A Modified Fatigue Life Prediction Model for Cyclic Hardening/Softening Steel
Abstract
1. Introduction
2. Materials and Methods
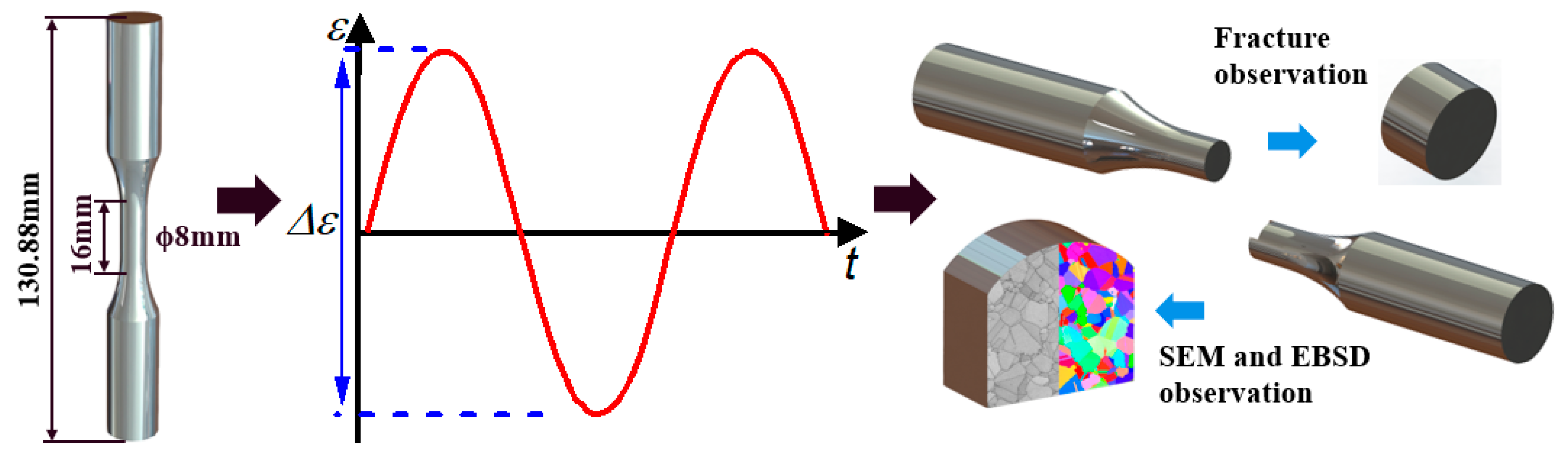
2.1. Materials and Experiments Methods
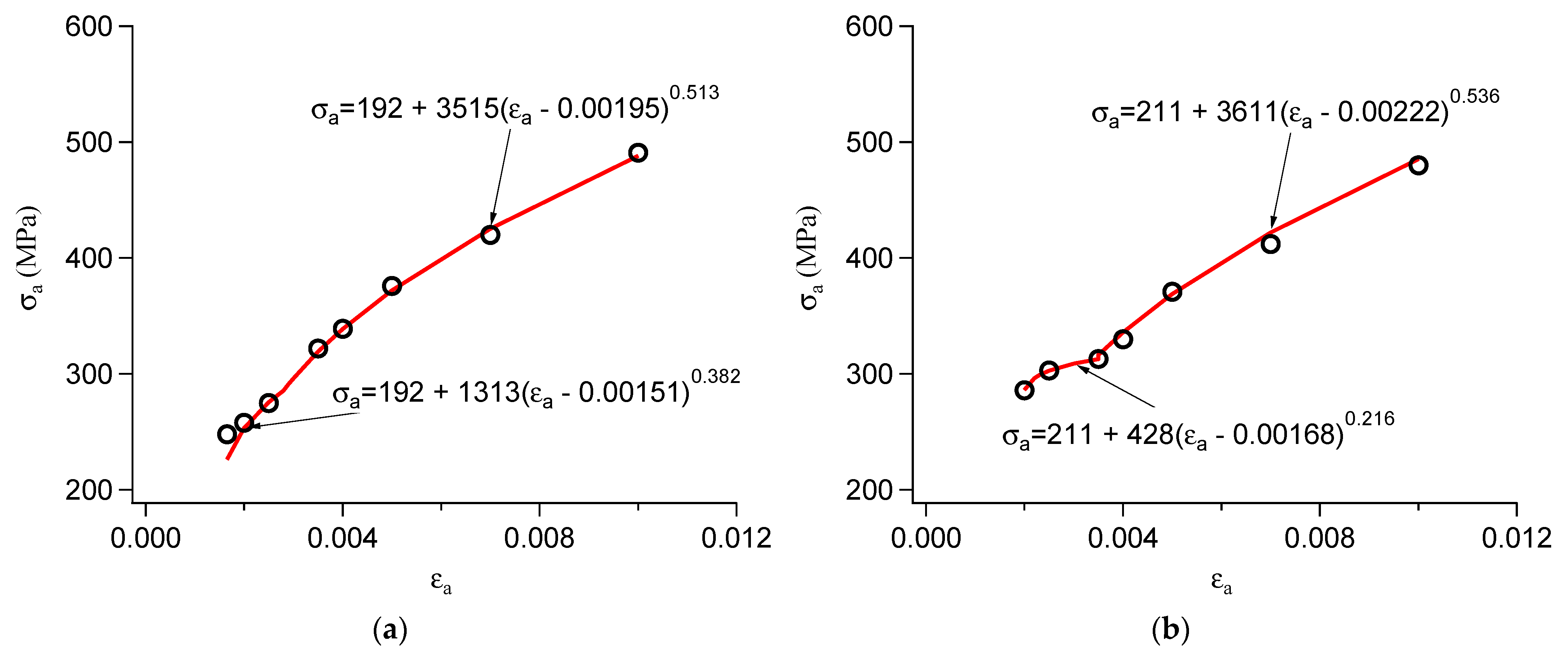
2.2. Fatigue Life Estimation Method
3. Fatigue Test Results
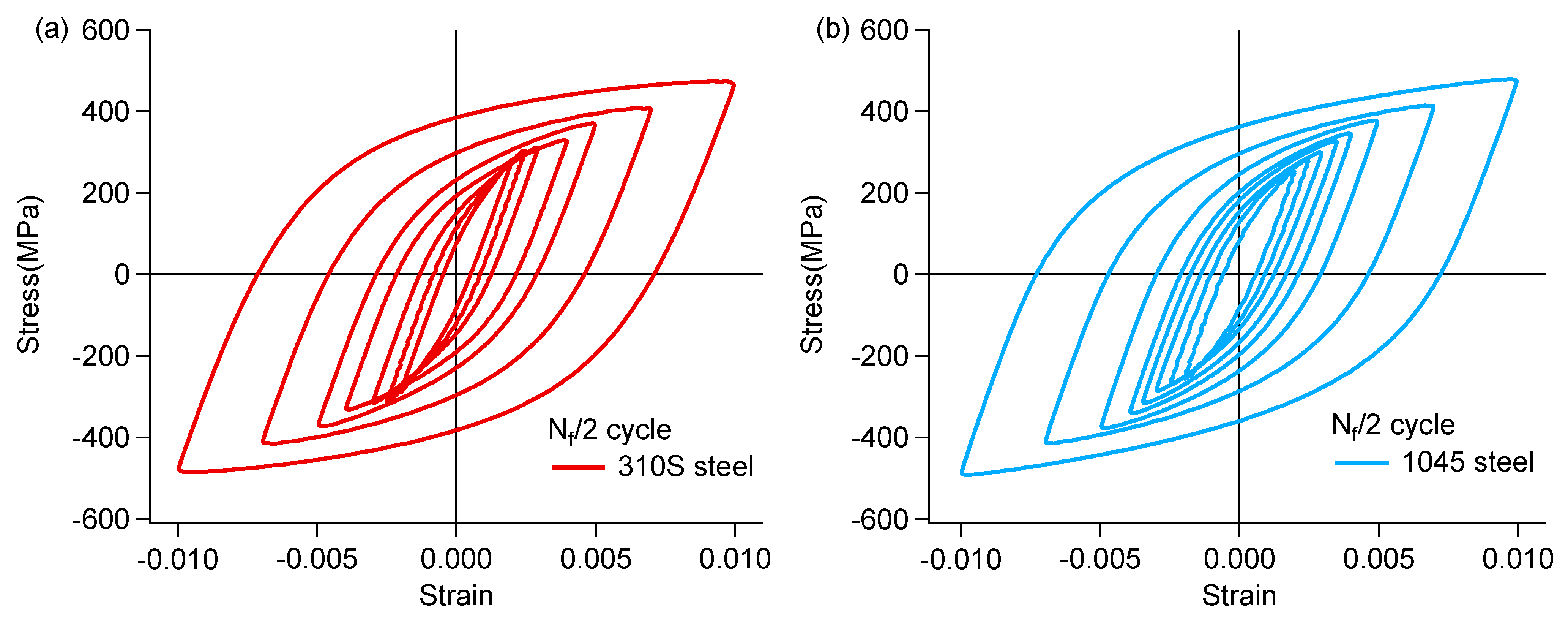
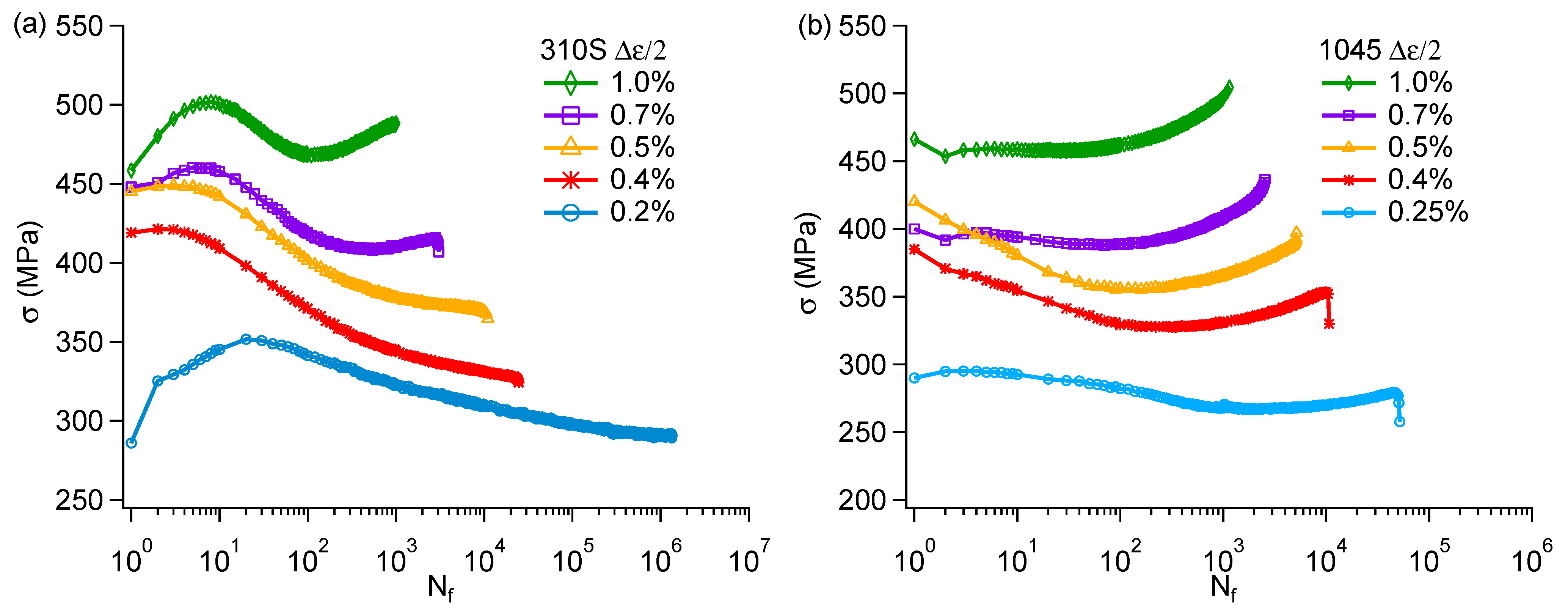
3.1. Fatigue Behavior
3.2. Fracture Morpholog
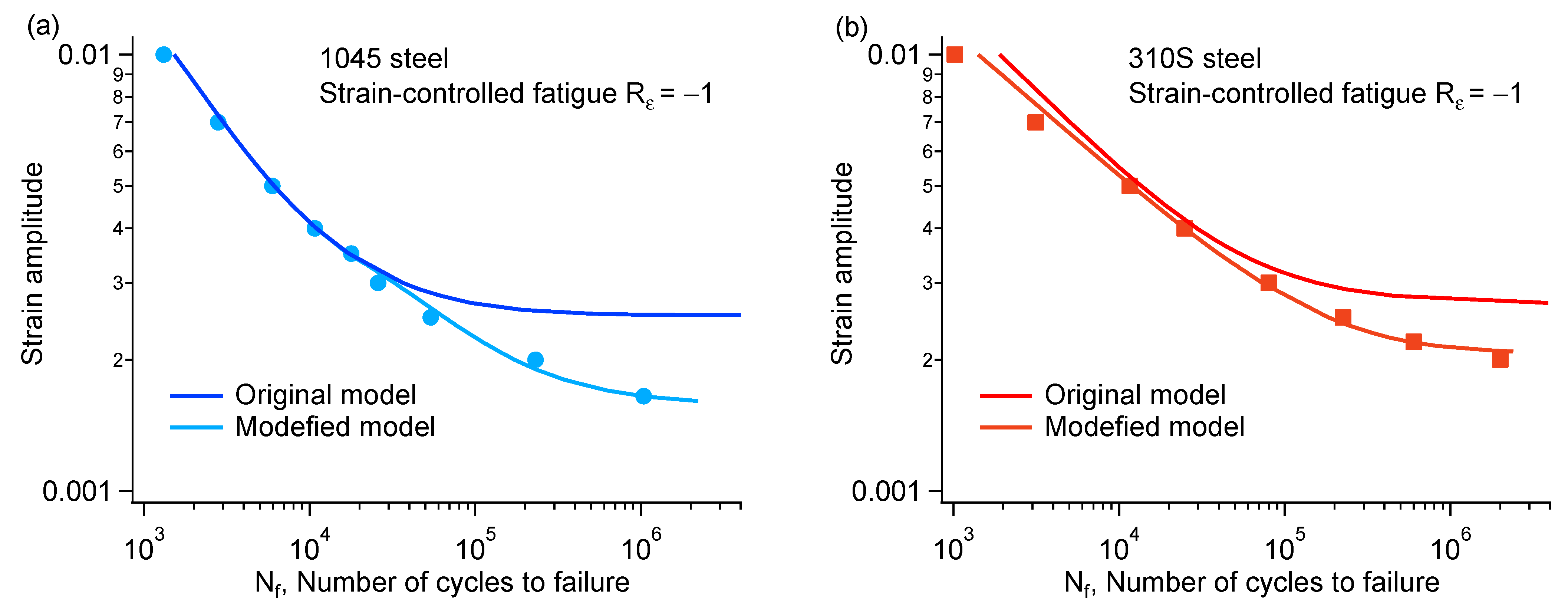
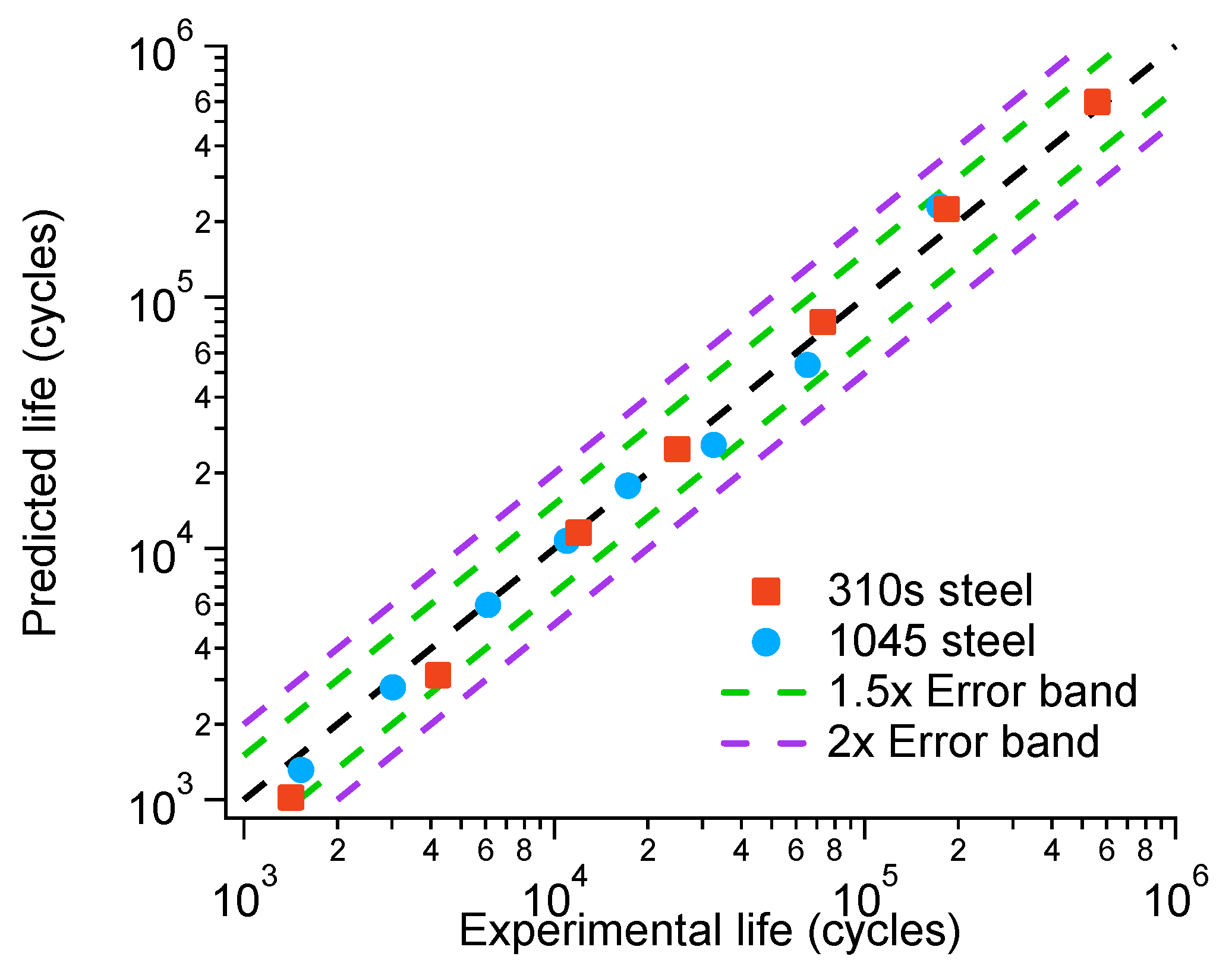
4. Fatigue Life Estimation Results
5. Conclusions
- (1)
- Based on a life prediction model using flow stress, this paper corrects the equation between cyclic plastic strain and flow stress by optimizing the calculation of cyclic plastic strain under different strain amplitudes.
- (2)
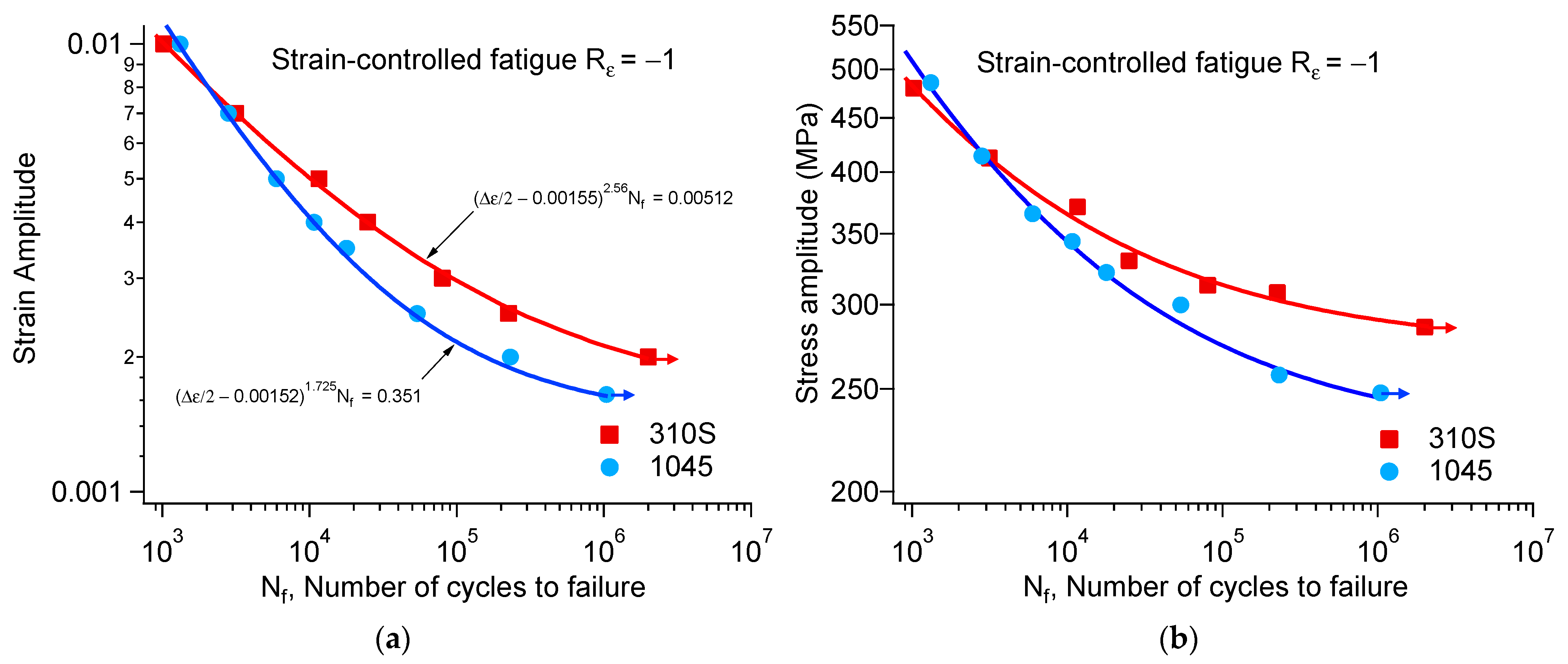
- Fatigue test results showed that 1045 carbon steel reached a fatigue life of 106 cycles at a strain amplitude of approximately 0.165%, while 310S stainless steel reached a fatigue life of 106 cycles at a strain amplitude of approximately 0.21%.
- (3)
- The revised model can effectively predict both high-cycle and low-cycle fatigue life across the entire ε-N curve. Compared with the original model, the prediction accuracy for high-cycle fatigue is improved. The error of the revised model is controlled within a 1.5× error band.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Kamal, M.; Rahman, M.M. Advances in fatigue life modeling: A review. Renew. Sustain. Energy Rev. 2018, 82, 940–949. [Google Scholar] [CrossRef]
- Santecchia, E.; Hamouda, A.M.S.; Musharavati, F.; Zalnezhad, E.; Cabibbo, M.; El Mehtedi, M.; Spigarelli, S. A Review on Fatigue Life Prediction Methods for Metals. Adv. Mater. Sci. Eng. 2016, 2016, 9573524. [Google Scholar] [CrossRef]
- Shiozawa, K.; Lu, L.; Ishihara, S. S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 781–790. [Google Scholar] [CrossRef]
- Hou, S.-q.; Xu, J.-q. Relationship among S-N curves corresponding to different mean stresses or stress ratios. J. Zhejiang Univ.-Sci. A 2015, 16, 885–893. [Google Scholar] [CrossRef]
- Hariharan, K.; Prakash, R.V.; Sathya Prasad, M. Weighted error criterion to evaluate strain–fatigue life prediction methods. Int. J. Fatigue 2011, 33, 727–734. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Castro, J.T.P.d. An improved strain-life model based on the Walker equation to describe tensile and compressive mean stress effects. Int. J. Fatigue 2022, 161, 106905. [Google Scholar] [CrossRef]
- Hirschberg, V.; Faust, L.; Wilhelm, M.; Rodrigue, D. Universal Strain-Life Curve Exponents for Thermoplastics and Elastomers under Tension-Tension and Torsion. Macromol. Mater. Eng. 2021, 306, 2100165. [Google Scholar] [CrossRef]
- Ma, S.; Duan, J.H.; Cheng, J.S.; Du, X.L.; Yuan, J.X.; Chen, P.H. Low-cycle fatigue fracture behavior and life prediction of 30CrMnSiA high-strength steel joint. J. Constr. Steel Res. 2025, 232, 109612. [Google Scholar] [CrossRef]
- He, H.; Liu, H.; Mura, A.; Zhu, C. Gear bending fatigue life prediction based on continuum damage mechanics and linear elastic fracture mechanics. Meccanica 2023, 58, 119–135. [Google Scholar] [CrossRef]
- Wang, F.; Cui, W. Recent Developments on the Unified Fatigue Life Prediction Method Based on Fracture Mechanics and its Applications. J. Mar. Sci. Eng. 2020, 8, 427. [Google Scholar] [CrossRef]
- Lei, D.; Zhang, P.; He, J.; Bai, P.; Zhu, F. Fatigue life prediction method of concrete based on energy dissipation. Constr. Build. Mater. 2017, 145, 419–425. [Google Scholar] [CrossRef]
- Wei, H.; Liu, Y. A critical plane-energy model for multiaxial fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1973–1983. [Google Scholar] [CrossRef]
- Meng, X.; Qu, C.; Fu, D.; Qu, C. Effects of Fatigue Damage on the Microscopic Modulus of Cortical Bone Using Nanoindentation. Materials 2021, 14, 3252. [Google Scholar] [CrossRef] [PubMed]
- Maciolek, A.; Wagener, R.; Melz, T. Review of and a new approach to elastic modulus evaluation for fatigue design of metallic components. Int. J. Fatigue 2021, 151, 106325. [Google Scholar] [CrossRef]
- He, J.; Hu, C.; Zhang, R.; Hu, P.; Xiao, C.; Wang, X. A new low-cycle and high-cycle fatigue life prediction criterion based on crystal plasticity finite element method. Int. J. Fatigue 2025, 197, 108903. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, Z.; Zheng, M.; Su, P. Fatigue life study of milled surfaces based on stress concentration factor. Surf. Topogr. Metrol. Prop. 2025, 13, 015013. [Google Scholar] [CrossRef]
- Lukáš, P.; Kunz, L. Cyclic plasticity and substructure of metals. Mater. Sci. Eng. A 2002, 322, 217–227. [Google Scholar] [CrossRef]
- Xu, J.; Huo, M.; Xia, R. Effect of cyclic plastic strain and flow stress on low cycle fatigue life of 316L(N) stainless steel. Mech. Mater. 2017, 114, 134–141. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, Z.; Wang, Y.; Chen, H.; Wang, P. Fatigue life prediction based on the hysteretic loop evolution of carbon steel under tensile cyclic loading. Eng. Fail. Anal. 2022, 142, 106787. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Y.; Xi, J.; Jiang, J.; Wang, Y.; Chen, A.; Nikbin, K. Energy dissipation-based LCF model for additive manufactured alloys with dispersed fatigue properties. Eng. Fail. Anal. 2024, 159, 108139. [Google Scholar] [CrossRef]
- Dong, Z.; Jiang, W.; Xie, X.; Wang, S.; Wan, Y.; Pei, X.; Tu, S.-t. Transition-behavior of fatigue crack with variation of stress amplitude for SAF2205 steel: Effect of dual-phase imbalance caused by welding. Int. J. Fatigue 2025, 198, 108978. [Google Scholar] [CrossRef]
- Su, R.; Li, H.; Wang, S.; Wang, D.; Guo, J.; Li, S.; Chen, H. Study on fatigue properties with composite waveform and variable amplitude of TC21 titanium alloy pulsed laser-arc hybrid welded joints. Eng. Fail. Anal. 2024, 165, 108797. [Google Scholar] [CrossRef]
- Droste, M.; Henkel, S.; Biermann, H.; Weidner, A. Influence of Plastic Strain Control on Martensite Evolution and Fatigue Life of Metastable Austenitic Stainless Steel. Metals 2022, 12, 1222. [Google Scholar] [CrossRef]
- Dan, W.J.; Hu, Z.G.; Zhang, W.G. Influences of cyclic loading on martensite transformation of TRIP steels. Met. Mater. Int. 2013, 19, 251–257. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Yu, Y.; Wu, W.; Wang, Z.; Lu, J.; Sun, Q.; Xie, L.; Hua, L. Fatigue life improvement of TC11 titanium alloy by novel electroshock treatment. Mater. Des. 2022, 221, 110902. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, X.; Zhang, Z.; Zhu, R.; Li, Y.; Zhang, F.; Yang, Z. Effect of phase transformation sequence on the low cycle fatigue properties of bainitic/martensitic multiphase steels. Int. J. Fatigue 2024, 178, 107995. [Google Scholar] [CrossRef]
- Moore, J.A.; Rusch, J.P.; Nezhad, P.S.; Manchiraju, S.; Erdeniz, D. Effects of martensitic phase transformation on fatigue indicator parameters determined by a crystal plasticity model. Int. J. Fatigue 2023, 168, 107457. [Google Scholar] [CrossRef]


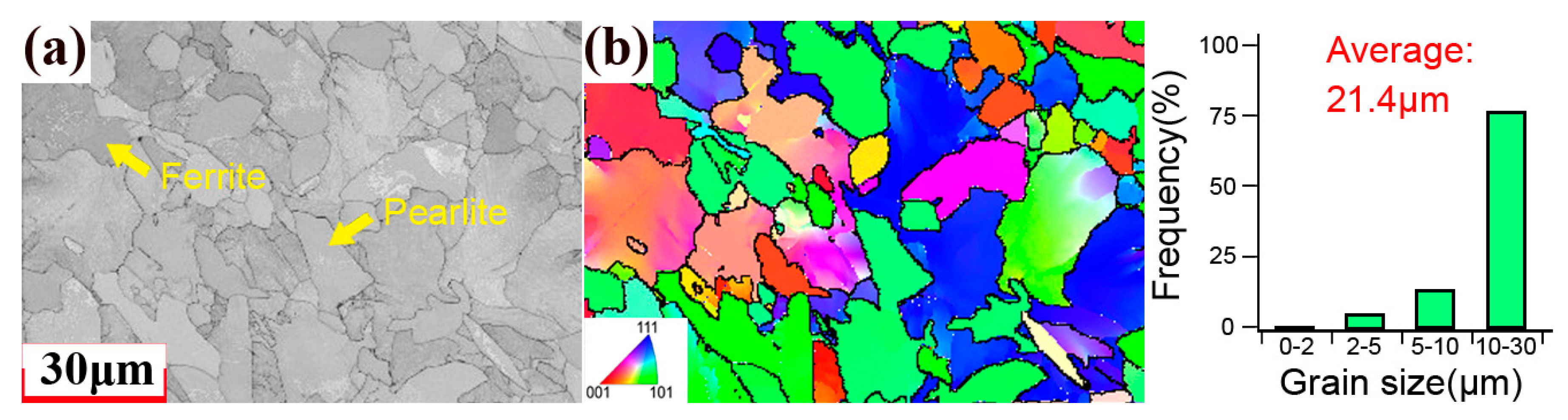





| Chemical Compositions | C | Si | Mn | P | S | Cr | Ni | Fe |
|---|---|---|---|---|---|---|---|---|
| 310S | 0.04 | 0.61 | 1.06 | 0.017 | 0.001 | 25.65 | 19.41 | balance |
| 1045 | 0.46 | 0.27 | 0.70 | 0.019 | 0.027 | / | / | balance |
| Spec. ID | ∆ε/2 (%) | f (Hz) | Nf (Cycles) | ∆σ/2 (MPa) |
|---|---|---|---|---|
| Z-04 | 1.00 | 0.2 | 1021 | 480.0 |
| Z-05 | 0.70 | 0.35 | 3137 | 412.5 |
| Z-03 | 0.50 | 0.6 | 11,590 | 370.9 |
| Z-07 | 0.40 | 1.0 | 24,887 | 330.1 |
| Z-06 | 0.30 | 1.0 | 80,466 | 312.9 |
| Z-11 | 0.25 | 2.0 | 225,073 | 308.1 |
| Z-13 | 0.20 | 5.0 | >2,000,000 | 285.8 |
| Spec. ID | ∆ε/2 (%) | f (Hz) | Nf (Cycles) | ∆σ/2 (MPa) |
|---|---|---|---|---|
| C-02 | 1.00 | 0.2 | 1316 | 485.8 |
| C-05 | 0.70 | 0.35 | 2809 | 414.4 |
| C-03 | 0.50 | 0.6 | 5956 | 365.5 |
| C-11 | 0.40 | 1.0 | 10,736 | 344.3 |
| C-12 | 0.35 | 1.0 | 17,820 | 321.8 |
| C-07 | 0.25 | 4.0 | 53,750 | 275.3 |
| C-01 | 0.20 | 5.0 | 230,670 | 257.6 |
| C-08 | 0.165 | 5.0 | 1,049,928 | 247.8 |
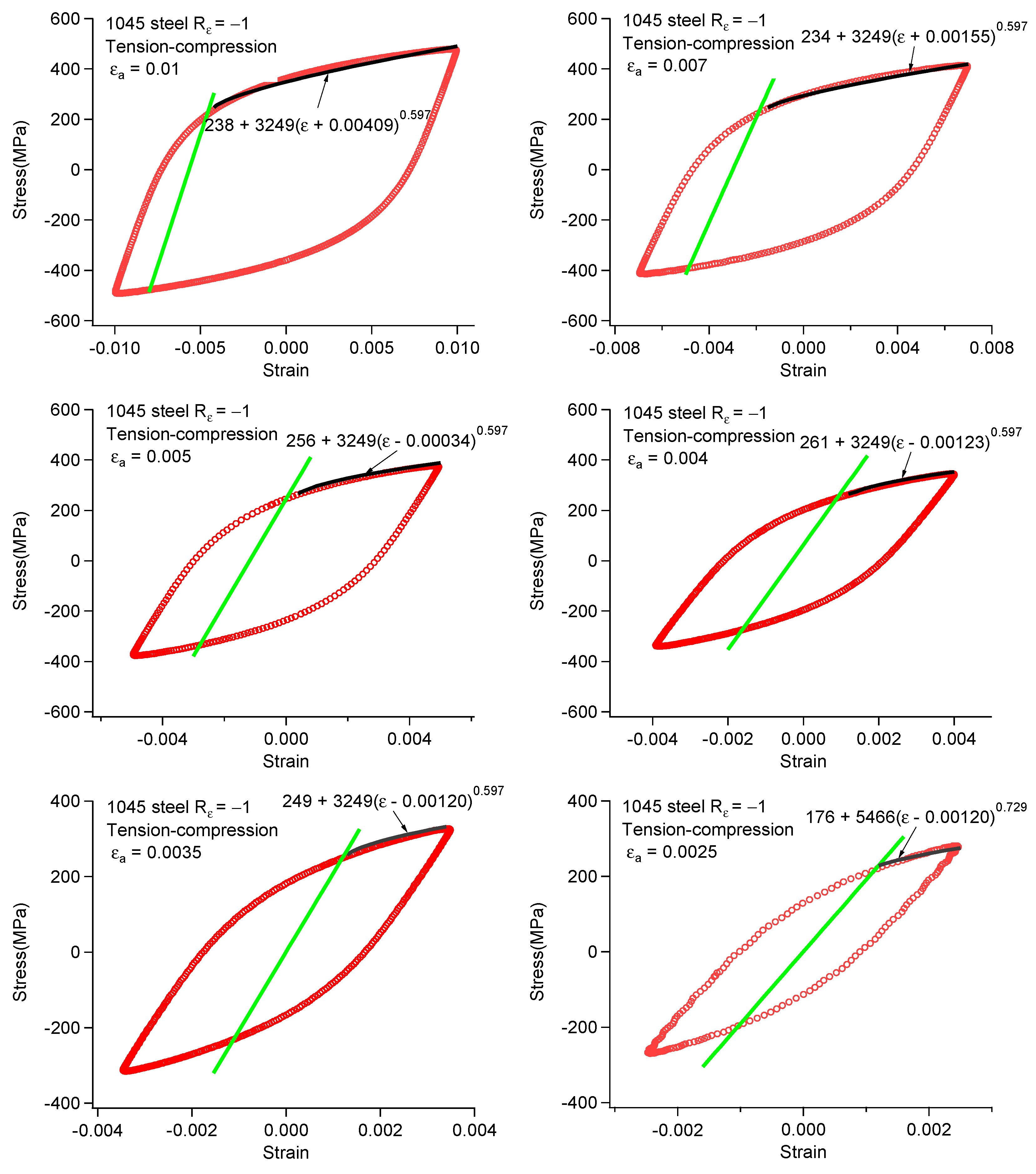
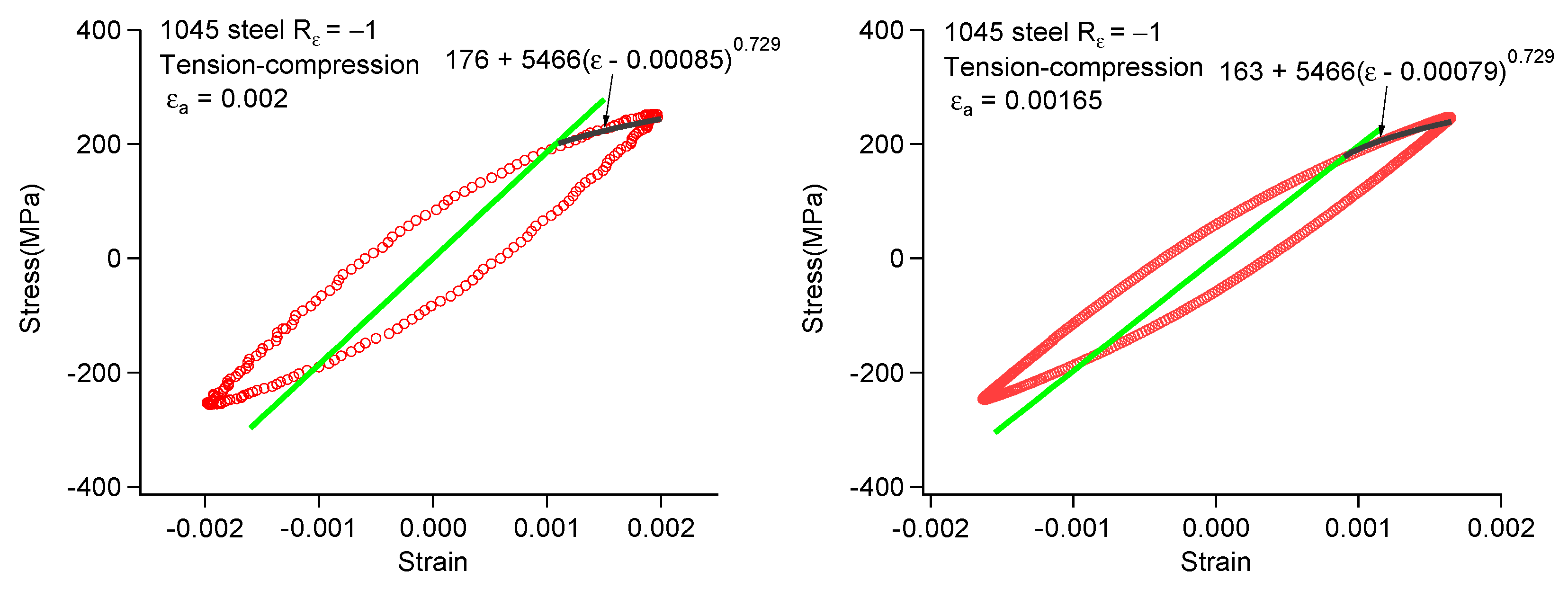
| 0.01 | 0.007 | 0.005 | 0.004 | 0.0035 | 0.0025 | 0.002 | 0.00165 | |
| 238 | 235 | 256 | 261 | 249 | 208 | 176 | 163 | |
| 0.00409 | 0.00155 | −0.00034 | −0.00123 | −0.001195 | −0.001 | −0.00085 | −0.00079 | |
| 491 | 410 | 376 | 339 | 322 | 275 | 258 | 248 |
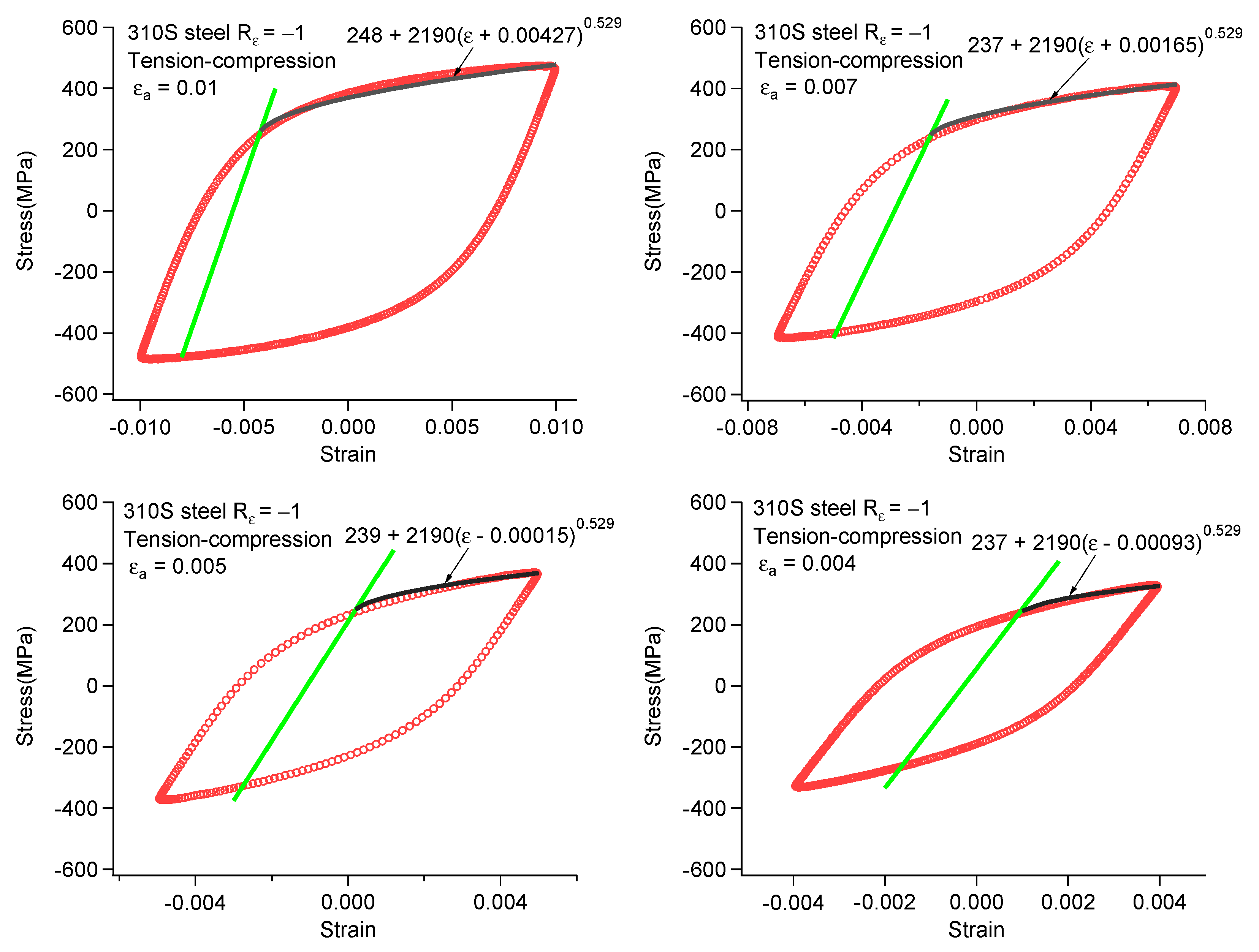
| 0.01 | 0.007 | 0.005 | 0.004 | 0.003 | 0.0025 | 0.002 | |
| 248 | 237 | 239 | 237 | 227 | 215 | 192 | |
| 0.00427 | 0.00165 | −0.00015 | −0.00093 | −0.00117 | −0.0011 | −0.00098 | |
| 480 | 412 | 371 | 330 | 313 | 303 | 286 |
| Strain Amplitude (%) | Absolute Deviation Value (%) | |
|---|---|---|
| 1045 | 310S | |
| 1.0 | 15.88 | 310S |
| 0.7 | 7.16 | 38.39 |
| 0.5 | 2.51 | 34.17 |
| 0.4 | 2.06 | 3.01 |
| 0.35 | 4.62 | 3.49 |
| 0.3 | / | / |
| 0.25 | 21.23 | 8.68 |
| 0.2 | 24.93 | 18.68 |
| 0.165 | 2.99 | 19.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Cai, Z.; Wang, H.; Xu, B.; Zhang, L.; Song, Y.; Gao, Z. A Modified Fatigue Life Prediction Model for Cyclic Hardening/Softening Steel. Materials 2025, 18, 3274. https://doi.org/10.3390/ma18143274
Shen Z, Cai Z, Wang H, Xu B, Zhang L, Song Y, Gao Z. A Modified Fatigue Life Prediction Model for Cyclic Hardening/Softening Steel. Materials. 2025; 18(14):3274. https://doi.org/10.3390/ma18143274
Chicago/Turabian StyleShen, Zhibin, Zhihui Cai, Hong Wang, Bo Xu, Linye Zhang, Yuxuan Song, and Zengliang Gao. 2025. "A Modified Fatigue Life Prediction Model for Cyclic Hardening/Softening Steel" Materials 18, no. 14: 3274. https://doi.org/10.3390/ma18143274
APA StyleShen, Z., Cai, Z., Wang, H., Xu, B., Zhang, L., Song, Y., & Gao, Z. (2025). A Modified Fatigue Life Prediction Model for Cyclic Hardening/Softening Steel. Materials, 18(14), 3274. https://doi.org/10.3390/ma18143274






