Modeling of Linear Die Filling Based on Dimensional Analysis Using DEM-CFD Methods
Abstract
1. Introduction
2. Numerical Modeling
2.1. Discrete Element Method
2.2. Computational Fluid Dynamics
2.3. Simulation Conditions
3. Results and Discussion
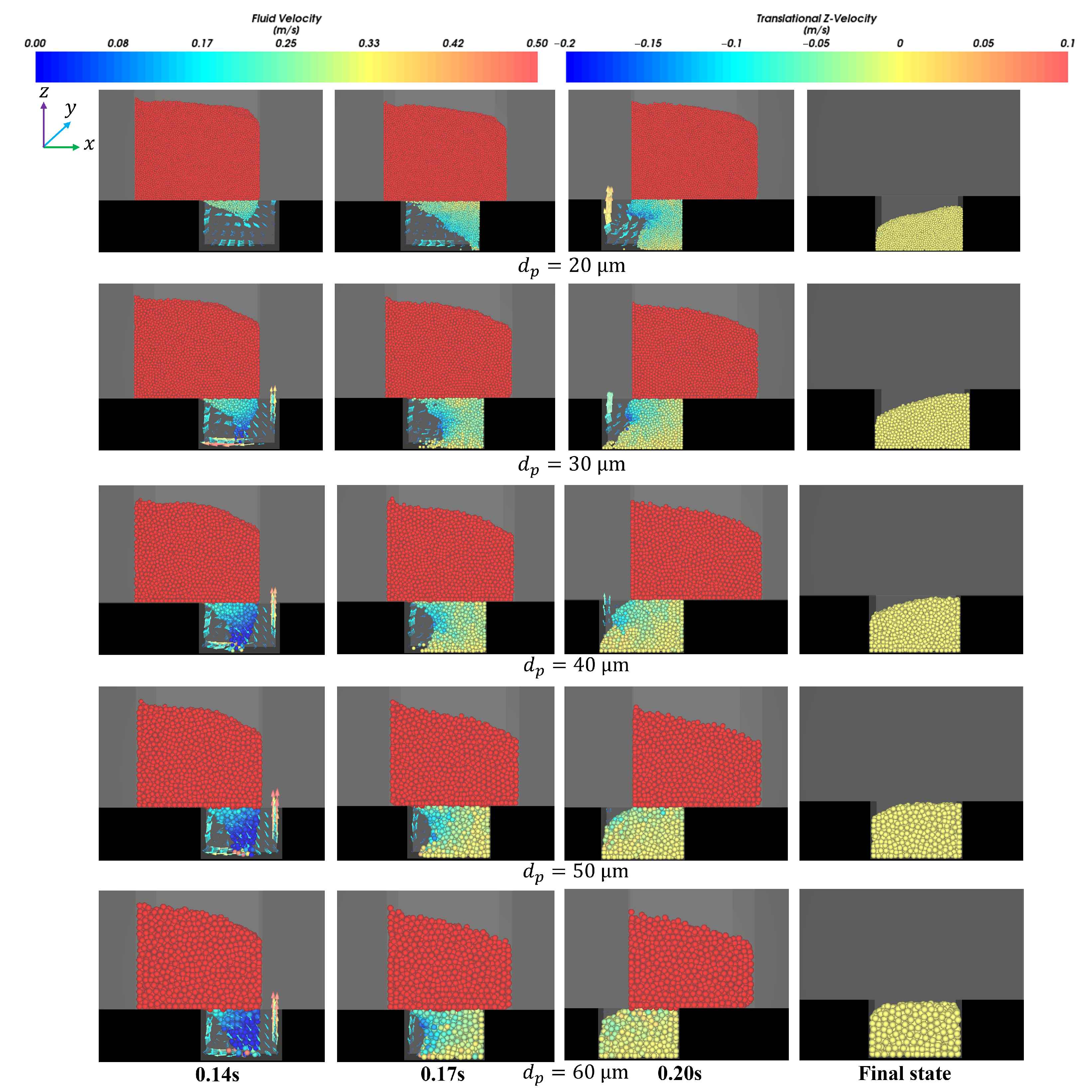
3.1. The Effect of Ratio Number
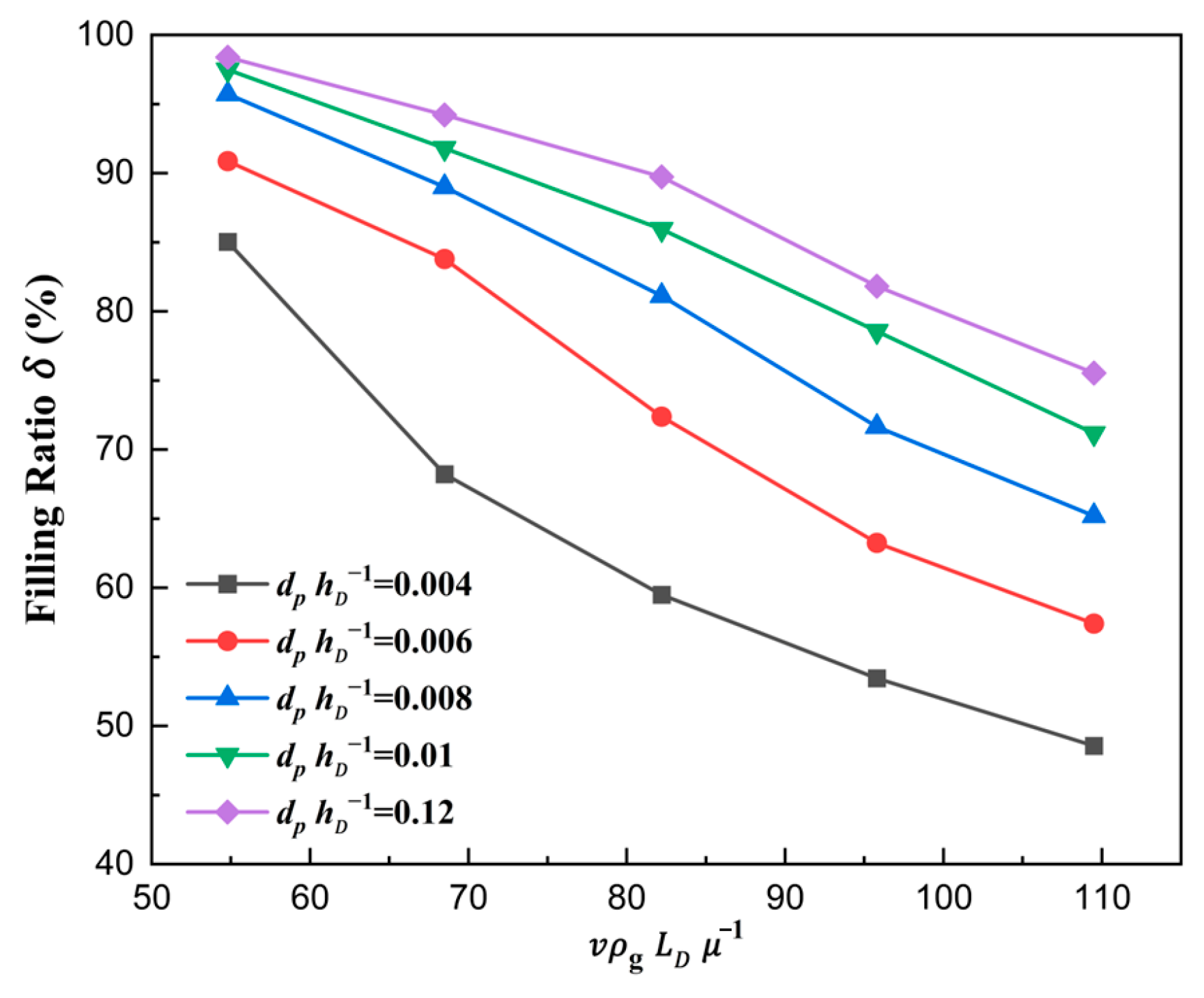
3.2. The Shoe Speed Number
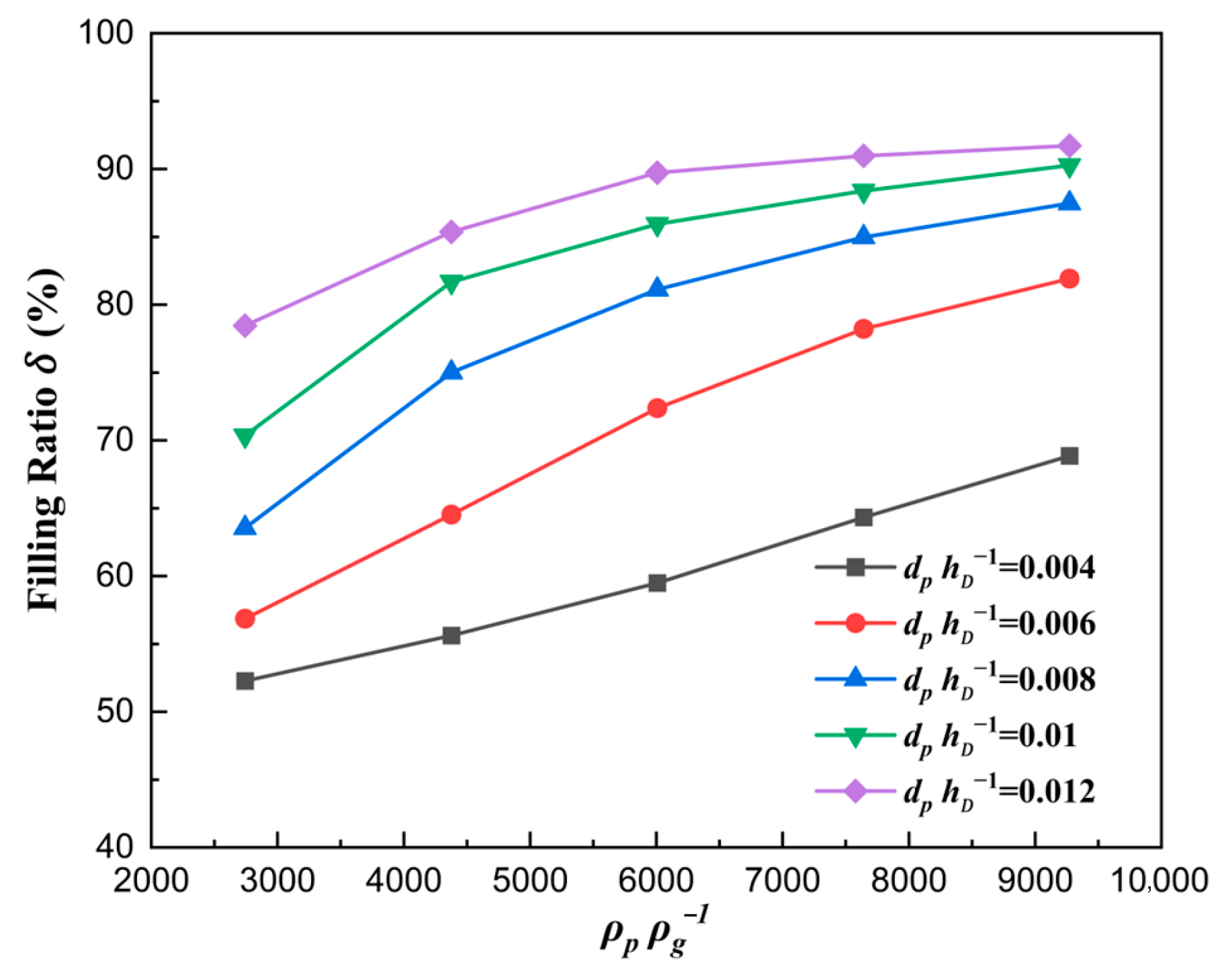
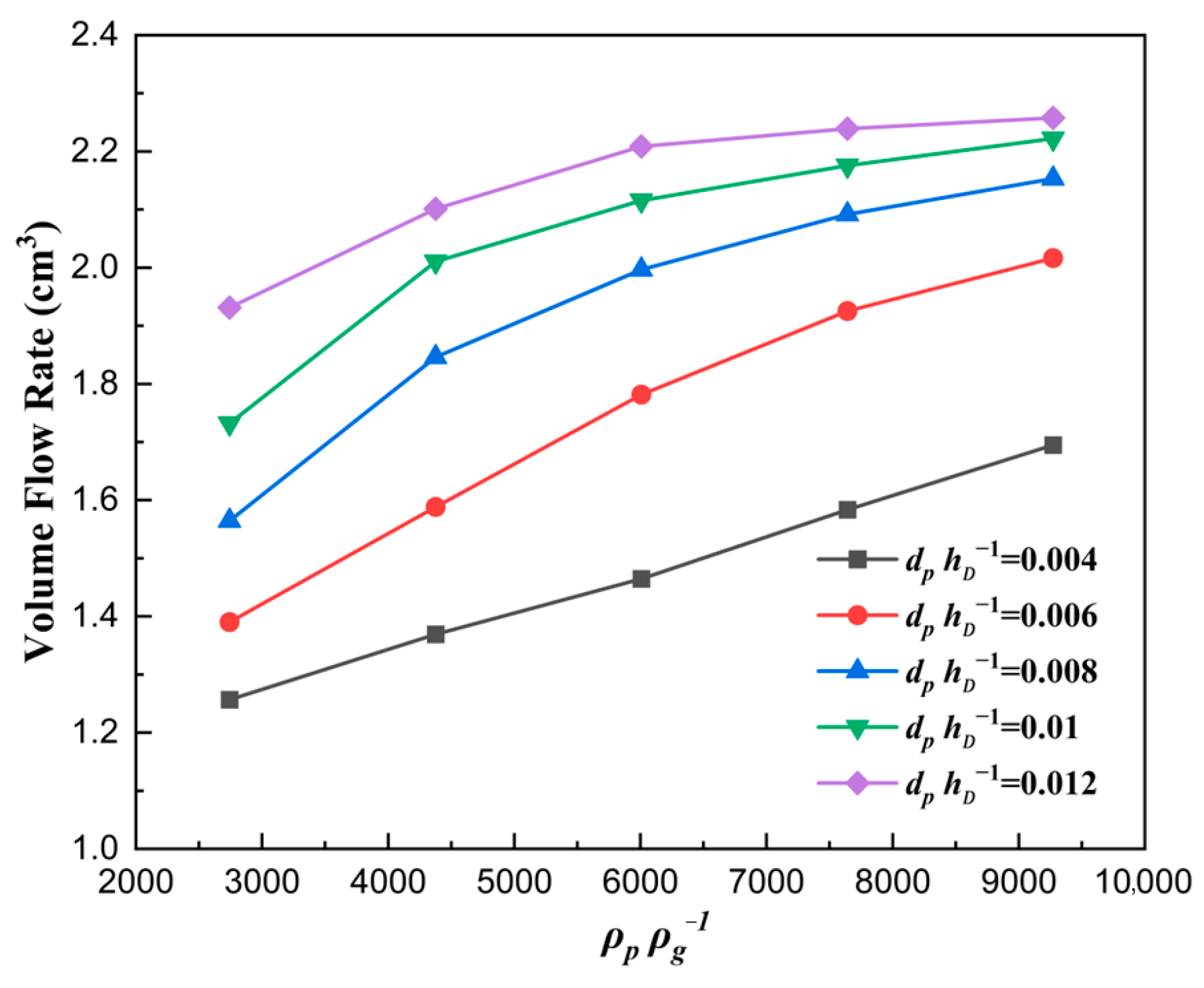
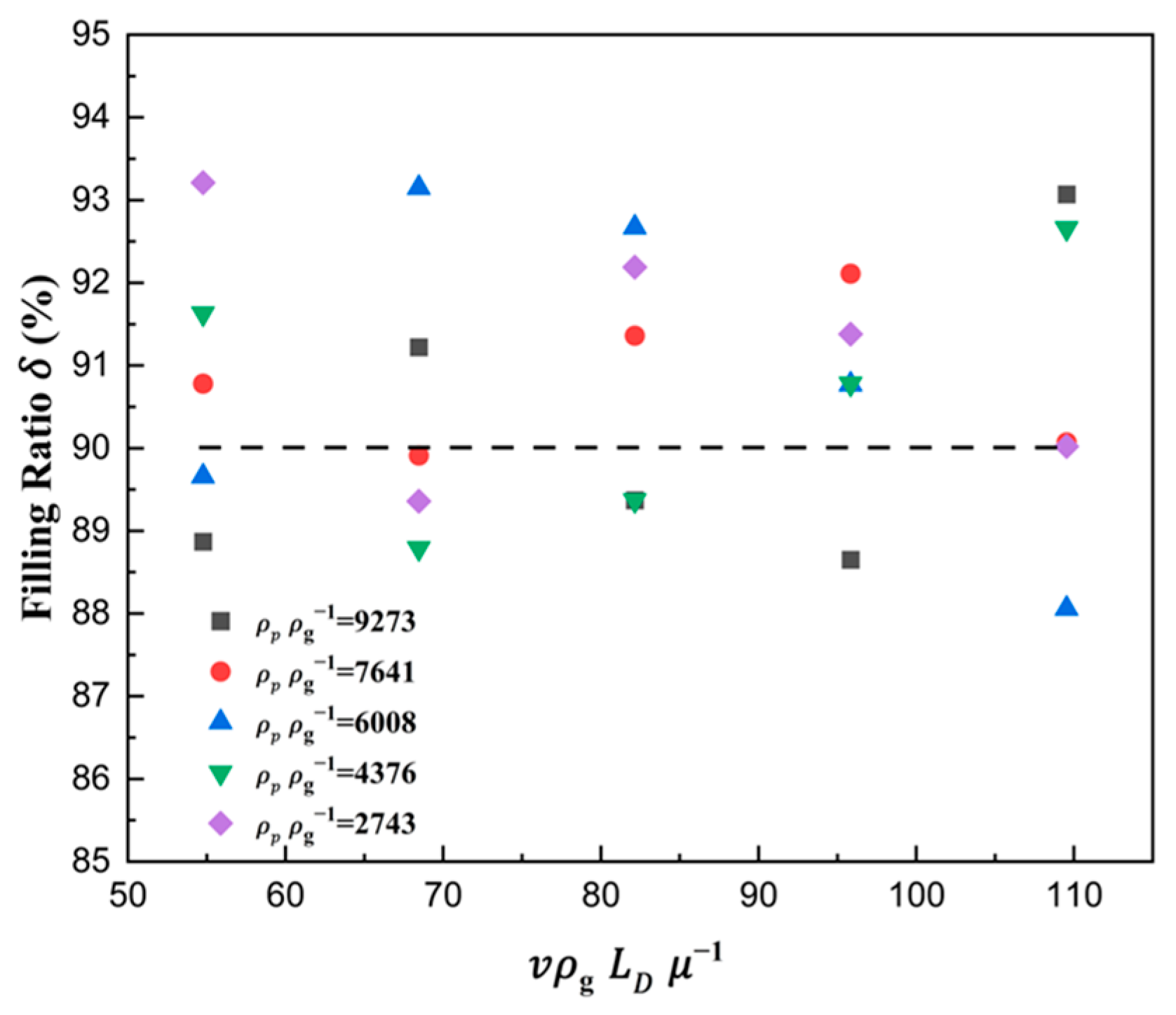
3.3. The Solid Density Number
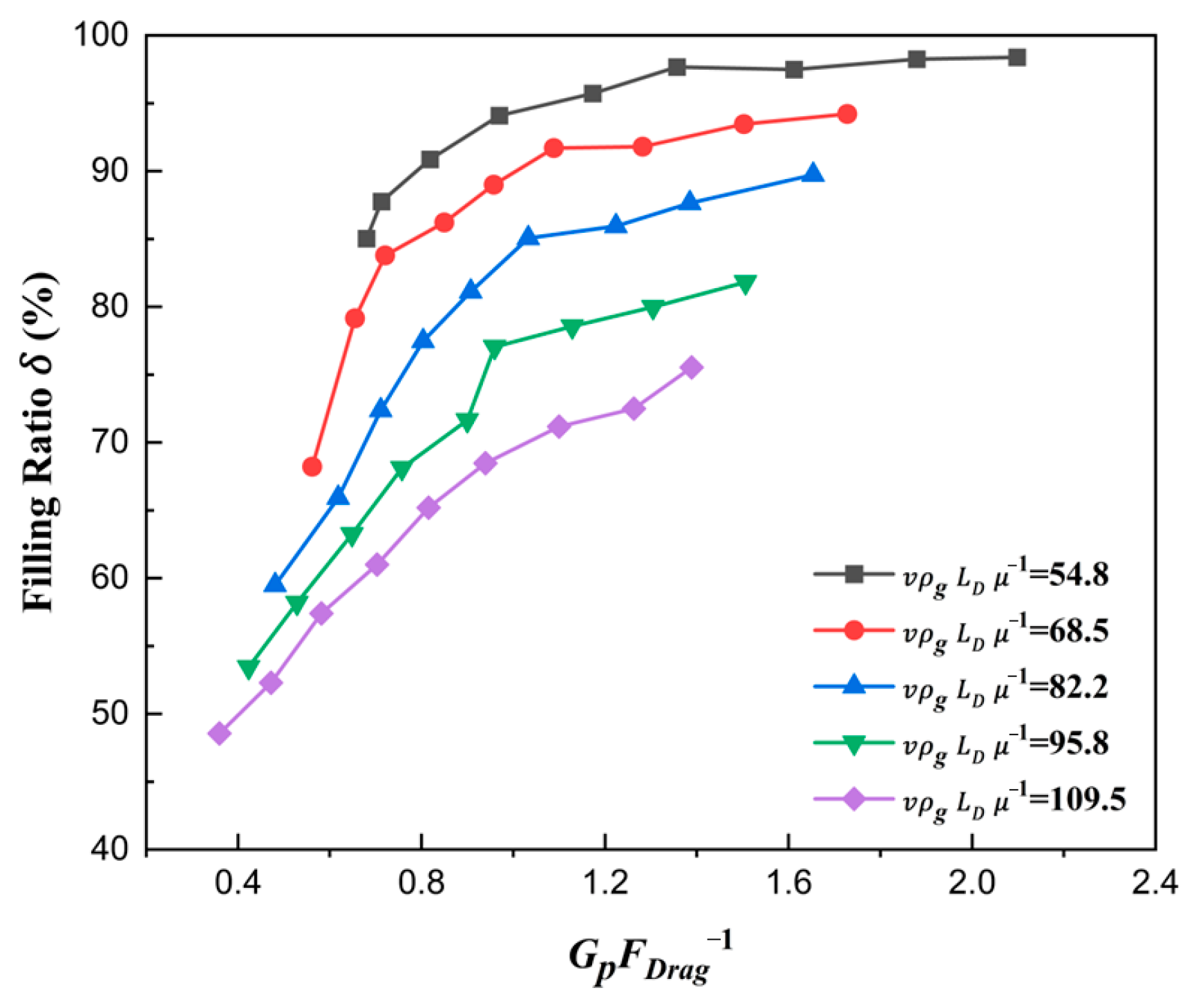
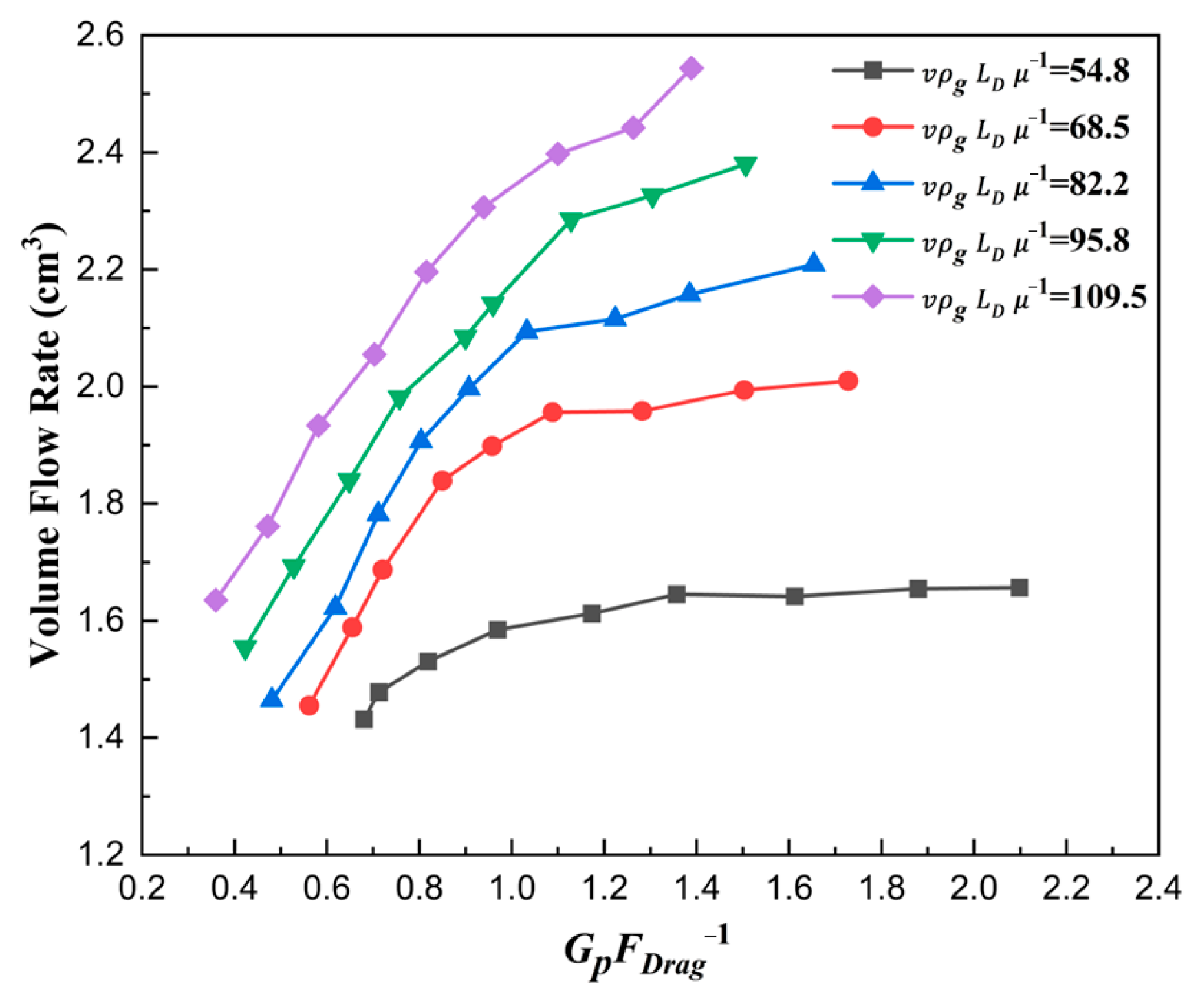
3.4. The Force Number
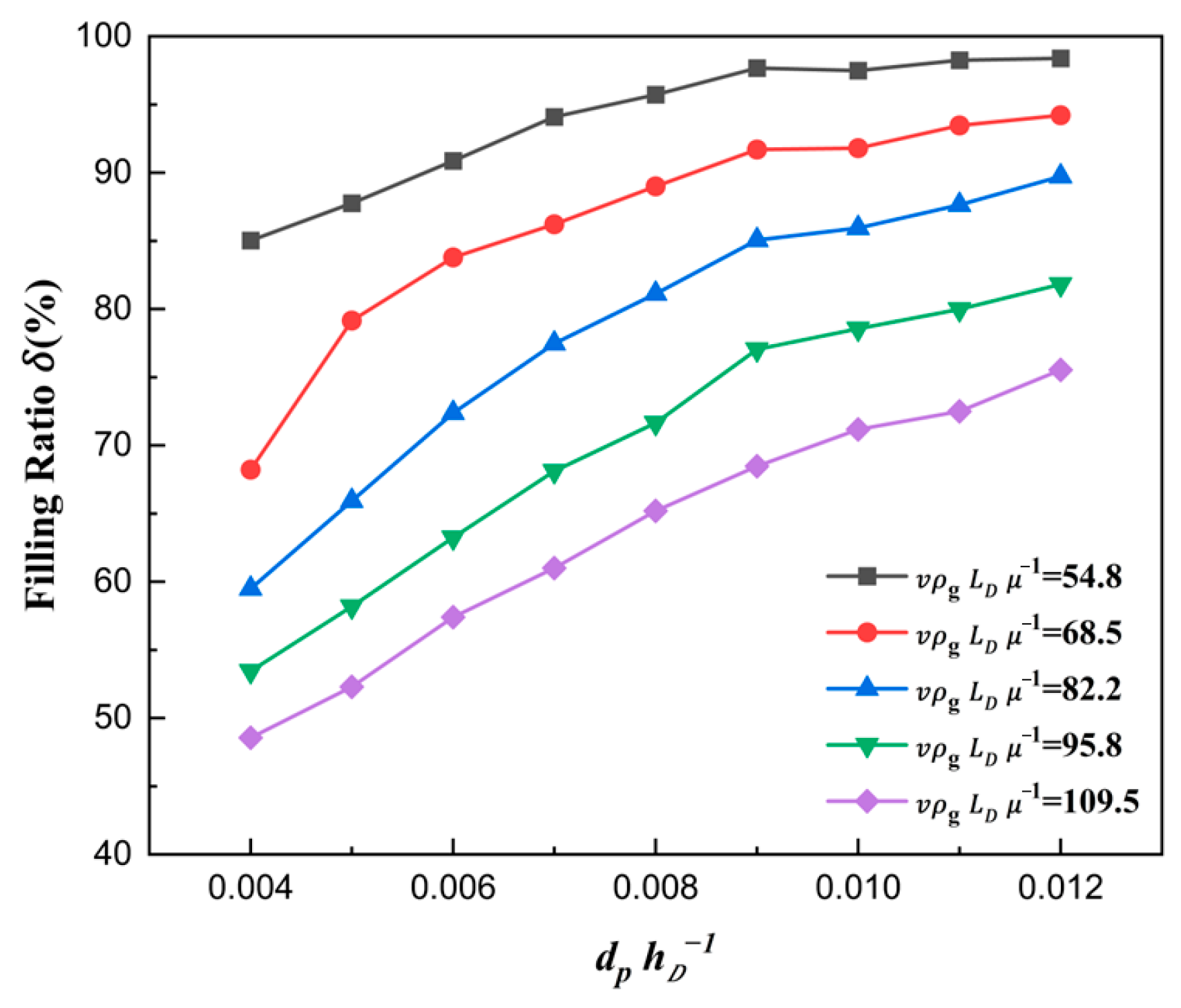
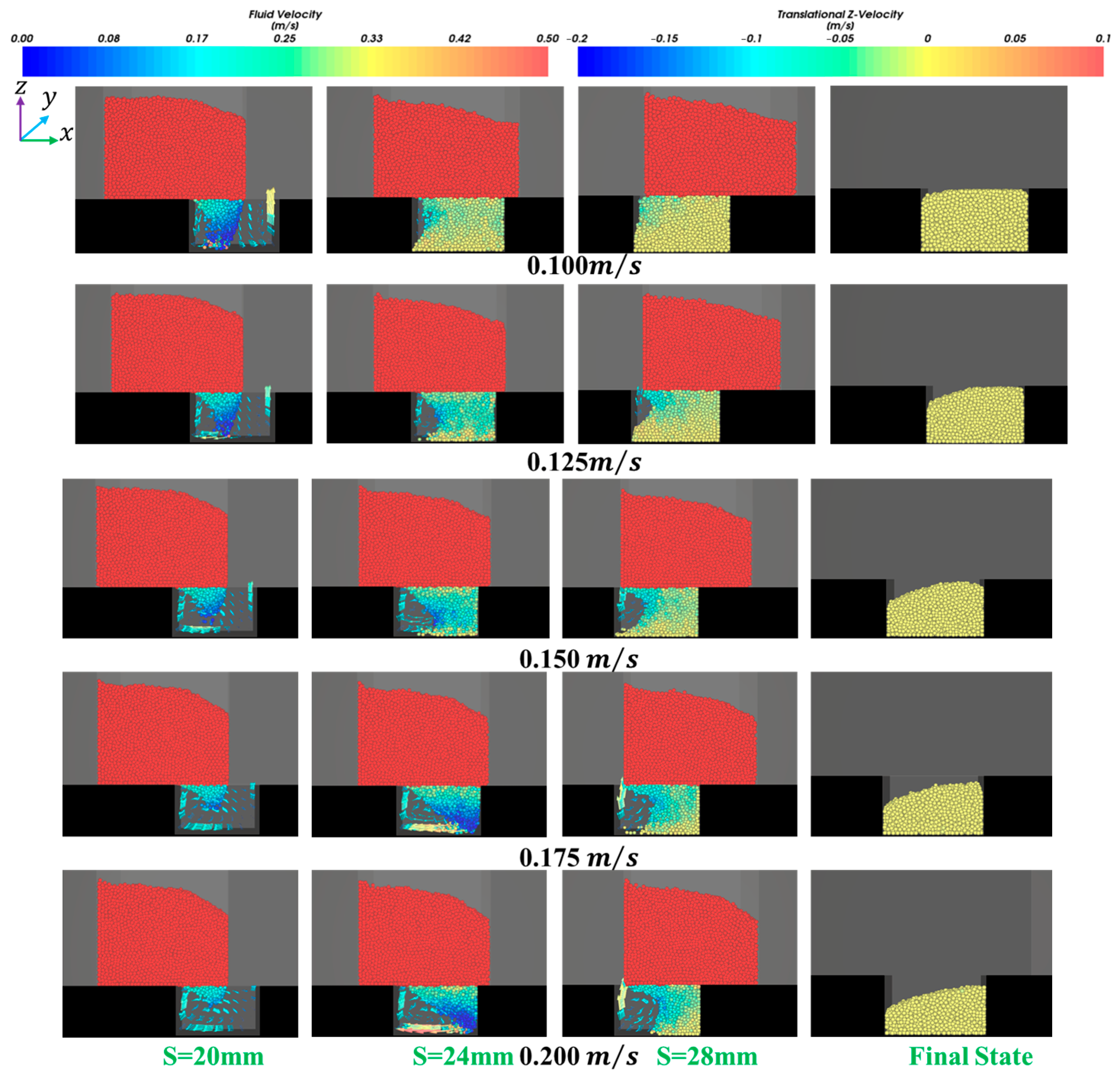
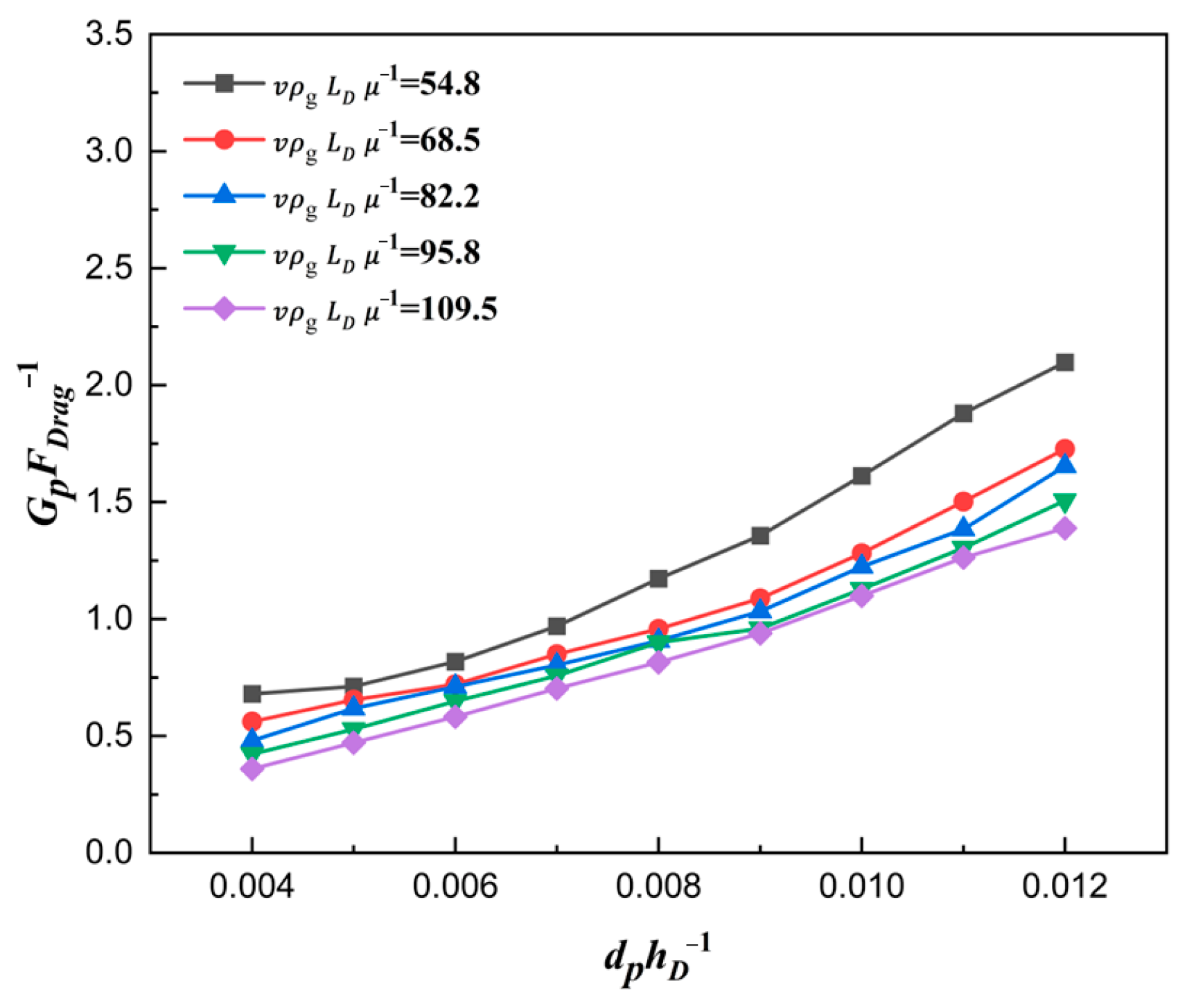
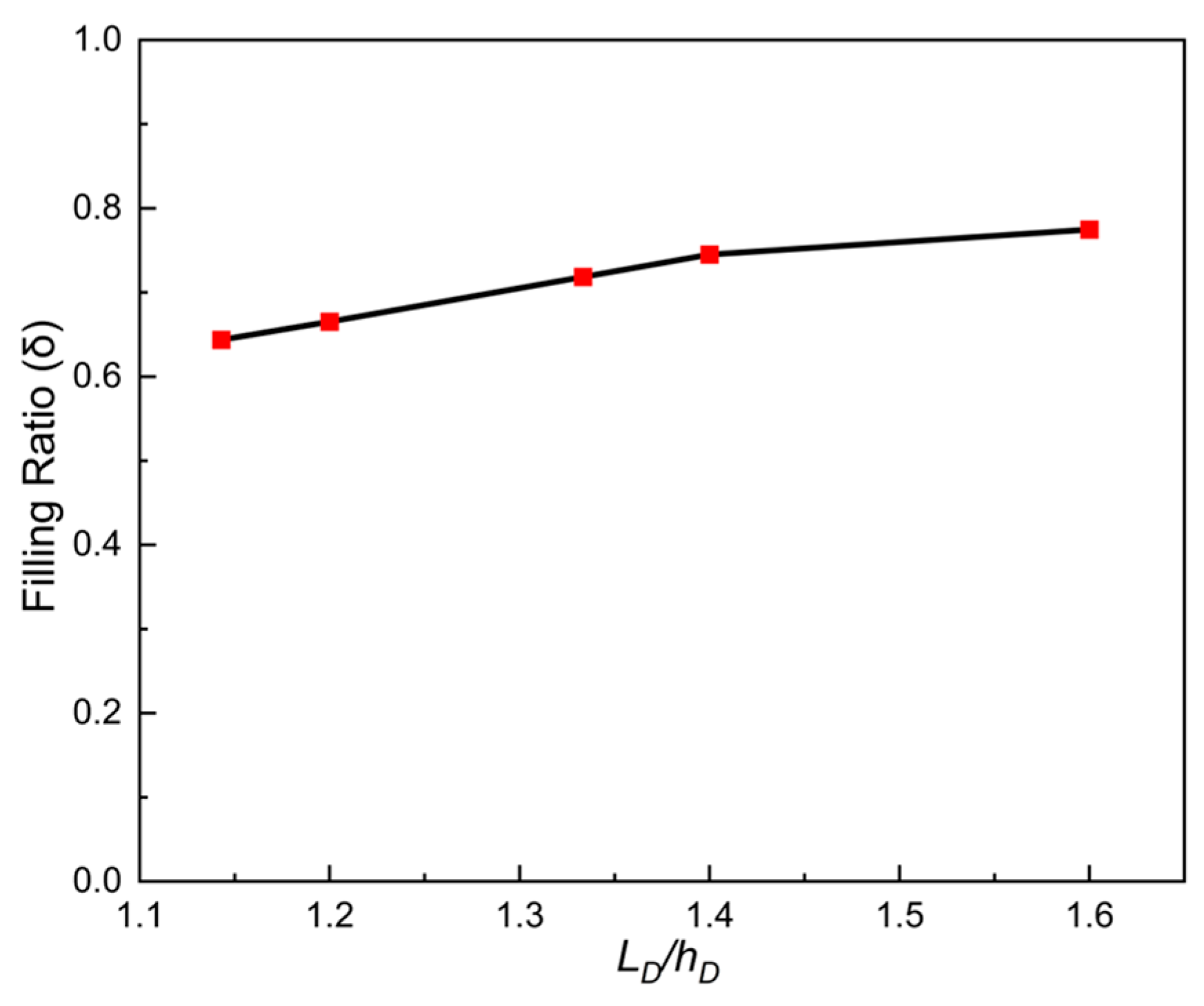
3.5. Geometric Parameters
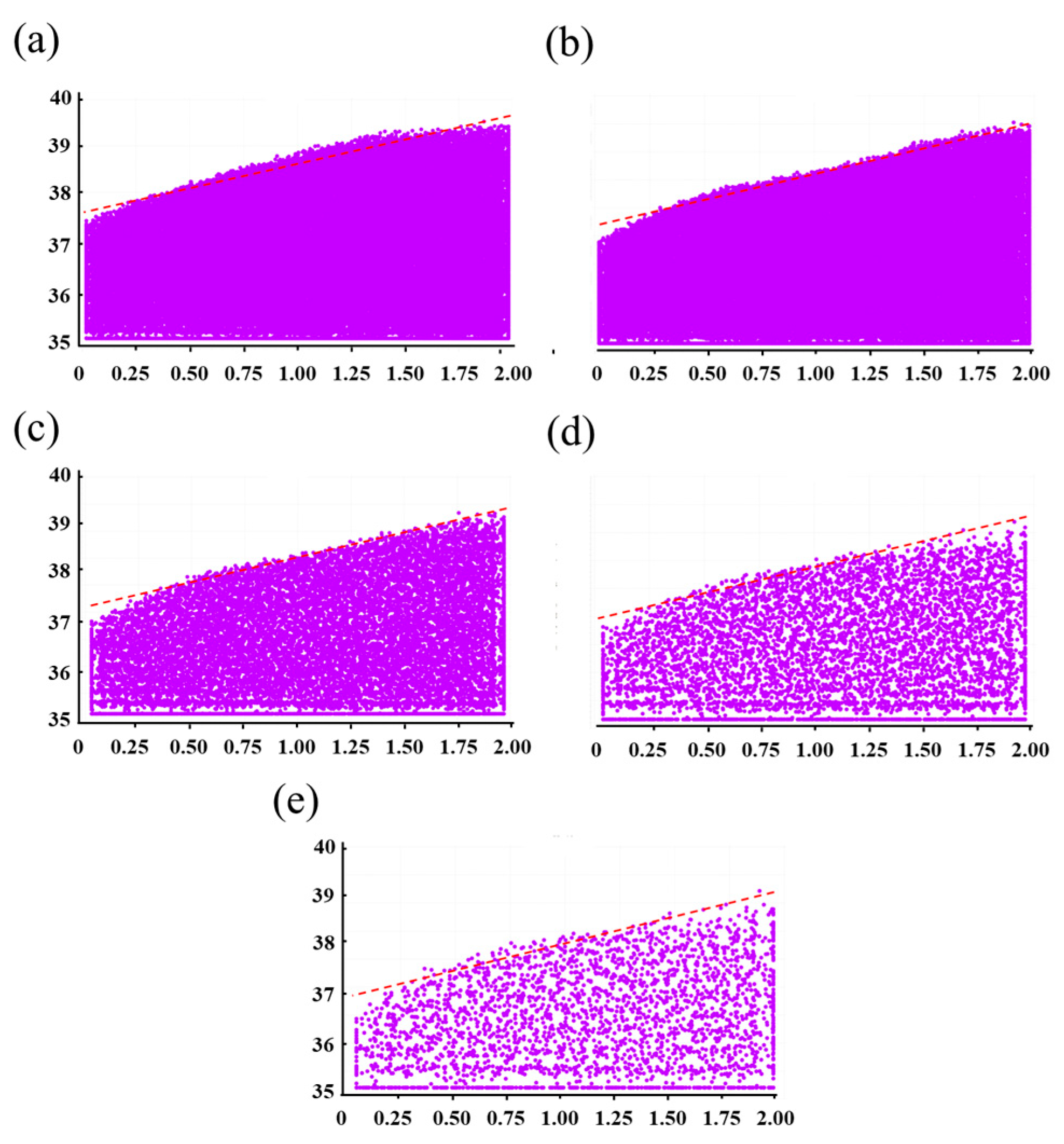
3.6. Modeling of Linear Die Filling
4. Conclusions
- (1)
- The coarse-grain DEM-CFD method was adopted, and the scale-up factor was verified. The static and dynamic repose angles in experiments and DEM simulations were used to determine the contact parameters. The scale-up factor was also determined by DEM simulations in die filling.
- (2)
- Based on dimensionless derivation and analysis, the ratio number of size , the solid density number , the shoe speed number , and force number were derived. The filling ratio increased with the increase in and and decreased with the increase in . The force number was found to be a key point determining the filling ratio. Due to the falling of the particles being hindered by the airflow, smaller proportions of drag forces relative to gravity result in larger filling ratios, which is the essence of filling.
- (3)
- A filling ratio of ninety percent was selected as a sign of full filling, and then, the corresponding critical value was obtained. A semi-empirical modeling of linear die filling, taking the critical value as the dependent variable and solid density number and shoe speed number as independent variables, was developed. Hence, this model can be used to design the smallest shoe speed to achieve complete die filling, optimize the parameters of die structures, and support process development.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Snick, B.; Holman, J.; Cunningham, C.; Kumar, A.; Vercruysse, J.; De Beer, T.; Remon, J.P.; Vervaet, C. Continuous direct compression as manufacturing platform for sustained release tablets. Int. J. Pharm. 2017, 519, 390–407. [Google Scholar] [CrossRef] [PubMed]
- Hildebrandt, C.; Gopireddy, S.R.; Fritsch, A.K.; Profitlich, T.; Scherliess, R.; Urbanetz, N.A. Evaluation and prediction of powder flowability in pharmaceutical tableting. Pharm. Dev. Technol. 2019, 24, 35–47. [Google Scholar] [CrossRef]
- Wu, C.; Guo, Y. Modelling of the flow of cohesive powders during pharmaceutical tabletting. J. Pharm. Pharmacol. 2010, 62, 1450–1451. Available online: https://research.birmingham.ac.uk/en/publications/modelling-of-the-flow-of-cohesive-powders-during-pharmaceutical-t (accessed on 25 May 2025).
- Mills, L.A.; Sinka, I.C. Effect of particle size and density on the die fill of powders. Eur. J. Pharm. Biopharm. 2013, 84, 642–652. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wu, C.Y.; Kafui, K.D.; Thornton, C. Numerical analysis of density-induced segregation during die filling. Powder Technol. 2010, 197, 111–119. [Google Scholar] [CrossRef]
- Wu, C.; Dihoru, L.; Cocks, A.C.F. The flow of powder into simple and stepped dies. Powder Technol. 2003, 134, 24–39. [Google Scholar] [CrossRef]
- Nwose, E.N.; Pei, C.; Wu, C.Y. Modelling die filling with charged particles using DEM/CFD. Particuology 2012, 10, 229–235. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.Y.; Kafui, K.D.; Thornton, C. 3D DEM/CFD analysis of size-induced segregation during die filling. Powder Technol. 2011, 206, 177–188. [Google Scholar] [CrossRef]
- Guo, Y.; Kafui, K.D.; Wu, C.Y.; Thornton, C.; Seville, J.P.K. coupled DEM/CFD analysis of the effect of air on powder flow during die filling. AICHE J. 2009, 55, 49–62. [Google Scholar] [CrossRef]
- Yao, H.; Mori, Y.; Takabatake, K.; Sun, X.; Sakai, M. Numerical investigation on the influence of air flow in a die filling process. J. Taiwan Inst. Chem. Eng. 2018, 90, 9–17. [Google Scholar] [CrossRef]
- Schomberg, A.K.; Kwade, A.; Finke, J.H. Modeling gravity filling of dies on a rotary tablet press. Powder Technol. 2023, 413, 117998. [Google Scholar] [CrossRef]
- Schiano, S.; Chen, L.; Wu, C. The effect of dry granulation on flow behaviour of pharmaceutical powders during die filling. Powder Technol. 2018, 337, 78–83. [Google Scholar] [CrossRef]
- Schneider, L.C.R.; Sinka, I.C.; Cocks, A.C.F. Characterisation of the flow behaviour of pharmaceutical powders using a model die–shoe filling system. Powder Technol. 2007, 173, 59–71. [Google Scholar] [CrossRef]
- Bobba, D.; Tabei, S.A.; Cherukuri, H.P.; Pando, M.A. DEM simulation of particle segregation in filling of vibratory dies. Adv. Powder Technol. 2020, 31, 3474–3484. [Google Scholar] [CrossRef]
- Zhong, W.; Zakhvatayeva, A.; Zhang, L.; Wu, C. Powder flow during linear and rotary die filling. Int. J. Pharm. 2021, 602, 120654. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, Y.; Zakhvatayeva, A.; Wang, X.; Liu, Z.; Yang, M.; Zheng, Q.; Wu, C. Influence of moisture content on die filling of pharmaceutical powders, J. Drug Deliv. Sci. Technol. 2022, 78, 103985. [Google Scholar] [CrossRef]
- Zheng, C.; Yost, E.; Muliadi, A.R.; Govender, N.; Zhang, L.; Wu, C. DEM analysis of the influence of stirrer design on die filling with forced powder feeding. Particuology 2024, 88, 107–115. [Google Scholar] [CrossRef]
- Jackson, I.C.S.A.S. The effect of suction during die fill on a rotary tablet press. Eur. J. Pharm. Biopharm. 2007, 65, 253–256. [Google Scholar] [CrossRef]
- Zakhvatayeva, A.; Zhong, W.; Makroo, H.A.; Hare, C.; Wu, C.Y. An experimental study of die filling of pharmaceutical powders using a rotary die filling system. Int. J. Pharm. 2018, 553, 84–96. [Google Scholar] [CrossRef]
- Zakhvatayeva, A.; Hare, C.; Wu, C.Y. Size-induced segregation during die filling. Int. J. Pharm. X 2019, 1, 100032. [Google Scholar] [CrossRef]
- Wu, T.; Li, F.; Liu, Q.; Ren, J.; Huang, J.; Qin, Z. Numerical Simulation and Analysis of the Impurity Removal Process of a Sugarcane Chopper Harvester Based on a CFD–DEM Model. Agriculture 2024, 14, 1392. [Google Scholar] [CrossRef]
- Mei, X.; Fang, X.; Zhang, L.; Wang, Y.; Tian, Y. Simulation and Optimization of Conveying Parameters for Vertical Screw Conveyor Based on CFD + DEM. Fluids 2025, 10, 171. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, Y.; Liu, M.; Wang, F.; Wang, Y.; Du, S.; Wang, W.; Hong, B. The Erosion Characteristics of a Needle Throttle Valve with Multiple Placement Schemes in a Shale Gas Field Based on CFD-DEM. Processes 2025, 13, 1833. [Google Scholar] [CrossRef]
- Yin, H.; Jin, H.; Liu, X.; Wang, C.; Chen, W.; Chen, F.; Xu, S.; Li, S. Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis. Processes 2025, 13, 1816. [Google Scholar] [CrossRef]
- Mendez, R.; Muzzio, F.; Velazquez, C. Study of the effects of feed frames on powder blend properties during the filling of tablet press dies. Powder Technol. 2010, 200, 105–116. [Google Scholar] [CrossRef]
- Widartiningsih, P.M.; Mori, Y.; Takabatake, K.; Wu, C.; Yokoi, K.; Yamaguchi, A.; Sakai, M. Coarse graining DEM simulations of a powder die-filling system. Powder Technol. 2020, 371, 83–95. [Google Scholar] [CrossRef]
- Sakai, M.; Abe, M.; Shigeto, Y.; Mizutani, S.; Takahashi, H.; Viré, A.; Percival, J.R.; Xiang, J.; Pain, C.C. Verification and validation of a coarse grain model of the DEM in a bubbling fluidized bed. Chem. Eng. J. 2014, 244, 33–43. [Google Scholar] [CrossRef]
- Sakai, M.; Takahashi, H.; Pain, C.C.; Latham, J.; Xiang, J. Study on a large-scale discrete element model for fine particles in a fluidized bed. Adv. Powder Technol. 2012, 23, 673–681. [Google Scholar] [CrossRef]
- Sakai, M.; Koshizuka, S. Large-scale discrete element modeling in pneumatic conveying. Chem. Eng. Sci. 2009, 64, 533–539. [Google Scholar] [CrossRef]
- Takabatake, K.; Mori, Y.; Khinast, J.G.; Sakai, M. Numerical investigation of a coarse-grain discrete element method in solid mixing in a spouted bed. Chem. Eng. J. 2018, 346, 416–426. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, Y.; Takabatake, K.; Yamaguchi, A.; Sakai, M. Coarse-grained DEM study of solids sedimentation in water. Powder Technol. 2020, 361, 21–32. [Google Scholar] [CrossRef]
- Mori, Y.; Wu, C.; Sakai, M. Validation study on a scaling law model of the DEM in industrial gas-solid flows. Powder Technol. 2019, 343, 101–112. [Google Scholar] [CrossRef]
- Thornton; Yin, K.K. Impact of elastic spheres with and without adhesion. Powder Technol. 1991, 65, 153–166. [Google Scholar] [CrossRef]
- Krajewski, G.; Matthews, D.R.H. Baayen, Analyzing linguistic data: A practical introduction to statistics using R. Cambridge: Cambridge University Press, 2008. Pp. 368. ISBN-13: 978-0-521-70918-7. J. Child Lang. 2010, 2, 465–470. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. ASME J. Appl. Mech. 1953, 3, 327–344. [Google Scholar] [CrossRef]
- Gidazpow, B.D. Multiphase Flow and Fluidization. Academic Press. J. Fluid Mech. 1995, 25, 405–407. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar] [CrossRef]
- Wen, C.Y.; Yu, Y.H. A generalized method for predicting the minimum fluidization velocity. AICHE J. 1966, 12, 610–612. [Google Scholar] [CrossRef]
- Lu, H.L.; Gidaspow, D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar] [CrossRef]
- Bierwisch; Kraft, T.; Riedel, H.; Moseler, M. Three-dimensional discrete element models for the granular statics and dynamics of powders in cavity filling. J. Mech. Phys. Solids 2009, 57, 10–31. [Google Scholar] [CrossRef]
- Kazidenov; Khamitov, F.; Amanbek, Y. Coarse-graining of CFD-DEM for simulation of sand production in the modified cohesive contact model. Gas Sci. Eng. 2023, 113, 204976. [Google Scholar] [CrossRef]
- Che, H.; Werner, D.; Seville, J.; Wheldon, T.K.; Windows-Yule, K. Evaluation of coarse-grained CFD-DEM models with the validation of PEPT measurements. Particuology 2023, 82, 48–63. [Google Scholar] [CrossRef]
- Renzo, D.; Napolitano, E.S.; Di Maio, F.P. Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes 2021, 9, 279. [Google Scholar] [CrossRef]
- Chen, X.; Elliott, J.A. On the scaling law of JKR contact model for coarse-grained cohesive particles. Chem. Eng. Sci. 2020, 227, 115906. [Google Scholar] [CrossRef]
- Wang, D.; Li, X. Study of airflow induced by regular particles in freefall through tubes. Adv. Powder Technol. 2020, 31, 169–180. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Zhang, D.; Jia, B.; Luo, H.; Hu, Y. Model for induced airflow velocity of falling materials in semi-closed transfer station based on similitude theory. Adv. Powder Technol. 2015, 26, 236–243. [Google Scholar] [CrossRef]
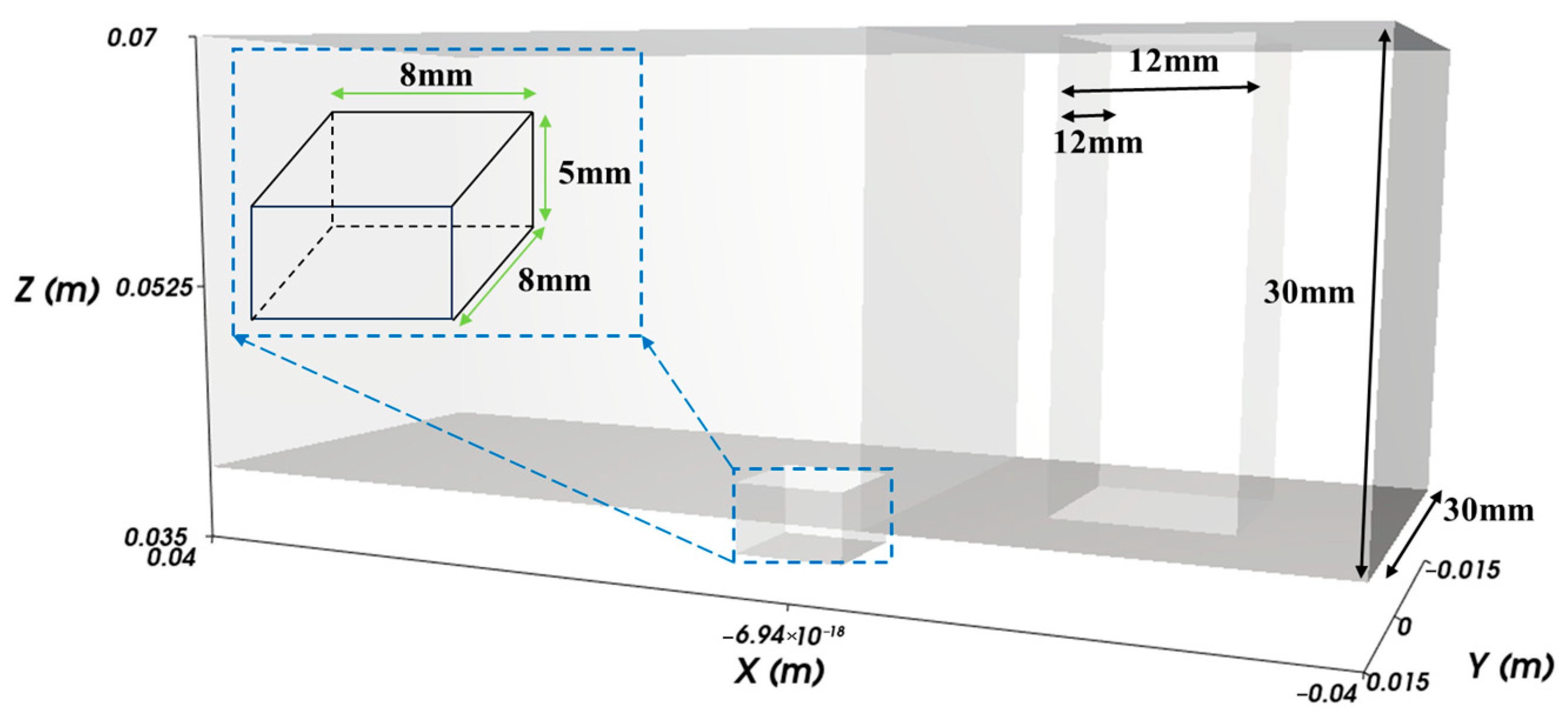






| The Solid | Symbol | Value | |
|---|---|---|---|
| Normal force model | Hertzian spring–dashpot model | ||
| Tangential force model | Mindlin–Deresiewicz model | ||
| Particle size () | 20~60 | ||
| Solid density (kg/m3) | 3360~11,360 | ||
| Young’s modulus | |||
| Poisson’s ratio | 0.3 | ||
| Friction coefficient | 0.67 | ||
| Rolling resistance | 0.218 | ||
| Restitution coefficients | 0.5 | ||
| CGM scale factor | 1, 4, 6, 8, 10 | ||
| The air | |||
| Density (kg/m3) | 1.225 | ||
| Viscosity () | |||
| Process | |||
| Shoe speed (m/s) | 0.100~0.200 |
| Scale-Up Factor | |||||
|---|---|---|---|---|---|
| Filling ratio (%) | 50.87 | 50.68 | 50.96 | 50.42 | 50.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhou, S.; Yan, S.; Tan, Y.; Zhang, J. Modeling of Linear Die Filling Based on Dimensional Analysis Using DEM-CFD Methods. Materials 2025, 18, 3261. https://doi.org/10.3390/ma18143261
Li J, Zhou S, Yan S, Tan Y, Zhang J. Modeling of Linear Die Filling Based on Dimensional Analysis Using DEM-CFD Methods. Materials. 2025; 18(14):3261. https://doi.org/10.3390/ma18143261
Chicago/Turabian StyleLi, Jie, Sunsheng Zhou, Shiyan Yan, Yuanqiang Tan, and Jiangtao Zhang. 2025. "Modeling of Linear Die Filling Based on Dimensional Analysis Using DEM-CFD Methods" Materials 18, no. 14: 3261. https://doi.org/10.3390/ma18143261
APA StyleLi, J., Zhou, S., Yan, S., Tan, Y., & Zhang, J. (2025). Modeling of Linear Die Filling Based on Dimensional Analysis Using DEM-CFD Methods. Materials, 18(14), 3261. https://doi.org/10.3390/ma18143261




