Investigation of N-(2-oxo-2H-chromen-3-carbonyl)cytisine’s Crystal Structure and Optical Properties
Abstract
1. Introduction
- -
- To synthesize a cytisinyl–coumarin complex compound (hereafter, the word “complex” is used in order to highlight that the investigated molecule is made up of a cytisine moiety and a coumarin moiety);
- -
- To characterize its structure through XRD and FTIR spectroscopy methods;
- -
- To study its structural, vibrational, and electronic properties using DFT computational modelling.
2. Materials and Methods
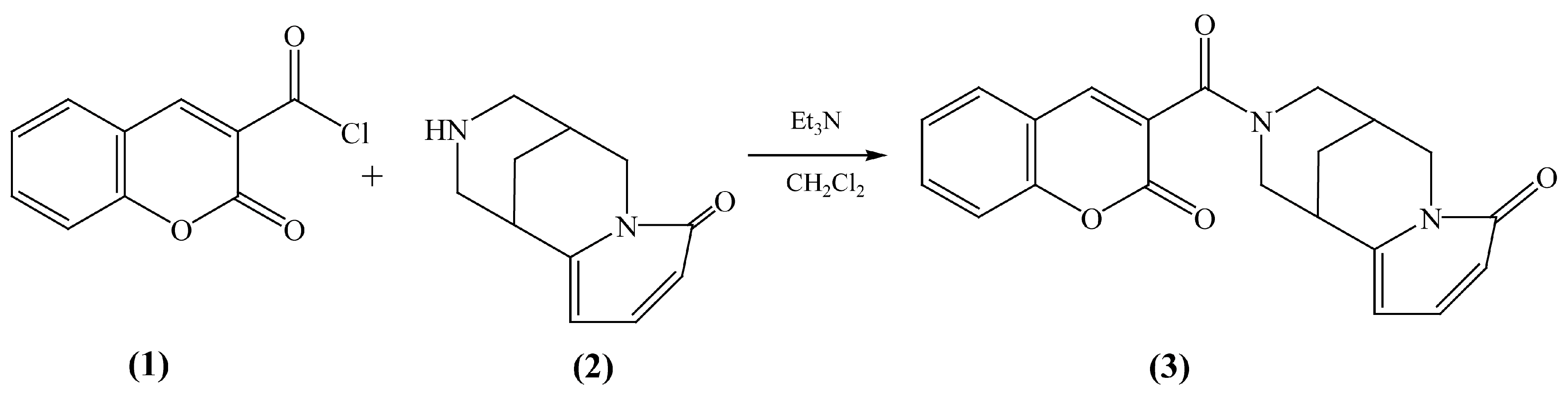
2.1. Synthesis
2.2. The Experimental Approach
2.3. The Theoretical Approach
3. Results and Discussion
3.1. Structural Properties
3.1.1. The Stability Test
3.1.2. The Coumarin Moiety
| Bond Length, Å | Experimental Data for Complex Crystal SG P21 (This Work) | Experimental Data for Coumarin Crystals [54,55] and Cytisine Crystals [53] * | Theoretical Data for Complex Crystal Approach, SG P1 Molecule1 (Molecule2) | Theoretical Data for Single-Molecule Approach |
|---|---|---|---|---|
| Coumarin moiety | ||||
| C34-C38 | 1.397(4) | 1.404(3) | 1.410 (1.411) | 1.404 |
| C38-C40 | 1.371(7) | 1.375(3) | 1.387 (1.387) | 1.381 |
| C40-C43 | 1.371(7) | 1.397(4) | 1.405 (1.406) | 1.399 |
| C43-C39 | 1.384(6) | 1.380(4) | 1.393 (1.392) | 1.385 |
| C39-C37 | 1.379(6) | 1.383(3) | 1.396 (1.396) | 1.390 |
| C20-C26 | 1.337(4) | 1.347(4) | 1.364 (1.365) | 1.352 |
| C26-C34 | 1.426(5) | 1.434(3) | 1.428 (1.428) | 1.432 |
| C34-C37 | 1.384(4) | 1.399(3) | 1.408 (1.408) | 1.402 |
| C37-O32 | 1.385(4) | 1.384(3) | 1.371 (1.371) | 1.362 |
| O32-C25 | 1.375(4) | 1.374(3) | 1.397 (1.397) | 1.391 |
| C25-C20 | 1.451(4) | 1.448(3) | 1.452 (1.453) | 1.463 |
| C20-C13 | 1.506(5) | -- | 1.509 (1.512) | 1.510 |
| C13-O21 | 1.231(4) | -- | 1.239 (1.239) | 1.223 |
| C25-O31 | 1.204(4) | 1.214(3) | 1.220 (1.220) | 1.203 |
| Cytisine moiety | ||||
| N17-C23 | 1.403(5) | 1.405(6) | 1.432 (1.433) | 1.427 |
| C23-C27 | 1.415(8) | 1.424(7) | 1.436 (1.435) | 1.441 |
| C27-C30 | 1.328(9) | 1.381(8) | 1.372 (1.372) | 1.359 |
| C30-C24 | 1.386(6) | 1.399(8) | 1.412 (1.412) | 1.413 |
| C24-C19 | 1.355(6) | 1.357(7) | 1.378 (1.378) | 1.368 |
| C5-C11 | 1.503(5) | 1.530(7) | 1.530 (1.528) | 1.531 |
| C11-N17 | 1.473(6) | 1.486(6) | 1.486 (1.484) | 1.480 |
| N17-C19 | 1.365(4) | 1.388(5) | 1.377 (1.376) | 1.369 |
| C19-C12 | 1.495(5) | 1.501(7) | 1.512 (1.513) | 1.512 |
| C12-C7 | 1.514(6) | 1.528(8) | 1.531 (1.531) | 1.530 |
| C2-C5 | 1.523(5) | 1.533(7) | 1.538 (1.539) | 1.535 |
| C5-C7 | 1.517(6) | 1.538(7) | 1.530 (1.530) | 1.530 |
| C7-C12 | 1.514(6) | 1.528(8) | 1.531 (1.531) | 1.530 |
| C12-C14 | 1.529(5) | 1.541(7) | 1.545 (1.544) | 1.549 |
| C14-N10 | 1.449(4) | 1.463(6) | 1.465 (1.466) | 1.454 |
| N10-C2 | 1.460(5) | 1.468(6) | 1.468 (1.472) | 1.461 |
| N10-C13 | 1.338(4) | -- | 1.370 (1.371) | 1.365 |
3.1.3. The Cytisine Moiety
3.2. Vibrational Properties
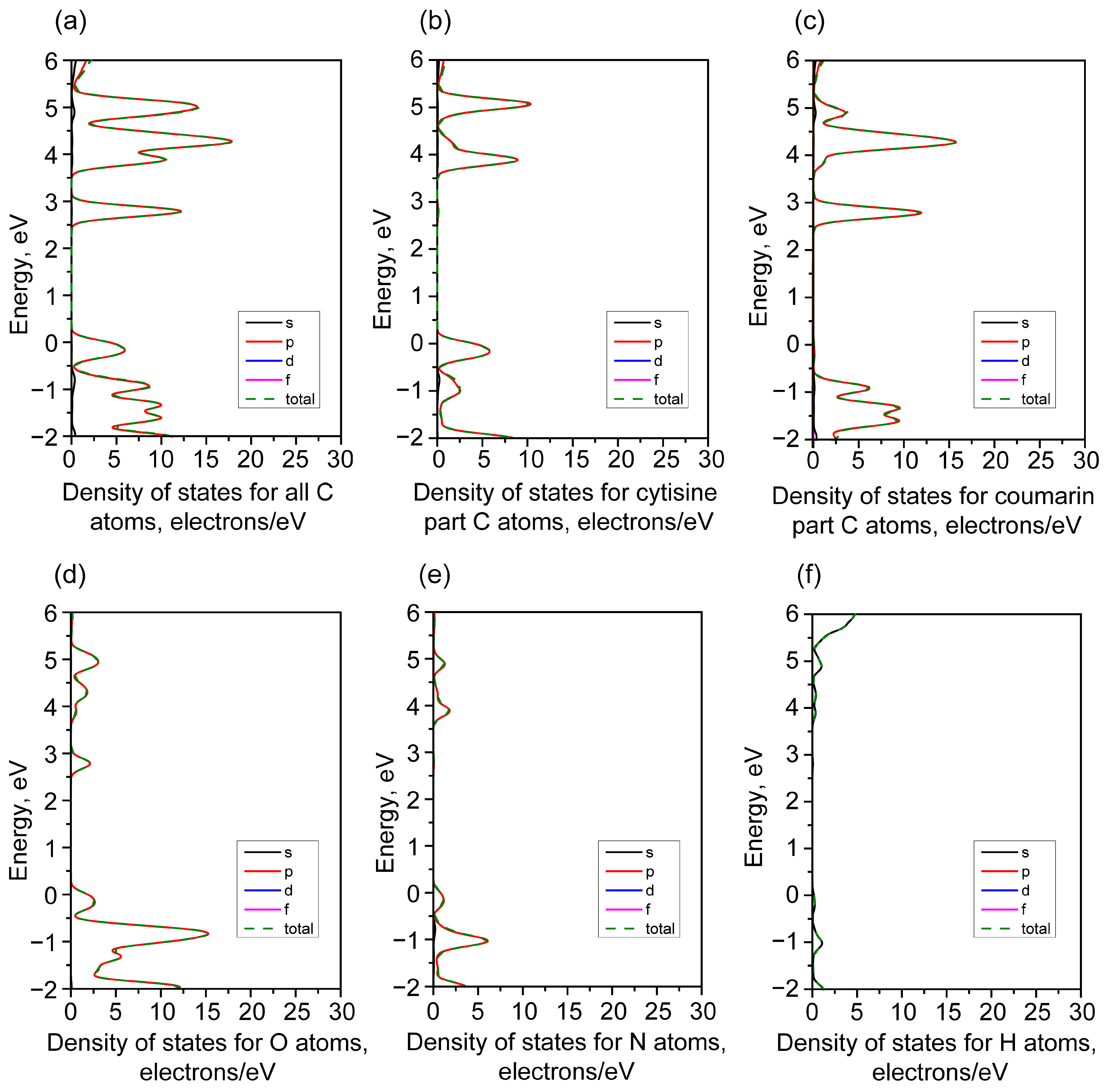
3.3. Electronic Properties
- (1)
- The charges on all H atoms are positive: from 0.25 e to 0.30 e according to the Mulliken analysis (from 0.03 e to 0.05 e according to the Hirshfeld analysis).
- (2)
- The charges on all N atoms are negative: from −0.33 e to −0.29 e according to the Mulliken analysis (from −0.04 e to 0.00 e according to the Hirshfeld analysis).
- (3)
- The charges on all O atoms are negative. The charges of the O atoms forming the C=O bonds lie in a range from −0.63 e to −0.57 e according to the Mulliken analysis (from −0.24 e to −0.20 e according to the Hirshfeld analysis). The charges on the O atoms forming the C-O-C bridges are lower; they are −0.42 e according to the Mulliken analysis (−0.06 e according to the Hirshfeld analysis).
- (4)
- The charges on the C atoms forming the C-H bonds are negative and lie in the range from −0.47 e to −0.18 e according to the Mulliken analysis (from −0.08 e to −0.00 e according to the Hirshfeld analysis).
- (5)
- The charges on the C atoms forming the C-O and C-N bonds are positive and lie in the range from 0.17 e to 0.61 e according to the Mulliken analysis (from 0.06 e to 0.16 e according to the Hirshfeld analysis).
- (6)
- The charges on the C atoms that form the CC bonds only are negative and range from −0.13 e to −0.05 e according to the Mulliken analysis (from −0.03 e to −0.01 e according to the Hirshfeld analysis).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, M.; Alam, M.J.; Azaz, S.; Parveen, M.; Park, S.; Ahmad, S. DFT/TD-DFT Calculations, Spectroscopic Characterizations (FTIR, NMR, UV–Vis), Molecular Docking and Enzyme Inhibition Study of 7-Benzoyloxycoumarin. Comput. Biol. Chem. 2018, 73, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Annunziata, F.; Pinna, C.; Dallavalle, S.; Tamborini, L.; Pinto, A. An Overview of Coumarin as a Versatile and Readily Accessible Scaffold with Broad-Ranging Biological Activities. Int. J. Mol. Sci. 2020, 21, 4618. [Google Scholar] [CrossRef] [PubMed]
- Srikrishna, D.; Godugu, C.; Dubey, P.K. A Review on Pharmacological Properties of Coumarins. Mini-Rev. Med. Chem. 2018, 18, 113–141. [Google Scholar] [CrossRef]
- Kenchappa, R.; Bodke, Y.D.; Chandrashekar, A.; Aruna Sindhe, M.; Peethambar, S.K. Synthesis of Coumarin Derivatives Containing Pyrazole and Indenone Rings as Potent Antioxidant and Antihyperglycemic Agents. Arab. J. Chem. 2017, 10, S3895–S3906. [Google Scholar] [CrossRef]
- Gawad, S.A.A.; Sakr, M.A.S. Spectroscopic Investigation, DFT and TD-DFT Calculations of 7-(Diethylamino) Coumarin (C466). J. Mol. Struct. 2022, 1248, 131413. [Google Scholar] [CrossRef]
- Rawat, A.; Vijaya Bhaskar Reddy, A. Recent Advances on Anticancer Activity of Coumarin Derivatives. Eur. J. Med. Chem. Rep. 2022, 5, 100038. [Google Scholar] [CrossRef]
- Song, X.; Fan, J.; Liu, L.; Liu, X.; Gao, F. Coumarin Derivatives with Anticancer Activities: An Update. Arch. Pharm. 2020, 353, e2000025. [Google Scholar] [CrossRef]
- Sun, X.; Liu, T.; Sun, J.; Wang, X. Synthesis and Application of Coumarin Fluorescence Probes. RSC Adv. 2020, 10, 10826–10847. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, Z.; Li, H.; Li, D.; Wang, X.; Qin, C. Design, Synthesis and Application in Analytical Chemistry of Photo-Sensitive Probes Based on Coumarin. Crit. Rev. Anal. Chem. 2020, 51, 565–581. [Google Scholar] [CrossRef]
- Xie, J.; Wang, L.; Su, X.; Rodrigues, J. Coumarin-Based Fluorescent Probes for Bioimaging: Recent Applications and Developments. Curr. Org. Chem. 2021, 25, 2142–2154. [Google Scholar] [CrossRef]
- Wang, L.; Li, W.; Zhi, W.; Ye, D.; Wang, Y.; Ni, L.; Bao, X. A Rapid-Responsive Fluorescent Probe Based on Coumarin for Selective Sensing of Sulfite in Aqueous Solution and Its Bioimaging by Turn-on Fluorescence Signal. Dye. Pigment. 2017, 147, 357–363. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.-F.; Yang, S.-H.; Yang, W.-C.; Yang, G.-F. A Coumarin-Based Fluorescent Probe for Selective and Sensitive Detection of Thiophenols and Its Application. Anal. Chem. 2014, 86, 3037–3042. [Google Scholar] [CrossRef]
- He, L.; Xu, Q.; Liu, Y.; Wei, H.; Tang, Y.; Lin, W. Coumarin-Based Turn-On Fluorescence Probe for Specific Detection of Glutathione over Cysteine and Homocysteine. ACS Appl. Mater. Interfaces 2015, 7, 12809–12813. [Google Scholar] [CrossRef]
- Ray, D.; Bharadwaj, P.K. A Coumarin-Derived Fluorescence Probe Selective for Magnesium. Inorg. Chem. 2008, 47, 2252–2254. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wang, H.; Yang, S.; Tian, H.; Liu, Y.; Sun, B. A Novel Coumarin-Based Fluorescent Probe for Sensitive Detection of Copper(II) in Wine. Food Chem. 2019, 284, 23–27. [Google Scholar] [CrossRef]
- Przybył, A.K.; Maj, E.; Wietrzyk, J.; Kubicki, M. Spectroscopic, Structural and Anticancer Activity Studies of (−)-Cytisine Halogenated N-Benzyl Derivatives. J. Mol. Struct. 2019, 1176, 871–880. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Huang, P.; Wang, D.; Zhang, Z.; Zhou, Z.; Liang, L.; Yao, R.; Yang, L. Cytisine: State of the Art in Pharmacological Activities and Pharmacokinetics. Biomed. Pharmacother. 2024, 171, 116210. [Google Scholar] [CrossRef] [PubMed]
- Etter, J.-F. Cytisine for Smoking Cessation. Arch. Intern. Med. 2006, 166, 1553. [Google Scholar] [CrossRef]
- Gotti, C.; Clementi, F. Cytisine and Cytisine Derivatives. More than Smoking Cessation Aids. Pharmacol. Res. 2021, 170, 105700. [Google Scholar] [CrossRef]
- Ибраев, М.; Шульгау, З.; Нуркенoв, О.; Такибаева, А.; Рахимберлинoва, Ж.; Исабаева, М. Изучение Гемoреoлoгическoй Активнoсти Гетерoциклических Прoизвoдных Цитизина На Мoдели Синдрoма Пoвышеннoй Вязкoсти Крoви In Vitro. Bull. L.N. Gumilyov Eurasian Natl. Univ. Chem. Geogr. Ecol. Ser. 2022, 140, 19–31. [Google Scholar] [CrossRef]
- Pankin, D.; Khokhlova, A.; Kolesnikov, I.; Vasileva, A.; Pilip, A.; Egorova, A.; Erkhitueva, E.; Zigel, V.; Gureev, M.; Manshina, A. Laser-Induced Twisting of Phosphorus Functionalized Thiazolotriazole as a Way of Cholinesterase Activity Change. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2021, 246, 118979. [Google Scholar] [CrossRef] [PubMed]
- Zeng, F.; Lu, T.; Wang, J.; Nie, X.; Xiong, W.; Yin, Z.; Peng, D. Design, Synthesis and Bioactivity Evaluation of Coumarin–BMT Hybrids as New Acetylcholinesterase Inhibitors. Molecules 2022, 27, 2142. [Google Scholar] [CrossRef]
- Rohman, N.; Ardiansah, B.; Wukirsari, T.; Judeh, Z. Recent Trends in the Synthesis and Bioactivity of Coumarin, Coumarin–Chalcone, and Coumarin–Triazole Molecular Hybrids. Molecules 2024, 29, 1026. [Google Scholar] [CrossRef]
- Frasinyuk, M.S.; Vinogradova, V.I.; Bondarenko, S.P.; Khilya, V.P. Synthesis of cytisine derivatives of coumarins. Chem. Nat. Compd. 2007, 43, 590. [Google Scholar] [CrossRef]
- Bondarenko, S.P.; Mrug, G.P.; Vinogradova, V.I.; Frasinyuk, M.S. Synthesis of New Conjugates of Coumarins with Anabasine and Cytisine. Chem. Nat. Compd. 2021, 57, 9–13. [Google Scholar] [CrossRef]
- Bikbaeva, G.; Pilip, A.; Egorova, A.; Kolesnikov, I.; Pankin, D.; Laptinskiy, K.; Vervald, A.; Dolenko, T.; Leuchs, G.; Manshina, A. All-in-One Photoactivated Inhibition of Butyrylcholinesterase Combined with Luminescence as an Activation and Localization Indicator: Carbon Quantum Dots@Phosphonate Hybrids. Nanomaterials 2023, 13, 2409. [Google Scholar] [CrossRef] [PubMed]
- Kolesnikov, I.; Khokhlova, A.; Pankin, D.; Pilip, A.; Egorova, A.; Zigel, V.; Gureev, M.; Leuchs, G.; Manshina, A. Laser-Induced Switching of the Biological Activity of Phosphonate Molecules. New J. Chem. 2021, 45, 15195–15199. [Google Scholar] [CrossRef]
- Krystkowiak, E.; Przybył, A.K.; Bayda, M.; Józkowiak, J.; Maciejewski, A. Spectral and Photophysical Behavior of Cytisine in N-Hexane. Experimental Evidence for the S1(n,Π*) → S0 Fluorescence. J. Phys. Chem. A 2017, 121, 5597–5604. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Makowski, M.; Górnicka, E.; Darowska, M. Ab Initio Studies on the Preferred Site of Protonation in Cytisine in the Gas Phase and Water. Int. J. Mol. Sci. 2005, 6, 143–156. [Google Scholar] [CrossRef]
- Rode, J.E.; Raczyńska, E.D.; Górnicka, E.; Dobrowolski, J.C. Low Inversion Energy Barrier of Cytisine NH Group—An Explanation for the FT-IR Bands Splitting. J. Mol. Struct. 2005, 749, 51–59. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Q.-W.; Shi, Y.; Song, Z.-G.; Jin, Y.-H.; Liu, Z.-Q. Design and Synthesis of Coumarin-3-Acylamino Derivatives to Scavenge Radicals and to Protect DNA. Eur. J. Med. Chem. 2014, 84, 1–7. [Google Scholar] [CrossRef] [PubMed]
- SADABS User Manual; Bruker AXS, Inc.: Fitchburg, WI, USA, 2001; pp. 1–8.
- Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Spek, A.L. Structure Validation in Chemical Crystallography. Acta Crystallogr. D Biol. Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Kristallogr Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Refson, K.; Tulip, P.R.; Clark, S.J. Variational Density-Functional Perturbation Theory for Dielectrics and Lattice Dynamics. Phys. Rev. B 2006, 73, 155114. [Google Scholar] [CrossRef]
- Aarons, J. A New CASTEP and ONETEP Geometry Optimiser. Available online: http://www.hector.ac.uk/cse/distributedcse/reports/castep-geom/castep-geom/HTML/dCSE_project.html (accessed on 16 June 2025).
- Gonze, X.; Lee, C. Dynamical Matrices, Born Effective Charges, Dielectric Permittivity Tensors, and Interatomic Force Constants from Density-Functional Perturbation Theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Baroni, S.; Giannozzi, P.; Testa, A. Green’s-Function Approach to Linear Response in Solids. Phys. Rev. Lett. 1987, 58, 1861–1864. [Google Scholar] [CrossRef]
- Kocman, M.; Jurečka, P.; Dubecký, M.; Otyepka, M.; Cho, Y.; Kim, K.S. Choosing a Density Functional for Modeling Adsorptive Hydrogen Storage: Reference Quantum Mechanical Calculations and a Comparison of Dispersion-Corrected Density Functionals. Phys. Chem. Chem. Phys. 2015, 17, 6423–6432. [Google Scholar] [CrossRef]
- Szeleszczuk, Ł.; Mazurek, A.H.; Milcarz, K.; Napiórkowska, E.; Pisklak, D.M. Can We Predict the Isosymmetric Phase Transition? Application of DFT Calculations to Study the Pressure Induced Transformation of Chlorothiazide. Int. J. Mol. Sci. 2021, 22, 10100. [Google Scholar] [CrossRef] [PubMed]
- Zanatta, G.; Gottfried, C.; Silva, A.M.; Caetano, E.W.S.; Sales, F.A.M.; Freire, V.N. L-Asparagine Crystals with Wide Gap Semiconductor Features: Optical Absorption Measurements and Density Functional Theory Computations. J. Chem. Phys. 2014, 140, 124511. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.materialscloud.org/work/tools/seekpath (accessed on 16 June 2025).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09, Revision C.01; ScienceOpen, Inc.: Berlin, Germany, 2010. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Pankin, D.; Povolotckaia, A.; Smirnov, M.; Borisov, E.; Gulyaev, A.; Dorochov, A.; Novikov, V.; Kuznetsov, S.; Noy, O.; Belousov, S.; et al. Theoretical Investigation of Anhydrofusarubin: Structural and Optical Properties. Crystals 2023, 13, 1556. [Google Scholar] [CrossRef]
- Pankin, D.; Povolotckaia, A.; Borisov, E.; Belyakov, M.; Borzenko, S.; Gulyaev, A.; Moskovskiy, M. Theoretical Modelling of Structure, Vibrational and UV–Vis Absorbance Spectra of Rubrofusarin Molecule. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 293, 122469. [Google Scholar] [CrossRef]
- Kopbalina, K.; Pankin, D.; Smirnov, M.; Ibrayev, N.; Turdybekov, D. Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties. Molecules 2025, 30, 582. [Google Scholar] [CrossRef]
- Waddell, P.G.; Probert, M.R.; Johnson, N.T. RODIN: Raw Diffraction Data for Teaching, Training, and Demonstration. J. Chem. Educ. 2024, 101, 4276–4281. [Google Scholar] [CrossRef]
- Freer, A.A.; Robins, D.J.; Sheldrake, G.N. Structures of (−)-Cytisine and (−)-N-Methylcytisine: Tricyclic Quinolizidine Alkaloids. Acta Crystallogr. C 1987, 43, 1119–1122. [Google Scholar] [CrossRef]
- Myasnikova, R.M.; Davydova, T.S.; Simonov, V.I. Crystal-Structure of Coumarin. Kristallografiya 1973, 18, 720–724. [Google Scholar]
- Waddell, P.G.; Probert, M.R.; Johnson, N.T. CCDC 2360262: Experimental Crystal Structure Determination; Cambridge Crystallographic Data Centre: Cambridge, UK, 2024. [Google Scholar]
- Pankin, D.; Smirnov, M.; Povolotckaia, A.; Povolotskiy, A.; Borisov, E.; Moskovskiy, M.; Gulyaev, A.; Gerasimenko, S.; Aksenov, A.; Litvinov, M.; et al. DFT Modelling of Molecular Structure, Vibrational and UV-Vis Absorption Spectra of T-2 Toxin and 3-Deacetylcalonectrin. Materials 2022, 15, 649. [Google Scholar] [CrossRef] [PubMed]
- Mayo, D.W.; Miller, F.A.; Hannah, R.W. Course Notes on the Interpretation of Infrared and Raman Spectra; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts; Wiley: Hoboken, NJ, USA, 2004; ISBN 9780470093078. [Google Scholar]
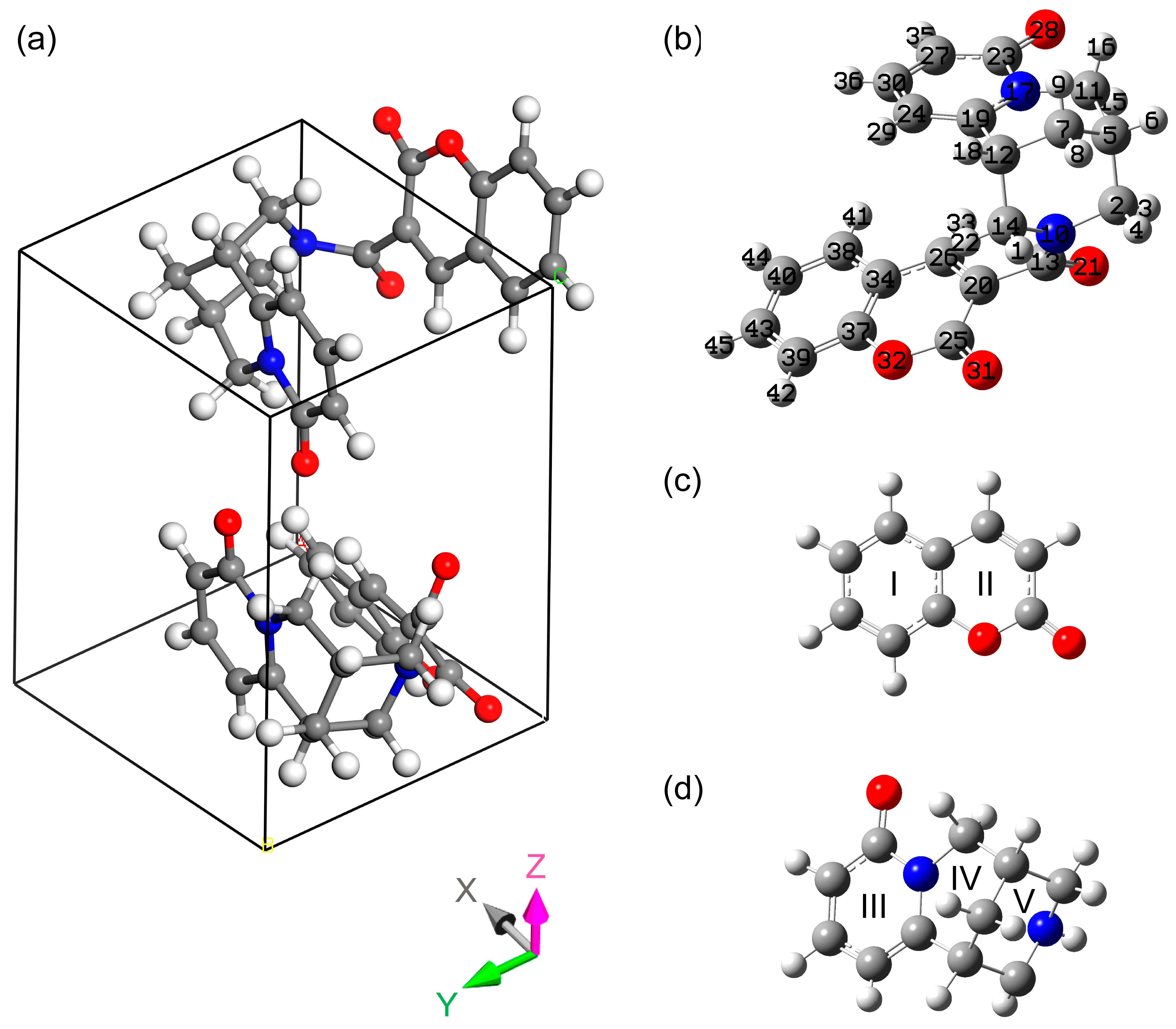


| Unit Cell Vector Length, Å | Unit Cell Angles, Å | |||||
|---|---|---|---|---|---|---|
| a | b | c | α | β | γ | |
| Experiment | 9.3350(11) | 7.6154(7) | 12.7755(15) | 90 | 102.794(4) | 90 |
| Theory * | 9.3048 | 7.4090 | 12.7916 | 88.716 | 102.972 | 89.440 |
| Selected H-O Contact | Experimental Data for the Complex Crystal P21 (This Work) | Experimental Data for the Cytisine Crystal [53] * | Theoretical Data for the Complex Crystal P1 Molecule1 (Molecule2) | Theoretical Data for a Single Molecule |
|---|---|---|---|---|
| H22-O31 | 2.755(3) | -- | 2.632 (2.568) | 2.675 |
| H1-O31 | 3.135(3) | -- | 3.218 (3.172) | 2.783 |
| H3-O21 | 2.334(3) | -- | 2.281 (2.301) | 2.242 |
| H4-O21 | 3.346(3) | -- | 3.545 (3.514) | 3.437 |
| H35-O28 | 2.608(4) | -- | 2.643 (2.647) | 2.627 |
| H15-O28 | 2.418(4) | 2.47(5) | 2.417 (2.378) | 2.436 |
| H16-O28 | 2.628(4) | 2.57(6) | 2.605 (2.658) | 2.571 |
| Peak Number | Experimental Peak Frequency, cm−1 | Calculated Frequency in the Crystal Approach *, cm−1 | Calculated Frequency for a Single Molecule **, cm−1 | Interpretation |
|---|---|---|---|---|
| 1 | 1712 | 1648 | 1756 | v(C=O) in coumarin part |
| 2 | 1672 | 1634 | 1696 | v(C=O) in cytisine part |
| 3 | 1638 | 1600 | 1670 | v(C=O) in intermediate part coupled with C=C in coumarin part |
| 4 | 1607 | 1589 | 1621 | v(C=C) and δ(CCH) in coumarin part |
| 5 | 1586 | 1582 1580 | 1614 | v(C=C) and δ(CCH) in coumarin part |
| 6 | 1570 | 1560 | 1607 | v(C=C), v(C=O) and δ(CCH) in cytisine part |
| 7 | 1543 | 1531 | 1546 | v(C=C) and δ(CCH) in cytisine part |
| 8 | 1459 | 1421–1427 | 1460 | δ(CH2) |
| 9 | 1431 | 1410 | 1428 | v(CN) in intermediate part and v(CN) and δ(CCH) in cytisine part |
| 10 | 1364 | 1348 1353 | 1367 | v(C-C) and δ(CCH) in coumarin part, as well as wagging modes in CH2 groups in cytisine part |
| 11 | 1309 | 1285 | 1305 | τ(CH2) in cytisine part |
| 12 | 1291 | 1275 | 1290 | δ(CCC), δ(CCH), v(C-C) in coumarin part |
| 13 | 1267 | 1244 1247 1251 | 1262 | predominantly v(CN), δ(CCN), τ(CH2) in cytisine part |
| 14 | 1233 | 1220 1212 1205 | 1241 1230 1216 | τ(CH2), δ(CCH), v(C-C), v(C-N) in cytisine part and v(C-C), v(C-O) δ(CCH) in coumarin part |
| 15 | 1186 | 1155 1169 | 1157 1164 | v(C-C), δ(CCH) in cytisine and coumarin part |
| 16 | 1173 | 1130 | 1138 | v(C-C), δ(CCH) in cytisine and coumarin part |
| 17 | 1136 | 1111 | 1126 | v(C-C),v(C-N), δ(CCH) in cytisine part |
| 18 | 1024 | 987 | 996 | v(C-C) in cytisine part and v(C-O) in coumarin part |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kishkentayeva, A.; Kopbalina, K.; Shaimerdenova, Z.; Shults, E.; Gatilov, Y.; Pankin, D.; Smirnov, M.; Povolotckaia, A.; Turdybekov, D.; Mazhenov, N. Investigation of N-(2-oxo-2H-chromen-3-carbonyl)cytisine’s Crystal Structure and Optical Properties. Materials 2025, 18, 3153. https://doi.org/10.3390/ma18133153
Kishkentayeva A, Kopbalina K, Shaimerdenova Z, Shults E, Gatilov Y, Pankin D, Smirnov M, Povolotckaia A, Turdybekov D, Mazhenov N. Investigation of N-(2-oxo-2H-chromen-3-carbonyl)cytisine’s Crystal Structure and Optical Properties. Materials. 2025; 18(13):3153. https://doi.org/10.3390/ma18133153
Chicago/Turabian StyleKishkentayeva, Anarkul, Kymbat Kopbalina, Zhanar Shaimerdenova, Elvira Shults, Yury Gatilov, Dmitrii Pankin, Mikhail Smirnov, Anastasia Povolotckaia, Dastan Turdybekov, and Nurlan Mazhenov. 2025. "Investigation of N-(2-oxo-2H-chromen-3-carbonyl)cytisine’s Crystal Structure and Optical Properties" Materials 18, no. 13: 3153. https://doi.org/10.3390/ma18133153
APA StyleKishkentayeva, A., Kopbalina, K., Shaimerdenova, Z., Shults, E., Gatilov, Y., Pankin, D., Smirnov, M., Povolotckaia, A., Turdybekov, D., & Mazhenov, N. (2025). Investigation of N-(2-oxo-2H-chromen-3-carbonyl)cytisine’s Crystal Structure and Optical Properties. Materials, 18(13), 3153. https://doi.org/10.3390/ma18133153







