Probabilistic Models for Two-Phase Materials
Abstract
1. Introduction
2. Level-Cut Random Fields
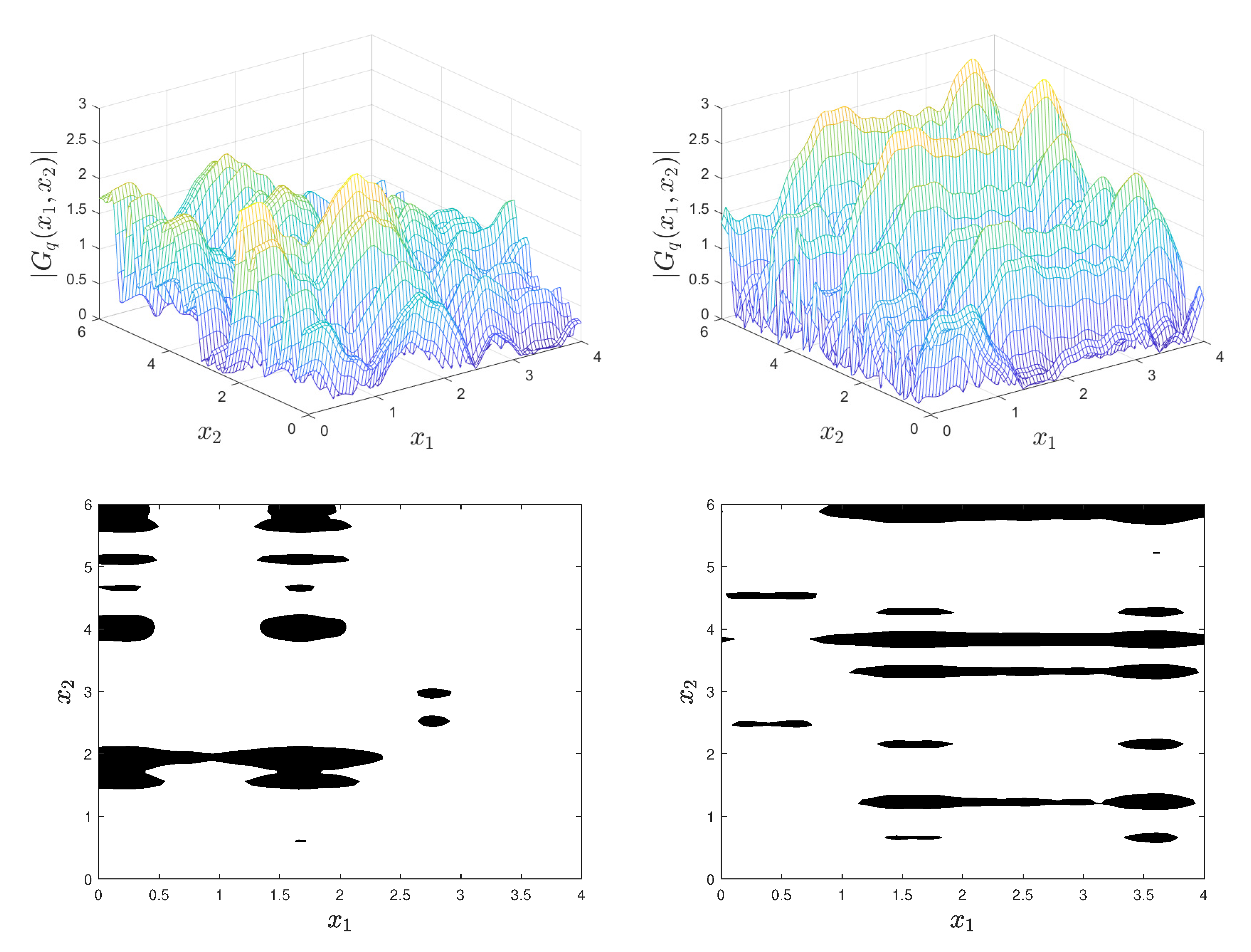
2.1. Gaussian Fields
2.1.1. Mean and Correlation Functions of Level-Cut Fields
2.1.2. Inclusion Properties
2.1.3. Monte Carlo Algorithm
- –
- Step 1: Generate samples of the Gaussian field by, e.g., one of the following two methods. The first represents by its values of the nodes of a dense mesh in D and generates samples of the resulting Gaussian vector by standard algorithms [13] (Sect. 5.2.1). The second method uses the spectral representation or related methods to generate directly realizations of [13] (Sect. 5.3.1). A simpler version of this method is used in the subsequent section.
- –
- Step 2: Identify the subsets of the realization of whose absolute values exceed specified levels and record the numbers, the volume, and other geometrical features of the generated subsets (inclusions).
- –
- Step 3: Estimate statistics of interest for the inclusions recorded in the previous step.
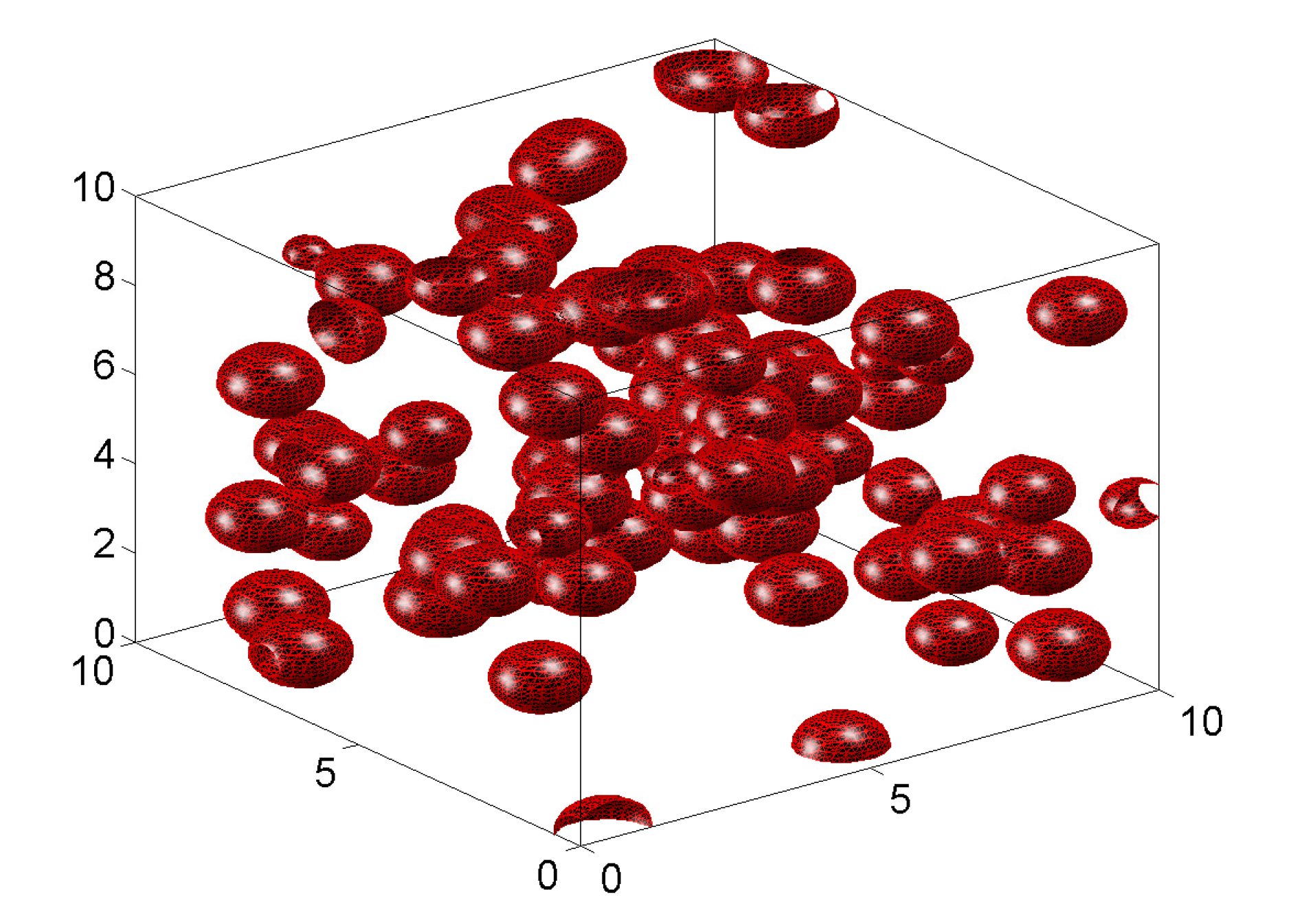
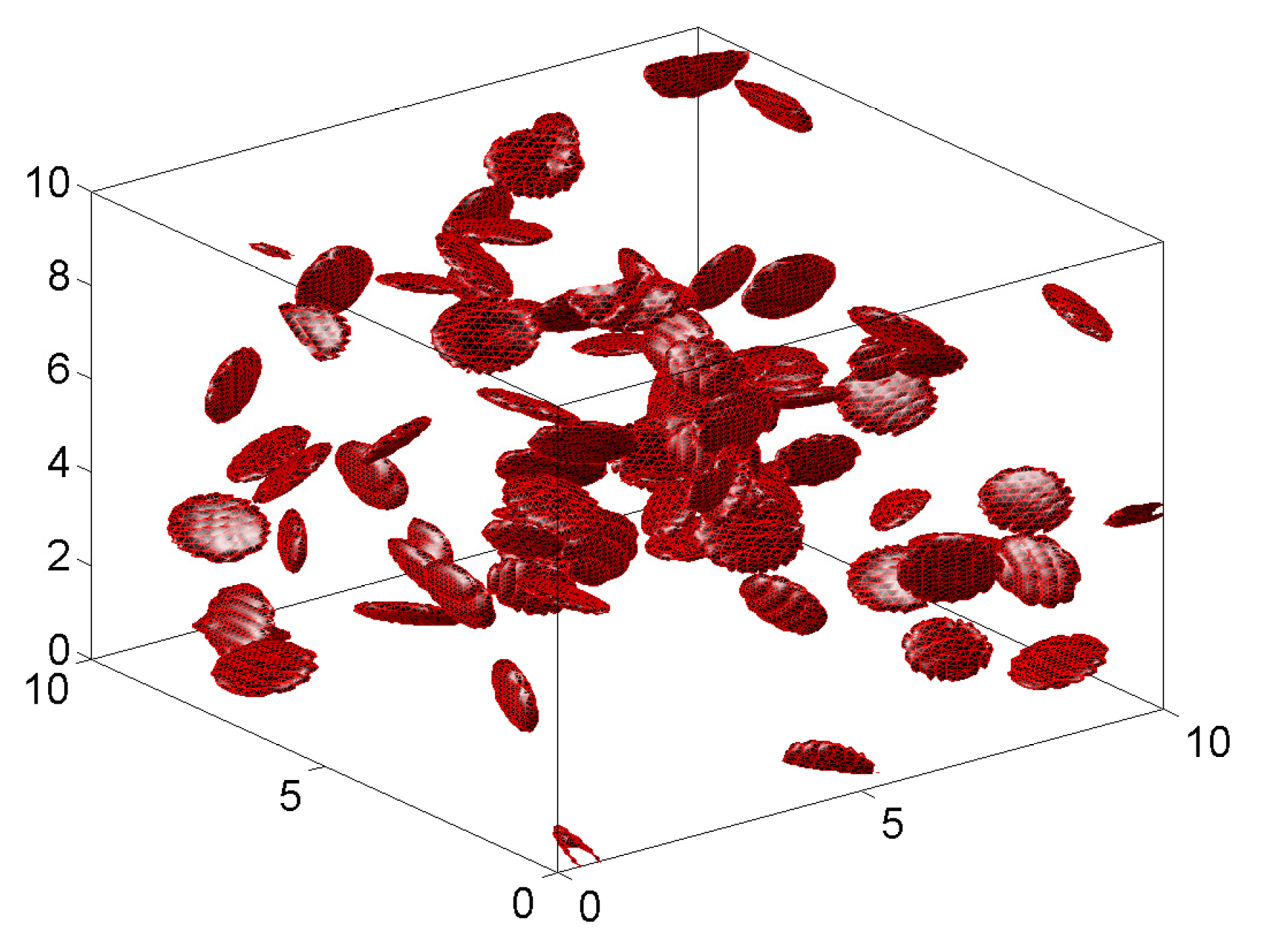
2.1.4. Two-Phase Synthetic Material Specimens
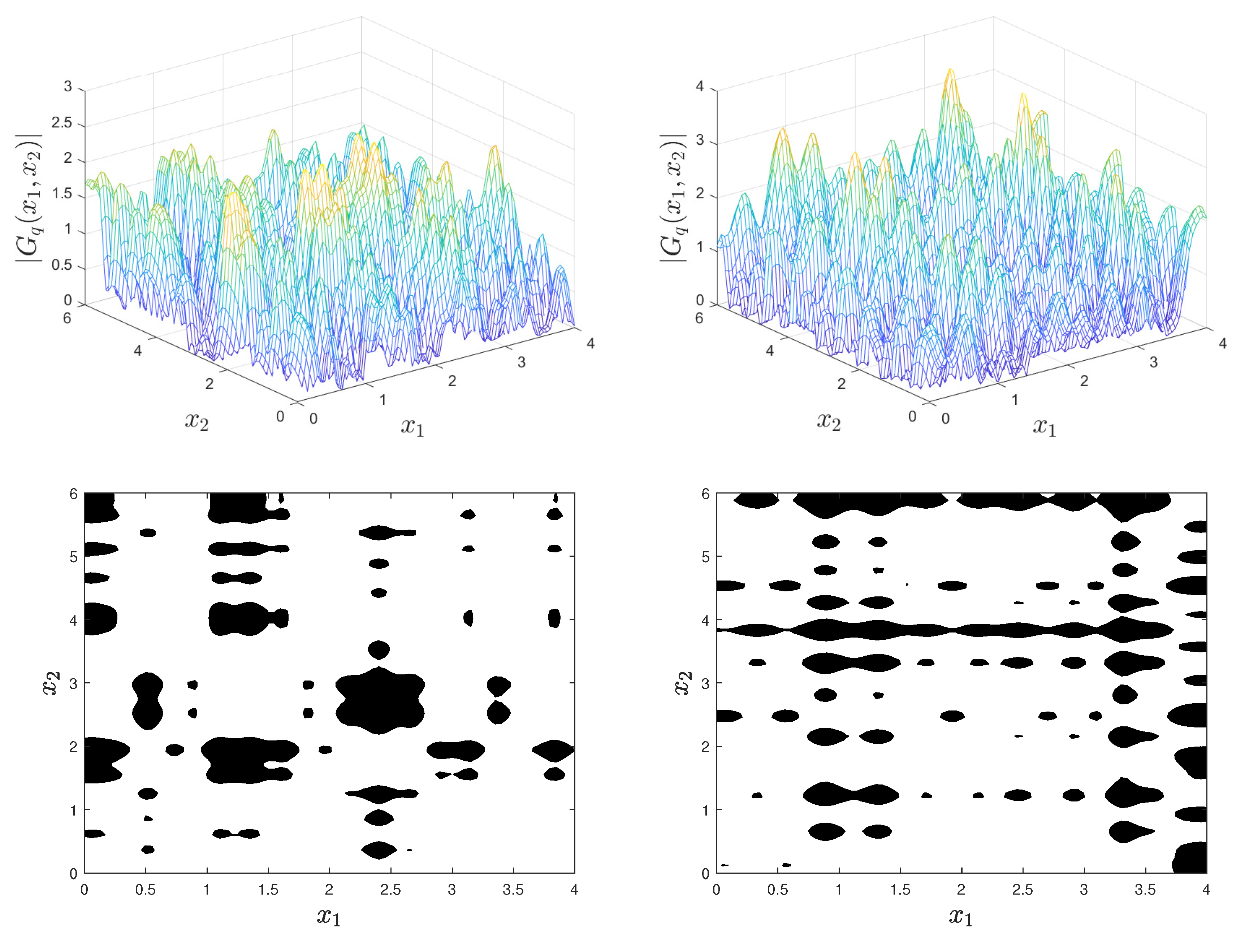
2.2. Filtered Poison Fields
2.2.1. Mean and Correlation Functions of Filtered Poisson Fields
2.2.2. Inclusion Properties
2.2.3. Monte Carlo Algorithm
- –
- Step 1: Generate independent samples of the Poisson random variable , which are integers by employing the methods described in, e.g., [15] (Sect. 4.6).
- –
- Step 2: For each sample of , generate independent uniformly distributed sets of points in and independent samples of and . Samples of and can be delivered by standard Monte Carlo algorithms. The rejection method can be used to generate independent uniformly distributed points in , see [5] (Sect. 2.2).
- –
- Step 3: Construct the corresponding realization of in (11) and the corresponding level-cut realizations, record cuts above , and estimate statistics of features of the resulting inclusions.
2.2.4. Two-Phase Synthetic Material Specimens
3. Mosaic Fields
3.1. Binomial Point Fields
3.2. Poisson Point Fields
3.3. Inclusion Properties
3.3.1. Monte Carlo Algorithm
- –
- Step 1: Generate samples of the Poisson random variable by employing the methods described in, e.g., [15] (Sect. 4.6).
- –
- Step 2: For each sample of , generate sets of independent uniformly distributed points in and random sets . There are several methods for generating realizations of binomial points in [5] (Sect. 2.2). For example, the rejection method generates independent, uniformly distributed points in a rectangle including the subset by using, e.g., the MATLAB (R2020) function , . Then, it retains from these points those which fall in .
- –
- Step 3: Construct the corresponding realization of the mosaic field and estimate statistics of features of the resulting inclusions.
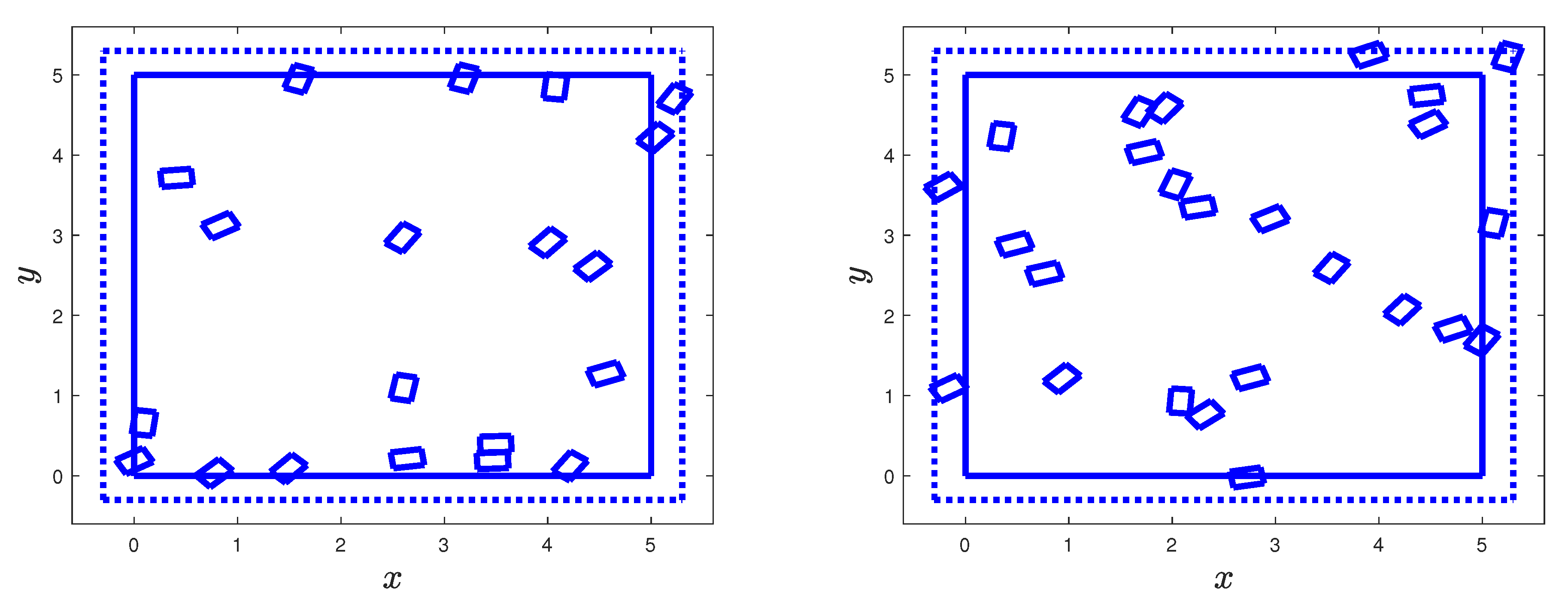
3.3.2. Two-Phase Synthetic Material Specimens
4. Tessellation Random Fields
4.1. Voronoi Tessellation
4.2. Inclusion Properties
4.2.1. Monte Carlo Algorithm
- –
- Step 1: Generate samples of the Poisson random variable by employing the methods described in, e.g., [15] (Sect. 4.6).
- –
- Step 2: For each sample of , generate sets of independent uniformly distributed points in D and use the voronoi MATLAB function to partition the specimen domain in Voronoi cells centered at the generated Poisson points.
- –
- Step 3: Toss a coin for each Voronoi cell and call it phase 1 (inclusion) with probability and estimate the statistics of features of the resulting inclusions.
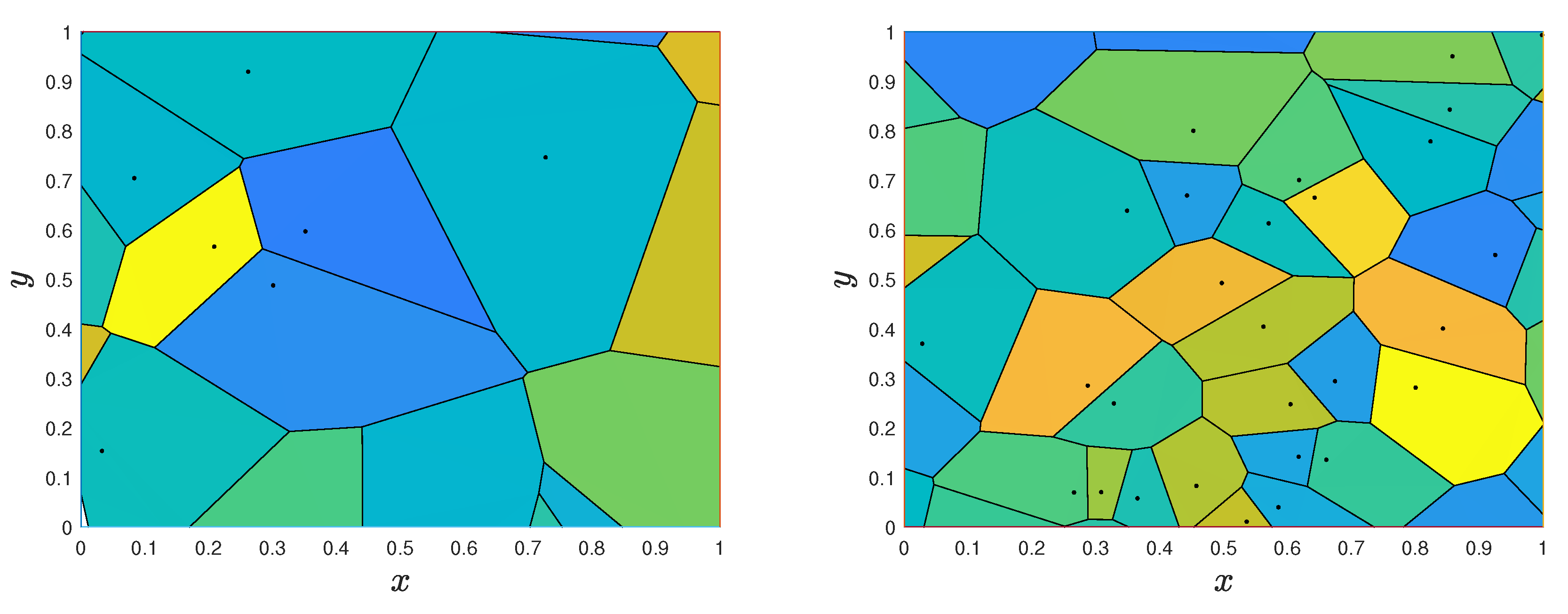
4.2.2. Two-Phase Synthetic Material Specimens
5. Conclusions
Funding
Conflicts of Interest
References
- Grigoriu, M.; Garboczi, E.J.; Kafali, C. Spherical harmonic-based random fields for aggregates used in concrete. Powder Technol. 2006, 166, 123–138. [Google Scholar] [CrossRef]
- Adler, R.J. The Geometry of Random Fields; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Aldous, D. Probability Approximations via the Poisson Clumping Heuristic; Springer: New York, NY, USA, 1989. [Google Scholar]
- Ostoja-Starzewski, M. Microstructural Randomness and Scaling in Mechanics of Materials; Chapman & Hall/CRC: New York, NY, USA, 2007. [Google Scholar]
- Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and Its Applications; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Torquato, S. Random Heterogeneous Materials. Microstructure and Macroscopic Properties; Springer: New York, NY, USA, 2002. [Google Scholar]
- Dirrler, M.; Dorr, C.; Schlather, M. A generalization of Matérn hard-core processes with applications to max-stable processes. J. Appl. Probab. 2020, 57, 1298–1312. [Google Scholar] [CrossRef]
- Grigoriu, M. Random field models for two-phase microstructures. J. Appl. Phys. 2003, 94, 3762–3770. [Google Scholar] [CrossRef]
- Grigoriu, M. Level-cut inhomogeneous filtered Poisson field for two-phase microstructures. Int. J. Numer. Methods Eng. 2009, 78, 215–228. [Google Scholar] [CrossRef]
- Quiblier, J.A. A new three-dimensional modeling technique for studying porous media. J. Colloid Interface Sci. 1984, 98, 84–102. [Google Scholar] [CrossRef]
- Torquato, S. Thermal conductivity of disordered heterogeneous media form the microstructure. Rev. Chem. Eng. 1987, 4, 151–204. [Google Scholar] [CrossRef]
- Field, R.; Grigoriu, M. Level cut gaussian random fields for transitions from laminar to turbulent flow. Probabilistic Eng. Mech. 2013, 28, 91–102. [Google Scholar] [CrossRef]
- Grigoriu, M. Stochastic Calculus. Applications in Science and Engineering; Birkhäuser: Boston, MA, USA, 2002. [Google Scholar]
- Johnson, N.L.; Kotz, S. Discrete Distributions; John Wiley & Sons, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Grigoriu, M. Applied Non-Gaussian Processes: Examples, Theory, Simulation, Linear Random Vibration, and MATLAB Solutions; Prentice Hall: Englewoods Cliffs, NJ, USA, 1995. [Google Scholar]
- Carroll, J.; Abuzaid, W.; Lambros, J.; Sehitoglu, H. An experimental methodology to relate local strain to microstructural texture. Rev. Sci. Instruments 2010, 81, 083703. [Google Scholar] [CrossRef] [PubMed]
- Grigoriu, M. Nearest neighbor probabilistic model for aluminum polycrystals. J. Eng. Mech. 2010, 136, 821–829. [Google Scholar] [CrossRef]
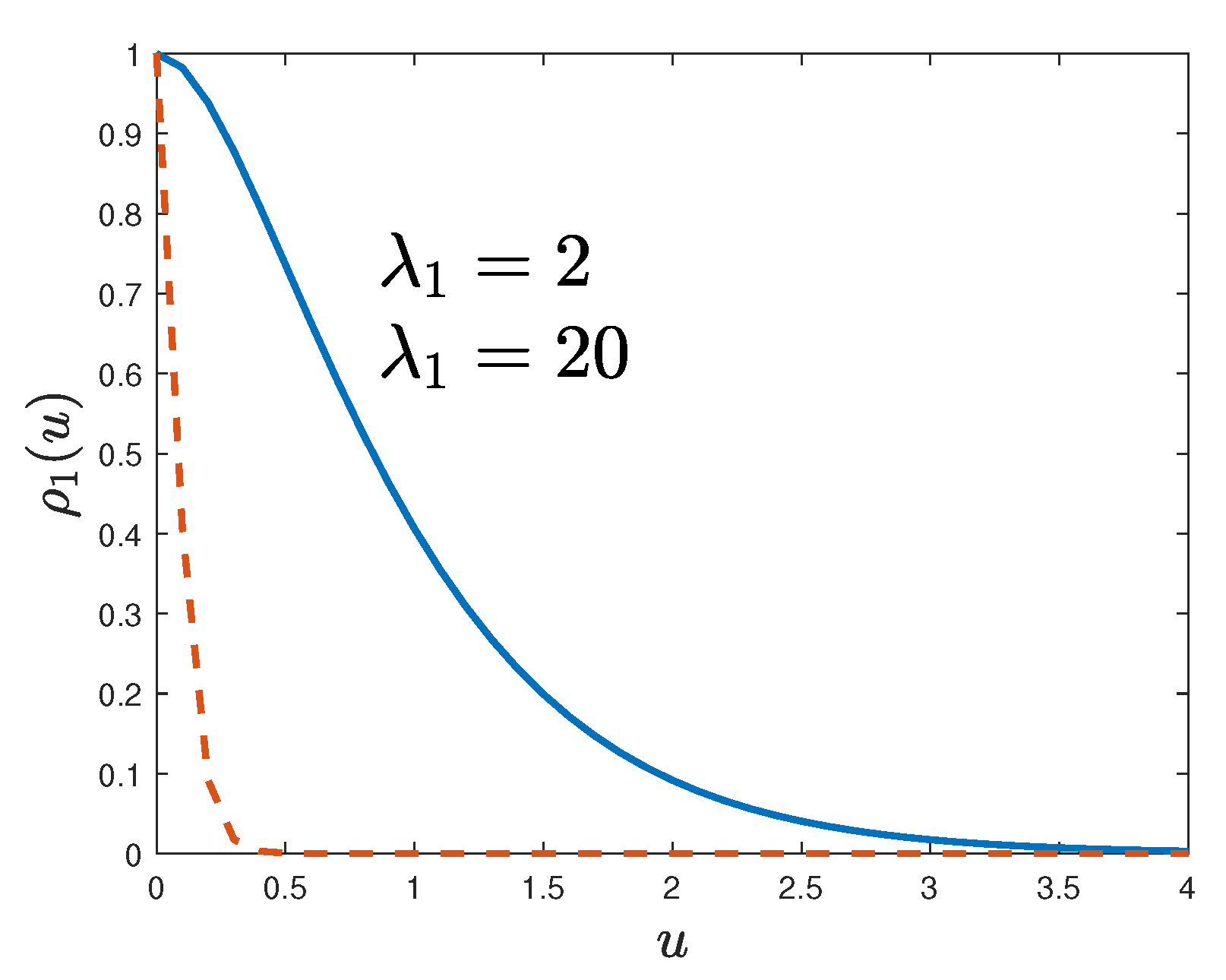

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoriu, M. Probabilistic Models for Two-Phase Materials. Materials 2025, 18, 3064. https://doi.org/10.3390/ma18133064
Grigoriu M. Probabilistic Models for Two-Phase Materials. Materials. 2025; 18(13):3064. https://doi.org/10.3390/ma18133064
Chicago/Turabian StyleGrigoriu, Mircea. 2025. "Probabilistic Models for Two-Phase Materials" Materials 18, no. 13: 3064. https://doi.org/10.3390/ma18133064
APA StyleGrigoriu, M. (2025). Probabilistic Models for Two-Phase Materials. Materials, 18(13), 3064. https://doi.org/10.3390/ma18133064




