Pore Structure Influence on Properties of Air-Entrained Concrete
Abstract
1. Introduction
2. Experimental Investigation
2.1. Materials
2.2. Methods
2.2.1. Consistency
2.2.2. Air Content
2.2.3. Compressive Strength
2.2.4. Ultrasonic Pulse Velocity
2.2.5. Freeze–Thaw Resistance (Direct Method)
- -
- the samples do not show any cracking,
- -
- the average mass loss of the samples does not exceed 5%,
- -
- the average reduction in compressive strength does not exceed 20%.
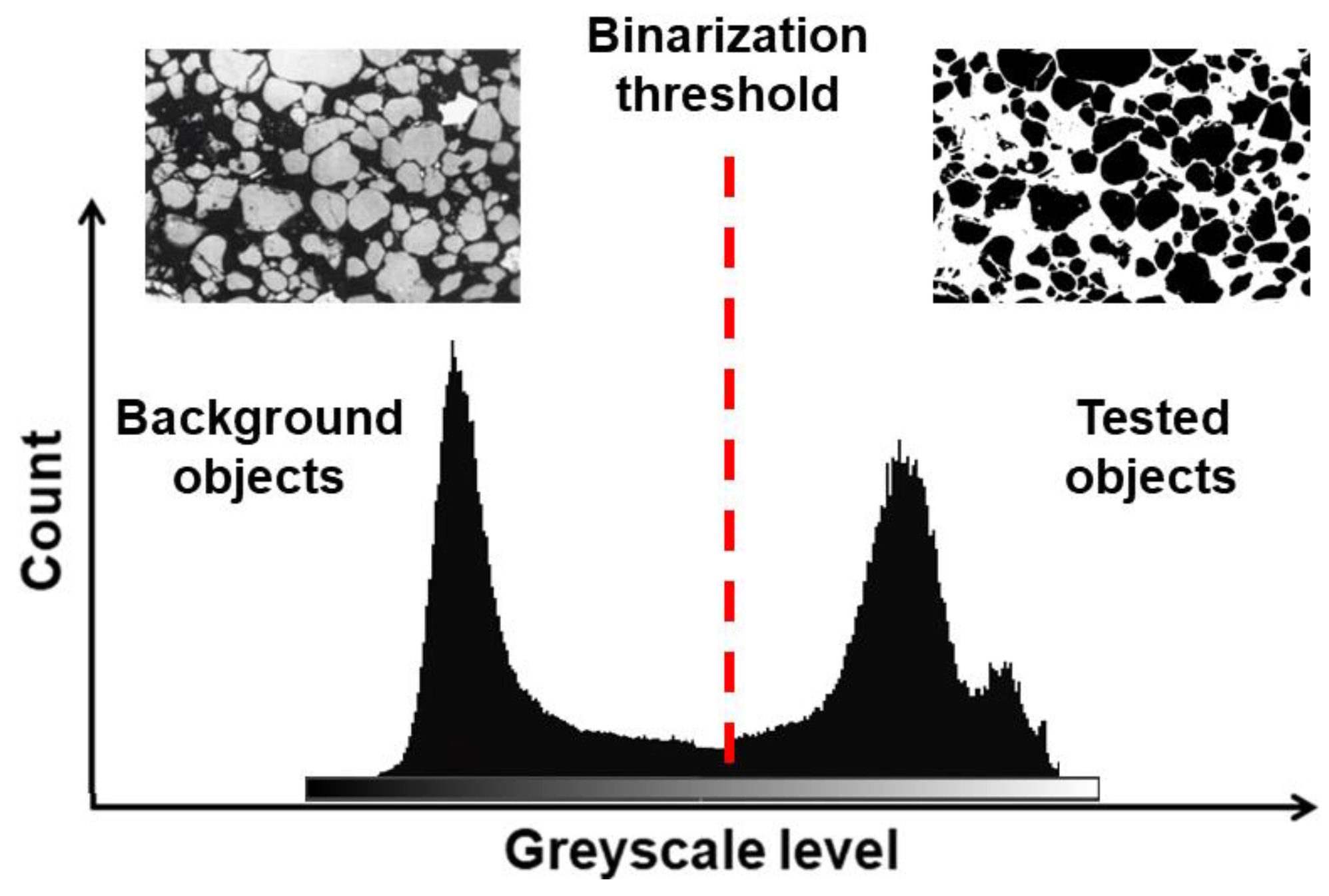
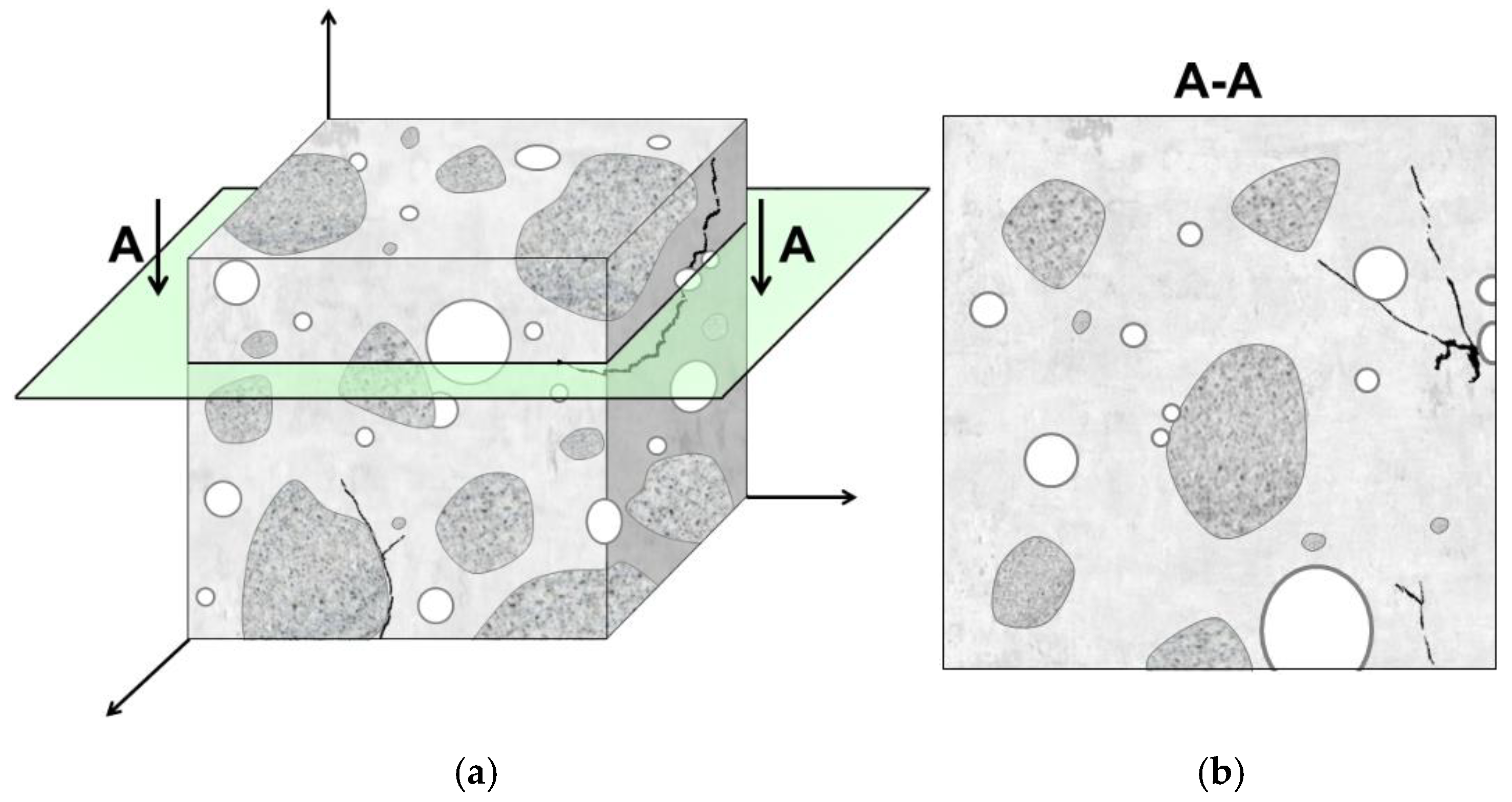
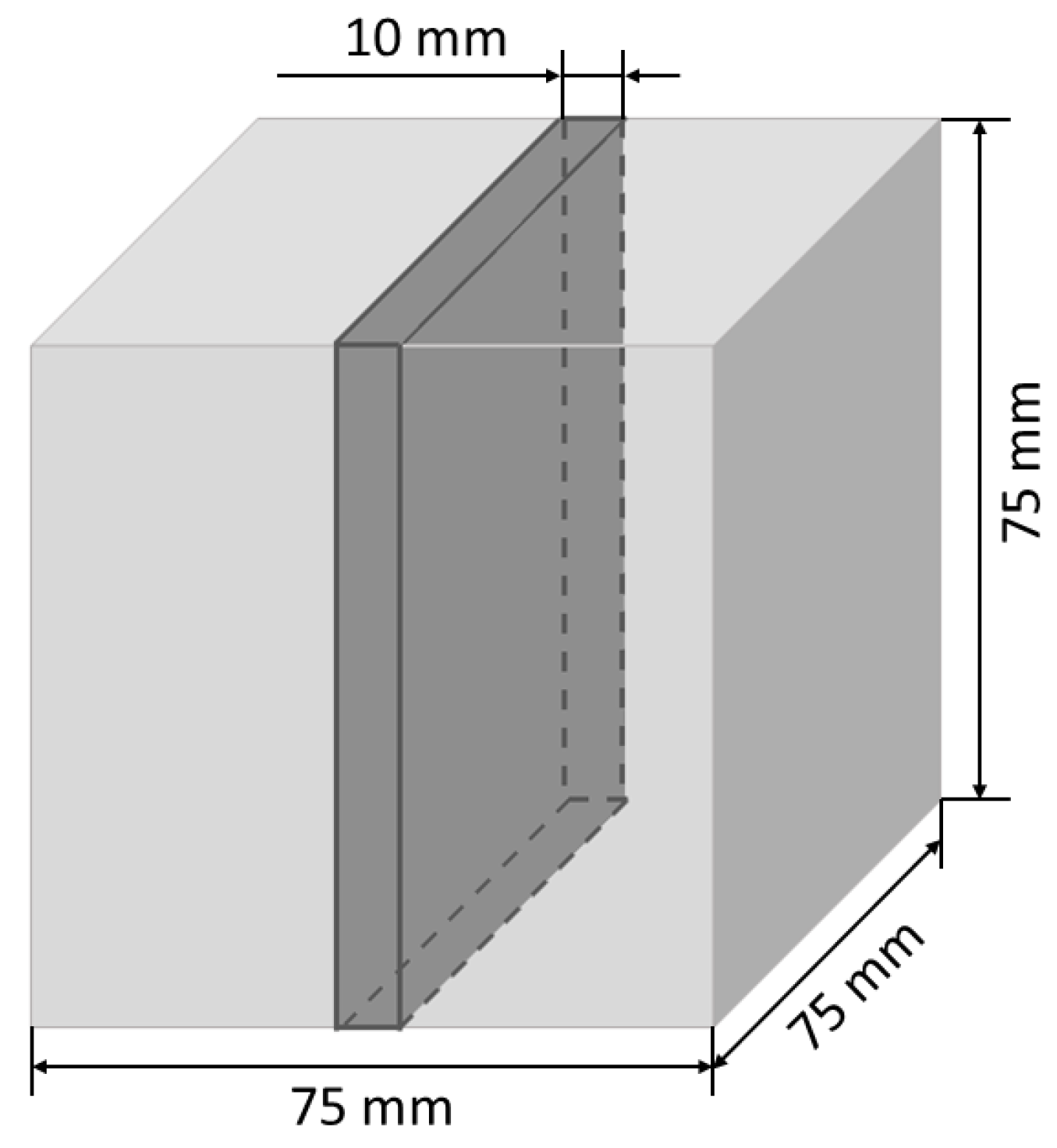
2.2.6. Pore Structure Analysis (Indirect Method)
2.2.7. Statistical Analysis
2.2.8. Summary of Experimental Plan
3. Results and Discussion
3.1. The Influence of the Air-Entraining Admixture on the Properties and Microstructure
3.1.1. Fresh Mix Properties
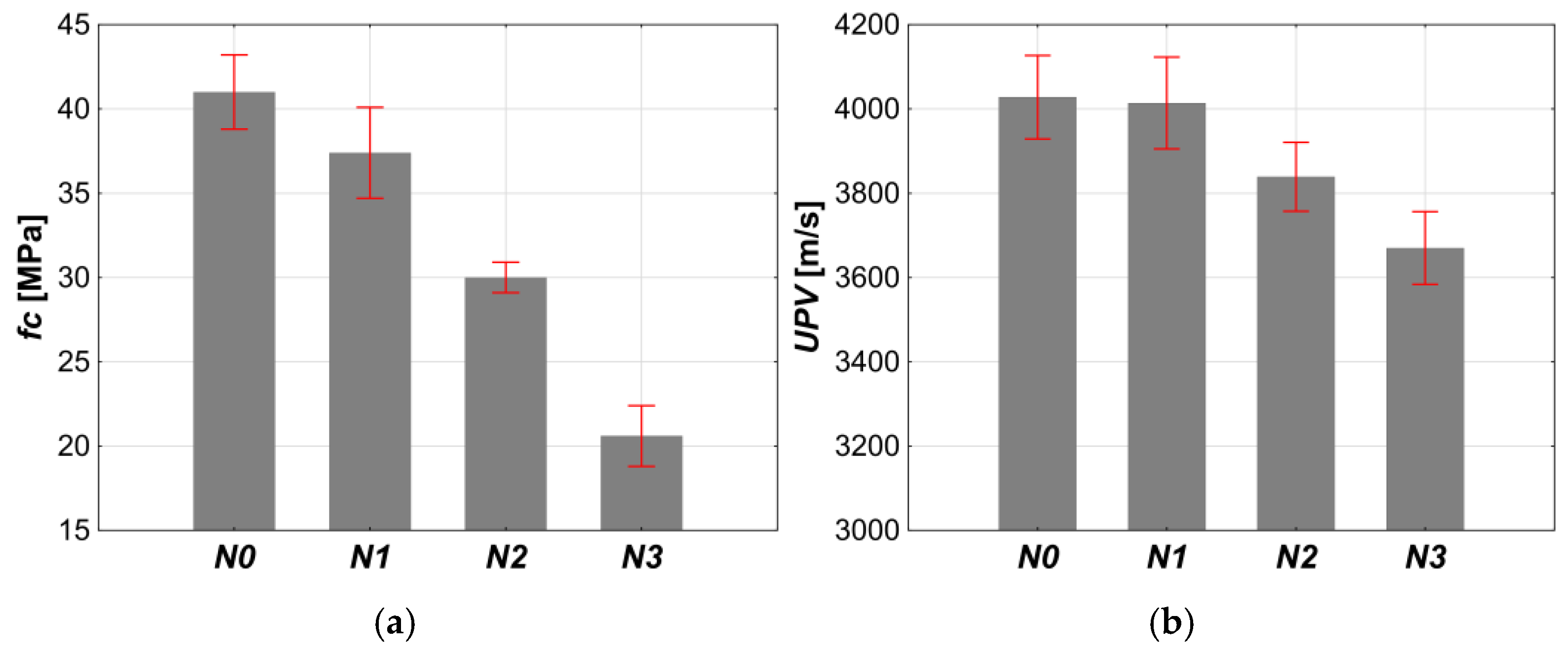
3.1.2. Compressive Strength and Ultrasonic Pulse Velocity of Concrete
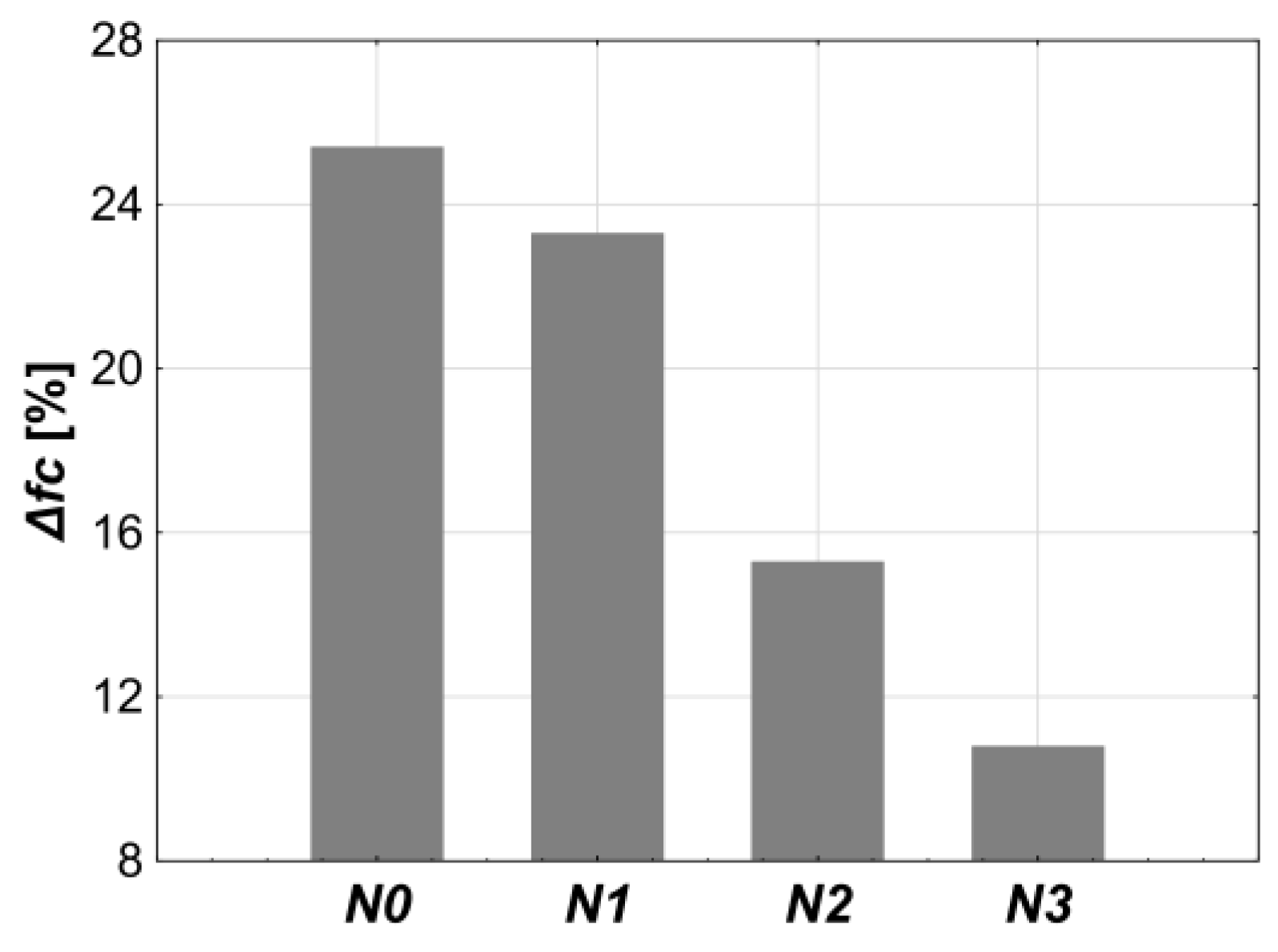
3.1.3. Freeze–Thaw Resistance of Concrete
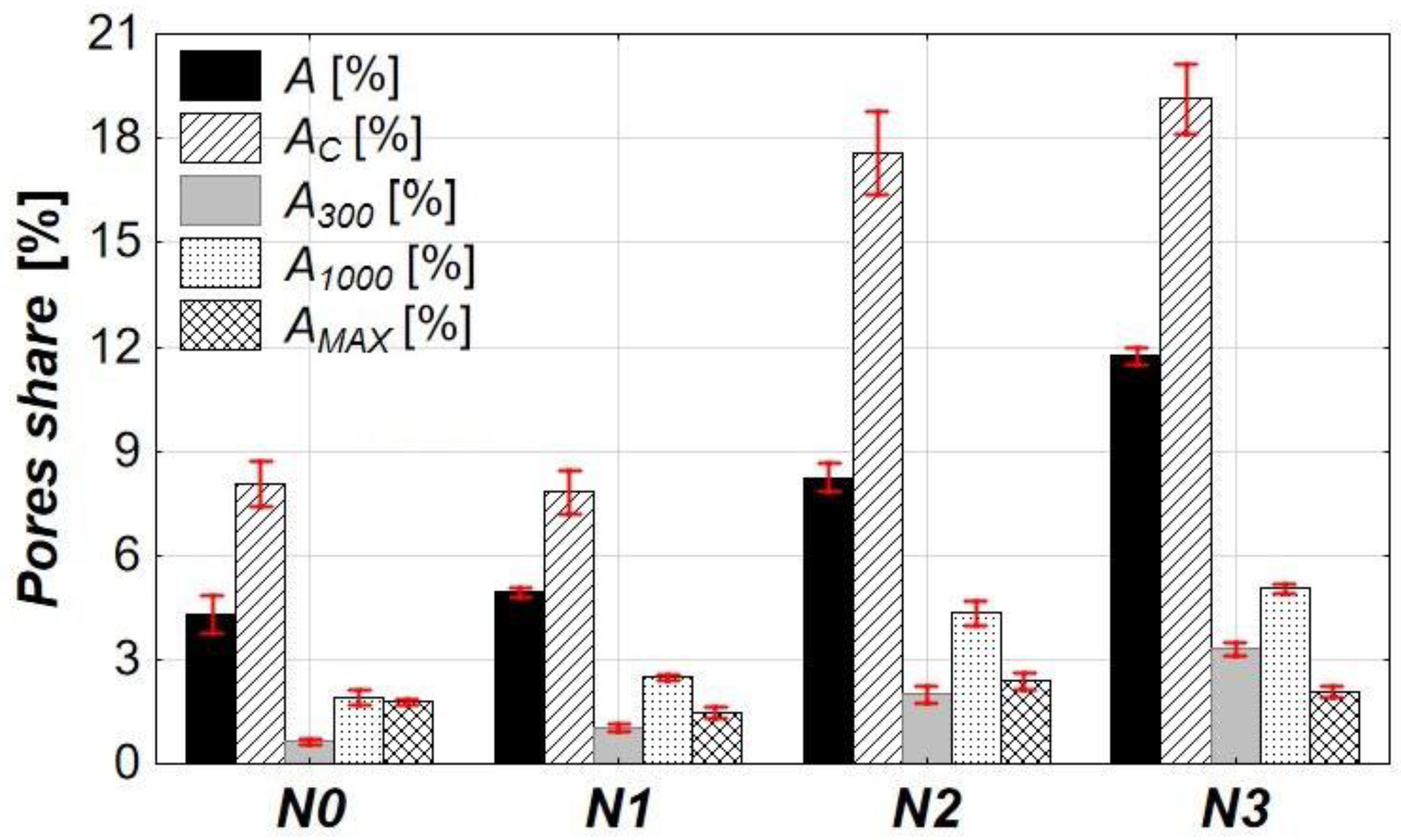
3.1.4. Pore Structure of Concrete
3.2. Analysis of Relations Between the Concrete Properties and the Quantative Parameters of Pore Structure
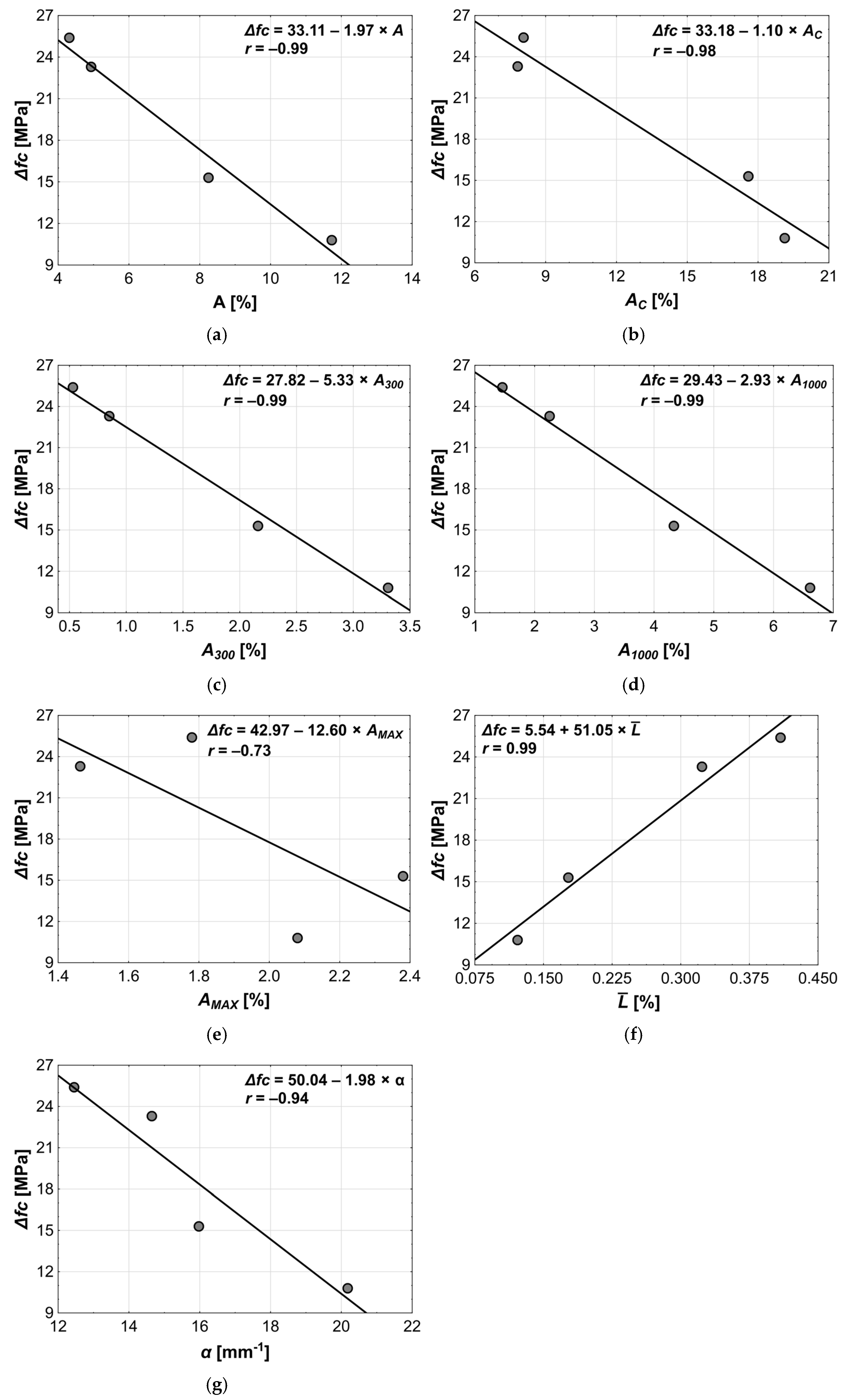
3.2.1. The Influence of the Pore Structure on the Compressive Strength
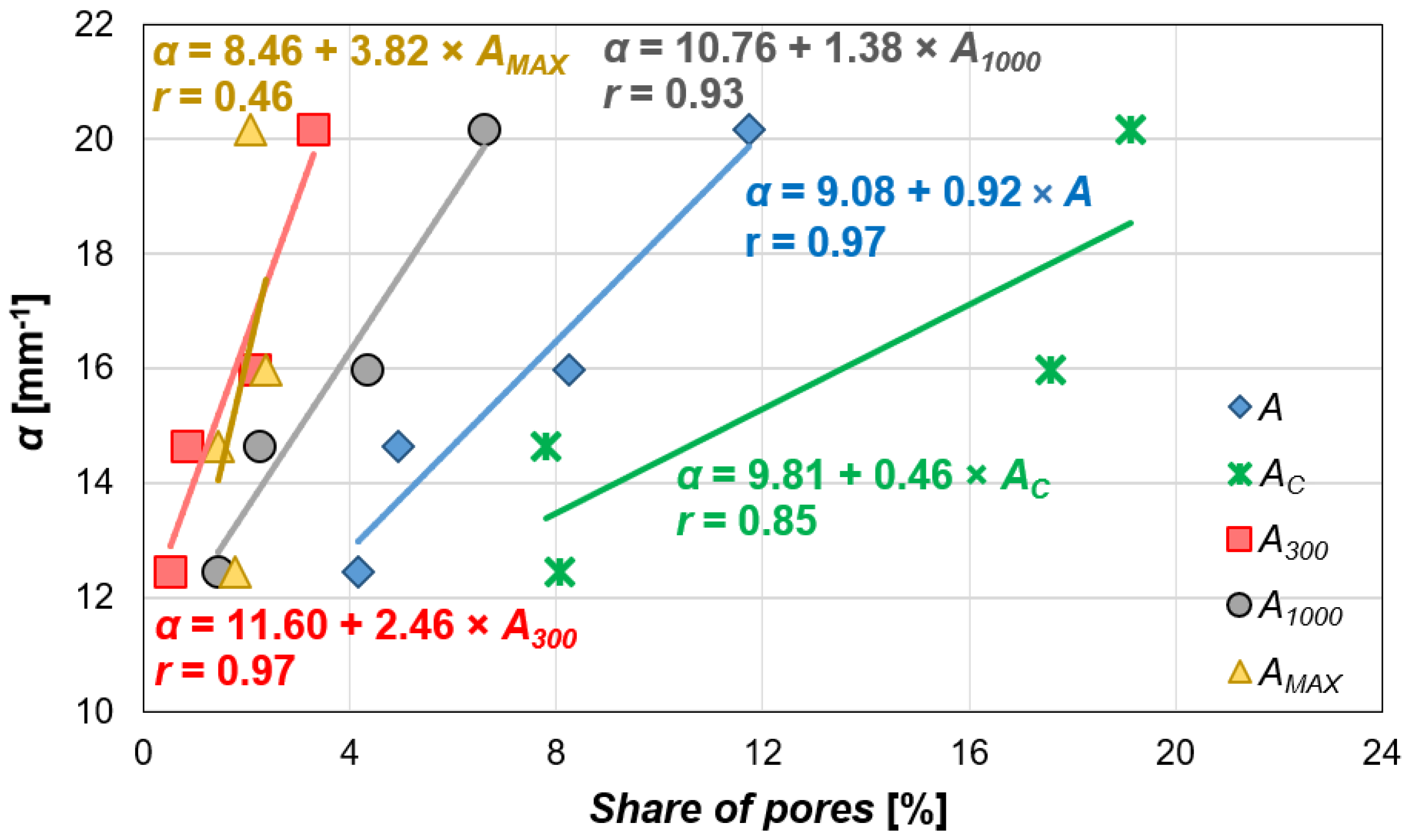
3.2.2. The Influence of the Pore Structure on the Ultrasonic Pulse Velocity
3.2.3. The Influence of the Pore Structure on the Freeze–Thaw Resistance
4. Conclusions
- –
- The image analysis method, supported by custom software, was successfully used to describe the air void structure in concrete.
- –
- The effectiveness of the air-entraining admixture was confirmed. It increased the air content in the fresh concrete mix and improved its workability. The entrained air remained in the hardened concrete as pores—mostly smaller than 1.0 mm. This led to the decrease in the compressive strength and the ultrasonic pulse velocity, but also improved the concrete’s resistance to freeze–thaw cycles.
- –
- The optimal admixture dosage was found to be 0.2% of the cement mass. At this level, the concrete showed the best balance between compressive strength and freeze–thaw resistance, confirmed by both indirect (pore structure) and direct (strength loss after freezing–thawing cycles) methods.
- –
- The ultrasonic pulse velocity proved to be a useful tool for evaluating the air entrainment quality, as it strongly correlates with both compressive strength and pore structure parameters defined in EN 480-11.
- –
- The pore structure parameter that best explains changes in compressive strength is the content of pores between 0.3 and 1.0 mm. The smaller pores—especially those uniformly distributed—are more favorable for concrete performance, whereas an increase in pore diameter reduces concrete’s load-bearing capacity.
- –
- The total pore content is the best predictor of ultrasonic pulse velocity, indicating that for ultrasonic wave propagation, the overall content of air voids in concrete is more important than their size. The wave velocity depends on the material’s elasticity, which in turn is affected by the content of air voids in the concrete. The higher the porosity, the lower the elastic modulus, and consequently, the lower the UPV.
- –
- For the freeze–thaw resistance (measured directly), the most important pore structure parameter is the content of pores smaller than 0.3 mm. This indicates that pores of this size are crucial for maintaining concrete durability under cyclic freezing and thawing conditions. It also confirms the effectiveness of the air-entraining admixture, which introduces air voids into the concrete—specifically those smaller than 0.3 mm.
- –
- The high quality of the regression models developed using stepwise forward selection showed that they can be used to predict compressive strength, ultrasonic pulse velocity, and freeze–thaw resistance based on stereological pore structure analysis.
- –
- The approach used in this study could be the first step toward fully automating the evaluation of freeze–thaw resistance by the image analysis method. The next step may involve applying deep learning algorithms.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Wu, S.; Zhou, J. Influence of Porosity on Compressive and Tensile Strength of Cement Mortar. Constr. Build. Mater. 2013, 40, 869–874. [Google Scholar] [CrossRef]
- Erniati; Tjaronge, M.W.; Zulharnah; Irfan, U.R. Porosity, Pore Size and Compressive Strength of Self Compacting Concrete Using Sea Water. Procedia Eng. 2015, 125, 832–837. [Google Scholar] [CrossRef]
- Lian, C.; Zhuge, Y.; Beecham, S. The relationship between porosity and strength for porous concrete. Constr. Build. Mater. 2011, 25, 4294–4298. [Google Scholar] [CrossRef]
- Naik, T.R. Concrete durability as influenced by density and/or porosity. In Proceedings of the Cement and Concrete Institute of Mexico Symposium: World of Concrete–Mexico, Guadalajara, Mexico, 4–7 June 1997. [Google Scholar]
- Yudenfreund, M.; Hanna, K.M.; Skalny, J.; Odler, I.; Brunauer, S. Hardened Portland cement pastes of low porosity. Part 5: Compressive strength. Cem. Concr. Res. 1972, 2, 731–743. [Google Scholar] [CrossRef]
- Zhao, H.; Xiao, Q.; Huang, D.; Zhang, S. Influence of Pore Structure on Compressive Strength of Cement Mortar. Sci. World J. 2014, 2024, 247058. [Google Scholar] [CrossRef] [PubMed]
- Claisse, P.A.; Cabrera, J.G.; Hunt, D.N. Measurement of porosity as a predictor of the durability performance of concrete with and without condensed silica fume. Adv. Cem. Res. 2001, 13, 165–174. [Google Scholar] [CrossRef]
- Li, Y.; Ma, H.; Wen, L.; Yuan, J.; Zhang, Y.; Li, Y.; Zhou, H.; Chen, J. Influence of Pore Size Distribution on Concrete Cracking with Different AEA Content and Curing Age Using Acoustic Emission and Low-Field NMR. J. Build. Eng. 2022, 58, 105059. [Google Scholar] [CrossRef]
- Sypek, M.; Latawiec, R.; Łaźniewska-Piekarczyk, B.; Pichór, W. Impact of Surfactant and Calcium Sulfate Type on Air-Entraining Effectiveness in Concrete. Materials 2022, 15, 985. [Google Scholar] [CrossRef]
- Talaat, A.; Emad, A.; Tarek, A.; Masbouba, M.; Essam, A.; Kohail, M. Factors Affecting the Results of Concrete Compression Testing: A Review. Ain Shams Eng. J. 2021, 12, 205–221. [Google Scholar] [CrossRef]
- Leventis, A.; Verganelakis, D.A.; Halse, M.R.; Webber, J.B.; Strange, J.H. Capillary Imbibition and Pore Characterisation in Cement Pastes. Transp. Porous Media 2000, 39, 143–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Zhang, R.; Yan, X.; Zhao, Z.; Zhu, Y. Effect of Constrictivity of Gel/Capillary Pores in Concrete on Chloride Ions Migration. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 4201–4213. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; An, M.; Sun, Y.; Yu, Z.; Huang, H. Factors Influencing the Capillary Water Absorption Characteristics of Concrete and Their Relationship to Pore Structure. Appl. Sci. 2022, 12, 2211. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete; Pearson Education Limited: London, UK, 2011. [Google Scholar] [CrossRef]
- Pawlowicz, J. Evaluation of Air Entraining Behaviour in Concrete Using Computer Aided Methods on Hardened Samples. Master’s Thesis, TU Delft University, Delft, The Netherlands, 2019. [Google Scholar]
- Kosmatka, S.H.; Wilson, M.L. Design and Control of Concrete Mixtures, 15th ed.; Engineering Bulletin 001.15; Portland Cement Association: Skokie, IL, USA, 2011. [Google Scholar]
- Lv, D.; Liu, H.; He, F.; Wang, W.; Miao, Q.; Li, H.; Wang, F.; Zhao, J.; Shi, C. Freeze–Thaw Damage Characteristics of Concrete Based on Compressive Mechanical Properties and Acoustic Parameters. Materials 2024, 17, 1010. [Google Scholar] [CrossRef]
- Zhao, Y.; Lian, S.; Bi, J.; Wang, C.; Zheng, K. Study on Freezing-Thawing Damage Mechanism and Evolution Model of Concrete. Theor. Appl. Fract. Mech. 2022, 121, 103439. [Google Scholar] [CrossRef]
- Luo, S.; Bai, T.; Guo, M.; Wei, Y.; Ma, W. Impact of Freeze–Thaw Cycles on the Long-Term Performance of Concrete Pavement and Related Improvement Measures: A Review. Materials 2022, 15, 4568. [Google Scholar] [CrossRef] [PubMed]
- Shang, H.S.; Song, Y.P. Experimental Study of Strength and Deformation of Plain Concrete under Biaxial Compression after Freezing and Thawing Cycles. Cem. Concr. Res. 2006, 36, 1857–1864. [Google Scholar] [CrossRef]
- Kelestemur, O.; Yildiz, S.; Gokcer, B.; Arici, E. Statistical Analysis for Freeze–Thaw Resistance of Cement Mortars Containing Marble Dust and Glass Fiber. Mater. Des. 2014, 60, 548–555. [Google Scholar] [CrossRef]
- Krstic, M.; Davalos, J.F.; Rossi, E.; Figueiredo, S.C.; Copuroglu, O. Freeze–Thaw Resistance and Air-Void Analysis of Concrete with Recycled Glass–Pozzolan Using X-ray Micro-Tomography. Materials 2021, 14, 154. [Google Scholar] [CrossRef]
- Li, G.; Hasholt, M.T.; Jensen, O.M. Air Void Analysis of Hardened Concrete Without Colour Enhancement. In Concrete Durability and Service Life Planning; Kovler, K., Ed.; Springer: Cham, Switzerland, 2020; Volume 26, pp. 79–83. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Kovler, K.; Zhutovsky, S.; Spatari, S.; Jensen, O. (Eds.) Concrete Durability and Service Life Planning. In RILEM Bookseries; Springer: Cham, Switzerland, 2020; Volume 26, pp. 127–134. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, E.; Wang, B.; Li, J.; Yao, T.; Zhang, Z. Effect of Porosity and Pore Size on the Axial Compressive Properties of Recycled Aggregate Concrete. Materials 2025, 18, 2830. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Z.; Zhang, L.; Zhang, J.; Zhang, X.; Zhang, Y.; Zhang, Q. Investigation on the Effect of Entrained Air on Pore Structure in Hardened Mortar and Concrete. Cem. Concr. Res. 2021, 139, 106230. [Google Scholar] [CrossRef]
- He, R.; Lu, N. Hydration, fresh, mechanical, and freeze–thaw properties of cement mortar incorporated with polymeric microspheres. Adv. Compos. Hybrid Mater. 2024, 7, 92. [Google Scholar] [CrossRef]
- Chen, Y.; Al-Neshawy, F.; Punkki, J. Investigation on the Effect of Entrained Air on Pore Structure in Hardened Concrete Using MIP. Constr. Build. Mater. 2021, 295, 123583. [Google Scholar] [CrossRef]
- Gagné, R. Science and Technology of Concrete Admixtures; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Szklarzyńska, M.; Gaudy, J.; Wojtysiak, Z. Air void characteristic in hardened, air entrained construction concrete in terms of specimens compacting method. In Proceedings of the XI Konferencja Dni Betonu, Wisła, Poland, 11–13 October 2021; Stowarzyszenie Producentów Cementu: Wisła, Poland, 2021; pp. 1117–1134. [Google Scholar]
- Schwoon, O. A New Efficient and Safe Admixture for Freeze/Thaw Resistant Concrete. In High Tech Concrete: Where Technology and Engineering Meet; Hordijk, D.A., Luković, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 2162–2168. [Google Scholar] [CrossRef]
- Guo, L.; Liu, J.; Zhou, M.; An, S. Effect of Sulfate Attack on Geopolymer Mortars at Early Ages of Exposure. Constr. Build. Mater. 2021, 274, 121835. [Google Scholar] [CrossRef]
- Li, W.; Pour-Ghaz, M.; Trtik, P.; Wyrzykowski, M.; Münch, B.; Lura, P.; Weiss, W.J. Using Neutron Radiography to Assess Water Absorption in Air Entrained Mortar. Constr. Build. Mater. 2016, 110, 98–105. [Google Scholar] [CrossRef]
- Zhang, P.; Wittmann, F.H.; Vogel, M.; Müller, H.S.; Zhao, T. Influence of Freeze-Thaw Cycles on Capillary Absorption and Chloride Penetration into Concrete. Cem. Concr. Res. 2017, 100, 60–67. [Google Scholar] [CrossRef]
- Nematzadeh, A.; Aytekin, B.; Mardani-Aghabaglou, A. Effect of Mineral Additives and Permeability Reducing Admixtures Having Different Action Mechanisms on Mechanical and Durability Performance of Cementitious Systems. Front. Struct. Civ. Eng. 2021, 15, 1277–1291. [Google Scholar] [CrossRef]
- Zhang, H. Concrete. In Building Materials in Civil Engineering; Zhang, H., Ed.; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Cambridge, UK, 2011; pp. 81–423. [Google Scholar] [CrossRef]
- Blikharskyy, Z.; Markiv, T.; Sobol, K.; Turba, Y.; Selejdak, J. The Effect of Air-Entraining Agent on the Properties of Mortars. Arch. Civ. Eng. 2023, 69, 147–156. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete, 5th ed.; Pearson Education: Harlow, UK, 2011. [Google Scholar]
- Güleryüz, E.; Özen, S.; Mardani-Aghabaglou, A. Effect of Utilization of Mineral Admixture on the Fresh and Hardened Properties of Air-Entrained Cement Mortars. Pamukkale Univ. J. Eng. Sci. 2020, 26, 1053–1061. [Google Scholar] [CrossRef]
- Abed, A.A.; Sołowski, W.T. Estimation of Water Retention Behaviour of Bentonite Based on Pore Structure Analysis. Constr. Build. Mater. 2021, 300, 123441. [Google Scholar] [CrossRef]
- Liu, L.; He, Z.; Cai, X.; Fu, S. Application of Low-Field NMR to the Pore Structure of Concrete. Appl. Magn. Reson. 2020, 52, 15–31. [Google Scholar] [CrossRef]
- Topcu, I.B.; Atesin, Ö.; Uygunoglu, T. Effect of High Dosage Air-Entraining Admixture Usage on Micro Concrete Properties. Int. J. Adv. Technol. Eng. Sci. 2017, 2, 1–11. [Google Scholar]
- Bednarek, M.; Grzybowski, M. Influence of Air-Entraining Admixture on Selected Properties of Concrete. MATEC Web Conf. 2018, 163, 05002. [Google Scholar]
- Łaźniewska-Piekarczyk, B. The Methodology for Assessing the Impact of New Generation Superplasticizers on Air Content in Self-Compacting Concrete. Constr. Build. Mater. 2014, 53, 488–502. [Google Scholar] [CrossRef]
- Yang, W. Is Air-Entraining Agent a Panacea for Solving Frost Resistance Problem? In The Issues and Discussion of Modern Concrete Science; Tsinghua University Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2015; pp. 53–68. [Google Scholar] [CrossRef]
- Fan, Y.F.; Luan, H.Y. Pore structure in concrete exposed to acid deposit. Constr. Build. Mater. 2013, 49, 407–416. [Google Scholar] [CrossRef]
- Kim, H.-T.; Razakamandimby, D.F.T.; Szilágyi, V.; Kis, Z.; Szentmiklósi, L.; Glinicki, M.A.; Park, K. Reconstruction of Concrete Microstructure Using Complementarity of X-ray and Neutron Tomography. Cem. Concr. Res. 2021, 148, 106540. [Google Scholar] [CrossRef]
- Han, J.; Wang, K.; Wang, X.; Monteiro, P.J.M. 2D image analysis method for evaluating coarse aggregate characteristic and distribution in concrete. Constr. Build. Mater. 2016, 127, 30–42. [Google Scholar] [CrossRef]
- Wawrzenczyk, J.; Kozak, W. A method of analyzing the porous microstructure in air-entrained concrete on the basis on 2D image analysis. Proc. Eng. 2015, 108, 102–107. [Google Scholar] [CrossRef]
- Ojala, T.; Chen, Y.; Punkki, J.; Al-Neshawy, F. Characteristics of entrained air voids in hardened concrete with the method of digital image analysis coupled with Schwartz-Saltykov conversion. Materials 2021, 14, 2439. [Google Scholar] [CrossRef]
- Kuziak, J.; Zalegowski, K.; Jackiewicz-Rek, J.; Stanisławek, E. Influence of the Type of Cement on the Action of the Admixture Containing Aluminum Powder. Materials 2021, 14, 2927. [Google Scholar] [CrossRef]
- Zalegowski, K.; Piotrowski, T.; Garbacz, A. Influence of Polymer Modification on the Microstructure of Shielding Concrete. Materials 2020, 13, 498. [Google Scholar] [CrossRef]
- Pourebrahimi, M.; Shahhosseini, V.; Ramezanianpour, A.A. Innovative Sieve Simulation and Microstructure Image Analysis Techniques for Estimation of Aggregate Size Distribution in Hardened Concrete. Constr. Build. Mater. 2023, 384, 131456. [Google Scholar] [CrossRef]
- Ye, G.; Hu, J.; van Breugel, K.; Stroeven, P. Characterization of the Development of Microstructure and Porosity of Cement-Based Materials by Numerical Simulation and ESEM Image Analysis. Mater. Struct. 2002, 35, 603–613. [Google Scholar] [CrossRef]
- Imtiaz, T.; Ahmed, A.; Hossain, M.S.; Faysal, M. Microstructure Analysis and Strength Characterization of Recycled Base and Sub-Base Materials Using Scanning Electron Microscope. Infrastructures 2020, 5, 70. [Google Scholar] [CrossRef]
- Bangaru, S.S.; Wang, C.; Zhou, X.; Hassan, M. Scanning Electron Microscopy (SEM) Image Segmentation for Microstructure Analysis of Concrete Using U-Net Convolutional Neural Network. Autom. Constr. 2022, 144, 104602. [Google Scholar] [CrossRef]
- Yuan, Y.; He, Z.; Niu, K.; Tian, B.; Chen, L.; Bai, W.; Zheng, S.; Yu, G. Analyzing Pore Evolution Characteristics in Cementitious Materials Using a Plane Distribution Model. Coatings 2023, 13, 2023. [Google Scholar] [CrossRef]
- Dequiedt, A.-S.; Coster, M.; Chermant, L.; Chermant, J.-L. Study of Phase Dispersion in Concrete by Image Analysis. Cem. Concr. Compos. 2001, 23, 215–226. [Google Scholar] [CrossRef]
- Xie, X.; Yu, Z.; Zhang, Y.; Wang, J.; Wang, X. Quick Image Analysis of Concrete Pore Structure Based on Deep Learning. Constr. Build. Mater. 2019, 211, 71–83. [Google Scholar] [CrossRef]
- Glinicki, M.A.; Litorowicz, A. Diagnosis of cracks in cement matrix composites using computer image analysis. Roads Bridges 2007, 3, 45–77. (In Polish) [Google Scholar]
- Ringot, E.; Bascoul, A. About the analysis of microcracking in concrete. Cem. Concr. Compos. 2001, 23, 261–266. [Google Scholar] [CrossRef]
- Dung, C.V.; Le, A.D. Autonomous Concrete Crack Detection Using Deep Fully Convolutional Neural Network. Autom. Constr. 2018, 99, 52–58. [Google Scholar] [CrossRef]
- Gonthina, M.; Chamata, R.; Duppalapudi, J.; Lute, V. Deep CNN-Based Concrete Cracks Identification and Quantification Using Image Processing Techniques. Asian J. Civ. Eng. 2023, 24, 727–740. [Google Scholar] [CrossRef]
- Avendaño, J.C.; Leander, J.; Karoumi, R. Image-Based Concrete Crack Detection Method Using the Median Absolute Deviation. Sensors 2024, 24, 2736. [Google Scholar] [CrossRef] [PubMed]
- Mertens, G.; Elsen, J. Use of Computer Assisted Image Analysis for the Determination of the Grain-Size Distribution of Sands Used in Mortars. Cem. Concr. Res. 2006, 36, 1453–1459. [Google Scholar] [CrossRef]
- Qian, H.; Li, Y.; Yang, J.; Xie, L.; Tan, K.H. Segmentation and Analysis of Cement Particles in Cement Paste with Deep Learning. Cem. Concr. Compos. 2023, 136, 104819. [Google Scholar] [CrossRef]
- Song, Y.; Huang, Z.; Lange, D.A. Deep Learning-Based Automated Image Segmentation for Concrete Petrographic Analysis. Cem. Concr. Res. 2020, 135, 106118. [Google Scholar] [CrossRef]
- EN 480-11:2008; Admixtures for Concrete, Mortar and Grout–Test Methods–Part 11: Determination of Air Void Characteristics in Hardened Concrete. European Committee for Standardization (CEN): Brussels, Belgium, 2008.
- Newlon, H.; Mitchell, T.M. Freezing and Thawing. In Significance of Test and Properties of Concrete and Concrete-Making Materials; Klieger, P., Lamond, J.F., Eds.; ASTM Publication: West Conshohocken, PA, USA, 1994. [Google Scholar]
- ACI Committee 201; Guide to durable concrete. ACI J. 1979, 74, 573–582.
- Material Specification for Concrete-Materials and Production, Metric; Ontario Provincial Standard Specification: Brampton, ON, Canada, 2014; OPSS.PROV 1350.
- Glinicki, M.A.; Jaskulski, R.; Dąbrowski, M. Design principles and testing of internal frost resistance of concrete for road structures–critical review. Roads Bridges -Drog. I Mosty 2016, 15, 21–43. [Google Scholar] [CrossRef]
- Wawrzenczyk, J.; Molendowska, A.; Kłak, A. Relationship between porosity characteristics and concrete frost durability in bridges. Struct. Environ. 2012, 4, 28–34. [Google Scholar]
- Glinicki, M.A. European requirements for air-entrained concrete in the XF class environment. Drogownictwo 2005, 3, 86–88. (In Polish) [Google Scholar]
- Wawrzeńczyk, J.; Kowalczyk, H. Simplified Method of Estimating the A300 Micropore Content in Air-Entrained Concrete. Materials 2023, 16, 2752. [Google Scholar] [CrossRef]
- Molendowska, A.; Wawrzeńczyk, J.; Kowalczyk, H. Development of the Measuring Techniques for Estimating the Air Void System Parameters in Concrete Using 2D Analysis Method. Materials 2020, 13, 428. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wei, D.; Zhou, Y.; Huang, Y.; Tie, B.; Lei, M. Mechanisms of Arsenate and Cadmium Co-immobilized on Ferrihydrite Inferred from Ternary Surface Configuration. Chem. Eng. J. 2021, 424, 130410. [Google Scholar] [CrossRef]
- Zalegowski, K.; Piotrowski, T.; Garbacz, A.; Adamczewski, G. Relation between microstructure, technical properties and neutron radiation shielding efficiency of concrete. Constr. Build. Mater. 2020, 235, 117389. [Google Scholar] [CrossRef]
- Zalegowski, K.; Garbacz, A. Analiza ilościowa mikrostruktury betonu (The quantitative image analysis of concrete microstructure). Inżynieria I Bud. 2016, 75, 417–424. [Google Scholar]
- Fonesca, P.C.; Scherer, G.W. An image analysis procedure to quantify the air void system of mortar and concrete. Mater. Struct. 2015, 48, 3087–3098. [Google Scholar] [CrossRef]
- Michałek, J.; Sobótka, M. Assessment of Internal Structure of Spun Concrete Using Image Analysis and Physicochemical Methods. Materials 2020, 13, 3987. [Google Scholar] [CrossRef]
- PN-B-06265:2018-10/Ap1:2019-05; Concrete–Specification, Performance, Production and Conformity–NATIONAL Annex to PN-EN 206+A1:2016-12. Polish Committee for Standardization: Warsaw, Poland, 2019.
- EN 206+A2:2021; Concrete–Specification, Performance, Production and Conformity. European Committee for Standardization: Brussels, Belgium, 2021.
- Zalegowski, K. Ultrasonic Quality Assessment of Polymer-Cement Concrete with PET Waste as the Aggregate. Arch. Civ. Eng. 2018, 64, 67–77. [Google Scholar] [CrossRef]
- Moura, M.A.d.N.; Moreno Junior, A.L.; Ferreira, G.C.d.S. Ultrasonic Testing on Evaluation of Concrete Residual Compressive Strength: A Review. Constr. Build. Mater. 2023, 373, 130887. [Google Scholar] [CrossRef]
- Lemus, R.M.; Ruiz, R.O.; Castellanos, E.N. Correlation between Compressive Strength of Concrete and Ultrasonic Pulse Velocity: A Case of Study and a New Correlation Method. Constr. Build. Mater. 2023, 369, 130569. [Google Scholar] [CrossRef]
- Rao, S.K.; Sravana, P.; Rao, T.C. Relationship between Ultrasonic Pulse Velocity and Compressive Strength for Roller Compacted Concrete Containing GGBS. Int. J. Appl. Eng. Res. 2016, 11, 2077–2084. [Google Scholar]
- Lencis, U.; Udris, A.; Kara De Maeijer, P.; Korjakins, A. Methodology for Determining the Correct Ultrasonic Pulse Velocity in Concrete. Buildings 2024, 14, 720. [Google Scholar] [CrossRef]
- Hasannejad, M.; Berenjian, J.; Pouraminian, M.; Larijani, A.S. Studying of microstructure, interface transition zone and ultrasonic wave velocity of high strength concrete by different aggregates. J. Build. Pathol. Rehabil. 2022, 7, 9. [Google Scholar] [CrossRef]
- Chryso Official Website. Available online: https://www.chryso.pl (accessed on 20 February 2025).
- EN 12350-2:2019; Testing Fresh Concrete–Part 2: Slump Test. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 12350-7:2019; Testing Fresh Concrete–Part 7: Air Content–Pressure Method. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 12390-2:2019; Testing Hardened Concrete–Part 2: Making and Curing Specimens for Strength Tests. European Committee for Standardization: Brussels, Belgium, 2019.
- EN 12504-4:2004; Testing Concrete in Structures–Part 4: Determination of Ultrasonic Pulse Velocity. European Committee for Standardization: Brussels, Belgium, 2004.
- Gundersen, H.J.G.; Jensen, E.B. The efficiency of systematic sampling in stereology and its prediction. J. Microsc. 1987, 147, 229–263. [Google Scholar] [CrossRef]
- Saltykov, S.A. Stereological Parameters of the Structure and Properties of Alloys. Metall. Sci. Heat Treat. 1972, 14, 1082–1085. [Google Scholar] [CrossRef]
- Metcalfe, A.; Green, D.; Greenfield, T.; Mansor, M.; Smith, A.; Tuke, J. Statistics in Engineering: With Examples in MATLAB® and R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Puthipad, N.; Suchi, M.; Rath, S.; Attachaiyawuth, A. Enhanced entrainment of fine air bubbles in self-compacting concrete with high volume of fly ash using defoaming agent for improved entrained air stability and higher aggregate content. Constr. Build. Mater. 2017, 144, 1–12. [Google Scholar] [CrossRef]
- Chia, K.H.; Zhang, M.H. Workability of air-entrained lightweight concrete from rheology perspective. Mag. Concr. Res. 2007, 59, 367–375. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI PRC-212.3-16: Report on Chemical Admixtures for Concrete; ACI: Farmington Hills, MI, USA, 2016. [Google Scholar]
- Al-Jabari, M. 1-Introduction to Concrete Chemistry. In Integral Waterproofing of Concrete Structures Advanced Protection Technologies of Concrete by Pore Blocking and Lining; Woodhead Publishing: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, X.; Zhang, Y. Effect of the Entrained Air Void on Strength and Interfacial Transition Zone of Air-Entrained Mortar. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2015, 30, 1020–1028. [Google Scholar] [CrossRef]
- Emamian, S.A.; Eskandari-Naddaf, H. Effect of Porosity on Predicting Compressive and Flexural Strength of Cement Mortar Containing Micro and Nano-Silica by ANN and GEP. Constr. Build. Mater. 2019, 218, 8–27. [Google Scholar] [CrossRef]
- Sánchez-Mendieta, C.; Galán-Díaz, J.J.; Martinez-Lage, I. Relationships between Density, Porosity, Compressive Strength and Permeability in Porous Concretes: Optimization of Properties through Control of the Water-Cement Ratio and Aggregate Type. J. Build. Eng. 2024, 97, 110858. [Google Scholar] [CrossRef]
- Soutsos, M.N.; Domone, P.L.; Halliwell, S.M. Ultrasonic Pulse Velocity Evaluation of Cementitious Materials. In Non-Destructive Testing Methods and New Applications; Eissa, M.E., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Benaicha, M.; Jalbaud, O.; Burtschell, Y. Ultrasonic Characterization and Mechanical Performance of Self-Compacting Concrete in Fresh and Hardened States. Ultrasonics 2025, 152, 107657. [Google Scholar] [CrossRef] [PubMed]
- Benaicha, M.; Jalbaud, O.; Hafidi Alaoui, A.; Burtschell, Y. Porosity Effects on Rheological and Mechanical Behavior of Self-Compacting Concrete. J. Build. Eng. 2022, 48, 103964. [Google Scholar] [CrossRef]
- Li, M.; Lai, Y.; Ma, D.; Wang, J.; Xu, L.; Gao, Z.; Liu, Y.; Li, L.; Guo, Y.; Zheng, L.; et al. Influence of Combined Air-Entraining Superplasticizer and Surface Treatments on Airport Pavement Concrete against Salt Freezing. Coatings 2023, 13, 372. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Z.; Yang, Y. Study of the Air-Entraining Behavior Based on the Interactions between Cement Particles and Selected Cationic, Anionic and Nonionic Surfactants. Materials 2020, 13, 3514. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Zhang, Y.; Wang, Y.; Zhang, Y.; Wang, Y. The Effectiveness of Different Additives on Concrete’s Freeze–Thaw Resistance. Materials 2023, 18, 978. [Google Scholar] [CrossRef]
- Góra, J.; Grzegorczyk-Frańczak, M. Frost Resistance of Concretes with Low-Clinker Cements Depending on Curing Time. Adv. Sci. Technol. Res. J. 2024, 18, 406–421. [Google Scholar] [CrossRef]
- Vu, V.H.; Tran, B.V.; Hoang, V.H.; Nguyen, T.H.G. The Effect of Porosity on the Elastic Modulus and Strength of Pervious Concrete. In Modern Mechanics and Applications; Tien Khiem, N., Van Lien, T., Xuan Hung, N., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Kim, W.; Jeong, K.; Choi, H.; Lee, T. Correlation analysis of ultrasonic pulse velocity and mechanical properties of normal aggregate and lightweight aggregate concretes in 30–60 MPa range. Materials 2022, 15, 2952. [Google Scholar] [CrossRef]









| Characteristic | Content [%] |
|---|---|
| Form | Liquid |
| Color | Straw yellow |
| Density | 1.003 ± 0.01 kg/dm3 |
| pH | 7 ± 1 |
| Chloride ion content | ≤0.1% |
| Alkali content | ≤1.0% |
| Symbol | Ingredients | |||
|---|---|---|---|---|
| Cement [kg] | Water [kg] | Aggregate [kg] | Air-Entering Admixture [% of Cement Mass] | |
| N0 | 320 | 177 | 1905 | 0.00 |
| N1 | 0.04 | |||
| N2 | 0.20 | |||
| N3 | 1.50 | |||
| Class | Slump Flow [mm] |
|---|---|
| S1 | 10–40 |
| S2 | 50–90 |
| S3 | 100–150 |
| S4 | 160–210 |
| S5 | ≥220 |
| Parameter | Definition |
|---|---|
| AA | Surface area of objects related to an image area |
| LA | Line length related to an image area |
| NA | Number of objects related to an image area |
| VV | Volume fraction of the selected objects in a volume unit of a material |
| SV | Surface area of selected objects in a volume unit of a material |
| LV | Line length in a volume unit of a material |
| NV | Number of elected objects in a volume of a material |
| Parameter | Short Description |
|---|---|
| A | Volume fraction of pores across full range of pore sizes |
| A300 | Volume fraction of pores of sizes below 0.3 mm |
| α | Specific surface area of pores across full range of pore sizes |
| Average maximum distance from any point in cement paste to edge of nearest pore | |
| A1000 | Volume fraction of pores of sizes between 0.3 mm and 1.0 mm |
| AMAX | Volume fraction of pores of sizes above 1.0 mm |
| AC | Volume fraction of pores across full range of pore sizes, excluding volume of coarse aggregate |
| Test | Sample Size (mm3) | No. of Samples |
|---|---|---|
| Freeze–thaw resistance | 100 × 100 × 100 | 12 |
| Compressive strength | 100 × 100 × 100 | 3 |
| Ultrasonic pulse velocity | 100 × 100 × 100 | 3 |
| Pore structure, i.e., air contents, specific surface area, spacing factor | 75 × 75 × 10 | 3 |
| Sample | AEA [%] | AC [%] | ST [mm] |
|---|---|---|---|
| N0 | 0.00 | 2.6 | 60 |
| N1 | 0.04 | 2.9 | 90 |
| N2 | 0.20 | 5.9 | 180 |
| N3 | 1.50 | 9.4 | 210 |
| Sample | AEA [%] | fc [MPa] | UPV [m/s] |
|---|---|---|---|
| N0 | 0.00 | 41.0 ± 2.2 | 4052 ± 48 |
| N1 | 0.04 | 37.4 ± 2.7 | 4043 ± 59 |
| N2 | 0.20 | 30.0 ± 0.9 | 3916 ± 86 |
| N3 | 1.50 | 20.6 ± 1.8 | 3735 ± 76 |
| Sample | AEA [%] | Δm [%] | Δfc [%] |
|---|---|---|---|
| N0 | 0.00 | 0.2 | 25.4 |
| N1 | 0.04 | 0.1 | 23.5 |
| N2 | 0.20 | 0.1 | 15.3 |
| N3 | 1.50 | 0.3 | 10.8 |
| Sample | AEA [%] | A [%] | AC [%] | A300 [%] | A1000 [%] | AMAX [%] | α [mm−1] | [mm] |
|---|---|---|---|---|---|---|---|---|
| N0 | 0.00 | 4.32 ± 0.54 | 8.06 ± 0.67 | 0.53 ± 0.10 | 1.46 ± 0.22 | 1.78 ± 0.09 | 12.45 ± 0.53 | 0.41 ± 0.02 |
| N1 | 0.04 | 4.93 ± 0.14 | 7.81 ± 0.63 | 0.85 ± 0.12 | 2.50 ± 0.08 | 1.46 ± 0.16 | 14.65 ± 0.98 | 0.32 ± 0.05 |
| N2 | 0.20 | 8.24 ± 0.39 | 16.59 ± 1.21 | 2.16 ± 0.25 | 4.33 ± 0.34 | 2.38 ± 0.18 | 15.97 ± 0.47 | 0.18 ± 0.02 |
| N3 | 1.50 | 11.73 ± 0.24 | 19.13 ± 1.01 | 3.31 ± 0.21 | 5.04 ± 0.15 | 2.08 ± 0.24 | 22.45 ± 0.97 | 0.12 ± 0.01 |
| N = 4 | Dependent variable—fc R = 0.9994; p < 0.0006; SEE = 0.3901 fc = 46.55 − 1.00 × A1000 | ||||
| β | SD β | B | SD B | p | |
| A1000 | −0.9994 | 0.0249 | −3.9041 | 0.0976 | <0.0001 |
| Constant | 46.5492 | 0.4072 | 0.0006 | ||
| N = 4 | Dependent variable—fc R = 0.9999; p < 0.0001; SEE = 0.0022 fc = 47.93 − 6.37 × A1000 + 4.47 × A300 | ||||
| β | SD β | B | SD B | p | |
| A1000 | −1.6304 | 0.0026 | −6.3691 | 0.0100 | <0.0001 |
| A300 | 0.6319 | 0.0026 | 4.4664 | 0.0181 | 0.0026 |
| Constant | 47.9330 | 0.0061 | <0.0001 | ||
| N = 4 | Dependent variable—UPV R = 0.9946; p < 0.0054; SEE = 18.8740 UPV = 25.13 − 3.19 × A | ||||
| β | SD β | B | SD B | p | |
| A | −0.9946 | A | −0.9946 | A | −0.9946 |
| Constant | Constant | Constant | |||
| N = 4 | Dependent variable—UPV R = 0.9999; p < 0.0027; SEE = 0.6939 UPV = 4453.98 − 117.89 × A + 200.75 × A300 | ||||
| β | SD β | B | SD B | p | |
| A | −2.7220 | A | −2.7220 | A | −2.7220 |
| A300 | 1.7305 | A300 | 1.7305 | A300 | 1.7305 |
| Constant | Constant | Constant | |||
| N = 4 | Dependent variable—Δfc R = 0.9945; p < 0.0055; SEE = 0.8779 Δfc = 27.81 − 5.33 × A300 | ||||
| β | SD β | B | SD B | p | |
| A300 | −0.9945 | A300 | −0.9945 | A300 | −0.9945 |
| Constant | 27.8149 | 0.8094 | 0.0008 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalegowski, K. Pore Structure Influence on Properties of Air-Entrained Concrete. Materials 2025, 18, 2885. https://doi.org/10.3390/ma18122885
Zalegowski K. Pore Structure Influence on Properties of Air-Entrained Concrete. Materials. 2025; 18(12):2885. https://doi.org/10.3390/ma18122885
Chicago/Turabian StyleZalegowski, Kamil. 2025. "Pore Structure Influence on Properties of Air-Entrained Concrete" Materials 18, no. 12: 2885. https://doi.org/10.3390/ma18122885
APA StyleZalegowski, K. (2025). Pore Structure Influence on Properties of Air-Entrained Concrete. Materials, 18(12), 2885. https://doi.org/10.3390/ma18122885






