Analysis of Key Material Parameters of Evaporator Wicks and Working Fluids for a Loop Heat Pipe Operating in the Temperature Range of 500–700 K
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
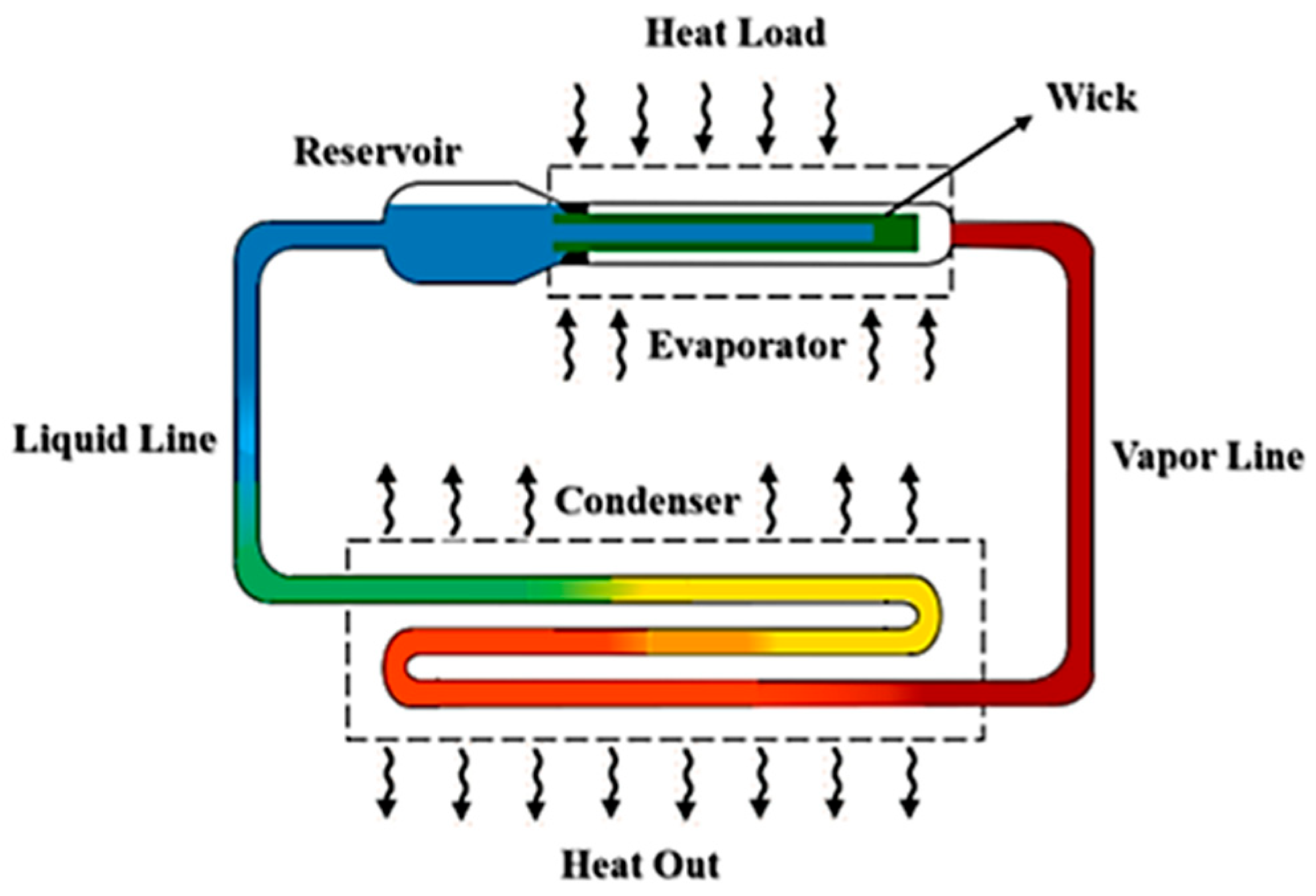
2.2. Methods
3. Results and Discussion
- The higher the porosity of the wick, the wider the temperature range for the criterion and the lower the pressure drop value;
- The bigger the size of the pore, the higher the pressure drop maintaining the criterion;
- The bigger the area of the wick, the wider the temperature range for the criterion and the lower the pressure drop value;
- The thicker the wick, the wider the temperature range for the criterion and the lower the pressure drop value.
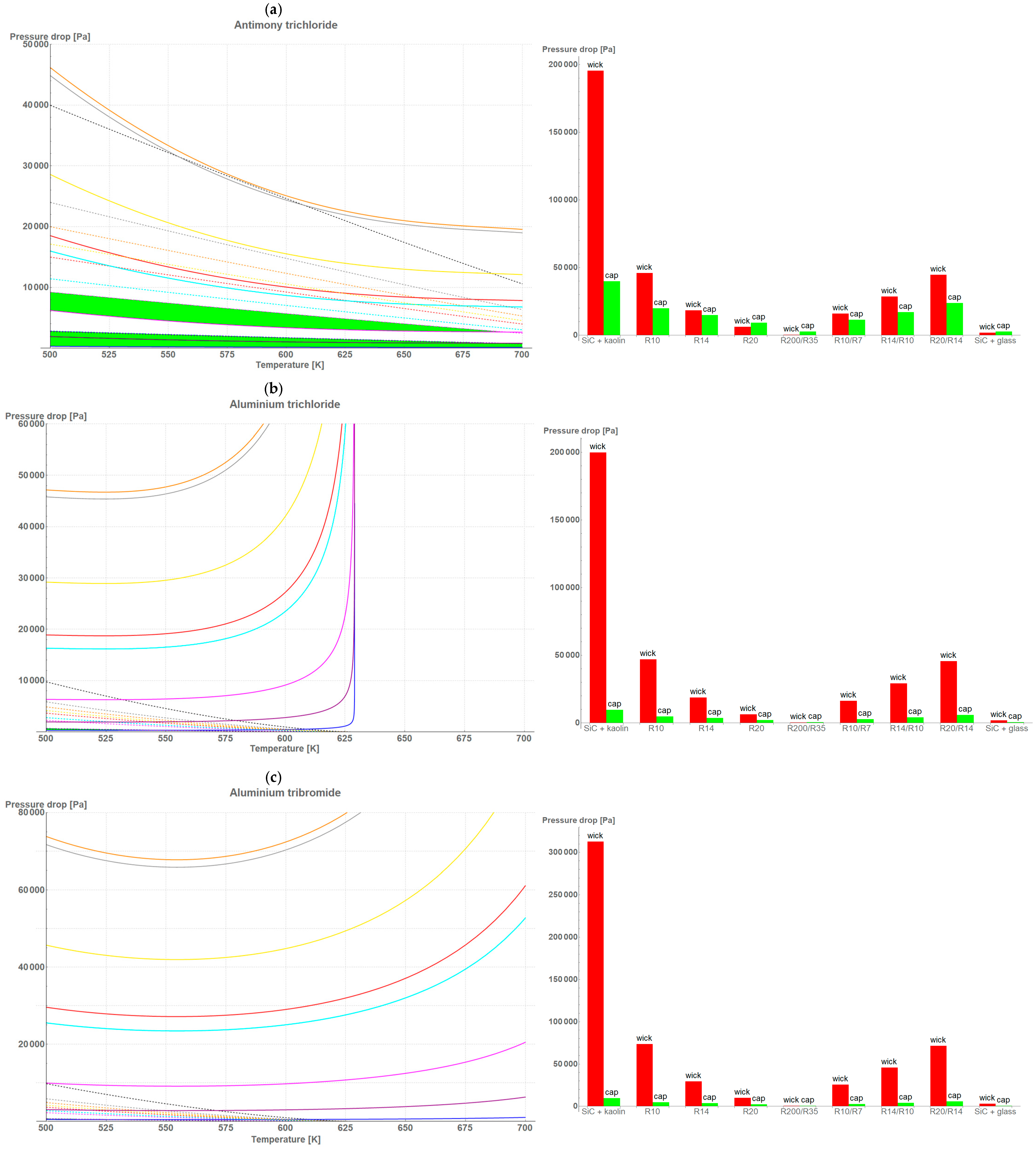

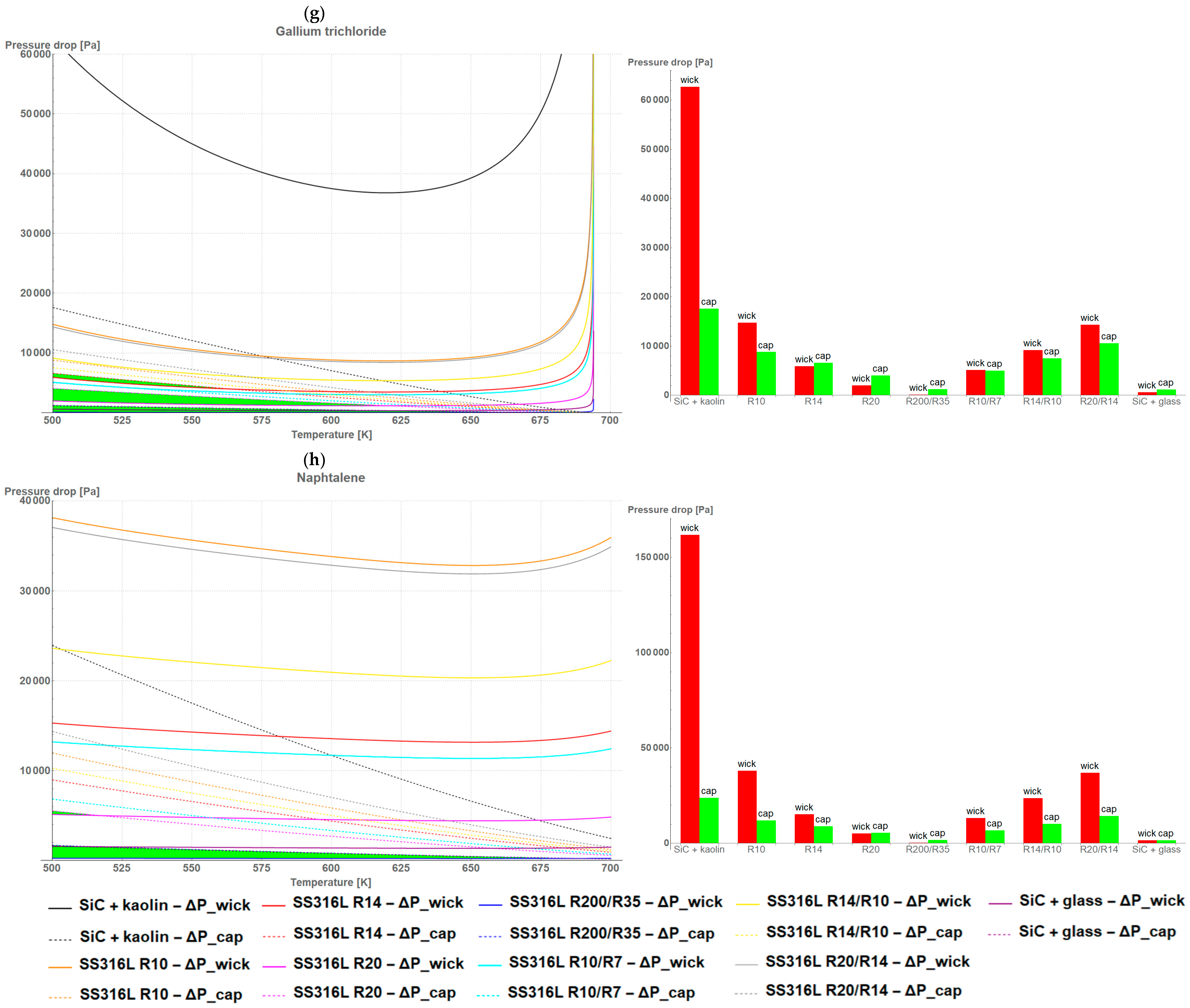
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| cap | capillary |
| crit | critical |
| F-LHP | flat-loop heat pipe |
| LHP | loop heat pipe |
| max | maximum |
| SS316L | type 316L stainless steel |
References
- Szymanski, P.; Law, R.; MᶜGlen, R.J.; Reay, D.A. Recent Advances in Loop Heat Pipes with Flat Evaporator. Entropy 2021, 23, 1374, Erratum in Entropy 2022, 24, 162. [Google Scholar] [CrossRef] [PubMed]
- Anderson, W.G.; Bland, J.J.; Fershtater, Y.; Goncharov, K.A.; Nikitkin, M.; Juhasz, A. High-temperature loop heat pipes. In Proceedings of the International Energy Conversion Engineering Conference (IECEC AP–18), Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Anderson, W.G.; Bienert, W. Loop heat pipe radiator trade study for the 300–550 K temperature range. AIP Conf. Proc. 2005, 746, 946–953. [Google Scholar]
- Anderson, W.G.; Dussinger, P.M.; Sarraf, D. High temperature water heat pipe life tests. AIP Conf. Proc. 2006, 813, 100–107. [Google Scholar] [CrossRef]
- Sarraf, D.B.; Anderson, W.G. High-temperature water heat pipes. In Proceedings of the 2006 IMAPS International Conference and Exhibition on High Temperature Electronics (HiTEC 2006), Minneapolis, MN, USA, 19–21 June 2006; pp. 549–556. [Google Scholar]
- Anderson, W.G.; Bonner, R.W.; Dussinger, P.M.; Hartenstine, J.R.; Sarraf, D.B.; Locci, I.E. Intermediate temperature fluids life tests—Experiments. In Proceedings of the 5th International Energy Conversion Engineering Conference, St. Louis, MO, USA, 25–27 June 2007; Volume 2, pp. 926–941. [Google Scholar] [CrossRef][Green Version]
- Anderson, W.G.; Tamanna, S.; Tarau, C.; Hartenstine, J.R.; Ellis, D.L. Intermediate temperature heat pipe life tests and analyses. In Proceedings of the 43rd International Conference on Environmental Systems, Vail, CO, USA, 14–18 July 2013; pp. 1–23. [Google Scholar]
- Devarakonda, A.; Anderson, W.G. Thermo-physical properties of intermediate temperature heat pipe fluids. AIP Conf. Proc. 2005, 746, 179–186. [Google Scholar] [CrossRef]
- Anderson, W.G.; Rosenfeld, J.H.; Angirasa, D.; Mi, Y. Evaluation of Heat Pipe Working Fluids In The Temperature Range 450 to 700 K. AIP Conf. Proc. 2004, 699, 20–27. [Google Scholar] [CrossRef]
- Anderson, W.G. Intermediate temperature fluids for heat pipes and loop heat pipes. In Proceedings of the 5th International Energy Conversion Engineering Conference and Exhibit (IECEC), St. Louis, MO, USA, 25–27 June 2007; Volume 2, pp. 1147–1164. [Google Scholar]
- Zhang, Y. (Ed.) Heat Pipes: Design, Applications and Technology; Nova Science Publishers: New York, NY, USA, 2018; ISBN 978-1-53613-908-2. [Google Scholar]
- Faghri, A.; Buchko, M.; Cao, Y. A study of high-temperature heat pipes with multiple heat sources and sinks: Part I—Experimental methodology and frozen startup profiles. J. Heat Transf. 1991, 113, 1003–1009. [Google Scholar] [CrossRef]
- Faghri, A.; Buchko, M.; Cao, Y. A study of high-temperature heat pipes with multiple heat sources and sinks: Part II—Analysis of continuum transient and steady-state experimental data with numerical predictions. J. Heat Transf. 1991, 113, 1010–1016. [Google Scholar] [CrossRef]
- Werner, T.C. Challenges in Operating Heat Pipes Above 350 °C. 2019. Available online: http://www.hexag.org/news/36/thomas_werner.pdf (accessed on 10 July 2023).
- Werner, T.C. Investigation of Novel Analytical Tools and Experimental Methods for the Development of Intermediate Temperature Heat Pipes. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2017. [Google Scholar]
- Werner, T.C.; Yan, Y.; Mullen, D.; Halimic, E. Experimental Analysis of a High Temperature Water Heat Pipe for Thermal Storage Applications. Therm. Sci. Eng. Prog. 2020, 19, 100564. [Google Scholar] [CrossRef]
- Werner, T.C.; Pickert, V.; Yan, Y. An Analytical Model and Comparative Fluid Analysis Tool for Screen and Sinter Wick Heat Pipes. In Proceedings of the 18th UK Heat Transfer Conference, Birmingham, UK, 9–11 September 2024; Available online: https://more.bham.ac.uk/ukhtc-2024/wp-content/uploads/sites/80/2024/09/UKHTC-2024_paper_49.pdf (accessed on 9 June 2025).
- Werner, T.C.; Yan, Y.; Karayiannis, T.; Pickert, V.; Critoph, R. Medium Temperature Heat Pipes—Applications, Challenges and Future Direction. Appl. Therm. Eng. 2024, 236, 121371. [Google Scholar] [CrossRef]
- Szymański, P.; Mikielewicz, D.; Fooladpanjeh, S. Current Trends in Wick Structure Construction in Loop Heat Pipes Applications: A Review. Materials 2022, 15, 5765. [Google Scholar] [CrossRef] [PubMed]
- Mantelli Heneiques, M.B. Thermosyphons and Heat Pipes: Theory and Applications; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Peterson, G.P. An Introduction to Heat Pipes: Modeling, Testing, and Applications; Wiley-Interscience: New York, NY, USA, 1994. [Google Scholar]
- Yaws, C.L. Chemical Property Handbook; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. REFPROP; Version 9.0; NIST—National Institute of Standards and Technology: Boulder, CO, USA, 2010. [Google Scholar]
- Dechema. Detherm. Available online: https://dechema.de/en/detherm.html (accessed on 1 January 2025).
- CoolProp. Available online: http://www.coolprop.org/ (accessed on 1 January 2025).
- CDS. National Chemical Database Service. Available online: https://www.rsc.org/journals-books-databases/databases-literature-updates/#databases (accessed on 1 January 2025).
- Siperm—Porous Metals and Components. Available online: https://www.siperm.com/ (accessed on 22 April 2025).
- Powloka—Powłoki Techniczne i Specjalistyczne. Available online: https://www.powloka.com/ (accessed on 22 April 2025).
- Szymański, P.; Song, I.-H.; Jeon, J.-H.; Radomski, P.; Miruszewski, T.; Mikielewicz, D. Experimental Investigation of the Structure of SiC Porous Ceramic in Application to LHP Evaporator Working in Medium-Temperature Heat Rejection Systems. In Proceedings of the Joint 22nd International Heat Pipe Conference (IHPC) and 16th International Heat Pipe Symposium (IHPS), Nakhon Pathom, Thailand, 24–28 November 2024. [Google Scholar]

| Wick | Materials | Shear Strength | Diameter | Thickness | Porosity | Pore Diameter |
|---|---|---|---|---|---|---|
| Ceramic | Silicon carbide + glass | 76 MPa | 0.06 m | 0.1 m | 23.5% | 44 μm |
| Ceramic | Silicon carbide + kaolin | 76 MPa | 0.06 m | 0.1 m | 35.0% | 3.0 μm |
| SS316L R10 | Stainless steel | 240 MPa | 0.06 m | 0.1 m | 35.5% | 6.0 μm |
| SS316L R14 | Stainless steel | 210 MPa | 0.06 m | 0.1 m | 38.5% | 8.0 μm |
| SS316L R20 | Stainless steel | 180 MPa | 0.06 m | 0.1 m | 39.6% | 13.0 μm |
| SS316L R200/R35 | Stainless steel | 80 MPa | 0.06 m | 0.1 m | 45.5% | 42.5 μm |
| SS316L R10/R7 | Stainless steel | 240 MPa | 0.06 m | 0.1 m | 35.0% | 5.0 μm |
| SS316L R14/R10 | Stainless steel | 210 MPa | 0.06 m | 0.1 m | 37.0% | 7.0 μm |
| SS316L R20/R14 | Stainless steel | 180 MPa | 0.06 m | 0.1 m | 39.0% | 10.5 μm |
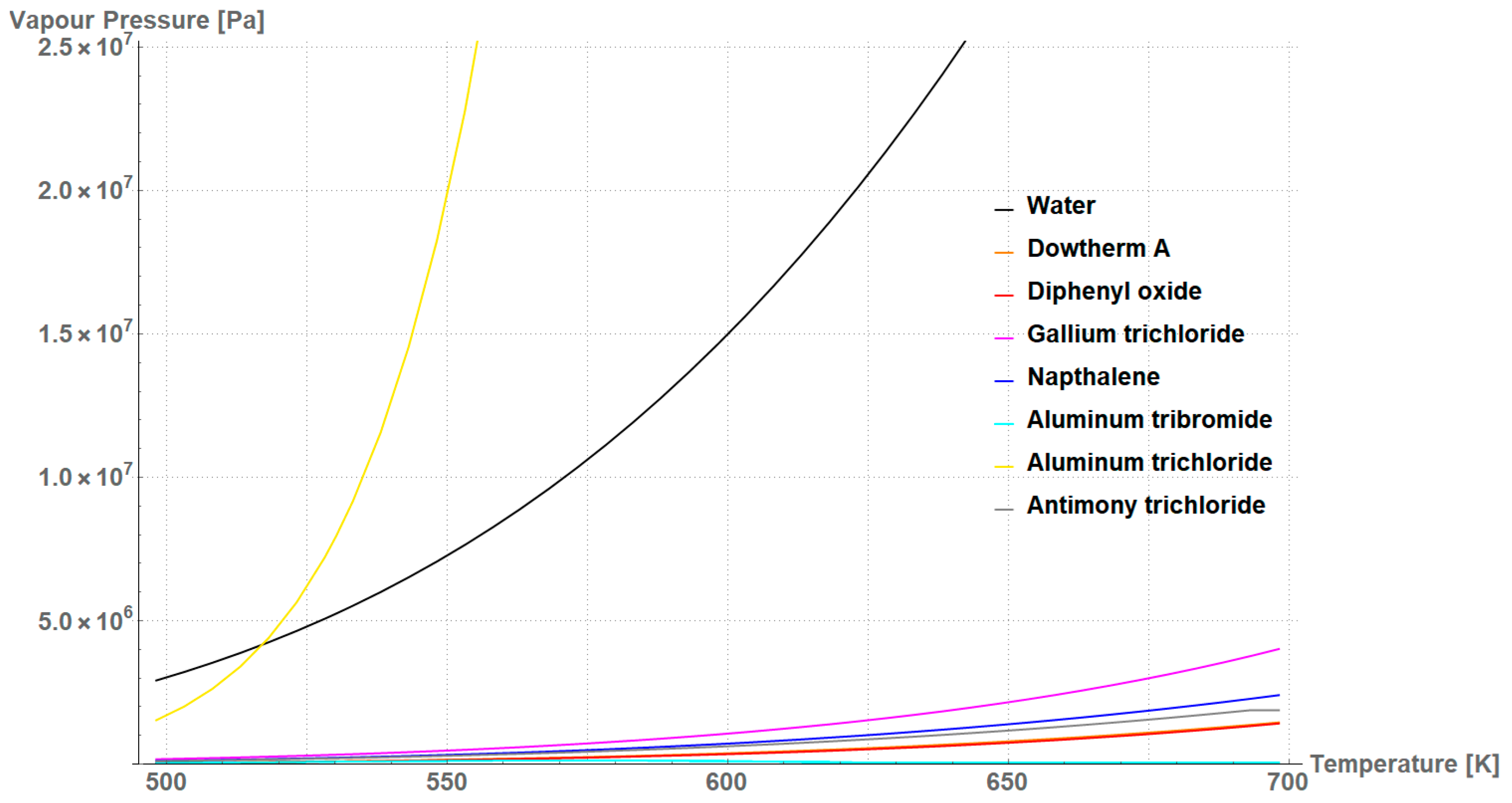
| Working Fluid | Chemical Formula | Melting Point | Boiling Point 1 | Critical Temperature | Critical Pressure |
|---|---|---|---|---|---|
| Water | H2O | 273.15 K | 373.15 K | 647.10 K | 22.12 MPa |
| Aluminum tribromide | AlBr3 | 370.65 K/366.15 K 2 | 528.15 K | 763.15 K | 2.89 MPa |
| Aluminum trichloride | AlCl3 | 453.15 K/373.15 K 2 | 455.85 K | 625.75 K | 2.60 MPa |
| Antimony trichloride | SbCl3 | 346.55 K | 496.65 K | 794.15 K | 4.82 MPa |
| Gallium trichloride | GaCl3 | 351.05 K/317.55 K 3 | 474.15 K | 694.15 K | 6.11 MPa |
| Diphenyl oxide | (C6H5)2O | 298.15 K | 531.70 K | 767.15 K | 3.29 MPa |
| Naphthalene | C10H8 | 351.35 K | 491.12 K | 748.35 K | 4.11 MPa |
| Dowtherm A | (C12H10)/(C12H10O) 4 | 285.15 K | 530.15 K | 770.15 K | 3.13 MPa |
| Working Fluid | Vapor Pressure (MPa) | Safety 1 | Potential of Evaporation 2 | Price (USD) 3 for 100 g | Assessment (0–1) | |
|---|---|---|---|---|---|---|
| Water | ✓ | 2.9216 | 0 | 167.4993 | 5.66 4 | 0.7497 |
| Aluminum tribromide | ✓ | 1.5366 | 5 | 2.1631 | 517.02 | 0.4890 |
| Aluminum trichloride | ✓ | 0.046335 | 5 | 1.3823 | 1851.06 | 0.5458 |
| Antimony trichloride | ✓ | 0.10325 | 3 | 9.0409 | 906.91 | 0.6434 |
| Gallium trichloride | ✓ | 0.17512 | 4 | 12.4307 | 4789.00 | 0.4189 |
| Diphenyl oxide | ✓ | 0.046893 | 3 | 6.2428 | 85.11 | 0.6869 |
| Naphthalene | ✓ | 0.11891 | 4 | 6.5514 | 185.11 | 0.6552 |
| Dowtherm A | ✓ | 0.049701 | 3 | 7.3383 | 21.22 | 0.6917 |
| T = 700 K | ||||||
| Water | X | - | 0 | - | 5.66 4 | 0.0000 |
| Aluminum tribromide | X | - | 5 | - | 517.02 | 0.0000 |
| Aluminum trichloride | X | - | 5 | - | 1851.06 | 0.0000 |
| Antimony trichloride | ✓ | 1.88546 | 3 | 5.6605 | 906.91 | 0.5262 |
| Gallium trichloride | X | - | 4 | - | 4789.00 | 0.0000 |
| Diphenyl oxide | ✓ | 1.4198 | 3 | 2.0564 | 85.11 | 0.6332 |
| Naphthalene | ✓ | 2.4087 | 4 | 0.7158 | 185.11 | 0.0000 |
| Dowtherm A | ✓ | 1.4580 | 3 | 2.0248 | 21.22 | 0.6458 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymański, P.; Radomski, P.; Jeon, J.-H.; Mikielewicz, D. Analysis of Key Material Parameters of Evaporator Wicks and Working Fluids for a Loop Heat Pipe Operating in the Temperature Range of 500–700 K. Materials 2025, 18, 2798. https://doi.org/10.3390/ma18122798
Szymański P, Radomski P, Jeon J-H, Mikielewicz D. Analysis of Key Material Parameters of Evaporator Wicks and Working Fluids for a Loop Heat Pipe Operating in the Temperature Range of 500–700 K. Materials. 2025; 18(12):2798. https://doi.org/10.3390/ma18122798
Chicago/Turabian StyleSzymański, Paweł, Piotr Radomski, Jae-Ho Jeon, and Dariusz Mikielewicz. 2025. "Analysis of Key Material Parameters of Evaporator Wicks and Working Fluids for a Loop Heat Pipe Operating in the Temperature Range of 500–700 K" Materials 18, no. 12: 2798. https://doi.org/10.3390/ma18122798
APA StyleSzymański, P., Radomski, P., Jeon, J.-H., & Mikielewicz, D. (2025). Analysis of Key Material Parameters of Evaporator Wicks and Working Fluids for a Loop Heat Pipe Operating in the Temperature Range of 500–700 K. Materials, 18(12), 2798. https://doi.org/10.3390/ma18122798





