Identification of Material Constants for Composite Materials Using a Sensitivity-Based Multi-Level Optimization Method
Abstract
1. Introduction
2. Formulation of the Sensitivity-Based Multi-Level Optimization Method
3. Natural Frequency Sensitivity Analysis of the Composite Plate
4. Feasibility Study of the Sensitivity-Based Multi-Level Optimization Method
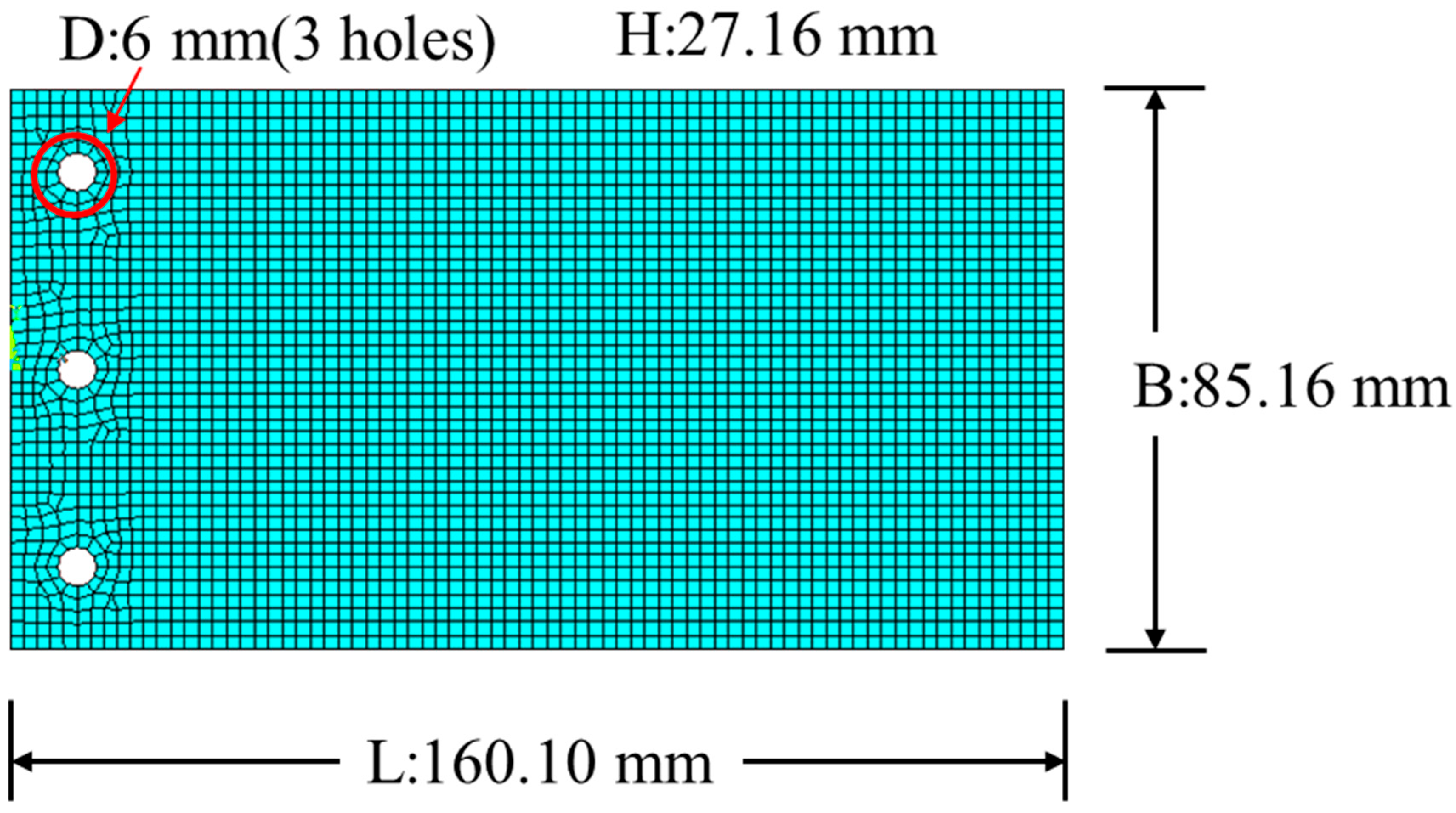
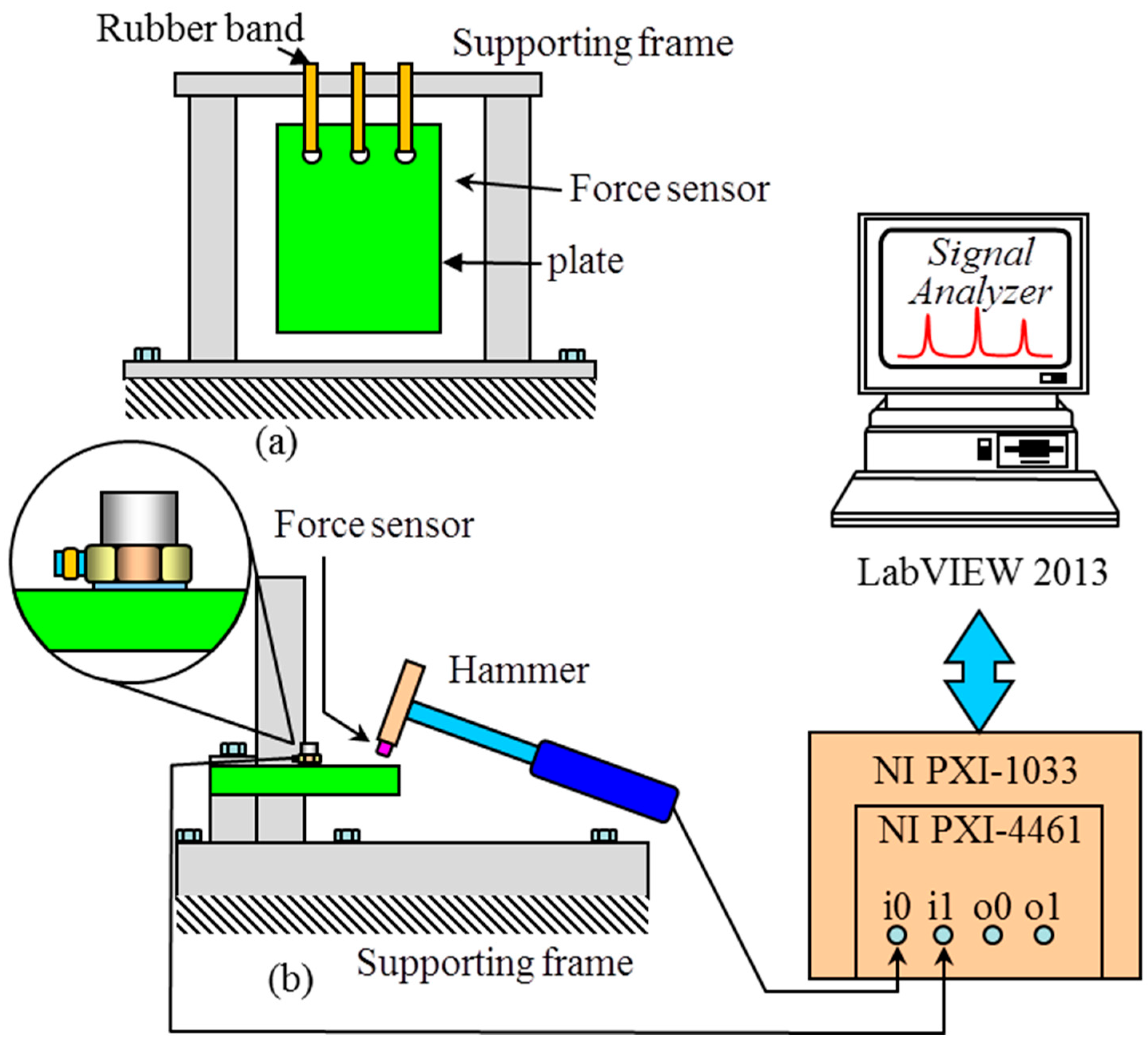
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ito, K. Identification method for material constants in Johnson–Cook model associated with strain-rate and temperature sensitivities using ball impact and indentation tests. J. Eng. Mater. Technol. 2022, 144, 041007. [Google Scholar] [CrossRef]
- Kam, T.Y.; Chen, C.M.; Yang, S.H. Material characterization of laminated composite materials using a three-point-bending technique. J. Compos. Struct. 2009, 88, 624–628. [Google Scholar] [CrossRef]
- Grédiac, M.; Toussaint, E.; Pierron, F. Special virtual fields for the direct determination of material parameters with the virtual fields method. 2—application to in-plane properties. Int. J. Solids Struct. 2002, 39, 2707–2730. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Fiborek, P.; Wandowski, T. Elastic constants identification of woven fabric reinforced composites by using guided wave dispersion curves and genetic algorithm. Compos. Struct. 2020, 249, 112569. [Google Scholar] [CrossRef]
- Rogers, W.P. Elastic property measurement using Rayleigh-lamb waves. Res. Nondestruct. Eval 1995, 6, 185–208. [Google Scholar] [CrossRef]
- Ong, W.; Rajic, N.; Chiu, W.; Rosalie, C. Determination of the elastic properties of woven composite panels for Lamb wave studies. Compos. Struct. 2016, 141, 24–31. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Fiborek, P.; Wandowski, T. Elastic constants identification of fibre-reinforced composites by using guided wave dispersion curves and genetic algorithm for improved simulations. Compos. Struct. 2021, 272, 114178. [Google Scholar] [CrossRef]
- Castellano, A.; Foti, P.; Fraddosio, A.; Marzano, S.; Piccioni, M.D. Mechanical characterization of CFRP composites by ultrasonic immersion tests: Experimental and numerical approaches. Compos. Part B Eng. 2014, 66, 299–310. [Google Scholar] [CrossRef]
- Kersemans, M.; Martens, A.; Lammens, N.; Van Den Abeele, K.; Degrieck, J.; Zastavnik, F.; Pyl, L.; Sol, H.; Van Paepegem, W. Identification of the elastic properties of isotropic and orthotropic thin-plate materials with the pulsed ultrasonic polar scan. Exp. Mech. 2014, 54, 1121–1132. [Google Scholar] [CrossRef]
- Lee, J. Identification of multiple cracks in a beam using natural frequencies. J. Sound Vib. 2009, 320, 482–490. [Google Scholar] [CrossRef]
- Xu, G.Y.; Zhu, W.D.; Emory, B.H. Experimental and numerical investigation of structural damage detection using changes in natural frequencies. J. Vib. Acoust. 2007, 129, 686–700. [Google Scholar] [CrossRef]
- Kim, J.T.; Ryu, Y.S.; Cho, H.M.; Stubbs, N. Damage identification in beam-type structures: Frequency-based method vs mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Vestroni, F.; Capecchi, D. Damage detection in beam structures based on frequency measurements. J. Eng. Mech. 2000, 126, 761–768. [Google Scholar] [CrossRef]
- Kosmatka, J.; Ricles, M. Damage detection in structures by modal vibration characterization. J. Struct. Eng. 1999, 125, 1384–1392. [Google Scholar] [CrossRef]
- Sheinman, I. Damage detection and updating of stiffness and mass matrices using mode data. Comput. Struct. 1996, 59, 149–156. [Google Scholar] [CrossRef]
- Pothisiri, T.; Hjelmstad, K. Structural damage detection and assessment from modal response. J. Eng. Mech. 2003, 129, 135–145. [Google Scholar] [CrossRef]
- Lu, Z.R.; Liu, J.K.; Huang, M.; Xu, W.H. Identification of local damages in coupled beam systems from measured dynamic responses. J. Sound Vib. 2009, 326, 177–189. [Google Scholar] [CrossRef]
- Lauwagie, T.; Sol, H.; Heylen, W.; Roebben, G. Determination of the in-plane elastic properties of the different layers of laminated plates by means of vibration testing and model updating. J. Sound Vib. 2004, 274, 529–546. [Google Scholar] [CrossRef]
- Hwang, S.F.; Wu, J.C.; He, R.S. Identification of effective elastic constants of composite plates based on a hybrid genetic algorithm. Compos. Struct. 2009, 90, 217–224. [Google Scholar] [CrossRef]
- Araujo, A.L.; Soares, C.M.M.; DeFreitas, M.J.M. Characterization of material parameters of composite plate specimens using optimization and experimental vibrational data. Compos. Part B Eng. 1996, 27, 185–191. [Google Scholar] [CrossRef]
- Lee, C.R.; Kam, T.Y. System identification of partially restrained composite plates using measured natural frequencies. J. Eng. Mech. 2006, 132, 841–850. [Google Scholar] [CrossRef]
- Lee, C.R.; Kam, T.Y. Identification of mechanical properties of elastically restrained laminated composite plates using vibration data. J. Sound Vib. 2006, 295, 999–1016. [Google Scholar] [CrossRef]
- Lee, C.R.; Kam, T.Y.; Sun, S.J. Free-vibration analysis and material constants identification of laminated composite sandwich plates. J. Eng. Mech. 2007, 133, 874–886. [Google Scholar] [CrossRef]
- Ayorinde, E.O.; Gibson, R.F. Elastic constants of orthotropic composite materials using plate resonance frequencies, classical lamination theory and an optimized three-mode Rayleigh formulation. Compos. Eng. 1993, 3, 395–407. [Google Scholar] [CrossRef]
- De Wilde, W.P. Identification of the rigidities of composite systems by mixed numerical/experimental techniques. In Mechanical Identification of Composites; Vautrin, A., Sol, H., Eds.; Springer: Dordrecht, The Netherlands, 1991. [Google Scholar] [CrossRef]
- Deobald, L.R.; Gibson, R.F. Determination of elastic constants of orthotropic plates by a modal analysis/Rayleigh–Ritz technique. J. Sound Vib. 1988, 124, 269–283. [Google Scholar] [CrossRef]
- Lai, T.C.; Lau, T.C. Determination of elastic constants of a generally orthotropic plate by modal analysis. Int. J. Anal. Exp. Modal Anal. 1993, 8, 15–33. [Google Scholar]
- Moussu, F.; Nivoit, M. Determination of elastic constants of orthotropic plates by a modal analysis/method of superposition. J. Sound Vib. 1993, 165, 149–163. [Google Scholar] [CrossRef]
- Fallstrom, K.E.; Jonsson, M. A nondestructive method to determine material properties in anisotropic plates. Polym. Compos. 1991, 12, 293–305. [Google Scholar] [CrossRef]
- Pedersen, P.; Frederiksen, P.S. Identification of orthotropic material moduli by a combined experimental/numerical approach. Measurement 1992, 10, 113–118. [Google Scholar] [CrossRef]
- Tam, J.H.; Ong, Z.C.; Lau, C.L.; Ismail, Z.; Ang, B.C.; Khoo, S.Y. Identification of material properties of composite plates using fourier-generated frequency response functions. Mech. Adv. Mater. Struct. 2017, 26, 119–128. [Google Scholar] [CrossRef]
- Sol, H.; Hua, J.; Visscher, J.; Vantomme, J.; Wilde, W.P. A mixed numerical/experimental technique for the nondestructive identification of the stiffness properties of fiber reinforced composite materials. NDT E Int. 1997, 30, 85–91. [Google Scholar] [CrossRef]
- Grediac, M.; Auslender, F.; Pierron, F. Applying the virtual fields method to determine the through-thickness moduli of thick composites with a nonlinear shear response. Compos. Part A 2001, 32, 1713–1725. [Google Scholar] [CrossRef]
- Gipple, K.L.; Hoyns, D. Measurement of the out-of-plane shear response of thick section composite materials using the V-notched beam specimen. J. Compos. Mater. 1994, 28, 543–572. [Google Scholar] [CrossRef]
- Frederiksen, P.S. Experimental procedure and results for the identification of elastic constants of thick orthotropic plates. J. Compos. Mater. 1997, 31, 360–382. [Google Scholar] [CrossRef]
- Hansen, L.U.; Horst, P. Multilevel optimization in aircraft structural design evaluation. Comput. Struct. 2008, 86, 104–118. [Google Scholar] [CrossRef]
- Maki, K.; Sbragio, R.; Vlahopoulos, N. System design of a wind turbine using a multi-level optimization approach. Renew. Energy 2012, 43, 101–110. [Google Scholar] [CrossRef]
- Ghanmi, S.; Guedri, M.; Bouazizi, M.L.; Bouhaddi, N. Robust multi-objective and multi-level optimization of complex mechanical structures. Mech. Syst. Signal Process. 2011, 25, 2444–2461. [Google Scholar] [CrossRef]
- Gong, H.; Chang, T.Y.P.; Li, G.Q. Multilevel optimization for structural design of tall buildings. Tall Build. 2005, 534–538. [Google Scholar] [CrossRef]
- Rodríguez-Segade, M.; Hernández, S.; Díaz, J. Multi-level and multi-objective structural optimization for hypersonic vehicle design. Aerosp. Sci. Technol. 2024, 152, 109346. [Google Scholar] [CrossRef]
- Logan, T.R.; Abdi, F.F.; Sobieszczanski-Sobieski, J. Multilevel optimization techniques for aircraft. Control. Dyn. Syst. 1993, 57, 25–54. [Google Scholar] [CrossRef]
- Li, Q.S.; Liu, D.K.; Zhang, N.; Tam, C.M.; Yang, L.F. Multi-level design model and genetic algorithm for structural control system optimization. Earthq. Eng. Struct. Dyn. 2001, 30, 927–942. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-objective design optimization of an IPMSM Based on Multilevel Strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Fischer, M.; Kennedy, D.; Featherston, C.A. Multilevel framework for optimization of lightweight structures. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 380–394. [Google Scholar] [CrossRef]
- Barthelemy, J.F.M.; Riley, M.F. Improved multilevel optimization approach for the design of complex engineering systems. AIAA J. 2021, 26, 353–360. [Google Scholar] [CrossRef]
- Sobieszczanski-Sobieski, J.; James, B.B.; Riley, M.F. Structural sizing by generalized, multilevel optimization. AIAA J. 2012, 25, 139–145. [Google Scholar] [CrossRef]
- Li, G.; Zhou, R.G.; Duan, L.; Chen, W.F. Multi-objective and multilevel optimization for steel frames. Eng. Struct. 1999, 21, 519–529. [Google Scholar] [CrossRef]
- Ding, Y. Multilevel optimization of frames with beams including buckling constraints. Comput. Struct. 1989, 32, 249–261. [Google Scholar] [CrossRef]
- Rothwell, A. Multi-level optimization of aircraft shell structures. Thin-Walled Struct. 1991, 11, 85–103. [Google Scholar] [CrossRef][Green Version]
- Heiko, E.; Becker, W.; Morris, A. Implementation of a multi-level optimisation methodology within the e-design of a blended wing body. Aerosp. Sci. Technol. 2004, 8, 145–153. [Google Scholar] [CrossRef]
- Huang, C.Y.; Kam, T.Y. A multi-Level optimization method for elastic constants identification of composite laminates. Appl. Sci. 2019, 9, 4267. [Google Scholar] [CrossRef]
- Kam, T.Y. Optimum design of laminated composite structures via a multilevel substructuring and optimization approach. Eng. Optim. 1992, 19, 81–100. [Google Scholar] [CrossRef]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design: With Applications; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Snyman, J.A. A new and dynamic method for unconstrained minimization. Appl. Math. Model. 1982, 6, 449–462. [Google Scholar] [CrossRef]
- Liu, C.W.; Kam, T.Y. Free vibration of rectangular composite cantilever plate and its application on material degradation assessment. Appl. Sci. 2003, 13, 5101. [Google Scholar] [CrossRef]
- ANSYS 19.5; ANSYS Inc: Canonsburg, PA, USA, 2022. Available online: https://www.ansys.com/products/structures/ansys-mechanical (accessed on 5 May 2025).
- Jones, R.M. Mechanics of Composite Material; McGraw-Hill Book Company: New York, NY, USA, 1975. [Google Scholar]
- Snyman, J.A.; Fatti, L.P. A multi-start global minimization algorithm with dynamic search trajectories. J. Optim. Theory Appl. 1987, 54, 121–141. [Google Scholar] [CrossRef]
- Global Optimization Toolbox-Matalb 2021a; The MathWorks, Inc USA: Natick, MA, USA, 2025; Available online: https://www.mathworks.com/products/global-optimization.html (accessed on 5 May 2025).

| Material Constant | Natural Frequency Number | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Percentage Change (%) | |||||
| E1 | −7.39 | −6.26 | −0.98 | −3.58 | −2.49 |
| E2 | −0.03 | −0.06 | −4.59 | −0.01 | −1.50 |
| G12 | −3.94 | −3.06 | −1.86 | −7.48 | −5.71 |
| G23 | 0.00 | −1.25 | −3.39 | 0.00 | −3.71 |
| ν12 | −0.06 | −0.05 | −0.01 | −0.03 | −0.10 |
| Material Constant | Natural Frequency Number | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Percentage Change (%) | |||||
| E1 | −6.68 | −6.68 | −3.26 | −4.72 | −3.20 |
| E2 | −0.44 | −0.46 | −0.20 | −0.62 | −0.21 |
| G12 | −2.99 | −3.01 | −5.54 | −4.32 | −5.73 |
| G23 | −0.92 | −0.40 | −1.78 | −1.29 | −1.75 |
| v12 | −0.06 | −0.06 | −0.01 | −0.04 | −0.03 |
| Material Constant | Natural Frequency Number | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Percentage Change (%) | |||||
| E1 | −5.63 | −7.44 | −2.17 | −3.58 | −3.92 |
| E2 | −0.79 | −0.58 | −0.25 | −0.41 | −0.27 |
| G12 | −4.03 | −2.76 | −6.66 | −5.36 | −5.59 |
| G23 | −0.45 | −0.74 | −1.27 | −1.33 | −1.59 |
| v12 | −0.29 | 0.09 | −0.02 | −0.01 | 0.01 |
| E1 (GPa) | G12 = G13 (GPa) | |
|---|---|---|
| True value | 89.60 | 3.58 |
| Starting point (E1, G12) | Identified value | |
| First (165.08, 2.64) | 89.60 | 3.60 |
| Second (117.46, 3.39) | 89.60 | 3.60 |
| Third (132.84, 2.94) | 90.14 | 3.58 |
| Fourth (103.06, 5.11) | 89.82 | 3.58 |
| Fivth (96.54, 6.37) | 89.24 | 3.58 |
| Average | 89.68 (0.09) * | 3.59 (0.16) |
| Standard deviation | 0.43238 | 0.00026 |
| COV (%) | 0.48 | 0.01 |
| E2 (GPa) | G23 (GPa) | |
|---|---|---|
| True value | 8.80 | 1.20 |
| Starting point (E2, G23) | Identified value | |
| First (11.02, 1.01) | 8.80 | 1.20 |
| Second (13.72, 1.54) | 8.80 | 1.20 |
| Third (5.79, 2.17) | 8.91 | 1.19 |
| Fourth (7.77, 2.23) | 8.80 | 1.20 |
| Fifth (12.92, 1.54) | 8.94 | 1.21 |
| Average | 8.85 (0.57) * | 1.20 (0.00) |
| Standard deviation | 0.01977 | 0.00028 |
| COV (%) | 0.22 | 0.02 |
| ν12 | |
|---|---|
| True value | 0.20 |
| Starting point (ν12) | Identified value |
| First (0.37) | 0.20 |
| Second (0.15) | 0.20 |
| Third (0.23) | 0.21 |
| Fourth (0.29) | 0.20 |
| Fifth (0.14) | 0.20 |
| Average | 0.20 (0.00) * |
| Standard deviation | 0.00023 |
| COV (%) | 0.12 |
| Level no. | Design Variable | True Value | Average | COV (%) |
|---|---|---|---|---|
| First | E1 (GPa) | 89.60 | 89.68 (0.09) * | 0.48 |
| G12 (GPa) | 3.58 | 3.59 (0.16) | 0.01 | |
| Second | E2 (GPa) | 8.80 | 8.85 (0.57) | 0.22 |
| G23 (GPa) | 1.20 | 1.20 (0.00) | 0.02 | |
| Third | v12 | 0.20 | 0.20 (0.00) | 0.12 |
| Material Constant | |||||||
|---|---|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | G12 (GPa) | G23 (GPa) | v12 | |||
| True value | 89.60 | 8.80 | 3.58 | 1.20 | 0.20 | ||
| Method | Number of starting points | Number of Eigenvalue problems | |||||
| Present | 89.68 (0.09) * | 8.85 (0.57) | 3.59 (0.16) | 1.20 (0.00) | 0.20 (0.00) | 15 | 150 |
| SGOM | 89.53 (0.08) | 8.83 (0.37) | 3.58 (0.00) | 1.19 (0.57) | 0.24 (22.16) | 20 | 340 |
| Matlab | 88.37 (0.68) | 8.88 (0.94) | 3.58 (0.00) | 1.48 (23.28) | 0.31 (54.24) | 1 | 281 |
| ANSYS | 89.86 (0.29) | 8.86 (0.70) | 3.58 (0.00) | 1.18 (1.33) | 0.13 (37.25) | 1 | 155 |
| E1 (GPa) | G12 = G13 (GPa) | G23 (GPa) | |
|---|---|---|---|
| True value | 89.60 | 3.58 | 1.20 |
| Starting point (E1, G12, G23) | Identified value | ||
| First (57.98, 2.30, 0.99) | 89.48 | 3.60 | 1.20 |
| Second (126.78, 6.67, 1.36) | 89.54 | 3.60 | 1.20 |
| Third (81.40, 6.17, 2.03) | 89.63 | 3.58 | 1.22 |
| Fourth (116.09, 6.49, 2.01) | 89.61 | 3.58 | 1.20 |
| Fivth (91.81, 2.53, 1.22) | 89.58 | 3.58 | 1.22 |
| Average | 89.17 (0.09) * | 3.59 (0.16) | 1.21 (0.56) |
| Standard deviation | 1.05834 | 0.00224 | 0.00060 |
| COV(%) | 1.19 | 0.06 | 0.05 |
| E2 (GPa) | ν12 | |
|---|---|---|
| True value | 8.80 | 0.20 |
| Starting point (E2, ν12) | Identified value | |
| First (12.76, 0.28) | 9.09 | 0.20 |
| Second (7.71, 0.31) | 8.53 | 0.20 |
| Third (14.21, 0.29) | 8.89 | 0.20 |
| Fourth (12.99, 0.29) | 9.05 | 0.21 |
| Fivth (8.14, 0.29) | 8.87 | 0.20 |
| Average | 8.89 (0.98) * | 0.20 (0.00) |
| Standard deviation | 0.19490 | 0.00010 |
| COV (%) | 2.19 | 0.05 |
| Level No. | Material Constants | True Value | Average | COV (%) |
|---|---|---|---|---|
| First | E1 (GPa) | 89.60 | 89.17 (0.09) * | 1.19 |
| G12 (GPa) | 3.58 | 3.58 (0.00) | 0.06 | |
| G23 (GPa) | 1.20 | 1.21 (0.00) | 0.05 | |
| Second | E2 (GPa) | 8.80 | 8.89 (0.57) | 2.19 |
| v12 | 0.20 | 0.20 (0.00) | 0.05 |
| E1 (GPa) | E2 (GPa) | |
|---|---|---|
| True value | 89.6 | 8.80 |
| Starting point (E1, E2) | Identified value | |
| First (88.26, 9.22) | 89.59 | 8.80 |
| Second (88.56, 9.60) | 89.57 | 8.80 |
| Third (90.33, 8.66) | 89.84 | 8.61 |
| Fourth (91.60, 6.62) | 89.67 | 8.80 |
| Fivth (88.27, 6.49) | 89.52 | 8.80 |
| Average | 89.64 (0.04) * | 8.76 (0.43) |
| Standard deviation | 0.06254 | 0.02754 |
| COV (%) | 0.07 | 0.31 |
| Material Constant | |||||||
|---|---|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | G12 (GPa) | G23 (GPa) | v12 | |||
| True value | 89.60 | 8.80 | 3.58 | 1.20 | 0.20 | ||
| Method | Number of starting points | Number of Eigenvalue problems | |||||
| Present | 89.64 (0.04) * | 8.76 (0.43) | 3.58 (0.00) | 1.20 (0.00) | 0.20 (0.00) | 15 | 150 |
| Stochastic global optimization | 89.69 (0.10) | 8.69 (1.28) | 3.58 (0.00) | 1.20 (0.00) | 0.20 (0.00) | 20 | 340 |
| Matlab | 88.47 (1.26) | 10.52 (19.53) | 3.46 (3.47) | 1.64 (36.76) | 0.30 (47.81) | 1 | 1004 |
| ANSYS | 89.18 (0.47) | 12.43 (41.25) | 3.69 (2.94) | 1.14 (5.04) | 0.13 (37.18) | 1 | 127 |
| E1 (GPa) | G12 = G13 | |
|---|---|---|
| True value | 89.60 | 3.58 |
| Starting point (E1, G12) | Identified value | |
| First (167.14, 6.15) | 88.17 | 3.58 |
| Second (144.60, 5.81) | 87.84 | 3.59 |
| Third (64.62, 6.04) | 88.55 | 3.55 |
| Fourth (57.31, 6.69) | 89.27 | 3.55 |
| Fivth (104.28, 5.39) | 90.28 | 3.33 |
| Average | 88.82 (0.87) * | 3.52 (1.76) |
| Standard deviation | 3.79170 | 0.04668 |
| COV (%) | 4.27 | 1.33 |
| E2 (GPa) | G23 (GPa) | ν12 | |
|---|---|---|---|
| True value | 8.80 | 1.20 | 0.20 |
| Starting point (E2, G23, ν12) | Identified value | ||
| First (14.80, 1.63, 0.14) | 9.61 | 1.27 | 0.21 |
| Second (11.89, 1.51, 0.34) | 8.62 | 1.19 | 0.19 |
| Third (14.59, 1.47, 0.20) | 9.16 | 1.27 | 0.21 |
| Fourth (8.43, 1.39, 0.17) | 8.36 | 1.13 | 0.20 |
| Fivth (5.80, 1.11, 0.37) | 8.67 | 1.24 | 0.20 |
| Average | 8.89 (0.97) * | 1.22 (1.84) | 0.20 (0.00) |
| Standard deviation | 0.99758 | 0.01442 | 0.00015 |
| COV(%) | 11.23 | 1.18 | 0.08 |
| Level No. | Material Constants | True Value | Average | COV (%) |
|---|---|---|---|---|
| First | E1 (GPa) | 89.60 | 88.24 (0.87) * | 4.27 |
| G12 (GPa) | 3.58 | 3.52 (1.76) | 1.33 | |
| Second | E2 (GPa) | 8.80 | 8.89 (0.97) | 11.23 |
| G23 (GPa) | 1.20 | 1.22 (1.84) | 1.18 | |
| v12 | 0.20 | 0.20 (0.00) | 0.08 |
| E1 (GPa) | E2 (GPa) | G12 = G13 (GPa) | G23(GPa) | |
|---|---|---|---|---|
| True value | 89.6 | 8.80 | 3.58 | 1.20 |
| Starting point (E1, E2, G12, G23) | Identified value | |||
| First (89.70, 9.22, 3.55) | 89.70 | 8.89 | 3.56 | 1.20 |
| Second (88.56, 9.60, 3.62) | 89.70 | 8.85 | 3.58 | 1.20 |
| Third (90.33, 8.66, 3.60) | 89.70 | 9.12 | 3.56 | 1.21 |
| Fourth (91.60, 6.62, 3.52) | 89.68 | 9.05 | 3.59 | 1.19 |
| Fivth (88.27, 6.49, 3.50) | 89.66 | 9.05 | 3.57 | 1.20 |
| Average | 89.69 (0.10) * | 8.99 (2.18) | 3.57 (0.38) | 1.20 (0.00) |
| Standard deviation | 0.00099 | 0.05473 | 0.00053 | 0.00007 |
| COV (%) | 0.00 | 0.61 | 0.01 | 0.01 |
| Material Constant | |||||||
|---|---|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | G12 (GPa) | G23 (GPa) | v12 | |||
| True value | 89.60 | 8.80 | 3.58 | 1.20 | 0.20 | ||
| Method | Number of starting points | Number of Eigenvalue problems | |||||
| Present | 89.69 (0.10) * | 8.99 (2.18) | 3.57 (0.38) | 1.20 (0.00) | 0.20 (0.00) | 15 | 150 |
| Stochastic global optimization | 89.40 (0.23) | 8.73 (0.78) | 3.59 (0.07) | 1.21 (0.56) | 0.20 (0.00) | 20 | 340 |
| Matlab | 86.11 (3.86) | 11.73 (33.30) | 3.43 (4.29) | 1.76 (47.03) | 0.28 (40.71) | 1 | 526 |
| ANSYS | 89.13 (7.22) | 15.05 (71.08) | 3.56 (0.55) | 1.20 (0.00) | 0.13 37.19 | 1 | 144 |
| Material Constant | Natural Frequency Number | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Percentage Change (%) | |||||
| E1 | −7.25 | −3.27 | −0.58 | −3.35 | −2.09 |
| E2 | −0.03 | −0.10 | −3.67 | −0.05 | −0.07 |
| G12 | −4.09 | −5.14 | −2.50 | −6.96 | −6.83 |
| G23 | 0.00 | −2.12 | −4.96 | −0.05 | −1.77 |
| ν12 | −0.06 | −0.04 | −0.01 | −0.05 | −0.04 |
| Level no. | Material Constants | Average | COV (%) |
|---|---|---|---|
| First | E1 (GPa) | 77.56 | 0.07 |
| G12 (GPa) | 4.12 | 0.05 | |
| Second | E2 (GPa) | 6.37 | 0.08 |
| G23 (GPa) | 1.33 | 0.61 | |
| Third | v12 | 0.372 | 0.01 |
| Natural Frequency (Hz) | f1 | f2 |
|---|---|---|
| Experimental | 2261 | 2470 |
| Theoretical (Original material constants) | 2663 (17.78) | 5237 (111.99) |
| Theoretical (Identified material constants) | 2280 (0.87) * | 2474 (0.15) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.W.; Kam, T.Y. Identification of Material Constants for Composite Materials Using a Sensitivity-Based Multi-Level Optimization Method. Materials 2025, 18, 2737. https://doi.org/10.3390/ma18122737
Liu CW, Kam TY. Identification of Material Constants for Composite Materials Using a Sensitivity-Based Multi-Level Optimization Method. Materials. 2025; 18(12):2737. https://doi.org/10.3390/ma18122737
Chicago/Turabian StyleLiu, Ching Wen, and Tai Yan Kam. 2025. "Identification of Material Constants for Composite Materials Using a Sensitivity-Based Multi-Level Optimization Method" Materials 18, no. 12: 2737. https://doi.org/10.3390/ma18122737
APA StyleLiu, C. W., & Kam, T. Y. (2025). Identification of Material Constants for Composite Materials Using a Sensitivity-Based Multi-Level Optimization Method. Materials, 18(12), 2737. https://doi.org/10.3390/ma18122737







