A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks
Abstract
1. Introduction
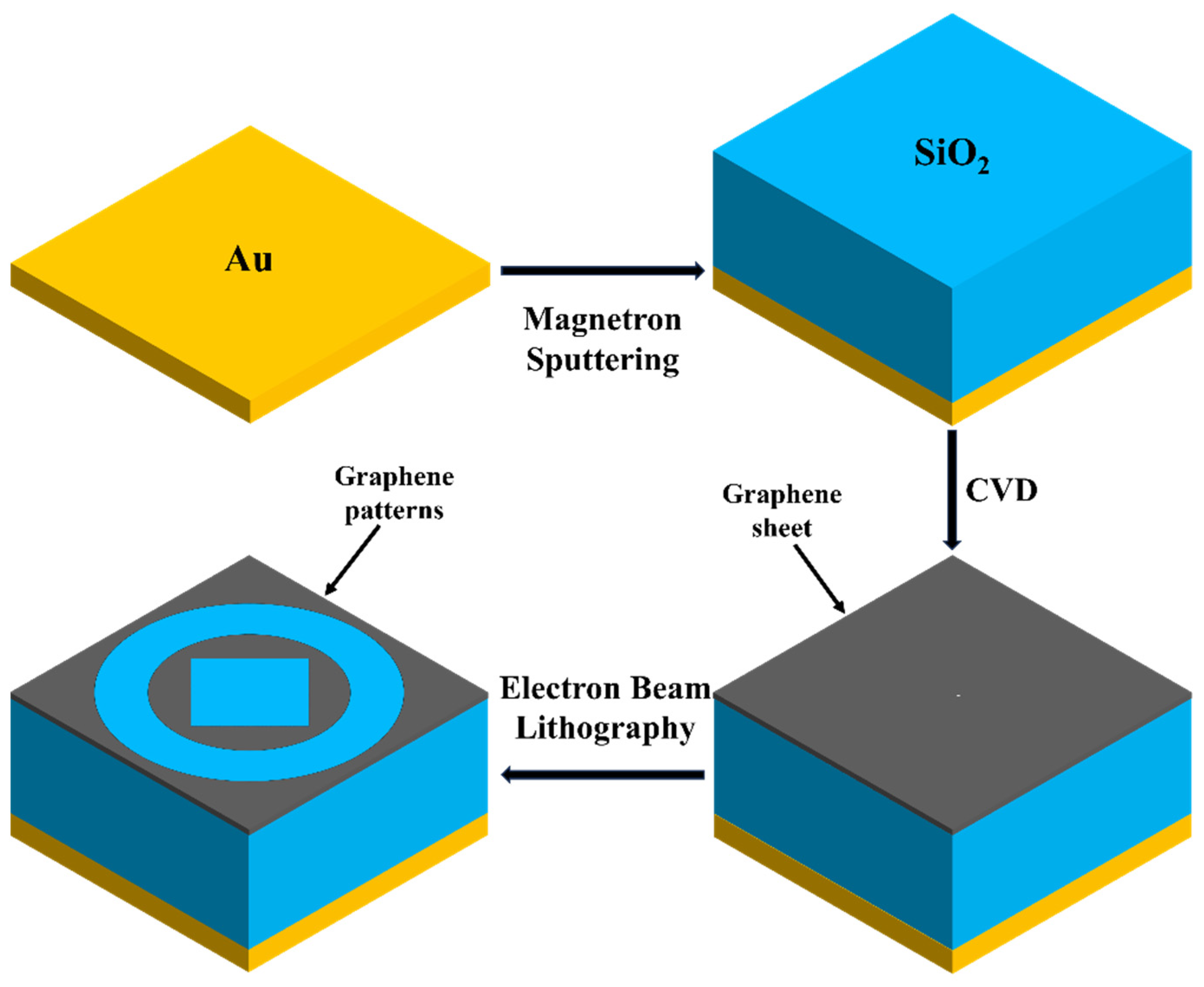
2. Numerical Model and Structural Design
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balashov, I.S.; Chezhegov, A.A.; Chizhov, A.S.; Grunin, A.A.; Anokhin, K.V.; Fedyanin, A.A. Light-stimulated adaptive artificial synapse based on nanocrystalline metal-oxide film. Opto-Electron. Sci. 2023, 2, 230016. [Google Scholar] [CrossRef]
- Jo, Y.; Park, H.; Yoon, H.; Kim, I. Advanced biological imaging techniques based on metasurfaces. Opto-Electron. Adv. 2024, 7, 240122. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Yang, H.; Wang, J.; Li, B.; Zhang, H.; Yi, Y. TiN-Only Metasurface Absorber for Solar Energy Harvesting. Photonics 2025, 12, 443. [Google Scholar] [CrossRef]
- Zeng, L.L.; Li, B.X.; Wen, R.Q.; Zhang, X.J. Plasmonic Sensor Based on Multi Fano Resonance in Inverse T Shape Structure for Detection of CO2 Concentration. IEEE Photonics J. 2023, 15, 2201805. [Google Scholar] [CrossRef]
- Hu, J.Y.; Tan, C.X.; Bai, W.D.; Li, Y.M.; Lin, Q.; Wang, L.L. Dielectric nanocavity-coupled surface lattice resonances for high-efficiency plasmonic sensing. J. Phys. D Appl. Phys. 2022, 55, 075105. [Google Scholar] [CrossRef]
- Rao, X.J.; Zhu, H.R.; Wang, X.X.; Chen, Y.Z.; Qi, Y.P.; Yang, H. High-sensitivity plasmonic refractive index sensor based on embedded gratings with triple self-reference characteristics. J. Opt. Soc. Am. B 2025, 42, 431–437. [Google Scholar] [CrossRef]
- Kang, D.H.; Heo, H.S.; Yang, Y.H.; Seong, J.; Kim, H.; Kim, J.; Rho, J. Liquid crystal-integrated metasurfaces for an active photonic platform. Opto-Electron. Adv. 2024, 7, 230216. [Google Scholar] [CrossRef]
- Yang, C.; Luo, M.H.; Ju, X.W.; Hu, J.Y. Ultra-narrow dual-band perfect absorber based on double-slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2024, 57, 345104. [Google Scholar] [CrossRef]
- Lv, J.; Ren, Y.; Wang, D.; Wang, J.; Lu, X.; Yu, Y.; Li, W.; Liu, Q.; Xu, X.; Liu, W.; et al. Optical switching with high-Q Fano resonance of all-dielectric metasurface governed by bound states in the continuum. Opt. Express 2024, 32, 28334–28347. [Google Scholar] [CrossRef]
- Cheng, S.B.; Li, W.X.; Zhang, H.F.; Akhtar, M.N.; Yi, Z.; Zeng, Q.D.; Ma, C.; Sun, T.Y.; Wu, P.H.; Ahmad, S. High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals. Opt. Commun. 2024, 569, 130816. [Google Scholar] [CrossRef]
- Li, Y.M.; Tan, C.X.; Hu, J.Y.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Zhang, Y.; Wang, L.L. Ultra-narrow band perfect absorbance induced by magnetic lattice resonances in dielectric dimer metamaterials. Results Phys. 2022, 39, 105730. [Google Scholar] [CrossRef]
- Tian, Y.X.; Dong, B.Y.; Li, Y.X.; Xiong, B.; Zhang, J.; Sun, C.; Hao, Z.; Wang, J.; Wang, L.; Han, Y.; et al. Photonics-assisted THz wireless communication enabled by wide-bandwidth packaged back-illuminated modified uni-traveling-carrier photodiode. Opto-Electron. Sci. 2024, 3, 230051. [Google Scholar] [CrossRef]
- Zhang, B.W.; Luo, Y.N. Dynamic optical tuning and sensing in L-shaped dirac semimetal-based terahertz metasurfaces. Phys. Lett. A 2025, 541, 130419. [Google Scholar] [CrossRef]
- Zeng, Z.L.; Liu, H.F.; Zhang, H.F.; Cheng, S.B.; Yi, Y.G.; Yi, Z.; Wang, J.Q.; Zhang, J.G. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Photonics Nanostruct. Fundam. Appl. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Rane, S.; Prabhu, S.; Chowdhury, D.R. Physics and applications of terahertz metagratings. Opto-Electron. Sci. 2024, 3, 230049. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.K.; Liu, S.T.; Zhang, Y. Highly efficient vectorial field manipulation using a transmitted tri-layer metasurface in the terahertz band. Opto-Electron. Adv. 2023, 6, 220012. [Google Scholar] [CrossRef]
- Liu, M.L.; Li, B.X.; Zeng, L.L.; Wei, Y.; Wen, R.Q.; Zhang, X.J.; Deng, C.S. Dynamic tunable narrow-band perfect absorber for fiber -optic communication band based on liquid crystal. J. Phys. D Appl. Phys. 2023, 56, 505102. [Google Scholar] [CrossRef]
- Xiang, T.; Sun, Z.; Wang, L.L.; Lin, Q.; Liu, G.D. Polarization independent perfect absorption of borophene metamaterials operating in the communication band. Phys. Scr. 2024, 99, 085519. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Musina, G.R.; Nikitin, P.V.; Dolganova, I.N.; Kucheryavenko, A.S.; Alekseeva, A.I.; Wang, Y.; Xu, D.; Shi, Q.; Tuchin, V.V.; et al. Terahertz technology in intraoperative neurodiagnostics: A review. Opto-Electron. Adv. 2023, 6, 220071. [Google Scholar] [CrossRef]
- Ai, Z.; Liu, H.F.; Cheng, S.B.; Zhang, H.F.; Yi, Z.; Zeng, Q.D.; Wu, P.H.; Zhang, J.G.; Tang, C.J.; Hao, Z.Q. Four peak and high angle tilted insensitive surface plasmon resonance graphene absorber based on circular etching square window. J. Phys. D Appl. Phys. 2025, 58, 185305. [Google Scholar] [CrossRef]
- Wang, H.Y.; Ma, R.; Liu, G.D.; Wang, L.L.; Lin, Q. Optical force conversion and conveyor belt effect with coupled graphene plasmon waveguide modes. Opt. Express 2023, 31, 32422. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.T.; Li, X.; Liu, G.D.; Wang, L.L.; Lin, Q. Analytical investigation of unidirectional reflectionless phenomenon near the exceptional points in graphene plasmonic system. Opt. Express 2023, 31, 30458. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.R.; Ji, C.; Tan, J.B.; Du, B.Q.; Zhao, X.F.; Yu, J.; Man, B.Y.; Xu, K.C.; Zhang, C.; Li, Z. Ferroelectrically modulate the Fermi level of graphene oxide to enhance SERS response. Opto-Electron. Adv. 2023, 6, 230094. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, L.G.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Extreme enhancement of optical force via the acoustic graphene plasmon mode. Opt. Express 2023, 31, 482723. [Google Scholar] [CrossRef] [PubMed]
- Maksimova, Y.; Pyankova, E.; Nesterova, L.; Maksimov, A. Effects of Graphene Derivatives and Near-Infrared Laser Irradiation on E. coli Biofilms and Stress Response Gene Expression. Int. J. Mol. Sci. 2025, 26, 4728. [Google Scholar] [CrossRef]
- Li, Z.T.; Cheng, S.B.; Zhang, H.F.; Yang, W.X.; Yi, Z.; Yi, Y.G.; Wang, J.Q.; Ahmad, S.; Raza, R. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Li, B.X.; Liu, M.L.; Wen, R.Q.; Wei, Y.; Zeng, L.L.; Deng, C.S. Dynamic control of Fano-like interference in the graphene periodic structure. J. Phys. D Appl. Phys. 2023, 56, 115104. [Google Scholar] [CrossRef]
- Januszko, A.; Górski, K.; Bogdanowicz, K.A.; Drabczyk, K.; Zdrojek, M.; Żerańska, K.; Pellowski, W.; Miedziak, J.; Iwan, A. Graphene Flakes and Ethylene–Vinyl Acetate-Based Sensor for Detecting Mechanical Damage in Photovoltaic Panels on Sound-Absorbing Screens: An Engineering Approach for Civil and Military Applications. Energies 2025, 18, 1817. [Google Scholar] [CrossRef]
- Zeng, T.Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Light-matter interactions enhanced by quasi-bound states in the continuum in a graphene-dielectric metasurface. Opt. Express 2021, 29, 40177–40186. [Google Scholar] [CrossRef]
- Shiraishi, N.; Lu, J.; Fauzi, F.B.; Imaizumi, R.; Tsukahara, T.; Mogari, S.; Iida, S.; Matsukura, Y.; Teramoto, S.; Yokoi, K.; et al. Basic Characteristics of Ionic Liquid-Gated Graphene FET Sensors for Nitrogen Cycle Monitoring in Agricultural Soil. Biosensors 2025, 15, 55. [Google Scholar] [CrossRef]
- Zhang, S.W.; Yang, H.; Tang, C.J.; Yi, Z.; Zhang, J.G.; Wang, J.Q.; Li, B.X. Multiple tunable six-peak graphene absorber for high-performance refractive index sensing. Phys. B Condens. Matter 2025, 708, 417225. [Google Scholar] [CrossRef]
- Zeng, Y.; Ling, Z.X.; Liu, G.D.; Wang, L.L.; Lin, Q. Tunable plasmonically induced transparency with giant group delay in gain-assisted graphene metamaterials. Opt. Express 2022, 30, 455954. [Google Scholar] [CrossRef]
- Tang, C.J.; Nie, Q.M.; Cai, P.G.; Liu, F.X.; Gu, P.; Yan, Z.D.; Huang, Z.; Zhu, M.W. Ultra-broadband near-infrared absorption enhancement of monolayer graphene by multiple-resonator approach. Diam. Relat. Mater. 2024, 141, 110607. [Google Scholar] [CrossRef]
- Chen, S.; Wu, X.H.; Fu, C.J. Active tuning of anisotropic phonon polaritons in natural van der Waals crystals with negative permittivity substrates and its application in energy transport. Opto-Electron. Sci. 2024, 3, 240002. [Google Scholar] [CrossRef]
- Yang, Q.; Yu, M.; Chen, Z.; Ai, S.; Kentsch, U.; Zhou, S.; Jia, Y.; Chen, F.; Liu, H. A novel approach towards robust construction of physical colors on lithium niobate crystal. Opto-Electron. Adv. 2025, 8, 240193. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, C.; Nong, H.; Weng, J.; Wang, D.; Yu, Y.; Zhang, J.; Zhang, C.; Yu, J.; Zhang, Z.; et al. Multi-photon neuron embedded bionic skin for high-precision complex texture and object reconstruction perception research. Opto-Electron. Adv. 2025, 8, 240152. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.; Yi, Z.; Wang, J.; Cheng, S.; Li, B.; Wu, P. High Absorption Broadband Ultra-Long Infrared Absorption Device Based on Nanoring–Nanowire Metasurface Structure. Photonics 2025, 12, 451. [Google Scholar] [CrossRef]
- Tan, Z.Q.; Lin, Q.; Du, W.J.; Wang, L.L.; Liu, G.D. Simultaneously enhance electric and magnetic Purcell factor by strong coupling between toroidal dipole quasi-BIC and electric dipole. J. Appl. Phys. 2025, 137, 033103. [Google Scholar] [CrossRef]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.X.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active Tunable Terahertz Band-width Absorber Based on single layer Graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, L.; Liu, G.; Wang, L.; Lin, Q. The total optical force exerted on black phosphorus coated dielectric cylinder pairs enhanced by localized surface plasmon. J. Appl. Phys. 2021, 130, 113103. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liu, M.S.; Yang, H.; Yi, Z.; Zhang, H.; Tang, C.J.; Deng, J.; Wang, J.Q.; Li, B.X. Photoelectric simulation of perovskite solar cells based on two inverted pyramid structures. Phys. Lett. A 2025, 552, 130653. [Google Scholar] [CrossRef]
- Hu, J.Y.; Bai, W.D.; Tan, C.X.; Li, Y.M.; Lin, Q.; Wang, L.L. Highly electric field enhancement induced by anapole modes coupling in the hybrid dielectric-metal nanoantenna. Opt. Commun. 2022, 511, 127987. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Lin, Q.; Yan, X.Q.; Wang, L.L.; Liu, G.D. Flat-band Friedrich-Wintgen bound states in the continuum based on borophene metamaterials. Opt. Express 2024, 32, 10669–10678. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Q.; Sun, J.Y.; Sun, S.; Zhang, H.; Wang, Q.Q.; Yang, J.Y.; Mei, Y.W. Numerical simulation of electromagnetically induced transparency in composite metamaterial. Phys. Scr. 2025, 100, 025512. [Google Scholar] [CrossRef]
- Li, W.X.; Cheng, S.B.; Yi, Z.; Zhang, H.F.; Song, Q.J.; Hao, Z.Q.; Sun, T.Y.; Wu, P.H.; Zeng, Q.D.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, G.D.; Wang, L. Active modulation of quasi-bound state in the continuum based on bulk Dirac semimetals metamaterial. Appl. Phys. Express 2022, 15, 032006. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cheng, S.B.; Zhang, H.F.; Yi, Z.; Tang, B.; Chen, J.; Zhang, J.G.; Tang, C.J. Ultra wideband absorption absorber based on Dirac semimetallic and graphene metamaterials. Phys. Lett. A 2024, 517, 129675. [Google Scholar] [CrossRef]
- Gu, X.; Liu, G.D.; Wang, L.L.; Lin, Q. Robust Fano resonance induced by topologically protected interface modes interference at gigahertz. Appl. Phys. Express 2022, 15, 082004. [Google Scholar] [CrossRef]
- Wang, J.Q.; Yang, J.Y.; Mei, Y.W. Non-radiating anapole state in dielectric nanostructures and metamaterials. J. Phys. D Appl. Phys. 2025, 58, 203001. [Google Scholar] [CrossRef]
- Yang, C.; Lin, Q.; Du, W.J.; Wang, L.L.; Liu, G.D. Bi-tunable absorber based on borophene and VO2 in the optical telecom-munication band. J. Opt. Soc. Am. B 2022, 39, 2969–2974. [Google Scholar] [CrossRef]
- Yan, X.; Lin, Q.; Wang, L.; Liu, G.D. Active absorption modulation by employing strong coupling between magnetic plasmons and borophene surface plasmons in the telecommunication band. J. Appl. Phys. 2022, 132, 063101. [Google Scholar] [CrossRef]
- Ling, Z.X.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Unified model for plasmon-induced transparency with direct and indirect coupling in borophene-integrated metamaterials. Opt. Express 2022, 30, 21966. [Google Scholar] [CrossRef] [PubMed]
- Long, T.; Zhang, L.; Wang, L.L.; Lin, Q. Tunable narrow transparency windows induced by the coupled quasi-guided modes in borophene plasmonic nanostructure. J. Phys. D Appl. Phys. 2022, 55, 315101. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Belhadj, W.; Wong, B.M. Quantum tunneling mechanisms in monolayer graphene modulated by multiple electrostatic barriers. Results Phys. 2021, 26, 104403. [Google Scholar] [CrossRef]
- Zhan, T.; Shi, X.; Dai, Y.; Liu, X.; Zi, J. Transfer matrix method for optics in graphene layers. J. Phys. Condens. Matter 2013, 25, 215301. [Google Scholar] [CrossRef]
- Yan, X.F.; Lin, Q.; Wang, L.L.; Liu, G.D. Tunable strong plasmon–exciton coupling based modulator employing borophene and deep subwavelength perovskite grating. J. Phys. D Appl. Phys. 2023, 56, 435106. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Ma, C.; Wu, P.; Zeng, Q.; Raza, R. Multi-functional metasurface: Ultra-wideband/multi-band absorption switching by adjusting guided mode resonance and local surface plasmon resonance effects. Commun. Theor. Phys. 2024, 76, 065701. [Google Scholar] [CrossRef]
- Wu, X.; Chen, J.; Wang, S.; Ren, Y.; Yang, Y.; He, Z. Sensing Based on Plasmon-Induced Transparency in H-Shaped Graphene-Based Metamaterials. Nanomaterials 2024, 14, 997. [Google Scholar] [CrossRef]
- Guo, X.C.; Tang, C.J.; Yi, Z.; Cheng, S.B.; Wang, J.Q.; Li, B.X. Design and application of multi-absorption and highly sensitive monolayer graphene microstructure absorption devices located at terahertz frequencies. Curr. Appl. Phys. 2025, 76, 16–25. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.T.; Wang, L.L.; Lin, Q. Unidirectional reflectionless propagation in borophene plasmonic metamaterials. J. Phys. D Appl. Phys. 2023, 57, 015103. [Google Scholar] [CrossRef]
- Gu, X.; Liu, X.; Yan, X.F.; Du, W.J.; Lin, Q.; Wang, L.L.; Liu, G.D. Polaritonic coherent perfect absorption based on self-hybridization of a quasi-bound state in the continuum and exciton. Opt. Express 2023, 31, 4691–4700. [Google Scholar] [CrossRef] [PubMed]
- Li, B.X.; Zeng, L.L.; Wen, R.Q.; Zhang, X.J. Dynamic Regulation of Multiple Fano Resonances Based on Liquid Crystal. IEEE Photonics J. 2023, 15, 2200506. [Google Scholar] [CrossRef]
- Liu, S.H.; Yang, H.; Tang, C.J.; Yi, Z.; Yi, Y.G.; Wang, J.Q.; Li, B.X. Highly sensitive photonic crystal optic fiber with annular stomatal arrangement for cervical cancer cell detection. Phys. Lett. A 2025, 548, 130574. [Google Scholar] [CrossRef]
- Li, Z.; Song, Q.J.; Jia, L.B.; Yi, Z.; Cheng, S.B.; Wang, J.Q.; Li, B.X. Actively tunable multi-frequency narrowband te-rahertz absorber using graphene metamaterials. Opt. Commun. 2025, 583, 131768. [Google Scholar] [CrossRef]
- Luo, M.H.; Hu, J.Y.; Li, Y.M.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Wang, L.L. Anapole-assisted ultra-narrow-band lattice resonance in slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2023, 56, 375102. [Google Scholar] [CrossRef]
- Yan, D.Y.; Tang, C.J.; Yi, Z.; Wang, J.Q.; Li, B.X. A fully symmetric solar absorber for thermophotovoltaic power generation. Phys. Lett. A 2025, 542, 130461. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lin, Q.; Wang, L.L.; Liu, G.D. Dynamic control of polarization conversion based on borophene nanostructures in optical communication bands. Phys. Scr. 2024, 99, 085531. [Google Scholar] [CrossRef]
- Ning, X.; Sun, T.Y.; Song, Q.J.; Yi, Z.; Cheng, S.B.; Wang, J.Q.; Zeng, Q.D.; Yi, Y.G. A modulated broadband polarimetric insensitive metamaterial absorber based on a monolayer of graphene. Commun. Theor. Phys. 2025, 77, 095702. [Google Scholar] [CrossRef]
- Veeraselvam, A.; Mohammed, G.N.A.; Savarimuthu, K. A Novel Ultra-Miniaturized Highly Sensitive Refractive Index-Based Terahertz Biosensor. J. Light. Technol. 2021, 39, 7281–7287. [Google Scholar] [CrossRef]
- Razani, A.H.N.; Rezaei, P.; Zamzam, P.; Khatami, S.A.; Daraei, O.M. Absorption-based ultra-sensitive RI sensor based on the flower-shaped graphene resonator for early detection of cancer. Opt. Commun. 2022, 524, 128775. [Google Scholar] [CrossRef]
- Nickpay, M.R.; Danaie, M.; Shahzadi, A. Graphene-based metamaterial absorber for refractive index sensing applications in terahertz band. Diam. Relat. Mater. 2022, 130, 109539. [Google Scholar] [CrossRef]
- Lu, W.Q.; Wu, P.H.; Bian, L.; Yan, J.Q.; Yi, Z.; Liu, M.S.; Tang, B.; Li, G.F.; Liu, C. Perfect adjustable absorber based on Dirac semi-metal high sensitivity four-band high frequency detection. Opt. Laser Technol. 2024, 174, 110650. [Google Scholar] [CrossRef]
- Hadipour, S.; Rezaei, P.; Norouzi-Razani, A. Multi band square-shaped polarization-insensitive graphene-based perfect absorber. Opt. Quant. Electron. 2024, 56, 471. [Google Scholar] [CrossRef]
- Khatami, S.A.; Rezaei, P.; Zamzam, P. Quad band metal-dielectric-metal perfect absorber to selective sensing application. Opt. Quant. Electron. 2022, 54, 638. [Google Scholar] [CrossRef]
- Khodadadi, B.; Babaeinik, M.; Ghods, V.; Rezaei, P. Triple-band metamaterial perfect absorber for refractive index sensing in THz frequency. Opt. Quant. Electron. 2023, 55, 431. [Google Scholar] [CrossRef]
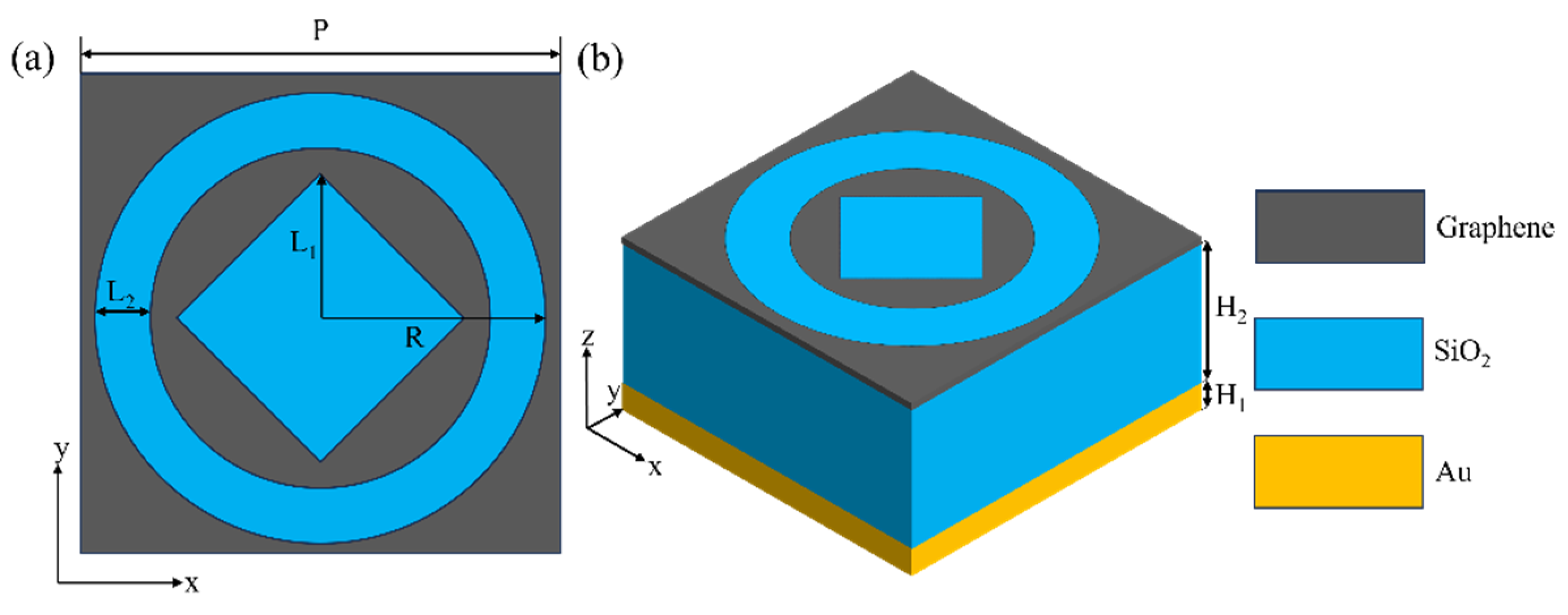







| Parmeter | L1 | L2 | R | P | H1 | H2 | Graphene Level |
|---|---|---|---|---|---|---|---|
| Value (μm) | 3 | 1.2 | 4.7 | 5 | 0.3 | 5 | 0.001 |
| Ref. | Materials | Peak Number | Average Absorption | Sensitivity [GHz/RIU] | Q- Factor | FOM (1/RIU) | Tunability |
|---|---|---|---|---|---|---|---|
| [69] | Au | 1 | Over 99% | 2100 | 6.8 | 7.03 | Yes |
| [70] | Graphene | 1 | 99.8% | 3923 | 14.92 | 6.111 | No |
| [71] | Graphene | 3 | 95.7% | 1791 | 32.354 | 7.046 | No |
| [72] | BDS | 4 | 99.9% | 560 | ~ | ~ | Yes |
| [73] | Graphene | 13 | 99.6% | ~ | ~ | ~ | No |
| [74] | Au | 4 | 98.22% | ~ | ~ | ~ | No |
| [75] | Graphene | 3 | 99.53% | 1387 | 12.62 | 1.612 | Yes |
| This work | Graphene | 5 | 98.9% | 4508.75 | 51.32 | 18.03 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Shi, P.; Yi, Z. A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks. Materials 2025, 18, 2601. https://doi.org/10.3390/ma18112601
Ma H, Shi P, Yi Z. A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks. Materials. 2025; 18(11):2601. https://doi.org/10.3390/ma18112601
Chicago/Turabian StyleMa, Hongyu, Pengcheng Shi, and Zao Yi. 2025. "A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks" Materials 18, no. 11: 2601. https://doi.org/10.3390/ma18112601
APA StyleMa, H., Shi, P., & Yi, Z. (2025). A Highly Sensitive Graphene-Based Terahertz Perfect Absorber Featuring Five Tunable Absorption Peaks. Materials, 18(11), 2601. https://doi.org/10.3390/ma18112601








