Predicting the Compressive Properties of Carbon Foam Using Artificial Neural Networks
Abstract
1. Introduction
2. Materials and Methods
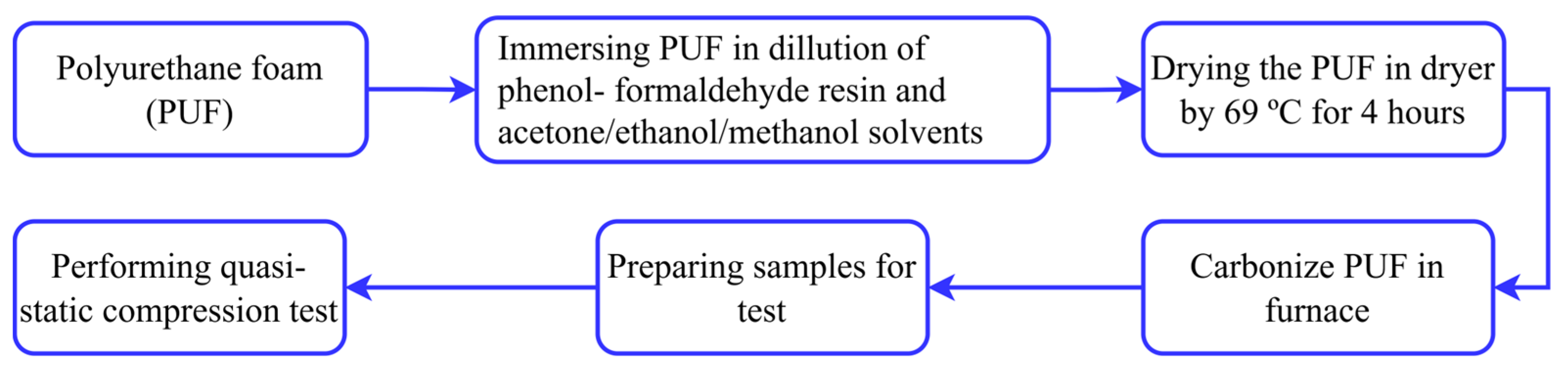
2.1. Materials
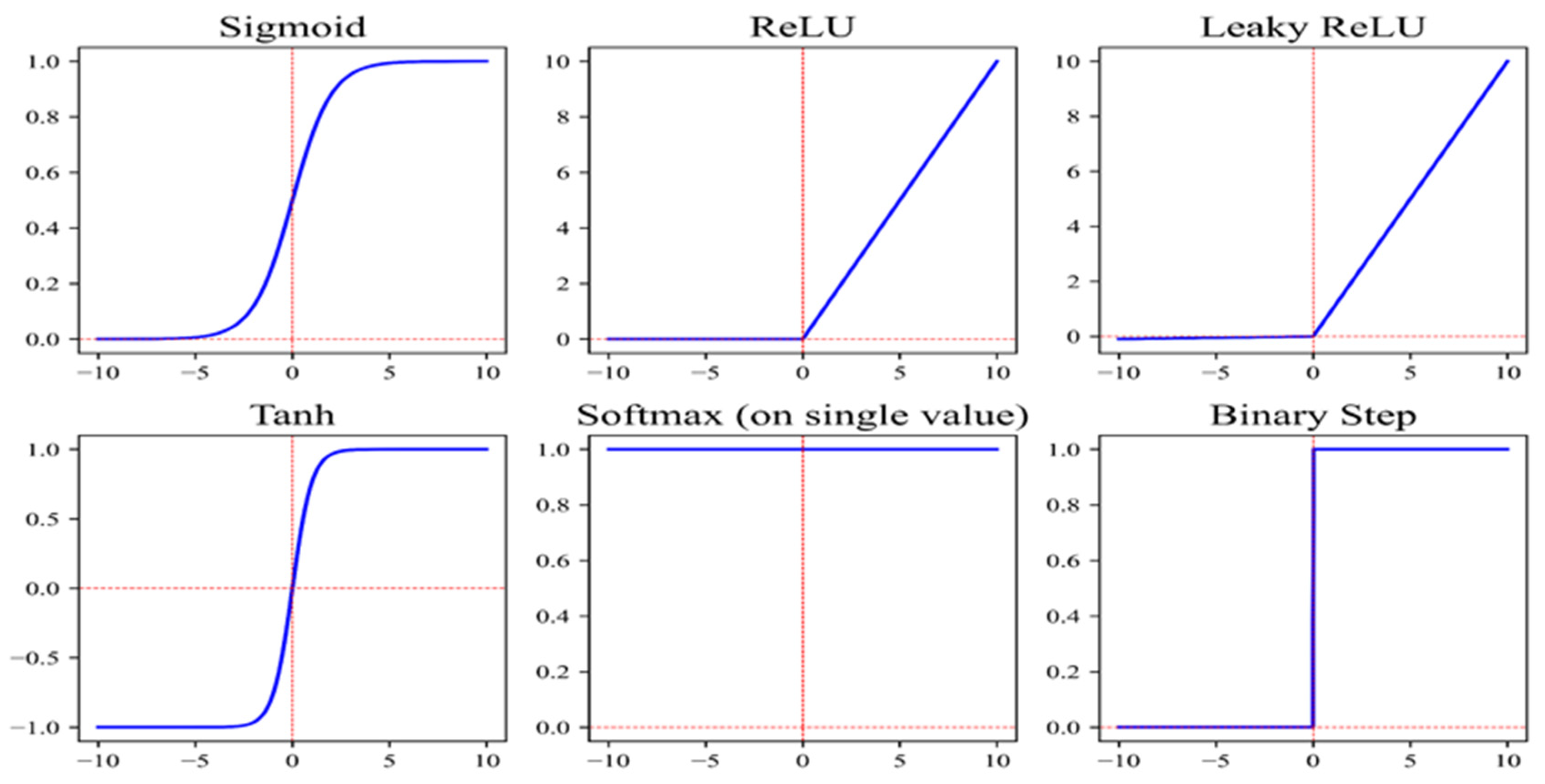
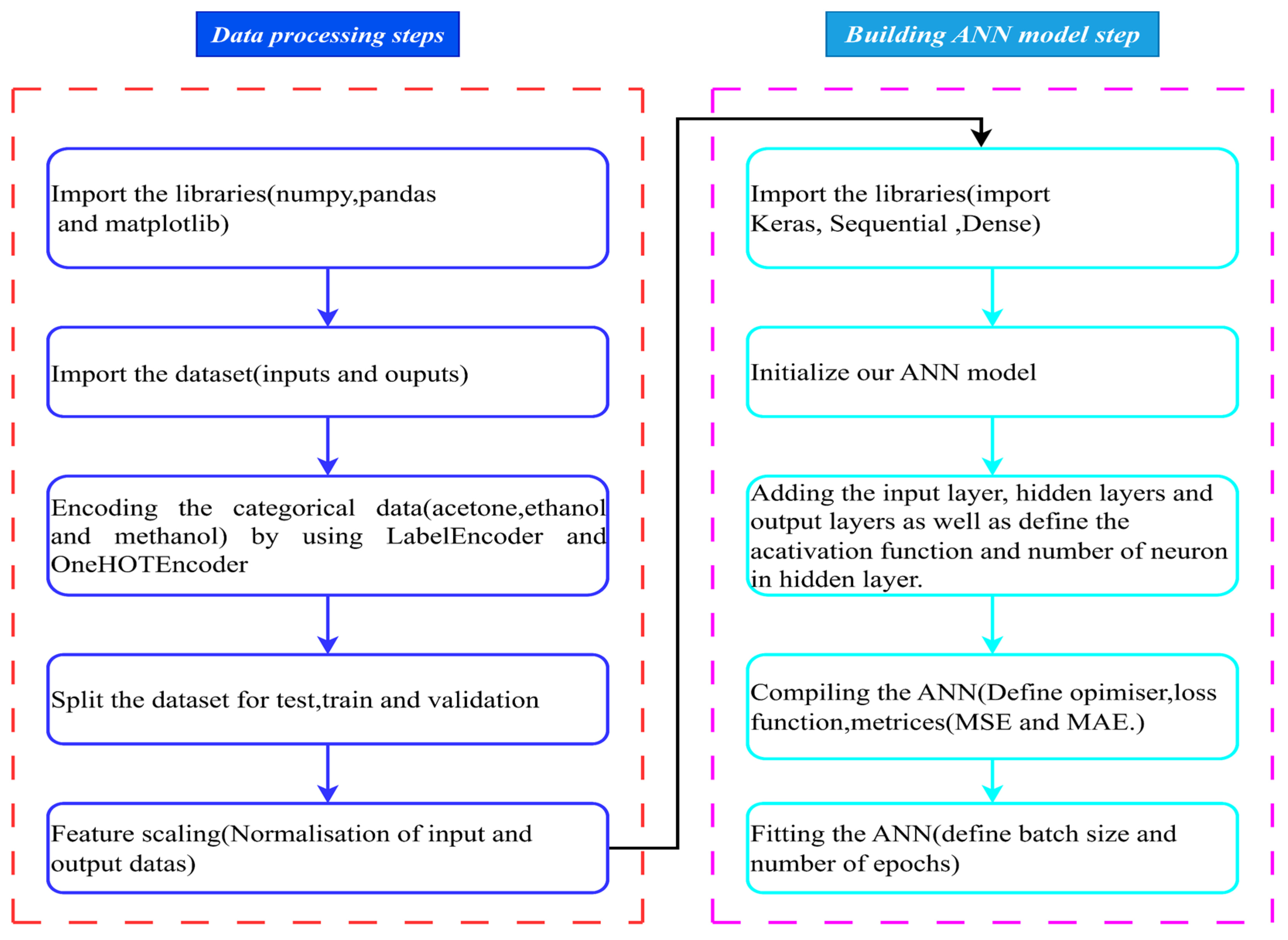
2.2. Artificial Neural Networks
2.2.1. Preparing the Training, Testing, and Validation Datasets
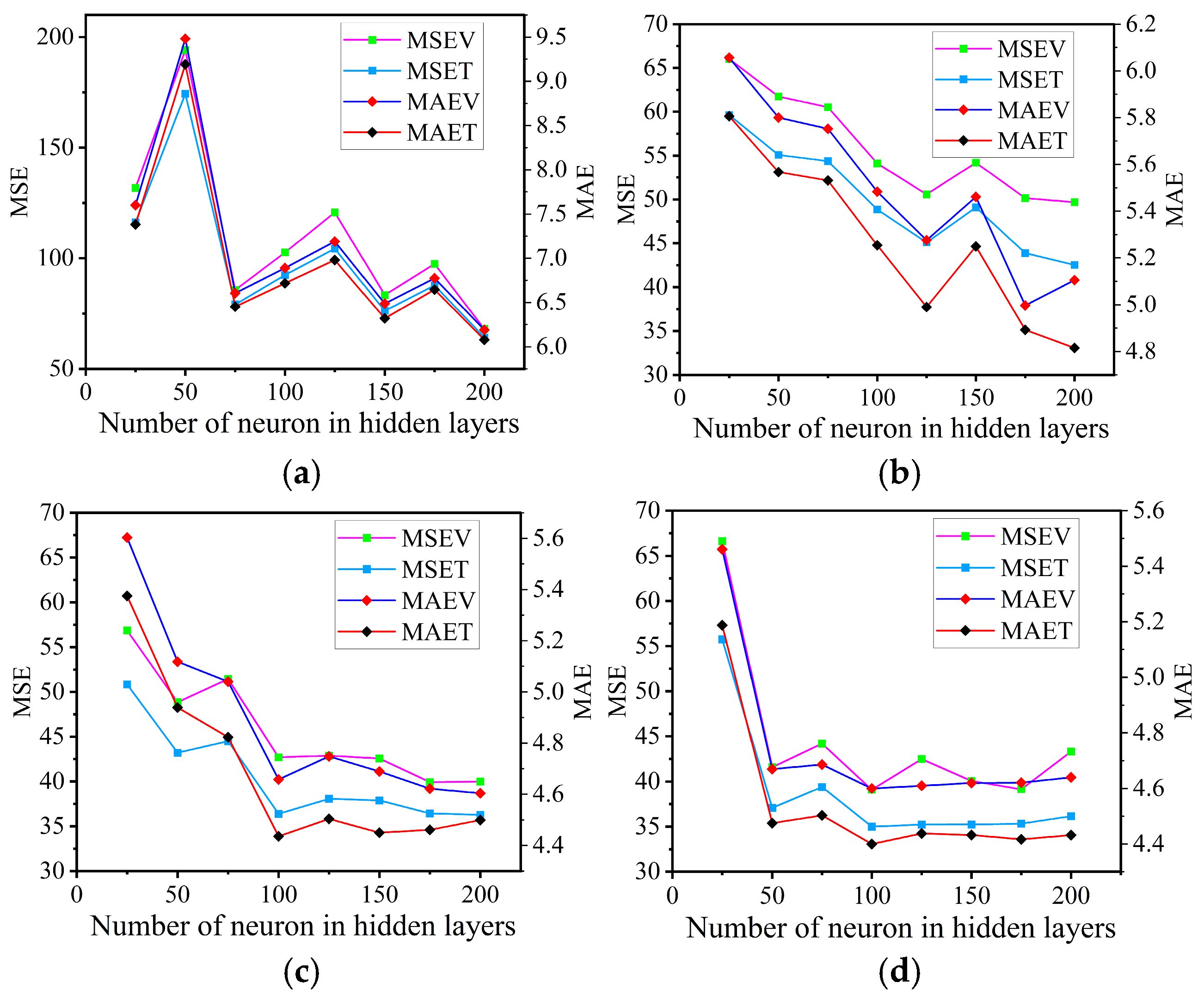
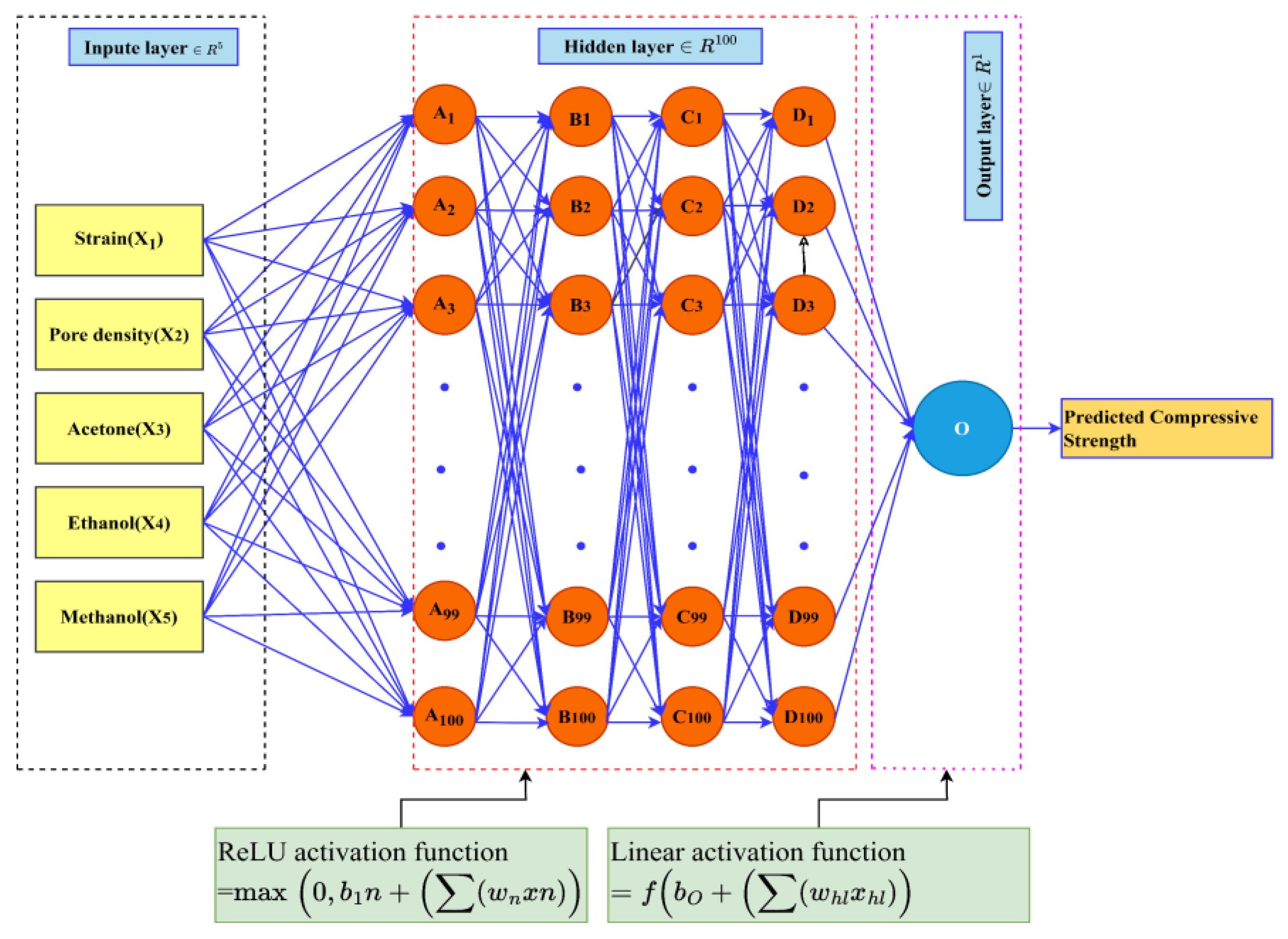
2.2.2. Construction of the ANN Model
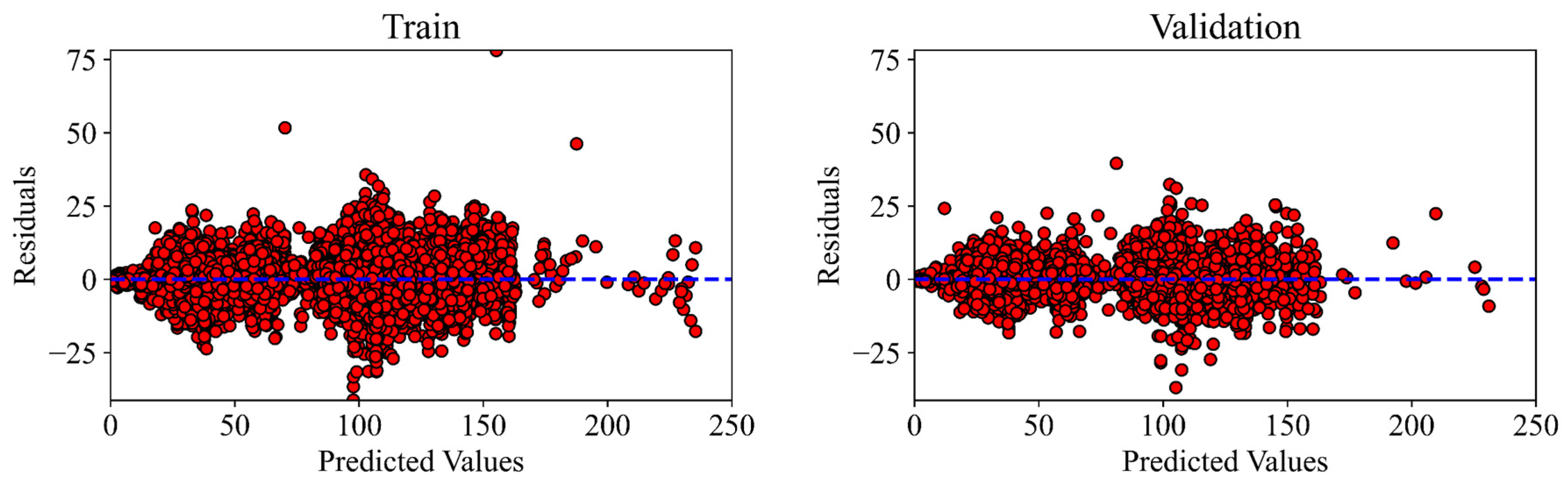
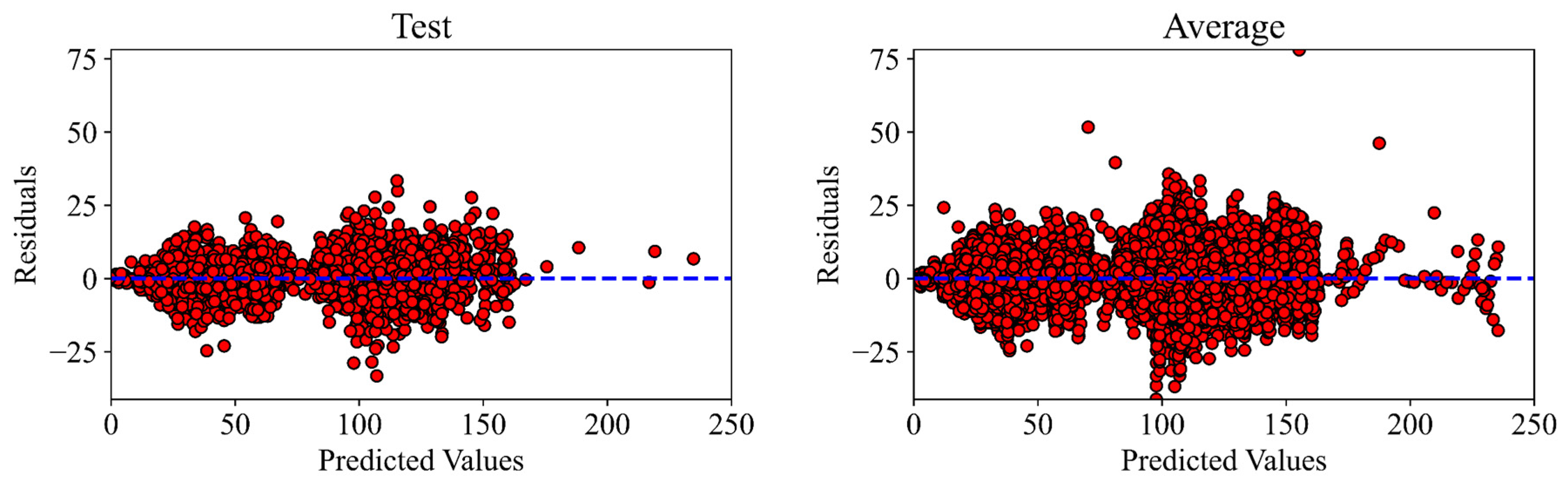
2.2.3. Evaluation of ANN Model Performance
2.2.4. Weight and Bias of the ANN Model
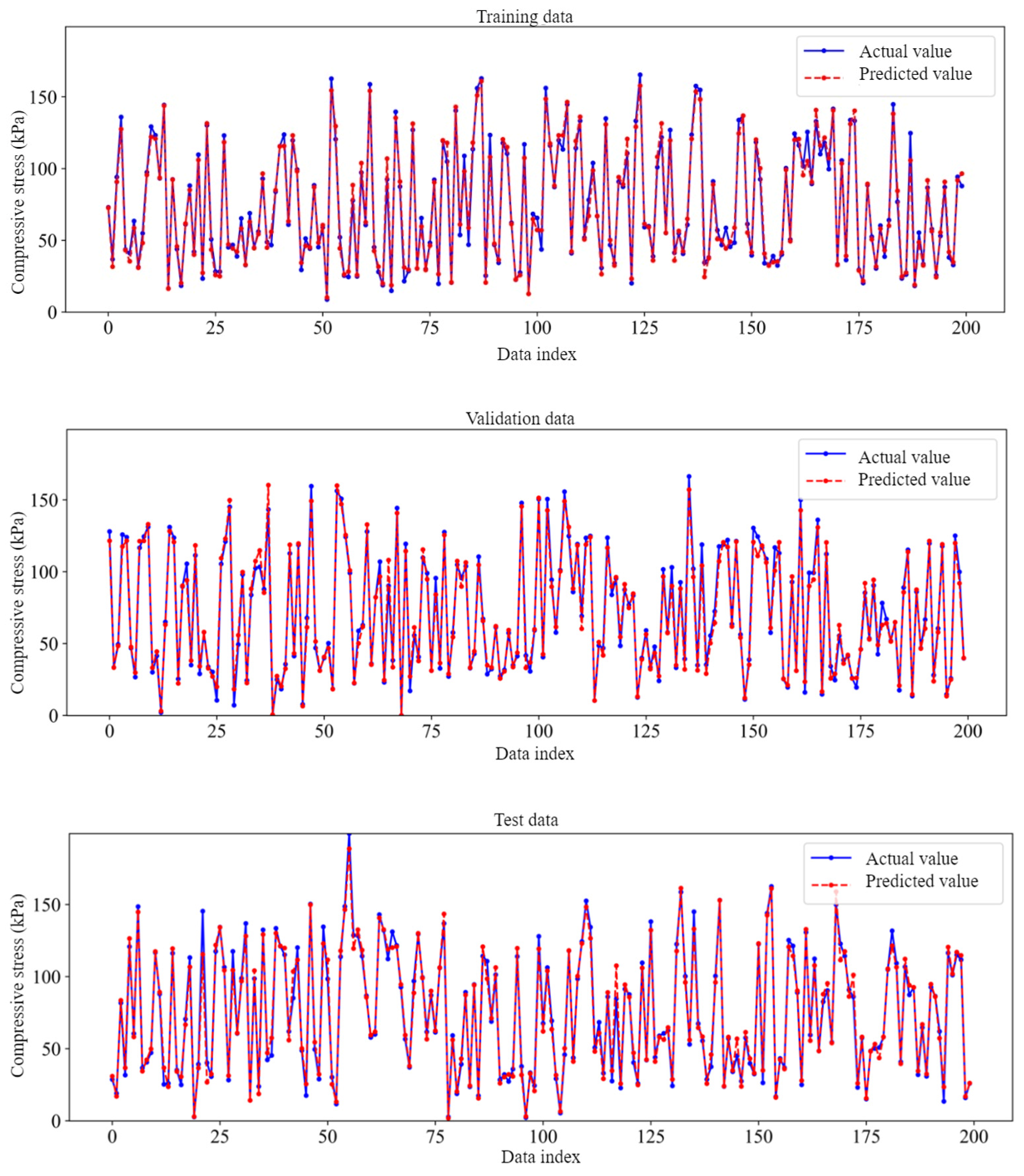
3. Discussion of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Liu, H.; Yang, Y.; Tian, N.; You, C.; Yang, Y. Foam-Structured Carbon Materials and Composites for Electromagnetic Interference Shielding: Design Principles and Structural Evolution. Carbon 2024, 217, 118608. [Google Scholar] [CrossRef]
- Fan, R.; Zheng, N.; Sun, Z. Enhanced Photothermal Conversion Capability of Melamine Foam-Derived Carbon Foam-Based Form-Stable Phase Change Composites. Energy Convers. Manag. 2022, 263, 115693. [Google Scholar] [CrossRef]
- Li, H.; Wang, B.; Zhang, Y.; Li, Y.; Hu, M.; Xu, J.; Cao, S. Synthesis of Carbon Nanofibers from Carbon Foam Composites via Oxyacetylene Torch Ablation. Mater. Manuf. Process 2015, 30, 54–58. [Google Scholar] [CrossRef]
- Bagal, R.; Bahir, M.; Lenka, N.; Patro, T.U. Polymer Derived Porous Carbon Foam and Its Application in Bone Tissue Engineering: A Review. Int. J. Polym. Mater. Polym. Biomater. 2023, 72, 909–924. [Google Scholar] [CrossRef]
- Seo, S.W.; Kang, S.C.; Im, J.S. Synthesis and Formation Mechanism of Pitch-Based Carbon Foam for Three-Dimensional Structural Applications. Inorg. Chem. Commun. 2023, 156, 111285. [Google Scholar] [CrossRef]
- Narasimman, R.; Prabhakaran, K. Preparation of Carbon Foams with Enhanced Oxidation Resistance by Foaming Molten Sucrose Using a Boric Acid Blowing Agent. Carbon 2013, 55, 305–312. [Google Scholar] [CrossRef]
- Kornievsky, A.; Nasedkin, A. Numerical Investigation of Mechanical Properties of Foams Modeled by Regular Gibson–Ashby Lattices with Different Internal Structures. Materialia 2022, 26, 101563. [Google Scholar] [CrossRef]
- Iqbal, N.; Mubashar, A.; Ahmed, S.; Arif, N.; Din, E.-U. Investigating Relative Density Effects on Quasi-Static Response of High-Density Rigid Polyurethane Foam (RPUF). Mater. Today Commun. 2022, 31, 103320. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G.; Ibba, A. Mechanical Models of Cellular Solids: Parameters Identification from Experimental Tests. Int. J. Impact Eng. 2007, 34, 3–27. [Google Scholar] [CrossRef]
- Ashby, M.F.; Medalist, R.F.M. The Mechanical Properties of Cellular Solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Mechanical Properties of Regular Porous Biomaterials Made from Truncated Cube Repeating Unit Cells: Analytical Solutions and Computational Models. Mater. Sci. Eng. C 2016, 60, 163–183. [Google Scholar] [CrossRef] [PubMed]
- Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical Properties of Open-Cell Rhombic Dodecahedron Cellular Structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Campoli, G.; Amin Yavari, S.; Sajadi, B.; Wauthle, R.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Mechanical Behavior of Regular Open-Cell Porous Biomaterials Made of Diamond Lattice Unit Cells. J. Mech. Behav. Biomed. Mater. 2014, 34, 106–115. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.-L. Micromechanical Modeling of Three-Dimensional Open-Cell Foams. In Advances in Soft Matter Mechanics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 213–258. ISBN 978-3-642-19372-9. [Google Scholar]
- An, Y.; Wen, C.; Hodgson, P.D.; Yang, C. Investigation of Cell Shape Effect on the Mechanical Behaviour of Open-Cell Metal Foams. Comput. Mater. Sci. 2012, 55, 1–9. [Google Scholar] [CrossRef]
- Shakibanezhad, R.; Sadighi, M.; Hedayati, R. Numerical and Experimental Study of Quasi-Static Loading of Aluminum Closed-Cell Foams Using Weaire–Phelan and Kelvin Tessellations. Transp. Porous Media 2022, 142, 229–248. [Google Scholar] [CrossRef]
- El Ghezal, M.I.; Maalej, Y.; Doghri, I. Micromechanical Models for Porous and Cellular Materials in Linear Elasticity and Viscoelasticity. Comput. Mater. Sci. 2013, 70, 51–70. [Google Scholar] [CrossRef]
- Gong, L.; Kyriakides, S.; Jang, W.-Y. Compressive Response of Open-Cell Foams. Part I: Morphology and Elastic Properties. Int. J. Solids Struct. 2005, 42, 1355–1379. [Google Scholar] [CrossRef]
- Gencel, O.; Nodehi, M.; Bozkurt, A.; Sarı, A.; Ozbakkaloglu, T. The Use of Computerized Tomography (CT) and Image Processing for Evaluation of the Properties of Foam Concrete Produced with Different Content of Foaming Agent and Aggregate. Constr. Build. Mater. 2023, 399, 132433. [Google Scholar] [CrossRef]
- Ghazi, A.; Berke, P.; Tiago, C.; Massart, T.J. Computed Tomography Based Modelling of the Behaviour of Closed Cell Metallic Foams Using a Shell Approximation. Mater. Des. 2020, 194, 108866. [Google Scholar] [CrossRef]
- Goga, V. New Phenomenological Model for Solid Foams. In Computational Modelling and Advanced Simulations; Murín, J., Kompiš, V., Kutiš, V., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 67–82. ISBN 978-94-007-0317-9. [Google Scholar]
- Luo, G.; Zhu, Y.; Zhang, R.; Cao, P.; Liu, Q.; Zhang, J.; Sun, Y.; Yuan, H.; Guo, W.; Shen, Q.; et al. A Review on Mechanical Models for Cellular Media: Investigation on Material Characterization and Numerical Simulation. Polymers 2021, 13, 3283. [Google Scholar] [CrossRef]
- Daxner, T. Finite Element Modeling of Cellular Materials. In Cellular and Porous Materials in Structures and Processes; Altenbach, H., Öchsner, A., Eds.; CISM International Centre for Mechanical Sciences; Springer: Vienna, Austria, 2010; Volume 521, pp. 47–106. ISBN 978-3-7091-0296-1. [Google Scholar]
- Martinsen, Ø.G.; Heiskanen, A. Data and Models. In Bioimpedance and Bioelectricity Basics; Elsevier: Amsterdam, The Netherlands, 2023; pp. 345–433. ISBN 978-0-12-819107-1. [Google Scholar]
- Casalino, G. [INVITED] Computational Intelligence for Smart Laser Materials Processing. Opt. Laser Technol. 2018, 100, 165–175. [Google Scholar] [CrossRef]
- Mears, L.; Stocks, S.M.; Sin, G.; Gernaey, K.V. A Review of Control Strategies for Manipulating the Feed Rate in Fed-Batch Fermentation Processes. J. Biotechnol. 2017, 245, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.A.; Zhang, X. Prediction of Oscillatory Heat Transfer Coefficient for a Thermoacoustic Heat Exchanger through Artificial Neural Network Technique. Int. J. Heat Mass Transf. 2018, 124, 1088–1096. [Google Scholar] [CrossRef]
- Mohanraj, M.; Jayaraj, S.; Muraleedharan, C. Applications of Artificial Neural Networks for Thermal Analysis of Heat Exchangers—A Review. Int. J. Therm. Sci. 2015, 90, 150–172. [Google Scholar] [CrossRef]
- Yadav, D.; Naruka, D.S.; Kumar Singh, P. Employing ANN Model for Prediction of Thermal Conductivity of CNT Nanofluids. In Proceedings of the 2020 International Conference on Contemporary Computing and Applications (IC3A), Lucknow, India, 5–7 February 2020; IEEE: New York, NY, USA, 2020; pp. 163–168. [Google Scholar]
- Habeeb, M.; Woon You, H.; Balasaheb Aher, K.; Balasaheb Bhavar, G.; Suryabhan Pawar, S.; Dnyaneshwar Gaikwad, S. Artificial Neural Networks for the Prediction of Mechanical Properties of CGNP/PLGA Nanocomposites. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Ismail, A.S.; Sathyamurthy, R.; Abdelhamid, T.; Edreis, E.M.A.; Kabeel, A.E.; Haiou, Z. An Artificial Neural Network Based Approach for Prediction the Thermal Conductivity of Nanofluids. SN Appl. Sci. 2020, 2, 235. [Google Scholar] [CrossRef]
- Hong, G.; Seong, N. Optimization of the ANN Model for Energy Consumption Prediction of Direct-Fired Absorption Chillers for a Short-Term. Buildings 2023, 13, 2526. [Google Scholar] [CrossRef]
- Dadrasi, A.; Albooyeh, A.R.; Fooladpanjeh, S.; Shad, M.D.; Beynaghi, M. RSM and ANN Modeling of the Energy Absorption Behavior of Steel Thin-Walled Columns: A Multi-Objective Optimization Using the Genetic Algorithm. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 563. [Google Scholar] [CrossRef]
- Di Benedetto, R.M.; Botelho, E.C.; Janotti, A.; Ancelotti Junior, A.C.; Gomes, G.F. Development of an Artificial Neural Network for Predicting Energy Absorption Capability of Thermoplastic Commingled Composites. Compos. Struct. 2021, 257, 113131. [Google Scholar] [CrossRef]
- Xiao, S.; Li, J.; Bordas, S.P.A.; Kim, T.-Y. Artificial Neural Networks and Their Applications in Computational Materials Science: A Review and a Case Study. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, pp. 1–33. ISBN 978-0-443-13705-1. [Google Scholar]
- Sriram, R.; Vaidya, U.K.; Kim, J.-E. Blast Impact Response of Aluminum Foam Sandwich Composites. J. Mater. Sci. 2006, 41, 4023–4039. [Google Scholar] [CrossRef]
- Maheo, L.; Viot, P.; Bernard, D.; Chirazi, A.; Ceglia, G.; Schmitt, V.; Mondain-Monval, O. Elastic Behavior of Multi-Scale, Open-Cell Foams. Compos. Part B Eng. 2013, 44, 172–183. [Google Scholar] [CrossRef]
- Zhuang, W.; Wang, E.; Zhang, H. Prediction of Compressive Mechanical Properties of Three-Dimensional Mesoscopic Aluminium Foam Based on Deep Learning Method. Mech. Mater. 2023, 182, 104684. [Google Scholar] [CrossRef]
- Raj, R.E.; Daniel, B.S.S. Prediction of Compressive Properties of Closed-Cell Aluminum Foam Using Artificial Neural Network. Comput. Mater. Sci. 2008, 43, 767–773. [Google Scholar] [CrossRef]
- Capuano, G.; Rimoli, J.J. Smart Finite Elements: A Novel Machine Learning Application. Comput. Methods Appl. Mech. Eng. 2019, 345, 363–381. [Google Scholar] [CrossRef]
- Zhuang, W.; Wang, E.; Zhang, H. Prediction of the Compressive Mechanical Properties and Reverse Structural Design of Two-Dimensional Mesoscopic Aluminum Foam Based on Deep Learning Methods. J. Mater. Sci. 2024, 59, 11416–11439. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, A.E.; Plascencia-Mora, H. A Machine Learning Approach to Estimate the Strain Energy Absorption in Expanded Polystyrene Foams. J. Cell Plast. 2022, 58, 399–427. [Google Scholar] [CrossRef]
- Hangai, Y.; Sakaguchi, Y.; Kitahara, Y.; Takagi, T.; Kenji, O.; Yuuki, T. Plateau Stress Estimation of Aluminum Foam by Machine Learning Using X-Ray Computed Tomography Images. Int. J. Adv. Manuf. Technol. 2024, 132, 5053–5061. [Google Scholar] [CrossRef]
- Hangai, Y.; Ozawa, S.; Okada, K.; Tanaka, Y.; Amagai, K.; Suzuki, R. Machine Learning Estimation of Plateau Stress of Aluminum Foam Using X-Ray Computed Tomography Images. Materials 2023, 16, 1894. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, A.E.; Plascencia-Mora, H. Modeling Hysteresis in Expanded Polystyrene Foams under Compressive Loads Using Feed-Forward Neural Networks. J. Cell Plast. 2023, 59, 269–292. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, A.E.; Plascencia-Mora, H.; Acevedo-Alvarado, M. Neural Network-Driven Interpretability Analysis for Evaluating Compressive Stress in Polymer Foams. J. Cell Plast. 2024, 60, 237–258. [Google Scholar] [CrossRef]
- Stręk, A.M.; Dudzik, M.; Machniewicz, T. Specifications for Modelling of the Phenomenon of Compression of Closed-Cell Aluminium Foams with Neural Networks. Materials 2022, 15, 1262. [Google Scholar] [CrossRef] [PubMed]
- Ozan, S.; Taskin, M.; Kolukisa, S.; Ozerdem, M.S. Application of ANN in the Prediction of the Pore Concentration of Aluminum Metal Foams Manufactured by Powder Metallurgy Methods. Int. J. Adv. Manuf. Technol. 2008, 39, 251–256. [Google Scholar] [CrossRef]
- Gahlen, P.; Mainka, R.; Stommel, M. Prediction of Anisotropic Foam Stiffness Properties by a Neural Network. Int. J. Mech. Sci. 2023, 249, 108245. [Google Scholar] [CrossRef]
- Pech-Mendoza, M.I.; Rodríguez-Sánchez, A.E.; Plascencia-Mora, H. Neural Networks-Based Modeling of Compressive Stress in Expanded Polystyrene Foams: A Focus on Bead Size Parameters. Proc. Inst. Mech. Eng. Part J. Mater. Des. Appl. 2024, 238, 1331–1341. [Google Scholar] [CrossRef]
- Aengchuan, P.; Boonpuek, P.; Klinsuk, J. Prediction of Stress Relaxation Behavior of Polymer Foam Using Artificial Neural Network. Mater. Sci. Forum 2024, 1126, 37–42. [Google Scholar] [CrossRef]
- Sheini Dashtgoli, D.; Taghizadeh, S.; Macconi, L.; Concli, F. Comparative Analysis of Machine Learning Models for Predicting the Mechanical Behavior of Bio-Based Cellular Composite Sandwich Structures. Materials 2024, 17, 3493. [Google Scholar] [CrossRef]
- Abdellatief, M.; Wong, L.S.; Din, N.M.; Ahmed, A.N.; Hassan, A.M.; Ibrahim, Z.; Murali, G.; Mo, K.H.; El-Shafie, A. Sustainable Foam Glass Property Prediction Using Machine Learning: A Comprehensive Comparison of Predictive Methods and Techniques. Results Eng. 2025, 25, 104089. [Google Scholar] [CrossRef]
- Salami, B.A.; Iqbal, M.; Abdulraheem, A.; Jalal, F.E.; Alimi, W.; Jamal, A.; Tafsirojjaman, T.; Liu, Y.; Bardhan, A. Estimating Compressive Strength of Lightweight Foamed Concrete Using Neural, Genetic and Ensemble Machine Learning Approaches. Cem. Concr. Compos. 2022, 133, 104721. [Google Scholar] [CrossRef]
- Wacławiak, K.; Myalski, J.; Gurmu, D.N.; Sirata, G.G. Experimental Analysis of the Mechanical Properties of Carbon Foams Under Quasi-Static Compressive Loads. Materials 2024, 17, 5605. [Google Scholar] [CrossRef]
- Bai, J.; Li, M.; Shen, J. Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms. Materials 2024, 17, 4222. [Google Scholar] [CrossRef]
- Mauro, A.W.; Revellin, R.; Viscito, L. Development and Assessment of Performance of Artificial Neural Networks for Prediction of Frictional Pressure Gradients during Two-Phase Flow. Int. J. Heat Mass Transf. 2024, 221, 125106. [Google Scholar] [CrossRef]
- Moheimani, R.; Gonzalez, M.; Dalir, H. An Integrated Nanocomposite Proximity Sensor: Machine Learning-Based Optimization, Simulation, and Experiment. Nanomaterials 2022, 12, 1269. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Singh, L.K.; Yadav, M.K. Utilization of ANN for the Prediction of Mechanical Properties in AlP0507-MWCNT-RHA Composites. Met. Mater. Int. 2024, 30, 1106–1122. [Google Scholar] [CrossRef]
- Akdag, U.; Komur, M.A.; Akcay, S. Prediction of Heat Transfer on a Flat Plate Subjected to a Transversely Pulsating Jet Using Artificial Neural Networks. Appl. Therm. Eng. 2016, 100, 412–420. [Google Scholar] [CrossRef]
- Shafabakhsh, G.H.; Ani, O.J.; Talebsafa, M. Artificial Neural Network Modeling (ANN) for Predicting Rutting Performance of Nano-Modified Hot-Mix Asphalt Mixtures Containing Steel Slag Aggregates. Constr. Build. Mater. 2015, 85, 136–143. [Google Scholar] [CrossRef]
- Jiang, H.; Xi, Z.; Rahman, A.A.; Zhang, X. Prediction of Output Power with Artificial Neural Network Using Extended Datasets for Stirling Engines. Appl. Energy 2020, 271, 115123. [Google Scholar] [CrossRef]
- Merayo, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of Mechanical Properties by Artificial Neural Networks to Characterize the Plastic Behavior of Aluminum Alloys. Materials 2020, 13, 5227. [Google Scholar] [CrossRef]
- Xue, J.; Shao, J.F.; Burlion, N. Estimation of Constituent Properties of Concrete Materials with an Artificial Neural Network Based Method. Cem. Concr. Res. 2021, 150, 106614. [Google Scholar] [CrossRef]
- Merayo Fernández, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of the Bilinear Stress-Strain Curve of Aluminum Alloys Using Artificial Intelligence and Big Data. Metals 2020, 10, 904. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Z.; Jia, Z.; Hou, M.; Yang, X.; Ying, X.; Ji, Z. Artificial Neural Network-Based Shelf Life Prediction Approach in the Food Storage Process: A Review. Crit. Rev. Food Sci. Nutr. 2024, 64, 12009–12024. [Google Scholar] [CrossRef]
- Bhagya Raj, G.V.S.; Dash, K.K. Comprehensive Study on Applications of Artificial Neural Network in Food Process Modeling. Crit. Rev. Food Sci. Nutr. 2022, 62, 2756–2783. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Y.; Zhang, Z.; Wang, Z.; Liu, B.; Liu, C.; Huang, C.; Dong, S.; Pu, X.; Wan, F. Plant Image Recognition with Deep Learning: A Review. Comput. Electron. Agric. 2023, 212, 108072. [Google Scholar] [CrossRef]
- Linkon, A.H.M.; Labib, M.M.; Hasan, T.; Hossain, M. Deep Learning in Prostate Cancer Diagnosis and Gleason Grading in Histopathology Images: An Extensive Study. Inform. Med. Unlocked 2021, 24, 100582. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, J. A Dual-Layer Attention-Based LSTM Network for Fed-Batch Fermentation Process Modelling. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2021; Volume 50, pp. 541–547. ISBN 978-0-323-88506-5. [Google Scholar]
- Parsa, M.; Rad, H.Y.; Vaezi, H.; Hossein-Zadeh, G.-A.; Setarehdan, S.K.; Rostami, R.; Rostami, H.; Vahabie, A.-H. EEG-Based Classification of Individuals with Neuropsychiatric Disorders Using Deep Neural Networks: A Systematic Review of Current Status and Future Directions. Comput. Methods Prog. Biomed 2023, 240, 107683. [Google Scholar] [CrossRef]
- Reyad, M.; Sarhan, A.M.; Arafa, M. A Modified Adam Algorithm for Deep Neural Network Optimization. Neural Comput. Appl. 2023, 35, 17095–17112. [Google Scholar] [CrossRef]
- Team, K. Keras Documentation: Getting Started with Keras. Available online: https://keras.io/getting_started/ (accessed on 11 March 2025).
- Pundhir, S.; Kumari, V.; Ghose, U. Performance Interpretation of Supervised Artificial Neural Network Highlighting Role of Weight and Bias for Link Prediction. In International Conference on Artificial Intelligence and Sustainable Engineering; Sanyal, G., Travieso-González, C.M., Awasthi, S., Pinto, C.M.A., Purushothama, B.R., Eds.; Lecture Notes in Electrical Engineering; Springer Nature: Singapore, 2022; Volume 836, pp. 109–119. ISBN 978-981-16-8541-5. [Google Scholar]
- Moosavi, S.R.; Wood, D.A.; Ahmadi, M.A.; Choubineh, A. ANN-Based Prediction of Laboratory-Scale Performance of CO2-Foam Flooding for Improving Oil Recovery. Nat. Resour. Res. 2019, 28, 1619–1637. [Google Scholar] [CrossRef]



| No | Author(s) | Objectives | Materials | Methodology | Key Findings/Results |
|---|---|---|---|---|---|
| 1 | Zhuang et al. [41] | To predict mechanical properties of aluminum foam | Aluminum foam | 2D convolutional neural network (2D-CNN) and conditional generative adversarial network (CGAN) | Achieved < 3% error in predicting mechanical properties of aluminum foam by using 2D-CNN. |
| 2 | Rodríguez-Sánchez et al. [42] | To map compressive stress response and energy absorption parameters of an expanded polystyrene foam | Expanded polystyrene foams | ANN | ANN model outperformed prediction capabilities of compressive strength and strain energy absorption of polystyrene foam and obtained errors around 2% of experimental data only. |
| 3 | Hangai et al. [43] | To estimate the plateau stress of aluminum foam | Aluminum foam | Supervised learning neural network model and X-ray computed tomography (CT) | Using an ANN is the most promising method and can train results obtained from advanced 3D imaging techniques such as CT-scan. |
| 4 | Hangai et al. [44] | To estimate the plateau stress of aluminum foam | Aluminum foam | CNN and X-ray CT | The plateau stresses estimated by machine learning and those obtained by the compression test were almost identical. |
| 5 | Rodríguez-Sánchez and Plascencia-Mora [45] | Predict the mechanical response of expanded polystyrene foam | Expanded polystyrene foams | Feed-forward ANN | ANN predicted the mechanical response almost the same with experimental values (errors of less than 3%). |
| 6 | Rodríguez-Sánchez and Plascencia-Mora [46] | Predict compressive stress responses of polymer foam by taking density, loading rate, and strain as input parameter | Expanded Polypropylene and expanded polystyrene foams | Feed-forwarded ANN with interpretability tool | Integration of interpretability tools with ANN models offers a robust method for material response analysis (compressive properties) and contributing to a deeper understanding of material science. |
| 7 | Stręk et al. [47] | Verify the possibility of describing compression phenomenon of closed-cell aluminum by ANNs | Closed-cell aluminum foams | ANNs and experimental | ANNs were found to be appropriate tools for building models of the compression phenomenon of aluminum foams. |
| 8 | Zhuang et al. [38] | To investigate the mechanical properties of Voronoi modeled aluminum foam | Aluminum foam | 3D-CNN and FEA | Deep learning has more advantages in efficiency and accuracy of predicting mechanical properties of cellular solids and is an effective alternative to numerical simulation. |
| 9 | Ozan et al. [48] | To study effect of fabrication parameters on the pore concentration of aluminum metal foam | Aluminum foam | ANN and experimental | The ANN was successfully used to predict the pore concentration % (volume) of aluminum foam related to fabrication parameters. |
| 10 | Gahlen et al. [49] | To predict the orthotropic stiffness tensor of anisotropic foam structures utilizing a tessellation-based foam RVE database | Low-density closed-cell PUR | FEA and ANN | The anisotropy of complex foam structures can be determined via the ANN within seconds instead of performing time-consuming simulations (up to hours). |
| 11 | Pech-Mendoza et al. [50] | To predict the compressive stress responses of polystyrene foams | Expanded polystyrene | ANN | The utility of ANNs in modeling the compressive behavior of polystyrene foams resulted in errors of less than 3% as compared to the experiment. |
| 12 | Aengchuan et al. [51] | To predict the stress relaxation of polymer foam | Polymer foam | Feed-forward ANN | The results demonstrate that the ANN model achieved highly accurate predictions for the relaxation stress of polymer foam. |
| 13 | Dashtgoli et al. [52] | To investigate the mechanical behavior of biocomposite cellular sandwich structures under quasi-static out-of-plane compression | Bio-based cellular composite | Machine learning (ML) | Advanced ML models gave accurate predictions of the mechanical behavior of biocomposites, enabling more efficient and cost-effective development. |
| 14 | Abdellatief et al. [53] | To predict porosity and compressive strength of foam glass | Foam glass (FG) | Gradient boosting (GB), random forest (RF), gaussian process regression (GPR), and linear regression (LR) | The optimization of FG was production by providing reliable tools for predicting and controlling porosity and compressive strength, reducing material waste, enhancing product quality, and streamlining manufacturing processes. |
| 15 | Salami et al. [54] | To develop ANN, GEP, and GBT models for predicting compressive strength of foamed concrete | Foamed concrete | ANN, gene expression programming (GEP), and gradient boosting tree (GBT) models | A GBT model offered reliable accuracy in predicting the compressive strength of foamed concrete. |
| Number of Hidden Layers | Epochs | Number of Neurons in Hidden Layers | Validation | Testing | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | R2 | MAE | MSE | R2 | MAE | |||
| 1 | 100 | 150 | 158.16 | 0.9130 | 8.34 | 137.65 | 0.9210 | 7.98 |
| 1000 | 125 | 117.10 | 0.9357 | 7.43 | 103.49 | 0.9409 | 7.15 | |
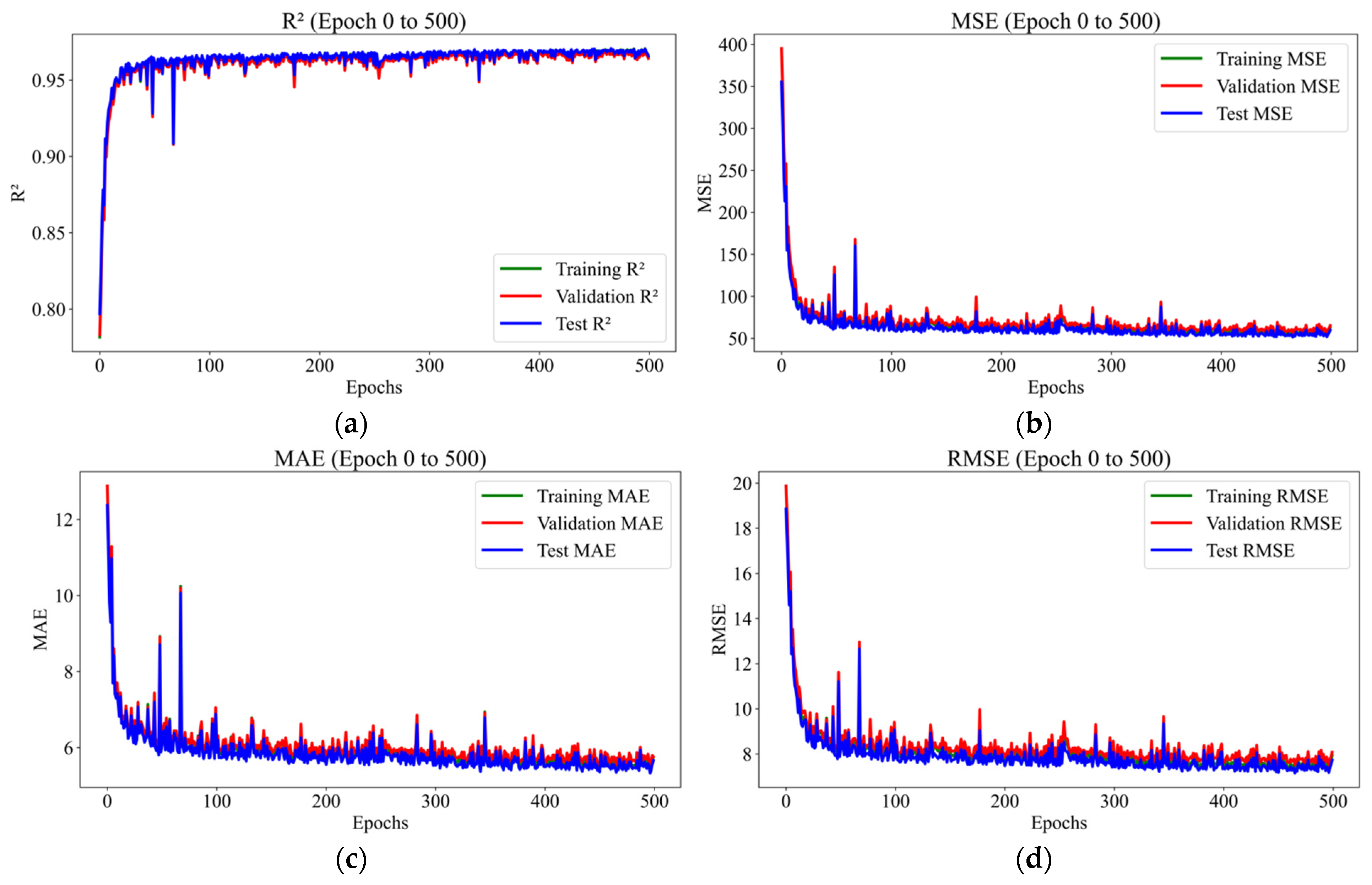
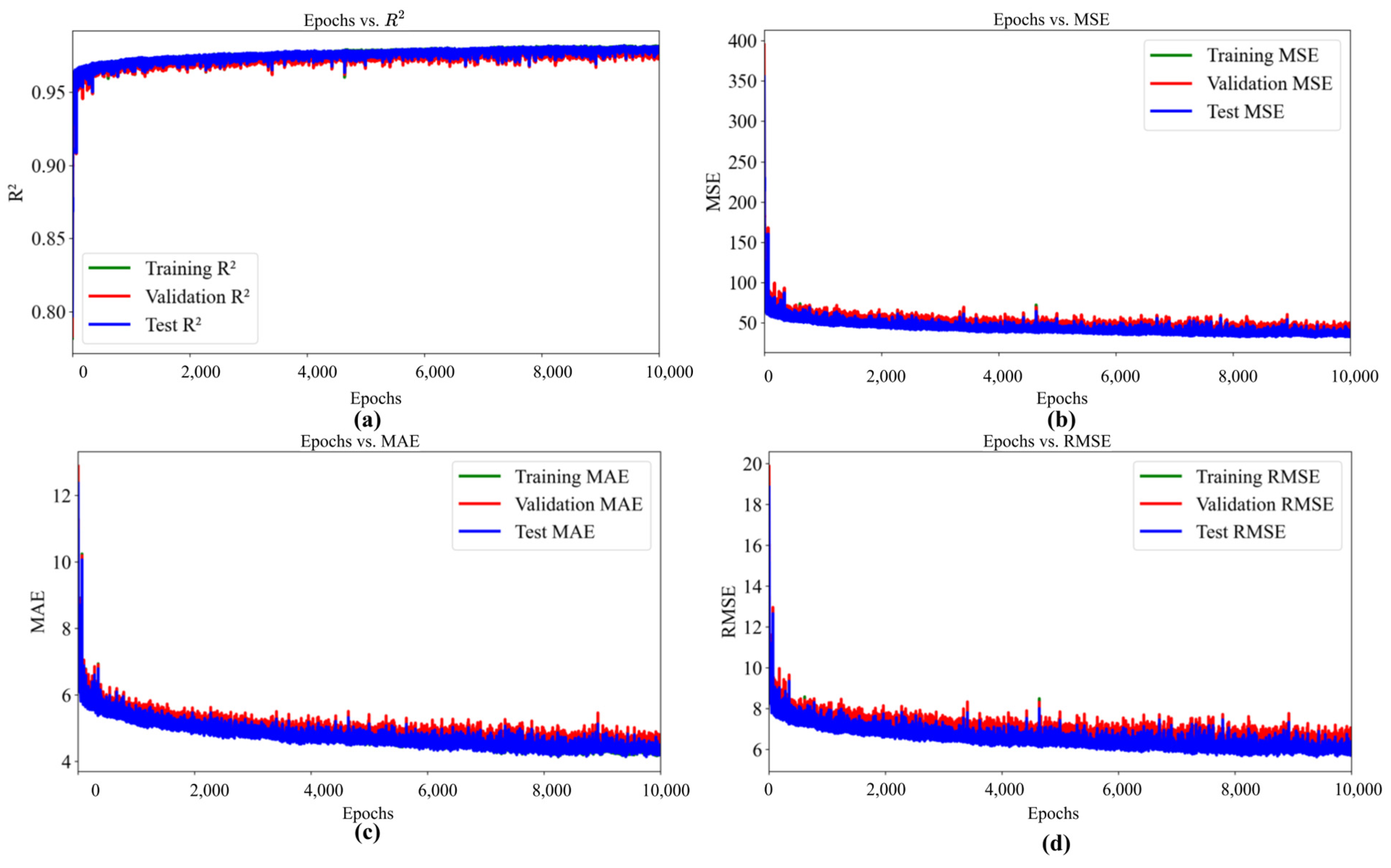
| 10,000 | 200 | 67.99 | 0.9630 | 6.19 | 64.19 | 0.9633 | 6.08 | |
| 2 | 100 | 200 | 81.88 | 0.9550 | 6.44 | 72.47 | 0.9590 | 6.27 |
| 1000 | 175 | 60.51 | 0.9668 | 5.72 | 54.88 | 0.9686 | 5.51 | |
| 10,000 | 200 | 49.69 | 0.9730 | 5.11 | 42.52 | 0.9760 | 4.86 | |
| 3 | 100 | 125 | 68.57 | 0.9620 | 6.17 | 61.58 | 0.9650 | 5.92 |
| 1000 | 200 | 53.15 | 0.9708 | 5.35 | 47.58 | 0.9728 | 5.14 | |
| 10,000 | 175 | 39.93 | 0.9780 | 4.62 | 36.44 | 0.9790 | 4.46 | |
| 4 | 100 | 100 | 65.74 | 0.9640 | 5.99 | 61.22 | 0.9650 | 5.89 |
| 1000 | 200 | 50.31 | 0.9724 | 5.21 | 45.47 | 0.9740 | 5.04 | |
| 10,000 | 100 | 39.10 | 0.9785 | 4.60 | 35.00 | 0.9801 | 4.40 | |
| Parameters | Specification |
|---|---|
| ANN types | Feed-forward Neural Networks |
| Loss function | Mean square error |
| Optimizer | Adam |
| Number of neurons in input layer | 5 |
| Number of hidden layers | 4 |
| Number of neurons in hidden layers | 100 |
| Number of neurons in output layer | 1 |
| Activation function in hidden layer | ReLU |
| Activation function in output layer | Linear |
| Input | Strain, pore density, and solvents |
| Output | Compressive stress |
| Training | Validation Data | Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | RMSE | R2 | MSE | MAE | RMSE | R2 | MSE | MAE | RMSE | R2 |
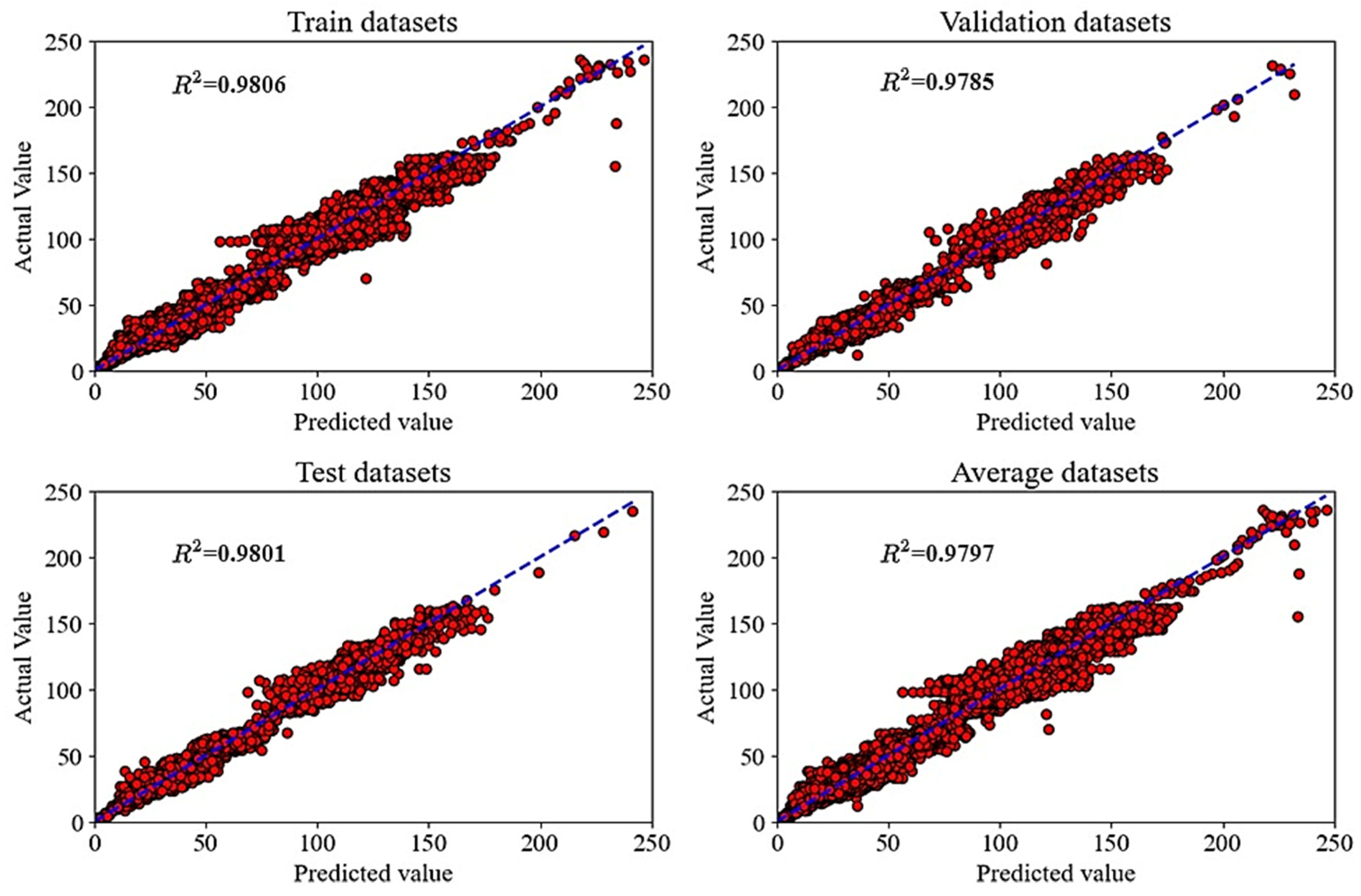
| 34.93 | 4.28 | 5.89 | 0.9806 | 39.1 | 4.6 | 6.22 | 0.9785 | 35 | 4.4 | 5.89 | 0.9801 |
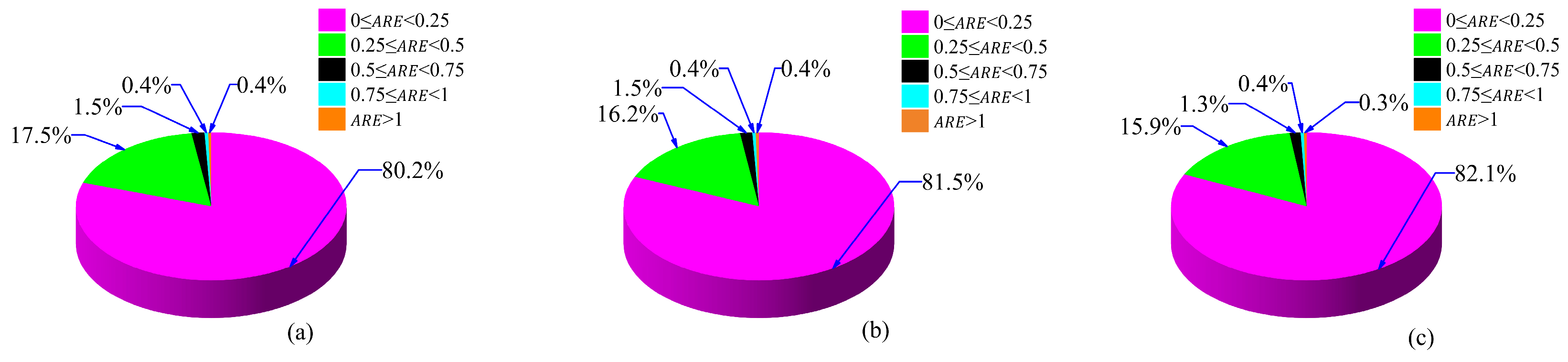
| Statical Parameters | Training Datasets | Validation Datasets | Testing Datasets |
|---|---|---|---|
| Minimum Error | 5.31 × 10−6 | 6.18 × 10−6 | 0 |
| Maximum Error | 1.95 | 1.96 | 1.77 |
| Mean | 8.16 × 10−2 | 8.8 × 10−2 | 8.58 × 10−2 |
| Standard Deviation | 1.13 × 10−1 | 1.22 × 10−1 | 1.21 × 10−1 |
| Lower 95% CI of mean | 7.98 × 10−2 | 8.39 × 10−2 | 8.17 × 10−2 |
| Upper 95% CI of mean | 8.34 × 10−2 | 9.22 × 10−2 | 9 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurmu, D.N.; Wacławiak, K.; Lemu, H.G. Predicting the Compressive Properties of Carbon Foam Using Artificial Neural Networks. Materials 2025, 18, 2516. https://doi.org/10.3390/ma18112516
Gurmu DN, Wacławiak K, Lemu HG. Predicting the Compressive Properties of Carbon Foam Using Artificial Neural Networks. Materials. 2025; 18(11):2516. https://doi.org/10.3390/ma18112516
Chicago/Turabian StyleGurmu, Debela N., Krzysztof Wacławiak, and Hirpa G. Lemu. 2025. "Predicting the Compressive Properties of Carbon Foam Using Artificial Neural Networks" Materials 18, no. 11: 2516. https://doi.org/10.3390/ma18112516
APA StyleGurmu, D. N., Wacławiak, K., & Lemu, H. G. (2025). Predicting the Compressive Properties of Carbon Foam Using Artificial Neural Networks. Materials, 18(11), 2516. https://doi.org/10.3390/ma18112516






