Hot Compression Behavior and Processing Maps of 6063 Aluminum Alloy Under Medium Strain Rate
Abstract
1. Introduction
2. Materials and Experimental Methods
3. The Construction of Processing Map
4. Results and Discussion
4.1. Initial Microstructure
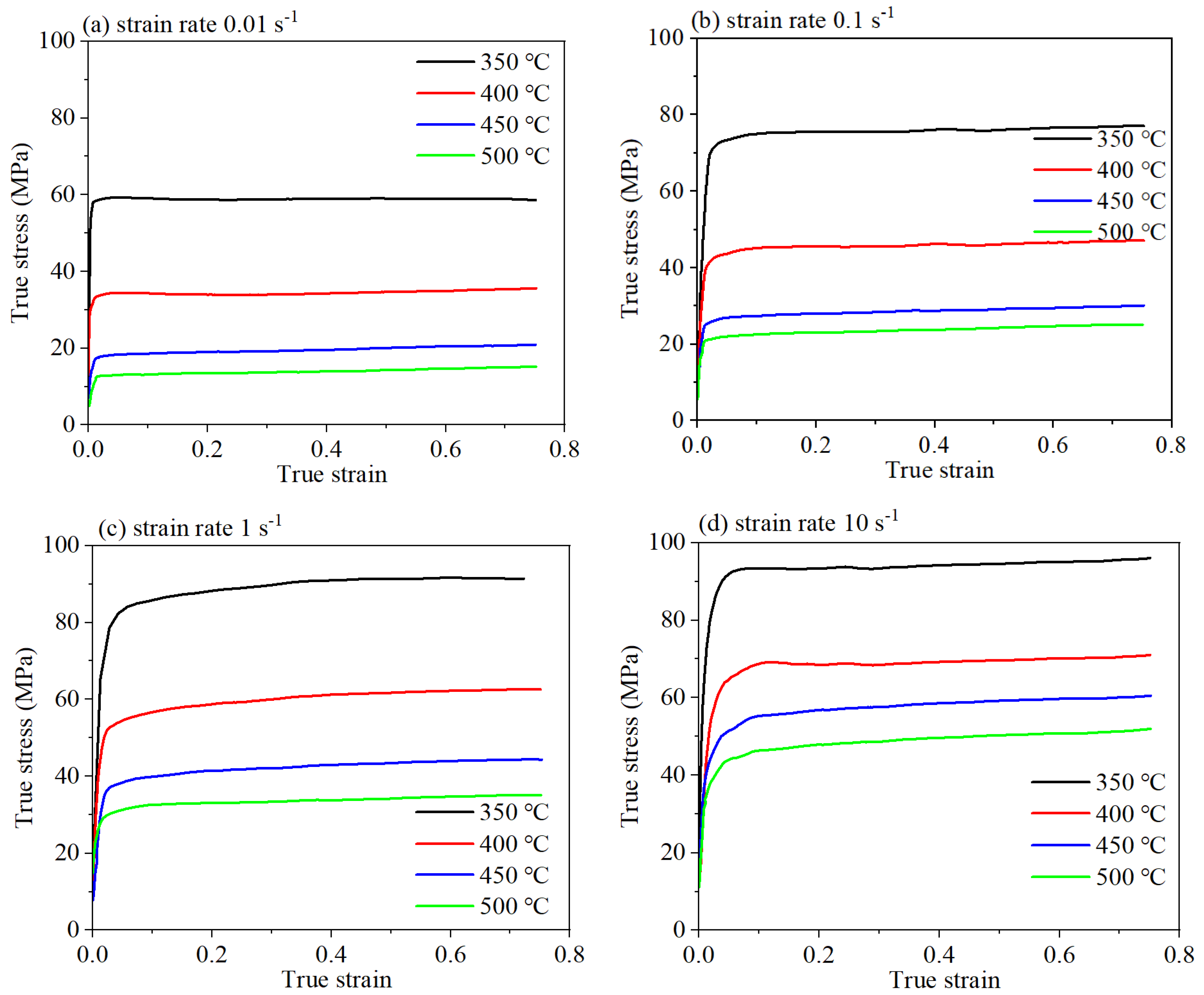
4.2. The True Stress–Strain Curve
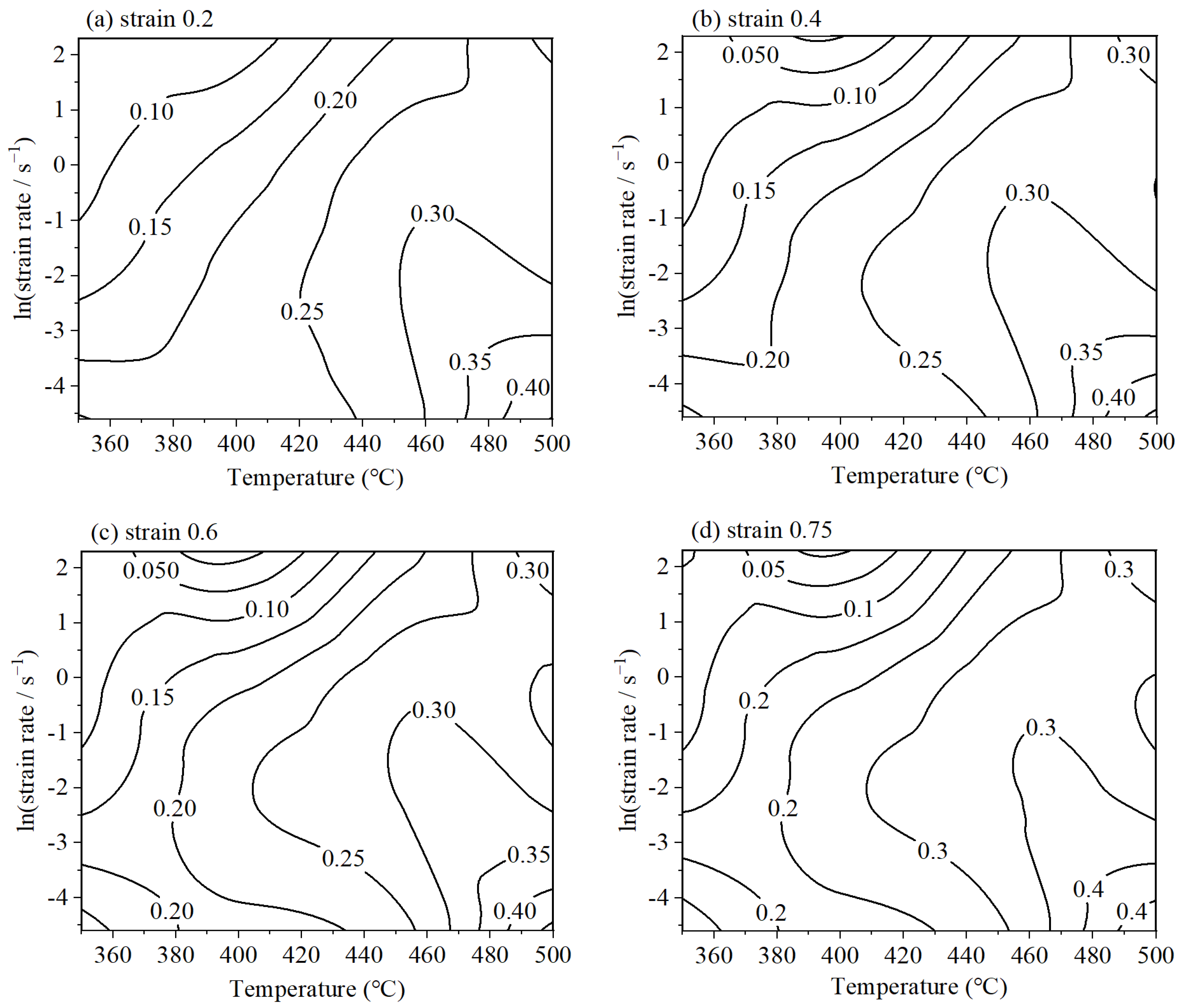
4.3. Processing Map
4.3.1. The Analysis of Strain Rate Sensitivity Factor m
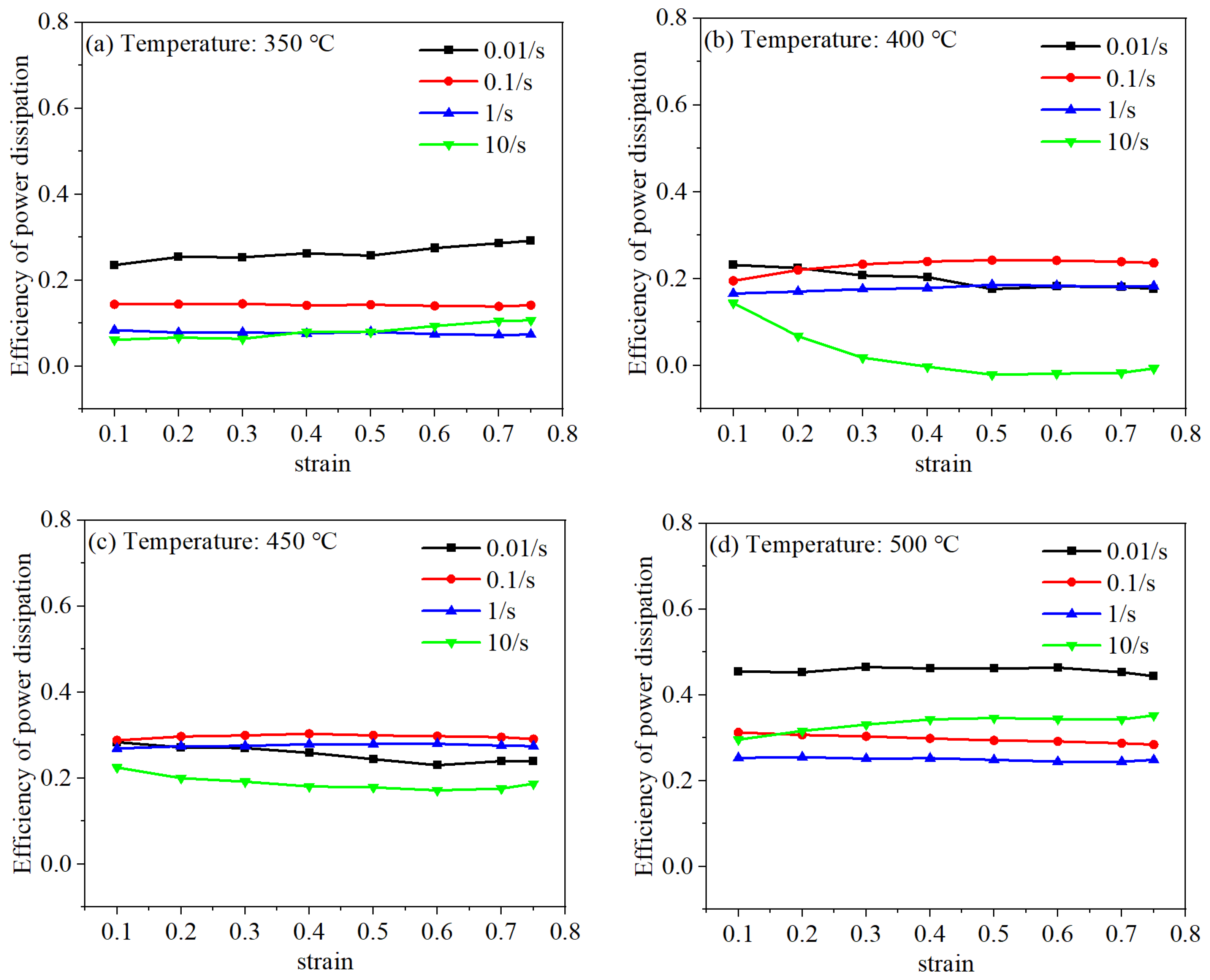
4.3.2. The Analysis of Power Dissipation Efficiency η
4.3.3. The Instability Parameter ξ
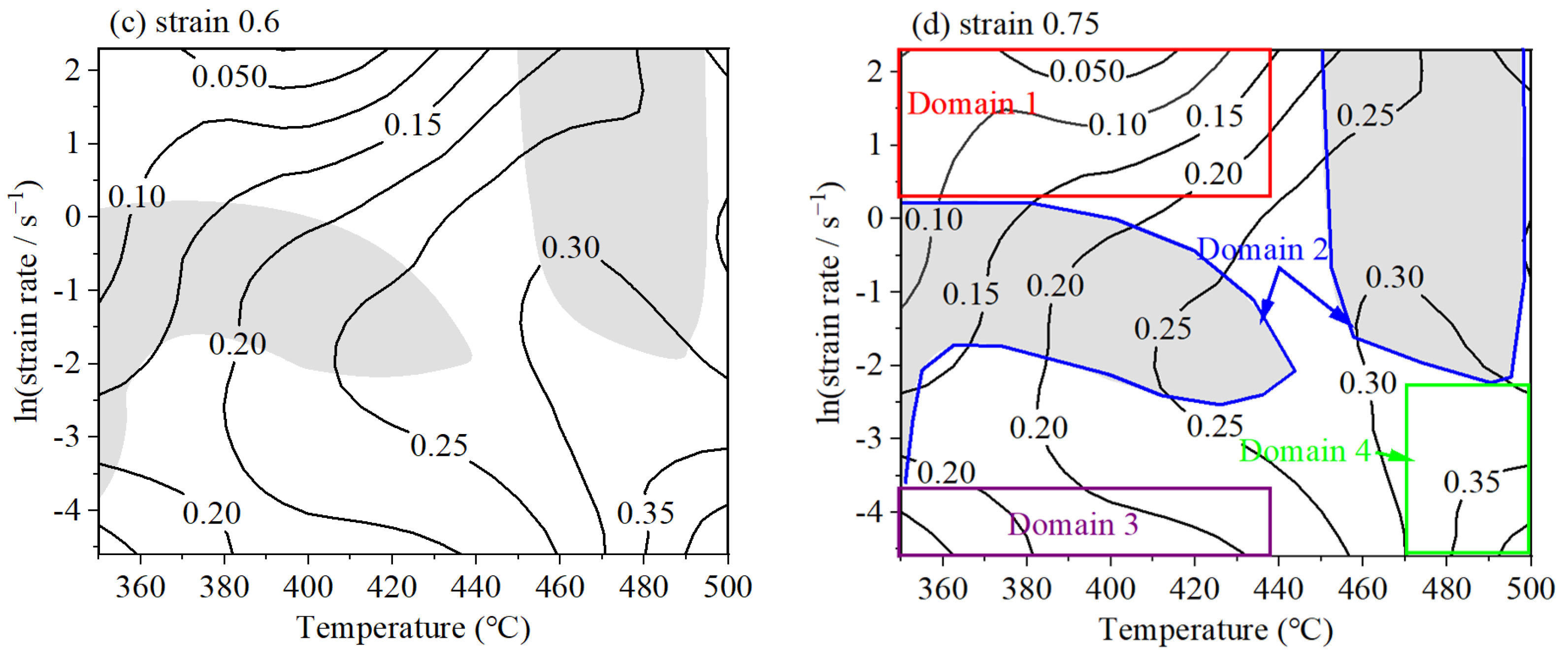
4.3.4. The Processing Map
4.4. Microstructure Observation
5. Conclusions
- The flow stress of the 6063 aluminum alloy increases significantly with rising strain rate and declines with increasing deformation temperatures during hot compression. A set of hot processing maps was established, and the optimal hot working conditions for the 6063 aluminum alloy at an applied strain of 0.75 were identified within the temperature and strain rate range (470–500 °C, 0.01–0.1108 s−1), achieving a peak efficiency of 0.4.
- During hot compression, the equiaxed grains elongate in the vertical direction of compression, and no voids or cracks are present. The density of dislocation increases with increasing strain rate and declining temperature. The main softening mechanism of the alloy is dynamic recovery. The microstructural observations align closely with the processing map outcomes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.S.; Yue, X.; Li, Q.Y.; Peng, H.; Dong, B.; Liu, T.; Yang, H.; Fan, J.; Shu, S.; Qiu, F.; et al. Development and applications of aluminum alloys for aerospace industry. J. Mater. Res. Technol. 2023, 27, 944–983. [Google Scholar] [CrossRef]
- Lv, Q.; Zhang, F.; Wei, H.; Li, Z.; Zhang, J. Effect of rare earth (La, Ce, Nd, Sc) on strength and toughness of 6082 aluminum alloy. Vacuum 2023, 215, 112333. [Google Scholar] [CrossRef]
- Tenali, N.; Ganesan, G.; Babu, P.R. An investigation on the mechanical and tribological properties of an ultrasonic-assisted stir casting Al-Cu-Mg matrix-based composite reinforced with agro waste ash particles. Appl. Eng. Lett. 2024, 9, 46–63. [Google Scholar] [CrossRef]
- Sharma, S.K.; Gajević, S.; Sharma, L.K.; Pradhan, R.; Sharma, Y.; Miletić, I.; Stojanović, B. Progress in Aluminum-Based Composites Prepared by Stir Casting: Mechanical and Tribological Properties for Automotive, Aerospace, and Military Applications. Lubricants 2024, 12, 421. [Google Scholar] [CrossRef]
- Chen, G.; Liu, J.; Dong, Z.; Shu, X.; Zhang, B. Underlying reasons of poor mechanical performance of thick plate aluminum-copper alloy vacuum electron beam welded joints. Vacuum 2020, 182, 109667. [Google Scholar] [CrossRef]
- Kumar, N. Severe Plastic Deformation of Al–Mg–Si Alloys Processed Through Rolling Techniques: A Review. Metallogr. Microstruct. Anal. 2022, 11, 353–404. [Google Scholar] [CrossRef]
- Han, Y.; Shao, D.; Chen, B.A.; Peng, Z.; Zhu, Z.X.; Zhang, Q.; Chen, X.; Liu, G.; Li, X.M. Effect of Mg/Si ratio on the microstructure and hardness–conductivity relationship of ultrafine-grained Al-Mg-Si alloys. J. Mater. Sci. 2017, 52, 4445–4459. [Google Scholar] [CrossRef]
- Omotoyinbo, J.A.; Oladele, I.O. The effect of plastic deformation and magnesium content on the mechanical properties of 6063 aluminium alloys. J. Miner. Mater. Charact. Eng. 2010, 9, 539–546. [Google Scholar] [CrossRef]
- Siddiqui, R.A.; Abdullah, H.A.; Al-Belushi, K.R. Influence of aging parameters on the mechanical properties of 6063 aluminium alloy. J. Mater. Process. Technol. 2000, 102, 234–240. [Google Scholar] [CrossRef]
- Lu, R.; Zheng, S.; Teng, J.; Hu, J.; Fu, D.; Chen, J.; Zhao, G.; Jiang, F.; Zhang, H. Microstructure, mechanical properties and deformation characteristics of Al-Mg-Si alloys processed by a continuous expansion extrusion approach. J. Mater. Sci. Technol. 2021, 80, 150–162. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, X.; Liu, M.; Liu, Z.; Luo, B.; Yu, K.; Li, Q.; Ran, J.; Zhao, P. Effect of hot rolling finishing temperature and intermediate annealing on the microstructure, texture evolution, and comprehensive properties of Al-Mg-Si alloy. J. Alloys Compd. 2024, 970, 172525. [Google Scholar] [CrossRef]
- Zhao, N.; Ma, H.; Hu, Z.; Yan, Y.; Chen, T. Microstructure and mechanical properties of Al-Mg-Si alloy during solution heat treatment and forging integrated forming process. Mater. Charact. 2022, 185, 111762. [Google Scholar] [CrossRef]
- Prasad, Y.; Seshacharyulu, T. Modelling of hot deformation for microstructural control. Int. Mater. Rev. 1998, 43, 243–258. [Google Scholar] [CrossRef]
- Prasad, Y.; Rao, K.P. Materials modeling and finite element simulation of isothermal forging of electrolytic copper. Mater. Des. 2011, 32, 1851–1858. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Q.; Wang, W.; Huang, Z.; Xiang, S.; Liu, B. Dynamic softening mechanisms and Zener-Hollomon parameter of Al–Mg–Si–Ce–B alloy during hot deformation. J. Mater. Res. Technol. 2021, 15, 6395–6403. [Google Scholar] [CrossRef]
- Ghosh, A.; Elasheri, A.; Parson, N.; Chen, X.-G. Hot deformation behavior and processing maps for an Al-Mg-Si-Zr-Mn Alloy. J. Alloys Metall. Syst. 2024, 6, 100077. [Google Scholar] [CrossRef]
- Feng, X.; Wang, Y.; Huang, Q.; Liu, H.; Zhang, Z. The dynamic recrystallization microstructure characteristics and the effects on static recrystallization and mechanical properties of Al–Mg–Si alloy. Mater. Sci. Eng. A 2024, 899, 146454. [Google Scholar] [CrossRef]
- Ke, B.; Ye, L.; Tang, J.; Zhang, Y.; Liu, S.; Lin, H.; Dong, Y.; Liu, X. Hot deformation behavior and 3D processing maps of AA7020 aluminum alloy. J. Alloys Compd. 2020, 845, 156113. [Google Scholar] [CrossRef]
- Miao, J.; Sutton, S.; Luo, A.A. Deformation microstructure and thermomechanical processing maps of homogenized AA2070 aluminum alloy. Mater. Sci. Eng. A 2022, 834, 142619. [Google Scholar] [CrossRef]
- Su, Y.; Kong, F.; You, F.; Wang, X.; Chen, Y. The high-temperature deformation behavior of a novel near-α titanium alloy and hot-forging based on the processing map. Vacuum 2020, 173, 109135. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Cao, L.; Liao, B.; Wang, Y.; Liu, Q. Hot deformation and dynamic recrystallization in Al-Mg-Si alloy. Mater. Charact. 2021, 173, 110976. [Google Scholar] [CrossRef]
- Qu, S.; Li, Y. Characterization of Hot Deformation Behavior and Processing Maps of Homogenized Al-Mg-Si-Sc-Zr Alloys. J. Mater. Eng. Perform. 2024, 34, 2435–2449. [Google Scholar] [CrossRef]
- Muhammad, M.; Nezhadfar, P.; Thompson, S.; Saharan, A.; Phan, N.; Shamsaei, N. A comparative investigation on the microstructure and mechanical properties of additively manufactured aluminum alloys. Int. J. Fatigue 2021, 146, 106165. [Google Scholar] [CrossRef]
- Cao, H.; Sun, Q.; Pu, Q.; Wang, L.; Huang, M.; Luo, Z.; Che, J. Effect of vacuum degree and T6 treatment on the microstructure and mechanical properties of Al–Si–Cu alloy die castings. Vacuum 2020, 172, 109063. [Google Scholar] [CrossRef]
- Snopiński, P.; Król, M.; Tański, T.; Pakuła, D.; Kříž, A. Effect of initial microstructure on hot deformation behavior of AlMg5Si2Mn alloy. Mater. Charact. 2021, 177, 111167. [Google Scholar] [CrossRef]
- Jin, D.; Li, H.; Zhu, Z.; Yang, C.; Chen, B.; Miao, Y. Effects of cooling rate in homogenization on microstructure, hot deformation resistance and subsequent age-hardening behavior of an Al–Mg–Si alloy. J. Mater. Res. Technol. 2023, 27, 3283–3300. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, F.; Zhu, E.; Gopi, K.R.; Farah, S.; An, X.; Yao, K.; Li, J.; Hashmi, A.F.; Liu, L. Investigation on the grain structure evolution and abnormal stress increase of Al–Mg–Si alloy during hot deformation. Met. Mater. Int. 2024, 30, 967–989. [Google Scholar] [CrossRef]
- Hu, M.; Sun, Y.; He, J.; Li, C.; Li, H.; Yu, L.; Liu, Y. Hot deformation behaviour and microstructure evolution of Al-3% Mg2Si alloy. Mater. Charact. 2022, 183, 111623. [Google Scholar] [CrossRef]
- Mirahmadi, D.; Dehghani, K.; Shamsipur, A.; Kalaki, A. Hot deformation behavior, microstructure evolution and processing map of Cu–2Be alloy. J. Mater. Res. Technol. 2023, 24, 376–394. [Google Scholar] [CrossRef]
- Volodko, S.; Yudin, S.; Korotitskiy, A.; Markova, G.; Cheverikin, V.; Permyakova, D.; Poliakov, M.; Titov, D.; Moskovkikh, D.; Kasimtsev, A. Hot deformation behavior of NiTiHf alloy under compression: Effect of deformation heating on flow softening. Mater. Charact. 2024, 212, 113981. [Google Scholar] [CrossRef]
- Yi, H.; Ding, J.; Ni, C.; Dai, J.; Tang, Y.; Chen, X.; Song, K.; Xia, X. Hot compression deformation behavior and processing maps of Al-0.5 Mg-0.4 Si-0.1 Cu alloy. J. Mater. Res. Technol. 2022, 19, 4890–4904. [Google Scholar] [CrossRef]
- Zhao, N.; Sun, Q.; Pang, Q.; Hu, Z. Comprehensive study of hot compression behaviors and microstructure evolution of solutionized 6082 aluminum alloy extruded bar. J. Alloys Compd. 2023, 931, 167541. [Google Scholar] [CrossRef]
- Prasad, Y.; Seshacharyulu, T. Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 1998, 243, 82–88. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Mo, Y.; Wang, H.; Xu, J. Hot deformation and processing maps of Al–Zn–Mg–Cu alloy under coupling-stirring casting. J. Mater. Res. Technol. 2019, 8, 1224–1234. [Google Scholar] [CrossRef]
- Chamanfar, A.; Alamoudi, M.T.; Nanninga, N.E.; Misiolek, W.Z. Analysis of flow stress and microstructure during hot compression of 6099 aluminum alloy (AA6099). Mater. Sci. Eng. A 2019, 743, 684–696. [Google Scholar] [CrossRef]
- Tang, J.; Wang, J.; Teng, J.; Wang, G.; Fu, D.; Zhang, H.; Jiang, F. Effect of Zn content on the dynamic softening of Al–Zn–Mg–Cu alloys during hot compression deformation. Vacuum 2021, 184, 109941. [Google Scholar] [CrossRef]
- Xia, E.; Ye, T.; Qiu, S.; Liu, L.; Luo, F.; Yue, H.; Wu, Y. Deformation Behavior and Processing Maps of 7075 Aluminum Alloy under Large-Strain Thermal Compression. Materials 2023, 16, 7432. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, G.; Zhang, J. A new constitutive model and hot processing map of 5A06 aluminum alloy based on high-temperature rheological behavior and higher-order gradients. Mater. Today Commun. 2023, 36, 106502. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, H.-D.; Li, G.-A.; Tang, X.-F.; Yi, P.-S.; Liu, Z.; Wang, X.-Y.; Jin, J.-S. Processing map and hot deformation behavior of squeeze cast 6082 aluminum alloy. Trans. Nonferrous Met. Soc. China 2022, 32, 2150–2163. [Google Scholar] [CrossRef]
- Zhao, H.; Ye, L.; Cheng, Q.; Kang, Y.; Zhang, W. Constitutive model and processing maps of 7055 aluminum alloy used for fasteners. Mater. Today Commun. 2022, 33, 104996. [Google Scholar] [CrossRef]
- Liu, W.; Man, Q.; Li, J.; Liu, L.; Zhang, W.; Wang, Z.; Pan, H. Microstructural evolution and vibration fatigue properties of 7075-T651 aluminum alloy treated by nitrogen ion implantation. Vacuum 2022, 199, 110931. [Google Scholar] [CrossRef]
- Xu, C.; Huang, J.; Jiang, F.; Jiang, Y. Dynamic recrystallization and precipitation behavior of a novel Sc, Zr alloyed Al-Zn-Mg-Cu alloy during hot deformation. Mater. Charact. 2022, 183, 111629. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Liu, Y. Dynamic recrystallization mechanisms of as-forged Al–Zn–Mg-(Cu) aluminum alloy during hot compression deformation. Mater. Sci. Eng. A 2023, 878, 145236. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, X.; Ye, L.; Gu, G.; Jiang, H.; Gui, X. Evolution of θ′ precipitate in aluminum alloy 2519A impacted by split Hopkinson bar. Mater. Sci. Eng. A 2015, 620, 241–245. [Google Scholar]
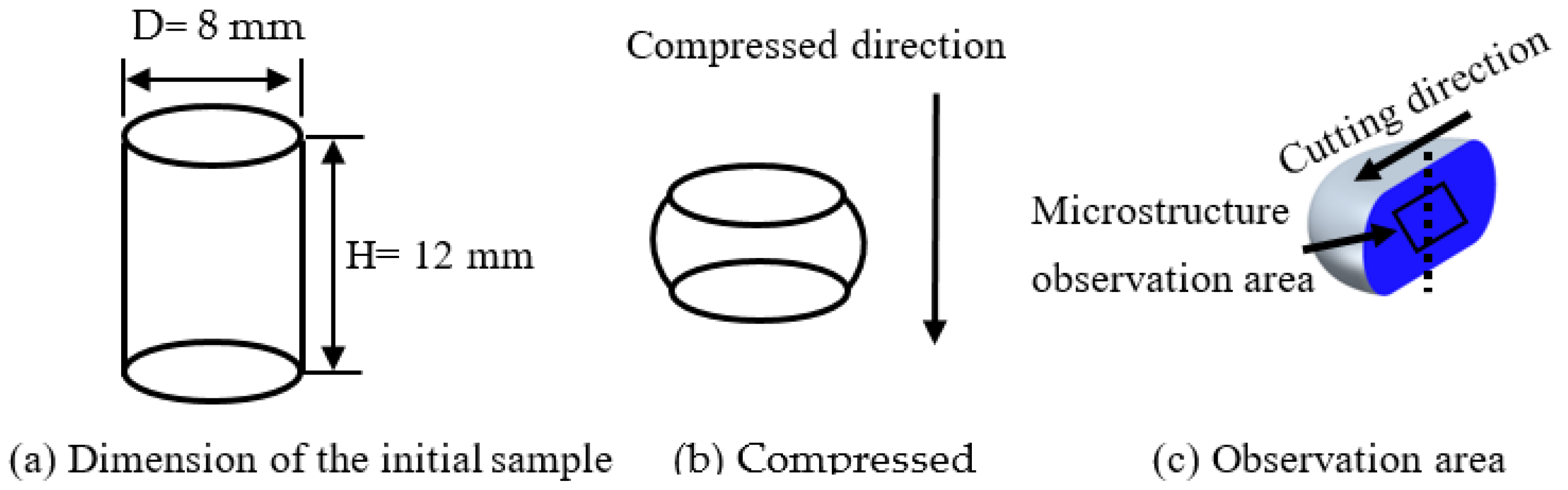






| Composition | Mg | Cu | Si | Cr | Fe | Zn | Mn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|
| Content (wt.%) | 0.65 | 0.1 | 0.46 | 0.1 | 0.18 | 0.1 | 0.05 | 0.08 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Shen, Q.; Chen, S.; Dong, L.; Xia, E.; Guo, P.; Luo, Y. Hot Compression Behavior and Processing Maps of 6063 Aluminum Alloy Under Medium Strain Rate. Materials 2025, 18, 2510. https://doi.org/10.3390/ma18112510
Wang Z, Shen Q, Chen S, Dong L, Xia E, Guo P, Luo Y. Hot Compression Behavior and Processing Maps of 6063 Aluminum Alloy Under Medium Strain Rate. Materials. 2025; 18(11):2510. https://doi.org/10.3390/ma18112510
Chicago/Turabian StyleWang, Zhenhu, Qincan Shen, Shuang Chen, Lijun Dong, Erli Xia, Pengcheng Guo, and Yajun Luo. 2025. "Hot Compression Behavior and Processing Maps of 6063 Aluminum Alloy Under Medium Strain Rate" Materials 18, no. 11: 2510. https://doi.org/10.3390/ma18112510
APA StyleWang, Z., Shen, Q., Chen, S., Dong, L., Xia, E., Guo, P., & Luo, Y. (2025). Hot Compression Behavior and Processing Maps of 6063 Aluminum Alloy Under Medium Strain Rate. Materials, 18(11), 2510. https://doi.org/10.3390/ma18112510








