Study on Winding Forming Process of Glass Fiber Composite Pressure Vessel
Abstract
1. Introduction
2. Finite Element Analysis of Blow Molding of Pressure Vessel
2.1. Structure Design of High-Density Polyethylene Lining
2.2. Lining Forming Process
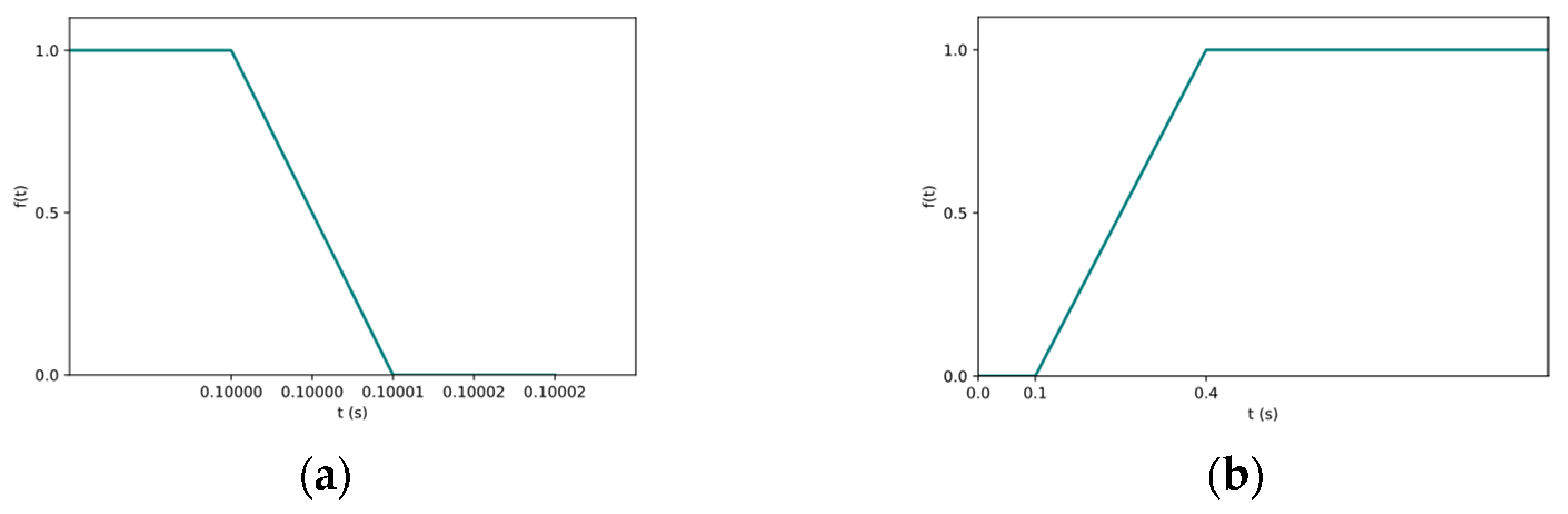
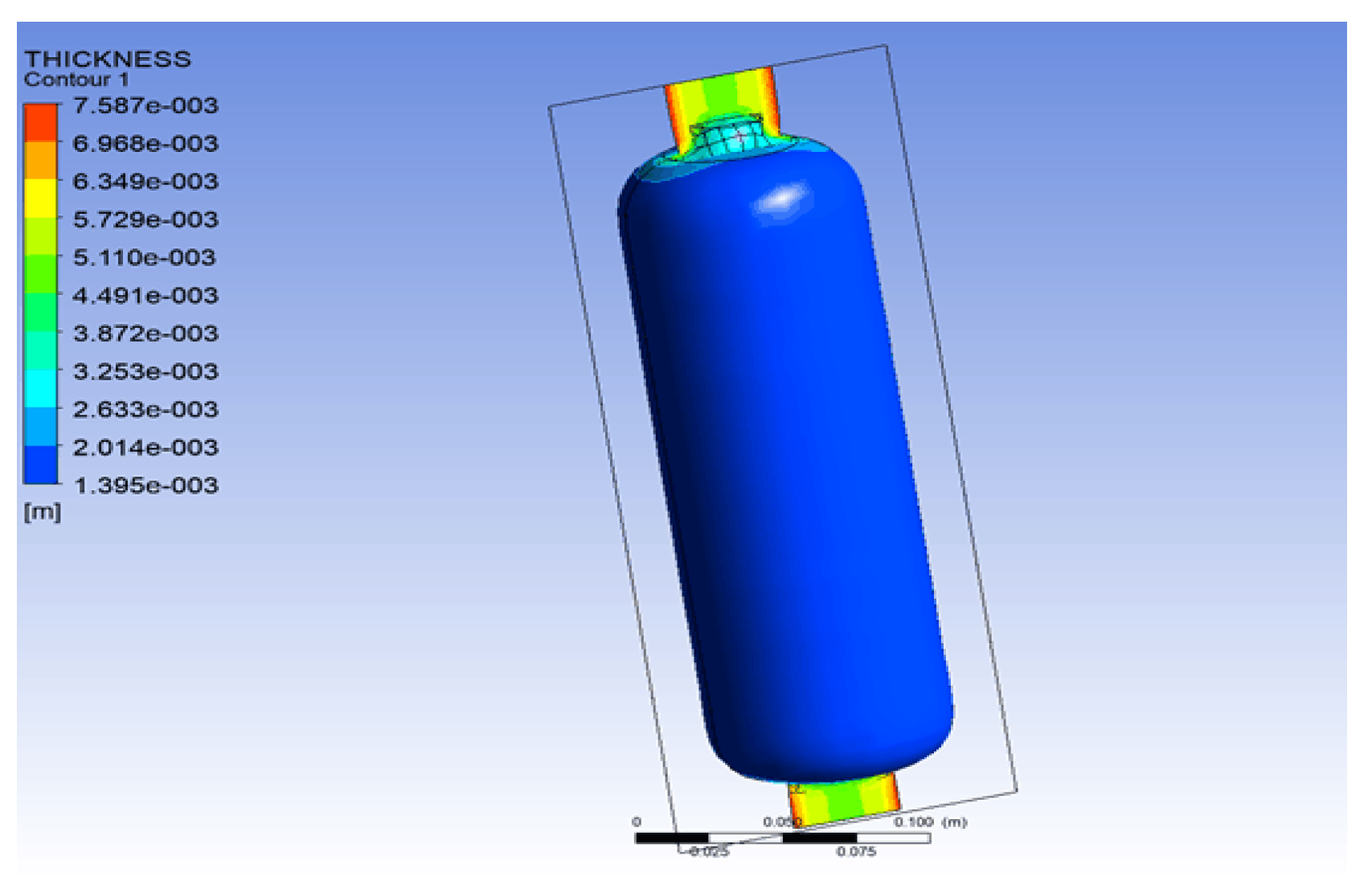
2.3. Finite Element Analysis of Lining Forming Process
3. Design and Simulation Analysis of Winding Process
3.1. Selection and Determination of Fiber Materials
3.2. Selection of Winding Forming Process
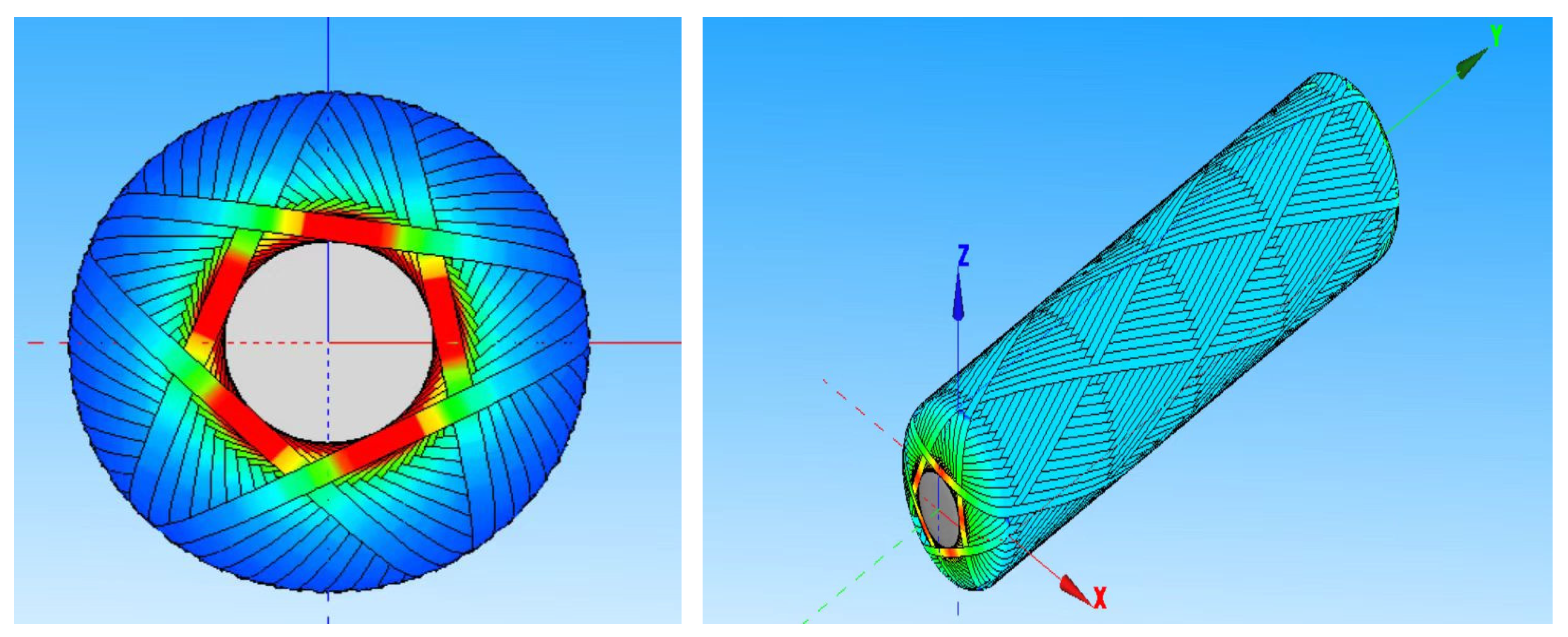
3.3. Simulation Analysis of CADWIND Winding Molding
4. Simulation Analysis of Glass Fiber Composite Pressure Vessel
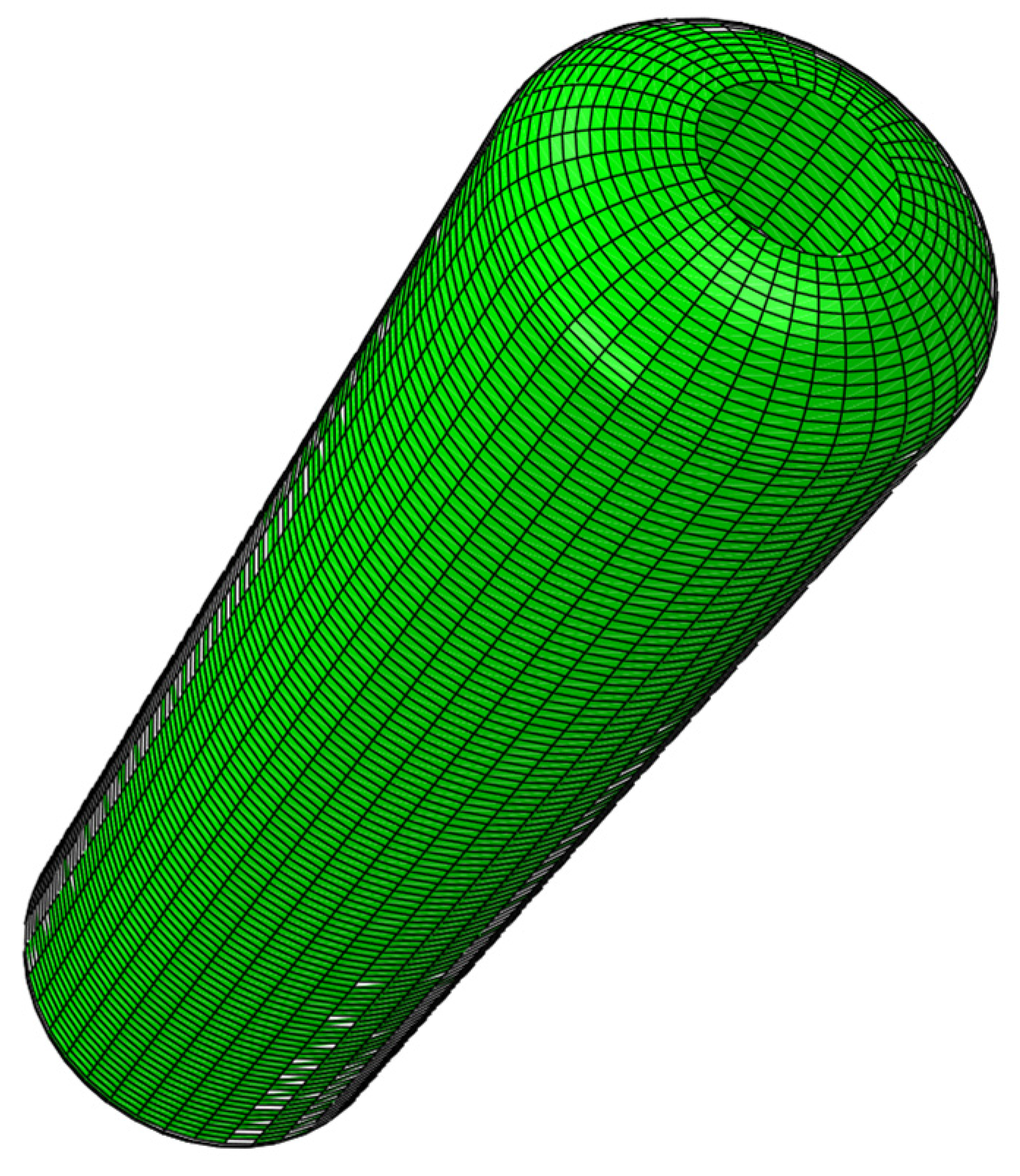
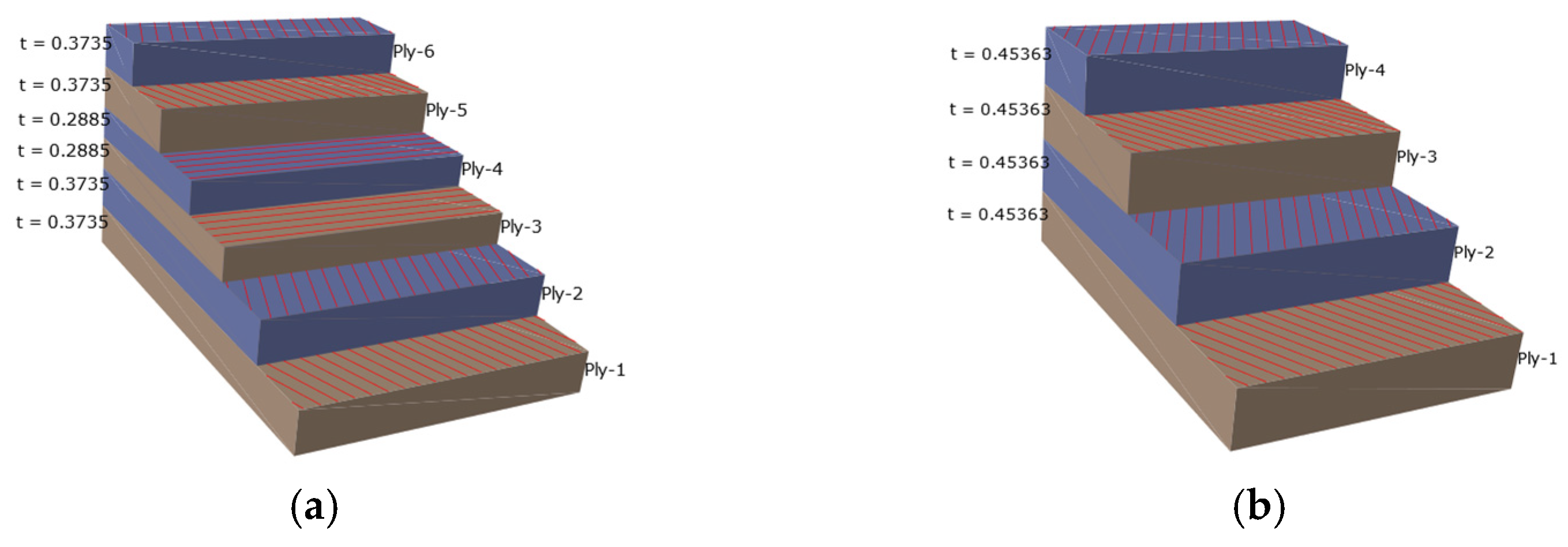
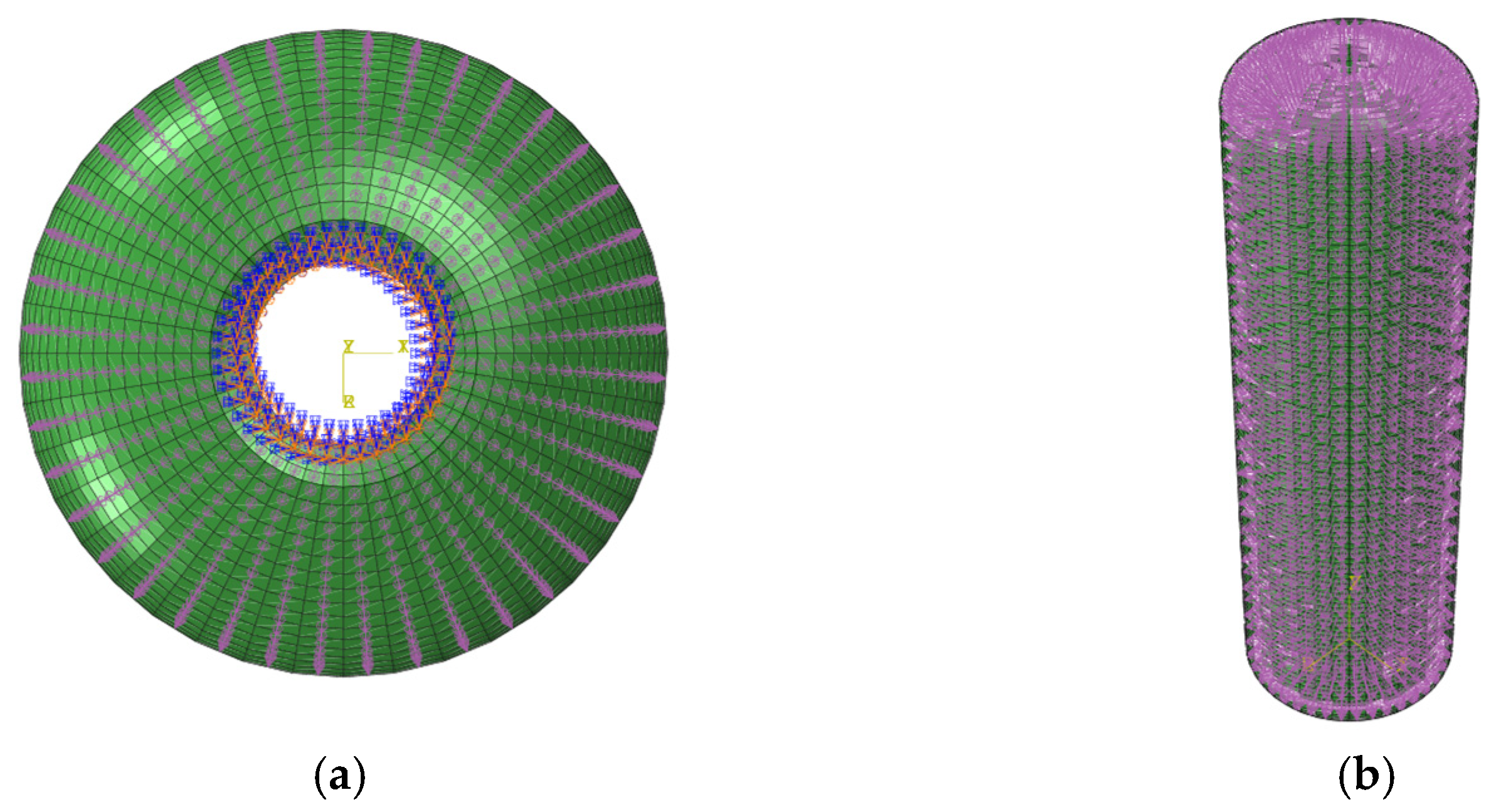
4.1. Establishment of Finite Element Model
- (1)
- Element Selection and Mesh Division
- (2)
- Material parameter setting
- (3)
- Boundary and load conditions
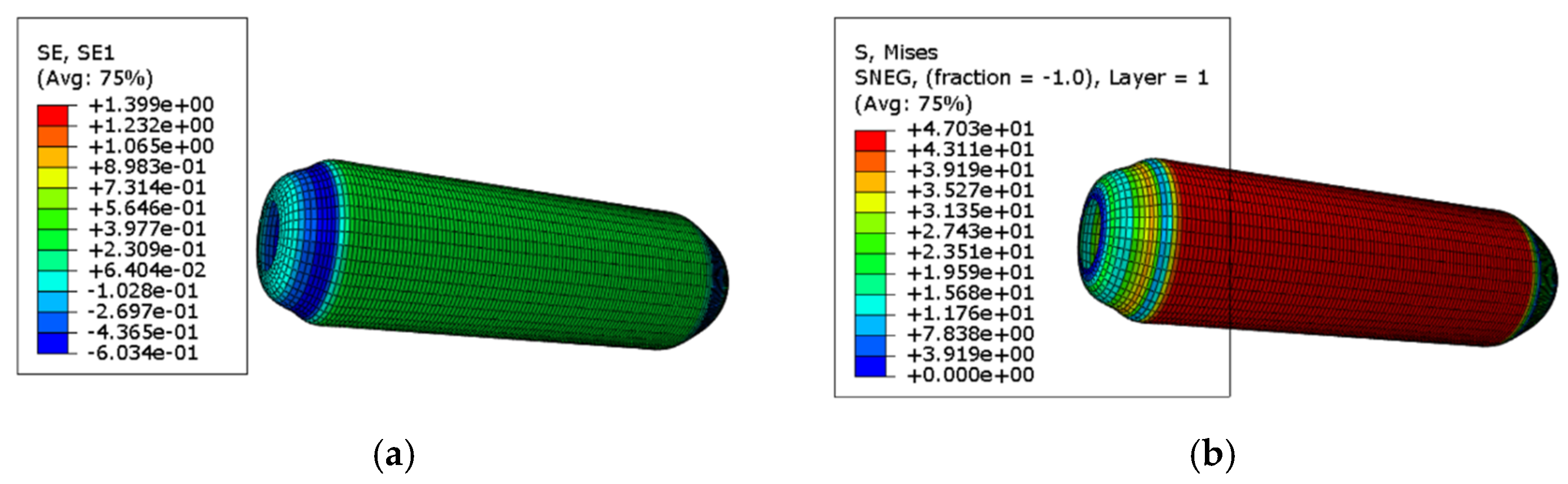
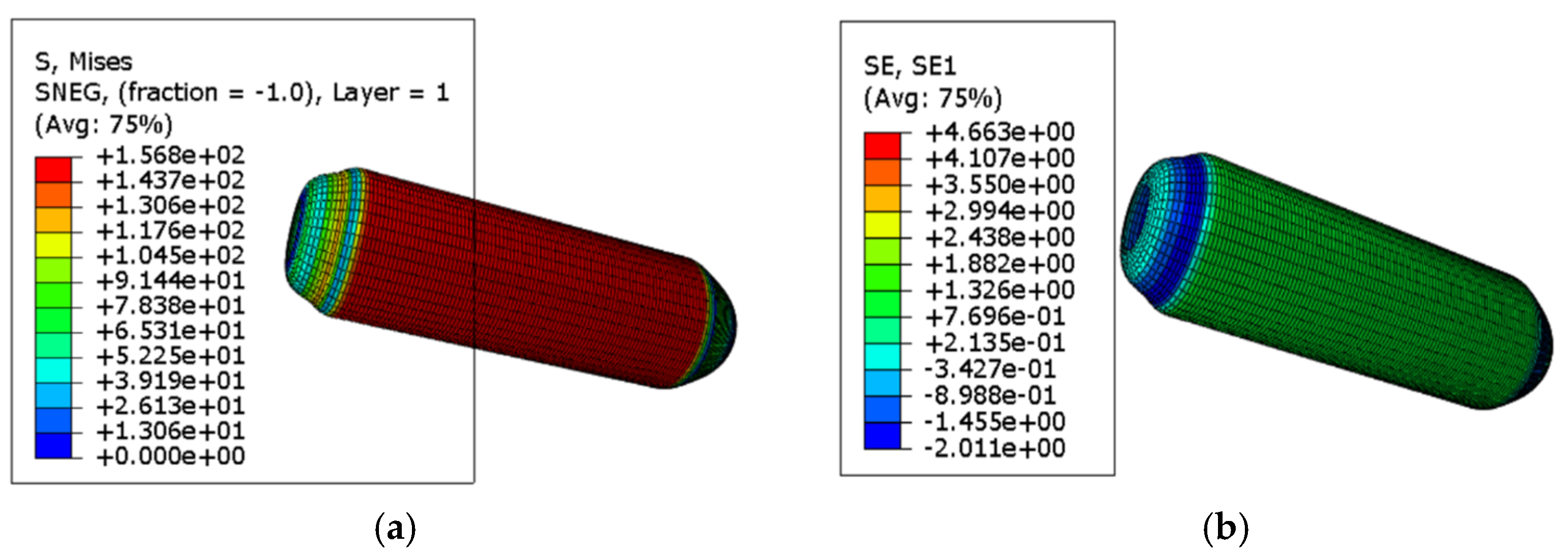
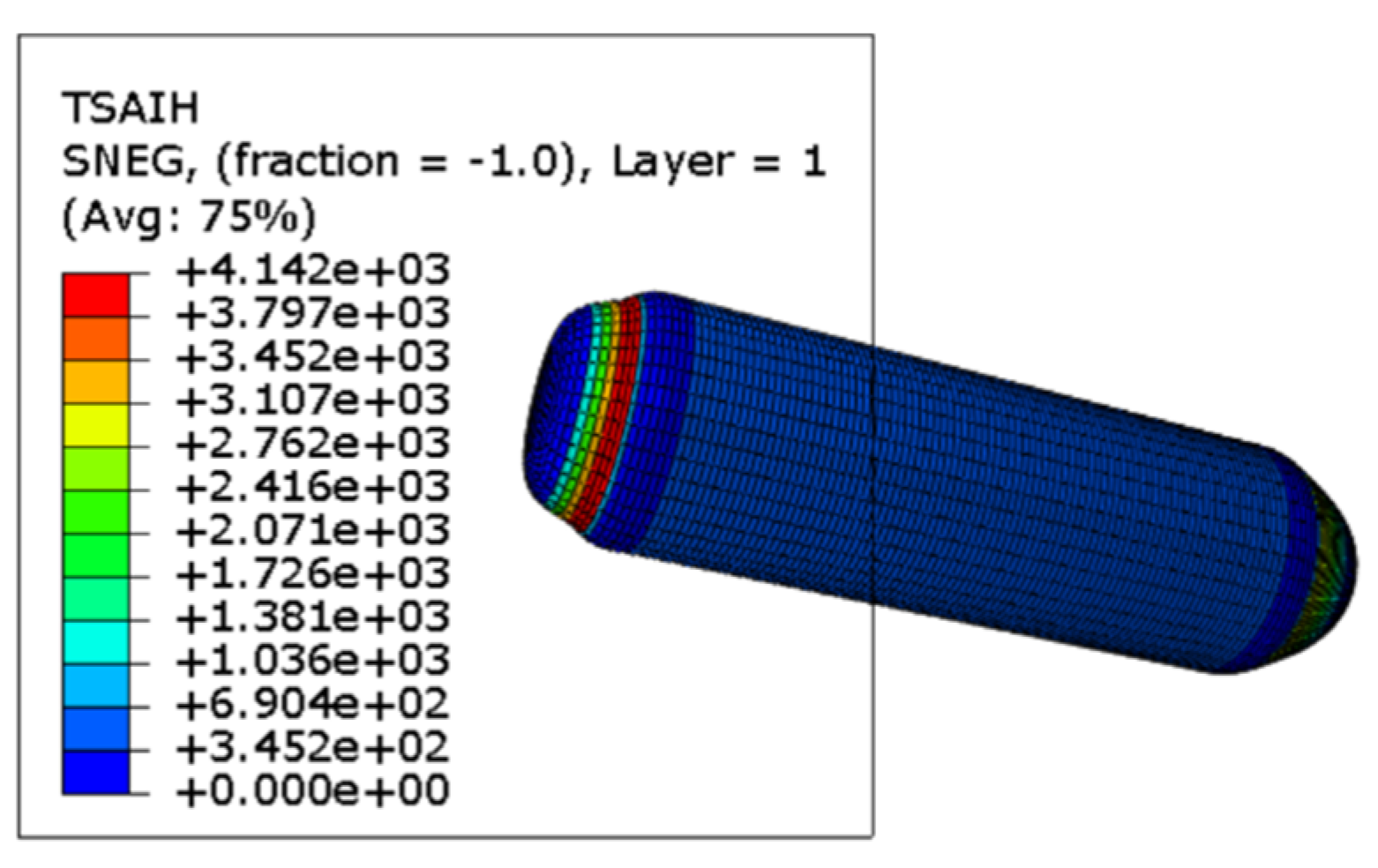
4.2. Simulation Result Analysis
5. Experimental Verification Analysis
5.1. Test Scheme Design
5.2. Winding Forming and Curing
5.3. Blasting Test
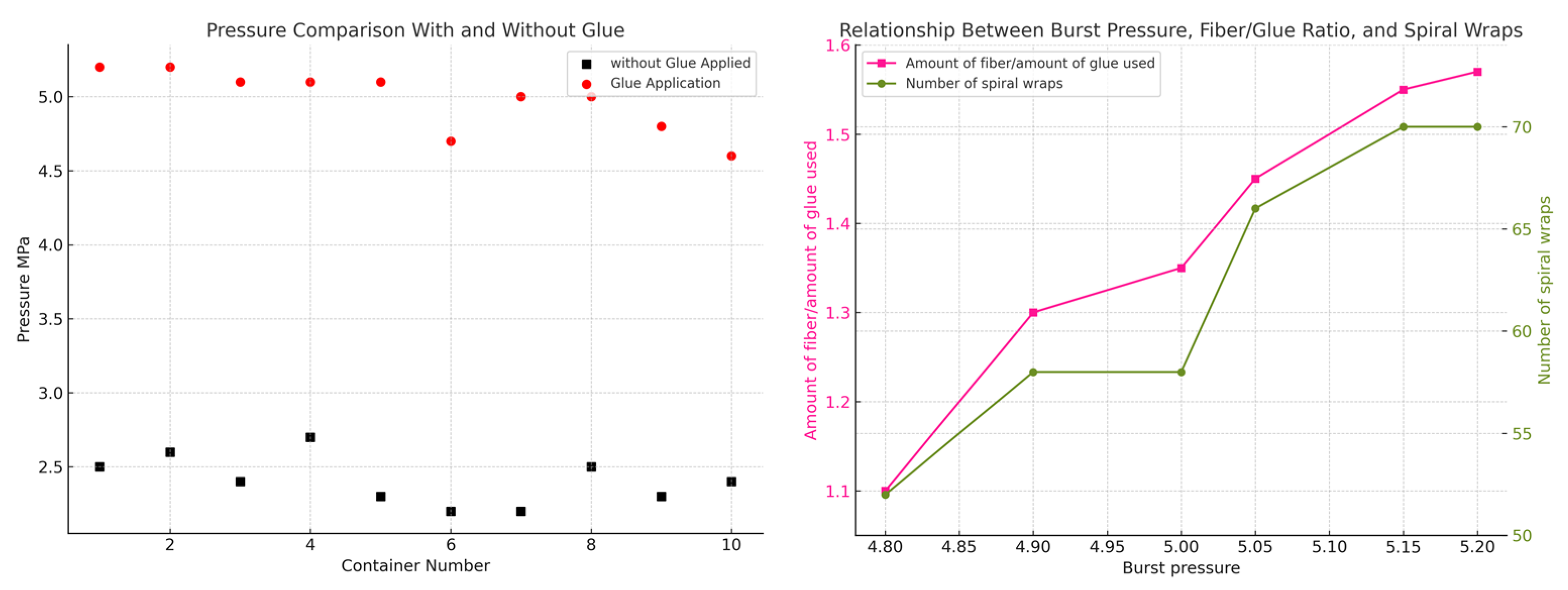
5.4. Analysis of Experimental Results
6. Conclusions
- (1)
- Feasibility of liner design and forming process
- (2)
- Accurate winding process design with high coverage
- (3)
- Excellent agreement between finite element prediction and burst testing
- (4)
- Good interfacial bonding and synergistic failure mechanism
- (5)
- Significant impact of sealing on vessel performance
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saharudin, M.S.; Hasbi, S.; Sahu, S.K.; Ma, Q.; Younas, M. Numerical Analysis and Life Cycle Assessment of Type V Hydrogen Pressure Vessels. J. Compos. Sci. 2025, 9, 75. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Song, H.; Li, K.; Hu, J. Layup Design and Mechanical Properties of an Optimal Dome Profile. Polym. Compos. 2024, 45, 14993–15004. [Google Scholar] [CrossRef]
- Zhang, N.; Gao, S.; Song, M.; Chen, Y.; Zhao, X.; Liang, J.; Feng, J. A Multiscale Study of CFRP Based on Asymptotic Homogenization with Application to Mechanical Analysis of Composite Pressure Vessels. Polymers 2022, 14, 2817. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, B.P.; Fursikov, P.V.; Volodin, A.A.; Bocharnikov, M.S.; Shimkus, Y.Y.; Kashin, A.M.; Yartys, V.A.; Chidziva, S.; Pasupathi, S.; Lototskyy, M.V. Metal Hydride Hydrogen Storage and Compression Systems for Energy Storage Technologies. Int. J. Hydrogen Energy 2021, 46, 13647–13657. [Google Scholar] [CrossRef]
- Daghighi, S.; Weaver, P.M. Nonconventional tow-steered pressure vessels for hydrogen storage. Compos. Struct. 2024, 334, 117970. [Google Scholar] [CrossRef]
- Saxena, A.; Findley, K.O. A Model to Account for the Effects of Load Ratio and Hydrogen Pressure on the Fatigue Crack Growth Behavior of Pressure Vessel Steels. Materials 2024, 17, 4308. [Google Scholar] [CrossRef]
- McKeen, L.W. Production of films, containers, and membranes. In Permeability Properties of Plastics and Elastomers; Elsevier: Amsterdam, The Netherlands, 2017; pp. 41–60. [Google Scholar]
- Sidorov, D.; Kolosov, A.; Kolosova, E.; Nosachova, J.; Glushchenko, M. Evaluating the Wall Thickness of a Blow Molding Billet; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Azeem, M.; Ya, H.H.; Alam, M.A.; Kumar, M.; Stabla, P.; Smolnicki, M.; Gemi, L.; Khan, R.; Ahmed, T.; Ma, Q.; et al. Application of Filament Winding Technology in Composite Pressure Vessels and Challenges: A Review. J. Energy Storage 2022, 49, 103468. [Google Scholar] [CrossRef]
- Behrens, B.; Brunotte, K.; Wester, H.; Kock, C. Targeted Adjustment of Residual Stresses in Hot-Formed Components by Means of Process Design Based on Finite Element Simulation. Arch. Appl. Mech. 2021, 91, 3579–3602. [Google Scholar] [CrossRef]
- Shah, S.P.; Maiaru, M. Effect of Manufacturing on the Transverse Response of Polymer Matrix Composites. Polymers 2021, 13, 2491. [Google Scholar] [CrossRef]
- Kutz, M. Applied Plastics Engineering Handbook: Processing, Sustainability, Materials, and Applications; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Dorp, E.R.-v.; Blume, C.; Haedecke, T.; Pata, V.; Reith, D.; Bruch, O.; Moeginger, B.; Hausnerova, B. Process-dependent Structural and Deformation Properties of Extrusion Blow Molding Parts. Polym. Test. 2019, 77, 105903. [Google Scholar] [CrossRef]
- Alcan, P.; Sözöz, H.; Aydoğmuş, S.B. Production of Market Bag and Their Stability and Optimization Parameters. Int. J. Adv. Sci. Technol. 2017, 103, 23–34. [Google Scholar] [CrossRef]
- Michels, P.; Bruch, O.; Evers-Dietze, B.; Grotenburg, D.; Dorp, E.R.-V.; Altenbach, H. Shrinkage Simulation of Blow Molded Parts Using Viscoelastic Material Models. Mater. Werkst. 2022, 53, 449–466. [Google Scholar] [CrossRef]
- Gao, S.; Qiu, Z.; Ouyang, J. The Improvement Effect and Mechanism of Longitudinal Ultrasonic Vibration on the Injection Molding Quality of a Polymeric Micro-Needle Array. Polymers 2019, 11, 151. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Xu, H.; Jia, X.; Zu, L.; Cheng, S.; Wang, H. Design of a 70 MPa Type IV Hydrogen Storage Vessel Using Accurate Modeling Techniques for Dome Thickness Prediction. Compos. Struct. 2020, 236, 111915. [Google Scholar] [CrossRef]
- Frueh, N.; Knippers, J. Multi-stage Filament Winding: Integrative Design and Fabrication Method for Fibre-Reinforced Composite Components of Complex Geometries. Compos. Struct. 2021, 268, 113969. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, X.; Wang, H.; Cao, J.; Yuan, Y. Prestressing Estimation for Multilayer Clamping High Pressure Vessel Laminates. J. Press. Vessel Technol. Trans. ASME 2024, 146, 051703. [Google Scholar] [CrossRef]
- Kangal, S.; Kartav, O.; Tanoglu, M.; Aktas, E.; Artem, H.S. Investigation of Interlayer Hybridization Effect on Burst Pressure Performance of Composite Overwrapped Pressure Vessels with Load-Sharing Metallic Liner. J. Compos. Mater. 2020, 54, 961–980. [Google Scholar] [CrossRef]
- Zu, L.; Xu, H.; Wang, H.; Zhang, B.; Zi, B. Design and Analysis of Filament-Wound Composite Pressure Vessels Based on Non-Geodesic Winding. Compos. Struct. 2019, 207, 41–52. [Google Scholar] [CrossRef]
- Javier, P.R.J.; Azdrubal, R.V.B.; Javier, B.O.F.; Daniel, R. The Role of Fiber-Matrix Compatibility in Vacuum Processed Natural Fiber/epoxy Biocomposites. Cellulose 2021, 28, 7845–7857. [Google Scholar] [CrossRef]
- Al-Tabbakh, A.A. Symmetry in Crystallography: Understanding the International Tables, by Paolo G. Radaelli. Contemp. Phys. 2017, 58, 371–373. [Google Scholar] [CrossRef]
- Andrews, S. Using Rotational Averaging to Calculate the Bulk Response of Isotropic and Anisotropic Samples from Molecular Parameters. J. Chem. Educ. 2004, 81, 877. [Google Scholar] [CrossRef]
- Suleman, K.; Bosi, F. Direct Stress Computations in Arbitrarily Shaped Thin Shells and Elliptic Bulge Tests. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478, 20220619. [Google Scholar] [CrossRef]
- Noraphaiphipaksa, N.; Poapongsakorn, P.; Hasap, A.; Kanchanomai, C. Failure Analysis of Pressure Vessel with Sight Ports Using Finite Element Analysis. Eng. Fail. Anal. 2020, 117, 104791. [Google Scholar] [CrossRef]
- Zimmermann, N.; Wang, P.H. A review of failure modes and fracture analysis of aircraft composite materials. Eng. Fail. Anal. 2020, 115, 104692. [Google Scholar] [CrossRef]
- Llobet, J.; Maimi, P.; Turon, A.; Bak, B.L.; Lindgaard, E.; Carreras, L.; Essa, Y.; Escalera, F.M.d.l. A Continuum Damage Model for Composite Laminates: Part IV—Experimental and Numerical Tests. Mech. Mater. 2020, 154, 103686. [Google Scholar] [CrossRef]
- Shi, J.; Wang, X.; Zhang, L.; Wu, Z.; Zhu, Z. Composite-Wedge Anchorage for Fiber-Reinforced Polymer Tendons. J. Compos. Constr. 2022, 26, 04022005. [Google Scholar] [CrossRef]
- Rafiee, R.; Torabi, M.A. Stochastic Prediction of Burst Pressure in Composite Pressure Vessels. Compos. Struct. 2017, 185, 573–583. [Google Scholar] [CrossRef]









| Name | Barrel Diameter | Head Height | Diameter of the Front Pole Hole | Height of Rear Head | Diameter of Rear Pole Hole | Head Type |
|---|---|---|---|---|---|---|
| Unit (mm) | 84.4 | 20 | 24 | 20 | 24 | ellipsoid |
| Bobbin Number | Single Bundle Yarn Width | Fiber Mass Content | Fiber Fineness | Fiber Density | Resin Density |
|---|---|---|---|---|---|
| 1 | 5 mm | 74% | 1200 g/kg | 1.8 g/cm3 | 1.2 g/cm3 |
| Number | Number of Contact Points | Winding Number | Degree of Coverage % |
|---|---|---|---|
| 1 | 13/5 | 67 | 107 |
| 2 | −18/7 | 70 | 112 |
| 3 | 18/7 | 77 | 123 |
| 4 | −23/9 | 64 | 102 |
| 5 | 23/9 | 74 | 118 |
| 6 | 21/8 | 76 | 122 |
| 7 | −13/5 | 73 | 117 |
| 8 | −28/11 | 79 | 126 |
| 9 | 28/11 | 89 | 142 |
| 10 | −29/11 | 66 | 106 |
| 11 | 29/11 | 79 | 126 |
| 12 | −21/8 | 71 | 114 |
| 13 | −5/2 | 63 | 101 |
| 14 | 8/3 | 69 | 110 |
| 15 | −8/3 | 69 | 107 |
| 16 | 5/2 | 70 | 107 |
| 17 | 27/10 | 89 | 142 |
| Name | Unit/GPa |
|---|---|
| Young’s modulus E1 | 39 |
| Young’s modulus E1 | 9 |
| Poisson’s ratio | 0.25 |
| Shear modulus G12 | 4.35 |
| Shear modulus G13 | 4.35 |
| Shear modulus G23 | 2.2 |
| Scheme Number | Specimen Number | Number of Spiral Winding Turns | Number of Toroidal Winding Layers | Whether the Head Is Coated with Glue |
|---|---|---|---|---|
| 1 | 1 | 67 | 1 | Yes |
| 2 | 67 | 1 | No | |
| 3 | 62 | 1 | Yes | |
| 2 | 4 | 57 | 1 | Yes |
| 5 | 52 | 1 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.; Zeng, W.; Li, F.; Tian, H.; Li, X. Study on Winding Forming Process of Glass Fiber Composite Pressure Vessel. Materials 2025, 18, 2485. https://doi.org/10.3390/ma18112485
Wu R, Zeng W, Li F, Tian H, Li X. Study on Winding Forming Process of Glass Fiber Composite Pressure Vessel. Materials. 2025; 18(11):2485. https://doi.org/10.3390/ma18112485
Chicago/Turabian StyleWu, Run, Wenlei Zeng, Fangfang Li, Haobin Tian, and Xuelei Li. 2025. "Study on Winding Forming Process of Glass Fiber Composite Pressure Vessel" Materials 18, no. 11: 2485. https://doi.org/10.3390/ma18112485
APA StyleWu, R., Zeng, W., Li, F., Tian, H., & Li, X. (2025). Study on Winding Forming Process of Glass Fiber Composite Pressure Vessel. Materials, 18(11), 2485. https://doi.org/10.3390/ma18112485






