Numerical Analysis of Slurry–Crack Coupling in Grouting Repair Process of Multiple Cracks in Concrete Material
Abstract
1. Introduction
2. Theory and Finite Element Model
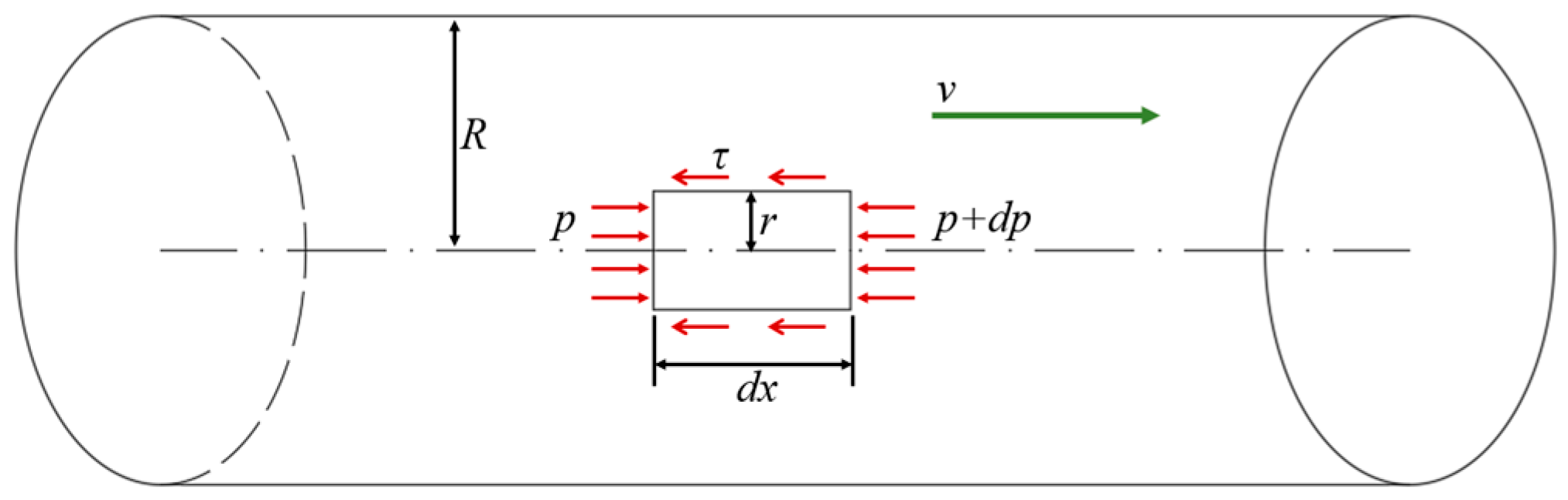
2.1. Grouting Continuity Equations in Concrete Crack
- The slurry is a homogeneous and incompressible fluid.
- The diffusion of the slurry in the pore–crack medium is regarded as an osmotic diffusion model, and the influence of the percolation effect during the diffusion process is ignored.
- The pore medium is homogeneous and isotropic.
- The slurry pressure is continuous at the junction of the cracked and porous media.
- Cement slurry can be considered as a Newtonian fluid [22]. The derivation is performed according to the constitutive equation of Newtonian fluids.
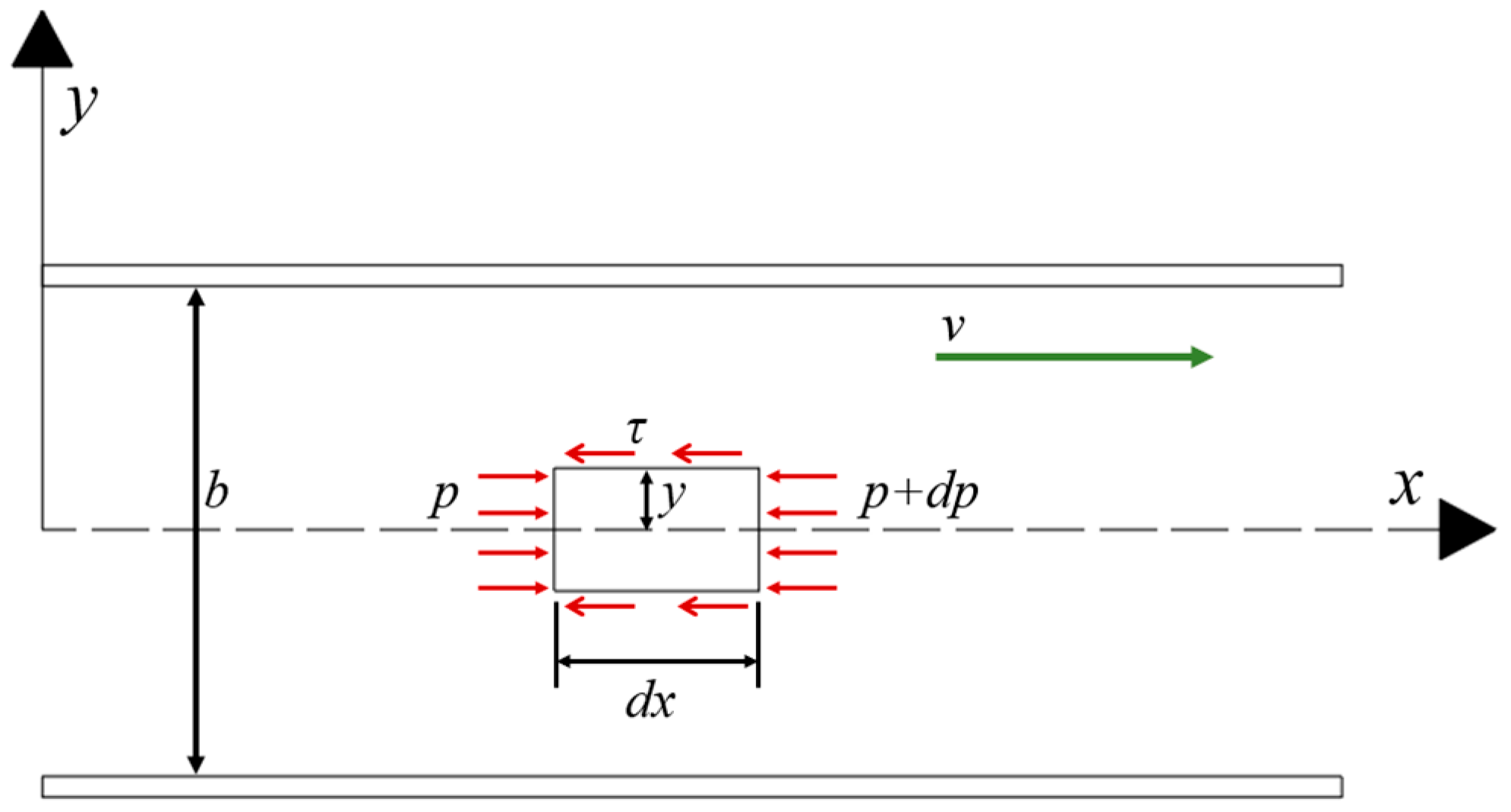
2.2. Description of Crack Opening Based on the Interfacial Layer Model
2.3. Finite Element Model of Multi-Cracked Concrete Grouting
3. Results and Discussion
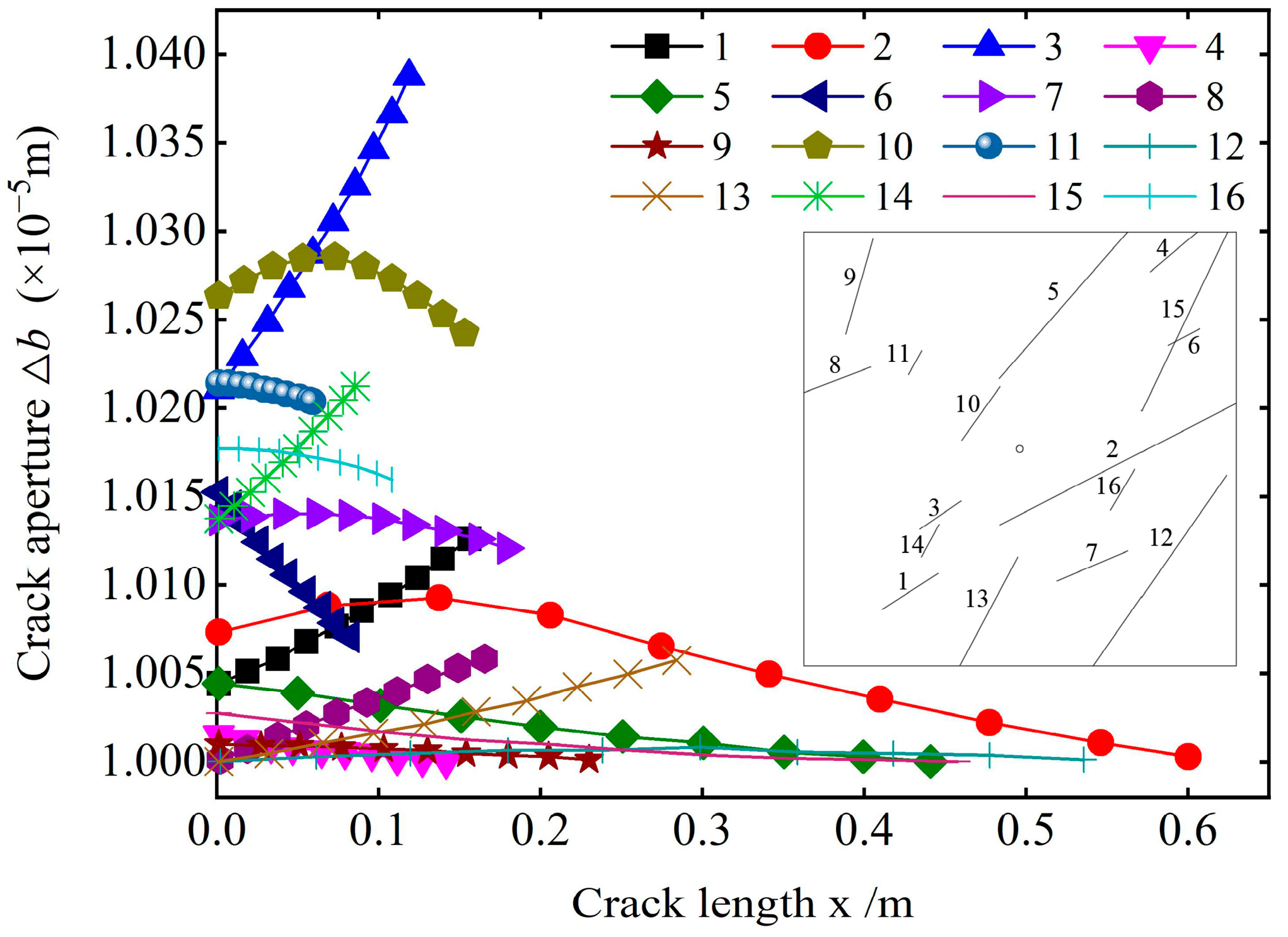
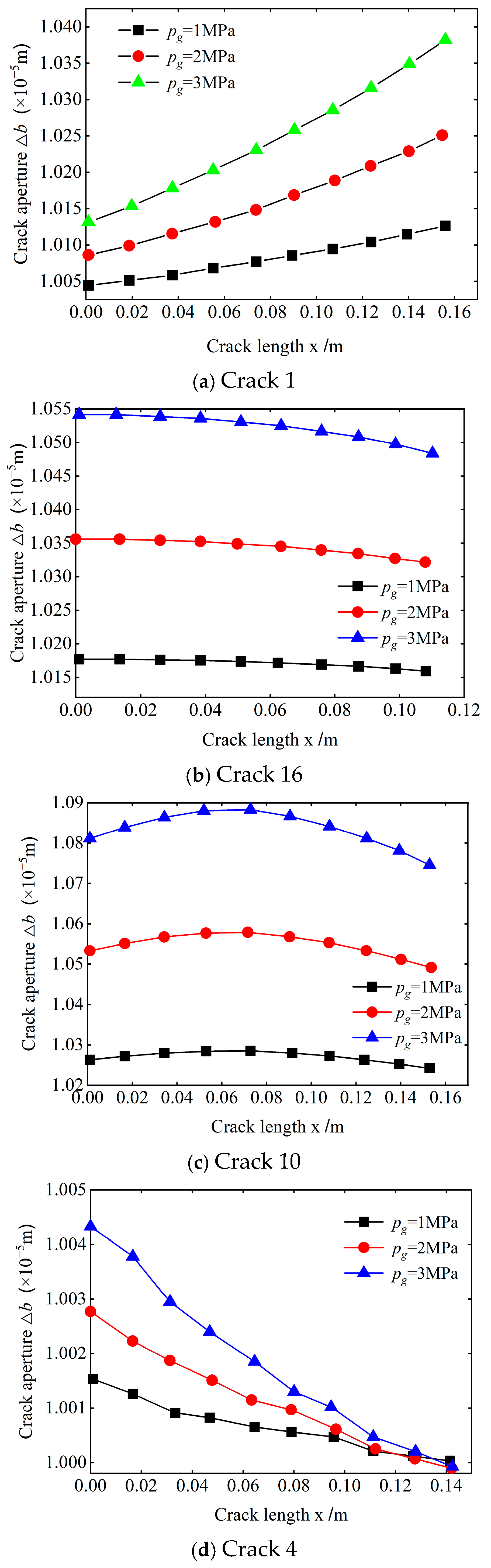
3.1. Calculation Results and Analysis Under Certain Crack Density
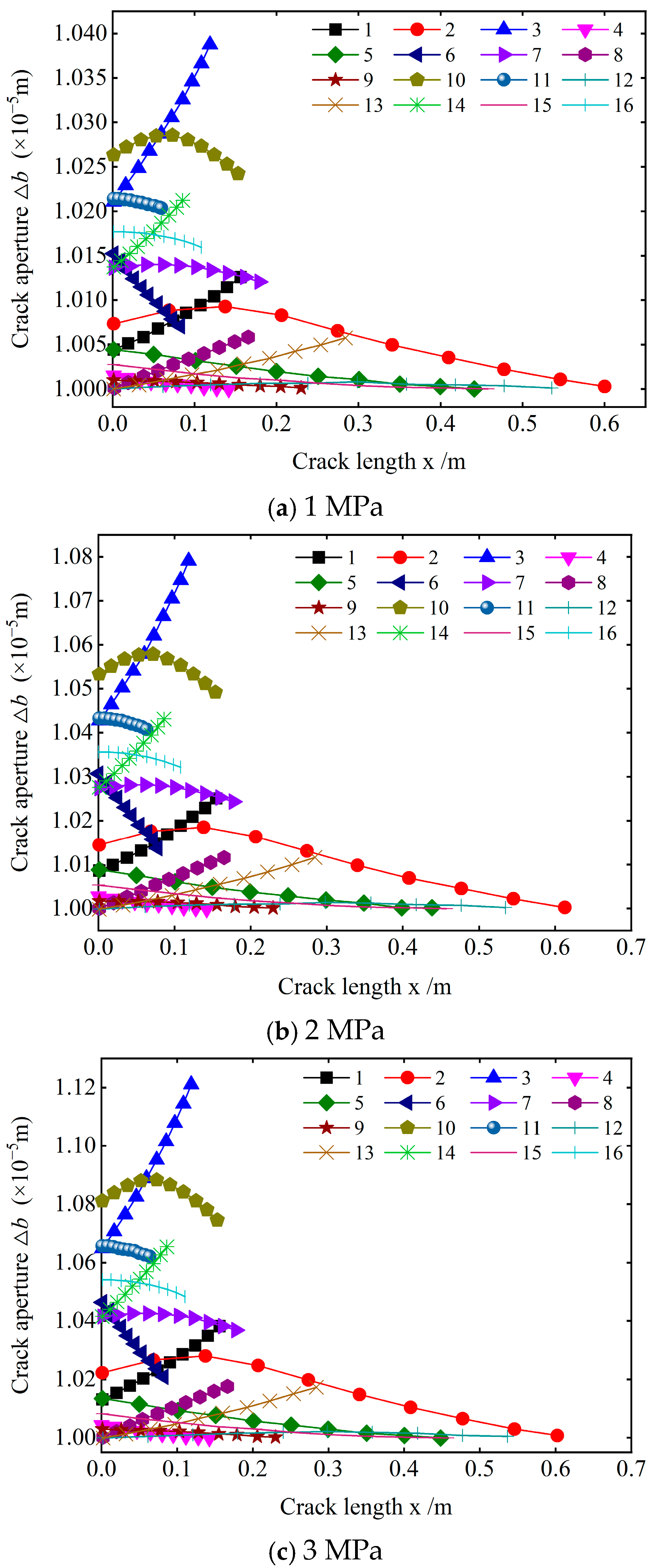
3.2. Sensitivity Analysis of Crack Aperture Under Different Grouting Pressures
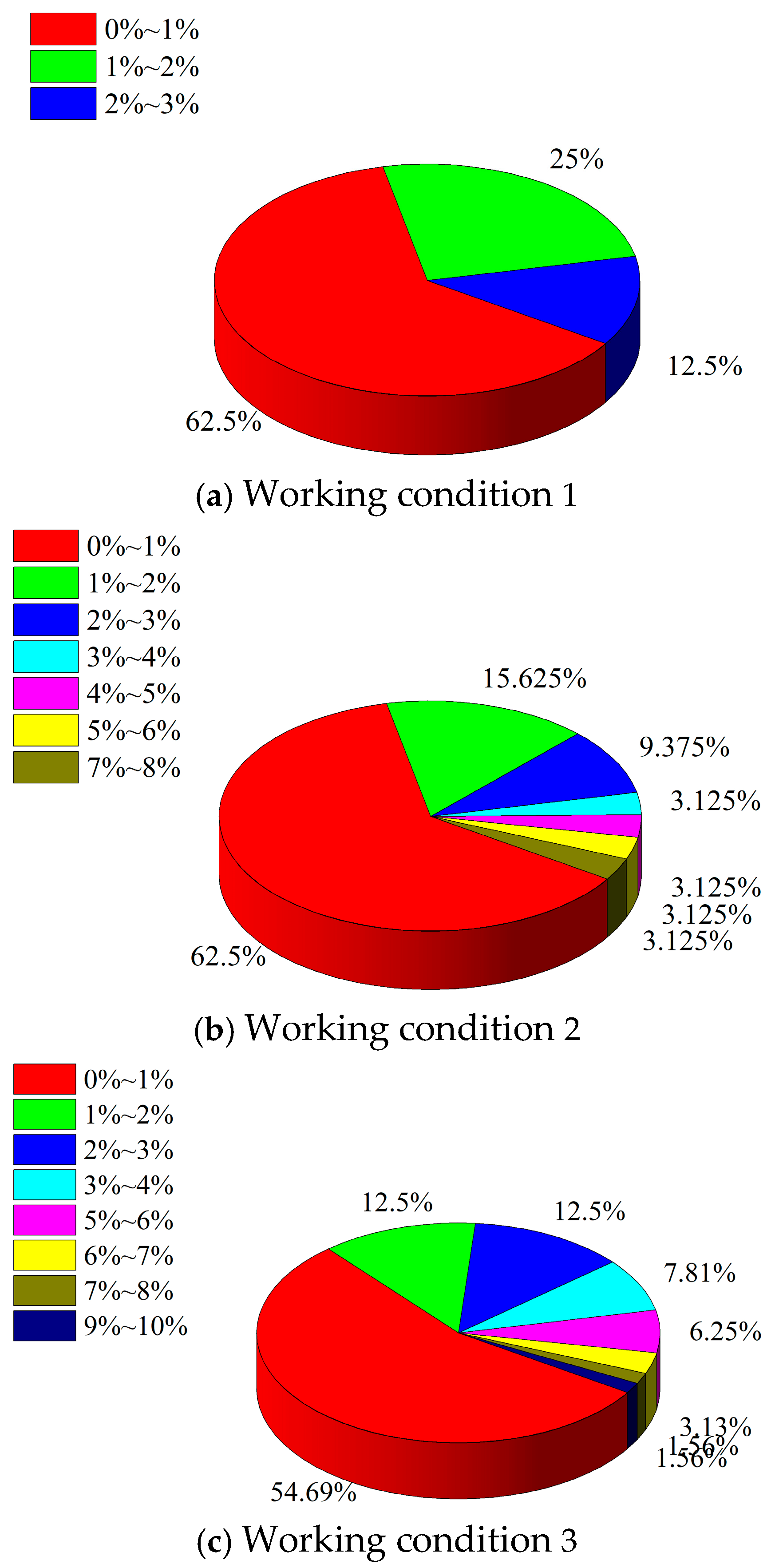
3.3. Calculation Results and Analysis Under Different Crack Densities
3.4. Discussion
4. Conclusions
- (1)
- When slurry is injected from a grouting hole to a certain position, four kinds of variation rules exist regarding the direction of the crack opening extension: gradual increase along the crack length; gradual decrease; first increasing and then decreasing; and, basically, remaining unchanged. This variation mainly depends on the distribution location and production status of the cracks.
- (2)
- As the grouting pressure increases, the variation law of the crack opening extension remains basically unchanged, but the crack opening per unit length obviously varies. Specifically, the increase in the crack opening per unit length under high grouting pressure is obviously greater than that under low grouting pressure. Along the crack distribution direction, the variation of the crack opening per unit length caused by different grouting pressures mainly exhibits four trends: gradual increase along the distribution direction; gradual decrease; first increasing and then decreasing; and, basically, remaining unchanged.
- (3)
- The average opening increment distribution of cracks obviously varies with the number of cracks in the region. The range of crack opening increment increases with the number of cracks in the region, but it does not exceed 10%. The number of cracks in a cracked concrete determines the size of the cracked concrete affected by the slurry–concrete crack coupling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, Y.X.; Yu, L.Y.; Qian, J.Y.; Li, W.; Zhang, T.; Zhou, L.J. Dynamic tensile behavior and crack propagation in coral aggregate seawater shotcrete: Experimental investigation and numerical simulation. Cement Concrete Comp. 2025, 159, 106010. [Google Scholar] [CrossRef]
- Li, Z.Q.; Nie, L.; Xue, Y.; Li, W.; Fan, K. Model Testing on the Processes, Characteristics, and Mechanism of Water Inrush Induced by Karst Caves Ahead and Alongside a Tunnel. Rock. Mech. Rock. Eng. 2025, 58, 5363–5380. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.S.; Wang, X.C.; Yu, L.Y.; Li, Z.Q. Synergistic effect of particle size, carboxymethyl starch and Na2CO3 on rheological and filtration property of bentonite-based material. Case Stud. Constr. Mat. 2024, 21, e03537. [Google Scholar] [CrossRef]
- Li, W.; Yu, L.Y.; Tan, Y.Z.; Wu, L.R.; Qian, J.Y. Mechanical properties and impact behavior of frozen clay: Insights from static mechanical tests, fly-plate tests, and split-Hopkinson pressure bar analysis. Phys. Fluids 2024, 36, 057138. [Google Scholar] [CrossRef]
- Li, W.; Yu, L.; Zhang, T. Quantitative analysis of grain size effect on tensile mechanical behavior of granite based on multi-level force chain networks. Comp. Part. Mech. 2024, 11, 2245–2266. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, C.; Li, Z.; Wang, A.; Gao, Y.; Wang, X. Experimental Study on Water-Plugging Performance of Grouted Concrete Crack. Materials 2024, 17, 1568. [Google Scholar] [CrossRef] [PubMed]
- Gustafson, G.; Claesson, J.; Fransson, A. Steering parameters for rock grouting. J. Appl. Math. 2013, 2013, 269594. [Google Scholar] [CrossRef]
- Zhou, M.R.; Chen, Z.C.; Luo, X.B.; Zhou, G.K.; Lu, C.G. Reinforcement mechanism of cement slurry grouting in collapsible loess. J. Build. Sci. Eng. 2017, 34, 65–70. [Google Scholar]
- Ruan, W.J. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts. Chin. J. Rock Mech. Eng. 2015, 24, 2709–2714. [Google Scholar]
- Li, S.C.; Liu, R.T.; Zhang, Q.S.; Sun, Z.Z.; Zhang, X.; Zhu, M.T. Research on c-s slurry diffusion mechanism with time-dependent behavior of viscosity. Chin. J. Rock Mech. Eng. 2013, 32, 2415–2421. [Google Scholar]
- Zhang, Q.S.; Zhang, L.Z.; Zhang, X.; Liu, R.T.; Zhu, M.T.; Zheng, D.Z. Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity. Chin. J. Rock Mech. Eng. 2015, 34, 1199–1210. [Google Scholar]
- Zhou, F.; Xu, Y.; Zhu, R.; Song, Z.; Zhai, D.Z.; Mou, Y.M. Diffusion characteristics of grouting slurry in sandy stratum. J. Build. Sci. Eng. 2020, 37, 182–192. [Google Scholar]
- Li, X.L.; Jin, D.; Wang, F.M.; Zhong, Y.H.; Zhang, B. Diffusion model of an ideal expansible grout in single fracture. Chin. J. Rock Mech. Eng. 2018, 37, 1207–1217. [Google Scholar]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock—New methods for calculation of penetration length, part I. Tunnel. Undergr. Space Technol. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Fransson, A.; Tsang, C.F.; Rutqvist, J.; Gustafson, G. A new parameter to assess hydromechanical effects in single-hole hydraulic testing and grouting. Int. J. Rock Mech. Min. Sci. 2007, 44, 1011–1021. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, S.C.; Liu, R.T.; Zhu, G.X.; Zhang, L.Z.; Pan, D. Analysis of coupling effect between grout and rock mass during jointed rock grouting. Chin. J. Rock Mech. Eng. 2015, S2, 4054–4062. [Google Scholar]
- Kim, H.M.; Lee, J.W.; Yazdani, M.; Tohidi, E.; Nejati, H.R.; Park, E.S. Coupled viscous fluid flow and joint deformation analysis for grout injection in a rock joint. Rock Mech. Rock Eng. 2017, 3, 627–638. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zhang, Q.S.; Liu, R.T.; Li, S.C. Grouting mechanism in fractured rock considering slurry-rock stress coupling effects. Chin. J. Geotech. Eng. 2018, 40, 1–9. [Google Scholar]
- Yang, M.J.; Chen, M.X.; He, Y.N. Simulating experiment for grouting seepage in rock mass. J. Exp. Mech. 2001, 1, 105–112. [Google Scholar]
- Yang, M.J.; Chen, M.X.; He, Y.N. Law of grouting penetrating through fracture network of rock mass. J. Hydraul. Eng. 2001, 7, 41–46. [Google Scholar]
- Zhang, Y.T. Rock Hydraulics and Engineering; China Water&Power Press: Beijing, China, 2005. [Google Scholar]
- Ruan, W.J. Research on diffusion of grouting and basic properties of grouts. Chin. J. Geotech. Eng. 2005, 27, 69–73. [Google Scholar]
- Kong, X.Y. Advanced Mechanics of Fluid in Porous Media; Press of University of Science and Technology of China: Hefei, China, 1999. [Google Scholar]
- Zhou, C.B.; Chen, Y.F.; Jiang, Q.H.; Rong, G. An interfacial layer model for coupled hydromechanical analysis in geological discontinuities. Chin. J. Rock Mech. Eng. 2008, 6, 1081–1093. [Google Scholar]
- Li, S.C.; Zheng, Z.; Liu, R.T.; Wang, X.; Zhang, L.; Wang, H. Analysis on fracture grouting mechanism considering grout-rock coupling effect. Chin. J. Rock Mech. Eng. 2017, 36, 812–820. [Google Scholar]
- Zhu, L.L. The Monte Carlo Method and Application. Ph.D. Thesis, Central China Normal University, Wuhan, China, 2014. [Google Scholar]
- Song, X.C.; Xu, W.Y. Numerical model of three-dimensional discrete fracture network for seepage in fractured rocks (I): Generation of fracture network. Chin. J. Rock Mech. Eng. 2004, 12, 2015–2020. [Google Scholar]
- Liu, R.C.; Li, B.; Jiang, Y.J. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, Z.H.; Peng, H.; Pu, H. The role of fracture surface roughness in macroscopic fluid flow and heat transfer in fractured rocks. Int. J. Rock Mech. Min. Sci. 2016, 87, 29–38. [Google Scholar] [CrossRef]


| Type 1 | Dip Angle/(°) | Trace Length/(m) | Density of Crack (Strips/m2) | |
|---|---|---|---|---|
| Mean Value | Variance | Mean Value | ||
| 1 | 28° | 6.6 | 0.37 | 16 |
| 62° | 4.3 | 0.34 | ||
| 2 | 28° | 6.6 | 0.37 | 32 |
| 62° | 4.3 | 0.34 | ||
| 3 | 28° | 6.6 | 0.37 | 64 |
| 62° | 4.3 | 0.34 | ||
| Parameters | The Value |
|---|---|
| Porosity of porous media | 0.22 |
| Permeability of porous media | 4 × 10−8 m2 |
| Elastic modulus | 5 × 102 MPa |
| Poisson’s ratio of concrete | 0.2 |
| Crack porosity | 1 |
| Slurry density | 2940 g/cm3 |
| Slurry viscosity | 0.08 Pa·s |
| Type | Characteristics of a Change in Opening | Typical Cracks |
|---|---|---|
| A | ① The crack opening gradually increases along the distribution direction. ② The crack opening greatly varies along the distribution direction. | 1, 3, 8, 13, 14 |
| B | ① The crack opening gradually decreases along the distribution direction. ② The variation of the crack opening is small. ③ The variation degree of the crack opening is obviously different, but the overall trend is the same. | 5, 6, 11, 15, 16 |
| C | ① The crack opening first increases and then decreases along the distribution direction. ② The variation degree of the crack opening is large. | 2, 7, 10 |
| D | ① There is no obvious change in the crack opening along the distribution direction. ② The variation degree of the crack opening is small. | 4, 9, 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, W.; Shen, M.; Wang, H. Numerical Analysis of Slurry–Crack Coupling in Grouting Repair Process of Multiple Cracks in Concrete Material. Materials 2025, 18, 2472. https://doi.org/10.3390/ma18112472
Wang X, Li W, Shen M, Wang H. Numerical Analysis of Slurry–Crack Coupling in Grouting Repair Process of Multiple Cracks in Concrete Material. Materials. 2025; 18(11):2472. https://doi.org/10.3390/ma18112472
Chicago/Turabian StyleWang, Xiaochen, Wei Li, Mingxiang Shen, and Hongtao Wang. 2025. "Numerical Analysis of Slurry–Crack Coupling in Grouting Repair Process of Multiple Cracks in Concrete Material" Materials 18, no. 11: 2472. https://doi.org/10.3390/ma18112472
APA StyleWang, X., Li, W., Shen, M., & Wang, H. (2025). Numerical Analysis of Slurry–Crack Coupling in Grouting Repair Process of Multiple Cracks in Concrete Material. Materials, 18(11), 2472. https://doi.org/10.3390/ma18112472







