Next Article in Journal
Influence of Raw Material Fineness on Clinker Burnability and Cement Performance
Previous Article in Journal
First-Principles Design of Qubits in Charged Carbon Nanomaterials
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 18
Issue 11
10.3390/ma18112452
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Overview of Torsion Tests on Fiber-Reinforced Concrete Beams

by
Jacek Domski
1,*,
Marek Lehmann
1,
Artur Sanok
1 and
Katarina Tvrda
2
1
Faculty of Civil Engineering, Environmental and Geodetic Sciences, Koszalin University of Technology, 75-453 Koszalin, Poland
2
Faculty of Civil Engineering, Slovak University of Technology in Bratislava, 813 68 Bratislava, Slovakia
*
Author to whom correspondence should be addressed.
Materials 2025, 18(11), 2452; https://doi.org/10.3390/ma18112452
Submission received: 14 April 2025 / Revised: 19 May 2025 / Accepted: 21 May 2025 / Published: 23 May 2025
(This article belongs to the Section Construction and Building Materials)
Browse Figures
Versions Notes

Abstract

:
The article presents the results of laboratory tests published in dozens of publications. These tests focused on reinforced concrete beams with additional dispersed reinforcement that were loaded with torsional moments. The results of cracking and ultimate stress were presented depending on various factors influencing the beam’s load-bearing capacity, i.e., the degree of fiber reinforcement Vf, the angle of rotation θ, the compressive strength of the concrete fc, the fiber slenderness l/d, the degree of conventional reinforcement ρtot, the proportions of the cross-section h/b, and the slenderness of the tested element. The frequency of occurrence of the aforementioned factors in the tests was also statistically analyzed. Additionally, the influence of fibers on the factors determining the torsional load-bearing capacity was examined. It has been shown that fibers can significantly contribute to increasing the torsional load-bearing capacity of beams and can even be characterized by a twofold increase. It has also been observed that despite the increased load-bearing capacity, beams with fibers are often characterized by lower torsional stiffness. Additionally, it has been found that fibers provide the greatest increase in load-bearing capacity for concretes with compressive strengths in the range of 25–45 MPa and for square cross-sections (b/h = 1.0). In addition, fibers can lead to the formation of torsional cracks at higher reinforcement factors (Vf). However, in terms of cooperation with conventional reinforcement, fibers are of little importance in transferring torsional stresses in the case of beams with a high conventional reinforcement factor ρtot > 3%.

1. Introduction

Torsion is an important issue in structural mechanics, influencing the design and analysis of various building elements. A proper understanding of the phenomenon of torsion is essential not only for ensuring the safety and durability of structures but also for the efficient use of building materials. This phenomenon occurs wherever loads do not act in a homogeneous manner. In the context of structures, torsion can be caused by various factors, including asymmetric load distribution, wind forces, and temperature changes. The issue becomes even more complex with the developing market for building materials, including the use of high-performance concrete and innovative solutions for reinforcing concrete structural elements.
In order to understand the influence of fibers on torsional load-bearing capacity, one of the most popular calculation models used to calculate reinforced concrete elements under torsion should be presented first (Figure 1). This model is a spatial truss, which, in its assumptions, resembles a truss used in shear calculations. The load-bearing capacity will therefore consist of individual components of the truss model: force Fsl in longitudinal bars placed at the corners of the cross-section, force Fsw in closed-tension stirrups, and additionally, the load-bearing capacity being influenced by a diagonally compressed concrete strut inclined at an angle θ. However, when discussing cross-sections made of fiber-reinforced concrete, the truss model described above should be modified. Figure 1 illustrates only those fibers that will be responsible for torsional load-bearing capacity, i.e., fibers that will bridge diagonal cracks. The diagonal arrangement of the fibers will result in a horizontal force Ffl and a vertical force Ffw, as additional factors increasing the torsional resistance. At the same time, according to the results of many studies, after the cracking of the torsion element, the concrete contained inside the cross-section near the center of gravity does not reach its full strength and is not subject to cracking. Hence, similarly to the case of reinforced concrete elements, its contribution is omitted in the calculations, and the cross-section is considered to be a thin-walled box section.
The aim of this review article is to analyze previous research on the torsion of structural elements made of concrete reinforced with dispersed reinforcement. The analysis used various journal databases, including Elsevier, MDPI, BazTech, DOAJ, Ebsco, Infona, ProQuest Central, Springer Link, Web of Science, Wiley Online Library, Hindawi, and Sciendo. A total of approximately 270 articles published between 1979 and 2024 and which fell within the researched thematic area were evaluated (Table A1). Ultimately, based on the analyses conducted by the authors of the referenced articles and the results obtained, 48 articles were selected for analysis in this paper. Figure 2 illustrates the number of beam elements used with the corresponding volume of dispersed reinforcement.
The mechanical properties in terms of compressive strength of composites with the addition of steel fibers were determined in each of the articles [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] (Table A3). The influence of fiber addition on compressive strength was evident in all cases. Unfortunately, not all mechanical properties were assessed during the tests and presented in the aforementioned articles. Tensile strength was determined in articles [1,3,9,10,12,14,15,16,17,18,19,20,21,22,23,24,26,27,28,29,30,31,32,33,34,35,36,38,39,40,43,46], which demonstrated a positive influence of fiber addition on this property. The modulus of elasticity was analyzed by the following authors: [5,6,11,14,15,16,17,18,19,20,32,34,35,36,38,39,40,45,46,47]. In this case, the impact of the addition was less clear, with either a slight increase or no observable influence of the dispersed reinforcement on this property. Some authors also investigated residual strength [5], where a significant effect of the addition of fibers, along with their percentage content in concrete, was observed on the improvement of the fiber-reinforced concrete class. A few researchers reported the properties of applied longitudinal [1,2,3,5,6,8,9,11,13,19,20,21,22,27,28,32,33,34,36,38,41,43,44,46,47], transverse [1,2,3,5,6,8,19,20,21,22,27,32,33,34,36,38,43,44,46,47], or dispersed [1,3,4,5,6,8,9,10,11,12,16,20,21,25,26,28,29,30,31,32,33,36,38,40,42,43,44,46,48] reinforcement (Table A3). Unfortunately, the absence of basic properties in all analyzed articles means that in several cases it was difficult to draw clear conclusions.
Analysis of the torsion phenomenon was conducted for rectangular elements with an aspect ratio of 1 to 2.5 (Table A2), featuring a longitudinal reinforcement ratio of up to 2.2%, transverse reinforcement of up to 1.7%, and dispersed reinforcement of up to 1.5% (by volume), as well as a composite strength of up to 70 MPa. These criteria were met by 33 articles, which were further analyzed in this article. The authors of the reviewed articles determined the cracking stress (corresponding to the cracking moment) [1,3,4,5,6,7,8,9,11,12,13,14,16,17,18,20,21,22,23,24,27,29,32,33], the ultimate stress (corresponding to the ultimate moment) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], the angle of rotation at the cracking moment [1,5,6,7,8,9,11,12,16,17,18,20,22,23,26], the angle of rotation at the maximum moment [1,4,5,6,7,8,9,10,11,12,14,16,17,18,19,20,21,22,23,26,32], the compressive strength [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], the longitudinal reinforcement ratio [1,2,3,4,5,6,7,8,9,11,12,13,16,17,18,19,20,21,22,23,24,27,28,32,33], and the transverse reinforcement ratio [1,2,3,4,5,7,8,9,12,16,17,18,19,20,21,22,23,24,27,32,33] (Table A4). Additionally, they examined the h/b ratio [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], the slenderness of the element [2,3,4,5,6,7,8,9,11,12,13,15,16,17,19,20,22,27,28,32], and fiber slenderness l/d [1,3,4,5,6,8,11,12,13,15,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. Unfortunately, many articles do not provide information on how the individual values were determined. The lack of this information may affect the results obtained and the conclusions drawn, especially when comparing results obtained by different authors.
All the analyzed articles emphasize the importance of modern building materials in this dynamically evolving field.
This review article attempts to examine and synthesize the latest achievements concerning the behavior of fiber-reinforced concrete beams subjected to torsion. It also comprehensively describes the factors influencing the torsional load-bearing capacity based on previous research, i.e., the compressive strength of concrete fc, the fiber slenderness l/d, the aspect ratio h/b, and the slenderness of the tested elements. By using relative torsional stresses (tu/tuo), the influence of the fibers themselves on the factors determining this load-bearing capacity for the results of the current research is also presented.
Based on the literature reviewed, it is evident that further research is necessary to gain a more comprehensive understanding of the influence of various factors on the load-bearing capacity of structures under torsional loads, and to develop more advanced theories and models that can be applied in engineering practice. Consequently, this review seeks not only to define the current state of knowledge in this field but also to indicate directions for future research that will contribute to the development of more effective and durable building solutions.

2. Results from the Conducted Literature Review

Based on the literature review conducted, it is possible to identify the fundamental properties specified by the majority of authors [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. First, the description of the results began with the stresses at which a reinforced concrete torsion element cracks (Figure 3a). In the case of reinforced concrete elements without the addition of dispersed reinforcement, the values of cracking stresses reach up to 16 MPa, while the addition of fibers in amounts of up to 0.5% increases this value to over 18 MPa. An amount of fibers in concrete at the level of 1.0% increases the stresses to 22 MPa, while an amount of 1.5% increases the value of cracking stresses to over 24 MPa. However, based on Figure 3b, it can be seen that most researchers achieved values of cracking stresses in the range of 2 to 6 MPa. In this range, the number of conducted tests in which fibers were used in amounts of 0.5% to 1% was the largest. This indicates that the addition of fibers in this amount gained the greatest interest from researchers, which can be explained by the effectiveness of their use in this amount.
Based on the literature review conducted, it can be concluded that the addition of fibers increases the value of the cracking moment compared to the element without dispersed reinforcement. This value increases with the increase in fiber content in the element [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. The literature review conducted shows, among other things, that non-dispersed reinforcement increases the cracking moment to a greater extent compared to traditional reinforcement, and that fibers have a greater effect on the cracking moment than on the maximum torsional strength [24].
Another important feature of torsionally stiffened elements, determined by researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], is their load-bearing capacity, understood as torsional strength (τu). The results of the literature review conducted in the field of the change in the value of torsional strength as a function of the amount of dispersed reinforcement used are presented in Figure 4a. It shows that the highest strength of about 34 MPa was obtained with the addition of fibers in an amount of 1.0%. Some of the researchers obtained relatively high values of torsional strength for elements without dispersed reinforcement, reaching even 32 MPa [4]. This is probably due to the significant amount of additional reinforcement in the tested element. However, most of the researchers obtained lower values of torsional strength (Figure 4b). For elements without dispersed reinforcement, the largest number of analyzed elements (26) yielded values in the range from 2 to 4 MPa. A total of 16 elements obtained stress values in the range from 4 to 6 MPa, while 12 elements were in the range from 6 to 8 MPa. Some researchers added fibers in amounts of up to 0.5%, which resulted in stress values mainly in the range from 2 to 10 MPa. However, the largest number of tested elements contained fibers in the range from 0.5 to 1.0% (47 beams); for this group, the stress value obtained was from 4 to 6 MPa. A relatively small number of the tested elements contained dispersed reinforcement in amounts above 1%, which may indicate the lack of feasibility and effectiveness of using a larger number of fibers in the twisted element.
Source materials show that the addition of fibers increases the torsional strength of beam elements [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. The amount of dispersed reinforcement used affects the torsional strength values. With an increase in the volume of fiber used, the torsional strength increases. However, not every amount of fibers improved this value. Fibers in the amount of about 0.3% had a negligible effect on the torsional strength value [20,21,23,24].
The torsion phenomenon is always accompanied by an angle of rotation. This can be measured and defined in various ways. In this article, it is assumed to be defined in rad/m. Based on the bibliographic query [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], it was determined that the angle of rotation changes depending on the stresses causing the cracking of the twisted element (Figure 5a). The highest value of the angle of rotation (θcr), about 0.08 rad/m, was obtained for an element containing fibers in an amount of up to 1%. This is a relatively high value compared to most of the presented results. Most researchers obtained a cracking angle of rotation no greater than 0.01 rad/m (Figure 5b). If we consider the results of strength at cracking of the twisted element, in this range, it can be seen that the addition of fibers causes a decrease in the angle of rotation [7]. This is undoubtedly related to the increase in the fracture energy of the twisted element [27].
The rotation angle was also analyzed for the ultimate stresses of the torsion element (Figure 6a). The highest value of the rotation angle (θu = 0.18 rad/m) was obtained for the ultimate stresses of about 11 MPa, while the highest stress value (τu = 34 MPa) was recorded for a rotation angle of 0.02 rad/m. This discrepancy in results indicates that the addition of fibers can cause an increase in the value of the rotation angle, which is visible in the greater ductility of the material [10,12,25,32], or that the addition of fibers reduces the rotation angle, thus increasing the torsional stiffness and strength of the element [13,21]. At the same time, it can be assumed that the rotation angle can be approximately the same for elements with and without dispersed reinforcement [31]. These discrepancies in results and conclusions drawn can be used to carry out verification tests. Additionally, when analyzing Figure 6b, it can be seen that the largest number of results for the angle of rotation corresponding to the ultimate moment was obtained for the value of 0.01 rad/m, which may indicate that some of the individual results defining significant angles of rotation are burdened with statistical error.
Compressive strength is a key parameter describing the properties of concrete. Its influence on other features of the cement composite is crucial. The addition of fibers to concrete means that the relationship between compressive strength and, among others, the strength of the torsional element is not clearly defined. The above relationship is presented in Figure 7a, illustrating the influence of the amount of applied dispersed reinforcement, obtained on the basis of works [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. It can be seen that compressive strength increases with the amount of applied dispersed reinforcement [3,10,25,29], and at the same time, the torsional strength of the element increases [12,32,33]. As can be seen from Figure 7b, most of the test elements were made of composites with strength in the range of 25 to 45 MPa. The largest number of test elements were made with the addition of steel fibers in amounts from 0 to 0.5% and from 0.5 to 1.0%, obtaining concretes with compressive strengths from 29 to 34 and from 39 to 44 MPa, respectively. Concrete with compressive strength values in these ranges are currently the most popular in residential construction.
Another important feature influencing the load-bearing capacity of twisted elements is the slenderness of the fibers used. As can be seen from the literature review, the efficiency of fibers depends, among other things, on their dimensions. The slenderness of fibers, i.e., the ratio of length to diameter, is the basic parameter describing them. Figure 8a shows the effect of the slenderness of fibers on the torsional strength of the element. It can be seen that the most effective fibers are those with an l/d ratio in the range of 60 to 80. It follows from this that regardless of the number of fibers used, the highest values of torsional load-bearing capacity were achieved in this range. Also, from Figure 8b, it can be concluded that the authors of publications [23,27,28,29] most often used fibers with a slenderness of 60 to 75, which probably resulted from their knowledge of the effect of the slenderness of fibers on the properties of the fresh mixture and the hardened composite [49].
Conventional reinforcement in torsion elements is the main factor determining their load-bearing capacity. In practically every research work, the influence of the amount of longitudinal and transverse reinforcement on torsional load-bearing capacity was analyzed [50,51]. The situation is similar in the case of beams in which fibers provide additional reinforcement. The histograms (Figure 9b,c) show that the most common longitudinal reinforcement ratio in beams ranged from 1.5% to 1.6%, while the most common transverse reinforcement ratios ranged from 0.2 to 0.4%. It is assumed that the load-bearing capacity of the elements under torsion can be achieved by joint plasticization of the longitudinal and transverse reinforcement—most often in the case of low ρl and ρw values, by plasticization of the transverse reinforcement—in the case of small ρw and large ρl, by plasticization of the longitudinal reinforcement where the ratio of reinforcement ratios is inverse, and for large ρl and ρw values, failure occurs through crushing of the concrete before the yield strength of the longitudinal and transverse reinforcement has been reached [52].
Due to the very complex effects of longitudinal and transverse reinforcement in torsion elements, it was decided to compare torsional stresses to the total longitudinal reinforcement ρl and transverse reinforcement ρw in the form of total reinforcement ratio ρtot in the analysis. A clear trend can be seen in the τu to ρtot graph (Figure 9a), where the increase in maximum stresses is accompanied by an increase in the reinforcement ratio. It should be noted that the increasing trend is contradicted by the research results from two articles [7,17], where the load-bearing capacity with a small reinforcement ratio reached a value similar to the case of a threefold higher reinforcement ratio in beams, according to other authors. However, it was decided not to reject the research results, thus showing possible variability despite the general trend in the graph. The influence of fiber content on cooperation with conventional reinforcement in transferring torsional stresses is presented in the next section.
The issue of the influence of cross-section dimensions on the torsional resistance of concrete elements was analyzed in the second half of the 20th century. Researchers agree that the aspect ratio of the cross-section has a large influence on the torsional resistance as well as on the change in the angle at which this resistance is achieved [53]. It is stated that square cross-section elements (h/b = 1) achieve greater torsional resistance than their counterparts with a cross-section proportion h/b > 1. Researchers also agree that torsional resistance decreases with the increase in the height of the cross-section, although no proportionally linear relationship between these two features has been found for h/b in the range <1:2>. At the same time, it is noted that with h/b > 2, the torsional resistance decreases linearly with the increase in height [52]. Figure 10a shows the dependence of torsional stresses on the cross-section proportions for beams with different fiber content and without fibers. According to the histogram, the most frequently tested elements are beams with a rectangular cross-section h/b = 2.0, followed by square cross-sections. Rectangular cross-sections with h/b < 2.0 were also noted, but in a relatively smaller number (see Figure 10b). Assuming that the most frequently tested elements are those with cross-sections h/d = 2 and h/d = 1, a clear trend of decreasing torsional stresses can be observed, and the difference in the achieved stresses is almost twofold: for beams with h/d = 1, the maximum stresses in the described beams were 28 MPa, and for beams with a cross-section h/b = 2, they were only 14 MPa. At the same time, it should be noted that there is no clear trend in the influence of steel fibers on the analyzed phenomenon, which suggests similar conclusions to those reached in the analysis of the influence of fibers on slenderness.
Figure 11a presents the relations between torsional stresses and torsional slenderness. Torsional slenderness is assumed to be the ratio of the support spacing to the radius of gyration of the cross-section under torsional stress. The issue of the influence of torsional slenderness is discussed in the literature, although it is not analyzed as often as, for example, the influence of cross-section dimensions [1]. In general, a tendency is observed in which stockier beams achieve higher torsional load-bearing capacities; the influence of slenderness disappears over time, and for beams with high but variable slenderness, it is essentially unnoticeable. The phenomenon described above is also visible in Figure 11a, but only with a significant increase in slenderness equal to 37–38, where stresses were achieved in the range from 2 to 10 MPa. More stocky beams with slenderness from 8 to 19 showed a similar level of torsional stresses, reaching values of up to 34 MPa, with slenderness of 11.7. Additionally, the scatter of results for stocky beams was noticeably larger than for slender beams. The most commonly adopted slenderness values in the tests were in the range of 12–16 and 36–38. Regarding dispersed reinforcement, it was found that the slenderness effect in beams with fibers is just as noticeable as that in beams without fibers, without the amount of fiber content having a significant influence. Hence, it can be assumed that dispersed reinforcement does not have a major impact on the potential reduction or intensification of the influence of beam slenderness on torsional stresses.

3. Analysis of Research Results from Conducted Literature Review

The previous section described the general dependencies of torsional stresses both at the moment of cracking and at the moment of reaching torsional capacity, along with different factors that determine this capacity. However, it should be noted that the described torsional capacity depends on the factors described earlier (i.e., cross-section geometry, reinforcement ratio, matrix compressive strength, or slenderness), and determining the efficiency of fibers in transferring torsional stresses by comparing only the load-bearing capacity values may be problematic. Therefore, it was decided that the fiber effect itself (the effect of fiber reinforcement) would be interpreted by the expression τ/τ0, in which the torsional stresses of reinforced concrete beams with fibers τ are divided by the torsional stresses of reference reinforced concrete beams without fibers τ0, with the same degree of reinforcement, cross-section geometry, slenderness, and matrix strength as the beams with fibers. This will allow the factors described above to be eliminated by focusing only on the dispersed reinforcement itself.
Figure 12 shows the relationship of τcr/τcr0 to the fiber content. The influence of fibers on the cracking stress is clearly visible, and their quantity alone influences the level of these stresses. It can be assumed that 0.5% fiber content increases the cracking moment by approx. 25%, 1.0% by approx. 40%, and 1.5% by approx. 60%. It should be noted, however, that this is a general upward trend, which did not always occur in the studies. According to the graph, some researchers noted similar or lower values of cracking stress in elements with fibers compared to those without [5,6,11,20,29]. Additionally, it cannot be clearly stated whether the addition of fibers in amounts greater than 1.5% contributes to the achievement of higher cracking moments by beams, due to the small number of results.
Figure 13 illustrates the relationship between the maximum torsional stresses and the maximum stresses in the reference beams, as well as the percentage of fiber content. As in the case of cracking stresses, fibers also have an effect on the torsional load-bearing capacity. This effect is variable and, depending on the test series, it can be marginal, in the order of a few percent, or even more than 2.5 times the load-bearing capacity of the reference beams. It should be noted, however, that no clear trend of increasing load-bearing capacity was observed with increasing fiber content. The reason for this may lie in the use of different types of fibers in the mixtures in terms of shape, the material from which they are made, and their slenderness. It is also worth noting that the high variability of the effect of fiber reinforcement may result from other factors, such as the degree of reinforcement or the compressive strength of the concrete.
Figure 14 shows the relationship between the τu/τu0 value and the compressive strength of the concrete used in beam tests. In the literature, there are analyses devoted to the influence of concrete compressive strength on torsional stresses; this influence is obvious, as presented in Figure 7a. However, when analyzing the effect of fiber reinforcement for different concrete strengths, a different trend was observed. The graph shows that regardless of the concrete class, whether in the order of 15 MPa or 65 MPa, fibers provide a minimum reinforcement threshold of about 25% at different levels of dispersed reinforcement. However, the graph also shows that for beams made of concrete with strengths between 25 and 45 MPa, some researchers achieved greater reinforcement effects in the range from 50% to 125%, and their occurrence was independent of the percentage of fiber content. The clear trend of more effective fiber action for concretes in the range of 25–45 MPa may result from the fact that the tensile strength of the matrix is too high in the case of higher concrete classes, which means that the fibers are less effective in transferring tensile stresses, while for concretes of lower strength, the fiber effectiveness may be offset by the generally low strength of the matrix, both in tension and compression, leading to lower values of maximum stresses in the tested elements. Finally, it should be remembered that the scatter of results in the graph may result from other factors mentioned above that affect the torsional load-bearing capacity.
The next figure shows the effect of fiber reinforcement depending on the cross-section dimensions of the tested beams. According to Figure 10a, the cross-sectional aspect ratio has a significant effect on achieving maximum torsional load-bearing capacity, and a similar trend can be observed when analyzing the τu/τu0 values. The influence of fibers for square cross-sections oscillated at a reinforcement level of up to approximately 100%, and in the case of the fiber reinforcement ratio of up to 1.0%, this influence decreased, reaching values of approximately 50%, for h/b equal to 2.0. A similar downward trend can be observed for beams reinforced with fibers in the range of 1.0% to 1.5%. Thus, it can be stated that, similarly to the case of torsional load-bearing capacity, the reinforcement effect also depends on the cross-section dimensions; however, when comparing Figure 10a and Figure 15, the decrease in the τu/τu0 value is less pronounced.
Figure 16 shows the dependence of the τu/τu0 values as a function of the rotation angle ratios for beams with fibers and the rotation angles of reference beams θu/θu0. According to the analysis presented in the previous section (see Figure 6a), the rotation angles took on different values, which were usually associated with factors such as concrete strength, cross-section dimensions, or reinforcement ratios. In order to better interpret the effect of fibers on the rotation angle, the reinforcement coefficient τu/τu0 and θu/θu0 values were compared, which is intended to help eliminate other factors influencing this angle, and thus the overall assessment of the torsional stiffness of the beams. When analyzing the values of the fiber reinforcement effect, a fairly clear pattern can be observed, where the results can be divided into three groups. The first group, constituting about 7.3% of the analyzed beams, consists of beams in which the addition of fibers resulted in a higher load-bearing capacity compared to the reference beams, while at the same time the torsional stiffness of the beams was greater or at least the same. For this population of results, the influence of fibers proved to be beneficial, improving torsional stiffness. The next group, comprising about 78% of the beams, consists of cases in which a greater increase in the angle of rotation was observed (maximum four times) in relation to the increase in load-bearing capacity, which resulted in a correspondingly lower torsional stiffness. The last group consists of elements for which a significantly greater increase in the angle of rotation was noted with small increases in load-bearing capacity—it is worth emphasizing that the percentage of such beams in the population was small. At the same time, no significant effect of the Vf fiber content on the improvement or deterioration of torsional stiffness was found, and in this case the factor is of secondary importance. It should be noted that in the previous analysis (Figure 5a), it was decided not to compare the effect of fiber reinforcement with the angle of rotation at cracking, due to the negligible influence of fibers on this aspect.
The relationship between the effect of fiber reinforcement and the reinforcement ratio is illustrated in Figure 17. Given the complex roles of both longitudinal and transverse reinforcement in transferring torsional stresses, the total reinforcement ratio ρtot was adopted as the sum of the longitudinal and transverse reinforcement ratios. Figure 17 shows a clear tendency for the reinforcement effect to decrease with increasing ρtot value, and this decreasing tendency occurs in each of the ranges of fiber reinforcement ratio Vf. For beams with a reinforcement ratio in the range <1;1.2>, the effects of fiber reinforcement reached values even above 100%, while for ρtot equal to 2.75, this effect decreased to approx. 35%. Finally, it can be assumed that an increase in the ρtot value by 1% results in a decrease in the fiber reinforcement effect of 50%, and for beams with ρtot above 3%, the addition of fibers may become ineffective from the point of view of torsional load capacity.

4. Future Research Directions

The analysis of the above-described factors influencing torsion leaves great possibilities for future research directions. The addition of fibers itself has a very random effect on the improvement of torsional load-bearing capacity, and it is possible that other factors contribute in this case to the randomness of the fiber’s influence, i.e., slenderness and aspect ratio. The trends concerning the influence of slenderness or the h/b ratio on torsional load-bearing capacity are usually presented for specific tests with appropriate initial assumptions, i.e., the degree of reinforcement and concrete strength. In this case, a number of additional tests should be performed—for example, considering different variants of h/b for different degrees of conventional reinforcement, different degrees of slenderness, and different degrees of fiber reinforcement. In a similar way, analysis of torsional slenderness and its influence on conventional reinforcement should be performed. Another aspect in which slenderness may be an important factor is the variable rotation angle. Due to the possible increase in load-bearing capacity, fibers have not always had a positive effect on the improvement of the angle increase, and thus on torsional stiffness. In this case, it would be necessary to perform an analysis of torsional stiffness for different fiber contents as well as for different degrees of slenderness of the elements. It should also be assumed that the interlocking of aggregate in concrete will affect the inclination of the angle of diagonal cracks and thus the subsequent stiffness; hence, performing tests for concretes with different aggregate fractions would be a good complement to the subject of stiffness after the cracking of the element. The above proposals are only the basic directions of research that should be carried out in the future in order to better understand the complex issue of torsion in reinforced concrete elements with fibers.

5. Conclusions

The issue of torsion in fiber-reinforced concrete elements is the subject of numerous studies and analyses, in which the authors examine various aspects of this complex phenomenon. Interpreting the previously described results, several conclusions can be drawn:
  • The effect of fibers on the magnitude of torsional cracking stresses can be significant for Vf values greater than 1%.
  • The influence of fiber reinforcement on load-bearing capacity can vary; it may either be minimal or result in nearly double the load-bearing capacity compared to the reference beams. Furthermore, the observed increase in load-bearing capacity does not have a clear correlation with the amount of fibers.
  • The greatest effect of fiber reinforcement on load-bearing capacity was observed for beams made of concrete with strengths ranging from 25 to 45 MPa.
  • The h/b cross-section proportions affect the effective performance of fibers. For square cross-sections, the increase in load-bearing capacity due to fibers is greater than that for rectangular cross-sections with an h/b ratio of 2.0.
  • Fibers have a small effect on improving torsional stiffness; rather, a reduction in stiffness itself was observed. At the same time, greater ductility was observed for beams that achieved greater rotation angles in relation to the reference beams.
  • The load-bearing capacity gain due to fibers decreased with the increase in the conventional reinforcement ratio, and at ρtot above 3% it was marginal.
Despite the considerable amount of research, significant variation in the results has been observed, along with a frequent lack of clear trends in individual analyses, indicating the need for further studies on fiber-reinforced concrete elements subjected to torsion. The above conclusions will allow for the appropriate preparation of a test program for torsion beams regarding element geometry, slenderness, and the amount of conventional reinforcement. Tests on beams made using waste materials are planned; the main material is to be waste fibers (derived from used car tires). Tests using aggregate obtained from ceramic and porcelain waste are also planned, including investigation of the effect of this aggregate together with waste fibers on load-bearing capacity and crack morphology in torsional conditions.

Author Contributions

Conceptualization, A.S., J.D. and M.L.; methodology, A.S., J.D. and M.L.; software, A.S. and M.L.; validation, A.S., J.D., K.T. and M.L.; formal analysis, A.S.; investigation, A.S.; resources, A.S.; data curation, A.S.; writing—original draft preparation, M.L., K.T. and J.D.; writing—review and editing, A.S., J.D., M.L. and K.T.; visualization, A.S.; supervision, J.D. and M.L.; funding acquisition, K.T.; project administration, J.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Nomenclature

bcross-section width
dfiber diameter
fccylindrical compressive strength
hcross-section height
h/bcross-section aspect ratio
lfiber length
l/dlength-to-diameter ratio of the fibers used
Lelement length
Pgauge length
Tcrcracking moment
Tumaximum moment
Vfvolumetric percentage of dispersed reinforcement used
ρllongitudinal reinforcement ratio
ρtotdegree of conventional reinforcement
ρwtransverse reinforcement ratio
τcrshear stresses of the cross-section for the cracking moment
τcr0shear stresses of the cross-section for the cracking moment of reference beams
τushear stresses of the cross-section for the maximum moment
τu0shear stresses of the cross-section for the maximum moment of reference beams
θangle of rotation
θcrangle at the cracking moment
θcr0angle at the cracking moment for reference beams
θuangle at the maximum moment
θu0angle at the maximum moment for reference beams

Appendix A

Table A1. The parameter ranges and property specifications of the components considered by the authors in their analytical framework.
Table A1. The parameter ranges and property specifications of the components considered by the authors in their analytical framework.
Characteristics/PropertiesCompartment
Aspect ratio h/bfrom 1 to 2.5
Longitudinal reinforcement ratio, ρlup to 2.2%
Transverse reinforcement, ρwup to 1.7%
Dispersed reinforcement (by volume), Vfup to 1.5%
Composite strength, fcfrom 9 to 70 MPa
Modulus of elasticity, Ecfrom 13 to 50 GPa
Tensile strength, ftfrom 0.1 to 11 MPa
Table A2. Geometry of research elements.
Table A2. Geometry of research elements.
Lp.b, mmh, mmL, mmP, mmh/bSlenderness
[1]A1-Con1001501500-1.50-
A1-M13-0.51001501500-1.50-
A1-M13-1.01001501500-1.50-
A1-M13-1.51001501500-1.50-
A1-H35-0.51001501500-1.50-
A1-H35-1.01001501500-1.50-
A1-H35-1.51001501500-1.50-
A2.25-Con1502251500-1.50-
A2.25-M13-0.51502251500-1.50-
A2.25-M13-1.01502251500-1.50-
A2.25-M13-1.51502251500-1.50-
A2.25-H35-0.51502251500-1.50-
A2.25-H35-1.01502251500-1.50-
A2.25-H35-1.51502251500-1.50-
A4-Con2003001500-1.50-
A4-M13-0.52003001500-1.50-
A4-M13-1.02003001500-1.50-
A4-M13-1.52003001500-1.50-
A4-H35-0.52003001500-1.50-
A4-H35-1.02003001500-1.50-
A4-H35-1.52003001500-1.50-
[2]B120020011006001.008.00
B220020011006001.008.00
B320020011006001.008.00
B420020011006001.008.00
B720020011006001.008.00
B820020011006001.008.00
B920020011006001.008.00
B1020020011006001.008.00
B1120020011006001.008.00
[3]B125025011506001.006.40
B2S25025011506001.006.40
B3H25025011506001.006.40
B4C25025011506001.006.40
[4]Control15025016508001.6711.69
1SF15025016508001.6711.69
[5]TB1-PC-L18300300270015001.0013.33
TB3-G25-L18300300270015001.0013.33
TB4-G25-L18300300270015001.0013.33
TB5-G50-L18300300270015001.0013.33
TB6-G50-L18300300270015001.0013.33
TB7-D25-L18300300270015001.0013.33
TB8-D25-L18300300270015001.0013.33
TB9-D50-L18300300270015001.0013.33
TB10-D10-L18300300270015001.0013.33
TB11-D50-L18-ST6/150300300270015001.0013.33
TB12-D50-L18-ST6/150300300270015001.0013.33
TB13-PC-L18-ST6/150300300270015001.0013.33
TB14-PC-L18-ST6/150300300270015001.0013.33
[6]TB1-PC300300270015001.0013.33
TB3-SFRC25300300270015001.0013.33
TB4-SFRC25300300270015001.0013.33
TB5-SFRC50300300270015001.0013.33
TB6-SFRC50300300270015001.0013.33
[7]B1300300250021001.0018.67
B2300300250021001.0018.67
B3300300250021001.0018.67
B4300300250021001.0018.67
B5300300250021001.0018.67
B6300300250021001.0018.67
B7300300250021001.0018.67
B8300300250021001.0018.67
B9300300250021001.0018.67
B10300300250021001.0018.67
B11300300250021001.0018.67
B12300300250021001.0018.67
B13300300250021001.0018.67
B14300300250021001.0018.67
B15300300250021001.0018.67
B16300300250021001.0018.67
B17300300250021001.0018.67
B18300300250021001.0018.67
B19300300250021001.0018.67
B20300300250021001.0018.67
[8]T-Reference20020015006001.008.00
T30SF20020015006001.008.00
T60SF20020015006001.008.00
[9]R115025013008001.6711.69
R215025013008001.6711.69
R315025013008001.6711.69
FR215025013008001.6711.69
FR315025013008001.6711.69
[10]A-VC Plain1002002300-2.00-
A-SFVC 501002002300-2.00-
A-SFVC 701002002300-2.00-
A-SFVC 1001002002300-2.00-
A-SCC Plain1002002300-2.00-
A-SFSCC 501002002300-2.00-
A-SFSCC 701002002300-2.00-
A-SFSCC 1001002002300-2.00-
A-RVC Plain1002002300-2.00-
A-RSFVC 501002002300-2.00-
A-RSFVC 701002002300-2.00-
A-RSFVC 1001002002300-2.00-
A-RSCC Plain1002002300-2.00-
A-RSFSCC 501002002300-2.00-
A-RSFSCC 701002002300-2.00-
A-RSFSCC 1001002002300-2.00-
B-VC Plain1002002300-2.00-
B-SFVC 501002002300-2.00-
B-SFVC 701002002300-2.00-
B-SFVC 1001002002300-2.00-
B-SCC Plain1002002300-2.00-
B-SFSCC 501002002300-2.00-
B-SFSCC 701002002300-2.00-
B-SFSCC 1001002002300-2.00-
B-RVC Plain1002002300-2.00-
B-RSFVC 501002002300-2.00-
B-RSFVC 701002002300-2.00-
B-RSFVC 1001002002300-2.00-
B-RSCC Plain1002002300-2.00-
B-RSFSCC 501002002300-2.00-
B-RSFSCC 701002002300-2.00-
B-RSFSCC 1001002002300-2.00-
[11]TB1-PC300300240012001.0010.67
TB2-SFRC25300300240012001.0010.67
TB3-SFRC50300300240012001.0010.67
[12]M0S200300150010001.5011.30
M0.5S200300150010001.5011.30
M1S200300150010001.5011.30
[13]B05-SF0-T150200200016001.3325.16
B06-SF0.5-T150200200016001.3325.16
B07-SF0.75-T150200200016001.3325.16
B08-SF1-T150200200016001.3325.16
[14]NWC1001501100-1.50-
NWFRC1001501100-1.50-
CSC1001501100-1.50-
CSFRC1001501100-1.50-
[15]MIX-1140140150014201.0027.05
MIX-2140140150014201.0027.05
[16]NWC150200150013001.3320.44
NWFRC-55150200150013001.3320.44
NWFRC-65150200150013001.3320.44
NWFRC-80150200150013001.3320.44
OPSC-0150200150013001.3320.44
OPSFRC-55150200150013001.3320.44
OPSFRC-65150200150013001.3320.44
OPSFRC-80150200150013001.3320.44
[17]Ap15015011858101.0014.40
A10015015011858101.0014.40
A8015015011858101.0014.40
Dp15015011858101.0014.40
D10015015011858101.0014.40
D8015015011858101.0014.40
Ep15015011858101.0014.40
E10015015011858101.0014.40
E8015015011858101.0014.40
[18]T01502001500-1.33-
T251502001500-1.33-
T501502001500-1.33-
T751502001500-1.33-
T1001502001500-1.33-
[19]TR-00150250220012001.6717.54
TS-15150250220012001.6717.54
[20]L08F00V0150200190010001.3315.73
L08F40V3150200190010001.3315.73
L08F40V6150200190010001.3315.73
L08F55V3150200190010001.3315.73
L08F55V6150200190010001.3315.73
L08F67V3150200190010001.3315.73
L08F67V6150200190010001.3315.73
L08F80V3150200190010001.3315.73
L08F80V6150200190010001.3315.73
L12F00V0150200190010001.3315.73
L12F40V3150200190010001.3315.73
L12F80V3150200190010001.3315.73
[21]R50C-P1002002000-2.00-
R50C-F11002002000-2.00-
R50C-F21002002000-2.00-
R50C-F31002002000-2.00-
R50C-F41002002000-2.00-
R50L-P1002002000-2.00-
R50L-F11002002000-2.00-
R50L-F21002002000-2.00-
R50L-F31002002000-2.00-
R50L-F41002002000-2.00-
R50T-P1002002000-2.00-
R50T-F11002002000-2.00-
R50T-F21002002000-2.00-
R50T-F31002002000-2.00-
R50T-F41002002000-2.00-
[22]RP0100200160013002.0027.18
RP1100200160013002.0027.18
RL0100200160013002.0027.18
RL1100200160013002.0027.18
RR0100200160013002.0027.18
RR1100200160013002.0027.18
[23]RL-P1002002200-2.00-
RL-F11002002200-2.00-
RL-F21002002200-2.00-
RL-F31002002200-2.00-
RL-F41002002200-2.00-
RT-P1002002200-2.00-
RT-F11002002200-2.00-
RT-F21002002200-2.00-
RT-F31002002200-2.00-
RT-F41002002200-2.00-
[24]R40C-P1002002000-2.00-
R40C-F11002002000-2.00-
R40C-F21002002000-2.00-
R40C-F31002002000-2.00-
R40C-F41002002000-2.00-
R40L-P1002002000-2.00-
R40L-F11002002000-2.00-
R40L-F21002002000-2.00-
R40L-F31002002000-2.00-
R40L-F41002002000-2.00-
R40T-P1002002000-2.00-
R40T-F11002002000-2.00-
R40T-F21002002000-2.00-
R40T-F31002002000-2.00-
R40T-F41002002000-2.00-
[25]LC1100200700-2.00-
LC1-0.5-32100200700-2.00-
LC1-1.0-32100200700-2.00-
LC1-1.5-32100200700-2.00-
LC2100200700-2.00-
LC2-0.5-25100200700-2.00-
LC2-1.0-25100200700-2.00-
LC2-1.5-25100200700-2.00-
LC2-0.5-32100200700-2.00-
LC2-1.0-32100200700-2.00-
LC2-1.5-32100200700-2.00-
NC100200700-2.00-
NC-0.5-32100200700-2.00-
NC-1.0-32100200700-2.00-
NC-1.5-32100200700-2.00-
HC100200700-2.00-
HC-0.5-25100200700-2.00-
HC-1.0-25100200700-2.00-
HC-1.5-25100200700-2.00-
HC-0.5-32100200700-2.00-
HC-1.0-32100200700-2.00-
HC-1.5-32100200700-2.00-
HC-0.5-50100200700-2.00-
HC-1.0-50100200700-2.00-
[26]P20-P1002002000-2.00-
P20-F11002002000-2.00-
P20-F21002002000-2.00-
P20-F31002002000-2.00-
P20-F41002002000-2.00-
P30-P1002002000-2.00-
P30-F11002002000-2.00-
P30-F21002002000-2.00-
P30-F31002002000-2.00-
P30-F41002002000-2.00-
P40-P1002002000-2.00-
P40-F11002002000-2.00-
P40-F21002002000-2.00-
P40-F31002002000-2.00-
P40-F41002002000-2.00-
P50-P1002002000-2.00-
P50-F11002002000-2.00-
P50-F21002002000-2.00-
P50-F31002002000-2.00-
P50-F41002002000-2.00-
[27]B1100200200018002.0037.64
B2100200200018002.0037.64
B3100200200018002.0037.64
B4100200200018002.0037.64
B5100200200018002.0037.64
B6100200200018002.0037.64
[28]B0.0-0100250219018502.5037.04
B0.5-0100250219018502.5037.04
B1.0-0100250219018502.5037.04
B1.5-0100250219018502.5037.04
B0.0-2a100250219018502.5037.04
B0.0-2b100250219018502.5037.04
B0.5-2100250219018502.5037.04
B1.0-2100250219018502.5037.04
B1.5-2100250219018502.5037.04
B0.0-4a100250219018502.5037.04
B0.0-4b100250219018502.5037.04
B0.5-4100250219018502.5037.04
B1.0-4100250219018502.5037.04
B1.5-4100250219018502.5037.04
[29]P1152.4304.81778-2.00-
P2152.4304.81778-2.00-
P3152.4304.81778-2.00-
P4152.4304.81778-2.00-
[30]1102102760-1.00-
2102102760-1.00-
3102102760-1.00-
4102102760-1.00-
5102102760-1.00-
6102102760-1.00-
7102102760-1.00-
8102102760-1.00-
9102102760-1.00-
10102102760-1.00-
11102102760-1.00-
12102102760-1.00-
13102102760-1.00-
14102102760-1.00-
15102102760-1.00-
[31]AP1001001000-1.00-
BP1001001000-1.00-
CP1001001000-1.00-
AF1001001000-1.00-
BF1001001000-1.00-
CF1001001000-1.00-
[32]B1150300200014002.0019.52
B4150300200014002.0019.52
[33]B-NC1001501500-1.50-
B-SSF-131001501500-1.50-
B-HSF-131001501500-1.50-
b—cross-section width, h—cross-section height, L—element length, P—gauge length, l/d—length-to-diameter ratio of the fibers used.
Table A3. Material data of test elements.
Table A3. Material data of test elements.
Lp.fc, MPaft, MPaEc, GPaρl, %fys, MPaρw, %fysw, MPal/dVf, %Type of Fiberff, MPa
[1]A1-Con24.4082.45-1.344550.94455-0--
A1-M13-0.533.2164.88-1.344550.94455650.5straight2500
A1-M13-1.041.8725.75-1.344550.94455651straight2500
A1-M13-1.542.5046.10-1.344550.94455651.5straight2500
A1-H35-0.529.2162.71-1.344550.94455640.5hooked900–2200
A1-H35-1.031.2884.15-1.344550.94455641hooked900–2200
A1-H35-1.536.3844.72-1.344550.94455641.5hooked900–2200
A2.25-Con24.4082.45-1.234550.38455-0--
A2.25-M13-0.533.2164.88-1.234550.38455650.5straight2500
A2.25-M13-1.041.8725.75-1.234550.38455651straight2500
A2.25-M13-1.542.5046.10-1.234550.38455651.5straight2500
A2.25-H35-0.529.2162.71-1.234550.38455640.5hooked900–2200
A2.25-H35-1.031.2884.15-1.234550.38455641hooked900–2200
A2.25-H35-1.536.3844.72-1.234550.38455641.5hooked900–2200
A4-Con24.4082.45-0.924550.22455-0--
A4-M13-0.533.2164.88-0.924550.22455650.5straight2500
A4-M13-1.041.8725.75-0.924550.22455651straight2500
A4-M13-1.542.5046.10-0.924550.22455651.5straight2500
A4-H35-0.529.2162.71-0.924550.22455640.5hooked900–2200
A4-H35-1.031.2884.15-0.924550.22455641hooked900–2200
A4-H35-1.536.3844.72-0.924550.22455641.5hooked900–2200
[2]B136.16--2.075200.79460-0--
B236.16--2.075200.79460-0.5hooked-
B336.16--2.075200.79460-0.75hooked-
B436.16--2.075200.79460-0.25hooked-
B751.76--2.075200.79460-0hooked-
B851.76--2.075200.79460-0.5hooked-
B951.76--2.075200.79460-0.75hooked-
B1067.84--2.075200.79460-0--
B1167.84--2.075200.79460-0.75hooked-
[3]B135.74.18-1.454450.23445-0-
B2S44.16.27-1.454450.23445501straight2850
B3H438.12-1.454450.23445601hooked>1000
B4C45.48.95-1.454450.23445831wavy>700
[4]Control45.1--1.49-0.29--0--
1SF47.3--1.49-0.29-671-2100
[5]TB1-PC-L1834.80-32.31.13512---0--
TB3-G25-L1842.08-34.21.13512--860.32hooked2200
TB4-G25-L1842.08-34.21.13512--860.32hooked2200
TB5-G50-L1841.84-34.21.13512--860.63hooked2200
TB6-G50-L1841.84-34.21.13512--860.63hooked2200
TB7-D25-L1841.28-341.13512--650.32hooked2300
TB8-D25-L1841.28-341.13512--650.32hooked2300
TB9-D50-L1841.04-341.13512--650.63hooked2300
TB10-D10-L1841.04-341.13512--650.63hooked2300
TB11-D50-L18-ST6/15041.04-341.135120.13523650.63hooked2300
TB12-D50-L18-ST6/15041.04-341.135120.13523650.63hooked2300
TB13-PC-L18-ST6/15039.60-33.61.135120.13523-0--
TB14-PC-L18-ST6/15039.60-33.61.135120.13523-0--
[6]TB1-PC34.80-32.31.13516---0--
TB3-SFRC2542.08-34.21.13516--860.32hooked2200
TB4-SFRC2542.08-34.21.13516--860.32hooked2200
TB5-SFRC5041.84-34.21.13516--860.63hooked2200
TB6-SFRC5041.84-34.21.13516--860.63hooked2200
[7]B124--0.70-0.44--0--
B222.4--0.70-0.44--0--
B320.8--0.70-0.44--0--
B420.8--0.70-0.44--0--
B520--0.70-0.44--0--
B625.6--0.70-0.44--0.5straight-
B724--0.70-0.44--0.5straight-
B822.4--0.70-0.44--0.5straight-
B921.6--0.70-0.44--0.5straight-
B1021.6--0.70-0.44--0.5straight-
B1128--0.70-0.44--1straight-
B1227.2--0.70-0.44--1straight-
B1324--0.70-0.44--1straight-
B1422.4--0.70-0.44--1straight-
B1521.6--0.70-0.44--1straight-
B1629.6--0.70-0.44--1.5straight-
B1727.2--0.70-0.44--1.5straight-
B1827.2--0.70-0.44--1.5straight-
B1924.8--0.70-0.44--1.5straight-
B2022.4--0.70-0.44--1.5straight-
[8]T-Reference34--1.544200.25420-0--
T30SF34--1.544200.25420400.38hooked1100
T60SF34--1.544200.25420400.76hooked1100
[9]R156.45.6-0.845000.52200-0--
R256.45.6-0.845000.52200-0--
R356.45.6-0.845000.52200-0--
FR256.45.6-0.845000.52200670.5hooked2300
FR356.45.6-0.845000.52200670.5hooked2300
[10]A-VC Plain16.962.31------0--
A-SFVC 5018.722.8-----500.5hooked275
A-SFVC 7019.522.75-----700.5hooked275
A-SFVC 10018.082.62-----1000.5hooked275
A-SCC Plain17.922.34------0--
A-SFSCC 5019.842.71-----500.5hooked275
A-SFSCC 7020.322.84-----700.5hooked275
A-SFSCC 10018.82.64-----1000.5hooked275
A-RVC Plain14.722.11------0--
A-RSFVC 5016.642.46-----500.5hooked275
A-RSFVC 7017.842.52-----700.5hooked275
A-RSFVC 10015.842.37-----1000.5hooked275
A-RSCC Plain16.242.15------0--
A-RSFSCC 5017.922.53-----500.5hooked275
A-RSFSCC 7018.642.62-----700.5hooked275
A-RSFSCC 10016.562.41-----1000.5hooked275
B-VC Plain64.484.67------0--
B-SFVC 5067.365.22-----500.5hooked275
B-SFVC 7068.485.36-----700.5hooked275
B-SFVC 10066.725.16-----1000.5hooked275
B-SCC Plain64.84.81------0--
B-SFSCC 5067.925.52-----500.5hooked275
B-SFSCC 7068.965.68-----700.5hooked275
B-SFSCC 10066.565.34-----1000.5hooked275
B-RVC Plain58.84.24------0--
B-RSFVC 5061.444.92-----500.5hooked275
B-RSFVC 7063.845.06-----700.5hooked275
B-RSFVC 10060.884.88-----1000.5hooked275
B-RSCC Plain59.924.56------0--
B-RSFSCC 5063.685.25-----500.5hooked275
B-RSFSCC 7064.45.38-----700.5hooked275
B-RSFSCC 10061.764.96-----1000.5hooked275
[11]TB1-PC32.32-311.13543---0--
TB2-SFRC2532.944-331.13543--860.32hooked>2200
TB3-SFRC5024.76-28.31.13543--860.64hooked>2200
[12]M0S363.6-1.13-0.79--0--
M0.5S424.6-1.13-0.79-750.5straight2850
M1S456-1.13-0.79-751straight2850
[13]B05-SF0-T32--1.34550---0--
B06-SF0.5-T32--1.34550--480.5hooked-
B07-SF0.75-T32--1.34550--480.75hooked-
B08-SF1-T32--1.34550--481hooked-
[14]NWC25.762.69------0--
NWFRC35.363.206------0.5--
CSC24.1362.35------0--
CSFRC26.1123.18------0.5--
[15]MIX-142.354.03------0--
MIX-245.725.26-----801.5--
[16]NWC25.363.8917.231.51-0.25--0--
NWFRC-5528.083.8919.591.51-0.25-550.5hooked-
NWFRC-6529.23.9521.431.51-0.25-650.5hooked-
NWFRC-8029.444.1120.711.51-0.25-800.5hooked-
OPSC-026.242.8313.251.51-0.25--0--
OPSFRC-5527.523.6316.21.51-0.25-550.5hooked-
OPSFRC-6528.483.8514.721.51-0.25-650.5hooked-
OPSFRC-8029.63.9115.481.51-0.25-800.5hooked-
[17]Ap32.843.1224.897-----0--
A10032.843.1224.8970.50-0.26--0--
A8032.843.1224.8970.50-0.33--0--
Dp33.293.7825.365-----0.4hooked-
D10033.293.7825.3650.50-0.26--0.4hooked-
D8033.293.7825.3650.50-0.33--0.4hooked-
Ep34.544.1526.184-----0.8hooked-
E10034.544.1526.1840.50-0.26--0.8hooked-
E8034.544.1526.1840.50-0.33--0.8hooked-
[18]T027.122.5913.871.51-0.25--0--
T2531.923.7315.671.51-0.25-640.25hooked-
T5032.964.1716.111.51-0.25-640.5hooked-
T7536.724.9516.291.51-0.25-640.75hooked-
T10037.845.4715.51.51-0.25-641hooked-
[19]TR-0046.863.39-2.145051.31466-0--
TS-1541.515.77-2.145051.31466601.5hooked-
[20]L08F00V034.83.5131.40.674600.34460-0--
L08F40V333.43.55300.674600.34460400.3hooked1200
L08F40V631.33.3529.90.674600.34460400.6hooked1200
L08F55V3313.0827.90.674600.34460550.3hooked1200
L08F55V630.93.4129.90.674600.34460550.6hooked1200
L08F67V332.73.4231.20.674600.34460670.3hooked1200
L08F67V629.53.1228.50.674600.34460670.6hooked1200
L08F80V331.93.4627.90.674600.34460800.3hooked1200
L08F80V6303.128.70.674600.34460800.6hooked1200
L12F00V034.83.5131.41.514600.34460-0--
L12F40V331.73.5829.61.514600.34460400.3hooked1200
L12F80V331.63.5627.51.514600.34460800.3hooked1200
[21]R50C-P50.122.9-1.574321.26432-0--
R50C-F150.953.11-1.574321.26432750.3straight295
R50C-F251.823.336-1.574321.26432750.6straight295
R50C-F352.453.88-1.574321.26432750.9straight295
R50C-F453.94.38-1.574321.26432751.2straight295
R50L-P50.212.89-1.574320.67432-0--
R50L-F151.053.04-1.574320.67432750.3straight295
R50L-F252.063.51-1.574320.67432750.6straight295
R50L-F353.413.87-1.574320.67432750.9straight295
R50L-F454.074.35-1.574320.67432751.2straight295
R50T-P51.352.91-0.574321.26432-0--
R50T-F152.63.29-0.574321.26432750.3straight295
R50T-F253.153.71-0.574321.26432750.6straight295
R50T-F354.124.05-0.574321.26432750.9straight295
R50T-F455.514.45-0.574321.26432751.2straight295
[22]RP013.5121.481.45-----0--
RP115.842.051.84----37.51hooked-
RL014.6961.561.471.57415---0--
RL113.6321.791.801.57415--37.51hooked-
RR016.0961.61.601.574150.50344-0--
RR115.1681.862.001.574150.5034437.51hooked-
[23]RL-P33.62.25-1.57-0.01--0--
RL-F135.22.81-1.57-0.01-750.3straight-
RL-F237.043.27-1.57-0.01-750.6straight-
RL-F337.73.81-1.57-0.01-750.9straight-
RL-F438.44.2-1.57-0.01-751.2straight-
RT-P32.482.2-0.21-1.68--0--
RT-F133.852.46-0.21-1.68-750.3straight-
RT-F234.443.35-0.21-1.68-750.6straight-
RT-F334.953.75-0.21-1.68-750.9straight-
RT-F435.253.95-0.21-1.68-751.2straight-
[24]R40C-P39.742.83-1.01-1.12--0--
R40C-F140.053.46-1.01-1.12-750.3straight-
R40C-F241.063.61-1.01-1.12-750.6straight-
R40C-F341.983.82-1.01-1.12-750.9straight-
R40C-F443.264.1-1.01-1.12-751.2straight-
R40L-P40.162.91-1.57-0.57--0--
R40L-F141.283.14-1.57-0.57-750.3straight-
R40L-F242.163.27-1.57-0.57-750.6straight-
R40L-F343.373.53-1.57-0.57-750.9straight-
R40L-F444.064.07-1.57-0.57-751.2straight-
R40T-P40.212.88-0.57-1.01--0--
R40T-F141.473.46-0.57-1.01-750.3straight-
R40T-F242.813.62-0.57-1.01-750.6straight-
R40T-F343.063.85-0.57-1.01-750.9straight-
R40T-F443.874.09-0.57-1.01-751.2straight-
[25]LC112-------0--
LC1-0.5-3212------470.5-650
LC1-1.0-3212------471-650
LC1-1.5-3212------471.5-650
LC29-------0--
LC2-0.5-259------420.5-650
LC2-1.0-259------421-650
LC2-1.5-259------421.5-650
LC2-0.5-329------470.5-650
LC2-1.0-329------471-650
LC2-1.5-329------471.5-650
NC30-------0--
NC-0.5-3230------470.5-650
NC-1.0-3230------471-650
NC-1.5-3230------471.5-650
HC61-------0--
HC-0.5-2561------420.5-650
HC-1.0-2561------421-650
HC-1.5-2561------421.5-650
HC-0.5-3261------470.5-650
HC-1.0-3261------471-650
HC-1.5-3261------471.5-650
HC-0.5-5061------570.5-650
HC-1.0-5061------571-650
[26]P20-P17.62.35------0--
P20-F117.9282.54-----750.3straight275
P20-F218.6082.75-----750.6straight275
P20-F319.322.82-----750.9straight275
P20-F420.3283-----751.2straight275
P30-P25.4882.7------0--
P30-F125.9283.05-----750.3straight275
P30-F226.5283.29-----750.6straight275
P30-F327.3683.71-----750.9straight275
P30-F428.0083.89-----751.2straight275
P40-P31.1922.95------0--
P40-F133.2323.39-----750.3straight275
P40-F233.763.52-----750.6straight275
P40-F334.4163.81-----750.9straight275
P40-F435.4483.99-----751.2straight275
P50-P41.0483.06------0--
P50-F141.9043.45-----750.3straight275
P50-F243.1283.8-----750.6straight275
P50-F343.83.98-----750.9straight275
P50-F444.044.33-----751.2straight275
[27]B135.474.26-1.57250---0--
B231.265.94-1.57250--750.6hooked-
B340.117.58-1.57250--751.2hooked-
B440.124.18-1.572500.35250-0--
B538.935.67-1.572500.35250750.6hooked-
B635.647.68-1.572500.35250751.2hooked-
[28]B0.0-037.933.14-260260260260-0--
B0.5-035.14.05-260260260260750.5hooked260
B1.0-039.085.13-260260260260751hooked260
B1.5-041.425.67-260260260260751.5hooked260
B0.0-2a40.723.15-0.90----0--
B0.0-2b36.593.22-0.90----0--
B0.5-234.163.94-0.90---750.5hooked260
B1.0-242.895.52-0.90---751hooked260
B1.5-240.016.06-0.90---751.5hooked260
B0.0-4a37.072.33-1.36----0--
B0.0-4b35.563.19-1.36----0--
B0.5-437.84.14-1.36---750.5hooked260
B1.0-439.144.73-1.36---751hooked260
B1.5-441.485.83-1.36---751.5hooked260
[29]P140.683.45------0--
P239.995.72-----600.7hooked930–1380
P343.446.34-----1001hooked930–1380
P435.855.31-----601.5hooked930–1380
[30]121.122.67------0--
220.962.8------0--
324.482.6------0--
429.043.32-----261straight300
525.843.32-----261straight300
629.283.55-----261straight300
7283.7-----391straight300
827.283.78-----391straight300
9284.04-----391straight300
1027.283.92-----531straight300
1128.163.83-----531straight300
1226.883.95-----531straight300
1325.843.99-----771straight300
1427.123.76-----771straight300
1526.163.8-----771straight300
[31]AP38.43.7------0-
BP26.82.8------0-
CP17.62.2------0-
AF39.844.2-----1500.7straight2000
BF283.5-----1500.7straight2000
CF21.62.7-----1500.7straight2000
[32]B140.24.2-1.24440.5
465.2		0.39418.6-0--
B447.84.2-1.24440.5
465.2		0.39418.6550.75wavy2400
[33]B-NC25.1282.73-2.094620.65437-0-
B-SSF-1327.643.24-2.094620.65437651straight<2100
B-HSF-1328.0643.31-2.094620.65437651hooked<2100
fc—cylindrical compressive strength, ft—tensile strength, Ec—modulus of elasticity, ρl—longitudinal reinforcement ratio, fys—yield strength of longitudinal reinforcement, ρw—transverse reinforcement ratio, fysw—plastic limit of stirrups, l/d—length-to-diameter ratio of the fibers used, Vf—volumetric percentage of dispersed reinforcement used, ff—tensile strength of fibers.
Table A4. Torsion test results of individual elements.
Table A4. Torsion test results of individual elements.
Lp.Tcr, kNmØcr, rad/mØcr, radØcr/Øcr0τcr, MPaτcr/τcr0Tu, kNmØu, rad/mØu, radØu/Øu0τu, MPaτu/τu0τu/τcr
[1]A1-Con0.90.0044-1.002.601.002.40.046-1.006.931.002.67
A1-M13-0.51.10.0023-0.523.171.222.70.056-1.227.791.132.45
A1-M13-1.01.20.0025-0.573.461.3330.0826-1.808.661.252.50
A1-M13-1.51.30.0023-0.523.751.443.30.092-2.009.521.382.54
A1-H35-0.51.50.007-1.594.331.672.80.1195-2.608.081.171.87
A1-H35-1.01.60.0071-1.614.621.783.30.1196-2.609.521.382.06
A1-H35-1.51.60.0036-0.824.621.783.90.102-2.2211.261.632.44
A2.25-Con3.30.008-1.002.821.005.90.0459-1.005.051.001.79
A2.25-M13-0.54.80.007-0.884.101.458.10.054-1.186.931.371.69
A2.25-M13-1.05.20.0042-0.534.451.588.70.068-1.487.441.471.67
A2.25-M13-1.56.50.0038-0.485.561.9710.40.04-0.878.891.761.60
A2.25-H35-0.53.50.0063-0.792.991.067.10.062-1.356.071.202.03
A2.25-H35-1.04.60.0077-0.963.931.398.80.107-2.337.521.491.91
A2.25-H35-1.55.20.004-0.504.451.5810.10.062-1.358.641.711.94
A4-Con6.80.0044-1.002.451.0010.20.029-1.003.681.001.50
A4-M13-0.58.80.0053-1.203.171.2915.90.058-2.005.741.561.81
A4-M13-1.010.30.006-1.363.721.5118.70.032-1.106.751.831.82
A4-M13-1.511.30.0065-1.484.081.6621.70.053-1.837.832.131.92
A4-H35-0.57.40.0042-0.952.671.0915.50.0505-1.745.591.522.09
A4-H35-1.09.50.0054-1.233.431.4019.10.052-1.796.891.872.01
A4-H35-1.5110.0061-1.393.971.6222.60.0475-1.648.152.222.05
[2]B1------24.68-0.01921.0014.821.00-
B2------30.99-0.02531.3218.611.26-
B3------31.37-0.0261.3518.831.27-
B4------29.69-0.0241.2517.831.20-
B7------35.66-0.0261.0021.411.00-
B8------38.83-0.0321.2323.311.09-
B9------39.64-0.03331.2823.801.11-
B10------42.04-0.03251.0025.241.00-
B11------46.29-0.0391.2027.791.10-
[3]B16.56-0.01711.002.021.009.5-0.03821.002.921.001.45
B2S8.25-0.02061.202.541.2611.5-0.04141.083.541.211.39
B3H9.35-0.02371.392.871.4312.8-0.03931.033.931.351.37
B4C9.86-0.02511.473.031.5013.2-0.03841.004.061.391.34
[4]Control8.3---6.241.0042.80.019-1.0032.201.005.16
1SF9.4---7.071.1344.90.02-1.0533.781.054.78
[5]TB1-PC-L1812.40.0008-1.002.211.0016.80.0013-1.002.991.001.35
TB3-G25-L1813.40.0009-1.132.381.0827.320.0124-9.524.861.632.04
TB4-G25-L18120.0008-1.032.130.9722.940.0075-5.784.081.371.91
TB5-G50-L1813.890.0008-1.012.471.1226.940.012-9.234.791.601.94
TB6-G50-L1813.740.0012-1.502.441.1124.630.0105-8.094.381.471.79
TB7-D25-L1811.920.0007-0.872.120.9620.270.0067-5.153.611.211.70
TB8-D25-L1815.960.001-1.262.841.2920.80.0032-2.423.701.241.30
TB9-D50-L1813.230.0006-0.782.351.0727.90.0094-7.254.961.662.11
TB10-D10-L1812.90.0008-0.962.291.0425.30.0195-15.004.501.511.96
TB11-D50-L18-ST6/15013.20.0007-1.051.051.1735.60.0312-2.336.331.692.70
TB12-D50-L18-ST6/15013.50.0008-1.312.401.19320.0309-2.305.691.522.37
TB13-PC-L18-ST6/15011.60.0006-1.002.061.0021.110.0117-1.003.761.001.82
TB14-PC-L18-ST6/150110.0006-1.001.961.0021.070.0152-1.003.751.001.92
[6]TB1-PC12.40.0008-1.002.211.0016.180.0013-1.002.881.001.30
TB3-SFRC2513.40.0009-1.132.381.0827.320.0154-12.304.861.692.04
TB4-SFRC25120.0008-1.032.130.9722.940.0075-6.024.081.421.91
TB5-SFRC5013.890.0008-1.012.471.1226.940.012-9.604.791.671.94
TB6-SFRC5013.740.0012-1.502.441.1124.630.0105-8.424.381.521.79
[7]B1900.022-1.0016.011.00950.0363-1.0016.901.001.06
B2820.0194-1.0014.591.00880.0332-1.0015.651.001.07
B3750.0166-1.0013.341.00780.0318-1.0013.881.001.04
B4710.0105-1.0012.631.00750.0175-1.0013.341.001.06
B5600.0072-1.0010.671.00700.0136-1.0012.451.001.17
B61060.0183-1.2118.861.401140.0447-1.6920.281.401.08
B71000.0161-1.0617.791.321030.0421-1.5918.321.271.03
B8950.0147-0.9716.901.26980.0316-1.1917.431.211.03
B9870.0077-0.5115.481.15950.0199-0.7516.901.171.09
B10800.0056-0.3714.231.06880.0154-0.5815.651.081.10
B111230.0133-0.8821.881.631330.0641-2.4223.661.641.08
B121180.0107-0.7020.991.561250.0543-2.0522.241.541.06
B131060.0096-0.6418.861.401140.0428-1.6220.281.401.08
B141020.0054-0.3618.141.351110.0374-1.4119.751.371.09
B15900.0049-0.3216.011.191050.0237-0.9018.681.291.17
B161380.0066-0.4424.551.831470.0777-2.9426.151.811.07
B171250.0052-0.3522.241.651330.0702-2.6523.661.641.06
B181140.0047-0.3120.281.511220.0532-2.0121.701.501.07
B191060.0038-0.2518.861.401170.0391-1.4820.811.441.10
B20950.003-0.2016.901.261150.0248-0.9420.461.421.21
[8]T-Reference0.290.0279-1.000.171.005.370.0445-1.003.221.0018.52
T30SF0.50.0283-1.010.301.727.50.0534-1.204.501.4015.00
T60SF0.60.0229-0.820.362.0711.060.0974-2.196.642.0618.43
[9]R15.70.0033-1.004.291.009.80.0103-1.007.371.001.72
R25.80.0027-1.004.361.007.60.0035-1.005.721.001.31
R37.50.0032-1.005.641.007.70.0036-1.005.791.001.03
FR27.20.0058-1.895.421.1410.10.0193-3.337.601.211.40
FR37.80.0034-1.115.871.2310.80.0122-2.108.121.291.38
[10]A-VC Plain------1.630.0055-1.003.311.00-
A-SFVC 50------1.80.0064-1.183.661.10-
A-SFVC 70------1.930.0068-1.253.921.18-
A-SFVC 100------1.840.0063-1.153.741.13-
A-SCC Plain------1.690.0057-1.003.441.00-
A-SFSCC 50------1.930.0071-1.253.921.14-
A-SFSCC 70------2.040.0075-1.314.151.21-
A-SFSCC 100------1.870.0069-1.213.801.11-
A-RVC Plain------1.490.005-1.003.031.00-
A-RSFVC 50------1.740.0055-1.103.541.17-
A-RSFVC 70------1.820.0061-1.233.701.22-
A-RSFVC 100------1.690.0057-1.153.441.13-
A-RSCC Plain------1.560.0051-1.003.171.00-
A-RSFSCC 50------1.820.0064-1.263.701.17-
A-RSFSCC 70------1.890.0068-1.323.841.21-
A-RSFSCC 100------1.720.0062-1.223.501.10-
B-VC Plain------3.570.0071-1.007.261.00-
B-SFVC 50------3.950.0095-1.348.031.11-
B-SFVC 70------4.080.0112-1.588.301.14-
B-SFVC 100------3.820.0091-1.287.771.07-
B-SCC Plain------3.70.0075-1.007.521.00-
B-SFSCC 50------4.240.0119-1.588.621.15-
B-SFSCC 70------4.380.0138-1.838.911.18-
B-SFSCC 100------4.120.0113-1.508.381.11-
B-RVC Plain------3.250.0065-1.006.611.00-
B-RSFVC 50------3.720.0086-1.327.561.14-
B-RSFVC 70------3.840.0102-1.577.811.18-
B-RSFVC 100------3.640.0082-1.267.401.12-
B-RSCC Plain------3.480.0069-1.007.081.00-
B-RSFSCC 50------4.080.0109-1.588.301.17-
B-RSFSCC 70------4.160.0122-1.778.461.20-
B-RSFSCC 100------3.780.0104-1.517.691.09-
[11]TB1-PC18.40.0016-1.003.271.0018.40.0016-1.003.271.001.00
TB2-SFRC2517.90.0015-0.913.180.9720.30.0084-5.383.611.101.13
TB3-SFRC5017.90.0016-0.973.180.9719.50.0021-1.323.471.061.09
[12]M0S20.40.0015-1.007.361.0025.90.0031-1.009.341.001.27
M0.5S26.30.0021-1.339.491.2943.10.0136-4.4315.551.661.64
M1S29.40.0022-1.4010.611.4446.70.0201-6.5416.851.801.59
[13]B05-SF0-T3.225---3.191.003.386-0.10951.003.351.001.05
B06-SF0.5-T4.192---4.151.304.353-0.11731.074.311.291.04
B07-SF0.75-T4.353---4.311.354.676-0.14541.334.631.381.07
B08-SF1-T4.745---4.701.475.061-0.18941.735.011.491.07
[14]NWC2.146---6.191.002.550.0624-1.007.361.001.19
NWFRC3.825---11.041.784.050.084-1.3511.691.591.06
CSC4.35---12.551.004.80.077-1.0013.851.001.10
CSFRC5.1---14.721.175.3250.0134-0.1715.371.111.04
[15]MIX-1------2.5-0.01271.004.381.00-
MIX-2------3.072-0.02251.775.381.23-
[16]NWC5.490.024-1.005.441.005.490.024-1.005.441.001.00
NWFRC-556.950.047-1.966.881.276.980.051-2.136.911.271.00
NWFRC-657.10.04-1.677.031.297.680.052-2.177.601.401.08
NWFRC-807.80.048-2.007.721.427.570.051-2.137.491.380.97
OPSC-05.490.052-1.005.441.005.50.052-1.005.451.001.00
OPSFRC-557.280.069-1.337.211.337.360.074-1.427.291.341.01
OPSFRC-657.770.068-1.317.691.427.880.077-1.487.801.431.01
OPSFRC-808.580.076-1.468.491.568.60.08-1.548.511.561.00
[17]Ap1.120.004-1.001.591.001.120.004-1.001.591.001.00
A1002.80.0014-1.003.981.006.440.0063-1.009.161.002.30
A803.360.0049-1.004.781.008.960.0411-1.0012.751.002.67
Dp2.380.0063-1.583.392.132.380.0063-1.583.392.131.00
D1002.920.0046-3.344.161.0411.480.0667-10.5816.341.783.93
D803.360.0013-0.274.781.0014.280.0769-1.8720.321.594.25
Ep2.80.0035-0.883.982.503.080.0131-3.274.382.751.10
E1004.480.0035-2.566.381.6017.360.0528-8.3824.712.703.88
E804.480.002-0.416.381.3318.480.0648-1.5826.302.064.13
[18]T05.270.068-1.005.221.005.280.068-1.005.231.001.00
T256.930.067-0.996.861.316.90.072-1.066.831.311.00
T507.230.078-1.157.161.377.320.085-1.257.251.391.01
T757.730.078-1.157.651.477.850.087-1.287.771.491.02
T1008.340.077-1.138.261.588.50.089-1.318.421.611.02
[19]TR-00------9.370.075-1.007.051.00-
TS-15------14.420.1045-1.3910.851.54-
[20]L08F00V04.930.0032-1.004.881.004.930.0032-1.004.881.001.00
L08F40V34.580.0032-1.014.530.934.580.0032-1.014.530.931.00
L08F40V64.620.0035-1.104.570.945.680.0648-20.255.621.151.23
L08F55V34.930.0038-1.194.881.004.940.0039-1.214.891.001.00
L08F55V65.10.004-1.235.051.035.870.0593-18.525.811.191.15
L08F67V34.850.0036-1.114.800.984.920.0056-1.764.871.001.01
L08F67V64.910.0036-1.134.861.005.880.0659-20.615.821.191.20
L08F80V34.80.0034-1.054.750.974.850.0041-1.284.800.981.01
L08F80V64.510.0036-1.134.460.915.490.0634-19.825.441.111.22
L12F00V04.450.0032-1.004.411.005.070.0346-1.005.021.001.14
L12F40V34.610.0037-1.164.561.046.010.0897-2.595.951.191.30
L12F80V34.470.0036-1.144.431.006.250.0935-2.706.191.231.40
[21]R50C-P2.0570.039-1.004.181.006.5840.138-1.0013.391.003.20
R50C-F12.1990.047-1.214.471.076.670.141-1.0213.561.013.03
R50C-F22.3670.052-1.334.811.156.7550.141-1.0213.741.032.85
R50C-F32.710.057-1.465.511.326.8410.141-1.0213.911.042.52
R50C-F43.0390.06-1.546.181.486.960.141-1.0214.151.062.29
R50L-P2.050.039-1.004.171.005.1310.173-1.0010.431.002.50
R50L-F12.1520.049-1.264.381.055.2160.173-1.0010.611.022.42
R50L-F22.4670.058-1.495.021.205.3020.176-1.0210.781.032.15
R50L-F32.7070.063-1.625.501.325.3870.179-1.0310.951.051.99
R50L-F43.020.068-1.746.141.475.4730.18-1.0411.131.071.81
R50T-P2.0660.034-1.004.201.005.6870.156-1.0011.561.002.75
R50T-F12.3230.045-1.324.721.125.7720.156-1.0011.741.012.48
R50T-F22.6020.043-1.265.291.265.8150.163-1.0411.821.022.23
R50T-F32.8270.053-1.565.751.375.90.163-1.0412.001.042.09
R50T-F43.090.061-1.796.281.505.9860.167-1.0712.171.051.94
[22]RP01.450.009-1.002.951.001.450.009-1.002.951.001.00
RP11.840.019-2.113.741.271.840.019-2.113.741.271.00
RL01.470.015-1.002.991.001.470.015-1.002.991.001.00
RL11.80.012-0.803.661.222.410.021-1.404.901.641.34
RR01.60.015-1.003.251.002.310.073-1.004.701.001.44
RR120.016-1.074.071.252.730.088-1.215.551.181.37
[23]RL-P1.5820.009-1.003.221.001.5820.0267-1.003.221.001.00
RL-F11.9520.01-1.113.971.232.010.0233-0.874.091.271.03
RL-F22.2540.01-1.114.581.422.2660.0267-1.004.611.431.01
RL-F32.5960.011-1.225.281.642.6080.03-1.125.301.651.00
RL-F42.7910.012-1.335.681.762.8220.03-1.125.741.781.01
RT-P1.5460.008-1.003.141.001.570.008-1.003.191.001.02
RT-F11.7210.009-1.133.501.111.7530.0233-2.913.561.121.02
RT-F22.290.01-1.254.661.482.090.0267-3.344.251.330.91
RT-F32.540.012-1.505.161.642.5660.03-3.755.221.631.01
RT-F42.6640.012-1.505.421.722.6940.028-3.505.481.721.01
[24]R40C-P1.982---4.031.005.516---11.221.002.78
R40C-F12.389---4.861.215.558---11.301.012.33
R40C-F22.489---5.061.265.687---11.561.032.28
R40C-F32.627---5.341.335.729---11.651.042.18
R40C-F42.809---5.711.425.815---11.821.052.07
R40L-P2.036---4.141.004.062---8.261.002.00
R40L-F12.189---4.451.084.105---8.351.011.88
R40L-F22.277---4.631.124.19---8.521.031.84
R40L-F32.449---4.981.204.233---8.611.041.73
R40L-F42.795---5.681.374.233---8.611.041.51
R40T-P2.016---4.101.003.763---7.651.001.87
R40T-F12.396---4.871.193.848---7.821.021.61
R40T-F22.504---5.091.243.934---8.001.051.57
R40T-F32.651---5.391.313.976---8.081.061.50
R40T-F42.806---5.711.394.019---8.171.071.43
[25]LC1------0.725---1.471.00-
LC1-0.5-32------0.772---1.571.06-
LC1-1.0-32------0.803---1.631.11-
LC1-1.5-32------0.848---1.721.17-
LC2------0.867---1.761.00-
LC2-0.5-25------0.864---1.761.00-
LC2-1.0-25------0.961---1.951.11-
LC2-1.5-25------1.102---2.241.27-
LC2-0.5-32------0.905---1.841.04-
LC2-1.0-32------1.004---2.041.16-
LC2-1.5-32------1.16---2.361.34-
NC------1.429---2.911.00-
NC-0.5-32------1.461---2.971.02-
NC-1.0-32------1.604---3.261.12-
NC-1.5-32------1.818---3.701.27-
HC------1.91---3.881.00-
HC-0.5-25------1.925---3.911.01-
HC-1.0-25------2.108---4.291.10-
HC-1.5-25------2.282---4.641.19-
HC-0.5-32------2.032---4.131.06-
HC-1.0-32------2.317---4.711.21-
HC-1.5-32------2.732---5.561.43-
HC-0.5-50------2.098---4.271.10-
HC-1.0-50------2.65---5.391.39-
[26]P20-P------1.7530.0057-1.003.561.00-
P20-F1------1.8810.0059-1.053.821.07-
P20-F2------1.9240.0061-1.083.911.10-
P20-F3------2.0950.0063-1.114.261.20-
P20-F4------2.2660.0064-1.144.611.29-
P30-P------1.9670.0048-1.004.001.00-
P30-F1------2.180.0059-1.244.431.11-
P30-F2------2.3510.0059-1.244.781.20-
P30-F3------2.5220.0068-1.435.131.28-
P30-F4------2.6510.0077-1.625.391.35-
P40-P------2.2660.0057-1.004.611.00-
P40-F1------2.3940.0066-1.164.871.06-
P40-F2------2.5220.0067-1.185.131.11-
P40-F3------2.6080.0088-1.555.301.15-
P40-F4------2.9070.0093-1.655.911.28-
P50-P------2.1380.0044-1.004.351.00-
P50-F1------2.3090.0067-1.514.691.08-
P50-F2------2.6510.0083-1.885.391.24-
P50-F3------2.950.0086-1.956.001.38-
P50-F4------2.9930.0086-1.966.091.40-
[27]B10.966---1.961.001.077---2.191.001.11
B21.033---2.101.071.408---2.861.311.36
B31.187---2.411.231.739---3.541.611.47
B41.297---2.641.001.712---3.481.001.32
B51.408---2.861.092.29---4.661.341.63
B61.518---3.091.172.842---5.781.661.87
[28]B0.0-0------2.68---4.161.00-
B0.5-0------2.99---4.641.12-
B1.0-0------2.8---4.351.04-
B1.5-0------3.56---5.531.33-
B0.0-2a------4.44---6.891.00-
B0.0-2b------4.89---7.591.00-
B0.5-2------4.81---7.471.03-
B1.0-2------5.09---7.901.05-
B1.5-2------6.19---9.611.25-
B0.0-4a------4.57---7.101.00-
B0.0-4b------5.58---8.661.00-
B0.5-4------5.36---8.321.06-
B1.0-4------5.32---8.261.05-
B1.5-4------6.25---9.701.23-
[29]P10.158---0.091.000.158---0.091.001.00
P20.17---0.101.080.17---0.101.081.00
P30.158---0.091.000.158---0.091.001.00
P40.155---0.090.980.155---0.090.981.00
[30]1------0.8437---3.821.00-
2------0.8142---3.691.00-
3------0.824---3.731.00-
4------0.9048---4.101.09-
5------0.9025---4.081.09-
6------0.8927---4.041.08-
7------0.9228---4.181.12-
8------0.922---4.171.11-
9------0.9152---4.141.11-
10------0.9221---4.171.11-
11------0.9633---4.361.16-
12------0.9025---4.081.09-
13------0.9957---4.511.20-
14------0.9319---4.221.13-
15------0.9593---4.341.16-
[31]AP------1.1---5.281.00-
BP------1.084---5.211.00-
CP------0.98---4.711.00-
AF------1.365---6.561.24-
BF------1.21---5.811.12-
CF------0.94---4.510.96-
[32]B112---7.231.0014.1120.0122-1.008.501.001.18
B413.05---7.861.0921.6720.0311-2.5513.061.541.66
[33]B-NC1-0.0021.002.891.003.4-0.02041.009.811.003.40
B-SSF-131.2-0.0021.003.461.204.2-0.03841.8812.121.243.50
B-HSF-131.1-0.00180.903.171.103.9-0.00350.1711.261.153.55
Tcr—cracking moment, θcr—angle at the cracking moment, θcr0—angle at the cracking moment for reference beams, τcr—shear stresses of the cross-section for the cracking moment, τcr0—shear stresses of the cross-section for the cracking moment of reference beams, Tu—maximum moment, θu—angle at the maximum moment, θu0—angle at the maximum moment for reference beams, τu—shear stresses of the cross-section for the maximum moment, τu0—shear stresses of the cross-section for the maximum moment of reference beams.

References

  1. Hassan, R.F.; Al-Salim, N.H.; Mohammed, N.S.; Hussein, H.H. Experimental study and theoretical pre-diction on torsional strength with different steel fiber reinforced concretes and Cross-Section areas. Eng. Struct. 2022, 251, 113559. [Google Scholar] [CrossRef]
  2. Hussain, H.K.; Zewair, M.S.; Ahmed, M.A. High Strength Concrete Beams Reinforced with Hooked Steel Fibers under Pure Torsion. Civ. Eng. J. 2022, 8, 92–104. [Google Scholar] [CrossRef]
  3. Abdullah, M.D.; Majeed, F.H.; Saleh, S.M. The Role of Fiber-Type Reinforcement in the Torsional Behavior of Solid and Hollow Reinforced Concrete Beams. Fibers 2022, 10, 80. [Google Scholar] [CrossRef]
  4. Karimipour, A.; de Brito, J.; Ghalehnovi, M.; Gencel, O. Torsional behaviour of rectangular high-performance fibre-reinforced concrete beams. Structures 2022, 35, 511–519. [Google Scholar] [CrossRef]
  5. Facconi, L.; Amin, A.; Minelli, F.; Plizzari, G. A unified approach for determining the strength of FRC beams subjected to torsion–Part II: Analytical modeling. Struct. Concr. 2021, 22, 3780–3797. [Google Scholar] [CrossRef]
  6. Facconi, L.; Minelli, F.; Ceresa; Plizzari, G. Steel fibers for replacing minimum reinforcement in beams under torsion. Mater Struct 2021, 54, 34. [Google Scholar] [CrossRef]
  7. Ahmed, M.A. Structural torsional response behavior and prediction for steel fiber-recycled aggregate concrete beams. Int. J. Geomate 2021, 21, 1–10. [Google Scholar] [CrossRef]
  8. Aydin, A.C.; Kiliç, M.; Maali, M.; AYRAK, B.B.; Tunç, E. The Torsional and Shear Behavior of Steel Fiber Reinforced RC Members. Architecture, Civil Engineering, Environment 2021, 14, 47–65. [Google Scholar] [CrossRef]
  9. Lau, C.K.; Htut, T.N.S.; Melling, J.J.; Chegenizadeh, A.; Ng, T.S. Torsional Behaviour of Steel Fibre Reinforced Alkali Activated Concrete. Materials 2020, 13, 3423. [Google Scholar] [CrossRef]
  10. Nitesh, K.J.N.S.; Rao, S.V.; Kumar, P.R. An experimental investigation on torsional behaviour of recycled aggregate based steel fiber reinforced self compacting concrete. J. Build. Eng. 2019, 22, 242–251. [Google Scholar] [CrossRef]
  11. Facconi, L.; Minelli, F.; Plizzari, G.; Ceresa, P. Experimental study on steel fiber reinforced concrete beams in pure torsion. In Proceedings of the Fib Symposium 2019: Concrete—Innovations in Materials, Design and Structures, Kraków, Poland, 27–29 May 2019; pp. 1811–1818. [Google Scholar]
  12. Al-Attar, T.; Qader, S.A.; Hussain, H. Torsional Behavior of Solid and Hollow Core Self Compacting Concrete Beams Reinforced with Steel Fibers. Eng. Technol. J. 2019, 37, 248–255. [Google Scholar] [CrossRef]
  13. Hameed, A.A.; Al-Sherrawi, M.H. Torsional Strength of Steel Fiber Reinforced Concrete Beams. Int. J. Civ. Eng. Technol. (IJCIET) 2018, 9, 1388–1396. Available online: http://www.iaeme.com/ijciet/issues.asp?JType=IJCIET&VType=9&IType=6 (accessed on 3 March 2023).
  14. George, A.; Sofi, A. Torsional Strengthening of Normal Weight Concrete and Light Weight Concrete Using Steel Fibres. Mater. Today Proc. 2017, 4, 9846–9850. [Google Scholar] [CrossRef]
  15. Patil, S.P.; Sangle, K.K. Tests of steel fibre reinforced concrete beams under predominant torsion. J. Build. Eng. 2016, 6, 157–162. [Google Scholar] [CrossRef]
  16. Yap, S.P.; Khaw, K.R.; Alengaram, U.J.; Jumaat, M.Z. Effect of fibre aspect ratio on the torsional behaviour of steel fibre-reinforced normal weight concrete and lightweight concrete. Eng. Struct. 2015, 101, 24–33. [Google Scholar] [CrossRef]
  17. Al-Khafaji, J.; Al-Shaarbaf, I.; Ra’idF, A. Torsional Behavior of Steel Fibers Reinforced Self-Compacting Concrete Beams. 2015. Available online: https://www.researchgate.net/publication/326960211_Torsional_Behavior_of_Steel_Fibers_Reinforced_Self-Compacting_Concrete_Beams (accessed on 28 March 2023).
  18. Yap, S.P.; Alengaram, U.J.; Jumaat, M.Z.; Khaw, K.R. Torsional behaviour of steel fibre-reinforced oil palm shell concrete beams. Mater. Des. 2015, 87, 854–862. [Google Scholar] [CrossRef]
  19. Ju, H.; Kim, K.S.; Lee, D.H.; Hwang, J.-H.; Choi, S.-H.; Oh, Y.-H. Torsional responses of steel fiber-reinforced concrete members. Compos. Struct. 2015, 129, 143–156. [Google Scholar] [CrossRef]
  20. Okay, F.; Engin, S. Torsional behavior of steel fiber reinforced concrete beams. Constr. Build. Mater. 2012, 28, 269–275. [Google Scholar] [CrossRef]
  21. Rao, G.; Seshu, R.; Warnitchai, P. Effect of Steel Fibers on the Behavior of Over-Reinforced Beams Subjected to Pure Torsion. Civ. Eng. Dimens. 2010, 12, 44–51. [Google Scholar]
  22. Chalioris, C.E.; Karayannis, C.G. Effectiveness of the use of steel fibres on the torsional behaviour of flanged concrete beams. Cem. Concr. Compos. 2009, 31, 331–341. [Google Scholar] [CrossRef]
  23. Rao, T.D.G.; Seshu, D.R. Torsional response of fibrous reinforced concrete members: Effect of single type of reinforcement. Constr. Build. Mater. 2006, 20, 187–192. [Google Scholar] [CrossRef]
  24. Rao, T.D.G.; Seshu, D.R. Analytical model for the torsional response of steel fiber reinforced concrete members under pure torsion. Cem. Concr. Compos. 2005, 27, 493–501. [Google Scholar] [CrossRef]
  25. Khaloo, A.R.; Sharifian, M. Experimental investigation of low to high-strength steel fiber reinforced lightweight concrete under pure torsion. Asian J. Civ. Eng. (Build. Hous.) 2005, 6, 533. [Google Scholar]
  26. Rao, T.D.G.; Seshu, D.R. Torsion of steel fiber reinforced concrete members. Cem. Concr. Res. 2003, 33, 1783–1788. [Google Scholar] [CrossRef]
  27. Ei-Niema, E.I. Fiber Reinforced Concrete Beams Under Torsion. ACI Struct. J. 1993, 90, 489–495. [Google Scholar] [CrossRef]
  28. Wafa, F.F.; Hasnat, A.; Tarabolsi, O.F. Prestressed Fiber Reinforced Concrete Beams Subjected to Torsion. ACI Struct. J. 1992, 89, 272–283. [Google Scholar] [CrossRef]
  29. Craig, R.J.; Parr, J.A.; Germain, E.; Mosquera, V.; Kamilares, S. Fiber Reinforced Beams in Torsion. ACI J. Proc. 1986, 83, 934–942. [Google Scholar] [CrossRef]
  30. Mansur, M.A.; Paramasivam, P. Steel fibre reinforced concrete beams in pure torsion. Int. J. Cem. Compos. Lightweight Concr. 1982, 4, 39–45. [Google Scholar] [CrossRef]
  31. Narayanan, R. Fibre reinforced concrete in pure torsion and in combined bending and torsion. Proc. Inst. Civ. Eng. 1979, 67, 987–1001. [Google Scholar] [CrossRef]
  32. Said, M.; Salah, A.; Erfan, A.; Esam, A. Experimental analysis of torsional behavior of hybrid fiber reinforced concrete beams. J. Build. Eng. 2023, 71, 106574. [Google Scholar] [CrossRef]
  33. Al-Salim, N.H.; Jaber, M.H.; Hassan, R.F.; Mohammed, N.S.; Hussein, H.H. Experimental Investigation of Compound Effect of Flexural and Torsion on Fiber-Reinforced Concrete Beams. Buildings 2023, 13, 1347. [Google Scholar] [CrossRef]
  34. Cao, X.; Zhang, W.J.; Ren, Y.C.; Fu, F.; Li, Y.H.; He, D.B.; Zheng, Y. Torsional capacity of ultra-high-performance concrete beams using rectangle stirrup. J. Build. Eng. 2023, 69, 106231. [Google Scholar] [CrossRef]
  35. Mahdi, M.S.; Mohaisen, S.K. Behavior of steel fiber self-compacting concrete hollow deep beams under torque. J. Eng. Sustain. Dev. 2022, 25, 22–33. [Google Scholar] [CrossRef]
  36. Zhou, J.; Li, C.; Feng, Z.; Yoo, D.-Y. Experimental investigation on torsional behaviors of ultrahigh-performance fiber-reinforced concrete hollow beams. Cem. Concr. Compos. 2022, 129, 104504. [Google Scholar] [CrossRef]
  37. Abdullah, M.D.; Malik, H.S. Experimental Study of Hollow RC Beams Strengthened by Steel Fiber under Pure Torsion. J. Eng. 2022, 2022, e3496809. [Google Scholar] [CrossRef]
  38. Li, C.; Zhou, J.; Ke, L.; Yu, S.; Li, H. Failure mechanisms and loading capacity prediction for rectangular UHPC beams under pure torsion. Eng. Struct. 2022, 264, 114426. [Google Scholar] [CrossRef]
  39. Mohammed Khalifah, Z.; Rasheed, M.M. The effect of sifcon on torsional behavior of reinforced concrete beams. J. Eng. Sustain. Dev. 2022, 26, 52–62. [Google Scholar] [CrossRef]
  40. Zhou, C.; Wang, J.; Jia, W.; Fang, Z. Torsional behavior of ultra-high performance concrete (UHPC) rectangular beams without steel reinforcement: Experimental investigation and theoretical analysis. Compos. Struct. 2022, 299, 116022. [Google Scholar] [CrossRef]
  41. Mures, J.K.; Chkheiwer, A.H.; Ahmed, M.A. Experimental Study on Torsional Behavior of steel Fiber Reinforced Concrete Members under Pure Torsion. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1090, 012065. [Google Scholar] [CrossRef]
  42. Mures, J.K.; Ahmed, M.A.I.; Chkheiwer, A.H. Torsional Behavior of High Strength Concrete Members Strengthened by Mixed Steel Fibers. J. Eng. 2021, 2021, e5539623. [Google Scholar] [CrossRef]
  43. Hassan, R.F.; Jaber, M.H.; Al-Salim, N.H.; Hussein, H.H. Experimental research on torsional strength of synthetic/steel fiber-reinforced hollow concrete beam. Eng. Struct. 2020, 220, 110948. [Google Scholar] [CrossRef]
  44. Ju, H.; Han, S.-J.; Zhang, D.; Kim, J.; Wu, W.; Kim, K.S. Estimation of Minimum Torsional Reinforcement of Reinforced Concrete and Steel Fiber-Reinforced Concrete Members. Adv. Mater. Sci. Eng. 2019, 2019, e4595363. [Google Scholar] [CrossRef]
  45. Waryosh, W.; Mohaisen, S.K.; Dkhel, R.H. Deformation responses of reinforced concrete beams under pure torsion. IOP Conf. Ser. Mater. Sci. Eng. 2018, 433, 012037. [Google Scholar] [CrossRef]
  46. Zhou, J.; Shen, W.; Wang, S. Experimental study on torsional behavior of FRC and ECC beams reinforced with GFRP bars. Constr. Build. Mater. 2017, 152, 74–81. [Google Scholar] [CrossRef]
  47. Yang, I.-H.; Joh, C.; Lee, J.W.; Kim, B.-S. Torsional behavior of ultra-high performance concrete squared beams. Eng. Struct. 2013, 56, 372–383. [Google Scholar] [CrossRef]
  48. Tegos, I.A. Fiber Reinforced Concrete Beams With Circular Section in Torsion. ACI Struct. J. 1989, 86, 473–482. [Google Scholar] [CrossRef]
  49. Naaman, A.E. Engineered Steel Fibers with Optimal Properties for Reinforcement of Cement Composites. J. Adv. Concr. Technol. 2003, 1, 241–252. [Google Scholar] [CrossRef]
  50. Buda-Ożóg, L. Numeryczna i doświadczalna analiza zginanych, skręcanych i ścinanych belek żelbeto-wych. J. Civ. Eng. Environ. Archit. 2017, XXXIV, 223–234. [Google Scholar] [CrossRef]
  51. Buda-Ozóg, L.; Sienkowska, K.; Skrzypczak, I. Reliability of beams subjected to torsion designed using STM. Arch. Civ. Eng. 2020, 66, 555–573. [Google Scholar] [CrossRef]
  52. Rahal, K.N. Analysis and design for torsion in reinforced and prestressed concrete beams. Struct. Engine-Ering Mech. 2001, 11, 575–590. [Google Scholar] [CrossRef]
  53. Samman, T.A.; Radain, T.A. Effect Of Aspect Ratio On Torsional Capacity Of High-Strength Plain Concrete Deep Beams. Eng. J. Qatar Univ. 1993, 6, 115–134. [Google Scholar]
Materials 18 02452 g001
Figure 1. Spatial truss model in torsion calculations.
Figure 1. Spatial truss model in torsion calculations.
Materials 18 02452 g001
Materials 18 02452 g002
Figure 2. Number of beam elements in which the appropriate amount of fibers is used [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].
Figure 2. Number of beam elements in which the appropriate amount of fibers is used [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].
Materials 18 02452 g002
Materials 18 02452 g003
Figure 3. The τcr parameter in the analyzed database [1,3,4,5,6,7,8,9,11,12,13,14,16,17,18,20,21,22,23,24,27,29,32,33]: (a) the relationship between the cracking stress τcr and the amount of dispersed reinforcement Vf; (b) histogram of the crack stress τcr as a function of the amount of dispersed reinforcement Vf.
Figure 3. The τcr parameter in the analyzed database [1,3,4,5,6,7,8,9,11,12,13,14,16,17,18,20,21,22,23,24,27,29,32,33]: (a) the relationship between the cracking stress τcr and the amount of dispersed reinforcement Vf; (b) histogram of the crack stress τcr as a function of the amount of dispersed reinforcement Vf.
Materials 18 02452 g003
Materials 18 02452 g004
Figure 4. The τu parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the amount of dispersed reinforcement Vf; (b) histogram of the ultimate stress τu as a function of the amount of dispersed reinforcement Vf.
Figure 4. The τu parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the amount of dispersed reinforcement Vf; (b) histogram of the ultimate stress τu as a function of the amount of dispersed reinforcement Vf.
Materials 18 02452 g004
Materials 18 02452 g005
Figure 5. The θcr parameter in the analyzed database [1,5,6,7,8,9,11,12,16,17,18,20,22,23,26]: (a) the relationship between the crack stress τcr and the rotation angle θcr; (b) histogram of the angle of rotation corresponding to the cracking stress θcr for different amounts of dispersed reinforcement in the twisted element.
Figure 5. The θcr parameter in the analyzed database [1,5,6,7,8,9,11,12,16,17,18,20,22,23,26]: (a) the relationship between the crack stress τcr and the rotation angle θcr; (b) histogram of the angle of rotation corresponding to the cracking stress θcr for different amounts of dispersed reinforcement in the twisted element.
Materials 18 02452 g005
Materials 18 02452 g006
Figure 6. The θu parameter in the analyzed database [1,4,5,6,7,8,9,10,11,12,14,16,17,18,19,20,21,22,23,26,32]: (a) the relationship between the ultimate stress τcr and the rotation angle θu; (b) histogram of the angle of rotation corresponding to the ultimate stress θu for different amounts of dispersed reinforcement in the twisted element.
Figure 6. The θu parameter in the analyzed database [1,4,5,6,7,8,9,10,11,12,14,16,17,18,19,20,21,22,23,26,32]: (a) the relationship between the ultimate stress τcr and the rotation angle θu; (b) histogram of the angle of rotation corresponding to the ultimate stress θu for different amounts of dispersed reinforcement in the twisted element.
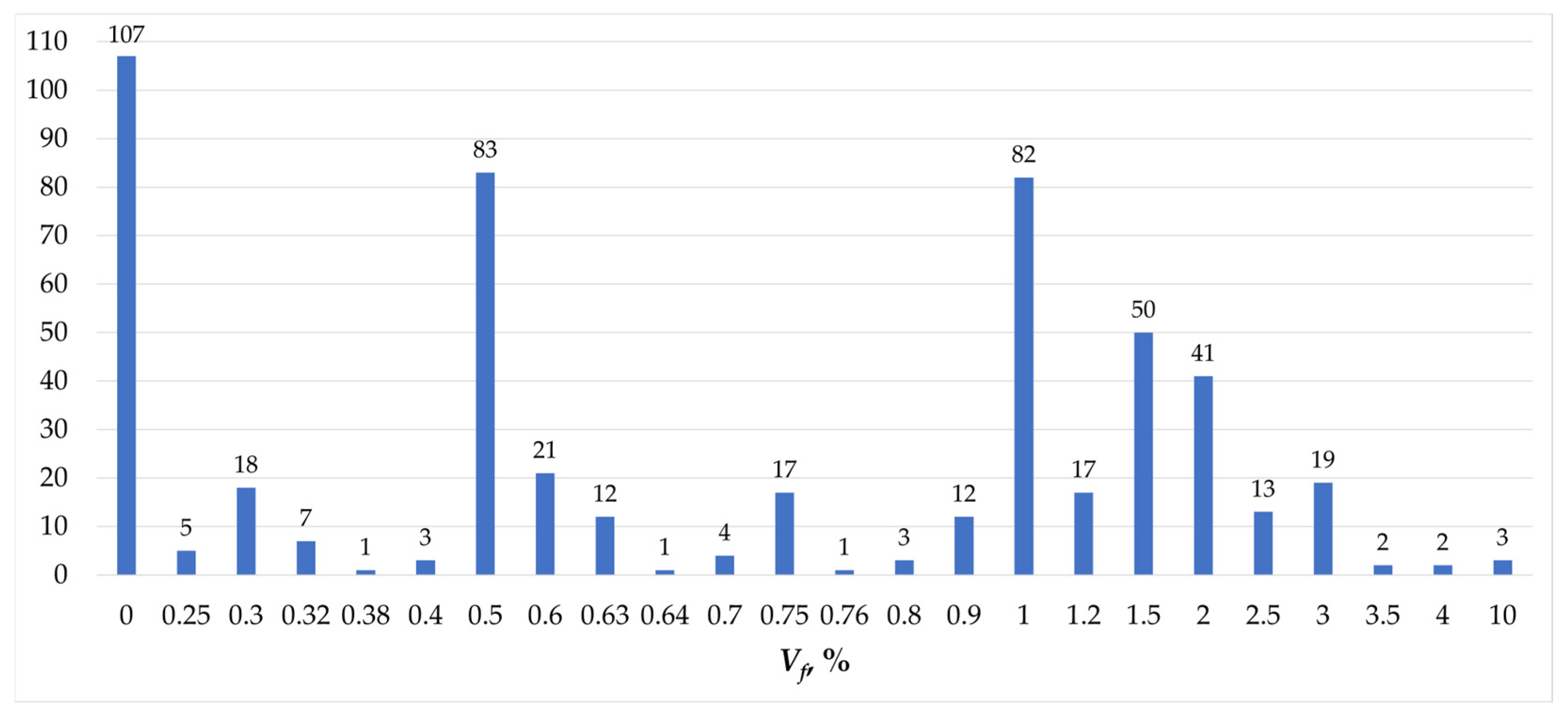
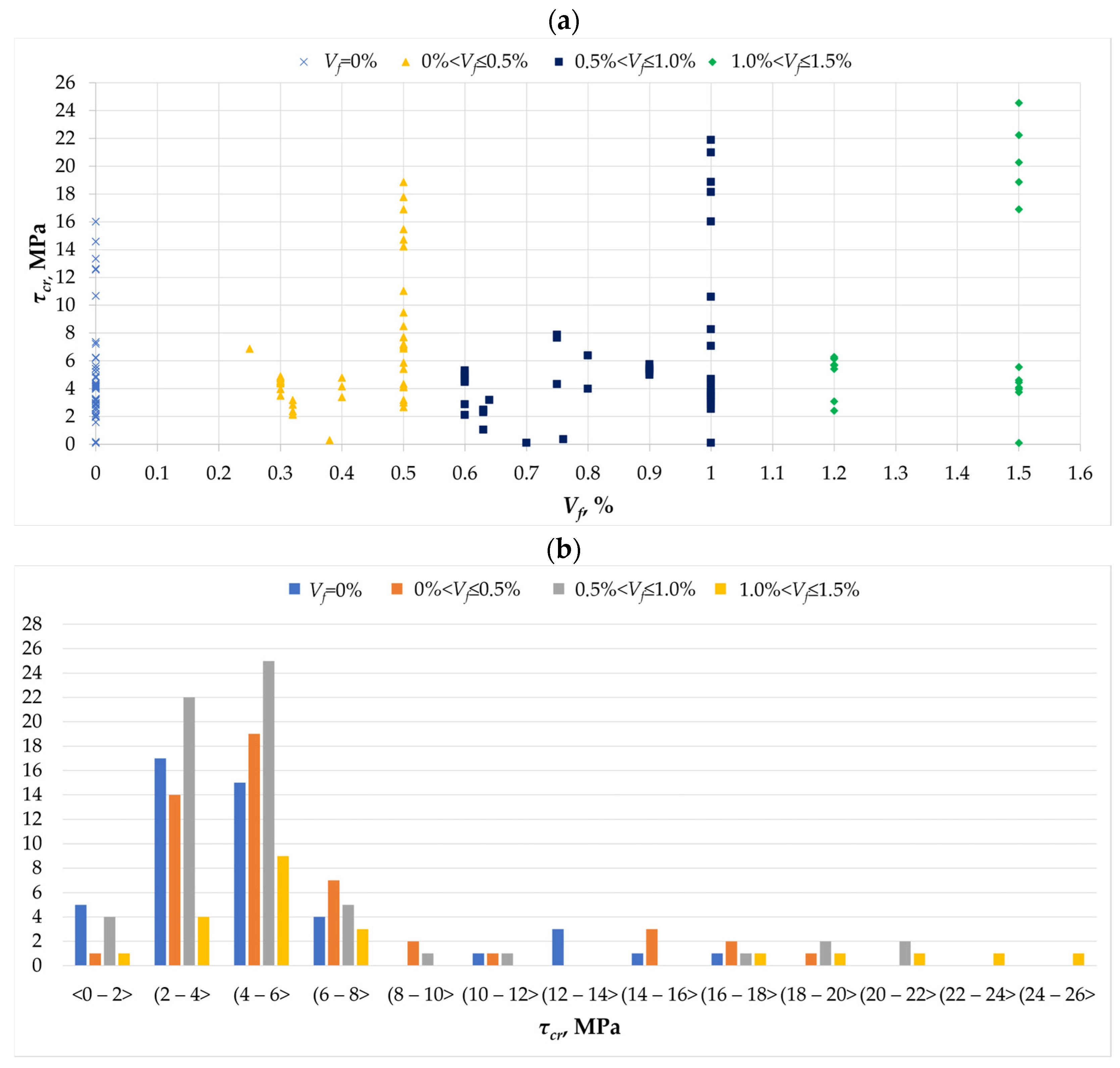
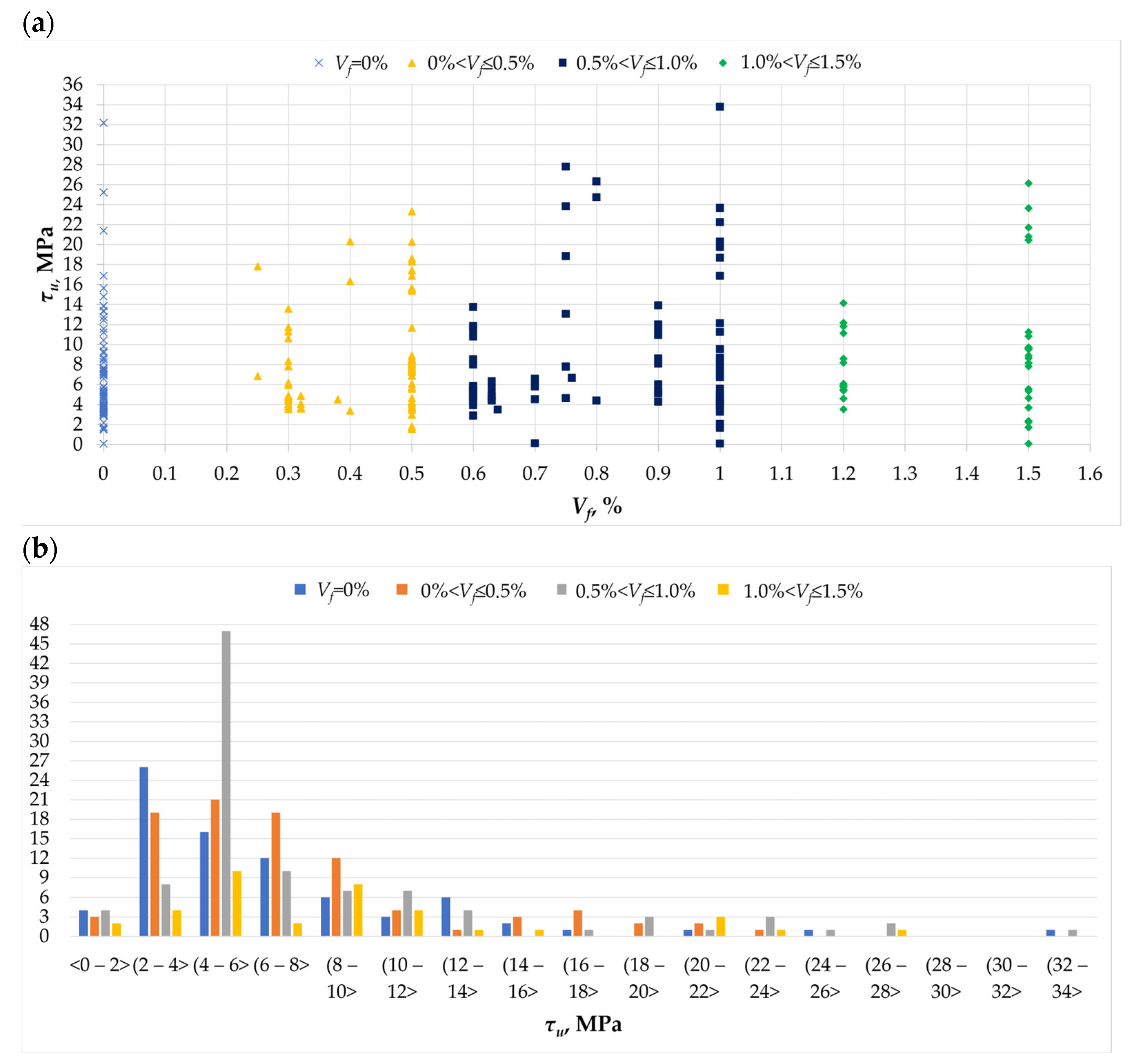
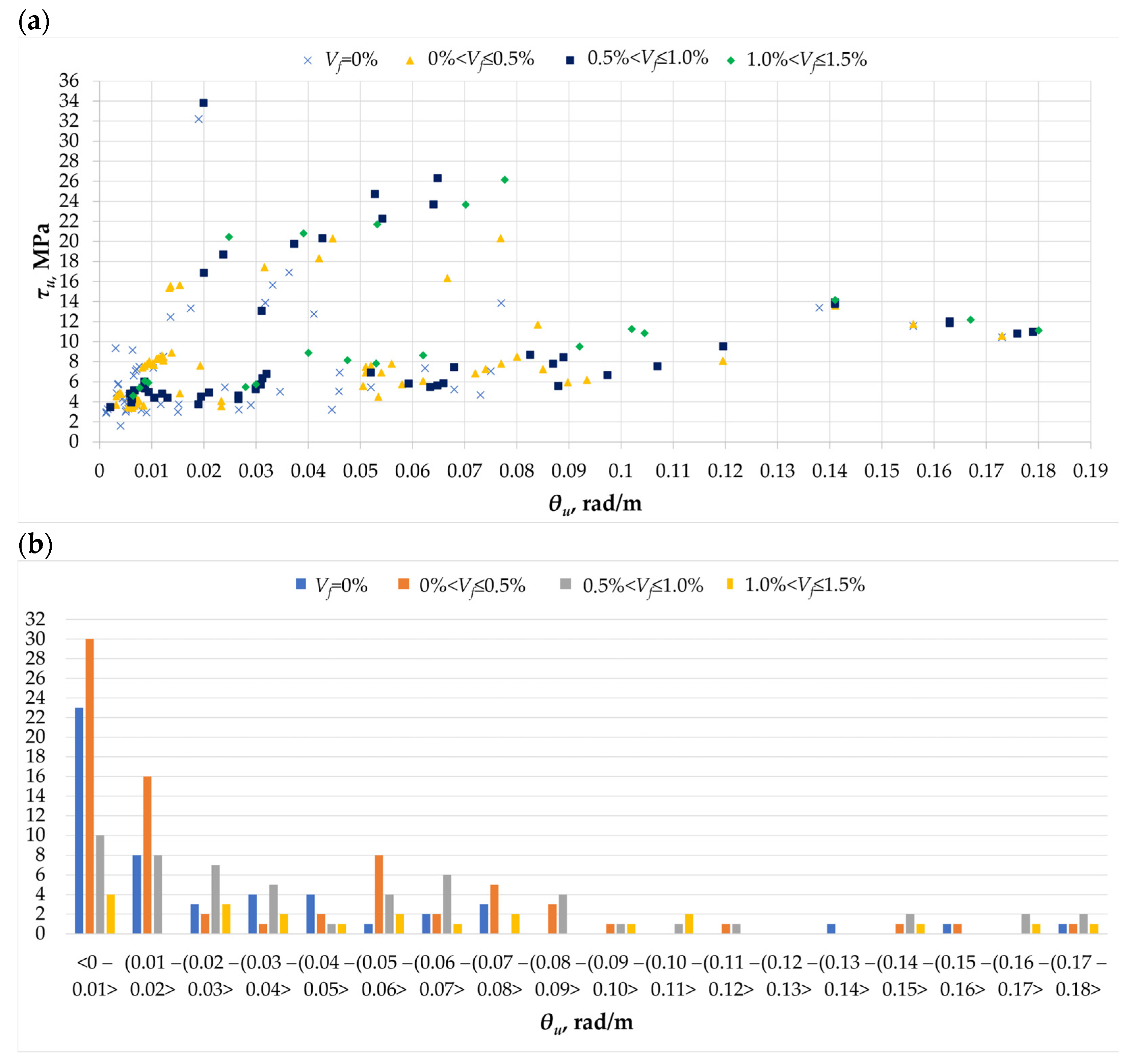
Materials 18 02452 g006
Materials 18 02452 g007
Figure 7. The fc parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the compressive strength fc; (b) histogram of compressive strength fc for different amounts of dispersed reinforcement.
Figure 7. The fc parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the compressive strength fc; (b) histogram of compressive strength fc for different amounts of dispersed reinforcement.
Materials 18 02452 g007
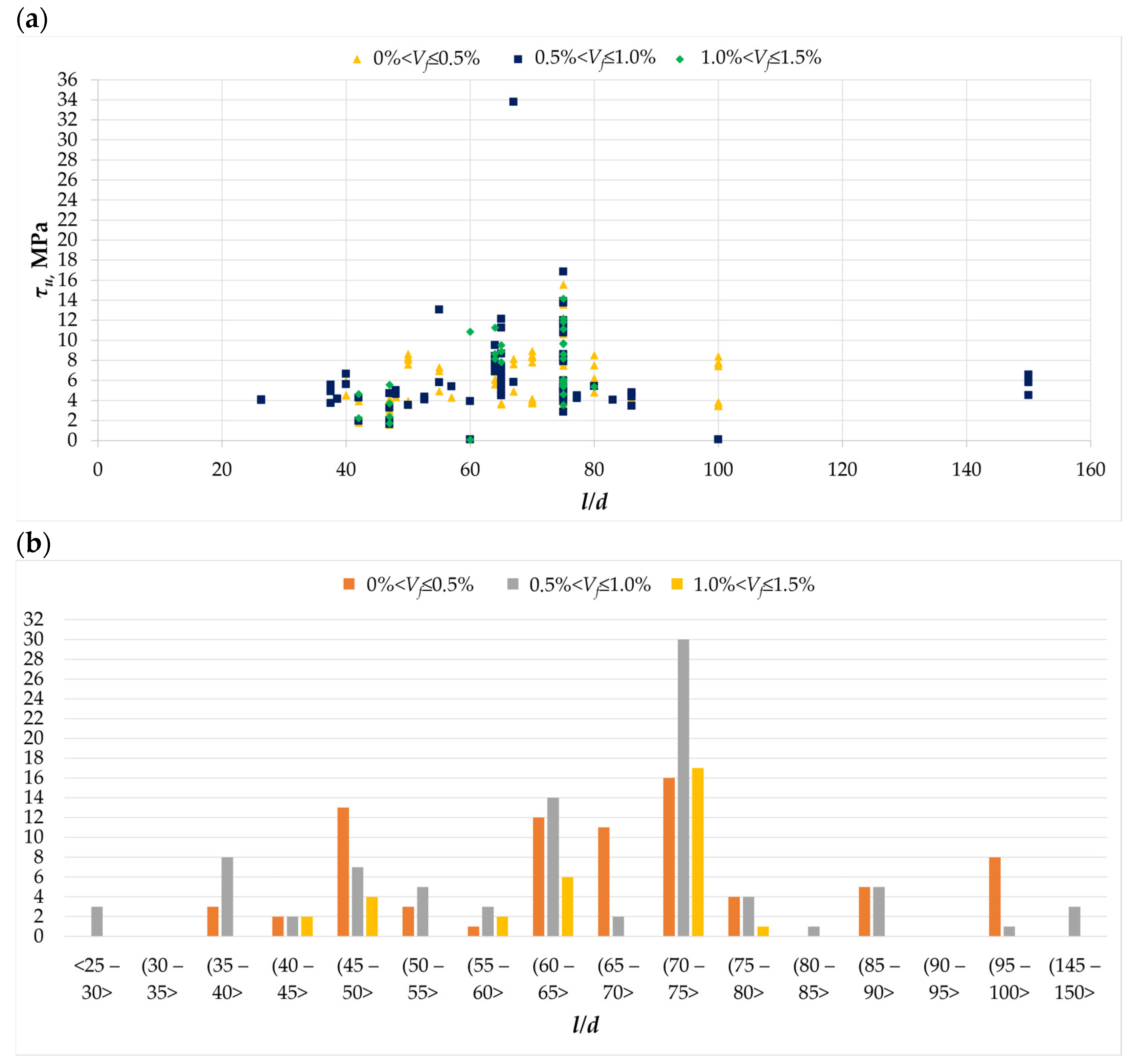
Materials 18 02452 g008
Figure 8. The l/d parameter in the analyzed database [1,3,4,5,6,8,11,12,13,15,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the fiber slenderness l/d; (b) histogram of fiber slenderness l/d for different amounts of dispersed reinforcement.
Figure 8. The l/d parameter in the analyzed database [1,3,4,5,6,8,11,12,13,15,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and the fiber slenderness l/d; (b) histogram of fiber slenderness l/d for different amounts of dispersed reinforcement.
Materials 18 02452 g008
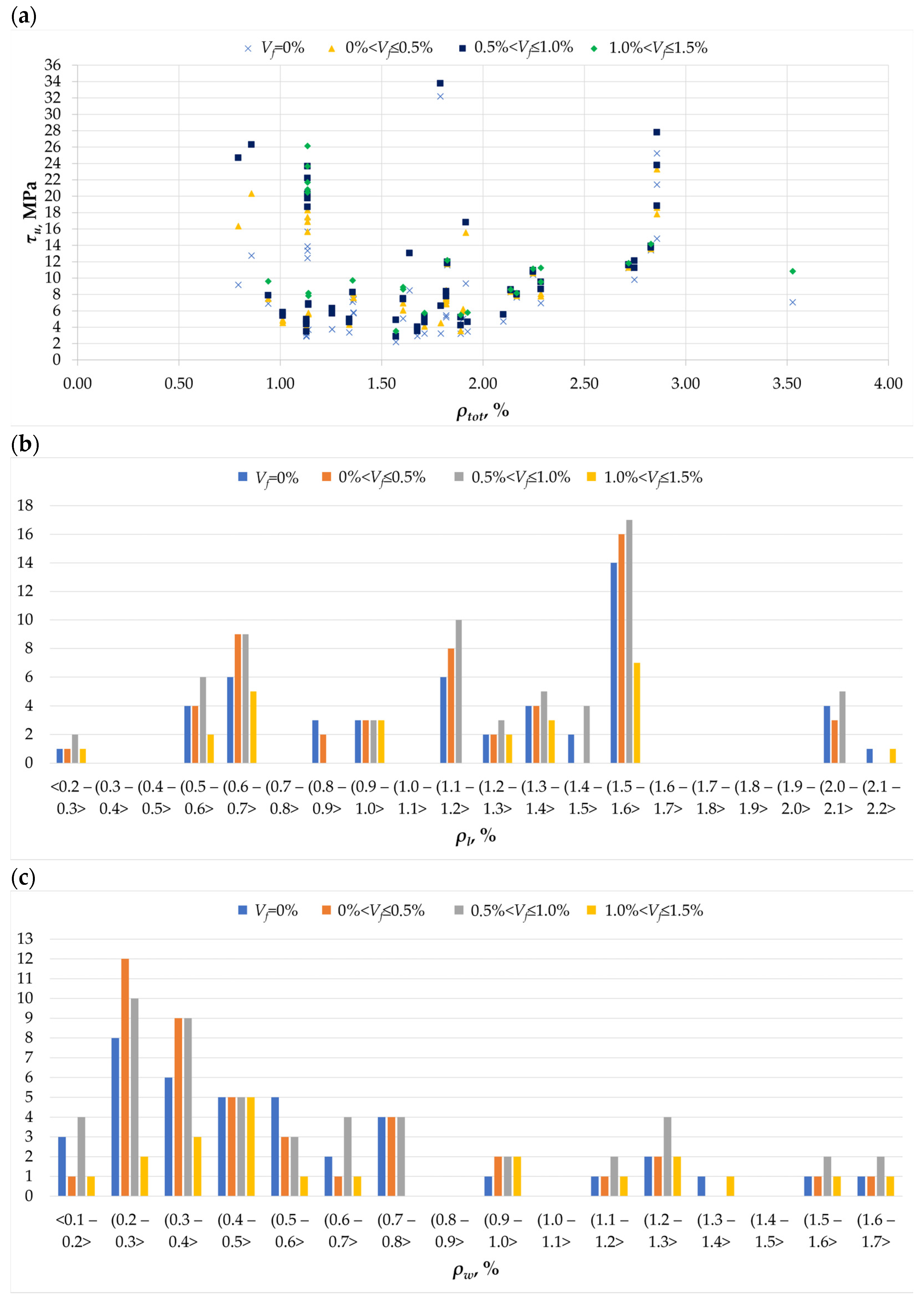
Materials 18 02452 g009
Figure 9. The parameters ρtot, ρl, and ρw in the analyzed database: (a) the relationship between the ultimate stress τu and total reinforcement ratio ρtot [1,2,3,4,5,6,7,8,9,11,12,13,16,17,18,19,20,21,22,23,24,27,28,32,33]: (b) histogram of longitudinal reinforcement ρl for different amounts of dispersed reinforcement in the twisted element [1,2,3,4,5,6,7,8,9,11,12,13,16,17,18,19,20,21,22,23,24,27,28,32,33]; (c) histogram of transverse reinforcement ρw for different amounts of dispersed reinforcement in the twisted element [1,2,3,4,5,7,8,9,12,16,17,18,19,20,21,22,23,24,27,32,33].
Figure 9. The parameters ρtot, ρl, and ρw in the analyzed database: (a) the relationship between the ultimate stress τu and total reinforcement ratio ρtot [1,2,3,4,5,6,7,8,9,11,12,13,16,17,18,19,20,21,22,23,24,27,28,32,33]: (b) histogram of longitudinal reinforcement ρl for different amounts of dispersed reinforcement in the twisted element [1,2,3,4,5,6,7,8,9,11,12,13,16,17,18,19,20,21,22,23,24,27,28,32,33]; (c) histogram of transverse reinforcement ρw for different amounts of dispersed reinforcement in the twisted element [1,2,3,4,5,7,8,9,12,16,17,18,19,20,21,22,23,24,27,32,33].
Materials 18 02452 g009
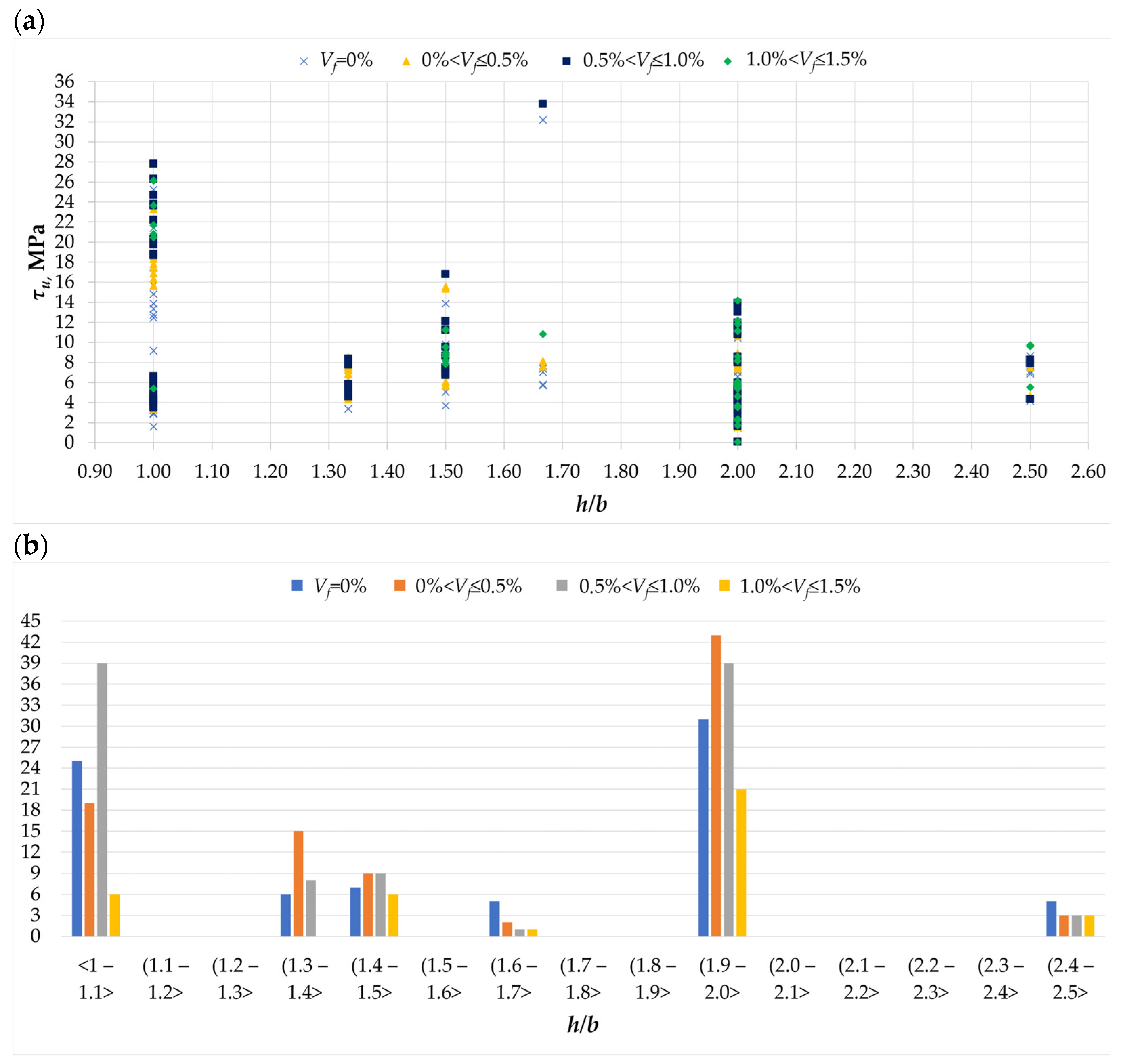
Materials 18 02452 g010
Figure 10. The h/b parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and aspect ratio h/b; (b) histogram of aspect ratio h/b for different amounts of dispersed reinforcement in the twisted element.
Figure 10. The h/b parameter in the analyzed database [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]: (a) the relationship between the ultimate stress τu and aspect ratio h/b; (b) histogram of aspect ratio h/b for different amounts of dispersed reinforcement in the twisted element.
Materials 18 02452 g010
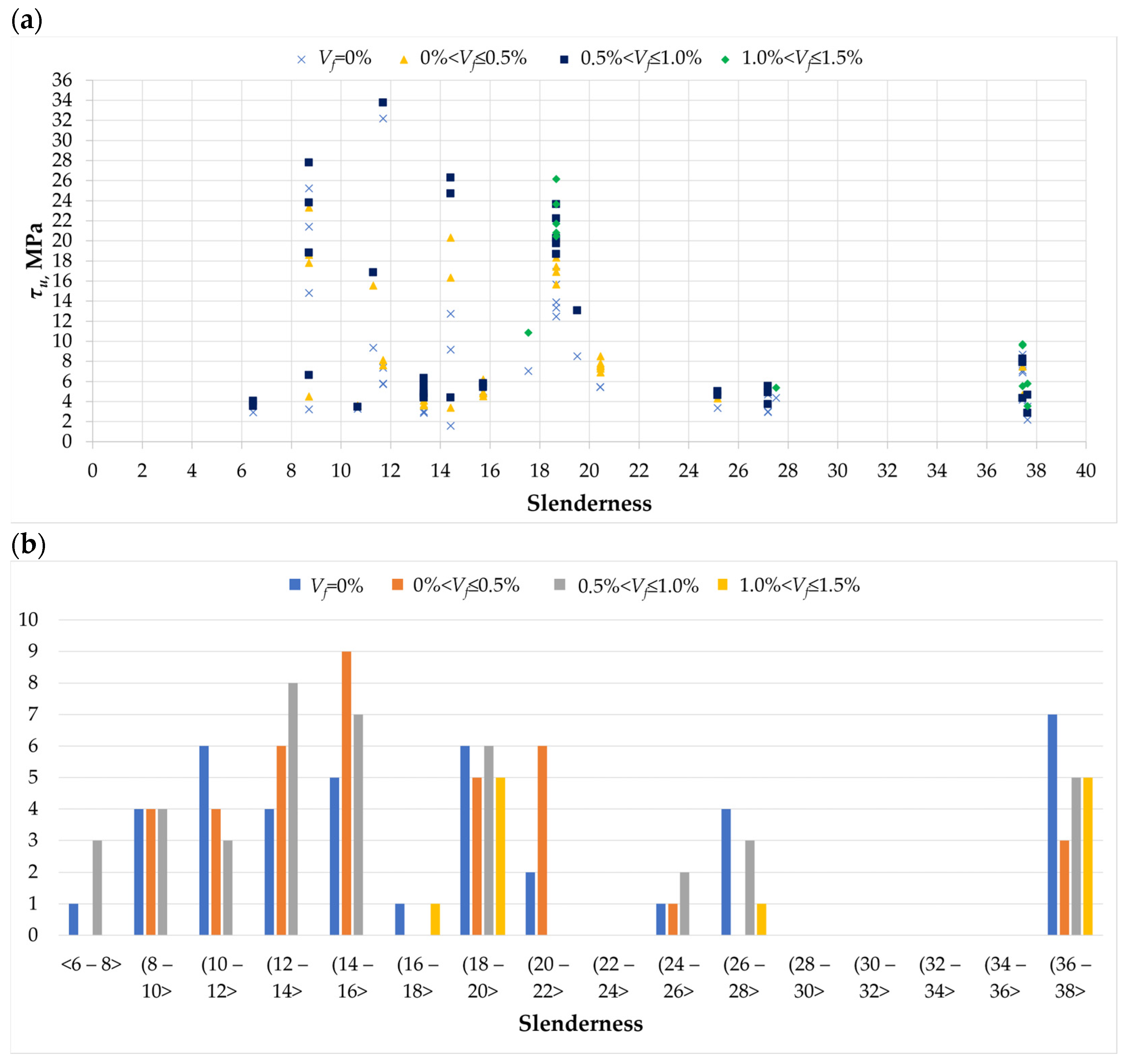
Materials 18 02452 g011
Figure 11. Slenderness in the analyzed database [2,3,4,5,6,7,8,9,11,12,13,15,16,17,19,20,22,27,28,32]: (a) the relationship between ultimate stress τu and slenderness of twisted elements; (b) histogram of slenderness ratios for elements with varying amounts of dispersed reinforcement in the twisted element.
Figure 11. Slenderness in the analyzed database [2,3,4,5,6,7,8,9,11,12,13,15,16,17,19,20,22,27,28,32]: (a) the relationship between ultimate stress τu and slenderness of twisted elements; (b) histogram of slenderness ratios for elements with varying amounts of dispersed reinforcement in the twisted element.
Materials 18 02452 g011
Materials 18 02452 g012
Figure 12. The relationship between the normalized crack stress τcr/τcr0 and the amount of dispersed reinforcement Vf [1,3,4,5,6,7,8,9,11,12,13,14,16,17,18,20,21,22,23,24,27,29,32,33].
Figure 12. The relationship between the normalized crack stress τcr/τcr0 and the amount of dispersed reinforcement Vf [1,3,4,5,6,7,8,9,11,12,13,14,16,17,18,20,21,22,23,24,27,29,32,33].
Materials 18 02452 g012
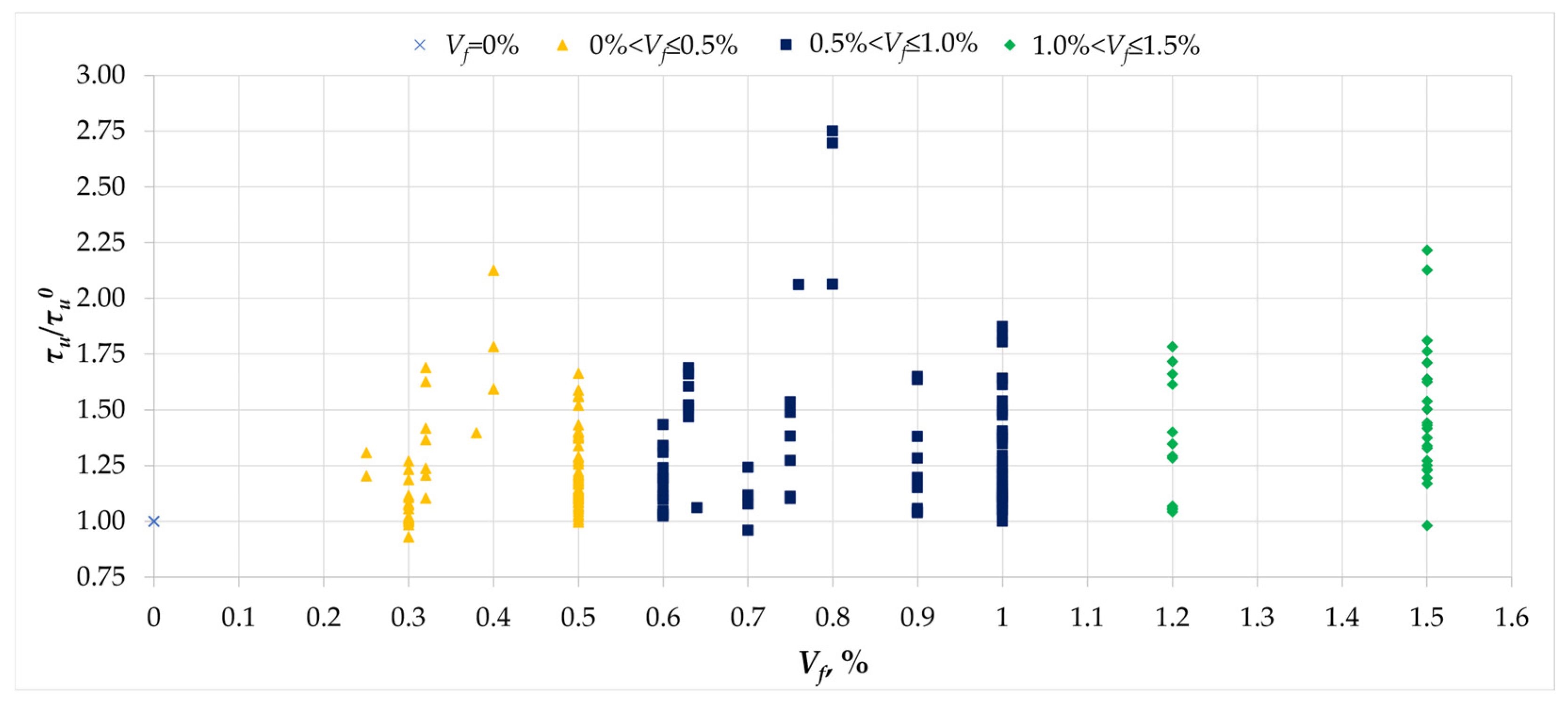
Materials 18 02452 g013
Figure 13. The relationship between the normalized ultimate stress τu/τu0 and the amount of dispersed reinforcement Vf [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Figure 13. The relationship between the normalized ultimate stress τu/τu0 and the amount of dispersed reinforcement Vf [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Materials 18 02452 g013
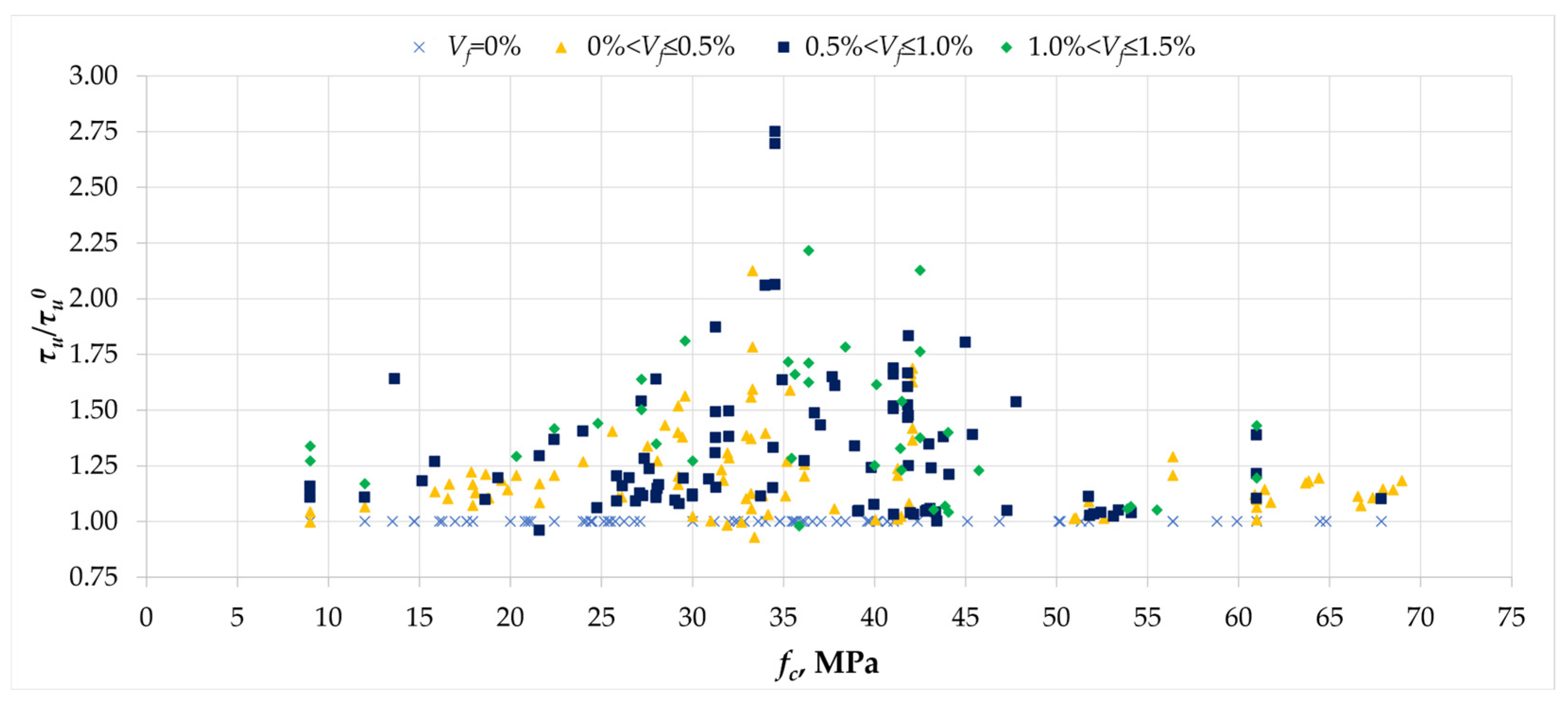
Materials 18 02452 g014
Figure 14. The relationship between the normalized ultimate stress τu/τu0 and the compressive strength fc [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Figure 14. The relationship between the normalized ultimate stress τu/τu0 and the compressive strength fc [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Materials 18 02452 g014
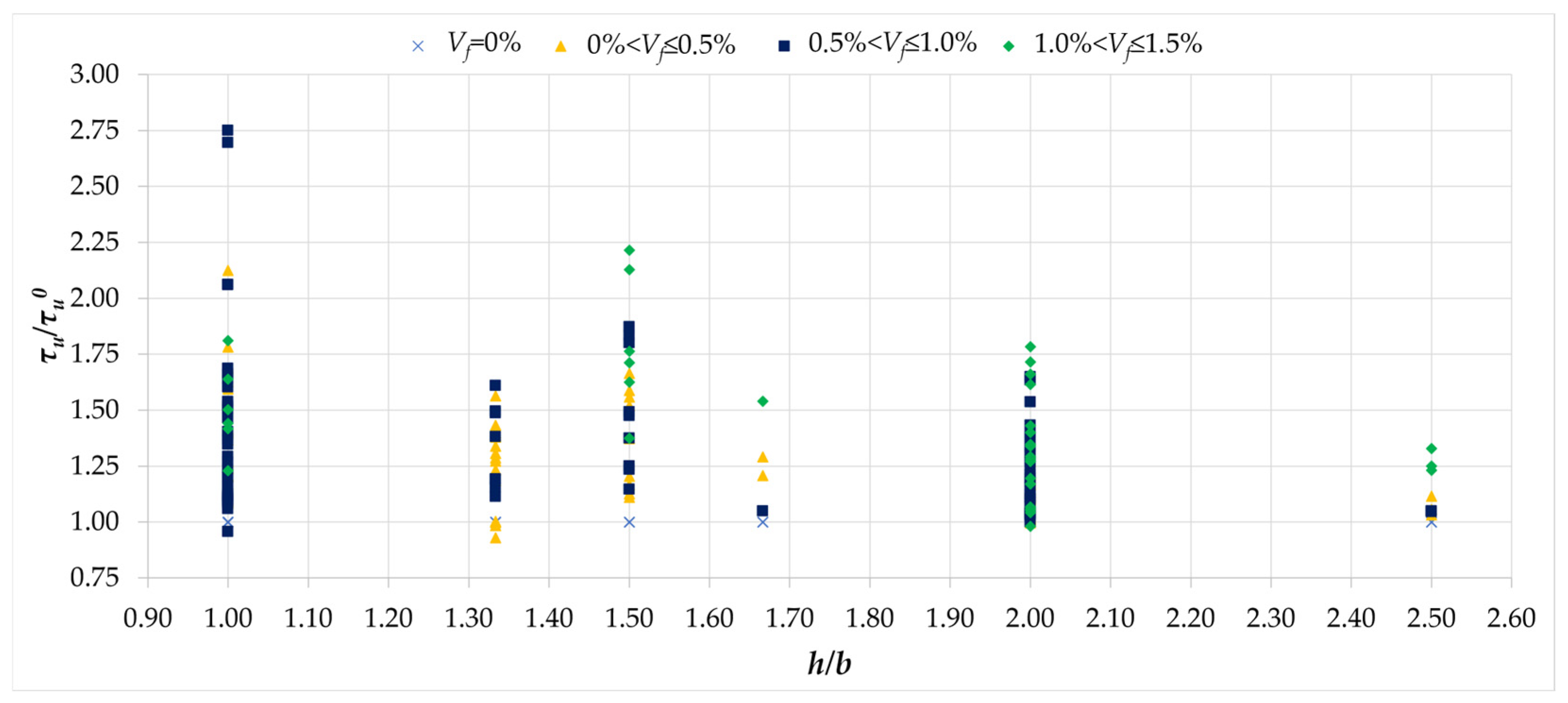
Materials 18 02452 g015
Figure 15. The relationship between the normalized ultimate stress τu/τu0 and aspect ratio h/b [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Figure 15. The relationship between the normalized ultimate stress τu/τu0 and aspect ratio h/b [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
Materials 18 02452 g015
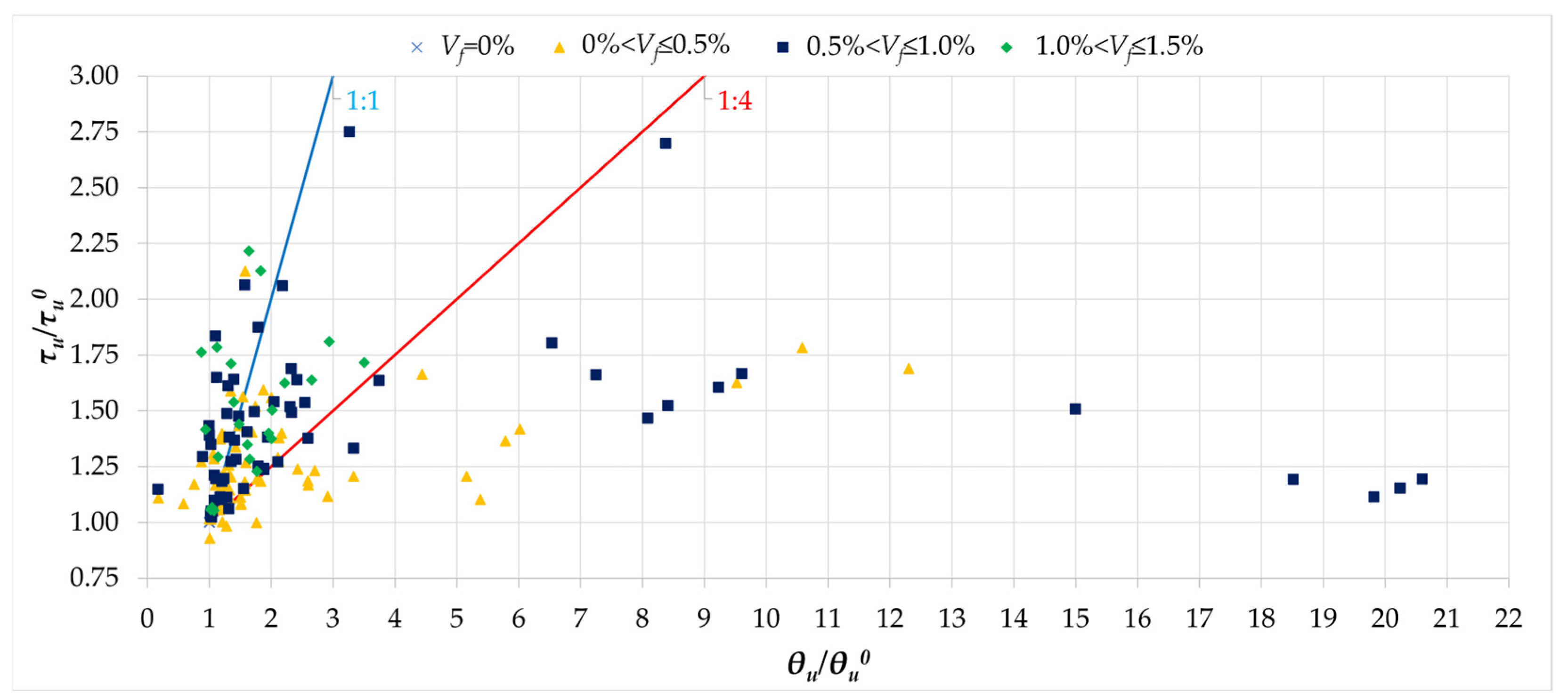
Materials 18 02452 g016
Figure 16. The relationship between the normalized ultimate stress τu/τu0 and normalized rotation angle θu/θu0 [1,4,5,6,7,8,9,10,11,12,14,16,17,18,19,20,21,22,23,26,32].
Figure 16. The relationship between the normalized ultimate stress τu/τu0 and normalized rotation angle θu/θu0 [1,4,5,6,7,8,9,10,11,12,14,16,17,18,19,20,21,22,23,26,32].
Materials 18 02452 g016
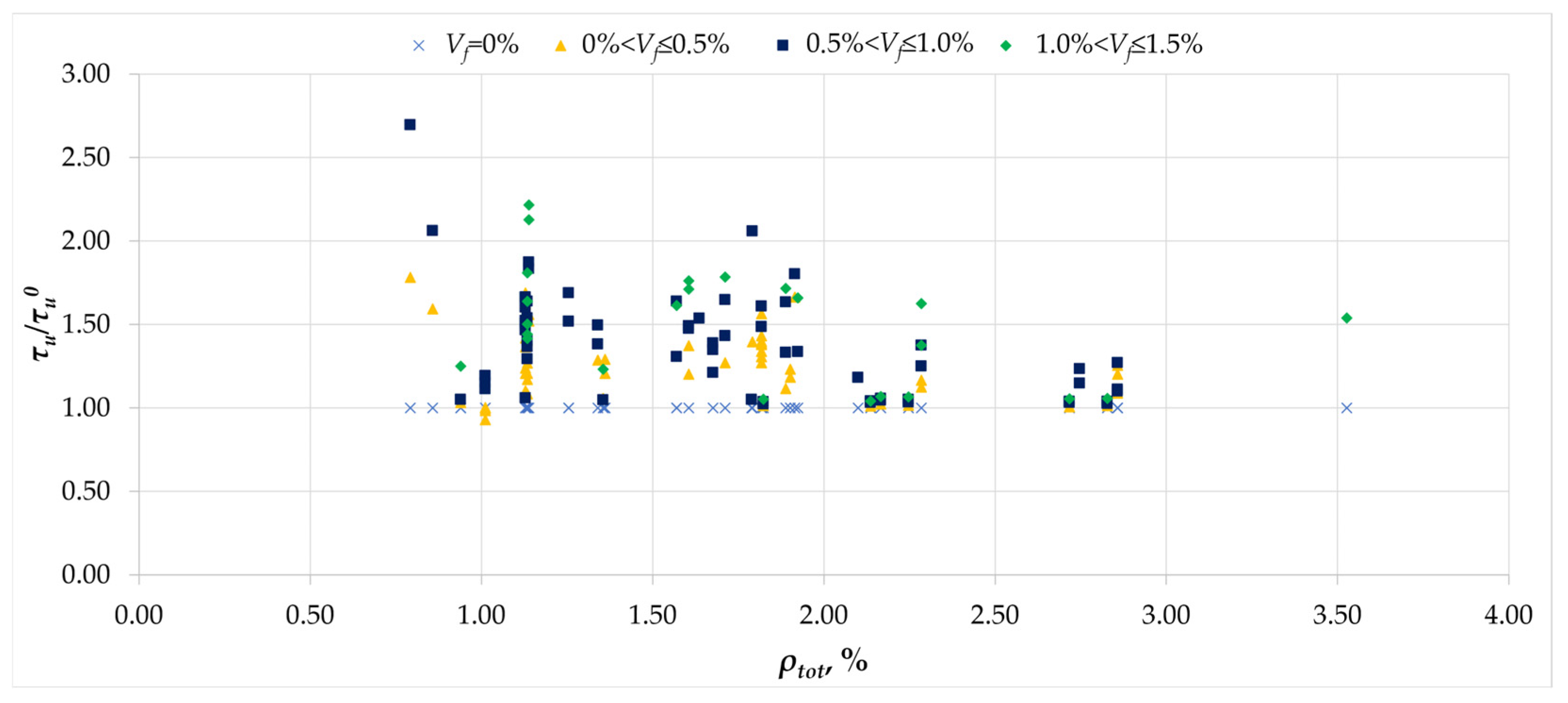
Materials 18 02452 g017
Figure 17. The relationship between the normalized ultimate stress τu/τu0 and total reinforcement ratio ρtot.
Figure 17. The relationship between the normalized ultimate stress τu/τu0 and total reinforcement ratio ρtot.
Materials 18 02452 g017
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Domski, J.; Lehmann, M.; Sanok, A.; Tvrda, K. Overview of Torsion Tests on Fiber-Reinforced Concrete Beams. Materials 2025, 18, 2452. https://doi.org/10.3390/ma18112452

AMA Style

Domski J, Lehmann M, Sanok A, Tvrda K. Overview of Torsion Tests on Fiber-Reinforced Concrete Beams. Materials. 2025; 18(11):2452. https://doi.org/10.3390/ma18112452

Chicago/Turabian Style

Domski, Jacek, Marek Lehmann, Artur Sanok, and Katarina Tvrda. 2025. "Overview of Torsion Tests on Fiber-Reinforced Concrete Beams" Materials 18, no. 11: 2452. https://doi.org/10.3390/ma18112452

APA Style

Domski, J., Lehmann, M., Sanok, A., & Tvrda, K. (2025). Overview of Torsion Tests on Fiber-Reinforced Concrete Beams. Materials, 18(11), 2452. https://doi.org/10.3390/ma18112452

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop