Advances in Optical Microfibers: From Fabrication to Functionalization and Sensing Applications
Abstract
1. Introduction
2. Principles of Operation
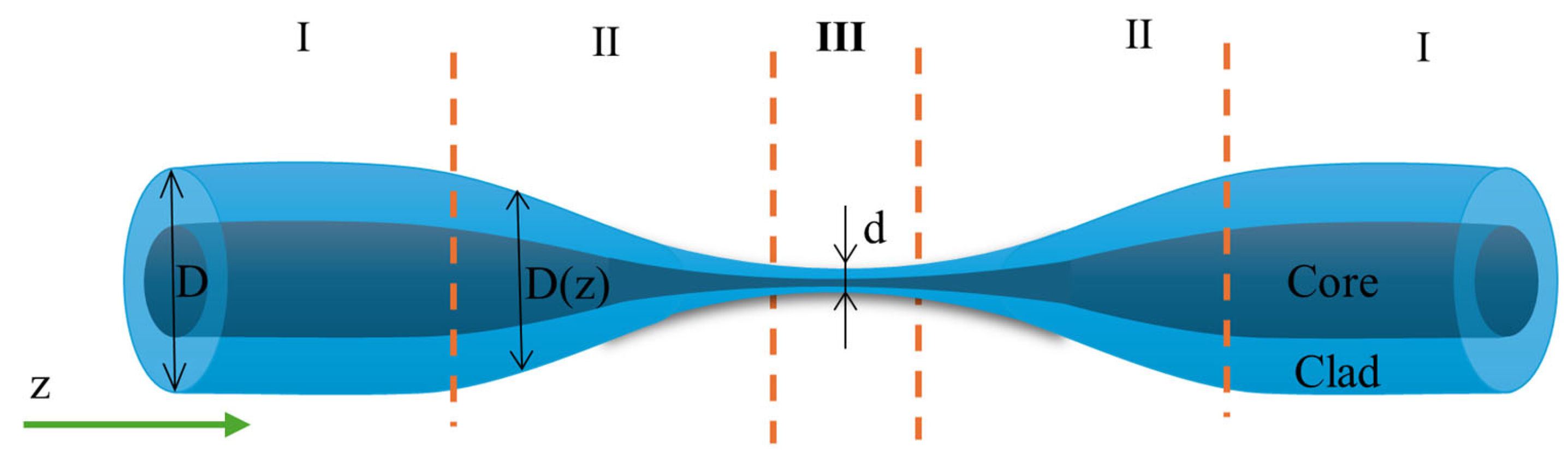
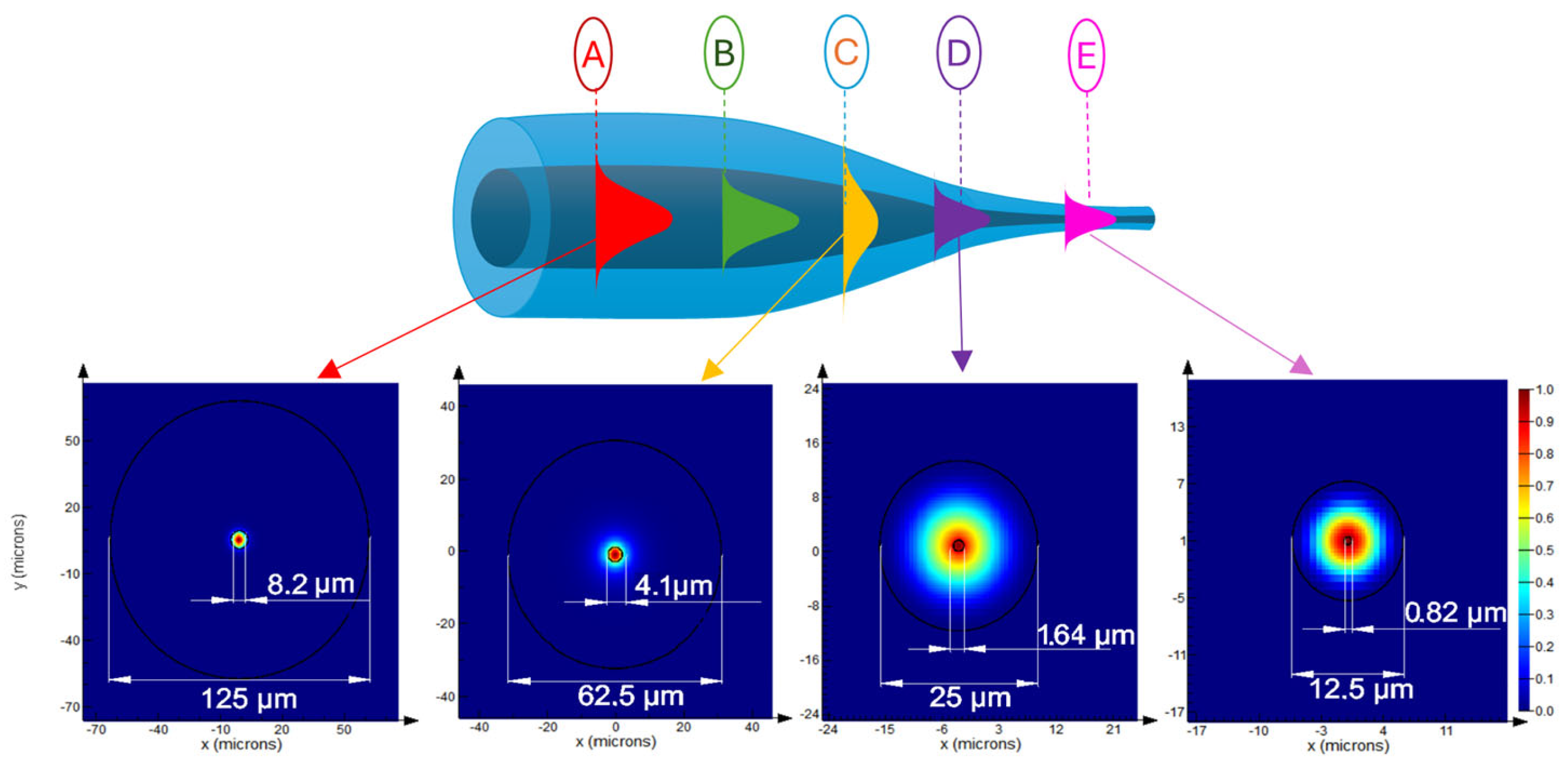
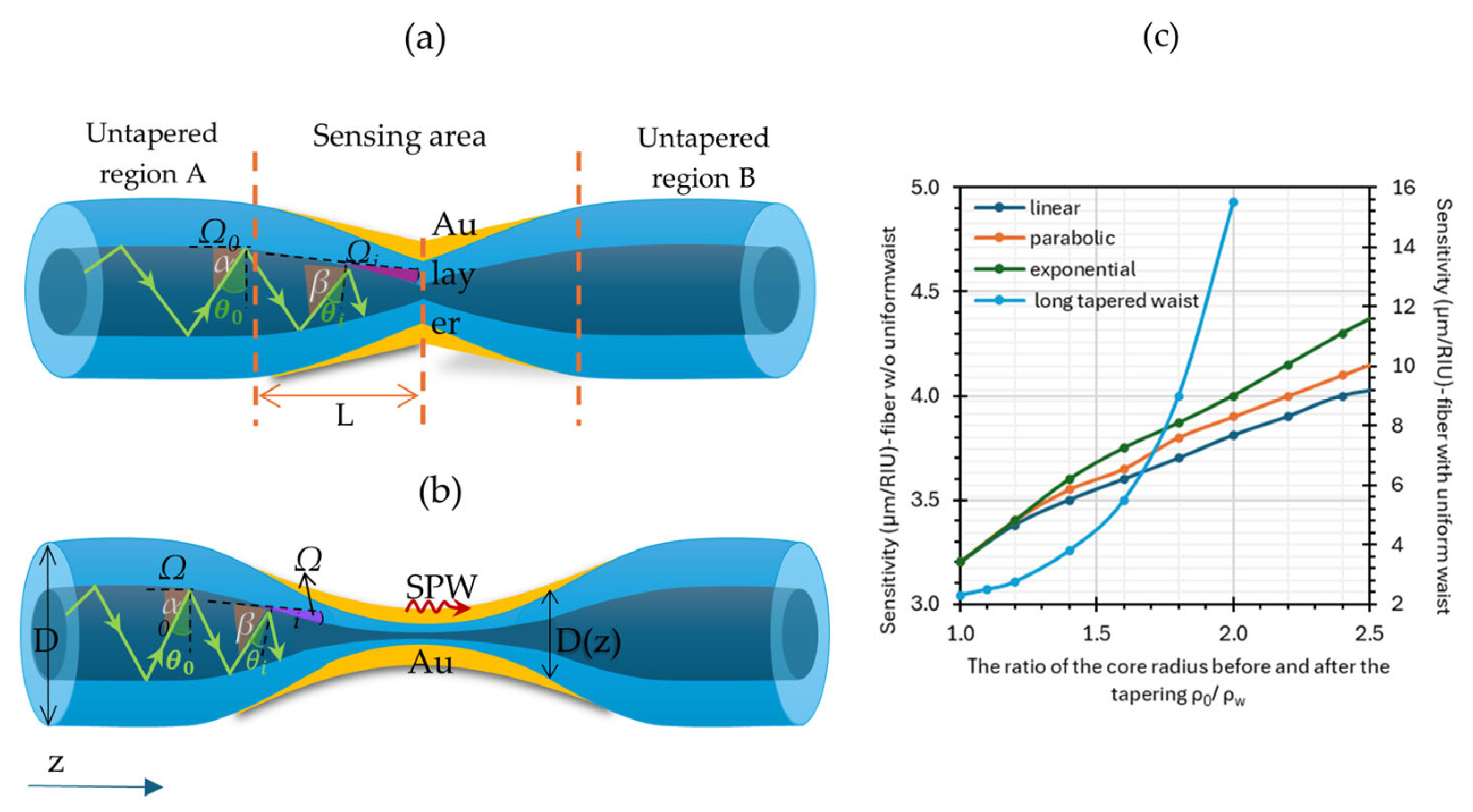
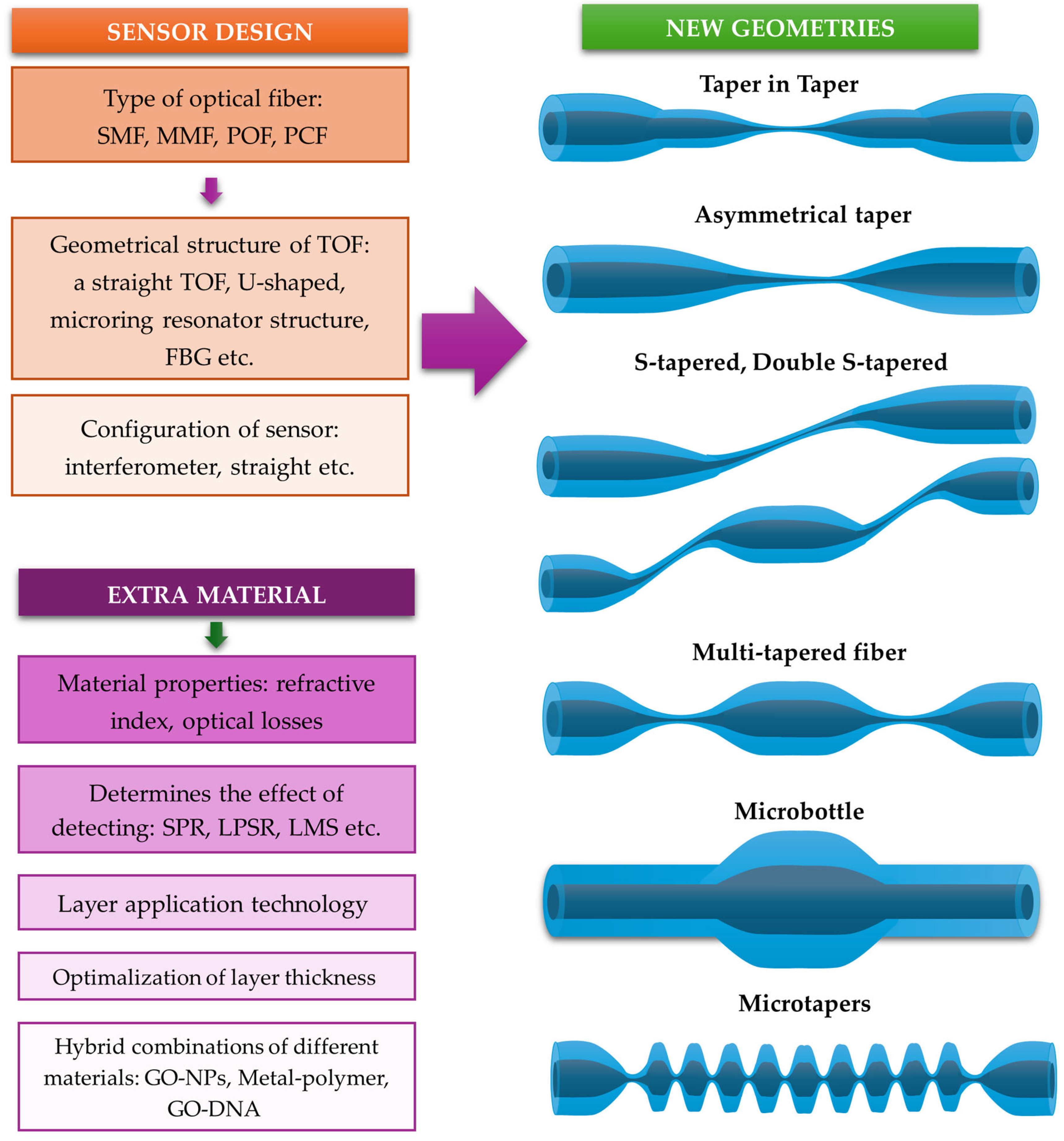
2.1. Fabrication of the TOF
2.2. EW and Sensory Properties of TOF
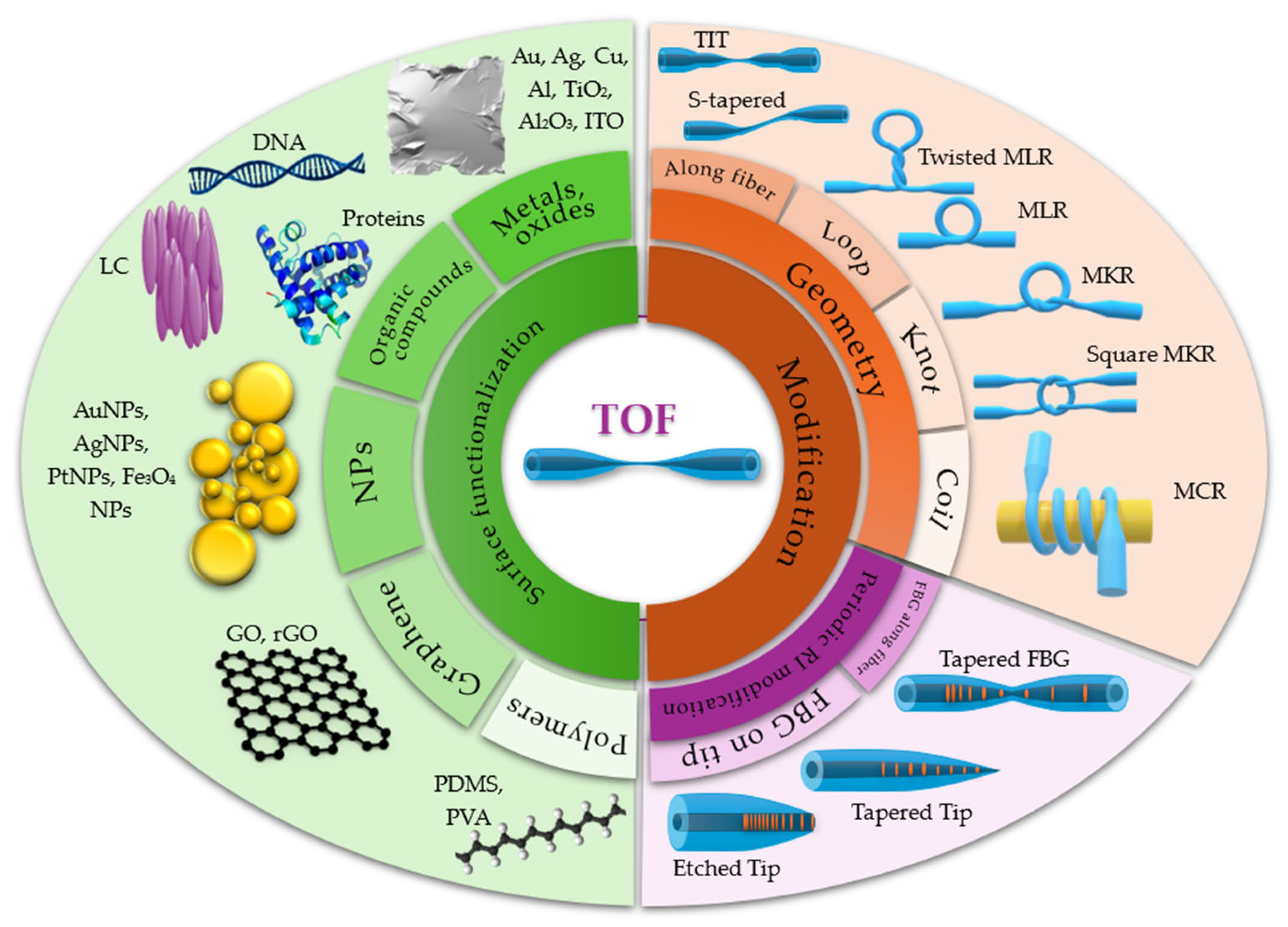
3. Overview of Selected Sensors Based on Microfibers
3.1. TOF Coated with Additional Functional Materials
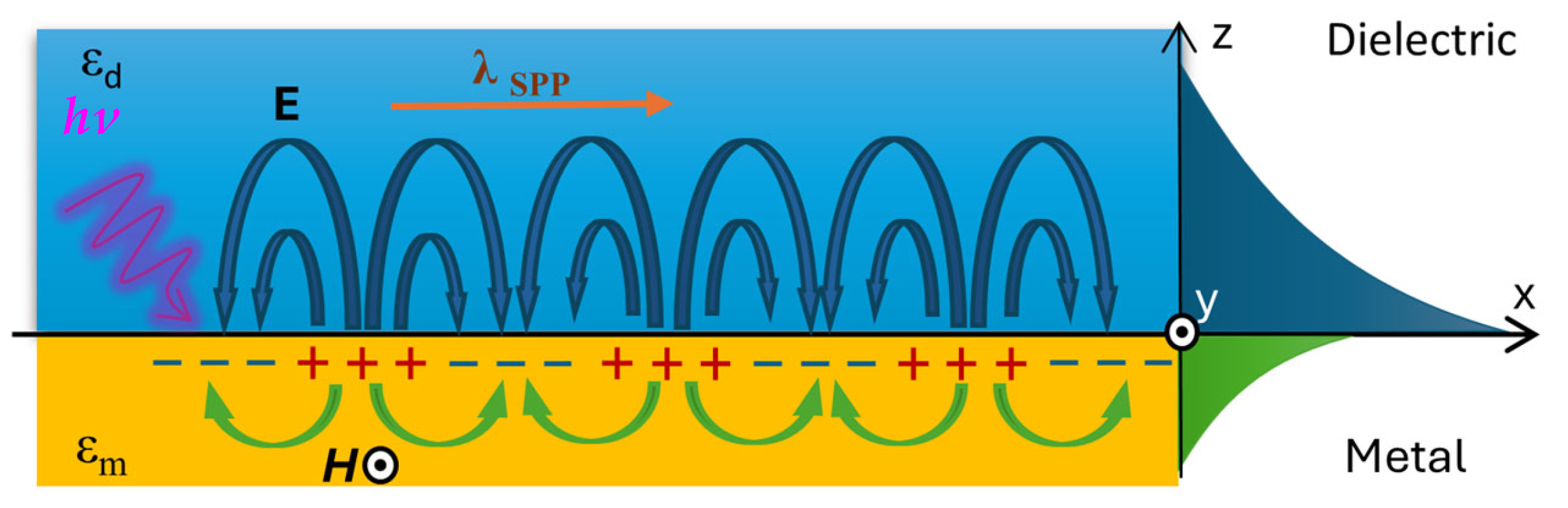
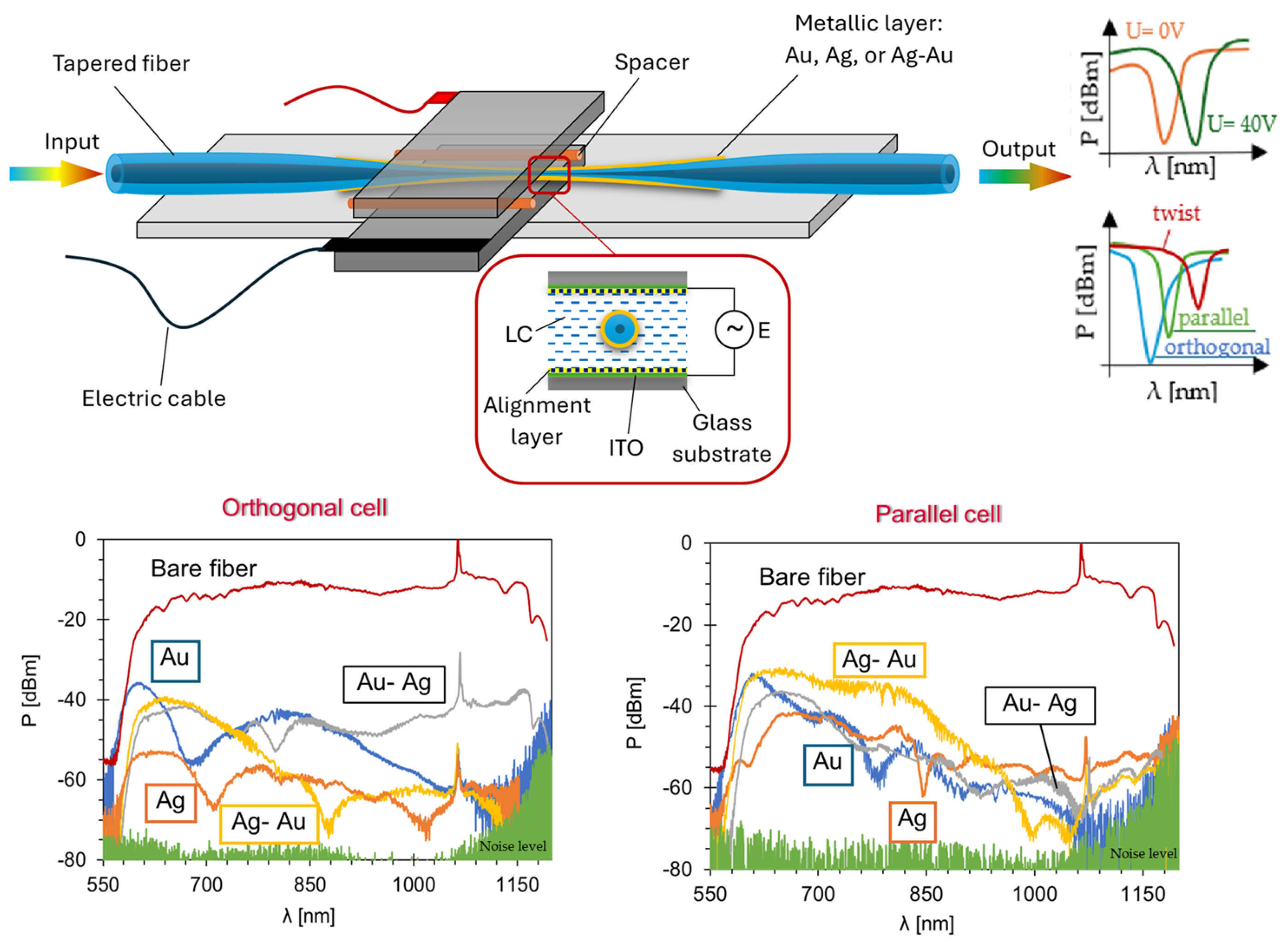
3.1.1. Metallic Layer Covers
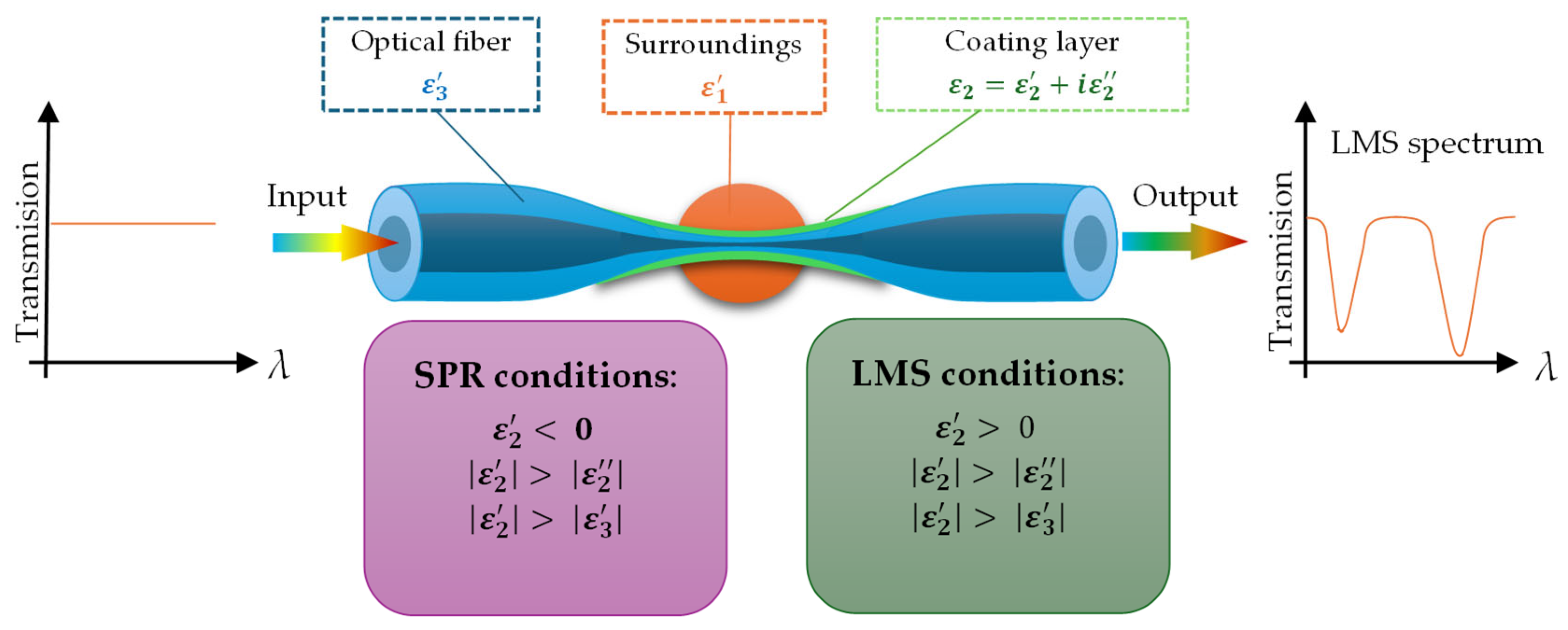
3.1.2. Oxide Coatings
- The permittivity value of the coating layer is higher than 0 (opposite to the SPR effect);
- The number of attenuation dips in LMR of more than one can be observed on the spectrum;
- LMS phenomena can be observed in a wide wavelength range—VIS and NIR;
- In the case of LMS, as the layer thickness increases, the number of dips and the wavelength range at which the effect can be observed increase;
- In comparison to SPR, where a film of metal is required, for LMS, a different material can be used, like polymers, oxides, or combinations of polymers and NPs;
- TM- and TE-polarized light can generate this effect in sensors.
3.1.3. Organic Compound Coatings
3.1.4. Polymeric Coatings
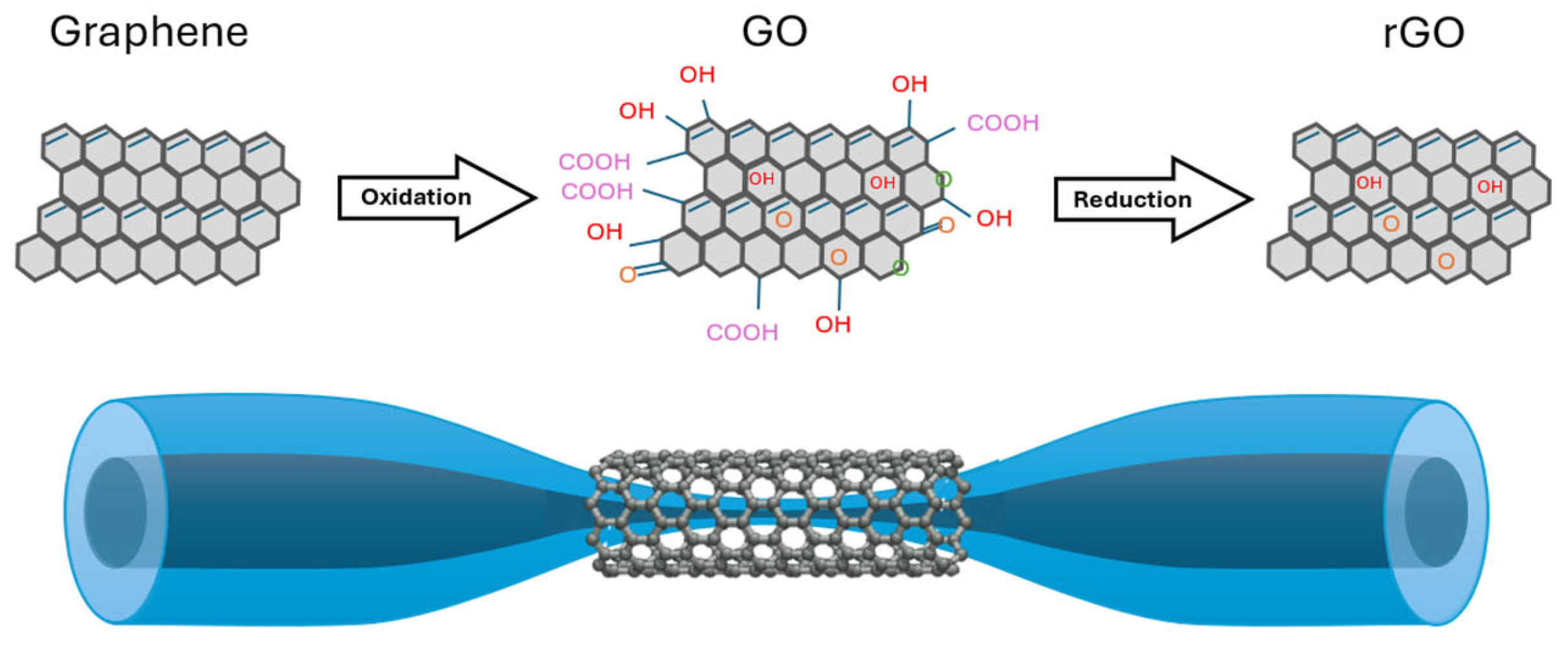
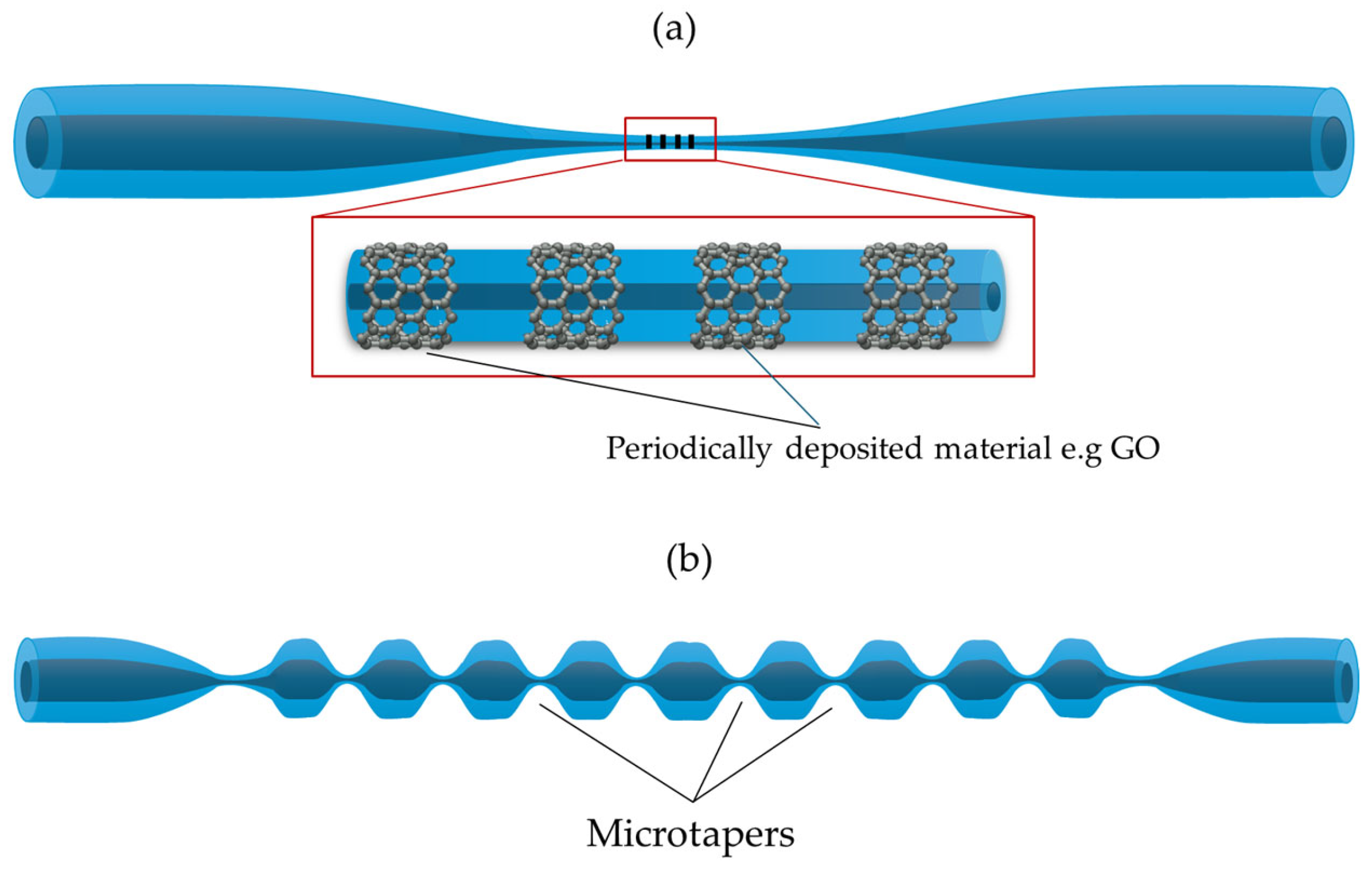
3.1.5. Graphene, Graphene Oxide, and Reduced Graphene Oxide Coatings
3.2. Loop, Knot, and Microcoil Sensors as Microring Resonators
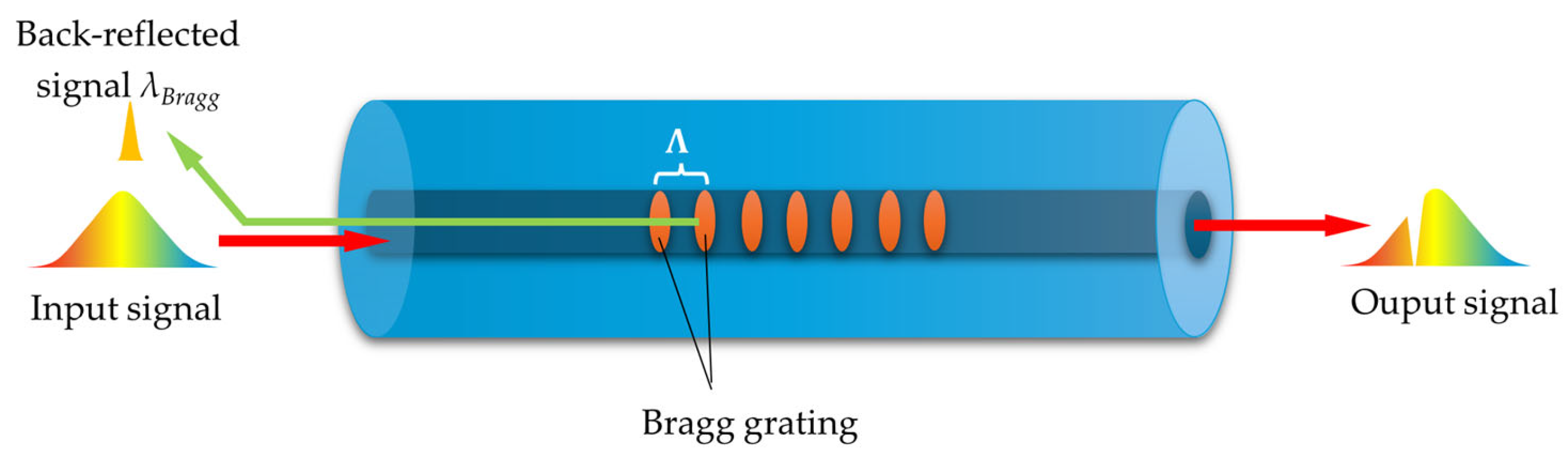
3.3. Fiber Bragg Gratings
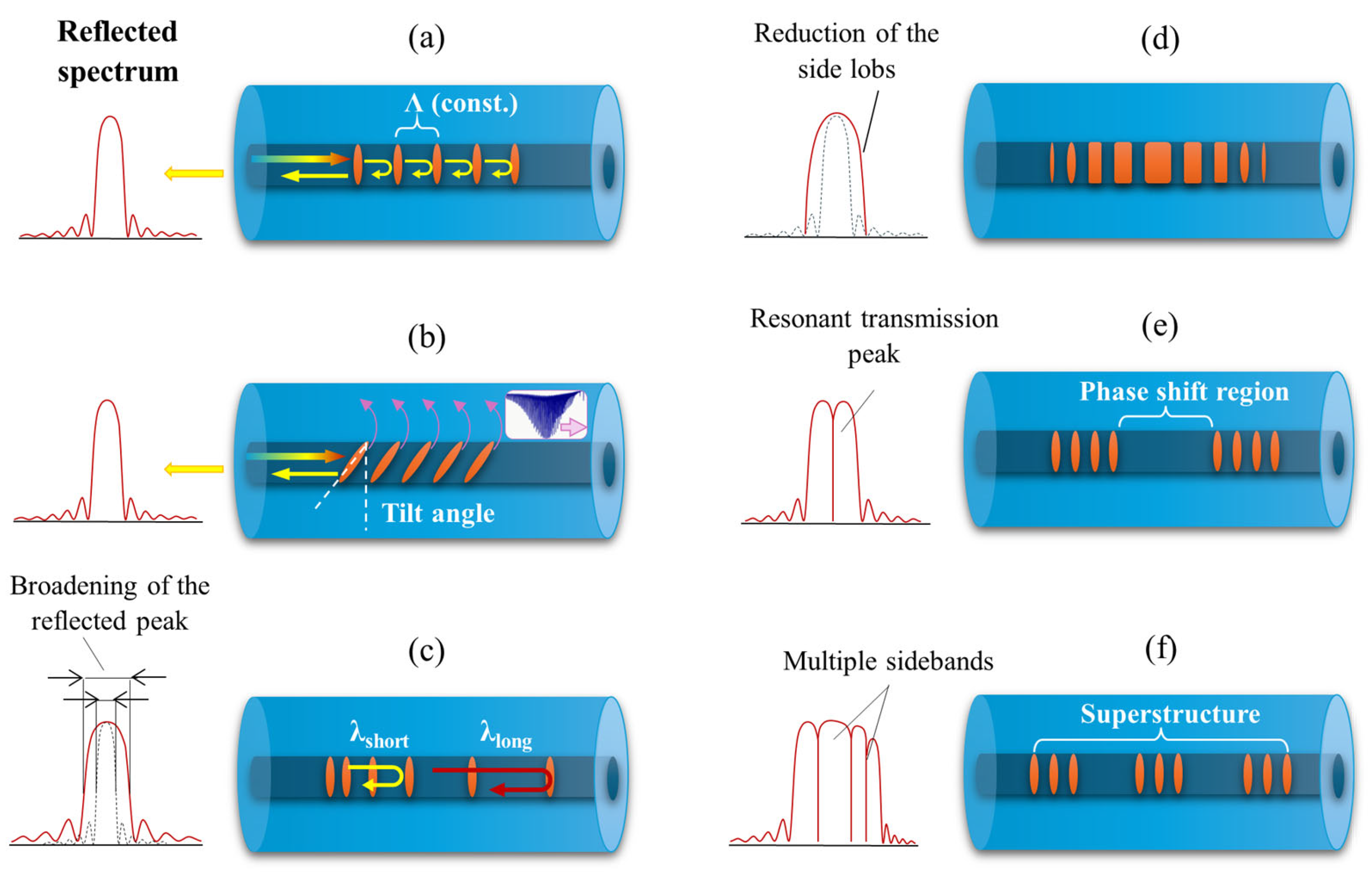
3.3.1. FBGs and LPGs
- Gratings with a constant period and perpendicular perturbation of the RI relative to the fiber axis (Figure 19a): However, such gratings may generate undesirable reflections at different wavelengths, which interfere with data transmission.
- Tilted where the RI perturbation is rotated by a certain angle θ, as shown in Figure 19b: Depending on the tilt angle of the grating, coupling of the core mode to several selected cladding modes may occur, which can lead to modifications in the position and shape of the reflected peak. This process can simultaneously significantly improve the resolution of the sensor [187].
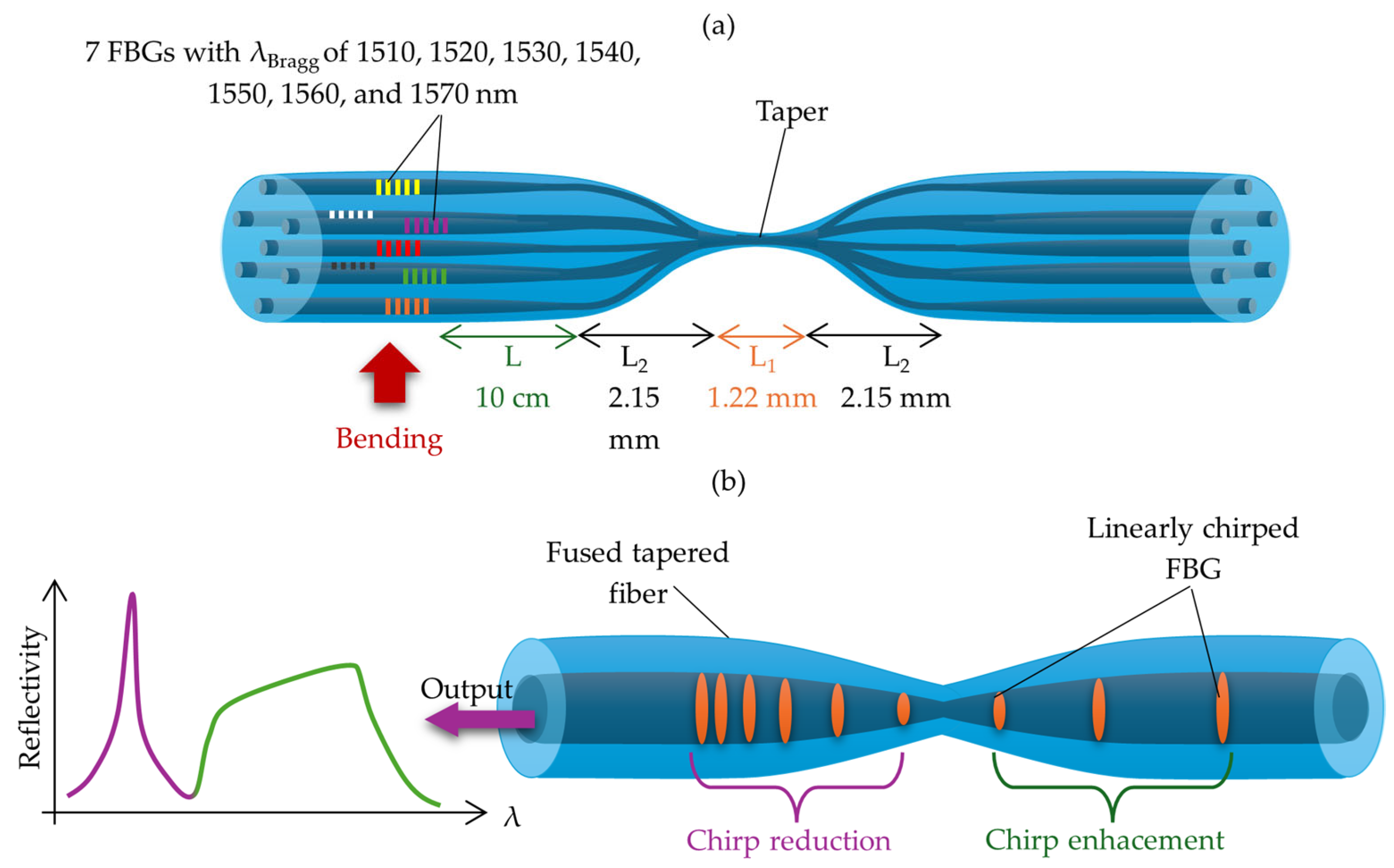
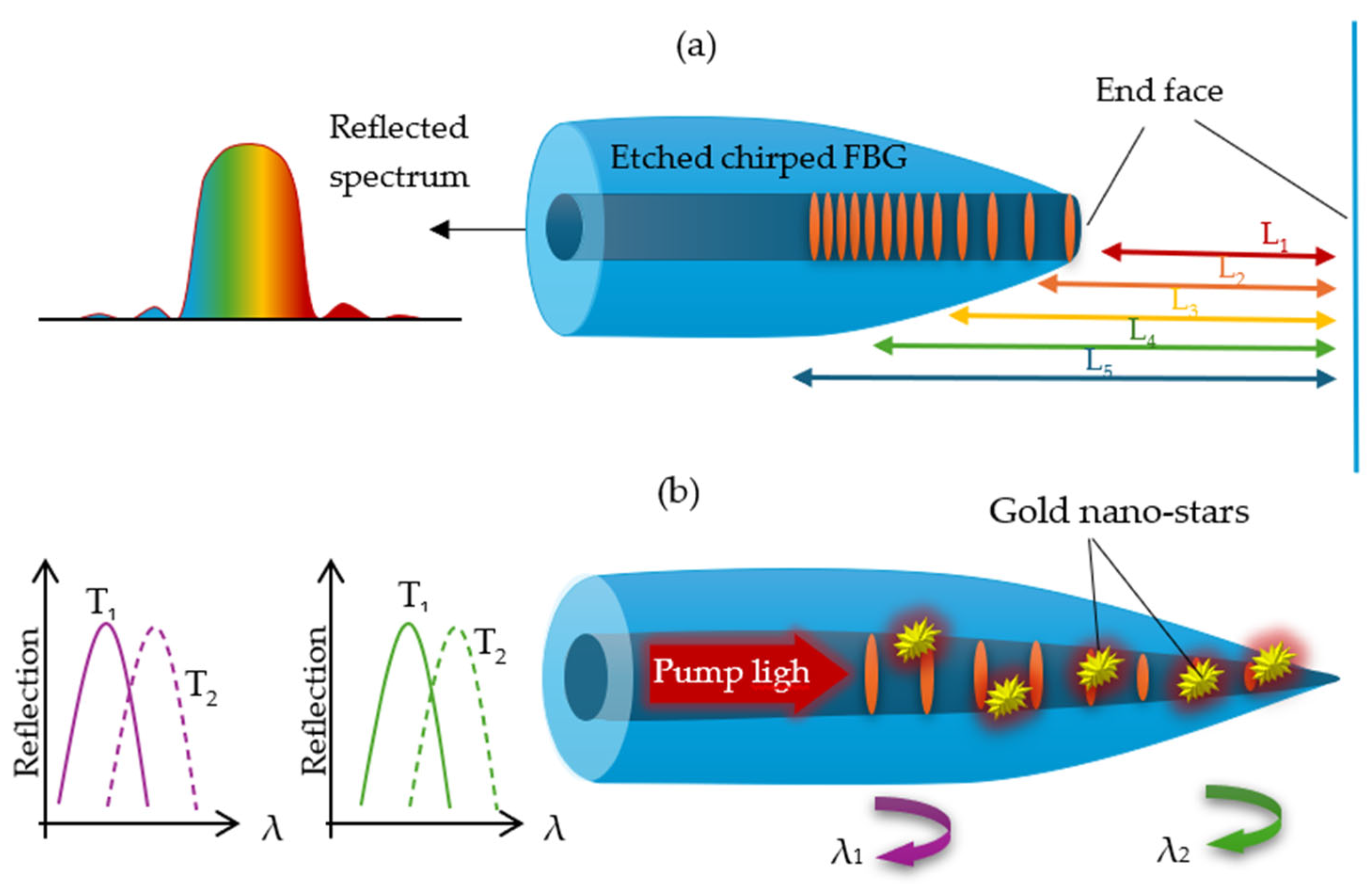
3.3.2. Tapered Fiber Bragg Gratings
4. Summary and Future Trends
- The TOF structure can be shaped by changing its dimensions and geometry;
- A variety of configuration sensors, like a straight TOF, TOFs as a part of interferometers, and TOFs with FBGs and LPGs, can be observed;
- More and more often, materials are combined in a hybrid form (two or three materials) to improve the parameters of the designed sensor;
- Depending on the coating material, different phenomena enable the detection of the measured parameter: SPR, LSPR, LMS, etc.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Dudek, M.; Kowalski, J.K.; Teisseyre, K. The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application. Sensors 2019, 19, 2699. [Google Scholar] [CrossRef]
- Gursel, A.T. Fiber Lasers and Their Medical Applications. In Optical Amplifiers—A Few Different Dimensions; IntechOpen: Rijeka, Croatia, 2018; pp. 83–113. [Google Scholar]
- Lee, C.M.; Engelbrecht, C.J.; Soper, T.D.; Helmchen, F.; Seibel, E.J. Scanning fiber endoscopy with highly flexible, 1-mm catheterscopes for wide-field, full-color imaging. Biophotonics 2010, 3, 385–407. [Google Scholar] [CrossRef] [PubMed]
- Wild, G.; Hinckley, S. Acousto-Ultrasonic Optical Fiber Sensors: Overview and State-of-the-Art. IEEE Sens. J. 2008, 8, 1184–1193. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, Y.; Wang, Z.; Yu, M.; Wu, C.; Chang, T.; Cui, H. Low-frequency fiber optic hydrophone based on weak value amplification. Opt. Express 2020, 28, 25935–25948. [Google Scholar] [CrossRef]
- Freitas, J. Recent developments in seismic seabed oil reservoir monitoring applications using fibre-optic sensing networks. Meas. Sci. 2011, 22, 052001. [Google Scholar] [CrossRef]
- Domański, A.W.; Lesiak; Milenko, K.; Budaszewski, D.; Chyłkowski, M.; Ertman, S.; Tefelska, M.; Woliński, T.R.; Jędrzejewski, K.; Lewandowski, L.; et al. Comparison of Bragg and Polarimetric Optical Fiber Sensors for Stress Monitoring in Composite Materials. Acta Phys. Pol. A 2009, 116, 294–297. [Google Scholar] [CrossRef]
- Badru, A.S. Optical Fibre Evanescent Field Techniques for Gas Detection; The University of Heriot-Watt and St Andrews University: Edinburgh, Scotland, 2008. [Google Scholar]
- Verma, R.K.; Gupta, D.B. Fiber optic SPR sensor for the detection of 3-pyridinecarboxamide (vitamin B3) using molecularly imprinted hydrogel. Sens. Actuators B Chem. 2013, 177, 279–285. [Google Scholar] [CrossRef]
- Gandhi, M.; Chu, S.; Senthilnathan, K.; Babu; Nakkeeran, K.; Li, Q. Recent Advances in Plasmonic Sensor-Based Fiber Optic Probes for Biological Applications. Appl. Sci. 2019, 9, 949. [Google Scholar] [CrossRef]
- Mitu, S.A.; Ahmed, K.; Zahrani, F.A.A.; Grover, A.; Rajan, M.S.M.; Moni, M.A. Development and analysis of surface plasmon resonance based refractive index sensor for pregnancy testing. Opt. Lasers Eng. 2021, 140, 106551. [Google Scholar] [CrossRef]
- Kosturek, R.; Wachowski, M.; Śnieżek, L.; Gloc, M. The influence of the post-weld heat treatment on the microstructure of inconel 625/carbon steel bimetal joint obtained by explosive weldin. Metals 2019, 9, 246. [Google Scholar] [CrossRef]
- Jinachandran, S.; Ning, Y.; Wu, B.; Li, H.; Xi, J.; Prusty, B.G.; Rajan, G. Cold Crack Monitoring and Localization in Welding Using Fiber Bragg Grating Sensors. IEEE Trans. Instrum. Meas. 2020, 69, 1557–9662. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, X.; Wang, L.; Lai, S.; Zhou, H.; Zhao, H.; Liao, Y. Progress of Optical Fiber Sensors and Its Application in Harsh Environment. Photonic Sens. 2011, 1, 84–89. [Google Scholar] [CrossRef][Green Version]
- Chen, J.H.; Li, D.R.; Xu, F. Optical microfiber sensors: Sensing mechanisms, and recent advances. J. Lightw. Technol. 2019, 37, 2577–2589. [Google Scholar] [CrossRef]
- Klantsataya, E.; Jia; Ebendorff-Heidepriem, H.; Monro, T.M.; François, A. Plasmonic Fiber Optic Refractometric Sensors: From Conventional Architectures to Recent Design Trends. Sensors 2017, 17, 12. [Google Scholar] [CrossRef]
- Cennamo, N.; Pesavento, M.; Arcadio, F.; Marzano, C.; Zeni, L. Advances in plastic optical fiber bio/chemical sensors to realize point-of-care-tests. TrAC Trends Anal. Chem. 2024, 177, 117797. [Google Scholar] [CrossRef]
- Zhong, X.; Xie, Q.; Liu, Y.; He, Y.; Zhong, N.; Zhang, Z.; Karimi-Maleh, H.; Peng, X.; Lichtfouse, E. Recent advances in optical fiber grating sensors for detection of organic substances. Chem. Eng. J. 2024, 492, 152260. [Google Scholar] [CrossRef]
- Maniewski, P.; Wörmann, T.J.; Pasiskevicius, V.; Holmes, C.; Gates, J.C.; Laurell, F. Advances in laser-based manufacturing techniques for specialty optical fiber. J. Am. Ceram. Soc. 2024, 107, 5143–5158. [Google Scholar] [CrossRef]
- Talataisong, W.; Brambilla, G.; Ismaeel, R. A Review of Microfiber-Based Temperature Sensors. Sensors 2018, 18, 461. [Google Scholar] [CrossRef]
- Joe, H.-E.; Yun, H.; Jo, S.-H.; Jun, M.B.G.; Min, B.-K. A review on Optical Fiber Sensors for Environmental Monitoring. Int. J. Precis. Eng. Manuf. Green Technol. 2018, 5, 173–191. [Google Scholar] [CrossRef]
- Tong, L.; Gattass, R.R.; Ashcom, J.B.; He, S.; Lou, J.; Shen, M.; Maxwell, I.; Mazur, E. Subwavelength-diameter silica wires. Nature 2003, 426, 816–819. [Google Scholar] [CrossRef]
- Briks, T.; Li, Y. The shape of fiber tapers. J. Light. Technol. 1992, 10, 432–438. [Google Scholar] [CrossRef]
- Grellier, A.; Zayer, N.; Pannell, C. Heat transfer modelling in CO2 laser processing of optical fibres. Opt. Commun. 1998, 152, 324–328. [Google Scholar] [CrossRef]
- Zhang, E.; Sacher, W.; Poon, J. Hydrofluoric acid flow etching of low-loss subwavelength-diameter biconical fiber tapers. Opt. Express 2010, 18, 22593–22598. [Google Scholar] [CrossRef]
- Orucevic, F.; Lef, V.; Hare, J. Transmittance and near-field characterization of sub-wavelength tapered optical fibers. Opt. Express 2007, 15, 13624–13629. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Chen, L.; Bao, X. Thermal and mechanical properties of tapered single mode fiber measured by OFDR and its application for high-sensitivity force measurement. Opt. Express 2012, 20, 14779–14788. [Google Scholar] [CrossRef]
- Xu, Y.; Fang, W.; Tong, L. Real-time control of micro/nanofiber waist diameter with ultrahigh accuracy and precision. Opt. Express 2017, 25, 10434–10440. [Google Scholar] [CrossRef]
- Jung, Y.; Brambilla, G.; Richardson, D.J. Broadband single-mode operation of standard optical fiber. Opt. Express 2008, 16, 14661–14667. [Google Scholar] [CrossRef]
- Yu, H.; Huang, Q.; Zhao, J. Fabrication of an Optical Fiber Micro-Sphere with a Diameter of Several Tens of Micrometers. Materials 2014, 7, 4878–4895. [Google Scholar] [CrossRef]
- Harun, S.W.; Lim, K.S.; Tio, C.K.; Dimyati, K.; Ahmed, H. Theoretical analysis and fabrication of tapered fiber. Optic 2013, 126, 538–543. [Google Scholar] [CrossRef]
- Teng, C.; Li, M.; Cheng, Y.; Peng, H.; Deng, S.; Deng, H.; Yuan, L.; Chen, M. Investigation of U-shape tapered plastic optical fibers based surface plasmon resonance sensor for RI sensing. Optik 2022, 251, 168461. [Google Scholar] [CrossRef]
- Mägi, E.; Steinvurzel; Eggleton, B. Tapered photonic crystal fibers. Opt. Express 2004, 12, 776–784. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, S.H.; Moghaddam, S.T. Optical microfiber loop resonator for gas pressure sensing. Phys. Open 2022, 13, 100118. [Google Scholar] [CrossRef]
- Wang, P.; Li, S.; Ling, F.; Farrell, G.; Lewis, E.; Yin, Y. All-optical modulator based on a microfibre coil resonator functionalized with MXene. Opt. Fiber Technol. 2022, 68, 102776. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, L.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Chirped fiber tip Fabry–Perot interferometer. Opt. Lett. 2017, 42, 3474–3477. [Google Scholar] [CrossRef]
- Jiang, Y.; Fang, Z.; Du, Y.; Lewis, E.; Farrell, G.; Wang, P. Highly sensitive temperature sensor using packaged optical microfiber coupler filled with liquids. Opt. Express 2018, 26, 356–366. [Google Scholar] [CrossRef]
- Zhu, S.; Pang, F.; Huang, S.; Zou, F.; Dong, Y.; Wang, T. High sensitivity refractive index sensor based on adiabatic tapered optical fiber deposited with nanofilm by ALD. Opt. Express 2015, 23, 13880–13888. [Google Scholar] [CrossRef]
- Yasin, M.; Irawati, N.; Isa, M.; Harun, S.; Ahmad, F. Graphene coated silica microfiber for highly sensitive magnesium sensor. Sens. Actuator A. Phys. 2018, 273, 67–71. [Google Scholar] [CrossRef]
- Leung, A.; Rijal, K.; Shankar, M.; Mutharasan, R. Effects of geometry on transmission and sensing potential of tapered fiber sensors. Biosens. Bioelectron. 2006, 21, 2202–2209. [Google Scholar] [CrossRef]
- Brambilla, G. Optical fibre nanowires and microwires: A review. J. Opt. 2010, 12, 043001. [Google Scholar] [CrossRef]
- Tong, L.; Lou, J.; Mazur, E. Single-mode guiding properties of subwavelength-diameter silica and silicon wire waveguides. Opt. Express 2004, 12, 1025–1035. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Z.; Pang, F.; Wang, T. Theoretical Analysis of Fiber-Optic Evanescent Wave Sensors. In Proceedings of the 2008 China-Japan Joint Microwave Conference, Shanghai, China, 10–12 September 2008; pp. 583–587. [Google Scholar]
- Li, J. A review: Development of novel fiber-optic platforms for bulk and surface refractive index sensing applications. Sens. Actuators Rep. 2020, 2, 1–14. [Google Scholar] [CrossRef]
- Gouveia, C.A.J.; Baptista, J.M.; Jorge, P. Refractometric Optical Fiber Platforms for Label Free Sensing. In Current Developments in Optical Fiber Technology, 1st ed.; InTech: London, UK, 2013; pp. 345–373. [Google Scholar]
- McCabe, S. An Investigation of Evanescent Wave Gas Sensing Zirconium Fluoride Optical Fibre. Ph.D. Thesis, Dublin City University, Dublin, Ireland, 1994. [Google Scholar]
- BGupta, D.; Singh, C.D. Evanescent-absorption coefficient for diffuse source illumination: Uniform- and tapered-fiber sensors. Appl. Opt. 1994, 33, 2737–2742. [Google Scholar]
- Elosua, C.; Arregui, F.; Del Villar, I.; Ruiz-Zamarreño, C.; Corres, J.; Bariain, C.; Goicoechea, J.; Hernaez, M.; Rivero; Socorro, A.; et al. Micro and Nanostructured Materials for the Development of Optical Fibre Sensors. Sensors 2017, 17, 2312. [Google Scholar] [CrossRef]
- Latifi, H.; Zibaii, M.; Hoseini, S.; Jorge, P. Nonadiabatic Tapered Optical Fiber for Biosensor Applications. Photonic Sens. 2012, 2, 340–356. [Google Scholar] [CrossRef]
- Jarzebinska, R.; Cheung, C.S.; James, S.W.; Ashwell, G.J.; Tatam, R. Response of the transmission spectrum of tapered optical fibres to the eposition of a nanostructured coating. In Proceedings of the SPIE 19th International Conference on Optical Fibre Sensors, Perth, WA, USA, 14 April 2008; p. 7004L. [Google Scholar]
- Ahmad, M.; Hench, L. Effect of taper geometries and launch angle on evenecsent wave penetration depth in optical fibers. Biosens. Bioelectron. 2005, 20, 1312–1319. [Google Scholar] [CrossRef]
- Corres, J.; Arregui, F.J.; Matias, I. Sensitivity optimization of tapered optical fiber humidity sensors by means of tuning the thickness of nanostructured sensitive coatings. Sens. Actuators B 2007, 122, 442–449. [Google Scholar] [CrossRef]
- Zhu, S.; Pang, F.; Wen, J.; Zhao, Z.; Wang, T. Temperature sensor nased on a tapered optical fiber with ALD nanofilm. Proc. SPIE 2005, 9634, 963474. [Google Scholar]
- Corres, J.; Bravo, J.; Matias, I.; Arregui, F. Nonadiabatic tapered single mode fiber coated with humidity sensitive nanofilms. IEEE Photonics Technol. Lett. 2006, 18, 935–937. [Google Scholar] [CrossRef]
- Pilla, P.; Malachovska, V.; Borriello, A.; Buosciolo, A.; Giordano, M.; Ambrosio, L.; Cutolo, A.; Cusano, A. Transitions mode long period grating biosensor with funkcional multilayer coatings. Opr. Express 2011, 19, 512–526. [Google Scholar] [CrossRef]
- Zubiate, P.; Zamarreño, C.R.; Del Villar, I.; Matias, I.R.; Arregui, F. Hight sensitive refractometers based on lossy mode resonance supported by ITO coated D-shape optical fibers. Opt. Express 2015, 23, 8045–8050. [Google Scholar] [CrossRef]
- Zhu, S.; Pang, F.; Huang, S.; Zou, F.; Guo, Q.; Wen, J.; Wang, T. High Sensitivity Refractometer Based on TiO2-Coated Adiabatic Tapered Optical Fiber via ALD Technology. Sensors 2016, 16, 1295. [Google Scholar] [CrossRef] [PubMed]
- Śmietana, M.; Mysliwiec, M.; Mikulic; Witkowski, B.; Bock, W. Capability for fine tuning of the refractive index sensing properties of long period gratings by atomic layer deposited Al2O3 overlaps. Sensors 2013, 13, 16372–16383. [Google Scholar] [CrossRef]
- Ritchie, R. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Zayts, A.V.; Smolyanionov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Maier, S.A. Chapter 1: Electromagnetics of Metals. In Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; pp. 5–19. [Google Scholar]
- Rifat, A.A.; Hasan, R.; Ahmed, R.; Miroshnichenko, E. Chapter 9 Microstructured Optical Fiber-Based Plasmonic Sensors. In Computational Photonic Sensors; Springer Nature: Berlin/Heidelberg, Germany, 2019; pp. 203–232. [Google Scholar]
- Novotny, L.; Hecht, B. Chapter 12: Surface plasmons. In Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2006; pp. 378–418. [Google Scholar]
- Gupta, B.D. Chapter 4 Surface Plasmon Resonance Based Fiber Optic Sensors. In Reviews in Plasmonics; Springer: Berlin/Heidelberg, Germany, 2010; p. 105. [Google Scholar]
- Hosoki, A.; Nishiyama, M.; Igawa, H.; Seki, A.; Watanabe, K.A. hydrogen curing effect on surface plasmon resonance fiber optic hydrogen sensors using an annealed Au/Ta2O5/Pd multi-layers film. Opt. Express 2014, 22, 18556–18563. [Google Scholar] [CrossRef]
- Ju, S.; Jeong, S.; Kim, Y.; Lee, S.-H.; Linganna, K.; Kim, C.; Han, W.-T. Effect of heat treatment of optical fiber incorporated with Au nano-particles on surface plasmon resonance. Opt. Mater. Express 2015, 5, 1440–1449. [Google Scholar] [CrossRef]
- Villuendas, F.; Pelayo, J. Optical fibre device for chemical seming based on surface plasmon excitridon. Sens. Actuators A Phys. 1990, 23, 1142–1145. [Google Scholar] [CrossRef]
- Jorgenson, R.; Yee, S. A fiber-optic chemical sensor based on surface plasmon resonance. Sens. Actuators B Chem. 1993, 12, 213–220. [Google Scholar] [CrossRef]
- Verma, R.K.; Sharma, A.K.; Gupta, B.D. Modeling of tapered fiber-optic surface plasmon resonance sensor with enhanced sensitivity. IEEE Photonics Technol. Lett. 2007, 19, 1786–1788. [Google Scholar] [CrossRef]
- Verma, R.K.; Sharma, A.K.; Gupta, B.D. Surface Plasmon Resonance based tapered fiber optic sensor with different taper profiles. Opt. Commun. 2008, 281, 1486–1491. [Google Scholar] [CrossRef]
- Popescu, A.; Baschir, L.; Savastru, D.; Stafe, M.; Vasile, G.; Miclos, S.; Negutu, C.; Mihaliesku, M.; Puscas, N. Analytical considerations and numerical simulations for surface plasmon resonance in four layers plasmonic structures which contain high refractive index waveguide. U.P.B. Sci. Bull. Ser. A 2015, 77, 233–244. [Google Scholar]
- Rosenblatt, G.; Simkhovich, B.; Bartal, G.; Orenstein, M. Nonmodal plasmonics: Controlling the forced optical response of nanostructures. Phys. Rev. 2020, 10, 011071. [Google Scholar] [CrossRef]
- Queiroz, I.; Melo, A.; Fernandes, F.; Fim, F.; Blair, S.; Mang, Y.; Moreira, C.; Cruz, R. Sensitivity enhancement of silver-based SPR sensors using ultrathin gold film and graphene overlay. In Proceedings of the Conference: 2020 IEEE International Instrumentation and Measurement Technology Conference, Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar]
- Mishra, K.S.; Gupta, B.D. Surface plasmon resonance based fiber optic pH sensor utilizing Ag/ITO/Al/hydrogel layers. Analyst 2013, 139, 2640. [Google Scholar] [CrossRef]
- Johnson, B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Xiong, K.; Tordera, D.; Emilsson, G.; Olsson, O.; Linderhed, U.; Jonsson, M.; Dahlin, A.B. Switchable Plasmonic Metasurfaces with High Chromaticity Containing Only Abundant Metals. Nano Lett. 2017, 11, 7033–7039. [Google Scholar] [CrossRef]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.; Meyer, S.P.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic films can easily be better: Rules and recipes. ACS Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef]
- Moreira, C.; Wang, Y.; Blair, S. Aluminum-Based Deep-Ultraviolet Surface Plasmon Resonance Sensor. Plasmonics 2020, 15, 1891–1901. [Google Scholar] [CrossRef]
- Werner, W.S.M.; Glantschnig, K.; Ambrosch-Draxl, C. Optical constants and inelastic electron-scattering data for 17 elemental metals. J. Phys. Chem. 2009, 38, 1013–1092. [Google Scholar] [CrossRef]
- García-Pardo, M.; Nieto-Pinero, E.; Petford-Long, A.; Serna, R.; Toudert, J. Active analog tuning of the phase of light in the visible regime by bismuth-based metamaterials. Nanophotonics 2020, 9, 1–12. [Google Scholar] [CrossRef]
- Johnson, B.; Christy, R.W. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Tittl, A.; Mai; Taubert, R.; Dregely, D.; Liu, N.; Giessen, H. Palladium-Based Plasmonic Perfect Absorber in the Visible Wavelength Range and Its Application to Hydrogen Sensing. Nano Lett. 2011, 11, 4366–4369. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Peng, Y.; Chen, X.; Zhang, S.; Zhao, Y. Optimization of tapered optical fiber sensor based on SPR for high sensitivity salinity measurement. Opt. Fiber Technol. 2023, 78, 103309. [Google Scholar] [CrossRef]
- Korec, J.; Stasiewicz, K.A.; Jaroszewicz, L.R.; Garbat, K. SPR Effect Controlled by an Electric Field in a Tapered Optical Fiber Surrounded by a Low Refractive Index Nematic Liquid Crystal. Materials 2020, 13, 4942. [Google Scholar] [CrossRef]
- Korec, J.; Stasiewicz, K.A.; Garbat, K.; Jaroszewicz, L.R. Enhancement of the SPR Effect in an Optical Fiber DeviceUtilizing a Thin Ag Layer and a 3092A Liquid Crystal Mixture. Molecules 2021, 26, 7553. [Google Scholar] [CrossRef]
- Korec, J.; Stasiewicz, K.A.; Jaroszewicz, L.R. SPR Sensor Based on a Tapered Optical Fiber with a Low Refractive Index Liquid Crystal Cladding and Bimetallic Ag–Au Layers. Sensors 2022, 22, 7192. [Google Scholar] [CrossRef]
- Alkhabet, M.M.; Girei, S.H.; Salih, H.K.; Thabit, R.; Issa, M.A.; Paiman, S.; Arsad, N.; Alresheedi, M.T.; Mahdi, M.A.; Yaacob, M.H. Room temperature operated hydrogen sensor using palladium coated on tapered optical fiber. Mater. Sci. Eng. B 2023, 287, 116092. [Google Scholar] [CrossRef]
- Peng, Y.; Qin, S.; Ye, Y.; Zhao, Y. Miniature fiber optic SPR high sensitivity humidity sensor based on coated polyvinyl alcohol film. Opt. Fiber Technol. 2024, 87, 103934. [Google Scholar] [CrossRef]
- Yang, X.; Guo, J.; Yang, F.; Yang, G.; Wu, Y.; Li, Z.; Liu, Y.; Yang, X.; Yao, J. Tapered optical fiber LRSPR biosensor based on gold nanoparticle amplification for label-free BSA detection. Sens. Actuators B Chem. 2025, 426, 136986. [Google Scholar] [CrossRef]
- Borjikhani, P.; Granpayeh, N.; Zibaii, M.I. High sensitivity tapered fiber refractive index biosensor using hollow gold nanoparticles. Sci. Rep. 2025, 15, 1458. [Google Scholar] [CrossRef]
- Kharissova, O.V.; Montano Gonzalez, G.A.; Madrid Rodarte, S.C.; Rico Mendez, M.; Aguilar, R.S. Tapered optical fiber sensor coated with carbon nanotubes containing functional groups or Fe nanoparticles for sensing applications. Nano-Struct. Nano-Objects 2024, 38, 101144. [Google Scholar] [CrossRef]
- Singh, S.; Mishra, S.K.; Gupta, B.D. Sensitivity enhancement of a surface plasmon resonance based fibre optic refractive index sensor utilizing an additional layer of oxides. Sens. Actuators A Phys. 2013, 193, 136–140. [Google Scholar] [CrossRef]
- Rani, M.; Sharma, N.K.; Salaj, V. Surface plasmon resonance based fiber optic sensor utilizing indium oxide. Optik 2013, 124, 5034–5038. [Google Scholar] [CrossRef]
- Socorro, A.; Del Villar, I.; Corres, J.; Matias, I.; Arregui, F. Lossy mode resonance dependence on the geometry of a taperedmonomode optical fiber. Sens. Actuators A Phys. 2012, 180, 25–31. [Google Scholar] [CrossRef]
- Gaur, D.S.; Purohit, A.; Mishra, S.K.; Mishra, A.K. An Interplay between Lossy Mode Resonance and Surface Plasmon Resonance and Their Sensing Applications. Biosensors 2022, 12, 721. [Google Scholar] [CrossRef]
- Vikas, V.; Mishra, S.K.; Mishra, A.K.; Saccomandi; Verma, R.K. Recent Advances in Lossy Mode Resonance—Based Fiber Optic Sensors: A Review. Micromachines 2022, 13, 1921. [Google Scholar] [CrossRef]
- Kischkat, J.; Peteres, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride. Appl. Opt. 2012, 51, 6789–6798. [Google Scholar] [CrossRef]
- Shah, K.; Sharma, N.K.; Sajal, V. SPR based fiber optic sensor with bi layers of indium tin oxide and platinum: A theoretical evaluation. Optik 2017, 135, 20–56. [Google Scholar] [CrossRef]
- Hagemann, H.J.; Gudat, W.; Kunz, C. Optical constants from the far infrared to the x-ray region: Mg, Al, Cu, Ag, Au, Bi, C, and Al2O3. J. Opt. Soc. Am. 1975, 65, 742–744. [Google Scholar] [CrossRef]
- Ascorbe, J.; Arregui, F.; Corres, J.; Matias, I. Optical Fiber Humidity Sensor Based on a Tapered optical fiber Asymmetrically coated with Indum Tin Oxide. In Proceedings of the IEEE Sensors, Valencia, Spain, 2–5 November 2014. [Google Scholar]
- Tiwari, D.; Mullaney, K.; Korposh, S.; James, S. Ammonia sensing using lossy mode resonance in a tapered optical fiber coated wth porphyrin-incorporated titanium dioxide. Proc. of SPIE 2016, 9916, 99161H-1-4. [Google Scholar]
- Vikas; Verma, R.K. Sensitivity enhancement of a lossy mode resonance based tapered fiber optic sensor with an optimum taper profile. J. Phys. D Appl. Phys. 2018, 51, 415302. [Google Scholar] [CrossRef]
- Akmar, N.; Yahyaa, M.; Rash, M.; Hamidc, Y.; Ibrahim, S.; Ongc, B.; Rahmanb, N.; Zainf, A.M.; Mahdia, M.; Yaacob, M. H2sensor based on tapered optical fiber coated with MnO2nanostructure. Sens. Actuators B Chem. 2017, 246, 421–427. [Google Scholar]
- Wang, Q.; Li, X.; Zhao, W.-M.; Jin, S. Lossy mode resonance-based fiber optic sensor using layer-by-layer SnO2 thin film and SnO2 nanoparticles. Appl. Surf. Sci. 2019, 492, 374–381. [Google Scholar] [CrossRef]
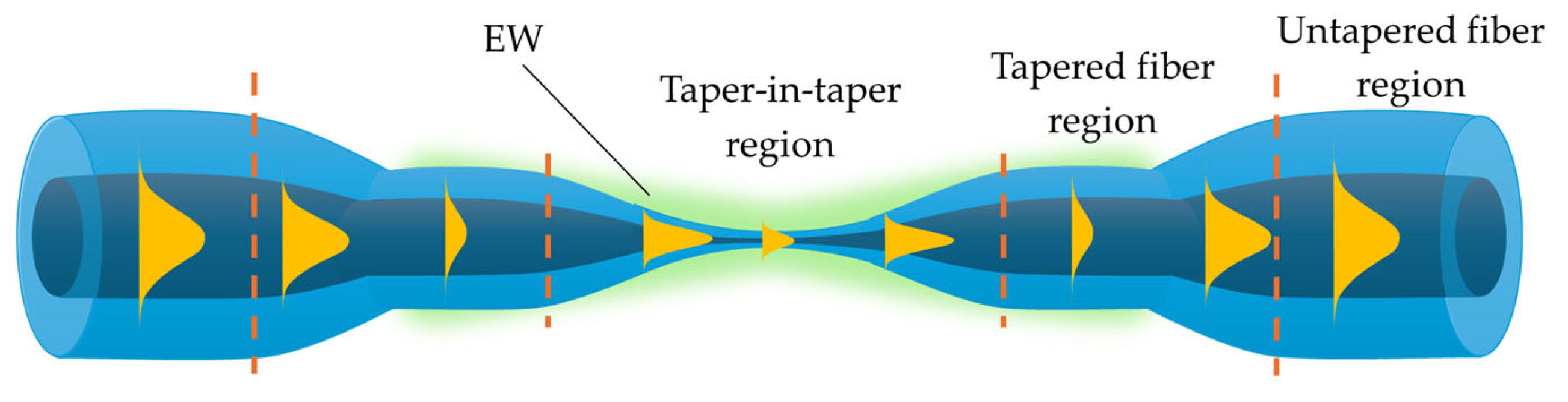
- Liu, F.; Zhang, W.; Lang, X.; Liu, X.; Singh, R.; Li, G.; Xie, Y.; Zhang, B.; Kumar, S. Development of Taper-in-Taper-Based Optical Fiber Sensors forChemical and Biological Sensing. Photonics 2023, 10, 567. [Google Scholar] [CrossRef]
- Wang, Z.; Singh, R.; Marques, C.; Jha, R.; Zhang, B.; Kumar, S. Taper-in-taper fiber structure-based LSPR sensor for alanine aminotransferase detection. Opt. Express 2021, 29, 43793–43810. [Google Scholar] [CrossRef]
- Liu, H.; Miao, Y.; Liu, B.; Lin, W.; Zhang, H.; Song, B.; Huang, M.; Lin, L. Relative Humidity Sensor Based on S-Taper Fiber Coated With SiO2 Nanoparticles. IEEE Sens. J. 2015, 15, 3424–3428. [Google Scholar] [CrossRef]
- Jarzebinska, R.; Korposh, S.; James, S.; Batty, W.; Tatam, R.; Lee, S.-W. Optical Gas Sensor Fabrication Based on Porphyrin-Anchored Electrostatic Self-Assembly onto Tapered Optical Fibers. Anal. Lett. 2012, 45, 1297–1309. [Google Scholar] [CrossRef]
- Tiwari, D.; Mullaney, K.; Korposh, S.; James, S.; Lee, S. Ammoniasensingusinglossymode resonances in a tapered optical fibre coated with porphyrin-incorporated titanium dioxide. In Proceedings of the Sixth European Workshop on Optical Fibre Sensors. International Society for Optics and Photonics, Limerick, Ireland, 31 May–3 June 2016; Volume 9916. [Google Scholar]
- Wang, Z.; Ma, H.; Yang, X.; Copner, N.; Jiang, Y.; Li, K. Ethanol sensor based on cascaded tapered optical fiber with surface modification of ZIF-8. Sens. Actuators B Chem. 2023, 402, 135084. [Google Scholar] [CrossRef]
- Zainuddin, N.; Chee, H.; Ahmad, M.M.; Mahdi, M.; Bakar, M.A.; Yaacob, M. Sensitive Leptospira DNA detection using tapered optical fiber sensor. J. Biophotonics 2018, 11, e201700363. [Google Scholar] [CrossRef]
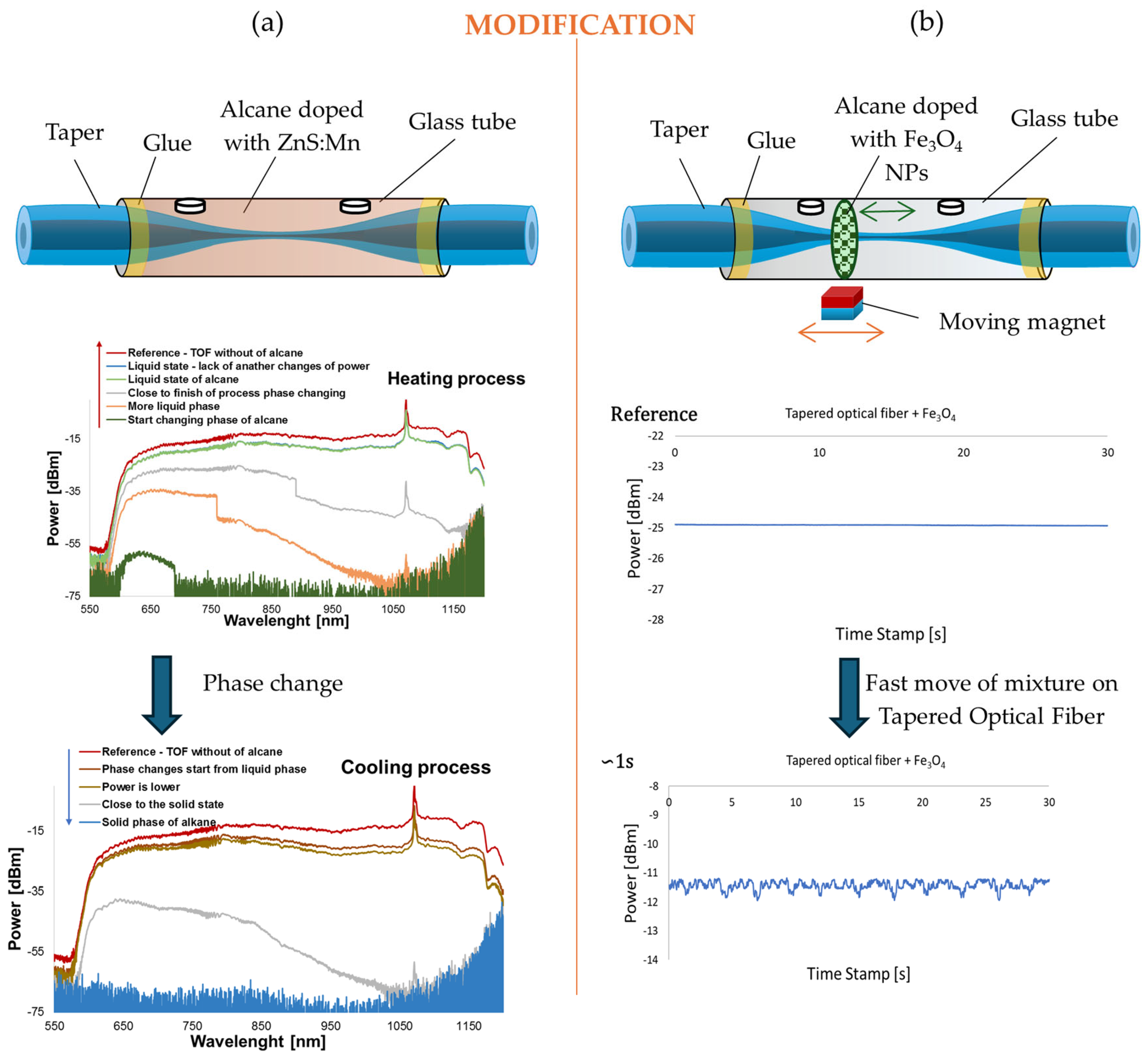
- Moś, J.E.; Stasiewicz, K.A.; Matras-Postołek, K.; Jaroszewicz, L.R. Thermo-Optical Switching Effect Based on a Tapered Optical Fiber and Higher Alkanes Doped with ZnS:Mn. Materials 2020, 13, 5044. [Google Scholar] [CrossRef]
- Stasiewicz, K.A.; Jakubowska, I.; Moś, J.E.; Marć; Paczesny, J.; Zbonikowski, R.; Jaroszewicz, L.R. Optical Properties of a Tapered Optical Fiber Coated with Alkanes Doped with Fe3O4 Nanoparticles. Sensors 2022, 22, 7801. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski, R.S.; Garbat, K.; Urban, S.; Woliński, T.R.; Dziaduszek, J.; Ogrodnik, T.; Siarkowska, A. Low-birefringence liquid crystal mixtures for photonic liquid crystal fibres application. Liq. Cryst. 2017, 44, 1911–1928. [Google Scholar] [CrossRef]
- Niewczas, M.; Stasiewicz, K.A.; Przybysz, N.; Pakuła, A.; Paczesny, J.; Zbonikowski, R.; Dziaduszek, J.; Kula; Jaroszewicz, L.R. Technology and research on the influence of liquid crystal cladding doped with magnetic Fe3O4 nanoparticles on light propagation in an optical taper sensor. Adv. Opt. Technol. 2024, 13, 1422695. [Google Scholar] [CrossRef]
- Moś, J.E.; Stasiewicz, K.A.; Jaroszewicz, L.R. Investigation of transmission properties of a tapered optical fibre with gold. Optoelectron. Rev. 2022, 30, e143936. [Google Scholar]
- Jakubowska, I.; Marć; Popiel, S.; Chruściel, M.; Stasiewicz, K.A.; Jaroszewicz, L.R. Photopolymer coating of tapered optical fiber for chemical sensors. Proc. SPIE 2019, 11199, 1119910. [Google Scholar]
- Li, T.; Dong, X.; Chan, C.; Zhao, C.; Zu, P. Humidity Sensor Based on a Multimode Fiber Taper Coated with Polyvinyl Alcohol Interacting with a Fiber Bragg Gratings. IEEE Sens. J. 2012, 12, 2205–2208. [Google Scholar] [CrossRef]
- Dai, X.; Ding, H.; Blanchetiere, C.; Mihailov, S. Chemical and Pressure Sensors Using Tapered Optical Fiber with Polymer Layer. Proc. of SPIE 2012, 8412G, 8412. [Google Scholar]
- Socorro, A.; Del Villar, I.; Corres, J.; Arregui, J.; Matias, I. Spectral width reduction in lossy mode resonance-based sensors by means of tapered optical fibre structures. Sens. Actuators B Chem. 2014, 200, 53–60. [Google Scholar] [CrossRef]
- Wang, Z.; Kong, L.; Chen, T.; Zhao, R.; Liua, Y.; Xie, Q.; He, Y.; Tang, H.; Wu, L.; Lai, D.; et al. Tapered optical fiber evanescent wave sensor for accurate in-situ detection of paper moisture content. Sens. Actuators B Chem. 2025, 426, 137119. [Google Scholar] [CrossRef]
- Stasiewicz, K.A.; Berski, W.; Jakubowska, I.; Kowerdziej, R.; Węgłowska, D.; Spadło, A. The Biopolymer Active Surface for Optical Fibre Sensors. Polymers 2024, 16, 2114. [Google Scholar] [CrossRef]
- Wang, W.; Jin, L.; Shi, G.; Xu, Z.; Guo, Y.; Yang, B.; Yang, Y.; Wu, J.; Suna, D.; Ma, J. Flexible wearable optical microfiber sensor for identifying bending direction and body temperature. Opt. Laser Technol. 2024, 179, 111281. [Google Scholar] [CrossRef]
- Li, F.; Su, X.; Mo, H.; Chen, Y.; Cao, J.; Dong, C.; Fang, Y.; Liu, C. Highly sensitive temperature sensor using femtosecond laser direct writing tapered fiber and coated with PDMS. Opt. Mater. 2024, 159, 116545. [Google Scholar] [CrossRef]
- Dai, P.; Cong, Z.; Sun, Y.; Yan, W.; Chen, P.; Wang, X.; Jiang, C. Bio-inspired flexible optical microfiber sensor with nanohemisphere array microstructure for ultra-sensitive detection of skin signals. Measurement 2024, 235, 114874. [Google Scholar] [CrossRef]
- Castrellon-Uribe, J.; Medina-Cabrera, J.J.; Soto-Robles, M.C.; Sandoval-Espino, J.A.; Nuñez-Gómez, R.E. Tapered Optical Fiber Coated With a Polyester Polymer as a Curvature Sensor. IEEE Photonics Technol. Lett. 2024, 36, 1281–1284. [Google Scholar] [CrossRef]
- Gong, Z.; Lei, Y.; Wang, Z.; Zhang, J.; Sun, Z.; Li, Y.; Huang, J.; Chan, C.; Ouyang, X. A Taper-in-Taper Structured Interferometric Optical Fiber Sensor for Cu2+ ion Detection. Sensors 2022, 22, 2709. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, A.; Li, T.; Dai, S.; Gan, N. An evanescent waves sensor based on polydopamine-gold coated chalcogenide tapered fiber for enzyme activity profiling. Infrared Phys. Technol. 2024, 141, 105469. [Google Scholar] [CrossRef]
- Chen, N.; Zhou, X.; Li, X. Highly Sensitive Humidity Sensor With Low-Temperature Cross-Sensitivity Based on a Polyvinyl Alcohol Coating Tapered Fiber. IEEE Trans. Instrum. Meas. 2020, 70, 3034154. [Google Scholar] [CrossRef]
- Girei, S.H.; Shabaneh, A.A.; Ngee-Lim, H.; Hamidon, M.N.; Mahdi, M.A.; Yaacob, M.H. Tapered optical fiber coated with graphene based nanomaterials for measurement of etanol concentrations in water. Opt. Rev. 2015, 22, 385–392. [Google Scholar] [CrossRef]
- Wang, S.; Feng, M.; Wu, S.; Wang, Q.; Zhang, L. Highly Sensitive Temperature Sensor Based on Gain Competition Mechanism Using Graphene Coated Microfiber. IEEE Photonics J. 2018, 10, 6802008. [Google Scholar] [CrossRef]
- Liu, Z.; Navik, R.; Tan, H.; Xiang, Q.; Wahyudiono; Goto, M.; Ibarra, R.M.; Zhao, Y. Graphene-based materials prepared by supercritical fluid technology and its application in energy storage. J. Supercrit. Fluids 2022, 188, 105672. [Google Scholar] [CrossRef]
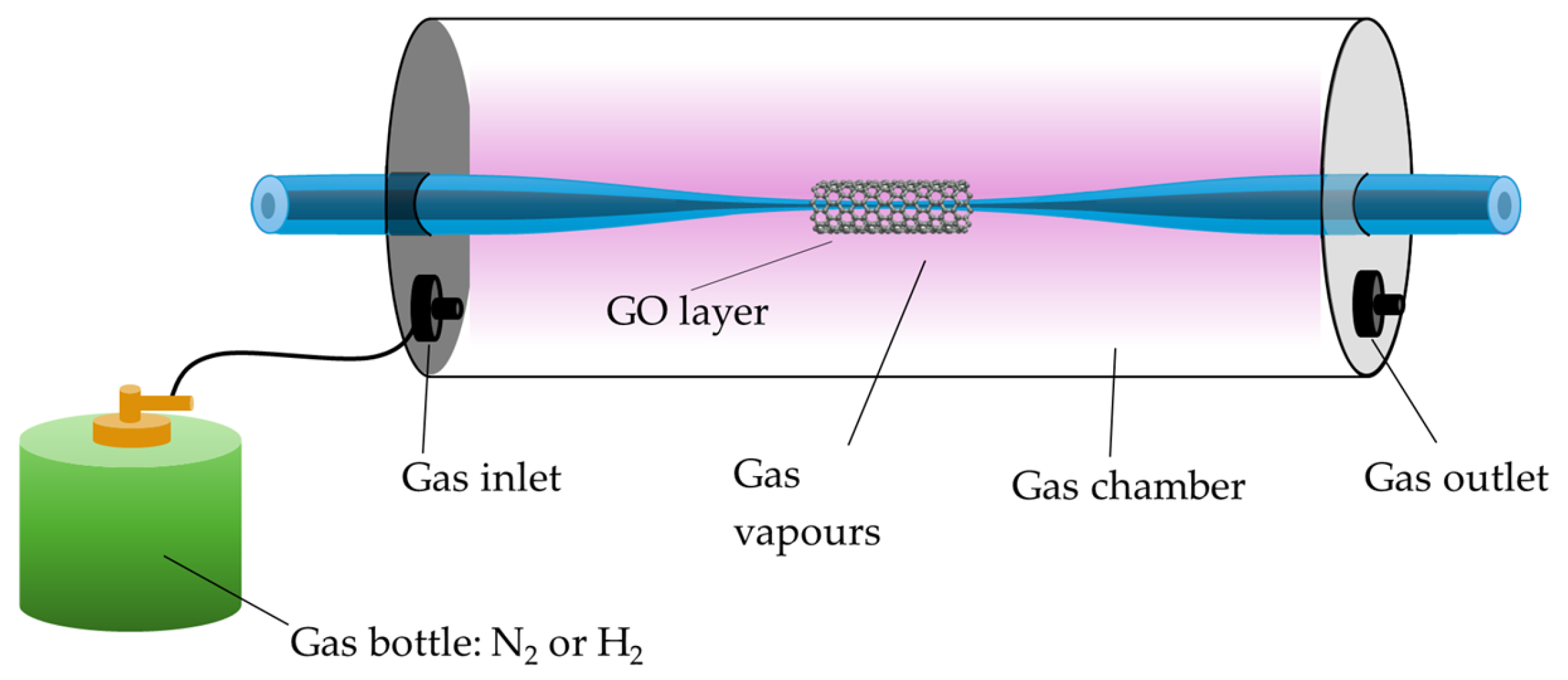
- Stasiewicz, K.A.; Jakubowska, I.; Moś, J.E.; Kosturek, R.; Kowiorski, K. In-Line Gas Sensor Based on the Optical Fiber Taper Technology with a Graphene Oxide Layer. Electronics 2023, 12, 830. [Google Scholar] [CrossRef]
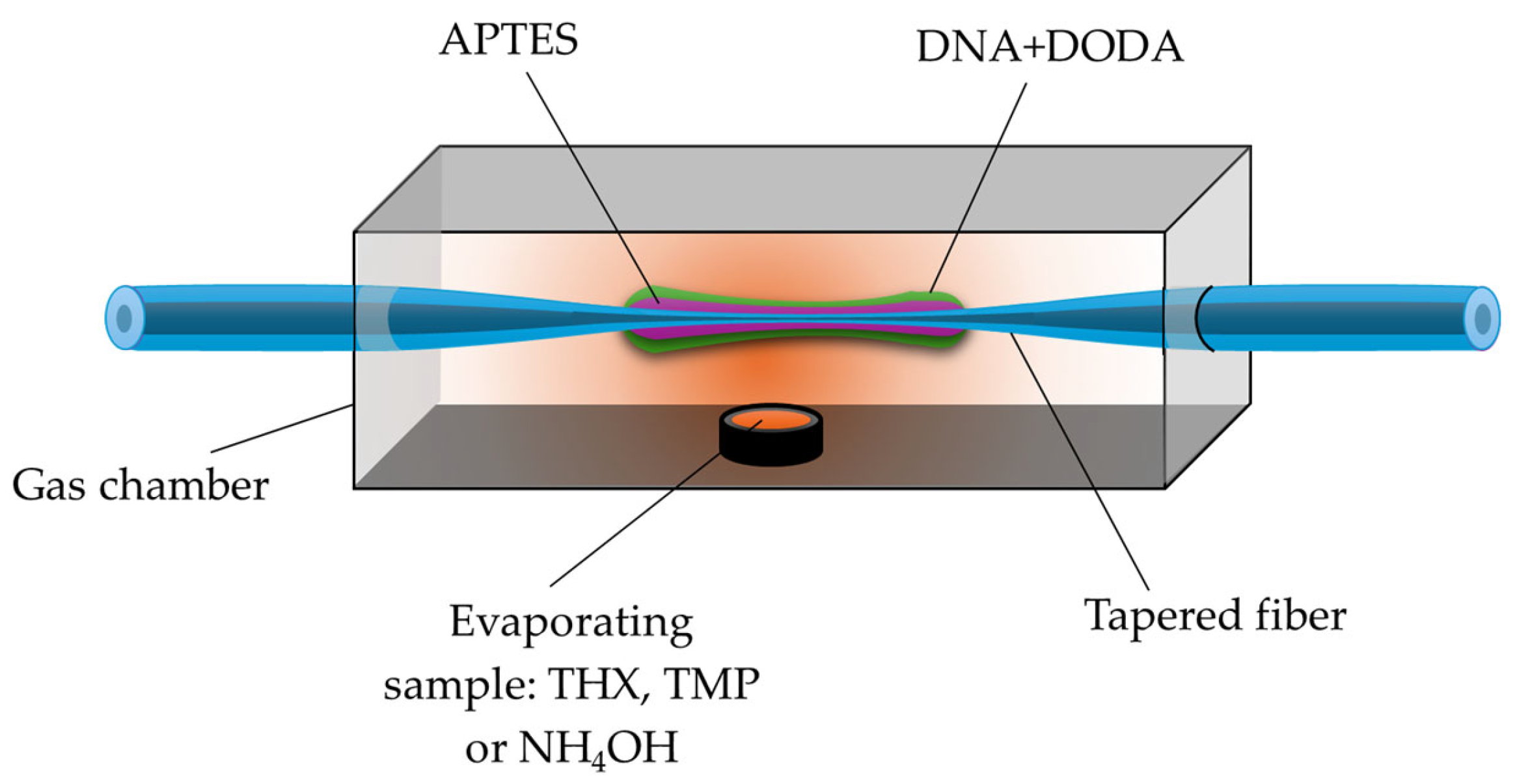
- Krawczyk, J.; Korec-Kosturek, J.; Kosturek, R.; Jakubowska, I.; Pakuła, A.; Djas, M.; Kowiorski, K.; Stasiewicz, K.A. Use of graphene oxide as an active layer on a tapered fibre for detection of volatile liquid vapours: Ammonium hydroxide, trimethyl phosphate, and 1,4-thioxane. Opto-Electron. Rev. 2025, 33, 1–8. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Dai, S. Chalcogenide glass-tapered fiber sensor modified by graphene oxide doped with platinum nanoparticles for high-sensitivity measurement. Results Phys. 2023, 47, 106348. [Google Scholar] [CrossRef]
- Wang, B.; Liu, S.; Gao, M.; Li, Y.; Yang, H.; Sun, C.I.; Guo, Q.; Yu, Y. A highly sensitive tapered fiber biosensor modified by PDMS combustion product and graphene oxide for MUC1 detection. Sens. Actuators Rep. 2025, 9, 100287. [Google Scholar] [CrossRef]
- Hernaez, M.; Mayes, A.G.; Melendi-Espina, S. Lossy Mode Resonance Generation by Graphene Oxide Coatings Onto Cladding-Removed Multimode Optical Fiber. IEEE Sens. J. 2019, 18, 6187–6192. [Google Scholar] [CrossRef]
- Syuhada, A.; Daud, S.; Aziz, M.S. Nonadiabatic Tapered Optical Fiber with GO/PVA Nanostructured Sensitive Coating for Humidity Sensing Application. Int. Laser Technol. Opt. Symp. 2019 2020, 1484, 012016. [Google Scholar] [CrossRef]
- Bakhshi, A.; Jalaly, M.; Vahedi, M. The effect of GO–Fe3O4 hybrid coating on the magnetic field detection by a tapered optical fiber sensor. Opt. Fiber Technol. 2022, 74, 103134. [Google Scholar] [CrossRef]
- Fan, H.; Lu, C.; He, H.; Fan, H. Graphene-Coated Twisted Taper for Highly Sensitive Sensing and All-Optical Modulation. IEEE Sens. J. 2023, 23, 4843–4848. [Google Scholar] [CrossRef]
- Fan, H.; Yin, Q.; Fan, H.; Lu, C. Graphene-coated three-twisted-taper and four-twisted-taper for highly sensitive temperature and strain sensing. Sens. Actuators A Phys. 2023, 357, 114366. [Google Scholar] [CrossRef]
- Brambilla, G.; Xu, F.; Horak; Jung, Y.; Koizumi, F.; Sessions, N.; Koukharenko, E.; Feng, X.; Murugan, G.S.; Wilkinson, J.S. Optical fiber nanowires and microwires: Fabrication and applications. Adv. Opt. Photonics 2009, 1, 107–161. [Google Scholar] [CrossRef]
- Shi, L.; Xu, Y.; Chen, X. Simulation of Optical Microfiber Loop Resonators for Ambient Refractive Index Sensing. Sensors 2007, 7, 689–696. [Google Scholar] [CrossRef]
- Lou, N.; Jha, R.; Dominguez-Juarez, J.L.; Finazzi, V.; Villatoro, J.; Badenes, G.; Pruneri, V. Embedded optical micro/nano-fibers for stable devices. Opt. Lett. 2010, 35, 571–573. [Google Scholar] [CrossRef]
- Cai, D.; Tong, T.; Zhang, Z.; Pan, J.; Zhang, L.; Tong, L. Functional Film Coated Optical Micro/Nanofibers for High-Performance Gas Sensing. IEEE Sensors J. 2019, 19, 9229–9234. [Google Scholar] [CrossRef]
- Sun, L.; Li, J.; Tan, Y.; Shen, X.; Xie, X.; Gao, S.; Guan, B.O. Miniature highly-birefringent microfiber loop with extremely-high refractive index sensitivity. Opt. Express 2012, 20, 10180–10185. [Google Scholar] [CrossRef]
- Jali, M.H.; Rahim, H.R.A.; Hamis, S.S.; Johari, M.A.M.; Yusof, H.H.M.; Thokchom, S.; Harun, S.W.; Khasanah, M.; Yasin, M. Microfiber loop resonator for formaldehyde liquid sensing. Optik 2019, 196, 163174. [Google Scholar] [CrossRef]
- Wu, X.; Tong, L. Optical microfibers and nanofibers. Nanophotonic 2013, 2, 407–428. [Google Scholar] [CrossRef]
- Yang, H.; Kong, L.; Li, L.; Wang, Y.; Li, X.; Wang, X.; Bo, Y.; Wang, Y.; Wei, Q.; Lu, X. Enhanced-sensitive dual microfiber knot resonators based sensor with vernier effect for simultaneous measurement of refractive index and temperature. Optik 2022, 250 Pt 1, 168350. [Google Scholar] [CrossRef]
- Tian, Q.; Yang, H.; Rong, Q.; Feng, Z.; Wang, R.; Zaini, M.K.A.; Lim, K.-S.; Ahmad, H.; Zhang; Ding, X.; et al. Highly sensitive micro-hygrometer based on microfiber knot resonator. Opt. Commun. 2019, 431, 88–92. [Google Scholar] [CrossRef]
- Cai, L.; Li, J. PDMS packaged microfiber knot resonator used for sensing longitudinal load change. J. Phys. Chem. Solids 2020, 138, 109268. [Google Scholar] [CrossRef]
- Yue-Yu, X.; Zhao-hui, Z.; Xiao-yong, J.; Hua, C. Simultaneous measurement of temperature and refractive index using microfiber knot resonators in Hi-Bi fiber loop mirrors. Optik 2020, 219, 165232. [Google Scholar]
- Zhai, X.; Zhang, W.; Cui, J.; Huang, H.; Wang, Y.; Zhang, G.; Wang, R.; Yang, Y.; Wang, Y. Underwater acoustic sensor based on microfiber knot resonator. Opt. Fiber Technol. 2024, 84, 103711. [Google Scholar] [CrossRef]
- Huang, H.; Cui, J.; Zhang, W.; Zhang, G.; Wang, R.; Yang, Y.; Wang, Y. A microfiber knot resonator for ultrasonic underwater detection. Opt. Fiber Technol. 2025, 91, 104152. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Li, Q.; Su, L.; Fu, X.; Jin, W.; Bi, W.; Fu, G. Ultrasound detection based on optical tapered-knot resonator sensor. Sens. Actuators A Phys. 2024, 369, 115214. [Google Scholar] [CrossRef]
- Sun, S.; Xu, Y.; Ren, L.; Xu, J.; Jia, T.; Zhang, L.; Xiao, J.; Wang, B.; Yang, W.; Cheng, S.; et al. Research on the gas refractive index sensing based on microfiber double-knot resonator with a parallel structure. Optik 2020, 204, 164207. [Google Scholar] [CrossRef]
- Yi, Y.; Jiang, Y.; Zhao, H.; Brambilla, G.; Fan, Y.; Wang, P. High-Sensitivity Humidity Sensor Based on Microknot Resonator Assisted Agarose-Coated Mach-Zehnder Interferometer. J. Light. Technol. 2022, 40, 2191–2196. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Wu, Y.; Rao, Y.-J.; Deng, Q.; Gong, Y. Hybrid Mach–Zehnder interferometer and knot resonator based on silica microfibers. Opt. Commun. 2010, 283, 2953–2956. [Google Scholar] [CrossRef]
- Shahal, S.; Duadi, H.; Linzon, Y.; Fridman, H. Complex Fiber Micro-Knots. Sensors 2018, 18, 1273. [Google Scholar] [CrossRef]
- Vienne, G.; Coillet, A.; Grelu; El Amraoui, M.; Jules, J.-C.; Smektala, F.; Tong, L. Demonstration of a reef knot microfiber resonator. Opt. Express 2009, 17, 6224–6229. [Google Scholar] [CrossRef]
- Sumetsky, M. Uniform coil optical resonator and waveguide transmission spectrum eigenmodes and dispersion relation. Opt. Express 2005, 13, 4331–4340. [Google Scholar] [CrossRef]
- Xu, F.; Brambilla, G.; Feng, J.; Lu, Y. Mathematical model for manufacturing microfiber coil resonator. Opt. Eng. 2010, 49, 044001-04001-4. [Google Scholar]
- Wu, Q.; Xiao, Y.; Zhao, G.; Song, Q. Evolutionary processes and applications of microfiber resonant Rings: A systematic exploration for sensitivity enhancement. Opt. Laser Technol. 2024, 174, 110567. [Google Scholar] [CrossRef]
- Chen, G.; Brambilla, B.; Newson, T. Inspection of electrical wires for insulation faults and current surges using sliding temperature sensor based on optical Microfibre coil resonator. Electron. Lett. 2013, 49, 46–47. [Google Scholar] [CrossRef]
- Ismaeel, R.; Lee, T.; Al-Saab, F.; Jung, Y.; Brambilla, G. A self-coupling multi-port microcoil resonator. Opt. Express 2012, 20, 8568–8574. [Google Scholar] [CrossRef]
- Talataisong, W.; Ismaeel, R.; Masoudi, A.; Beresna, M.; Brambilla, G. Magnetic field sensor based on multi-port microcoil resonator. In Proceedings of the Proceedings Volume 10323, 25th International Conference on Optical Fiber Sensors, Jeju, Republic of Korea, 24–28 April 2017; Volume 1032309. [Google Scholar]
- Zain, H.A.; Batumalay, M.; Haris, H.; Saad, I.; Muhammad, A.; Mustaffa, S.N.; Markom, A.M.; Rahim, H.R.A.; Tan, S.J.; Harun, S.W. Review of Microbottle Resonators for Sensing Applications. Micromachines 2023, 14, 734. [Google Scholar] [CrossRef]
- Guo, G. Superstructure fiber Bragg gratings for simultaneous temperature and strain measurement. Optik 2019, 182, 331–340. [Google Scholar] [CrossRef]
- Xu, J.; Liu, T.; Dai, X.; Su, Y.; Shi, J.; Zheng, Y.; Dai, S.; Zhang, P. Multi-mode fiber Bragg grating for simultaneous detection of strain, torsion and temperature. Opt. Laser Technol. 2024, 179, 111293. [Google Scholar] [CrossRef]
- Chen, C.; Wu, Q.; Zhang, Y.; Fan, B.; Xiong, K. Multi-directional strain measurement under thermomechanical loading using embedded phase-shifted fiber Bragg grating. Measurement 2023, 220, 113297. [Google Scholar] [CrossRef]
- Bhatti, H.S.; Aizzuddin, A.M.; Hadeed, M.; Vorathin, E.; Mohammad, H.; Lim, K.S. Temperature and chirp compensated fibre Bragg grating geophone for improved seismic detection. Opt. Commun. 2025, 579, 131533. [Google Scholar] [CrossRef]
- Abeywardena, C.I.; Zhang, Q.; Korposh, S.; Morgan, S.; Bull, S.; Carreia, R. Highly sensitive optical fibre Bragg grating contact pressure sensor embedded in a polymer layer: Modelling and experimental validation. Results Opt. 2024, 14, 100604. [Google Scholar] [CrossRef]
- Zhang, R.; Dou, H.; Zhang; Liu, J.; Wu, X. Dual-axis fiber Bragg grating tilt sensor based on universal joint structure. Opt. Fiber Technol. 2024, 87, 103898. [Google Scholar] [CrossRef]
- Le, H.-D.; Chiang, C.-C.; Nguyen, C.-N.; Hsu, H.-C. A fiber Bragg grating acceleration sensor based on a circular flexure hinge structure for medium- and high-frequency vibration measurements. Optik 2023, 280, 170790. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, Q.; Zhang, Y.; Ibrahim, R.; Li, D. A miniature triaxial force sensor based on fiber Bragg gratings for flexible endoscopic robot. Measurement 2024, 232, 114645. [Google Scholar] [CrossRef]
- Ams, M.; Dekker; Gross, S.; Withford, M.J. Fabricating waveguide Bragg gratings (WBGs) in bulk materials using ultrashort laser pulses. Nanophotonics 2017, 6, 743–763. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Mihailov, S.J. Femtosecond laser writing of fiber Bragg gratings using the phase mask technique: A geometrical optics analysis based on the Bravais refractive index. Opt. Express 2024, 32, 14685–14704. [Google Scholar] [CrossRef]
- Tahir, B.; Ali, J.; Rahman, R.A. Fabrication of fiber grating by phase mask and its sensing application. J. Optoelectron. Adv. Mater. 2006, 8, 1604–1609. [Google Scholar]
- Yao, G.; Huang, J.; Liu, W. Influence of light incident angle on fiber grating fabrication. IOP Conf. Ser. Mater. Sci. Eng. 2018, 382, 052040. [Google Scholar] [CrossRef]
- Przhiialkovskii, D.V.; Butov, O.V. High-precision point-by-point fiber Bragg grating inscription. Results Phys. 2021, 30, 104902. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, B.; He, J.; Hou, M.; Bao, W.; Wang, Y. High-Efficiency Inscription of Fiber Bragg Grating Array with High-Energy Nanosecond-Pulsed Laser Talbot Interferometer. Sensors 2020, 20, 4307. [Google Scholar] [CrossRef]
- Paixão, T.; Pereira, L.; MIn, R.; Blanc, W.; Tosi, D.; Molardi, C.; Marques, C.; Antunes, P. Inscription of a fiber Bragg grating and a Fabry-Pérot interferometer on a MgO-doped optical fiber. In Proceedings of the International Microwave and Optoelectronics Conference, Aveiro, Portugal, 10–14 November 2019. [Google Scholar]
- Williams, R.J.; Krämer, R.G.; Nolte, S.; Withford, M.J. Femtosecond direct-writing of low-loss fiber Bragg gratings using a continuous core-scanning technique. Opt. Lett. 2013, 38, 1918–1920. [Google Scholar] [CrossRef]
- Gao, C.; Zhao, R.; Wu, B.; Li, H.; Ye, X.; Wang, M.; Xu, X.; Wang, Z. Femtosecond laser direct writing large-area fiber Bragg grating based on diaphragm shaping. Opt. Express 2024, 32, 18582–18593. [Google Scholar] [CrossRef]
- Zhu, Q.; Tian, T.; Ma, Y.; Zhu, Y.; Geng, T.; Yuan, L. A highly sensitive refractive index sensor based on super-structured long-period fiber grating. Opt. Fiber Technol. 2025, 90, 104123. [Google Scholar] [CrossRef]
- Xu, F.; Dai, R.; Guo, Y.; Hu, M.; Wang, X.; Zhao, Y. High-sensitive glucose sensor based on tilted fiber Bragg gratings. Opt. Commun. 2024, 569, 130861. [Google Scholar] [CrossRef]
- Mandal, H.N.; Sidhishwari, S. Apodized chirped fiber Bragg grating for measuring the uniform and non-uniform characteristics of physical parameters. Measurement 2025, 240, 115606. [Google Scholar] [CrossRef]
- Singh, J.; Khare, A.; Kumar, S. Design of Gaussian Apodized Fiber Bragg Grating and its applications. Int. J. Eng. Sci. Technol. 2010, 2, 1914–1924. [Google Scholar]
- Luo, Y.; Liang, H.; Ju, W.; Chen, J.; Lin, X.; Qiu, Q.; Zhang, Z.; Wang, X.; Xing, Y.; Dai, N.; et al. High-brightness 980 nm all-fiber oscillator with 27 % slope efficiency using chirped and tilted fiber Bragg grating. Opt. Fiber Technol. 2025, 89, 104054. [Google Scholar] [CrossRef]
- Cai, J.; Liu, H.; Liu, Y.; Lin, Z.; Yang, X.; Yang, H.; Shu, X. A small-period long-period fiber grating biosensor based on immobilization of concanavalin A on polydopamine nanospheres for simultaneous detection of D-glucose and temperature. Measurement 2025, 242, 115877. [Google Scholar] [CrossRef]
- Yu, Y.; Yi, Q.; Gao, Z. Temperature and refractive index sensing using a chirped tilted fiber Bragg grating (CTFBG) cascaded with a fiber Bragg grating (FBG). Instrum. Sci. Technol. 2025, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Shum; Cheng, X.; Ngo, N.Q.; Li, S.Y. Analysis of linearly tapered fiber Bragg grating for dispersion slope compensation. IEEE Photonics Technol. Lett. 2003, 15, 1389–1391. [Google Scholar] [CrossRef]
- Lima, H.F.; Antunes, F.; Pinto, J.L.; Nogueira, R.N. Simultaneous Measurement of Strain and Temperature With a Single Fiber Bragg Grating Written in a Tapered Optical Fiber. IEEE Sens. J. 2010, 10, 269–273. [Google Scholar] [CrossRef]
- Osuch, T. Tapered and linearly chirped fiber Bragg gratings with co-directional and counter-directional resultant chirps. Opt. Commun. 2016, 366, 194–199. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, L.; Dong, M.; Lou, X.; Liu, F. A Temperature Fiber Sensor Based on Tapered Fiber Bragg Grating Fabricated by Femtosecond Laser. Appl. Sci. 2018, 8, 2616. [Google Scholar] [CrossRef]
- Afroozeh, A. Highly Sensitive FBG Based Sensor for Temperature Measurement. Plasmonics 2021, 16, 1973–1982. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, K.; Wu, Q.; Liu, J.; Yan, K.; Wang, J. Batch fabrication of the smooth-surfaced and tailored-diameter microfiber Bragg grating sensors using hydrothermal method and its characteristics. Opt. Fiber Technol. 2023, 81, 103534. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, Y.; Zhang, L.; Zhang, F.; Nie, Z.; Wang, M. Research on vector bending sensors based on taper-drawn seven-core fiber Bragg grating. Opt. Fiber Technol. 2024, 88, 103975. [Google Scholar] [CrossRef]
- Markowski, K.; Araszkiewicz; Bojarczuk, J.; Perlicki, K. High-sensitivity chirped tapered fiber-Bragg-grating-based Fabry–Perot cavity for strain measurements. Opt. Lett. 2020, 45, 2838–2841. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Tang, X.; Liu, Z.; Zhang, Y.; Sha, C.; Zhang, M.; Wei, J.; Zhang, J.; Yuan, L. Photosensitive Polymer-Based Micro-Nano Long-Period Fiber Grating for Refractive Index Sensing. J. Light. Technol. 2021, 99, 1–7. [Google Scholar] [CrossRef]
- Li, B.; Chen, J.-H.; Xu, F.; Lu, Y.-Q. Periodic micro-structures in optical microfibers induced by Plateau-Rayleigh instability and its applications. Opt. Express 2017, 25, 4326–4334. [Google Scholar] [CrossRef]
- Jie, D.; Sang, M.; Wang, S.; Xu, T. Refractive Index Sensor Based on Graphene Oxide-Coated Long-Period Fiber Grating Inscribed in a Two-Mode Fiber. IEEE Access 2020, 8, 109028–109037. [Google Scholar]
- Cheng, Z.; Goda, K. Design of waveguide-integrated graphenedevices for photonic gas sensing. Nanotechnology 2017, 27, 505206. [Google Scholar] [CrossRef]
- Wang, R.; Ren, Z.; Kong, D.; Hu, B.; He, Z. Highly Sensitive Label-Free Biosensor Based on Graphene-Oxide Functionalized Micro-Tapered Long Period Fiber Grating. Opt. Mater. 2020, 109, 110253. [Google Scholar] [CrossRef]
- Zawisza, R.; Eftimov, T.; Mikulic; Bock, W.J.; Jaroszewicz, L.R. Ambient Refractive-Index Measurement with Simultaneous Temperature Monitoring Based on a Dual-Resonance Long-Period Grating Inside a Fiber Loop Mirror Structure. Sensors 2018, 18, 2370. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Hu, D.; Li, Z.; Xu, Z.; Ran, Y.; Guan, B. Assembly tapered fiber Bragg grating tip with gold nanostars for heat generation and gradient temperature sensing. Opt. Laser Technol. 2024, 175, 110759. [Google Scholar] [CrossRef]
- Wei, W.; Nong, J.; Zhang, G.; Tang, L.; Jiang, X.; Chen, N.; Luo, S.; Lan, G.; Zhu, Y. Graphene-Based Long-Period Fiber Grating Surface Plasmon Resonance Sensor for High-Sensitivity Gas Sensing. Sensors 2017, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Mehdi, I.; Mehdi, M.; Hussain, S.; Guo, J.; Shi, J.; Ali, S.; Mehdi, R.; Zhu, S.; Ghaffar, A.; et al. Twisted tapered plastic optical fiber sensor: An alternative approach for multi-variant alcohol detection. Opt. Commun. 2025, 577, 131386. [Google Scholar] [CrossRef]
- Zulkeflee, N.N.; Kamil, Y.M.; Mashohor, S.; Bakar, M.H.A. Functionalized cascaded tapered optical fiber sensor for simultaneous detection of dengue II E and SARS-CoV-2 S proteins. Biosens. Bioelectron. 2025, 277, 117200. [Google Scholar] [CrossRef]
- Zhao, W.-M.; Wang, Q. A high sensitivity refractive index sensor based on three-level gradient structure S-tapered fiber mode-mode interferometer. Measurement 2019, 139, 49–60. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Wang, J.; Shen, J.; Meiqin, Z.; Mengxing, H. Fabrication and sensing characterization of an S-tapered fiber probe. AIP Adv. 2020, 10, 075306. [Google Scholar] [CrossRef]
- Correia, R.; James, S.; Lee, S.-W.; Morgan, S.; Korposh, S.; Lee, S.-W.; Korposh, S. Biomedical application of optical fibre sensors. J. Opt. 2018, 20, 073003. [Google Scholar] [CrossRef]
- Zhu, G.; Agrawal, N.; Singh, R.; Kumar, S.; Zhang, B.; Saha, C.; Kumar, C. A novel periodically tapered structure-based gold nanoparticles and graphene oxide–Immobilized optical fiber sensor to detect ascorbic acid. Opt. Laser Technol. 2020, 127, 106156. [Google Scholar] [CrossRef]
- Vasconcelos, H.C.A.S.G.; de Almeida, J.M.M.M.; Saraiva, C.M.T.; da Silva Jorge, A.; Coelho, L.C.C. Mach-Zehnder Interferometers Based on Long Period Fiber Grating Coated with Titanium Dioxide for Refractive Index Sensing. J. Light. Technol. 2019, 37, 4584–4589. [Google Scholar] [CrossRef]
- Mumtaz, F.; Roman, M.; Zhang, B.; Huang, J. Assembly-free ultra-sensitive miniaturized strain sensor based on an asymmetric optical fiber taper. Measurement 2023, 211, 112655. [Google Scholar] [CrossRef]

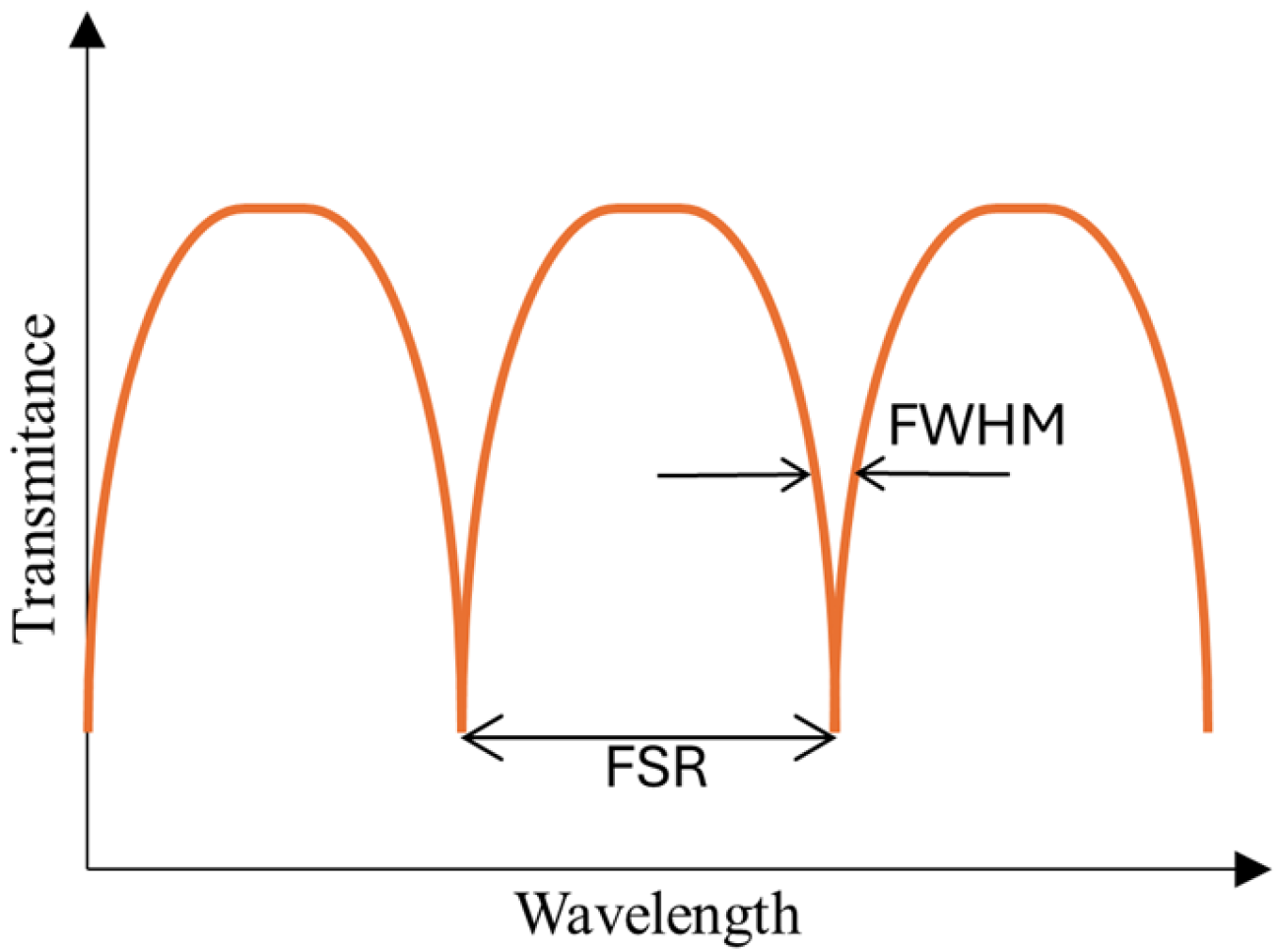
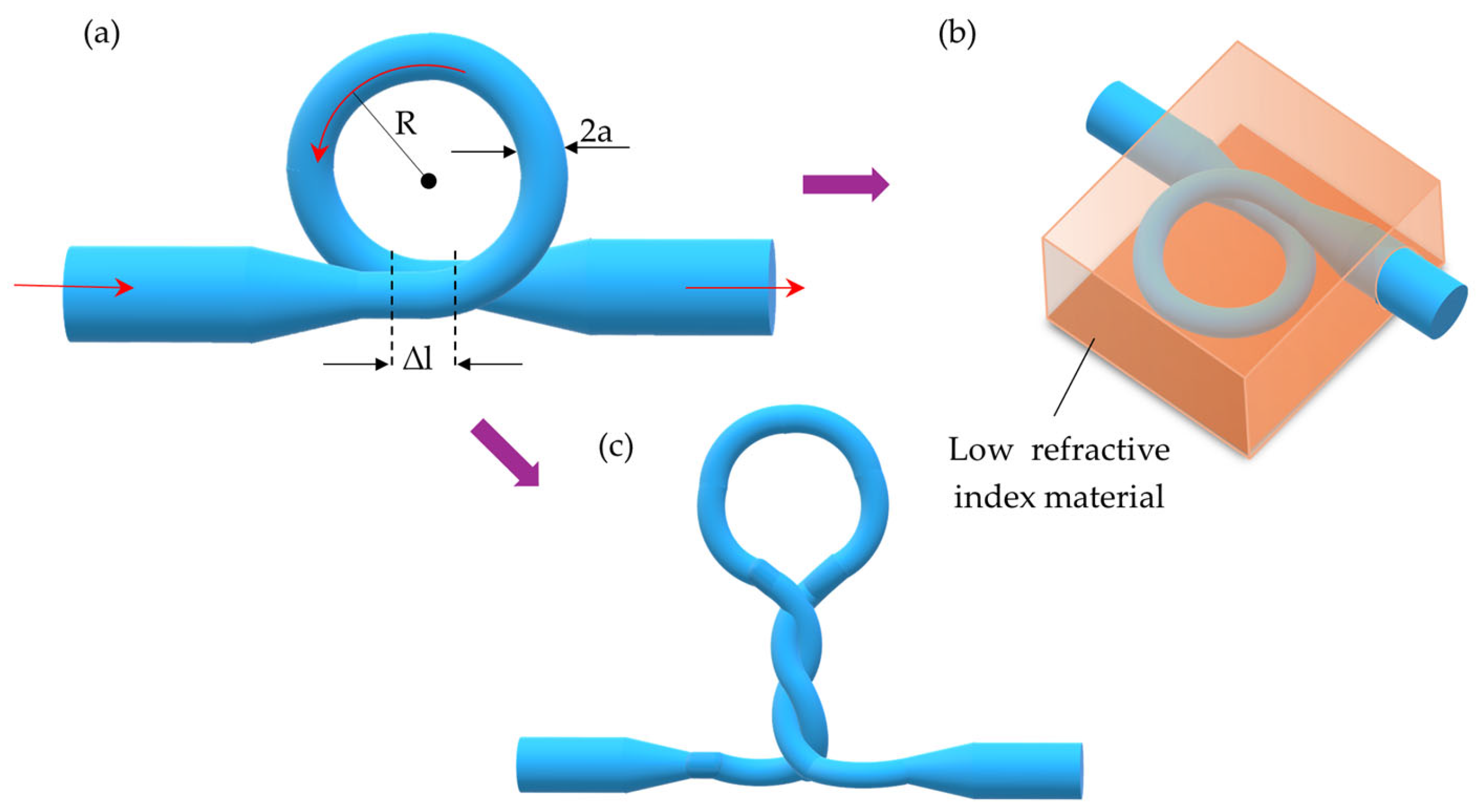
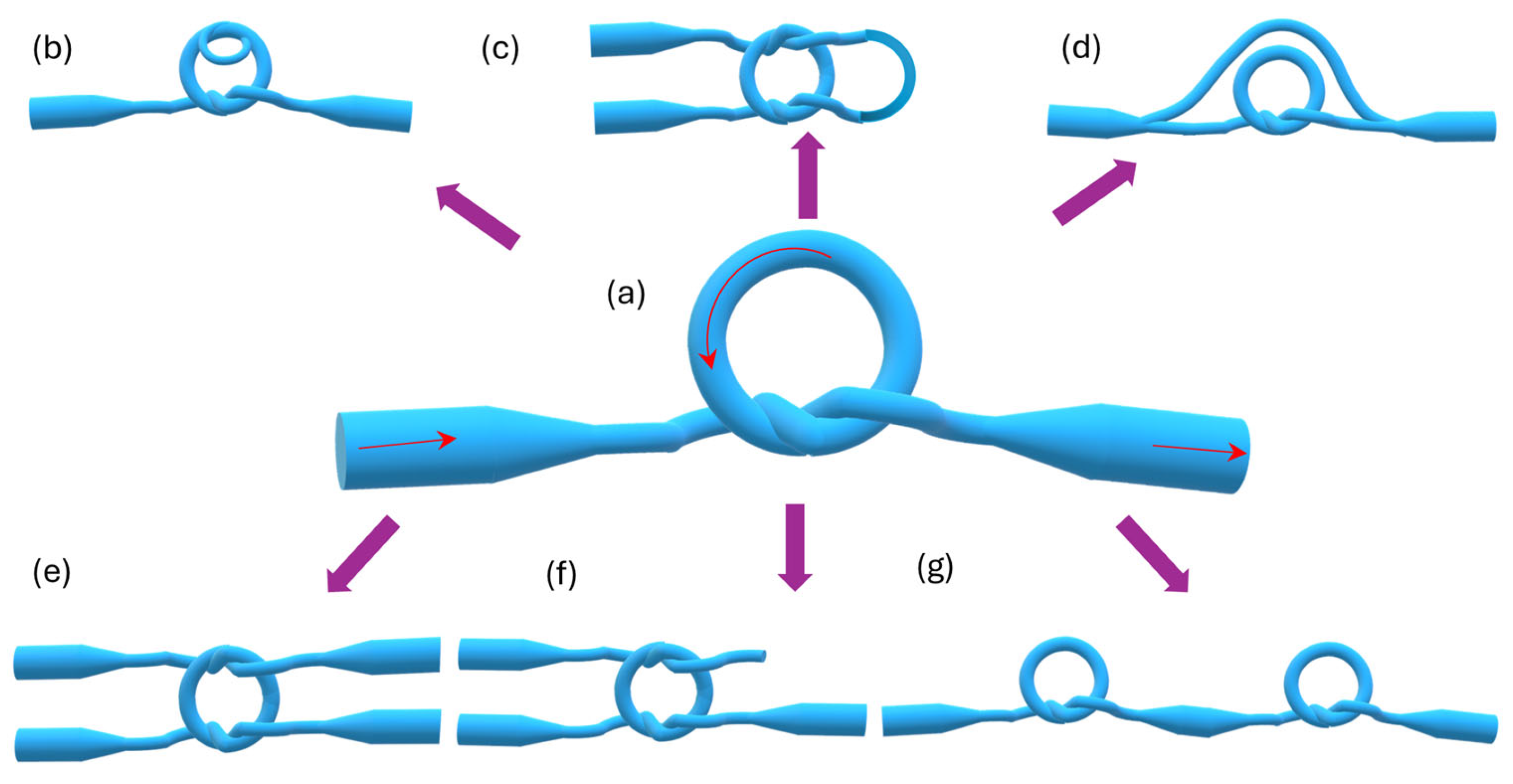
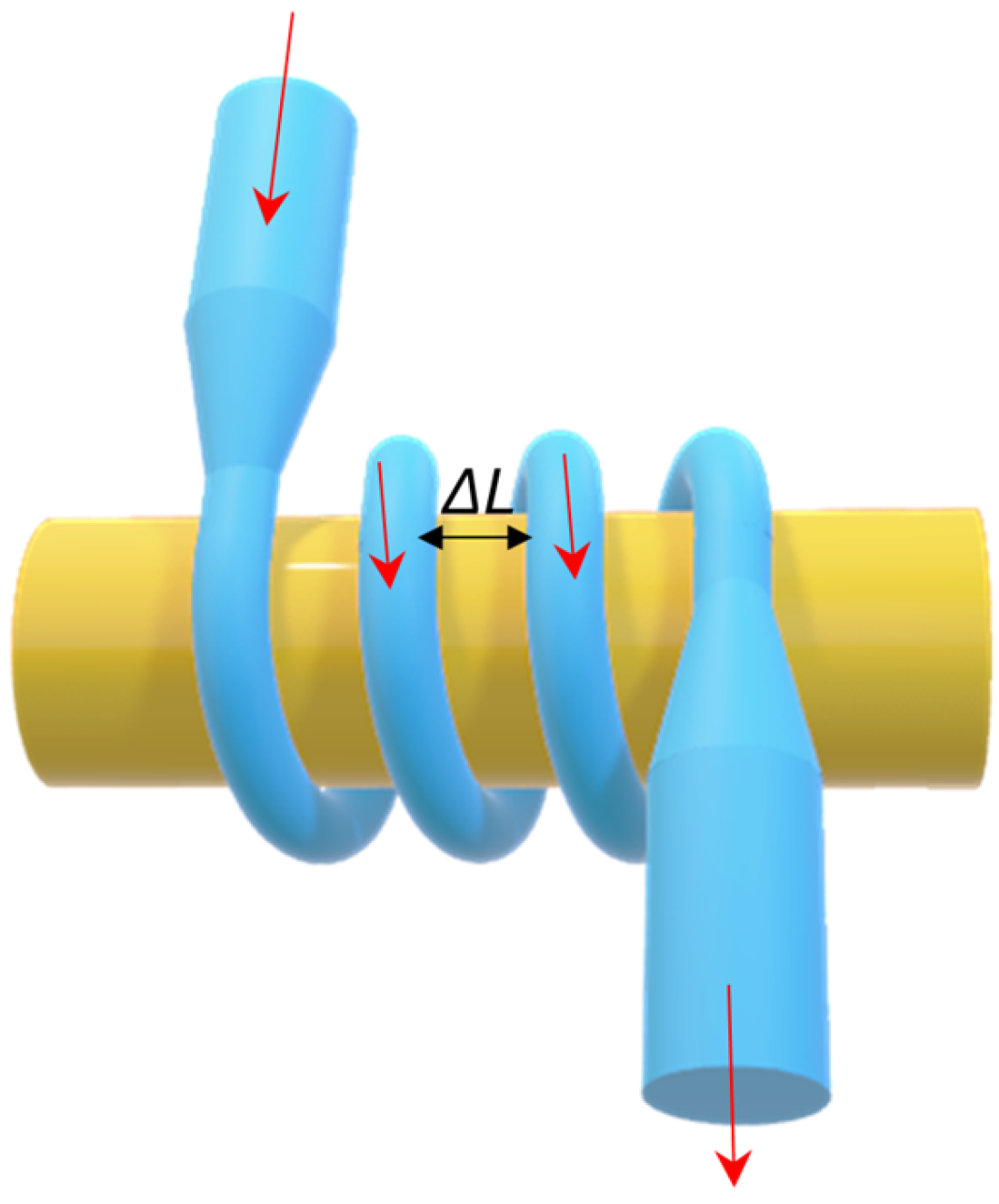
| Metal | εr + iεi * | εr/εi | Operating Wavelength Range | Refs. |
|---|---|---|---|---|
| Au | −11.36 + 1.23i | 9.23 | VIS | [72,73] |
| Ag | −18.22 + 0.48i | 37.9 | VIS | [74,75] |
| Cu | −12.46 + 0.65i | 19.2 | VIS-IR | [76,77] |
| Al | −43.42 + 15.40i | 2.82 | UV-NIR | [78,79] |
| Bi | −23.44 + 2.18i | 10.7 | UV-NIR | [80,81] |
| Pd | −15.27 + 15.17i | 1.01 | NIR-IR | [82,83] |
| Material | εr + iεi * | Ref. |
|---|---|---|
| SiO2 | 2.08 + 0.000058i | [98] |
| ITO | 3.24 + 0.01i | [99] |
| TiO2 | 5.92 + 0.00048i | [98] |
| Al2O3 | 3.15 + 0.0078i | [100] |
| Properties of Sensor | Geometric Parameter on Which It Depends | Dimension |
|---|---|---|
| High Sensitivity | 2a | small |
| hardly dependent on R | small | |
| Higher Q-Factor | 2a | large |
| R | large | |
| Δl | appropriate | |
| Lower Detection Limit Factor | 2a | large |
| R | large | |
| Δl | appropriate | |
| Large FSR—Related to Wide Dynamic Measurement Range | 2a | small |
| hardly dependent on R | small |
| Modified Parameter | Modification Increasing (↑)/Decreasing (↓) | Effect on Resonant Parameter | |
|---|---|---|---|
| Parameter | Effect | ||
| Diameter of the supporting rod | ↑ | FSR | ↓ |
| Gap between the coils | ↓ | FWHM | ↓ |
| Q-factor | ↑ | ||
| Er * | ↑ | ||
| Number of coils | ↑ | FWHM | ↓ |
| Q-factor | ↑ | ||
| Optical loss coefficient | ↑ | Er* | ↑ |
| Feature | LPG | FBG |
|---|---|---|
| Working principle | Coupling of core modes to cladding modes | Fresnel reflection according to the Bragg condition |
| Grating period | 100–1000 μm | ~0.5 μm |
| Operating mode | Transmission (light passes through the grating) | Reflection (light reflects from the grating) |
| Bands in the spectrum | Losses in the transmission spectrum | Reflection in the reflection spectrum |
| Sensitivity to temperature changes | High | Average |
| Sensitivity to the surrounding RI | Very high | Low |
| Type | Active Material | Principle/Method | Measured Factor | Range | Sensitivity | Ref. |
|---|---|---|---|---|---|---|
| TOF | Au NPs | LSPR | BSA | 1 ng/mL –10 mg/mL | 19.46 nm/log(ng/mL) | [90] |
| TOF | Au film | SPR | Salinity | 0–40‰ | 0.708 nm/‰ | [84] |
| Twisted TPOF * | - | Coupling method | Alcohol: ethanol, propanol, butanol, and pentanol | - | 506 %/RIU | [209] |
| U-shaped TPOF | Au film | SPR | RI | 1.335–1.41 | 1534.53 nm/RIU | [32] |
| TOF | Au and PVA | SPR | Humidity Temperature | 46–93 %RH | 1.542 nm/%RH | [89] |
| TOF | Pd | SPR | Hydrogen | 0.125–2.00 % H2 | −18.645 % | [88] |
| Cascaded SMTF ** | Protein antibodies | Cascaded interferometric effect | Dengue II E and SARS-CoV-2 S proteins | 0.0–1.0 nM | 6.91 nm/nM and 9.96 nm/nM | [210] |
| TOF | PVA/DE | EW | Paper moisture content | - | 0.1662 %/%ω | [122] |
| TOF | MoS2 and PDMS | Interferometer | Bending curvature Temperature | 4.31–6.10 m−1 35–42 °C | 23.62 nm/m−1 2.70 nm/m−1 1.10 nm/°C | [124] |
| TOF sandwiched in PDMS film | PDMS with NHSA *** | Self-mixing interference | Blood pressure | - | 0.0138 mV/kPa | [126] |
| TOF modified using femtosecond laser pulses | PDMS | Mach–Zehnder interferometer | Temperature | 30–65 °C | 616.3 pm/°C | [125] |
| TOF | GO–Fe3O4 | EW | Magnetic field | 0–60 mT | 99–324 pW/mT | [140] |
| 2-twisted TOF | - | SPP, multi-mode interference | Temperature Tensile strain | 30–60 °C 0–90 με | −73.7 pm/°C −163.5 pm/με | [141] |
| 2-twisted TOF | Graphene | −127.2 pm/°C −173.9 pm/με | ||||
| 3-twisted TOF | −66.2 pm/°C −173.4 pm/με | [142] | ||||
| 4-twisted TOF | −61.7 pm/°C −103.2 pm/με | |||||
| Non-adiabatic TOF | - GO/PVA | EW | Humidity | 20–99.9 % | 0.00106 a.u. (%)−1 0.00624 a.u.(%)−1 | [139] |
| TOF | PDMS and GO | EW | MUC1 protein | 10–400 μg/ml | 2.11 dB/log(C(μg/mL)) 0.11 pM (detection limit) | [137] |
| TIT | ZnO-NPs | EW | Creatine Ethanol solution | 0–2000 μM 0–100% | 0.11 a.u./μM 4.06 a.u./% | [106] |
| S-tapered | SiO2 NPs | EW | Humidity | 83.8–95.2 %RH | 1.1718 nm/%RH and 0.441 dB/%RH | [108] |
| TIT | AuNPs/MoS2NP/CeO2-Ns | LSPR | Alanine aminotransferase | 10–1000 U/L | 4.1 pm/(U/L) | [107] |
| TOF | Aldehyde modifier | EW | Leptospira DNA | 0.1–1.0 nM | 1.2862 nm/nM | [112] |
| TOF | Zeolite imidazole framework ZIF-8 | The Vernier effect | Ethanol (gas concentration) RI | 0–140 ppm - | 0.1411 nm/ppm 18,366.17 nm/RIU | [111] |
| TOF | PVA | EW | Humidity | 30–90 %RH | 0.119 nm/%RH | [130] |
| Asymmetric TFBG | - | Fresnel reflection | Temperature | 30–350 °C | 12.3 pm/°C | [196] |
| FBG | - | Fresnel reflection | Temperature | 0–140 °C | 717 1/°C | [197] |
| SCF FBG | - | Fresnel reflection | Vector bending | - | 127 pm/m−1 | [199] |
| Chirped TFBG | - | Fresnel reflection/Fabry–Perot | Strain Temperature | - | 5 μm/με 8.9 Chirped 6 pm/°C | [200] |
| Etched chirped TFBG tip | - | Fabry–Perot cavity | Temperature | 25–65 °C | ~11 pm/°C | [36] |
| MKR | PDMS | Acoustic sensor | −135.8 dB | [154] | ||
| MKR | PDMS | Strain sensor | 94.5 pm/N | [152] | ||
| DMKR | - | The Vernier effect | RI and temperature | 1.3375–1.3359 0–25.3 °C | 12523 nm/RIU 0.91998 nm/°C | [150] |
| MKR–U-shaped MZ interferometer | Agarose | The Vernier effect | Humidity | 60–95% RH | 2.442 nm/%RH | [158] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korec-Kosturek, J.; Moś, J.E. Advances in Optical Microfibers: From Fabrication to Functionalization and Sensing Applications. Materials 2025, 18, 2418. https://doi.org/10.3390/ma18112418
Korec-Kosturek J, Moś JE. Advances in Optical Microfibers: From Fabrication to Functionalization and Sensing Applications. Materials. 2025; 18(11):2418. https://doi.org/10.3390/ma18112418
Chicago/Turabian StyleKorec-Kosturek, Joanna, and Joanna E. Moś. 2025. "Advances in Optical Microfibers: From Fabrication to Functionalization and Sensing Applications" Materials 18, no. 11: 2418. https://doi.org/10.3390/ma18112418
APA StyleKorec-Kosturek, J., & Moś, J. E. (2025). Advances in Optical Microfibers: From Fabrication to Functionalization and Sensing Applications. Materials, 18(11), 2418. https://doi.org/10.3390/ma18112418








