Damage Quantitative Detection of Curved Composite Laminates Based on Improved Particle Swarm Optimization Algorithm
Abstract
1. Introduction
2. Mathematical Model of Damage Detection Method Based on Vibration Response Parameters
2.1. Parameterization of Damage
2.2. Damage Location Recognition Algorithm Based on Finite Difference Method
2.3. Objective Function of Optimization Algorithm Based on Vibration Response Parameters
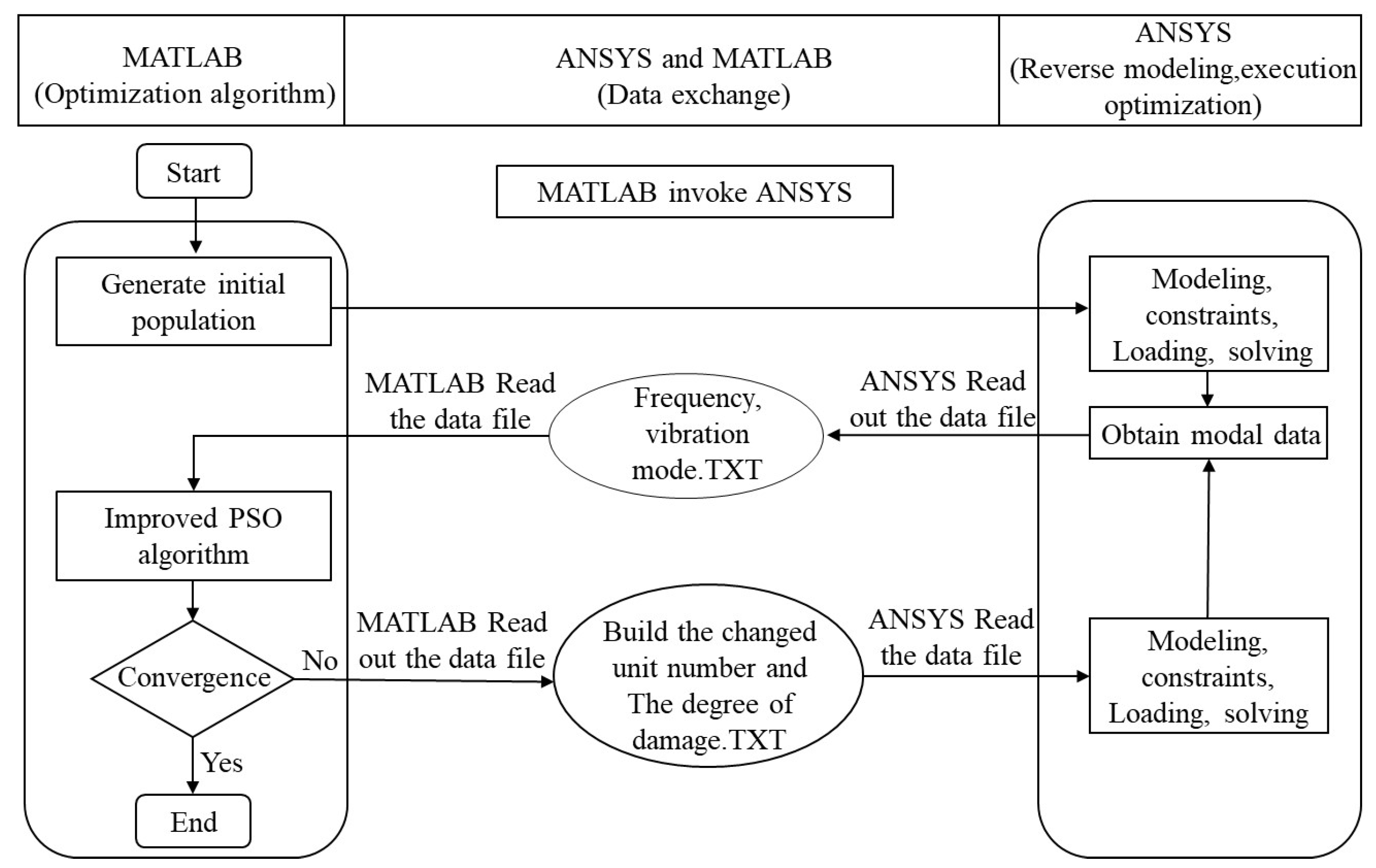
2.4. Damage Quantitative Identification Algorithm Based on IPSO
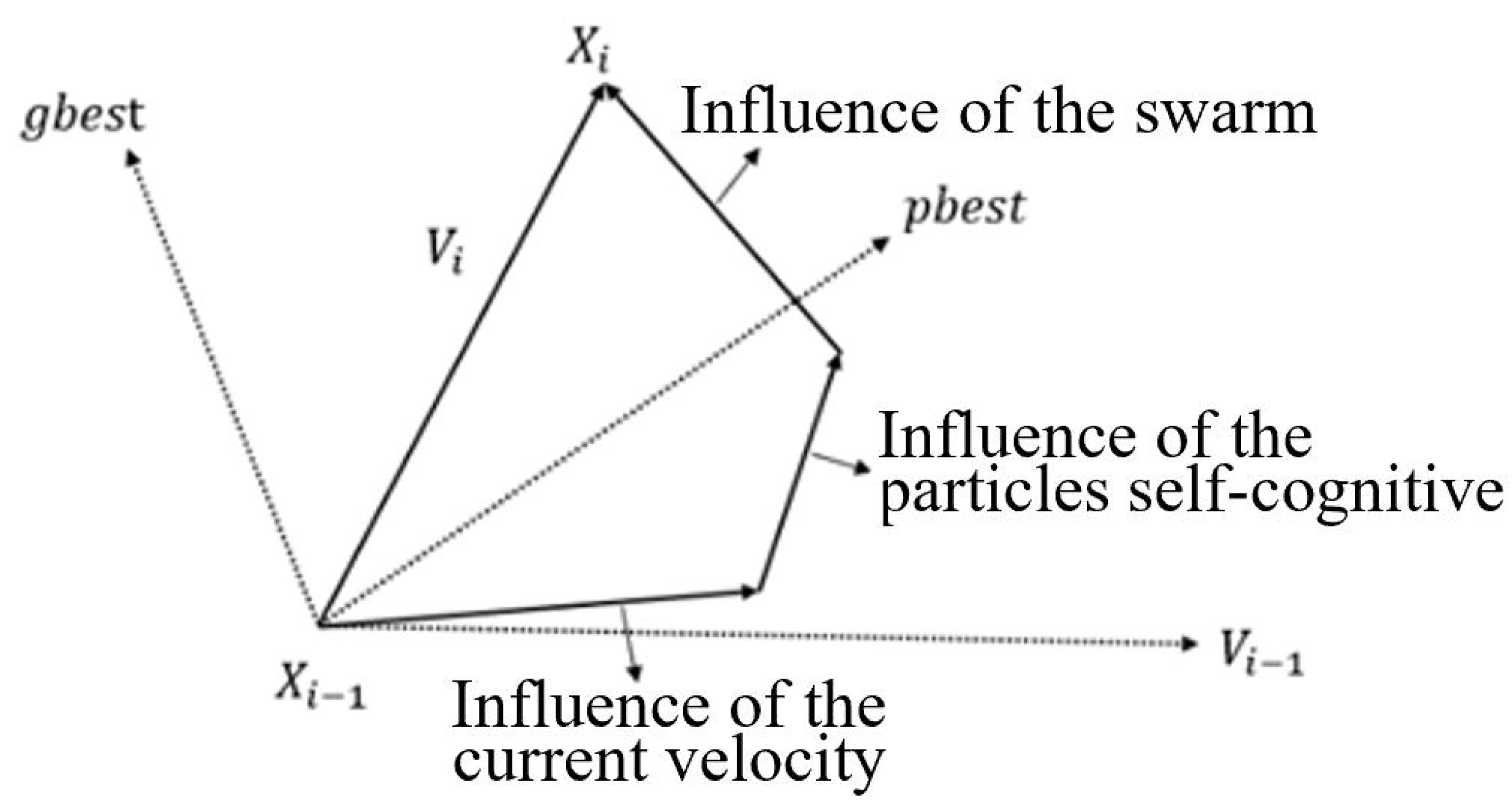
2.4.1. Standard PSO Algorithm
2.4.2. Improved PSO Algorithm
3. Numerical Simulation Verification of Damage Detection Method
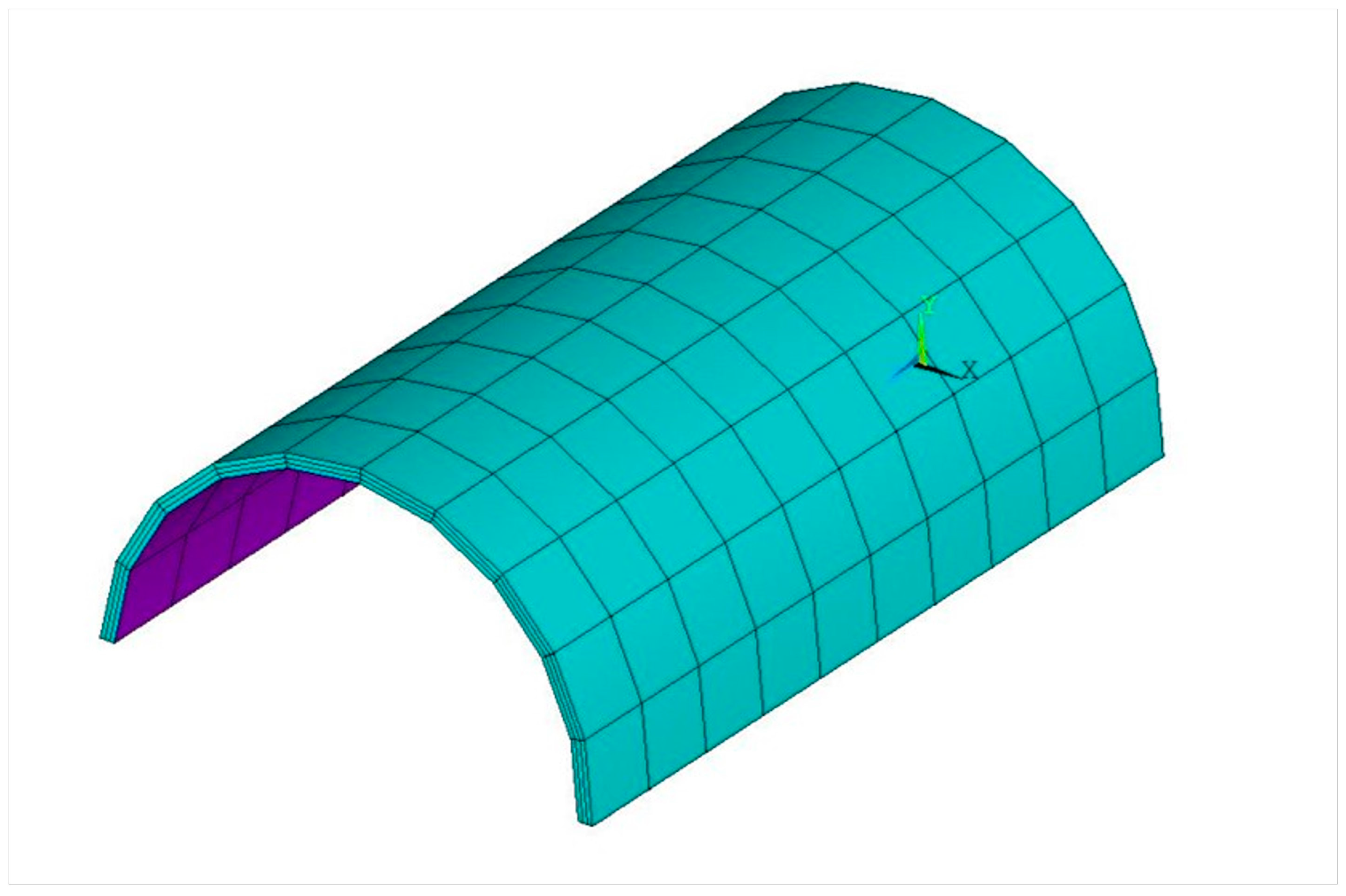
3.1. Finite Element Model of Curved Laminated Plate
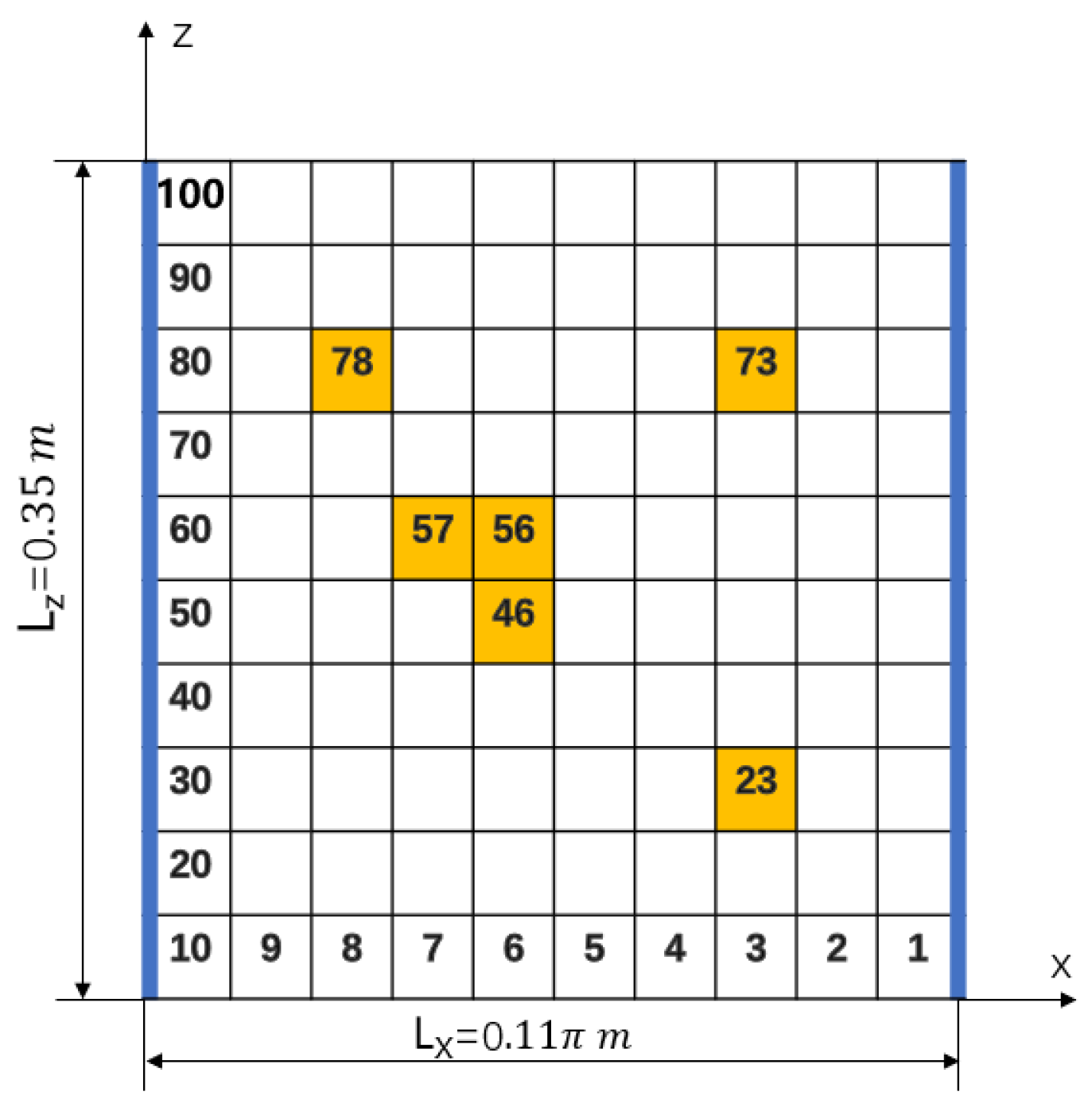
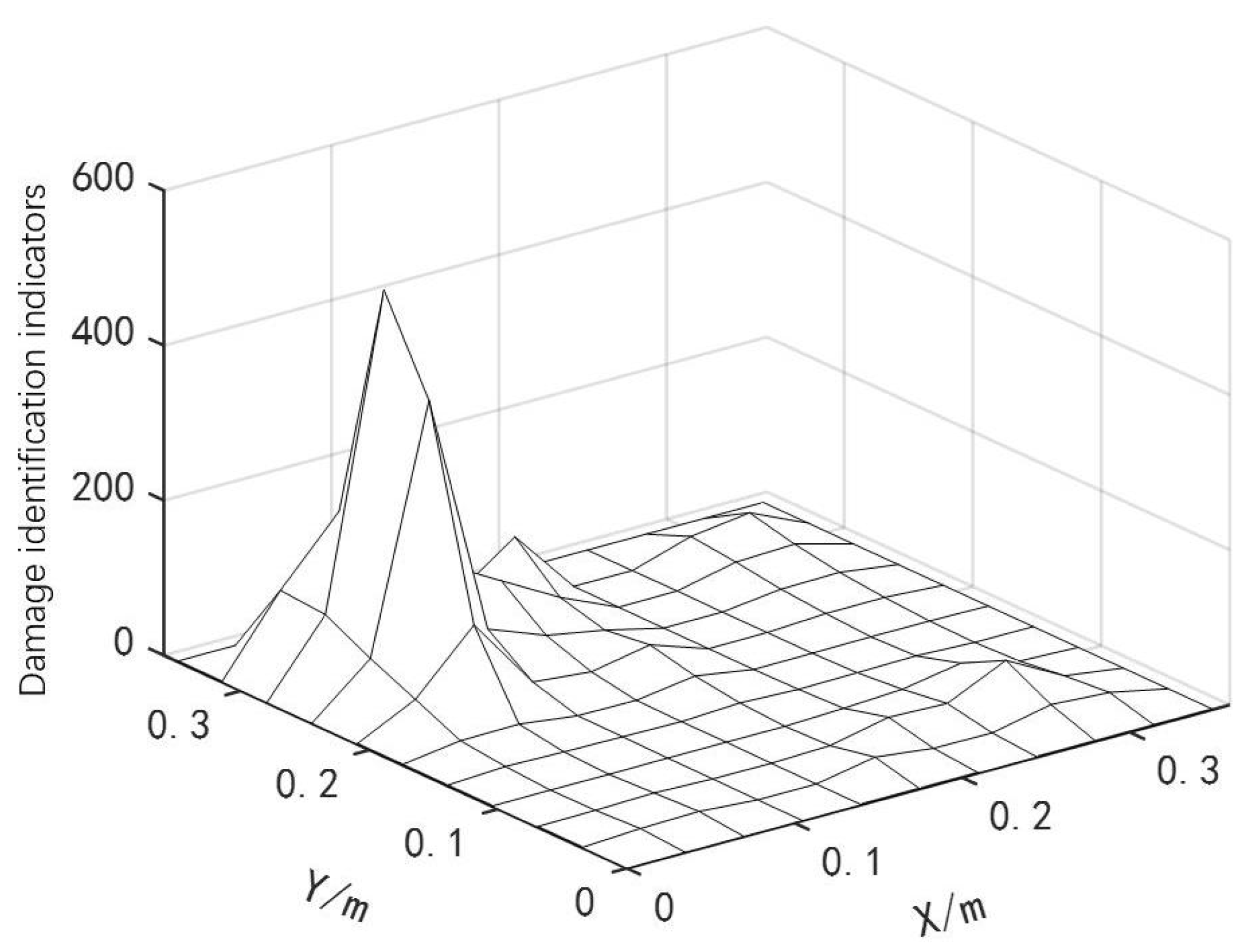
3.2. Detection Results of Different Damage Conditions
Two Discrete Damage Locations
3.3. Two Consecutive Damages
3.3.1. Three Damages
3.3.2. Four Damages
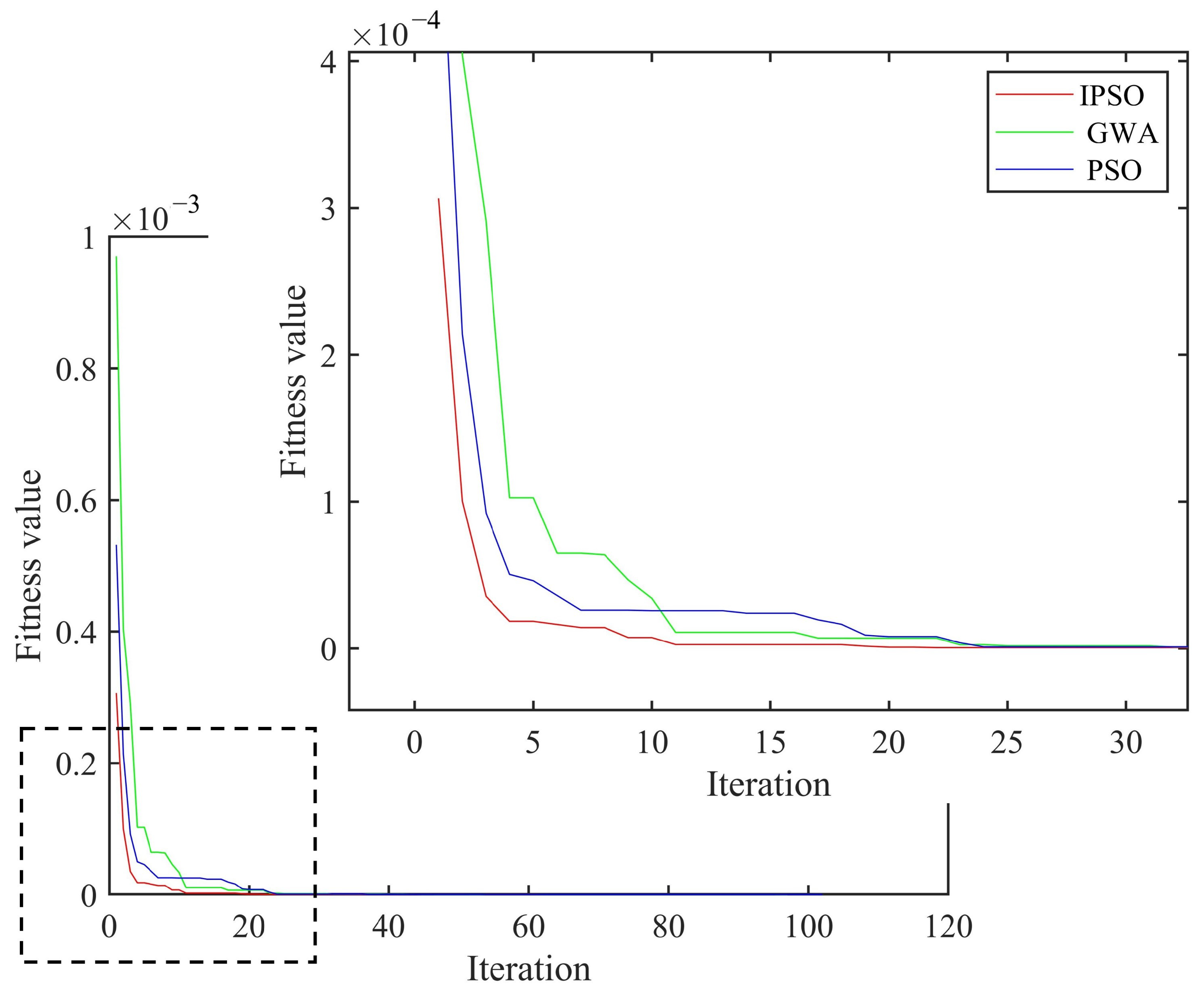
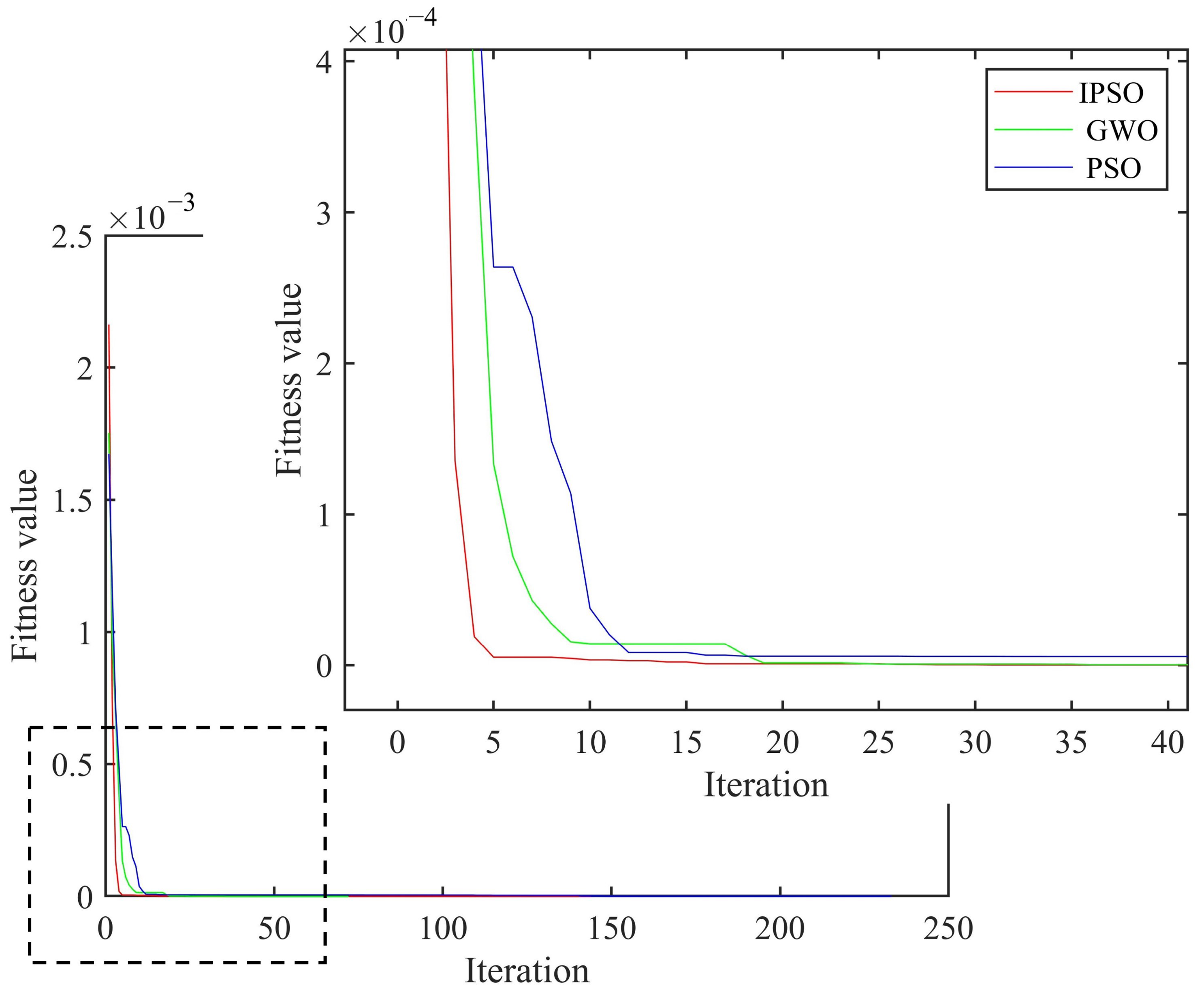
3.4. Analysis of Damage Detection Ability of IPSO Algorithm
3.4.1. The Influence of the Damage Degree on the Detection Ability of the Algorithm
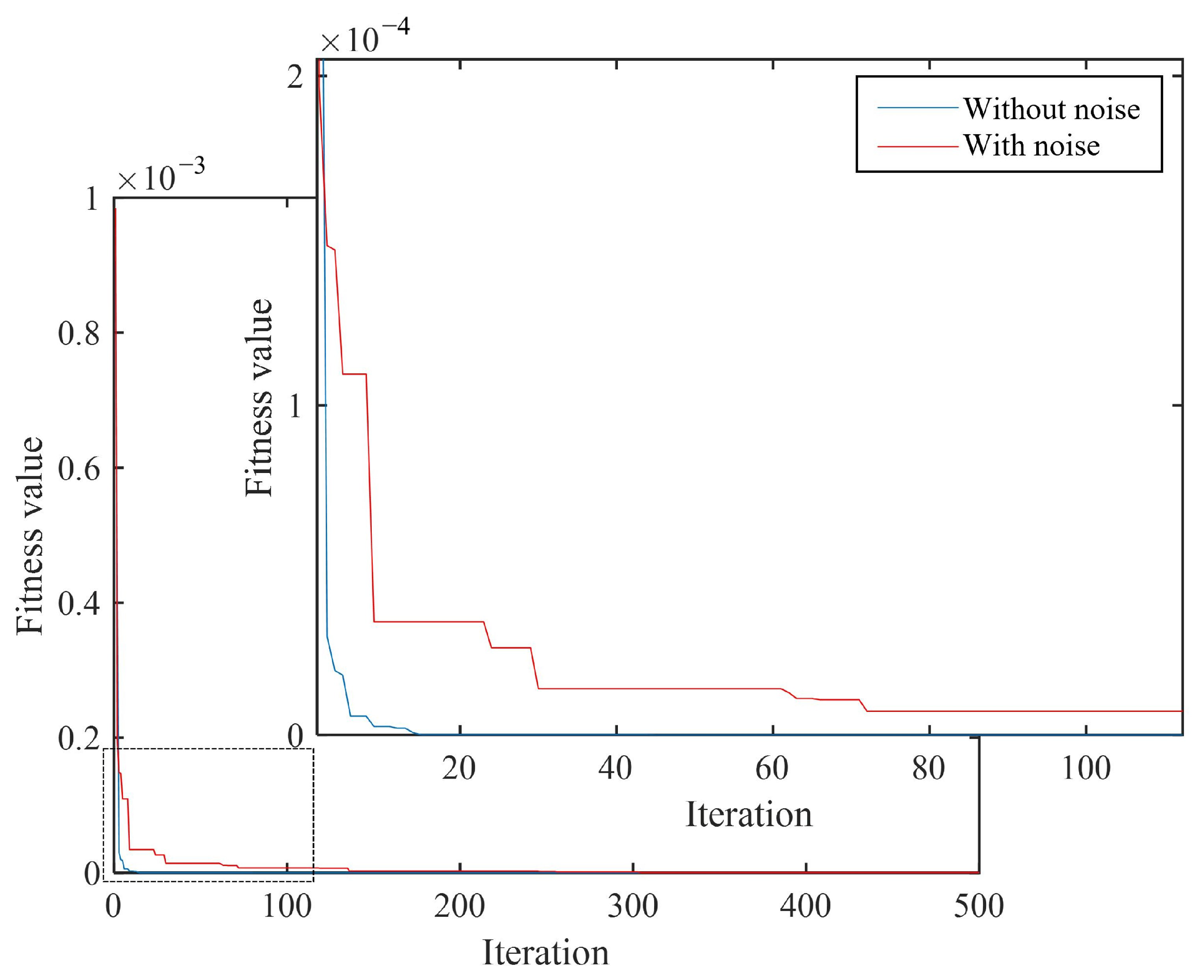
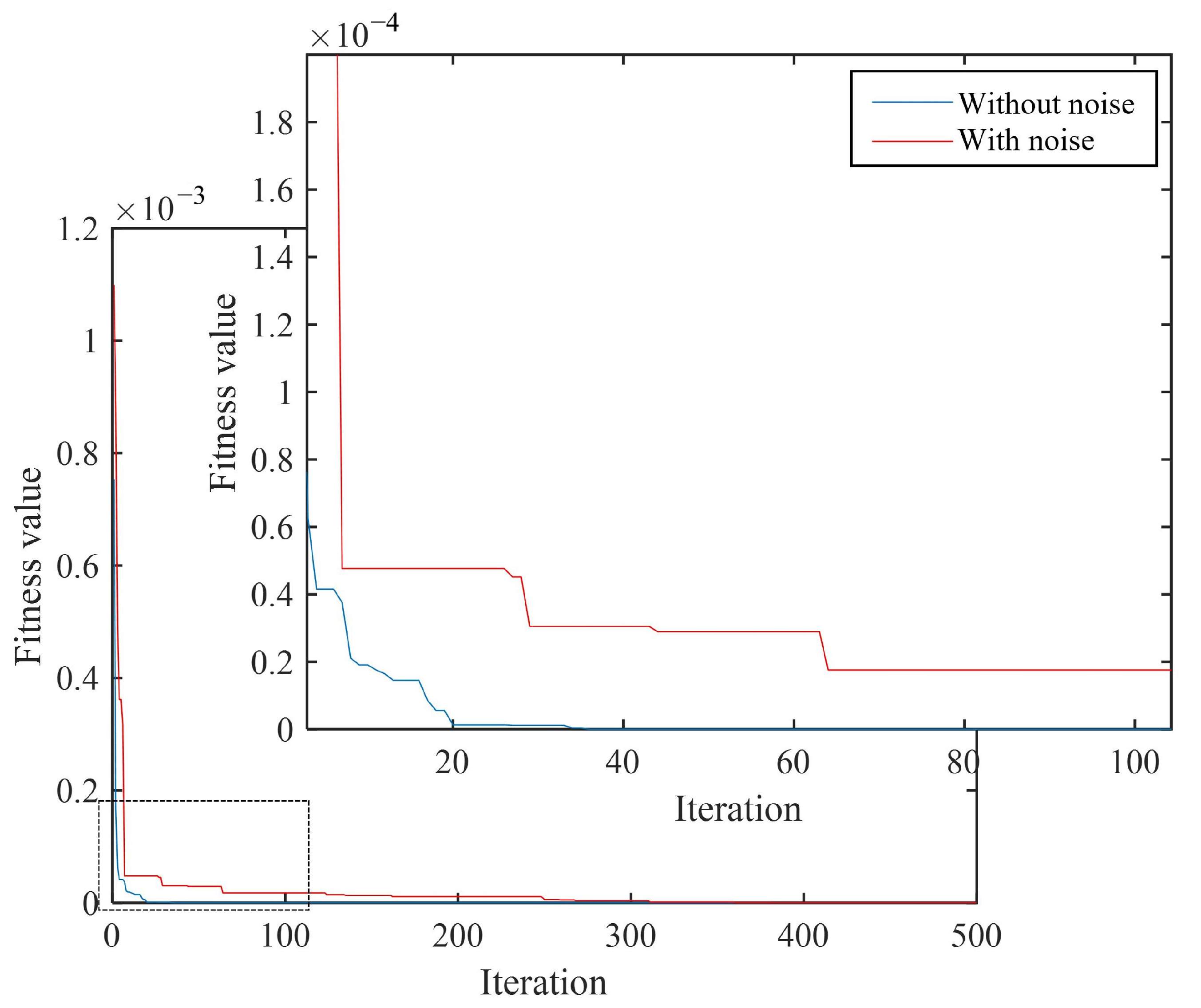
3.4.2. The Influence of Noise on the Detection Ability of the Algorithm
4. Experimental Verification
4.1. Test System
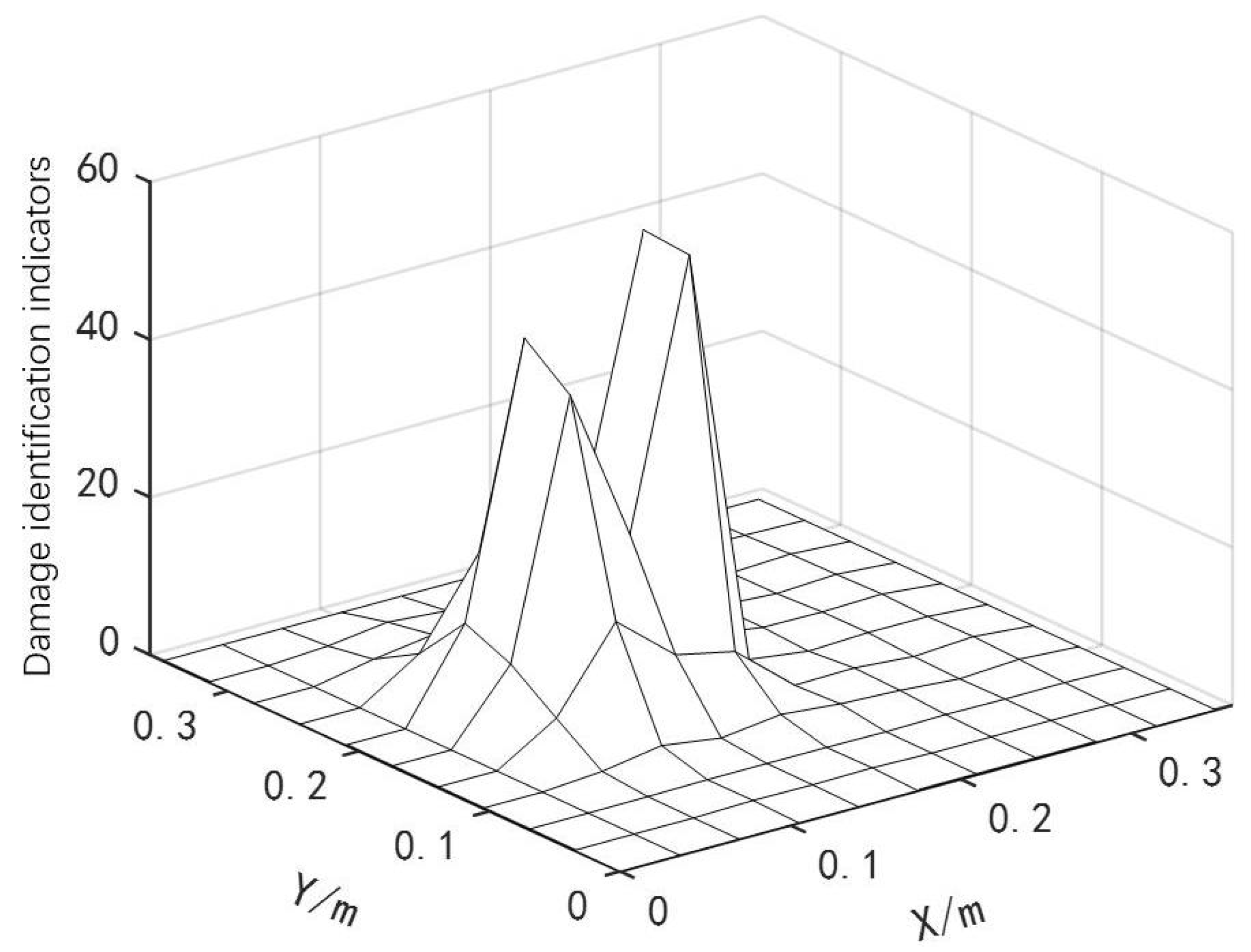
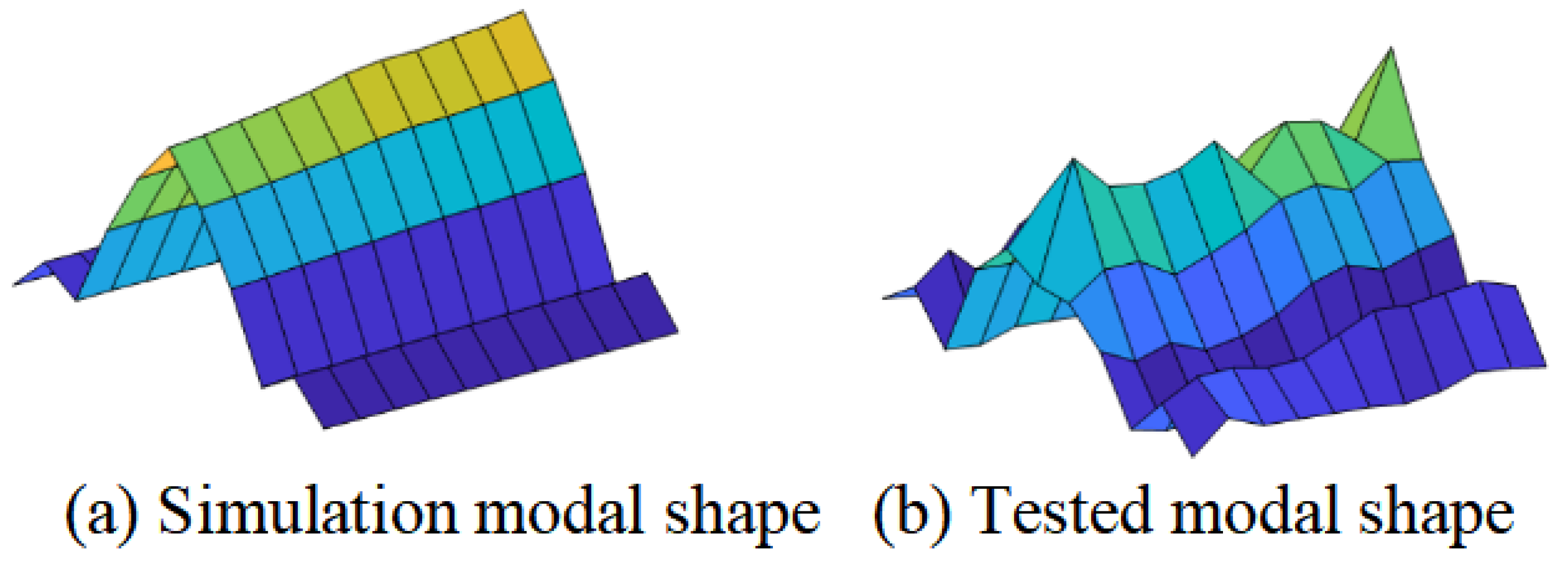
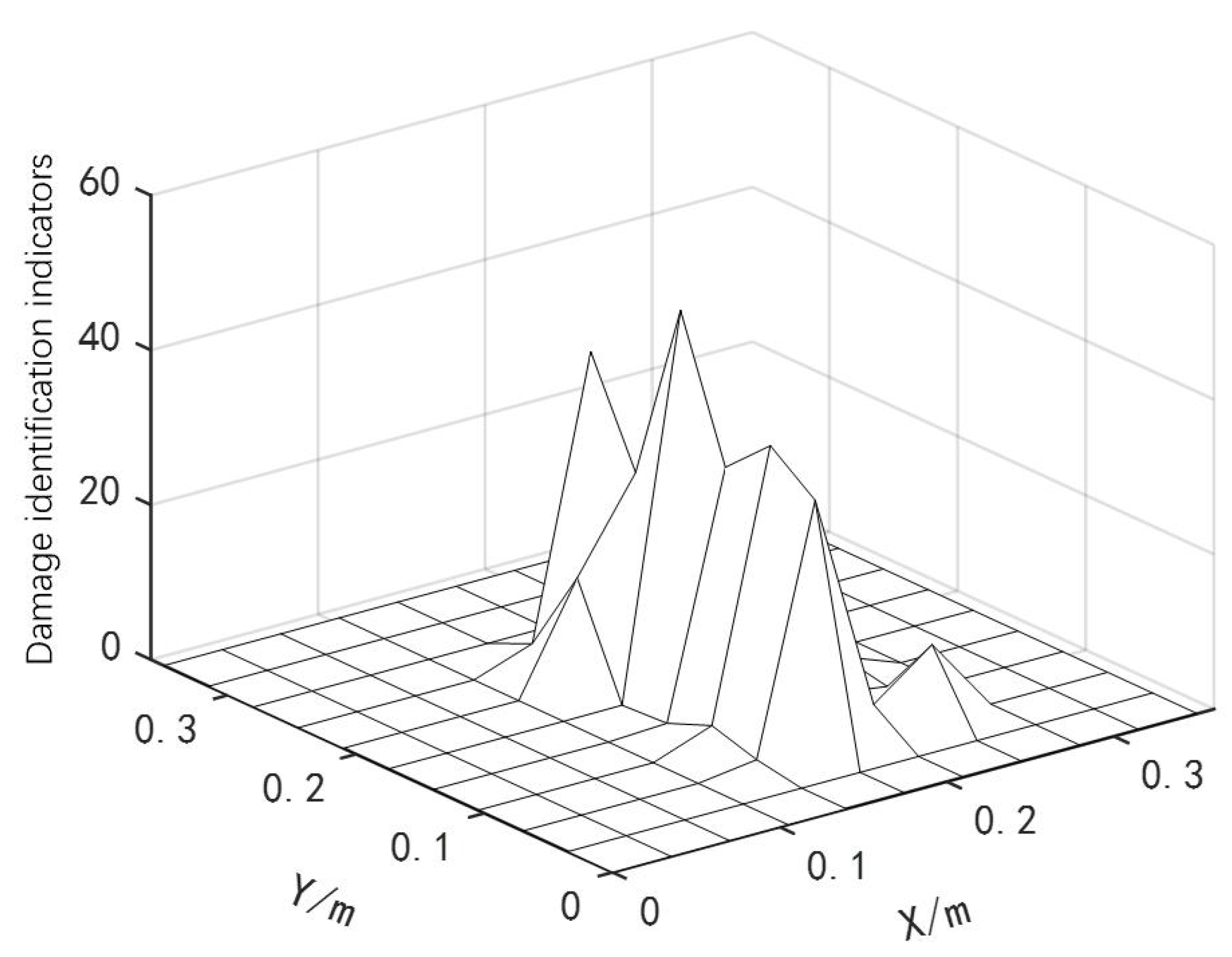
4.2. Analysis of Experimental Measurement Signal and Processing Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bardenhagen, A.; Sethi, V.; Gudwani, H. Spider-silk composite material for aerospace application. Acta Astronaut. 2022, 193, 704–709. [Google Scholar]
- Yang, H.; Yang, Z.; Yang, L.; San, Y.N.; Lin, K.X.; Wu, Z.J. Progress in ultrasonic testing and imaging method for damage of carbon fiber composites. Acta Mater. Compos. Sin. 2023, 40, 4295–4317. [Google Scholar]
- Jia, Z.; Fu, R.; Wang, F. Research Advance Review of Machining Technology for Carbon Fiber Reinforced Polymer Composite Components. J. Mech. Eng. 2023, 59, 348–374. [Google Scholar]
- Singh, T.; Sehgal, S. Structural Health Monitoring of Composite Materials. Arch. Comput. Methods Eng. 2022, 29, 1997–2017. [Google Scholar] [CrossRef]
- Yao, S.; Zhou, M.; Xing, J. Study on Local High-Velocity-Impact Characteristics of Carbon Fiber Composite Laminates Based on Experimental Image Sequences. Materials 2025, 18, 1833. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Li, Z.; Chen, J. Application of two dimensional Morlet wavelet transform in damage detection for composite laminates. Compos. Struct. 2023, 318, 117091. [Google Scholar] [CrossRef]
- Yan, L.; Xiaolei, L.; Jie, G.; Cunfu, H. Analysis of Lamb Wave Dispersion Characteristics of Thermoelastic Anisotropic Laminates Based on the Polynomial Method. Chin. J. Theor. Appl. Mech. 2023, 55, 1939–1949. [Google Scholar]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E. Vibration-based crack prediction on a beam model using hybrid butterfly optimization algorithm with artificial neural network. Front. Struct. Civ. Eng. 2022, 16, 976–989. [Google Scholar] [CrossRef]
- Niu, Z.; Wu, F.; Han, Z.; Zhuo, Y.; Che, A.; Zhu, H. An Improved Generalized Flexibility Sensitivity Method for Structural Damage Detection. J. Shanghai Jiaotong Univ. 2023, 57, 1–20. [Google Scholar]
- He, W.; He, K.; Wang, G. An improved method for modal shape identification of loaded bridges based on frequency variation. J. Vib. Shock 2023, 42, 189–196, 283. [Google Scholar]
- Le, T.C.; Ho, D.D.; Nguyen, C.T.; Huynh, T.C. Structural Damage Localization in Plates Using Global and Local Modal Strain Energy Method. Adv. Civ. Eng. 2022, 18, 4456439. [Google Scholar] [CrossRef]
- Mahdavi, S.; Xu, C. Time-Domain Structural Damage Identification Using Ensemble Bagged Trees and Evolutionary Optimization Algorithms. Struct. Control Health Monit. 2023, 2023, 6321012. [Google Scholar] [CrossRef]
- Guedria, N.B. An accelerated differential evolution algorithm with new operators for multi-damage detection in plate-like structures. Appl. Math. Model. 2020, 80, 366–383. [Google Scholar] [CrossRef]
- Banimahd, S.A. Structural Damage Detection Using Artificial Bee Colony Optimization Algorithm. Modares Civ. Eng. J. 2019, 19, 17–29. [Google Scholar]
- Liu, R.; Zhang, Q.; Jiang, F.; Zhou, J.; He, J.; Mao, Z. Research on Deformation Prediction of VMD-GRU Deep Foundation Pit Based on PSO Optimization Parameters. Materials 2024, 17, 2198. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yue, H.; Zhang, C.; Dai, W.; Guo, C.; Li, Q.; Zhang, J. Fatigue Life Prediction of 2024-T3 Al Alloy by Integrating Particle Swarm Optimization—Extreme Gradient Boosting and Physical Model. Materials 2024, 17, 5332. [Google Scholar] [CrossRef] [PubMed]
- Tian, S.; Xiao, Y.; Liu, J.; Fan, J.; Xie, G.; Du, W. Vibration based numerical and experimental analysis on debonding defect identification for lattice sandwich plate. Int. J. Appl. Electromagn. Mech. 2019, 59, 1431–1439. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 12, pp. 1941–1948. [Google Scholar]
- Schemmel, R.; Krieger, V.; Hemsel, T.; Sextro, W. Co-simulation of MATLAB and ANSYS for ultrasonic wire bonding process optimization. Microelectron. Reliab. 2021, 119, 114077. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, W.; Gong, W. Local Stress Analysis of Railway Steel Truss Bridge Based on Co-simulation Method. J. China Railw. Soc. 2021, 43, 144–152. [Google Scholar]
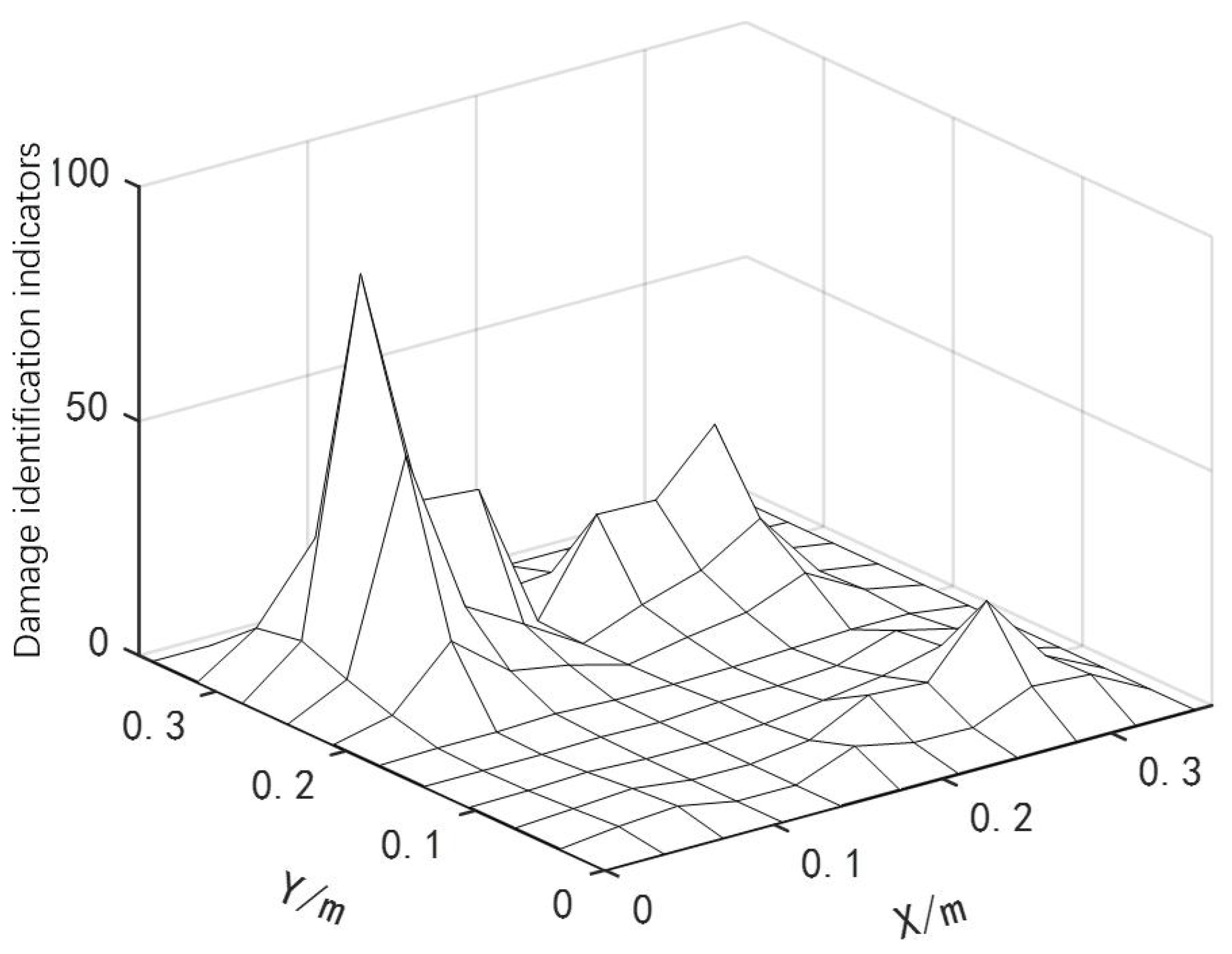
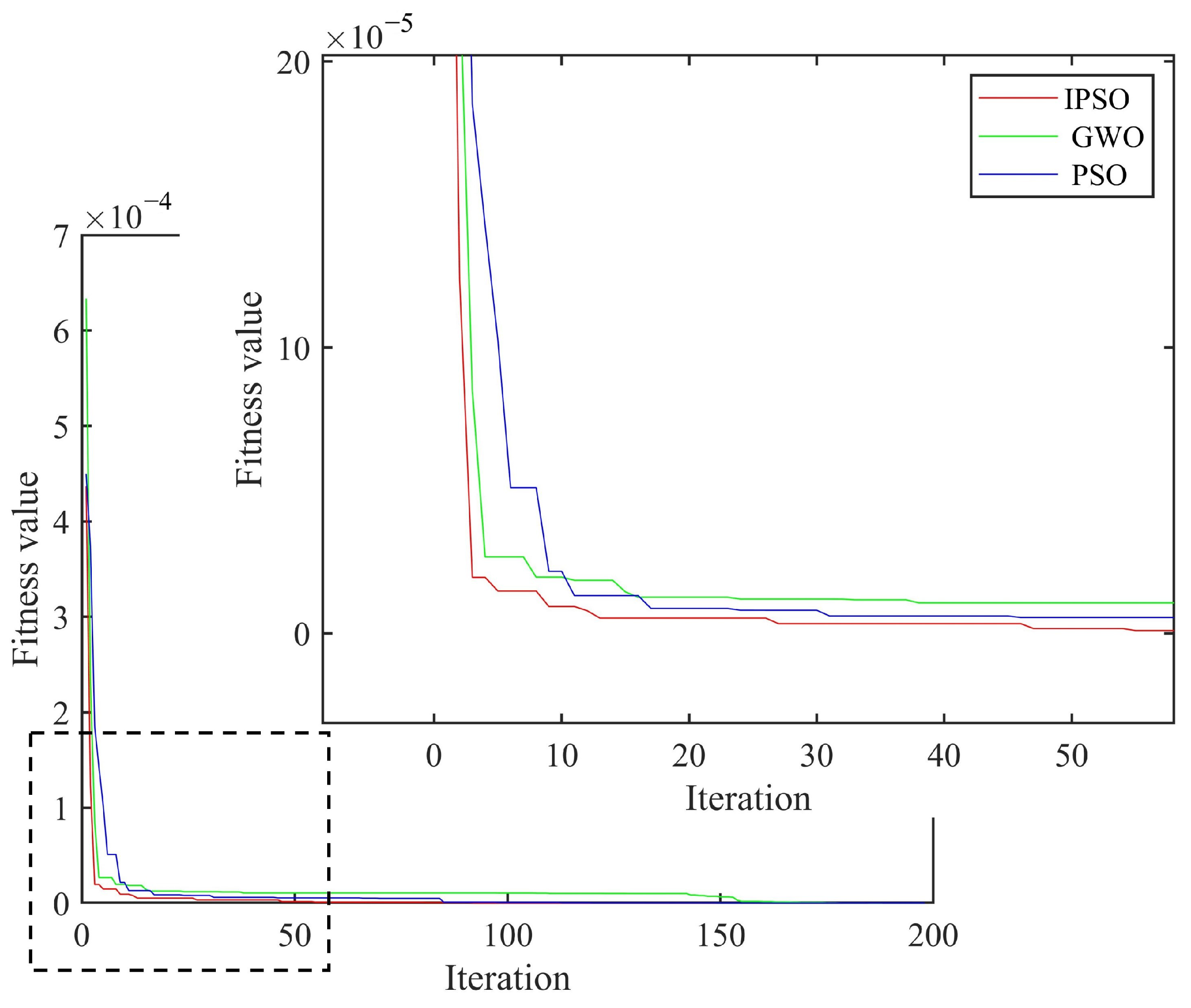
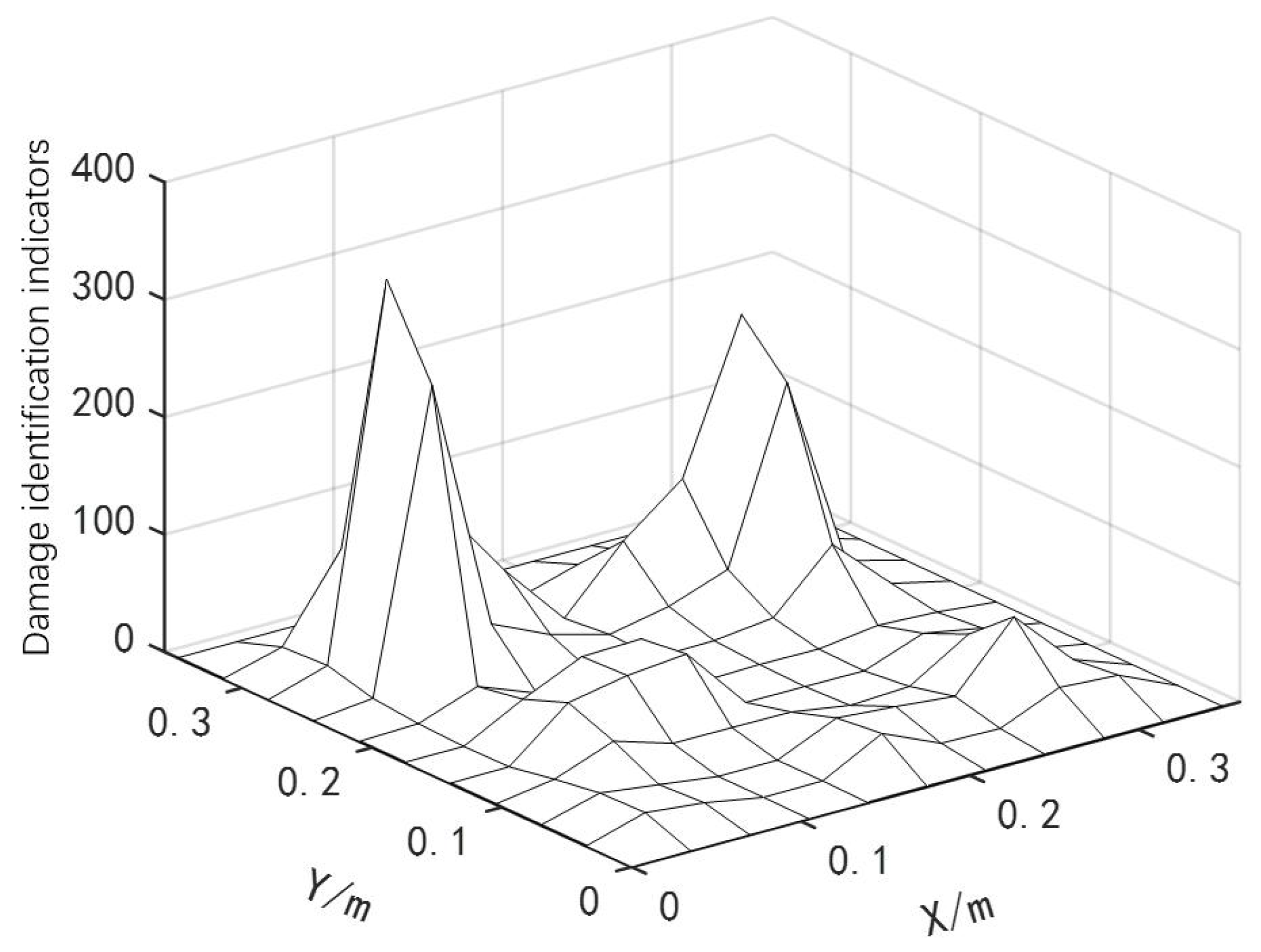
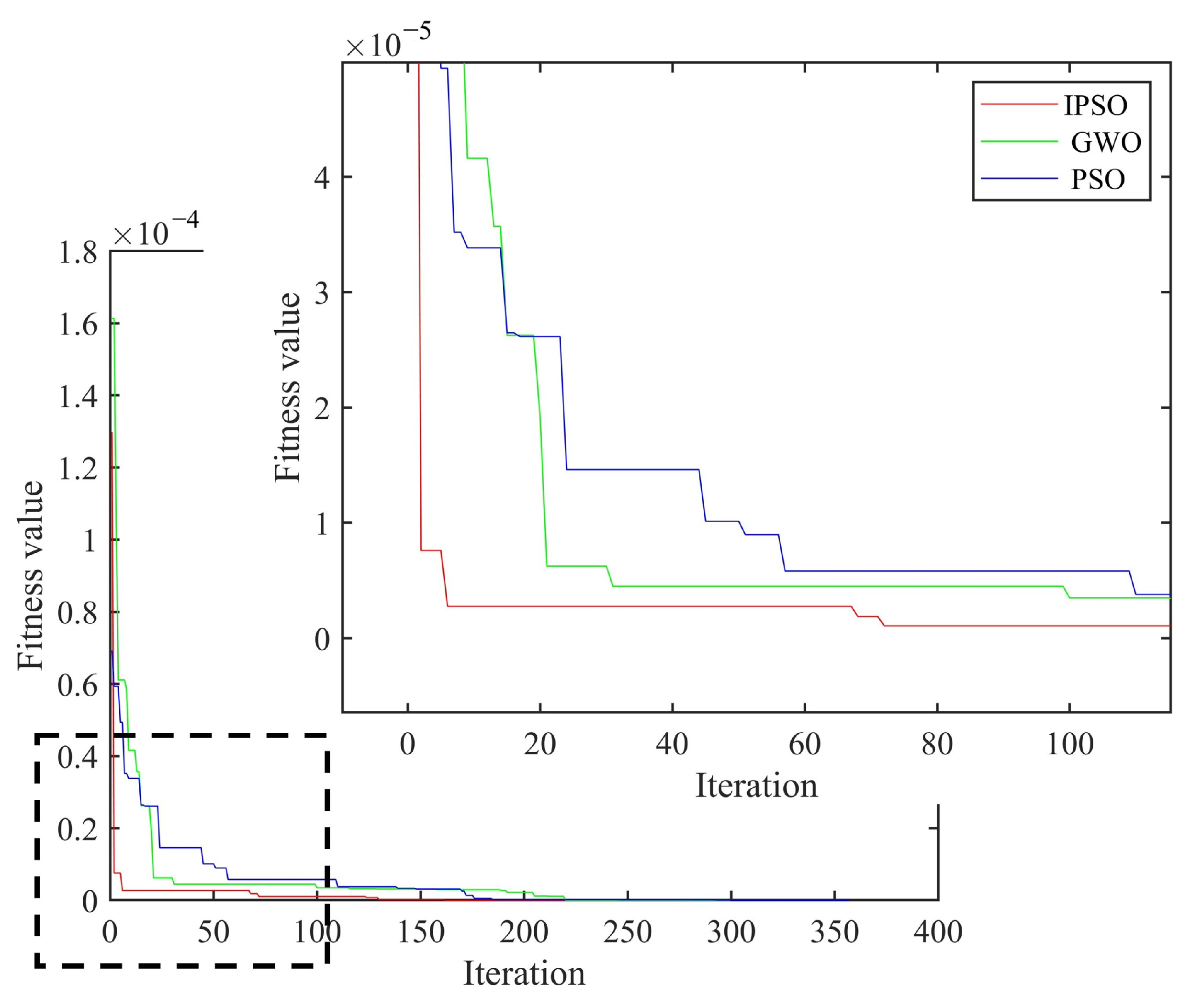




| Num. | Damage Condition | Number of Damage Unit | Damage Degree |
|---|---|---|---|
| 1 | Two discrete damage types | 23/78 | 30%/70% |
| 2 | Two consecutive damage types | 56/57 | 30%/30% |
| 3 | Three damage types | 23/73/78 | 20%/30%/40% |
| 4 | Four damage types | 23/46/73/78 | 30%/60%/60%/70% |
| Algorithm Name | Preset Value | Detected Value | Number of Convergences | Error (%) |
|---|---|---|---|---|
| PSO | 0.3/0.7 | 0.3040/0.7036 | 102 | 1.33/0.51 |
| GWO | 0.3/0.7 | 0.3030/0.6960 | 97 | 1.0/0.57 |
| IPSO | 0.3/0.7 | 0.3005/0.6993 | 60 | 0.17/0.10 |
| Algorithm Name | Preset Value | Detected Value | Number of Convergences | Error (%) |
|---|---|---|---|---|
| PSO | 0.3/0.3 | 0.295/0.297 | 151 | 1.6/1.0 |
| GWO | 0.3/0.3 | 0.296/0.297 | 144 | 1.3/1.0 |
| IPSO | 0.3/0.3 | 0.2985/0.2994 | 93 | 0.50/0.20 |
| Algorithm Name | Preset Value | Detected Value | Number of Convergences | Error (%) |
|---|---|---|---|---|
| PSO | 0.2/0.3 | 0.196/0.311 | 198 | 2.0/3.33 |
| /0.4 | /0.413 | /3.25 | ||
| GWO | 0.2/0.3 | 0.203/0.303 | 188 | 1.5/1.0 |
| /0.4 | /0.412 | /3 | ||
| IPSO | 0.2/0.3 | 0.196/0.3012 | 149 | 0.15/0.27 |
| /0.4 | /0.4014 | /0.37 |
| Algorithm Name | Preset Value | Detected Value | Number of Convergences | Error (%) |
|---|---|---|---|---|
| PSO | 0.3/0.6 | 0.305/0.611 | 357 | 1.66/1.83 |
| /0.6/0.7 | 0.591/0.689 | 1.5/1.57 | ||
| GWO | 0.3/0.6 | 0.296/0.589 | 305 | 1.3/1.83 |
| /0.6/0.7 | 0.604/0.703 | 0.66/0.42 | ||
| IPSO | 0.3/0.6 | 0.3014/0.6004 | 226 | 0.46/0.06 |
| /0.6/0.7 | 0.6002/0.7012 | 0.03/0.17 |
| Damage Degree | 5% | 10% | 70% | 95% |
|---|---|---|---|---|
| Damage unit number | 56 | 56 | 56 | 56 |
| Optimal solution | 0.0523 | 0.1028 | 0.7009 | 0.9494 |
| Average solution | 0.0510 | 0.1014 | 0.6999 | 0.9517 |
| Standard deviation | 0.0027 | 0.0030 | 0.0037 | 0.0023 |
| Error (%) | 2.00 | 1.40 | 0.01 | 0.18 |
| Without Noise | With Noise | |||
|---|---|---|---|---|
| Damage unit number | 23 | 78 | 23 | 78 |
| Optimal solution | 0.3005 | 0.7003 | 0.3059 | 0.6914 |
| Average solution | 0.3005 | 0.6993 | 0.2870 | 0.6822 |
| Standard deviation | 0.0024 | 0.0013 | 0.0151 | 0.0160 |
| Error (%) | 0.17 | 0.10 | 4.31 | 2.54 |
| Without Noise | With Noise | |||
|---|---|---|---|---|
| Damage unit number | 56 | 57 | 56 | 57 |
| Optimal solution | 0.2985 | 0.2994 | 0.2807 | 0.3039 |
| Average solution | 0.2994 | 0.2994 | 0.3171 | 0.2838 |
| Standard deviation | 0.0033 | 0.0014 | 0.0324 | 0.0164 |
| Error (%) | 0.20 | 0.20 | 5.70 | 5.40 |
| Modal Order | Simulation Frequency (Hz) | Experimental Frequency (Hz) | Relative Error (%) |
|---|---|---|---|
| 1 | 88.561 | 76.433 | 13.69 |
| 2 | 194.39 | 185.432 | 4.61 |
| 3 | 198.21 | 189.377 | 4.46 |
| 4 | 327.33 | 341.807 | 4.42 |
| 5 | 360.31 | 354.737 | 1.55 |
| The First Run Results | The Second Run Results | The Third Run Results | |
|---|---|---|---|
| Damage unit number | 56 | 56 | 56 |
| Damage degree | 0.9836 | 0.9765 | 0.9890 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Wang, S.; Chen, Z.; Hao, R.; Qin, Z.; Ma, J.; Xu, L. Damage Quantitative Detection of Curved Composite Laminates Based on Improved Particle Swarm Optimization Algorithm. Materials 2025, 18, 2317. https://doi.org/10.3390/ma18102317
Tian S, Wang S, Chen Z, Hao R, Qin Z, Ma J, Xu L. Damage Quantitative Detection of Curved Composite Laminates Based on Improved Particle Swarm Optimization Algorithm. Materials. 2025; 18(10):2317. https://doi.org/10.3390/ma18102317
Chicago/Turabian StyleTian, Shuxia, Shunqiang Wang, Zhenmao Chen, Ran Hao, Zhihui Qin, Jiangdong Ma, and Linfeng Xu. 2025. "Damage Quantitative Detection of Curved Composite Laminates Based on Improved Particle Swarm Optimization Algorithm" Materials 18, no. 10: 2317. https://doi.org/10.3390/ma18102317
APA StyleTian, S., Wang, S., Chen, Z., Hao, R., Qin, Z., Ma, J., & Xu, L. (2025). Damage Quantitative Detection of Curved Composite Laminates Based on Improved Particle Swarm Optimization Algorithm. Materials, 18(10), 2317. https://doi.org/10.3390/ma18102317






