Sensitivity Analysis and Influence Evaluation of Progressive Wall Thickness of Honeycomb Structures as Energy Absorber Produced by Additive Technology Multi-Jet Fusion
Abstract
:1. Introduction
1.1. Cellular Structures
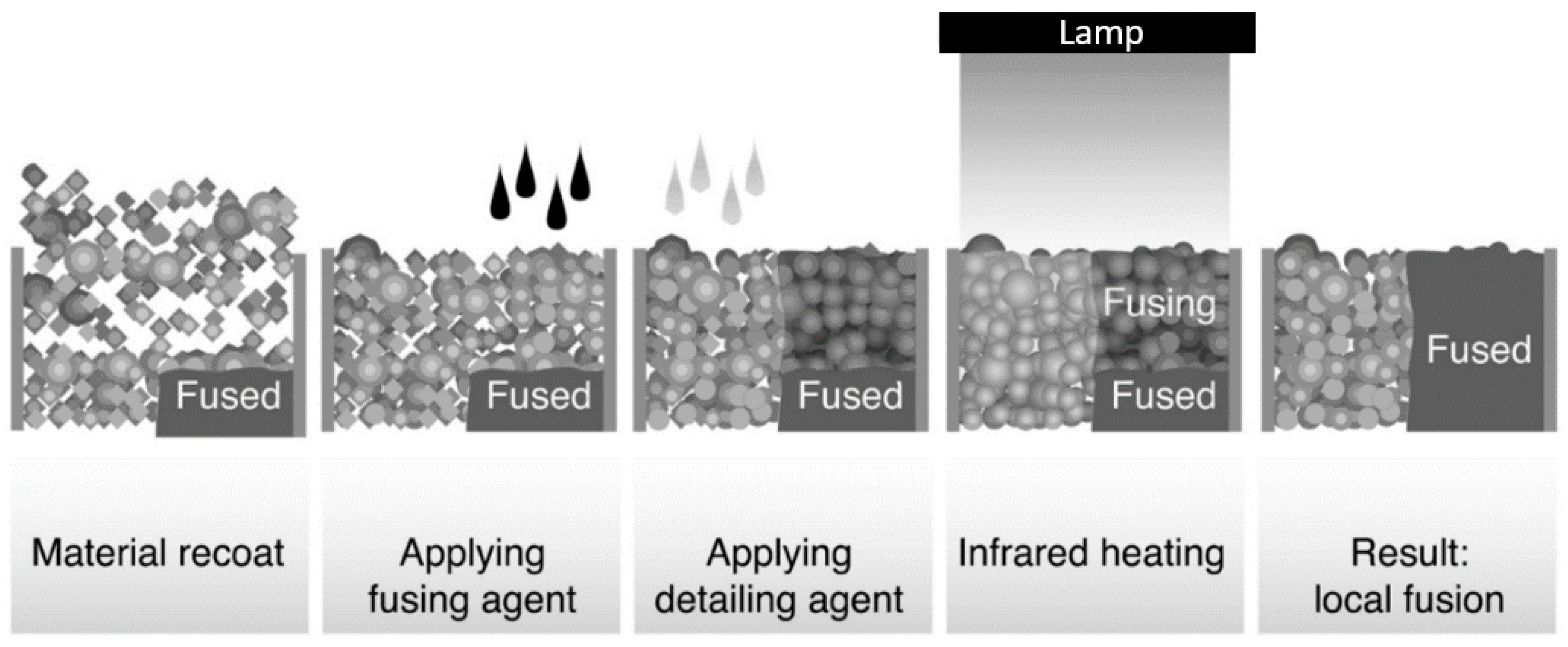
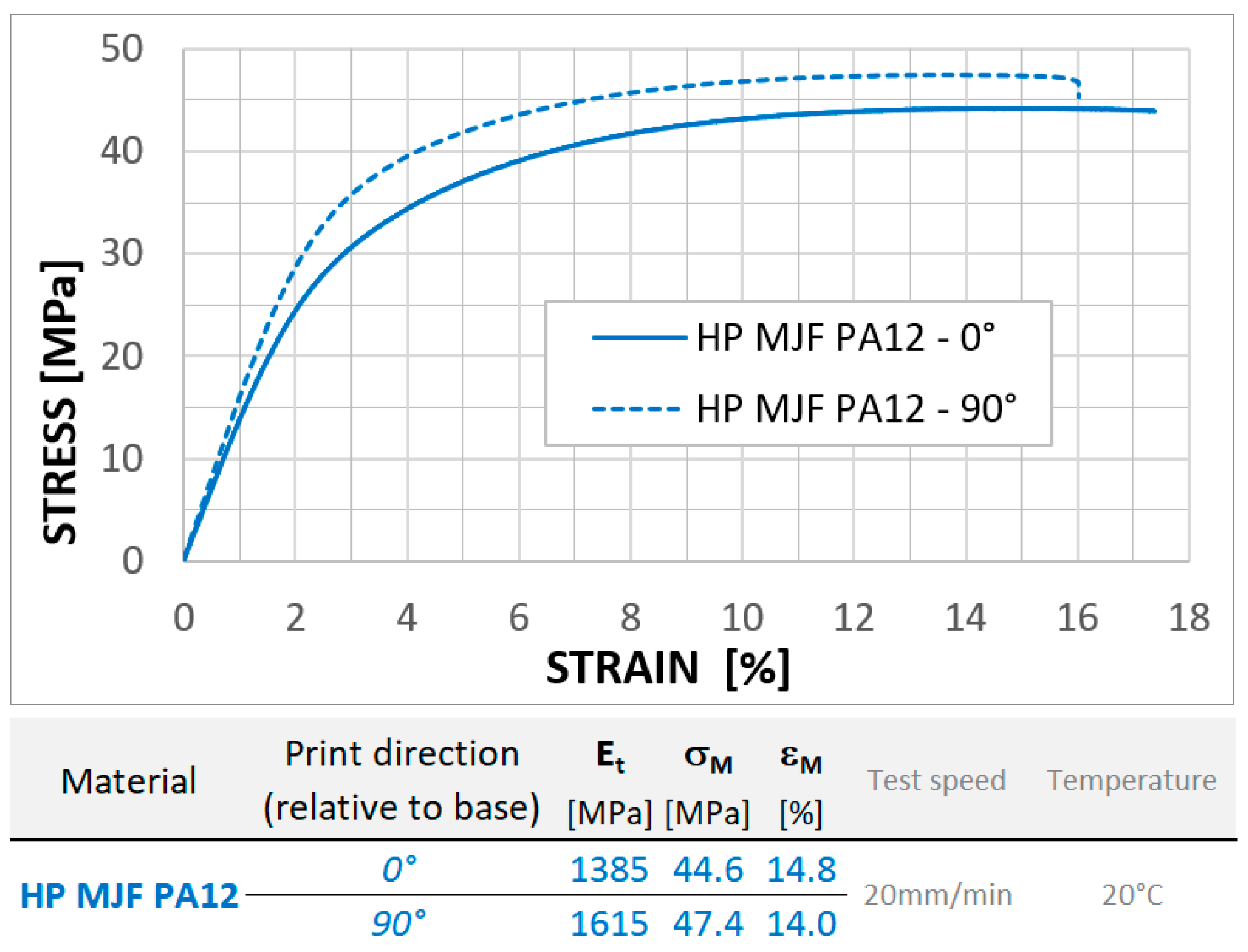
1.2. Three-Dimensional Printing Technology and Material
1.3. Cellular Structures Made by Additive Technologies
2. Investigation of Dynamic Properties of Honeycombs Based on Experimental and Numerical Methods
2.1. Numerical Analyses
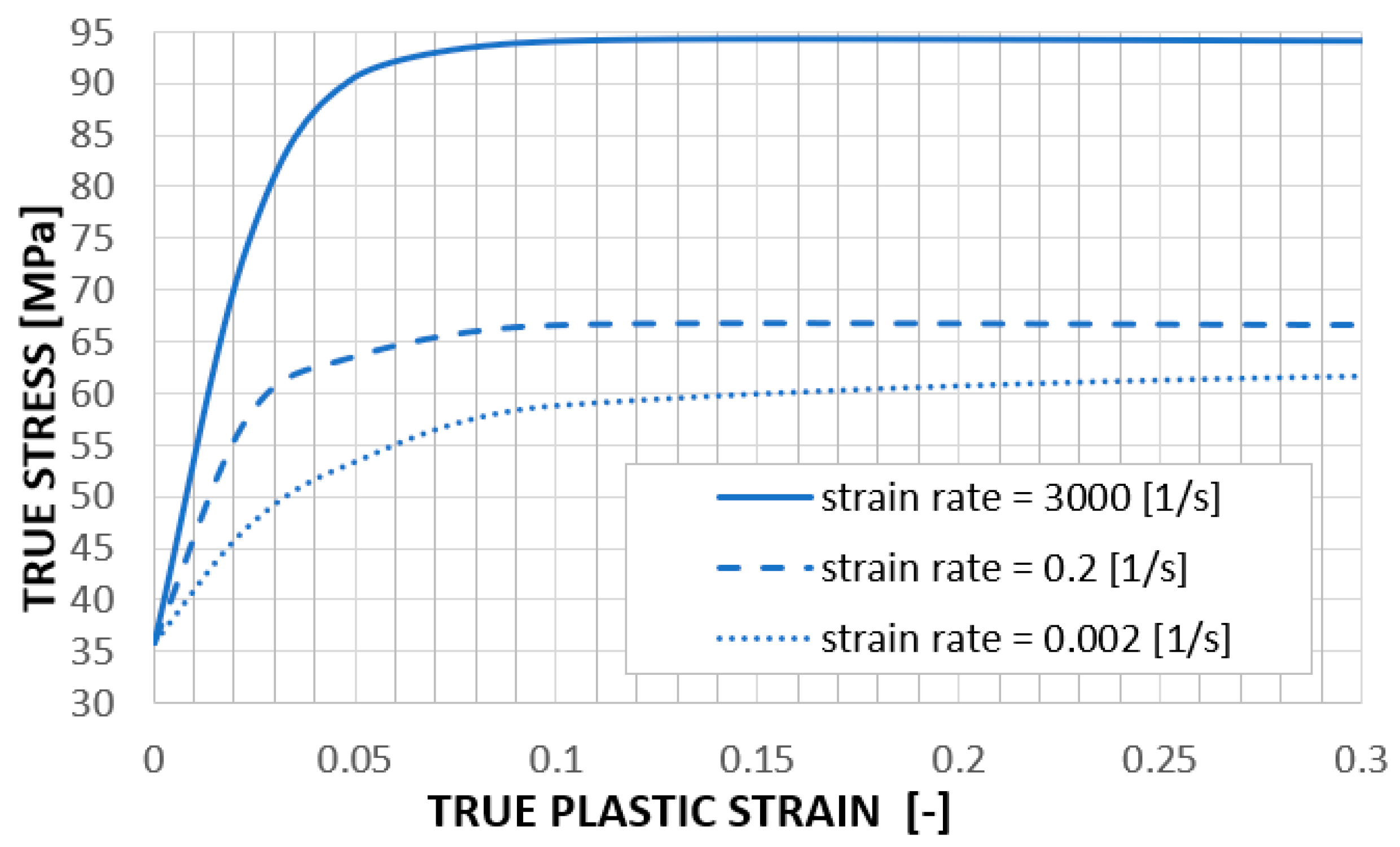
2.1.1. Dynamic Phenomena in Numerical Simulations: Explicit Finite Element Analysis (FEA)
2.1.2. Pam-Crash: FEM-Based Computational Solver
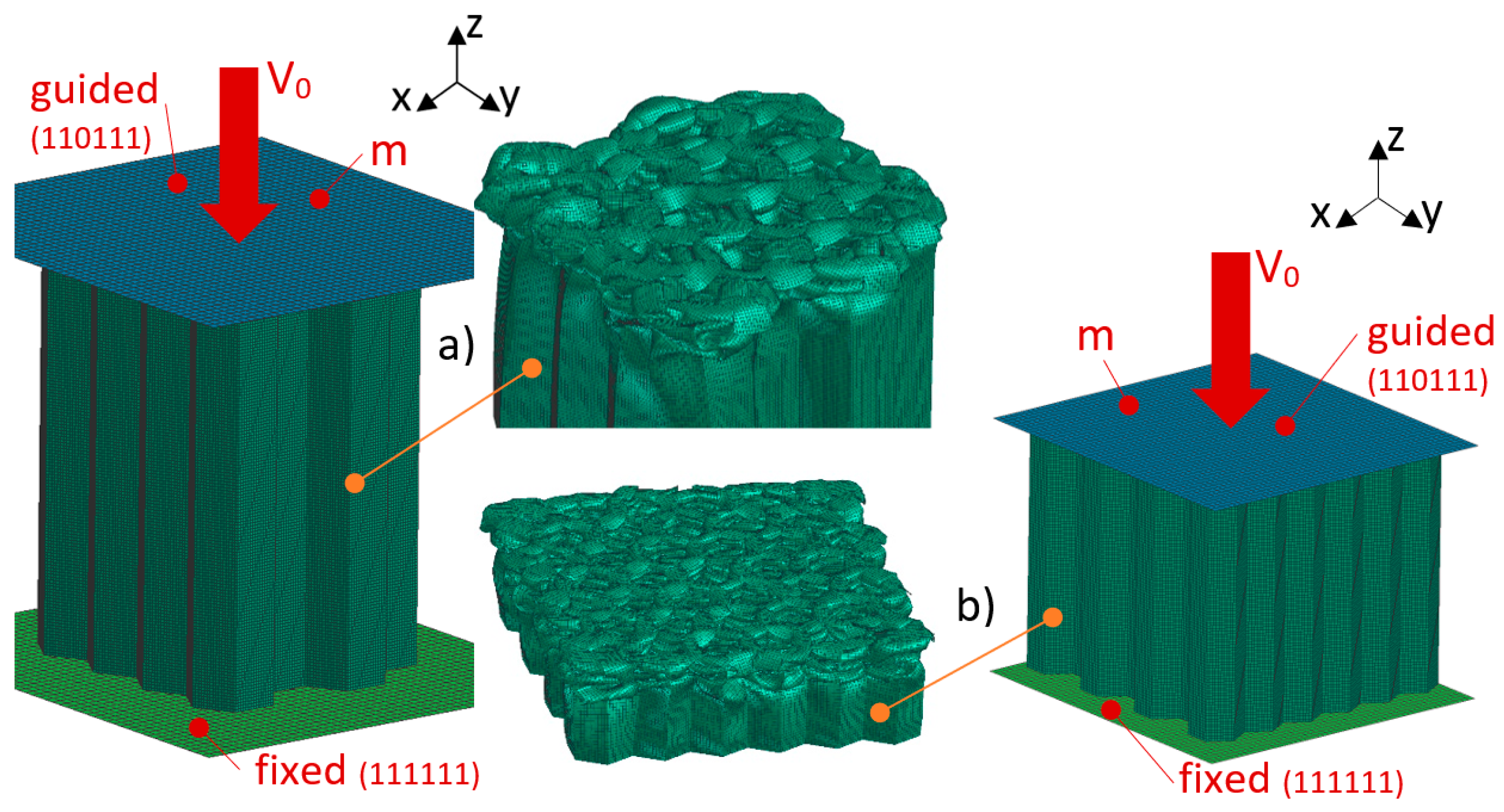
2.1.3. Computational Model for FEA
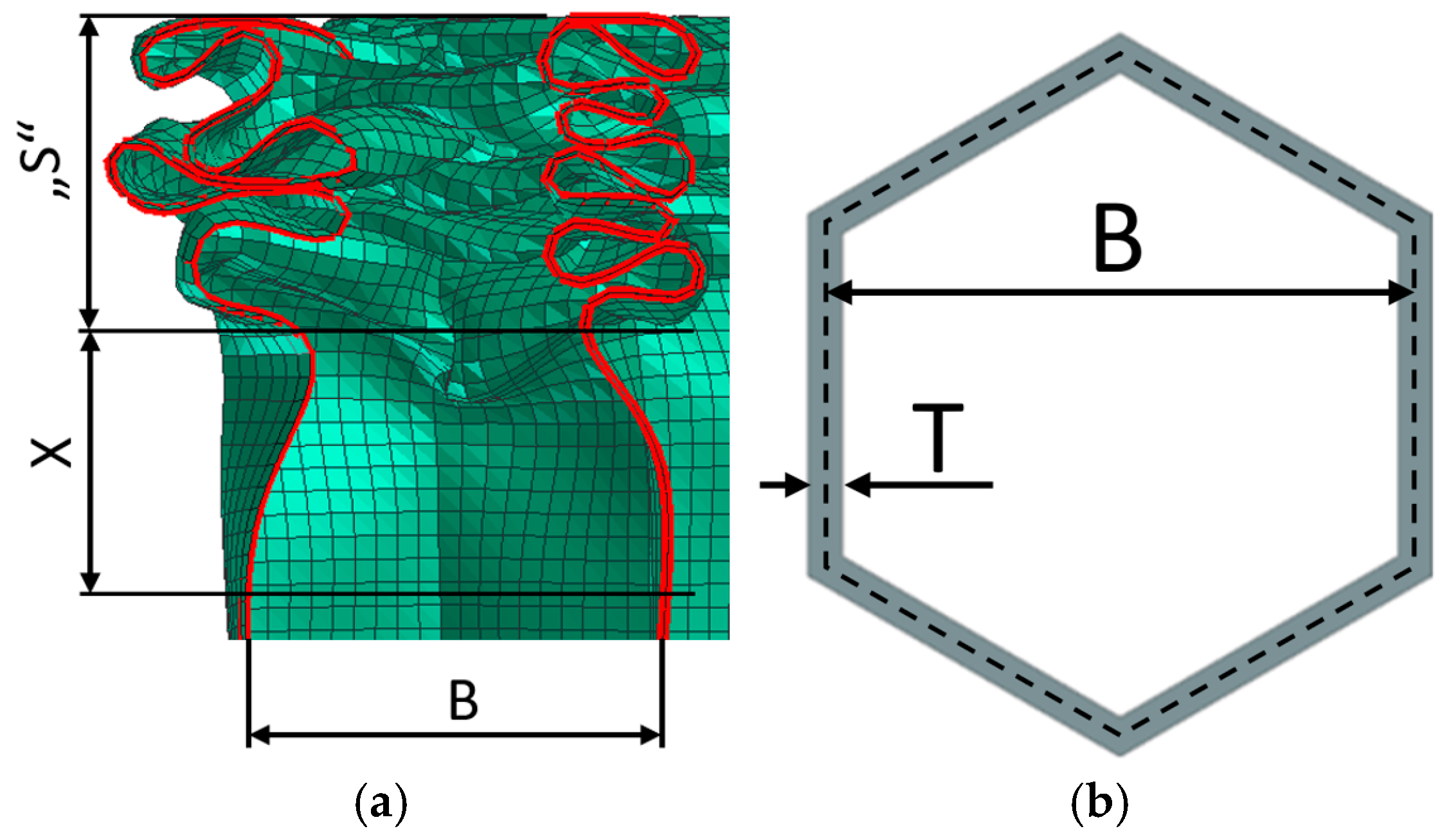
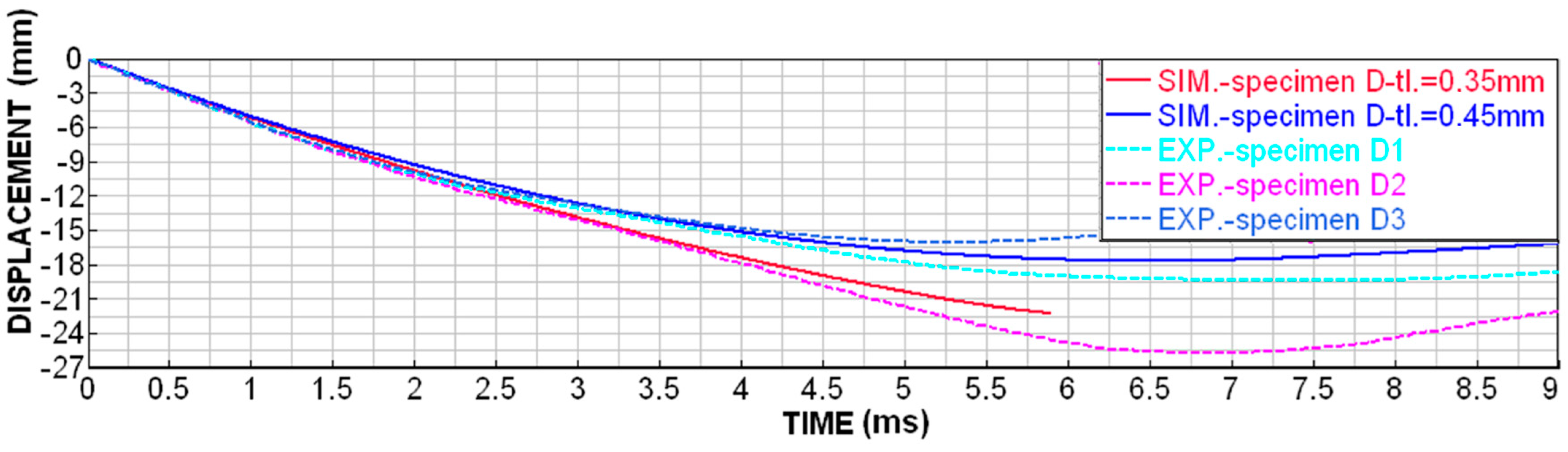
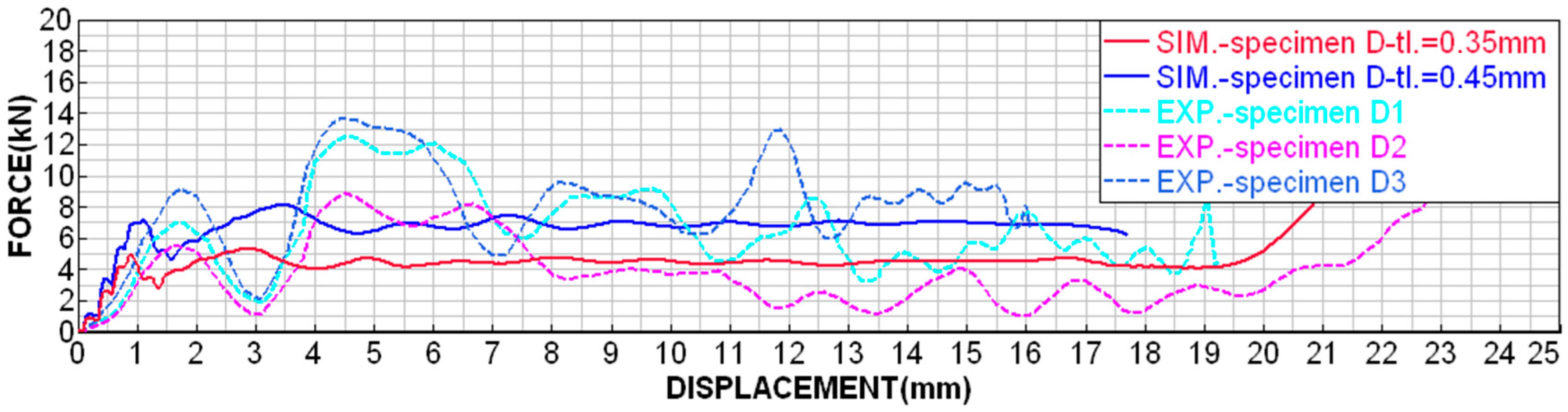
2.2. Validation of Numerical Simulations According to Experimental Testing
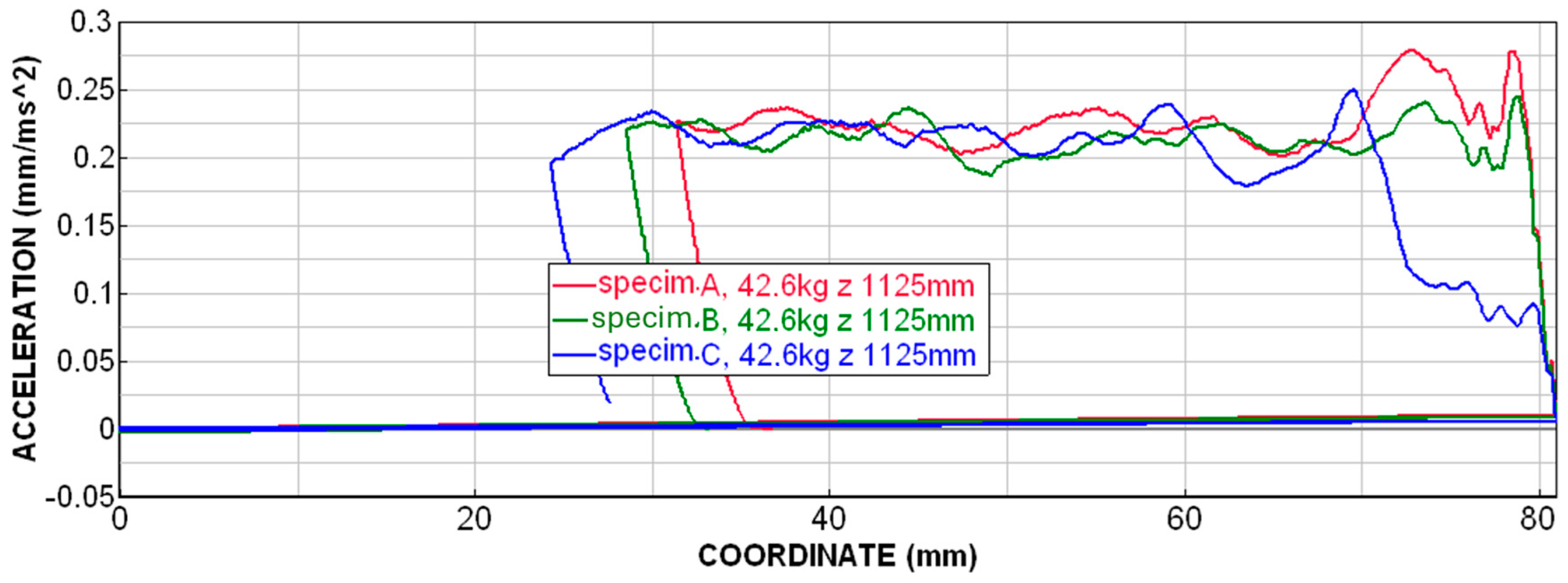
2.2.1. Experimental Testing
2.2.2. Validation of Numerical Simulations
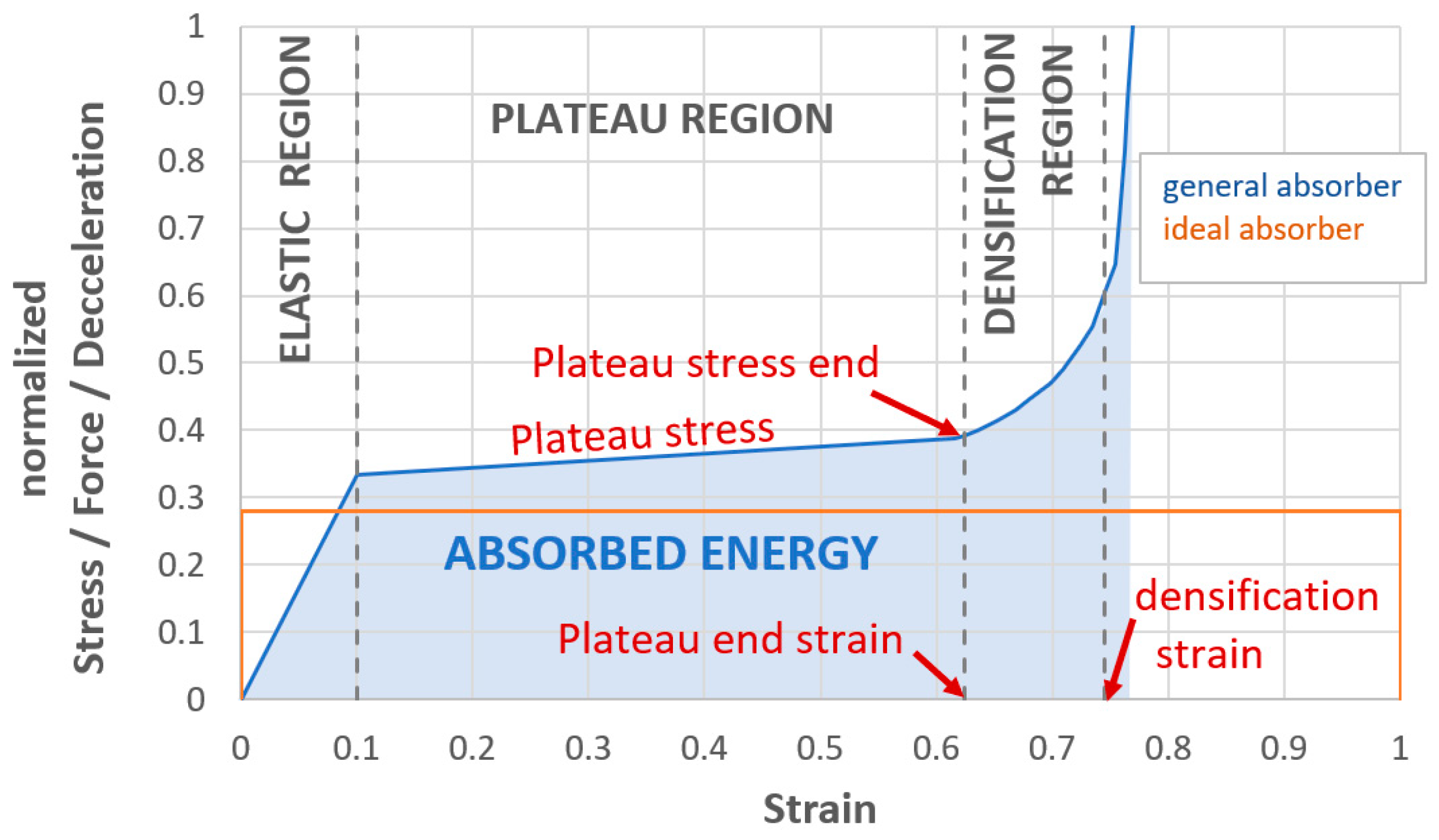
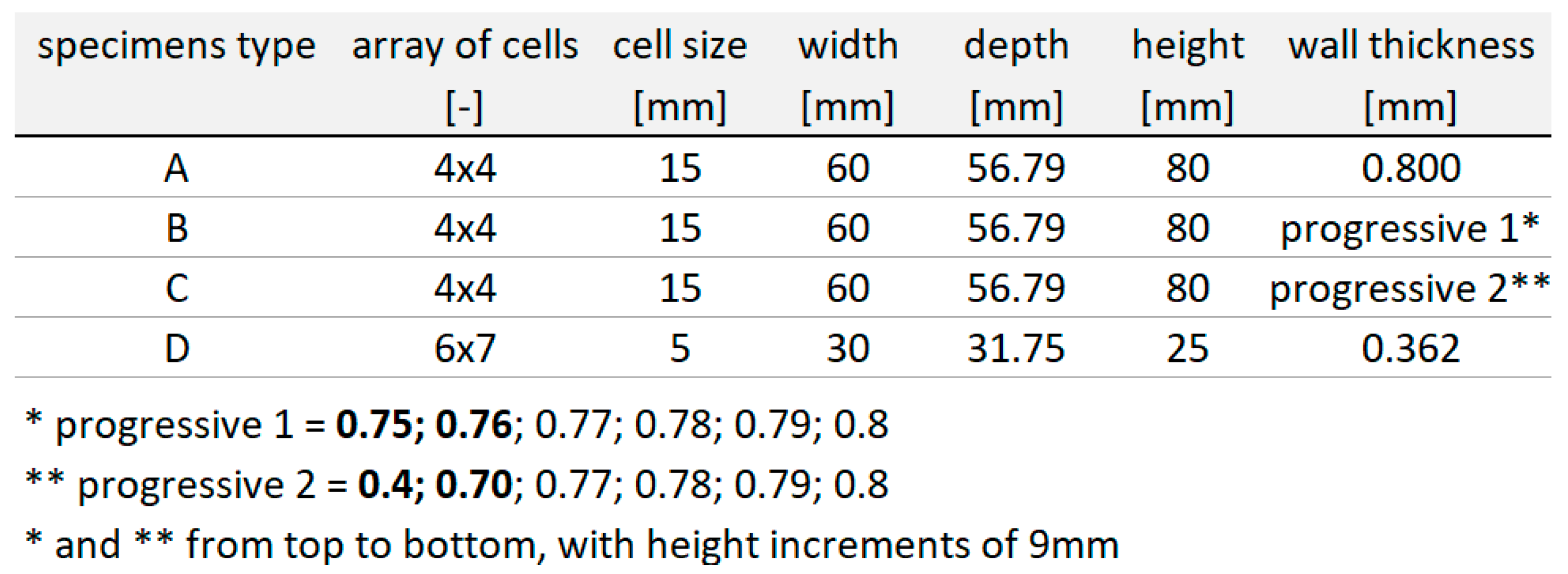
2.3. Evaluation of the Parameters Affecting the Properties of the Honeycomb
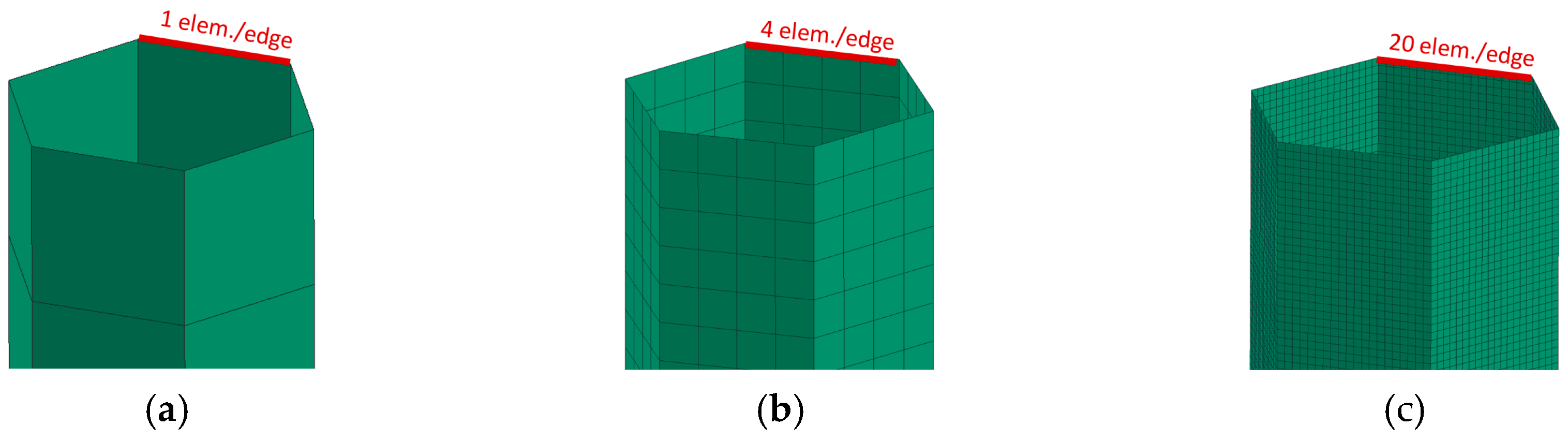
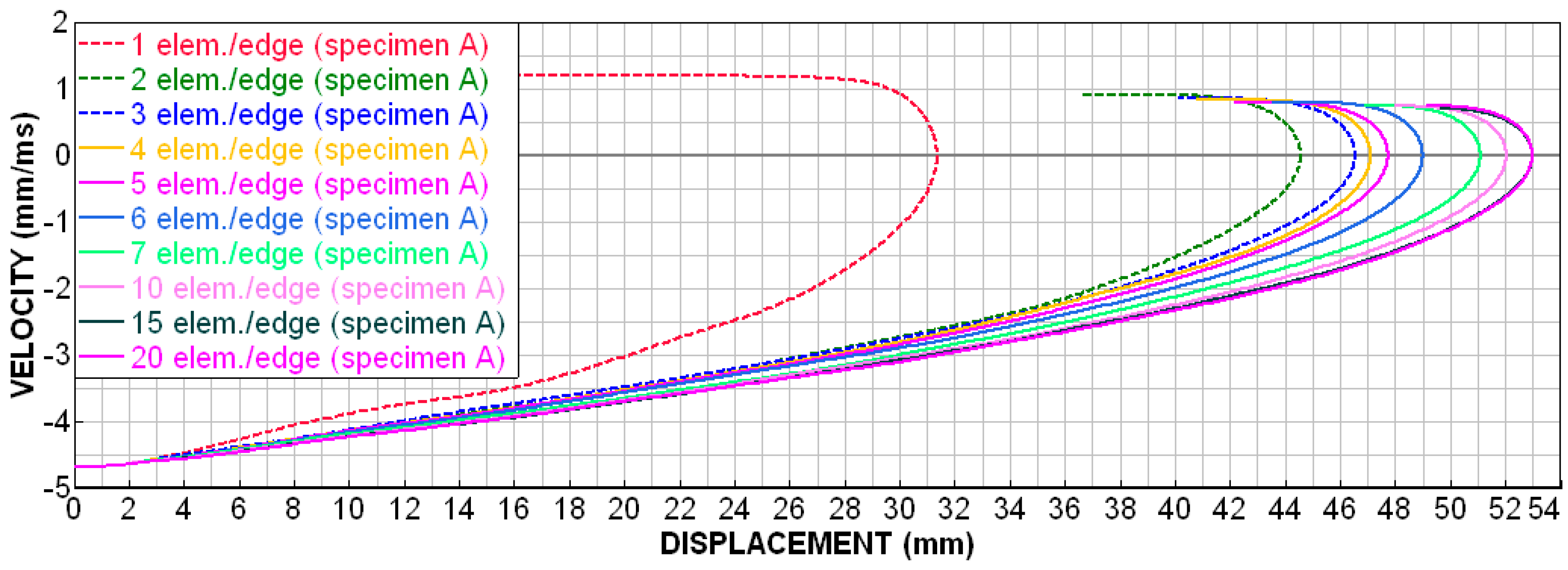
2.4. Sensitivity Analysis—Size of FEM Mesh Elements
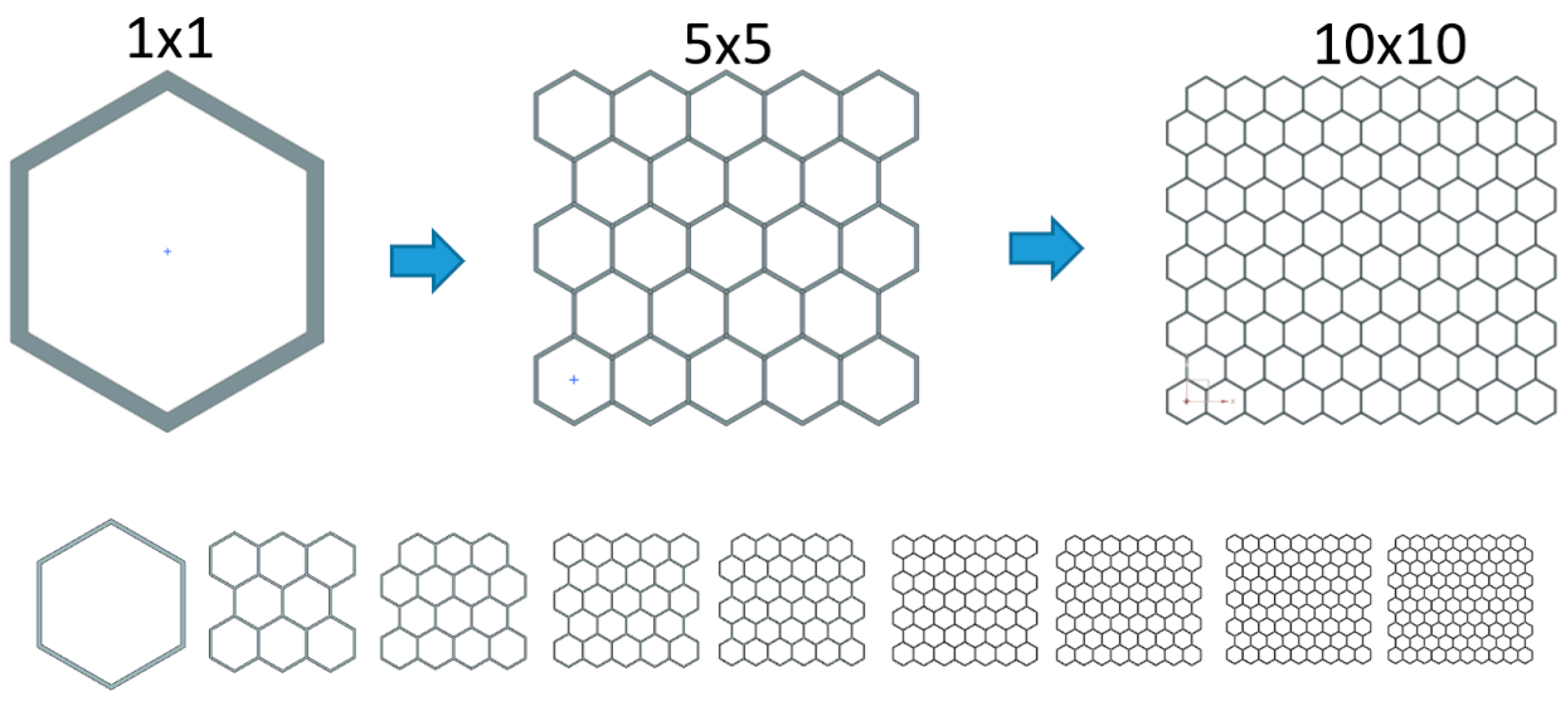
2.5. Sensitivity Analysis—Size of Cell Size
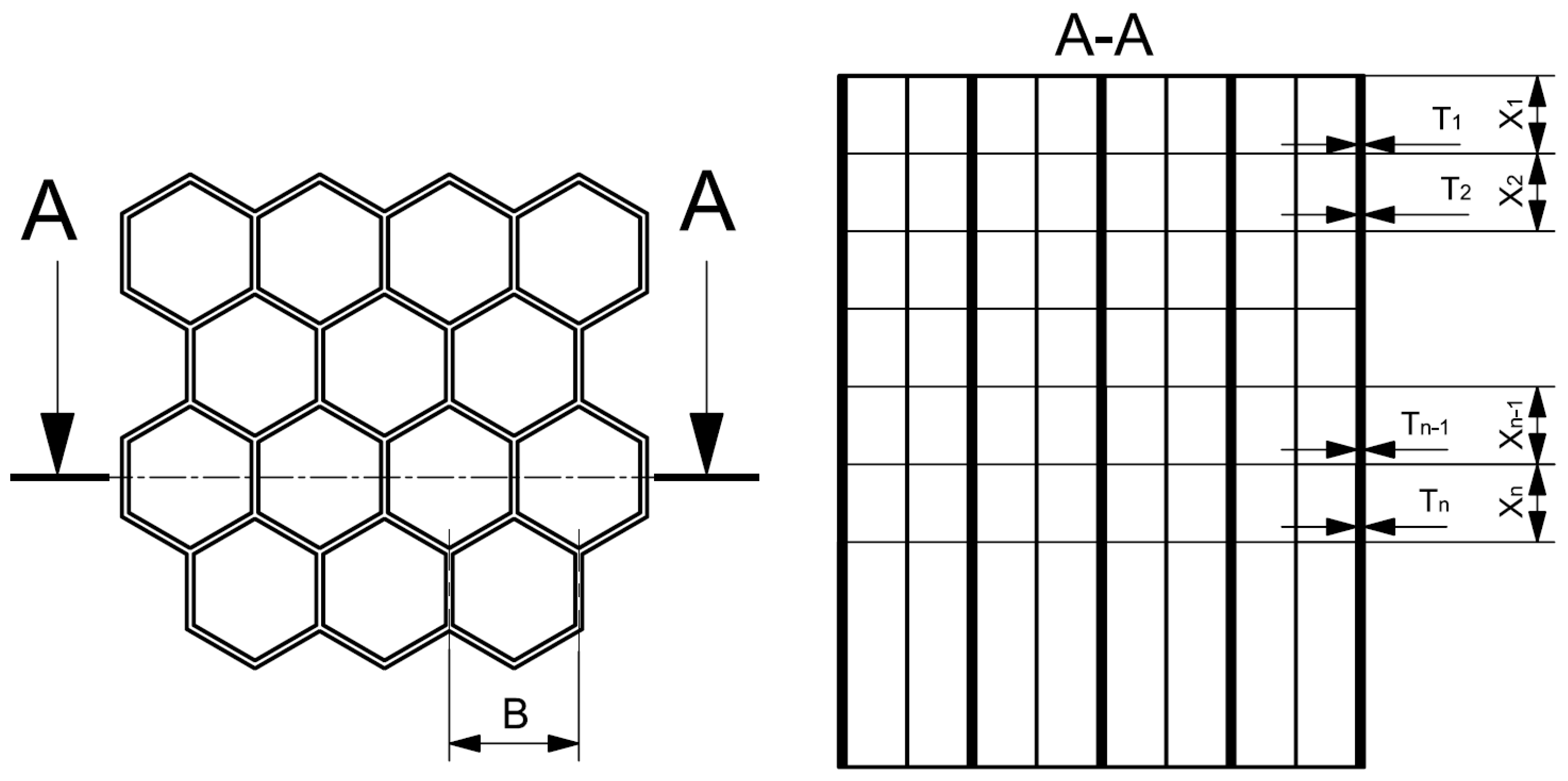
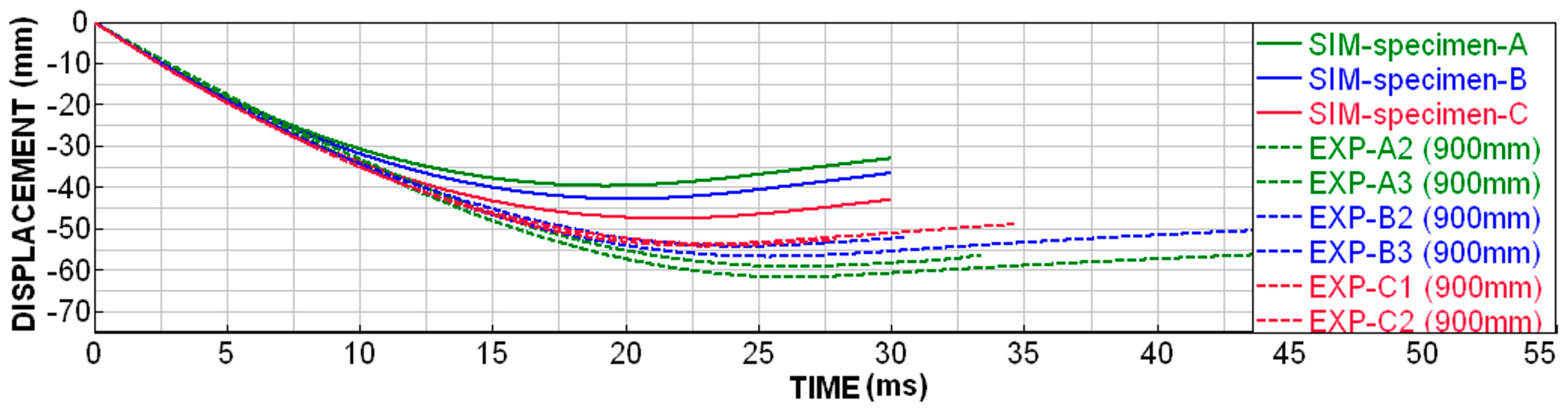
2.6. Effect of Progressive Honeycomb Wall Thickness
3. Summarization and Discussion of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Špirk, S.; Křížek, M.; Jeníček, S. Polyurethane foam behaviour during impact. In IOP Conference Series: Materials Science and Engineering, MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; ISSN 2261236X. [Google Scholar] [CrossRef]
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef]
- Srivastava, V.; Srivastava, R. On the polymeric foams: Modeling and properties. J. Mater. Sci. 2014, 49, 2681–2692. [Google Scholar] [CrossRef]
- Gorguluarslan, R.; Gandhi, U.; Mandapati, R.; Choi, S. Design and fabrication of periodic lattice-based cellular structures. Comput. Aided Des. Appl. 2015, 13, 50–62. [Google Scholar] [CrossRef]
- Sedlacek, F.; Lasova, V. Optimization of Additive Manufactured Components Using Topology Optimization. Struct. Integr. 2019, 5, 106–107. [Google Scholar] [CrossRef]
- Pflug, J.; Czarnecki, T. Continuous honeycomb production technology. JEC Composites Magazine, March 2014; 111–113. [Google Scholar]
- Ráž, K.; Chval, Z.; Kemka, V. Parametric Production of Prostheses Using the Additive Polymer Manufacturing Technology Multi Jet Fusion. Materials 2024, 17, 2347. [Google Scholar] [CrossRef]
- Farkas, A.Z.; Galatanu, S.-V.; Nagib, R. The Influence of Printing Layer Thickness and Orientation on the Mechanical Properties of DLP 3D-Printed Dental Resin. Polymers 2023, 15, 1113. [Google Scholar] [CrossRef]
- Ráž, K.; Chval, Z.; Thomann, S. Minimizing Deformations during HP MJF 3D Printing. Materials 2023, 16, 7389. [Google Scholar] [CrossRef] [PubMed]
- Habib, F.; Iovenitti, P.; Masood, S.; Nikzad, M.; Ruan, D. Design and evaluation of 3D printed polymeric cellular materials for dynamic energy absorption. Int. J. Adv. Manuf. Technol. 2019, 103, 2347–2391. [Google Scholar] [CrossRef]
- Osswald, P.V.; Obst, P.; Capote, G.A.M.; Friedrich, M.; Rietzel, D.; Witt, G. Failure criterion for PA 12 multi-jet fusion additive manufactured parts. Addit. Manuf. 2020, 37, 101668. [Google Scholar] [CrossRef]
- Riedelbauch, J.; Rietzel, D.; Witt, G. Analysis of material aging and the influence on the mechanical properties of polyamide 12 in the Multi Jet Fusion process. Addit. Manuf. 2019, 27, 259–266. [Google Scholar] [CrossRef]
- Guessasma, S.; Belhabib, S. The Influence of Microstructural Arrangement on the Failure Characteristics of 3D-Printed Polymers: Exploring Damage Behaviour in Acrylonitrile Butadiene Styrene. Materials 2024, 17, 2699. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy absorption in lattice structures in dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Linul, E.; Şerban, D.A.; Voiconi, T.; Marşavina, L.; Sadowski, T. Energy—Absorption and efficiency diagrams of rigid PUR foams. Key Eng. Mater. 2013, 601, 246–249. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalapati, S.; Feih, S. Printing and characterisation of Kagome lattice structures by fused deposition modelling. Mater. Des. 2018, 137, 266–275. [Google Scholar] [CrossRef]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D printed stretching-dominated micro-trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar] [CrossRef]
- Mohsenizadeh, M.; Gasbarri, F.; Munther, M.; Beheshti, A.; Davami, K. Additively-manufactured lightweight Metamaterials for energy absorption. Mater. Des. 2018, 139, 521–530. [Google Scholar] [CrossRef]
- Atalay Kalsen, T.S.; Karadağ, H.B.; Eker, Y.R. The Out-Of-Plane Compression Behavior of In Situ Ethylene Vinyl Acetate (EVA)-Foam-Filled Aluminum Honeycomb Sandwich Structures. Materials 2023, 16, 5350. [Google Scholar] [CrossRef]
- Zhao, G.; Fu, T.; Li, J. Study on Concave Direction Impact Performance of Similar Concave Hexagon Honeycomb Structure. Materials 2023, 16, 3262. [Google Scholar] [CrossRef] [PubMed]
- Raz, K.; Chval, Z.; Sedlacek, F. Compressive strength prediction of quad-diametral lattice structures. Key Eng. Mater. 2020, 847, 69–74. [Google Scholar] [CrossRef]
- Raz, K.; Chval, Z. Development of a computational model of lattice structure. In IOP Conference Series: Materials Science and Engineering, MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2022. [Google Scholar]
- Spirk, S.; Kepka, M. Tests and Simulations for Assessment of Electric Buses Passive Safety. Procedia Eng. 2015, 114, 338–345. [Google Scholar] [CrossRef]
- Belytschko, T.; Lin, J.I.; Chen-Shyh, T. Explicit algorithms for the nonlinear dynamics of shells. Comput. Methods Appl. Mech. Eng. 1984, 42, 225–251. [Google Scholar] [CrossRef]
- Kühne, R. Electric buses—An energy efficient urban transportation means. Energy 2010, 35, 4510–4513. [Google Scholar] [CrossRef]
- Virtual Performance Solution—Solver Reference Manual; ESI Group: Bagneux, France, 2017.
- Xu, Q.; An, H. A class of domain decomposition based nonlinear explicit–implicit iteration algorithms for solving diffusion equations with discontinuous coefficient. J. Comput. Appl. Math. 2021, 386, 113232. [Google Scholar] [CrossRef]
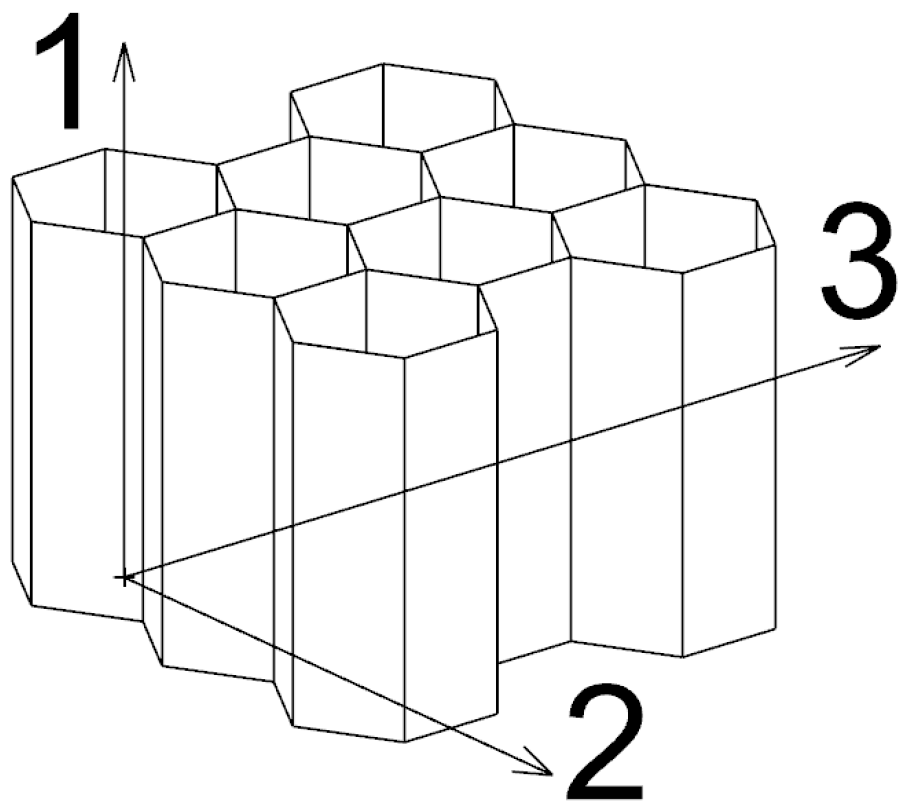









| INPUTS | OUTPUTS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Material | Geometric Parameters of Honeycomb | Load | ||||||||
| Width/Depth | Height | B | T | Mass | Velocity | E | aAVERAGE | Hdef. | A | |
| def. | def. | def. | def. | def. | def. | def. | def. | def. | def. | def. |
| def. | X-times def. | def. | def. | def. | def. | def. | def. | X-times def. | (1/X)-times def. | X-times def. |
| def. | X-times def. Y-times def. | def. | def. | def. | def. | def. | def. | (X ∗ Y)-times def. | (1/(X ∗ Y))-times def. | (X ∗ Y)-times def. |
| def. | def. | def. | def. | def. | X-times def. | def. | X-times def. | (1/X)-times def. | X-times def. | def. |
| def. | X-times def. | def. | def. | def. | X-times def. | def. | X-times def. | def. | def. | X-times def. |
| def. | def. | X-times def. | def. | def. | def. | def. | def. | def. | def. | def. |
| def. | def. | def. | def. | def. | def. | X-times def. | (X2)-times def. | def. | def. | def. |
| Array of Cells [-] | Cell Size [mm] | Model Width [mm] | Model Depth [mm] | Wall Thickness [mm] | Absorbed Energy * [J] | decc. MAX [m/s2] | decc. AVERAGE * [m/s2] |
|---|---|---|---|---|---|---|---|
| 1 × 1 | 60 | 60 | 69.28 | 1.832 | 124 | 243 | 119 |
| 3 × 3 | 20 | 60 | 57.74 | 0.956 | 210 | 272 | 199 |
| 4 × 4 | 15 | 60 | 56.79 | 0.800 | 241 | 279 | 227 |
| 5 × 5 | 12 | 60 | 55.43 | 0.637 | 249 | 277 | 236 |
| 6 × 6 | 10 | 60 | 54.84 | 0.557 | 260 | 292 | 249 |
| 7 × 7 | 8.57 | 60 | 54.43 | 0.477 | 262 | 300 | 251 |
| 8 × 8 | 7.50 | 60 | 54.13 | 0.429 | 269 | 310 | 257 |
| 9 × 9 | 6.67 | 60 | 53.91 | 0.381 | 272 | 310 | 262 |
| 10 × 10 | 6 | 60 | 53.69 | 0.349 | 279 | 320 | 268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalina, T.; Chval, Z.; Sedlacek, F.; Spirk, S. Sensitivity Analysis and Influence Evaluation of Progressive Wall Thickness of Honeycomb Structures as Energy Absorber Produced by Additive Technology Multi-Jet Fusion. Materials 2025, 18, 1. https://doi.org/10.3390/ma18010001
Kalina T, Chval Z, Sedlacek F, Spirk S. Sensitivity Analysis and Influence Evaluation of Progressive Wall Thickness of Honeycomb Structures as Energy Absorber Produced by Additive Technology Multi-Jet Fusion. Materials. 2025; 18(1):1. https://doi.org/10.3390/ma18010001
Chicago/Turabian StyleKalina, Tomas, Zdenek Chval, Frantisek Sedlacek, and Stanislav Spirk. 2025. "Sensitivity Analysis and Influence Evaluation of Progressive Wall Thickness of Honeycomb Structures as Energy Absorber Produced by Additive Technology Multi-Jet Fusion" Materials 18, no. 1: 1. https://doi.org/10.3390/ma18010001
APA StyleKalina, T., Chval, Z., Sedlacek, F., & Spirk, S. (2025). Sensitivity Analysis and Influence Evaluation of Progressive Wall Thickness of Honeycomb Structures as Energy Absorber Produced by Additive Technology Multi-Jet Fusion. Materials, 18(1), 1. https://doi.org/10.3390/ma18010001







