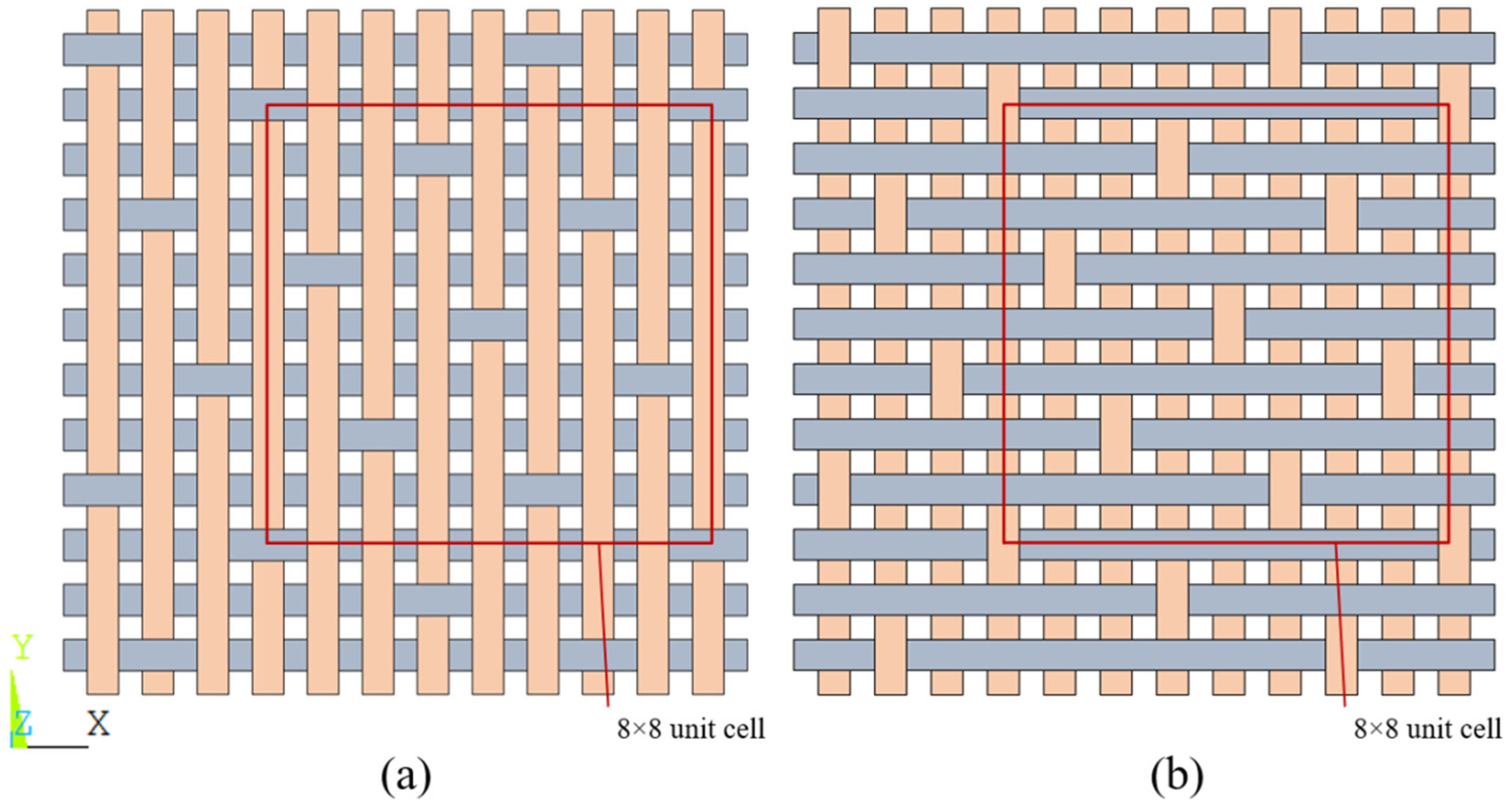
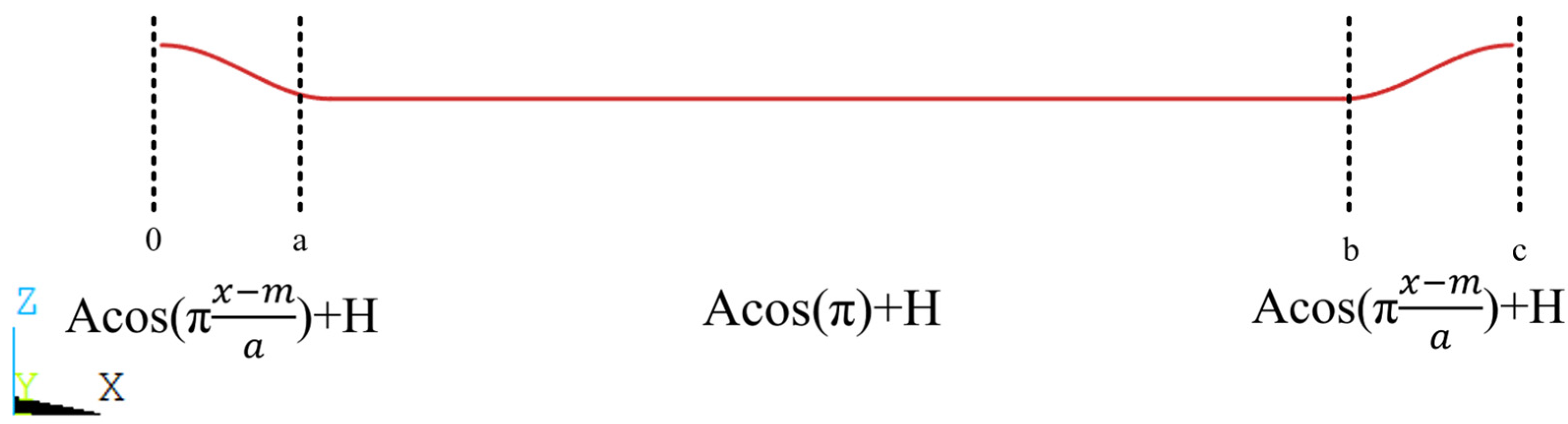
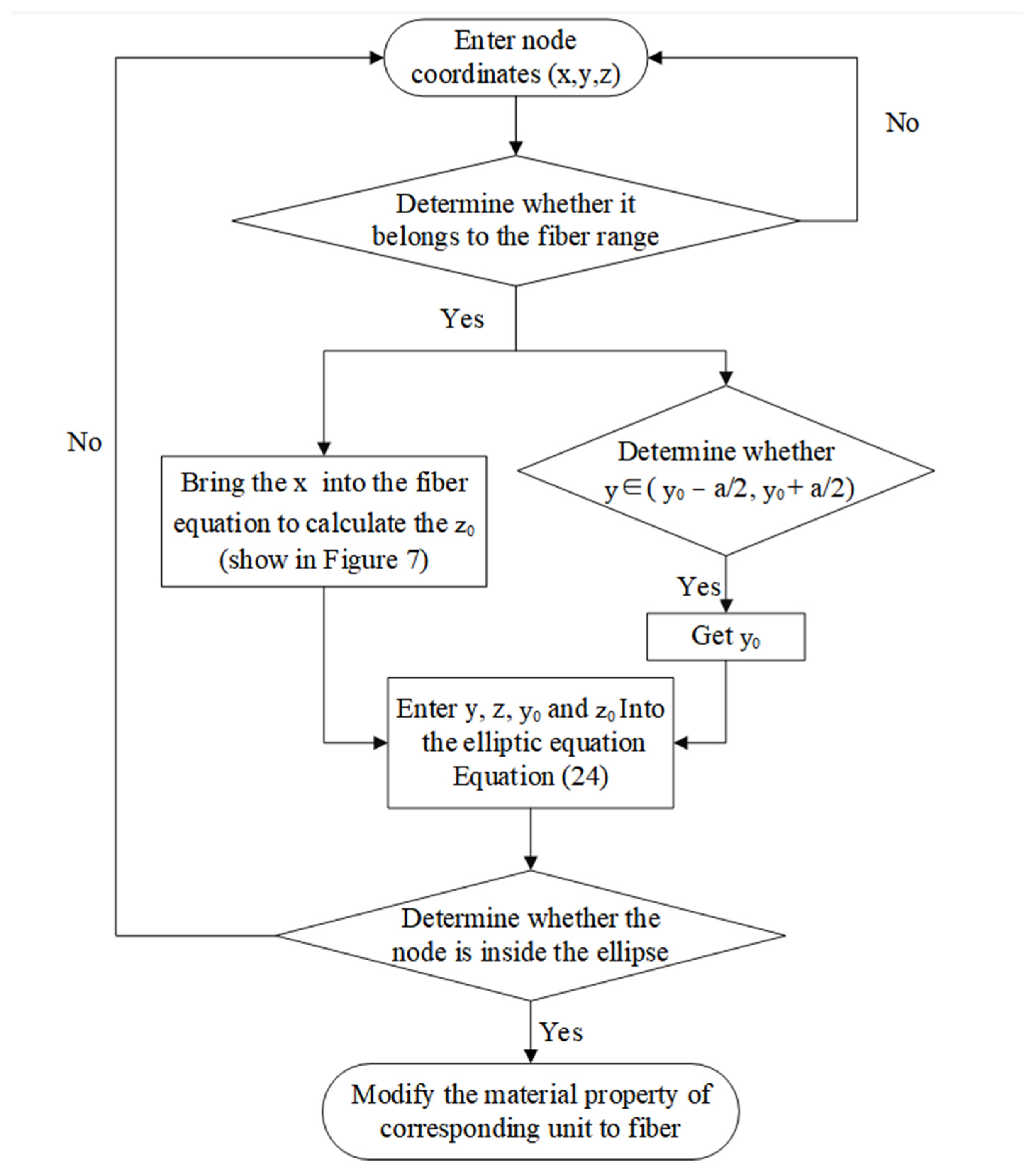
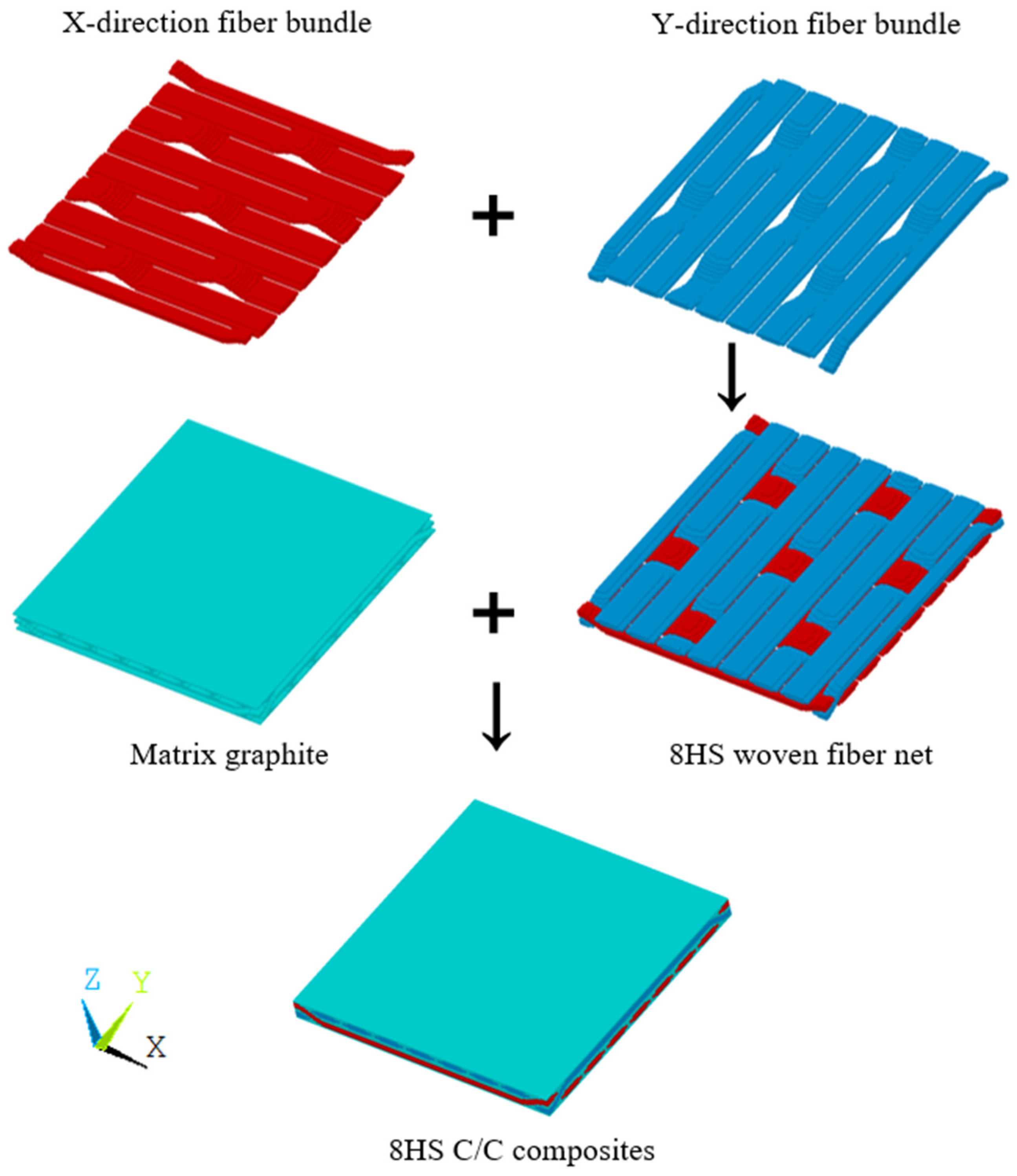
1. Introduction
Carbon-fiber-reinforced carbon matrix (C/C) composites exhibit a series of excellent properties such as low density, high strength, high plasticity, and impact resistance, and they are a widely used braided material [
1]. In terms of the fiber reinforcement orientation, they can be divided into unidirectional (UD), two-directional, and three-directional forms. The research and application of UD fiber-reinforced composites have been quite extensive, but their transverse performance defects cannot be ignored. Nowadays, braided composites have been widely used in various fields due to their more attractive transverse characteristics than UD composites [
2].
C/C composites are widely used in high-temperature environments. Their thermo-mechanical performance at high temperatures affects their application. The properties of braided C/C composites are mainly affected by the method of weaving, the material type of the fibers and matrix, and the volume fraction of each component [
3]. According to different weaving methods, they can be divided into woven, knitted, and nonwoven types. In terms of weaving efficiency, manufacturing costs, and overall performance, woven fabric has more advantages than knitted fabric, and it is the most widely used fabric structure. The carbon fabric preforms of the most common 2D C/C composites are usually woven in plain, twill, and satin patterns, and the resulting C/C composites have a lower modulus than the fibers themselves due to the curvature and wavy appearance of the fiber bundles at the knitting junction.
To fully understand the role of C/C composites in high-temperature environments, their thermo–mechanical properties were investigated. Chen [
4] tested the compression, bending, and tensile properties of carbon fiber/silicon (C/SiC) composites from room temperature up to 1000 °C and analyzed the fracture micromorphology of the composites. Cheng [
5] first studied the bending performance of C/C composites at a temperature of 2600 °C and observed their plastic deformation at high temperatures.
Currently, tests at high temperatures (above 1600 °C) are difficult, and the high cost of material production and characterization, the time cost, and doubts about the accuracy of the results have prompted scholars to investigate the properties of composites using theoretical methods and numerical methods.
Theoretically, works based on theoretical analytical methods include those by Tran et al. [
6] using the Mori–Tanaka [
7] method to derive the Eshelby spherical non-uniformity problem and predict the equivalent properties of gradient composites containing spherical inclusions. The classical methods, such as the self-consistent method and Mori–Tanaka method, reflect the average of the stress and strain of representative volume elements, which can solve some problems in the calculation of the material properties, but most of them are still limited to the calculation of the linear and nonlinear basic mechanical properties of heterogeneous materials. Meanwhile, many assumptions and premises proposed by commonly used semi-analytical methods about the microstructure limit the application of theoretical methods in material research with complex microstructures. Therefore, more accurate and convenient simulation methods for composite materials have become the focus of research.
Numerically, with the wide application of large-scale commercial finite element software, RVE, a representative volumetric element method based on finite element software, has also been used to analyze the equivalent properties of composites with complex shapes. Pahr et al. [
8] found that the FEM can study the macroscopic mechanical properties of heterogeneous materials in more detail than experiments. Salviato [
9] analyzed the in-layer size effect of textile composite structures from both experimental and numerical aspects. Using the three-dimensional finite element method (FEM), Galatti et al. [
10] performed a preliminary prediction of the mechanical behavior for composite materials fabricated by continuous filament fabrication (CFF). Srivastava [
11] predicted the effect of embedding graphene sheets (GSs) into the carbon matrix of 4D-C/C composites on the elastic modulus through the FEM. The representative volume element (RVE) method has been used to predict the properties of braided composites, but it lacks a strict mathematical framework to clarify the relationship between the equivalent properties and material layout. In contrast, the asymptotic homogenization method (AHM) was born from strict mathematical theory and has a higher computational efficiency [
12].
The detailed numerical calculation of the structural–mechanical behavior of composites is time-consuming, which can be significantly improved by the homogenization method [
12]. The AHM is considered for the calculation of the thermodynamic properties of composite materials.
In the 1970s, scholars introduced the homogenization theory proposed by Benssousan [
13] and Sanchez-Palencia [
14] into the study of heterogeneous materials. This method is utilized to analyze material systems with multiple scales, enabling the connection between the microscopic scale containing the second phase space and the macroscopic scale of the overall structure. Compared to the RVE method, this approach offers advantages such as not requiring a global periodicity assumption and allowing different microstructures at various points within the macroscopic structure. Based on this method, Guedes [
15] pioneered a computational program that merges the AHM with the FEM to determine the effective elastic moduli of composite materials, thereby advancing the practical application of the AHM in engineering domains. Harsanyi [
16] applied the AHM to solve the equivalent properties of plate and shell structures with microstructures. Macedo et al. [
17] extended this theory to the failure judgment of composites. Dutra et al. [
18] integrated the AHM with commercial finite element software to compute the equivalent properties of materials, providing a comprehensive framework of the requisite procedures to further facilitate the multidisciplinary application of the AHM across various engineering fields. Wei [
19] combined the AHM and the multiphase FEM to study the performance of 3D braided composites, focused on exploring the influence of voids and interphase defects on their effective thermal expansion coefficient.
In the performance prediction of woven composites, both Barile [
20] and Holmes [
21] conducted relevant research on plain-weave composites. Axinte [
22] established six different models of satin-fabric-reinforced composites. Naylor [
23] conducted tensile tests on 5-harness satin (5HS)-weave carbon fiber epoxy composites. Skinner [
24] used the 5HS weaving method to enhance carbon fiber/silicon carbide matrix composite (C/SiC) CMCs and studied their nonlinear constitutive behavior considering damage. Alshahrani [
25] used frame tests to investigate the deformation mechanism of 8HS carbon/epoxy prepreg under in-plane shear. Aghaei [
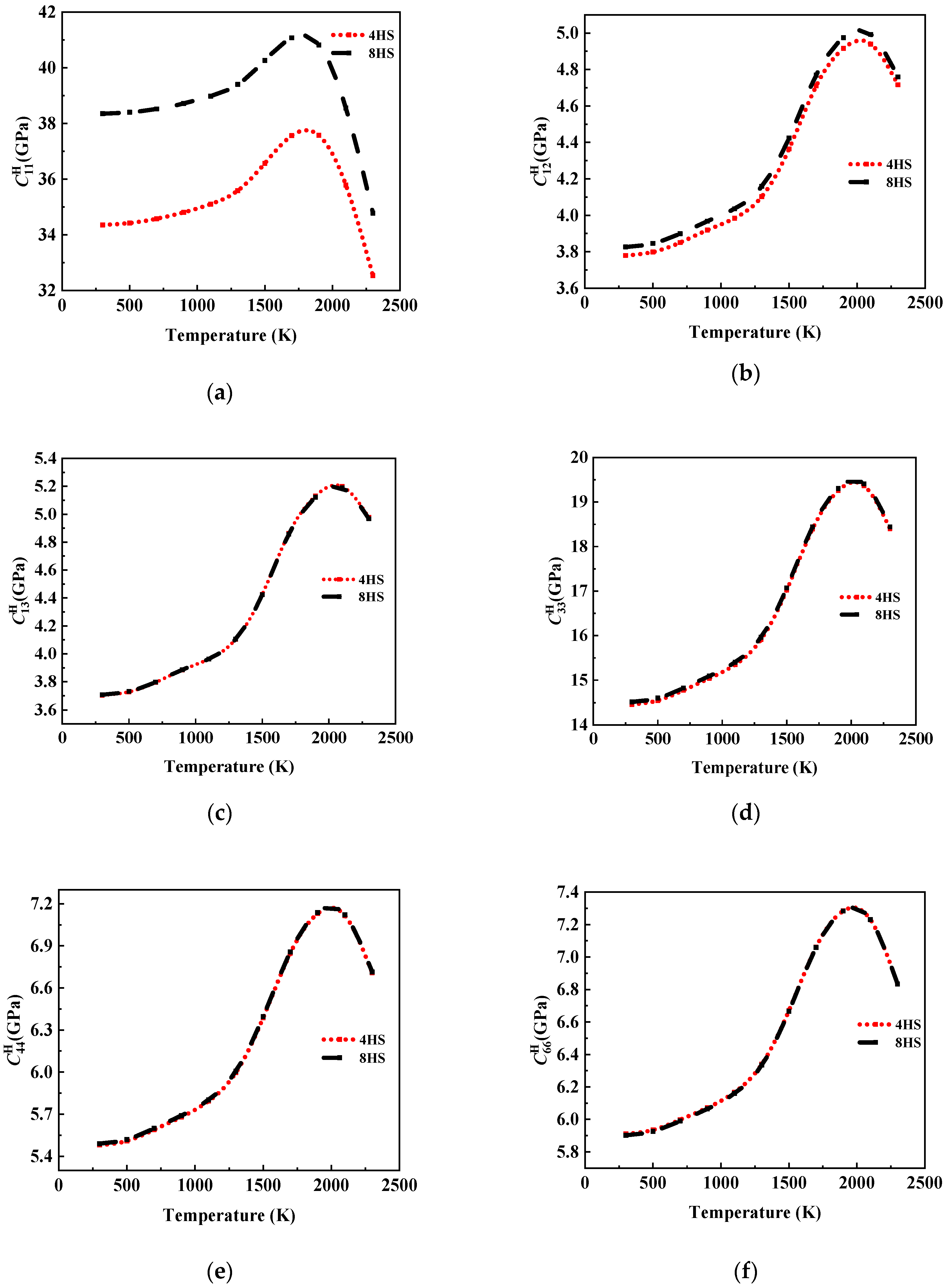
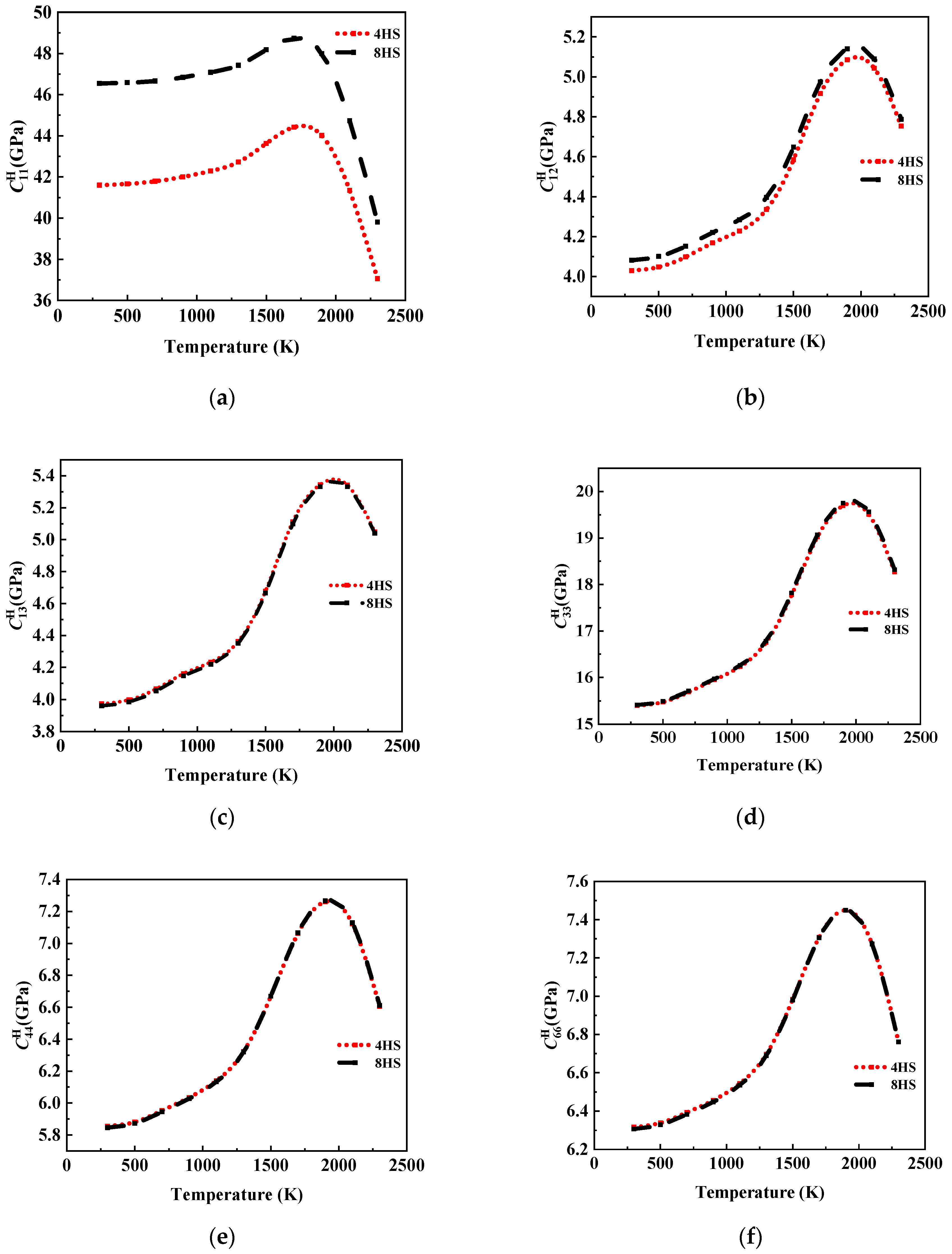
26] experimentally compared the effects of plain, 5HS, and 8HS weaving on the mechanical properties of glass fiber/epoxy composites. The results showed a slight edge in the tensile modulus for the 8HS over the 5HS and plain weave methods.
Considering the influence of temperature on the mechanical properties of materials, Karpov [
27] studied the mechanical properties of 4D C/C composites in the temperature range of 20~2800 °C and provided the reasons why the mechanical properties of the studied materials had a special temperature dependence. Priyanka [
28] fabricated mixed carbon–Kevlar fiber composites using plain and 2 × 2 twill weaves and tested them for their tensile strength, compressive resistance, bending, and low-velocity impact. Cheng [
29] studied the mechanical behavior of plain-weave C/C composites at high temperatures. Skinner [
30] simulated the mechanical response of plain-weave (C/SiC) CMCs in the temperature range from room temperature to 1200 °C. Petkov [
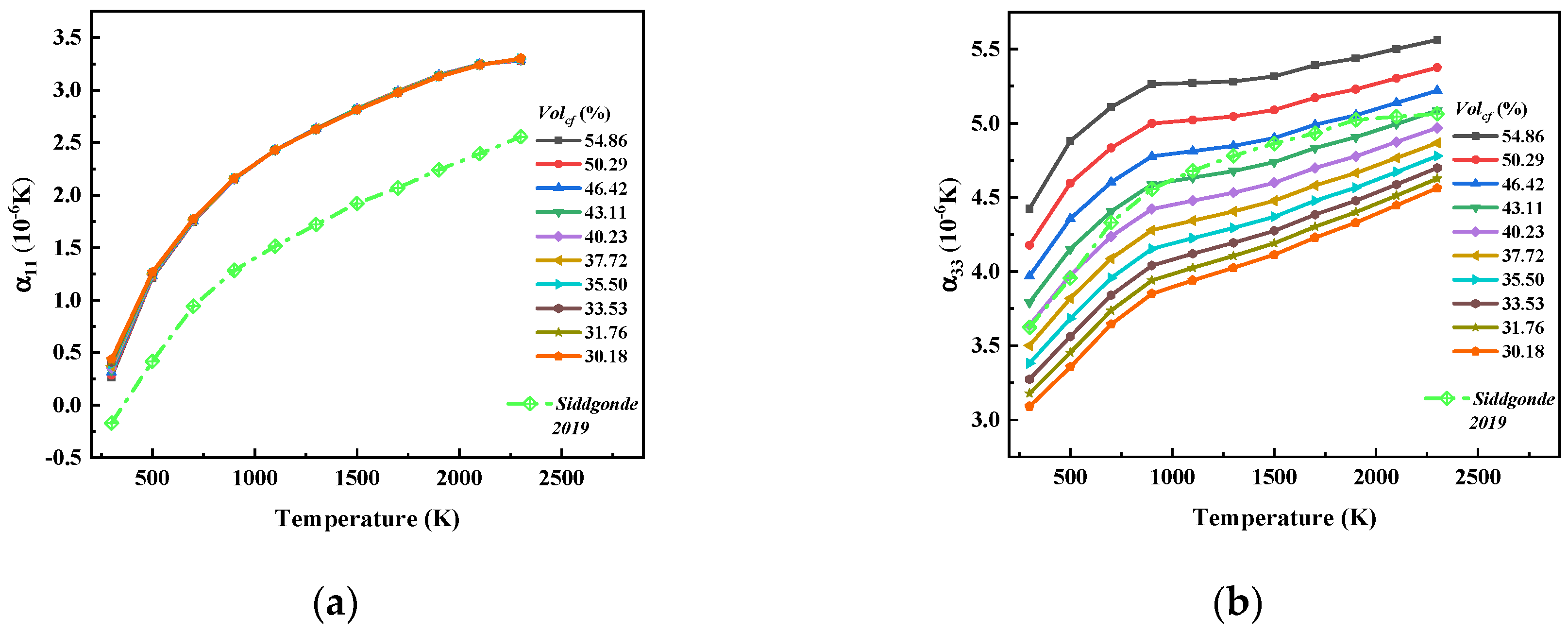
31] studied the weight loss and damage development of 8HS carbon-fiber-reinforced polyimide composites in high-temperature (288 °C and 320 °C) environments in air. Siddgonde [
32] studied the RVE model of 5HS C/C composites and predicted their thermo-elastic properties at high temperatures but did not consider the effect of the carbon fiber volume fraction on them. Xu [
33] found through experimental research that 8HS C/C composites treated at specific high temperatures exhibit better overall performance.
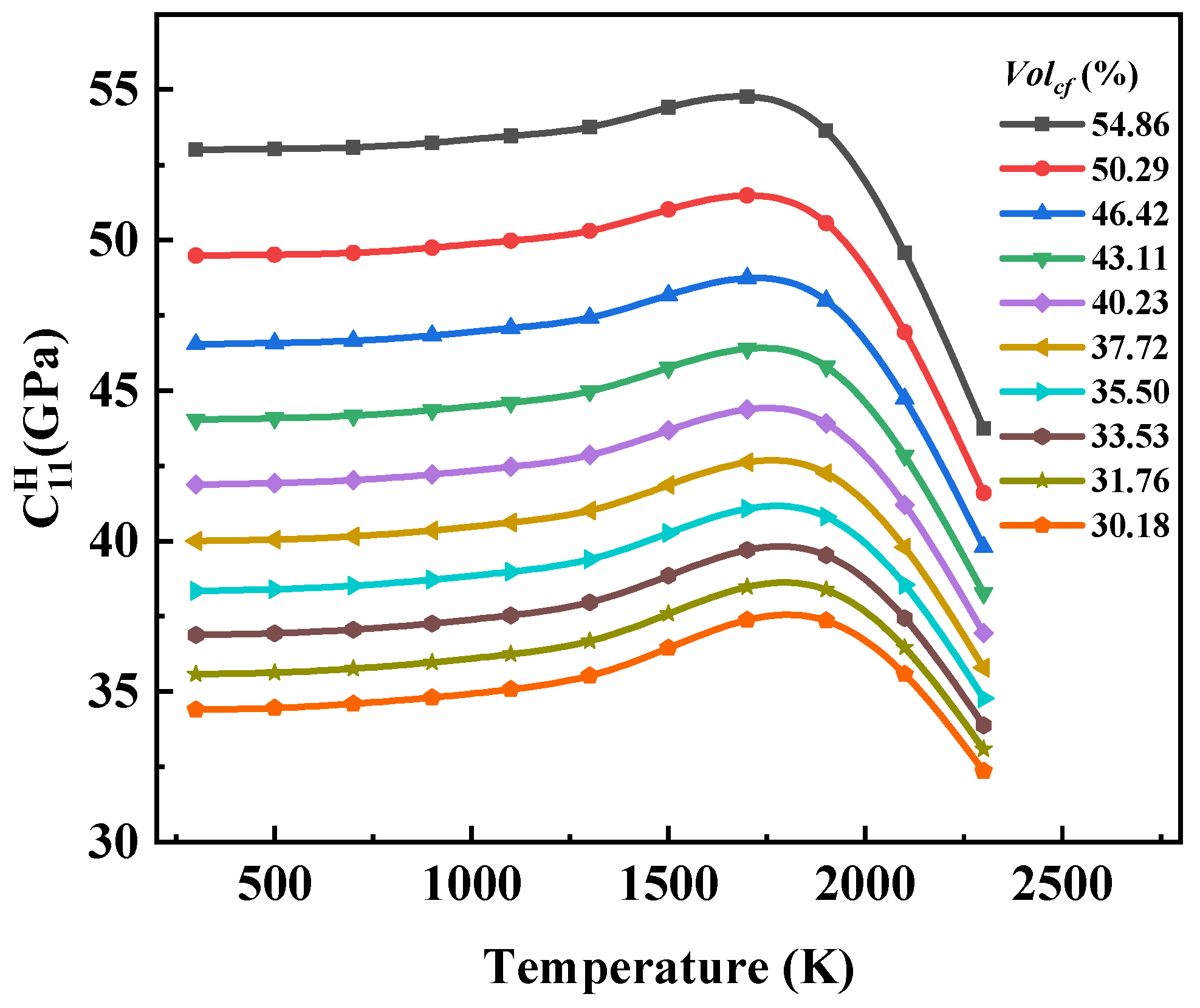
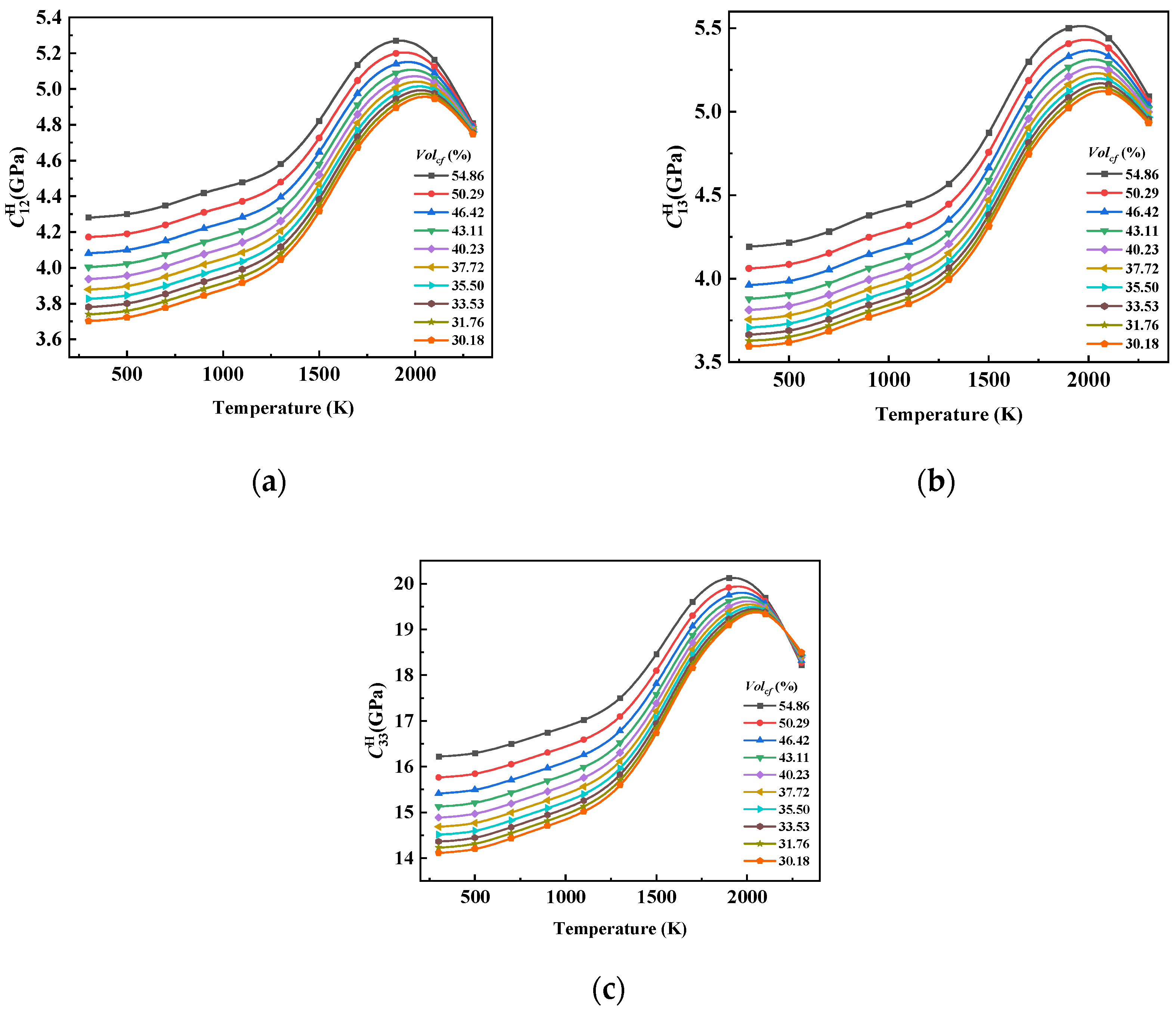
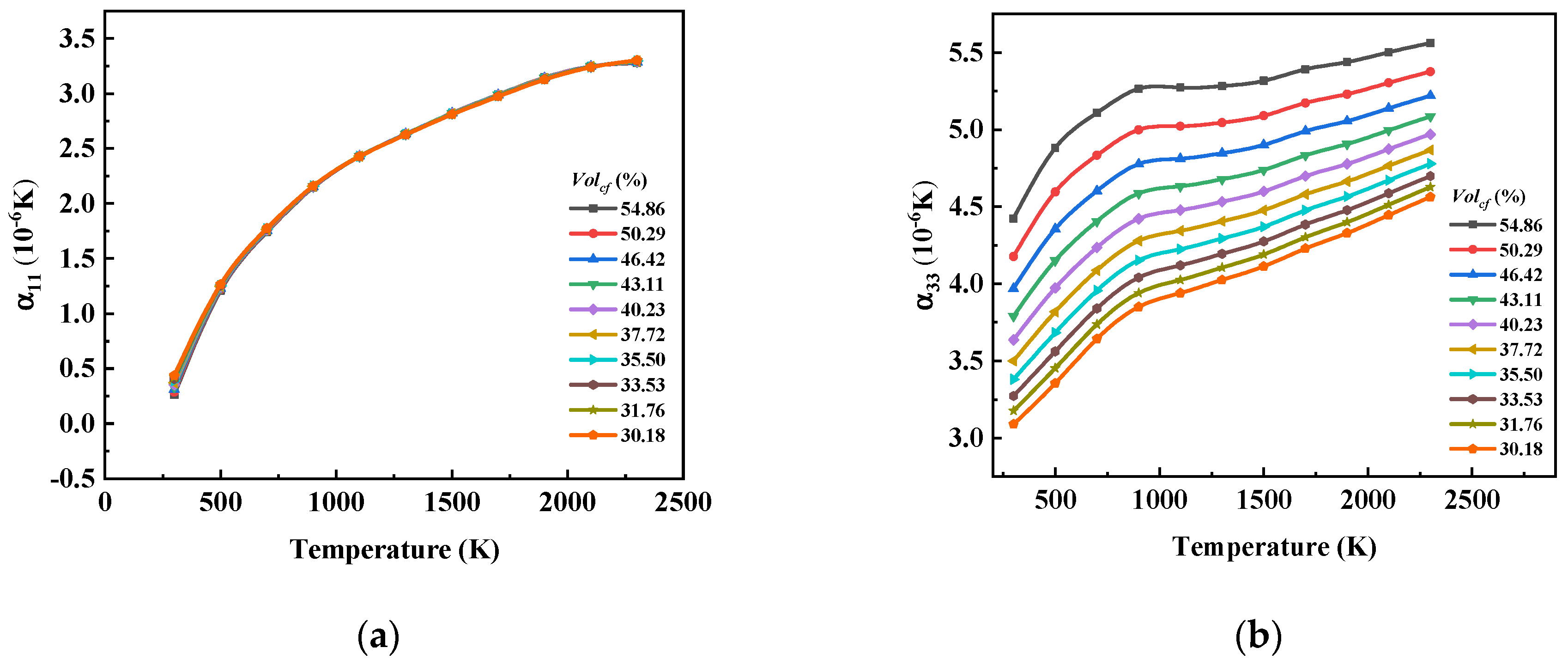
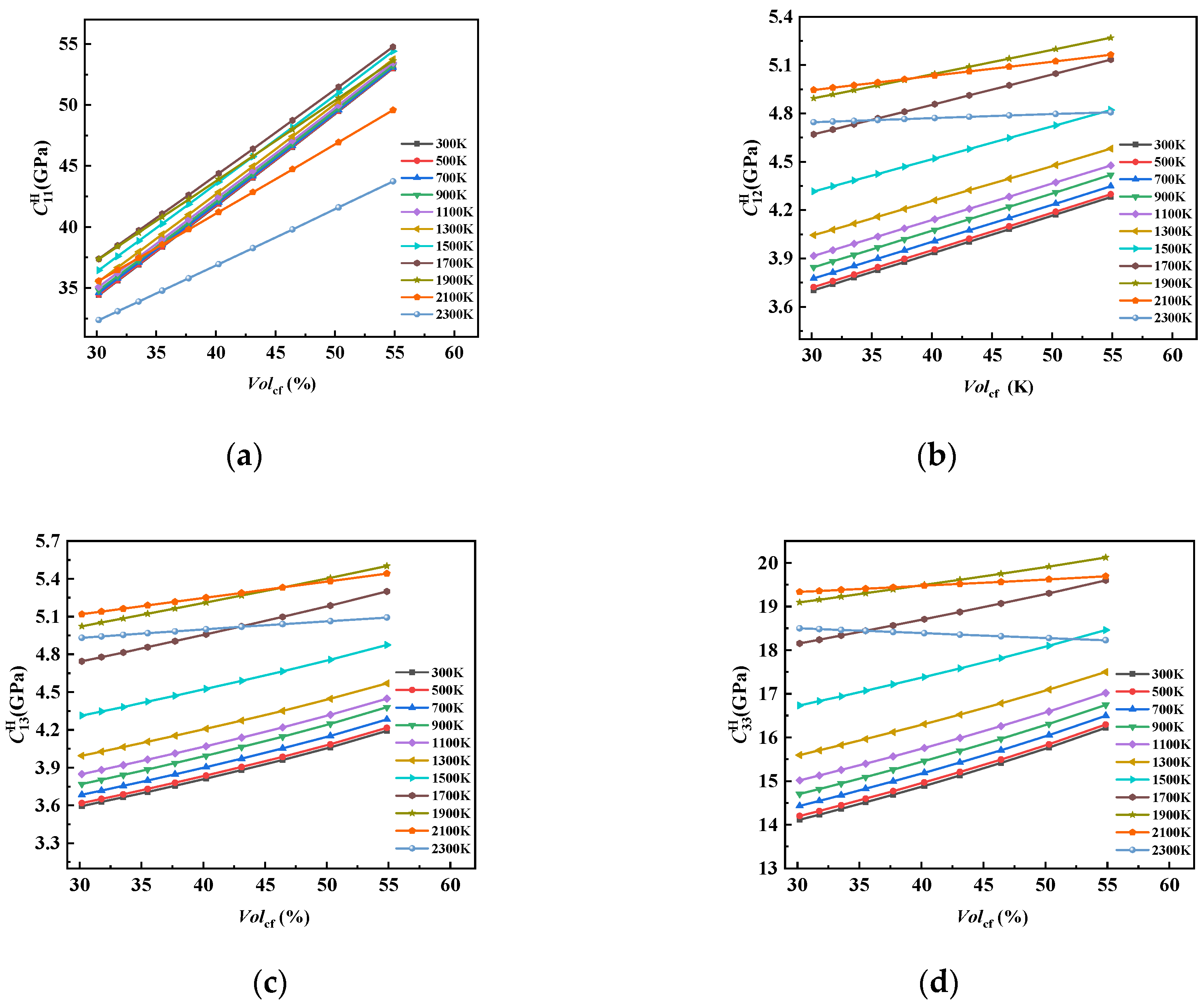
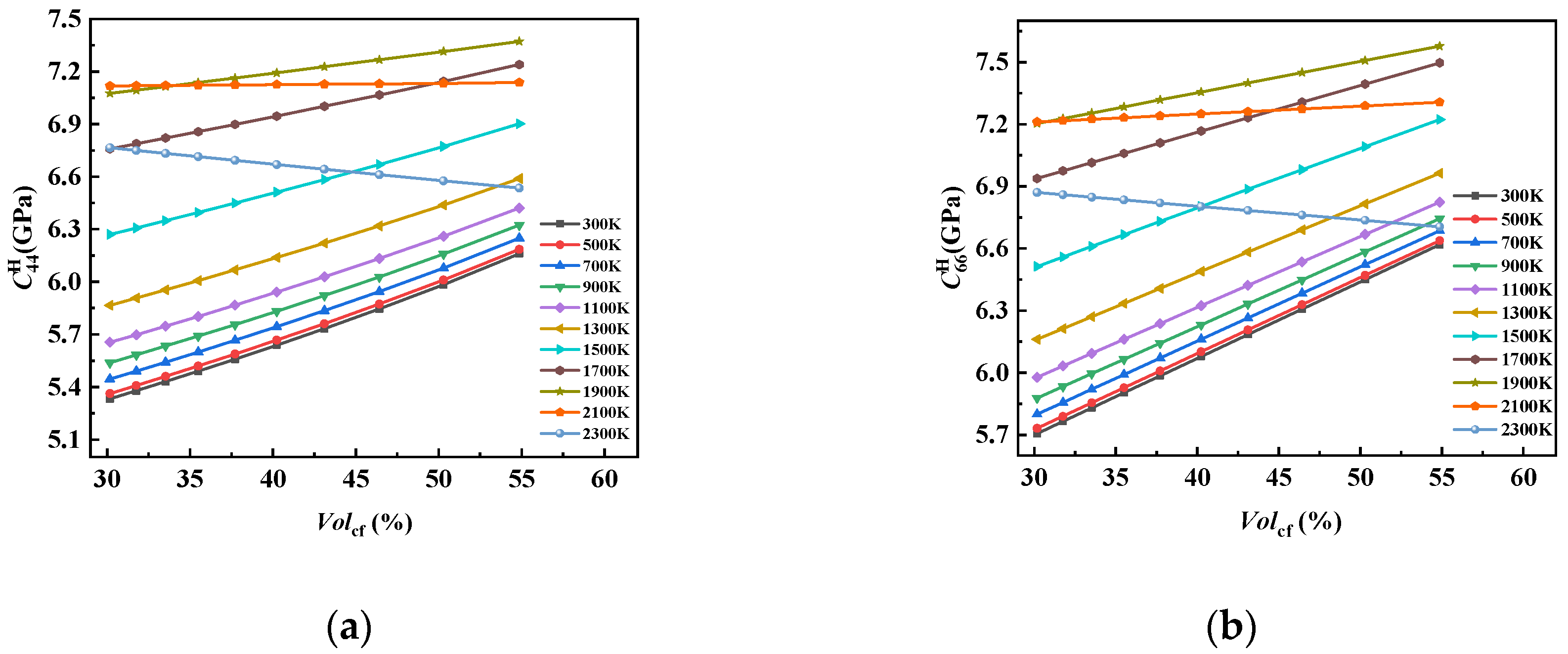
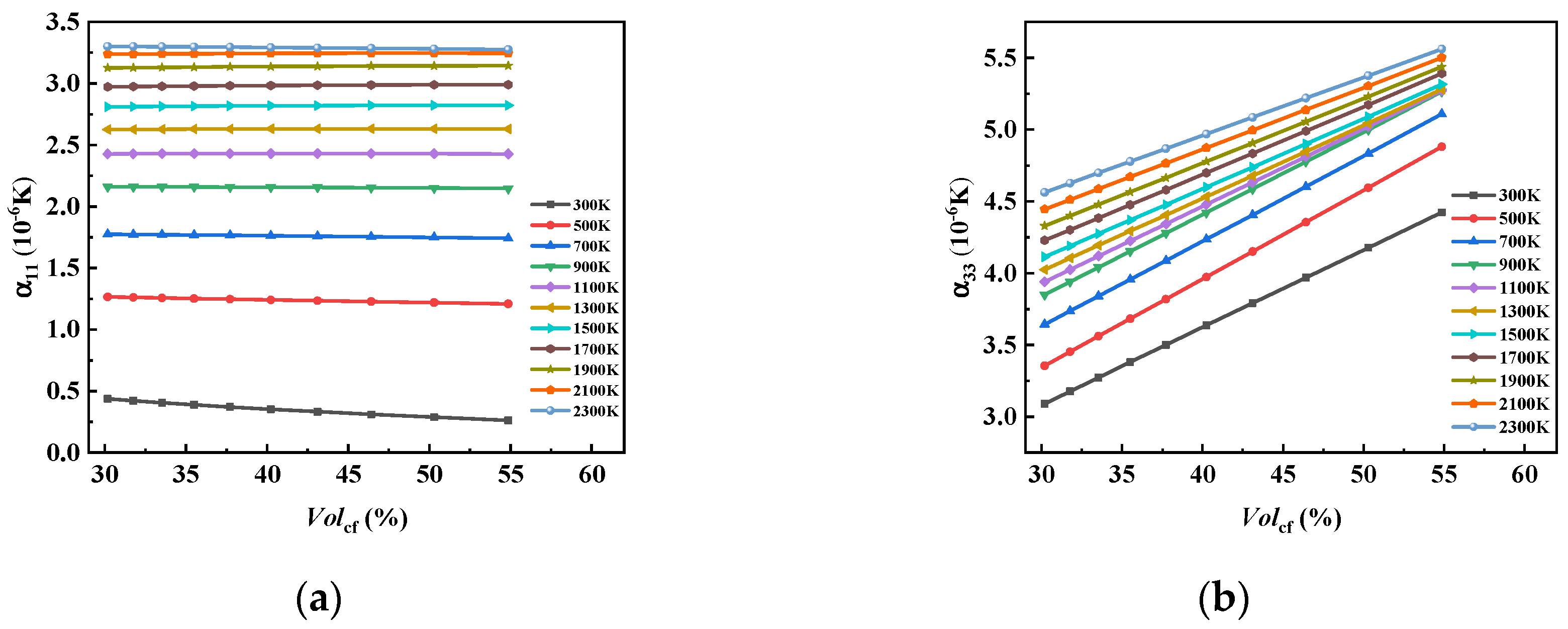
In this paper, considering that there is still a gap in the research on the equivalent of 8HS C/C composites related to temperature as well as the advantages of asymptotic homogenization methods in predicting the performance of periodic composite materials, we prepared 8HS C/C composites and conducted structural characterization. By combining the asymptotic homogenization method (AHM) with the finite element method (FEM), we calculated the elastic constants and thermal expansion coefficients of representative volume element (RVE) models by varying carbon fiber volume fractions at different temperatures, and we then explored the temperature dependence of the 8HS C/C composites properties. Additionally, the effects of the 4HS and 8HS weaving methods on the equivalent elastic constants of the composites were compared.
2. Asymptotic Homogenization Theory and Its Application
As a multi-scale analysis method, the asymptotic homogenization method [
12,
34] encompasses two spatial scales: micro scale and macro scale. This technique views the composite material as being composed of a repeated microstructure with a periodic and high non-uniformity.
2.1. Equivalent Elastic Tensor Asymptotic Homogenization Equation
Assuming that
is a three-dimensional simply connected bounded field with a perfectly smooth boundary, the thermo-mechanical coupling equilibrium of the structure in this region is described by the relevant dynamic equation and the heat conduction equation.
On the boundary
, the displacement
, where,
represents the stress acting on Ω;
is the force;
is the macroscopic coordinate; and
is thermal cycle vector. The stress–strain relationship in linear thermo-mechanical problems can be expressed as
The above formula is further expressed as
where
;
is the elastic constant tensor;
is the CTE;
is the total strain;
is thermal strain;
is the temperature field; the temperature difference is
; and
is the initial temperature.
The expression of the thermal cycle tensor,
, is as follows:
where
is the heat conduction tensor. These coefficients follow symmetry, with
and
.
The micro and macro scales are related by a very small positive number,
ε.
is the microscale coordinate system, and
is the macroscopic coordinate system.
When , heterogeneous macrostructures can be regarded as homogeneous macrostructures.
In a two-scale system, all structural field variables,
q, are functions of the macroscopic coordinates
and microscopic coordinates
, as
. Its partial derivative with respect to
is expressed as:
Therefore, Equations (4) and (5) become (8) and (9), respectively.
The displacement and temperature are asymptotically expanded to an infinite series with a small parameter,
ε, as follows:
Similarly, asymptotic expansions of stress and heat flow can be obtained, as follows:
After a series of formula transformations, the governing equation of the thermo-elastic problem can be expressed as [
35]
where
is the elastic constant tensor;
is the coefficient of thermal expansion;
is the temperature difference;
and
are the body force and the surface force, respectively;
is an arbitrary function;
is the period of the function; and
is the boundary of the region Ω.
The feature functions
and
can be defined to represent the relationship between
u(0) and
u(1):
Based on the asymptotic expansion method, the equivalent thermal performance prediction formula of composite materials considering the thermo-mechanical coupling effect is expressed as
When the asymptotic homogenization method is used to predict the equivalent properties, the corresponding characteristic fields and must be solved, but the complex microstructure of the composite material makes it difficult to obtain to an analytical solution of the characteristic fields. Therefore, numerical methods such as the finite element method were used to solve the characteristic fields required for the performance prediction, and the equivalent properties of the composite material were calculated based on the numerical solution of the characteristic fields.
Based on the characteristic displacement, the equivalent elastic tensor is re-expressed as follows [
36]:
where
is the unit strain applied to the node and
is the characteristic strain.
According to Sigmund’s work [
37], the above formula can be written in matrix form as follows:
where
CH is the equivalent elastic tensor.
Based on the finite element discrete form,
,
, and
; [
B] is the derivative matrix of the form function,
is the stiffness matrix; and
is the force matrix. Then, we obtain the finite element form of the asymptotic homogenization formula for the elasticity matrix [
35].
where [
χ0] is the displacement field generated by the unit prestrain field and [
χ*] is the characteristic displacement field obtained by solving the periodic boundary problem.
Similarly,
,
, and
; [
B] is the derivative matrix of the form function;
is the stiffness matrix; and
is the solution of the case where all the nodal degrees of freedom are constrained and the load (−1K) is applied at the nodes. Then, we obtain the finite element form of the asymptotic homogenization formula for the thermoelastic constant [
35].
2.2. Periodic Boundary Condition
When applying the AHM to predict the equivalent mechanical properties of composite materials, the whole structure of the material is not required. A representative region that contains all the essential details of the microscopic structure is used. There is a boundary between the representative region and the surrounding periodic region of the composite. Therefore, when considering the boundary of the selected representative region, appropriate boundary conditions must be introduced to achieve the numerical homogenization of the effective mechanical properties of the composite. A previous study [
38] has pointed out that when predicting the equivalent properties of composites, boundary conditions that satisfy Hill’s energy law [
39] must be selected, including a uniform stretching boundary, a linear displacement boundary, and periodic boundary. However, the linear displacement boundary condition usually leads to higher results, while the uniform stretching boundary condition is the opposite and is a better choice than the periodic boundary condition.
For an RVE area
, the border
is divided into two parallel parts of the relative
and
, and the two parts meet as
and
. Any material node on the surface
can find a corresponding point on the surface
,and the normal vector on both surfaces satisfies
. By coupling the structural field values of the corresponding nodes, the general form of the equation used is
where superscript
and
represent the corresponding set of nodes on two parallel surfaces of the cell, and
is the perturbation applied to the reference point. At the same time, it is necessary to classify the nodes on the boundary so that the boundary node traversal is not repeated.
2.3. Finite Element Implementation of AHM
- (1)
Calculate the elasticity matrix.
Step 1: Construct and apply a six-node displacement field on the RVE and solve to obtain the node reaction force .
Step 2: Apply the node reaction field and the periodic boundary conditions (Equation (23)) on the RVE. Apply a fixed constraint to one vertex of the model. Then, solve to obtain the characteristic displacement field .
Step 3: Apply the characteristic displacement field on the RVE and solve to obtain the nodal reaction force .
Step 4: Calculate the elastic constants, , from Equation (21).
- (2)
Calculate the CTE.
Step 1: Apply thermal loads (−1K) on each node with the boundary condition that all the nodal degrees of freedom are constrained and solve to obtain the corresponding nodal reaction force .
Step 2: Apply the nodal reaction force and periodic boundary conditions (Equation (23)) on the RVE and solve to obtain the characteristic displacement field .
Step 3: Apply the characteristic displacement field on each node and solve to obtain the corresponding nodal reaction force .
Step 4: Calculate the effective thermoelastic constant, , from Equation (22).
Step 5: Calculate the effective CTE from Equation (18).
2.4. Verification of Asymptotic Homogenization
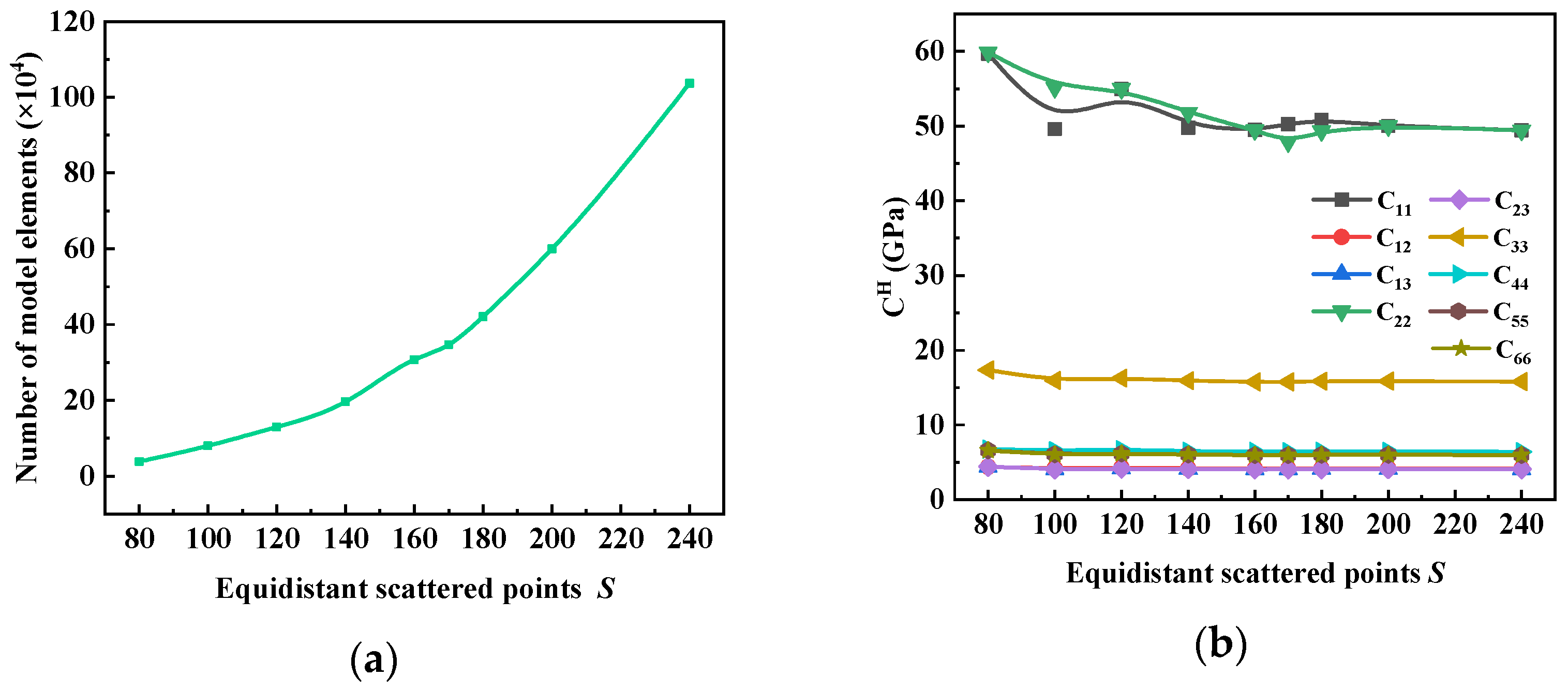
In order to explore the correctness of the calculation model, the same model was used in this section, and the size of RVE and grid were adjusted according to the size given in the literature.
Since it is not common to study the elastic properties of 8HS C/C composites with detailed model data, the correctness of the calculation model was explored using a 4HS C/C composite instead. The model building and property prediction methods used in this study were adopted to predict the elastic properties of 4-harness satin-weave-reinforced composites (4HS), and a single-cell model was established according to the sizes in the literature [
40]. The adopted carbon fiber was T800-12K. The matrix was a shape-memory resin. The volume fractions of the fiber and resin were 45% and 55%, respectively.
The calculation results of this article and the experimental results of the reference [
40] are shown in
Table 1. The results in the reference study were obtained by experiments, and the experimental results were affected by the test method and material defects. The calculation in this paper did not take into account other adverse factors affecting the performance. The calculated performance was ideal, the overall value was close, and the calculation error was less than 6%, so it was considered that the calculation accuracy of this method was reasonable.