Thermo-Hydric Study of Wood-Based Materials under Thermal Comfort Conditions
Abstract
1. Introduction
- Developing new general methods;
- Utilizing alternative energy sources and minimizing heat losses to the atmosphere;
- Implementing low-cost methods, such as artificial intelligence or simulations, for potential energy savings;
- Coordinating processes for efficient energy use;
- Emphasizing environmentally friendly solutions and reducing greenhouse gas emissions.
- Theoretical foundations and mathematical modelling: Describing phenomena within materials by extrapolating prior research to our context. A new formulation is developed to describe moisture transfer phenomena (diffusivity) in wood-based materials under specific thermal comfort conditions, subsequently used in the simulation.
- Numerical simulation and analysis: Visualize these phenomena and determine the required drying time to reach specific MC values (12% and 8%). Wood-based materials are assumed to be porous media, and diffusivity is derived from the first approach.
- Experimental study: Tracking MC evolution in two types of wood-based materials (melamine and MDF samples) over drying time for each extreme condition of the thermal comfort zone. The drying time for specific MC values is deduced.
- Artificial neural network (ANN) implementation: Combined with experimental data to build a generalized model calculating drying time under any environmental condition in the thermal comfort zone. The numerical model in MATLAB calculates the required time to reach 12% and 8% MC values. Drying time results are compared by calculating the percent error (PE) and subsequently discussed.
2. Detailed Problem Definition and Research Justification
2.1. Phenomenon Description
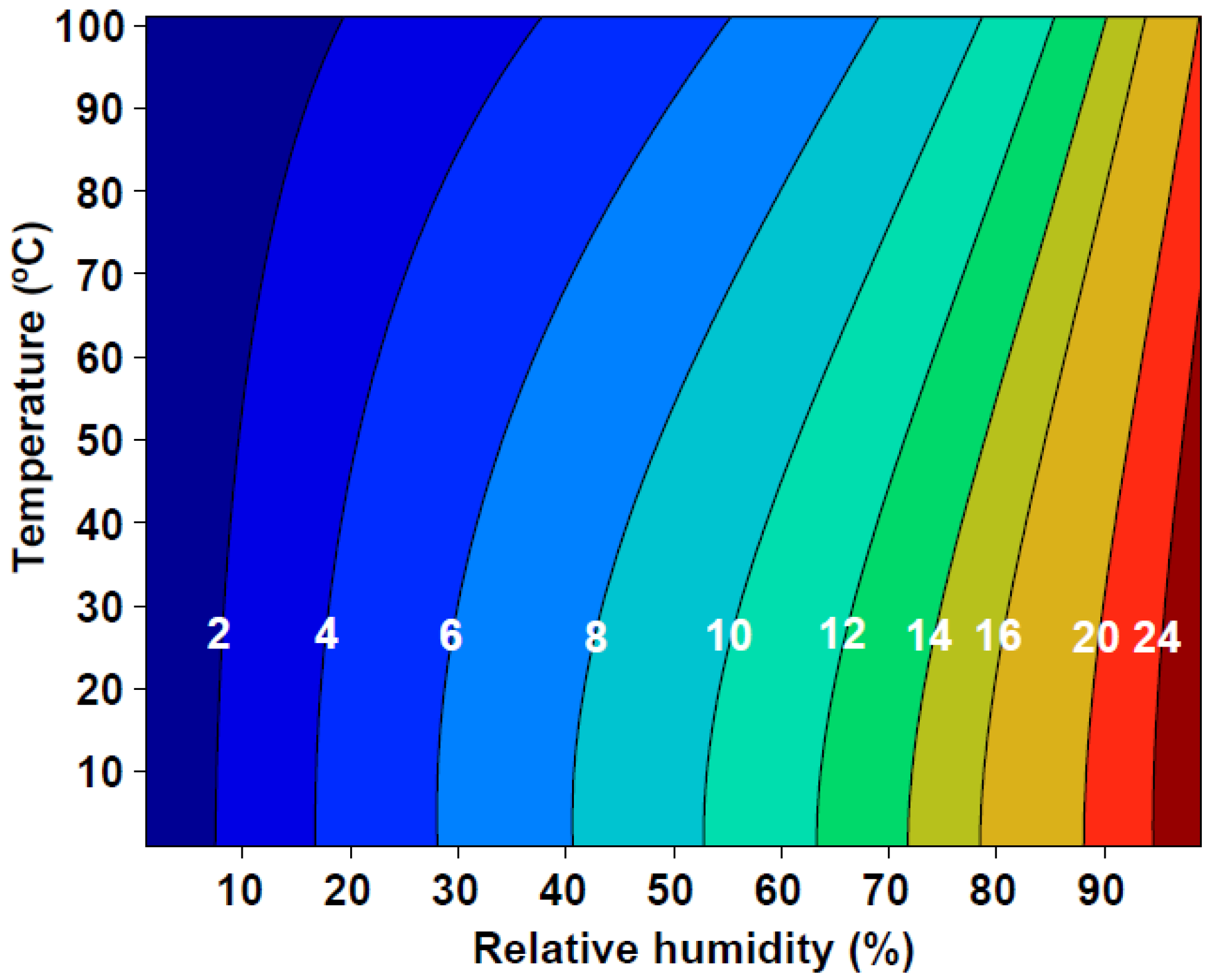
2.2. Thermal Comfort
2.3. Conceptual Formulation Overview
2.3.1. Moisture Content (MC)
2.3.2. Equilibrium Moisture Content (EMC)
2.4. Determination of Test Parameters
3. Theoretical Foundations and Mathematical Modelling
3.1. Literature Review
3.2. Development of the Mathematical Model
4. Numerical Simulation and Analysis
4.1. General Description
4.2. Governing Equations
- (1)
- The mass transfer of moisture occurs in vapor form.
- (2)
- Drying is merely driven by natural heat and mass transfer (natural drying).
- (3)
- The diffusion is based on an approximative equation.
4.2.1. Heat Transfer in Porous Media
4.2.2. Moisture Transport in Porous Media (Diffusion Model)
4.2.3. Input Parameters
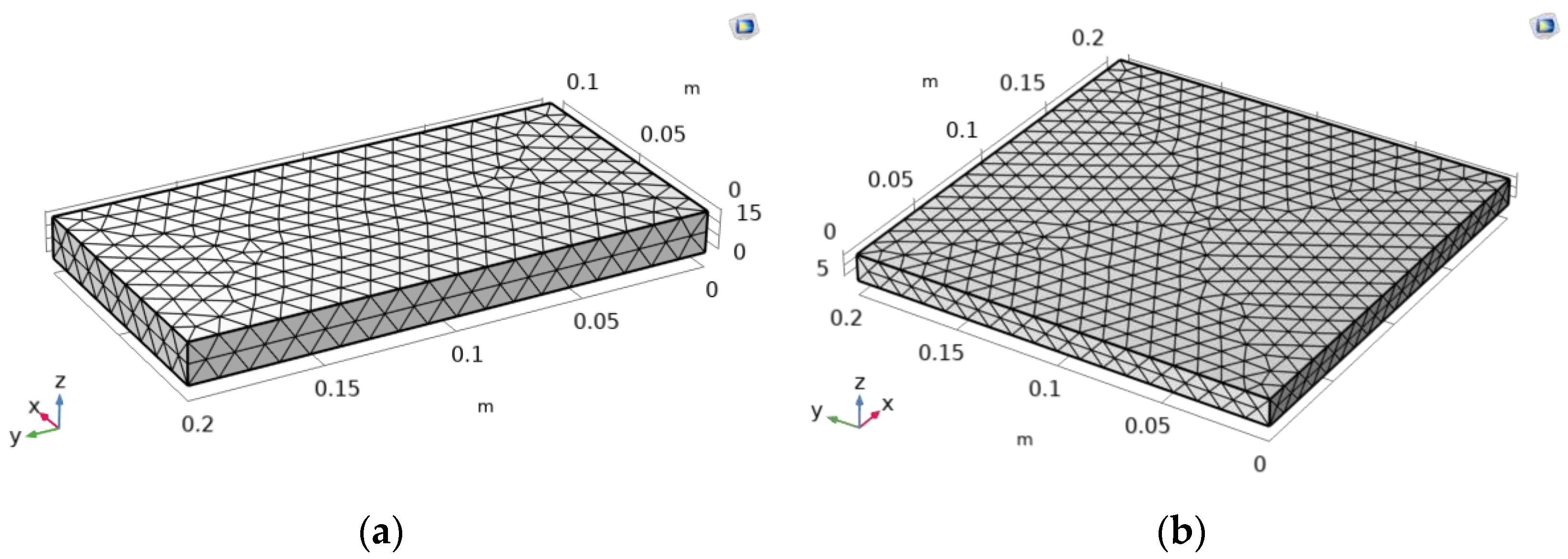
4.3. Geometry and Mesh Generation
4.4. Simulation Results and Discussion
- (1)
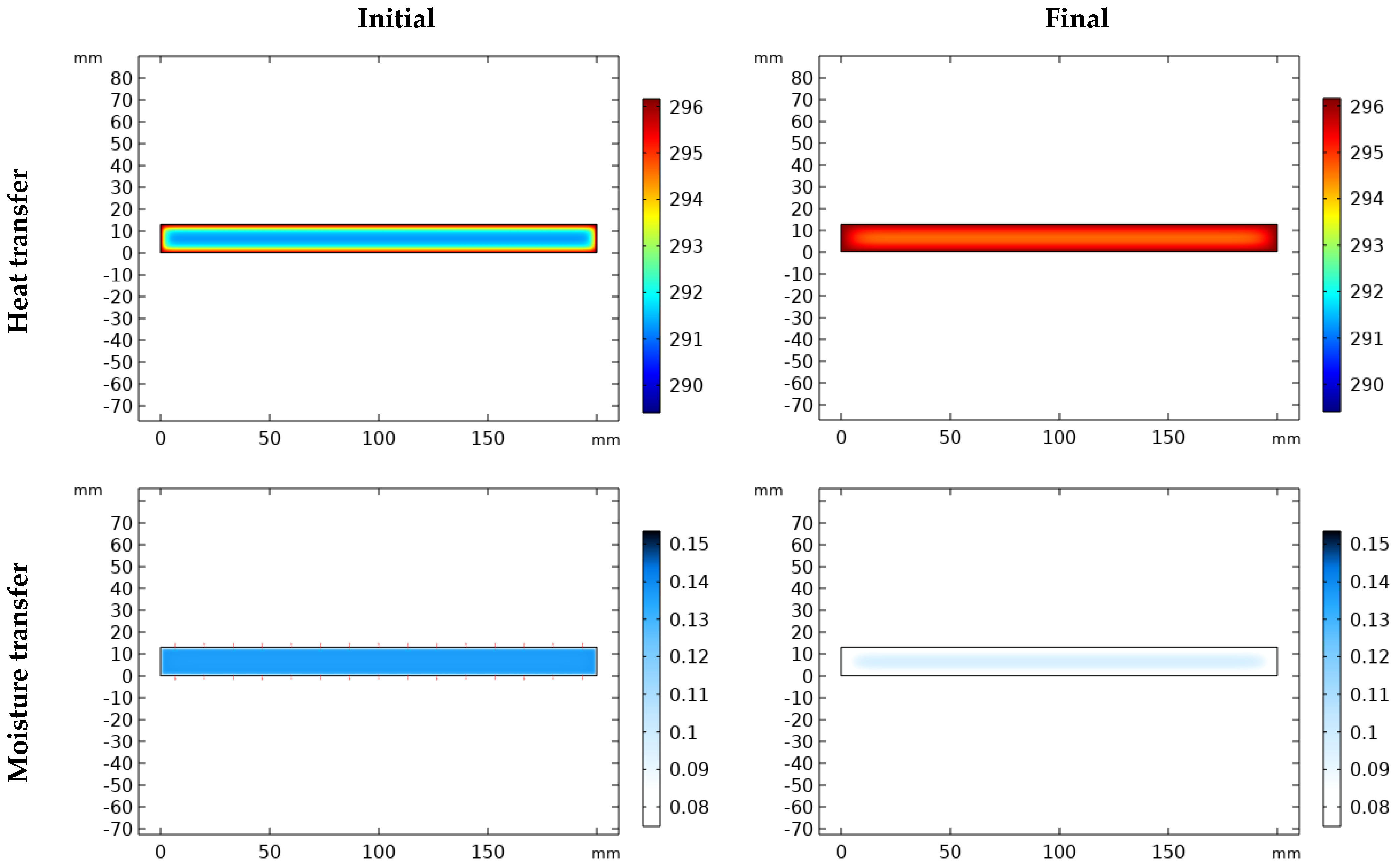
- Heat and moisture distribution: To show the transfer phenomena inside the material, the cross-section of the samples is presented according to the width and thickness. Figure 5 and Figure 6 show the evolution of combined heat and mass transfer in melamine and MDF, respectively. The heat transfer illustrates the temperature distribution and its evolution over time, from 0 to 2 h (depending on the condition), until it reaches a steady state. Notably, MDF reaches this state more rapidly than melamine due to the differences in their heat capacities within the temperature range of 292.15 °K and 300.15 °K (CP (melamine) > CP (MDF)). Furthermore, the boundaries of the specimen are influenced before the core. Moisture transfer occurs faster in MDF than in melamine and requires more time than heat transfer alone. When moisture transfer is combined with heat transfer, the drying process accelerates significantly compared to moisture transfer alone (more than 240 h). Therefore, temperature emerges as the pivotal factor in drying, particularly in drying time.
- (2)
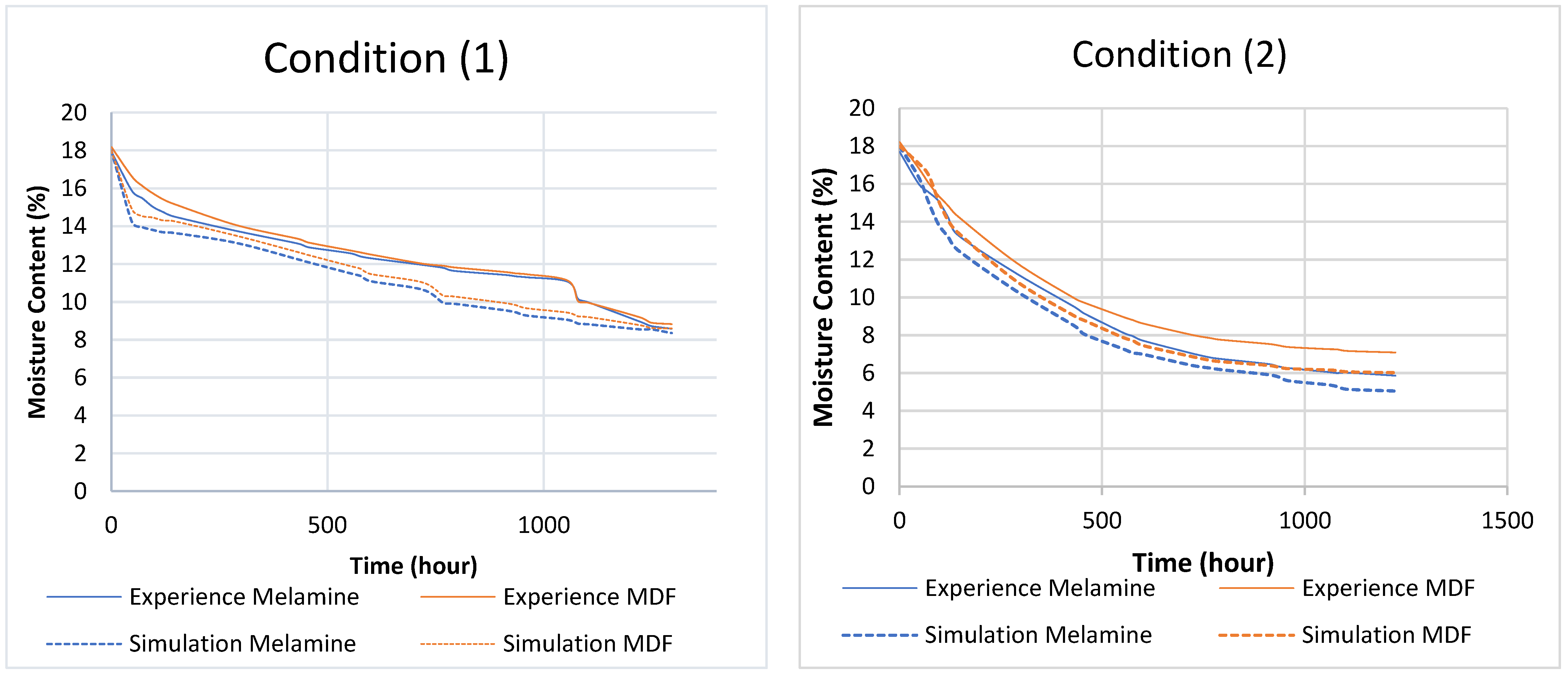
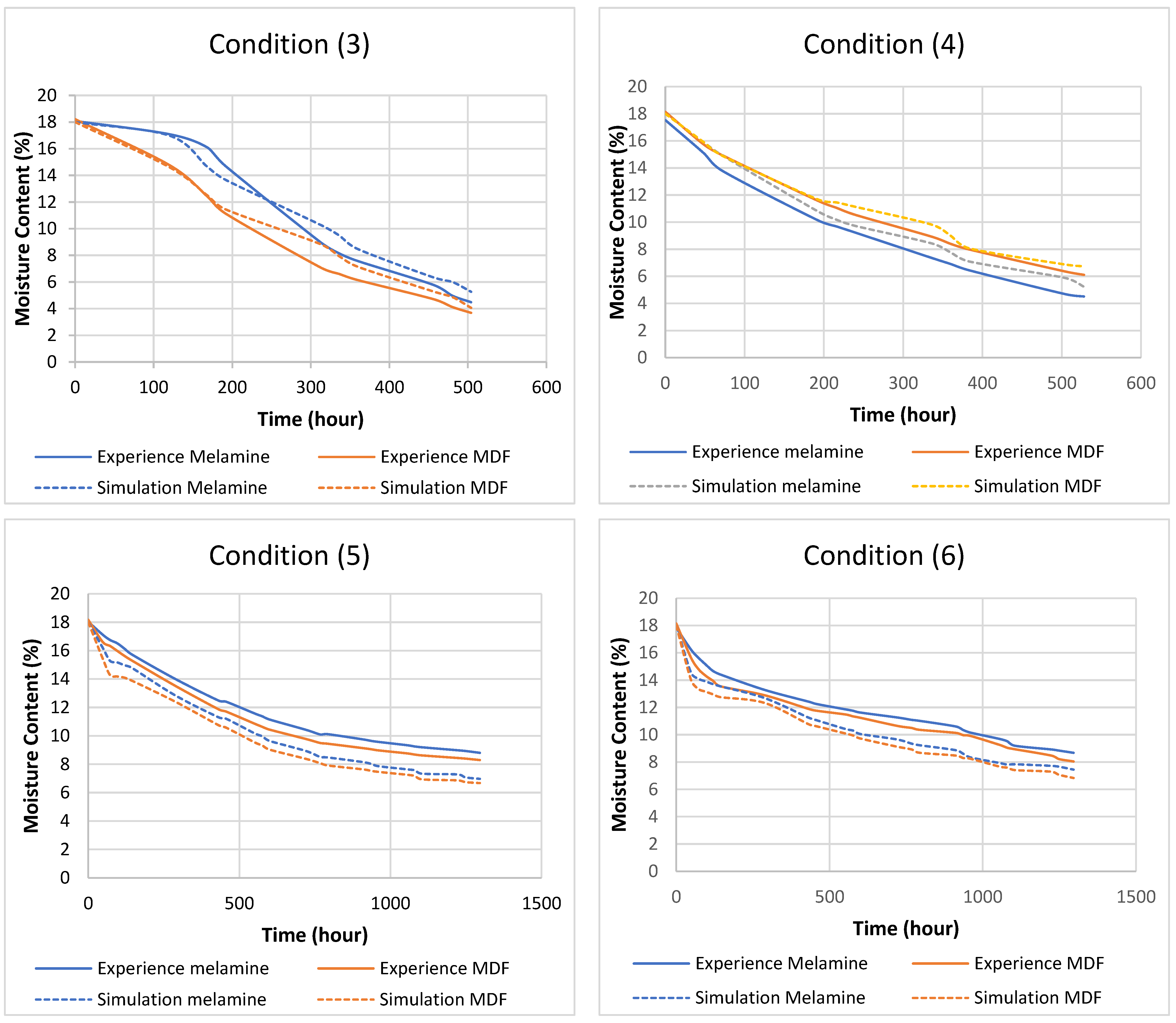
- Moisture content Graph: The simulation provides a detailed view of the phenomenon. Figure 7a,b illustrate the drying process for condition (5) (Table 1), divided into two stages. The first stage is characterized by a rapid drop in moisture content within a short period (2 h). This phenomenon results from the combined effects of heat and moisture transfer. The second stage features a gradual decrease in moisture content as the temperature stabilizes throughout the specimen until it reaches the equilibrium moisture content (EMC) or the desired values. The overall curve shape is consistent across all conditions, with differences primarily observed in the duration of each stage and the final moisture content. A comprehensive comparison of all graphs is presented in Section 7.2.
- The factors influencing the simulation are associated with the materials (such as the particles’ heterogeneity, nature, or size, and additives), the approximation equations, and the phenomenon’s complexity.
- Simulation allows us to visualize moisture content evolution within the materials and identify the stages of the phenomenon.
- Temperature plays the primary role in drying, especially for drying time.
- Like most wood-based materials, melamine and MDF exhibit comparable general behavior in response to their environment.
5. Experimental Study
5.1. Methodology of the Experimental Study
- Step 1: Drying until obtaining the anhydride mass, mdry. All samples were placed in a kiln dryer at 80 °C and measured their weight daily using a precision balance until it became stable (no weight variation). The final weight represented the anhydride mass mdry (0% moisture).
- Step 2: Attaining maximum moisture level (saturated moisture). After the anhydrite samples were obtained, they were placed in a conditioning chamber under extreme humidity conditions (23 °C, 95%) and obtained the maximum wetted mass mwet by measuring the weight until it became stable. This step allowed us to determine the maximum wetted mass (saturated moisture).
- Step 3: Applying test parameters. The final step involved applying the test parameters outlined in Table 1 and calculating the time required to reach 12% or 8% moisture content levels. During this step, moisture content variations were measured over time. This experience aimed to establish the necessary drying time for each sample.
- i: Test number (1 to 2). For the average, the letter M is used.
- X: Material (M for MDF, P for melamine).
- j: Number of test conditions (1 to 6).
5.2. Test Devices
- Kiln dryer: A kiln dryer assures the experience parameters of the first step at 80 °C.
- Weighing (precision balance): The precision balance measures the weight accurately, with a precision of 0.01 g and a maximum capacity of 1000 g.
- Conditioning chamber: The conditioning chamber ensures the experience parameters of the second and third steps with real-time control.
5.3. Materials
- Melamine:
- The test samples were 200 mm (length) × 100 mm (width) × 15.8 mm (thickness);
- Samples number: 12 (1P1, 1P2, 1P3, 1P4, 1P5, 1P6, 2P1, 2P2, 2P3, 2P4, 2P5, 2P6);
- Density: 728 kg/m3 (calculated).
- MDF:
- The test samples were 200 mm (length) × 200 mm (width) × 12.7 mm (thickness);
- Samples number:12 (1M1, 1M2, 1M3, 1M4, 1M5, 1M6, 2M1, 2M2, 2M3, 2M4, 2M5, 2M6);
- Density: 728 kg/m3 (calculated).
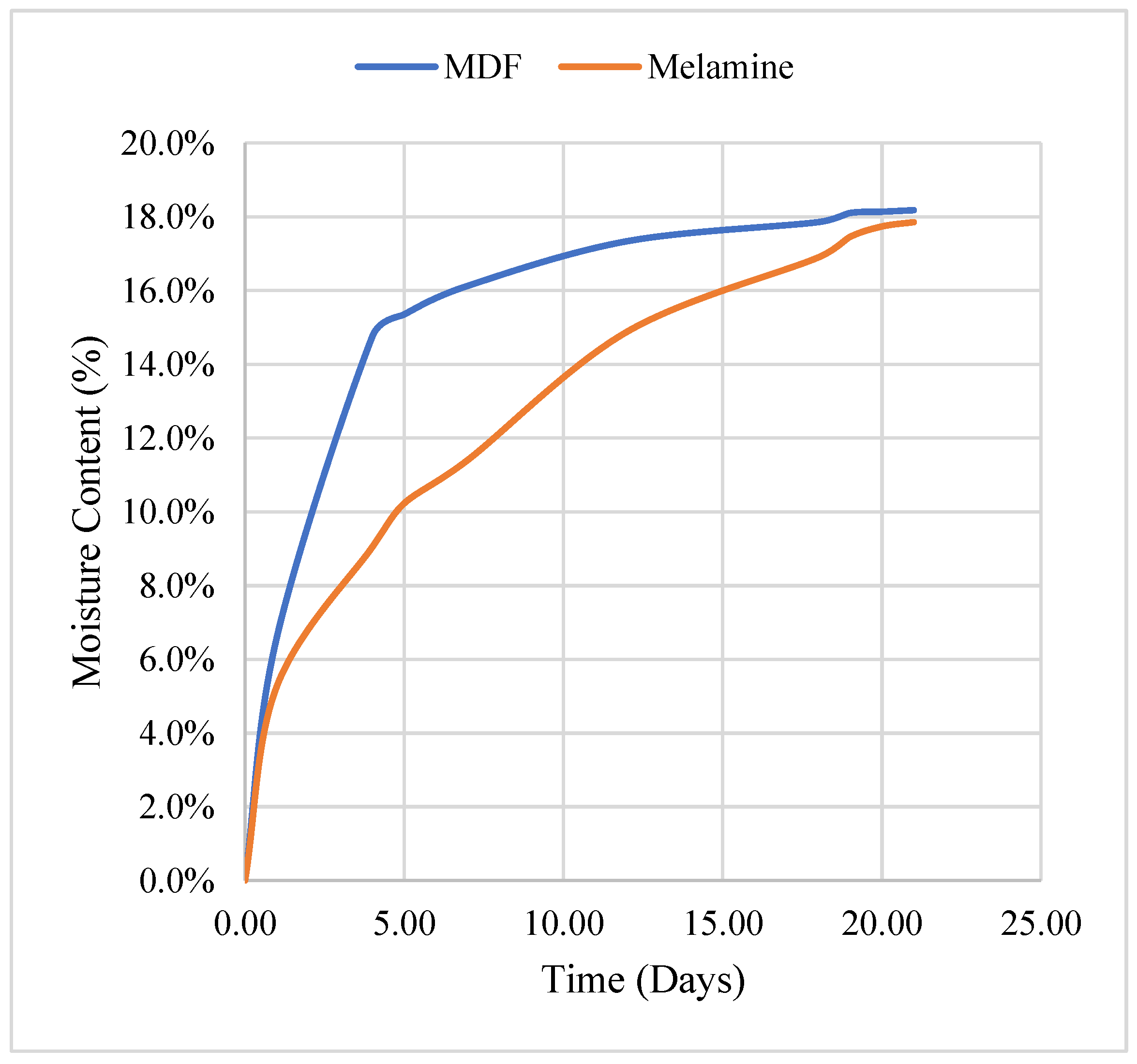
5.4. Experimental Results and Discussion
- Drying (desorption) and wetting (adsorption) are inverse processes.
- The graphs present a pseudo-exponential form.
- The sample exposed to higher temperatures dried faster.
- The sample exposed to lower air humidity also dried faster.
- MDF dries, under most conditions, faster than melamine.
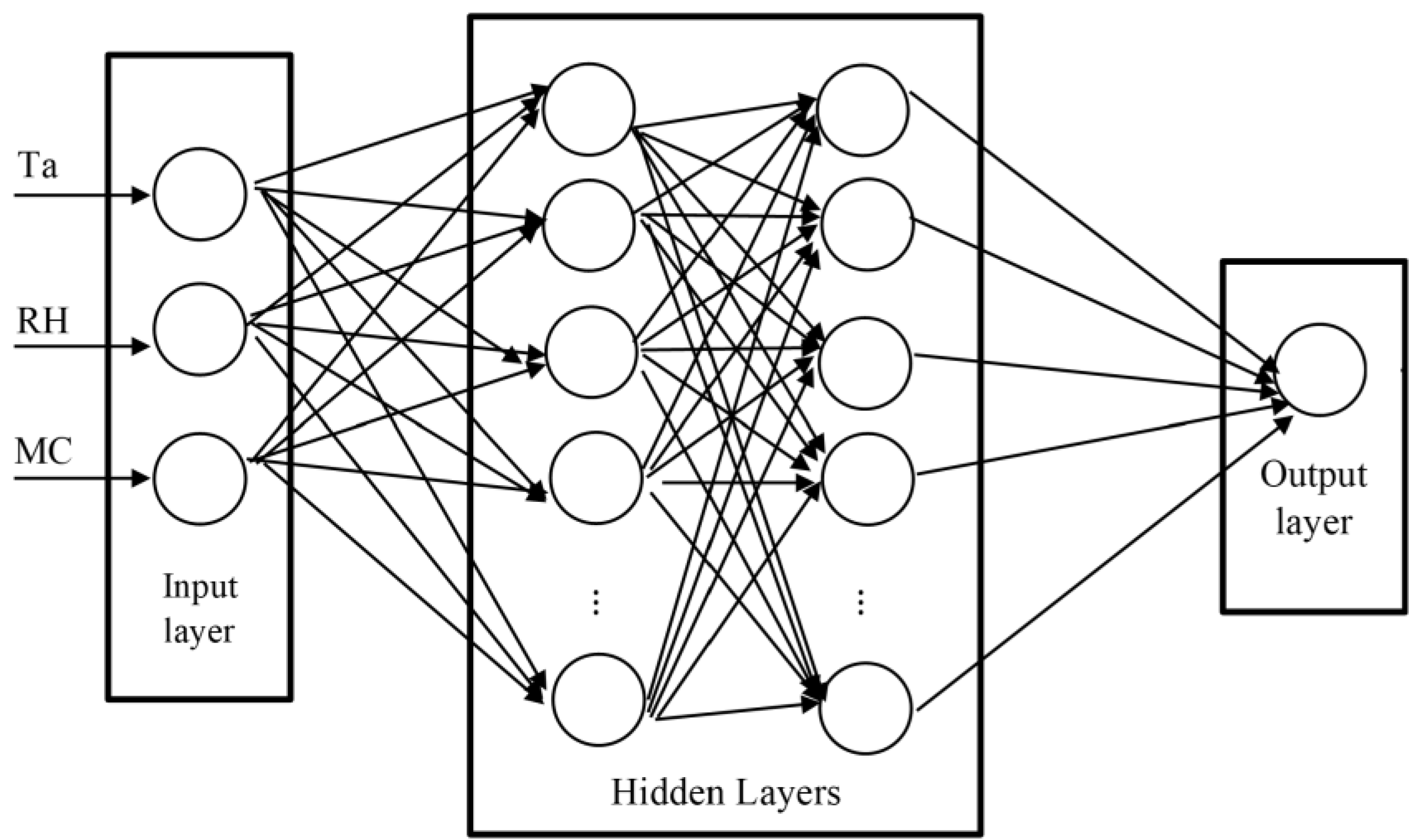
6. ANN Design and Implementation
6.1. General Description
- Firstly, determine the ANN architecture.
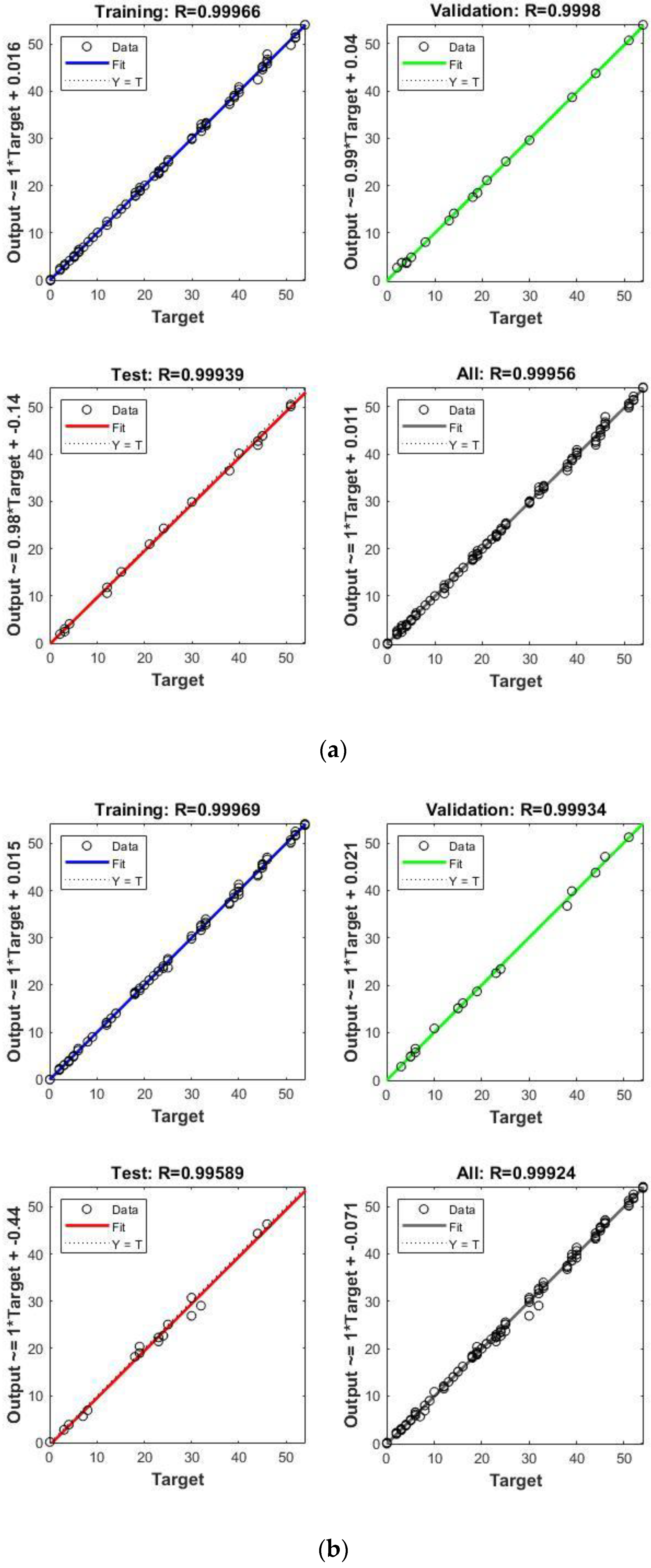
- Secondly, train the model, and validate its final configuration by calculating the mean squared error (MSE) and the coefficient of regression R.
- Thirdly, once the neural network predicts the time required to reach moisture content (MC) levels of 12% and 8%, compare these predictions with the experimental results by calculating the errors.
6.2. Model Building
6.3. Performance Parameters
6.4. ANN Results and Discussion
7. Comparative Analysis
7.1. Comparison Criterion
7.2. Experience vs. Simulation
7.3. Experience vs. ANN
7.4. Interpretation of Comparison Results
7.5. Comparative Analysis with Previous Studies
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haddouche, M.; Ilinca, A. Energy Efficiency and Industry 4.0 in Wood Industry: A Review and Comparison to Other Industries. Energies 2022, 15, 2384. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Y.; Wang, Z.; Zhao, Z.; Yi, S. Reducing wood drying time by application of ultrasound pretreatment. Dry. Technol. 2016, 34, 1141–1146. [Google Scholar] [CrossRef]
- Barbosa de Lima, A.G.; da Silva, J.V.; Pereira, E.M.A.; dos Santos, I.B.; de Lima, W.M.P.B. Drying of Bioproducts: Quality and Energy Aspects. In Drying and Energy Technologies; Delgado, J.M.P.Q., Barbosa de Lima, A.G., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–18. [Google Scholar] [CrossRef]
- Brandão, R.J.; Borel, L.D.M.S.; Marques, L.G.; Prado, M.M. Heat and Mass Transfer, Energy and Product Quality Aspects in Drying Processes Using Infrared Radiation. In Drying and Energy Technologies; Delgado, J.M.P.Q., Barbosa de Lima, A.G., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 111–130. [Google Scholar] [CrossRef]
- Ahmadinia, S.; Palviainen, M.; Kiuru, P.; Routa, J.; Sikanen, L.; Urzainki, I.; Laurén, A.A. Forest chip drying in self-heating piles during storage as affected by temperature and relative humidity conditions. Fuel 2022, 324, 124419. [Google Scholar] [CrossRef]
- Routa, J.; Kolström, M.; Sikanen, L. Dry matter losses and their economic significance in forest energy procurement. Int. J. For. Eng. 2018, 29, 53–62. [Google Scholar] [CrossRef]
- Fritzell, E.; Melander, O.; Rasmuson, A. The Drying Kinetics and Equilibrium Moisture Content of MDF Fibers. Dry. Technol. 2009, 27, 993–998. [Google Scholar] [CrossRef]
- Tomczak, K.; Tomczak, A.; Jelonek, T. Effect of Natural Drying Methods on Moisture Content and Mass Change of Scots Pine Roundwood. Forests 2020, 11, 668. [Google Scholar] [CrossRef]
- Glass, S.; Zelinka, S. Moisture Relations and Physical Properties of Wood; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
- Liu, R.; Liu, M.; Qu, Y.; Huang, A.; Ma, E. Dynamic moisture sorption and formaldehyde emission behavior of three kinds of wood-based panels. Eur. J. Wood Wood Prod. 2018, 76, 1037–1044. [Google Scholar] [CrossRef]
- Suchsland, O. Linear hygroscopic expansion of selected commercial particleboards. For. Prod. J. 1972, 22, 28–32. [Google Scholar]
- Wu, Q. Application of nelson’s sorption isotherm to wood composites and overlays. Wood Fiber Sci. 1999, 31, 187–191. [Google Scholar]
- Wu, Q.; Suchsland, O. Prediction of moisture content and moisture gradient of an overlaid particleboard. Wood Fiber Sci. 1996, 28, 227–239. [Google Scholar]
- Böhm, M.; Kobeticova, K.; Prochazka, J.; Černý, R. Moisture sorption and thickness swelling of wood-based materials intended for structural use in humid conditions and bonded with melamine resin. IOP Conf. Ser. Mater. Sci. Eng. 2019, 549, 012042. [Google Scholar] [CrossRef]
- Irle, M.; Barbu, M.; Niemz, P.; Carvalho, L.; Martins, J.; Costa, C.; Launey, M.; Sernek, M.; Dunky, M.; Aderhold, J.; et al. Wood-Based Panels: An Introduction for Specialists; Brunel University Press: London, UK, 2010. [Google Scholar]
- Thibeault, F.; Marceau, D.; Younsi, R.; Kocaefe, D. Numerical and experimental validation of thermo-hygro-mechanical behaviour of wood during drying process. Int. Commun. Heat Mass Transf. 2010, 37, 756–760. [Google Scholar] [CrossRef]
- Composite Panel Association. Technical Bulletin; Dimensional Stability of Particleboard and Medium Density Fiberboard (MDF); Composite Panel Association: Leesburg, VA, USA, 1997. [Google Scholar]
- Composite Panel Association. Technical Bulletin; Storage and Handling of Particleboard and Medium Density Fiberboard (MDF); Composite Panel Association: Leesburg, VA, USA, 2000. [Google Scholar]
- ASHRAE Standard 55a; R American Society of Heating, R.a.A.C.E.; American Society of Heating: Atlanta, GA, USA, 1995.
- Nelson, R.M. A model for sorption of water vapor by cellulosic materials. Wood Fiber Sci. 1983, 15, 8–22. [Google Scholar]
- Ganev, S.; Cloutier, A.; Beauregard, R.; Gendron, G. Effect of panel moisture content and density on moisture movement in MDF. Wood Fiber Sci. 2003, 35, 68–82. [Google Scholar]
- Siau, J.F. Transport Processes in Wood; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Cloutier, A.; Fortin, Y. A model of moisture movement in wood based on water potential and the determination of the effective water conductivity. Wood Sci. Technol. 1993, 27, 95–114. [Google Scholar] [CrossRef]
- Crank, J.; Park, G. An evaluation of the diffusion coefficient for chloroform in polystyrene from simple absorption experiments. Trans. Faraday Soc. 1949, 45, 240–249. [Google Scholar] [CrossRef]
- Luikov, A.V. Heat and Mass Transfer in Capillary-Porous Bodies. In Advances in Heat Transfer; Irvine, T.F., Hartnett, J.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1966; Volume 1, pp. 123–184. [Google Scholar]
- Simpson, W.T. Predicting equilibrium moisture content of wood by mathematical models. Wood Fiber Sci. 1973, 5, 41–49. [Google Scholar]
- Simpson, W.T. Measuring dependence of diffusion coefficient of wood on moisture concentration by adsorption experiments. Wood Fiber Sci. 1974, 5, 299–307. [Google Scholar]
- Liu, J.Y. A new method for separating diffusion coefficient and surface emission coefficient. Wood Fiber Sci. 1989, 21, 133–141. [Google Scholar]
- Simpson, W.T.; Liu, J.Y. Dependence of the water vapor diffusion coefficient of aspen (Populus spec.) on moisture content. Wood Sci. Technol. 1991, 26, 9–21. [Google Scholar] [CrossRef]
- Whitaker, S. Simultaneous Heat, Mass, and Momentum Transfer in Porous Media: A Theory of Drying. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1977; Volume 13, pp. 119–203. [Google Scholar]
- Stanish, M.; Schajer, G.; Kayihan, F. A mathematical model of drying for hygroscopic porous media. AIChE J. 1986, 32, 1301–1311. [Google Scholar] [CrossRef]
- Fortin, Y. Moisture Content-Matric Potential Relationship and Water Flow Properties of Wood at High Moisture Contents. Text. 1980. Available online: https://open.library.ubc.ca/collections/831/items/1.0095222 (accessed on 1 November 2023).
- Cloutier, A.; Fortin, Y. “Moisture content” water potential relationship of wood from saturated to dry conditions. Wood Sci. Technol. 1991, 25, 263–280. [Google Scholar] [CrossRef]
- Liping, C.; Deku, S. Modelling of the moisture transfer process in particleboards. Holz als Roh-und Werkstoff 1992, 50, 395–399. [Google Scholar] [CrossRef]
- Wu, Q.; Xiong, M. A Simulation of Moisture Diffusion Process in Furniture-grade Medium Density Fibreboard. In Proceedings of the 7th International IUFRO Wood Drying Conference, Tsukuba, Japan, 9–13 July 2001; pp. 222–227. [Google Scholar]
- Cai, L.; Wang, F. Steady and unsteady state moisture movement in particleboards. Holz als Roh- und Werkstoff 1994, 52, 304–306. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. (Eds.) Chapter 2—Properties of Gases and Liquids. In Principles of Environmental Physics, 4th ed.; Academic Press: Boston, MA, USA, 2013; pp. 5–23. [Google Scholar] [CrossRef]
- Čermák, P.; Horáček, P.; Rademacher, P. Measured temperature and moisture profiles during thermal modification of beech (Fagus sylvatica L.) and spruce (Picea abies L. Karst.) wood. Holzforschung 2014, 68, 175–183. [Google Scholar] [CrossRef]
- Autengruber, M.; Lukacevic, M.; Füssl, J. Finite-element-based moisture transport model for wood including free water above the fiber saturation point. Int. J. Heat Mass Transf. 2020, 161, 120228. [Google Scholar] [CrossRef]
- Yang, Q. Study on the specific heat of wood by statistical mechanics. J. For. Res. 2000, 11, 265–268. [Google Scholar] [CrossRef]
- Li, K.Y.; Fleischmann, C.M.; Spearpoint, M.J. Determining thermal physical properties of pyrolyzing New Zealand medium density fibreboard (MDF). Chem. Eng. Sci. 2013, 95, 211–220. [Google Scholar] [CrossRef]
- Tenwolde, A.; Mcnatt, J.D.; Krahn, L. Thermal Properties of Wood and Wood Panel Products for Use in Buildings; Forest Service: Madison, WI, USA, 1988. [Google Scholar]






| Test # | Initial Test Conditions | Initial EMC Melamine (%) | Initial EMC MDF (%) | Corrected Test Conditions | EMC Melamine (%) | EMC MDF (%) |
|---|---|---|---|---|---|---|
| 1 | 23 °C and 77% | 15.0 | 14.0 | 23 °C and 65% | 12.3 | 11.5 |
| 2 | 26 °C and 57% | 11.1 | 10.2 | 26 °C and 57% | 11.1 | 10.2 |
| 3 | 27 °C and 20% | 5.8 | 4.9 | 27 °C and 20% | 5.8 | 4.9 |
| 4 | 20 °C and 31% | 7.5 | 6.6 | 20 °C and 31% | 7.5 | 6.6 |
| 5 | 19 °C and 87% | 18.5 | 17.5 | 19 °C and 65% | 12.5 | 11.7 |
| 6 | 23 °C and 63% | 11.9 | 11.0 | 23 °C and 63% | 11.9 | 11.0 |
| Year | Author (s) | Expression | Advantage | Limits |
|---|---|---|---|---|
| 1949 | Crank and Park [25] | D = (0.049 a2)/t0.5 | Easy in application and calculus. | Significant error. Many missed parameters. |
| 1956 | Crank [24] | D = (0.1976 l2)/t0.5 | Easy in application and calculus. | Significant error. Many missed parameters. |
| 1966 | Luikov [26] | Kim, ε, Pn, K0 and Lu: Variable parameters | Analytic resolution. General formula considering both mass and heat transfer. | Depending on a lot of parameters. Difference from specimen surface to center. |
| 1974 | Simpson [24] | S: Averages of dealing with the concentration depending on the diffusion coefficient. and are the values of S at the points X = m(ΔX) at T = (n + 1) ΔT and T = n (ΔT), respectively, and Sm + 1 and Sm − 1 are the values of S at X = (m + 1)(ΔX) and X = X = (m − 1)(ΔX) at T = n (ΔT). | Series of approximations that are repeated until certain experimental and calculated values agree. Good match with experience results. | Large lumber of successive approximations. A high-speed computer is necessary to apply the method. |
| 1977 | Whitaker [31] | D: drying diffusion coefficient S: fractional moisture saturation | Analytic resolution. Based on simultaneous heat, mass, and momentum transfer in porous media. | Many assumptions (neglected parameters) and approximations to solve the problem. A lot of calculations. |
| 1984 | Siau [22] | L = thickness in direction of flow, cm; t = time, s. E = dimensionless term. D’ = diffusion coefficient which includes diffusion coefficient D and surface emission coefficient S | Analytic equation. Simple to calculate. | Includes unknown variable S (surface emission coefficient). |
| 1986 | Stanish [32] | (The conservation equation for air) | Simulated and experimental results revealed minor changes in the model parameter set. | Computational resolution by finite elements. |
| 1989 | Liu [29] | Use of surface emission coefficient S with diffusion D to obtain global phenomena understanding. | Significant error. Many missed parameters. | |
| 1991 | Simpson et Liu [30] | D = A exp (B m) A and B are coefficients determined by non-linear regression | Treats high-level moisture. Easy to apply. | Proceeding by two approximations. A and B numerical value changing with approximation. Adjusted parameters by experience. |
| 1993 | Cloutier and Fortin [24] (based on [25,30,31] works) | [Kx]xi,tj = effective water conductivity in the direction of flow x at position xi and time tj; [∂I/∂t]xi,tj = −(flow through plane xi at time tj); [∂ψ/∂x]xi,tj = ψ gradient at xi and tj. C: moisture concentration ψ: water potential (See Figure 1) | Combining analytic and experimental resolution. Less error and more precision than another formula. | Many notions and equations are to be considered. Needs a small gap between points, so more computing resources. |
| 1992 | L. Cai and S. Deku [35] | D’ = b0 + b1M + b2M2 + b3M3 | The diffusion D’ was expressed as a function of water content M with a third-degree polynomial. Use of the FEM. | Neglects the resistance of the surface in the unsteady regime. Error about 10% between experiment and FEM. |
| 1994 | L. Cai, F. and Wang [37] | (1) The diffusion coefficients of moisture movement perpendicular (d) and parallel (d) (2) Usins Liu [29] and Siau [22] equations to determine the diffusion coefficient (3) Regression equation Y = b + aX a,b depending on parameters on materials and direction (4) Determinate a simple relationship between moisture M, Diffusion D, and time t, for each case (example: M = 1.4774 t 0.178 with correlation coefficient R = 0.9710) | Treat both steady-state and unsteady-state. Determines diffusion coefficient D for both parallel and perpendicular orientations. Determines the linear relationship between diffusion D and moisture M for each case. | No general equation (equation for each case). A lot of approximation. Uses experience and graphic analysis to determine diffusion d for the steady state (giving the results by direct values). |
| 1996 | Wu and Suchsland [13] | Determinate the moisture content MC in two ways and compare between them: Predicting: Equation (5) and D Wi = specimen weight at time ‘‘i” W1 = initial specimen weight, WE = specimen weight at equilibrium, L = half specimen thickness. Measuring: Using Simpson’s [27] equation to determine the diffusion coefficient Comparing the two approaches | Good agreement between predicted and measured MC for three different panels. Demonstrates the backer can reduce the extent of the moisture differential and swelling stress imbalance. | The moisture profile is supposed uniform across the specimen thickness. Using experimental results that cannot fully create the assumed conditions. |
| 2001 | Wu Q, and Xiong M [36] | K (p,x) = 0.00431 − 0.00107p + 0.00192x + 0.0005p2 − 0.0192x2 + 0.000206.x.p | No big calculation and complex formula. Dedicated to MDF and particle boards. | A small range of temperature and humidity. |
| Parameter | Type | Definition | Value/Expression | Reference |
|---|---|---|---|---|
| T | Boundary conditions | Temperature (°K) | 292.15–300.15 | Table 1 |
| RH | Boundary conditions | Relative humidity | 20–65% | Table 1 |
| T_ini | Initial conditions | Initial temperature (°K) | 291.15 | Present work |
| MC_ini | Initial conditions | Initial moisture content | 18% | Present work |
| MC_fin | Boundary conditions | Final moisture content | EMC | Present work |
| D | Diffusion (m2/s) | Equation (15) | Present work | |
| CP_Melamine | Specific heat capacity of melamine (J/kg·K) | [40,41] | ||
| CP_MDF | Specific heat capacity of MDF (J/kg·K) | [42,43] |
| Test # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | |
| Element size (mm) | 14 | 100 | 10.8 | 60 | 8 | 38 | 5.6 | 30 | 3.6 | 20 | 2 | 16 | 0.8 | 11 | 0.3 | 7 | 0.04 | 4 |
| Calculation time | 14 min 21 s | 4 min 58 s | 6 min 20 s | 4 min 57 s | 7 min 53 s | 11 min 22 s | 45 min 31 s | 1 h 50 min 40 s | 2 h 15 min 21 s | |||||||||
| Relative error | 21.67% | 19.22% | 16.90% | 15.28% | 11.69% | 4.70% | 2.50% | 0.6% | 0.5% | |||||||||
| Material | Dimensions (L × W × T) [mm] | Sample Numbers | Density (kg/m3) |
|---|---|---|---|
| Melamine | 200 × 100 × 15.8 | 1P1, 1P2, 1P3, 1P4, 1P5, 1P6, 2P1, 2P2, 2P3, 2P4, 2P5, 2P6 | 728 (calculated) |
| MDF | 200 × 200 × 12.7 | 1M1, 1M2, 1M3, 1M4, 1M5, 1M6, 2M1, 2M2, 2M3, 2M4, 2M5, 2M6 | 728 (calculated) |
| MDF | Melamine | ||||||
|---|---|---|---|---|---|---|---|
| First Test | Second Test | First Test | Second Test | ||||
| Sample | Weight (g) | Sample | Weight (g) | Sample | Weight (g) | Sample | Weight (g) |
| 1M1 | 355.18 | 2M1 | 370.91 | 1P1 | 222.45 | 2P1 | 227.16 |
| 1M2 | 362.58 | 2M2 | 371.37 | 1P2 | 237.39 | 2P2 | 233.99 |
| 1M3 | 359.39 | 2M3 | 378.33 | 1P3 | 228.89 | 2P3 | 217.08 |
| 1M4 | 369.35 | 2M4 | 371.08 | 1P4 | 239.87 | 2P4 | 235.74 |
| 1M5 | 372.93 | 2M5 | 375.71 | 1P5 | 222.88 | 2P5 | 235.27 |
| 1M6 | 378.50 | 2M6 | 385.99 | 1P6 | 236.58 | 2P6 | 224.70 |
| Time (Days) | MC (%) Melamine | MC (%) MDF |
|---|---|---|
| 0.00 | 0.0% | 0.0% |
| 1.00 | 5.3% | 6.6% |
| 4.00 | 9.0% | 14.8% |
| 5.00 | 10.2% | 15.4% |
| 7.00 | 11.4% | 16.1% |
| 12.00 | 14.9% | 17.3% |
| 18.00 | 16.9% | 17.9% |
| 19.00 | 17.5% | 18.1% |
| 20.00 | 17.7% | 18.1% |
| 21.00 | 17.9% | 18.2% |
| Test # | Test Conditions | Melamine (Days) | MDF (Days) | ||
|---|---|---|---|---|---|
| 12% | 8% | 12% | 8% | ||
| 1 | 23 °C and 65% | 30 | 66 | 25 | 58 |
| 2 | 26 °C and 57% | 13 | 33 | 7 | 19 |
| 3 | 27 °C and 20% | 10.4 | 14.3 | 7.3 | 10.4 |
| 4 | 20 °C and 31% | 5.4 | 12.6 | 7.4 | 16 |
| 5 | 19 °C and 65% | 21 | 70 | 18 | 60 |
| 6 | 23 °C and 63% | 23 | 68 | 18 | 54 |
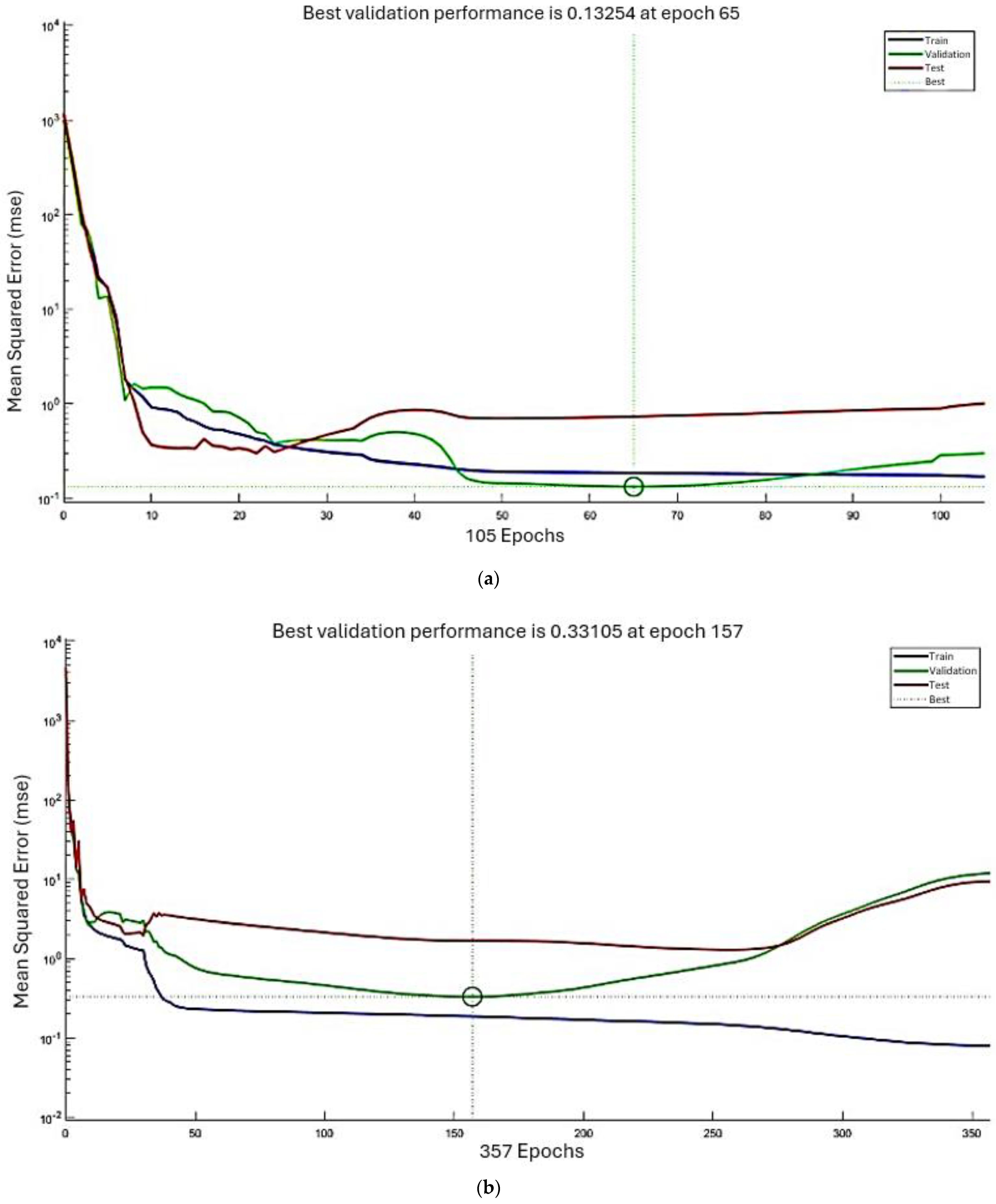
| Material | ANN Architecture | MSE Training | MSE Validation | R | Linear Regression Model |
|---|---|---|---|---|---|
| Melamine | [3-10-7-1] | 0.17 | 0.13 | 0.99956 | Output = 1*Target + 0.011 |
| MDF | [3-10-10-1] | 0.08 | 0.33 | 0.99924 | Output = 1*Target + 0.071 |
| Condition | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Melamine | Minimum error | 0.3% | 1.7% | 0.5% | 2.7% | 0.2% | 0.9% |
| Maximum error | 18.6% | 14.6% | 20.7% | 25.4% | 20.8% | 22.2% | |
| Average errors | 9.6% | 8.9% | 10.8% | 10.1% | 13.1% | 14.2% | |
| MDF | Minimum error | 1.1% | 1.2% | 0.6% | 0.2% | 0.9% | 0.8% |
| Maximum error | 15.7% | 15.5% | 24.6% | 10.3% | 19.8% | 22.2% | |
| Average errors | 8.3% | 10.7% | 10.7% | 4.4% | 13.5% | 14.2% |
| Condition | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Melamine (8%) Experience | 66 | 33 | 14.3 | 12.6 | 70 | 68 |
| Melamine (8%) ANN | 66.3 | 33.51 | 14.26 | 12.76 | 67.66 | 69.04 |
| PE | 0.46% | 1.55% | 0.27% | 1.27% | 3.35% | 1.53% |
| Average | 1.40% | |||||
| Melamine (12%) Experience | 30 | 13 | 10.4 | 5.4 | 21 | 23 |
| Melamine (12%) ANN | 29.05 | 12.69 | 9.91 | 5.42 | 20.68 | 21.86 |
| PE | 3.17% | 2.39% | 4.70% | 0.37% | 1.52% | 4.94% |
| Average | 2.85% | |||||
| MDF (8%) Experience | 58 | 19 | 10.4 | 16 | 60 | 54 |
| MDF (8%) ANN | 58.44 | 19.5 | 10.6 | 16.15 | 61.24 | 54.11 |
| PE | 0.77% | 2.64% | 1.88% | 0.94% | 2.07% | 0.21% |
| Average | 1.42% | |||||
| MDF (12%) Experience | 25 | 7 | 7.3 | 7.4 | 18 | 18 |
| MDF (12%) ANN | 24.79 | 7.18 | 7.51 | 7.65 | 17.58 | 17.73 |
| PE | 0.85% | 2.60% | 2.81% | 3.43% | 2.31% | 1.48% |
| Average | 2.25% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddouche, M.; Martini, F.; Chaouch, M.; Ilinca, A. Thermo-Hydric Study of Wood-Based Materials under Thermal Comfort Conditions. Materials 2024, 17, 1177. https://doi.org/10.3390/ma17051177
Haddouche M, Martini F, Chaouch M, Ilinca A. Thermo-Hydric Study of Wood-Based Materials under Thermal Comfort Conditions. Materials. 2024; 17(5):1177. https://doi.org/10.3390/ma17051177
Chicago/Turabian StyleHaddouche, Mohamed, Fahed Martini, Mounir Chaouch, and Adrian Ilinca. 2024. "Thermo-Hydric Study of Wood-Based Materials under Thermal Comfort Conditions" Materials 17, no. 5: 1177. https://doi.org/10.3390/ma17051177
APA StyleHaddouche, M., Martini, F., Chaouch, M., & Ilinca, A. (2024). Thermo-Hydric Study of Wood-Based Materials under Thermal Comfort Conditions. Materials, 17(5), 1177. https://doi.org/10.3390/ma17051177









