New Method for Detecting Flange Fracture Initiation in Incremental Radial Extrusion
Abstract
1. Introduction
2. Materials and Methods
- ε—effective strain;
- ε1, ε2, ε3—principal strains;
- —effective strain rate;
- C—value of the integral according to the normalized Cockcroft-Latham fracture criterion;
- σ1, σ2, σ3—principal stresses;
- σi—effective stress.
- Stress triaxiality
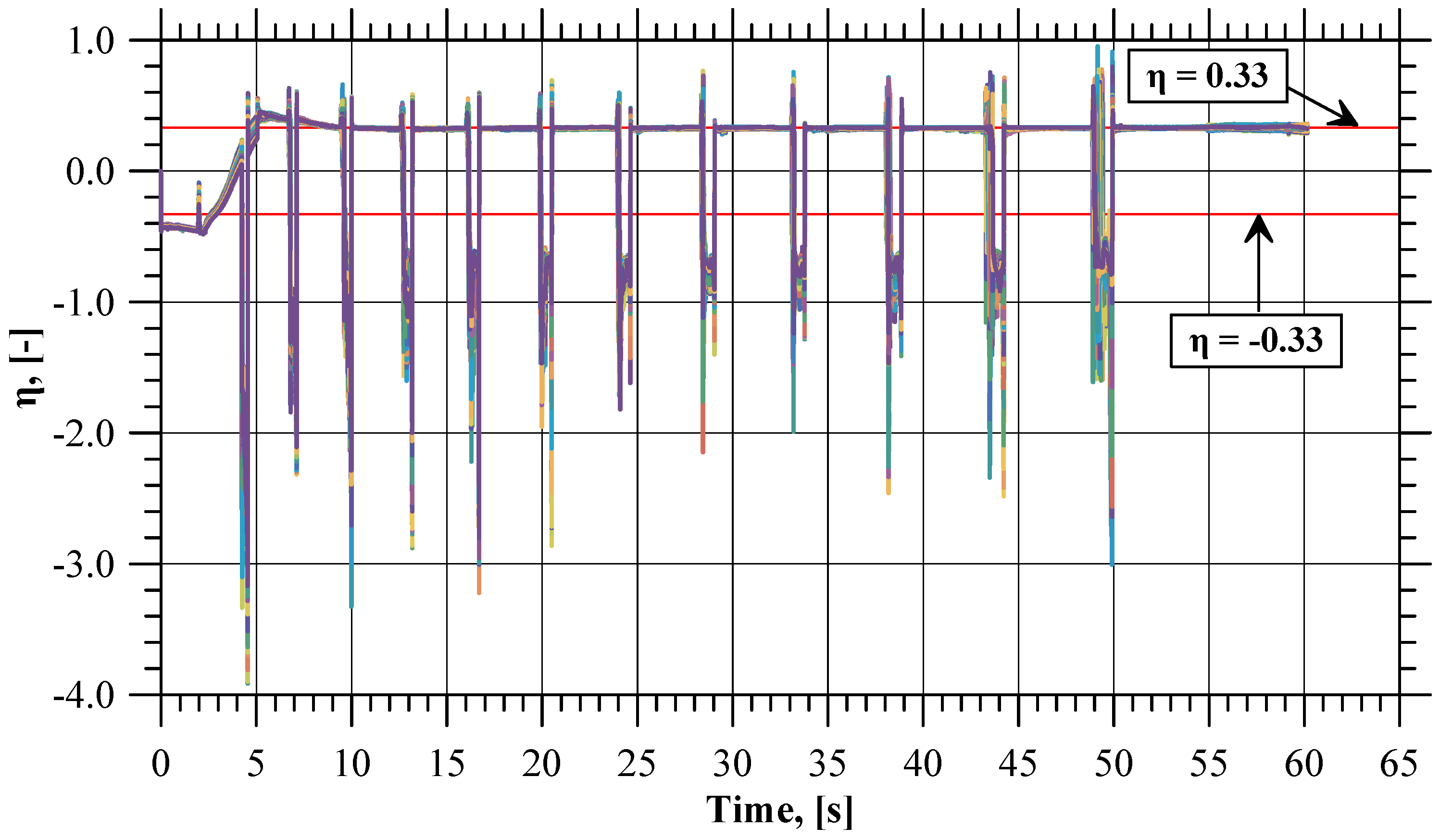
- Ratio between the maximum and the minimum effective strain at a given moment of time in all sensors:
- Increase in the effective strain value in individual sensors:
- Ratio between the maximum and the minimum value of the normalized Cockcroft–Latham fracture criterion integral at a given moment of time in all sensors:
- Increase in the value of the normalized Cockcroft–Latham fracture criterion integral in individual sensors:
- σm—mean stress;
- εi−s1, εi−s2, εi−s3, …, εi−s180—effective strain at the i-th moment of time in sensors s1, s2, s3, …, s180;
- εi,sj—effective strain at the i-th moment of time in the j-th sensor;
- Ci−s1, Ci−s2, Ci−s3, …, Ci−s180—values of the normalized Cockcroft-Latham fracture criterion integral at the i-th moment of time in sensors s1, s2, s3, …, s180;
- Ci,sj—values of the the normalized Cockcroft–Latham fracture criterion integral at the i-th moment of time in the j-th sensor.
- FEM analysis of the incremental radial flange extrusion process;
- Determination of the distribution of effective strains, strain rates, and values of the normalized Cockcroft–Latham fracture criterion integral in extruded parts;
- Determination of parameters describing the scatter and increment of effective strains, strain rates and normalized Cockcroft–Latham fracture criterion integral values on the flange edge;
- Determination of the moment of change in the values of the above parameters;
- Determination of the maximum flange diameter.
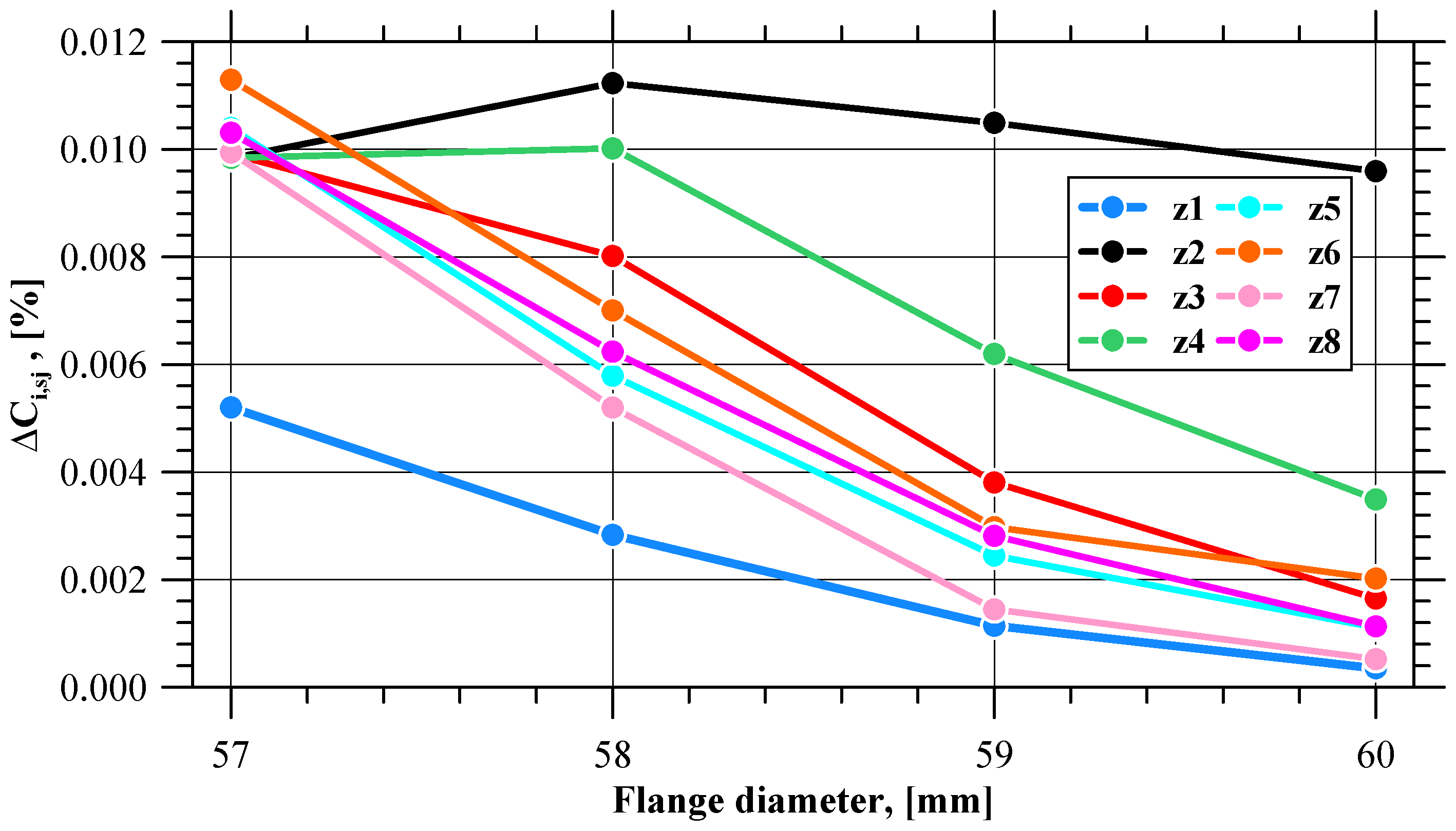
3. Results
4. Discussion
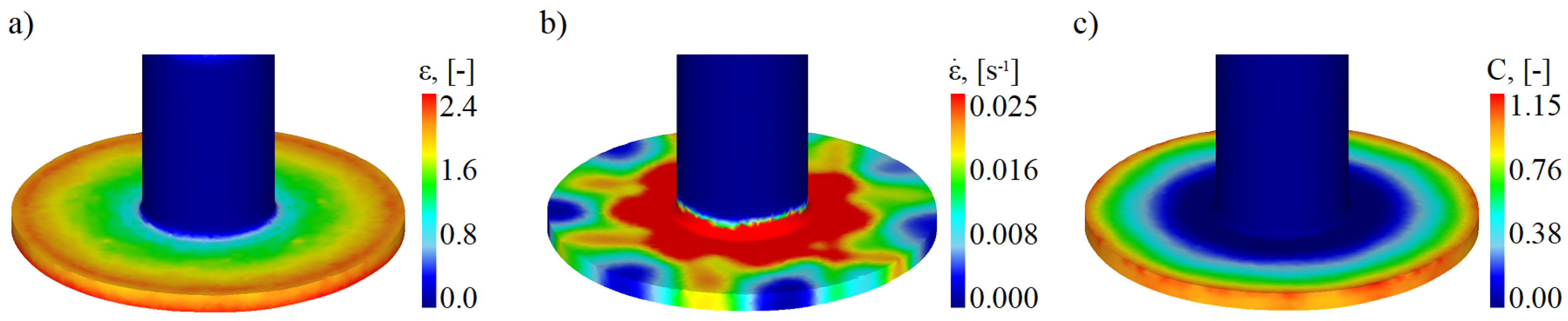
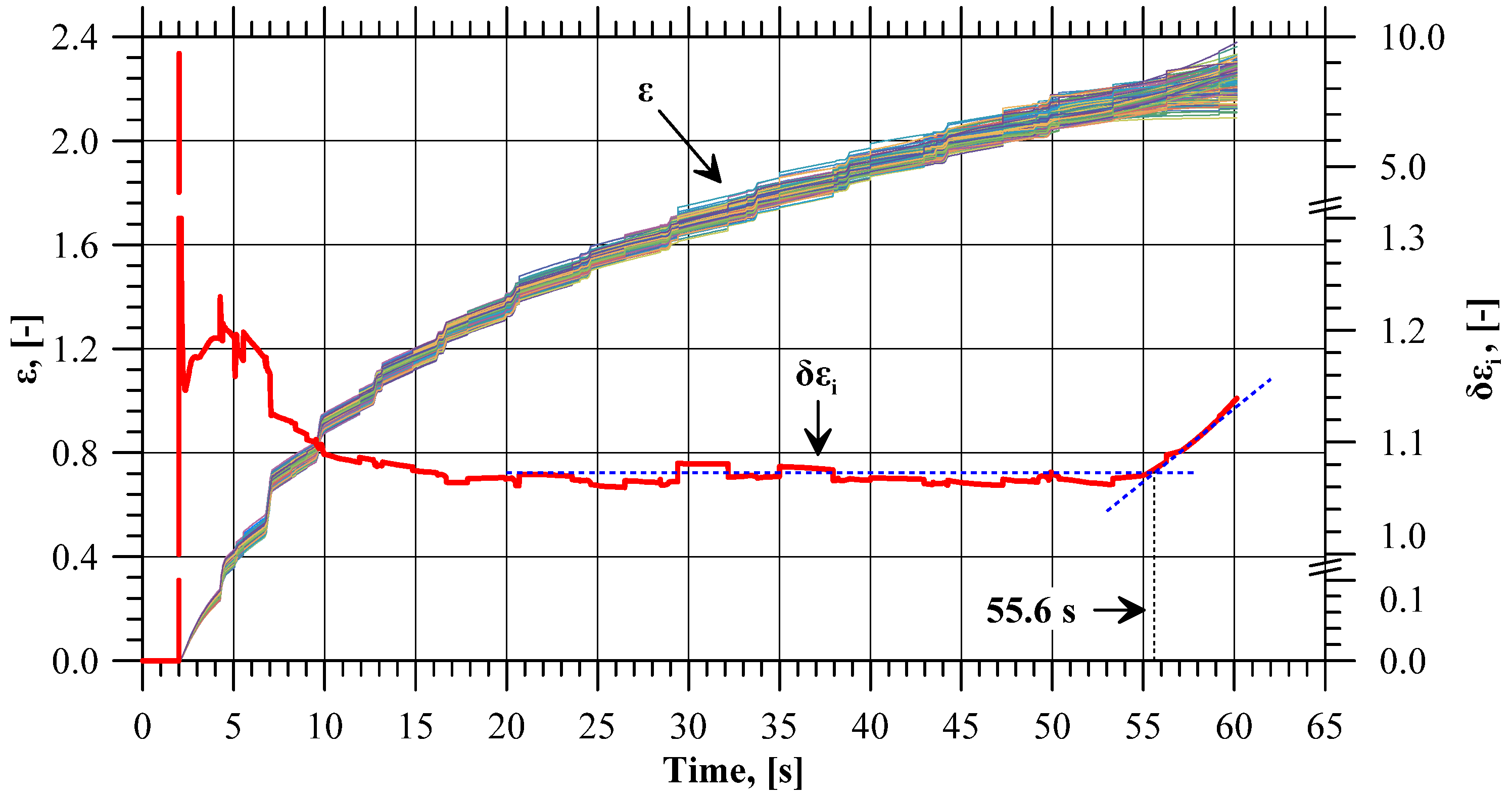
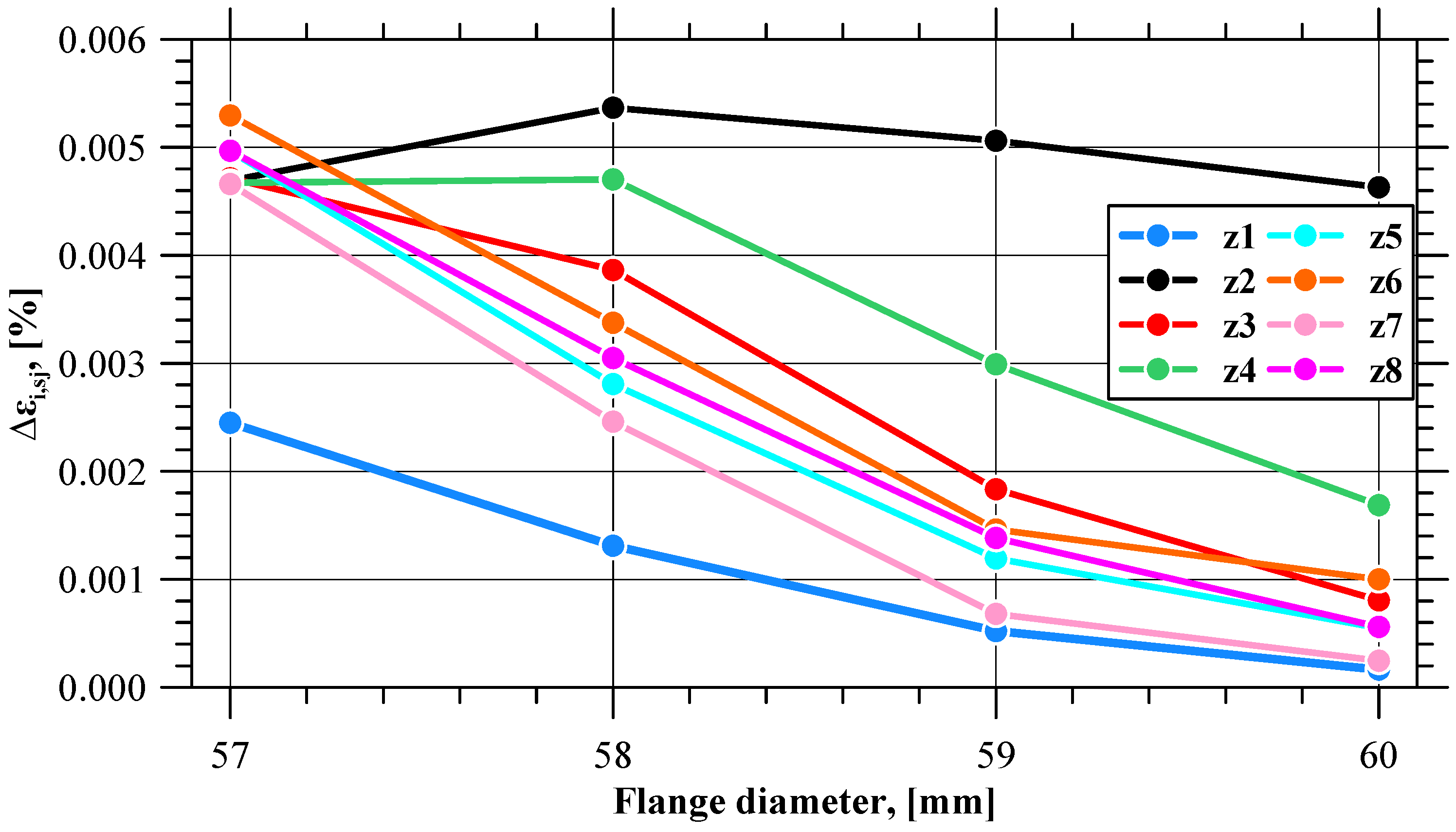
4.1. Effective Strain
4.2. Strain Rate
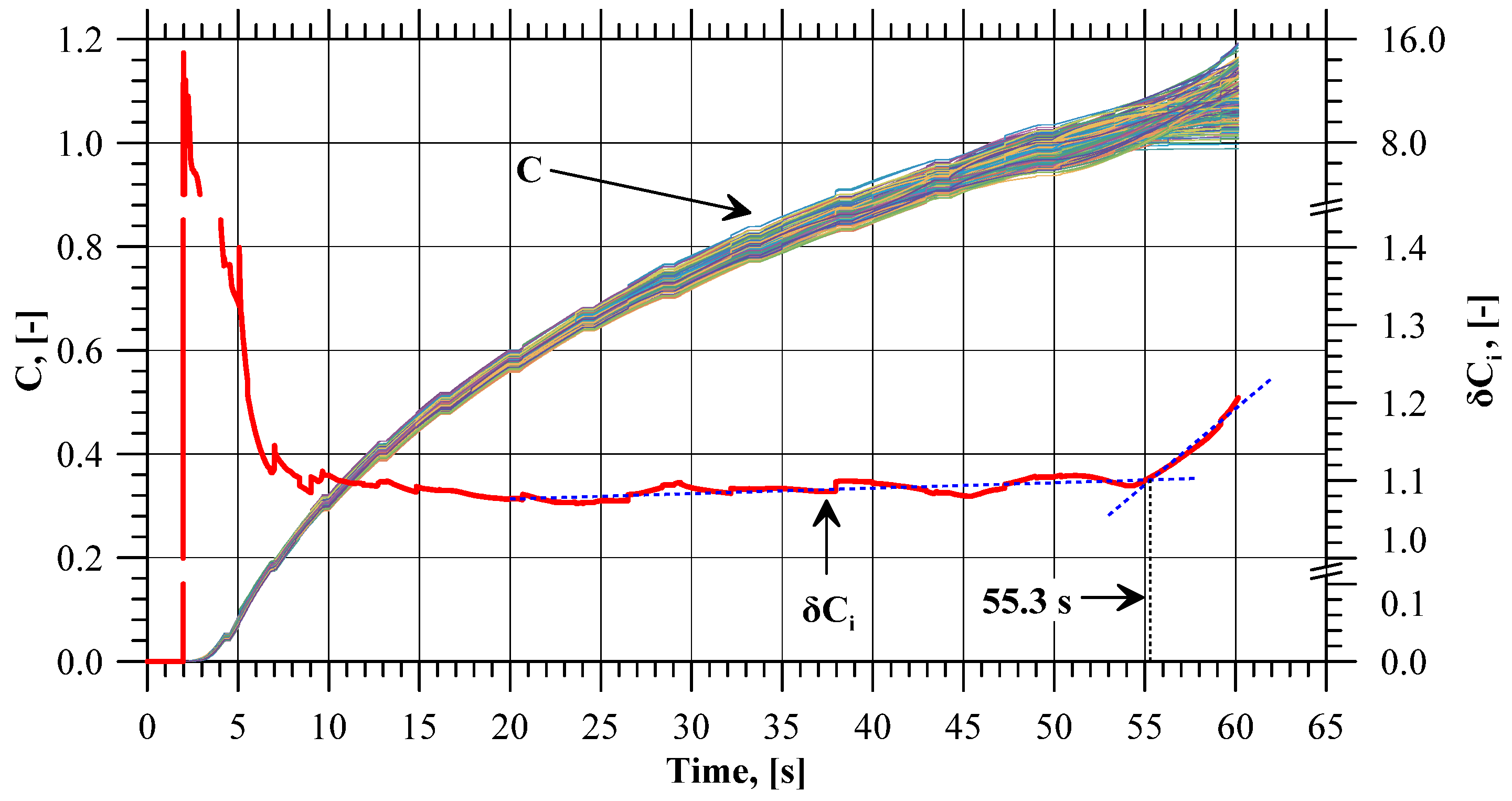
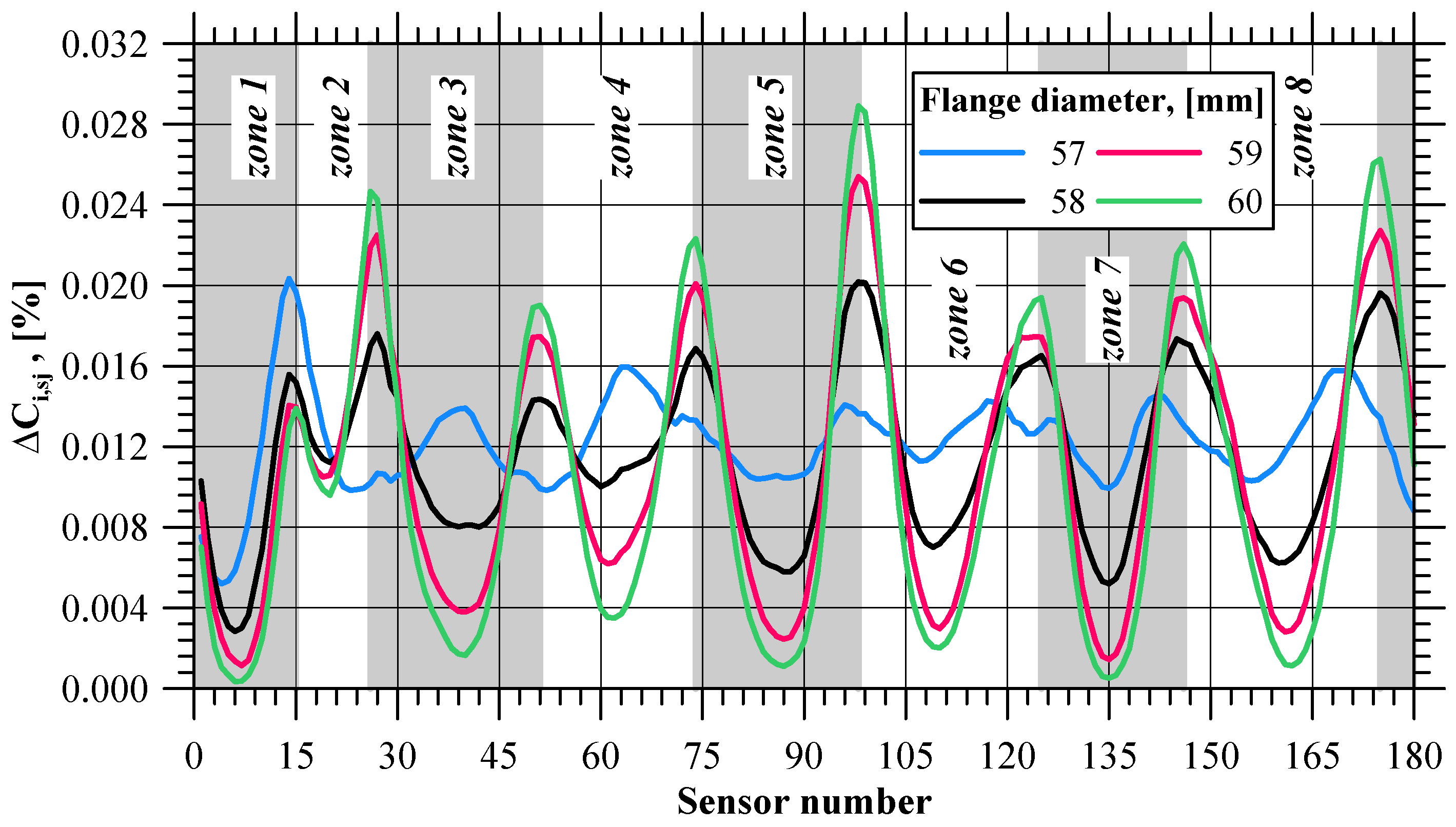
4.3. Cockcroft–Latham Integral
5. Conclusions
- Incremental radial extrusion makes it possible to form flanges on hollow parts, these flanges having constant thickness and a relatively large outside diameter;
- The use of rings with an increasing inside diameter for constraining the free flow of material in the radial direction causes a cyclic change in the state of strain and stress in the flange, which has a positive effect on the quality of the extruded parts;
- When material fracture initiates, the values of effective strain, strain rate, and the normalized Cockcroft–Latham fracture criterion integral on the flange edge begin to differ from those in other zones of the flange;
- The identification of the moments of changes in the values of the above-mentioned parameters, and thus the determination of flange fracture initiation, is possible via only numerical results analysis, which means that the proposed method for a limited flange diameter calculation does not require the performance of additional experiments aimed at calibrating or determining the limit parameters of the extruded material.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matsumoto, R.; Hayashi, K.; Utsunomiya, H. Experimental and numerical analysis of friction in high aspect ratio combined forward-backward extrusion with retreat and advance pulse ram motion on a servo press. J. Mater. Process Tech. 2014, 214, 936–944. [Google Scholar] [CrossRef]
- Maeno, T.; Mori, K.; Ichikawa, Y.; Sugawara, M. Use of liquid lubricant for backward extrusion of cup with internal splines using pulsating motion. J. Mater. Process Tech. 2017, 244, 273–281. [Google Scholar] [CrossRef]
- Lowrie, J.; Ngaile, G. Novel extrusion punch design for elimination of punch ejection load and enhanced lubrication. Manuf. Lett. 2015, 5, 12–16. [Google Scholar] [CrossRef]
- Fatemi-Varzaneh, S.M.; Zarei-Hanzaki, A.; Naderi, M.; Roostaei, A.A. Deformation homogeneity in accumulative back extrusion processing of AZ31 magnesium alloy. J. Alloys Compd. 2010, 507, 207–214. [Google Scholar] [CrossRef]
- Faraji, G.; Jafarzadeh, H.; Jeong, H.J.; Mashhadi, M.M.; Kim, H.S. Numerical and experimental investigation of the deformation behavior during the accumulative back extrusion of an AZ91 magnesium alloy. Mater. Des. 2012, 35, 251–258. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Z.; Yu, J.; Xue, Y. A novel backward extrusion process through rotating die and open punch. Procedia Eng. 2017, 207, 383–388. [Google Scholar] [CrossRef]
- Szota, P.; Mróz, S.; Stefanik, A.; Laber, K.; Mola, R. Theoretical and experimental analysis of the backward extrusion process with a rotational die of AZ31 alloy. Metalurgija 2021, 60, 36–38. Available online: https://hrcak.srce.hr/file/357468 (accessed on 8 January 2024).
- Che, X.; Wang, Q.; Dong, B.; Meng, M.; Zhang, Z. Numerical and experimental analysis of rotating backward extrusion as a new SPD process. Met. Mater. Int. 2020, 26, 1786–1796. [Google Scholar] [CrossRef]
- Che, X.; Dong, B.; Liu, K.; Wang, Q.; Meng, M.; Gao, Z.; Ma, J.; Yang, F.; Zhang, Z. An investigation on the microstructure and texture of an AZ80 cup-shaped piece processed by rotating backward extrusion. Materials 2020, 13, 3690. [Google Scholar] [CrossRef]
- Jafarzadeh, H.; Babaei, A.; Esmaeili-Goldarag, F. Friction stir radial backward extrusion (FSRBE) as a new grain refining technique. Arch. Civ. Mech. Eng. 2018, 18, 1374–1385. [Google Scholar] [CrossRef]
- Sheng, K.; Lu, L.; Xiang, Y.; Ma, M.; Wu, Z. Crack behavior in Mg/Al alloy thin sheet during hot compound extrusion. J. Magnes. Alloy 2019, 7, 717–724. [Google Scholar] [CrossRef]
- Tian, Y.; Hu, H.; Liang, P.; Zhang, D.; Ou, Z. Influences of expanding angles on extrusion-shearing-expanding processing of AZ31 magnesium alloy thin-walled tubes. Int. J. Adv. Manuf. Tech. 2022, 118, 751–758. [Google Scholar] [CrossRef]
- Ou, Z.; Hongjun, H.; Gang, H.; Hui, Z.; Zhongwen, O. A new method of processing magnesium alloy thin-walled tube by direct extrusion and corrugated equal channel angular extrusion. Int. J. Adv. Manuf. Tech. 2022, 122, 4029–4039. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A.; Dziubińska, A. The influence of tool geometry on the course of flanges radial extrusion in hollow parts. Arch. Civ. Mech. Eng. 2017, 17, 986–996. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A.; Samołyk, G. Flange formation in aluminium alloy EN AW 6060 tubes by radial extrusion with the use of a limit ring. Arch. Civ. Mech. Eng. 2019, 19, 1020–1028. [Google Scholar] [CrossRef]
- Ko, D.C.; Kim, B.M. The prediction of central burst defects in extrusion and wire drawing. J. Mater. Process Tech. 2000, 102, 19–24. [Google Scholar] [CrossRef]
- Saanouni, K.; Mariage, J.F.; Cherouat, A.; Lestriez, P. Numerical prediction of discontinuous central bursting in axisymmetric forward extrusion by continuum damage mechanics. Comput. Struct. 2004, 82, 2309–2332. [Google Scholar] [CrossRef]
- Soyarslan, C.; Tekkaya, A.E.; Akyuz, U. Application of continuum damage mechanics in discontinuous crack formation: Forward extrusion Chevron predictions. ZAMM Z. Angew. Math. Mech. 2008, 88, 436–453. [Google Scholar] [CrossRef]
- Soyarslan, C.; Tekkaya, A.E. Prevention of internal cracks in forward extrusion by means of counter pressure: A numerical treatise. Steel Res. Int. 2009, 80, 671–679. [Google Scholar] [CrossRef]
- Choi, J.S.; Lee, H.C.; Im, Y.T. A study on chevron crack formation and evolution in a cold extrusion. J. Mech. Sci. Technol. 2010, 24, 1885–1890. [Google Scholar] [CrossRef]
- Balasundar, I.; Raghu, T. On the die design for repetitive upsetting – extrusion (RUE) process. Int. J. Mater. Form. 2013, 6, 289–301. [Google Scholar] [CrossRef]
- Sebek, F.; Kubik, P.; Petruska, J. Chevron crack prediction using the extremely low stress triaxiality test. MM Sci. J. 2015, 6, 201518. [Google Scholar] [CrossRef]
- Terhorst, M.; Feuerhack, A.; Trauth, D.; Klocke, F. Extension of the normalized Cockcroft and Latham criterion with temperature-dependent critical damage values for predicting chevron cracks in solid forward extrusion. Int. J. Mater. Form. 2016, 9, 449–456. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.; Chen, X.; Xu, X. Cracking behavior and prediction criterion of spray-deposited 2195 Al–Li alloy extrusion profile. Int. J. Adv. Manuf. Tech. 2022, 120, 5969–5984. [Google Scholar] [CrossRef]
- Kubik, P.; Petruska, J.; Judas, J.; Sebek, F. Computational prediction of chevron cracking during multi-pass cold forward extrusion. J. Manuf. Process 2023, 102, 154–168. [Google Scholar] [CrossRef]
- Park, J.J. Finite-element analysis of radial extrusion for a thin disk with severe-plastic deformation. Met. Mater. Int. 2012, 18, 439–444. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Cristino, V.A.; Montanari, L.; Silva, M.B.; Atkins, A.G.; Martins, P.A.F. Fracture in hole-flanging produced by single point incremental forming. Int. J. Mech. Sci. 2014, 83, 146–154. [Google Scholar] [CrossRef]
- Kubik, P.; Sebek, F.; Hulka, J.; Petruska, J. Calibration of ductile fracture criteria at negative stress triaxiality. Int. J. Mech. Sci. 2016, 108–109, 90–103. [Google Scholar] [CrossRef]
- Pater, Z.; Tomczak, J.; Bulzak, T. Rotary compression as a new calibration test for prediction of a critical damage value. J. Mater. Res. Tech. 2020, 9, 5487–5498. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A.; Samołyk, G. Theoretical and experimental analysis of a new process for forming flanges on hollow parts. Materials 2020, 13, 4088. [Google Scholar] [CrossRef] [PubMed]
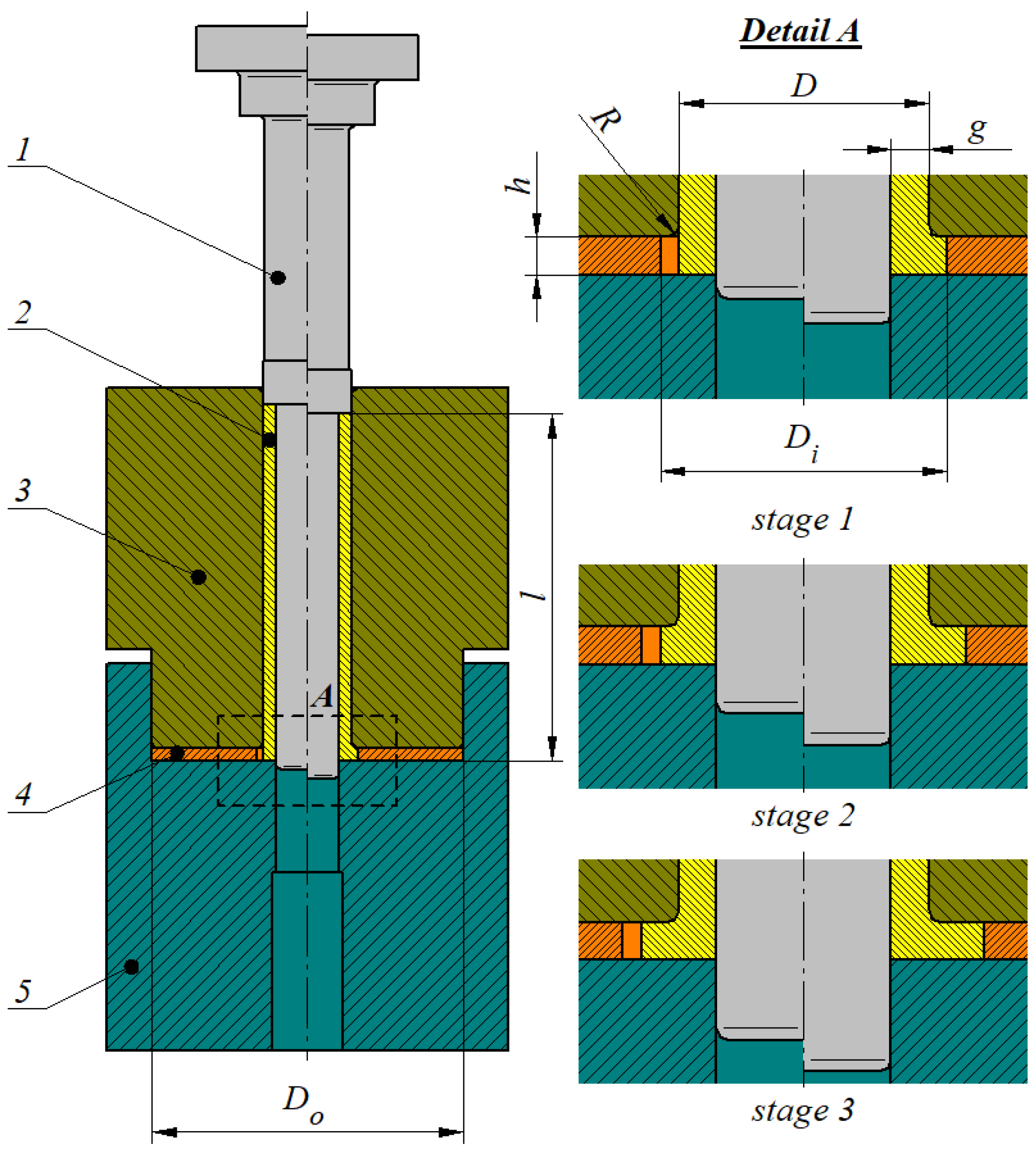
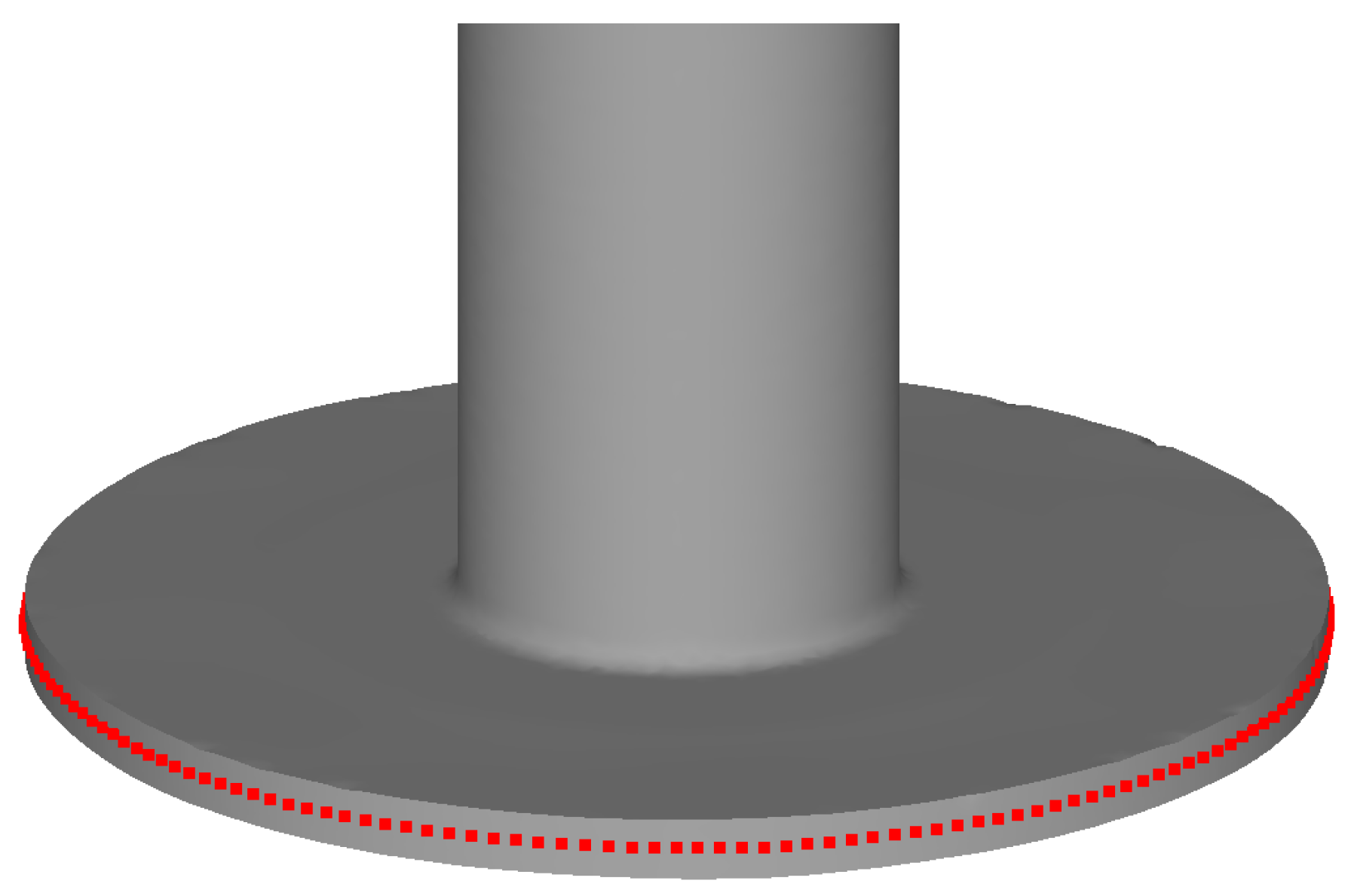




| Name of the Parameter | Parameter Value |
|---|---|
| Billet material | aluminum alloy EW AW 6060 in annealed state |
| Billet dimensions | D = 20 mm, g = 3 mm, l = 80 mm |
| Container working edge rounding radius | R = 1 mm |
| Ring dimensions | Di = 23, 26, 29, 32, 35, 38, 41, 44, 47, 50, 53, 56 mm, Do = 70 mm, h = 3 mm |
| FEM software | Deform-3D v11 |
| Flow curve equation for tested aluminum alloy | σp = 147.5·ε0.2 where σp—plastic stress, ε—strain |
| Initial temperature of billet and tools | 20 °C |
| Coefficient of heat transfer between workpiece and tools and between workpiece and environment | 12 kW/m2K, 0.02 kW/m2K |
| Friction factor between workpiece and tools | 0.2 |
| Punch velocity | 50 mm/min |
| Testing machine used in experiments | Instron 1000HDX |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiarski, G. New Method for Detecting Flange Fracture Initiation in Incremental Radial Extrusion. Materials 2024, 17, 1054. https://doi.org/10.3390/ma17051054
Winiarski G. New Method for Detecting Flange Fracture Initiation in Incremental Radial Extrusion. Materials. 2024; 17(5):1054. https://doi.org/10.3390/ma17051054
Chicago/Turabian StyleWiniarski, Grzegorz. 2024. "New Method for Detecting Flange Fracture Initiation in Incremental Radial Extrusion" Materials 17, no. 5: 1054. https://doi.org/10.3390/ma17051054
APA StyleWiniarski, G. (2024). New Method for Detecting Flange Fracture Initiation in Incremental Radial Extrusion. Materials, 17(5), 1054. https://doi.org/10.3390/ma17051054








