Relative Entropy Application to Study the Elastoplastic Behavior of S235JR Structural Steel
Abstract
1. Introduction
2. Theoretical Background
Governing Equations
- (i)
- Kullback–Leibler and Jeffreys’ relative entropies
- (ii)
- the squared Hellinger relative entropy
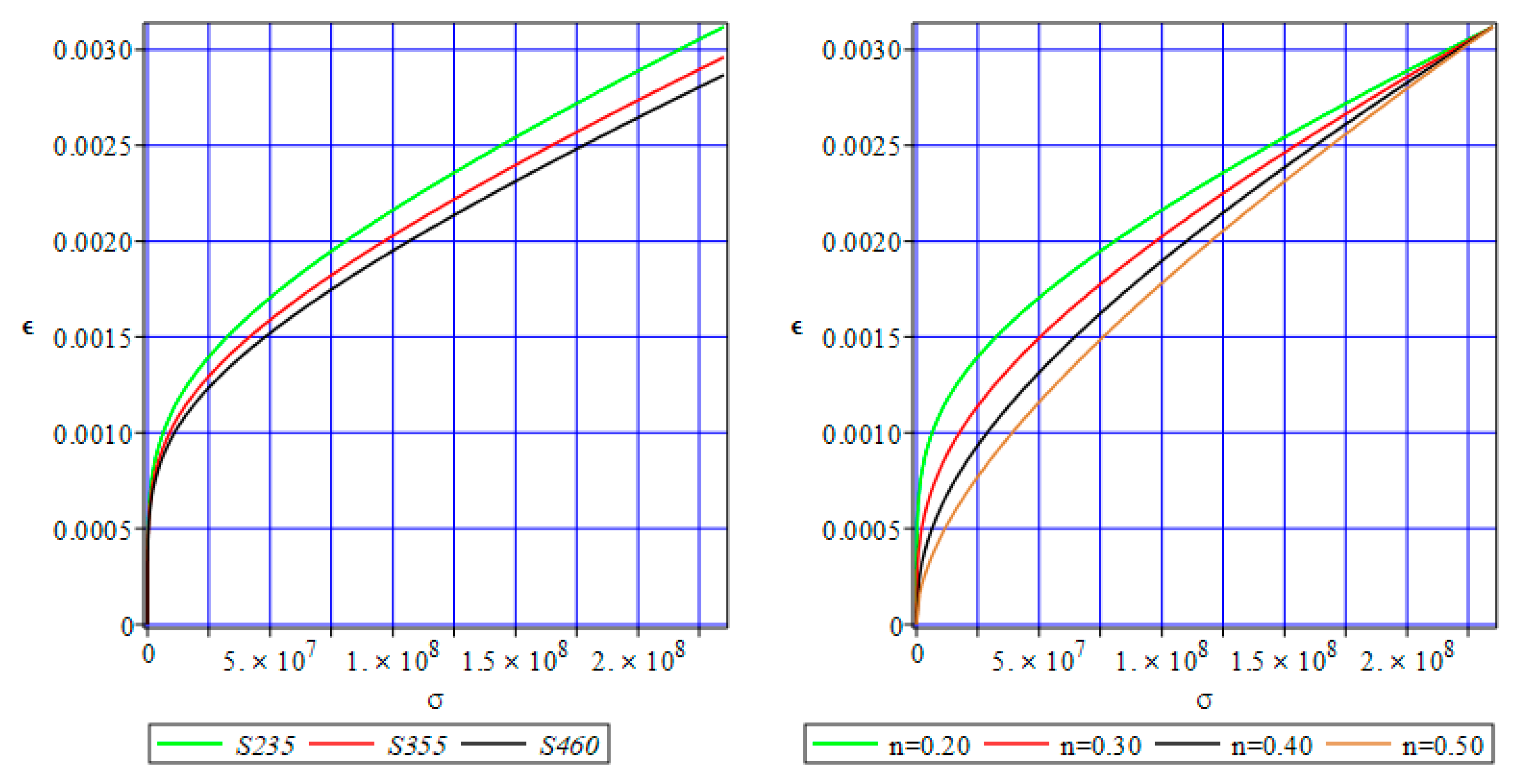
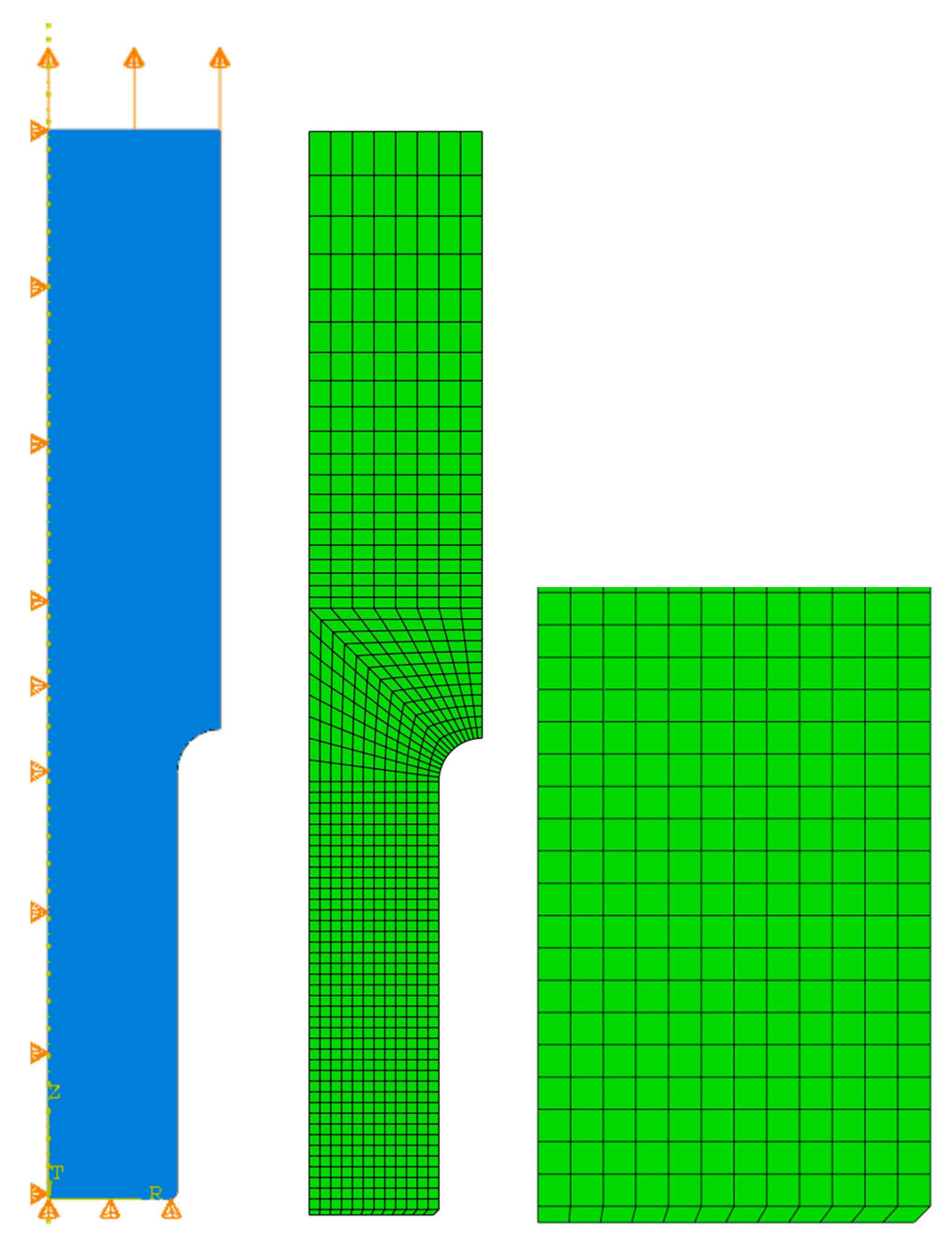
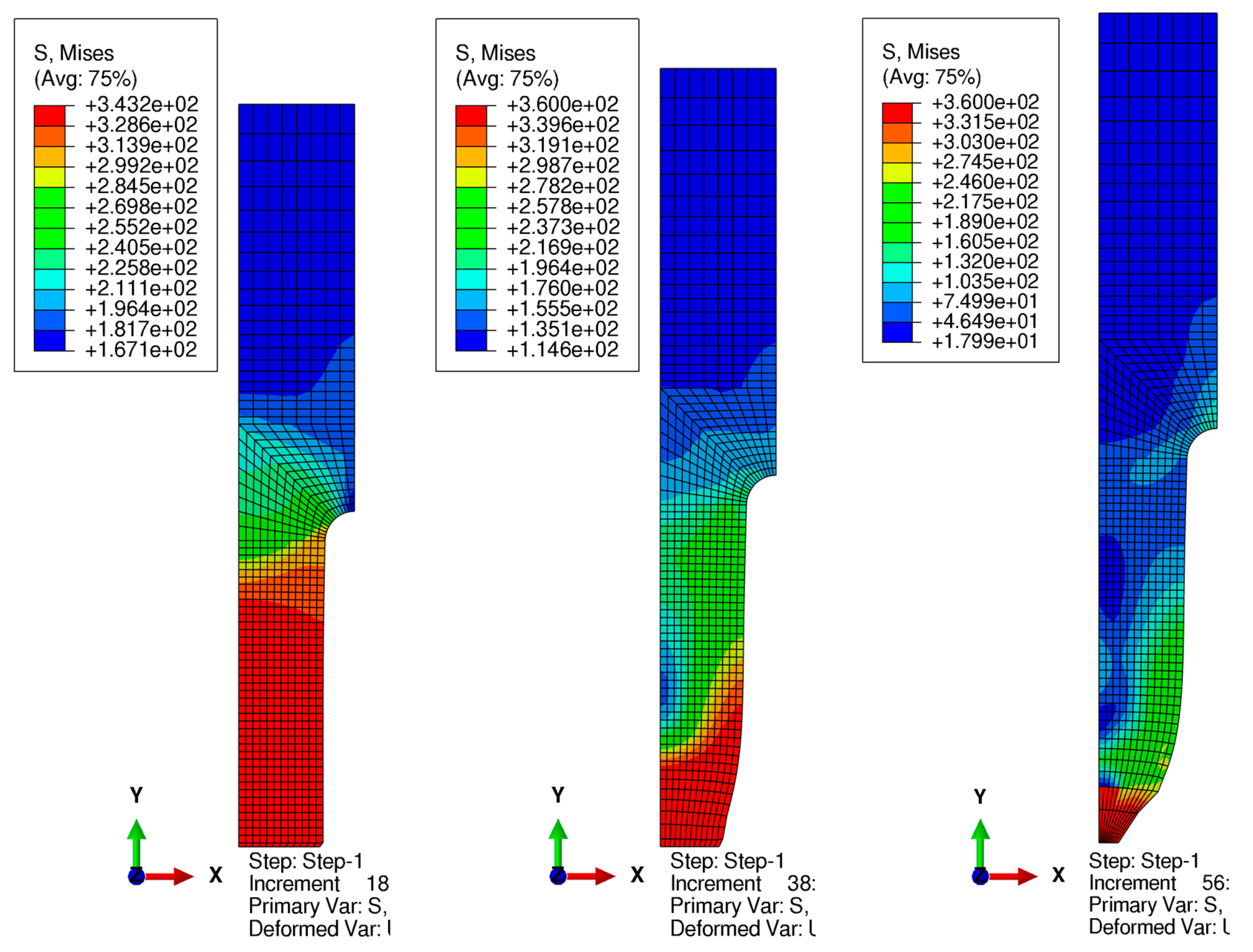
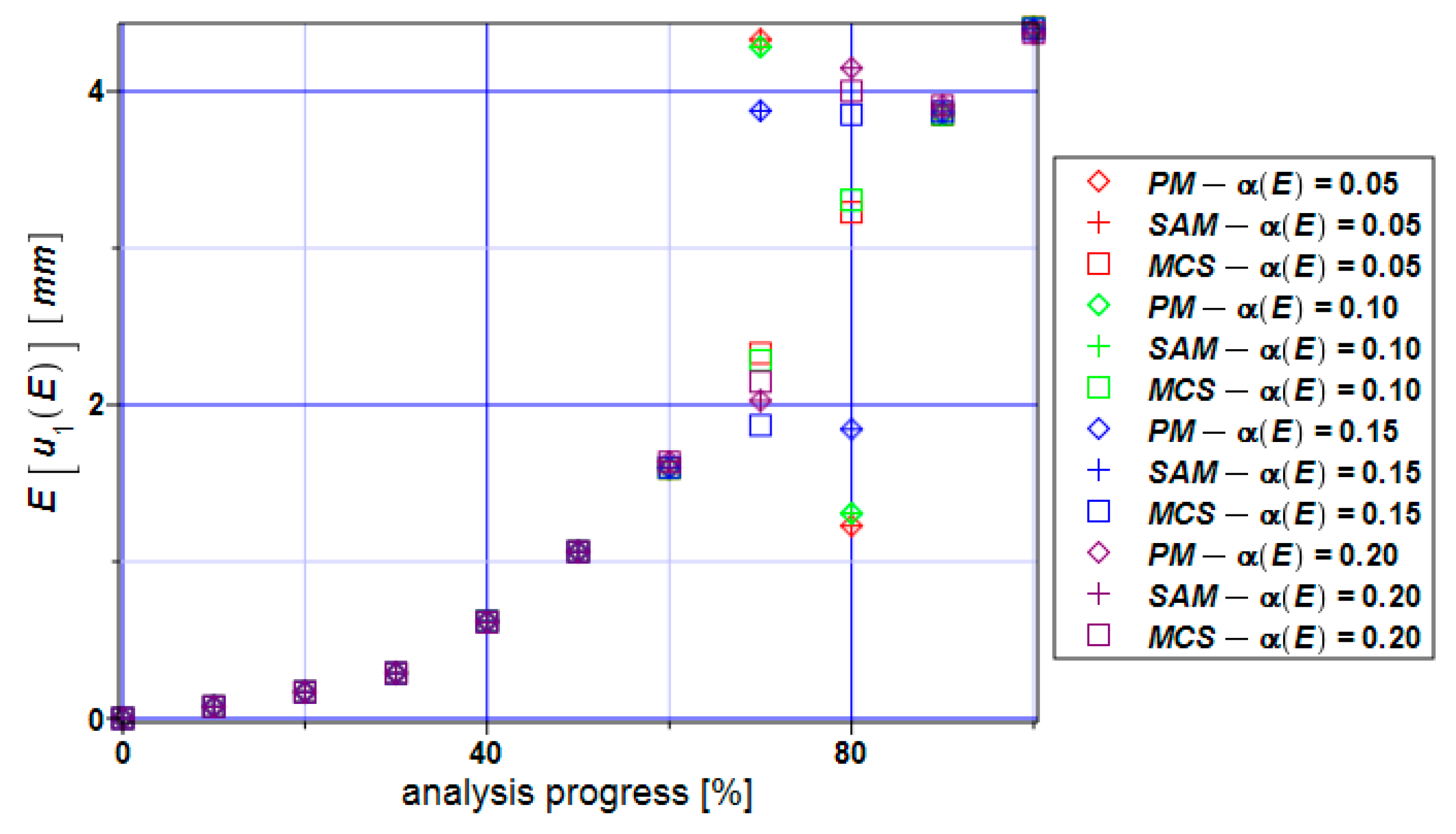
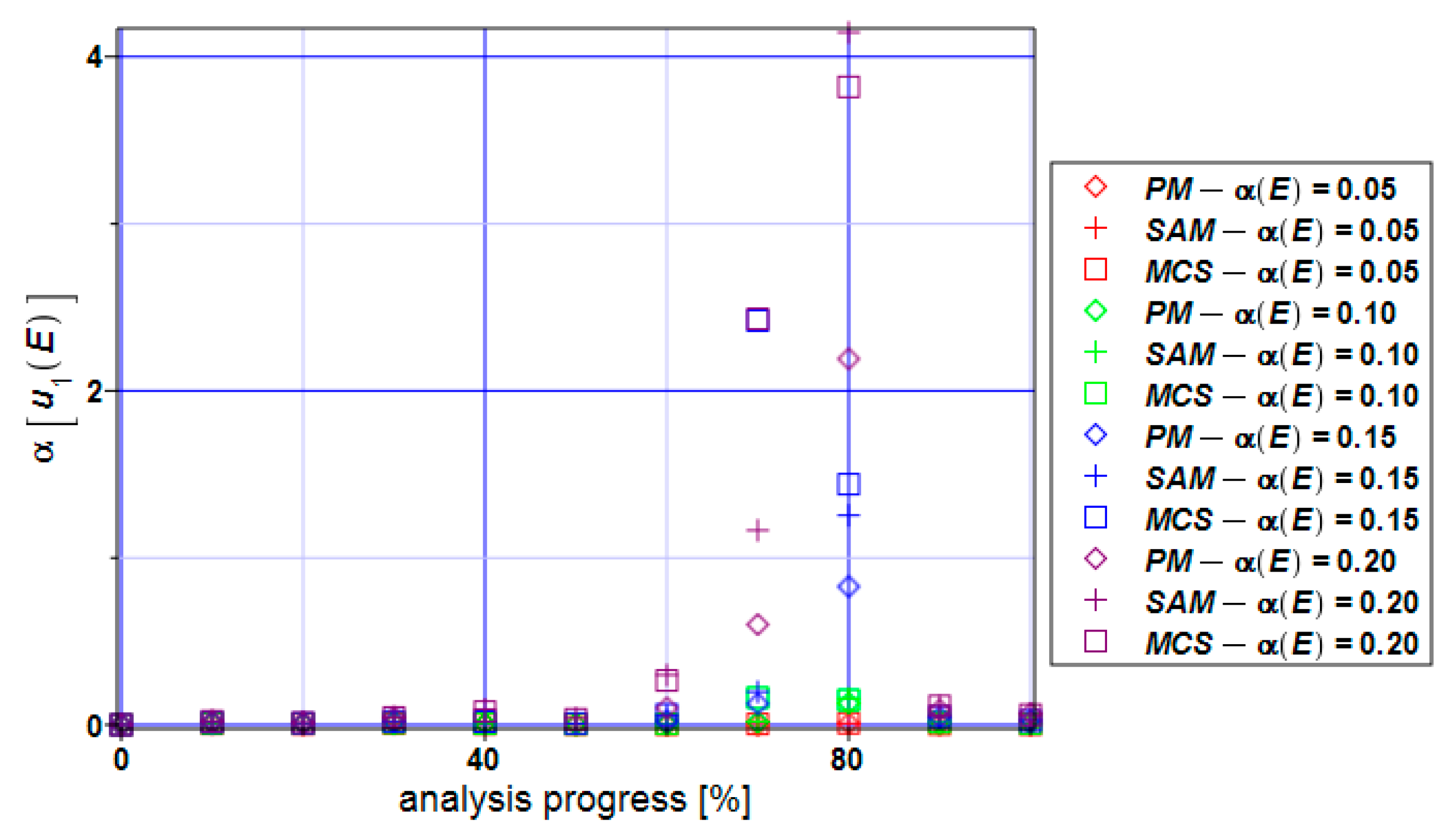
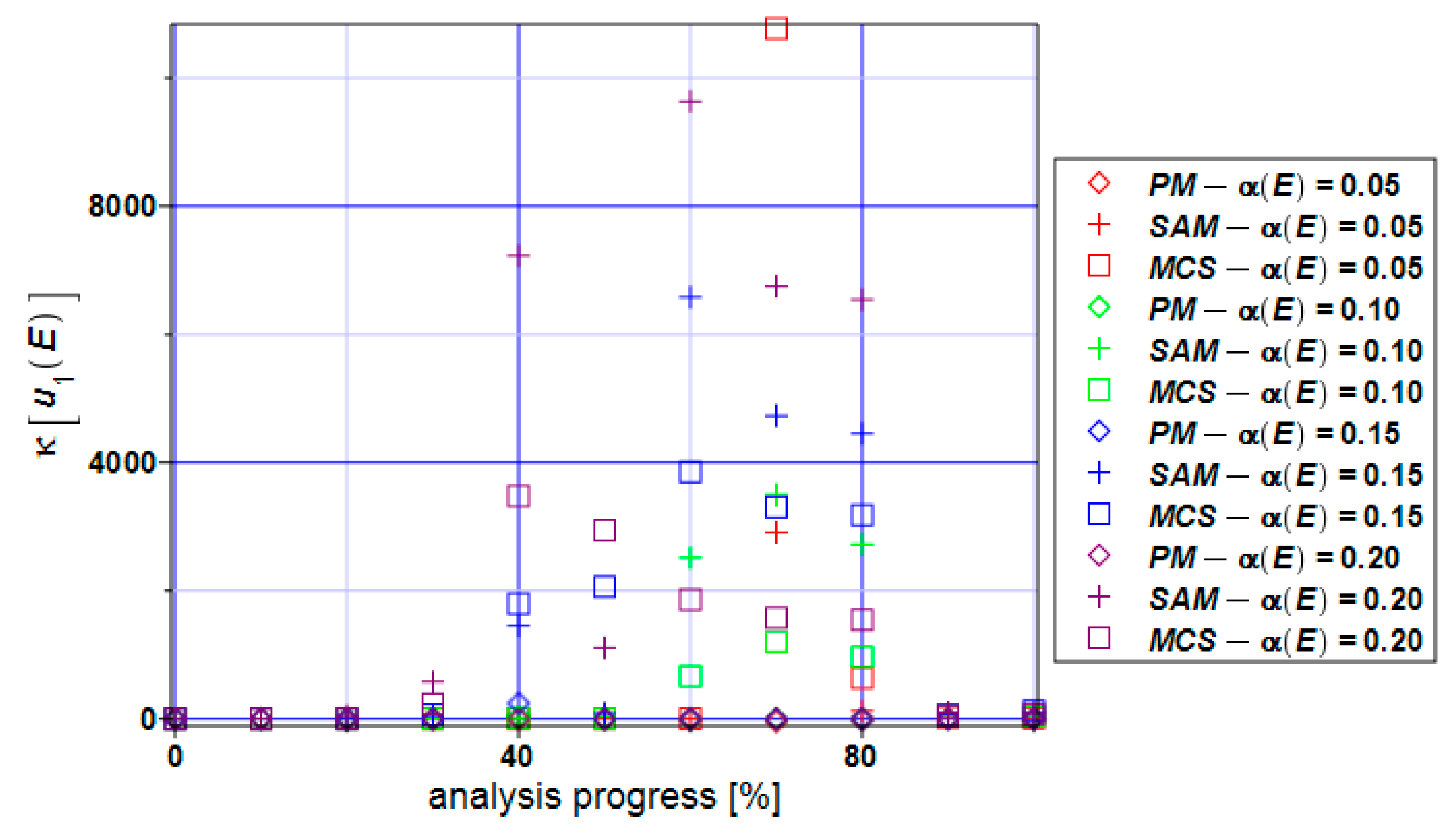
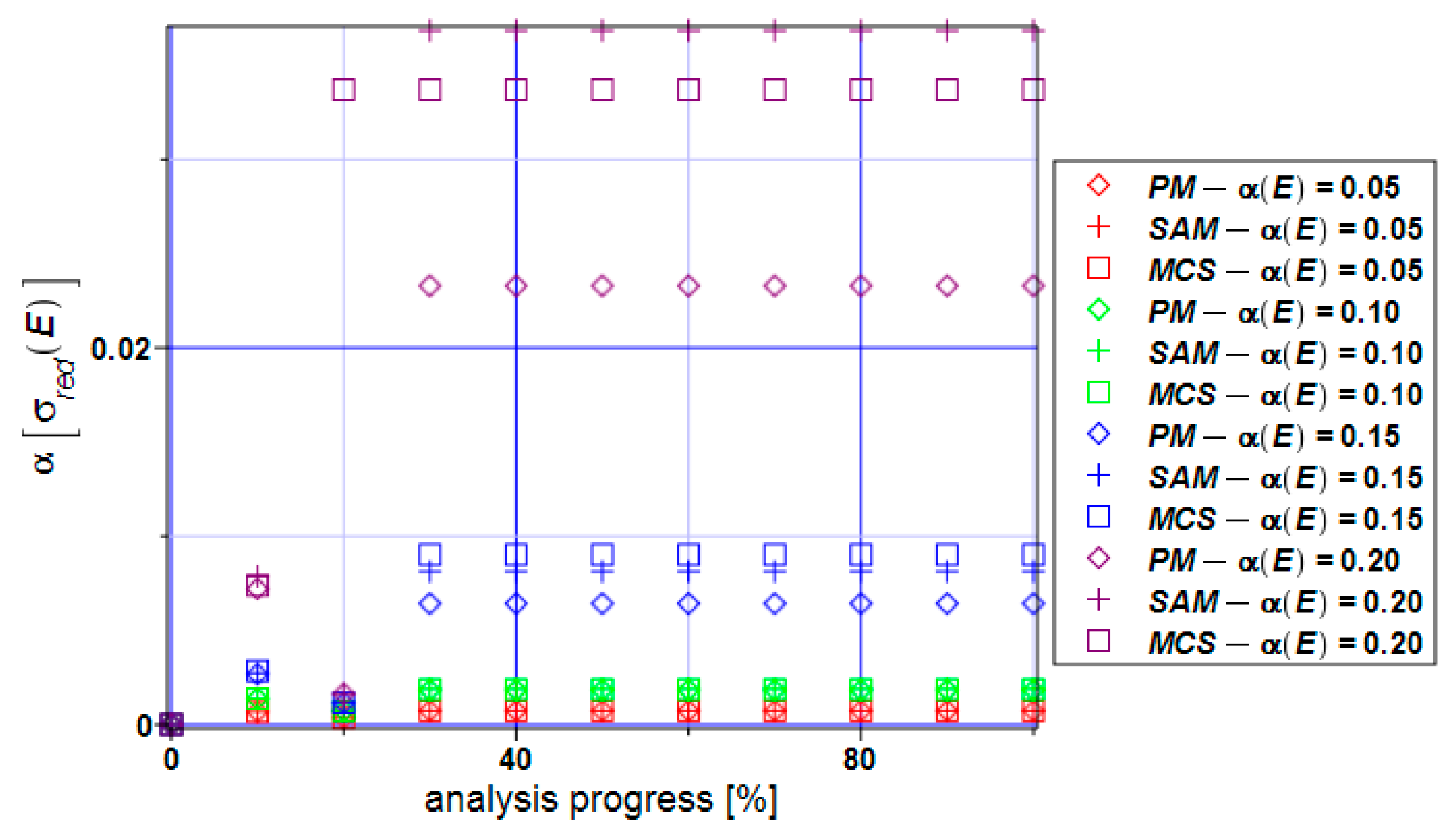
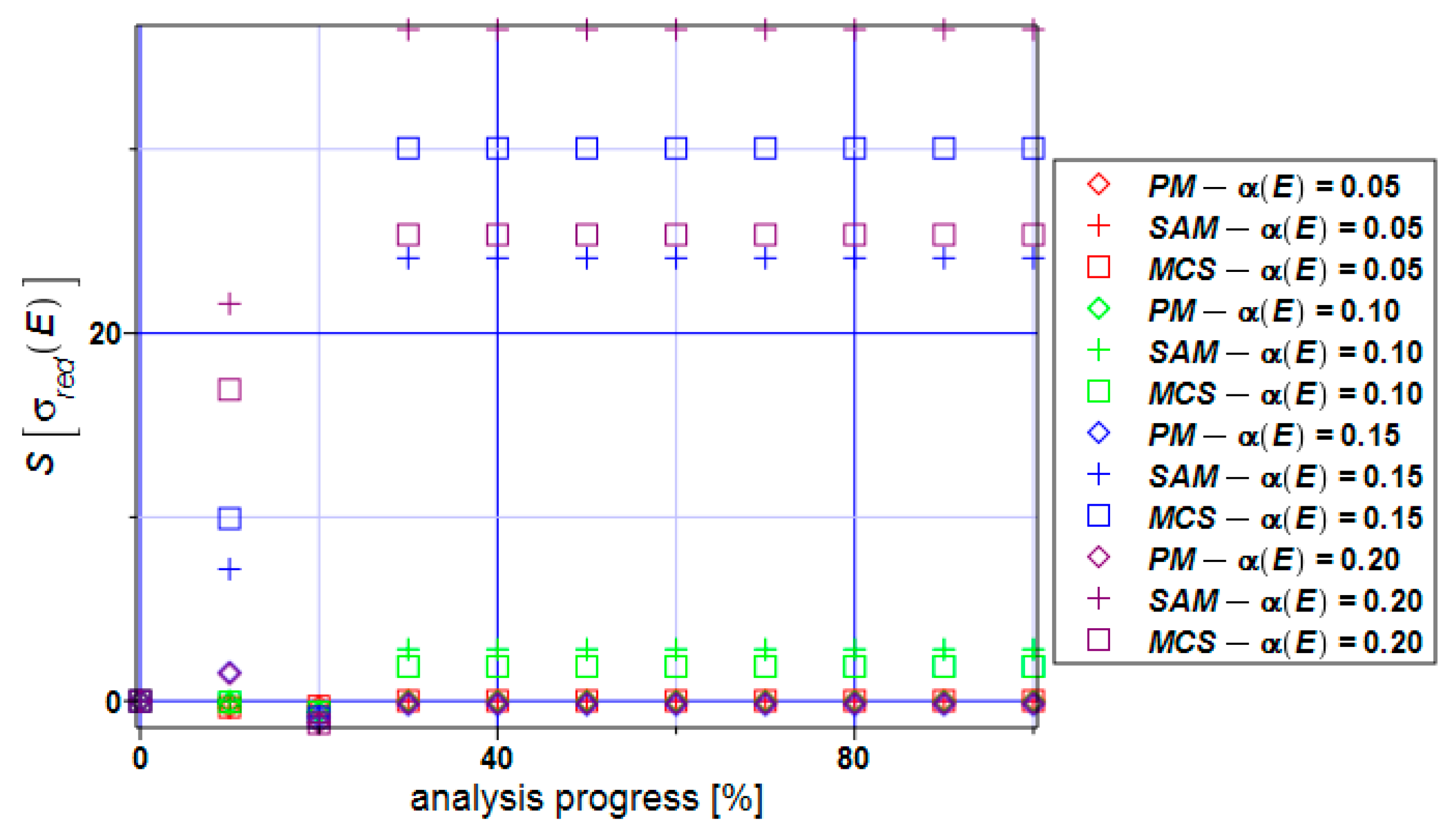
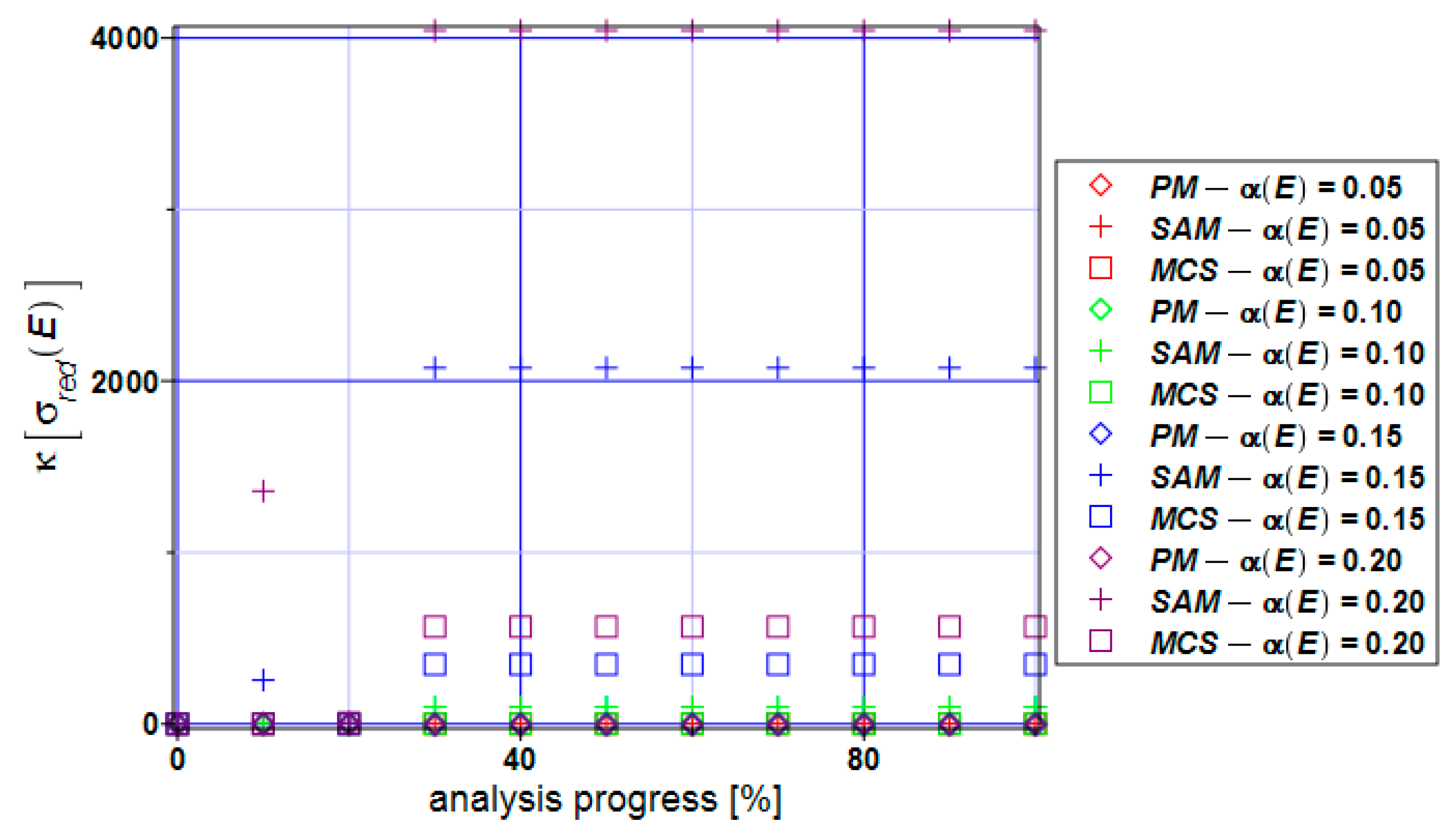
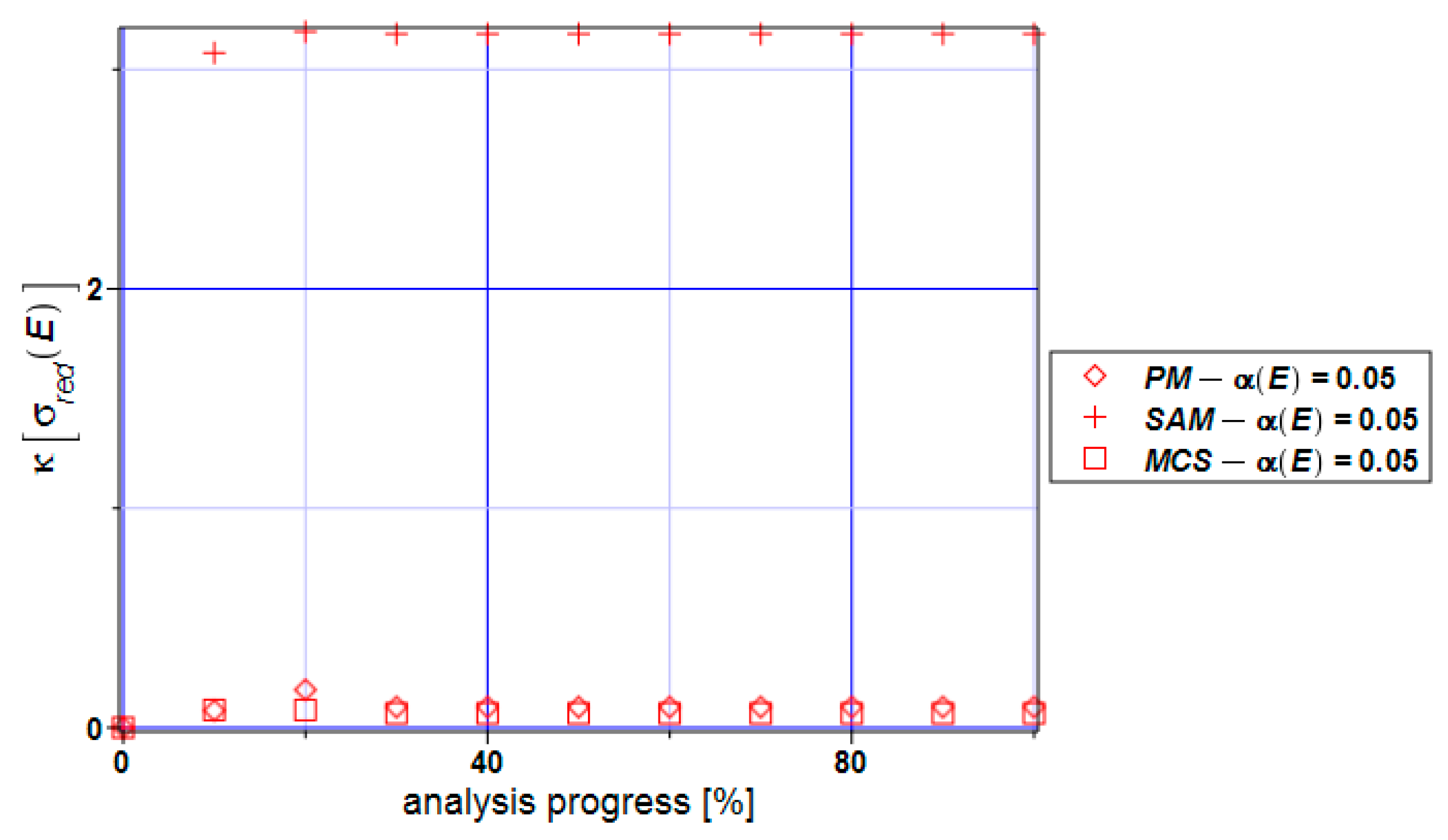
3. Numerical Simulation of Uniform Extension of the Steel Cylinder
4. Concluding Remarks
- Statistical dispersion of the input uncertainty on the level of 5% enables for treating structural responses inherent in the ULS and SLS as Gaussian, which may further simplify both the uncertainty analysis and the reliability assessment;
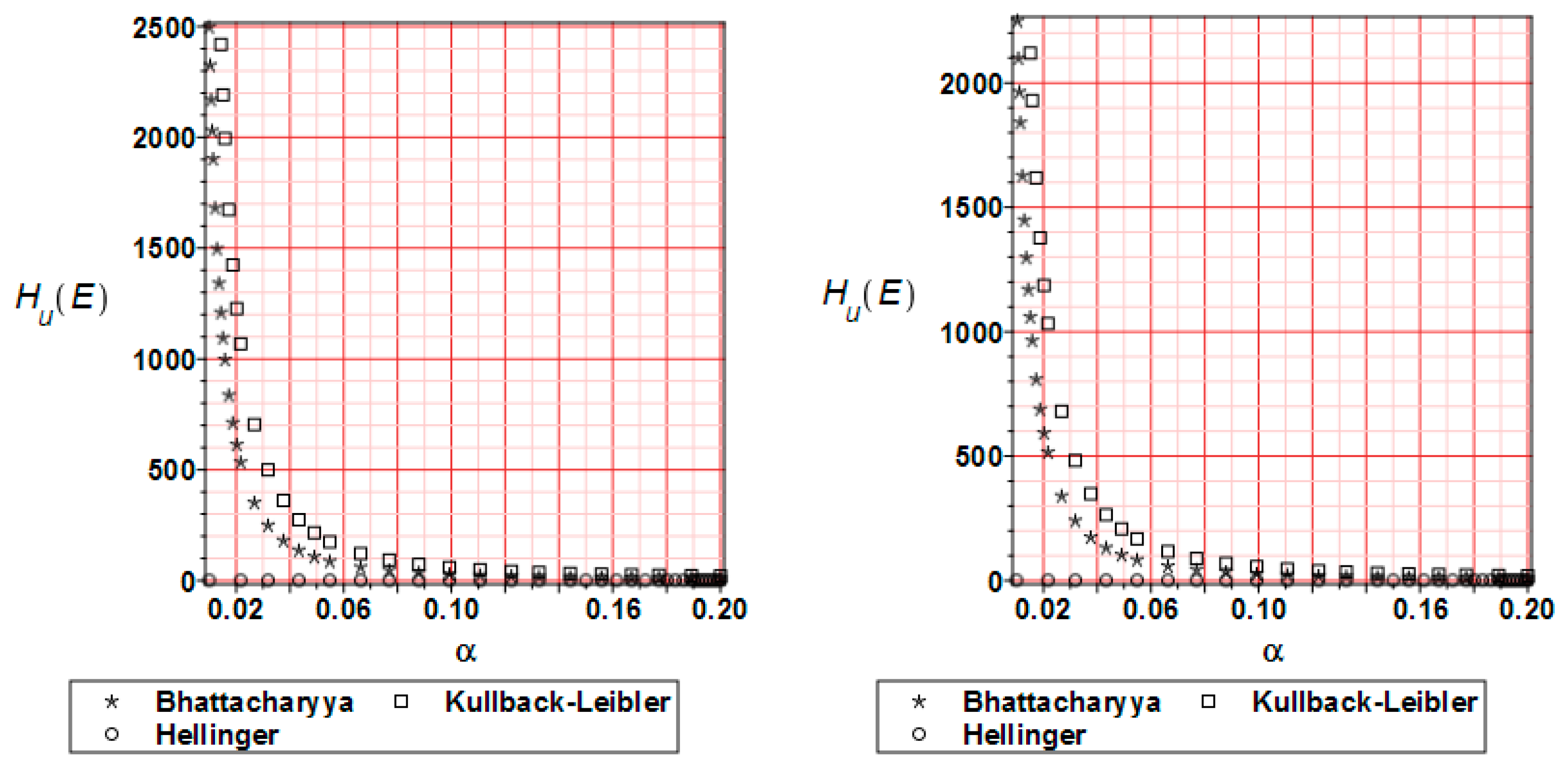
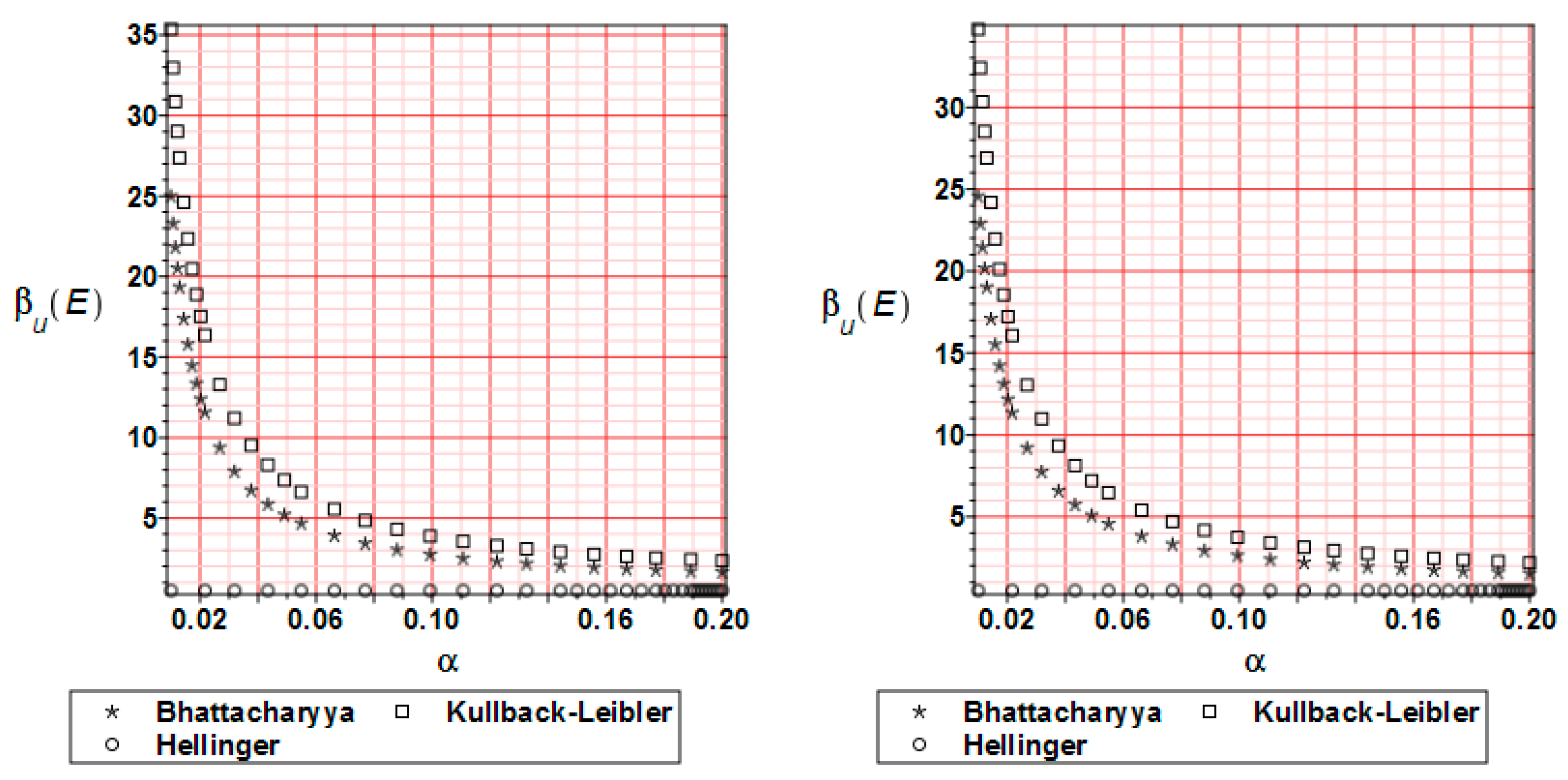
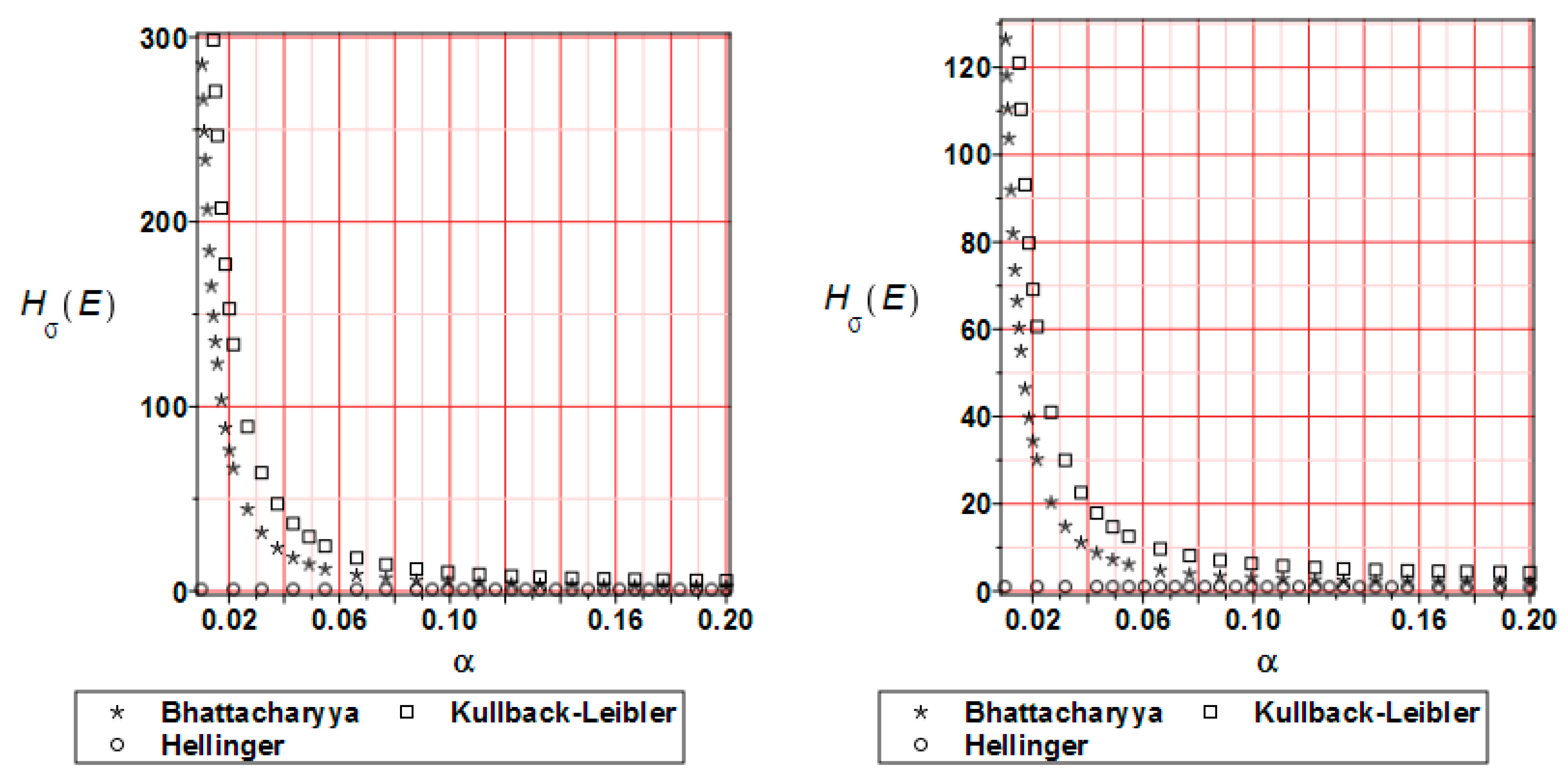
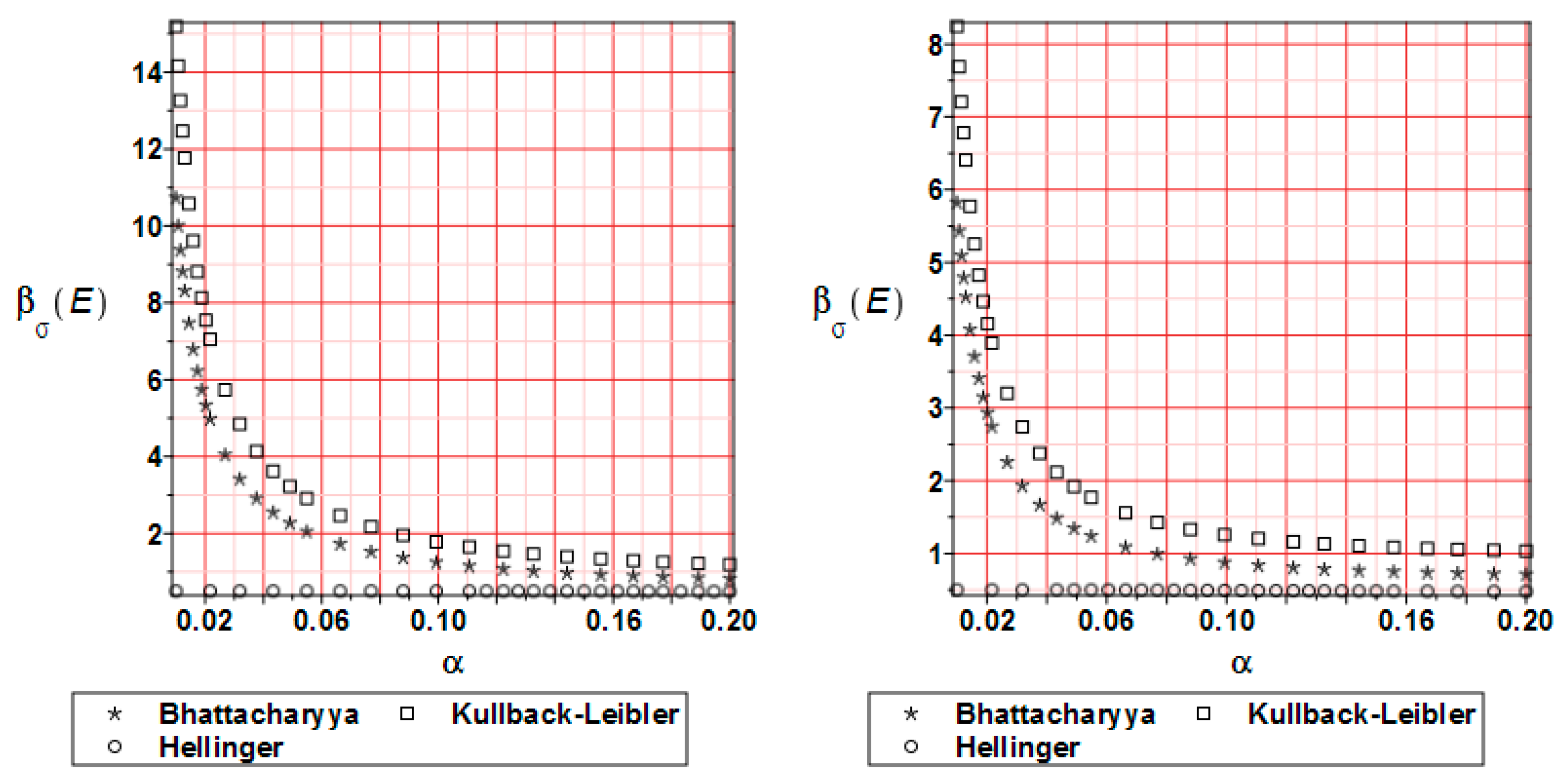
- The distribution of the reliability index β based on the relative entropy and relative entropy H have similar characters but their values differ by 10–20 times;
- The reliability index based on relative entropy according to the Bhattacharyya and Kullback–Leiber method for reduced stress brings numerical values quite close to the reliability index based on the FORM method;
- The Jeffreys and Hellinger’s approximation cannot be directly used for safety assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melchers, R.E. Structural Reliability Analysis and Prediction; Wiley: Chichester, UK, 2002. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress–Strain Curves by Three Parameters, Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Wei, D.; Elgindi, M.B.M. Finite element analysis of the Ramberg-Osgood bar. Am. J. Comp. Math. 2013, 3, 211–216. [Google Scholar] [CrossRef]
- Gadamchetty, G.; Pandey, A.; Gawture, M. On Practical implementation of the Ramberg-Osgood Model for FE Simulation. SAE Int. J. Mat. Manuf. 2016, 9, 200–205. [Google Scholar] [CrossRef]
- Anatolyevich, B.P.; Yakovlevna, G.N. Generalization of the Ramberg–Osgood Model for Elastoplastic Materials. J. Mater. Eng. Perform. 2019, 28, 7342–7346. [Google Scholar] [CrossRef]
- Elruby, A.Y.; Nakhla, S. Extending the Ramberg–Osgood Relationship to Account for Metal Porosity. Metall. Mater. Trans. A 2019, 50, 3121–3131. [Google Scholar] [CrossRef]
- Skelton, R.P.; Maier, H.J.; Christ, H.-J. The Bauschinger effect, Masing model and the Ramberg–Osgood relation for cyclic deformation in metals. Mater. Sci. Eng. 1997, 238, 377–390. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Li, C. An improved method for estimation of Ramberg–Osgood curves of steels from monotonic tensile properties. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 412–426. [Google Scholar] [CrossRef]
- Niesłony, A.; el Dsoki, C.; Kaufmann, H.; Krug, P. New method for evaluation of the Manson–Coffin–Basquin and Ramberg–Osgood equations with respect to compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]
- Basan, R.; Fralunović, M.; Prebil, I.; Kunc, R. Study on Ramberg-Osgood and Chaboche models for 42CrMo4 steel and some approximations. J. Constr. Steel Res. 2017, 136, 65–74. [Google Scholar] [CrossRef]
- Kaldjiian, M.J. Moment-Curvature of Beams as Ramberg-Osgood Functions. J. Struct. Div. 1967, 93, 53–65. [Google Scholar] [CrossRef]
- Mostaghel, N.; Byrd, R.A. Inversion of Ramberg–Osgood equation and description of hysteresis loops. Int. J. Non-Linear Mech. 2002, 37, 1319–1335. [Google Scholar] [CrossRef]
- Papadimitriou, A.G.; Buckovalas, G.D. Plasticity model for sand under small and large cyclic strains: A multiaxial formulation. Soil Dyn. Earthq. Eng. 2002, 22, 191–204. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Strąkowski, M.; Kamiński, M. Stochastic Finite Element Method elasto-plastic analysis of the necking bar with material microdefects. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2019, 5, 030908. [Google Scholar] [CrossRef]
- Kossakowski, P. The numerical modeling of failure of 235JR steel using Gurson-Tvergaard-Needleman material model. Roads Bridges 2012, 11, 295–310. [Google Scholar]
- Qu, P.; Sun, Y.; Sumelka, W. Review on Stress-Fractional Plasticity Models. Materials 2022, 15, 7802. [Google Scholar] [CrossRef]
- Buryachenko, V. Elastic-plastic behavior of elastically homogeneous materials with a random field of inclusions. Int. J. Plast. 1999, 15, 687–720. [Google Scholar] [CrossRef]
- Kamiński, M. Probabilistic characterization of porous plasticity in solids. Mech. Res. Commun. 1999, 26, 99–106. [Google Scholar] [CrossRef]
- Kamiński, M. The Stochastic Perturbation Method for Computational Mechanic; Wiley: Chichester, UK, 2013. [Google Scholar]
- Hamada, M.S.; Wilson, A.G.; Reese, C.S.; Martz, H.F. Bayesian Reliability, Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Cardoso, J.B.; de Almeida, J.R.; Dias, J.M.; Coelho, P.G. Structural reliability analysis using Monte Carlo simulation and neural networks. Adv. Eng. Softw. 2008, 39, 505–513. [Google Scholar] [CrossRef]
- Ghanem, R.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Kleiber, M.; Hien, T.D. The Stochastic Finite Element Method; Wiley: Chichester, UK, 1992. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Renyi, A. On measures of information and entropy. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1960; pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Zhao, Y.-G.; Ono, T. Moment methods for structural reliability. Struct. Saf. 2001, 23, 47–75. [Google Scholar] [CrossRef]
- Lopez, R.H.; Beck, A.T. Reliability-Based Design Optimization Strategies Based on FORM: A Review. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 506–514. [Google Scholar] [CrossRef]
- Cai, G.Q.; Elishakoff, I. Refined second-order reliability analysis. Struct. Saf. 1994, 14, 267–276. [Google Scholar] [CrossRef]
- Tichy, M. First-order third-moment reliability method. Struct. Saf. 1994, 16, 189–200. [Google Scholar] [CrossRef]
- Peng, X.; Geng, L.; Liyan, W.; Liu, G.R.; Lam, K.Y. A stochastic finite element method for fatigue reliability analysis of gear teeth subjected to bending. Comput. Mech. 1988, 21, 253–261. [Google Scholar] [CrossRef]
- Donald, M.J. On the relative entropy. Commun. Math. Phys. 1986, 105, 13–34. [Google Scholar] [CrossRef]
- Rauber, T.W.; Braun, T.; Berns, K. Probabilistic distance measures of the Dirichlet and Beta distributions. Patt. Recognit. 2008, 41, 637–645. [Google Scholar] [CrossRef]
- Namdari, A.; Li, Z. A review of entropy measures for uncertainty quantification of stochastic processes. Adv. Mech. Eng. 2019, 11, 168781401985735. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Hellinger, E. Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen. J. Reine Angew. Math. (Crelles J.) 1909, 136, 210–271. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Nielsen, F. Fast approximations of the Jeffreys divergence between univariate Gaussian mixtures via mixture conversions to exponential-polynomial distributions. Entropy 2021, 23, 1417. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Teixeira, R.; O’Connor, A.; Nogal, M. Probabilistic Sensitivity Analysis of OWT using a transformed Kullback-Leibler discrimination. Struct. Saf. 2019, 81, 101860. [Google Scholar] [CrossRef]
- Ghasemi, S.H.; Nowak, A.S. Reliability index for non-normal distributions of limit state functions. Struct. Eng. Mech. 2017, 62, 365–372. [Google Scholar] [CrossRef]
- Kleiber, M.; Woźniak, C. Nonlinear Mechanics of Structures; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Oden, J.T. Finite Elements of Nonlinear Continua; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.C. The Finite Element Method, 4th ed.; McGraw Hill: New York, NY, USA, 1989. [Google Scholar]
- Bjorck, A. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Aravas, N. On the numerical integration of a class of pressure-dependent plasticity models. Int. J. Numer. Methods Eng. 1987, 24, 1395–1416. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, Z.; Zhang, J.; Bian, J.; Wang, C. Rolling bearing state assessment based on the composite multiscale weight slope entropy and hierarchical prototype-based approach. Adv. Mech. Eng. 2022, 14, 16878132221137419. [Google Scholar] [CrossRef]
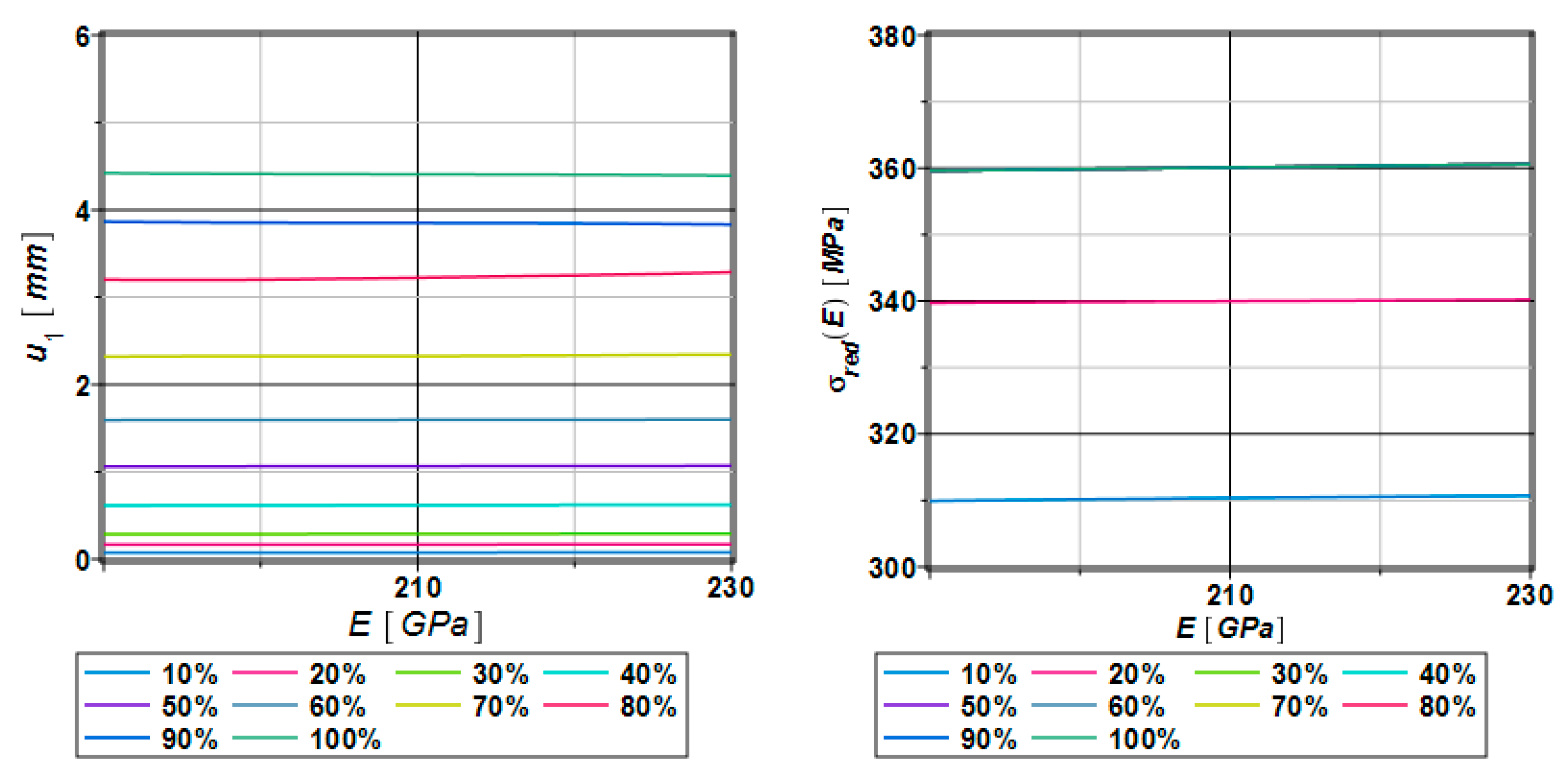


| Analysis Progress [%] | RMS Error |
|---|---|
| 10 | 0.00129528 |
| 20 | 0.000244397 |
| 30 | 0.00147109 |
| 40 | 0.0000566029 |
| 50 | 0.0000711416 |
| 60 | 0.0000900214 |
| 70 | 0.00223297 |
| 80 | 0.00420256 |
| 90 | 0.00127888 |
| 100 | 0.000428241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, M.; Strąkowski, M. Relative Entropy Application to Study the Elastoplastic Behavior of S235JR Structural Steel. Materials 2024, 17, 727. https://doi.org/10.3390/ma17030727
Kamiński M, Strąkowski M. Relative Entropy Application to Study the Elastoplastic Behavior of S235JR Structural Steel. Materials. 2024; 17(3):727. https://doi.org/10.3390/ma17030727
Chicago/Turabian StyleKamiński, Marcin, and Michał Strąkowski. 2024. "Relative Entropy Application to Study the Elastoplastic Behavior of S235JR Structural Steel" Materials 17, no. 3: 727. https://doi.org/10.3390/ma17030727
APA StyleKamiński, M., & Strąkowski, M. (2024). Relative Entropy Application to Study the Elastoplastic Behavior of S235JR Structural Steel. Materials, 17(3), 727. https://doi.org/10.3390/ma17030727








