Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Chemicals
2.2. Adsorbent Fabrication
2.3. Adsorbent Characterization
2.4. Batch Adsorption Experiments
2.5. Adsorption Kinetics
2.6. Adsorption Isotherms
2.7. Packed Bed Adsorption Simulation
3. Results
3.1. Adsorbent Characterization
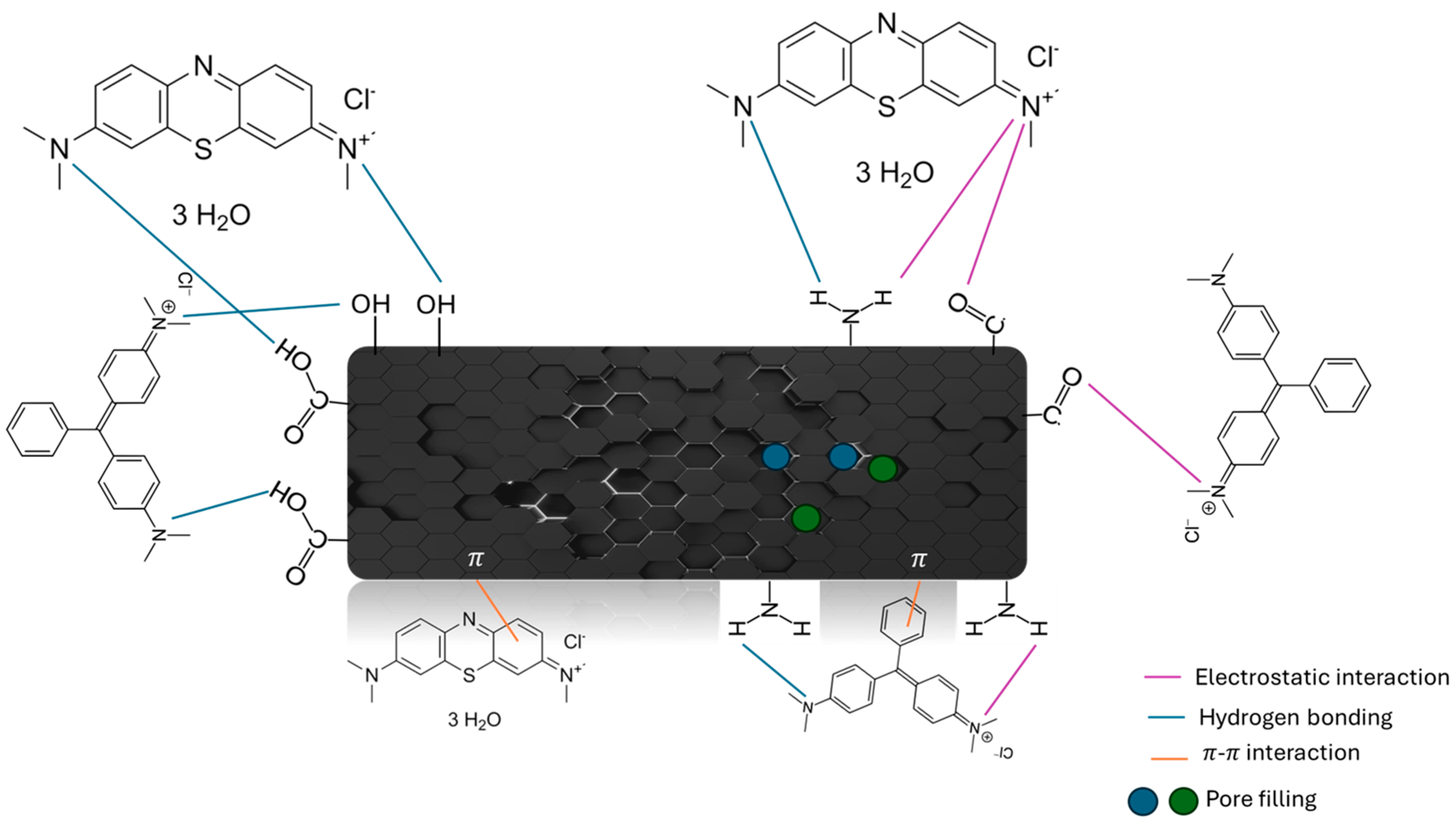
3.2. Dye Adsorption Studies
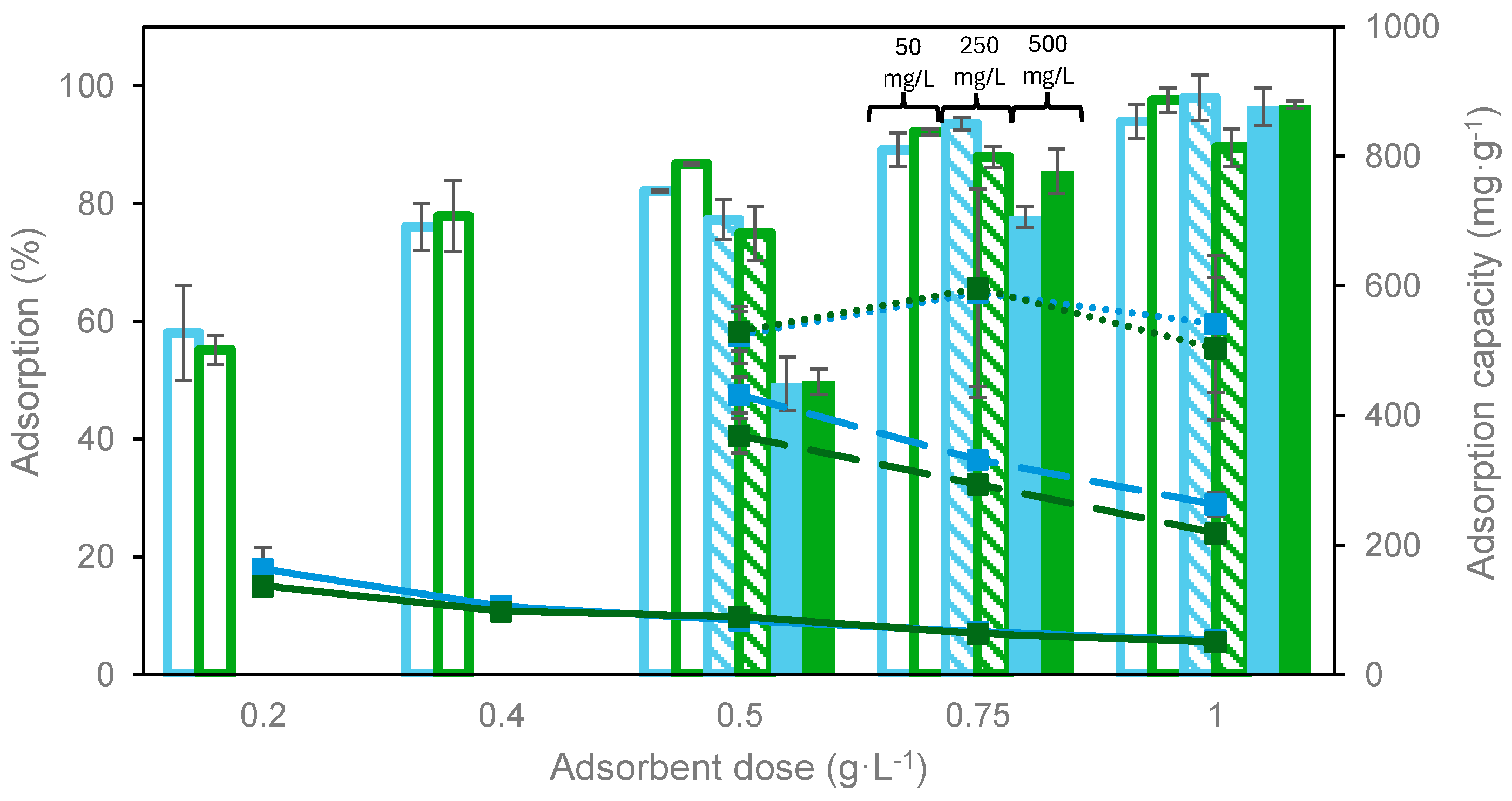
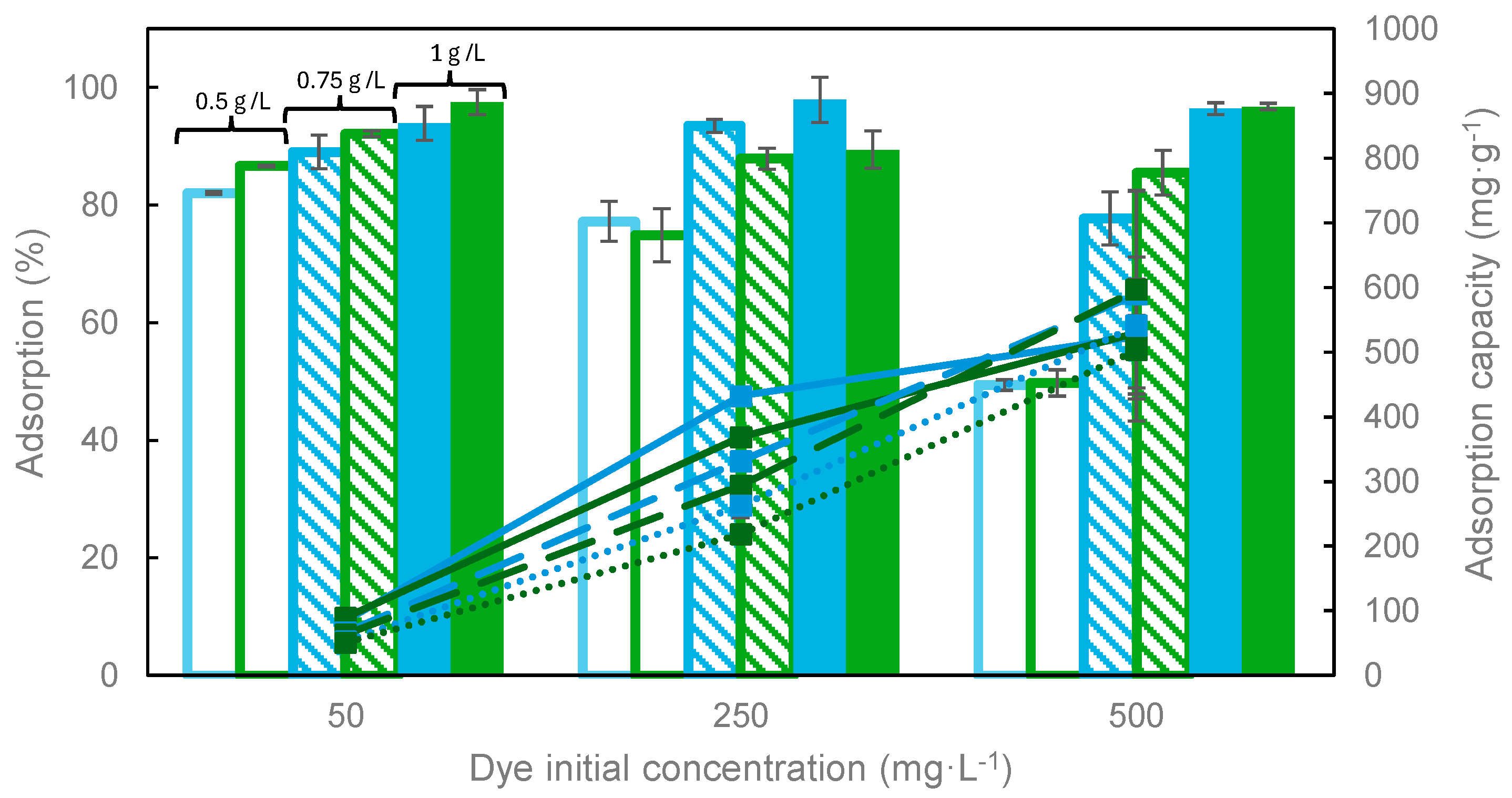
3.2.1. Effect of Adsorbent Dosage and Initial Dye Concentration
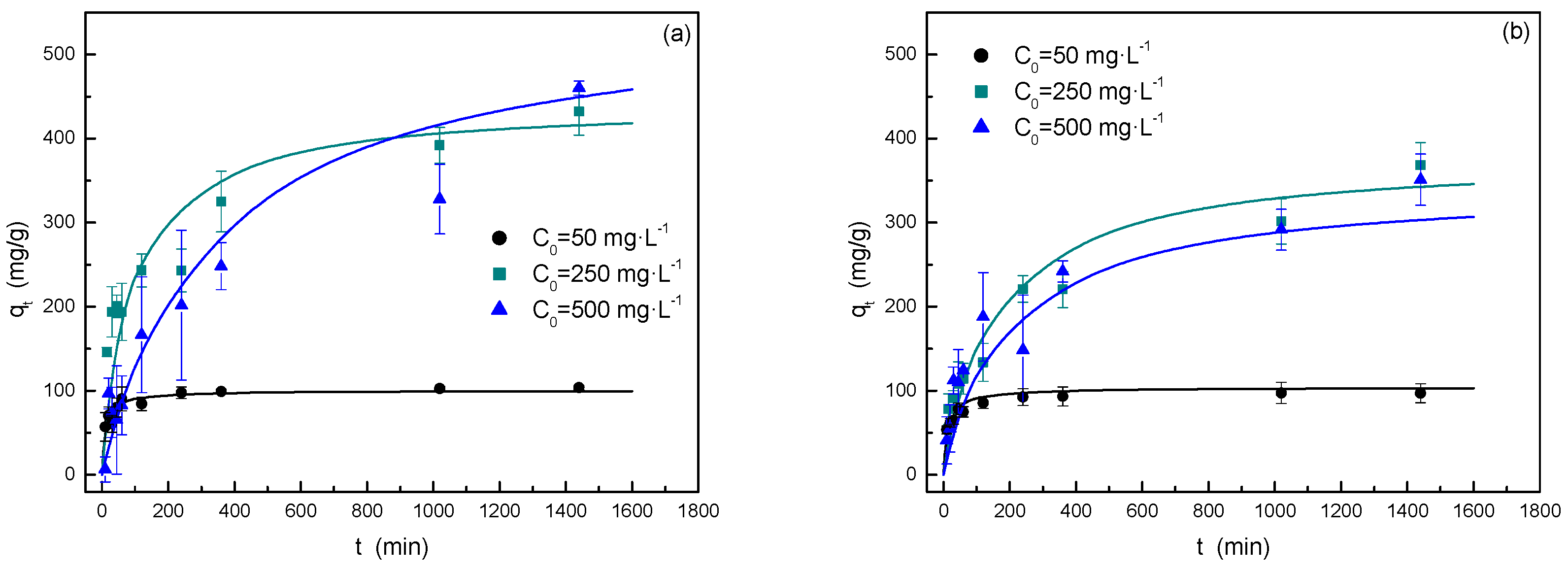
3.2.2. Adsorption Kinetics
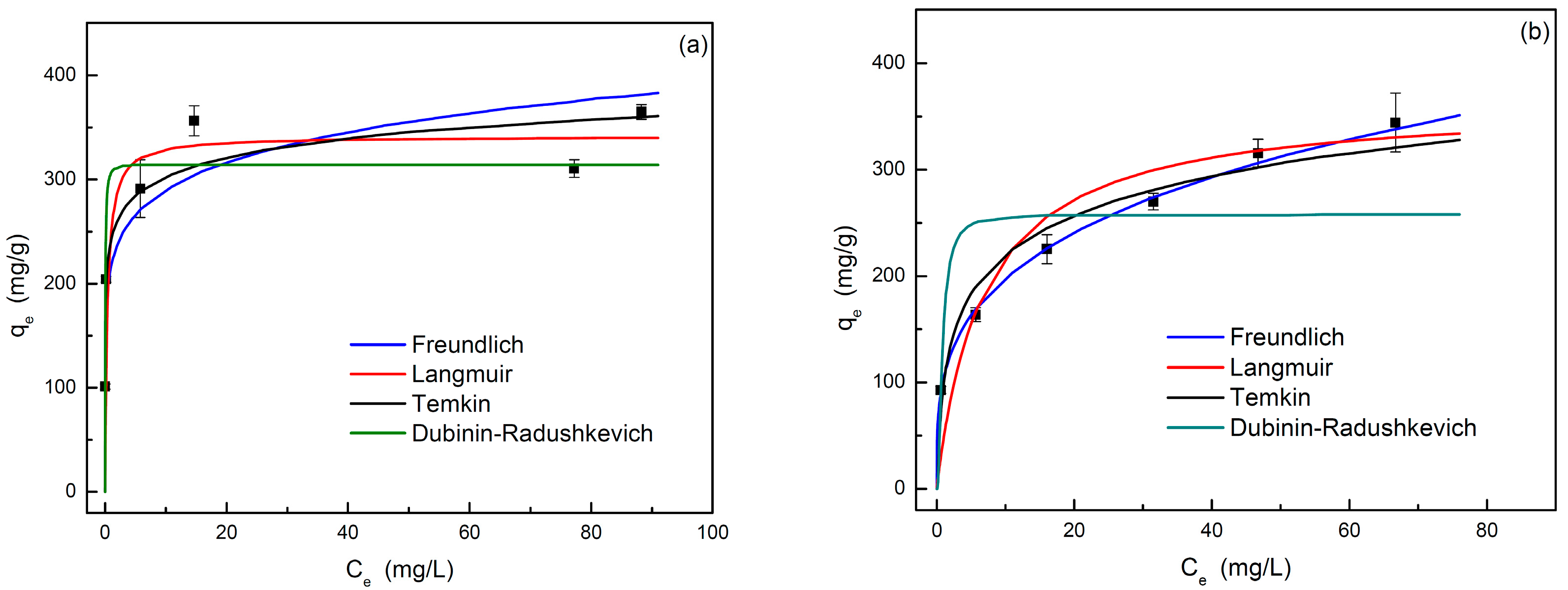
3.2.3. Adsorption Equilibrium
3.3. Simulation of Dyes Adsorption in a Packed-Bed
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lotfy, H.R.; Roubik, H. Water purification using activated carbon prepared from agriculture waste—Overview of a recent development. Biomass Convers. Biorefin. 2023, 13, 15577–15590. [Google Scholar] [CrossRef]
- Ullah Khan, W.; Ahmed, S.; Dhoble, Y.; Madhav, S. A critical review of hazardous waste generation from textile industries and associated ecological impacts. J. Indian Chem. Soc. 2023, 100, 100829. [Google Scholar] [CrossRef]
- Shakoor, S.; Nasar, A. Adsorptive treatment of hazardous Methylene Blue dye from artificially contaminated water using Cucumis sativus peel waste as a low-cost adsorbent. Groundw. Sustain. Dev. 2017, 5, 152–159. [Google Scholar] [CrossRef]
- Wisniewska, M.; Urban, T.; Tokarska, K.; Marciniak, P.; Giel, A.; Nowick, P. Removal of organic dyes, polymers and surfactants using carbonaceous materials derived from walnut shells. Materials 2024, 17, 1987. [Google Scholar] [CrossRef]
- Santos, D.H.S.; Duarte, J.L.S.; Tonholo, J.; Meili, L.; Zanta, C.L.P.S. Saturated activated carbon regeneration by UV-light, H2O2 and Fenton reaction. Sep. Purif. Technol. 2020, 250, 117112. [Google Scholar] [CrossRef]
- Santos, D.H.S.; Xiao, Y.; Chaukura, N.; Hill, J.M.; Selvasembian, R.; Zanta, C.L.P.S.; Meili, L. Regeneration of dye-saturated activated carbon through advanced oxidative processes: A review. Heliyon 2022, 8, e10205. [Google Scholar] [CrossRef]
- Plassard, F.; Winiarski, T.; Petit-Ramel, M. Retention and distribution of three heavy metals in a carbonated soil: Comparison between batch and unsaturated column studies. J. Contam. Hydrol. 2000, 42, 99–111. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, L.K.; Gaur, J. Metal sorption by algal biomass: From batch to continuous system. Algal Res. 2016, 18, 95–109. [Google Scholar] [CrossRef]
- Selambakkannu, S.; Othman, N.A.F.; Bakar, K.A.; Karim, Z.A. Adsorption studies of packed bed column for the removal of dyes using amine functionalized radiation induced grafted fiber. SN Appl. Sci. 2019, 1, 175. [Google Scholar] [CrossRef]
- Li, L.; Sun, F.; Gao, J.; Wang, L.; Pi, S.; Zhao, G. Broadening the pore size of coal-based activated carbon via a washing-free chem-physical activation method for high-capacity dye adsorption. RSC Adv. 2018, 8, 14488. [Google Scholar] [CrossRef]
- Amran, F.; Zaini, M.A.A. Effects of chemical activating agents on physical properties of activated carbons—A commentary. Water Prac. Technol. 2020, 15, 863–876. [Google Scholar] [CrossRef]
- Carabineiro, S.A.C.; Thavorn-Amornsri, T.; Pereira, M.F.R.; Serp, P.; Figueiredo, J.L. Comparison between activated carbon, carbon xerogel and carbon nanotubes for the adsorption of the antibiotic ciprofloxacin. Catal. Today 2012, 186, 29–34. [Google Scholar] [CrossRef]
- Juela, D.M. Comparison of the adsorption capacity of acetaminophen on sugarcane bagasse and corn cob by dynamic simulation. Sustain. Environ. Res. 2020, 30, 23. [Google Scholar] [CrossRef]
- Pimentel, C.H.; Díaz-Fernández, L.; Gómez-Díaz, D.; Freire, M.S.; González-Álvarez, J. Separation of CO2 using biochar and KOH and ZnCl2 activated carbons derived from pine sawdust. J. Environ. Chem. Eng. 2023, 11, 111378. [Google Scholar] [CrossRef]
- Sayğili, H.; Güzel, F. Usability of activated carbon with well-developed mesoporous structure for the decontamination of malachite green from aquatic environments: Kinetic, equilibrium and regeneration studies. J. Porous Mater. 2018, 25, 477–488. [Google Scholar] [CrossRef]
- Thang, N.H.; Khang, D.S.; Hai, T.D.; Nga, D.T.; Tuan, P.D. Methylene blue adsorption mechanism of activated carbon synthesised from cashew nut shells. RSC Adv. 2021, 11, 26563–26570. [Google Scholar] [CrossRef]
- Freire, M.S.; Gómez Díaz, D.; González Álvarez, J.; Pimentel, C.H. Preparation of activated carbon from pine (Pinus radiata) sawdust by chemical activation with zinc chloride for wood dye adsorption. Biomass Convers. Biorefin. 2023, 13, 16537–16555. [Google Scholar]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodríguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution. Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Manyá, J.J.; González, B.; Azuara, M.; Arner, G. Ultra-microporous adsorbents prepared from vine shoots-derived biochar with high CO2 uptake and CO2/N2 selectivity. Chem. Eng. J. 2018, 345, 631–669. [Google Scholar] [CrossRef]
- Giles, C.H.; MacEwan, T.; Nakhwa, S.; Smith, D. A system of classification of solution adsorption isotherms and its use in diagnosis of adsorption mechanisms and in measurement of specific surface area solids. J. Chem. Soc. 1960, 14, 3973–3993. [Google Scholar] [CrossRef]
- Spessato, L.; Bedin, K.C.; Cazetta, A.L.; Souza, I.P.A.F.; Duarte, V.A.; Crespo, L.H.S.; Silva, M.C.; Pontes, R.M.; Almeida, V.C. KOH-super activated carbon from biomass waste: Insights into the paracetamol adsorption mechanism and thermal regeneration cycles. J. Hazard. Mater. 2019, 371, 499–505. [Google Scholar] [CrossRef]
- Shikuku, V.O.; Mishra, T. Adsorption isotherm modeling for methylene blue removal onto magnetic kaolinite clay: A comparison of two-parameter isotherms. Appl. Water Sci. 2021, 11, 103. [Google Scholar] [CrossRef]
- Jawad, A.H.; Malek, N.N.A.; Khadiran, T.; Alothman, Z.A.; Yaseen, Z.M. Mesoporous high-surface-area activated carbon from biomass waste via microwave-assisted-H3PO4 activation for methylene blue dye adsorption: An optimized process. Diam. Relat. Mat. 2022, 128, 109288. [Google Scholar] [CrossRef]
- Jasri, K.; Abdulhameed, A.S.; Jawad, A.H.; Alothman, Z.A.; Yousef, T.A.; Al Duaij, O.K. Mesoporous activated carbon produced from mixed wastes of oil palm frond and palm kernel shell using microwave radiation-assisted K2CO3 activation for methylene blue dye removal: Optimization by response surface methodology. Diam. Relat. Mat. 2023, 131, 109581. [Google Scholar] [CrossRef]
- Baysal, M.; Bilge, K.; Yılmaz, B.; Papila, M.; Yürüm, Y. Preparation of high surface area activated carbon from waste-biomass of sunflower piths: Kinetics and equilibrium studies on the dye removal. J. Environ. Chem. Eng. 2018, 6, 1702–1713. [Google Scholar] [CrossRef]
- Jahan, K.; Singh, V.; Mehrotra, N.; Rathore, K.; Verma, V. Development of activated carbon from KOH activation of pre-carbonized chickpea peel residue and its performance for removal of synthetic dye from drinking water. Biomass Convers. Biorefin. 2023, 13, 6913–6923. [Google Scholar] [CrossRef]
- Jawad, A.H.; Abdulhameed, A.S.; Bahrudin, N.N.; Hum, N.N.M.F.; Surip, S.N.; Syed-Hassan, S.S.A.; Yousif, E.; Sabar, S. Microporous activated carbon developed from KOH activated biomass waste: Surface mechanistic study of methylene blue dye adsorption. Water Sci. Technol. 2021, 84, 1858–1872. [Google Scholar] [CrossRef]
- Ali, F.; Bibi, S.; Ali, N.; Ali, Z.; Said, A.; Wahab, Z.U.; Bilal, M.; Iqbal, H.M.N. Sorptive removal of malachite green dye by activated charcoal: Process optimization, kinetic, and thermodynamic evaluation. Case Stud. Chem. Environ. Eng. 2020, 2, 100025. [Google Scholar] [CrossRef]
- Sharma, G.; Sharma, S.; Kumar, A.; Naushad, M.; Du, B.; Ahamad, T.; Ghfar, A.A.; Alqadami, A.A.; Stadler, F.J. Honeycomb structured activated carbon synthesized from Pinus roxburghii cone as effective bioadsorbent for toxic malachite green dye. J. Water Process Eng. 2019, 32, 100931. [Google Scholar] [CrossRef]
- Merrad, S.; Abbas, M.; Trari, M. Adsorption of malachite green onto walnut shells: Kinetics, thermodynamic, and regeneration of the adsorbent by chemical process. Fibers Polym. 2023, 24, 1067–1081. [Google Scholar] [CrossRef]
- Yildiz, H.; Gülşen, H.; Şahin, Ö.; Baytar, O.; Kutluay, S. Novel adsorbent for malachite green from okra stalks waste: Synthesis, kinetics and equilibrium studies. Int. J. Phytoremediat. 2023, 10, 1–13. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Ahmad, M.A.; Yahaya, N.K.E.M.; Karim, J. Adsorption of malachite green by activated carbon derived from gasified Hevea brasiliensis root. Arab. J. Chem. 2021, 14, 103104. [Google Scholar] [CrossRef]
- Qu, W.; Yuan, T.; Yin, G.; Xu, S.; Zhang, Q.; Su, H. Effect of properties of activated carbon on malachite green adsorption. Fuel 2019, 249, 45–53. [Google Scholar] [CrossRef]
- Zainol, N.B. Aspen Simulation of Methylene Blue Adsorption Using Coconut Shell Based Activated Carbon. Bachelor’s Thesis, Universiti Sains Malaysia, Pulau Pinang, Malaysia, 2021. [Google Scholar]
- Hameed, A.; Hameed, B.H.; Almomani, F.A.; Usman, M.; Ba-Abbad, M.M.; Khraisheh, M. Dynamic simulation of lead (II) metal adsorption from water on activated carbons in a packed-bed column. Biomass Convers. Biorefin. 2024, 14, 8283–8292. [Google Scholar] [CrossRef]
- Rahimi, V.; Ferreiro-Salgado, A.; Gómez-Díaz, D.; Freire, M.S.; González-Álvarez, J. Evaluating the performance of carbon-based adsorbents fabricated from renewable biomass precursors for post-combustion CO2 capture. Sep. Purif. Technol. 2024, 344, 127110. [Google Scholar] [CrossRef]
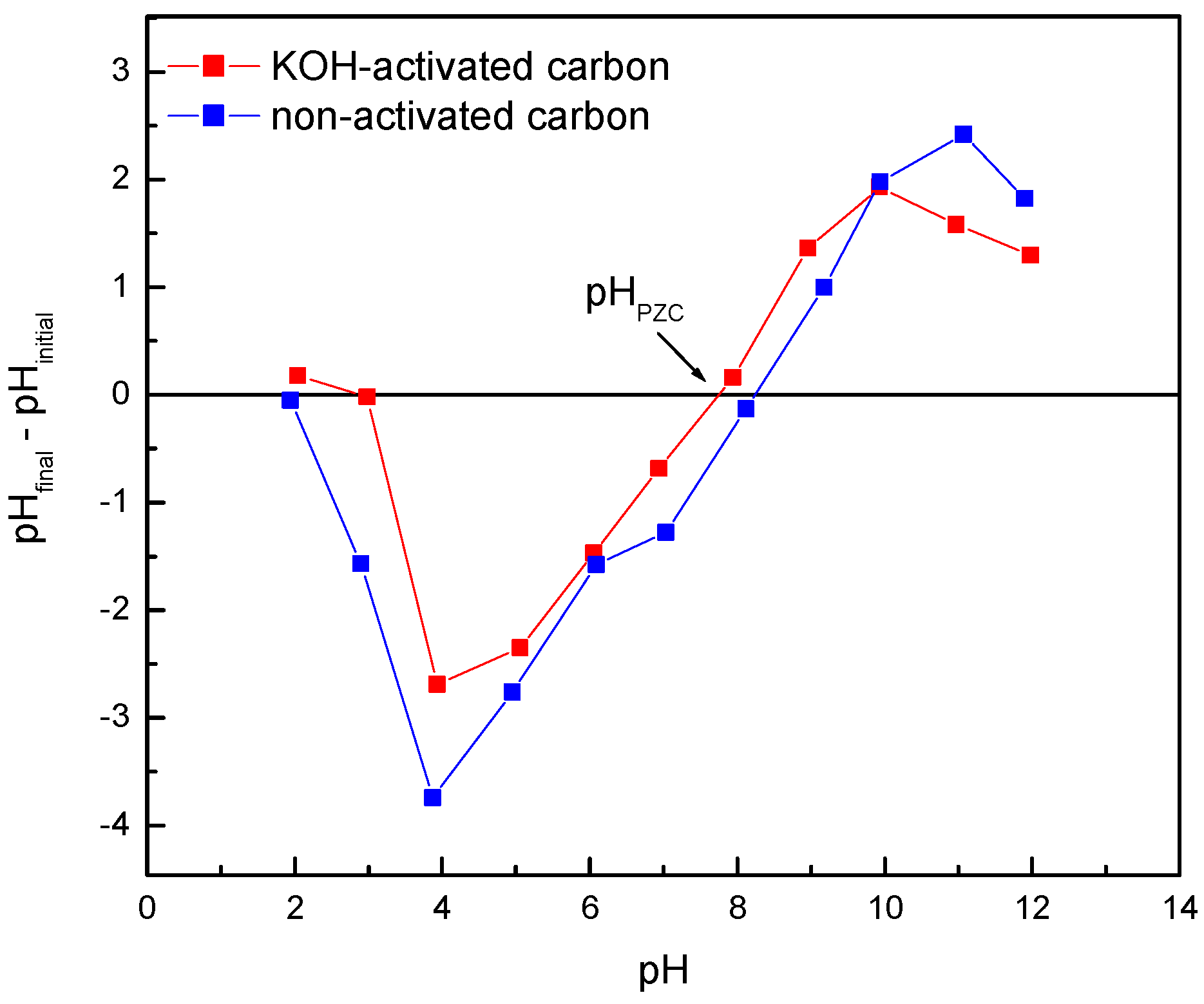


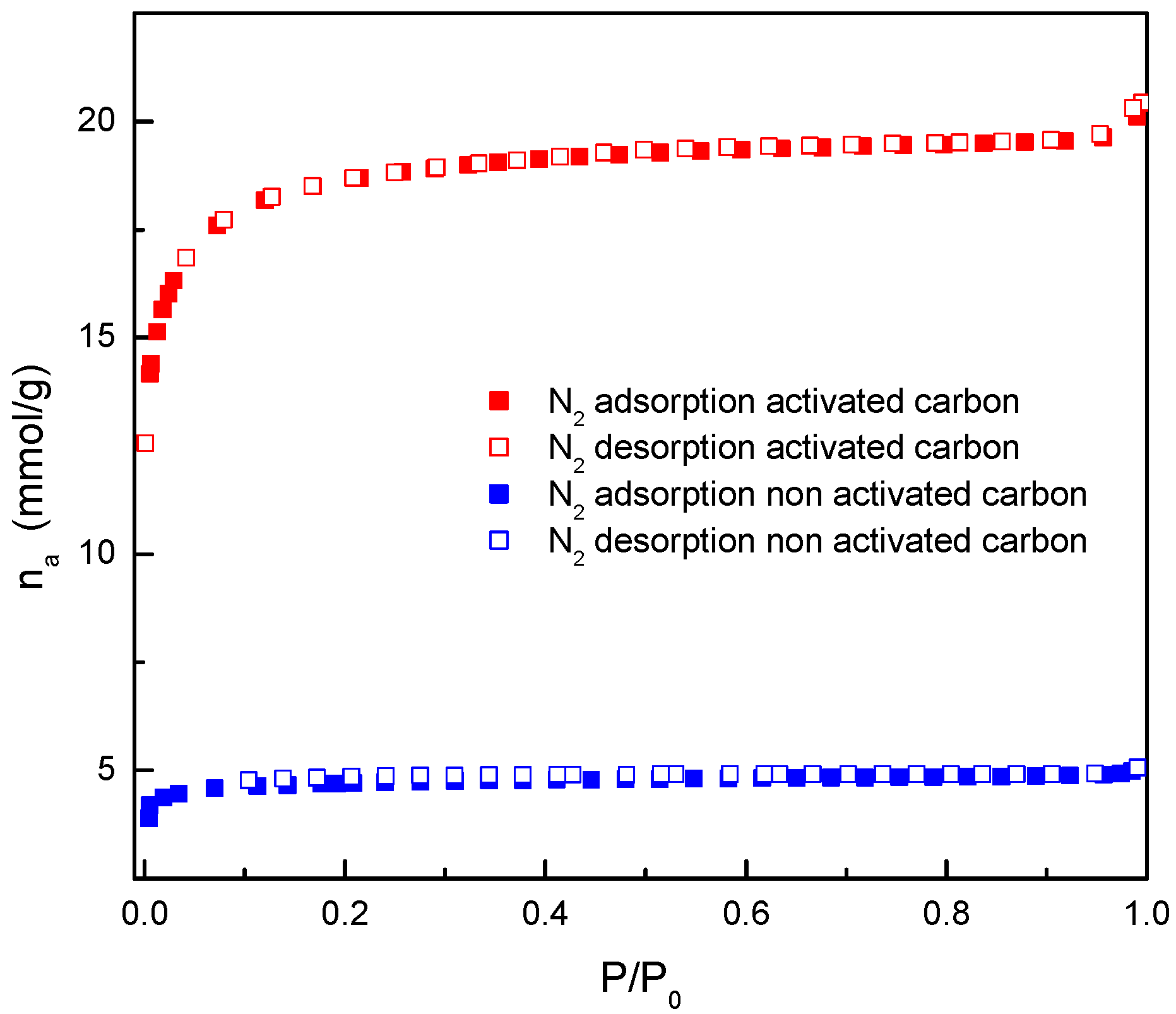
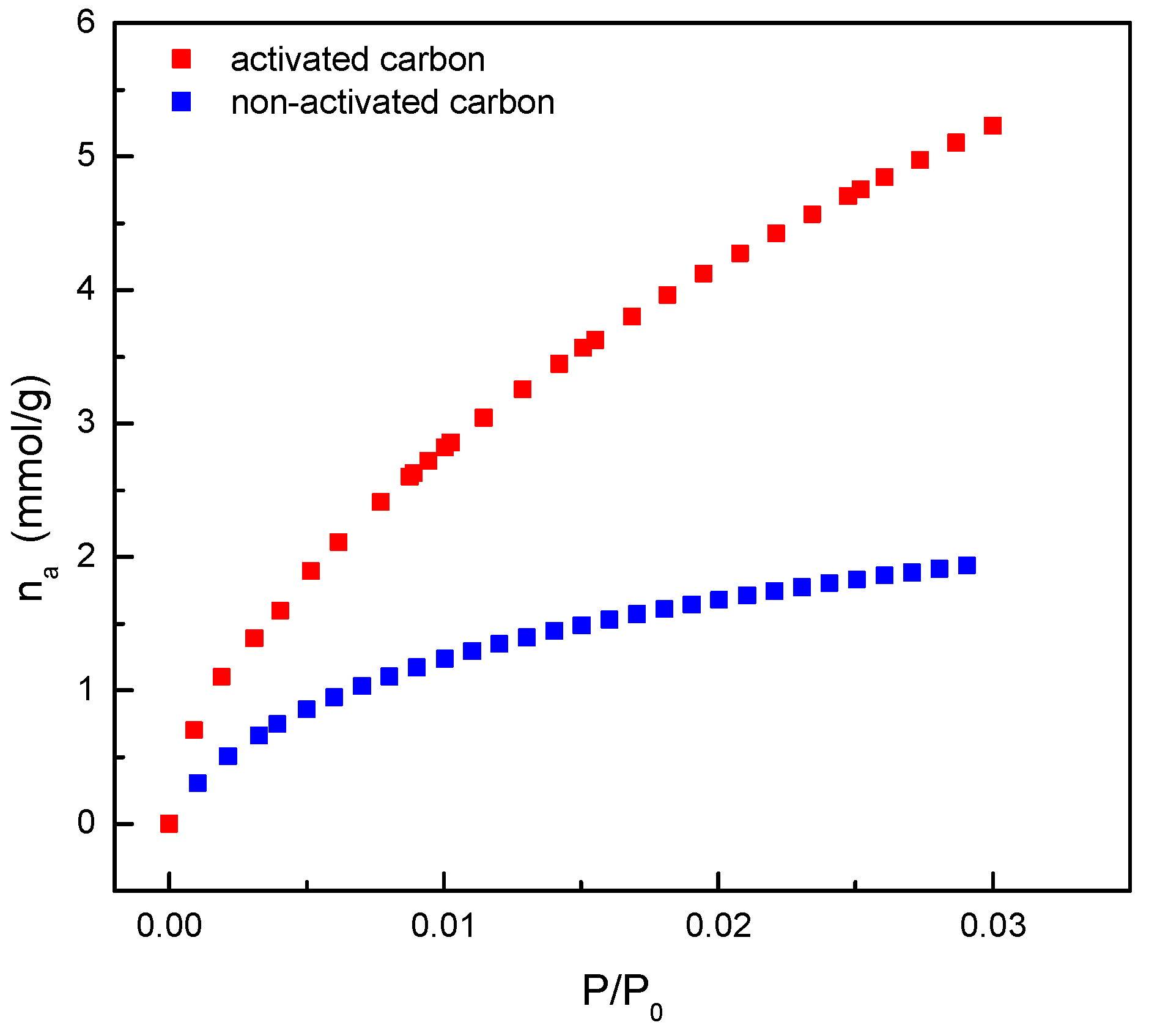
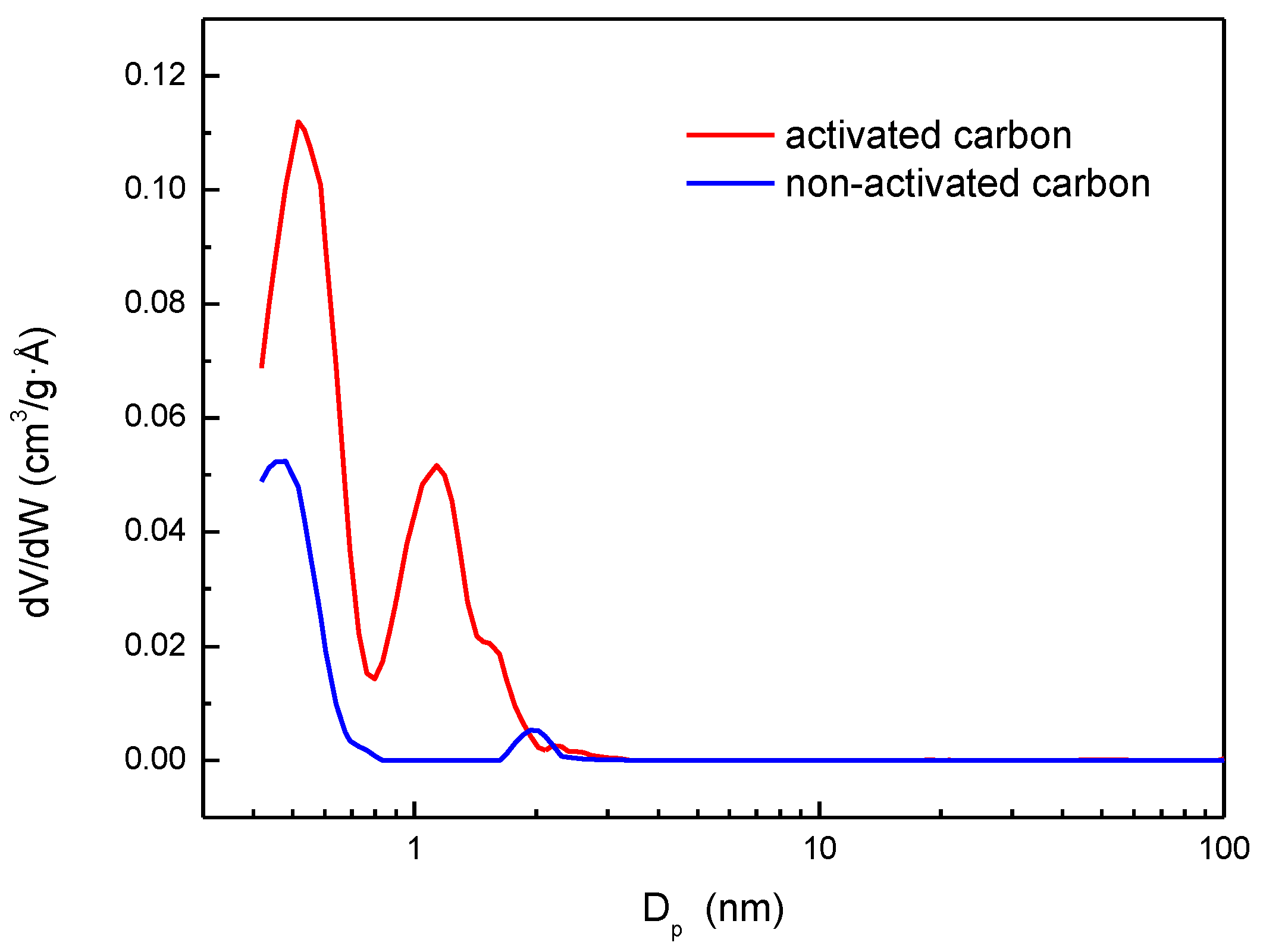

| Parameter | Non-Activated Carbon | Activated Carbon |
|---|---|---|
| Surface area (m2/g) N2 at 77 K (BET) | 294 ± 7 | 1577 ± 13 |
| Average pore size (Å) N2 at 77 K (BET) | 21.8 | 17.7 |
| Surface area (m2/g) CO2 at 273 K (BET) | 268 ± 1 | 772 ± 12 |
| Total pore volume (cm3/g) at P/Po = 0.99 | 0.161 | 0.697 |
| Microporosity (%) | 92.7 | 78.2 |
| Kinetic Model | Parameter | Methylene Blue | Malachite Green |
|---|---|---|---|
| C0 = 50 mg·L−1 | |||
| Adsorption half-time | t1/2 (min) | 10.9 | 13.8 |
| Pseudo-second-order | qe (mg·g−1) | 100.4 | 104.0 |
| k2 (g·mg−1·min−1) | 9.16·10−4 | 6.96·10−4 | |
| R2 | 0.9998 | 0.9998 | |
| Intraparticle diffusion | kid,1 (mg·g−1·min0.5) | 11.87 | 14.68 |
| C1 (mg·g−1) | 7.55 | 1.77 | |
| R2 | 0.9243 | 0.9753 | |
| kid,2 (mg·g−1·min0.5) | 0.286 | 3.02 | |
| C2 (mg·g−1) | 93.03 | 53.14 | |
| R2 | 0.6673 | 0.9075 | |
| kid,3 (mg·g−1·min0.5) | - | 0.273 | |
| C3 (mg·g−1) | - | 93.41 | |
| R2 | - | 0.8709 | |
| C0 = 250 mg·L−1 | |||
| Adsorption half-time | t1/2 (min) | 86.5 | 150.1 |
| Pseudo-second-order | qe (mg·g−1) | 441.1 | 378.6 |
| k2 (g·mg−1·min−1) | 2.62·10−5 | 1.76·10−5 | |
| R2 | 0.9880 | 0.9747 | |
| Intraparticle diffusion | kid,1 (mg·g−1·min0.5) | 35.85 | 13.02 |
| C1 (mg·g−1) | 1.69 | 13.12 | |
| R2 | 0.9974 | 0.9619 | |
| kid,2 (mg·g−1·min0.5) | 7.65 | 7.55 | |
| C2 (mg·g−1) | 148.3 | 73.23 | |
| R2 | 0.9640 | 0.9769 | |
| kid,3 (mg·g−1·min0.5) | - | - | |
| C3 (mg·g−1) | - | - | |
| R2 | - | - | |
| C0 = 500 mg·L−1 | |||
| Adsorption half-time | t1/2 (min) | 327.1 | 189.2 |
| Pseudo-second-order | qe (mg·g−1) | 551.9 | 343.2 |
| k2 (g·mg−1·min−1) | 5.54·10−6 | 1.54·10−5 | |
| R2 | 0.9966 | 0.9933 | |
| Intraparticle diffusion | kid,1 (mg·g−1·min0.5) | 10.43 | 11.46 |
| C1 (mg·g−1) | 22.47 | 20.48 | |
| R2 | 0.9397 | 0.8573 | |
| kid,2 (mg·g−1·min0.5) | 1.25 | 3.31 | |
| C2 (mg·g−1) | 419.7 | 205.9 | |
| R2 | 0.7235 | 0.9763 | |
| kid,3 (mg·g−1·min0.5) | - | - | |
| C3 (mg·g−1) | - | - | |
| R2 | - | - | |
| Equilibrium Model | Parameter | Methylene Blue | Malachite Green |
|---|---|---|---|
| Langmuir | qm,L (mg·g−1) | 341.3 | 363.6 |
| kL (L·mg−1) | 2.64 | 0.15 | |
| R2 | 0.989 | 0.982 | |
| Freundlich | N | 7.9 | 3.6 |
| kF (mg·g−1·(L·mg−1)−1/n) | 217.0 | 103.5 | |
| R2 | 0.896 | 0.998 | |
| Temkin | BT (J·mol−1) | 26.4 | 53.2 |
| kT (L·mg−1) | 9514.8 | 6.3 | |
| R2 | 0.910 | 0.948 | |
| Dubinin–Radushkevich | qm,DR (mg·g−1) | 314.2 | 257.6 |
| kDR (mol2·kJ−2) | 8.54·10−9 | 1.83·10−7 | |
| R2 | 0.919 | 0.730 |
| Precursor Material | Dye | Capacity (mg·g−1) | S/L (g·L−1) | Reference |
|---|---|---|---|---|
| Almond shell | MB | 341 | 0.5 | This work |
| Walnut shell | MB | 247 | 0.5 | [4] |
| Rubber seed pericarp | MB | 348 | 0.6 | [23] |
| Oil palm frond and palm kernel shell | MB | 332 | 2.5 | [24] |
| Sunflower pith | MB | 581 | 1.0 | [25] |
| Chickpea peel | MB | 200 | 0.8 | [26] |
| Sugarcane bagasse waste | MB | 142 | 5.0 | [27] |
| Almond shell | MG | 364 | 0.5 | This work |
| Charcoal | MG | 27 | 0.4 | [28] |
| Pinus roxburghii cone | MG | 250 | 0.7 | [29] |
| Walnut shell | MG | 155 | 0.6 | [30] |
| Okra stalks | MG | 100 | 1.0 | [31] |
| Hevea brasiliensis root | MG | 260 | 1.0 | [32] |
| Peach pit | MG | 70 | 2.0 | [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rial, A.; Pimentel, C.H.; Gómez-Díaz, D.; Freire, M.S.; González-Álvarez, J. Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies. Materials 2024, 17, 6077. https://doi.org/10.3390/ma17246077
Rial A, Pimentel CH, Gómez-Díaz D, Freire MS, González-Álvarez J. Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies. Materials. 2024; 17(24):6077. https://doi.org/10.3390/ma17246077
Chicago/Turabian StyleRial, Adrián, Catarina Helena Pimentel, Diego Gómez-Díaz, María Sonia Freire, and Julia González-Álvarez. 2024. "Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies" Materials 17, no. 24: 6077. https://doi.org/10.3390/ma17246077
APA StyleRial, A., Pimentel, C. H., Gómez-Díaz, D., Freire, M. S., & González-Álvarez, J. (2024). Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies. Materials, 17(24), 6077. https://doi.org/10.3390/ma17246077






