Polycrystalline Films of Indium-Doped PbTe on Amorphous Substrates: Investigation of the Material Based on Study of Its Structural, Transport, and Optical Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples Fabrication
2.2. Samples Characterization
2.3. Experimental Data Processing Using Images and Theoretical Models
3. Results
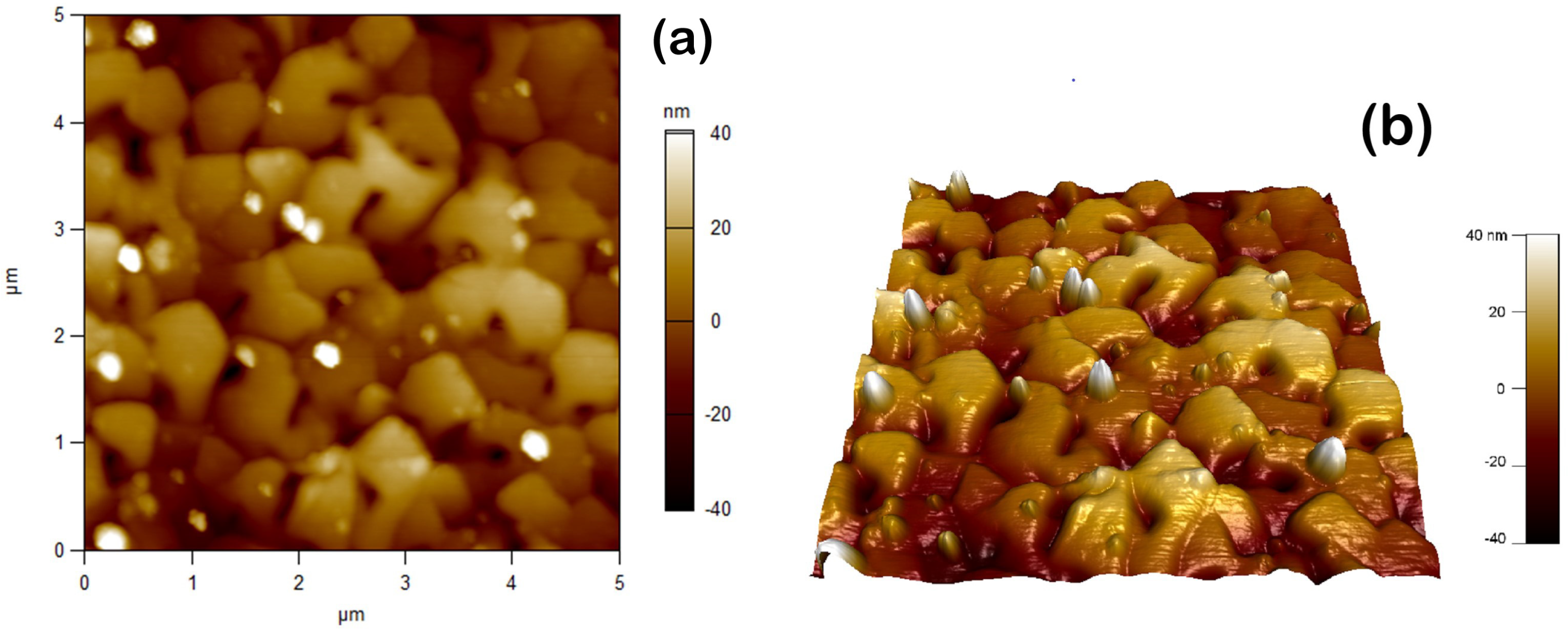
3.1. Structural Properties
3.2. Charge-Carrier-Related Properties
3.3. Infrared Transmission Spectra
4. Discussion
4.1. Morphology, Texture, and Surface Roughness
4.2. Electron Density and Transport Properties
4.3. Transmission Spectra
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LC | Lead chalcogenide |
| LTC | Lead–tin chalcogenide |
| IR | Infrared |
| TE | Thermoelectric |
| TEG | TE generator |
| PD | Photon/photo detector |
| PC | Photo-conductive |
| PCD | PC detector |
| CBD | Chemical bath deposition |
| CVD | Chemical vapor deposition |
| PVD | Physical vapor deposition |
| RT | Room temperature |
| EBPVD | Electron-beam-assisted physical vapor deposition |
| KPI | Kapton® polyimide |
| SOI | Silicon on insulator |
| SOX | Silicon dioxide |
| a-SOX | Amorphous SOX |
| XRD | X-ray diffraction |
| SEM | Scanning electron microscope/microscopy |
| HRSEM | High-resolution SEM |
| TEM | Transmission electron microscope/microscopy |
| STEM | Scanning TEM |
| HRTEM | High-resolution TEM |
| AFM | Atomic force microscope/microscopy |
| EDXS | Energy-dispersive X-ray spectroscopy |
| HAADF | High-angle annular dark field |
| MBE | Molecular-beam epitaxy |
| HWE | Hot-wall epitaxy |
Appendix A. Assessing the Dislocation Density
Appendix B. Modeling the Optical Properties of Planar Multilayered Structures
Appendix B.1. Outline
Appendix B.2. Mathematical Method
Appendix B.3. Effects of Super-Wavelength-Thick Layers
References
- Smith, R.A. Infra-red photo-conductors. Adv. Phys. 1953, 2, 321–369. [Google Scholar] [CrossRef]
- Dalven, R. A review of the semiconductor properties of PbTe, PbSe, PbS and PbO. Infrared Phys. 1969, 9, 141–184. [Google Scholar] [CrossRef]
- Ravich, Y.I.; Efimova, B.A.; Smirnov, I.A. Semiconducting Lead Chalcogenides; Monographs on Semiconductor Physics; Stil’bans, L.S., Ed.; Plenum Press & Springer Science+Business Media: New York, NY, USA, 1970; Volume 5. [Google Scholar]
- Nimtz, G.; Schlicht, B. Narrow-Gap Lead Salts. In Narrow-Gap Semiconductors; Springer Tracts in Modern, Physics; Höhler, G., Niekisch, E.A., Eds.; Springer Science+Business Media: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1983; Chapter 1; Volume 98, pp. 1–117. [Google Scholar]
- Ravich, Y.I. Lead Chalcogenides: Basic Physical Features. In Lead Chalcogenides Physics & Applications; Properties of Semiconductors and Superlattices; Khokhlov, D., Manasreh, M.O., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2003; Chapter 1; Volume 18, pp. 3–34. [Google Scholar]
- Rowe, D.M. (Ed.) Thermoelectrics Handbook: Macro to Nano; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Li, L.; Chen, Z.; Zhou, M.; Huang, R. Developments in semiconductor thermoelectric materials. Front. Energy 2011, 5, 125–136. [Google Scholar] [CrossRef]
- Gayner, C.; Kar, K.K. Recent advances in thermoelectric materials. Prog. Mater. Sci. 2016, 83, 330–382. [Google Scholar] [CrossRef]
- Tan, G.; Ohta, M.; Kanatzidis, M.G. Thermoelectric power generation: From new materials to devices. Philos. Transact. A Math. Phys. Eng. Sci. 2019, 377, 20180450. [Google Scholar] [CrossRef]
- Giri, J.M.; Nain, P.K.S. Review of recent progress in thermoelectric materials. In Proceedings of the Advances in Engineering Materials; Sharma, B.P., Rao, G.S., Gupta, S., Gupta, P., Prasad, A., Eds.; Springer Nature Singapore Pte Ltd.: Singapore, 2021; pp. 269–280. [Google Scholar]
- Gelbstein, Y.; Dashevsky, Z.; Dariel, M.P. High performance n-type PbTe-based materials for thermoelectric applications. Phys. B Condens. Matter 2005, 363, 196–205. [Google Scholar] [CrossRef]
- LaLonde, A.D.; Pei, Y.; Wang, H.; Snyder, G.J. Lead telluride alloy thermoelectrics. Mater. Today 2011, 14, 526–532. [Google Scholar] [CrossRef]
- Su, C.H. Design, growth and characterization of PbTe-based thermoelectric materials. Prog. Cryst. Growth Charact. Mater. 2019, 65, 47–94. [Google Scholar] [CrossRef]
- Parashchuk, T.; Dashevsky, Z.; Wojciechowski, K. Feasibility of a high stable PbTe:In semiconductor for thermoelectric energy applications. J. Appl. Phys. 2019, 37, 245103. [Google Scholar] [CrossRef]
- Shtern, Y.; Sherchenkov, A.; Shtern, M.; Rogachev, M.; Pepelyaev, D. Challenges and perspective recent trends of enhancing the efficiency of thermoelectric materials on the basis of PbTe. Mater. Today Commun. 2023, 37, 107083. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Rogalski, A. Infrared Detectors, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Rogalski, A. History of infrared detectors. Opto-Electron. Rev. 2012, 20, 279–308. [Google Scholar] [CrossRef]
- Hodes, G. Chemical Solution Deposition of Semiconductor Films; Marcel Dekker, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Morosanu, C.E. Thin Films by Chemical Vapour Deposition; Thin Films Science and Technology; Siddall, G., Ed.; Elsevier: Amsterdam, The Netherlands, 1990; Volume 7. [Google Scholar]
- Mattox, D.M. Handbook of Physical Vapor Deposition (PVD) Processing, 2nd ed.; Elsevier Inc., William Andrew: Oxford, UK, 2010. [Google Scholar]
- Vineis, C.J.; Shakouri, A.; Majumdar, A.; Kanatzidis, M.G. Nanostructured thermoelectrics: Big efficiency gains from small features. Adv. Mater. 2010, 22, 3970–3980. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Li, Z.; Fan, T.; Xiao, C.; Xie, Y. Defects engineering with multiple dimensions in thermoelectric materials. AAAS Res. 2020, 2020, 9652749. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, Y.; Han, J.; Liu, W.; Nan, C.; Lin, Y.; Hu, M.; Xu, B. Strong phonon localization in PbTe with dislocations and large deviation to Matthiessen’s rule. NPJ Comput. Mater. 2019, 5, 97. [Google Scholar] [CrossRef]
- Abdellaoui, L.; Chen, Z.; Yu, Y.; Luo, T.; Hanus, R.; Schwarz, T.; Bueno Villoro, R.; Cojocaru-Miredin, O.; Snyder, G.J.; Raabe, D.; et al. Parallel dislocation networks and Cottrell atmospheres reduce thermal conductivity of PbTe thermoelectrics. Adv. Funct. Mater. 2021, 31, 2101214. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, L.D. Charge and phonon transport in PbTe-based thermoelectric materials. NPJ Quantum Mater. 2018, 3, 55. [Google Scholar] [CrossRef]
- D’Souza, R.; Cao, J.; Querales-Flores, J.D.; Fahy, S.; Savić, I. Electron-phonon scattering and thermoelectric transport in p-type PbTe from first principles. Phys. Rev. B 2020, 102, 115204. [Google Scholar] [CrossRef]
- Wojciechowski, K.T.; Parashchuk, T.; Wiendlocha, B.; Cherniushok, O.; Dashevsky, Z. Highly efficient n-type PbTe developed by advanced electronic structure engineering. J. Mater. Chem. C 2020, 8, 13270–13285. [Google Scholar] [CrossRef]
- Parashchuk, T.; Wiendlocha, B.; Cherniushok, O.; Knura, R.; Wojciechowski, K.T. High thermoelectric performance of p-type PbTe enabled by the synergy of resonance scattering and lattice softening. ACS Appl. Mater. Interfaces 2021, 13, 49027–49042. [Google Scholar] [CrossRef]
- Chepkasov, I.V.; Kvashnin, A.G.; Radina, A.D.; Matsokin, N.A.; Jalolov, F.N.; Kvashnin, D.G.; Oganov, A.R.; Dashevsky, Z. Origin of brittle behavior of doped PbTe-based thermoelectric materials. Appl. Phys. Lett. 2024, 124, 022104. [Google Scholar] [CrossRef]
- Dashevsky, Z.; Mamykin, S.; Dzundza, B.; Auslender, M.; Shneck, R. A review of nanocrystalline film thermoelectrics on lead chalcogenide semiconductors: Progress and application. Energies 2023, 16, 3774. [Google Scholar] [CrossRef]
- International Thermoelectric Society. 2024. Available online: https://its.org/ (accessed on 1 October 2024).
- Dornhaus, R.; Nimtz, G. The Properties and Applications of the Hg1−xCdxTe Alloy System. In Narrow-Gap Semiconductors; Springer Tracts in Modern Physics; Höhler, G., Niekisch, E.A., Eds.; Springer Science+Business Media: Berlin/Heidelberg, Germany, 1983; Chapter 2; Volume 98, pp. 119–300. [Google Scholar]
- Rogalski, A. HgCdTe infrared detector material: History, status and outlook. Rep. Prog. Phys. 2005, 68, 2267–2336. [Google Scholar] [CrossRef]
- Dashevsky, Z.M.; Rulenko, M.P. Effect of increasing the diffusion length of charge carriers in polycrystalline PbTe films. Phys. Techn. Semicond. 1993, 27, 662–666. [Google Scholar]
- Springholz, G. Molecular Beam Epitaxy of IV-VI Heterostructures and Superlattices. In Lead Chalcogenides. Physics and Applications; Properties of Semiconductors and Superlattices; Khokhlov, D., Manasreh, M.O., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2003; Chapter 3; Volume 18, pp. 123–200. [Google Scholar]
- Dashevsky, Z.; Kreizman, R.; Dariel, M.P. Physical properties and inversion of conductivity type in nanocrystalline PbTe films. J. Appl. Phys. 2005, 98, 94309. [Google Scholar] [CrossRef]
- Dashevsky, Z. High Photosensitive Films of Lead Chalcogenides. In Handbook of Nanostructures and Nanodevices; Balandin, A.A., Wang, K.L., Eds.; American Scientific Publishers: Valencia, CA, USA, 2006; Chapter 11; Volume 2, pp. 335–359. [Google Scholar]
- Preier, H. Recent advances in lead-chalcogenide diode lasers. Appl. Phys. 1979, 20, 189–206. [Google Scholar] [CrossRef]
- Partin, D.L. Lead salt quantum effect structures. IEEE J. Quantum Electron. 1988, 24, 1716–1726. [Google Scholar] [CrossRef]
- Preier, H. Physics and applications of IV-VI compound semiconductor lasers. Semicond. Sci. Technol. 1990, 5, S12–S20. [Google Scholar] [CrossRef]
- Emtage, P.R. Auger recombination and junction resistance in lead-tin telluride. J. Appl. Phys. 1976, 47, 2565–2568. [Google Scholar] [CrossRef]
- Ziep, O.; Mocker, M.; Genzow, D.; Herrmann, K.H. Auger recombination in PbSnTe-like semiconductors. Phys. Status Solidi (b) 1978, 90, 197–205. [Google Scholar] [CrossRef]
- Mocker, M.; Ziep, O. Intrinsic recombination in dependence on doping concentration and excitation level application to lead chalcogenides. Phys. Status Solidi (b) 1983, 115, 415–425. [Google Scholar] [CrossRef]
- Klann, R.; Höfer, T.; Buhleier, R.; Elsaesser, T.; Tomm, J.W. Fast recombination processes in lead chalcogenide semiconductors studied via transient optical nonlinearities. J. Appl. Phys. 1995, 77, 277–286. [Google Scholar] [CrossRef]
- Findlay, P.C.; Pidgeon, C.R.; Kotitschke, R.; Hollingworth, A.; Murdin, B.N.; Langerak, C.J.G.M.; van der Meer, A.F.G.; Ciesla, C.M.; Oswald, J.; Homer, A.; et al. Auger recombination dynamics of lead salts under picosecond free-electron-laser excitation. Phys. Rev. B 1998, 58, 12908–12915. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, J.X.; Van de Walle, C.G. Anomalous Auger recombination in PbSe. Phys. Rev. Lett. 2020, 125, 037401. [Google Scholar] [CrossRef] [PubMed]
- Charache, G.W.; Baldasaro, P.F.; Danielson, L.R.; DePoy, D.M.; Freeman, M.J.; Wang, C.A.; Choi, H.K.; Garbuzov, D.Z.; Martinelli, R.U.; Khalfin, V.; et al. InGaAsSb thermophotovoltaic diode: Physics evaluation. J. Appl. Phys. 1999, 85, 2247–2252. [Google Scholar] [CrossRef]
- Levinshtein, M.; Rumyantsev, S.; Shur, M. (Eds.) Handbook Series on Semiconductor Parameters; World Scientific Publishing Co., Pte., Ltd.: Singapore, 1996; Volume I. [Google Scholar]
- Levinshtein, M.; Rumyantsev, S.; Shur, M. (Eds.) Handbook Series on Semiconductor Parameters; World Scientific Publishing Co., Pte., Ltd.: Singapore, 1999; Volume II. [Google Scholar]
- Zogg, H. Lead Chalcogenide Infrared Detectors Grown on Silicon Substrates. In Lead Chalcogenides. Physics and Applications; Properties of Semiconductors and Superlattices; Khokhlov, D., Manasreh, M.O., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2003; Chapter 11; Volume 18, pp. 587–616. [Google Scholar]
- Wang, J.; Hu, J.; Sun, X.; Agarwal, A.M.; Kimerling, L.C.; Lim, D.R.; Synowicki, R.A. Structural, electrical, and optical properties of thermally evaporated nanocrystalline PbTe films. J. Appl. Phys. 2008, 104, 53707. [Google Scholar] [CrossRef]
- Dobrovolsky, A.; Chernichkin, V.; Belogorokhov, I.; Dashevsky, Z.; Kasiyan, V.; Ryabova, L.; Khokhlov, D. Transport properties and photo-conductivity of nanocrystalline PbTe(In) films. Phys. Status Solidi C Curr. Top. Solid State Phys. 2010, 7, 869–872. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Becla, P.; Agarwal, A.M.; Kimerling, L.C. Room-temperature oxygen sensitization in highly textured, nanocrystalline PbTe films: A mechanistic study. J. Appl. Phys. 2011, 110, 83719. [Google Scholar] [CrossRef]
- Dzundza, B.; Nykyruy, L.; Parashchuk, T.; Ivakin, E.; Yavorsky, Y.; Chernyak, L.; Dashevsky, Z. Transport and thermoelectric performance of n-type PbTe films. Phys. B Condens. Matter 2020, 588, 412178. [Google Scholar] [CrossRef]
- Qiu, J.; Liu, Y.; Zhang, G.; Shi, K.; Li, Y.; Luo, Y. Modified vapor phase deposition technology for high-performance uncooled MIR PbSe detectors. RSC Adv. 2021, 11, 34908–34914. [Google Scholar] [CrossRef]
- Kovalyuk, V.; Sheveleva, E.; Auslender, M.; Goltsman, G.; Shneck, R.; Dashevsky, Z. Polycrystalline PbTe: In films on amorphous substrate: Structure and physical properties. Materials 2022, 15, 8383. [Google Scholar] [CrossRef] [PubMed]
- Kovalyuk, V.; Sheveleva, E.; Mel’nikov, A.; Auslender, M.; Goltsman, G.; Shneck, R.; Dashevsky, Z. Persistent photoconductivity of polycrystalline Pb1−xSnxTe: In films on an amorphous substrate in the telecom wavelength range. J. Appl. Phys. 2023, 134, 195702. [Google Scholar] [CrossRef]
- Su, P.; Pujari, R.; Boodhoo, V.; Aggarwal, S.; Bhattacharya, P.; Maksimov, O.; Wada, K.; Merlo, S.; Bhandari, H.B.; Kimerling, L.C.; et al. Ternary lead chalcogenide alloys for mid-infrared detectors. J. Electron. Mater. 2020, 49, 4577–4580. [Google Scholar] [CrossRef]
- Dashevsky, Z.; Kasiyan, V.; Radovsky, G.; Shufer, E.; Auslender, M. Mid-infrared photoluminescence of PbSe film structures up to room temperature. In Proceedings of the 6th International Conference on Advanced Optical Materials and Devices, Riga, Latvia, 24–27 August 2008; Volume 7142, pp. 172–183. [Google Scholar]
- Radovsky, G.; Dashevsky, Z.; Kasiyan, V.; Auslender, M.; Hava, S. Polycrystalline PbSe on a polyimide substrate. J. Alloys Compd. 2010, 501, 6–13. [Google Scholar] [CrossRef]
- Jang, M.H.; Litwin, P.M.; Yoo, S.S.; McDonnell, S.J.; Dhar, N.K.; Gupta, M.C. Mid-wavelength infrared photo response and band alignment for sensitized PbSe thin films. J. Appl. Phys. 2019, 126, 105701. [Google Scholar] [CrossRef]
- Jang, M.H.; Yoo, S.S.; Kramer, M.T.; Dhar, N.K.; Gupta, M.C. Electrical transport properties of sensitized PbSe thin films for IR imaging sensors. Semicond. Sci. Technol. 2019, 34, 065009. [Google Scholar] [CrossRef]
- Jang, M.H.; Kramer, M.T.; Yoo, S.S.; Gupta, M.C. Laser annealing to improve PbSe thin film photosensitivity and specific detectivity. Appl. Opt. 2020, 59, 9409–9414. [Google Scholar] [CrossRef]
- Shelton, D.; Sigley, J.; Nicholas, R.; Driggers, R. Potential and limitations for very-high-operating-temperature (VHOT) MWIR focal plane arrays using halogen-passivated PbSe. Proc. SPIE 2018, 10624, 1062411. [Google Scholar]
- Vergara, G.; Montojo, M.T.; Torquemada, M.C.; Rodrigo, M.T.; Sánchez, F.; Gómez, L.J.; Almazán, R.M.; Verdú, M.; Rodríguez, P.; Villamayor, V.; et al. Polycrystalline lead selenide: The resurgence of an old infrared detector. Opto-Electron. Rev. 2007, 15, 110–117. [Google Scholar] [CrossRef]
- Sierra, C.; Torquemada, M.; Vergara, G.; Rodrigo, M.; Gutiérrez, C.; Pérez, G.; Génova, I.; Catalán, I.; Gómez, L.; Villamayor, V.; et al. Multicolour PbSe sensors for analytical applications. Sens. Actuators B Chem. 2014, 190, 464–471. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Becla, P.; Agarwal, A.M.; Kimerling, L.C. Resonant-cavity-enhanced mid-infrared photodetector on a silicon platform. Opt. Express 2010, 18, 12890–12896. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zens, T.; Hu, J.; Becla, P.; Kimerling, L.C.; Agarwal, A.M. Monolithically integrated, resonant-cavity-enhanced dual-band mid-infrared photodetector on silicon. Appl. Phys. Lett. 2012, 100, 211106. [Google Scholar] [CrossRef]
- Mendez-Rial, R.; Souto-Lopez, A.; Garcia-Diaz, A. MWIR infrared gating imaging with uncooled PbSe FPAs for surveillance applications. Proc. SPIE 2018, 10677, 1–6. [Google Scholar]
- Rivera, C.; Alvarez, M. Assessment of PbSe photoconductors for the realization of free-space midinfrared optical communication links. IEEE Photonics Technol. Lett. 2012, 24, 267–269. [Google Scholar] [CrossRef]
- Shufer, E.; Dashevsky, Z.; Kasiyan, V.; Flitsiyan, E.; Chernyak, L.; Gartsman, K. Electrical conductivity and minority carrier diffusion in thermally oxidized PbTe thin films. Phys. B Condens. Matter 2010, 405, 1058–1061. [Google Scholar] [CrossRef]
- Jost, S. Identifying the physical mechanisms of polycrystalline lead salt photoconductors. J. Appl. Phys. 2022, 132, 64503. [Google Scholar] [CrossRef]
- Heo, S.H.; Yoo, J.; Lee, H.; Jang, H.; Jo, S.; Cho, J.; Baek, S.; Yang, S.E.; Gu, D.H.; Mun, H.J.; et al. Solution-processed hole-doped SnSe thermoelectric thin-film devices for low-temperature power generation. ACS Energy Lett. 2022, 7, 2092–2101. [Google Scholar] [CrossRef]
- Ishibe, T.; Komatsubara, Y.; Ishikawa, K.; Takigawa, S.; Naruse, N.; Mera, Y.; Yamashita, Y.; Ohishi, Y.; Nakamura, Y. Boosting thermoelectric performance in epitaxial GeTe film/Si by domain engineering and point defect control. ACS Appl. Mater. Interfaces 2023, 15, 26104–26110. [Google Scholar] [CrossRef]
- Dashevsky, Z.; Horichok, I.; Maksymuk, M.; Muchtar, A.R.; Srinivasan, B.; Mori, T. Feasibility of high performance in p-type Ge1−xBixTe materials for thermoelectric modules. J. Am. Ceram. Soc. 2022, 105, 4500–4511. [Google Scholar] [CrossRef]
- Askerov, B.M. Electron Transport Phenomena in Semiconductors, English Translation from Russian of 1985 Nauka ed.; World Scientific Publishing Co., Pte., Ltd.: Singapore, 1994. [Google Scholar]
- Volkov, B.A.; Ryabova, L.I.; Khokhlov, D.R. Mixed-valence impurities in lead telluride-based solid solutions. Physics–Uspekhi 2002, 45, 819–846. [Google Scholar] [CrossRef]
- Kaǐdanov, V.I.; Ravich, Y.I. Deep and resonance states in AIVBVI semiconductors. Sov. Phys. Usp. 1985, 28, 31–54. [Google Scholar] [CrossRef]
- Kaǐdanov, V.I. Resonance (quasilocal) states in AIVBVI semiconductors. In Proceedings of the Defects in Semiconductors I; Trans Tech Publications, Ltd.: Bäch, Switzerland, 1993; Volumes 103–105, pp. 387–406. [Google Scholar]
- SOI Wafers, Siegert Inc. 2023. Available online: https://www.siegertwafer.com/SOI_Wafers.html (accessed on 12 July 2024).
- Kapton® Polyimide, DuPont™. 2023. Available online: https://www.dupont.com/electronics-industrial/kapton-polyimide-film.html#null (accessed on 12 July 2024).
- Thompson, C.V. Structure evolution during processing of polycrystalline films. Annu. Rev. Mater. Sci. 2000, 30, 159–190. [Google Scholar] [CrossRef]
- Weeks, R.A.; Nelson, C.M. Irradiation effects and short-range order in fused silica and quartz. J. Appl. Phys. 1960, 31, 1555–1558. [Google Scholar] [CrossRef]
- Silica—Silicon Dioxide (SiO2), AZO Materials. 2023. Available online: https://www.azom.com/properties.aspx?ArticleID=1114 (accessed on 13 November 2024).
- Atanova, A.; Seregin, D.; Zhigalina, O.; Khmelenin, D.; Orlov, G.; Turkina, D.; Sigov, A.; Vorotilov, K. Control of columnar grain microstructure in CSD LaNiO3 films. Molecules 2023, 28, 1938. [Google Scholar] [CrossRef]
- Belenchuk, A.; Shapoval, O.; Kantser, V.; Fedorov, A.; Schunk, P.; Schimmel, T.; Dashevsky, Z. Growth of (111)-oriented PbTe thin films on vicinal Si(111) and on Si(100) using fluoride buffers. J. Cryst. Growth 1999, 198/199, 1216–1221. [Google Scholar] [CrossRef]
- Belenchuk, A.; Fedorov, A.; Huhtinen, H.; Kantser, V.; Laiho, R.; Shapoval, O.; Zakhvalinskii, V. Growth of (111)-oriented PbTe films on Si(001) using a BaF2 buffer. Thin Solid Films 2000, 358, 277–282. [Google Scholar] [CrossRef]
- Dashevsky, Z.; Belenchuk, A.; Gartstein, E.; Shapoval, O. PbTe films grown by hot wall epitaxy on sapphire substrates. Thin Solid Films 2004, 461, 256–265. [Google Scholar] [CrossRef]
- Ugai, Y.A.; Samoylova, A.M.; Sharov, M.K.; Tadeev, A.V. Crystal microstructure of PbTe/Si and PbTe/SiO2/Si thin flms. Thin Solid Films 1998, 336, 196–200. [Google Scholar] [CrossRef]
- Krishnan, K.; Stout, P.; Watanabe, M. Characterization of Semiconductor Silicon Using Fourier Transform Infrared Spectrometry. In Practical Fourier Transform Infrared Spectroscopy; Ferraro, J., Krishnan, K., Eds.; Academic Press, Inc.: New York, NY, USA, 1990; Chapter 6; pp. 285–349. [Google Scholar]
- Swanepoel, R. Determination of the thickness and optical constants of amorphous silicon. J. Phys. E Sci. Instrum. 1983, 16, 1214–1222. [Google Scholar] [CrossRef]
- Hordon, M.; Averbach, B. X-ray measurements of dislocation density in deformed copper and aluminum single crystals. Acta Metall. 1961, 9, 237–246. [Google Scholar] [CrossRef]
- Meng, Y.; Ju, X.; Yang, X. The measurement of the dislocation density using TEM. Mater. Charact. 2021, 175, 111065. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Heavens, O.S. Optical Properties of Thin Solid Films, Reissue of 1965 ed.; Dover Publications, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Knittl, Z. Optics of Thin Films (An Optical Multilayer Theory), 3rd ed.; Wiley & Sons: New York, NY, USA, 1976. [Google Scholar]
- Sturm, J.C.; Reaves, C.M. Silicon temperature measurement by infrared absorption. Fundamental processes and doping effects. IEEE Trans. Electron. Dev. 1992, 39, 81–88. [Google Scholar] [CrossRef]
- McMahon, H.O. Thermal radiation from partially transparent reflecting bodies. J. Opt. Soc. Am. 1950, 40, 376–380. [Google Scholar] [CrossRef]
- Timans, P.J. Emissivity of silicon at elevated temperatures. J. Appl. Phys. 1993, 74, 6353–6364. [Google Scholar] [CrossRef]
- Timans, P.J. The thermal radiative properties of semiconductors. In Advances in Rapid Thermal and Integrated Processing; Roozeboom, F., Ed.; Springer: Dordrecht, The Netherlands, 1996; Chapter 1; pp. 35–101. [Google Scholar]
- Hava, S.; Auslender, M.; Lacquet, B.; Coetzer, P.; Swart, P. IR transmission and reflection study of lamellar silicon grating-wafer structures. Infrared Phys. Technol. 1995, 36, 639–647. [Google Scholar] [CrossRef]







| Specimen | Mean Film Thickness | Mean Lateral Grain Size w, | Dislocations Density |
|---|---|---|---|
| SOX | 90 | ||
| SOX | |||
| SOX | |||
| SOX−4 |
| Specimen | In Content | Substrate Temperature , °C | Mean Film Thickness | Mean Lateral Grain Size w, |
|---|---|---|---|---|
| KPI−1 | 300 | 2 ± 0.10 | ||
| KPI−2 | 350 | 3 ± 0.15 | ||
| KPI−3 † | 350 | 3 ± 0.15 | ||
| KPI−4 | 250 | 2 ± 0.10 | ||
| KPI−5 | 325 | 3 ± 0.15 | ||
| KPI−6 | 325 | 4 ± 0.20 |
| Specimen | |||||
|---|---|---|---|---|---|
| SOX−1 | 4.8 | 700 | 6500 | ||
| SOX−2 | 5.1 | 800 | 7200 | ||
| SOX−3 | 5.0 | 850 | 8000 | ||
| SOX−4 | 5.0 | 900 | 8800 |
| Specimen | |||||
|---|---|---|---|---|---|
| KPI−1 | – | – | – | ||
| KPI−2 | 8.3 | 630 | 1900 | 1600 | |
| KPI−3 | 910 | 8000 | |||
| KPI−4 | 500 | 950 | 725 | ||
| KPI−5 | 9.4 | 500 | 1050 | 800 | |
| KPI−6 | 500 | 2050 | 1750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jopp, J.; Kovalyuk, V.; Towe, E.; Shneck, R.; Dashevsky, Z.; Auslender, M. Polycrystalline Films of Indium-Doped PbTe on Amorphous Substrates: Investigation of the Material Based on Study of Its Structural, Transport, and Optical Properties. Materials 2024, 17, 6058. https://doi.org/10.3390/ma17246058
Jopp J, Kovalyuk V, Towe E, Shneck R, Dashevsky Z, Auslender M. Polycrystalline Films of Indium-Doped PbTe on Amorphous Substrates: Investigation of the Material Based on Study of Its Structural, Transport, and Optical Properties. Materials. 2024; 17(24):6058. https://doi.org/10.3390/ma17246058
Chicago/Turabian StyleJopp, Jürgen, Vadim Kovalyuk, Elias Towe, Roni Shneck, Zinovi Dashevsky, and Mark Auslender. 2024. "Polycrystalline Films of Indium-Doped PbTe on Amorphous Substrates: Investigation of the Material Based on Study of Its Structural, Transport, and Optical Properties" Materials 17, no. 24: 6058. https://doi.org/10.3390/ma17246058
APA StyleJopp, J., Kovalyuk, V., Towe, E., Shneck, R., Dashevsky, Z., & Auslender, M. (2024). Polycrystalline Films of Indium-Doped PbTe on Amorphous Substrates: Investigation of the Material Based on Study of Its Structural, Transport, and Optical Properties. Materials, 17(24), 6058. https://doi.org/10.3390/ma17246058







