Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies
Highlights
- Asymptotic homogenization method is used to study the viscoelastic behavior of lattice structures.
- Effective moduli of tetrahedron-based and octet-truss topologies are obtained.
- Finite element method and experimental tests are used for validation of AH method.
- Both cell types exhibit stress relaxation over time, indicating their viscoelastic nature.
Abstract
1. Introduction
2. Materials and Methods
2.1. Designs
2.2. Material Model
2.3. Asymptotic Homogenization (AH)
2.3.1. Viscoelastic Moduli
2.3.2. Poisson’s Ratio
2.4. Periodic Boundary Condition
2.5. Finite Element Modeling Using ABAQUS
2.6. Experiments
3. Results and Discussion
3.1. Octet-Truss Unit Cell
3.1.1. Quasi-Static Compressive Tests Results
3.1.2. Numerical Results
Viscoelastic Moduli
Poisson’s Ratio
3.2. Tetrahedron-Based
Poisson’s Ratio
3.3. Performance Comparison: Octet-Truss vs. Tetrahedron-Based Unit Cells
3.4. von Mises Stress Analysis
3.4.1. Octet-Truss Unit Cell
3.4.2. Tetrahedron-Based Unit Cell
4. Conclusions
- From experimental tests, it was observed that density significantly affects mechanical properties in octet-truss lattices. Both yield strength and elastic modulus increased relatively non-linearly with density. Interestingly, the decrease in elastic modulus (13%) was smaller than the decrease in yield strength (48%) for a relative density reduction from 50% to 30%.
- A strong correlation existed between relative density and the effective elastic modulus of both unit cell designs. The tetrahedron-based structure exhibited significantly higher (longitudinal and shear) modulus compared to the octet-truss, particularly at higher densities. For instance, at 50% relative density, the tetrahedron’s longitudinal and shear moduli surpassed those of the octet-truss by 61.5% and 40.5%, respectively (based on the AH method). This highlights the trade-off between porosity (important for tissue in-growth) and mechanical support. For applications requiring high load-bearing capability, the tetrahedron-based design has shown to be preferable, especially at higher densities.
- Both unit cells exhibited minimal changes in moduli and a near-constant Poisson’s ratio (varying from 0.34 to 0.349 for octet-truss and 0.3258 to 0.3161 for tetrahedron) under the test conditions (PEEK polymer at room temperature). While statistically insignificant, the potential time-dependent stiffness reduction should be considered for long-term simulations.
- Both cell types exhibited stress relaxation over time, indicating their viscoelastic nature. The tetrahedral unit cell exhibited a higher initial stress () due to its inherent stiffness compared to the octet-truss ().
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arabnejad, S.; Johnston, R.B.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-strength porous biomaterials for bone replacement: A strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef]
- Hedayati, R.; Ghavidelnia, N.; Sadighi, M.; Bodaghi, M. Improving the accuracy of analytical relationships for mechanical properties of permeable metamaterials. Appl. Sci. 2021, 11, 1332. [Google Scholar] [CrossRef]
- Ghavidelnia, N.; Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M. Development of porous implants with non-uniform mechanical properties distribution based on CT images. Appl. Math. Model. 2020, 83, 801–823. [Google Scholar] [CrossRef]
- Hedayati, R.; Yousefi, A.; Dezaki, M.L.; Bodaghi, M. Analytical relationships for 2D Re-entrant auxetic metamaterials: An application to 3D printing flexible implants. J. Mech. Behav. Biomed. Mater. 2023, 143, 105938. [Google Scholar] [CrossRef] [PubMed]
- Tabata, Y. Biomaterial technology for tissue engineering applications. J. R. Soc. Interface 2009, 6 (Suppl. S3), S311–S324. [Google Scholar] [CrossRef] [PubMed]
- K Singh, N.; Singh, N.K.; Pandit, D.; Saxena, K.K. Recent trends in bio-materials and advances in design of spinal fusion implants. Adv. Mater. Process. Technol. 2022, 8 (Suppl. S4), 2122–2141. [Google Scholar] [CrossRef]
- White, E.W.; Weber, J.N.; Roy, D.M.; Owen, E.L.; Chiroff, R.T.; White, R.A. Replamineform porous biomaterials for hard tissue implant applications. J. Biomed. Mater. Res. 1975, 9, 23–27. [Google Scholar] [CrossRef] [PubMed]
- Oveissi, F.; Naficy, S.; Lee, A.; Winlaw, D.S.; Dehghani, F. Materials and manufacturing perspectives in engineering heart valves: A review. Mater. Today Bio. 2020, 5, 100038. [Google Scholar] [CrossRef] [PubMed]
- Eltom, A.; Zhong, G.; Muhammad, A. Scaffold techniques and designs in tissue engineering functions and purposes: A review. Adv. Mater. Sci. Eng. 2019, 2019, 3429527. [Google Scholar] [CrossRef]
- Melancon, D.; Bagheri, Z.S.; Johnston, R.B.; Liu, L.; Tanzer, M.; Pasini, D. Mechanical characterization of structurally porous biomaterials built via additive manufacturing: Experiments, predictive models, and design maps for load-bearing bone replacement implants. Acta Biomater. 2017, 63, 350–368. [Google Scholar] [CrossRef]
- Ghavidelnia, N.; Salami, S.J.; Hedayati, R. Analytical relationships for yield stress of five mechanical meta-biomaterials. Mech. Based Des. Struct. Mach. 2022, 50, 3452–3474. [Google Scholar] [CrossRef]
- Koloushani, M.; Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M. CT-based micro-mechanical approach to predict response of closed-cell porous biomaterials to low-velocity impact. J. Imaging 2018, 4, 49. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Q.; Yarlagadda, P.K.D.V.; Zhu, F.; Li, Q.; Li, Z. Single-parameter mechanical design of a 3D-printed octet truss topological scaffold to match natural cancellous bones. Mater. Des. 2021, 209, 109986. [Google Scholar] [CrossRef]
- Egan, P.F. Integrated design approaches for 3D printed tissue scaffolds: Review and outlook. Materials 2019, 12, 2355. [Google Scholar] [CrossRef] [PubMed]
- Watts, S. Elastic response of hollow truss lattice micro-architectures. Int. J. Solids Struct. 2020, 206, 472–564. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, F.; Gao, H.; Li, X. Elastically isotropic truss-plate-hybrid hierarchical microlattices with enhanced modulus and strength. Small 2023, 19, 2206024. [Google Scholar] [CrossRef]
- Bhat, C.; Kumar, A.; Lin, S.-C.; Jeng, J.-Y. Design, fabrication, and properties evaluation of novel nested lattice structures. Addit. Manuf. 2023, 68, 103510. [Google Scholar] [CrossRef]
- Dadashi, A.; Rahimi, G.H. A novel analytical solution for determining the shear behavior of the lattice structure based on the Primitive unit cell considering the shear and bending effect. Mech. Based Des. Struct. Mach. 2024, 1–26. [Google Scholar] [CrossRef]
- Doodi, R.; Gunji, B.M. Experimental and numerical investigation on novel three-dimensional printed bio-inspired hexagonal lattices for energy absorption and stiffness behavior. Mech. Based Des. Struct. Mach. 2024, 1–17. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of deformation of a porous viscoelastic anisotropic solid. J. Appl. Phys. 1956, 27, 459–467. [Google Scholar] [CrossRef]
- Barbero, E.; Luciano, R. Micromechanical formulas for the relaxation tensor of linear viscoelastic composites with transversely isotropic fibers. Int. J. Solids Struct. 1995, 32, 1859–1872. [Google Scholar] [CrossRef]
- Yi, Y.-M.; Park, S.-H.; Youn, S.-K. Asymptotic homogenization of viscoelastic composites with periodic microstructures. Int. J. Solids Struct. 1998, 35, 2039–2055. [Google Scholar] [CrossRef]
- Yi, Y.-M.; Park, S.-H.; Youn, S.-K. Design of microstructures of viscoelastic composites for optimal damping characteristics. Int. J. Solids Struct. 2000, 37, 4791–4810. [Google Scholar] [CrossRef]
- Liu, S.; Chen, K.-Z.; Feng, X.-A. Prediction of viscoelastic property of layered materials. Int. J. Solids Struct. 2004, 41, 3675–3688. [Google Scholar] [CrossRef]
- Tran, A.B.; Yvonnet, J.; He, Q.-C.; Toulemonde, C.; Sanahuja, J. A simple computational homogenization method for structures made of linear heterogeneous viscoelastic materials. Comput. Methods Appl. Mech. Eng. 2011, 200, 2956–2970. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Liu, S.; Wang, J. A novel implementation of asymptotic homogenization for viscoelastic composites with periodic microstructures. Compos. Struct. 2019, 208, 276–286. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, R.; Otero, J.A.; Cruz-González, O.L.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Sabina, F.J.; Padilla, P.; Lebon, F.; Sevostianov, I. Computation of the relaxation effective moduli for fibrous viscoelastic composites using the asymptotic homogenization method. Int. J. Solids Struct. 2020, 190, 281–290. [Google Scholar] [CrossRef]
- Glaesener, R.N.; Bastek, J.-H.; Gonon, F.; Kannan, V.; Telgen, B.; Spöttling, B.; Steiner, S.; Kochmann, D.M. Viscoelastic truss metamaterials as time-dependent generalized continua. J. Mech. Phys. Solids 2021, 156, 104569. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; American Mathematical Society: Providence, RI, USA, 2011; Volume 374. [Google Scholar]
- Guedes, J.; Kikuchi, N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput. Methods Appl. Mech. Eng. 1990, 83, 143–198. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Andrianov, I.V.; Danishevskyy, V.V. Asymptotic homogenization of composite materials and structures. Appl. Mech. Rev. 2009, 62, 030802. [Google Scholar] [CrossRef]
- Dinh, T.D.; Weeger, O.; Kaijima, S.; Yeung, S.-K. Prediction of mechanical properties of knitted fabrics under tensile and shear loading: Mesoscale analysis using representative unit cells and its validation. Compos. Part B Eng. 2018, 148, 81–92. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.M.; Wang, Z.; Li, Q.; Wu, X.; Zhou, S. A comparison of fast Fourier transform-based homogenization method to asymptotic homogenization method. Compos. Struct. 2020, 238, 111979. [Google Scholar] [CrossRef]
- Alinia, M.; Nopour, R.; Aghdam, M.M.; Hedayati, R. The effect of auxeticity on the vibration of conical sandwich shells with ring support under various boundary conditions. Eng. Anal. Bound. Elem. 2023, 152, 130–147. [Google Scholar] [CrossRef]
- Abedini, B.; Hedayati, R.; Aghdam, M.M.; Sadighi, M. Thermomechanical behavior of lattice structures: An analytical, numerical, and experimental study. Mech. Based Des. Struct. Mach. 2023, 1–24. [Google Scholar] [CrossRef]
- Alavi, M.; Hedayati, R.; Sadigh, M.I. Gradient 2D re-entrant cores for sandwich structures under low-velocity impact. J. Sandw. Struct. Mater. 2024. accepted. [Google Scholar] [CrossRef]
- Talebi, S.; Hedayati, R.; Sadighi, M. Dynamic crushing behavior of closed-cell aluminum foams based on different space-filling unit cells. Arch. Civ. Mech. Eng. 2021, 21, 99. [Google Scholar] [CrossRef]
- Refai, K.; Montemurro, M.; Brugger, C.; Saintier, N. Determination of the effective elastic properties of titanium lattice structures. Mech. Adv. Mater. Struct. 2020, 27, 1966–1982. [Google Scholar] [CrossRef]
- Gao, Q.; Ding, Z.; Liao, W.-H. Effective elastic properties of irregular auxetic structures. Compos. Struct. 2022, 287, 115269. [Google Scholar] [CrossRef]
- Zhu, Y.; Luo, Y.; Gao, D.; Yu, C.; Ren, X.; Zhang, C. In-plane elastic properties of a novel re-entrant auxetic honeycomb with zigzag inclined ligaments. Eng. Struct. 2022, 268, 114788. [Google Scholar] [CrossRef]
- Johnston, S.R.; Reed, M.; Wang, H.V.; Rosen, D.W. Analysis of Mesostructure Unit Cells Comprised of Octet-Truss Structures. In Proceedings of the 2006 International Solid Freeform Fabrication Symposium; Mechanical Engineering Department, The University of Texas at Austin: Austin, TX, USA, 2006; Available online: https://hdl.handle.net/2152/80129 (accessed on 20 April 2024).
- Abdelhamid, M.; Czekanski, A. Impact of the lattice angle on the effective properties of the octet-truss lattice structure. J. Eng. Mater. Technol. 2018, 140, 041010. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Lv, W.; Li, D.; Dong, L. Study on mechanical properties of a hierarchical octet-truss structure. Compos. Struct. 2020, 249, 112640. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, C.; Xing, B.; Shen, M.; Zhao, Z. Mechanical properties of zirconia octet truss structures fabricated by DLP 3D printing. Mater. Res. Express 2020, 7, 085201. [Google Scholar] [CrossRef]
- Gibson, L.J. Cellular solids. Mrs Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials. Mech. Mater. 2012, 46, 57–68. [Google Scholar] [CrossRef]
- Bagheri, A.; Buj-Corral, I.; Ferrer Ballester, M.; Magdalena Pastor, M.; Roure Fernandez, F. Determination of the elasticity modulus of 3D-printed octet-truss structures for use in porous prosthesis implants. Materials 2018, 11, 2420. [Google Scholar] [CrossRef]
- Olivas-Alanis, L.H.; Fraga-Martínez, A.A.; García-López, E.; Lopez-Botello, O.; Vazquez-Lepe, E.; Cuan-Urquizo, E.; Rodriguez, C.A. Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials 2023, 16, 1025. [Google Scholar] [CrossRef]
- Song, J.; Zhou, W.; Wang, Y.; Fan, R.; Wang, Y.; Chen, J.; Lu, Y.; Li, L. Octet-truss cellular materials for improved mechanical properties and specific energy absorption. Mater. Des. 2019, 173, 107773. [Google Scholar] [CrossRef]
- Xue, Y.; Mu, J.; Huang, Y.; Shi, Z. Experimental and Simulation Analysis on the Mechanical Behavior of 3D-Enhanced Al-Based Tetrahedral Lattice Materials. Phys. Status Solidi (A) 2023, 220, 2200580. [Google Scholar] [CrossRef]
- Hedayati, R.; Alavi, M.; Sadighi, M. Effect of Degradation of Polylactic Acid (PLA) on Dynamic Mechanical Response of 3D Printed Lattice Structures. Materials 2024, 17, 3674. [Google Scholar] [CrossRef]
- Feng, J.; Liu, B.; Lin, Z.; Fu, J. Isotropic octet-truss lattice structure design and anisotropy control strategies for implant application. Mater. Des. 2021, 203, 109595. [Google Scholar] [CrossRef]
- Goldberg, M. Three infinite families of tetrahedral space-fillers. J. Comb. Theory Ser. A 1974, 16, 348–354. [Google Scholar] [CrossRef][Green Version]
- Moussa, A.; Melancon, D.; El Elmi, A.; Pasini, D. Topology optimization of imperfect lattice materials built with process-induced defects via powder bed fusion. Addit. Manuf. 2021, 37, 101608. [Google Scholar] [CrossRef]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and characterization of a porosity graded lattice structure for additively manufactured biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- Deshpande, V.; Ashby, M.; Fleck, N. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Stiffness and strength of tridimensional periodic lattices. Comput. Methods Appl. Mech. Eng. 2012, 229, 27–43. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725. [Google Scholar] [CrossRef]
- Victrex, A Comprehensive Review of the Materials Properties of VICTREX® PEEK™ High Performance Polymer, in MATERIAL PROPERTIES GUIDE. Available online: https://www.victrex.com (accessed on 20 February 2024).
- Olasz, L.; Gudmundson, P. Viscoelastic model of cross-linked polyethylene including effects of temperature and crystallinity. Mech. Time-Depend. Mater. 2005, 9, 23–44. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cheng, G.-D.; Cai, Y.-W.; Xu, L. Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech. Sin. 2013, 29, 550–556. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]
- Sun, C.-T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]

































 | ||
|---|---|---|
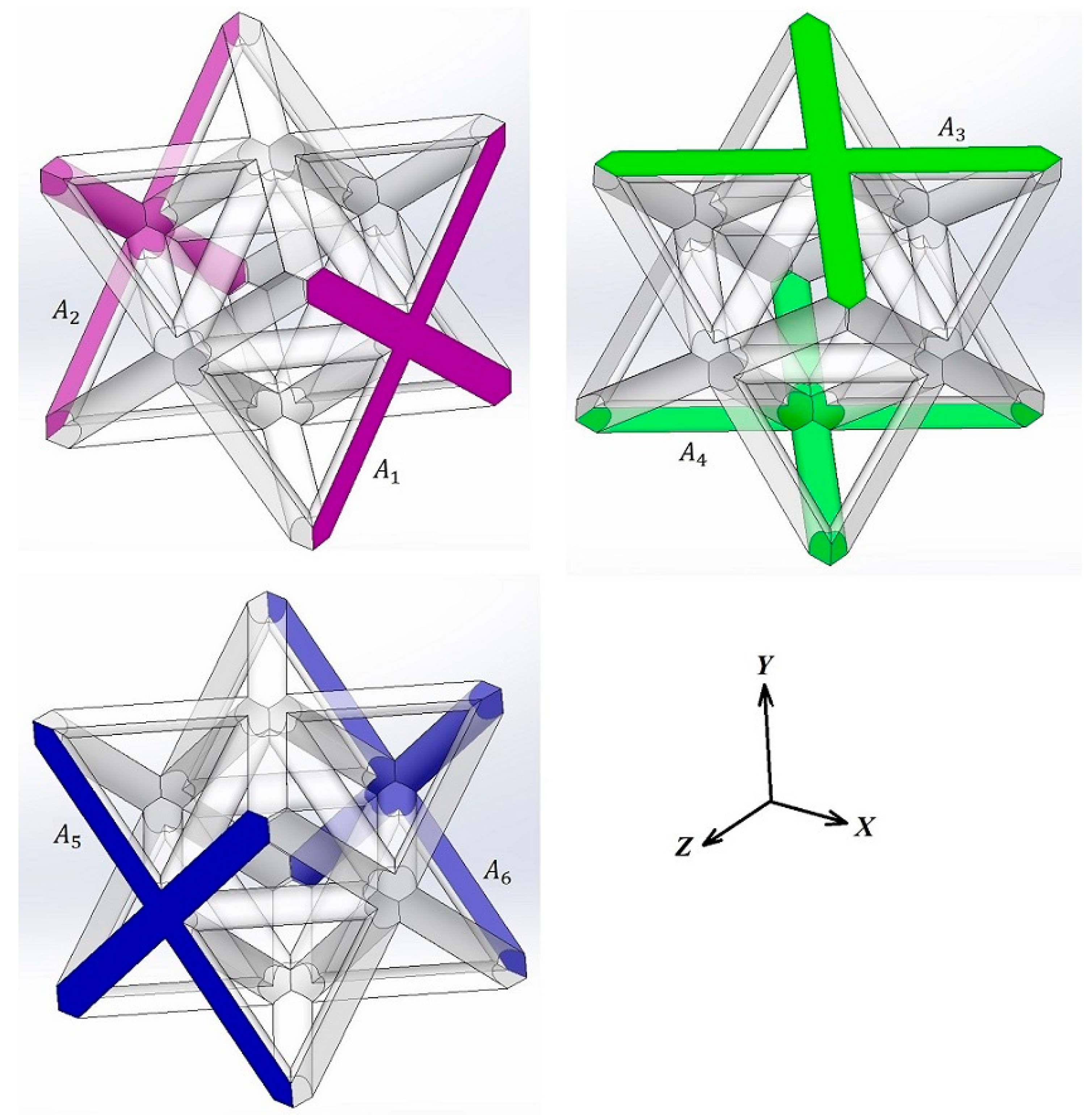
| Side | Relative Length | Angle |
| AB | ||
| AC | ||
| AD | ||
| BC | ||
| BD | ||
| CD | ||
| Long-term |
| Indices | Boundary Condition | Effective Modulus Components |
|---|---|---|
| , | ||
| , | ||
| , |
| AH | FE | Deshpande et al. [67] | AH | FE | Deshpande et al. [67] | ||
|---|---|---|---|---|---|---|---|
| Beginning of loading | 5 | 141.8 | 133.5 | 180.4 | 101.4 | 96.3 | 90.2 |
| 10 | 305 | 283 | 360.8 | 208.5 | 199.1 | 180.4 | |
| 18.5 | 593 | 561.4 | 667.54 | 402.3 | 379.7 | 333.8 | |
| 30 | 1115.8 | 1040.6 | 1082.5 | 701.3 | 667.2 | 541.2 | |
| 50 | 2263.1 | 2075.2 | 1804.2 | 1308.1 | 1224.6 | 902.1 | |
| After a long period | 5 | 120.6 | 122.1 | 165 | 92 | 88.1 | 82.5 |
| 10 | 260.8 | 258.9 | 330 | 190.2 | 182.1 | 165 | |
| 18.5 | 507.9 | 513.4 | 610.5 | 362.2 | 347.3 | 305.25 | |
| 30 | 961.8 | 951.7 | 990 | 646.7 | 610.3 | 495 | |
| 50 | 1971.7 | 1897.5 | 1650 | 1154.7 | 1120.3 | 825 | |
| Beginning of Loading | After a Long Period | |||
|---|---|---|---|---|
| AH | FE | AH | FE | |
| 5 | 0.3489 | 0.3392 | 0.3485 | 0.3389 |
| 10 | 0.3472 | 0.3401 | 0.3467 | 0.3397 |
| 18.5 | 0.3476 | 0.3391 | 0.3469 | 0.3384 |
| 30 | 0.3415 | 0.3362 | 0.3409 | 0.3353 |
| 50 | 0.3408 | 0.3303 | 0.3401 | 0.3288 |
| AH | FE | Deshpande et al. [67] | AH | FE | Deshpande et al. [67] | ||
|---|---|---|---|---|---|---|---|
| Beginning of loading | 5 | 94.1 | 86.7 | 161.3 | 152.1 | 94.1 | 86.7 |
| 10 | 199.1 | 193.2 | 364 | 342.9 | 199.1 | 193.2 | |
| 18.5 | 437.3 | 412.5 | 803.9 | 750.6 | 437.3 | 412.5 | |
| 30 | 868.7 | 795.1 | 1593.2 | 1502.7 | 868.7 | 795.1 | |
| 50 | 1838 | 1655.1 | 3654.5 | 3431.2 | 1838 | 1655.1 | |
| After a long period | 5 | 85.8 | 79.3 | 137 | 139.1 | 85.8 | 79.3 |
| 10 | 181.1 | 176.7 | 312.3 | 313.5 | 181.1 | 176.7 | |
| 18.5 | 393.8 | 377.3 | 691.3 | 686.2 | 393.8 | 377.3 | |
| 30 | 792.8 | 727.4 | 1398.9 | 1373.5 | 792.8 | 727.4 | |
| 50 | 1687.6 | 1515.2 | 3243 | 3134.9 | 1687.6 | 1515.2 | |
| Beginning of Loading | After a Long Period | |||
|---|---|---|---|---|
| AH | FE | AH | FE | |
| 5 | 0.3258 | 0.3207 | 0.3254 | 0.3204 |
| 10 | 0.3251 | 0.3226 | 0.3247 | 0.3222 |
| 18.5 | 0.3249 | 0.3231 | 0.3246 | 0.3225 |
| 30 | 0.3217 | 0.3211 | 0.3208 | 0.32 |
| 50 | 0.3186 | 0.3131 | 0.3161 | 0.3113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hedayati, R.; Shokrnia, M.; Alavi, M.; Sadighi, M.; Aghdam, M.M. Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies. Materials 2024, 17, 5865. https://doi.org/10.3390/ma17235865
Hedayati R, Shokrnia M, Alavi M, Sadighi M, Aghdam MM. Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies. Materials. 2024; 17(23):5865. https://doi.org/10.3390/ma17235865
Chicago/Turabian StyleHedayati, Reza, Mohammad Shokrnia, Melikasadat Alavi, Mojtaba Sadighi, and Mohammad Mohammadi Aghdam. 2024. "Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies" Materials 17, no. 23: 5865. https://doi.org/10.3390/ma17235865
APA StyleHedayati, R., Shokrnia, M., Alavi, M., Sadighi, M., & Aghdam, M. M. (2024). Viscoelastic Behavior of Cellular Biomaterials Based on Octet-Truss and Tetrahedron Topologies. Materials, 17(23), 5865. https://doi.org/10.3390/ma17235865








