Thermal Conversion of Coal Bottom Ash and Its Recovery Potential for High-Value Products Generation: Kinetic and Thermodynamic Analysis with Adiabatic TD24 Predictions
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Chemical and Structural Characterization
2.3. The Radiochemical Characterization
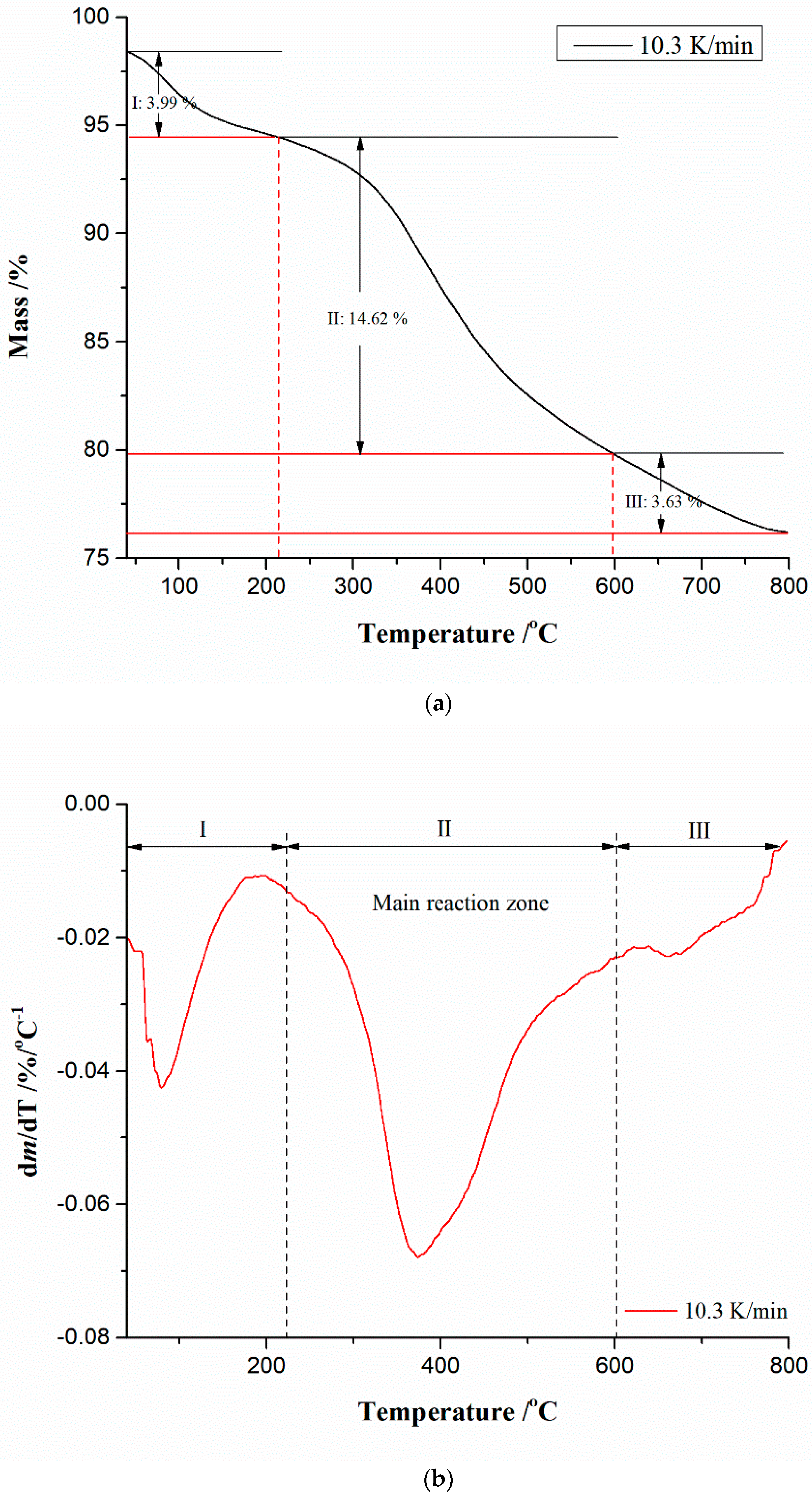
2.4. Thermal Decomposition Analysis Using the Simultaneous Thermogravimetry (TG) and Derivative Thermogravimetry (DTG) Measurements
3. Model-Free and Model-Based Kinetic Analysis with the Process Simulations
4. Results and Discussion
4.1. Chemical Characteristics of CBA-TB
4.2. Results Related to the Radiological Characterization of CBA-TB
4.3. XRD Analysis of CBA-TB
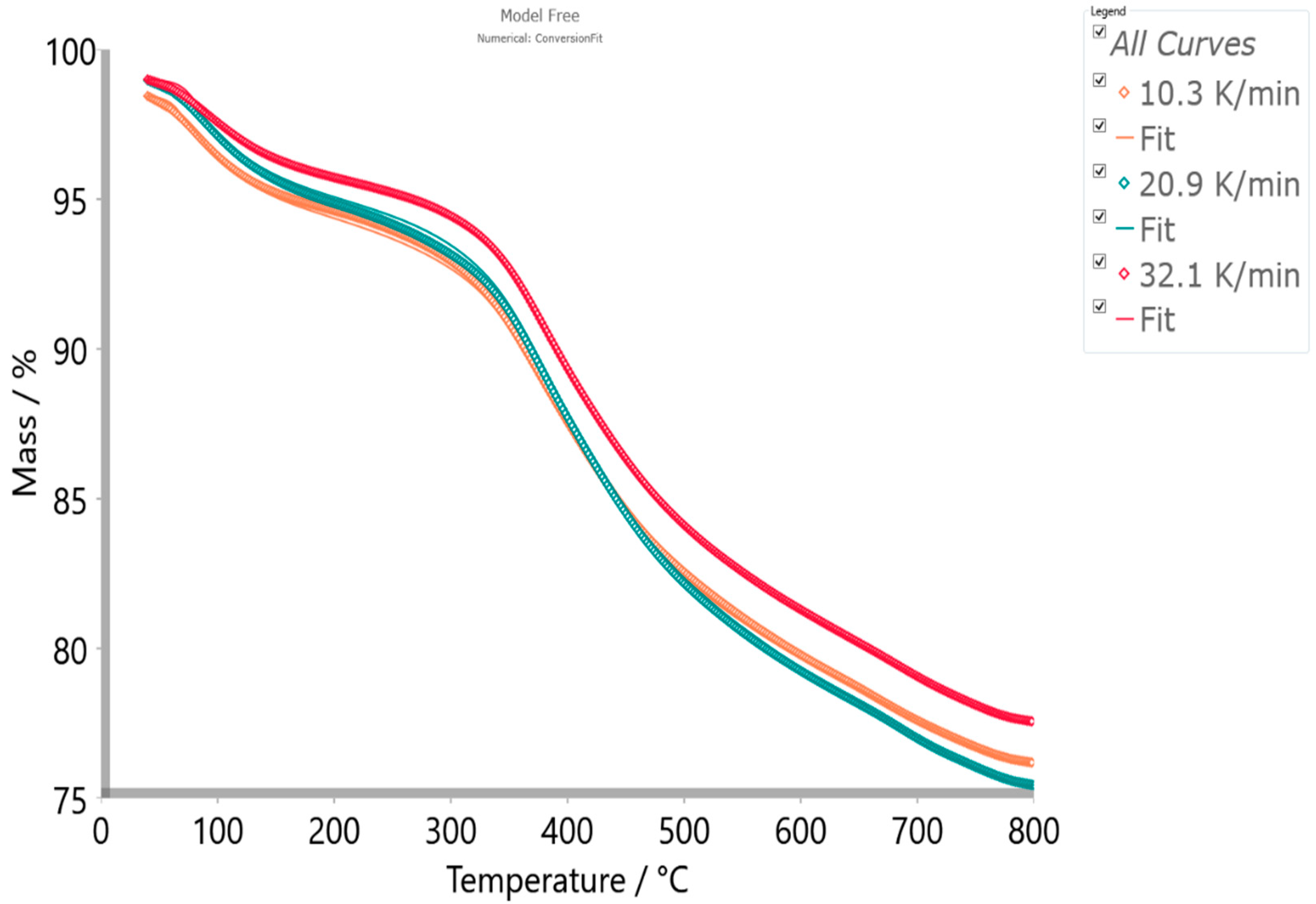
4.4. TG-DTG Analysis of CBA-TB Thermal Conversion Process
4.5. Results of a Detailed Kinetic Analysis of the CBA-TB Thermal Conversion Process
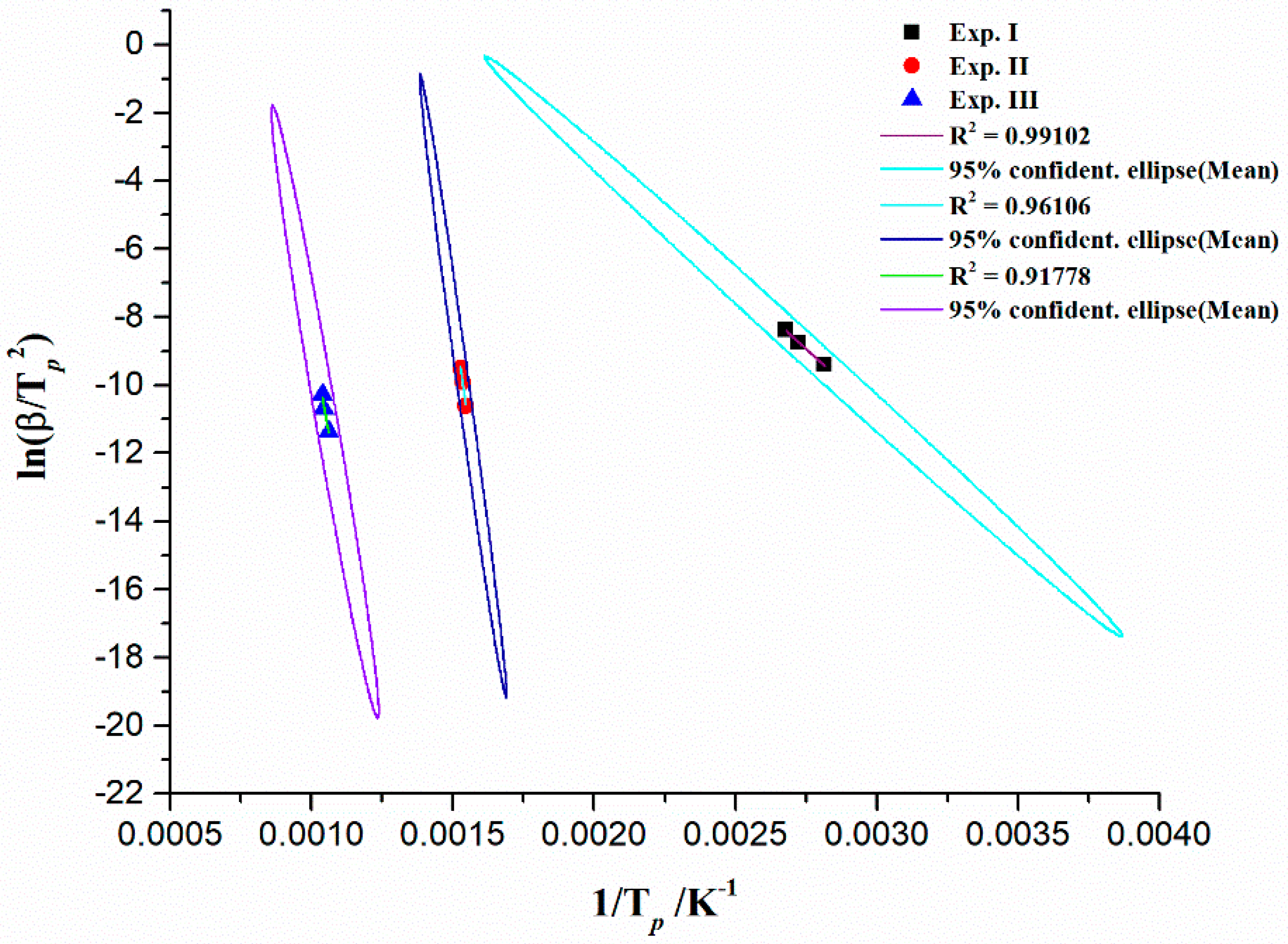
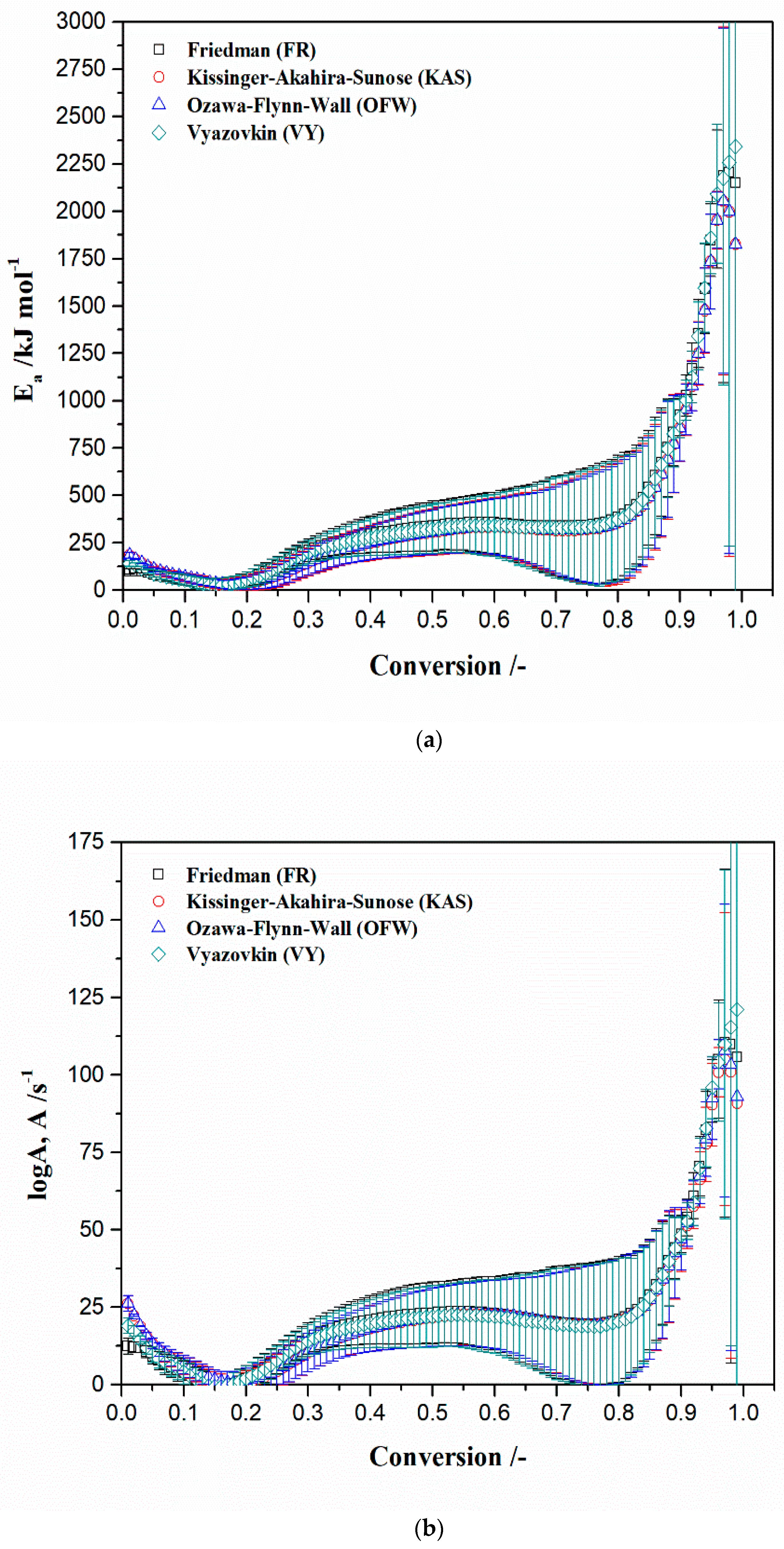
4.5.1. Model-Free Kinetics
Kinetic Compensation Effect (KCE) from Isoconversional (Model-Free) Approach
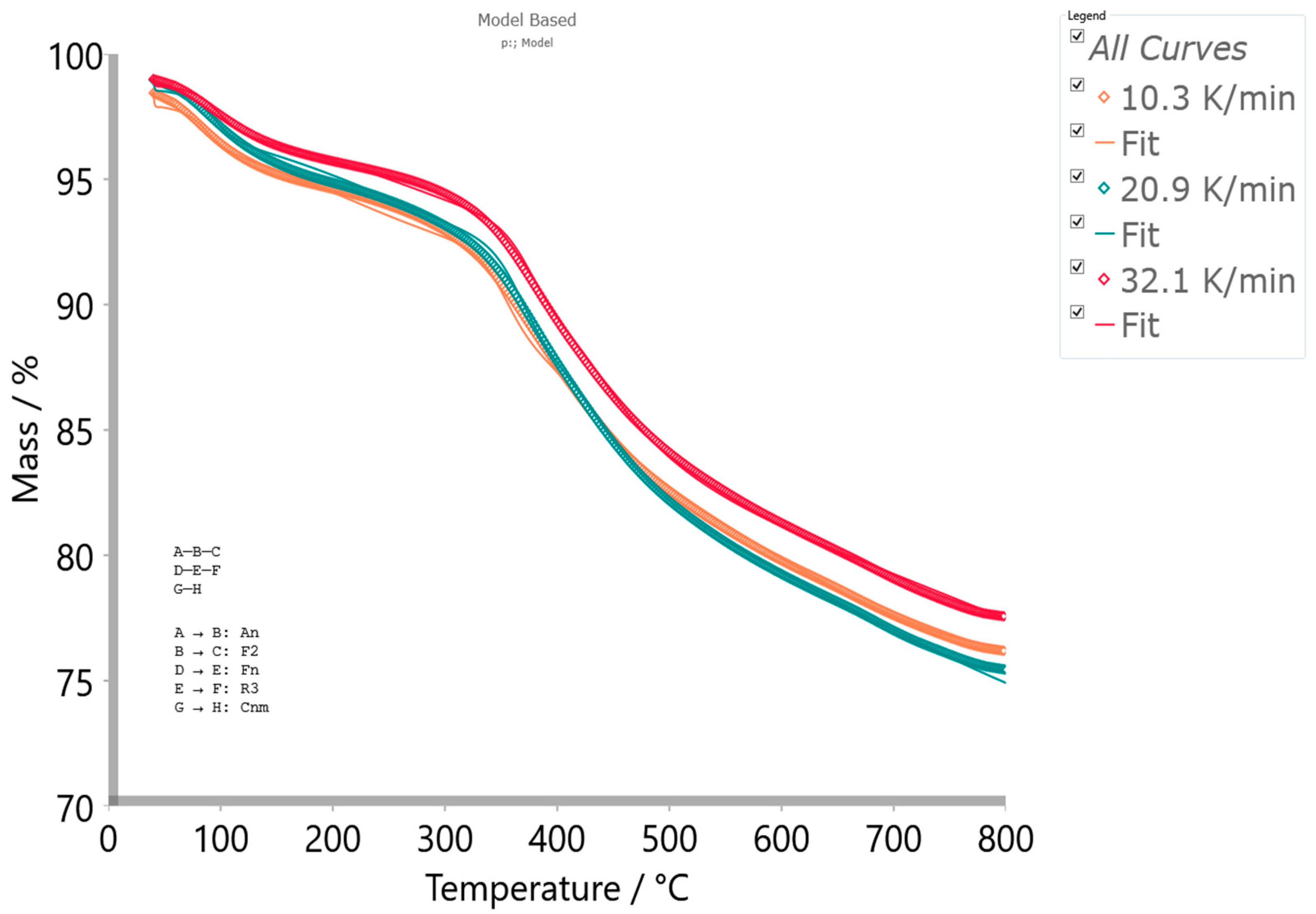
4.5.2. Model-Based Kinetics
- The first step () in the sequential reaction stage (see Equation (5)) which takes place in the temperature range of ΔT = 40–700 °C, is attributed to the reduction reaction of the ferric oxide (hematite) into iron(II, III) oxide (known as black iron oxide–magnetite) with the release of molecular oxygen, and the simultaneous elimination of the physically adsorbed water:Fe2O3(s) → (2/3)Fe3O4(s) + (1/6)O2(g)↑.
- The second step () in the sequential process stage (see Equation (5)) which occurs in the temperature range of ΔT = 200–800 °C can be attributed to Fe3O4-FeO interconversion, strongly assisted by the oxygen emission from previous step (Fe3O4 is the intermediate chemical specie “B”), favors the production of FeO (wüstite) [80]:which represents the final reaction product. This reaction was additionally promoted by the presence of CO liberated from CBA-TB, since that sample has high affinity for the association of present carbon and high oxygen concentrations towards CO generation. So, the second-order (F2) kinetics identified for the current reaction step is related to concentrations of Fe3O4 and CO present within the reaction system, which could be a platform for oxidation-reduction (redox) reaction (where CO is a reducing agent, while Fe3O4 is an oxidizing agent) forming a significant amount of iron(II) oxide, with allocation of CO2 as by-product.
- In addition, the first reaction step () in another sequential stage (see Equation (6)) which takes place in the temperature range of ΔT = 40–200 °C exhibits strong overlapping behavior with previous sequential stage, especially with A → B reaction step, in the lower temperature zone. This step was characterized by anorthite (CaAl2Si2O8) P1–I1 phase transition occurring up to temperature of T = 200 °C [84,85]. Actual designed experimental conditions for thermal decomposition of CBA-TB specimen are sufficient for thermal disordering pathway, whereby I1 phase may occurs at the lower temperatures, whereabouts pressure in the system is a high (in general, P1–I1 phase transition occurs from “low pressure” into “high pressure” system behavior) [86]. This transition is associated with a re-organization of the lattice modes, accompanied with structural changes. These changes indicate on the onset of strong distortion of the aluminosilicate framework of the I1 phase but the duration of this distortion does not go to infinity with further increase of the pressure in a system [87]. It is interesting to note that depending on magnitude of this pressure in the system, the kinetic character of this transition will also depend. It was founded that I1 phase of anorthite is stable at least up to 8.8 GPa but at a higher pressure out of 8.8 GPa, specifically on 10 GPa, the transition is the first-order in its nature [87]. For the actual step, we obtained that the kinetics of the transition goes by n-th order kinetics, with n = 1.975 (Table 9), indicating that a stable anorthite I1 phase has been reached, where no further transformation into a new high-pressure polymorph occurs. Namely, the first-order and n-th-order transition kinetics can be referred to as unstable ‘very high-pressure’ and stable ‘high-pressure’ anorthite I1 phase formation [88], which also affects the value of activation energy (Table 9). The P1–I1 phase transition is strongly influenced by both the composition and the temperature. Therefore, the activation energy for thermal disordering strongly depends on composition and temperature, especially on the ratio of SiO2/CaO present in the studied sample. For our sample, this ratio amounts of SiO2/CaO = 4.92. As this ratio is higher, the higher the E value (Table 9). On the other hand, the weak crystallization tendency of anorthite is guided by the increased SiO2/Al2O3 ratio [89]. For the investigated sample, the indicated ratio amounts to the SiO2/Al2O3 = 2.04. The increase of this ratio above 2.00 causes an increase in an energy barrier for the crystallization. The SiO2/Al2O3 ratio slightly exceeds the above-indicated value of 2.00, which is enough to prevent the trigger for the pure crystallization process.
- The second reaction step () within the sequential stage described by Equation (6) occurs in the temperature range of ΔT = 200–800 °C, and this can be attributed to anorthite I1 phase breakdown reaction. The actual reaction includes an anorthite softening step or nucleation, where the incongruent melting product can be obtained at temperatures above T ~700 °C [90]. The process was governed by thermal dissolution, which starts on the grain with the most soluble surface, most likely as ‘crystallographic’ controlled. The mechanism proceeds through a phase boundary-controlled reaction (R3, contracting volume 3D, with a geometrical factor of n = 2/3). The geometric contraction volume (R3) model is associated with low activation energy (Ea = 30.830 kJ/mol; Table 9) for the migration of tetrahedrally bonded atoms. It is possible that there is a pronounced meta-stability near the phase boundaries, which inhibits the formation of inter-growths. Since the observed kinetics does not take place according to the first-order kinetics but according to deceleratory contracting reaction mechanism (R3), there is a high probability that the transition takes place through retarding a variation of Al-Si order with an increasing temperature. As the final product, CaO·Al2O3·2SiO2 melts with CaO allocation are obtained [91].
- The last one, the single-step reaction () (see Equation (7)), which takes place in the temperature range of ΔT = 300–800 °C is characterized by Cnm model—n-th order and m-power reaction with autocatalysis (Table 9). The current reaction step has autocatalytic nature with an activation energy of 224.651 kJ/mol, with acceleratory portion order of m = 0.170 (the product involvements in reaction acting as the catalyst) and n-th order exponent of n = 6.392 that characterizes consumption of the reactant (Table 9). It is interesting to note that this reaction appears in the decomposition zone, where “shoulder” feature arises (see previous results). This stage can be attributed to the chromium-incorporated SiO2 decomposition, which is more thermally resistant than the CrO3 specie alone. This is probably a consequence of the highly dispersed chromium on the silica surface, resulting in the decomposition of “impregnated” catalyst by the following reaction:Silica/Cr(VI) → Silica/Cr(II) + O2(gaseous)↑.
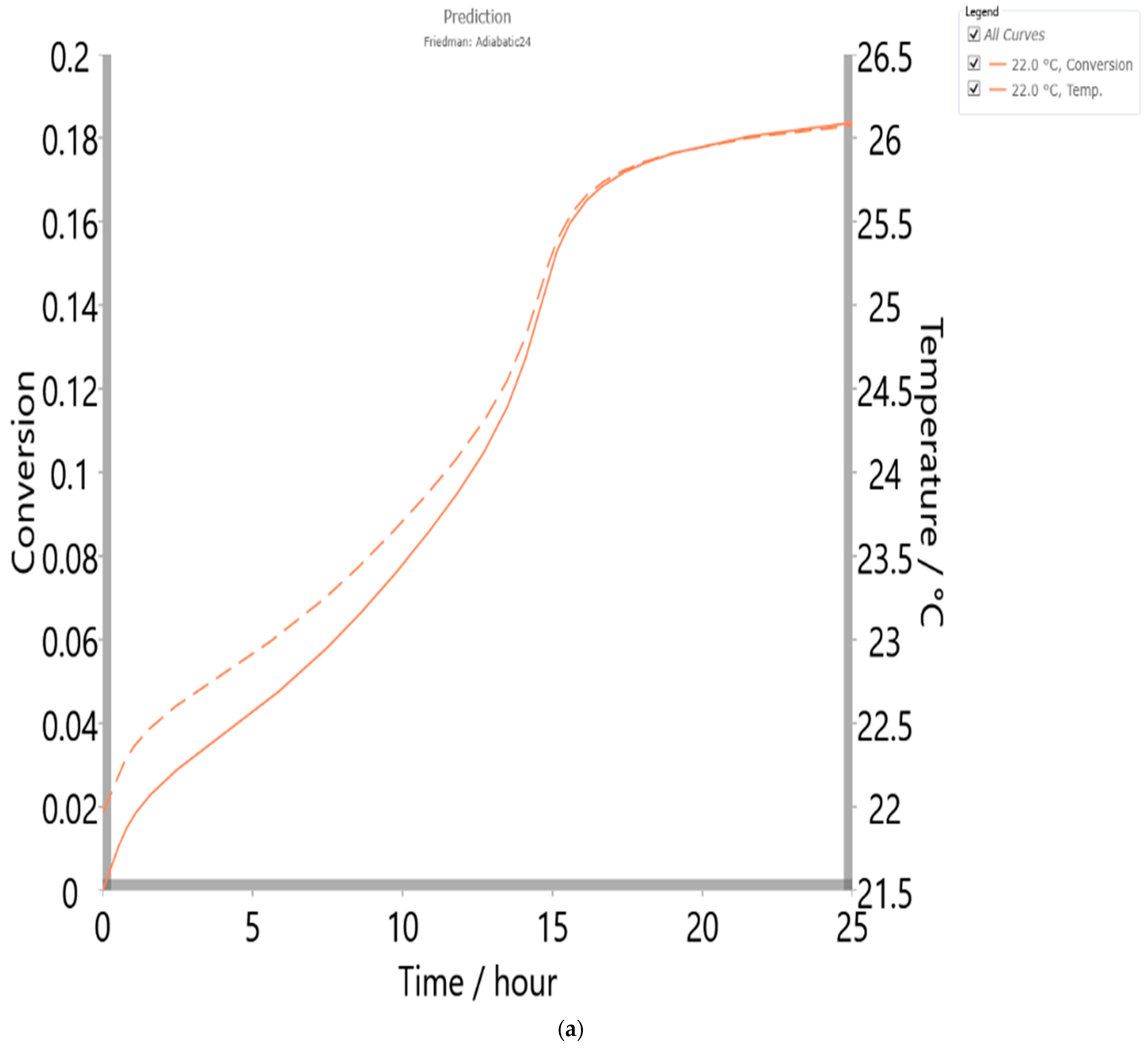
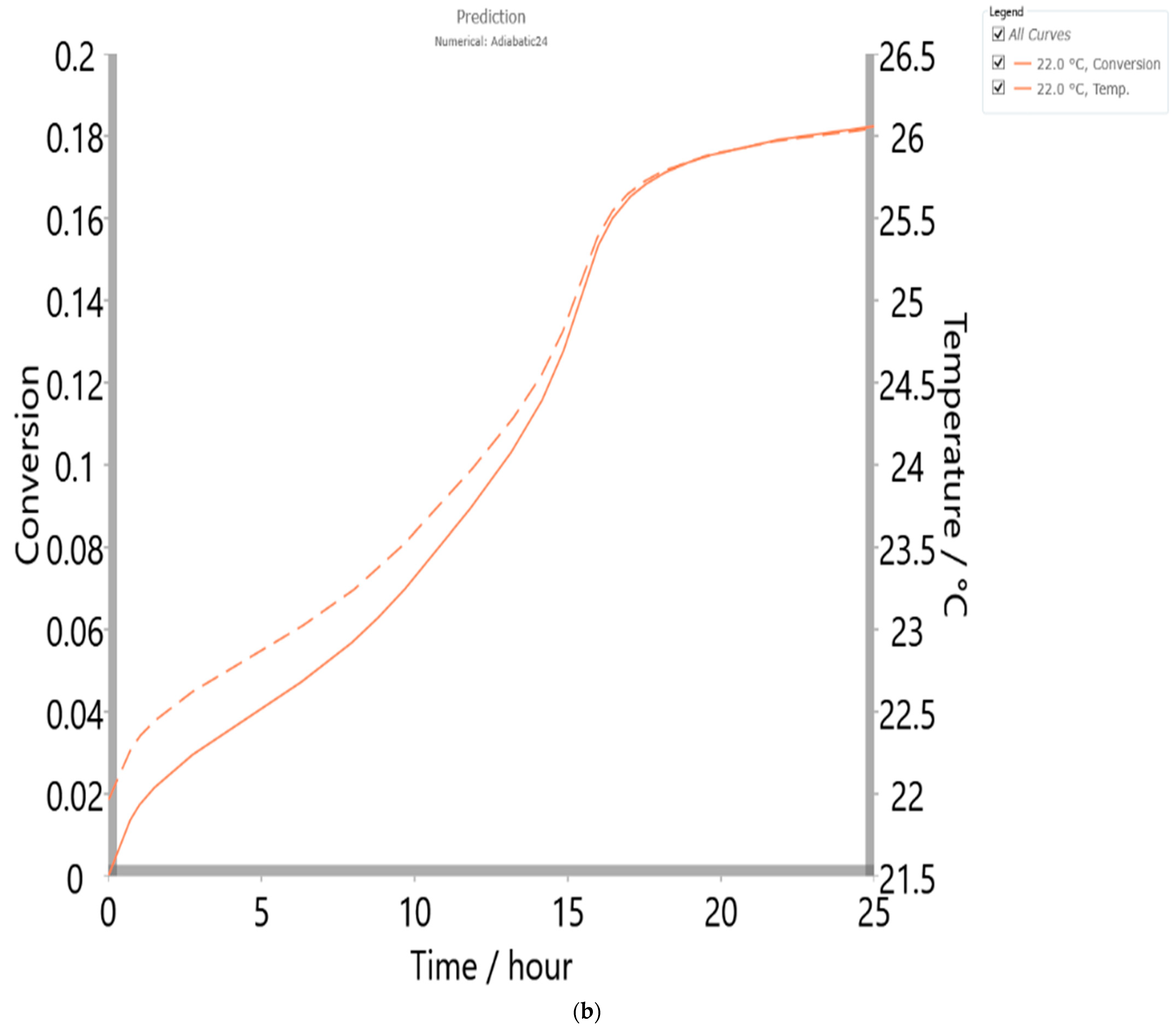
4.6. Thermal Safety Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| IEA | International Energy Agency |
| EU | European Union |
| CCP | Combustion coal products |
| LOI | Loss of ignition |
| TEKO-B | Coal-fired power plant “Kostolac B” |
| MTSR | Maximum temperature of synthesis reaction |
| TMR | The time to the maximum rate |
| CBA | Coal bottom ash |
| CBA-TB | Coal bottom ash collected in coal-fired power plant “Kostolac B” |
| WD-XRF | Wavelength-dispersive equipped X-ray fluorescence |
| ICP-MS | Inductively coupled plasma mass spectrometry |
| HMs | Heavy metals |
| XRD | X-ray diffraction |
| XRPD | X-ray powder diffraction |
| IAEA | International Atomic Energy Agency |
| MARLAP | Multi-Agency Radiological Laboratory Analytical Protocols |
| TG | Thermogravimetry |
| DTG | Derivative thermogravimetry |
| FR | Friedman method |
| KAS | Kissinger-Akahira-Sunose method |
| OFW | Ozawa-Flynn-Wall method |
| VY | Vyazovkin method |
| KCE | Kinetic compensation effect |
| NLLS | The non-linear least square |
| ASTM | American Society for Testing and Materials |
| LEAF | Leaching Environmental Assessment Framework |
| IARC | International Agency for Research on Cancer |
| TA | Thermo-analytical |
| AED | The activation energy distribution |
| ddf | Density distribution function |
| MR | Mean residual |
| IKR | Isokinetic relationship |
| MW | Molecular weight |
| Δmsample | the mass of powdered sample (mg) |
| T | the temperature (°C and/or K) |
| ΔT | the temperature range (interval) (°C) |
| logA | the logarithm of pre-exponential factor (-) |
| A | the pre-exponential factor (s−1) |
| Ea | the activation energy (effective) (kJ mol−1) |
| Δmres | the residual mass of the sample (expressed in%) |
| Tp | the maximum (peak) temperature (°C) |
| Rmax | the maximum reaction rate (%/min) |
| TD24 | initial temperature for an adiabatic process with time to the maximum rate equals to 24 h (°C) |
| ΔH* | changes in the activation enthalpy (kJ mol−1) |
| ΔS* | changes in the activation entropy (J mol−1 K−1) |
| ΔG* | changes in Gibbs free energy of activation (kJ mol−1) |
| Φ(Ea)exp | experimentally obtained density distribution function of activation energies (mol (kJ)−1) |
| Φ(Ea) | theoretically derived density distribution function (LogNormal) of activation energies (mol (kJ)−1) |
| dEa | infinitesimally small change of Ea (kJ mol−1) |
| ΔEa | the final change of Ea, the Ea increment (kJ mol−1) |
| Φo | the onset of the distribution (mol (kJ)−1) |
| A* | the area of the distribution function (kJ mol−1) |
| Ea,c | the central distribution value (median) (kJ mol−1) |
| kiso | the artificial isokinetic rate constant (s−1) |
| Tiso | the artificial isokinetic temperature (°C) |
| a | the KCE constant _ intercept value (s−1) |
| b | the KCE constant _ slope value (mol (kJ)−1) |
| Texp | experimental temperature value (°C) |
| Ea(α) | conversion dependent effective activation energy (kJ mol−1) |
| A(α) | conversion dependent pre-exponential factor (effective) (s−1) |
| [E, A, f(α)] | the kinetic triplet |
| E | the activation energy for the individual reaction step (kJ mol−1) |
| A | the pre-exponential factor for individual reaction step (s−1) |
| n | the reaction order |
| m | the autocatalysis reaction power exponent |
| P | the pressure (GPa) |
| Kcat | the autocatalysis factor |
| T* | the average temperature at maximum reaction rates, throughout all heating rates applied (°C and/or K) |
| dT/dt | the self-heat rate (K/s and/or K/min) |
| Greek Letters | |
| α | the conversion (the extent of reaction) (-) |
| β | the heating rate (K/min) |
| γ | the skewness |
| θ | the Bragg angle (°) |
| λ | the wavelength of Cu Ka radiation (Å) |
| φ | the gas flow rate (mL/min) |
| σ | the standard deviation (kJ mol−1) |
| ϕ | the thermal inertia factor (-) |
References
- IEA, International Energy Agency. Coal 2022—Analysis and Forecast to 2025. 2022, pp. 5–107. Available online: www.iea.org (accessed on 15 February 2022).
- Holechek, J.L.; Geli, H.M.E.; Sawalhah, M.N.; Valdez, R. A Global assessment: Can renewable energy replace fossil fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Pavlychenko, A.; Shustov, O.; Bielov, O.; Adamchuk, A.; Kozhantov, A. Integrated use of lignite resources to provide fuel for the energy sector of Ukraine in the war and post-war periods. Ind. Technol. Syst. Technol. Syst. Power Sup. 2023, 1, 32–39. [Google Scholar] [CrossRef]
- Janicka, J.; Debiagi, P.; Scholtissek, A.; Dreizler, A.; Epple, B.; Pawellek, R.; Maltsev, A.; Hasse, C. The potential of retrofitting existing coal power plants: A case study for operation with green iron. Appl. Energy 2023, 339, 120950. [Google Scholar] [CrossRef]
- Aydın, S.; Baradan, B. Effect of pumice and fly ash incorporation on high temperature resistance of cement based mortars. Cem. Concr. Res. 2007, 37, 988–995. [Google Scholar] [CrossRef]
- Kayali, O.; Ahmed, M.S. Assessment of high volume replacement fly ash concrete—Concept of performance index. Constr. Build. Mater. 2013, 39, 71–76. [Google Scholar] [CrossRef]
- Kolker, A.; Scott, C.; Hower, J.C.; Vazquez, J.A.; Lopano, C.L. Distribution of rare earth elements in coal combustion fly ash, determined by SHRIMP-RG ion microprobe. Int. J. Coal Geol. 2017, 184, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Zhuang, X.; Querol, X.; Font, O.; Moreno, N. A review on the applications of coal combustion products in China. Int. Geol. Rev. 2017, 60, 1–46. [Google Scholar] [CrossRef]
- Bheel, N.; Khoso, S.; Baloch, M.H.; Benjeddou, O.; Alwetaishi, M. Use of waste recycling coal bottom ash and sugarcane bagasse ash as cement and sand replacement material to produce sustainable concrete. Environ. Sci. Pollut. Res. 2022, 29, 52399–52411. [Google Scholar] [CrossRef]
- Embong, R.; Kusbiantoro, A.; Muthusamy, K.; Ismail, N. Recycling of coal bottom ash (CBA) as cement and aggregate replacement material: A review. In Proceedings of the 4th National Conference on Wind & Earthquake Engineering, Putrajaya, Malaysia, 16–17 October 2020; IOP Publishing: Bristol, UK, 2021; Volume 682, p. 012035. [Google Scholar] [CrossRef]
- Hollanda, L.R.; Bezerra de Souza, J.A.; Foletto, E.L.; Dotto, G.L.; Chiavone-Filho, O. Applying bottom ash as an alternative Fenton catalyst for effective removal of phenol from aqueous environment. Environ. Sci. Pollut. Res. 2023, 30, 120763–120774. [Google Scholar] [CrossRef]
- Saha, D.; Roychowdhury, T. Characterisation of coal and its combustion ash: Recognition of environmental impact and remediation. Environ. Sci. Pollut. Res. 2023, 30, 37310–37320. [Google Scholar] [CrossRef]
- Argiz, C.; Moragues, A.; Menéndez, E. Use of ground coal bottom ash as cement constituent in concretes exposed to chloride environments. J. Clean. Prod. 2018, 170, 25–33. [Google Scholar] [CrossRef]
- Rafieizonooz, M.; Mirza, J.; Salim, M.R.; Hussin, M.W.; Khankhaje, E. Investigation of coal bottom ash and fly ash in concrete as replacement for sand and cement. Constr. Build. Mater. 2016, 116, 15–24. [Google Scholar] [CrossRef]
- Singh, M.; Siddique, R. Compressive strength, drying shrinkage and chemical resistance of concrete incorporating coal bottom ash as partial or total replacement of sand. Constr. Build. Mater. 2014, 68, 39–48. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Shin, S. An evaluation of the physical and chemical stability of dry bottom ash as a concrete light weight aggregate. Materials 2021, 14, 5291. [Google Scholar] [CrossRef] [PubMed]
- Abbas, S.; Arshad, U.; Abbass, W.; Nehdi, M.L.; Ahmed, A. Recycling untreated coal bottom ash with added value for mitigating alkali-silica reaction in concrete: A sustainable approach. Sustainability 2020, 12, 10631. [Google Scholar] [CrossRef]
- MARLAP. Multi-Agency Radiological Laboratory Analytical Protocols Manual; MARLAP: Boston, MA, USA, 2004; Volume II, 12-1–12-44.
- IAEA, International Atomic Energy Agency. Measurement of Radionuclides in Food and The Environment. A Guidebook; Technical Reports Series No. 295; IAEA: Vienna, Austria, 1989. [Google Scholar]
- Friedman, H.L. Kinetic of thermal degradation of char-forming plastics from thermogravometry. Application to a phenolic plastic. J. Polym. Sci. Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Rep. Res. Chiba Inst. Technol. (Sci. Technol.) 1971, 16, 22–31. [Google Scholar]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. General treatment of the thermogravimetry of polymers. J. Res. Natl. Bur. Stand. A Phys. Chem. 1966, 70A, 487–523. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Dollimore, D. Linear and nonlinear procedures in isoconversional computations of the activation energy of nonisothermal reactions in solids. J. Chem. Inf. Comput. Sci. 1996, 36, 42–45. [Google Scholar] [CrossRef]
- Vyazovkin, S. Model-free kinetics—Staying free of multiplying entities without necessity. J. Therm. Anal. Calorim. 2006, 83, 45–51. [Google Scholar] [CrossRef]
- Doyle, C. Series approximations to the equation of thermogravimetric data. Nature 1965, 207, 290–291. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Linert, W. The application of isoconversional methods for analyzing isokinetic relationships occurring at thermal decomposition of solids. J. Solid State Chem. 1995, 114, 392–398. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J.P. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Pérez-Maqueda, L.; Criado, J. The accuracy of Senum and Yang’s approximations to the Arrhenius integral. J. Therm. Anal. Calorim. 2000, 60, 909–915. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Moukhina, E. Initial kinetic parameters for the model-based kinetic method. High Temp. High Press. 2013, 42, 287–302. [Google Scholar]
- NETZSCH Kinetics Neo Software, Version 2.6.0.1. 2022. Available online: https://kinetics.netzsch.com/en (accessed on 19 March 2023).
- Frank-Kamenetskii, D.A. Diffusion and Heat Transfer in Chemical Kinetics; Plenum Press: New York, NY, USA; London, UK, 1969. [Google Scholar]
- Dien, J.M.; Fierz, H.; Stoessel, F.; Killé, G. The thermal risk of autocatalytic decompositions: A kinetic study. Chimia 1994, 48, 542–550. [Google Scholar] [CrossRef]
- Pastré, J.; Wörsdörfer, U.; Keller, A.; Hungerbühler, K. Comparison of different methods for estimating TMRad from dynamic DSC measurements with ADT 24 values obtained from adiabatic Dewar experiments. J. Loss Prev. Process Ind. 2000, 13, 7–17. [Google Scholar] [CrossRef]
- Ticmanis, U.; Pantel, G.; Wilker, S.; Kaiser, M. Precision required for parameters in thermal safety simulations. In Proceedings of the 32nd International Annual Conference of ICT, Karlsruhe, Germany, 3–6 July 2001; p. 135. [Google Scholar]
- Folly, P. Thermal stability of explosives. Chimia 2004, 58, 394–400. [Google Scholar] [CrossRef]
- Roduit, B. Advanced Kinetics-Based Simulation Method for Determination of the Thermal Aging, Thermal Runaway TMRad and SADT Using DSC. Analysis Report (Example) The AKTS AG Advanced Kinetics and Technology Solutions. pp. 22–29. Available online: https://www.akts.com (accessed on 11 June 2008).
- Kossoy, A.; Misharev, P.; Belochvostov, V. Peculiarities of Calorimetric Data Processing for Kinetics Evaluation in Reaction Hazard Assessment. In Proceedings of the 53rd Annual Calorimetry Conference, Midland, MI, USA, 9–14 August 1998; pp. 1–9. [Google Scholar]
- Fisher, H.G.; Forrest, H.S.; Grossel, S.S.; Huff, J.E.; Muller, A.R.; Noronha, J.A.; Shaw, D.A.; Tilley, B.J. Emergency Relief System Design Using DIERS Technology: The Design Institute for Emergency Relief Systems (DIERS) Project Manual, 1st ed.; Wiley-AIChE: Hoboken, NJ, USA, 1993; pp. 1–576. ISBN 978-0-816-90568-3. [Google Scholar] [CrossRef]
- Huff, J.E. Emergency venting requirements. Plant/Operat. Prog. 1982, 1, 211–229. [Google Scholar] [CrossRef]
- Argiz, C.; Menéndez, E.; Sanjuán, M.A. Effect of mixes made of coal bottom ash and fly ash on the mechanical strength and porosity of Portland cement. Mater. Construcc. 2013, 63, 49–64. [Google Scholar] [CrossRef]
- Menéndez, E.; Argiz, C.; Recino, H.; Ángel Sanjuán, M. Characterization of mortars made with coal ashes identified as a way forward to mitigate climate change. Crystals 2022, 12, 557. [Google Scholar] [CrossRef]
- Menéndez, E.; Argiz, C.; Ángel Sanjuán, M. Chloride induced reinforcement corrosion in mortars containing coal bottom ash and coal fly ash. Materials 2019, 12, 1933. [Google Scholar] [CrossRef]
- Kim, H.K.; Lee, H.K. Coal bottom ash in field of civil engineering: A review of advanced applications and environmental considerations. KSCE J. Civil Eng. 2015, 19, 1802–1818. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Tian, C.; Li, H.; Shao, X.; Zheng, C. Mineralogy and chemical composition of high-calcium fly ashes and density fractions from a coal-fired power plant in China. Energy Fuels 2010, 24, 834–843. [Google Scholar] [CrossRef]
- Strzałkowska, E. Morphology, chemical and mineralogical composition of magnetic fraction of coal fly ash. Int. J. Coal Geol. 2021, 240, 103746. [Google Scholar] [CrossRef]
- Ma, X.; He, T.; Da, Y.; Xu, Y.; Wan, Z. Physical properties, chemical composition, and toxicity leaching of incineration fly ash by multistage water washing. Environ. Sci. Poll. Res. 2023, 30, 80978–80987. [Google Scholar] [CrossRef]
- Sadon, S.N.; Beddu, S.; Naganathan, S.; Kamal, N.L.M.; Hassan, H. Coal bottom ash as sustainable material in concrete—A review. Ind. J. Sci. Technol. 2017, 10, 1–10. [Google Scholar] [CrossRef]
- Arickx, S.; De Borger, V.; Van Gerven, T.; Vandecasteele, C. Effect of carbonation on the leaching of organic carbon and of copper from MSWI bottom ash. Waste Manag. 2010, 30, 1296–1302. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Tao, R.; Tan, H.; Zhou, A.; Deng, S.; Wang, X.; Zhang, Q. Migration characteristics and ecological risk assessment of heavy metals in ash from sewage sludge co-combustion in coal-fired power plants. Fuel 2023, 333, 126420. [Google Scholar] [CrossRef]
- Santos, R.M.; Mertens, G.; Salman, M.; Cizer, Ö.; Van Gerven, T. Comparative study of ageing, heat treatment and accelerated carbonation for stabilization of municipal solid waste incineration bottom ash in view of reducing regulated heavy metal/metalloid leaching. J. Environ. Manag. 2013, 128C, 807–821. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Shehnazdeep; Bhardwaj, A. Reviewing the role of coal bottom ash as an alternative of cement. Constr. Build. Mater. 2020, 233, 117276. [Google Scholar] [CrossRef]
- Argiz, C.; Menéndez, E.; Moragues, A.; Ángel Sanjuán, M. Recent advances in coal bottom ash use as a new common Portland cement constituent. Struct. Eng. Int. 2014, 24, 503–508. [Google Scholar] [CrossRef]
- LEAF, Leaching Environmental Assessment Framework. 2018. Available online: www.vanderbilt.edu/leaching/leaf/ (accessed on 30 November 2018).
- Saha, D.; Chatterjee, D.; Chakravarty, S.; Mazumder, M. Trace element geochemistry and mineralogy of coal from Samaleswari open cast coal block (S-OCB), Eastern India. Phys. Chem. Earth Parts A/B/C 2018, 104, 47–57. [Google Scholar] [CrossRef]
- IARC, International Agency for Research on Cancer. Agents Classified by the IARC Monographs. 2023, Volumes 1–117. Available online: http://monographs.iarc.fr/ENG/Classification/ClassificationsAlphaOrder.pdf (accessed on 4 March 2024).
- Huggins, F.E.; Senior, C.L.; Chu, P.; Ladwig, K.; Huffman, G.P. Selenium and arsenic speciation in fly ash from full-scale coal-burning utility plants. Environ. Sci. Technol. 2007, 41, 3284–3289. [Google Scholar] [CrossRef]
- Ángel Sanjuán, M.; Quintana, B.; Argiz, C. Coal bottom ash natural radioactivity in building materials. J. Radioanal. Nucl. Chem. 2019, 319, 91–99. [Google Scholar] [CrossRef]
- Boukhair, A.; Belahbib, L.; Azkour, K.; Nebdi, H.; Benjelloun, M.; Nourreddine, A. Measurement of natural radioactivity and Radon exhalation rate in coal ash samples from a thermal power plant. World J. Nucl. Sci. Technol. 2016, 6, 153–160. [Google Scholar] [CrossRef]
- Caridi, F.; Spoto, S.E.; Mottese, A.F.; Paladini, G.; Crupi, V.; Belvedere, A.; Marguccio, S.; D’Agostino, M.; Faggio, G.; Grillo, R.; et al. Multivariate statistics, mineralogy, and radiological hazards assessment due to the natural radioactivity content in pyroclastic products from Mt. Etna, Sicily, Southern Italy. Int. J. Environ. Res. Public Health 2022, 19, 11040. [Google Scholar] [CrossRef]
- Ángel Sanjuán, M.; Suarez-Navarro, J.A.; Argiz, C.; Estévez, E. Radiation dose calculation of fine and coarse coal fly ash used for building purposes. J. Radioanal. Nucl. Chem. 2021, 327, 1045–1054. [Google Scholar] [CrossRef]
- Pöykiö, R.; Manskinen, K.; Nurmesniemi, H.; Dahl, O. Comparison of trace elements in bottom ash and fly ash from a large-sized (77 MW) multi-fuel boiler at the power plant of a fluting board mill, Finland. Energy Expl. Exploit. 2011, 29, 217–234. [Google Scholar] [CrossRef]
- Wongsa, A.; Zaetang, Y.; Sata, V.; Chindaprasirt, P. Properties of lightweight fly ash geopolymer concrete containing bottom ash as aggregates. Constr. Build. Mater. 2016, 111, 637–643. [Google Scholar] [CrossRef]
- Klima, K.M.; Schollbach, K.; Brouwers, H.J.H.; Yu, Q. Thermal and fire resistance of Class F fly Ash based geopolymers—A review. Constr. Build. Mater. 2022, 323, 126529. [Google Scholar] [CrossRef]
- ASTM E2890-12; Standard Test Method for Kinetic Parameters for Thermally Unstable Materials by Differential Scanning Calorimetry Using the Kissinger Method. ASTM International: West Conshohocken, PA, USA, 2012.
- Lei, J.; Ye, X.; Wang, H.; Zhao, D. Insights into pyrolysis kinetics, thermodynamics, and the reaction mechanism of wheat straw for its resource utilization. Sustainability 2023, 15, 12536. [Google Scholar] [CrossRef]
- Choudhary, J.; Alawa, B.; Chakma, S. Insight into the kinetics and thermodynamic analyses of co-pyrolysis using advanced isoconversional method and thermogravimetric analysis: A multi-model study of optimization for enhanced fuel properties. Process Saf. Environ. Prot. 2023, 173, 507–528. [Google Scholar] [CrossRef]
- Patil, Y.; Ku, X.; Vasudev, V. Pyrolysis characteristics and determination of kinetic and thermodynamic parameters of raw and torrefied Chinese fir. ACS Omega 2023, 8, 34938–34947. [Google Scholar] [CrossRef]
- Singh, S.; Patil, T.; Tekade, S.P.; Gawande, M.B.; Sawarkar, A.N. Studies on individual pyrolysis and co-pyrolysis of corn cob and polyethylene: Thermal degradation behavior, possible synergism, kinetics, and thermodynamic analysis. Sci. Total Environ. 2021, 783, 147004. [Google Scholar] [CrossRef]
- Raj, S. Significance of Activation Energy in Process Metallurgy. Master’s Thesis, Master in Technology in Metallurgical and Material Engineering. National Institute of Technology, Rourkela, India, 2013; pp. 39–43. [Google Scholar]
- De Filippis, P.; De Caprariis, B.; Scarsella, M.; Verdone, N. Double distribution activation energy model as suitable tool in explaining biomass and coal pyrolysis behavior. Energies 2015, 8, 1730–1744. [Google Scholar] [CrossRef]
- Groppo, E.; Lamberti, C.; Bordiga, S.; Spoto, G.; Zecchina, A. The structure of active centers and the ethylene polymerization mechanism on the Cr/SiO2 catalyst: A frontier for the characterization methods. Chem. Rev. 2005, 105, 115–184. [Google Scholar] [CrossRef]
- Zapata, P.M.C.; Nazzarro, M.S.; Parentis, M.L.; Gonzo, E.E.; Bonini, N.A. Effect of hydrothermal treatment on Cr-SiO2 mesoporous materials. Chem. Eng. Sci. 2013, 101, 374–381. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Kinetic modelling of waste wood devolatilization during pyrolysis based on thermogravimetric data and solar pyrolysis reactor performance. Fuel 2020, 261, 116459. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Bian, H. A combined kinetic analysis for thermal characteristics and reaction mechanism based on non-isothermal experiments: The case of poly(vinyl alcohol) pyrolysis. Therm. Sci. Eng. Prog. 2023, 39, 101692. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Chen, Z.; Zeilstra, C.; Van Der Stel, J.; Sietsma, J.; Yang, Y. Reduction mechanism of fine hematite ore particles in suspension. Metall. Mater. Transac. B 2021, 52, 2239–2252. [Google Scholar] [CrossRef]
- Yan, Z.; FitzGerald, S.; Crawford, T.M.; Mefford, O.T. Oxidation of wüstite rich iron oxide nanoparticles via post-synthesis annealing. J. Magn. Mag. Mater. 2021, 539, 168405. [Google Scholar] [CrossRef]
- Jozwiak, W.K.; Kaczmarek, E.; Maniecki, T.P.; Ignaczak, W.; Maniukiewicz, W. Reduction behavior of iron oxides in hydrogen and carbon monoxide atmospheres. Appl. Catal. A Gen. 2007, 326, 17–27. [Google Scholar] [CrossRef]
- Bagatini, M.C.; Zymla, V.; Osório, E.; Vilela, A.C.F. Carbon gasification in self-reducing mixtures. ISIJ Int. 2014, 54, 2687–2696. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, H.; Chen, S.; Jiang, B. A microwave-assisted Boudouard reaction: A highly effective reduction of the greenhouse gas CO2 to useful CO feedstock with semi-coke. Molecules 2021, 26, 1507. [Google Scholar] [CrossRef]
- Van Tendeloo, G.; Ghose, S.; Amelinckx, S. A dynamical model for the P1—I1 phase transition in anorthite, CaAl2Si2O8. I. Evidence from electron microscopy. Phys. Chem. Miner. 1989, 16, 311–319. [Google Scholar] [CrossRef]
- Gorelova, L.A.; Vereshchagin, O.S.; Bocharov, V.N.; Krivovichev, S.V.; Zolotarev, A.A.; Rassomakhin, M.A. CaAl2Si2O8 polymorphs: Sensitive geothermometers and geospeedometers. Geosci. Front. 2023, 14, 101458. [Google Scholar] [CrossRef]
- Németh, P.; Tribaudino, M.; Bruno, E.; Buseck, P.R. TEM investigation of Ca-rich plagioclase: Structural fluctuations related to the I1-P1 phase transition. Am. Mineral. 2007, 92, 1080–1086. [Google Scholar] [CrossRef]
- Daniel, I.; Gillet, P.; McMillan, P.F.; Wolf, G.; Verhelst, M.A. High-pressure behavior of anorthite: Compression and amorphization. J. Geophys. Res. Solid Earth 1997, 102, 10313–10325. [Google Scholar] [CrossRef]
- Pakhomova, A.; Simonova, D.; Koemets, I.; Koemets, E.; Aprilis, G.; Bykov, M.; Gorelova, L.; Fedotenko, T.; Prakapenka, V.; Dubrovinsky, L. Polymorphism of feldspars above 10 GPa. Nat. Commun. 2020, 11, 2721. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Bai, J.; Vassilev, S.V.; Kong, L.; Li, H.; Bai, Z.; Li, W. The crystallization behavior of anorthite in coal ash slag under gasification condition. Chem. Eng. J. 2022, 445, 136683. [Google Scholar] [CrossRef]
- Pina, C.M.; Jordan, G. Reactivity of Mineral Surfaces at Nano-scale: Kinetics and Mechanisms of Growth and Dissolution. In Nanoscopic Approaches in Earth and Planetary Sciences, 1st ed.; Brenker, F.E., Jordan, G., Eds.; Geo Science World: McLean, VA, USA, 2010; Chapter 7; Volume 8, pp. 239–323. ISBN 9780903056489. [Google Scholar] [CrossRef]
- Lin, S.-M.; Yu, Y.-L.; Zhong, M.-F.; Yang, H.; Liu, Y.; Li, H.; Zhang, C.-Y.; Zhang, Z.-J. Preparation of anorthite/mullite in situ and phase transformation in porcelain. Materials 2023, 16, 1616. [Google Scholar] [CrossRef]
- McDaniel, M.P.; Johnson, M.M. A comparison of CrSiO2 and CrAlPO4 polymerization catalysts: I. Kinetics. J. Catal. 1986, 101, 446–457. [Google Scholar] [CrossRef]
- Jóźwiak, W.K.; Lana, I.G.D. Interactions between the chromium oxide phase and support surface; redispersion of α-chromia on silica, alumina and magnesia. J. Chem. Soc. Faraday Transac. 1997, 93, 2583–2589. [Google Scholar] [CrossRef]
- Park, H.D.; Comito, R.J.; Wu, Z.; Zhang, G.; Ricke, N.; Sun, C.; Van Voorhis, T.; Miller, J.T.; Román-Leshkov, Y.; Dincă, M. Gas-phase ethylene polymerization by single-site Cr centers in a metal-organic framework. ACS Catal. 2020, 10, 3864–3870. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, C.; Zhang, M.; Fang, K. Design of ZSM-5 encapsulating FeMnK nanocatalysts for light olefins synthesis with enhanced carbon utilization efficiency. Fuel 2023, 335, 126745. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, X.; Meng, F.; Chen, L.; Guo, Z.; Chen, W. Model identification and classification of autocatalytic decomposition kinetics. J. Therm. Anal. Calorim. 2023, 148, 5455–5470. [Google Scholar] [CrossRef]
- Roduit, B.; Borgeat, C.; Berger, B.; Folly, P.; Alonso, B.; Aebischer, J.N. The prediction of thermal stability of self-reactive chemicals—From milligrams to tons. J. Therm. Anal. Calorim. 2005, 80, 91–102. [Google Scholar] [CrossRef]
- Wu, X.-J.; Zhu, Y.; Chen, L.-P.; Chen, W.-H.; Guo, Z.-C. Effect of reaction type on TMRad, TD24 and other data obtained by adiabatic calorimetry. J. Therm. Anal. Calorim. 2022, 147, 5883–5896. [Google Scholar] [CrossRef]






| Content of Basic Component (%) | Heavy Metals (mg·kg−1) | ||
|---|---|---|---|
| SiO2 | 46.84 (52.2) a, (52.2) b, (52.4) c, (48.2) d | Pb | 10.6 |
| Al2O3 | 22.99 (27.5) a, (27.5) b, (27.5) c, (25.55) d | Cd | 0.0 |
| TiO2 | 1.08 (1.53) a, (0.97) c, (1.5) d | Zn | 13.4 |
| Fe2O3 | 9.40 (6.0) a, (6.0) b, (6.6) c, (5.86) d | Cu | 40.9 |
| CaO | 9.51 (5.9) a, (5.9) b, (2.4) c, (7.07) d | Ni | 79.5 |
| MgO | 4.37 (1.7) a, (1.7) b, (1.83) c, (1.28) d | Cr | 802.5 |
| SO3 | 1.83 (0.13) a, (0.13) b, (0) c, (0.15) d | Hg | 0.0 |
| Na2O | 0.29 (0.36) c | As | 62.8 |
| K2O | 1.00 (0.57) a, (0.57) b, (3.48) c | Ba | 69.0 |
| P2O5 | 0.10 (0.74) a, (0.74) b, (0.12) c, (0.96) d | Sb | 0.6 |
| Loss to fire * * Determined at 1000 °C | 2.59 (1.8) a, (3.8) c, (1.85) d | Se | 0.2 |
| Radionuclide | 226Ra | 232Th | 40K | 235U | 238U | 137Cs | Gross Alpha Activity | Gross Beta Activity |
|---|---|---|---|---|---|---|---|---|
| CBA-TB | 34 ± 2 (65.96) a, (84) b | 20 ± 2 (96.5) a, (79) b | 103 ± 10 (974) a, (168) b | 0.8 ± 0.1 | 18 ± 4 | <0.1 | <154 | <308 |
| β (K min−1) | Rmax (%/min) | Tp (°C) | ||||
|---|---|---|---|---|---|---|
| I | II | III | I | II | III | |
| 10.3 | 1.935 | 3.186 | 0.996 | 82 | 374 | 670 |
| 20.9 | 3.573 | 6.905 | 2.065 | 94 | 378 | 686 |
| 32.1 | 4.424 | 11.473 | 3.277 | 100 | 382 | 690 |
| Method/ASTM E2890 | Region | ||
|---|---|---|---|
| Kinetic Parameters | I | II | III |
| Ea (kJ·mol−1) | 62.66 ± 0.51 | 490.28 ± 8.31 | 385.44 ± 9.60 |
| A (s−1) | 1.67 × 107 | 9.48 × 1037 | 1.95 × 1019 |
| Thermodynamic Parameters | Heating Rate, β (K min−1) | Region | ||
|---|---|---|---|---|
| I | II | III | ||
| ΔH* (kJ·mol−1) | 10.3 | 59.71 | 484.90 | 377.60 |
| 20.9 | 59.61 | 484.87 | 377.47 | |
| 32.1 | 59.56 | 484.83 | 377.43 | |
| Average | 59.63 | 484.87 | 377.50 | |
| ΔG* (kJ·mol−1) | 10.3 | 101.05 | 182.45 | 277.17 |
| 20.9 | 102.45 | 180.58 | 275.46 | |
| 32.1 | 103.15 | 178.71 | 275.04 | |
| Average | 102.22 | 180.58 | 275.89 | |
| ΔS* (J·mol−1·K−1) | 10.3 | −116.41 | 467.35 | 106.49 |
| 20.9 | −116.68 | 467.30 | 106.35 | |
| 32.1 | −116.82 | 467.25 | 106.31 | |
| Average | −116.64 | 467.30 | 106.38 | |
| LogNormal ddf Parameters | |
|---|---|
| Φo × 10−4 (mol (kJ)−1) | 2.009 ± 0.004 |
| A* (kJ mol−1) | 2.302 ± 0.326 |
| Ea,c (kJ mol−1) | 337.23 ± 3.61 |
| σ (kJ mol−1) | 0.052 ± 0.012 |
| Method/Model | Fit to | R2 | Sum of Dev. Squares | Mean Residual (MR) | F-Test |
|---|---|---|---|---|---|
| Friedman | TG-signal | 0.99983 | 22.591 | 0.109 | 1.028 |
| Numerical | TG-signal | 0.99983 | 21.976 | 0.101 | 1.000 |
| Ozawa–Flynn–Wall | TG-signal | 0.98598 | 1811.935 | 1.147 | 82.450 |
| Kissinger–Akahira–Sunose | TG-signal | 0.98968 | 1337.008 | 0.940 | 60.839 |
| Vyazovkin | TG-signal | 0.99977 | 29.300 | 0.120 | 1.333 |
| KCE-Branch | Δα | a (s−1) | b (mol·(kJ)−1) | kiso (s−1) | Tiso (°C) |
|---|---|---|---|---|---|
| Region I | 0.01–0.14 | −5.09443 ± 0.15241 | 0.17048 ± 0.00212 | 8.04581 × 10−6 | 432.38 |
| Region II | 0.15–0.54 | −1.88189 ± 0.2233 | 0.07626 ± 9.06241 × 10−4 | 0.01313 | 1304.07 |
| Transition * | 0.55–0.73 | −43.07192 ± 3.87238 | 0.18758 ± 0.0112 | 8.47383 × 10−44 | 368.06 |
| Region III | 0.74–0.99 | 2.65488 ± 0.29398 | 0.04922 ± 2.58568 × 10−4 | 4.51731 × 102 | 2170.55 |
| p:, Model | |
|---|---|
| Model Scheme: A─B─C D─E─F G─H | |
| Step: A → B | |
| Reaction Type: An | |
| Concentration equation a: d(a→b)/dt = A·n·a·[−ln(a)][(n − 1)/n]·exp[−Ea/(RT)] | |
| Activation energy (Ea) (kJ·mol−1) | 24.842 |
| Log(PreExp), logA, A (s−1) | 0.011 |
| Dimension, n | 0.652 |
| Contribution | 0.215 |
| Step: B → C | |
| Reaction Type: F2 | |
| Concentration equation b: d(b→c)/dt = A·b2·exp[−Ea/(RT)] | |
| Activation energy (Ea) (kJ·mol−1) | 217.334 |
| Log(PreExp), logA, A (s−1) | 16.209 |
| Contribution | 0.181 |
| Step: D → E | |
| Reaction Type: Fn | |
| Concentration equation a: d(d→e)/dt = A·dn·exp[−Ea/(RT)] | |
| Activation energy (Ea) (kJ·mol−1) | 107.084 |
| Log(PreExp), logA, A (s−1) | 13.734 |
| React. Order, n | 1.975 |
| Contribution | 0.064 |
| Step: E → F | |
| Reaction Type: R3 | |
| Concentration equation b: d(e→f)/dt = A·3(e(2/3))·exp[−Ea/(RT)] | |
| Activation energy (Ea) (kJ·mol−1) | 30.830 |
| Log(PreExp), logA, A (s−1) | −1.712 |
| Contribution | 0.304 |
| Step: G → H | |
| Reaction Type: Cnm | |
| Concentration equation a,b: d(g→h)/dt = A·gn·[1 + AutocatPreExp·hm]·Exp[−Ea/(RT)] | |
| Activation energy (Ea) (kJ·mol−1) | 224.651 |
| Log(PreExp), logA, A (s−1) | 6.086 |
| React. Order, n | 6.392 |
| Log(AutocatPreExp) | 8.701 |
| Autocat. Power, m | 0.170 |
| Contribution | 0.236 |
| Method/Model | Friedman/Numerical/p:, |
|---|---|
| Enthalpy (ΔH) (J·g−1) | 112.00 |
| Specific heat (J·g−1·K−1) | 5.00 |
| Phi (ϕ) (dimensionless) | 1.00 |
| TMR adiabatic (h) | 24.00 |
| Temp. initial (°C) | 21.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janković, B.; Janković, M.; Mraković, A.; Krneta Nikolić, J.; Rajačić, M.; Vukanac, I.; Sarap, N.; Manić, N. Thermal Conversion of Coal Bottom Ash and Its Recovery Potential for High-Value Products Generation: Kinetic and Thermodynamic Analysis with Adiabatic TD24 Predictions. Materials 2024, 17, 5759. https://doi.org/10.3390/ma17235759
Janković B, Janković M, Mraković A, Krneta Nikolić J, Rajačić M, Vukanac I, Sarap N, Manić N. Thermal Conversion of Coal Bottom Ash and Its Recovery Potential for High-Value Products Generation: Kinetic and Thermodynamic Analysis with Adiabatic TD24 Predictions. Materials. 2024; 17(23):5759. https://doi.org/10.3390/ma17235759
Chicago/Turabian StyleJanković, Bojan, Marija Janković, Ana Mraković, Jelena Krneta Nikolić, Milica Rajačić, Ivana Vukanac, Nataša Sarap, and Nebojša Manić. 2024. "Thermal Conversion of Coal Bottom Ash and Its Recovery Potential for High-Value Products Generation: Kinetic and Thermodynamic Analysis with Adiabatic TD24 Predictions" Materials 17, no. 23: 5759. https://doi.org/10.3390/ma17235759
APA StyleJanković, B., Janković, M., Mraković, A., Krneta Nikolić, J., Rajačić, M., Vukanac, I., Sarap, N., & Manić, N. (2024). Thermal Conversion of Coal Bottom Ash and Its Recovery Potential for High-Value Products Generation: Kinetic and Thermodynamic Analysis with Adiabatic TD24 Predictions. Materials, 17(23), 5759. https://doi.org/10.3390/ma17235759







