A Modification of the Ostergren Model for Thermomechanical Fatigue Life Prediction of Die-Casting Die Steel
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Li, S.; Ren, Y.; Hou, X.; Yang, H.; Zhang, S. Thermo-mechanical fatigue behavior and microstructure evolution of 4Cr5Mo3V hot work die steel. Int. J. Fatigue 2024, 183, 108263. [Google Scholar] [CrossRef]
- Riccardo, G.; Rivolta, B.; Gorla, C.; Concli, F. Cyclic behavior and fatigue resistance of AISI H11 and AISI H13 tool steels. Eng. Fail. Anal. 2021, 121, 105096. [Google Scholar] [CrossRef]
- Liu, M.; Sang, B.; Hao, C.; Chen, G.; Yan, J. Thermal fatigue life prediction method for die casting mold steel based on the cooling cycle. J. Mater. Process. Technol. 2023, 321, 118131. [Google Scholar] [CrossRef]
- Schlayer, M.; Warwas, M.; Seifert, T. A temperature-dependent viscoplasticity model for the hot work steel X38CrMoV5-3, including thermal and cyclic softening under thermomechanical fatigue loading. Materials 2023, 16, 994. [Google Scholar] [CrossRef] [PubMed]
- Hawryluk, M.; Lachowicz, M.; Łukaszek-Sołek, A.; Lisiecki, Ł.; Ficak, G.; Cygan, P. Structural features of fatigue crack propagation of a forging die made of chromium–molybdenum–vanadium tool steel on its durability. Materials 2023, 16, 4223. [Google Scholar] [CrossRef] [PubMed]
- Mackey, B.T.; Sangid, M.D. Phasing effects on thermo-mechanical fatigue damage investigated via crystal plasticity modeling. Mater. Sci. Eng. A 2024, 903, 146642. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, B.; Hu, D.; Jiang, K.; Mao, J.; Jing, F. A critical-plane-based thermomechanical fatigue lifetime prediction model and its application in nickel-based single-crystal turbine blades. Mater. High Temp. 2019, 36, 325–334. [Google Scholar] [CrossRef]
- Szmytka, F.; Oudin, A. A reliability analysis method in thermomechanical fatigue design. Int. J. Fatigue 2013, 53, 82–91. [Google Scholar] [CrossRef]
- Fang, J.R.; Jiang, Q.C.; Guan, Q.F. The characteristics of fatigue under isothermal and thermo-mechanical load in Cr-Ni-Mo cast hot work die steel. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 481–488. [Google Scholar] [CrossRef]
- Jiang, B.; Li, X.C.; Zuo, P.P.; Wu, X.C. Study on isothermal fatigue life prediction model of a new type hot stamping die steel 4Cr2Mo2V. Eng. Fail. Anal. 2022, 136, 106211. [Google Scholar]
- Ghalehbandi, S.M.; Biglari, F. Predicting damage and failure under thermomechanical fatigue in hot forging tools. Eng. Fail. Anal. 2020, 113, 104545. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.; Fan, Z.; Dong, J. Thermomechanical Fatigue Mechanical Behavior and Life Prediction of Coke Drum with Cr-Mo Steel. J. Mater. Eng. Perform. 2023, 32, 7611–7621. [Google Scholar] [CrossRef]
- Liu, K.; Wang, S.; Pan, L.; Chen, X.-G. Thermo-mechanical fatigue behavior and resultant microstructure evolution in Al-Si 319 and 356 cast alloys. Materials 2023, 16, 829. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Lee, J.M.; Kim, Y.; Koo, J.M.; Seok, C.S.; Kim, Y.J. Thermo mechanical fatigue life prediction of Ni-based superalloy IN738LC. Int. J. Precis. Eng. Manuf. 2017, 18, 561–566. [Google Scholar] [CrossRef]
- Yun, H.S.; Jaeyeong, P.; Koo, J.S.; Nahm, S.H. Deformation behavior and crack mechanism of a first generation single-crystal Ni-based superalloys under thermomechanical fatigue loading. Eng. Fract. Mech. 2024, 296, 109820. [Google Scholar]
- Liu, R.; Zhang, Z.J.; Zhang, P.; Zhang, Z.F. Extremely-low-cycle fatigue behaviors of Cu and Cu-Al alloys: Damage mechanisms and life prediction. Acta Mater. 2015, 83, 341–356. [Google Scholar] [CrossRef]
- Shao, C.W.; Zhang, P.; Liu, R.; Zhang, Z.J.; Pang, J.C.; Zhang, Z.F. Low-cycle and extremely-low-cycle fatigue behaviors of high-Mn austenitic TRIP/TWIP alloys: Property evaluation, damage mechanisms and life prediction. Acta Mater. 2016, 103, 781–795. [Google Scholar] [CrossRef]
- Zuo, P.P.; Wu, X.C.; Zeng, Y.; He, X.J. In-phase and out-of-phase thermomechanical fatigue behavior of 4Cr5MoSiV1 hot work die steel cycling from 400 °C to 700 °C. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 159–169. [Google Scholar] [CrossRef]
- ASTM E2368-24; Standard Practice for Strain Controlled Thermomechanical Fatigue Testing. ASTM International: West Conshohocken, PA, USA, 2024.
- Pan, X.M.; Li, X.; Chang, L.; Zhang, G.D.; Xue, F.; Zhao, Y.F.; Zhou, C.Y. Thermal-mechanical fatigue behavior and lifetime prediction of P92 steel with different phase angles. Int. J. Fatigue 2018, 109, 126–136. [Google Scholar] [CrossRef]
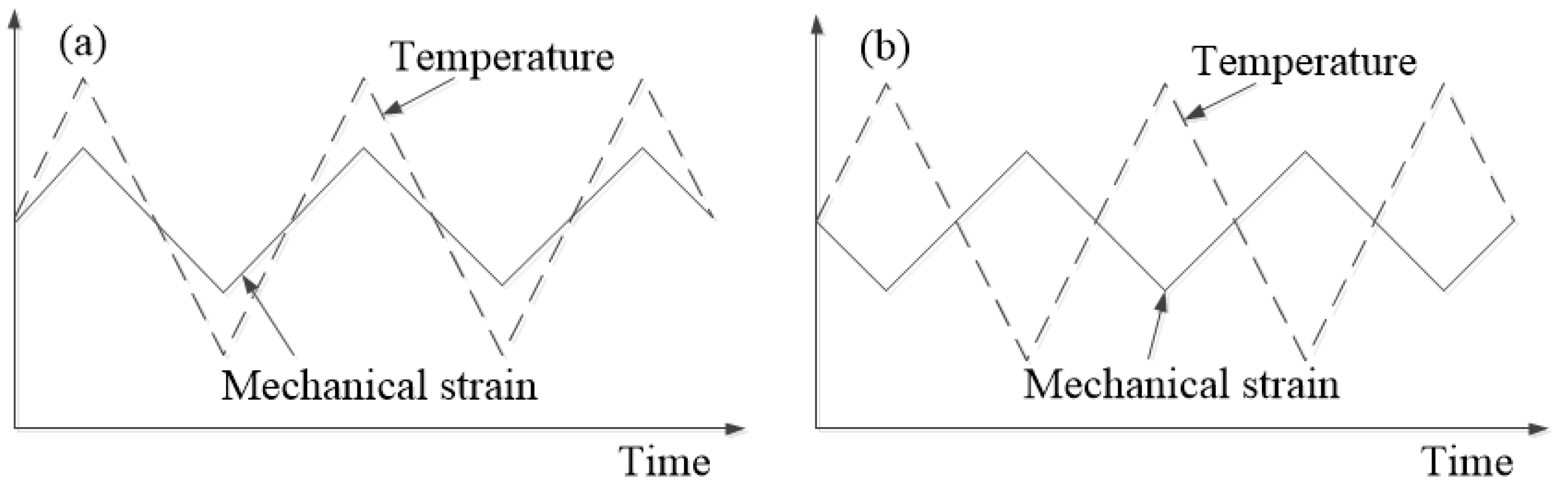
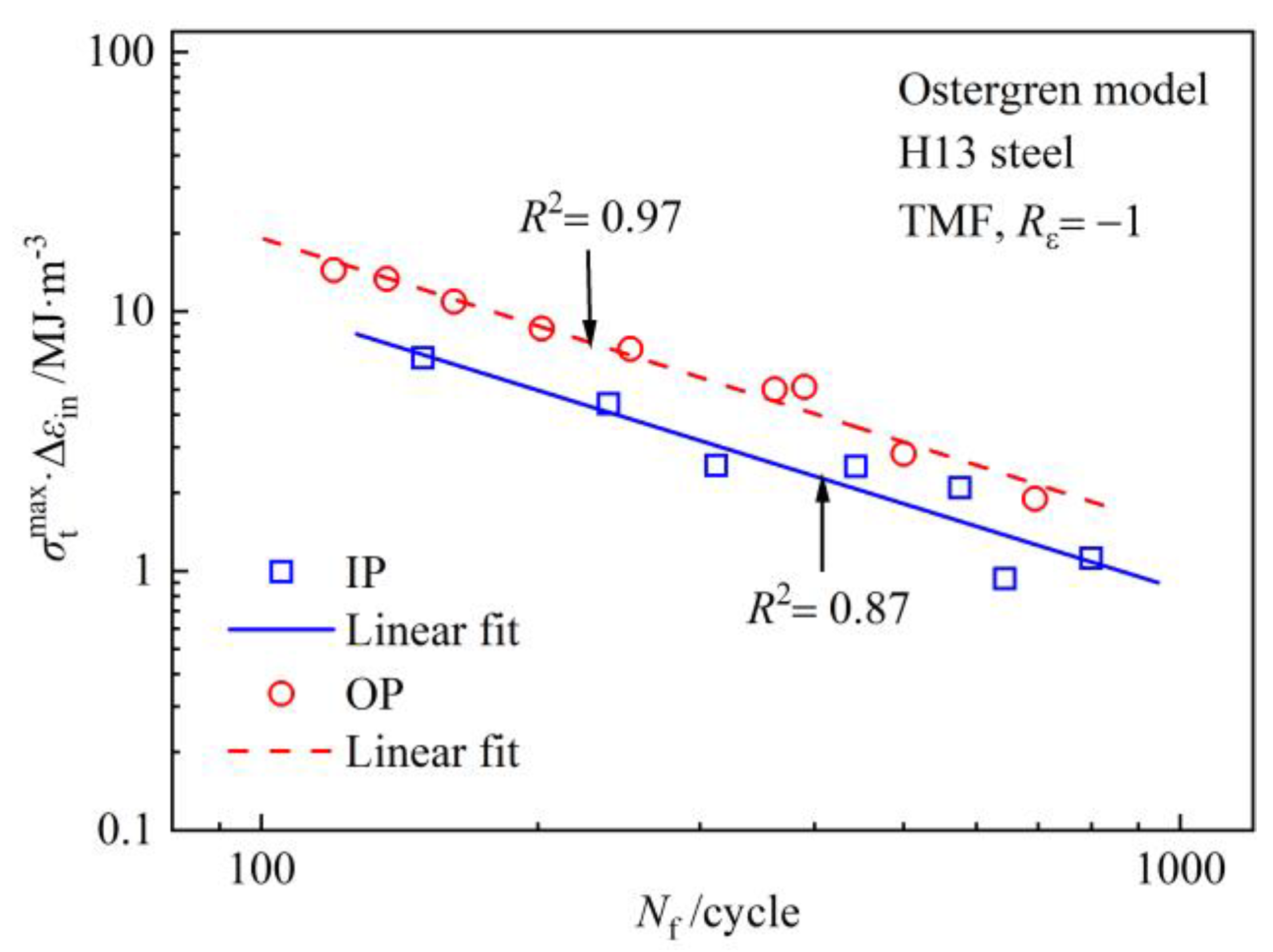


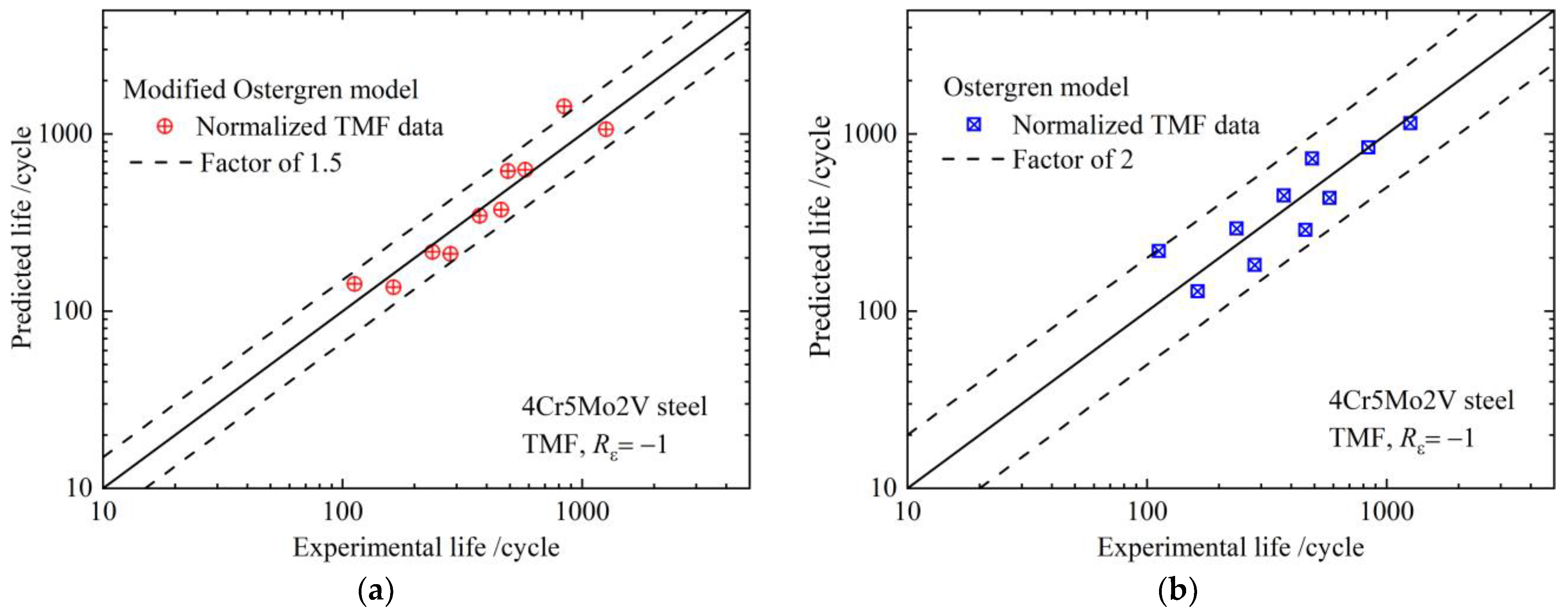
| Loading Type | /% | /MPa | /MPa | /% | |
|---|---|---|---|---|---|
| IP | 0.5 | 800 | 171.9 | 626.9 | 0.65 |
| 0.7 | 576 | 214.6 | 733.7 | 0.97 | |
| 0.9 | 444 | 211.9 | 758.0 | 1.19 | |
| OP | 0.5 | 500 | 462.2 | 627.2 | 0.61 |
| 0.7 | 390 | 526.4 | 762.2 | 0.97 | |
| 0.9 | 252 | 531.1 | 804.5 | 1.35 | |
| 1.1 | 162 | 663.3 | 1016.3 | 1.64 | |
| 1.3 | 120 | 720.5 | 1125.8 | 2.00 |
| Loading Type | /% | /MPa | /MPa | /% | |
|---|---|---|---|---|---|
| IP | 0.5 | 645 | 423.8 | 1400.2 | 0.22 |
| 0.7 | 313 | 478.7 | 1539.9 | 0.53 | |
| 0.9 | 239 | 523.2 | 1609.4 | 0.84 | |
| 1.1 | 150 | 606.3 | 1775.6 | 1.09 | |
| OP | 0.5 | 695 | 948.4 | 1393.0 | 0.20 |
| 0.7 | 362 | 982.1 | 1525.7 | 0.51 | |
| 0.9 | 202 | 1144.6 | 1784.7 | 0.75 | |
| 1.1 | 137 | 1128.7 | 1791.1 | 1.18 |
| Loading Type | /% | /MPa | /MPa | /% | |
|---|---|---|---|---|---|
| IP | 0.5 | 1258 | 473.6 | 1454.9 | 0.17 |
| 0.6 | 490 | 534.1 | 1611.5 | 0.27 | |
| 0.7 | 373 | 519.3 | 1560.4 | 0.51 | |
| 0.9 | 237 | 651.3 | 1852.8 | 0.70 | |
| 1.1 | 112 | 609.3 | 1851.5 | 1.08 | |
| OP | 0.5 | 841 | 999.7 | 1511.4 | 0.12 |
| 0.6 | 579 | 1099.9 | 1712.1 | 0.25 | |
| 0.7 | 459 | 1012.6 | 1592.0 | 0.46 | |
| 0.9 | 282 | 1151.2 | 1851.4 | 0.72 | |
| 1.1 | 163 | 1171.2 | 1919.9 | 1.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, P.; He, X.; Ji, J.; Wu, X. A Modification of the Ostergren Model for Thermomechanical Fatigue Life Prediction of Die-Casting Die Steel. Materials 2024, 17, 5744. https://doi.org/10.3390/ma17235744
Zuo P, He X, Ji J, Wu X. A Modification of the Ostergren Model for Thermomechanical Fatigue Life Prediction of Die-Casting Die Steel. Materials. 2024; 17(23):5744. https://doi.org/10.3390/ma17235744
Chicago/Turabian StyleZuo, Pengpeng, Xijuan He, Jie Ji, and Xiaochun Wu. 2024. "A Modification of the Ostergren Model for Thermomechanical Fatigue Life Prediction of Die-Casting Die Steel" Materials 17, no. 23: 5744. https://doi.org/10.3390/ma17235744
APA StyleZuo, P., He, X., Ji, J., & Wu, X. (2024). A Modification of the Ostergren Model for Thermomechanical Fatigue Life Prediction of Die-Casting Die Steel. Materials, 17(23), 5744. https://doi.org/10.3390/ma17235744







