Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive
Abstract
1. Introduction
2. Materials and Methods
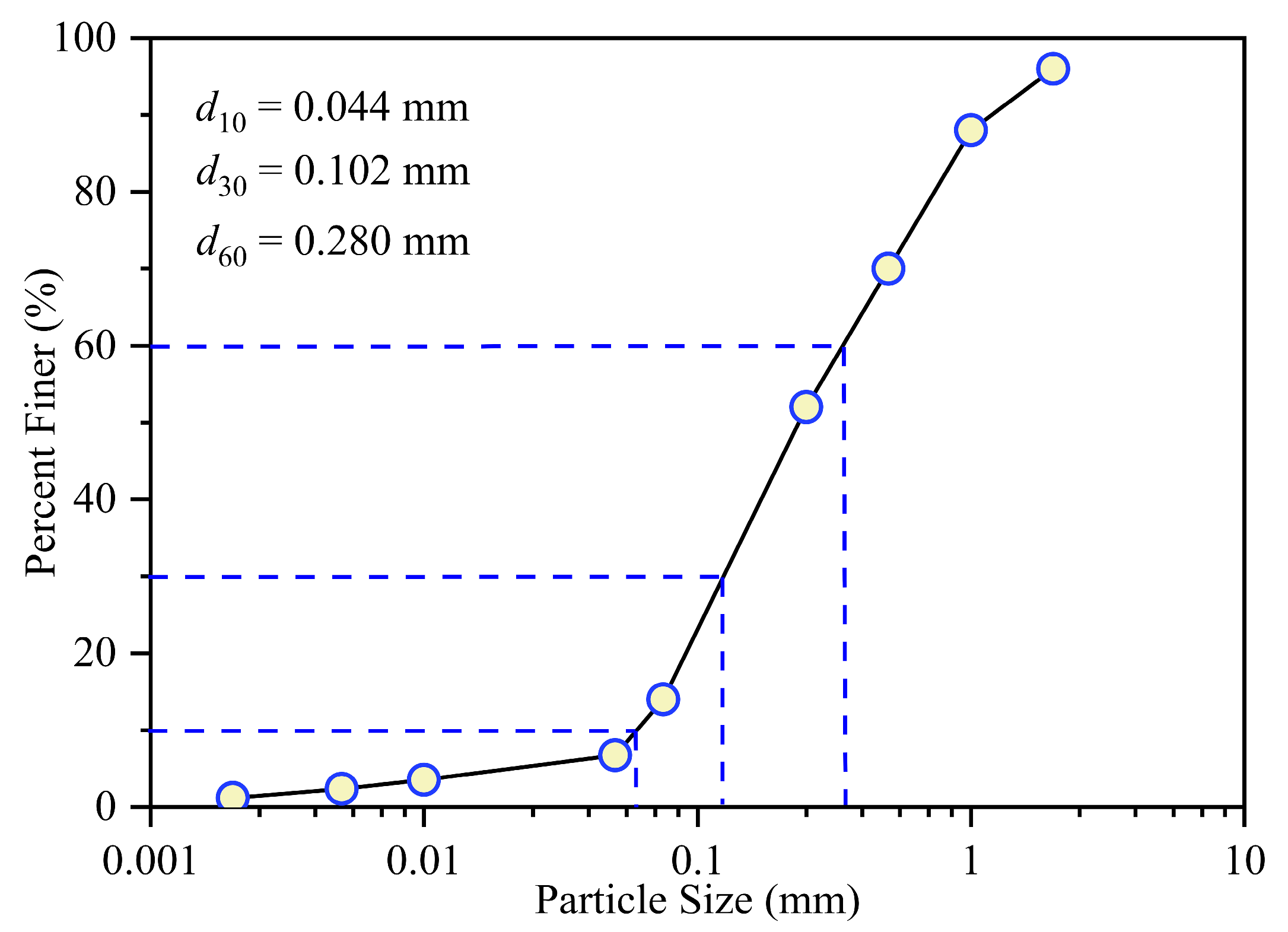
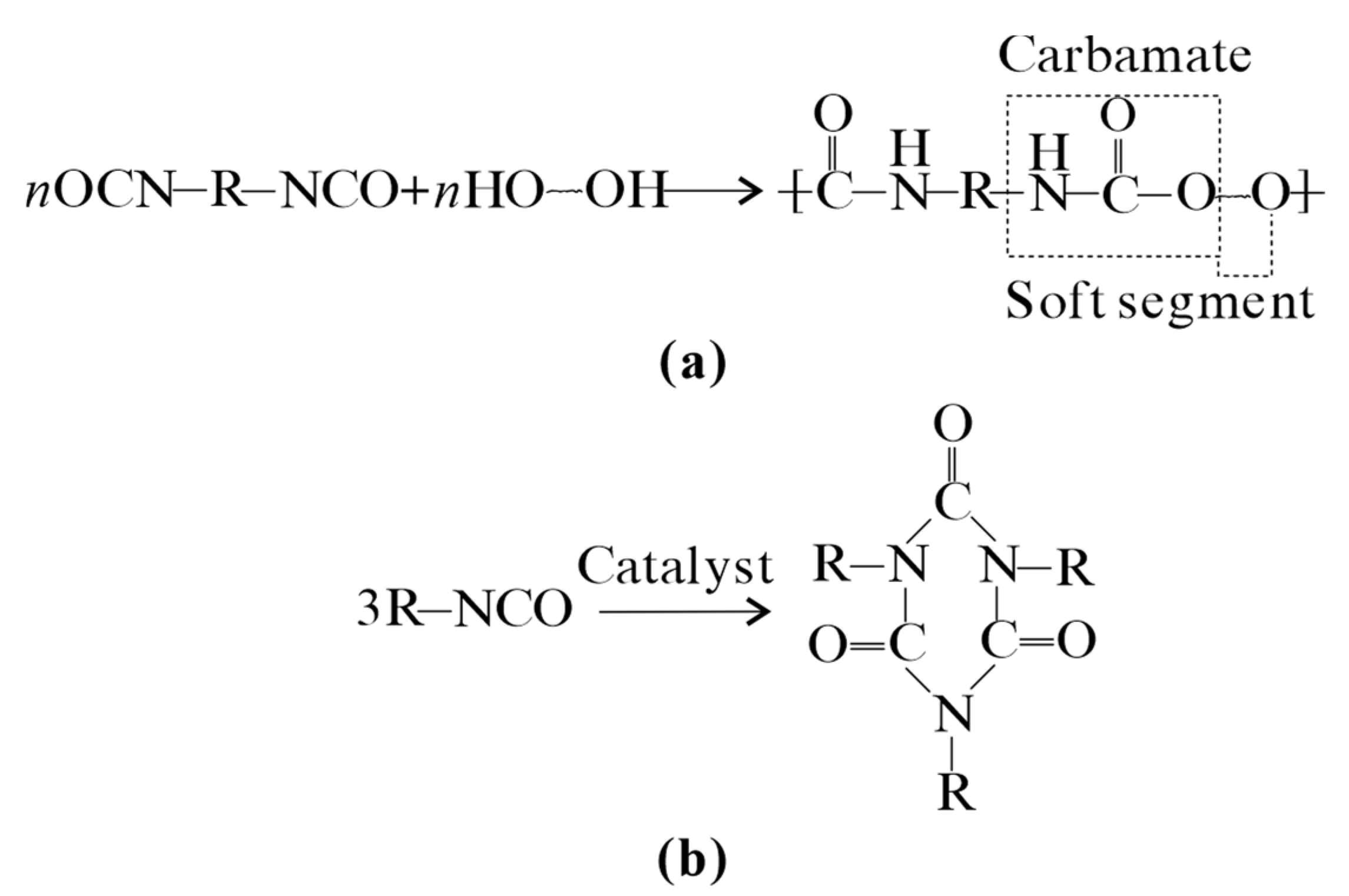
2.1. Calcareous Sand and Permeable Polymer Adhesive Materials
2.2. Sample Preparation
2.3. Test Equipment and Procedures
2.3.1. Compression Creep Test
2.3.2. Direct Shear Test
2.3.3. Triaxial Shear Test
2.3.4. Microstructural Analysis
3. Results and Discussion
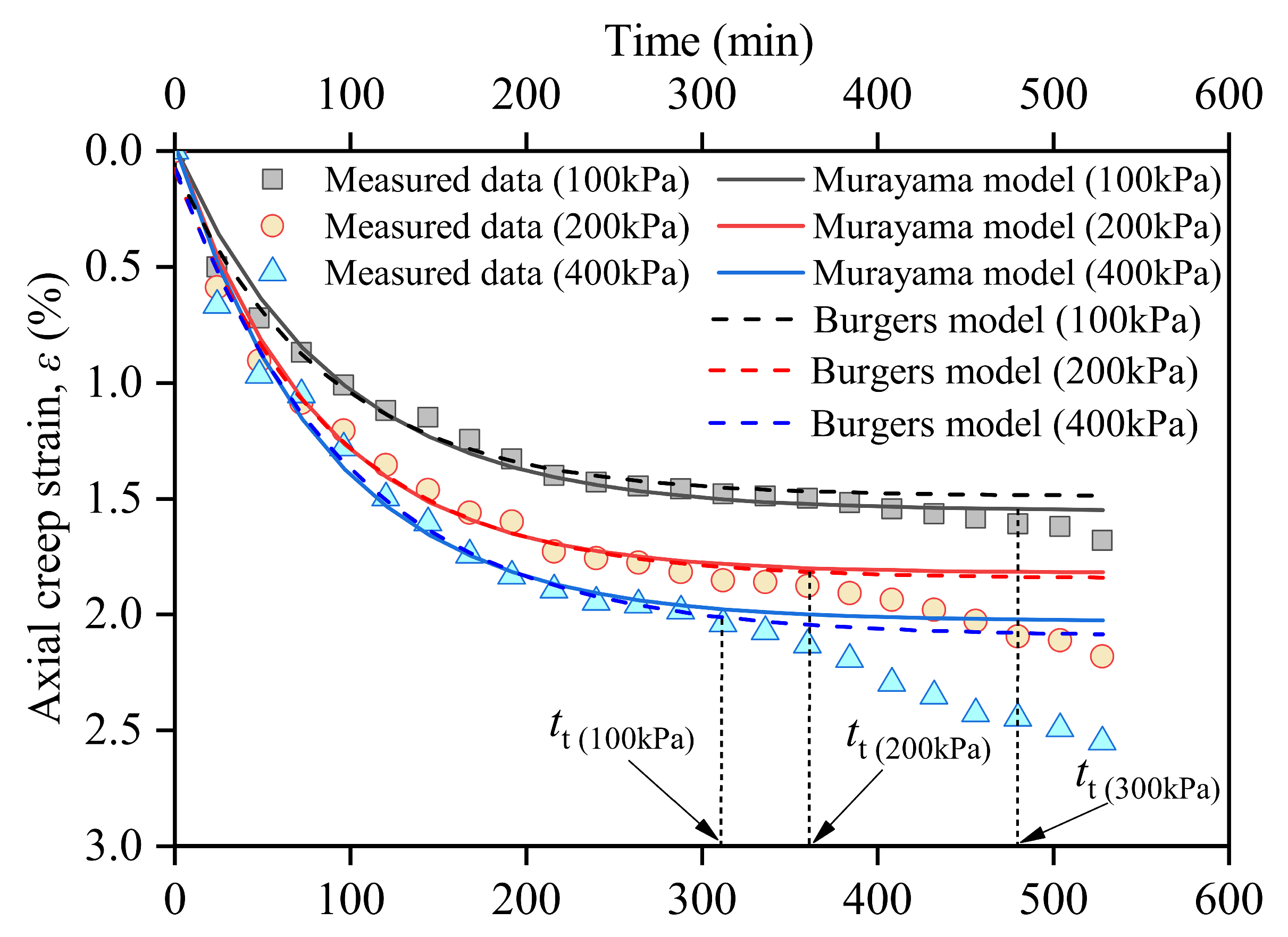
3.1. Compression Creep Development with Elapsed Time
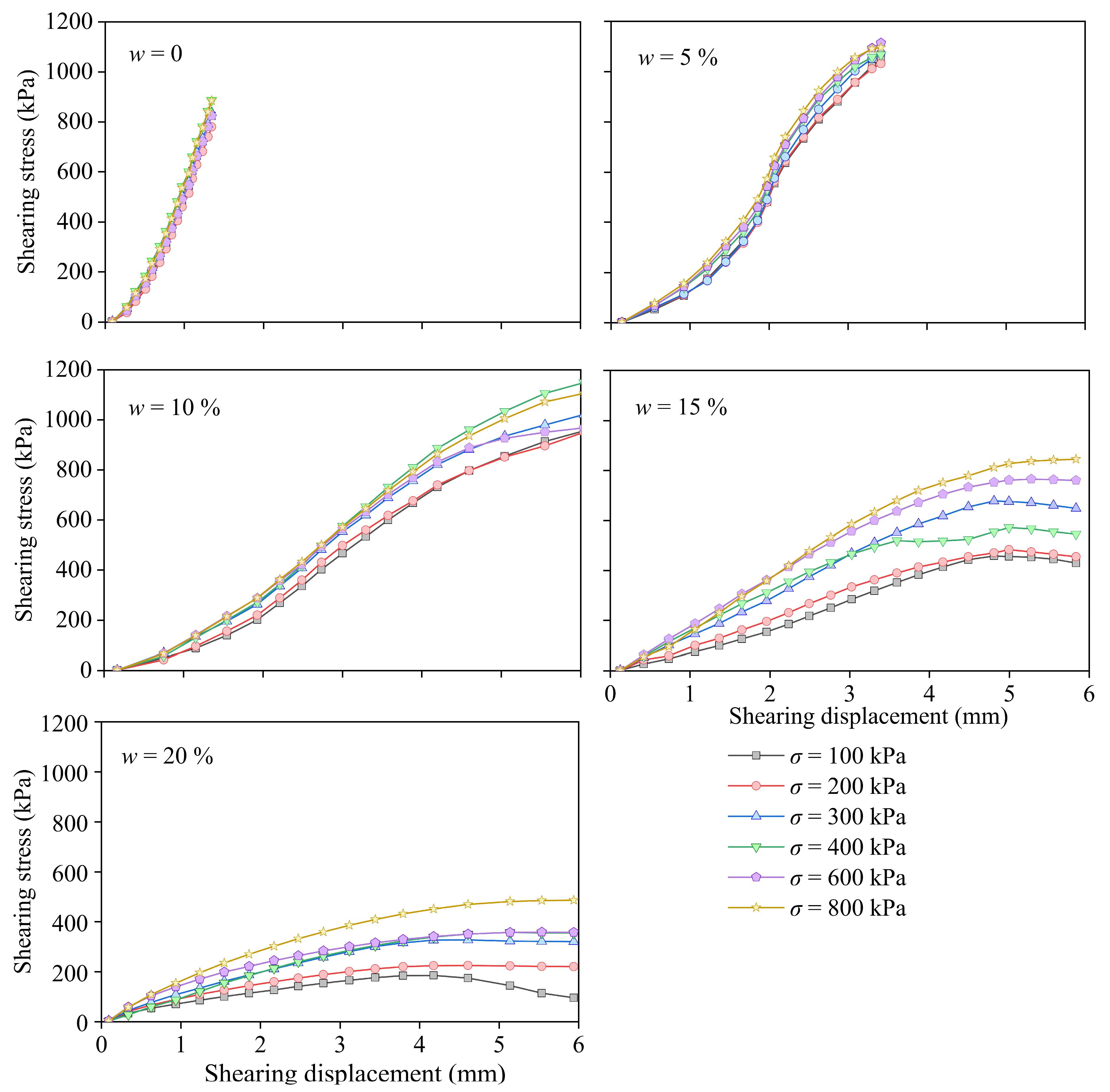
3.2. Direct Shear Strength Analysis
3.3. Triaxial Shear Strength Analysis
3.4. Microstructural Mechanism Analysis of the PPA Reinforced Calcareous Sand
4. Conclusions
- (1)
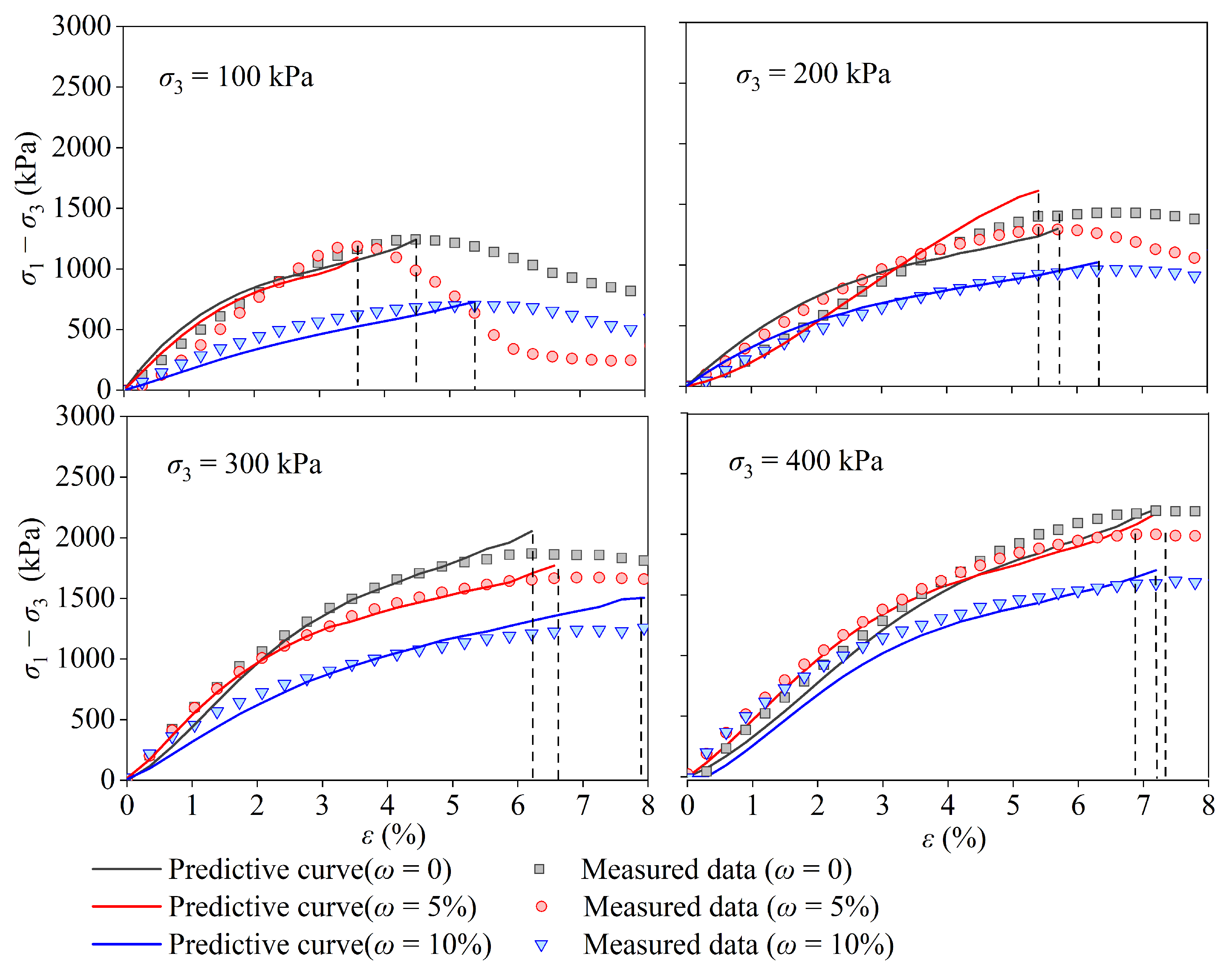
- There are time thresholds (tt) in the strain–time curves. Before tt, the measured and predicted values of the Burgers and Murayama models were consistent, and the compressive deformation rate changed from fast to slow. After the tt, the measured deformation data began to increase again, and neither the Burgers nor Murayama models reflected this restarted deformation. The deviation after tt was caused by the crushing of the calcareous sand particles and cutting failure of the PPA. The larger the confinement pressure, the later tt occurs.
- (2)
- Compared with the direct shear strength of fiber- and geogrid-reinforced calcareous sands, that reinforced by PPA is approximately nine times greater, which has great practical engineering value. The moisture content (w) and vertical normal stress play important roles in determining the direct shear strength of the PPA-reinforced calcareous sand. The influence of normal stress is not significant when the w is less than 10% because when the moisture content is low, the water is mainly wrapped around the solid particles and has not yet formed a connecting water bridge between the particles, which has little effect on the diffusion of the PPA. Under higher moisture content conditions (w is larger than 10%), the shear strength increased with the increase in vertical normal stress.
- (3)
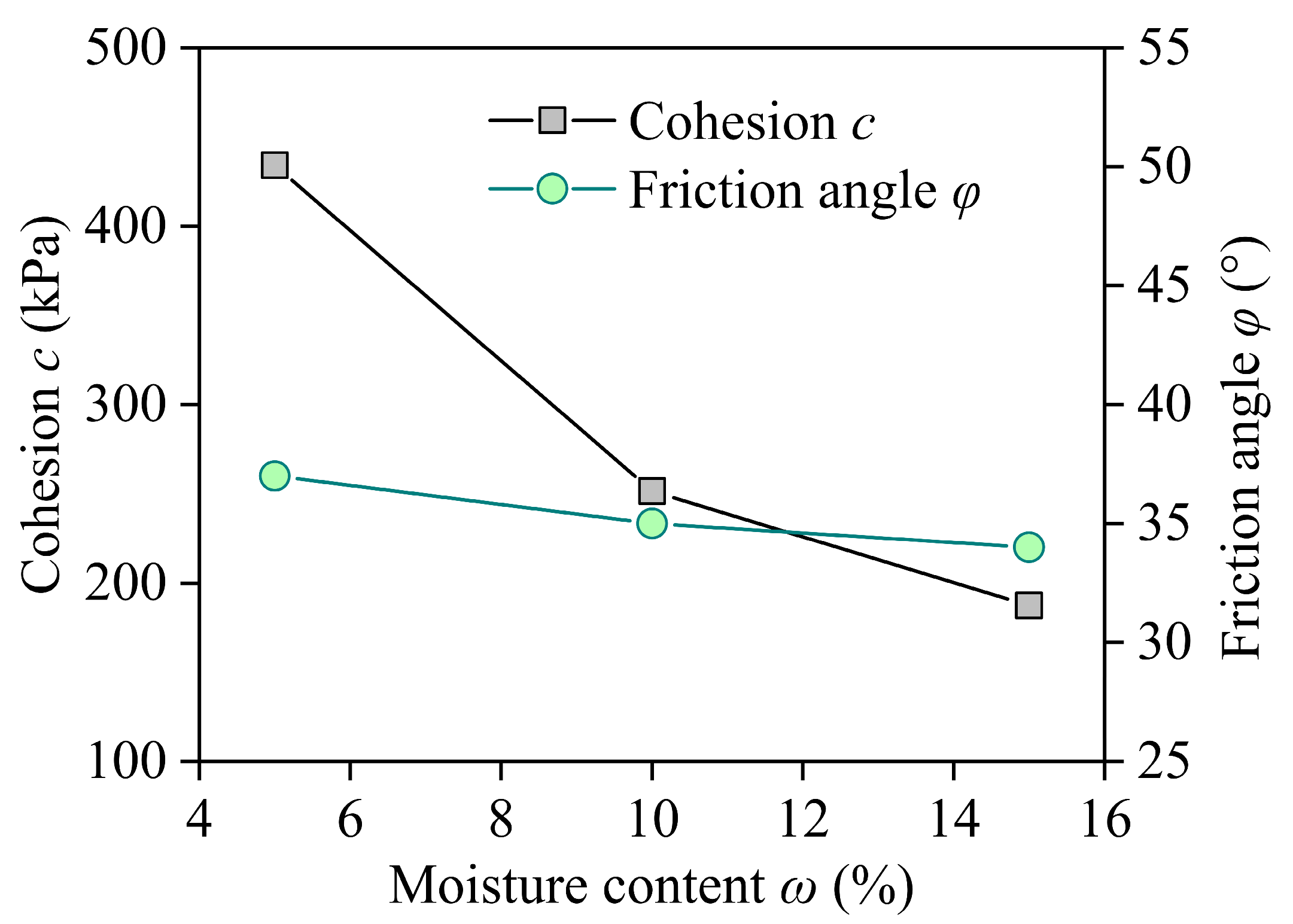
- Strain-softening features were observed in the relationship between and under low confining conditions (100 and 200 kPa). The greater the confining pressure, the higher the peak strength. Before softening occurs, the relationship between and can be effectively described by the classic Duncan–Chang model, with R2 being greater than 0.93. The higher the moisture content, the lower the peak strength. The moisture content significantly affects the cohesive force but has little influence on the internal friction angle and Poisson’s ratio.
- (4)
- The distribution of PPA and pores was determined by the moisture content. The higher the moisture content, the larger the number of pores formed after grouting with PPA. When w is 0, almost all the pores can be filled with PPA. When w is 5%, evenly distributed small pores can be observed, and when w is 10%, interconnected macropores can be observed. Therefore, in actual projects, groundwater must be pumped out before grouting the PPA into a calcareous sand foundation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.S.; Zhang, J.H.; Long, Z.L.; Kuang, D.M.; Cai, Y. Effects of particle size on the particle breakage of calcareous sands under impact loadings. Constr. Build. Mater. 2022, 341, 127809. [Google Scholar] [CrossRef]
- Zhang, Q.; Ye, W.; Liu, Z.; Wang, Q.; Chen, Y. Influence of injection methods on calcareous sand cementation by EICP technique. Constr. Build. Mater. 2023, 363, 129724. [Google Scholar] [CrossRef]
- Chen, Q.; Peng, W.; Yu, R.; Tao, G.; Nimbalkar, S. Laboratory Investigation on Particle Breakage Characteristics of calcareous sands. Adv. Civ. Eng. 2021, 2021, 8867741. [Google Scholar] [CrossRef]
- Cao, D.F.; Zhu, H.H.; Guo, C.C.; Wu, J.H.; Fatahi, B. Investigating the hydro-mechanical properties of calcareous sand foundations using distributed fiber optic sensing. Eng. Geol. 2021, 295, 106440. [Google Scholar] [CrossRef]
- Wang, X.; Shan, Y.; Cui, J.; Zhong, Y.; Shen, J.H.; Wang, X.Z.; Zhu, C.Q. Dilatancy of the foundation filling material of island-reefs in the South China Sea. Constr. Build. Mater. 2022, 323, 126524. [Google Scholar] [CrossRef]
- Jafarian, Y.; Javdanian, H.; Haddad, A. Dynamic properties of calcareous and siliceous sands under isotropic and anisotropic stress conditions. Soils Found. 2018, 58, 172–184. [Google Scholar] [CrossRef]
- Shen, J.; Wang, X.; Wang, X.; Yao, T.; Wei, H.; Zhu, C. Effect and mechanism of fines content on the shear strength of calcareous sand. Bull. Eng. Geol. Environ. 2021, 80, 7899–7919. [Google Scholar] [CrossRef]
- Ding, X.M.; Luo, Z.G.; Ou, Q. Mechanical property and deformation behavior of geogrid reinforced calcareous sand. Geotext. Geomembr. 2022, 50, 618–631. [Google Scholar] [CrossRef]
- Zhao, J.; Ou, Q.; Ding, X.; Chen, Z. Model test study on the response of coral sand foundation reinforced by vibroflotation. Acta Geotech. 2023, 18, 6201–6212. [Google Scholar] [CrossRef]
- Shan, Y.; Liang, J.; Tong, H.; Yuan, J.; Zhao, J. Effect of different fibers on small-strain dynamic properties of microbially induced calcite precipitation–fiber combined reinforced calcareous sand. Constr. Build. Mater. 2022, 322, 126343. [Google Scholar] [CrossRef]
- Zeng, H.; Yin, L.Y.; Tang, C.S.; Zhu, C.; Cheng, Q.; Li, H.; Lv, C.; Shi, B. Tensile behavior of bio-cemented, fiber-reinforced calcareous sand from coastal zone. Eng. Geol. 2021, 294, 106390. [Google Scholar] [CrossRef]
- Rezvani, R. Shearing response of geotextile-reinforced calcareous soils using monotonic triaxial tests. Mar. Georesour. Geotechnol. 2019, 38, 238–249. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, T.; Meng, Q.; Wang, X.; He, J. Experimental evaluation of the shear behavior of fiber-reinforced calcareous sands. Int. J. Géoméch. 2018, 18, 04018175. [Google Scholar] [CrossRef]
- Ye, J.; Haiyilati, Y.; Cao, M.; Zuo, D.; Chai, X. Creep characteristics of calcareous coral sand in the South China Sea. Acta Geotech. 2022, 17, 5133–5155. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, L.; Wang, M.; Lv, Y.; Dong, L.; Fan, P. A creep constitutive model incorporating deformation mechanisms for crushable calcareous sand. Arab. J. Geosci. 2018, 11, 623. [Google Scholar] [CrossRef]
- Lv, Y.; Li, F.; Liu, Y.; Fan, P.; Wang, M. Comparative study of coral sand and silica sand in creep under general stress states. Can. Geotech. J. 2017, 54, 1601–1611. [Google Scholar] [CrossRef]
- Lade, P.V.; Liggio, C.D.; Nam, J. Nam, Strain Rate, creep, and stress drop-creep experiments on crushed coral sand. J. Geotech. Geoenviron. Eng. 2009, 135, 941–953. [Google Scholar] [CrossRef]
- Wang, D.L.; Tang, C.S.; Pan, X.H.; Liu, B.; Shi, B. Coupling effect of fiber reinforcement and MICP stabilization on the tensile behavior of calcareous sand. Eng. Geol. 2023, 317, 107090. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, J.-F.; Zhuang, X.-Y. Undrained cyclic behaviors of fiber-reinforced calcareous sand under multidirectional simple shear stress path. Acta Geotech. 2023, 18, 2929–2943. [Google Scholar] [CrossRef]
- Xu, X.; Guo, H.; Li, M.; Deng, X. Bio-cementation improvement via CaCO3 cementation pattern and crystal polymorph: A review. Constr. Build. Mater. 2021, 297, 123478. [Google Scholar] [CrossRef]
- Zhang, W.; Ju, Y.; Zong, Y.; Qi, H.; Zhao, K. In situ real-time Study on dynamics of microbially induced calcium carbonate precipitation at a Single-Cell Level. Environ. Sci. Technol. 2018, 52, 9266–9276. [Google Scholar] [CrossRef] [PubMed]
- Tao, G.; Yuan, J.; Chen, Q.; Peng, W.; Yu, R.; Basack, S. Chemical stabilization of calcareous sand by polyurethane foam adhesive. Constr. Build. Mater. 2021, 295, 123609. [Google Scholar] [CrossRef]
- Tan, H.; Yu, C.; Sun, Y. Improved mechanical performance of gravel reinforced by polyurethane polymer adhesive. J. Mater. Civ. Eng. 2023, 35, 04023045. [Google Scholar] [CrossRef]
- Hao, Y.; Guo, C.; Shi, M.; Wang, F.; Xia, Y.; Wang, C. Application of polymer split grouting technology in earthen dam: Diffusion law and applicability. Constr. Build. Mater. 2023, 369, 130612. [Google Scholar] [CrossRef]
- Wang, C.; Diao, Y.; Guo, C.; Li, P.; Du, X.; Pan, Y. Two-stage column–hemispherical penetration diffusion model considering porosity tortuosity and time-dependent viscosity behavior. Acta Geotech. 2022, 18, 2661–2680. [Google Scholar] [CrossRef]
- Wang, C.; Guo, C.; Du, X.; Shi, M.; Liu, Q.; Xia, Y. Reinforcement of silty soil with permeable polyurethane by penetration injection. Constr. Build. Mater. 2021, 310, 124829. [Google Scholar] [CrossRef]
- Dudley, C. Classification of soils for engineering purposes. In Annual Book of ASTM Standards; American Society for Testing and Materials: West Conshohocken, PA, USA, 1985; pp. 395–408. [Google Scholar]
- Abell, A.B.; Willis, K.L.; Lange, D.A. Mercury intrusion porosimetry and image analysis of cement-based materials. J. Colloid Interface Sci. 1999, 211, 39–44. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and the Geometry of Nature; WH Freeman: Ney York, NY, USA, 1982. [Google Scholar]
- Xu, L.J.; Wang, R.; Xu, D.S.; Wang, X.Z.; Meng, Q.S.; Zhu, C.Q. Review of particle breakage measurement methods for calcareous sand. Adv. Civ. Eng. 2022, 2022, 6477197. [Google Scholar] [CrossRef]
- Murayama, S.; Michihiro, K.; Sakagami, T. Creep Characteristics of sands. Soils Found. 1984, 24, 1–15. [Google Scholar] [CrossRef]
- Yu, D.; Ye, J.; Yao, L. Prediction of the long-term settlement of the structures built on a reclaimed coral reef island: An aircraft runway. Bull. Eng. Geol. Environ. 2020, 79, 4549–4564. [Google Scholar] [CrossRef]
- Choo, H.; Kwon, M.; Touiti, L.; Jung, Y.H. Creep of calcareous sand in Tunisia: Effect of particle breakage at low stress level. Int. J. Geo-Eng. 2020, 11, 16. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, C.; Cao, D.; Ni, P.; Wang, F. An experimental study on the cutting failure of polymer grouting. Constr. Build. Mater. 2020, 258, 119582. [Google Scholar] [CrossRef]
- Sayde, C.; Gregory, C.; Gil-Rodriguez, M.; Tufillaro, N.; Tyler, S.; van de Giesen, N.; English, M.; Cuenca, R.; Selker, J.S. Feasibility of soil moisture monitoring with heated fiber optics. Water Resour. Res. 2010, 46, W06201. [Google Scholar] [CrossRef]
- Xu, L.; Wang, R.; Xu, D.; Wang, J.; Wang, X.; Meng, Q. Interface shear behavior of geogrid-reinforced calcareous sand under large-scale monotonic direct Shear. Int. J. Geosynth. Ground Eng. 2022, 8, 66. [Google Scholar] [CrossRef]
- Kondner, R.L. Hyperbolic Stress-Strain Response: Cohesive Soils. J. Soil Mech. Found. Div. 1963, 89, 115–143. [Google Scholar] [CrossRef]
- Jia, P.; Khoshghalb, A.; Chen, C.; Zhao, W.; Dong, M.; Esgandani, G.A. Modified Duncan-Chang Constitutive Model for Modeling Supported Excavations in Granular Soils. Int. J. Géoméch. 2020, 20, 04020211. [Google Scholar] [CrossRef]
- Duncan, J.M.; Chang, C.Y. Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found. Div. 1970, 96, 1629–1653. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, X.; Shen, J.H.; Cui, J.; Zhu, C.Q.; Wang, X.Z. Experimental Study on the Impact of Water Content on the Strength Parameters of Coral Gravelly Sand. J. Mar. Sci. Eng. 2020, 8, 634. [Google Scholar] [CrossRef]
- Wang, X.; Cui, J.; Zhu, C.Q.; Wu, Y.; Wang, X.Z. Experimental study of the mechanical behavior of calcareous sand under repeated loading-unloading. Bull. Eng. Geol. Environ. 2021, 80, 3097–3113. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Chen, X.; Cao, P.; Cao, L.; Chen, W. Mechanical Properties and Constitutive Model of Calcareous Sand Strengthened by MICP. J. Mar. Sci. Eng. 2023, 11, 819. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z.; Wang, Z.; Chen, Q.; Ma, D. Critical Dynamic Stress and Cumulative Plastic Deformation of Calcareous Sand Filler Based on Shakedown Theory. J. Mar. Sci. Eng. 2023, 11, 195. [Google Scholar] [CrossRef]
- Kumar, J.; Madhusudhan, B. Effect of relative density and confining pressure on Poisson ratio from bender and extender elements tests. Geotech. 2010, 60, 561–567. [Google Scholar] [CrossRef]
- Lv, C.; Wu, H.; Shi, M.; Zhang, D. Experimental study on the mechanical strength, deformation behavior and infiltration characteristics of coral sand. Sustainability 2024, 16, 3479. [Google Scholar] [CrossRef]
- Bowman, E.T.; Soga, K. Soga, Creep, ageing and microstructural change in dense granular materials. Soils Found. 2003, 43, 107–117. [Google Scholar] [CrossRef]
- Magazzù, A.; Marcuello, C. Investigation of soft matter nanomechanics by atomic force microscopy and optical tweezers: A comprehensive review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Zhang, J.; Liu, Y.; Xie, S. Pore characteristics of calcium sulfoaluminate cement paste with impact of supplementary cementitious materials and water to binder ratio. Powder Technol. 2021, 387, 146–155. [Google Scholar] [CrossRef]
- Lu, S.-G.; Malik, Z.; Chen, D.-P.; Wu, C.-F. Porosity and pore size distribution of Ultisols and correlations to soil iron oxides. Catena 2014, 123, 79–87. [Google Scholar] [CrossRef]








| Element | Na | Mg | Al | Si | P | S | Cl | K | Ca | Fe | Sr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Percentage (%) | 0.666 | 2.556 | 0.037 | 0.223 | 0.037 | 0.378 | 0.260 | 0.031 | 93.888 | 0.057 | 1.867 |
| Ingredient Name | Molecular Formula | Density g/mL | Content | Features | |
|---|---|---|---|---|---|
| A | Polymeric MDI | C15H10N2O2 | 1.2 | 50–70% | Brown liquid with a pungent odor |
| MDI | C15H10N2O2 | 1.19 | 30–50% | White or yellow flakes or crystals | |
| B | Polyether polyols | C8H22O7 | 1.02 | 30–60% | Light yellow transparent liquid |
| Tris Nphosphate | C9H18Cl3O4P | Null | 10–40% | Transparent, colorless, viscous | |
| Tests | Moisture (%) | (kPa) | (kPa) | Dry Density (g/cm3) |
|---|---|---|---|---|
| Compression | 10 | 100, 200, 400 | 0 | 1.45 |
| Direct shear | 0, 5, 10, 15, 20 | 100, 200, 300, 400, 600, 800 | 0 | 1.45 |
| Triaxial shear | 0, 5, 10 | / | 100, 200, 300, 400 | 1.45 |
| Models | 100 kPa | 200 kPa | 400 kPa | |||
|---|---|---|---|---|---|---|
| R2 | RMSD | R2 | RMSD | R2 | RMSD | |
| Burgers | 0.981 | 0.071 | 0.961 | 0.128 | 0.944 | 0.221 |
| Murayama | 0.987 | 0.559 | 0.989 | 0.137 | 0.986 | 0.193 |
| σ3 (kPa) | w = 5% | w = 10% | w = 15% | |||
|---|---|---|---|---|---|---|
| R2 | RMSD (kPa) | R2 | RMSD (kPa) | R2 | RMSD (kPa) | |
| 100 | 0.964 | 76.75 | 0.934 | 134.82 | 0.983 | 105.32 |
| 200 | 0.969 | 89.06 | 0.959 | 158.51 | 0.986 | 125.32 |
| 300 | 0.981 | 84.84 | 0.987 | 37.97 | 0.976 | 96.66 |
| 400 | 0.986 | 97.79 | 0.982 | 72.50 | 0.962 | 91.68 |
| σ3/kPa | w = 5% | w = 10 | w = 15 | |||
|---|---|---|---|---|---|---|
| μ | R2 | μ | R2 | μ | R2 | |
| 100 | 0.222 | 0.970 | 0.177 | 0.895 | 0.224 | 0.971 |
| 200 | 0.234 | 0.973 | 0.124 | 0.960 | 0.152 | 0.935 |
| 300 | 0.301 | 0.985 | 0.113 | 0.936 | 0.100 | 0.982 |
| 400 | 0.140 | 0.913 | 0.296 | 0.979 | 0.140 | 0.962 |
| Porosity (%) | Average Pore Diameter (nm) | Media Pore Diameter, V (mm) | Median Pore Diameter, A (nm) | Backbone Fractal Dimension | Percolation Fractal Dimension |
|---|---|---|---|---|---|
| 37.88 | 474.95 | 1.16 | 80.74 | 3.00 | 2.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, D.; Fan, L.; Huang, R.; Guo, C. Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive. Materials 2024, 17, 5277. https://doi.org/10.3390/ma17215277
Cao D, Fan L, Huang R, Guo C. Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive. Materials. 2024; 17(21):5277. https://doi.org/10.3390/ma17215277
Chicago/Turabian StyleCao, Dingfeng, Lei Fan, Rui Huang, and Chengchao Guo. 2024. "Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive" Materials 17, no. 21: 5277. https://doi.org/10.3390/ma17215277
APA StyleCao, D., Fan, L., Huang, R., & Guo, C. (2024). Investigation of the Mechanical Properties of Reinforced Calcareous Sand Using a Permeable Polyurethane Polymer Adhesive. Materials, 17(21), 5277. https://doi.org/10.3390/ma17215277





