Dynamics of a Magnetic Polaron in an Antiferromagnet
Abstract
1. Introduction
2. t-J Model and Methodologies
3. Results and Discussion
3.1. Nonequilibrium Quantum Dynamics of a Single Hole
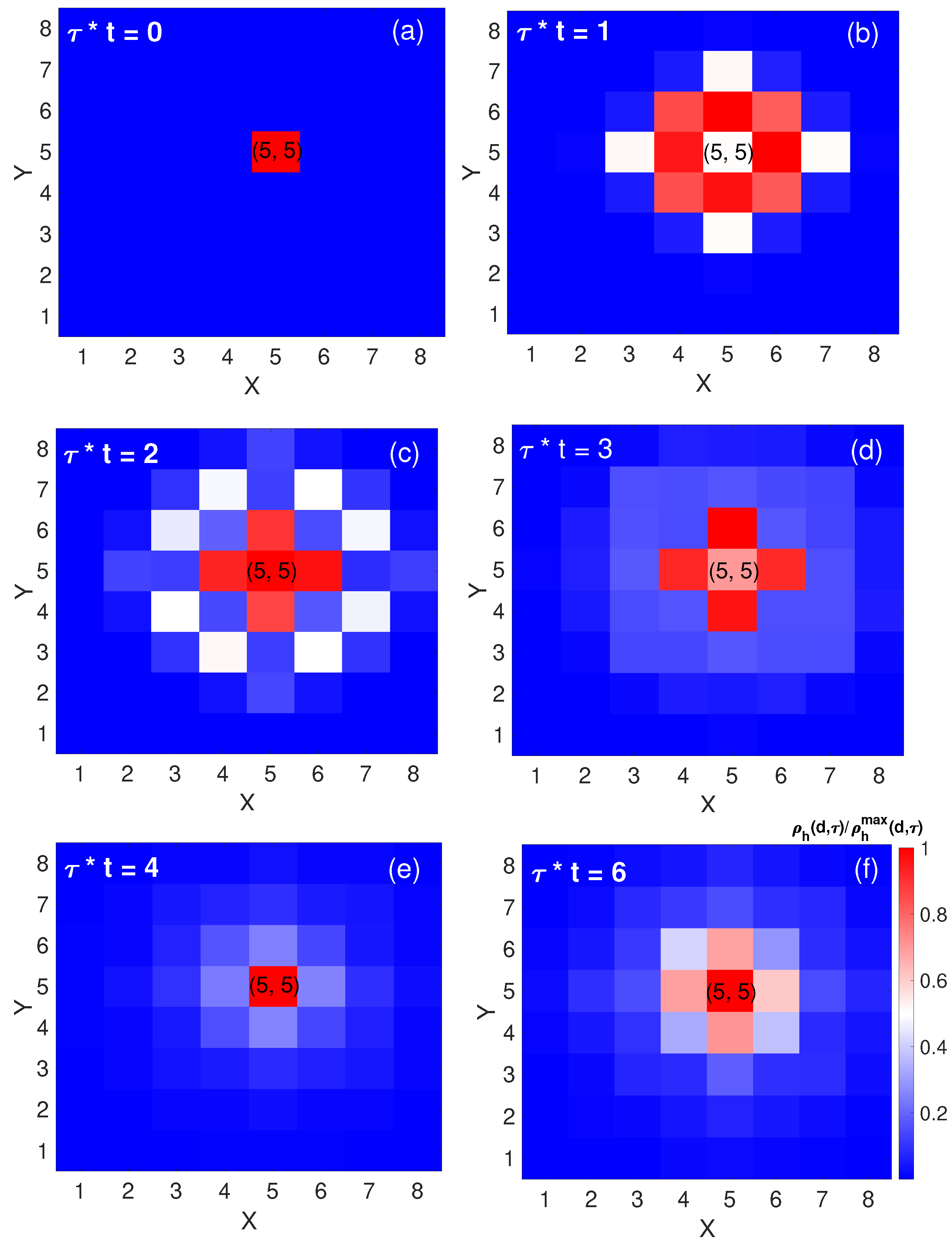
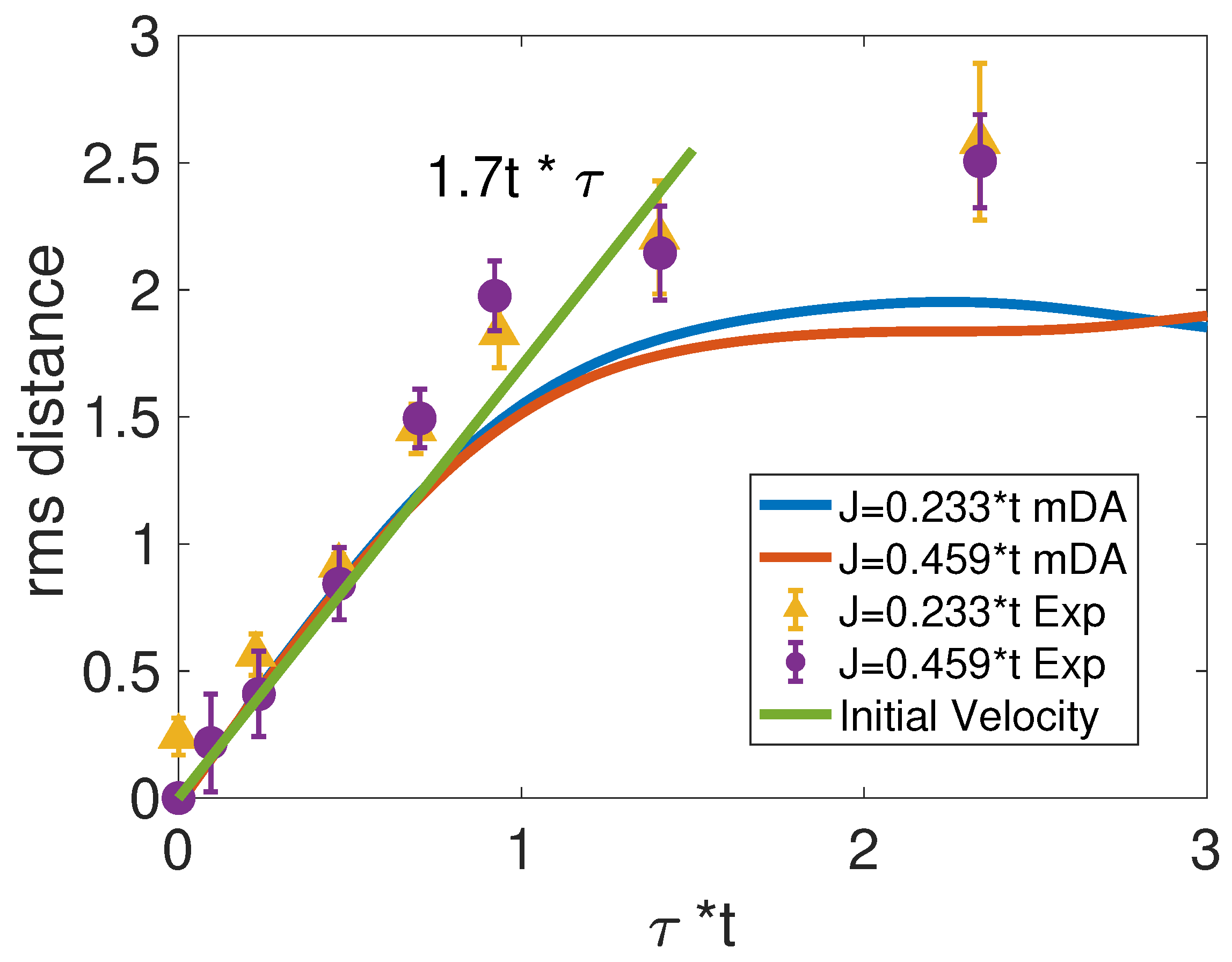
3.1.1. Spatial Spread of a Single Hole
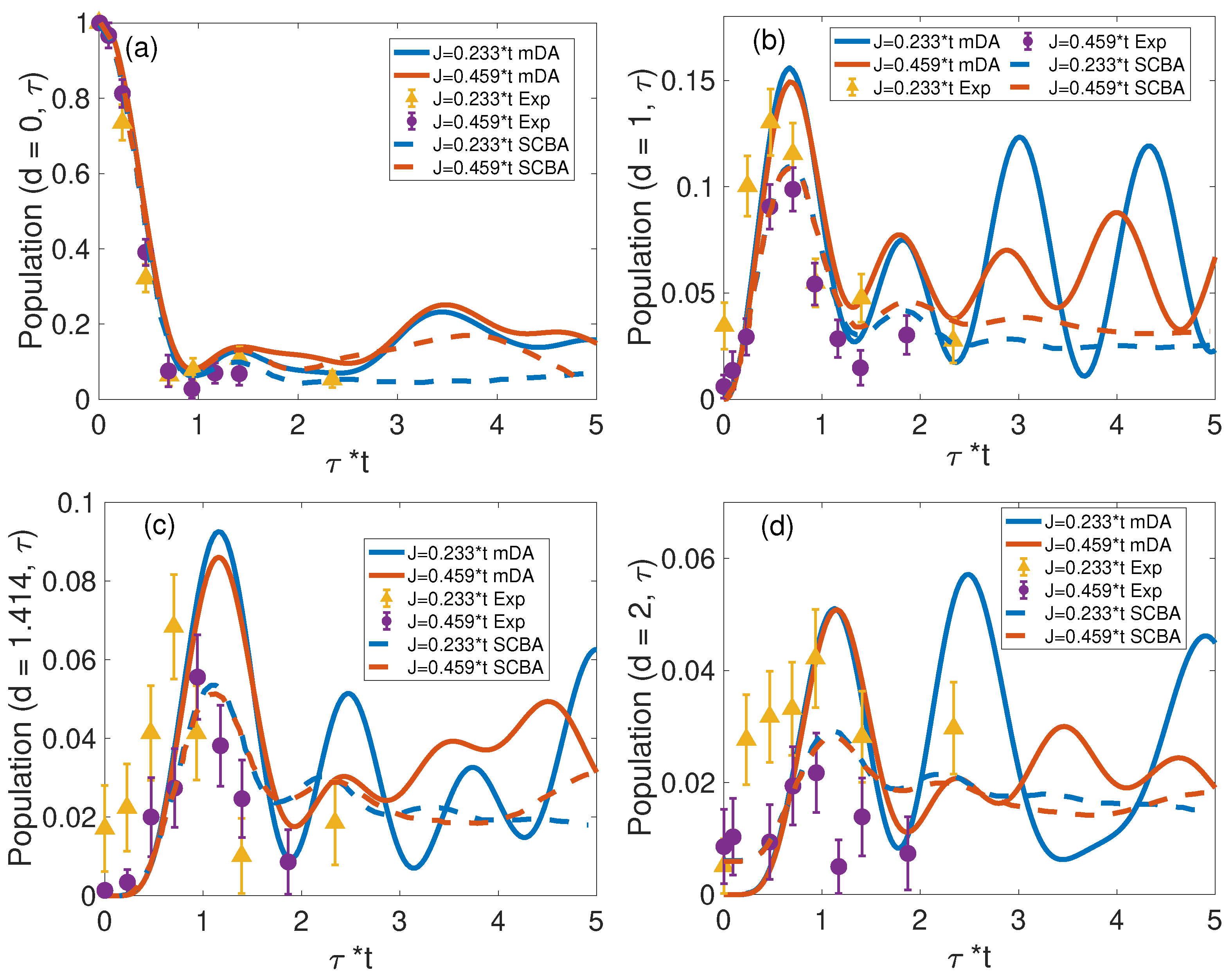
3.1.2. Population Dynamics Comparison with SCBA Method and Experimental Data
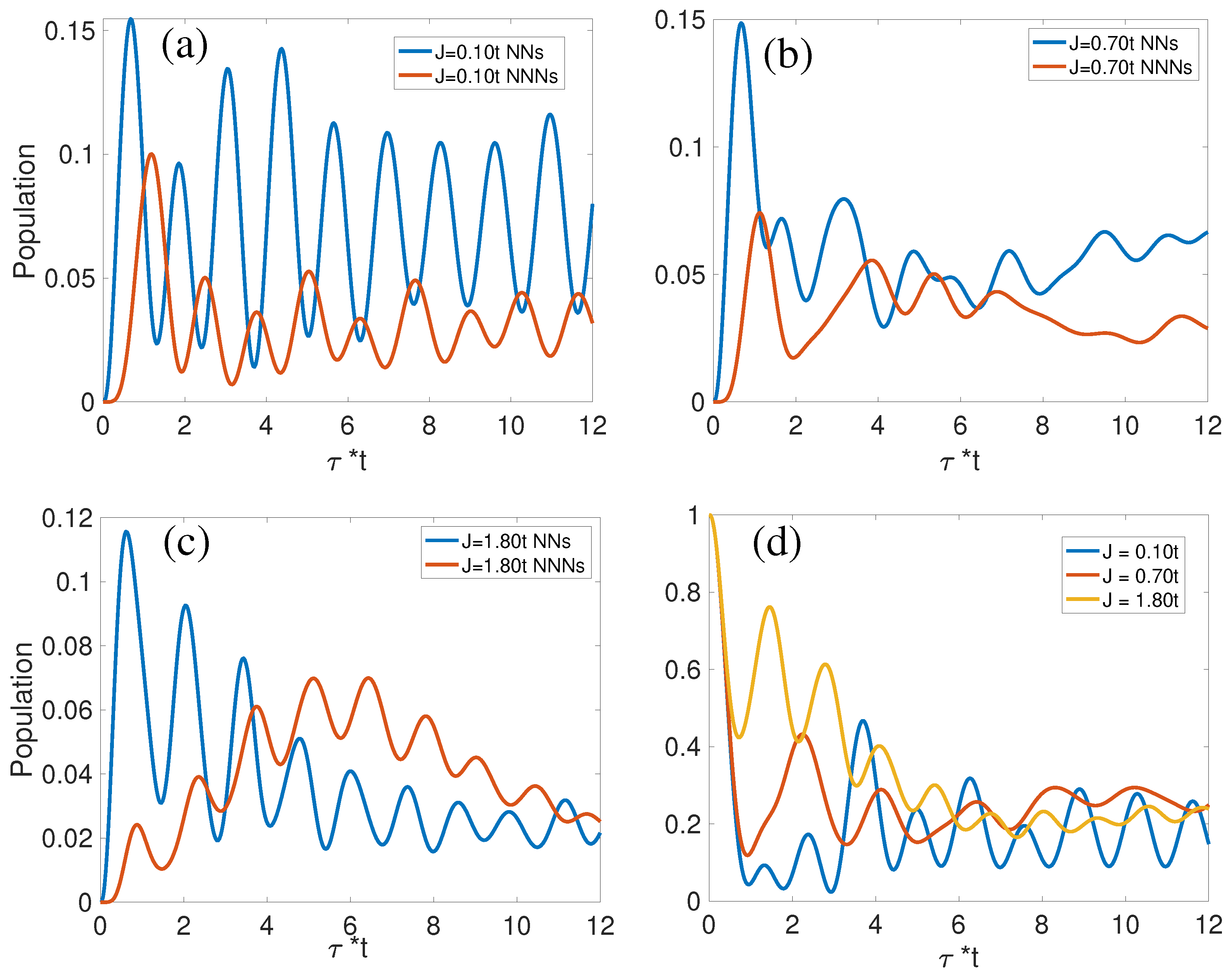
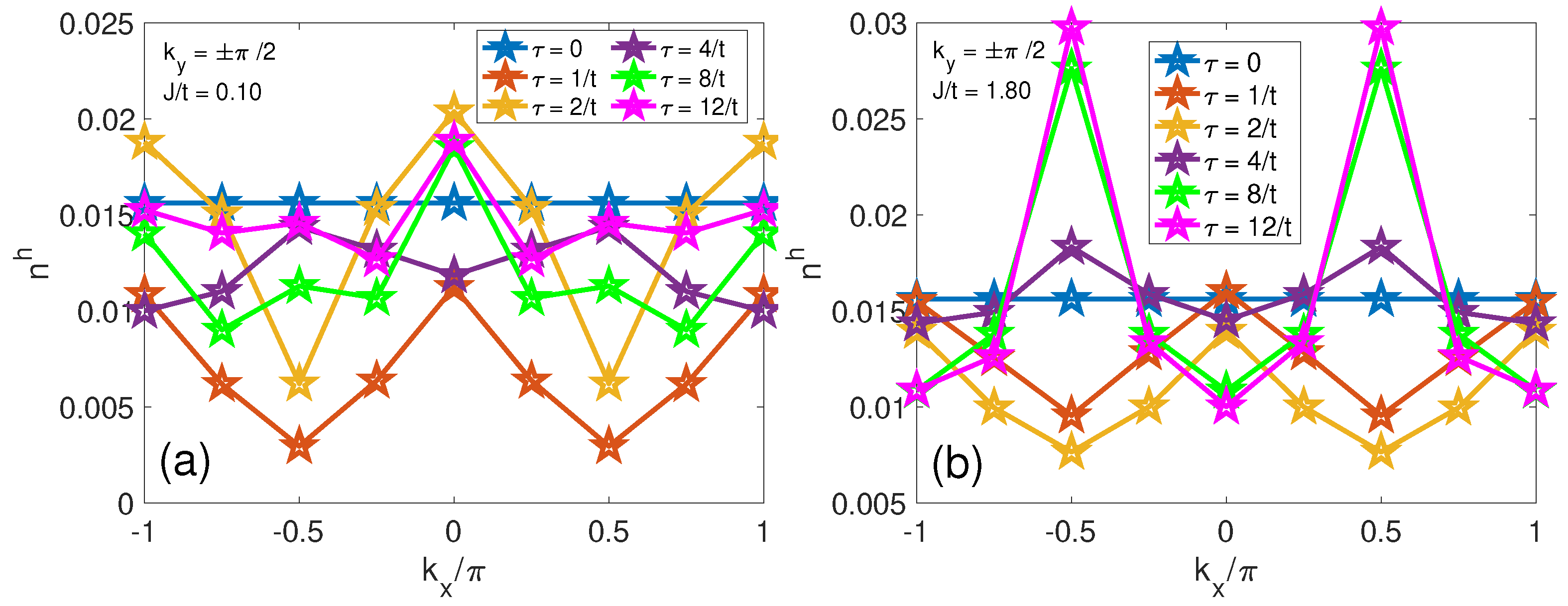
3.1.3. Site-Dependent Hole Dynamics across Diverse Spin–Spin Interaction Regimes
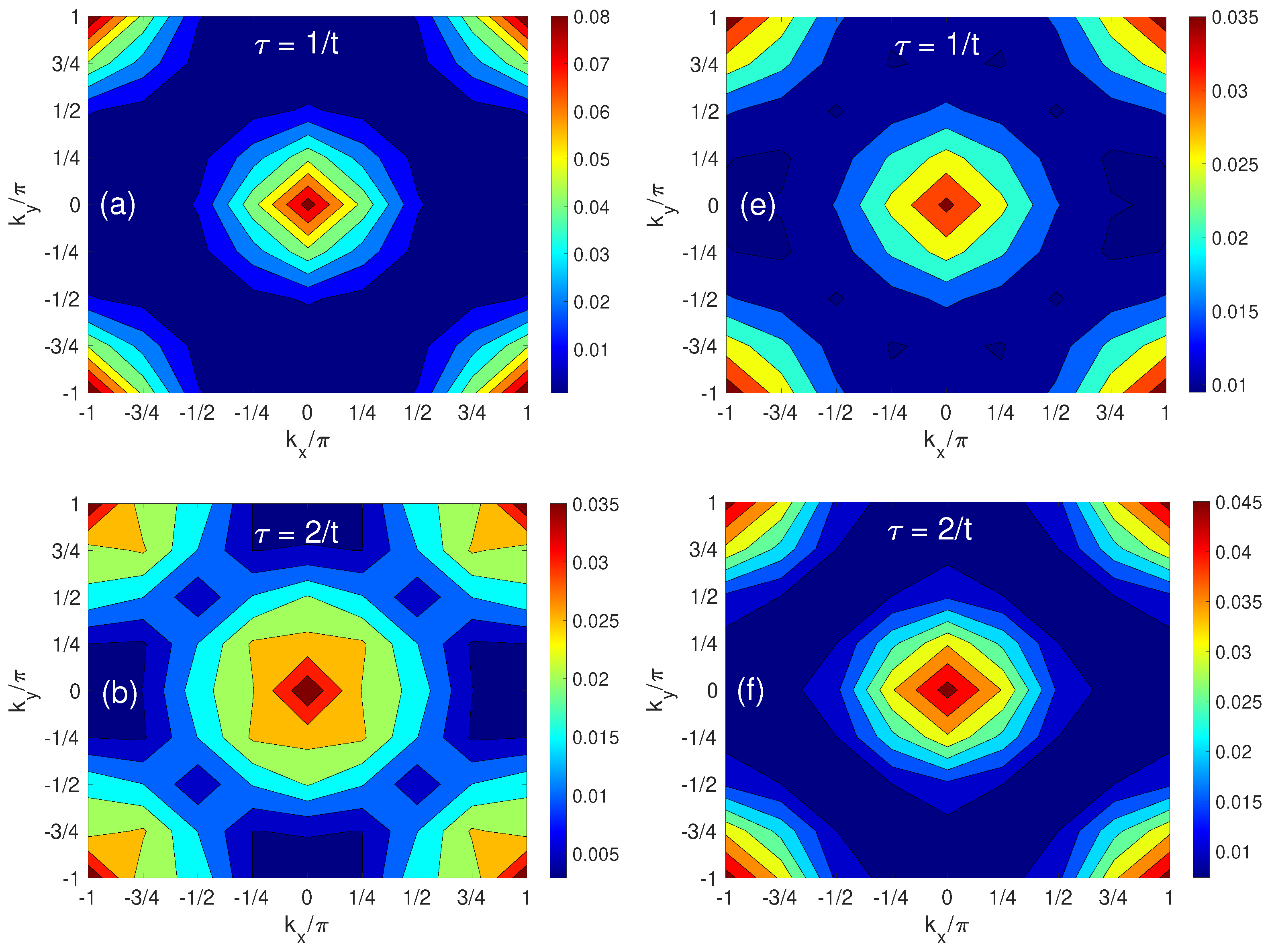
3.1.4. Momentum–Space Profile of a Solitary Hole
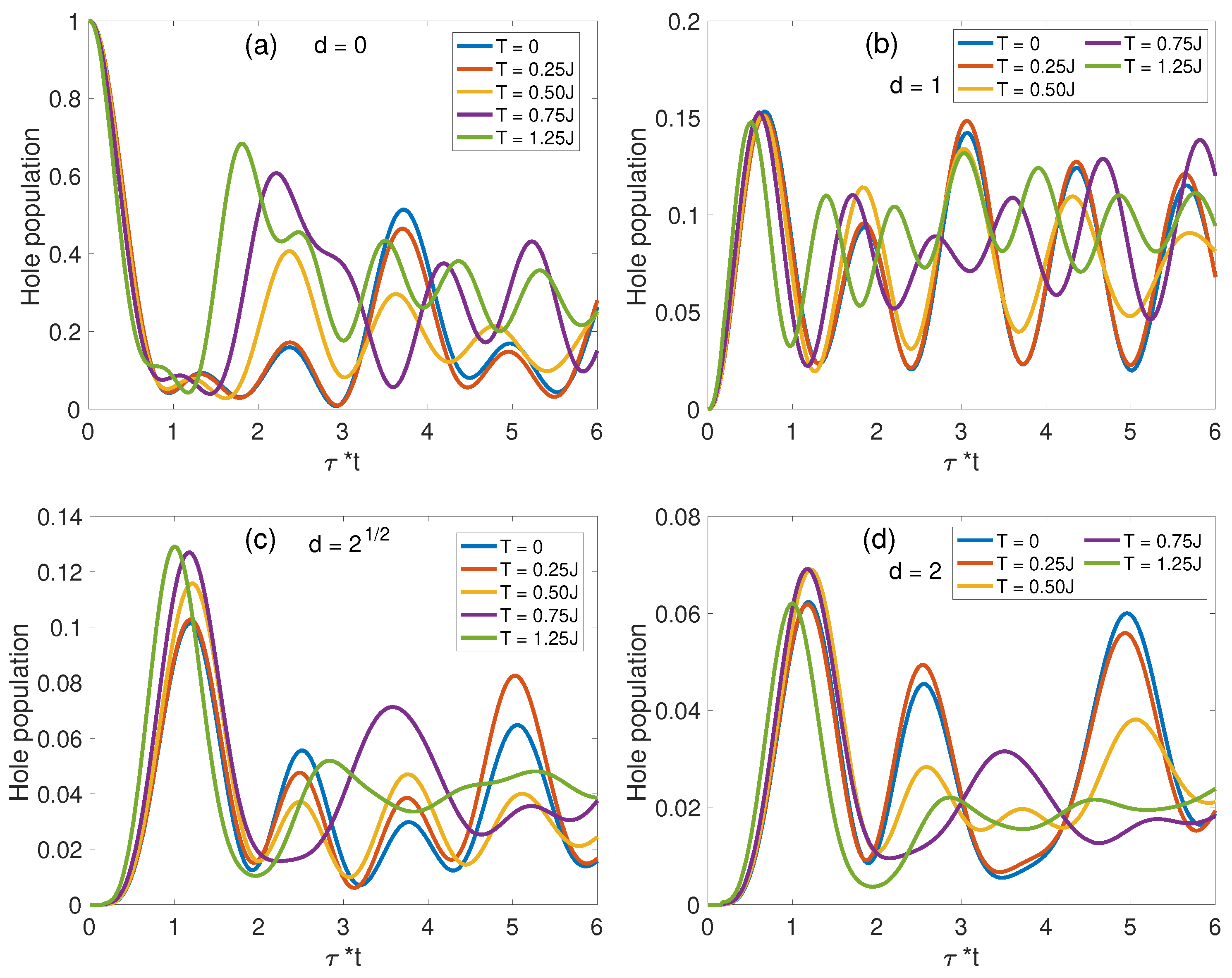
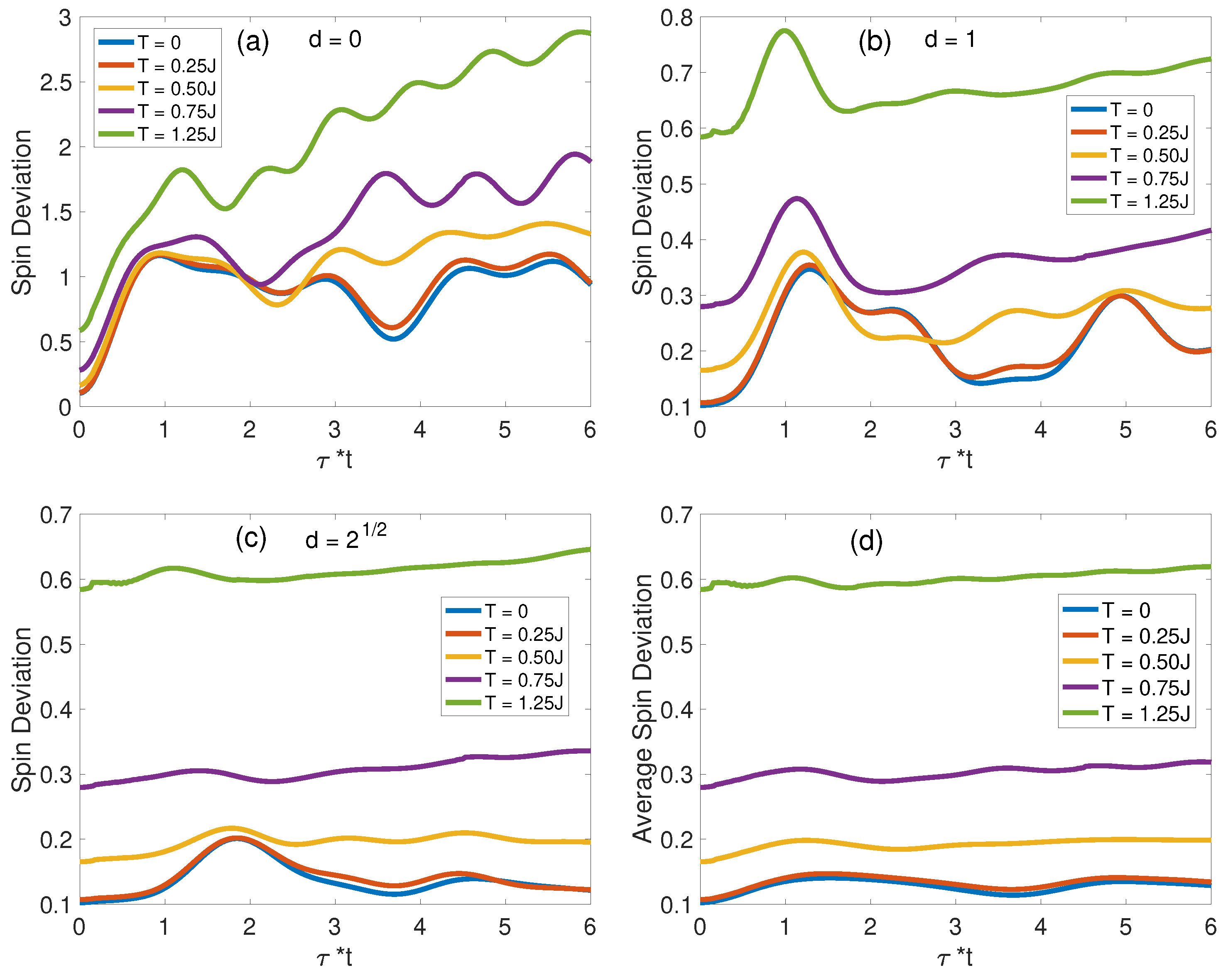
3.2. Analysis of Hole Dynamics and Spin Deviations at Finite Temperatures
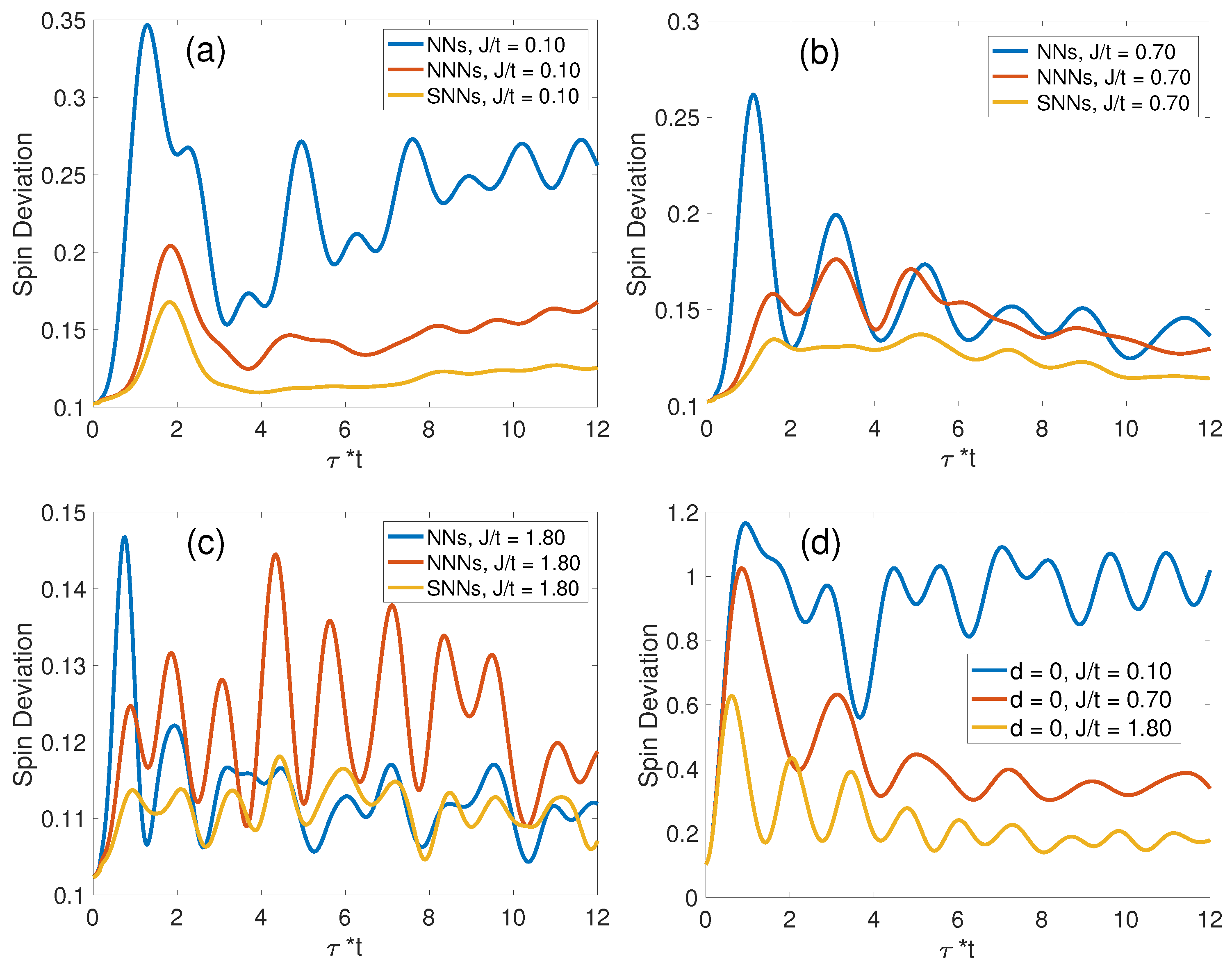
3.2.1. Zero-Temperature Spin Deviations
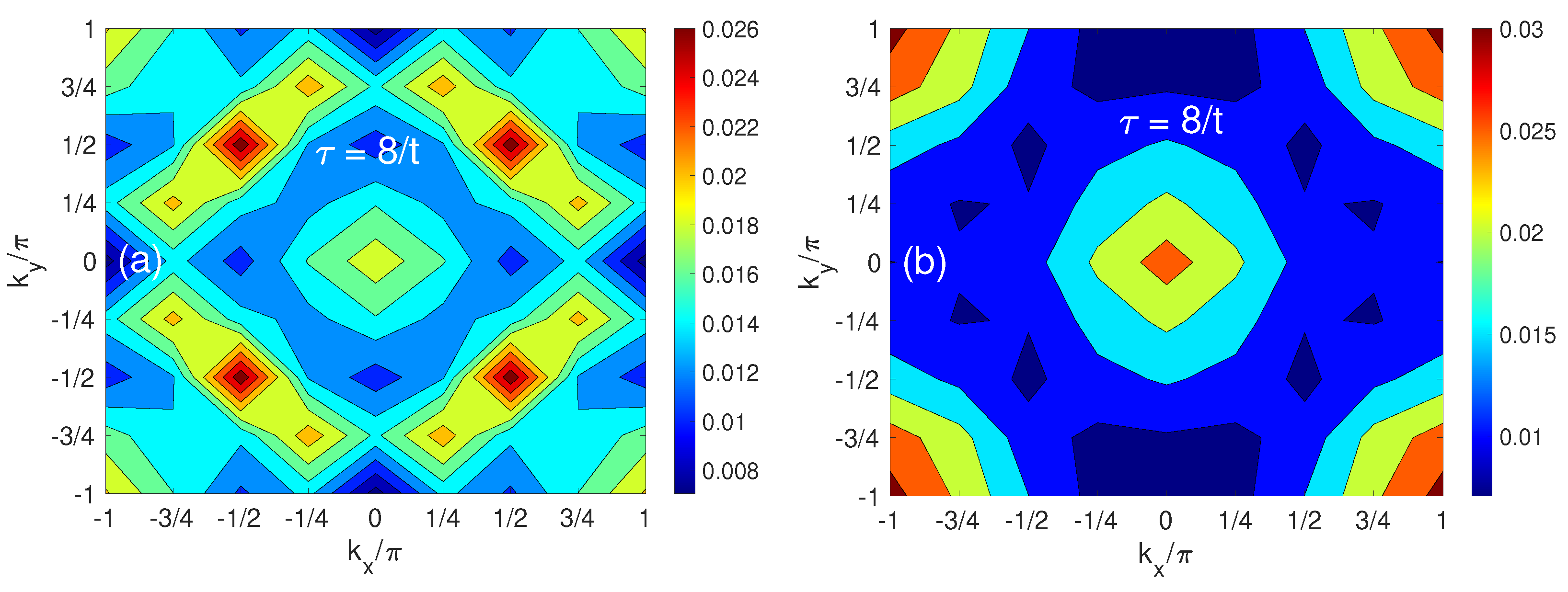
3.2.2. Finite-Temperature Hole Population Dynamics
3.2.3. Finite-Temperature Spin Deviation Evolutions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Antiferromagnetic |
| 2D | Two-dimensional |
| ARPES | Angle-resolved photoemission spectroscopy |
| SCBA | Self-consistent Born approximation |
| mDA | Multiple Davydov Ansatz |
| TFD | Thermo-field dynamics |
| NNs | Nearest neighbors |
| NNNs | Next-nearest neighbors |
| SNNs | Second-nearest neighbors |
| SLP | Spin-lattice polaron |
Appendix A. Derivation of Hole–Magnon Dynamics in the t-J Model
References
- Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179. [Google Scholar] [CrossRef] [PubMed]
- Boyce, B.R.; Skinta, J.A.; Lemberger, T.R. Effect of the pseudogap on the temperature dependence of the magnetic penetration depth in YBCO films. Phys. Supercond. 2000, 341, 561–562. [Google Scholar] [CrossRef]
- Brinckmann, J.; Lee, P.A. Renormalized mean-field theory of neutron scattering in cuprate superconductors. Phys. Rev. B 2001, 65, 014502. [Google Scholar] [CrossRef]
- Brinckmann, J.; Lee, P.A. Slave Boson approach to neutron scattering in YBa2Cu3O6+y superconductors. Phys. Rev. Lett. 1999, 82, 2915. [Google Scholar] [CrossRef]
- Padilla, W.J.; Lee, Y.S.; Dumm, M.; Blumberg, G.; Ono, S.; Segawa, K.; Komiya, S.; Ando, Y.; Basov, D.N. Constant effective mass across the phase diagram of high-Tc cuprates. Phys. Rev. B 2005, 72, 060511. [Google Scholar] [CrossRef]
- Senthil, T.; Lee, P.A. Cuprates as doped U(1) spin liquids. Phys. Rev. B 2005, 71, 174515. [Google Scholar] [CrossRef]
- Senthil, T.; Motrunich, O. Microscopic models for fractionalized phases in strongly correlated systems. Phys. Rev. B 2002, 66, 205104. [Google Scholar]
- Senthil, T.; Vishwanath, A.; Balents, L.; Sachdev, S.; Fisher, M.P. Deconfined quantum critical points. Science 2004, 303, 1490–1494. [Google Scholar]
- Ussishkin, I.; Sondhi, S.L.; Huse, D.A. Gaussian superconducting fluctuations, thermal transport, and the Nernst effect. Phys. Rev. Lett. 2002, 89, 287001. [Google Scholar] [CrossRef]
- Vojta, M.; Sachdev, S. Charge order, superconductivity, and a global phase diagram of doped antiferromagnets. Phys. Rev. Lett. 1999, 83, 3916. [Google Scholar] [CrossRef]
- Wen, H.-H.; Li, S. Materials and novel superconductivity in iron pnictide superconductors. Annu. Rev. Condens. Matter Phys. 2011, 2, 121. [Google Scholar] [CrossRef]
- Wosnitza, J. Superconductivity in layered organic metals. Crystals 2012, 2, 248. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef] [PubMed]
- Dagotto, E. Correlated electrons in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 763. [Google Scholar]
- Lee, P.A.; Nagaosa, N.; Wen, X.-G. Doping a mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17. [Google Scholar]
- Carlström, J.; Prokof’ev, N.; Svistunov, B. Quantum Walk in Degenerate Spin Environments. Phys. Rev. Lett. 2016, 116, 247202. [Google Scholar] [PubMed]
- Kanasz-Nagy, M.; Lovas, I.; Grusdt, F.; Greif, D.; Greiner, M.; Demler, E.A. Quantum correlations at infinite temperature: The dynamical nagaoka effect. Phys. Rev. B 2017, 96, 014303. [Google Scholar]
- Grusdt, F.; Zhu, Z.; Shi, T.; Demler, E. Meson formation in mixed-dimensional t-J models. SciPost Phys. 2018, 5, 057. [Google Scholar]
- Grusdt, F.; Kanasz-Nagy, M.; Bohrdt, A.; Chiu, C.S.; Ji, G.; Greiner, M.; Greif, D.; Demler, E. Parton Theory of Magnetic Polarons: Mesonic Resonances and Signatures in Dynamics. Phys. Rev. X 2018, 8, 011046. [Google Scholar]
- Nielsen, K.K.; Bastarrachea-Magnani, M.A.; Pohl, T.; Bruun, G.M. Spatial structure of magnetic polarons in strongly interacting antiferromagnets. Phys. Rev. B 2021, 104, 155136. [Google Scholar] [CrossRef]
- Brown, P.T.; Mitra, D.; Guardado-Sanchez, E.; Nourafkan, R.; Reymbaut, A.; Hébert, C.-D.; Bergeron, S.; Tremblay, A.-M.S.; Kokalj, J.; Huse, D.A.; et al. Bad metallic transport in a cold atom Fermi-Hubbard system. Science 2019, 363, 379. [Google Scholar] [CrossRef]
- Koepsell, J.; Vijayan, J.; Sompet, P.; Grusdt, F.; Hilker, T.A.; Demler, E.; Salomon, G.; Bloch, I.; Gross, C. Imaging magnetic polarons in the doped Fermi-Hubbard model. Nature 2019, 572, 358. [Google Scholar]
- Ji, G.; Xu, M.; Kendrick, L.H.; Chiu, C.S.; Brüggenjürgen, J.C.; Greif, D.; Bohrdt, A.; Grusdt, F.; Demler, E.; Lebrat, M.; et al. Coupling a Mobile Hole to an Antiferromagnetic Spin Background: Transient Dynamics of a Magnetic Polaron. Phys. Rev. X 2021, 11, 021022. [Google Scholar] [CrossRef]
- Koepsell, J.; Bourgund, D.; Sompet, P.; Hirthe, S.; Bohrdt, A.; Wang, Y.; Grusdt, F.; Demler, E.; Salomon, G.; Gross, C.; et al. Microscopic evolution of doped Mott insulators from polaronic metal to Fermi liquid. Science 2021, 374, 82. [Google Scholar]
- Gall, M.; Wurz, N.; Samland, J.; Chan, C.F.; Köhl, M. Competing magnetic orders in a bilayer Hubbard model with ultracold atoms. Nature 2021, 589, 40. [Google Scholar] [CrossRef] [PubMed]
- Hirthe, S.; Chalopin, T.; Bourgund, D.; Bojovic, P.; Bohrdt, A.; Demler, E.; Grusdt, F.; Bloch, I.; Hilker, T.A. Magnetically mediated hole pairing in fermionic ladders of ultracold atoms. Nature 2022, 613, 463–467. [Google Scholar] [CrossRef] [PubMed]
- Schmitt-Rink, S.; Varma, C.M.; Ruckenstein, A.E. Spectral Function of Holes in a Quantum Antiferromagnet. Phys. Rev. Lett. 1988, 60, 2793. [Google Scholar] [CrossRef]
- Liu, Z.; Manousakis, E. Spectral function of a hole in the t-J model. Phys. Rev. B 1991, 44, 2414. [Google Scholar]
- Damascelli, A.; Hussain, Z.; Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473. [Google Scholar] [CrossRef]
- Marshall, D.S.; Dessau, D.S.; Loeser, A.G.; Park, C.-H.; Matsuura, A.Y.; Eckstein, J.N.; Bozovic, I.; Fournier, P.; Kapitulnik, A.; Spicer, W.E.; et al. Unconventional electronic structure evolution with hole doping in Bi2Sr2CaCu2O8+δ: Angle-resolved photoemission results. Phys. Rev. Lett. 1996, 76, 4841. [Google Scholar] [CrossRef]
- Eder, R.; Ohta, Y.; Sawatzky, G.A. Doping-dependent quasiparticle band structure in cuprate superconductors. Phys. Rev. B 1997, 55, R3414. [Google Scholar]
- Kim, C.; White, P.J.; Shen, Z.-X.; Tohyama, T.; Shibata, Y.; Maekawa, S.; Wells, B.O.; Kim, Y.J.; Birgeneau, R.J.; Kastner, M.A. Systematics of the photoemission spectral function of cuprates: Insulators and hole-and electron-doped superconductors. Phys. Rev. Lett. 1998, 80, 4245. [Google Scholar] [CrossRef]
- Yin, W.-G.; Gong, C.-D.; Leung, P.W. Origin of the extended Van Hove region in cuprate superconductors. Phys. Rev. Lett. 1998, 81, 2534. [Google Scholar] [CrossRef]
- Shraiman, B.I.; Siggia, E.D. Mobile Vacancies in a Quan- tum Heisenberg Antiferromagnet. Phys. Rev. Lett. 1988, 61, 467. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Lee, P.A.; Read, N. Motion of a single hole in a quantum antiferromagnet. Phys. Rev. B 1989, 39, 6880. [Google Scholar] [CrossRef]
- Martinez, G.; Horsch, P. Spin polarons in the t-J model. Phys. Rev. B 1991, 44, 317. [Google Scholar] [CrossRef]
- Marsiglio, F.; Ruckenstein, A.E.; Schmitt-Rink, S.; Varma, C.M. Spectral function of a single hole in a two-dimensional quantum antiferromagnet. Phys. Rev. B 1991, 43, 10882. [Google Scholar] [CrossRef]
- Chernyshev, A.L.; Leung, P.W. Holes in the t-J z model: A diagrammatic study. Phys. Rev. B 1999, 60, 1592. [Google Scholar] [CrossRef]
- Diamantis, N.G.; Manousakis, E. Dynamics of string-like states of a hole in a quantum antiferromagnet: A diagrammatic monte carlo simulation. New J. Phys. 2021, 23, 123005. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Pohl, T.; Bruun, G.M. Nonequilibrium Hole Dynamics in Antiferromagnets: Damped Strings and Polarons. Phys. Rev. Lett. 2022, 129, 246601. [Google Scholar] [PubMed]
- Nazarenko, A.; Dagotto, E. Hole dispersion and symmetry of the superconducting order parameter for underdoped CuO2 bilayers and the three-dimensional antiferromagnets. Phys. Rev. B 1996, 54, 13158. [Google Scholar] [CrossRef]
- Yin, W.-G.; Gong, C.-D. Quasiparticle bands in the realistic bilayer cuprates. Phys. Rev. B 1997, 56, 2843. [Google Scholar] [CrossRef]
- Yin, W.-G.; Gong, C.-D. Quasiparticle bands and superconductivity for the multiple-layer and three-dimensional superlattice t-J models. Phys. Rev. B 1998, 57, 11743. [Google Scholar]
- Hida, K. Quantum disordered state without frustration in the double layer Heisenberg antiferromagnet: Dimer expansion and projector monte carlo study. J. Phys. Soc. Jpn. 1992, 61, 1013. [Google Scholar]
- Sandvik, A.W.; Scalapino, D.J. Order-Disorder Transition in a Two-Layer Quantum Antiferromagnet. Phys. Rev. Lett. 1994, 72, 2777. [Google Scholar]
- Scalettar, R.T.; Cannon, J.W.; Scalapino, D.J.; Sugar, R.L. Magnetic and pairing correlations in coupled Hubbard planes. Phys. Rev. B 1994, 50, 13419. [Google Scholar] [CrossRef] [PubMed]
- Millis, A.J.; Monien, H. Spin gaps and bilayer coupling in YBa2Cu3O7-δ and YBa2Cu4O8. Phys. Rev. B 1994, 50, 16606. [Google Scholar] [CrossRef]
- Plakida, N.M.; Oudovenko, V.S.; Yushankhai, V.Y. Temperature and doping dependence of the quasiparticle spectrum for holes in the spin-polaron model of copper oxides. Phys. Rev. B 1994, 50, 6431. [Google Scholar] [CrossRef]
- Igarashi, J.-I.; Fulde, P. Motion of a single hole in a quantum antiferromagnet at finite temperatures. Phys. Rev. B 1993, 48, 998–1007. [Google Scholar]
- Yanga, D.M.; Morales, A.A. The finite temperature Green’s function method for the spin-polaron problem. Phys. C Supercond. 2000, 341, 147–148. [Google Scholar]
- Schrieffer, J.R.; Wen, X.-G.; Zhang, S.-C. Spin-bag mechanism of high-temperature superconductivity. Phys. Rev. Lett. 1988, 60, 944. [Google Scholar] [CrossRef]
- Zhao, Y. The hierarchy of Davydov’s Ansätze: From guesswork to numerically “exact” many-body wave functions. J. Chem. Phys. 2023, 158, 080901. [Google Scholar]
- Takahashi, Y.; Umezawa, H. Thermo field dynamics. Int. J. Mod. Phys. B. 1996, 10, 1755. [Google Scholar]
- Suzuki, M. Density Matrix Formalism, Double-Space and Thermo Field Dynamics in Non-Equilibrium Dissipative Systems. Int. J. Mod. Phys. B. 1991, 05, 1821. [Google Scholar]
- Ramšak, A.; Horsch, P. Spin polarons in the t-J model: Shape and backflow. Phys. Rev. B 1993, 48, 10559. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, R.; Gelin, M.F. Finite temperature quantum dynamics of complex systems: Integrating thermo-field theories and tensor-train methods. WIREs Comput. Mol. Sci. 2021, 11, e1539. [Google Scholar]
- Zhao, Y.; Chen, G.; Yu, L. Lattice and Spin Polarons in Two Dimensions. J. Chem. Phys. 2000, 113, 6502–6508. [Google Scholar] [CrossRef]
- Suzuki, M. Thermo field dynamics of quantum spin systems. J. Stat. Phys. 1986, 42, 1047. [Google Scholar] [CrossRef]
- Borrelli, R.; Gelin, M.F. Quantum electron-vibrational dynamics at finite temperature: Thermo field dynamics approach. J. Chem. Phys. 2016, 145, 224101. [Google Scholar] [PubMed]
- Chen, L.; Zhao, Y. Finite temperature dynamics of a Holstein polaron: The thermo-field dynamics approach. J. Chem. Phys. 2017, 147, 214102. [Google Scholar] [CrossRef] [PubMed]
- Izyumov, Y.A. Strongly correlated electrons: The tJ model. Phys.-Uspekhi 1997, 405, 445. [Google Scholar] [CrossRef]
- Rezende, S.M.; Azevedo, A.; Rodríguez-Suárez, R.L. Introduction to antiferromagnetic magnons. J. Appl. Phys. 2019, 126, 151101. [Google Scholar] [CrossRef]
- Zheng, F.; Shen, Y.; Sun, K.; Zhao, Y. Photon-assisted Landau-Zener transitions in a periodically driven Rabi dimer coupled to a dissipative mode. J. Chem. Phys. 2021, 154, 044102. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Gelin, M.F.; Zhao, Y. Accurate Simulation of Spectroscopic Signatures of Cavity-Assisted, Conical-Intersection-Controlled Singlet Fission Processes. J. Phys. Chem. Lett. 2022, 13, 4280–4288. [Google Scholar]
- Chen, L.; Gelin, M.F.; Domcke, W.; Zhao, Y. Theory of femtosecond coherent double-pump single-molecule spectroscopy:Application to light harvesting complexes. J. Chem. Phys. 2015, 142, 164106. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Shen, K.; Gelin, M.F.; Zhao, Y. Exciton Dynamics and Time-Resolved Fluorescence in Nanocavity-Integrated Monolayers of Transition-Metal Dichalcogenides. J. Phys. Chem. Lett. 2022, 14, 221–229. [Google Scholar] [CrossRef]
- Manousakis, E. String excitations of a hole in a quantum antiferromagnet and photoelectron spectroscopy. Phys. Rev. B. 2007, 75, 035106. [Google Scholar]
- Leung, P.W.; Gooding, R.J. Dynamical properties of the single-hole t-J model on a 32-site square lattice. Phys. Rev. B 1995, 52, R15711. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wang, Q.R.; Qi, Y.; Sheng, D.N.; Weng, Z.Y. Single-hole wave function in two dimensions: A case study of the doped Mott insulator. Phys. Rev. B 2019, 99, 205128. [Google Scholar] [CrossRef]
- Hubig, C.; Bohrdt, A.; Knap, M.; Grusdt, F.; Cirac, J.I. Evaluation of time-dependent correlators after a local quench in iPEPS: Hole motion in the t-J model. SciPost Phys. 2020, 8, 021. [Google Scholar] [CrossRef]
- Pryadko, L.P.; Kivelson, S.A.; Zachar, O. Incipient Order in the t-J Model at High Temperatures. Phys. Rev. Lett. 2004, 92, 067002. [Google Scholar] [PubMed]
- Olsson, K.S.; An, K.; Li, X. Magnon and phonon thermometry with inelastic light scattering. J. Phys. D Appl. Phys. 2018, 51, 133001. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Rösch, O. Electron-phonon coupling in the self-consistent Born approximation of the t-J model. Phys. Rev. B 2006, 73, 174521. [Google Scholar] [CrossRef]
- Bohrdt, A.; Greif, D.; Demler, E.; Knap, M.; Grusdt, F. Angle-resolved photoemission spectroscopy with quantum gas microscopes. Phys. Rev. B 2018, 97, 125117. [Google Scholar] [CrossRef]
- Bohrdt, A.; Demler, E.; Pollmann, F.; Knap, M.; Grusdt, F. Parton theory of angle-resolved photoemission spectroscopy spectra in antiferromagnetic Mott insulators. Phys. Rev. B 2020, 102, 035139. [Google Scholar] [CrossRef]
- Kato, K.; Yokoyama, T.; Ishihara, H. Functionalized High-Speed Magnon Polaritons Resulting from Magnonic Antenna Effect. Phys. Rev. Appl. 2023, 19, 034035. [Google Scholar]
- Nyhegn, J.H.; Bruun, G.M.; Nielsen, K.K. Wave function and spatial structure of polarons in an antiferromagnetic bilayer. Phys. Rev. B 2023, 108, 075141. [Google Scholar] [CrossRef]
- Nielsen, K.K. Exact dynamics of two holes in two-leg antiferromagnetic ladders. Phys. Rev. B 2023, 108, 085125. [Google Scholar] [CrossRef]
- Kogoj, J.; Lenarčič, Z.; Golež, D.; Mierzejewski, M.; Prelovšek, P.; Bonča, J. Multistage dynamics of the spin-lattice polaron formation. Phys. Rev. B 2014, 90, 125104. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, K.; Gelin, M.F.; Sun, K.; Zhao, Y. Dynamics of a Magnetic Polaron in an Antiferromagnet. Materials 2024, 17, 469. https://doi.org/10.3390/ma17020469
Shen K, Gelin MF, Sun K, Zhao Y. Dynamics of a Magnetic Polaron in an Antiferromagnet. Materials. 2024; 17(2):469. https://doi.org/10.3390/ma17020469
Chicago/Turabian StyleShen, Kaijun, Maxim F. Gelin, Kewei Sun, and Yang Zhao. 2024. "Dynamics of a Magnetic Polaron in an Antiferromagnet" Materials 17, no. 2: 469. https://doi.org/10.3390/ma17020469
APA StyleShen, K., Gelin, M. F., Sun, K., & Zhao, Y. (2024). Dynamics of a Magnetic Polaron in an Antiferromagnet. Materials, 17(2), 469. https://doi.org/10.3390/ma17020469





