Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling
Abstract
1. Introduction
1.1. Dynamic and Static Flow Stress with Thermal Softening of Ti64
1.2. Mechanical Model of Flow Stress Behavior
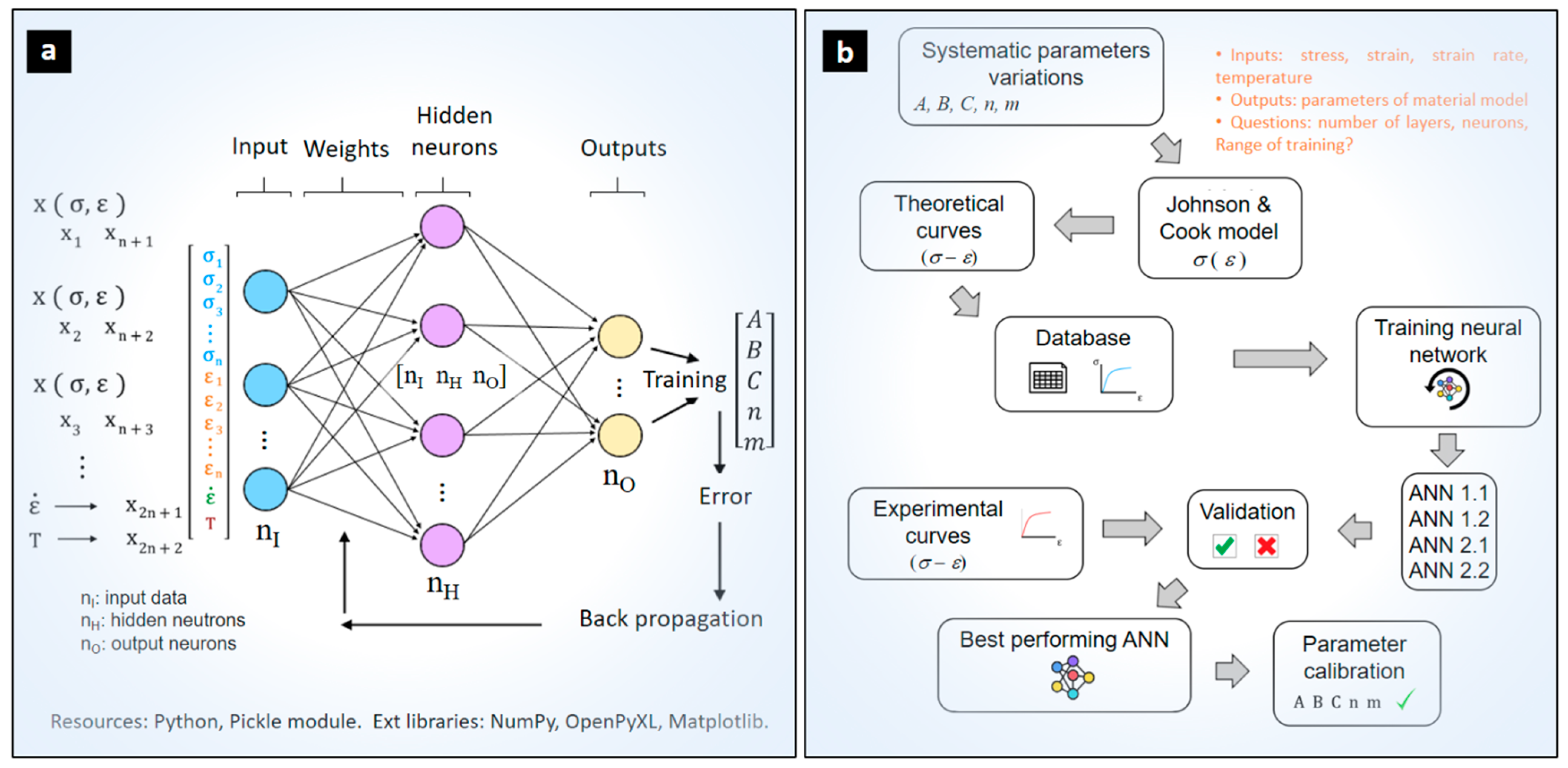
2. Model Calibration Strategy Based on Feed-Forward Backpropagation Neural Network
2.1. Modeling of Feed-Forward Neural Networks
2.2. Database Generation, Training, and Calibration Strategy Using ANN Configurations
3. Results and Discussion
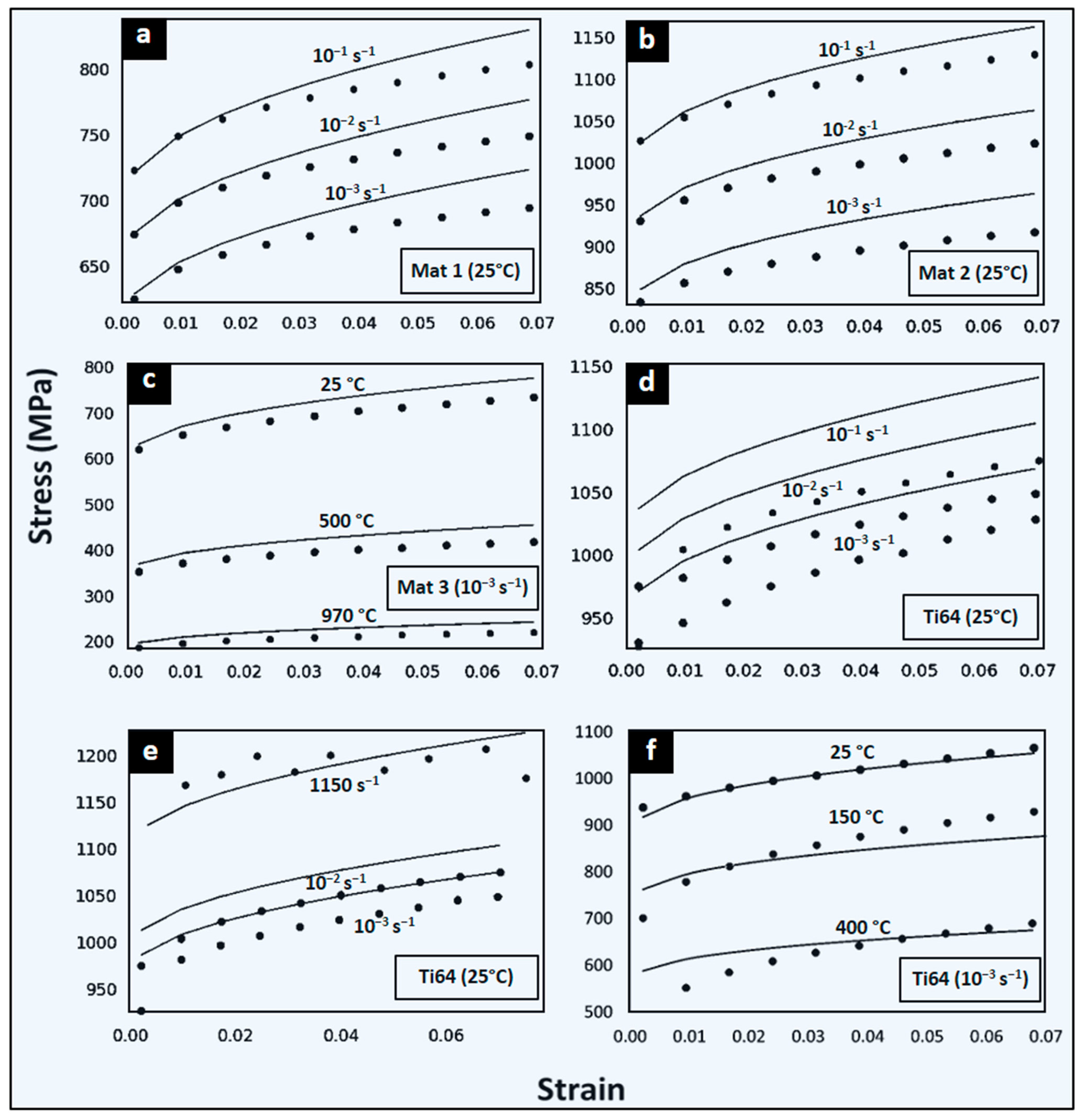
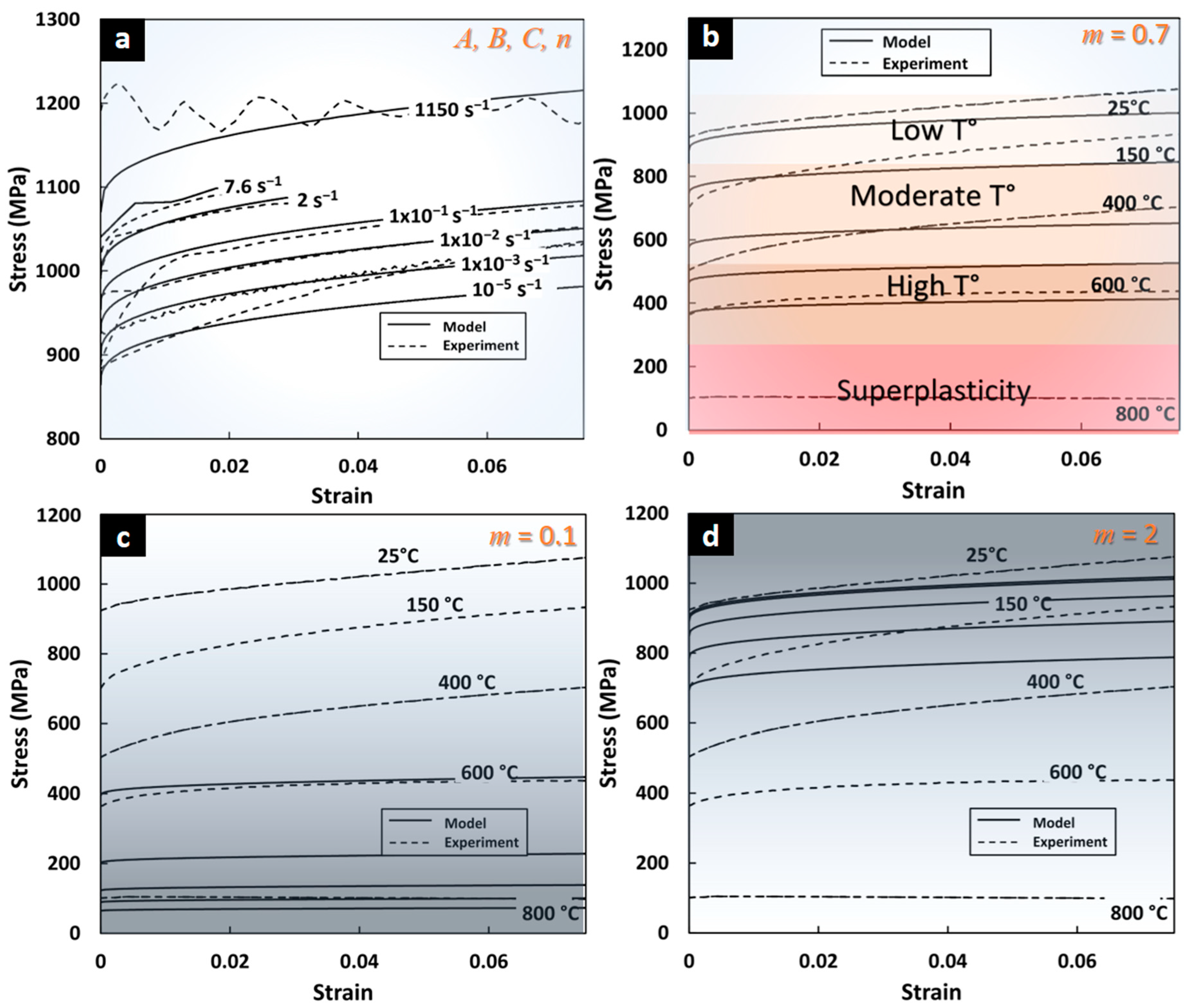
3.1. Quasi-Static and Dynamic Predictions of Flow Stress with ANN-Based Strategy
3.2. Assessment of JC Model in Superplasticity
4. Conclusions
- The implemented method applied to the parameter calibration of the Johnson–Cook model with the proposed feed-forward ANN architecture of 66 inputs, 30 hidden, and 5 output neurons provides the most accurate results. Input of only three experimental stress–strain curves at different strain rates is required to obtain an adequate set of model parameters with a prediction accuracy of 96.5% (GMAPE of 4.5%).
- The analysis and optimization of the JC model indicates that a high accuracy of the flow stress strain response for the Ti64 alloy is achieved for strain rate range between 10−3 and 1000 s−1, and for temperatures between 25 and 400 °C, with a prediction accuracy of 95% (GMAPE of 5%).
- The prediction accuracy of an ANN-based calibration strategy of JC flow stress model is slightly better than the direct optimization method, and requires less number of input stress–strain curves.
- Superplastic behavior and moderate temperature (above 400 °C) is not adequately modeled by JC. This finding is also similar to the calibration results using other models such as Northon–Hoff [40].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Serope, K.; Schmid, S.R. Manufacturing Engineering and Technology, 4th ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Özel, T.; Karpat, Y. Identification of constitutive material model parameters for high-strain rate metal cutting conditions using evolutionary computational algorithms. Mater. Manuf. Process. 2007, 22, 659–667. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, X.; Guo, H.; Xu, S.; Li, H.; Nishiwaki, S.; Chen, Y.; Takezawa, A. Multiscale topology optimization of biodegradable metal matrix composite structures for additive manufacturing. Appl. Math. Model. 2023, 114, 799–822. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Duchêne, L.; Hashemi, N.; Tran, H.S.; Carrus, R.; Mertens, A.; Habraken, A.M. Optimizing laser power of directed energy deposition process for homogeneous AISI M4 steel microstructure. Opt. Laser Technol. 2022, 163, 109426. [Google Scholar] [CrossRef]
- Sepúlveda, H.; Valle, R.; Pincheira, G.; Prasad, C.S.; Salas, A.; Medina, C.; Tuninetti, V. Dynamic numerical prediction of plasticity and damage in a turbofan blade containment test. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 2251–2560. [Google Scholar] [CrossRef]
- Cao, Z.; Fei, Q.; Jiang, D.; Kapania, R.K.; Wu, S.; Jin, H. A sensitivity-based nonlinear finite element model updating method for nonlinear engineering structures. Appl. Math. Model. 2021, 100, 632–655. [Google Scholar] [CrossRef]
- Bustos, F.; Hinojosa, J.; Tuninetti, V. Computational Comparison of Performance of Different Steel Plate Shear Yielding Dampers. Buildings 2023, 13, 793. [Google Scholar] [CrossRef]
- Fylstra, D.; Lasdon, L.; Watson, J.; Waren, A. Design and use of the Microsoft Excel Solver. Interfaces 1998, 28, 29–55. [Google Scholar] [CrossRef]
- Lasdon, L.; Fox, R.; Ratner, M. Nonlinear optimization using the generalized. Inform. Rech. Opérationn 1974, 3, 73–103. [Google Scholar]
- Bergs, T.; Hardt, M.; Schraknepper, D. Determination of Johnson-Cook material model parameters for AISI 1045 from orthogonal cutting tests using the Downhill-Simplex algorithm. Procedia Manuf. 2020, 48, 541–552. [Google Scholar] [CrossRef]
- Tuninetti, V. Alternative experimental method for characterizing the deformation behavior of Ti6Al4V at constant strain rates over the full elastoplastic range. Int. J. Mater. Form. 2019. preprint. [Google Scholar]
- Rojas-Ulloa, C.; Bouffioux, C.; Jaramillo, A.F.; García-Herrera, C.M.; Hussain, T.; Duchêne, L.; Riu, G.; Josep Roa, J.; Flores, P.; Marie Habraken, A.; et al. Nanomechanical Characterization of the Deformation Response of Orthotropic Ti–6Al–4V. Adv. Eng. Mater. 2021, 23, 2001341. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Flores, P.; Pincheira, G.; Duchêne, L.; Habraken, A.-M. Impact of distortional hardening and the strength differential effect on the prediction of large deformation behavior of the Ti6Al4V alloy. Meccanica 2019, 54, 1823–1840. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Valenzuela, M.; Tuninetti, V.; Habraken, A.M. Identification and validation of an extended Stewart-Cazacu micromechanics damage model applied to Ti–6Al–4V specimens exhibiting positive stress triaxialities. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1248–1261. [Google Scholar] [CrossRef]
- Lee, H.; Huen, W.Y.; Vimonsatit, V.; Mendis, P. An Investigation of Nanomechanical Properties of Materials using Nanoindentation and Artificial Neural Network. Sci. Rep. 2019, 9, 13189. [Google Scholar] [CrossRef] [PubMed]
- Uz, M.M.; Hazar Yoruç, A.B.; Cokgunlu, O.; Aydoğan, C.S.; Yapici, G.G. A comparative study on phenomenological and artificial neural network models for high temperature flow behavior prediction in Ti6Al4V alloy. Mater. Today Commun. 2022, 33, 104933. [Google Scholar] [CrossRef]
- Kalina, K.A.; Linden, L.; Brummund, J.; Metsch, P.; Kästner, M. Automated constitutive modeling of isotropic hyperelasticity based on artificial neural networks. Comput. Mech. 2022, 69, 213–232. [Google Scholar] [CrossRef]
- Zhang, A.; Mohr, D. Using neural networks to represent von Mises plasticity with isotropic hardening. Int. J. Plast. 2020, 132, 102732. [Google Scholar] [CrossRef]
- Marouani, H.; Aguir, H. Identification of material parameters of the Gurson-Tvergaard-Needleman damage law by combined experimental, numerical sheet metal blanking techniques and artificial neural networks approach. Int. J. Mater. Form. 2012, 5, 147–155. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Zhao, Y.Q.; Han, Y.F.; Ma, X. Intelligent method to develop constitutive relationship of Ti-6Al-2Zr-1Mo-1V alloy. Trans. Nonferrous Met. Soc. China Engl. Ed. 2012, 22, 1457–1461. [Google Scholar] [CrossRef]
- Xie, G.; Jia, H.; Li, H.; Zhong, Y.; Du, W. A life prediction method of mechanical structures based on the phase field method and neural network. Appl. Math. Model. 2023, 119, 782–802. [Google Scholar] [CrossRef]
- Gorji, M.B.; Mozaffar, M.; Heidenreich, J.N.; Cao, J.; Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity. J. Mech. Phys. Solids 2020, 143, 103972. [Google Scholar] [CrossRef]
- Li, L.F.; Chen, C.Q. Equilibrium-based convolution neural networks for constitutive modeling of hyperelastic materials. J. Mech. Phys. Solids 2022, 164, 104931. [Google Scholar] [CrossRef]
- Lecarme, L. Viscoplasticity, Damage, and Fracture of Ti-6Al-4V. Ph.D. Thesis, Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2013. [Google Scholar]
- Tuninetti, V. Experimental and Numerical Study of the Quasi-Static Behavior of Ti–6Al–4v. Ph.D. Thesis, Univertisé de Liège, Liège, Belgium, 2014. [Google Scholar]
- Peirs, J. Experimental Charcterisation and Modelling of the Dynamic Behaviour of the Titanium Alloy Ti6Al4V. Ph.D. Thesis, Ghent University, Gent, Belgium, 2012. [Google Scholar]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.M. Experimental characterization of the compressive mechanical behaviour of Ti6Al4V alloy at constant strain rates over the full elastoplastic range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Sepúlveda, H.; Pincheira, G.; Flores, P.; Duchêne, L.; Habraken, A.M. Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy. Phys. Sci. Forum 2022, 4, 2. [Google Scholar] [CrossRef]
- Kara, F.; Aslantaş, K.; Çiçek, A. Prediction of cutting temperature in orthogonal machining of AISI 316L using artificial neural network. Appl. Soft Comput. J. 2016, 38, 64–74. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, D.; Zhou, J.; Zuo, S.; Zhang, P. Comparison of the Warm Deformation Constitutive Model of GH4169 Alloy Based on Neural Network and the Arrhenius Model. Metals 2022, 12, 1429. [Google Scholar] [CrossRef]
- Titu, N.A.; Baucum, M.; No, T.; Trotsky, M.; Karandikar, J.; Schmitz, T.L.; Khojandi, A. Estimating Johnson-Cook material parameters using neural networks. Procedia Manuf. 2021, 53, 680–689. [Google Scholar] [CrossRef]
- Deb, S.; Muraleedharan, A.; Immanuel, R.J.; Panigrahi, S.K.; Racineux, G.; Marya, S. Establishing flow stress behaviour of Ti-6Al-4V alloy and development of constitutive models using Johnson-Cook method and Artificial Neural Network for quasi-static and dynamic loading. Theor. Appl. Fract. Mech. 2022, 119, 103338. [Google Scholar] [CrossRef]
- Yousfi, W.; Darnis, P.; Cahuc, O.; Laheurte, R.; Calamaz, M. 3D modeling of strain fields and strain rate in the cutting area: Application to milling. Int. J. Adv. Manuf. Technol. 2016, 84, 2207–2218. [Google Scholar] [CrossRef]
- Golasiński, K.; Pieczyska, E.; Maj, M.; Staszczak, M.; Świec, P.; Furuta, T.; Kuramoto, S. Investigation of strain rate sensitivity of Gum Metal under tension using digital image correlation. Arch. Civ. Mech. Eng. 2020, 20, 53. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Klippel, H.; Roethlin, M.; Wegener, K. An improved thermal model for SPH metal cutting simulations on GPU. Appl. Math. Model. 2021, 100, 728–750. [Google Scholar] [CrossRef]
- Ning, J.; Liang, S.Y. Inverse identification of Johnson-Cook material constants based on modified chip formation model and iterative gradient search using temperature and force measurements. Int. J. Adv. Manuf. Technol. 2019, 102, 2865–2876. [Google Scholar] [CrossRef]
- He, Z.; Guo, X.; Xuan, H.; Shan, X.; Fan, X.; Chen, C.; Hong, W. Characteristics and mechanisms of turboshaft engine axial compressor casing containment. Chin. J. Aeronaut. 2021, 34, 171–180. [Google Scholar] [CrossRef]
- Rai, R.; Kumar, G.; Dagar, S.; Somashekar, V.; Ahmed, C. Numerical simulation of ballistic impact on aluminium 5083-H116 plate with Johnson cook plasticity model. Mater. Today Proc. 2021, 46, 10619–10627. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Feng, D.-L.; Lien, F.-S.; Yee, E.; Deng, S.-X.; Gao, F.; Peng, C. Numerical modelling of interaction between aluminium structure and explosion in soil. Appl. Math. Model. 2021, 99, 760–784. [Google Scholar] [CrossRef]
- Tuninetti, V.; Habraken, A.M. Impact of anisotropy and viscosity to model the mechanical behavior of Ti-6Al-4V alloy. Mater. Sci. Eng. A 2014, 605, 39–50. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Hunt, J. Working with Excel Files. In Advanced Guide to Python 3 Programming; Springer International Publishing: Cham, Switzerland, 2019; pp. 249–255. ISBN 978-3-030-25943-3. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Sim, K.H.; Ri, Y.C.; Jo, C.H.; Kim, O.J.; Kim, R.S.; Pak, H. Modified Zerilli-Armstrong and Khan-Huang-Liang constitutive models to predict hot deformation behavior in a powder metallurgy Ti-22Al-25Nb alloy. Vacuum 2023, 210, 111749. [Google Scholar] [CrossRef]
- Stoffel, M.; Bamer, F.; Markert, B. Neural network based constitutive modeling of nonlinear viscoplastic structural response. Mech. Res. Commun. 2019, 95, 85–88. [Google Scholar] [CrossRef]
- Linka, K.; Hillgärtner, M.; Abdolazizi, K.P.; Aydin, R.C.; Itskov, M.; Cyron, C.J. Constitutive artificial neural networks: A fast and general approach to predictive data-driven constitutive modeling by deep learning. J. Comput. Phys. 2021, 429, 110010. [Google Scholar] [CrossRef]

| ANN | Number of Input σ-ε Curves | Range [mm/mm] | Discrete Points per Curve | Discrete Strain Step | Number of Hidden Layers | Neurons per Layer |
|---|---|---|---|---|---|---|
| 1.1 | 3 | [0.002–0.075] | 74 | 0.001 | 1 | [450 30 5] |
| 1.2 | 2 | [450 30 15 5] | ||||
| 2.1 | 10 | 0.0074 | 1 | [66 30 5] | ||
| 2.2 | 2 | [66 30 15 5] |
| Input Material Dataset | Input Stress–Strain Data | GMAPE by ANN Configuration (%) | |||||
|---|---|---|---|---|---|---|---|
| Material | [A, B, C, n, m] | Strain Rate (s−1) | T (°C) | ANN 1.1 [450 30 5] | ANN 1.2 [450 30 15 5] | ANN 2.1 [66 30 5] | ANN 2.2 [66 30 15 5] |
| Mat 1 | [630, 252, 0.0105, 0.28, -] | [10−3, 10−2 10−1] | [25, 25, 25] | 5.5 | 9.7 | 2.0 | 4.1 |
| Mat 2 | [900, 360, 0.015, 0.52, -] | [10−3, 10−2, 10−1] | [25, 25, 25] | 3.0 | 7.5 | 2.7 | 6.2 |
| Mat 3 | [630, 468, 0.0105, 0.4, 0.7] | [10−3, 10−3, 10−3] | [25, 500, 970] | 7.4 | 8.3 | 6.5 | 9.1 |
| Ti64 | (Exp. data) | [10−3, 10−2, 10−1] | [25, 25, 25] | 19 | 23 | 5.2 | 2.7 |
| [10−3, 10−2, 1150] | [25, 25, 25] | 14 | 14 | 2.6 | 2.5 | ||
| [10−3, 10−3, 10−3] | [25, 150, 400] | 13 | 9.2 | 3.6 | 3.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuninetti, V.; Forcael, D.; Valenzuela, M.; Martínez, A.; Ávila, A.; Medina, C.; Pincheira, G.; Salas, A.; Oñate, A.; Duchêne, L. Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling. Materials 2024, 17, 317. https://doi.org/10.3390/ma17020317
Tuninetti V, Forcael D, Valenzuela M, Martínez A, Ávila A, Medina C, Pincheira G, Salas A, Oñate A, Duchêne L. Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling. Materials. 2024; 17(2):317. https://doi.org/10.3390/ma17020317
Chicago/Turabian StyleTuninetti, Víctor, Diego Forcael, Marian Valenzuela, Alex Martínez, Andrés Ávila, Carlos Medina, Gonzalo Pincheira, Alexis Salas, Angelo Oñate, and Laurent Duchêne. 2024. "Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling" Materials 17, no. 2: 317. https://doi.org/10.3390/ma17020317
APA StyleTuninetti, V., Forcael, D., Valenzuela, M., Martínez, A., Ávila, A., Medina, C., Pincheira, G., Salas, A., Oñate, A., & Duchêne, L. (2024). Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling. Materials, 17(2), 317. https://doi.org/10.3390/ma17020317






