Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms
Abstract
1. Introduction
2. Project Background of Station-Bridge
3. Analytical Model of Train-Track-Station System
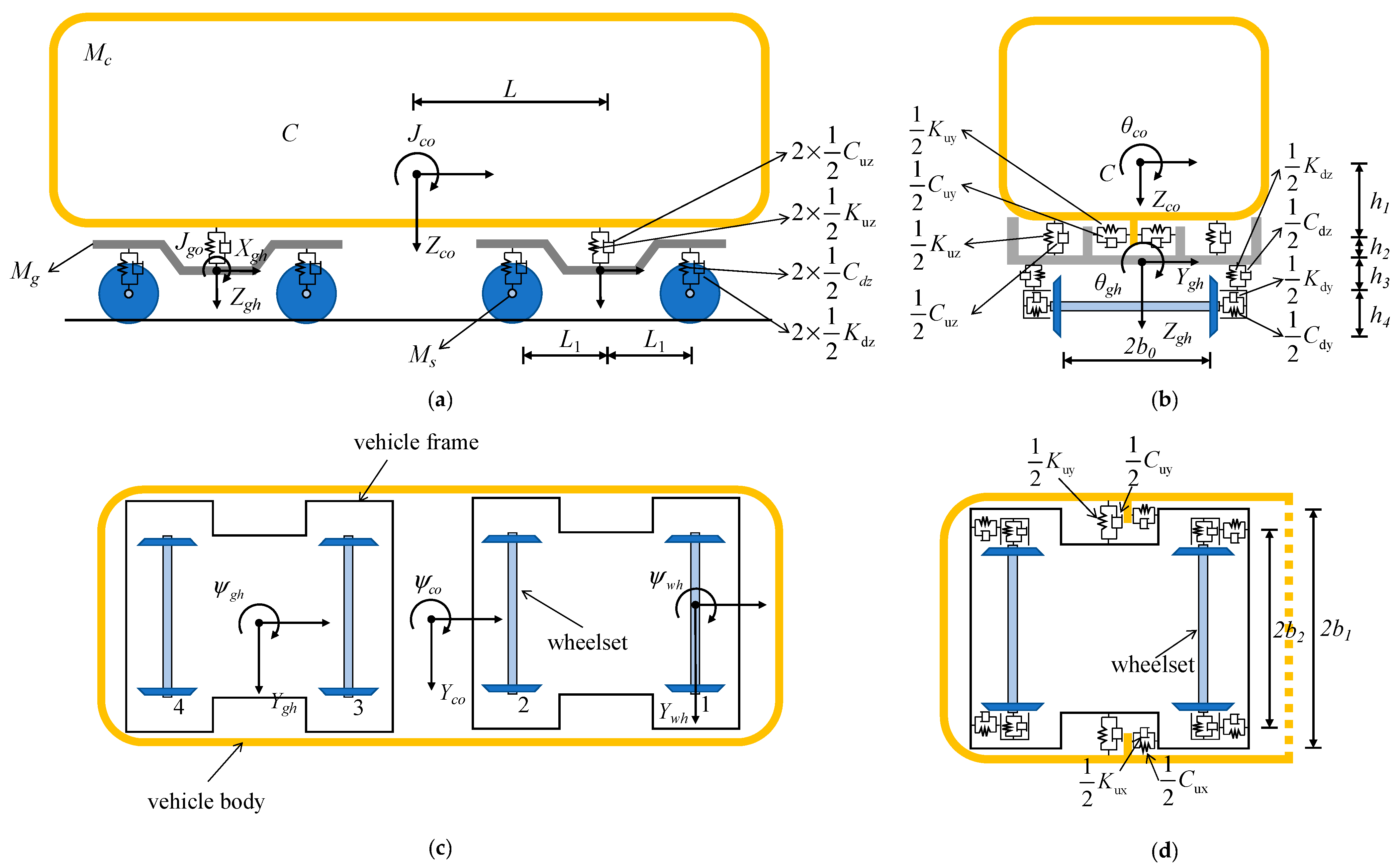
3.1. High-Speed Train and Track Irregularity
- (1)
- The body, bogie, and wheelset are assumed to be rigid;
- (2)
- The longitudinal vibration of locomotives and vehicles, and their effects on bridge vibration and travel speed, are not considered;
- (3)
- Vibrations in the wheelsets, bogies, and body are relatively minor;
- (4)
- The train suspension system is simulated with linear springs and viscous damping;
- (5)
- The wheelset and steel rail are in close contact in the vertical direction, and the vertical displacement of the wheelset and the rail are identical;
- Vertical profile:
- Alignment:
- Cross-level and gauge:where and are, respectively, the PSD functions of the cross-level and gauge track irregularities [cm2/(rad/m)], and is the cutoff frequency (rad/m). The standard track spectra are divided into six grades, and parameters of grade-6 are listed in Table 3. In the table, the maximum allowable train speeds related to different grades in accordance with the running safety standard are also given.
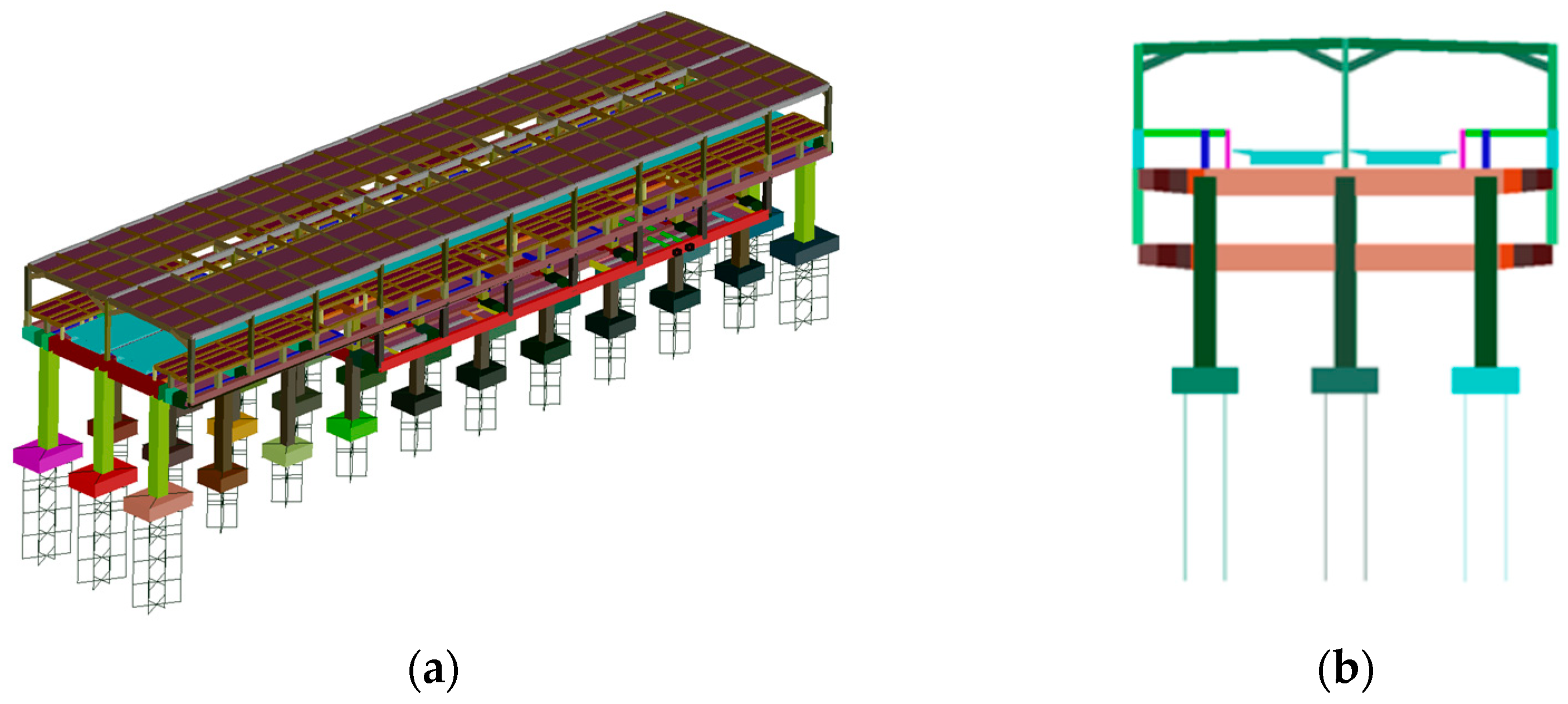
3.2. Finite Element Models of Track-Station System
3.3. Train-Track-Station Coupling Model
4. Dynamic Response Analysis for Train-Track-Station System
4.1. Relationship between Vehicle Parameters and Station Dynamic Response
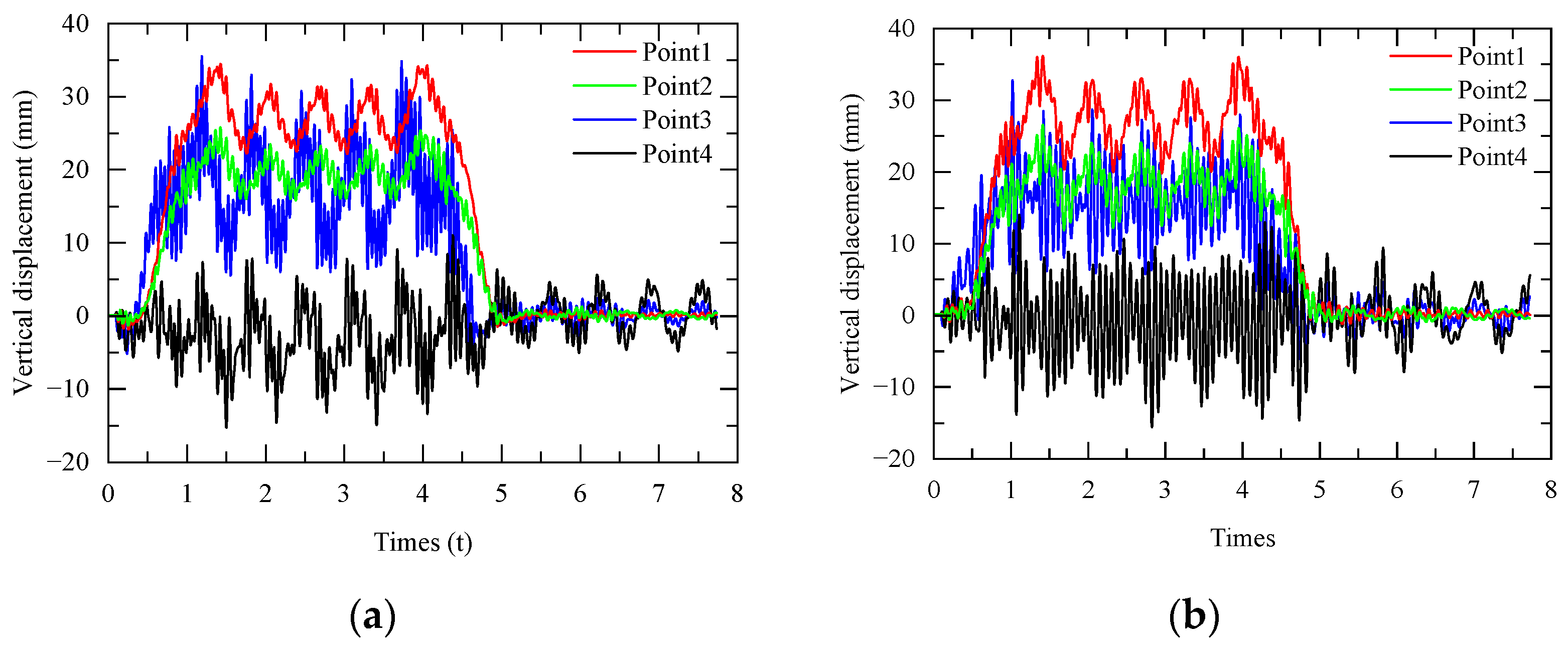
4.1.1. Single-Line Train Operation
4.1.2. Double-Line Train Operation
4.2. Analysis of Station Structural Parameters
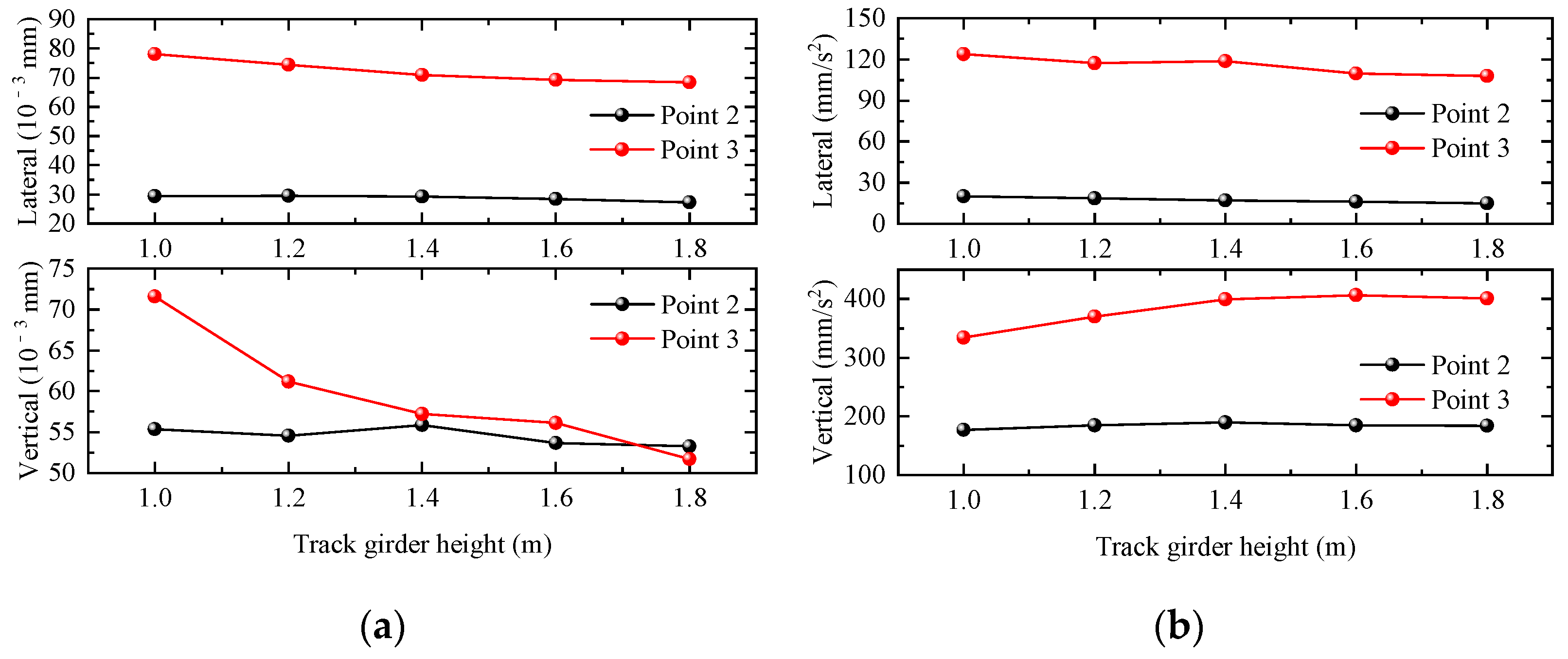
4.2.1. Track Girder Height
4.2.2. Thickness of Rail-Bearing Layer
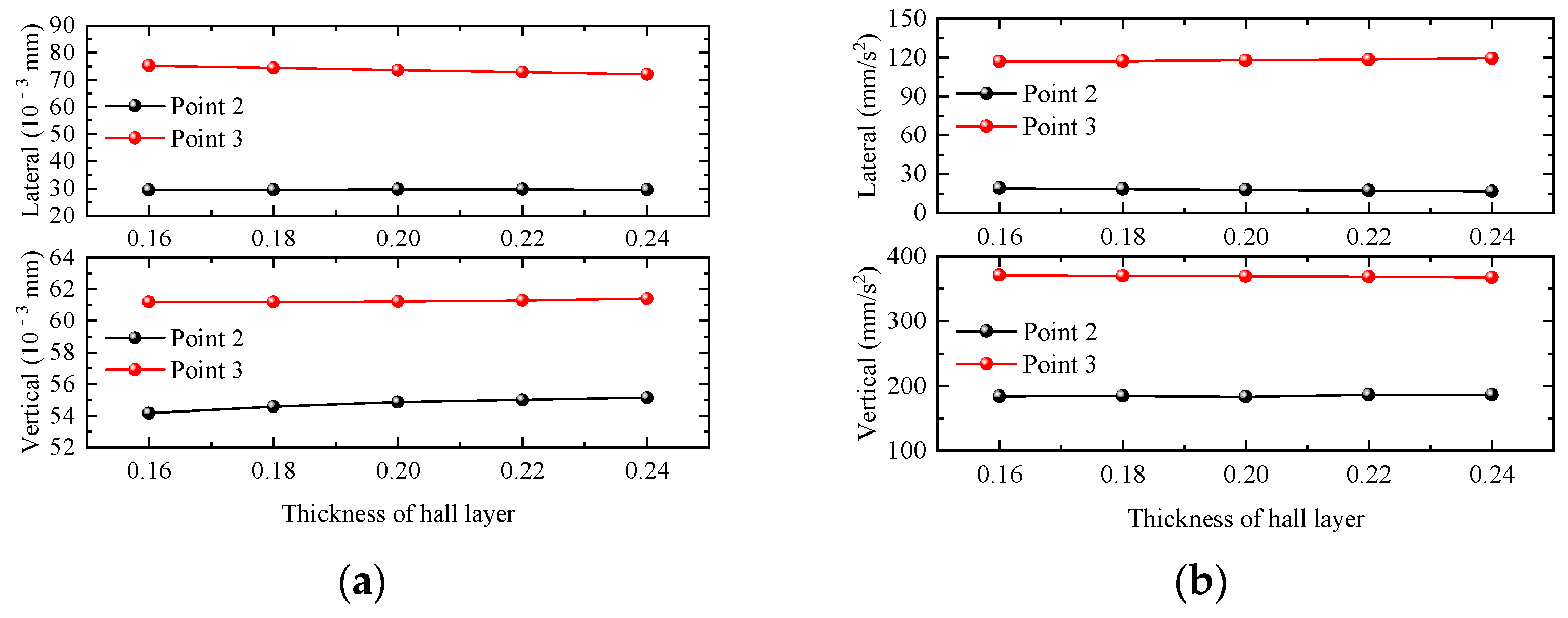
4.2.3. Thickness of Hall Layer
4.2.4. Thickness of Platform Level
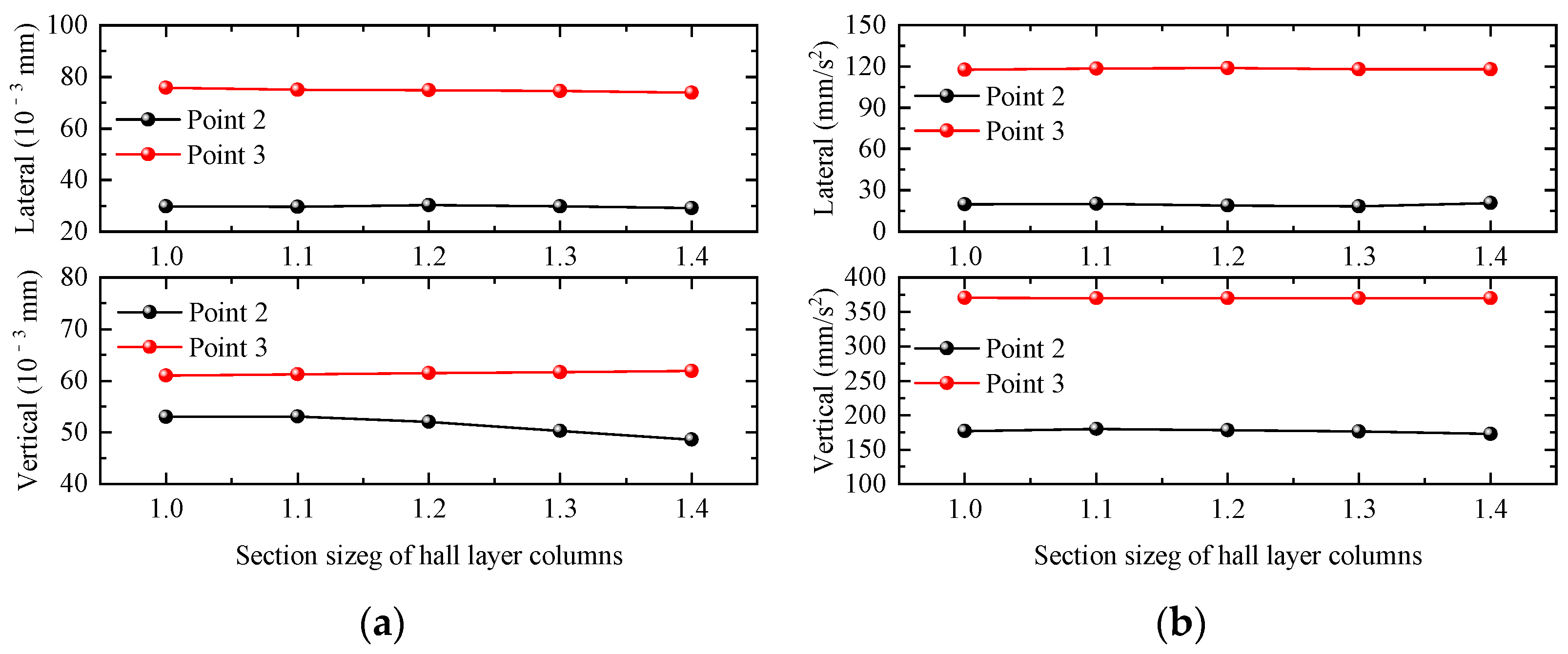
4.2.5. Section Size of Hall Layer Columns
5. Conclusions
- (1)
- Under the same traveling condition, the vertical acceleration of the rail-bearing layer of the integrated station is smaller than that of the rail-bearing layer of the combined station, while the vertical accelerations of the platform layer and hall layer of the integrated station are opposite to each other. When the train passes through the station at low speeds of 80 km/h and 90 km/h, the vertical acceleration at the station concourse level of the two types of stations is basically the same, and the vertical acceleration at the platform level of the integrated station is obviously larger than that of the combined station;
- (2)
- When the train passes through the station with high speed, the vertical accelerations of the platform level and station-hall level of the integrated station are larger than that of combined station under an unloaded double-line working condition, which indicates that the combined station has better dynamic performance under complicated working conditions. The combined dynamic performance of the combined station is better than that of integrated station, but there are problems such as the increased height of the whole station caused by the bridge box girder, the waterproofing problem of the track layer, the inconvenience of maintenance and replacement of the track girder support, etc. Therefore, comprehensive consideration should be given to the selection of the combined station based on various aspects;
- (3)
- For the integrated station-bridge structure, appropriately increasing the thickness of the floor slab at the rail bearing level has the most obvious effect on the reduction in the dynamic response of the station structure, and the dynamic responses of the waiting hall and the platform are significantly reduced; followed by increasing the thickness of the floor slab at the platform level, which can significantly reduce the dynamic response of the floor slab at the platform level; and then increasing the height of the rail beams, which can significantly reduce the displacement response of the floor slab at the platform level and the floor slab at the platform hall. Increasing the thickness of the floor slab at the waiting hall and the cross-section size of the frame columns of the waiting hall has little effect on the dynamic response of the station structure. Then, increasing the heights of track beams can significantly reduce the displacement response of platform floor slabs and station-hall floor slabs, while increasing the thickness of waiting-hall floor slabs and the cross-section size of waiting-hall frame columns has little effect on the dynamic response of the station structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, R.Q. Study on Economic Characteristics of Urban Rail Transit Elevated Line. Railw. Stand. Des. 2017, 61, 51–54. [Google Scholar]
- Feldmann, M.; Heinemeyer, C.; Kühn, B.; Sedlacek, G. Prediction of the dynamic behavior of bridges and roof of the railway main station Berlin. ZEV Rail Glas. Ann. 2006, 130, 314–326. [Google Scholar]
- Crispino, M.; D’apuzzo, M. Measurement and prediction of traffic-induced vibrations in a heritage building. J. Sound Vib. 2001, 246, 319–335. [Google Scholar] [CrossRef]
- Zhu, Z.; Davidson, M.T.; Harik, I.E.; Zhi-wu, Y. Train-induced vibration characteristics of an integrated high-speed railway station. J. Perform. Constr. Facil. 2017, 31, 04017010. [Google Scholar] [CrossRef]
- Cui, C.C.; Lei, X.Y.; Zhang, L. Study on vehicle-induced vibration response characteristics of an integrated traffic hub. Noise Vib. Control. 2017, 37, 144–150. [Google Scholar]
- Fang, L.M.; Zhu, Z.H.; Wang, L.D.; Yu, Z. Analysis of train induced random vibration of high-speed railway station with “integral station-bridge structure. J. China Railw. Soc. 2017, 39, 117–125. [Google Scholar]
- Li, Z.C.; Ran, W.M.; Yi, B.; Li, X.Z.; Zhang, X. Vibration Analysis of Integrated Transport Hub Station Structure under Train Load. Railw. Stand. Des. 2018, 62, 127–131. [Google Scholar]
- Ran, W.; Li, Z.; Li, X.; Yi, B.; Zhang, X. Frequency-domain analysis method for vibration responses of a high-speed railway station structure under train load excitation. J. Vib. Shock. 2018, 37, 218–224. [Google Scholar]
- Xie, W.P.; Yang, Y.Z.; Li, W. Research on vibration and structural noise measurement of subway elevated station combination of bridge and construction. J. Railw. Sci. Eng. 2021, 18, 1837–1845. [Google Scholar]
- Ba, Z.; Jiao, P.; Liang, J.; Liu, G.; Gao, Y. Actual measurement and analysis of station vibration induced by high-speed train. J. Tianjin Univ. (Sci. Technol.) 2020, 53, 1211–1217. [Google Scholar]
- Minseu, K.; Sanghyun, C. Vibration Control of a Railroad Station Using a Multiple Tuned Mass Damper Technique. J. Korean Soc. Hazard Mitig. 2017, 17, 37–43. [Google Scholar] [CrossRef]
- Yong, Y.; Kwon, S.-J.; Choi, S. Development of Vibration Mitigation Method for a Railway Station Using a Tuned-Mass-Dampered Platform. J. Korean Soc. Hazard Mitig. 2016, 16, 77–82. [Google Scholar] [CrossRef]
- Cai, C.; Deng, S.; He, X.; Zhou, Y.; Yu, K.; Wu, Y. Vibration measurement and analysis of an elevated station of Dongguan-Shenzhen intercity railway. J. Railw. Sci. Eng. 2022, 19, 1395–1403. [Google Scholar]
- Xia, H.; Gao, F.; Wu, X.; Zhang, N.; De Roeck, G.; Degrande, G. Running train induced vibrations and noises of elevated railway structures and their influences on environment. Front. Archit. Civ. Eng. China 2009, 3, 9–17. [Google Scholar] [CrossRef]
- Ju, S.H.; Lin, H.T.; Chen, T.K. Studying characteristics of train-induced ground vibrations adjacent to an elevated railway by field experiments. J. Geotech. Geoenvironmental Eng. 2007, 133, 1302–1307. [Google Scholar] [CrossRef]
- Yang, N.; Guo, T.; Sun, G. Train-induced vibration on elevated railway station. J. Cent. South Univ. 2013, 20, 3745–3753. [Google Scholar] [CrossRef]
- Tanabe, M.; Sogabe, M.; Wakui, H.; Matsumoto, N.; Tanabe, Y. Exact time integration for dynamic interaction of high-speed train and railway structure including derailment during an earthquake. J. Comput. Nonlinear Dyn. 2016, 11, 031004. [Google Scholar] [CrossRef]
- Lu, H.; Zhu, J.; Zhou, L. Research on vibration characteristics of a straddle-type station induced by moving trains. Eng. Res. Express 2024, 6, 025104. [Google Scholar] [CrossRef]
- Cui, K.; Su, L. Dynamic finite element analysis of an elevated station-track structure coupled system under resonance. Teh. Vjesn. 2019, 26, 449–456. [Google Scholar] [CrossRef]
- Zhao, Y.C.; Li, W.H. Research on Structure Type’s Assortment and Their Applicability of Elevated Station of Urban Rail Transi. Railw. Stand. Des. 2013, 01, 85–89. [Google Scholar]
- Guo, T.; Zhi, G.; Zhu, R.; Zhang, L. Train-Induced Vibration Characteristics of a Double-Story High-Speed Railway Station. J. Perform. Constr. Facil. 2024, 38, 04024008. [Google Scholar] [CrossRef]
- Deng, Z.M. Structural Vibration Analysis and Vibration Control Study on The New Changsha Railway Station. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
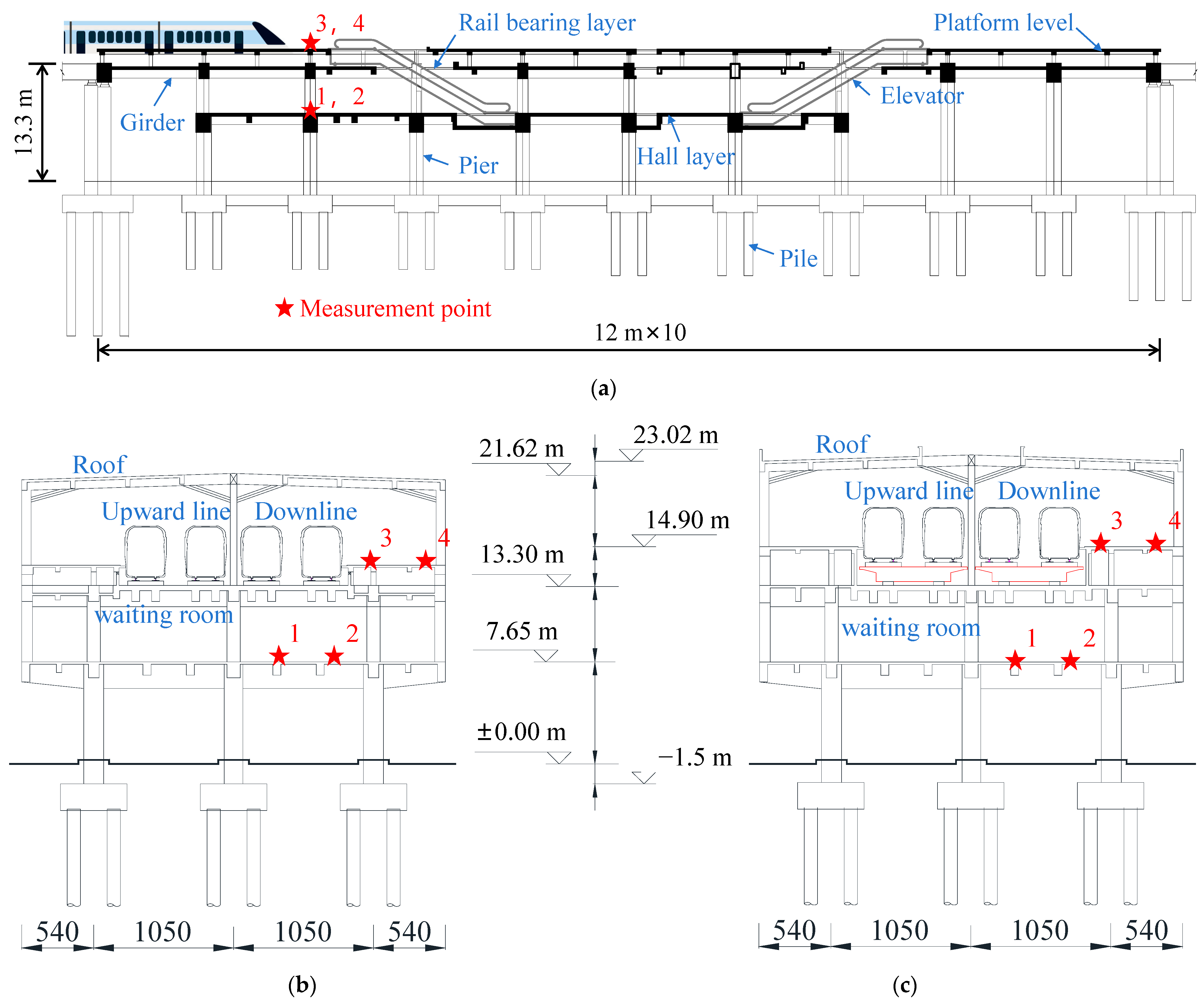








| Comparison Program | Plan A: Integrated Station-Bridge Structure | Plan B: Combined Station-Bridge Structure | Plan C: Separated Station-Bridge Structure |
|---|---|---|---|
| Load transfer relationship | The structure is cast-in-place as a whole. Train loads are dispersed through the beam-column system and then transferred to the ground floor frame columns. | The track girders are prefabricated and simply supported on the cover girders. Train loads are transferred to the cover beams and piers. | The train load is directly transferred to the bridge and is not transferred to the station. |
| Structural characteristics | Good structural integrity and seismic performance, seamless cast-in-place structure for track level girders and slabs | Poor structural integrity and seismic performance. There are longitudinal joints between the track girders and the main body of the station, and transverse joints between the track girders. Maintenance and overhaul of track beam supports are not easy to operate. | The bridge structure and the building structure are two completely independent systems, making the structural design relatively simple; the vibration interference from train operation on the concourse and platform levels is minimal. |
| Building arrangement | Flexible structural arrangement, smaller beam member sizes, less building height occupied. Relatively small column cross-section at station-hall level. Smaller lifting height of escalator. | Beam members are larger in size and take up more building height. Pier sections are generally larger. Escalator lifting heights are larger. | Beam members are larger in size and take up more building height. Pier sections are generally larger. Escalator lifting heights are larger. |
| Engineering investment | Relatively economical cost | Relatively higher cost |
| Parameters | Notation |
|---|---|
| Mass of car body, mass of bogie, mass of wheelset | |
| Distance between the center of gravity of the vehicle and the transverse spring. | |
| Distance between the center of gravity of the frame and the central transverse spring | |
| Distance between the center of gravity of the frame and the transverse spring of the axle box | |
| Distance between the center of gravity of the wheelset and the transverse spring of the axle box | |
| Half of the distance between the centers of gravity of the front and rear bogies. | |
| Rotation inertia of car body and frame | |
| Half length of the wheelbase | |
| Half the length of the train axle | |
| Half the distance of the car body’s lateral suspension system | |
| Half the width of the train car body | |
| The degrees of freedom of the vehicle body’s lateral swing, floating, rolling, pitching, and yawing | |
| The degrees of freedom of the vehicle wheelset’s lateral swing and yawing. | |
| The degrees of freedom of the vehicle frame’s lateral swing and yawing | |
| Stiffness of the suspension systems between the car body and the bogie | |
| Stiffness of the suspension systems between the bogie and wheelset | |
| Damping coefficient between the car body and the bogie | |
| Damping coefficient between frame and wheelset |
| Parameters | Value | Unit |
|---|---|---|
| Av | 0.0339 | cm2/(rad/m) |
| Aa | 0.0339 | cm2/(rad/m) |
| Ωs | 0.438 | rad/m |
| Ωc | 0.8245 | rad/m |
| Speed allowance | 176 | km/h |
| Integrated Station-Bridge System | Combined Station-Bridge System | |
|---|---|---|
| Number of nodes | 5149 | 5573 |
| Number of beam elements | 5077 | 5089 |
| Number of shell elements | 4152 | 4152 |
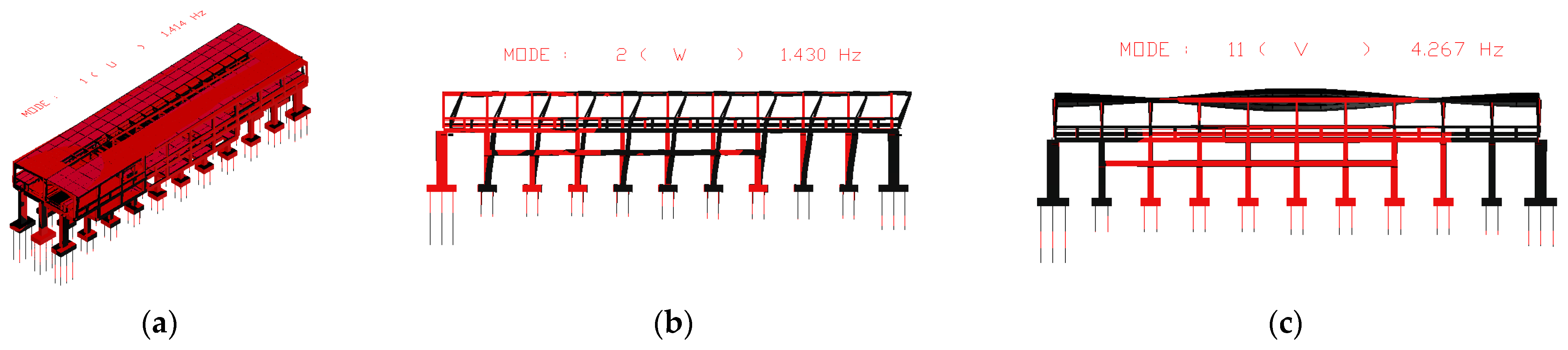
| Order | Mode Shape | Mode Frequency (Hz) | |
|---|---|---|---|
| Integrated Station-Bridge System | Combined Station-Bridge System | ||
| 1 | First-order antisymmetric transverse bending of the main structure | 1.534 | 1.414 |
| 2 | First-order longitudinal drift for beams, columns and canopies | 1.542 | 1.430 |
| 3 | Second-order transverse bends in the main structure | 1.685 | 1.538 |
| 4 | Longitudinal drift of the second order of the beam canopy | 2.369 | 2.161 |
| 5 | Third-order transverse bends in the main structure | 2.829 | 2.513 |
| 6 | Fourth-order transverse bends in the main structure | 2.964 | 2.635 |
| 7 | Column structure transverse bending | 3.633 | 3.633 |
| 8 | Canopy first-order vertical bend | 3.763 | 3.763 |
| 9 | Canopy second-order vertical bend | 3.862 | 3.862 |
| 10 | Canopy third-order vertical bend | 4.044 | 4.044 |
| 11 | Canopy third-order vertical bend | 4.394 | 4.267 |
| Measurement Point | Peak Acceleration (mm/s2) | |
|---|---|---|
| Measured Value | Calculated Value | |
| Point 1 | 42.46 | 32.98 |
| Point 2 | 50.96 | 38.37 |
| Point 3 | 123.86 | 152.57 |
| Point 4 | 107.75 | 101.50 |
| Table | Train Operating Conditions | Train Formation | Vehicle Weight | Vehicle Velocity (km/h) | Track Irregularities |
|---|---|---|---|---|---|
| Type B vehicle | Single-lane passages | Four-car consist train (T + M + M + T) | Dead-load, Over-load | 80, 90, 100, 110, 120 | American 6-level spectrum track irregularity |
| Type B vehicle | Double-lane passages |
| Station Area | Vehicle Velocity (km/h) | Vertical Acceleration (mm/s2) | |||
|---|---|---|---|---|---|
| Dead-Load | Over-Load | ||||
| Plan A | Plan B | Plan A | Plan B | ||
| Rail bearing layer | 80 | 581.03 | 604.25 | 857.06 | 912.95 |
| 90 | 636.99 | 657.74 | 923.03 | 963.14 | |
| 100 | 660.38 | 698.78 | 937.85 | 998.96 | |
| 110 | 666.62 | 683.07 | 946.03 | 984.41 | |
| 120 | 612.79 | 618.12 | 891.85 | 915.62 | |
| Hall layer | 80 | 101.71 | 77.70 | 102.96 | 100.49 |
| 90 | 92.94 | 81.87 | 111.48 | 95.98 | |
| 100 | 127.37 | 74.50 | 136.90 | 83.21 | |
| 110 | 175.32 | 99.61 | 206.19 | 126.83 | |
| 120 | 186.93 | 94.66 | 188.63 | 116.61 | |
| Platform level | 80 | 151.66 | 122.42 | 142.76 | 134.02 |
| 90 | 145.23 | 97.20 | 137.49 | 110.71 | |
| 100 | 146.84 | 90.83 | 167.31 | 116.95 | |
| 110 | 215.00 | 114.73 | 233.41 | 151.25 | |
| 120 | 237.26 | 138.27 | 226.36 | 166.55 | |
| Station Area | Vehicle Velocity (km/h) | Vertical Acceleration (mm/s2) | |||
|---|---|---|---|---|---|
| Dead-Load | Over-Load | ||||
| Plan A | Plan B | Plan A | Plan B | ||
| Rail bearing layer | 80 | 584.37 | 601.73 | 860.85 | 909.12 |
| 90 | 637.48 | 660.08 | 924.81 | 965.94 | |
| 100 | 661.37 | 699.47 | 939.15 | 999.65 | |
| 110 | 665.69 | 684.43 | 945.53 | 985.65 | |
| 120 | 613.19 | 618.57 | 892.55 | 916.40 | |
| Hall layer | 80 | 113.59 | 76.65 | 106.46 | 99.32 |
| 90 | 92.62 | 89.76 | 104.37 | 98.70 | |
| 100 | 131.08 | 77.88 | 143.00 | 97.40 | |
| 110 | 192.26 | 127.60 | 223.70 | 149.57 | |
| 120 | 214.01 | 149.92 | 233.03 | 193.67 | |
| Platform level | 80 | 170.05 | 120.78 | 169.31 | 131.25 |
| 90 | 174.51 | 117.55 | 168.83 | 132.82 | |
| 100 | 178.47 | 101.56 | 199.95 | 140.24 | |
| 110 | 258.18 | 149.72 | 285.04 | 172.53 | |
| 120 | 314.16 | 178.43 | 319.12 | 192.19 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Liu, J.; Cui, R. Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms. Materials 2024, 17, 4387. https://doi.org/10.3390/ma17174387
Guo X, Liu J, Cui R. Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms. Materials. 2024; 17(17):4387. https://doi.org/10.3390/ma17174387
Chicago/Turabian StyleGuo, Xiangrong, Jianghao Liu, and Ruibo Cui. 2024. "Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms" Materials 17, no. 17: 4387. https://doi.org/10.3390/ma17174387
APA StyleGuo, X., Liu, J., & Cui, R. (2024). Research on Train-Induced Vibration of High-Speed Railway Station with Different Structural Forms. Materials, 17(17), 4387. https://doi.org/10.3390/ma17174387






