Optimization Method of Floating Fixture Layout for Distortion Control of Low-Stiffness Thin-Walled Beams
Abstract
:1. Introduction
2. Optimization of Fixture Layout
2.1. Construction of an Objective Function
- (1)
- Calculation of thin plate model
- (2)
- Calculation of the fixed beam model
- (3)
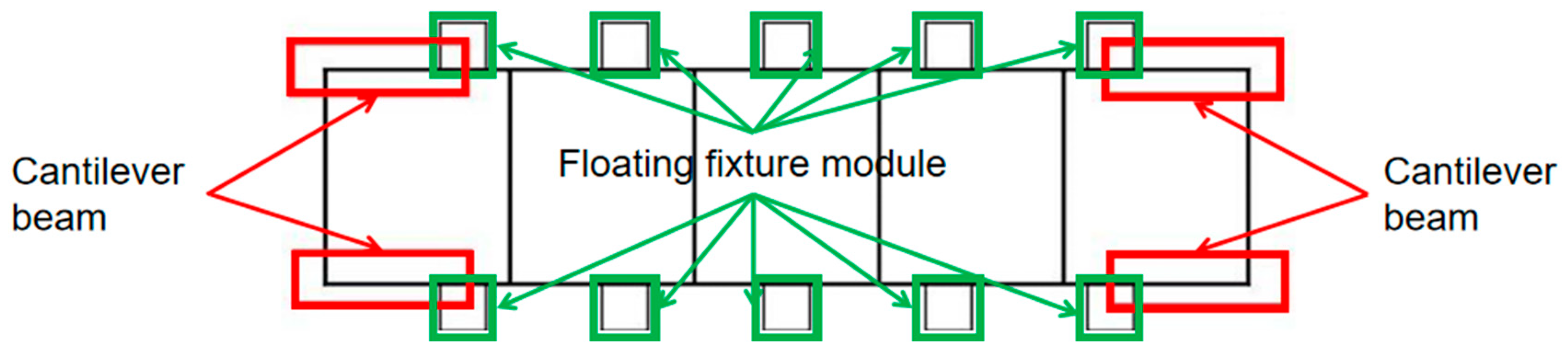
- Calculation of cantilever beam model
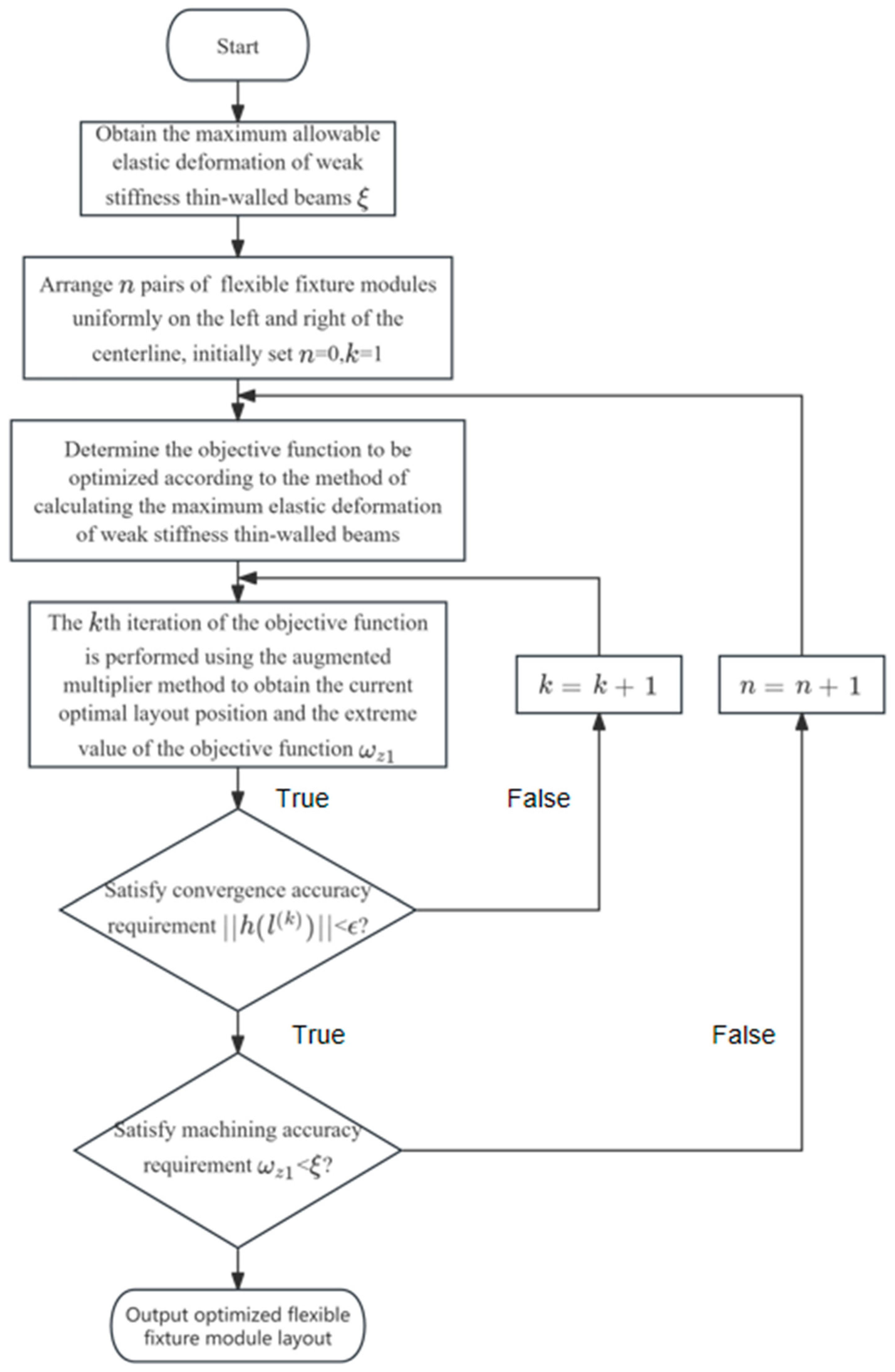
2.2. Fixture Layout Optimization Method
2.3. Augmented Multiplier Method
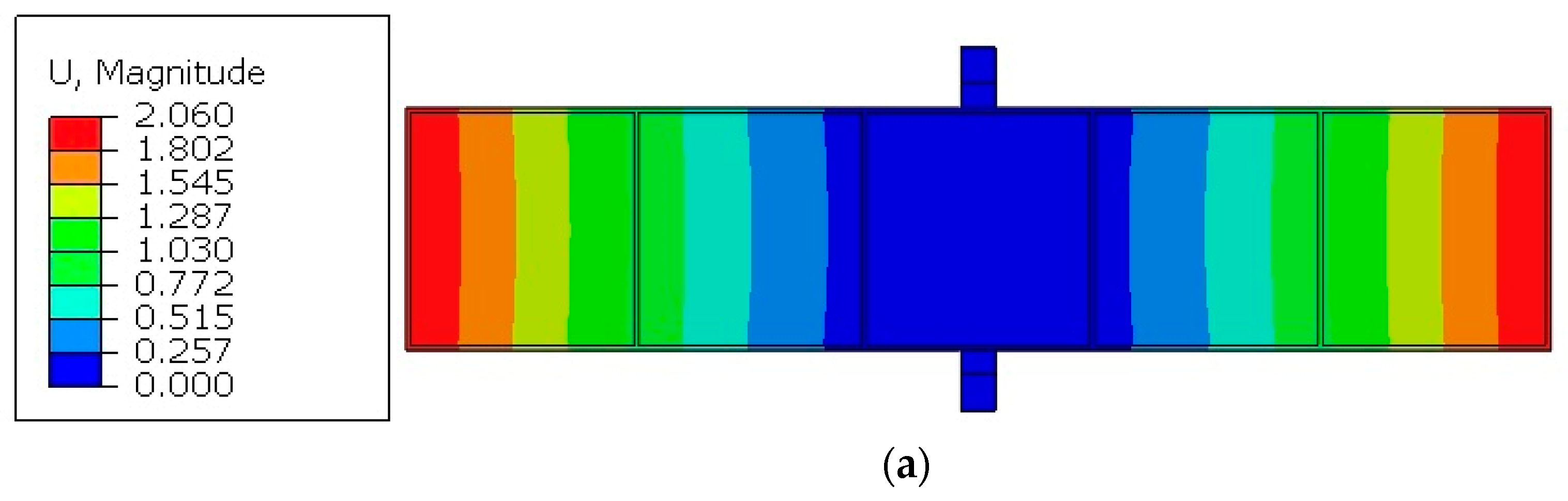
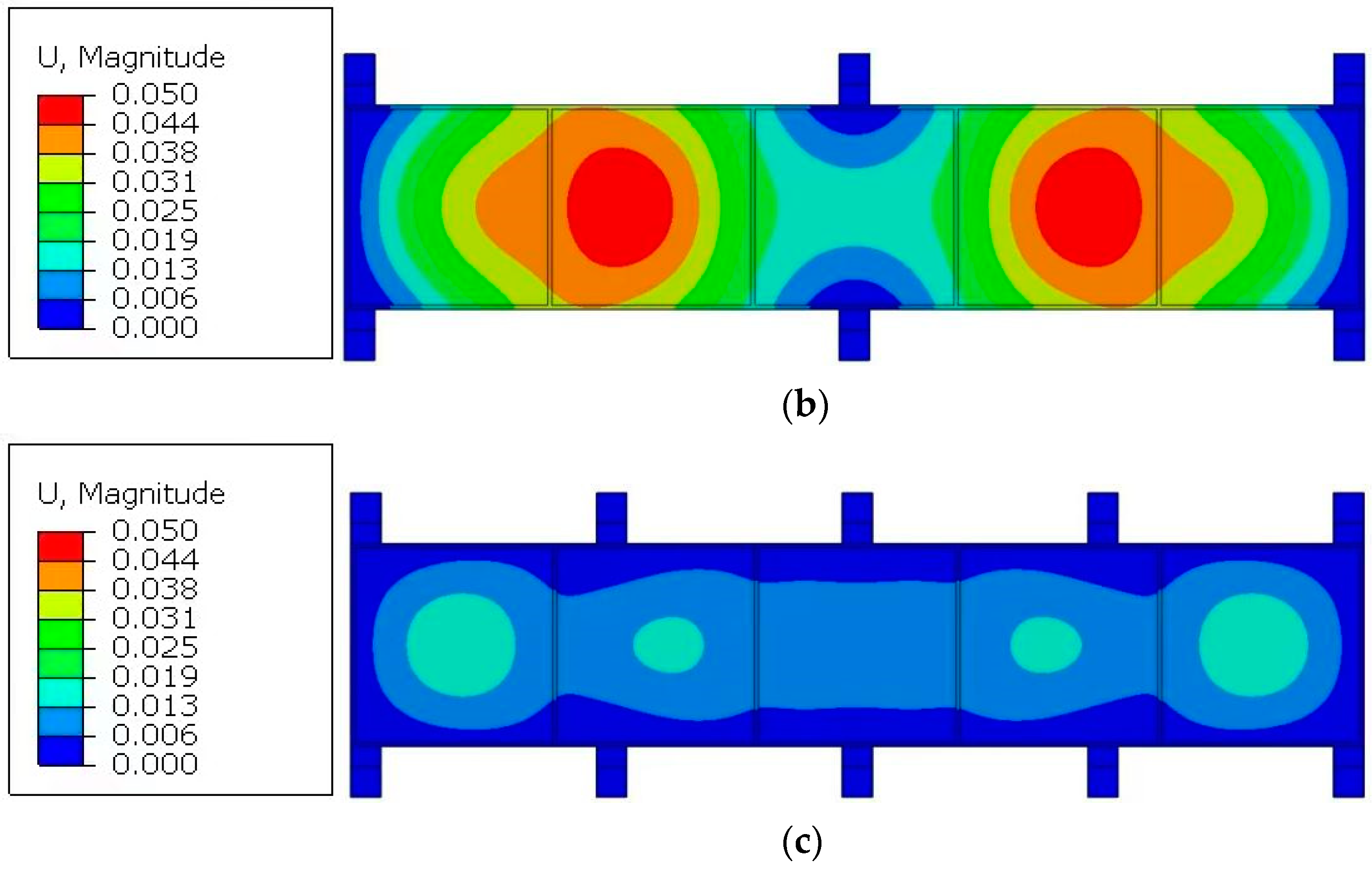
3. Simulation of Example
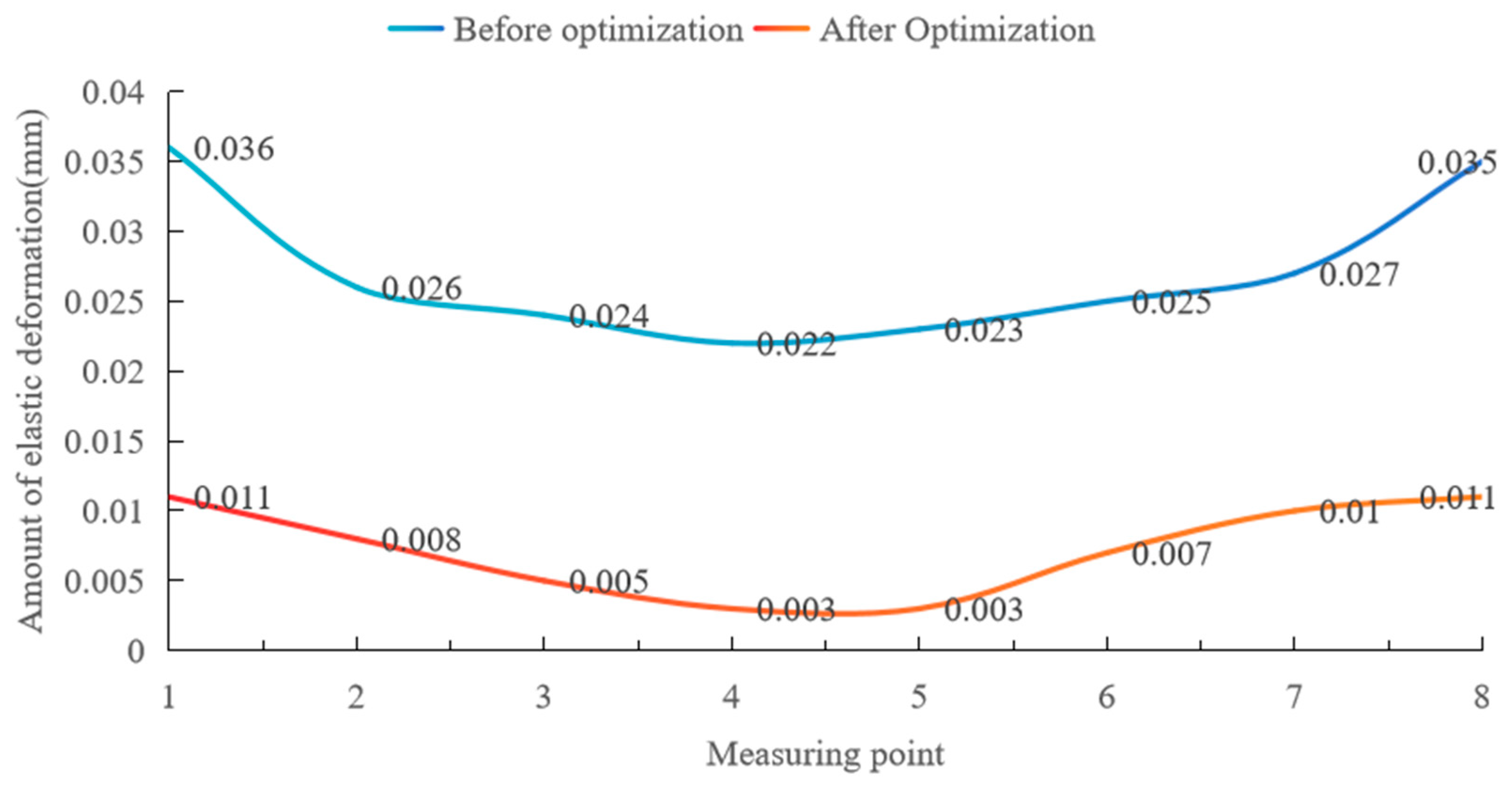
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, B. Research based on aircraft assembly frame design technology. Sci. Technol. Innov. Herald 2022, 17, 2–3. [Google Scholar]
- Xue, Y.X.; Xin, H.; Sun, J.F.; Meng, H.; Song, W.W. Analysis and process scheme design of processing distortion of thin-walled parts of aviation aluminum alloy. Tool Eng. 2023, 57, 125–128. [Google Scholar]
- Chen, T.; Xu, Y.; Huang, B.; Shi, Y.; Zhang, J.; Li, L.; Meng, Y.; Li, X. Aero-Engine Blade Cryogenic Cooling Milling Deformation Simulation and Process Parameter Optimization. Materials 2023, 16, 4072. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.-N.; Li, X.-W.; Zhu, K.; Zhang, Y.-A.; Li, Z.-H.; Yan, H.-W.; Wen, K. Influence of Material Removal Strategy on Machining Deformation of Aluminum Plates with Asymmetric Residual Stresses. Materials 2023, 16, 2033. [Google Scholar] [CrossRef]
- Peng, Y.Z. The influence of initial residual stress on the machining distortion of thin-walled rotary parts was explored. Int. Combust. Eng. Parts 2020, 5, 102–103. [Google Scholar]
- Liu, S.M.; Hu, B.Q.; Zhang, C.L.; Luo, Z.Z. Research on processing distortion control technology of thin-walled parts based on floating fixture adaptive machining technology. Aero. Manuf. Technol. 2023, 66, 70–77. [Google Scholar]
- Guo, F.; Ye, J. Contact model and elastic deformation analysis of plate structure based on the discrete element method. Arch. Appl. Mech. 2022, 92, 2513–2523. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhou, B.H.; Yu, J.B.; Zheng, Y.; Liu, J.F. Development of Fixture Layout Optimization for Thin-Walled Parts: A Review. Chin. J. Mech. Eng. 2024, 37, 17. [Google Scholar] [CrossRef]
- Liu, S.; Ma, F.; Zhu, F.S. Adaptive clamping design for machining large structural parts of aircraft based on TRIZ. Aero. Manuf. Technol. 2021, 64, 90–95. [Google Scholar]
- Zhang, C.H.; Yu, S.H.; Zhou, L.F. Optimization analysis of clamping layout of thin-walled ring parts of aero engine. Manuf. Technol. Mach. Tool 2021, 1, 21–24. [Google Scholar]
- Michael, T.R.F.; Hariharasakthisudhan, P.; Andrews, A.; Prince, A.B. Optimization of flexible fixture layout to improve form quality using parametric finite element model and mixed discrete-integer genetic algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 1, 236. [Google Scholar]
- Fountas, N.A.; Vaxevanidis, N.M.; Stergiou, C.I.; Benhadj-Djilali, R. Globally optimal tool paths for sculptured surfaces with emphasis on machining error and cutting posture smoothness. Int. J. Prod. Res. 2019, 57, 5478–5498. [Google Scholar] [CrossRef]
- Park, S.H.; Nam, E.; Gang, M.G.; Min, B.K. Post-machining Deformation Analysis for Virtual Machining of Thin Aluminium Alloy Parts. Int. J. Precis. Eng. Manuf. 2019, 20, 687–691. [Google Scholar] [CrossRef]
- Hajimiri, H.; Abedini, V.; Shakeri, M.; Siahmargoei, M.H. Simultaneous fixturing layout and sequence optimization based on genetic algorithm and finite element method. Int. J. Adv. Manuf. Technol. 2018, 97, 3191–3204. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Deptuła, A.; Urbanowicz, K.; Nugaras, J.; Królczyk, G.; Żak, K. Performance evaluation of extruded polystyrene foam for aerospace engineering applications using frequency analyses. Int. J. Adv. Manuf. Technol. 2023, 126, 5515–5526. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Y.P.; Zhang, H.R.; Jiao, D. Mechanical design and simulation of aircraft long truss cut-edge floating fixture. Manuf. Technol. Mach. Tool. 2017, 6, 172–175. [Google Scholar]
- Wang, W.; Men, X.R. Study on adsorption force optimization of suction cup floating tooling based on Abaqus. Mech. Eng. 2022, 7, 39–41. [Google Scholar]
- Yue, C.X.; Zhou, T.X.; Qin, Y.Y.; Wang, L.; Hu, D.S. Research progress on processing condition monitoring in the milling process of aerospace thin-walled parts. Aero. Manuf. Technol. 2023, 6, 30–43. [Google Scholar]
- Men, X.C.; Wang, Z.Q.; Du, Z.C.; Li, C.; Chang, Z.P. Optimization method for clamping of aviation thin-walled parts to minimize strain energy. Manuf. Technol. Mach. Tool 2023, 3, 141–148. [Google Scholar]
- Hao, X.Z.; Li, Y.G. Adaptive machining method of large structural parts floating fixture. J. Mech. Eng. 2020, 56, 35. [Google Scholar]
- Zheng, Y.; Wu, D.B.; Wang, H.; Liang, J.L.; Liu, X.P. Machining fixture and deformation control of aero-engine thin-walled casing. Int. J. Adv. Manuf. Technol. 2023, 129, 5601–5614. [Google Scholar] [CrossRef]
- Papadimitriou, D.; Vũ, B.C. An augmented Lagrangian method for nonconvex composite optimization problems with nonlinear constraints. Optim. Eng. 2023, 1–70. [Google Scholar] [CrossRef]
- Dai, Y.H.; Zhang, L.W. The Rate of Convergence of Augmented Lagrangian Method for Minimax Optimization Problems with Equality Constraints. J. Oper. Res. Soc. China 2022, 12, 265–297. [Google Scholar] [CrossRef]
- Sun, Q.; Zhou, J.; Li, P. Simulations and Experiments on the Micro-Milling Process of a Thin-Walled Structure of Al6061-T6. Materials 2022, 15, 3568. [Google Scholar] [CrossRef] [PubMed]
- Li, E.M.; Zhou, J.T.; Yang, C.S.; Wang, M.W.; Zhang, S.S. Clamping force prediction based on the deep spatio-temporal network for machining process of deformable parts. Sci. Rep. 2023, 13, 7012. [Google Scholar] [CrossRef]
- Huan, H.X.; Zhang, K.; Xu, J.H.; Xu, W.Q.; Wang, M.X. Machining deformation control methods and analysis of a thin-walled gear spoke plate. Int. J. Adv. Manuf. Technol. 2023, 127, 1317–1331. [Google Scholar] [CrossRef]
- Lu, D. Machining Deformation Prediction and Clamping Layout Optimization of Aviation Integral Structural Parts. Ph.D. Thesis, Shandong University, Jinan, China, 2007. [Google Scholar]







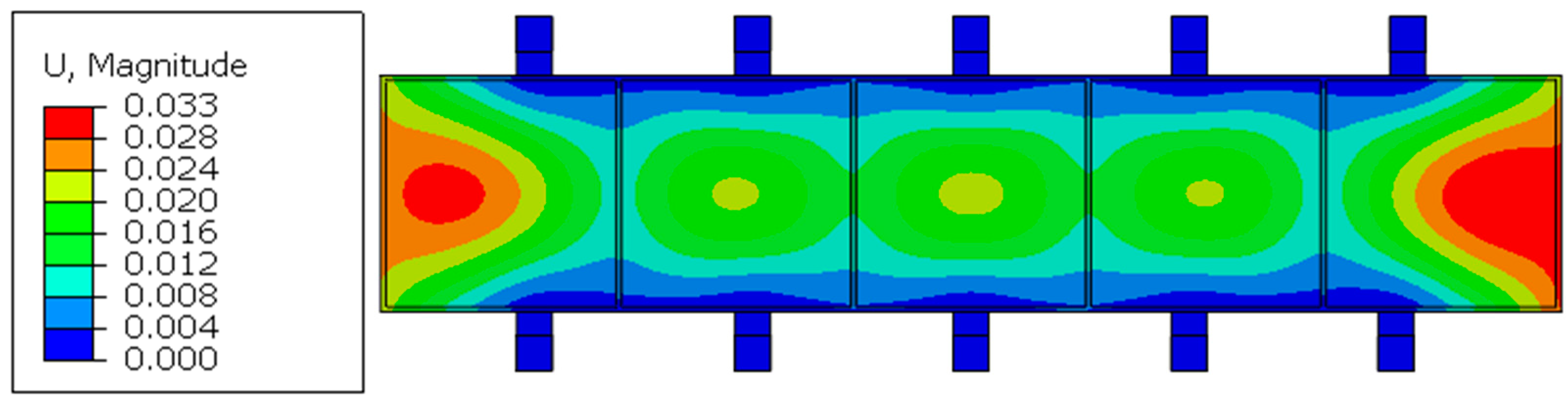


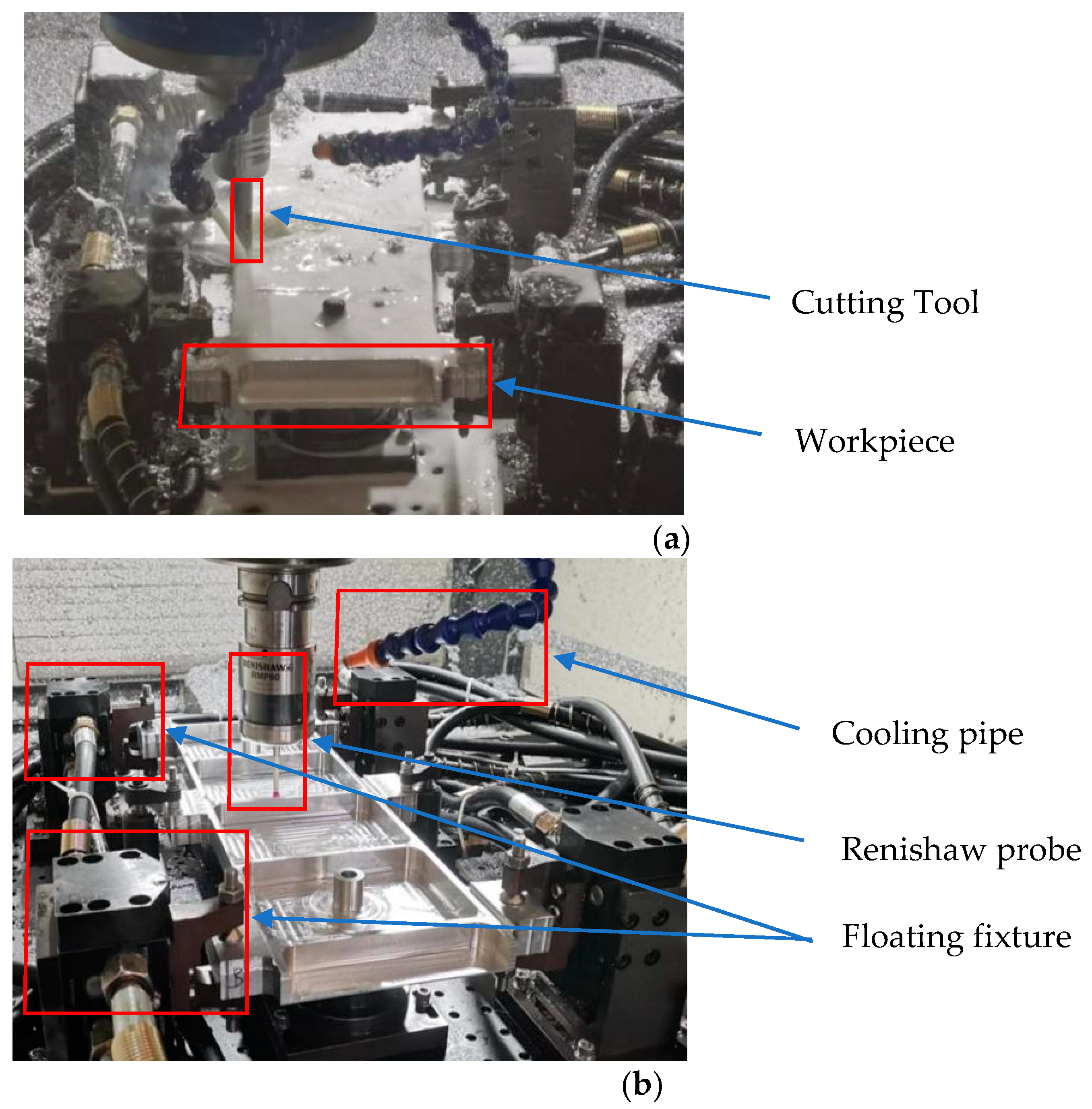
| a/b | 1 | 2 | 3 | 4 | ∞ |
|---|---|---|---|---|---|
| 0.0611 | 0.0788 | 0.0790 | 0.0791 | 0.0791 |
| Logarithm of Fixture Points n | Fixture Module Spacing l/mm | Clamp Module on Edge of Beam ln+1/mm | /mm | Relative Error/% | Average Relative Error/% | |
|---|---|---|---|---|---|---|
| 0 | 0 | 496 | 2.542 | 2.060 | 18.96 | |
| 1 | 495 | 0 | 0.060 | 0.049 | 18.33 | 17.43 |
| 2 | 247.5 | 0 | 0.020 | 0.017 | 15.00 |
| Cutting Parameters | Value |
|---|---|
| Cutting depth ap (mm) | 1 |
| Cutting width ae (mm) | 6 |
| Spindle speed n (rpm) | 800 |
| Feed speed f (mm/min) | 4000 |
| Tool diameter (mm) | 8 |
| Tool tooth number (N) | 3 |
| Measuring Point Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Reduced value/mm | 0.025 | 0.018 | 0.019 | 0.019 | 0.020 | 0.018 | 0.017 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Wang, J.; Mu, Z.; Gu, Y.; Du, Z.; He, W.; Aw, K.; Yang, Y. Optimization Method of Floating Fixture Layout for Distortion Control of Low-Stiffness Thin-Walled Beams. Materials 2024, 17, 4226. https://doi.org/10.3390/ma17174226
Feng J, Wang J, Mu Z, Gu Y, Du Z, He W, Aw K, Yang Y. Optimization Method of Floating Fixture Layout for Distortion Control of Low-Stiffness Thin-Walled Beams. Materials. 2024; 17(17):4226. https://doi.org/10.3390/ma17174226
Chicago/Turabian StyleFeng, Junping, Jiawei Wang, Zhuang Mu, Yifei Gu, Zongyang Du, Wenbo He, Kean Aw, and Yinfei Yang. 2024. "Optimization Method of Floating Fixture Layout for Distortion Control of Low-Stiffness Thin-Walled Beams" Materials 17, no. 17: 4226. https://doi.org/10.3390/ma17174226
APA StyleFeng, J., Wang, J., Mu, Z., Gu, Y., Du, Z., He, W., Aw, K., & Yang, Y. (2024). Optimization Method of Floating Fixture Layout for Distortion Control of Low-Stiffness Thin-Walled Beams. Materials, 17(17), 4226. https://doi.org/10.3390/ma17174226







