A Smart, Data-Driven Approach to Qualify Additively Manufactured Steel Samples for Print-Parameter-Based Imperfections
Abstract
1. Introduction
2. Methods
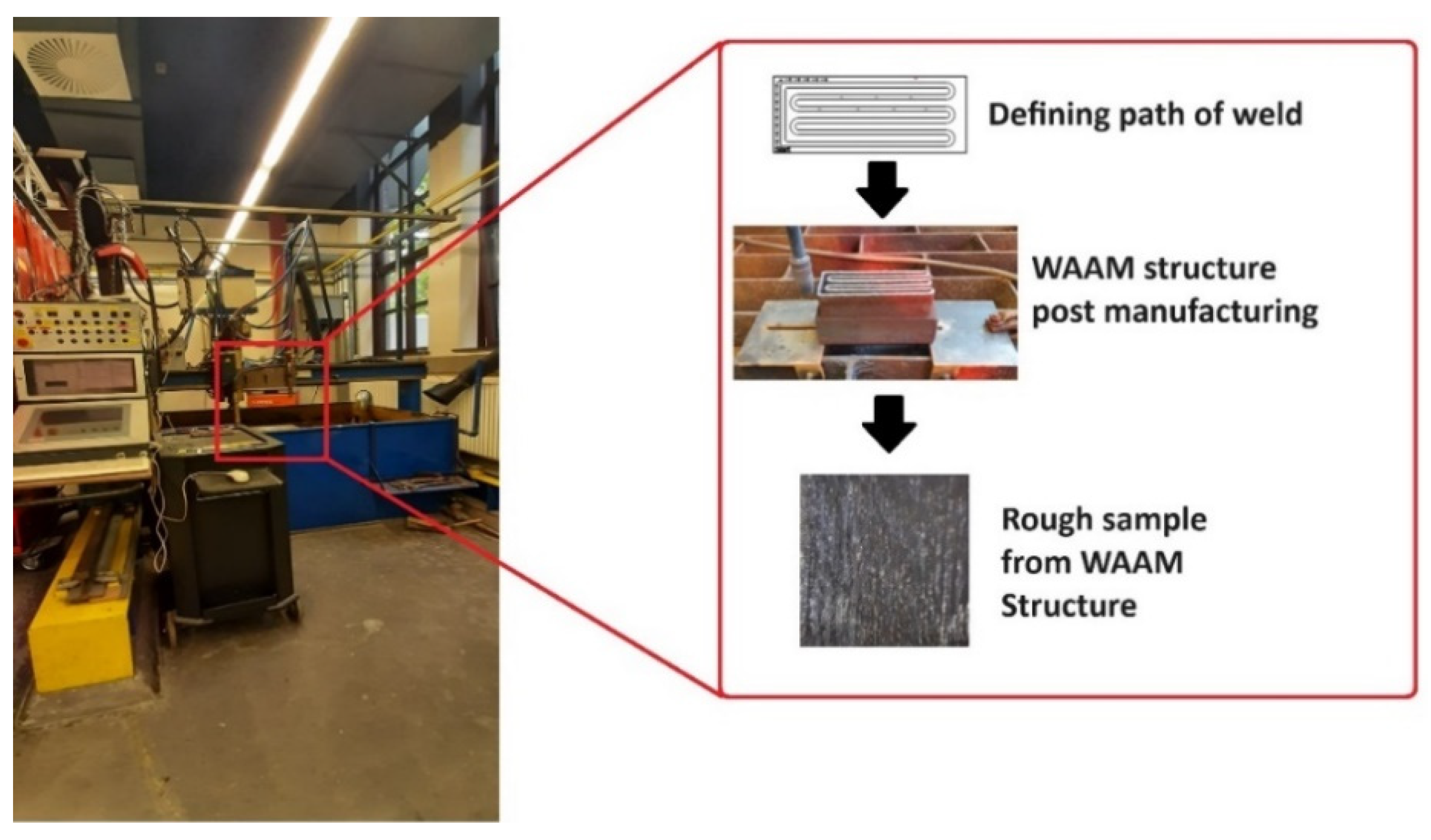
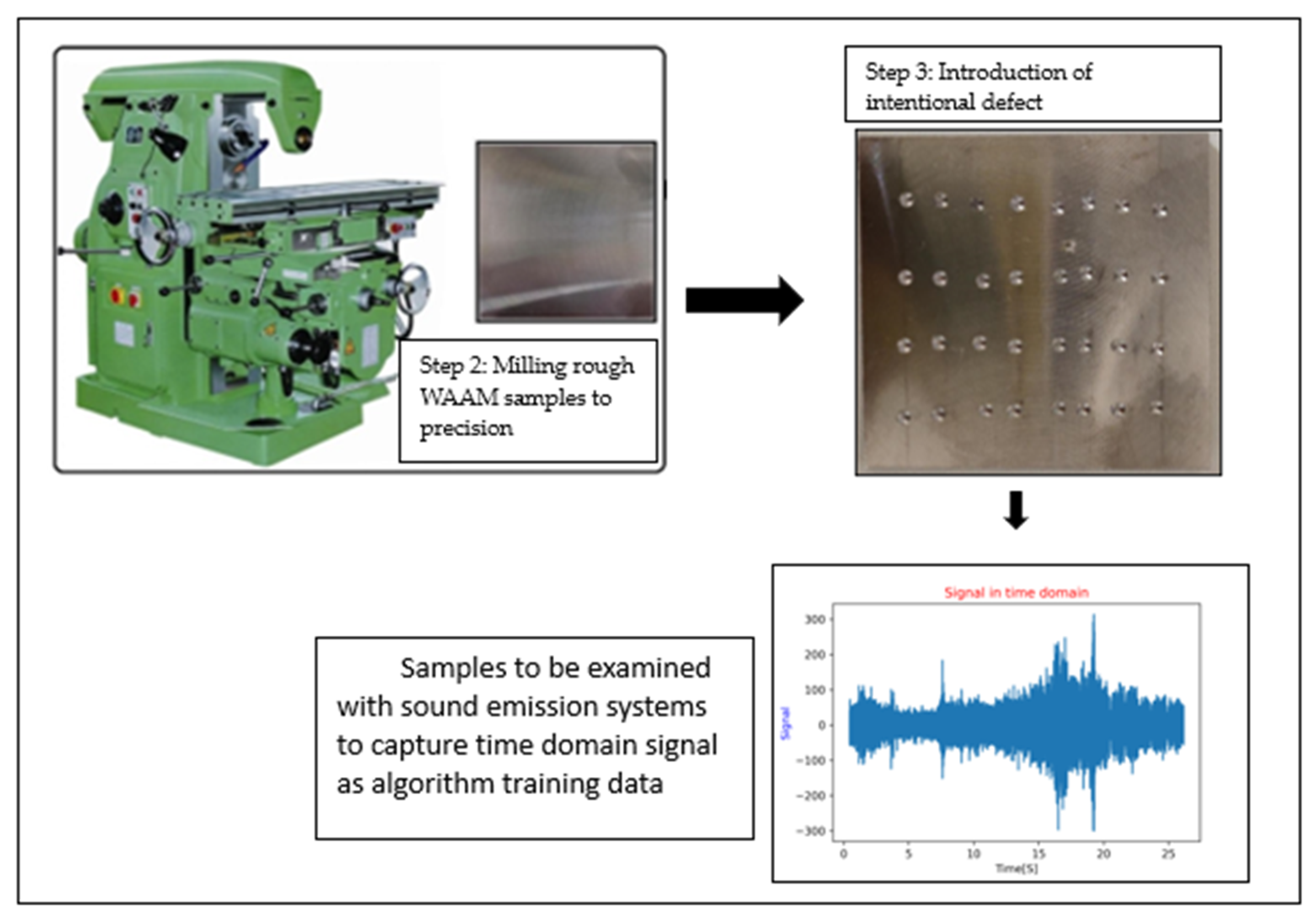
2.1. Sample Preparation from WAAM
2.2. Density Measurements
2.3. FEM Method for Database Enhancement
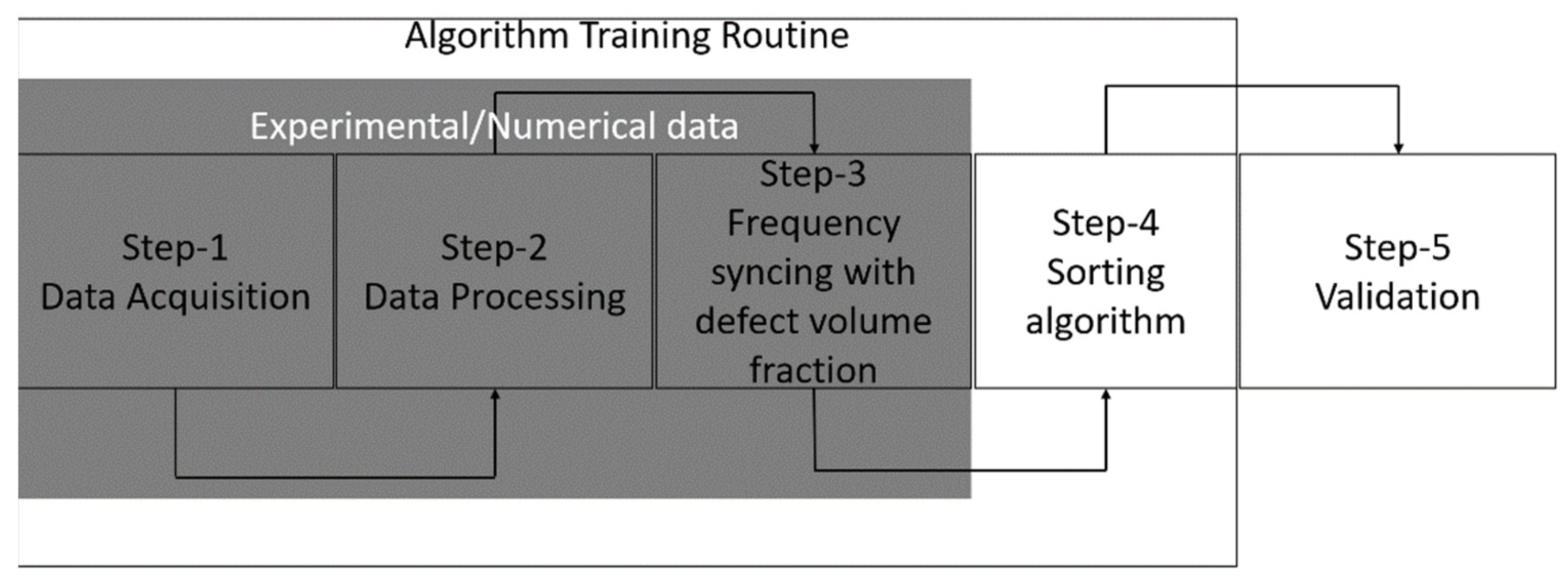
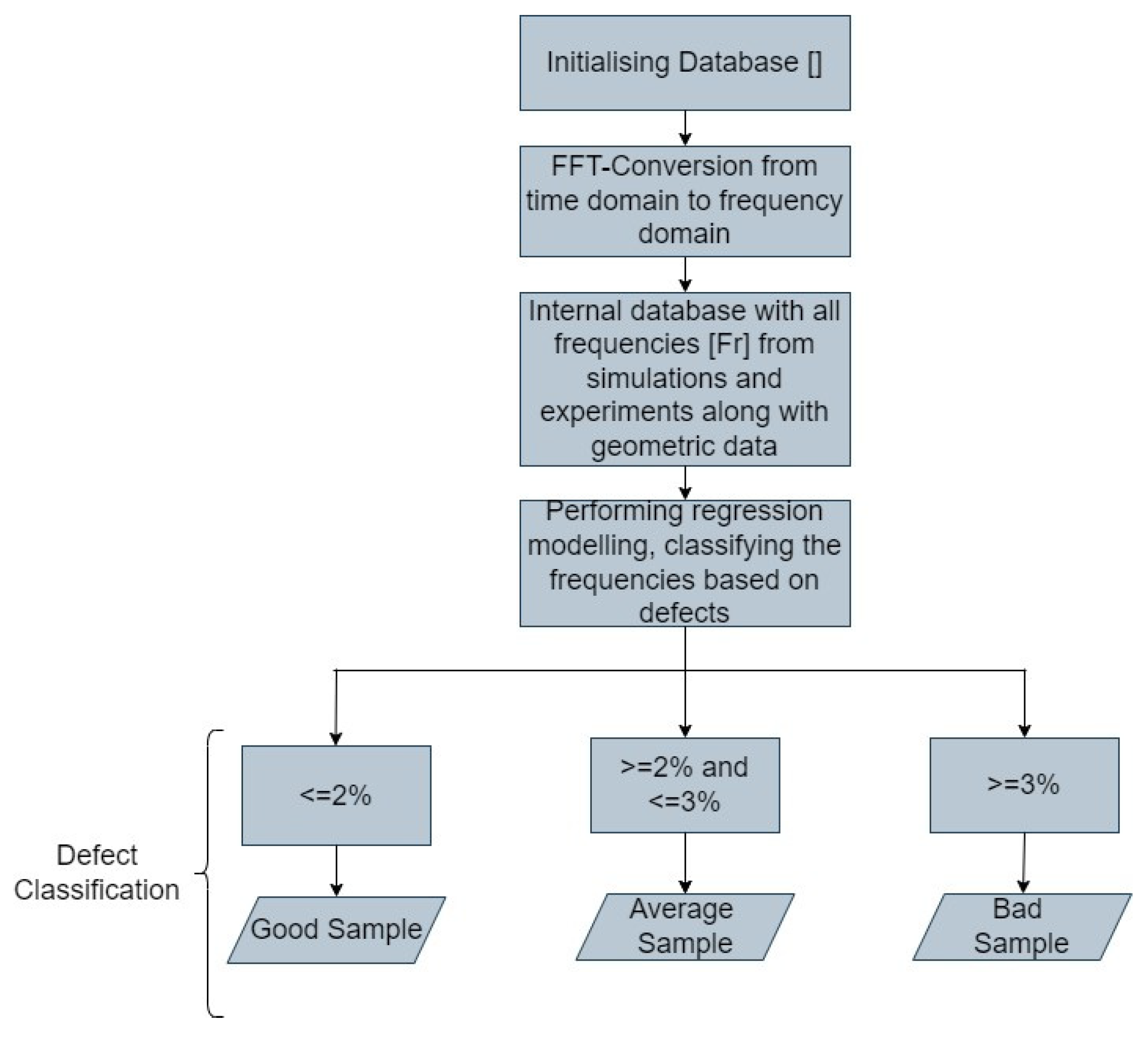
2.4. Resonant Frequency Measurement and Developing the Alogrithm
2.4.1. Brief Overview of the Methodology
2.4.2. Resonant Frequency Measurement Equipment
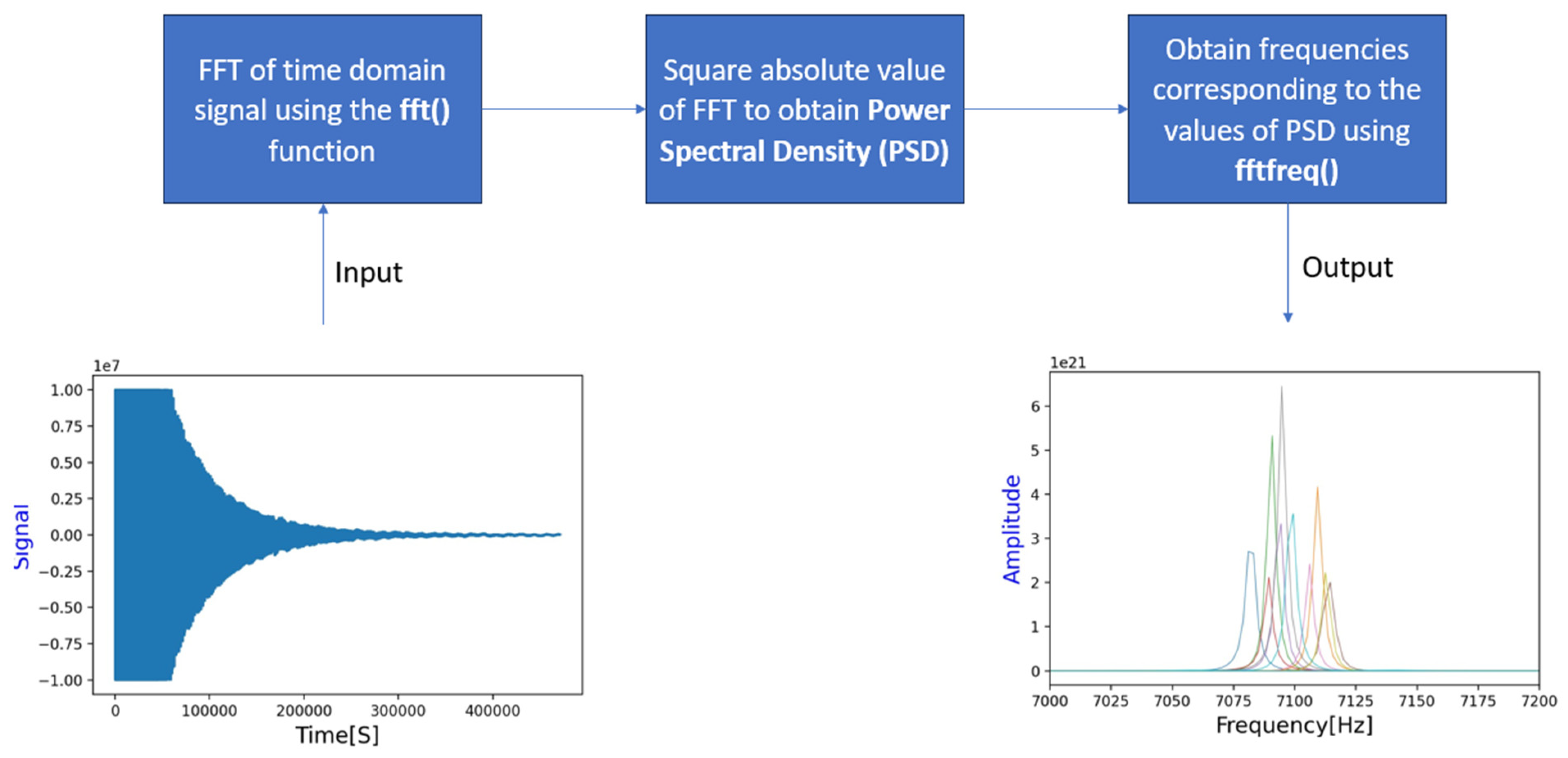
2.4.3. Experimental Data (Signal) Acquisition and Processing
2.4.4. Overview on the Development of the Algorithm
3. Results and Discussion
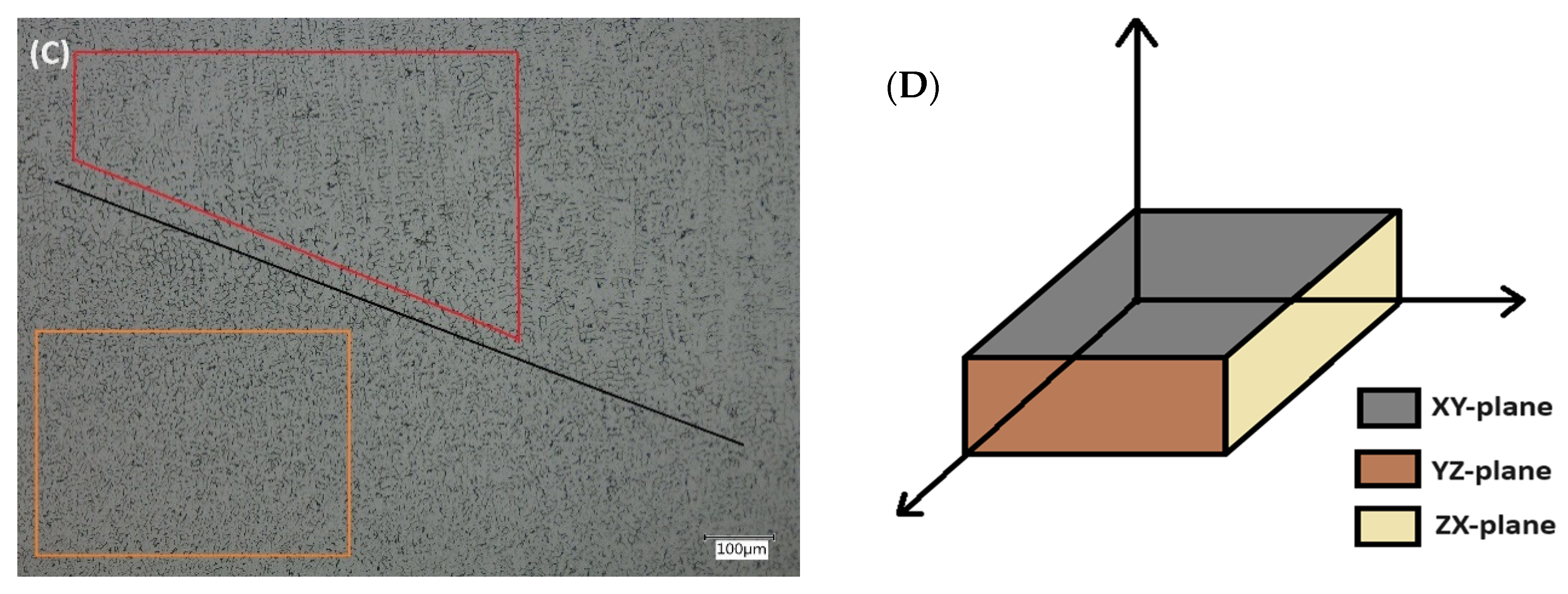
3.1. Density Measurements and Micrography
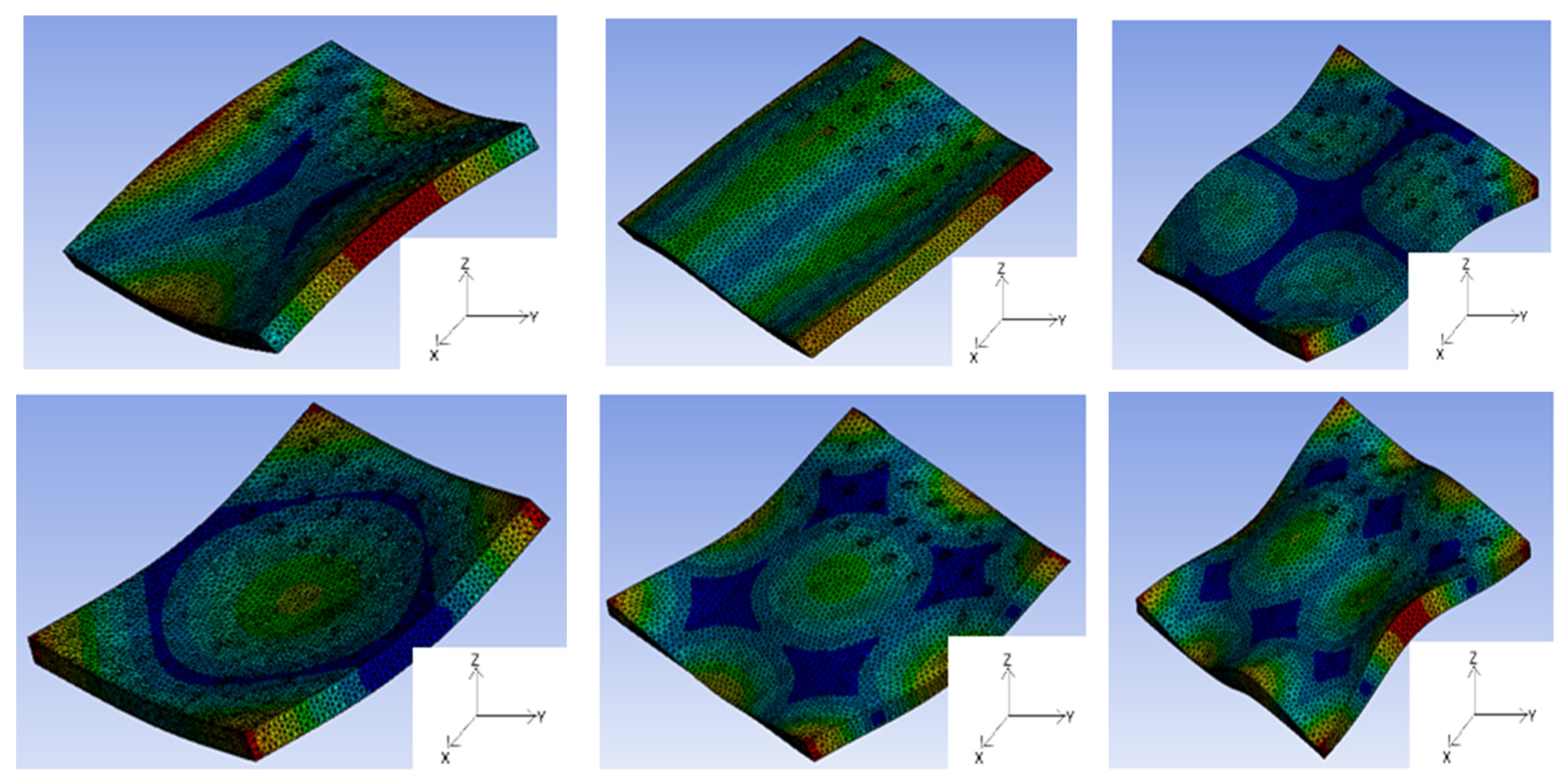
3.2. FEM-Simulated Sample Frequencies with/without Defects
- (a)
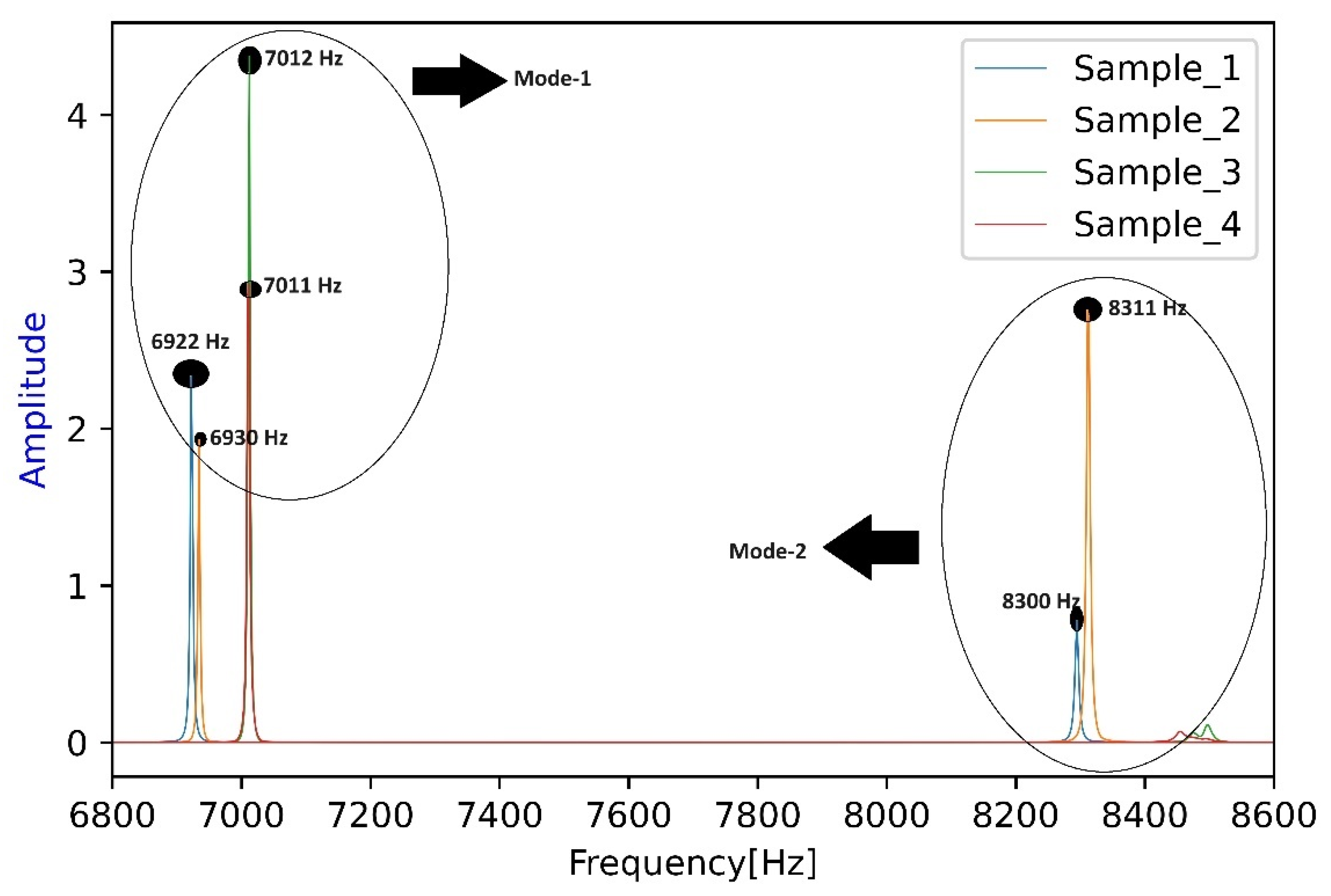
- Without defect: This information is elaborated in column 2 [0% porosity]. A parametric study was performed to ascertain the frequency shift by keeping the geometry fixed (dimensions are same as that used in experiments), while the E-modulus is varied between a range of 180–200 GPa. Finally, at 190 GPa, the frequency difference between FEM and experimental values (7030 and 7018 Hz, respectively) were narrowed down to just 0.17%. This inference serves an important function, which is identifying the correct resonant frequency from experiments and cancelling out the others.
- (b)
- Frequency shifts with increasing defect percent: Samples with varying amounts of porosity are shown in column 3. The frequency shifts with respect to each mode can be seen as well.
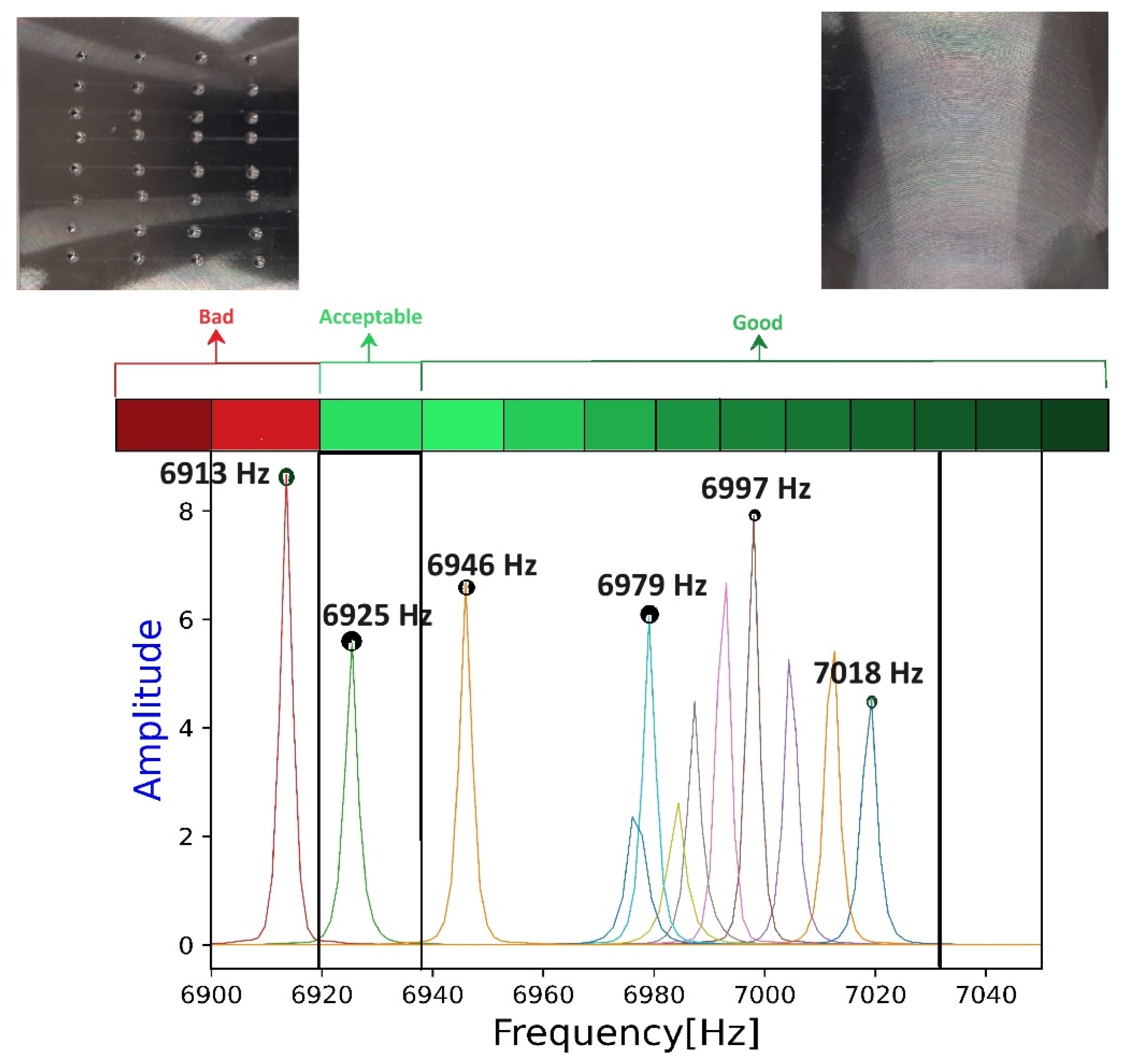
3.3. Defect Classification Based on Generated (Training-Set) Data
3.4. Defect Classification Based on Testing Dataset (Validation)
3.5. Future Work
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| WAAM | Wire arc additive manufacturing |
| RFM | Resonant frequency method |
| ISO | International Organisation for Standardisation |
| FEM/FEA | Finite element method/Finite element analysis |
| GMAW | Gas metal arc welding |
| GTAW | Gas tungsten arc welding |
| NDT | Non-destructive testing |
| XCT | X-ray computer tomography |
| RUS | Resonant ultrasound spectroscopy |
| ART | Acoustic resonance testing |
| SCNN | Spectral convolution neural network |
| TS | Travel speed |
| WFS | Wire weed speed |
| CAD | Computer-aided design |
| FFT | Fast Fourier transform |
References
- Rossin, J.; Goodlet, B.; Torbet, C.; Musinski, W.; Cox, M.; Miller, J.; Groeber, M.; Mayes, A.; Biedermann, E.; Smith, S.; et al. Assessment of grain structure evolution with resonant ultrasound spectroscopy in additively manufactured nickel alloys. Mater. Charact. 2020, 167, 110501. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Seifi, M. Metal additive manufacturing: A review of mechanical properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- DIN EN ISO/ASTM 52900:2022-03; Additive Fertigung-Grundlagen-Terminologie/Additive Manufacturing-Generl Principles-Fundamentals and Vocabulary. Deutsches Institut für Normung: Berlin, Germany, 2022.
- Keller, T.; Lindwall, G.; Ghosh, S.; Ma, L.; Lane, B.M.; Zhang, F.; Kattner, U.R.; Lass, E.A.; Heigel, J.C.; Idell, Y.; et al. Application of finite element, phase-field, and calphad-based methods to additive manufacturing of ni-based superalloys. Acta Mater. 2017, 139, 244–253. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, D. Wire-feed additive manufacturing of metal components: Technologies, developments and future interests. Int. J. Adv. Manuf. Technol. 2015, 81, 465–481. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H.; Xu, J.; Norrish, J. A review of the wire arc additive manufacturing of metals: Properties, defects and quality improvement. J. Manuf. Process. 2018, 35, 127–139. [Google Scholar] [CrossRef]
- Ya, W.; Hamilton, K. On-demand spare parts for the marine industry with directed energy deposition: Propeller use case. In Industrializing Additive Manufacturing-Proceedings of Additive Manufacturing in Products and Applications-AMPA20107; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 70–81. [Google Scholar]
- Seifi, M.; Salem, A.; Beuth, J.; Harrysson, O.; Lewandowski, J.J. Overview of materials qualification needs for metal additive manufacturing. JOM 2016, 68, 747–764. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Kruth, J.-P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Heinrich, M.; Valeske, B.; Rabe, U. Efficient detection of defective parts with acoustic resonance testing using synthetic training data. Appl. Sci. 2022, 12, 7648. [Google Scholar] [CrossRef]
- Obaton, A.-F.; Wang, Y.; Butsch, B.; Huang, Q. A non-destructive resonant acoustic testing and defect classification of additively manufactured lattice structures. Weld. World 2021, 65, 361–371. [Google Scholar] [CrossRef]
- ISO 5817:2014(E); Welding–Fusion-Welded Joints in Steel, Nickel, Titanium and Their Alloys (Beam Welding Excluded)–Quality Levels for Imperfections. ISO: Genève, Switzerland, 2014.
- Braun, M.; Schubnell, J.; Sarmast, A.; Subramanian, H.; Reissig, L.; Altenhöner, F.; Sheikhi, S.; Renken, F.; Ehlers, S. Mechanical behaviour of additively and conventionally manufactured 316L stainless steel plates joined by gas metal arc welding. J. Mat. Res. Tech. 2023, 24, 1692–1705. [Google Scholar] [CrossRef]
- ASTM B962-23; Standard Test Methods for Density of Compacted or Sintered Powder Metallurgy (PM) Products Using Archimedes Principle. ASTM International: West Conshohocken, PA, USA, 2023.
- Sufiiarov, V.; Popovich, A.; Borisov, E.; Polozov, I.; Masaylo, D.; Orlov, A. The effect of layer thickness at selective laser melting. Procedia Eng. 2017, 174, 126–134. [Google Scholar] [CrossRef]
- Pisarciuc, C.; Dan, I.; Cioară, R. The influence of mesh density on the results obtained by finite element analysis of complex bodies. Materials 2023, 16, 2555. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, Y.; Li, Z.; Davies, C.; Maharaj, C.; Dear, J.; Hooper, P. Acoustic resonance testing of additive manufactured lattice structures. Addit. Manuf. 2018, 24, 566–576. [Google Scholar] [CrossRef]
- DIN EN 843-2; Hochleistungskeramik-Mechanische Eigenschaften Monolithischer Keramik bei Raumtemperatur-Teil2: Bestimmung des Elastizitätsmoduls, Schubmoduls und der Poissonzahl. Deutsches Institut für Normung: Berlin, Germany, 2007. (In German)
- Collins, P.; Brice, D.; Samimi, P.; Ghamarian, I.; Fraser, H. Microstructural control of additively manufactured metallic materials. Annu. Rev. Mater. Res. 2016, 46, 63–91. [Google Scholar] [CrossRef]
- Müller, M. Book: Fundamentals of Music Processing; Chapter: The Fourier Transform in a Nutshell; Springer: Cham, Switzerland, 2015; pp. 39–114. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- ISO/ASTM 52922-F3413-19-Guide; Guide for Additive Manufacturing—Design—Directed Energy Deposition. ASTM: ASTM International: West Conshohocken, PA, USA, 2019.
- Schaeffler, A.L. Constitution diagram for stainless stee. Met. Prog. 1949, 56, 680. [Google Scholar]
- Delong, W.T. Ferrite in austenitic stainless steel weld metal. Weld. Res. 1974, 53, 273–286. [Google Scholar]
- Belotti, L.P.; Van Dommelen, J.A.W.; Geers, M.G.D.; Goulas, C.; Ya, W.; Hoefnagels, J.P.M. Microstructural characteristics of thick walled wire arc additively manufactured stainless steel. J. Mater. Process. Technol. 2022, 299, 117373. [Google Scholar] [CrossRef]
- Inoue, H.; Koseki, T.; Ohkita, S.; Fuhi, M. Formation mechanism of vermicular and lacy ferrite in austenitic stainless steel weld metals. Sci. Technol. Weld. Join. 2000, 5, 385–396. [Google Scholar] [CrossRef]
- Suutala, N.; Takalo, T.; Moisio, T. The relationship between solidification and microstructure in austenitic and austenitic-ferritic stainless steel welds. Met. Trans. A 1979, 10, 512–514. [Google Scholar] [CrossRef]
- Wang, C.; Liu, T.; Zhu, P.; Lu, Y.; Shoji, T. Study on microstructure and tensile properties of 316L stainless steel fabricated by CMT wire and arc additive manufacturing. Mater. Sci. Eng. A 2020, 796, 140006. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T. Free vibrations and static analysis of functionally graded sandwich plates with three-dimensional finite elements. Meccanica 2020, 55, 815–832. [Google Scholar] [CrossRef]




| Cr | Ni | Mo | Mn | Si | C | N | Nb | P | Fe | |
|---|---|---|---|---|---|---|---|---|---|---|
| Wire 316LSi | 18.65 | 11.64 | 2.29 | 1.76 | 0.65 | 0.026 | 0.035 | 0.016 | 0.003 | 64.62 |
| Material | Density [kg/m3] | E-Modulus [GPa] | Poisson’s Ratio |
|---|---|---|---|
| 316LSi | 7837 | 190 | 0.27 |
| Defect/Porosity Concentratin [%] | Sample Classification |
|---|---|
| Good | |
| and | Acceptable |
| Bad |
| Sample | Density (kg/m3) | E-Modulus (GPa) |
|---|---|---|
| Wrought | 7990 | 190 |
| WAAM | 7837 | 169 |
| Def [%] | 0% | 0.22% | 0.31% | 0.43% | 0.52% | 0.65% | 0.76% | 0.91% | 1.02% | 2.04% | 3.06% | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mode | ||||||||||||
| 1 | 7030 | 7024 | 7016 | 7009 | 7007 | 7002 | 6999 | 6994 | 6991 | 6966 | 6954 | |
| 2 | 8293 | 8297 | 8297 | 8296 | 8294 | 8289 | 8288 | 8289, | 8287 | 8268 | 8216 | |
| 3 | 11,644 | 11,647 | 11,642 | 11,635 | 11,628 | 11,619 | 11,612 | 11,608 | 11,602 | 11,565 | 11,517 | |
| 4 | 11,943 | 11,946 | 11,943 | 11,935 | 11,928 | 11,915 | 11,907 | 11,904 | 11,895 | 11,850 | 11,802 | |
| 5 | 19,610 | 19,612 | 19,597 | 19,579 | 19,570 | 19,571 | 19,553 | 19,538 | 19,528 | 19,461 | 19,383 | |
| 6 | 20,869 | 20,865 | 20,846 | 20,833 | 20,822 | 20,828 | 20,814 | 20,796 | 20,785 | 20,679 | 20,604 | |
| 7 | 20,950 | 20,953 | 20,951 | 20,948 | 20,946 | 20,943 | 20,942 | 20,940 | 20,937 | 20,797 | 20,663 | |
| 8 | 22,684 | 22,685 | 22,672 | 22,653 | 22,640 | 22,625 | 22,606 | 22,594 | 22,580 | 22,510 | 22,446 | |
| 9 | 25,130 | 25,133 | 25,118 | 25,102 | 25,090 | 25,089 | 25,072 | 25,058 | 25,045 | 24,927 | 24,827 | |
| 10 | 33,007 | 32,999 | 32,980 | 32,972 | 32,958 | 32,936 | 32,928 | 32,913 | 32,900 | 32,756 | 32,640 | |
| 11 | 33,576 | 33,571 | 33,538 | 33,512 | 33,493 | 33,504 | 33,479 | 33,444 | 33,424 | 33,299 | 33,218 | |
| 12 | 36,455 | 36,454 | 36,420 | 36,414 | 36,400 | 36,377 | 36,369 | 36,333 | 36,320 | 36,173 | 36,041 | |
| Pores % w.r.t Surface Area | Mass [g] | Frequency-Exp [Hz] | Frequency-FEM [Hz] | Category | |
|---|---|---|---|---|---|
| 0 | 0 | 80.05 | 7018 | 7030 | I-Good |
| 1 | 0.22 | 80.03 | 7012 | 7024 | |
| 2 | 0.31 | 80.01 | 7004 | 7016 | |
| 3 | 0.43 | 79.99 | 6997 | 7009 | |
| 4 | 0.52 | 79.97 | 6992 | 7077 | |
| 5 | 0.65 | 79.95 | 6987 | 7002 | |
| 6 | 0.76 | 79.93 | 6984 | 6999 | |
| 7 | 0.91 | 79.92 | 6979 | 6994 | |
| 8 | 1.02 | 79.90 | 6976 | 6991 | |
| 9 | 2.04 | 79.76 | 6946 | 6966 | |
| 10 | 3.06 | 79.62 | 6925 | 6945 | II-Acceptable |
| 11 | 4.02 | 79.48 | 6913 | 6930 | III-Bad |
| Sample No. | Classification | ||||
|---|---|---|---|---|---|
| Good | Good | Good | Acceptable | Bad | |
| 1 | 7014 | 7006 | 6901 | ||
| 2 | 7016 | 6915 | |||
| 3 | 7017 | 6980 | 6897 | ||
| 4 | 7013 | 7009 | 6933 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaparthi, S.; Subadra, S.P.; Sheikhi, S. A Smart, Data-Driven Approach to Qualify Additively Manufactured Steel Samples for Print-Parameter-Based Imperfections. Materials 2024, 17, 2513. https://doi.org/10.3390/ma17112513
Alaparthi S, Subadra SP, Sheikhi S. A Smart, Data-Driven Approach to Qualify Additively Manufactured Steel Samples for Print-Parameter-Based Imperfections. Materials. 2024; 17(11):2513. https://doi.org/10.3390/ma17112513
Chicago/Turabian StyleAlaparthi, Suresh, Sharath P. Subadra, and Shahram Sheikhi. 2024. "A Smart, Data-Driven Approach to Qualify Additively Manufactured Steel Samples for Print-Parameter-Based Imperfections" Materials 17, no. 11: 2513. https://doi.org/10.3390/ma17112513
APA StyleAlaparthi, S., Subadra, S. P., & Sheikhi, S. (2024). A Smart, Data-Driven Approach to Qualify Additively Manufactured Steel Samples for Print-Parameter-Based Imperfections. Materials, 17(11), 2513. https://doi.org/10.3390/ma17112513






