Modelling a Response of Complex-Phase Steel at High Strain Rates
Abstract
1. Introduction
2. Materials and Methods
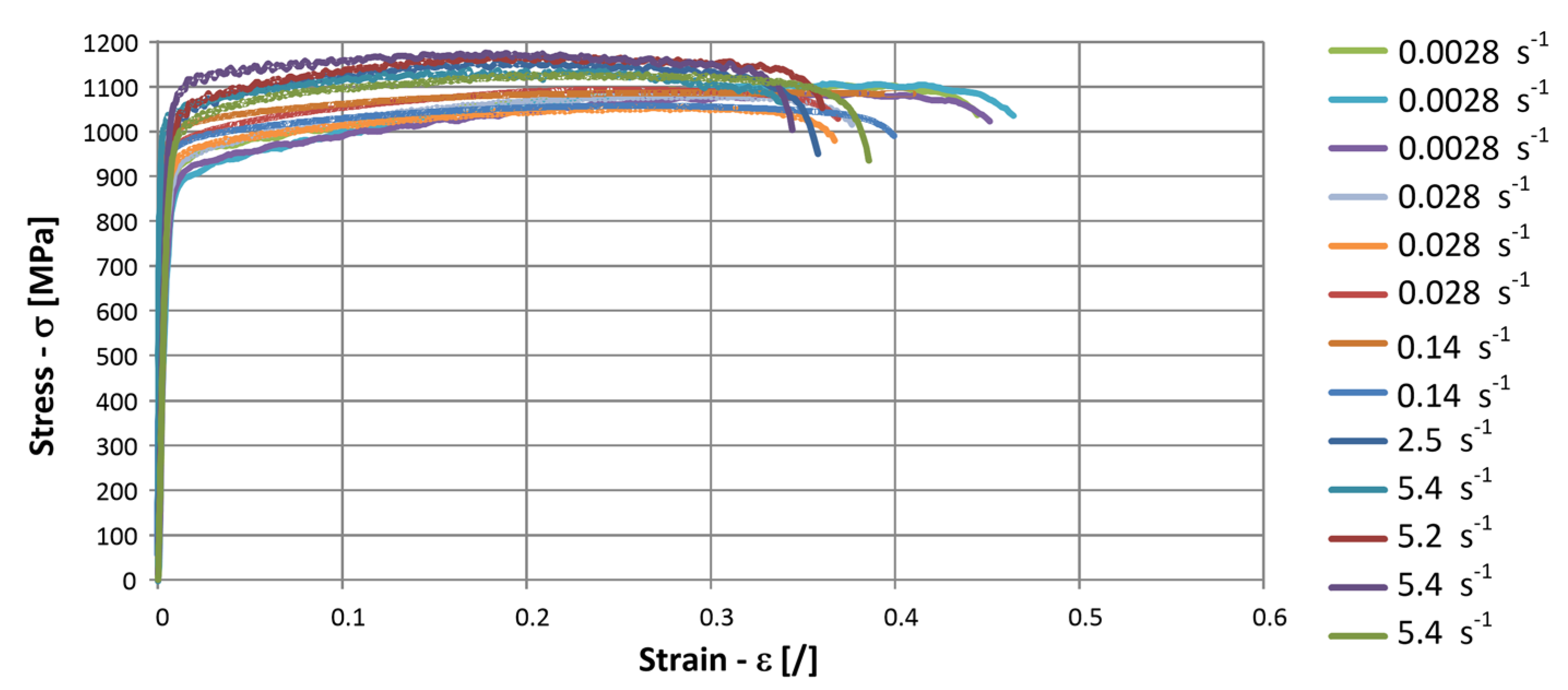
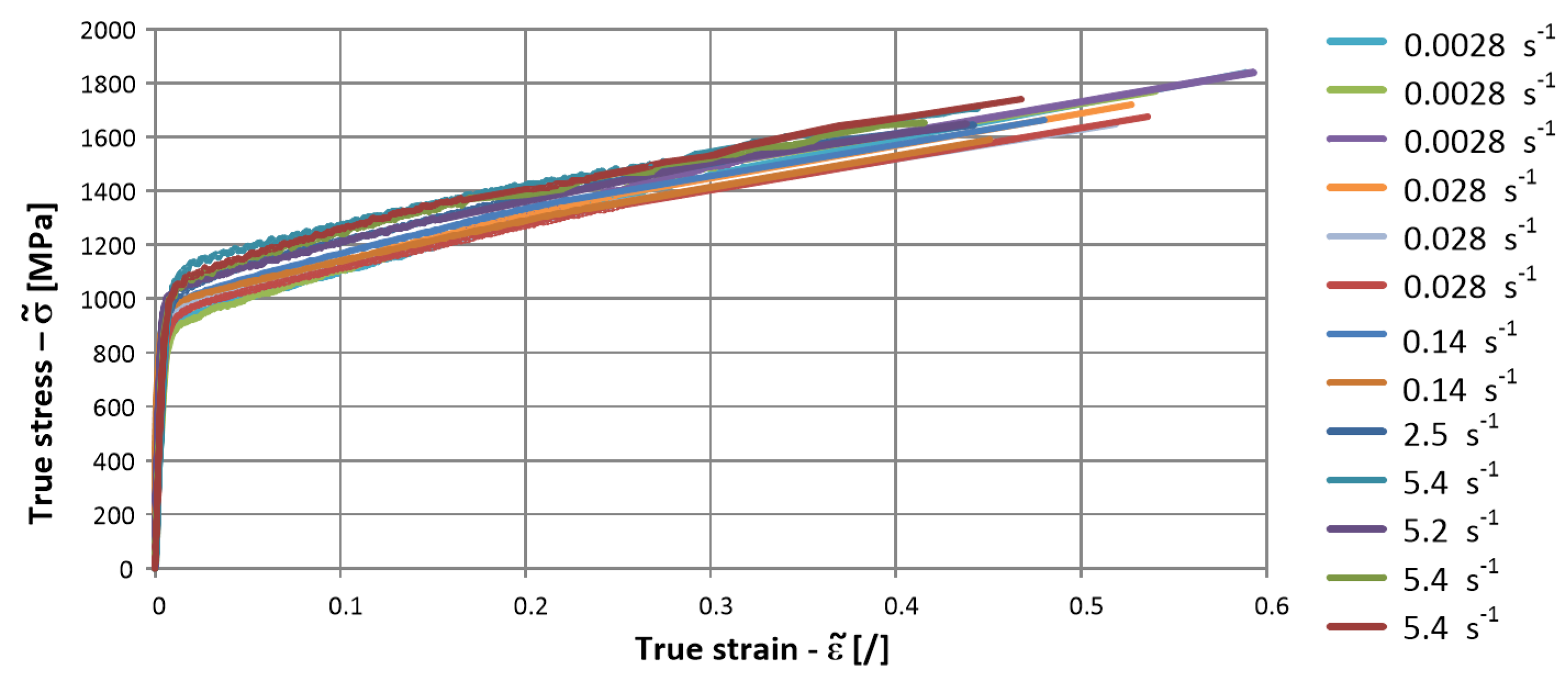
2.1. Tensile Stress–Strain Curves at Different Low-Strain Rates
2.2. Experimental Determination of Material Behaviour at High Strain Rates
2.3. Identification of the Strain-Rate-Dependent Material Parameters
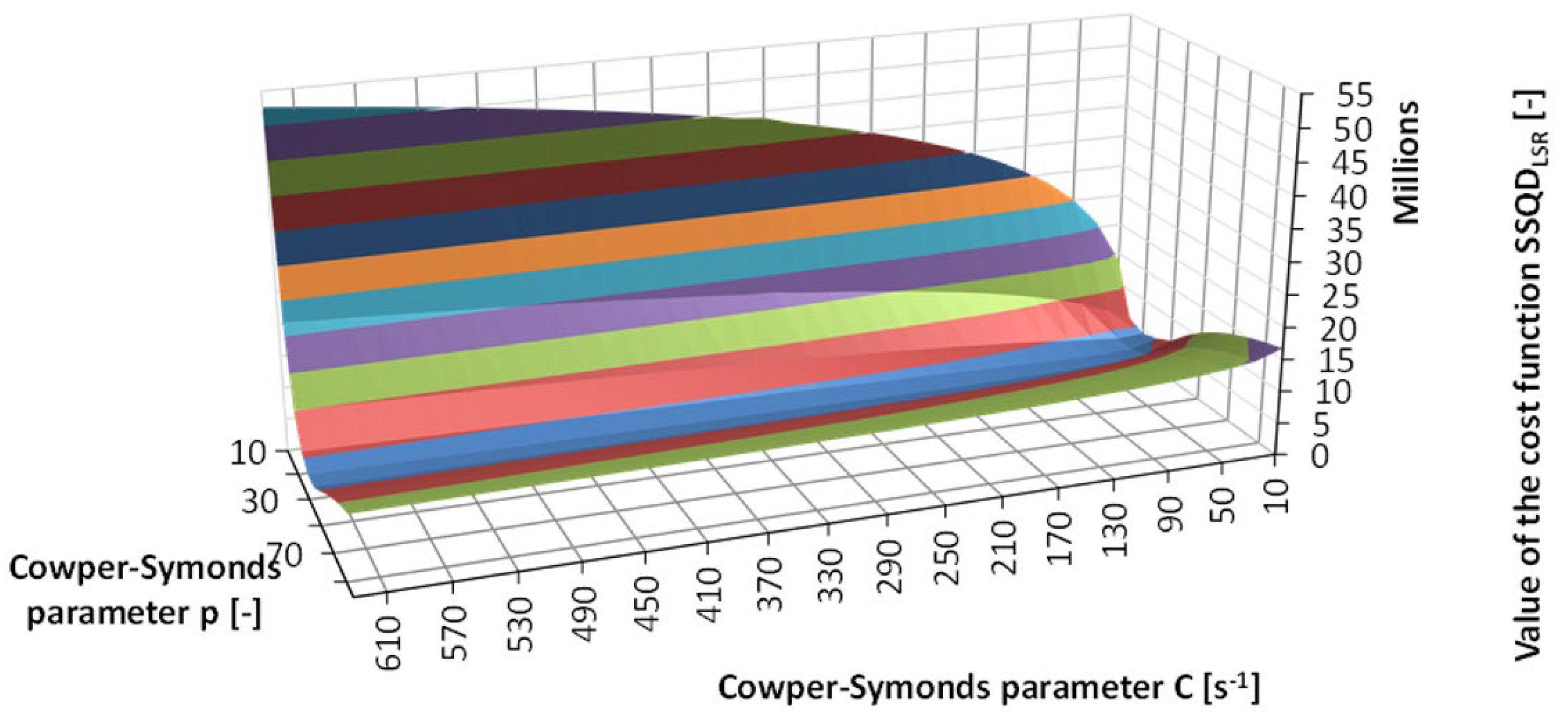
- A rough estimation of the three parameters SIGY, C, and p was first conducted with a grid-search method for the tensile tests at low strain rates.
- After the first phase, the SIGY parameter was fixed, and the two parameters, C and p, were fine-tuned using a reverse-engineering approach combined with a genetic algorithm optimisation procedure in the second phase.
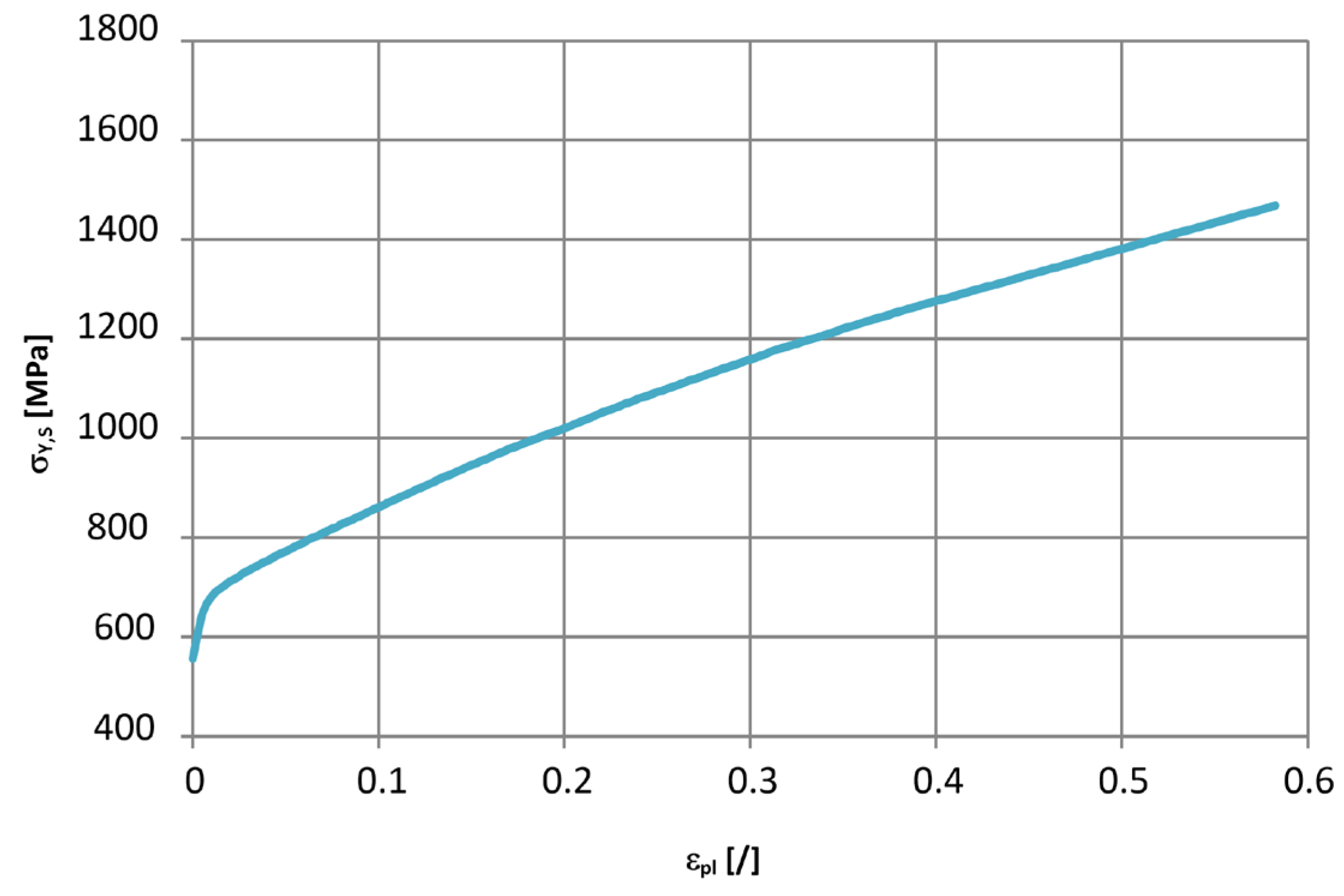
2.3.1. PHASE 1—Rough Estimation on the Basis of the Tensile Tests at a Low Strain Rate
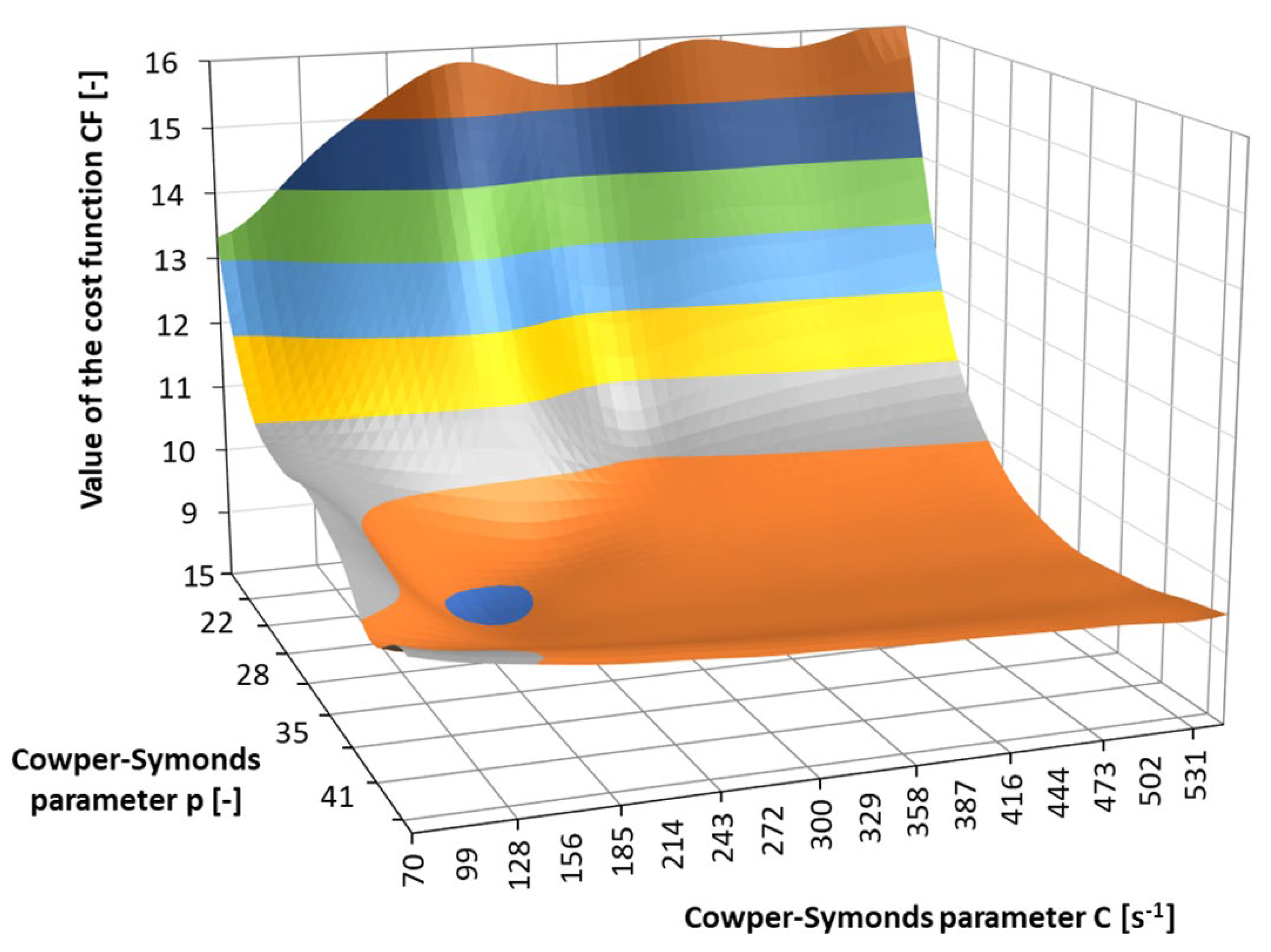
2.3.2. PHASE 2—Enhanced Estimation Based on the Reverse-Engineering Approach
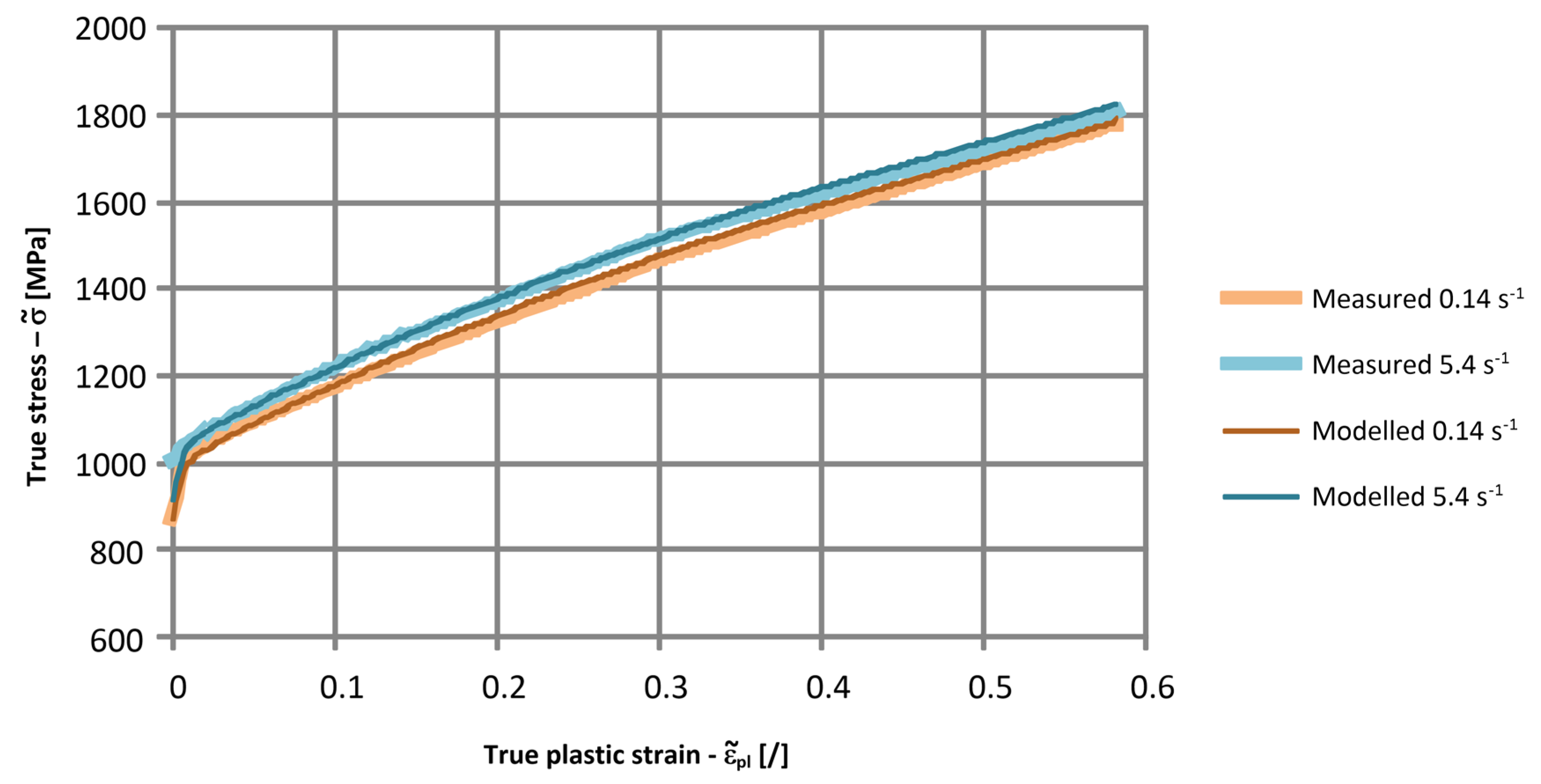
3. Results
4. Discussion
5. Conclusions
- The estimated values of the Cowper–Symonds parameters p and C differ somewhat from the data in the literature for similar materials.
- Parameter estimates are strongly dependent on the applied testing methods and strain rates.
- Due to the shape of the multi-criteria cost function, a wide domain of the combinations for the material parameters p and C yield acceptable results.
- Estimated values of the material parameters also depend on the mathematical formulation for the strain-rate effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hallquist, J.O. LS-DYNA Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Version 2006; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Hernandez, C.; Maranon, A.; Ashcroft, I.A.; Casas-Rodriguez, J.P. A Computational Determination of the Cowper–Symonds Parameters from a Single Taylor Test. Appl. Math. Model. 2013, 37, 4698–4708. [Google Scholar] [CrossRef]
- Škrlec, A.; Klemenc, J. Estimating the Strain-Rate-Dependent Parameters of the Johnson-Cook Material Model Using Optimisation Algorithms Combined with a Response Surface. Mathematics 2020, 8, 1105. [Google Scholar] [CrossRef]
- Li, H.; Li, F.; Zhang, R.; Zhi, X. High Strain Rate Experiments and Constitutive Model for Q390D Steel. J. Constr. Steel Res. 2023, 206, 107933. [Google Scholar] [CrossRef]
- Gupta, M.K.; Singh, N.K.; Gupta, N.K. Deformation Behaviour and Notch Sensitivity of a Super Duplex Stainless Steel at Different Strain Rates and Temperatures. Int. J. Impact Eng. 2023, 174, 104494. [Google Scholar] [CrossRef]
- Qin, J.; Chen, R.; Wen, X.; Lin, Y.; Liang, M.; Lu, F. Mechanical Behaviour of Dual-Phase High-Strength Steel under High Strain Rate Tensile Loading. Mater. Sci. Eng. A 2013, 586, 62–70. [Google Scholar] [CrossRef]
- Huh, H.; Kim, S.-B.; Song, J.-H.; Lim, J.-H. Dynamic Tensile Characteristics of TRIP-Type and DP-Type Steel Sheets for an Auto-Body. Int. J. Mech. Sci. 2008, 50, 918–931. [Google Scholar] [CrossRef]
- Yu, H.; Guo, Y.; Lai, X. Rate-Dependent Behavior and Constitutive Model of DP600 Steel at Strain Rate from 10−4 to 103 s−1. Mater. Des. 2009, 30, 2501–2505. [Google Scholar] [CrossRef]
- Shang, M.; Yang, H.; Su, A.; Wang, Y. Strain-Rate and Stress-State Dependent Ductile Fracture Model of S690 High-Strength Steel. J. Constr. Steel Res. 2023, 204, 107852. [Google Scholar] [CrossRef]
- Yang, X.; Yang, H.; Lai, Z.; Zhang, S. Dynamic Tensile Behavior of S690 High-Strength Structural Steel at Intermediate Strain Rates. J. Constr. Steel Res. 2020, 168, 105961. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Zhang, H.; Zhao, J.; Song, Q. A Rate-Dependent Damage Model to Characterize Dynamic Fracture Behavior of Ti6Al4V under High Strain Rate Loading. Eng. Fract. Mech. 2022, 274, 108781. [Google Scholar] [CrossRef]
- Mahalle, G.; Kotkunde, N.; Gupta, A.K.; Singh, S.K. Cowper-Symonds Strain Hardening Model for Flow Behaviour of Inconel 718 Alloy. Mater. Today Proc. 2019, 18, 2796–2801. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Machine-Learning Based Temperature- and Rate-Dependent Plasticity Model: Application to Analysis of Fracture Experiments on DP Steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar] [CrossRef]
- Shang, H.; Wu, P.; Lou, Y.; Wang, J.; Chen, Q. Machine Learning-Based Modeling of the Coupling Effect of Strain Rate and Temperature on Strain Hardening for 5182-O Aluminum Alloy. J. Mater. Process. Technol. 2022, 302, 117501. [Google Scholar] [CrossRef]
- SZBS800 Multiphase Steels: Bainitic Grade. Salzgitter Flachstahl GmbH. Available online: https://www.salzgitter-flachstahl.de/fileadmin/footage/media/gesellschaften/szfg/informationsmaterial/produktinformationen/warmgewalzte_produkte/eng/szbs800.pdf (accessed on 26 February 2024).
- ASTM E8/E8M; Test Methods for Tension Testing of Metallic Materials. E28 Committee. ASTM International: West Conshohocken, PA, USA, 2024.
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, 4th ed.; Pearson: Boston, MA, USA, 2013; ISBN 978-0-13-139506-0. [Google Scholar]
- Mirone, G.; Barbagallo, R.; Bua, G.; De Caro, D.; Ferrea, M.; Tedesco, M.M. A Simple Procedure for the Post-Necking Stress-Strain Curves of Anisotropic Sheet Metals. Metals 2023, 13, 1156. [Google Scholar] [CrossRef]
- ASTM D5420; Test Method for Impact Resistance of Flat, Rigid Plastic Specimen by Means of a Striker Impacted by a Falling Weight (Gardner Impact). D20 Committee; ASTM International: West Conshohocken, PA, USA, 2021.
- Klemenc, J.; Fajdiga, M. Joint Estimation of E–N Curves and Their Scatter Using Evolutionary Algorithms. Int. J. Fatigue 2013, 56, 42–53. [Google Scholar] [CrossRef]
- Cadoni, E.; Forni, D. Strain-Rate Effects on S690QL High Strength Steel under Tensile Loading. J. Constr. Steel Res. 2020, 175, 106348. [Google Scholar] [CrossRef]
- Gao, S.; Yu, X.; Li, Q.; Sun, Y.; Hao, Z.; Gu, D. Research on Dynamic Deformation Behavior and Constitutive Relationship of Hot Forming High Strength Steel. J. Mater. Res. Technol. 2024, 28, 1694–1712. [Google Scholar] [CrossRef]
- Zeng, X.; Huo, J.S. Rate-Dependent Constitutive Model of High-Strength Reinforcing Steel HTRB600E in Tension. Constr. Build. Mater. 2023, 363, 129824. [Google Scholar] [CrossRef]
- Singh, N.K.; Cadoni, E.; Singha, M.K.; Gupta, N.K. Dynamic Tensile Behavior of Multi Phase High Yield Strength Steel. Mater. Des. 2011, 32, 5091–5098. [Google Scholar] [CrossRef]
- Cadoni, E.; Dotta, M.; Forni, D.; Tesio, N. High Strain Rate Behaviour in Tension of Steel B500A Reinforcing Bar. Mater Struct 2015, 48, 1803–1813. [Google Scholar] [CrossRef]
- Zeng, X.; Huo, J.; Wang, H.; Wang, Z.; Elchalakani, M. Dynamic Tensile Behavior of Steel HRB500E Reinforcing Bar at Low, Medium, and High Strain Rates. Materials 2020, 13, 185. [Google Scholar] [CrossRef] [PubMed]







| C | Si | Mn | P | S | Al | B | Cu |
|---|---|---|---|---|---|---|---|
| max. | max. | max. | max. | max. | min. | max. | max. |
| 0.18% | 1.00% | 2.20% | 0.05% | 0.01% | 0.015–1.2% | 0.005% | 0.2% |
| Specimen Number | Impact Angle aj [°] | Ball Velocity vj [m/s] |
|---|---|---|
| 20210503_H800-1 | 0 | 111.5 |
| 20231108_H800-1 | 0 | 133.3 |
| 20210504_H800-1 | 0 | 155.3 |
| 20231108_H800-3 | 20 | 111.2 |
| 20231108_H800-2 | 20 | 132.6 |
| 20210714_H800-1 | 20 | 154.2 |
| 20210507_H800-2 | 35 | 113.1 |
| 20231110_H800-1 | 35 | 131.9 |
| 20210713_H800-1 | 35 | 153.5 |
| SIGY [MPa] | C [s−1] | p [/] |
|---|---|---|
| 200 | 1 | 0.1 |
| 300 | 2.5 | 0.25 |
| 400 | 5 | 0.5 |
| 500 | 10 | 1 |
| 600 | 50 | 2.5 |
| 100 | 5 | |
| 250 | 10 | |
| 500 | 15 | |
| 2500 | 25 | |
| 10,000 | 50 | |
| 100 |
| p [/] | C [s−1] | p [/] | C [s−1] |
|---|---|---|---|
| 10 | 10 | 80 | 190 |
| 15 | 30 | 90 | 210 |
| 20 | 50 | 100 | 230 |
| 25 | 70 | 250 | |
| 30 | 90 | 270 | |
| 40 | 110 | 300 | |
| 50 | 130 | 600 | |
| 60 | 150 | 1000 | |
| 70 | 170 | 1500 |
| p [/] | C [s−1] | p [/] | C [s−1] |
|---|---|---|---|
| 15 | 70 | 35 | 390 |
| 20 | 150 | 40 | 470 |
| 25 | 230 | 45 | 550 |
| 30 | 310 |
| Specimen Number | Impact Angle αj [°] | Ball Velocity vj [m/s] | Y-Coordinate of max. Indentation Yj,exp [mm] | Maximum Indentation Depth Hj,exp [mm] |
|---|---|---|---|---|
| 20210503_H800-1 | 0 | 111.5 | 29.762 | 5.768 |
| 20231108_H800-1 | 0 | 133.3 | 29.282 | 8.057 |
| 20210504_H800-1 | 0 | 155.3 | 29.716 | 8.497 |
| 20231108_H800-3 | 20 | 111.2 | 30.306 | 5.975 |
| 20231108_H800-2 | 20 | 132.6 | 29.575 | 6.940 |
| 20210714_H800-1 | 20 | 154.2 | 32.632 | 8.025 |
| 20210507_H800-2 | 35 | 113.1 | 32.325 | 5.726 |
| 20231110_H800-1 | 35 | 131.9 | 32.331 | 6.055 |
| 20210713_H800-1 | 35 | 153.5 | 33.821 | 6.911 |
| Material Name | EN Code | Testing Method | p [-] | C [s−1] |
|---|---|---|---|---|
| S690QL ultra-high-strength steel—EN 10025 [22] | 1.8931 | Low strain rates 10−3 s−1: Zwick/Roell—Z50 (ZwickRoell GmbH & Co., Ulm, Germany) Medium strain rates 3 s−1–30 s−1: Hydro-pneumatic machine; High strain rates 250 s−1–950 s−1: Split Hopkinson Tensile Bar | 2.3 to 4.49 | 121,783 to 212,352 |
| Hot-forming steel 22MnB5 [23] | 1.5528 | Low strain rates 10−3 s−1: WDW-100E uniaxial tensile testing machine; High strain rates 2000 s−1–4000 s−1: Split Hopkinson Pressure Bar | 3.2050 | 6277.8 |
| S690 high-strength structural steel [11] | 1.3964 | Low strain rates 10−3 s−1: universal electromechanical testing machine; Intermediate strain rates 10 s−1–200 s−1: High-speed tensile testing machine | 6.1–6.7 | 1.2 × 107 to 3.3 × 107 |
| high-strength reinforcing steel HTRB600E [24] | Low strain rates: below 2 × 10−3 s−1: electromechanical universal testing machine; Elevated strain rates 0.018–585 s−1: high-speed servo-hydraulic tensile testing machine Zwick/Roell HTM5020 | 5.925 to 6.027 | 1.83 × 107 to 8.67 × 107 | |
| Q390D steel [5] | Low strain rates 8.4 × 10−4 s−1: INSTRON 5569 uniaxial tensile testing machine (Instron, Norwood, MA, USA); High strain rates 837.1 s−1–3368.1 s−1: Split Hopkinson pressure Bar | 1.31 to 2.4 | 3097.14 to 3861.44 | |
| Duplex Stainless Steel 2507 [6] | 1.4410 | Low strain rates 0.0001–0.1: electromechanical universal testing machine (Zwick/Roell Z250) | 1.7566 | 2.68274 |
| MP800HY Steel [25] | Low strain rates 10−3 s−1: Zwick/Roell—Z50; Medium strain rates 5 s−1–25 s−1: Hydro-pneumatic machine; High strain rates 250 s−1–750 s−1: modified Hopkinson Bar | 2.2146 | 32,338 | |
| steel B500A [26] | Low strain rates 10−4 s−1: universal electromechanical testing machine; High strain rates 250 s−1–1000 s−1: Split Hopkinson Tensile Bar | 1.654 to 4.4677 | 5.574 to 525.444 | |
| Steel HRB500E [27] | Low strain rates 2.5 × 10−4–5.3 × 10−1 s−1: universal electromechanical testing machine; High strain rates 0.1 s−1–550 s−1: Zwick/Roell HTM5020 servo-hydraulic high-speed testing machine | 4.906 | 264,713 | |
| SZBS800 steel | 1.0998 | Low strain rates: 100 kN MTS Landmark testing machine; High strain rates: shooting ball into flat specimen | 30.4 | 172.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Škrlec, A.; Kocjan, T.; Nagode, M.; Klemenc, J. Modelling a Response of Complex-Phase Steel at High Strain Rates. Materials 2024, 17, 2302. https://doi.org/10.3390/ma17102302
Škrlec A, Kocjan T, Nagode M, Klemenc J. Modelling a Response of Complex-Phase Steel at High Strain Rates. Materials. 2024; 17(10):2302. https://doi.org/10.3390/ma17102302
Chicago/Turabian StyleŠkrlec, Andrej, Tadej Kocjan, Marko Nagode, and Jernej Klemenc. 2024. "Modelling a Response of Complex-Phase Steel at High Strain Rates" Materials 17, no. 10: 2302. https://doi.org/10.3390/ma17102302
APA StyleŠkrlec, A., Kocjan, T., Nagode, M., & Klemenc, J. (2024). Modelling a Response of Complex-Phase Steel at High Strain Rates. Materials, 17(10), 2302. https://doi.org/10.3390/ma17102302









