Exploration of Alloying Elements of High Specific Modulus Al–Li Alloy Based on Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset Construction
2.2. Feature Space Construction
2.3. Machine Learning
2.4. Experiments
3. Results and Discussion
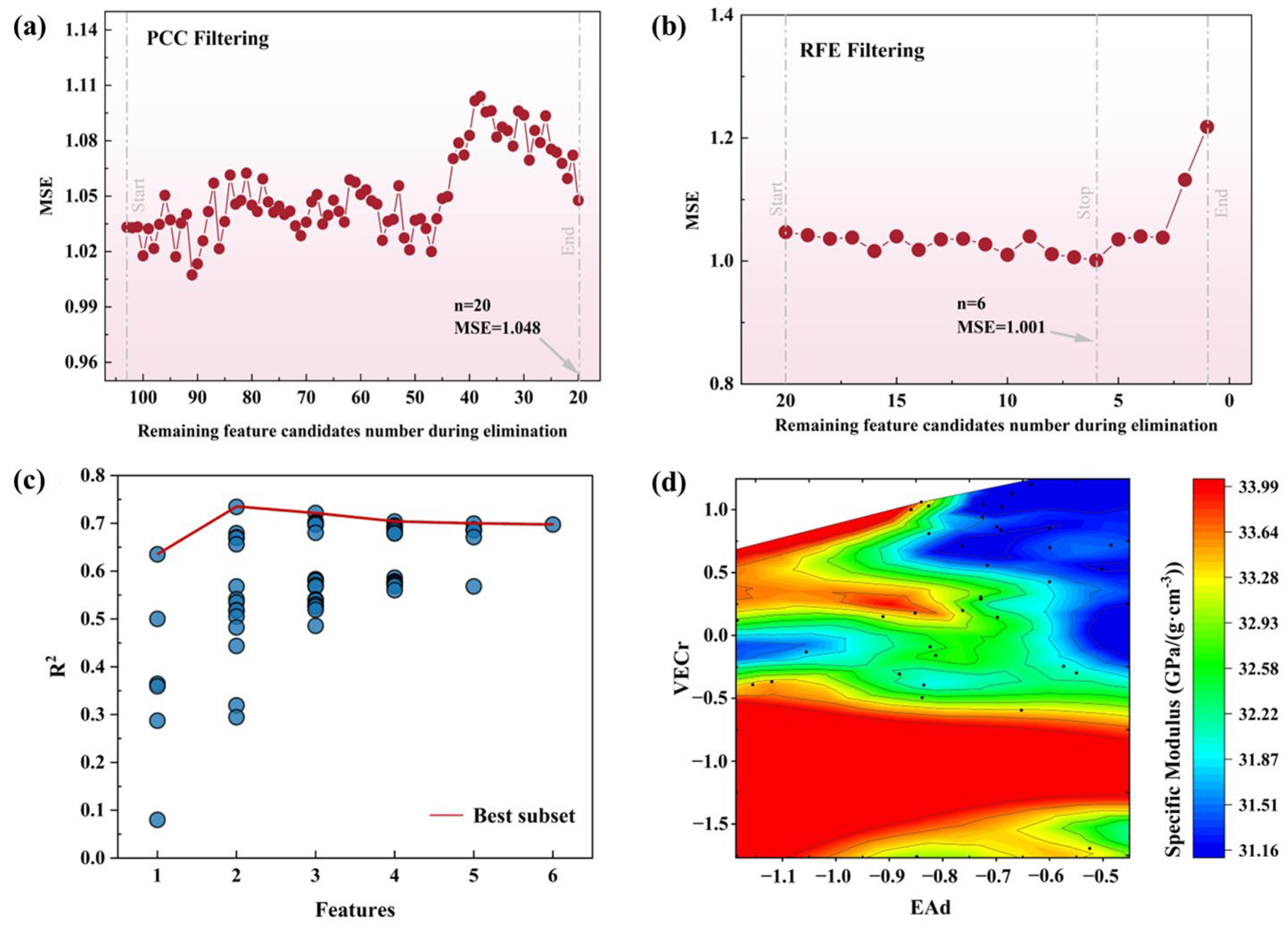
3.1. Elements Filtering
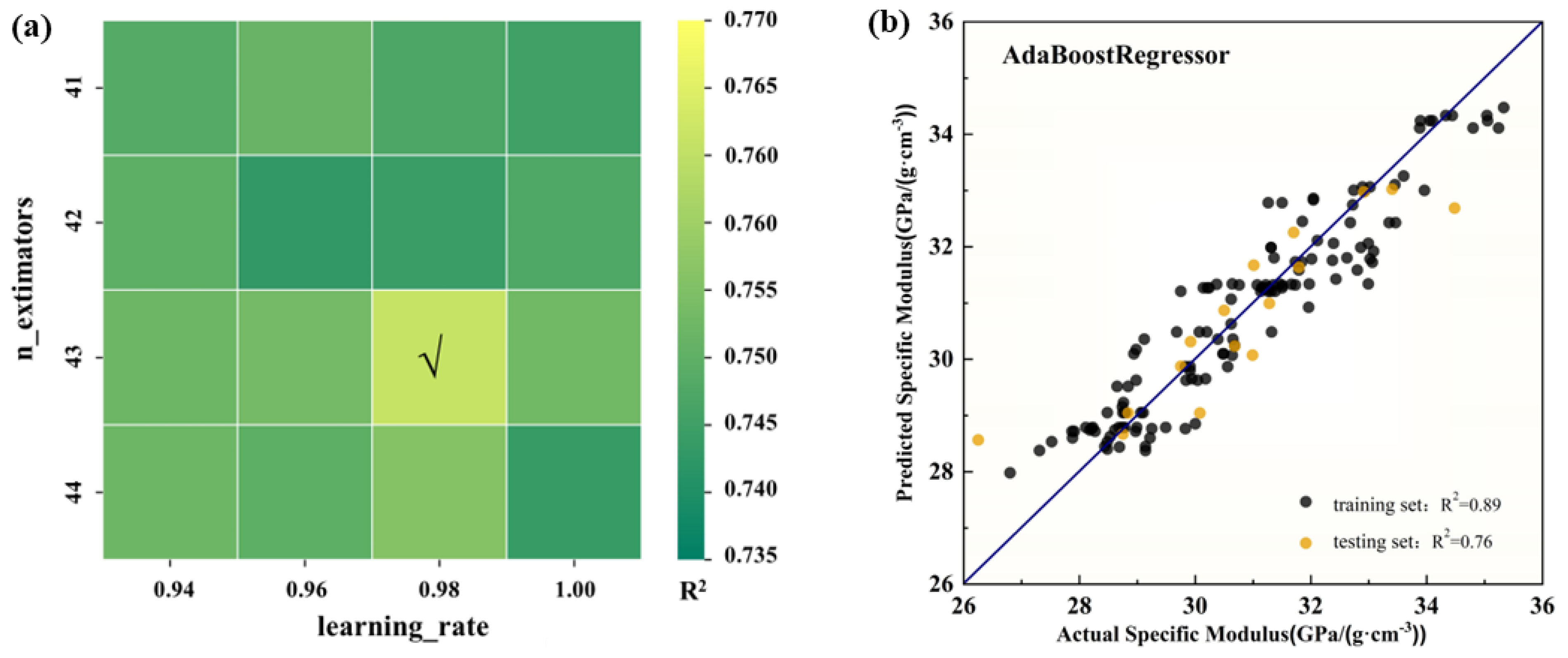
3.2. Model Construction
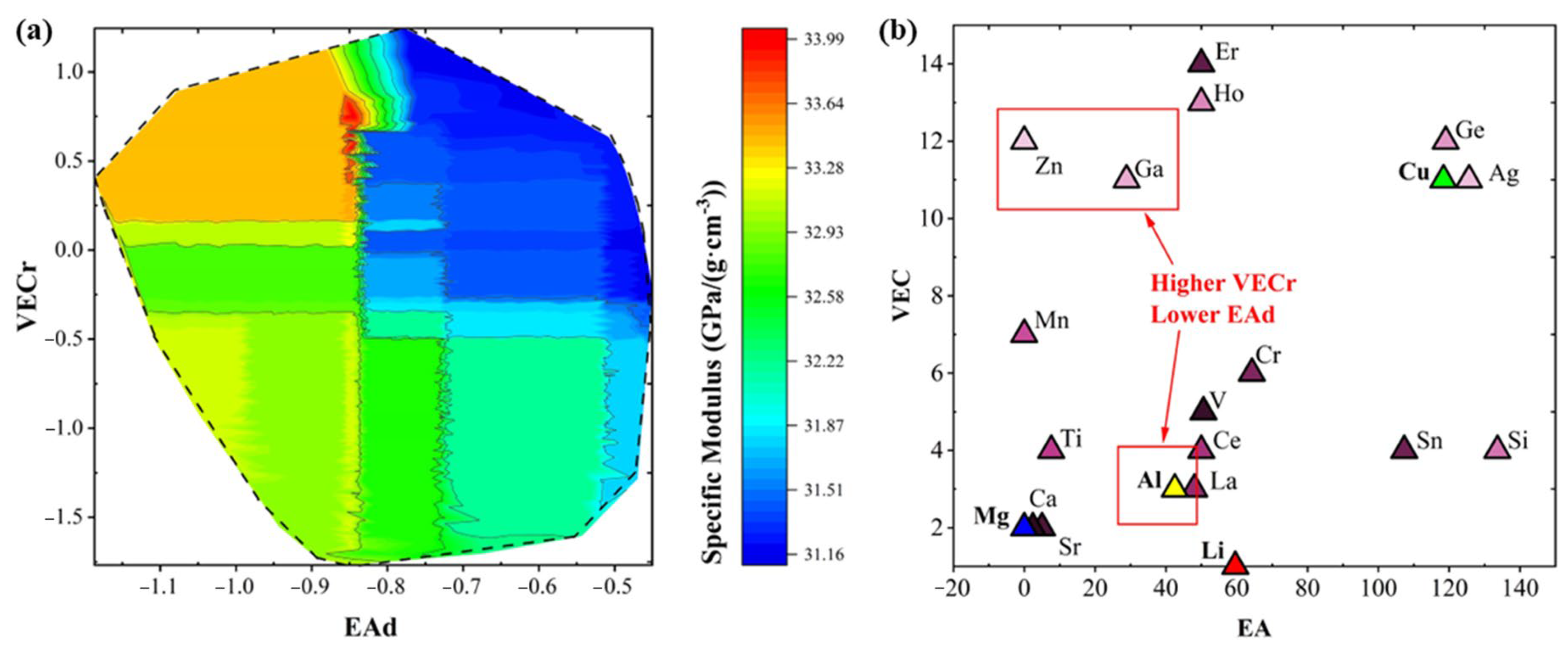
3.3. Virtual Alloy Search Space Prediction
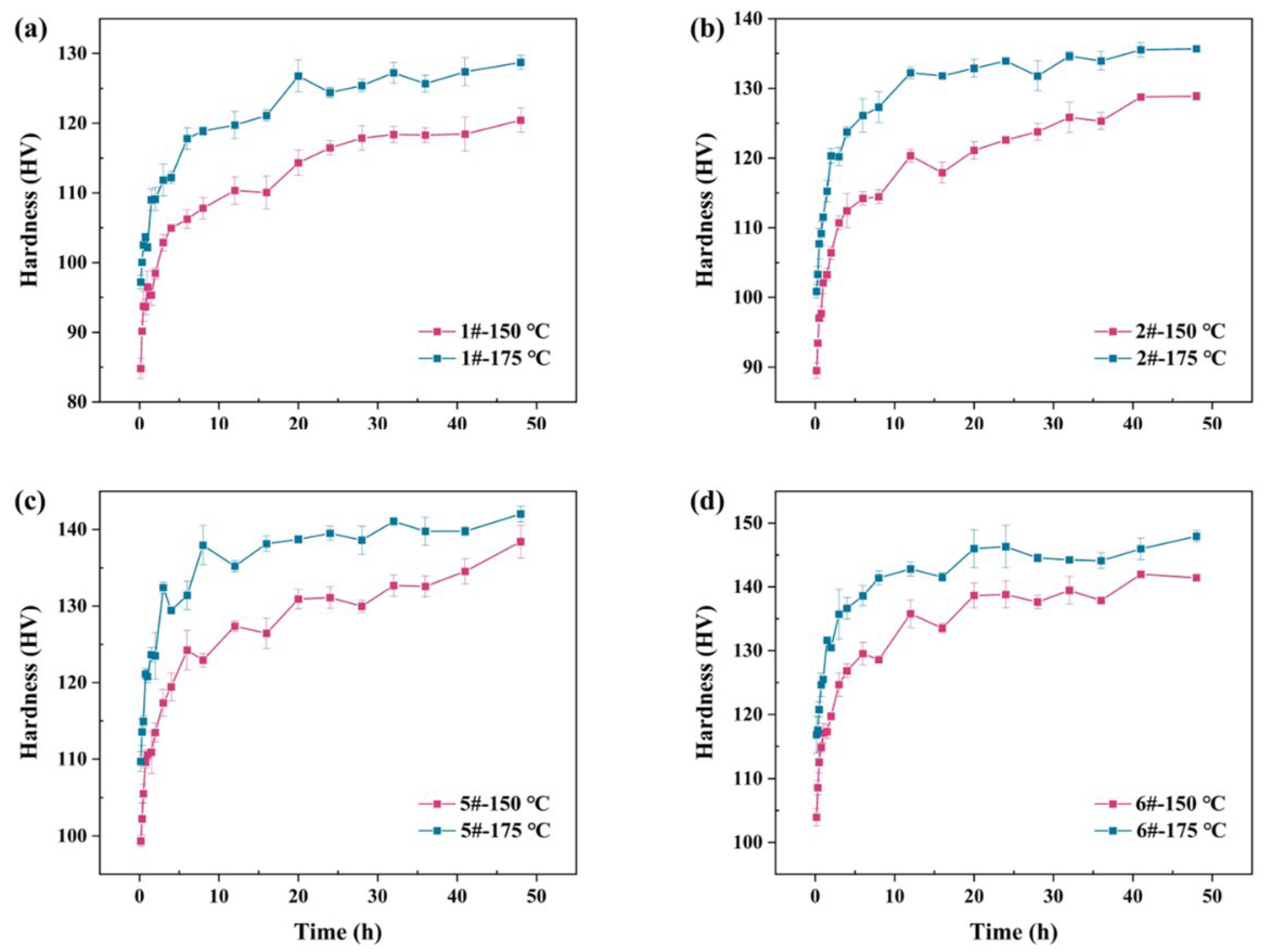
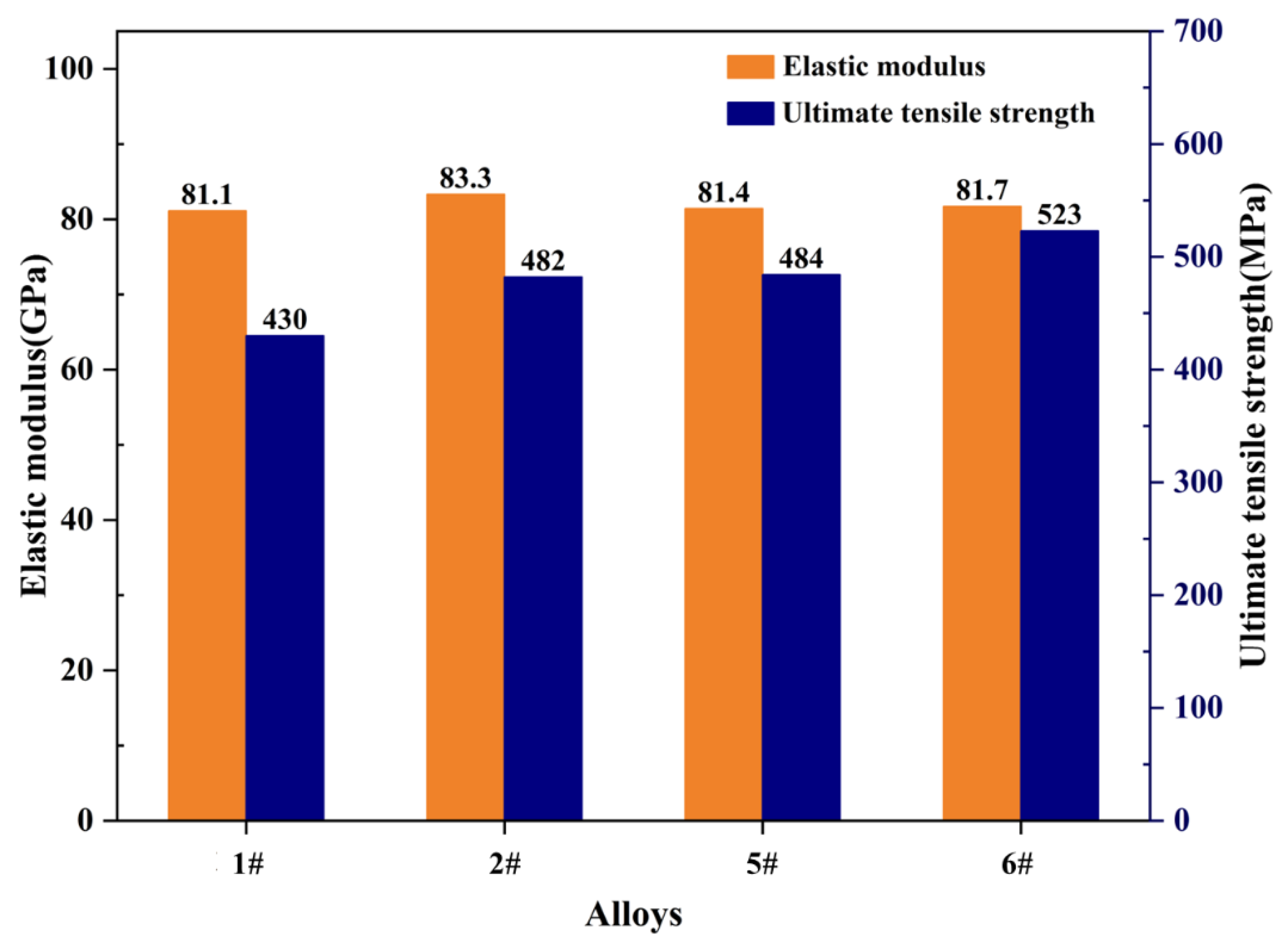
3.4. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rioja, R.J.; Liu, J. The evolution of Al-Li base products for aerospace and space applications. Metall. Mater. Trans. A 2012, 43, 3325–3337. [Google Scholar] [CrossRef]
- Rajendran, V.; Kumaran, S.M.; Jayakumar, T.; Palanichamy, P.; Shankar, P.; Raj, B. Microstructure and ultrasonic behaviour on thermal heat-treated Al-Li 8090 alloy. J. Alloys Compd. 2009, 478, 147–153. [Google Scholar] [CrossRef]
- Steglich, D.; Wafai, H.; Besson, J. Interaction between anisotropic plastic deformation and damage evolution in Al 2198 sheet metal. Eng. Fract. Mech. 2010, 77, 3501–3518. [Google Scholar] [CrossRef]
- El-Aty, A.A.; Xu, Y.; Guo, X.; Zhang, S.H.; Ma, Y.; Chen, D. Strengthening mechanisms, deformation behavior, and anisotropic mechanical properties of Al-Li alloys: A review. J. Adv. Res. 2018, 10, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, G.; Peng, X.; Guo, G.; Liu, S.; Liang, X. Research on microstructure and mechanical properties of 2050 Al-Li alloy during non-isothermal aging. J. Alloys Compd. 2022, 906, 163977. [Google Scholar] [CrossRef]
- Santos, M.C.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.S.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Rioja, R.J. Fabrication methods to manufacture isotropic Al-Li alloys and products for space and aerospace applications. Mater. Sci. Eng. A 1998, 257, 100–107. [Google Scholar] [CrossRef]
- Rambabu PP NK, V.; Eswara Prasad, N.; Kutumbarao, V.V.; Wanhill RJ, H. Aluminium alloys for aerospace applications. In Aerospace Materials and Material Technologies: Volume 1: Aerospace Materials; Springer: Berlin/Heidelberg, Germany, 2017; pp. 29–52. [Google Scholar]
- Li, S.; Yue, X.; Li, Q.; Peng, H.; Dong, B.; Liu, T.; Yang, H.; Fan, J.; Shu, S.; Qiu, F.; et al. Development and applications of aluminum alloys for aerospace industry. J. Mater. 2023, 27, 944–983. [Google Scholar] [CrossRef]
- Rao, M.S.; Padal, K.B. New developments of aluminium alloys for future generation applications—A review. AIP Conf. Proc. 2022, 2648, 030011. [Google Scholar]
- Rioja, R.J.; Denzer, D.K.; Mooy, D.; Venema, G. Lighter and stiffer materials for use in space vehicles. In ICAA13 Pittsburgh: Proceedings of the 13th International Conference on Aluminum Alloys, Pittsburgh, PA, USA, 3–7 June 2012; Springer: Berlin/Heidelberg, Germany, 2016; pp. 593–598. [Google Scholar]
- Wanhill, R.; Bray, G. Aerostructural design and its application to aluminum-lithium alloys. In Aluminum-Lithium Alloys; Elsevier: Amsterdam, The Netherlands, 2014; pp. 27–58. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Li, Y.; Xiao, W.; Wen, K.; Li, Z.; Zhang, Y.; Xiong, B. Machine learning assisted design of aluminum-lithium alloy with high specific modulus and specific strength. Mater. Des. 2023, 225, 111483. [Google Scholar] [CrossRef]
- Meng, L.; Zheng, X. Overview of the effects of impurities and rare earth elements in Al-Li alloys. Mater. Sci. Eng. A 1997, 237, 109–118. [Google Scholar] [CrossRef]
- Tsai, Y.C.; Chou, C.Y.; Lee, S.L.; Lin, C.K.; Lin, J.C.; Lim, S.W. Effect of trace La addition on the microstructures and mechanical properties of A356 (Al–7Si–0.35 Mg) aluminum alloys. J. Alloys Compd. 2009, 487, 157–162. [Google Scholar] [CrossRef]
- Tsai, Y.C.; Lee, S.L.; Lin, C.K. Effect of trace Ce addition on the microstructures and mechanical properties of A356 (Al-7Si-0.35 Mg) aluminum alloys. J. Chin. Inst. Eng. 2011, 34, 609–616. [Google Scholar] [CrossRef]
- Mao, F.; Yan, G.; Xuan, Z.; Cao, Z.; Wang, T. Effect of Eu addition on the microstructures and mechanical properties of A356 aluminum alloys. J. Alloys Compd. 2015, 650, 896–906. [Google Scholar] [CrossRef]
- Qiu, H.; Yan, H.; Hu, Z. Effect of samarium (Sm) addition on the microstructures and mechanical properties of Al-7Si-0.7 Mg alloys. J. Alloys Compd. 2013, 567, 77–81. [Google Scholar] [CrossRef]
- Qiu, C.; Miao, S.; Li, X.; Xia, X.; Ding, J.; Wang, Y.; Zhao, W. Synergistic effect of Sr and La on the microstructure and mechanical properties of A356. 2 alloy. Mater. Des. 2017, 114, 563–571. [Google Scholar] [CrossRef]
- Fang, H.-C.; Chen, K.-H.; Zhang, Z.; Zhu, C.-J. Effect of Yb additions on microstructures and properties of 7A60 aluminum alloy. Trans. Nonferrous Met. Soc. 2008, 18, 28–32. [Google Scholar] [CrossRef]
- Gupta, R.; Wang, Y.; Zhang, R.; Sukiman, N.; Davies, C.; Birbilis, N. Imparting sensitization resistance to an Al-5Mg alloy via neodymium additions. Corrosion 2013, 69, 4. [Google Scholar] [CrossRef]
- Wen, S.P.; Xing, Z.B.; Huang, H.; Li, B.L.; Wang, W.; Nie, Z.R. The effect of erbium on the microstructure and mechanical properties of Al-Mg-Mn-Zr alloy. Mater. Sci. Eng. A 2009, 516, 42–49. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- Durodola, J.F. Machine learning for design, phase transformation and mechanical properties of alloys. Prog. Mater. Sci. 2022, 123, 100797. [Google Scholar] [CrossRef]
- Juneja, R.; Yumnam, G.; Satsangi, S.; Singh, A.K. Coupling the high-throughput property map to machine learning for predicting lattice thermal conductivity. Chem. Mater. 2019, 31, 5145–5151. [Google Scholar] [CrossRef]
- Bash, D.; Cai, Y.; Chellappan, V.; Wong, S.L.; Yang, X.; Kumar, P.; Tan, J.D.; Abutaha, A.; Cheng, J.J.; Lim, Y.F.; et al. Multi-fidelity high-throughput optimization of electrical conductivity in P3HT-CNT composites. Adv. Funct. Mater. 2021, 31, 2102606. [Google Scholar] [CrossRef]
- Bhandari, U.; Rafi, R.; Zhang, C.; Yang, S. Yield strength prediction of high-entropy alloys using machine learning. Mater. Today Commun. 2021, 26, 101871. [Google Scholar] [CrossRef]
- Rickman, J.M.; Chan, H.M.; Harmer, M.P.; Smeltzer, J.A.; Marvel, C.J.; Roy, A.; Balasubramanian, G. Materials informatics for the screening of multi-principal elements and high-entropy alloys. Nat. Commun. 2019, 10, 2618. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef]
- Pearson, K., VII. Note on regression and inheritance in the case of two parents. Proc. Roy. Soc. 1895, 58, 240–242. [Google Scholar]
- Furlanello, C.; Serafini, M.; Merler, S.; Jurman, G. An accelerated procedure for recursive feature ranking on microarray data. Neural Netw. 2003, 16, 641–648. [Google Scholar] [CrossRef] [PubMed]
- Narendra, P.M.; Fukunaga, K. A branch and bound algorithm for feature subset selection. IEEE Trans Comput. 1977, 26, 917–922. [Google Scholar] [CrossRef]
- Uesugi, T.; Higashi, K. First-principles studies on lattice constants and local lattice distortions in solid solution aluminum alloys. Comput. Mater. Sci. 2013, 67, 1–10. [Google Scholar] [CrossRef]
- Czerwinski, F. Cerium in aluminum alloys. J. Mater. Sci. 2020, 55, 24–72. [Google Scholar] [CrossRef]
- Rogachev, S.; Naumova, E.; Vasileva, E.; Magurina, M.Y.; Sundeev, R.; Veligzhanin, A. Structure and mechanical properties of Al–Ca alloys processed by severe plastic deformation. Mater. Sci. Eng. A 2019, 767, 138410. [Google Scholar] [CrossRef]
- Borzone, G.; Parodi, N.; Ferro, R.; Bros, J.; Dubès, J.; Gambino, M. Heat capacity and phase equilibria in rare earth alloy systems. R-rich R-Al alloys (R = La, Pr and Nd). J. Alloys Compd. 2001, 320, 242–250. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, Z.; Li, H.; Lin, Y.; Li, N.; Gong, T.; Zhang, R.; Liu, H. Effects of holmium additions on microstructure and properties of A356 aluminum alloys. Metals 2018, 8, 849. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Q.; Shi, Y.; Zhao, G.; Zhang, R. Microstructure and mechanical properties of Gd-modified A356 aluminum alloys. J. Rare Earths 2015, 33, 1004–1009. [Google Scholar] [CrossRef]
- Xu, H.; Liu, R.; Choudhary, A.; Chen, W. A machine learning-based design representation method for designing heterogeneous microstructures. J. Mech. Eng. 2015, 137, 051403. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Browne, M.W. Cross-validation methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef]
- Kumaran, S.M.; Priyadharsini, N.; Rajendran, V.; Jayakumar, T.; Palanichamy, P.; Shankar, P.; Raj, B. In situ high temperature ultrasonic evaluation for on-line characterisation of fine scale precipitation reactions in 8090 Al-Li alloy. Mater. Sci. Eng. A 2006, 435–436, 29–39. [Google Scholar] [CrossRef]
- Chen, A.; Peng, Y.; Zhang, L.; Wu, G.; Li, Y. Microstructural evolution and mechanical properties of cast Al-3Li-1.5Cu-0.2Zr alloy during heat treatment. Mater. Charact. 2016, 114, 234–242. [Google Scholar] [CrossRef]


| Elements | Elemental Contents Range/wt.% | Counts |
|---|---|---|
| Al | 90.36~96.79 | 151 |
| Li | 0.49~3.78 | 151 |
| Cu | 0.04~4.7 | 134 |
| Mg | 0.015~5.9 | 133 |
| Zn | 0.001~1.31 | 67 |
| Ti | 0.01~0.6 | 39 |
| Mn | 0.005~0.86 | 91 |
| Cr | 0.0004~0.1 | 25 |
| Zr | 0.01~1 | 128 |
| Fe | 0.012~0.58 | 85 |
| Si | 0.0025~0.85 | 79 |
| Sc | 0.0433~0.31 | 13 |
| Ag | 0.005~0.62 | 61 |
| Definition | Descriptor | Unit | Symbol | Type |
|---|---|---|---|---|
| Number of Neutrons | N | - | NN | int |
| Atomic Number | Z | - | NA | int |
| Relative Atomic Mass | - | WA | float | |
| Density | D | float | ||
| Melting Temperature | °C | TM | float | |
| Boiling Temperature | °C | TB | float | |
| Valence Electrons | - | - | VE | float |
| Group Number in Periodic Table | Gn | - | G | int |
| Period Number in Periodic Table | Pn | - | P | int |
| Heat of Fusion | HF | float | ||
| Specific Heat Capacity | C | SH | float | |
| Coefficient of Thermal Expansion | °C−1 | CTE | float | |
| Enthalpy of Vaporization | VH | float | ||
| Ionic Charge | - | - | IC | float |
| Numbers of Valence Electrons | - | - | VEC | int |
| Atomic Ionization Energy | eV | EAI | float | |
| Atomic Radius | pm | RA | float | |
| Covalent Radius | pm | RC | float | |
| Conductivity | C | float | ||
| Resistivity | R | R | float | |
| Volume of Lattice | VL | float | ||
| Number of Space Group | - | - | NSG | int |
| Electronegative | - | EN | float | |
| Electron Affinity | EA | EA | float | |
| The 1st Ionization Weight | 1WI | float | ||
| The 2nd Ionization Weight | 2WI | float |
| M1/wt.% | M2/wt.% | ||
|---|---|---|---|
| Zn | 83.1 | Au | 0.44 |
| Ag | 53.56 | Gd | 0.4 |
| Ga | 19.95 | Yb | 0.3 |
| Ge | 5.54 | Sb | 0.28 |
| Ho | 5.2 | Ni | 0.24 |
| Si | 1.56 | Nb | 0.23 |
| Sm | 1.37 | In | 0.17 |
| Mn | 1.24 | Nd | 0.17 |
| Ti | 1.18 | Sc | 0.16 |
| Ce | 1.0 | Bi | 0.15 |
| La | 1.0 | Zr | 0.15 |
| Cr | 0.69 | Be | 0.1 |
| Sn | 0.64 | Eu | 0.1 |
| Er | 0.6 | Pr | 0.1 |
| Sr | 0.6 | Y | 0.1 |
| V | 0.58 | W | 0.08 |
| Ca | 0.5 | Fe | 0.05 |
| Alloys | Nominal Elemental Content/wt.% | Specific Modulus GPa/(g·cm−3) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Li | Cu | Mg | Zr | Ag | Mn | M | |||
| 1# | 2.4 | 0.1 | 0.1 | 0.1 | 0.3 | 0.3 | Ag | 3.9 | 33.905 |
| 2# | 2.3 | 0.1 | 0.4 | 0.1 | 0.3 | 0.3 | Ho | 3.7 | 33.986 |
| 3# | 2.3 | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 | Ge | 3.9 | 33.986 |
| 4# | 2.4 | 0.3 | 1.2 | 0.1 | 0.3 | 0.3 | Ge | 2.6 | 33.264 |
| 5# | 2.5 | 0.3 | 1.1 | 0.1 | 0.3 | 0.3 | Zn | 2.6 | 33.264 |
| 6# | 2.4 | 1.3 | 1.7 | 0.1 | 0.3 | 0.3 | Ga | 1.1 | 33.137 |
| Alloys | M1 | Density/(g·cm−3) | Specific Modulus /(GPa/(g·cm−3)) | Error/% |
|---|---|---|---|---|
| 1# | Ag | 2.639 | 30.315 | −10.59 |
| 2# | Ho | 2.622 | 30.890 | −9.11 |
| 3# | Ge | 2.644 | 29.461 | −13.31 |
| 4# | Ge | 2.604 | 29.760 | −10.53 |
| 5# | Zn | 2.582 | 31.178 | −6.27 |
| 6# | Ga | 2.593 | 30.891 | −6.78 |
| Alloys | Homogenization Regimes |
|---|---|
| 1# | 540 °C/48 h |
| 2# | 540 °C/24 h |
| 5# | 540 °C/24 h |
| 6# | 530 °C/48 h |
| Alloys | M1 | Density/(g·cm−3) | Specific Modulus/(GPa/(g·cm−3)) | Error/% |
|---|---|---|---|---|
| 1# | Ag | 2.633 | 30.803 | −9.15 |
| 2# | Ho | 2.634 | 31.620 | −6.96 |
| 5# | Zn | 2.582 | 31.526 | −5.23 |
| 6# | Ga | 2.591 | 31.531 | −4.85 |
| Benchmark alloy | 2.625 | 31.691 | / | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, X.; Li, Y.; Gao, G.; Wen, K.; Li, Z.; Zhang, Y.; Xiong, B. Exploration of Alloying Elements of High Specific Modulus Al–Li Alloy Based on Machine Learning. Materials 2024, 17, 92. https://doi.org/10.3390/ma17010092
Li H, Li X, Li Y, Gao G, Wen K, Li Z, Zhang Y, Xiong B. Exploration of Alloying Elements of High Specific Modulus Al–Li Alloy Based on Machine Learning. Materials. 2024; 17(1):92. https://doi.org/10.3390/ma17010092
Chicago/Turabian StyleLi, Huiyu, Xiwu Li, Yanan Li, Guanjun Gao, Kai Wen, Zhihui Li, Yongan Zhang, and Baiqing Xiong. 2024. "Exploration of Alloying Elements of High Specific Modulus Al–Li Alloy Based on Machine Learning" Materials 17, no. 1: 92. https://doi.org/10.3390/ma17010092
APA StyleLi, H., Li, X., Li, Y., Gao, G., Wen, K., Li, Z., Zhang, Y., & Xiong, B. (2024). Exploration of Alloying Elements of High Specific Modulus Al–Li Alloy Based on Machine Learning. Materials, 17(1), 92. https://doi.org/10.3390/ma17010092





