Two-Dimensional Damage Localization Using a Piezoelectric Smart Aggregate Approach—Implementation on Arbitrary Shaped Concrete Plates
Abstract
:1. Introduction
2. Hybrid Approach for Two-Dimensional Damage Detection and Localization
3. Numerical Modeling of PZT SA Actuator and Wave Propagation
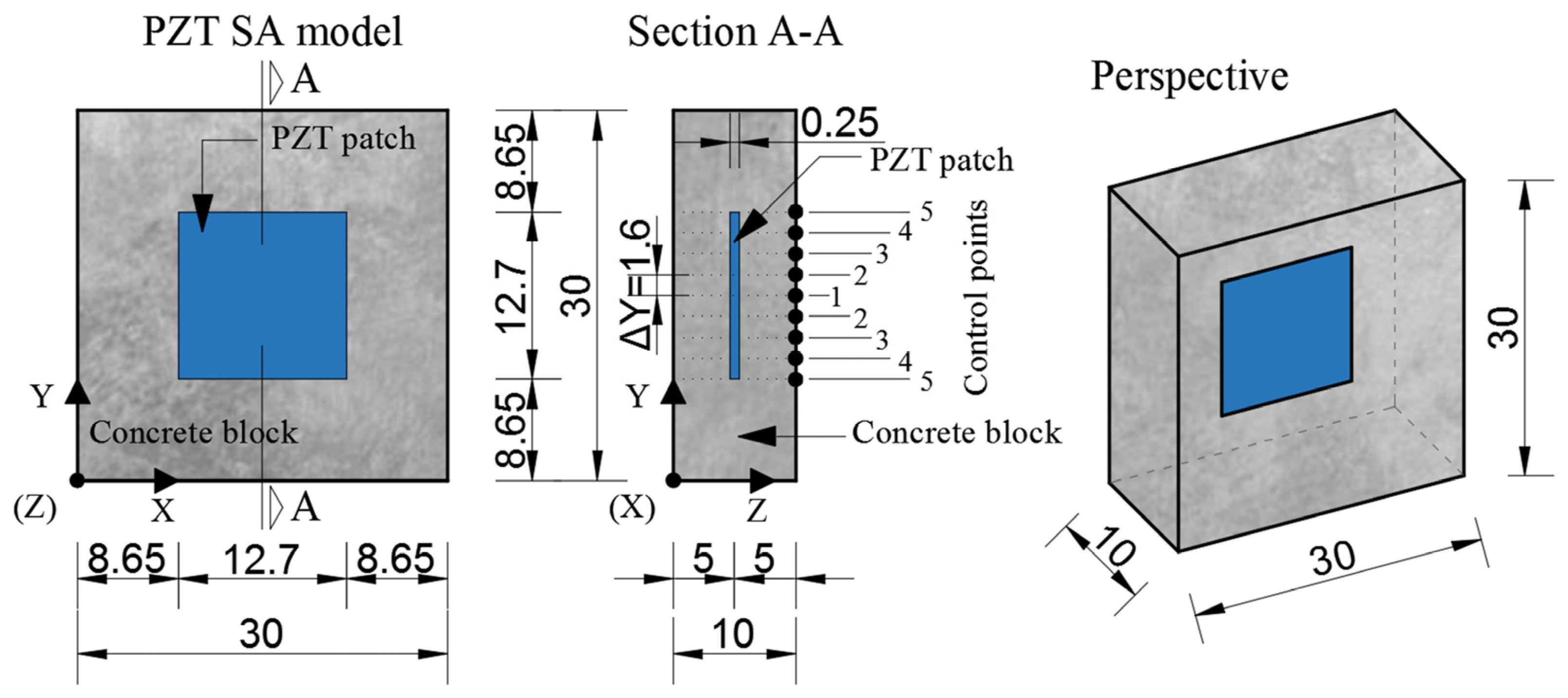
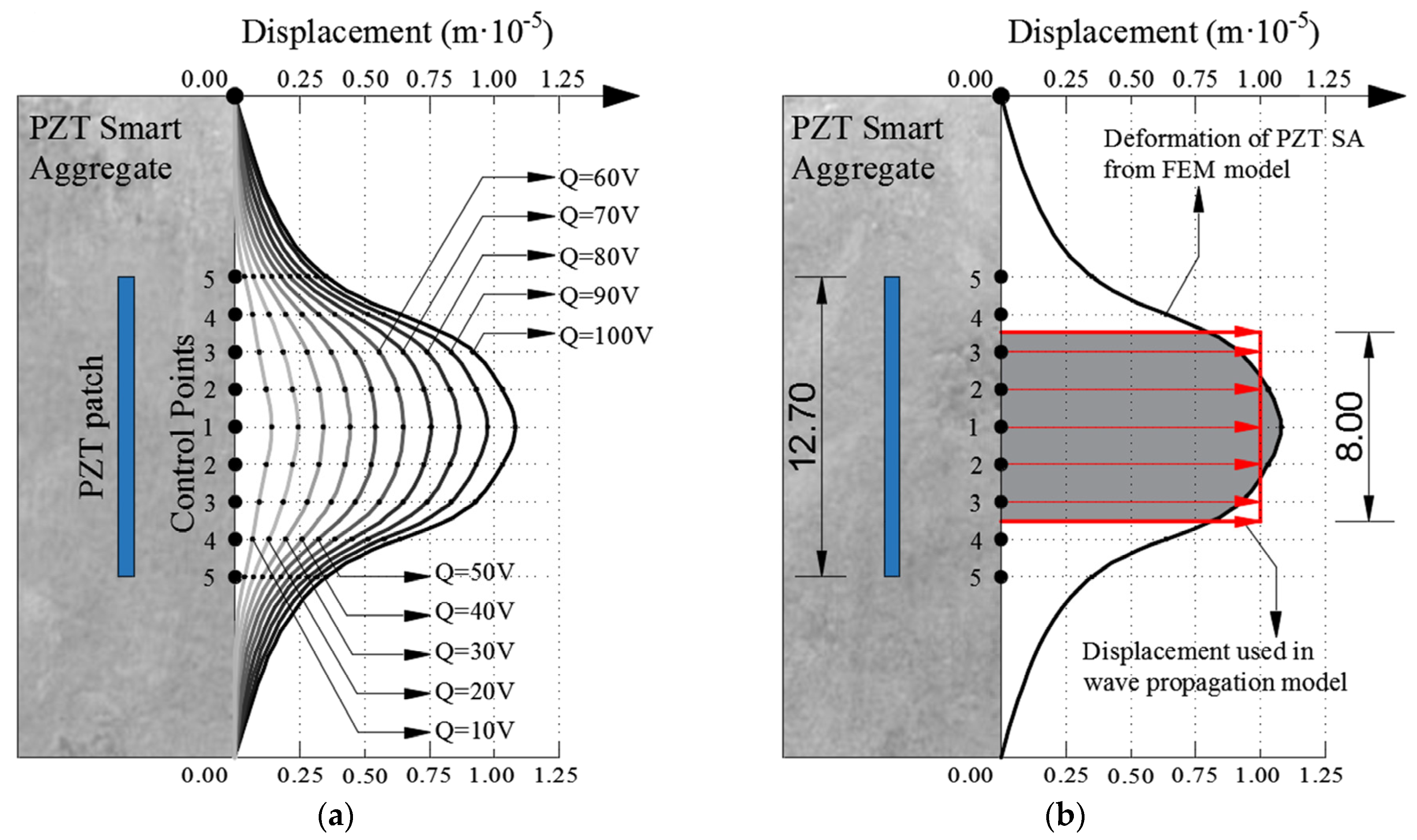
3.1. Numerical Modeling of PZT SAs
3.2. Numerical Modeling of Wave Propagation
4. Experimental and Numerical Verification of Hybrid Damage Localization Approach
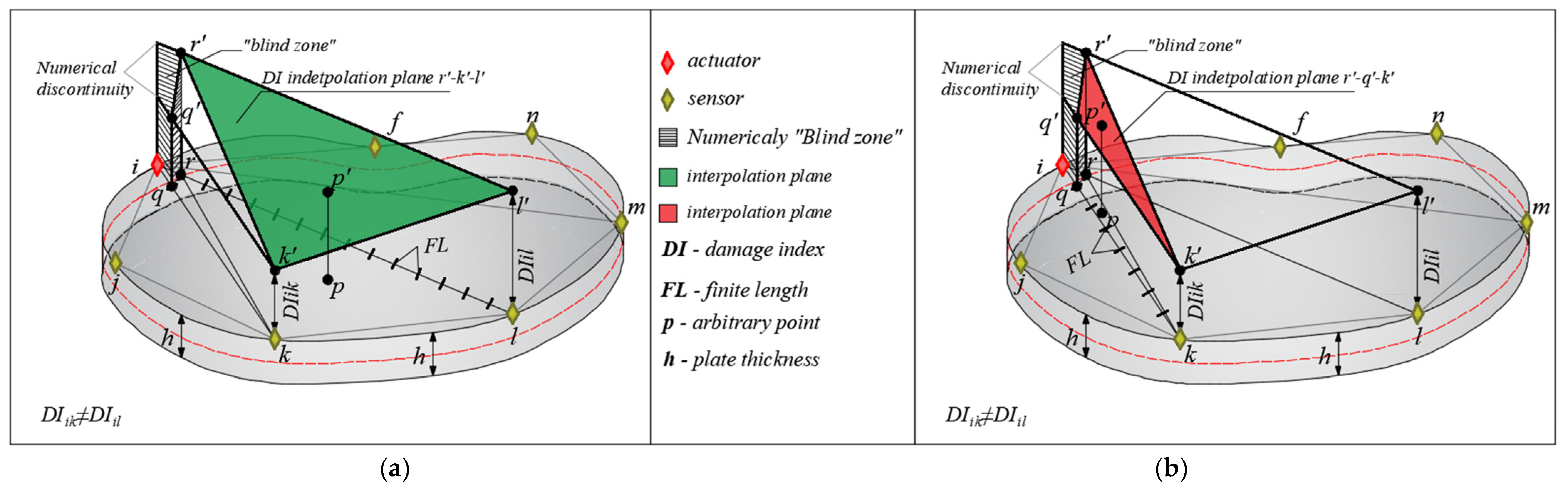
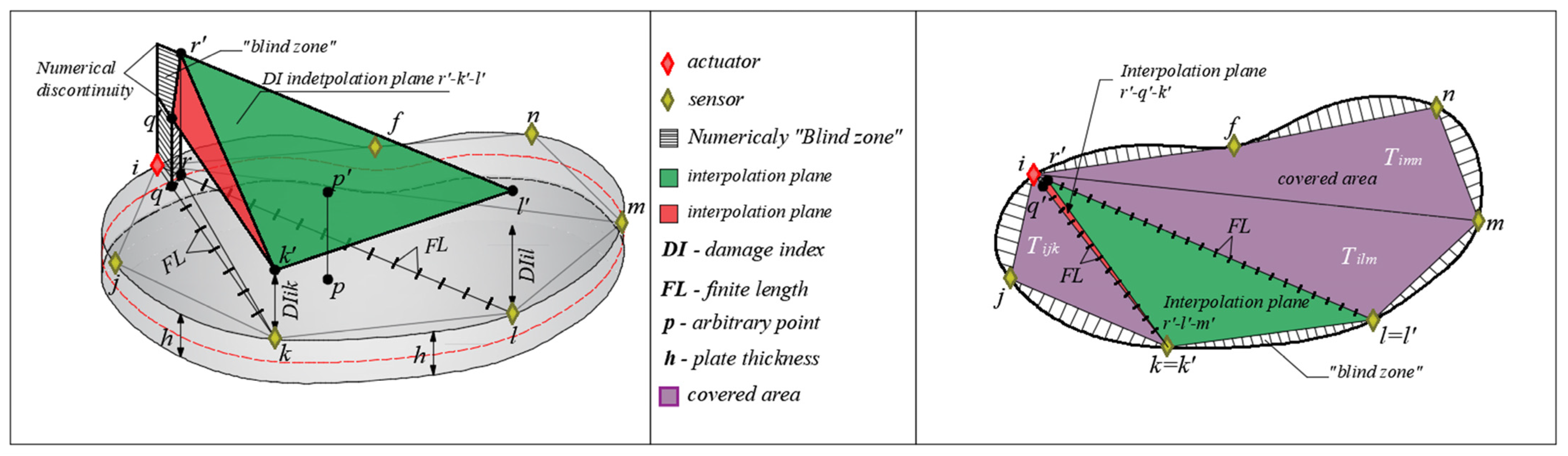
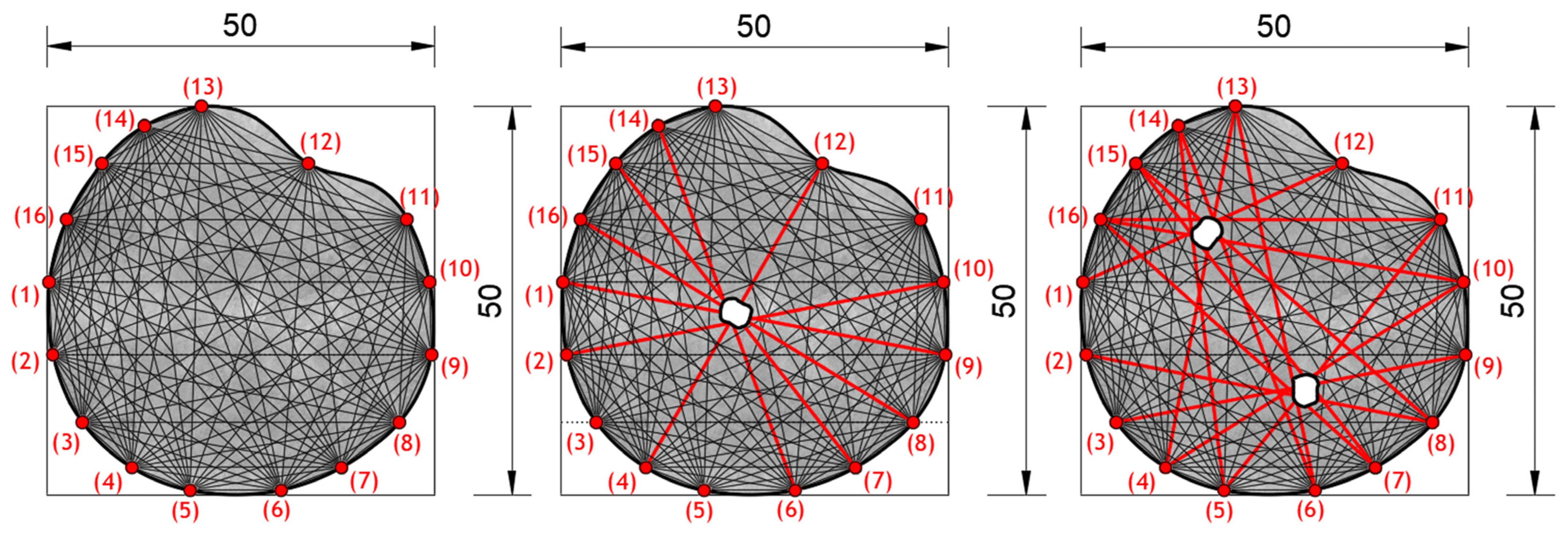
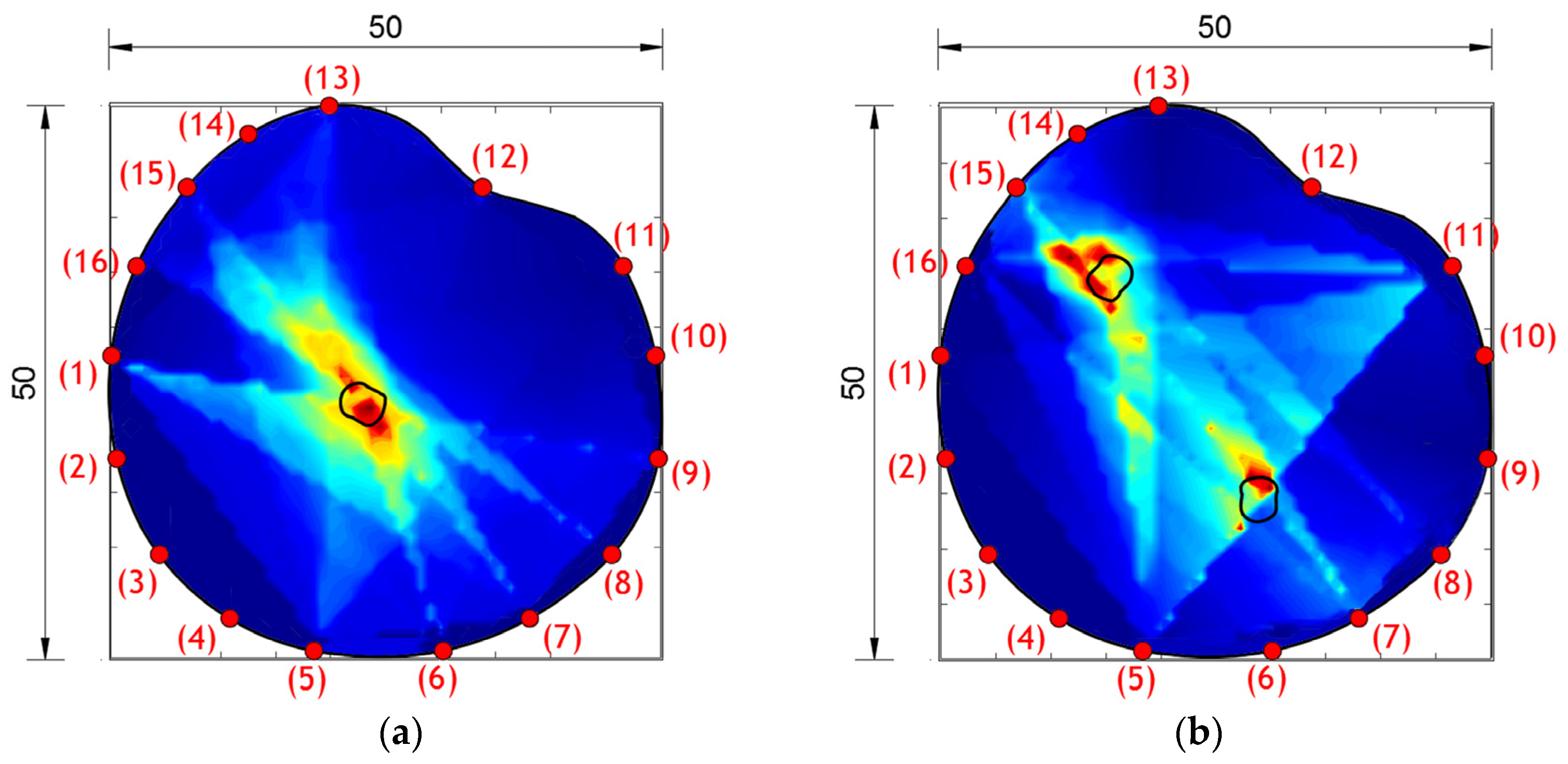
5. Implementation of Hybrid Damage Localization on Arbitrary Shaped Concrete Plate
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boller, C. Encyclopedia of Structural Health Monitoring; Boller, C., Chang, F.-K., Fujino, Y., Eds.; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-470-05822-0. [Google Scholar]
- Adams, D. Health Monitoring of Structural Materials and Components; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-470-03313-5. [Google Scholar]
- Balageas, D.; Frityen, C.P.; Guemes, A. Structural Health Monitoring; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-1-905-20901-9. [Google Scholar]
- Chang, P.C.; Flatau, A.; Liu, S.C. Review Paper: Health Monitoring of Civil Infrastructure. Struct. Health Monit. 2003, 2, 257–267. [Google Scholar] [CrossRef]
- Qin, L. Development and Application of Cement-Based Piezoelectric Composite in Concrete Behavior Monitoring. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2008. [Google Scholar]
- Pan, W.H.; Sun, X.D.; Wu, L.M.; Yang, K.K.; Tang, N. Damage Detection of Asphalt Concrete Using Piezo-Ultrasonic Wave Technology. Materials 2019, 12, 443. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Stasyewski, W.J.; Swamy, R.N. Smart Sensing Technologies for Structural Health Monitoring of Civil Engineering Structures. Adv. Civ. Eng. 2010, 2010, 724962. [Google Scholar] [CrossRef]
- Abdul, A.; Bisma, P.; Md Abdul, R.; Yasser, E.I.; Asraar, A.; Meftah, H.; Nagma, P.; Jalal, M.Z. A Review of Piezoelectric Material-Based Structural Control and Health Monitoring Techniques for Engineering Structures: Challenges and Opportunities. Actuators 2021, 10, 101. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, H.; Zhang, G.; Ayhan, B.; Yan, F.; Kwan, C.; Rose, J.L. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization and growth monitoring. Smart Mater. Struct. 2007, 16, 1208. [Google Scholar] [CrossRef]
- Ihn, J.B.; Chang, F.K. Pitch-catch Active Sensing Methods in Structural Health Monitoring for Aircraft Structures. Struct. Health Monit. 2008, 7, 5–15. [Google Scholar] [CrossRef]
- Smithard, J.; Rajic, N.; Velden, S.; Norman, P.; Rosalie, C.; Galea, S.; Mei, H.; Lin, B.; Giurgiutiu, V. An Advanced Multi-Sensor Acousto-Ultrasonic Structural Health Monitoring System: Development and Aerospace Demonstration. Materials 2017, 10, 832. [Google Scholar] [CrossRef] [PubMed]
- Giurgiutiu, V.; Zagrai, A.; Bao, J.J. Piezoelectric Wafer Embedded Active Sensors for Aging Aircraft Structural Health Monitoring. Struct. Health Monit. 2002, 1, 41–61. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical System from Changes in Their Vibration Characteristics: A Literature Review; Shock and Vibration Digest; LANL: Los Alamos, NM, USA, 1996. [Google Scholar] [CrossRef]
- Sinou, J.J. A Review of Damage Detection and Health Monitoring of Mechanical Systems from Changes in the Measurement of Linear and Non-Linear Vibrations; Mechanical Vibrations: Measurements, Effects and Control; Sapri, R.C., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 643–702. [Google Scholar]
- Nugroho, W.H.; Purnomo, N.J.H.; Soedarto, T. An experimental work on wireless structural health monitoring system applying on a submarine model scale. J. Phys. Conf. Ser. 2016, 776, 012094. [Google Scholar] [CrossRef]
- Perez, I.; Diulio, M.; Maley, S.; Phan, N. Structural Health Management in the NAVY. Struct. Health Monit. 2010, 9, 199–207. [Google Scholar] [CrossRef]
- Farrar, C.; Park, G.; Angel, M.; Bement, M.; Salvino, L. Structural Health Monitoring for Ship Structures. In Proceedings of the 7th International Workshop on Structural Health Monitoring, Palo Alto, CA, USA, 9 September 2009. [Google Scholar]
- Naoum, M.C.; Papadopoulos, N.A.; Voutetaki, M.E.; Chalioris, C.E. Structural Health Monitoring of Fiber-Reinforced Concrete Prisms with Polyolefin Macro-Fibers Using a Piezoelectric Materials Network under Various Load-Induced Stress. Buildings 2023, 13, 2465. [Google Scholar] [CrossRef]
- Suzuki, A.; Liao, W.; Shibata, D.; Yoshino, Y.; Kimuro, Y.; Shimoi, N. Structural Damage Detection Technique of Secondary Building Components Using Piezoelectric Sensors. Buildings 2023, 13, 2368. [Google Scholar] [CrossRef]
- Kang, J.D.; Baek, E.R.; Park, S.H. Evaluation of Vibration Detection Using Smartphones in a Two-Story Masonry-Infilled RC Frame Building. Buildings 2023, 13, 1069. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An Introduction to Structural Health Monitoring, New Trends in Vibration Based Structural Health Monitoring; Deraemaeker, A., Worden, K., Eds.; Springer: New York, NY, USA, 2010; ISBN 978-3-7091-0398-2. [Google Scholar]
- Mal, A.; Ricci, F.; Banerjee, S.; Shih, F. A Conceptual Structural Health Monitoring System based on Vibration and Wave Propagation. Struct. Health Monit. 2005, 4, 283–293. [Google Scholar] [CrossRef]
- Esmaeel, R.; Briand, J.; Taheri, F. Computational simulation and experimental verification of a new vibration-based structural health monitoring approach using piezoelectric sensors. Struct. Health Monit. 2011, 11, 237–250. [Google Scholar] [CrossRef]
- Deng, F.; Liu, Y.; Zhuge, X.; Huang, J. Progress on the Research of Ultrasonic Guided Wave Structural Health Monitoring in the Changing Ambient. J. Mech. Eng. 2016, 52, 1–7. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Predictive simulation of guided-wave structural health monitoring. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, OR, USA, 26–29 March 2017. [Google Scholar]
- Wang, Z.; Zhong, Y.; Zhou, J.; Li, C.; Zhong, L. Environmental Effects on Piezoelectric Sensors Array Signals and a Compensated Damage Imaging Method. Materials 2021, 14, 6742. [Google Scholar] [CrossRef]
- Shiveley, S.; Douglass, A.; Posch, B.; Harley, J. Guided wave structural health monitoring wath large data sets. In Proceedings of the IEEE International Ultrasonic Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar] [CrossRef]
- Filho, J.V.; Baptista, F.G.; Inman, D.J. Time-domain analysis of piezoelectric impedance based structural health monitoring using multilevel wavelet decomposition. Mech. Syst. Signal Process. 2011, 25, 1550–1558. [Google Scholar] [CrossRef]
- An, K.Y.; Sohn, H. Integrated impedance and guided wave-based damage detection. Mech. Syst. Signal Process. 2012, 28, 50–62. [Google Scholar] [CrossRef]
- Ali, L.; Khan, S.; Iqbal, N.; Bashmal, S.; Hameed, H.; Bai, Y. An Experimental Study of Damage Detection on Typical Joints of Jackets Platform Based on Electro-Mechanical Impedance Technique. Materials 2021, 14, 7168. [Google Scholar] [CrossRef]
- Lavrentyev, A.I.; Stucky, P.A.; Veronesi, W.A. Feasibility of ultrasonic and eddy current methods for measurement of residual stress in shot peened metals. AIP Conf. Proc. 2000, 509, 1621–1628. [Google Scholar] [CrossRef]
- Azari, H.; Nazarian, S.; Yuan, D. Assessing sensitivity of impact echo and ultrasonic surface waves methods for nondestructive evaluation of concrete structures. Constr. Build. Mater. 2014, 71, 384–391. [Google Scholar] [CrossRef]
- Jeong, H. Application of Odd Harmonic Resonances of a Single Crystal to Generation and Reception of Superharmonic Waves for Sensitive Monitoring of Heat-Treated Materials. Materials 2023, 16, 4777. [Google Scholar] [CrossRef] [PubMed]
- Kee, S.H.; Zhu, J. Using air-coupled sensors to determine the depth of a surface-breaking crack in concrete. J. Acoust. Soc. Am. 2010, 123, 1279–1287. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Ziehl, P.H. Evaluation of Reinforced Concrete Beam Specimens with Acoustic Emission and Cyclic Load Test Methods. ACI Struct. J. 2009, 106, 12. [Google Scholar]
- Altammar, H.; Dhingra, A.; Salowitz, N. Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending. Actuators 2019, 8, 70. [Google Scholar] [CrossRef]
- Milovanović, B.; Pečur, I.B. Review of Active IR Thermography for Detection and Characterization of Defects in Reinforced Concrete. J. Imaging 2016, 2, 11. [Google Scholar] [CrossRef]
- Costa, D.D.; Valenca, J.; Julio, E.; Araujo, H. Crack propagation monitoring using an image deformation approach. Struct. Control Health Monit. 2016, 24, e1973. [Google Scholar] [CrossRef]
- Reagan, D.; Sabato, A.; Niezrecki, C. Feasibility of using Digital Image Correlation for Unmanned Aerial Vehicle Structural Health Monitoring of Bridges. Struct. Health Monit. 2017, 17, 1056–1072. [Google Scholar] [CrossRef]
- Gao, W.; Huo, L.; Li, H.; Song, G. An embedded tubular PZT transducers based damage imaging method for two-dimensional concrete structures. IEEE 2018, 6, 30100–30109. [Google Scholar] [CrossRef]
- Kijanka, P.; Urban, M.W. Local Phase Velocity Based Imaging; A New Technique Used for Ultrasonic Shear Wave Elastography. IEEE Trans. Med. Imaging 2019, 38, 894–908. [Google Scholar] [CrossRef] [PubMed]
- Barouni, A.K.; Saravanos, D.A. A Layerwise semi-analytical method of modeling guided wave propagation in laminated composite infinite plates with induced surface excitation. Wave Motion 2017, 68, 56–77. [Google Scholar] [CrossRef]
- Jing, J.; Quek, S.T.; Quan, W. Wave boundary element method to study Lamb wave propagation in plates. J. Sound Vib. 2005, 288, 195–213. [Google Scholar]
- Giurgiutiu, V.; Shen, Y. Combined analytical FEM approach for efficient simulation of Lamb wave damage detection. Ultrasonics 2016, 69, 116–128. [Google Scholar]
- Delsando, P.P.; Scalerandi, M. A spring model for the simulation of the propagation of ultrasonic pulses through imperfect contants interfaces. J. Acoust. Soc. Am. 1998, 104, 2584–2591. [Google Scholar] [CrossRef]
- Gao, L.; Liu, K.X.; Liu, Y. A meshless method for stress-wave propagation in anisotropic and cracked media. Int. J. Eng. Sci. 2007, 45, 601–616. [Google Scholar] [CrossRef]
- Lee, B.C.; Stasyewski, W.J. Lamb wave propagation modelling for damage detection: I. Two dimensional analysis. Smart Mater. Struct. 2007, 16, 249. [Google Scholar] [CrossRef]
- Wang, J.; Xu, B.; Liu, Q.; Quan, R.; Ma, X. Feasibility of Stress Wave-Based Debond Defect Detection for RCFSTs Considering the Influence of Randomly Distributed Circular Aggregates with Mesoscale Homogenization Methodology. Materials 2023, 16, 3120. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Vincenzi, N. Structural and Elastodynamic Analysis of Rotary Transfer Machines by Finite Element Model. J. Serbian Soc. Comput. Mech. 2017, 11, 1–16. [Google Scholar] [CrossRef]
- Chatterjee, A.; Ranjan, V.; Azan, M.S.; Rao, M. Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate. Appl. Sci. 2019, 9, 745. [Google Scholar] [CrossRef]
- Song, F.; Huang, G.L.; Kim, J.H.; Haran, S. On the study of surface wave propagation in concrete structures using a piezoelectric actuator/sensor system. Smart Mater. Struct. 2008, 17, 055024. [Google Scholar] [CrossRef]
- Cheng, C.; Lu, Z.; Yang, J.; Gong, X.; Ke, Q. Modulating the Performance of the SAW Strain Sensor Based on Dual-Port Resonator Using FEM Simulation. Materials 2023, 16, 3269. [Google Scholar] [CrossRef] [PubMed]
- Marković, N.; Nestorović, T.; Stojić, D. Numerical modeling of damage detection in concrete beams using piezoelectric patches. Mech. Res. Commun. 2015, 64, 15–22. [Google Scholar] [CrossRef]
- Stojić, D.; Nestorović, T.; Marković, N.; Cvetković, R.; Stojić, N. Detection of damage to reinforced-concrete structures using piezoelectric smart aggregates. Građevinar 2016, 68, 371–380. [Google Scholar]
- Marković, N.; Nestorović, T.; Stojić, D.; Marjanović, M.; Stojković, N. Hybrid approach for two dimensional damage localiyation using piezoelectric smart aggregates. Mech. Res. Commun. 2017, 85, 69–75. [Google Scholar] [CrossRef]
- Song, G.; Olmi, C.; Gu, H. An overheight vehicle-bridge collision monitoring system using piezoellctric transducers. Smart Mater. Struct. 2007, 16, 462. [Google Scholar] [CrossRef]
- Wu, F.; Chang, F.K. Debond Detection using Embedded piezoelectric elements for reinforced concrete structures—Part II: Analysis and algorithm. Struct. Health Monit. 2006, 5, 17–28. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Ye, L.; Wang, D. Guided waves for damage detection in rebar-reinforced concrete beams. Constr. Build. Mater. 2013, 47, 370–378. [Google Scholar] [CrossRef]
- Liu, T.; Huang, Y.; Zou, D.; Teng, J.; Li, B. Exploratory study on water seepage monitoring of concrete structures using piezoelectric based smart aggregates. Smart Mater. Struct. 2013, 22, 065002. [Google Scholar] [CrossRef]
- Song, G.; Sethi, V.; Li, H.N. Vibration control of civil structures using piezoelectric smart materials: A review. Eng. Struct. 2006, 28, 1513–1524. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L. Smart Agregates: Multi-functional sensors for concrete structures—A tutorial and review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregates for compressive stress monitoring. Smart Mater. Struct. 2012, 21, 105035. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C. Concrete structural health monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2007, 16, 959. [Google Scholar] [CrossRef]
- Hu, B.; Kundu, T.; Grill, W.; Liu, B.; Toufigh, V. Embedded Piezoelectric Sensors for Health Monitoring of Concrete Structures. ACI Mater. J. 2013, 110, 149–158. [Google Scholar]
- Lu, Y.; Li, Z.; Liao, W.I. Damage monitoring of reinforced concrete frames under seismic loading using cement-based piezoelectric sensor. Mater. Struct. 2011, 44, 1273–1285. [Google Scholar] [CrossRef]
- Yao, Y.; Ellen, S.T.; Glišić, B. Crack detection and characterization techniques—An overview. Struct. Control Health Monit. 2014, 21, 1387–1413. [Google Scholar] [CrossRef]
- Seppanen, A.; Hallaji, M.; Pour-Ghaz, M. Electrical impedance tomography-based sensing skin for detection of damage in concrete. In Proceedings of the 11th European Conference on Non-Destructive Testing—ECNDT 2014, Prague, Czech Republic, 6–10 October 2014. [Google Scholar]
- Aggelis, D.G.; Shiotani, T.; Momoki, S.; Hirama, A. Acoustic Emission and Ultrasonic for Damage Characterization of Concrete Elements. ACI Mater. J. 2009, 106, 509. [Google Scholar]
- Stojić, N.; Nestorović, T.; Stojić, D.; Marković, N.; Stojković, N.; Velimirović, N. Energy based three-dimensional damage index for monitoring and damage detection of concrete structures. Građevinar 2021, 73, 1223–1238. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]





| PZT Material Properties | |||||
|---|---|---|---|---|---|
| Density (kg/m3) | Dielectric Properties (CV−1/m) · 10−8 | ||||
| ρ = 7500 | D11 = 1.505 | D22 = 1.301 | D33 = 1.505 | ||
| Piezoelectric properties (F/m) · 10−10 | |||||
| d111 = 0 | d122 = 0 | d133 = 0 | d112 = 7.41 | d113 = 0 | d123 = 0 |
| d211 = −2.74 | d222 = 5.93 | d233 = −2.74 | d212 = 0 | d213 = 0 | d223 = 0 |
| d311 = 0 | d322 = 0 | d333 = 0 | d312 = 0 | d313 = 0 | d323 = 7.41 |
| Material characteristics—Engineering constants | |||||
| E1 = 60.61 GPa | E2 = 48.31 GPa | E3 = 60.61 GPa | ν12 = 0.512 | ν13 = 0.289 | ν23 = 0.408 |
| G12 = 23.0 GPa | G13 = 23.5 GPa | G23 = 23.0 GPa | |||
| Concrete Material Properties | |||||
| Young’s modulus of elasticity (GPa) | Poisson’s ratio | Rayleigh damping coefficients | Density (kg/m3) | ||
| 44.30 | 0.15 | α = 2050 (1/s) | β = 1.10 · 10−8 (s) | 2400 | |
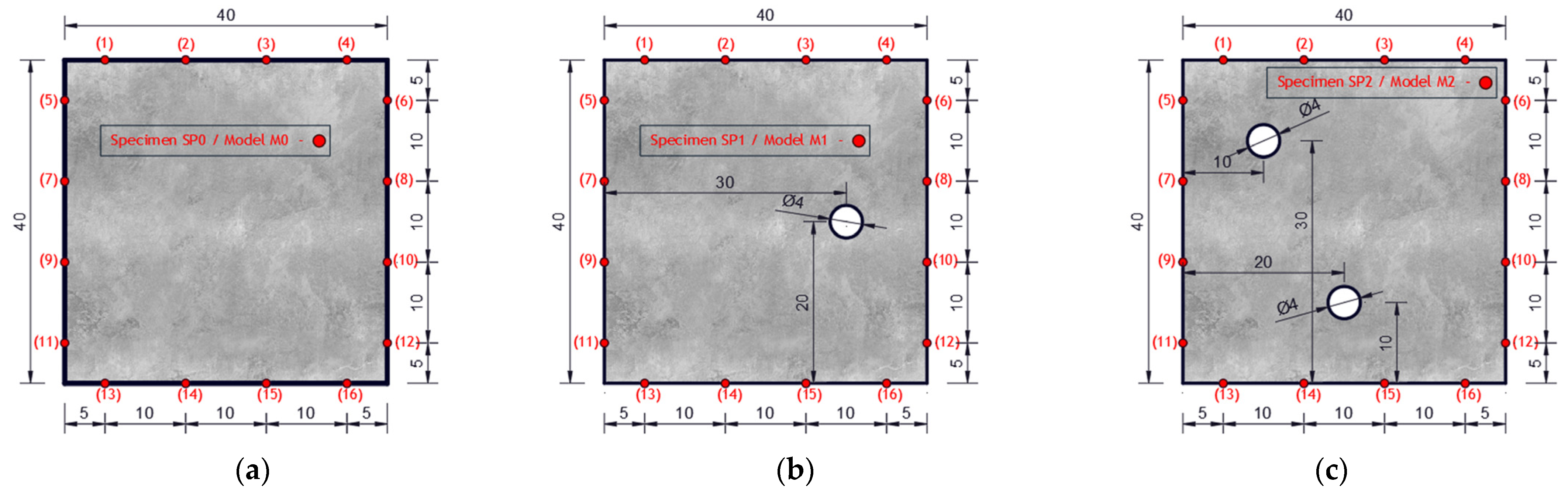
| Marks of Experimental Samples—SPi | Weight—Wi (kg) | Density—ρi (kg/m3) | Mean Value ρmean (kg/m3) | Deviation · 100(%) |
|---|---|---|---|---|
| Plate without damage: SP0 | 15.292 | 2389.375 | 2377.3 | 0.505 |
| Plate with one hole: SP1 | 15.068 | 2373.025 | 0.180 | |
| Plate with two damages: SP2 | 14.982 | 2378.280 | 0.040 | |
| Concrete ingredients | Fine-grained sand (kg/m3) | Coarse-grained sand (kg/m3) | Cement (kg/m3) | Water (kg/m3) |
| 685.00 | 1135.00 | 405.00 | 182.00 |
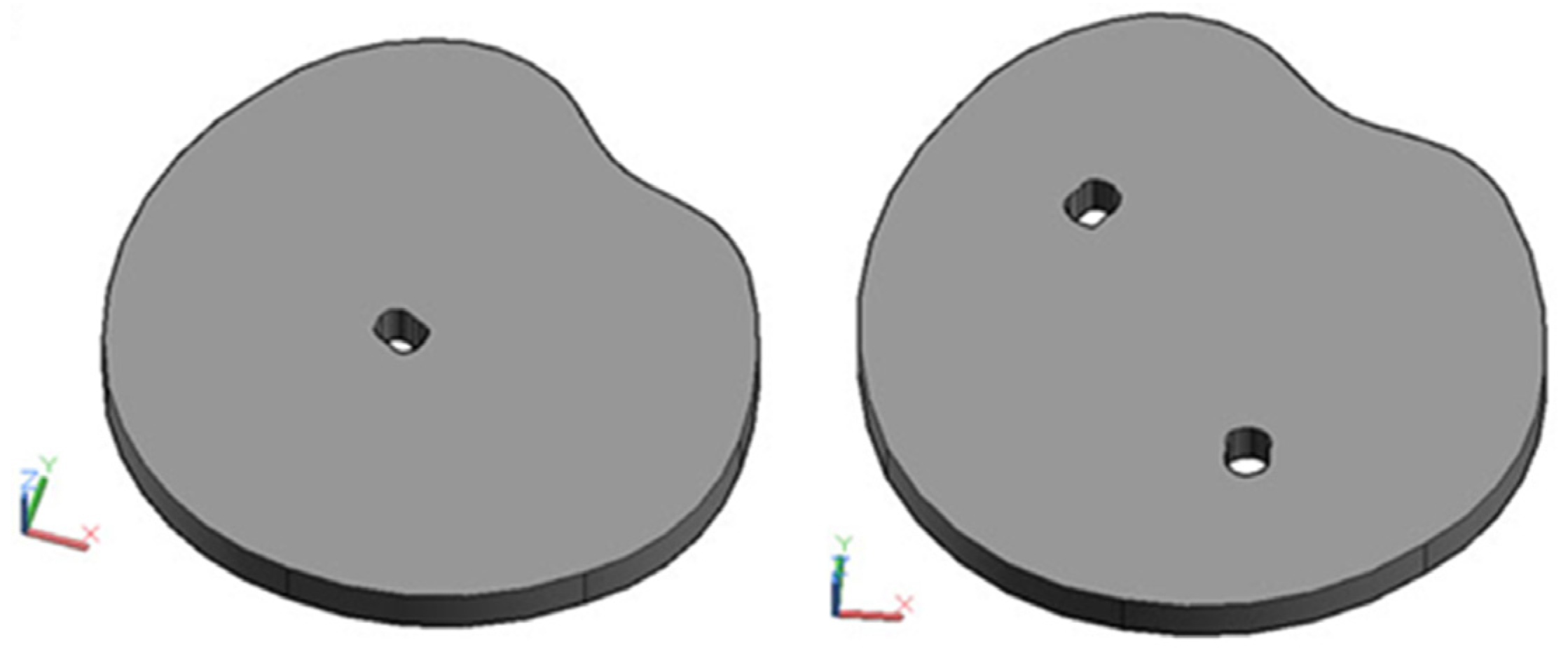
| Number of PZT Actuators/Sensors for Models with Arbitrary Shape | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| Models with 16 PZT actuators/sensors—XY coordinates | ||||||||||||||||
| X | 0.21 | 0.69 | 4.53 | 10.89 | 18.47 | 30.16 | 37.96 | 45.37 | 49.59 | 49.34 | 46.4 | 33.7 | 19.87 | 12.56 | 7.03 | 2.49 |
| Y | 27.36 | 18.04 | 9.34 | 3.52 | 0.58 | 0.58 | 3.52 | 9.34 | 18.04 | 27.36 | 35.46 | 42.01 | 50.0 | 47.47 | 42.61 | 35.46 |
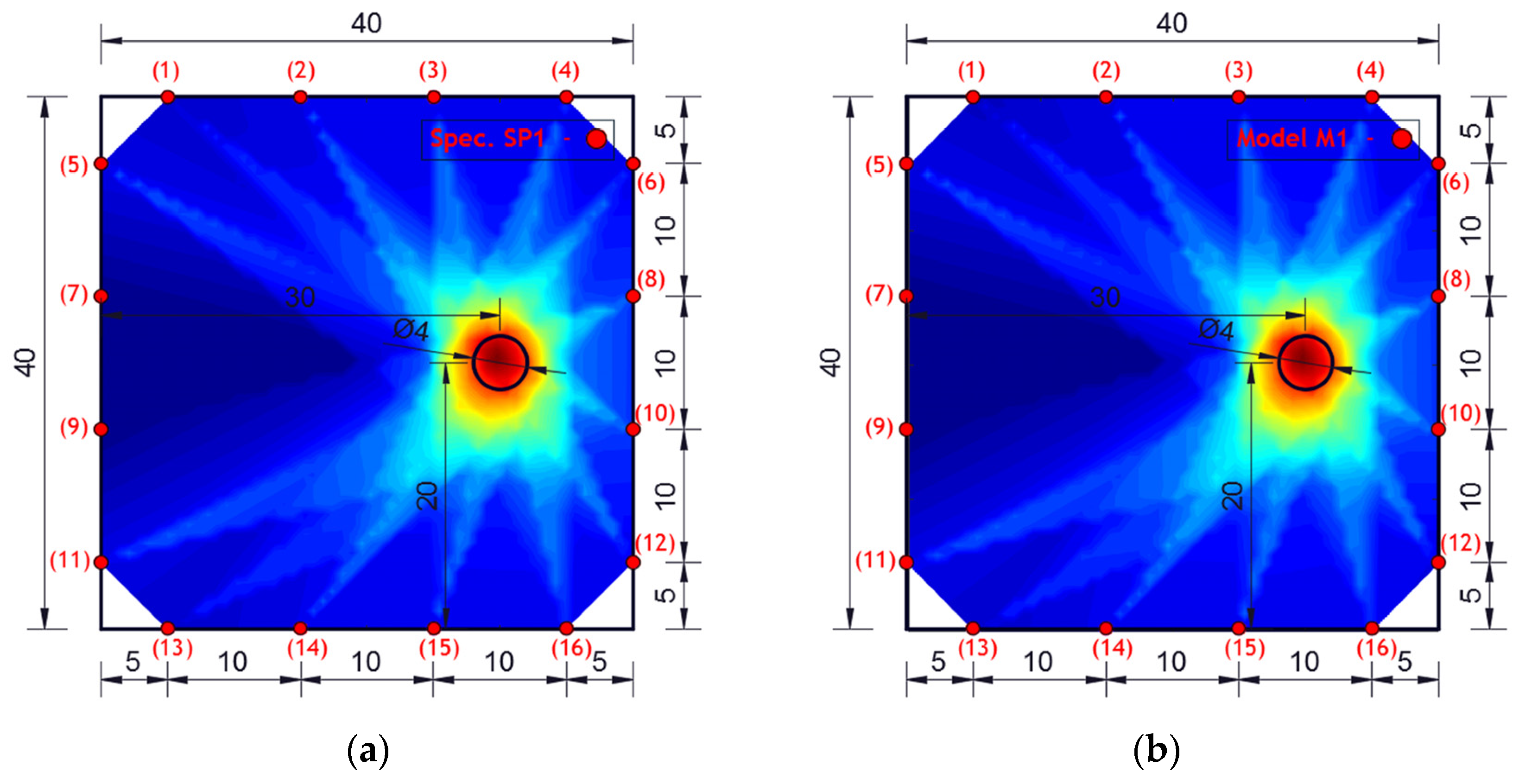
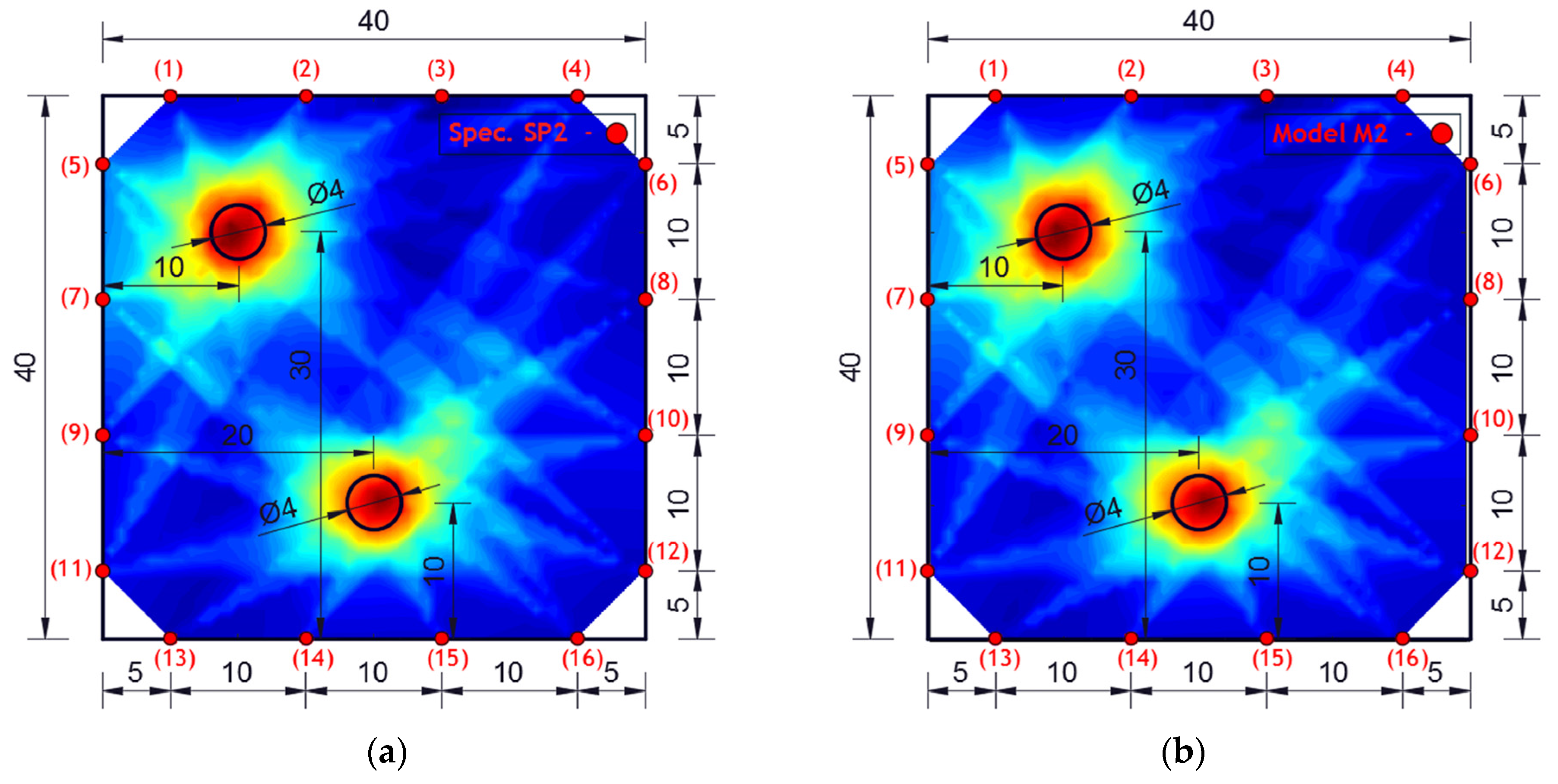
| M1 | M2 | SP1 | SP2 | MAR1 | MAR2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| a1 (%) | 96.18 | 89.18 | 88.92 | 94.72 | 90.63 | 91.18 | 46.52 | 20.57 | 30.05 |
| a2 (%) | 7.27 | 17.39 | 17.76 | 8.14 | 15.75 | 15.22 | 85.71 | 98.46 | 200.0 |
| a3 (%) | 96.84 | 92.43 | 92.07 | 95.13 | 93.12 | 92.95 | 69.94 | 40.82 | 90.30 |
| Ar (cm2) | 12.57 | 12.57 | 12.57 | 12.57 | 12.57 | 12.57 | 6.32 | 6.32 | 6.29 |
| Ah (cm2) | 12.98 | 13.16 | 13.65 | 13.21 | 13.50 | 13.52 | 4.42 | 2.58 | 5.68 |
| Ai (cm2) | 12.09 | 11.21 | 11.17 | 11.91 | 11.39 | 11.46 | 2.94 | 1.30 | 1.89 |
| Ao (cm2) | 0.89 | 1.95 | 2.47 | 1.30 | 2.11 | 2.06 | 2.52 | 1.28 | 3.78 |
| Marks | Analysis | Dimensions (cm) | Number of PZT SAs | Damage Detection | Damage Localization | Damage Quantification |
|---|---|---|---|---|---|---|
| SP1 | Experimental | 40 × 40 × 4 | 16 | Successfull | Successfull | Successfull |
| SP2 | Experimental | 40 × 40 × 4 | 16 | Successfull | Successfull | Successfull |
| M1 | Numerical | 40 × 40 × 4 | 16 | Successfull | Successfull | Successfull |
| M2 | Numerical | 40 × 40 × 4 | 16 | Successfull | Successfull | Successfull |
| MAR 1 | Numerical | Arbitrary | 16 | Successfull | Partially successfull | Partially successfull |
| MAR 2 | Numerical | Arbitrary | 16 | Successfull | Partially successfull | Partially successfull |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marković, N.; Grdić, D.; Stojković, N.; Topličić-Ćurčić, G.; Živković, D. Two-Dimensional Damage Localization Using a Piezoelectric Smart Aggregate Approach—Implementation on Arbitrary Shaped Concrete Plates. Materials 2024, 17, 218. https://doi.org/10.3390/ma17010218
Marković N, Grdić D, Stojković N, Topličić-Ćurčić G, Živković D. Two-Dimensional Damage Localization Using a Piezoelectric Smart Aggregate Approach—Implementation on Arbitrary Shaped Concrete Plates. Materials. 2024; 17(1):218. https://doi.org/10.3390/ma17010218
Chicago/Turabian StyleMarković, Nemanja, Dušan Grdić, Nenad Stojković, Gordana Topličić-Ćurčić, and Darko Živković. 2024. "Two-Dimensional Damage Localization Using a Piezoelectric Smart Aggregate Approach—Implementation on Arbitrary Shaped Concrete Plates" Materials 17, no. 1: 218. https://doi.org/10.3390/ma17010218
APA StyleMarković, N., Grdić, D., Stojković, N., Topličić-Ćurčić, G., & Živković, D. (2024). Two-Dimensional Damage Localization Using a Piezoelectric Smart Aggregate Approach—Implementation on Arbitrary Shaped Concrete Plates. Materials, 17(1), 218. https://doi.org/10.3390/ma17010218







