Regularities in the Evolution of Thermoelastic Martensitic Transformations during Cooling/Heating in the Free State and under Load of Titanium Nickelide Alloyed with Niobium
Abstract
1. Introduction
2. Materials and Methods
2.1. Alloy Preparation
2.2. Structure Characterization Methods
2.3. The Study of the Nature of Martensitic Transformation
3. Thermodynamics of Thermoelastic Martensitic Transformations
4. Results and Discussion
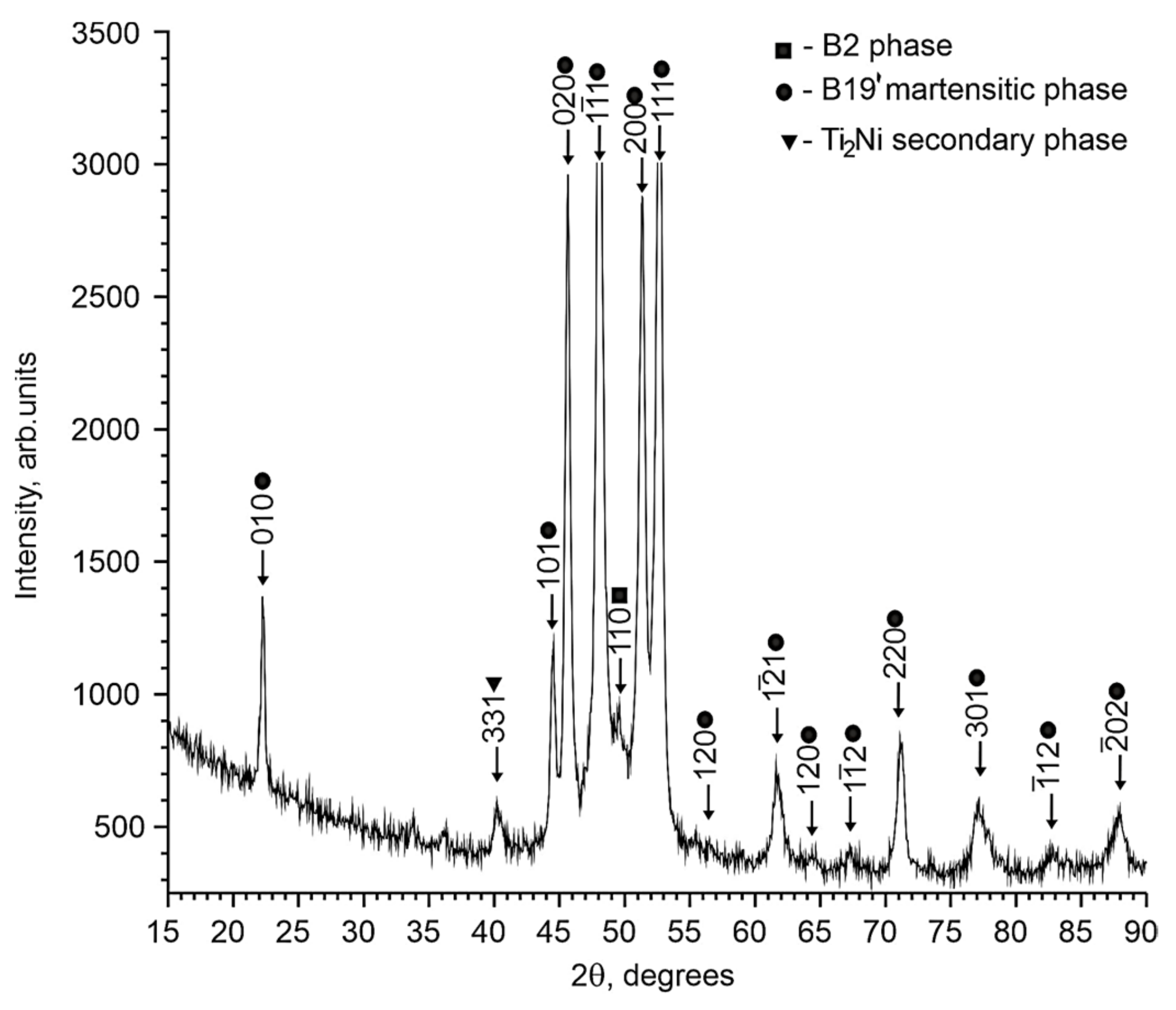
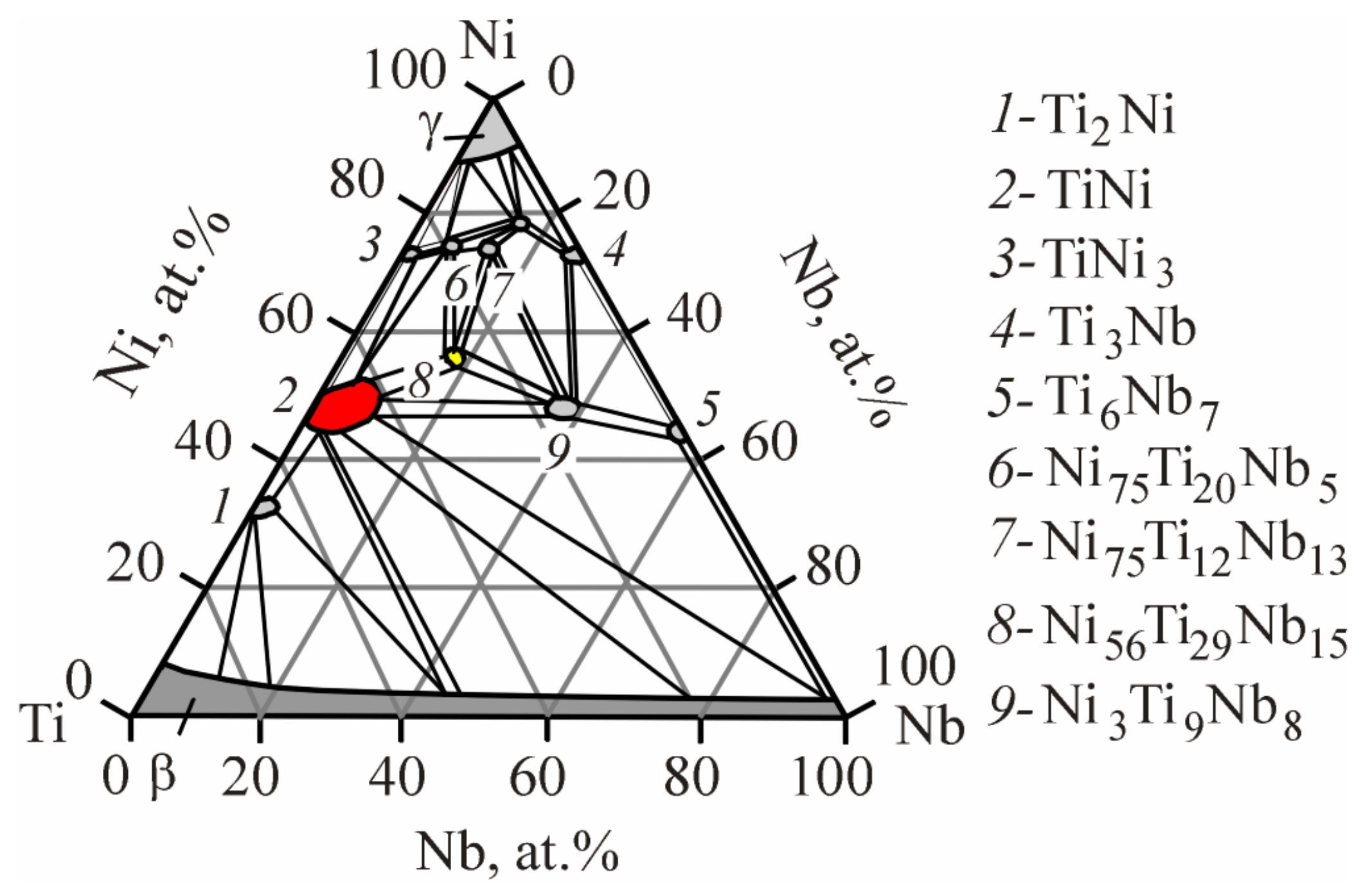
4.1. Structural and Phase States of TiNi-Based Alloys Doped with Nb
4.2. Microstructure of TiNi-Based Alloys Doped with Nb
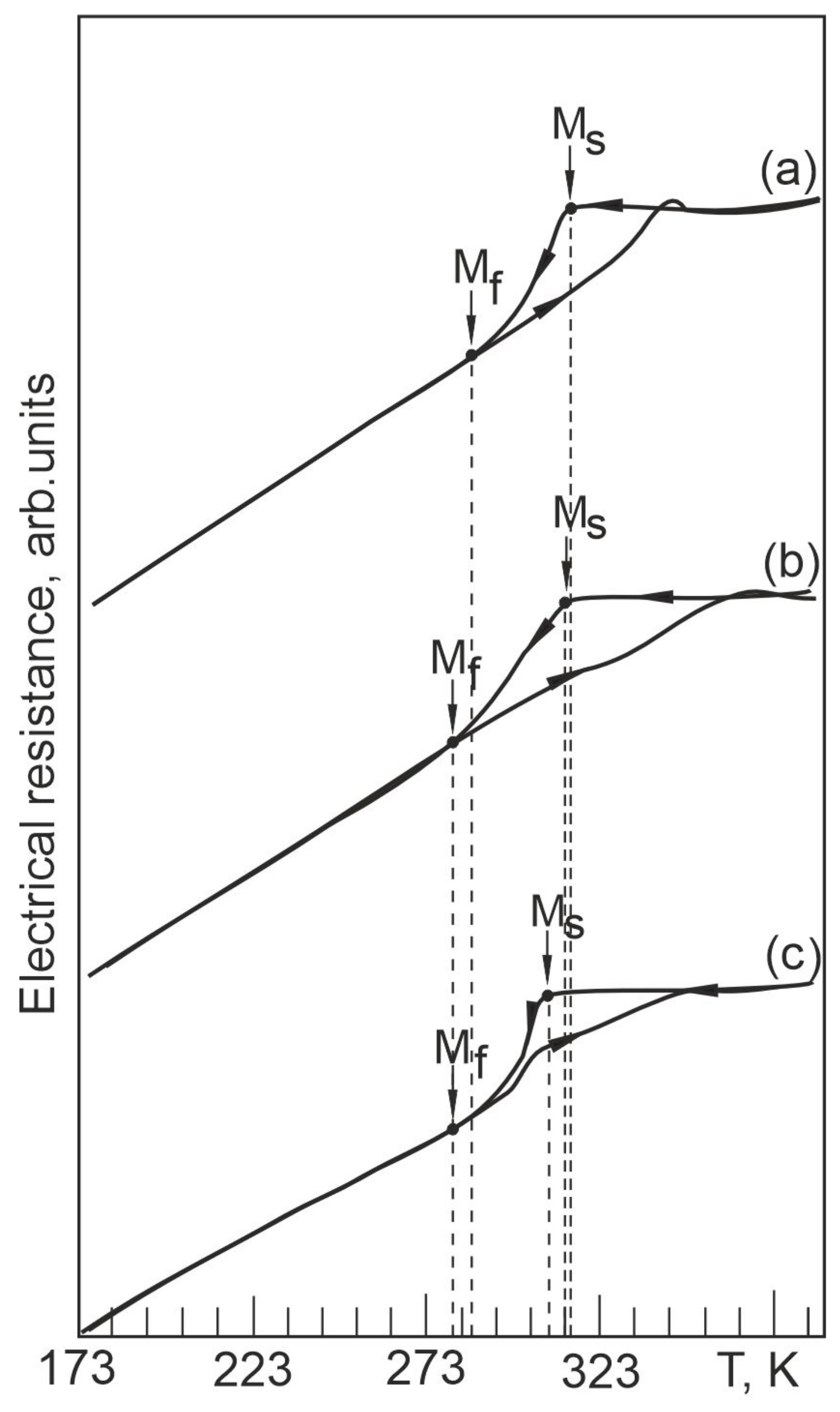
4.3. Temperature Dependences of Electrical Resistance in Nb-Doped TiNi-Based Alloys
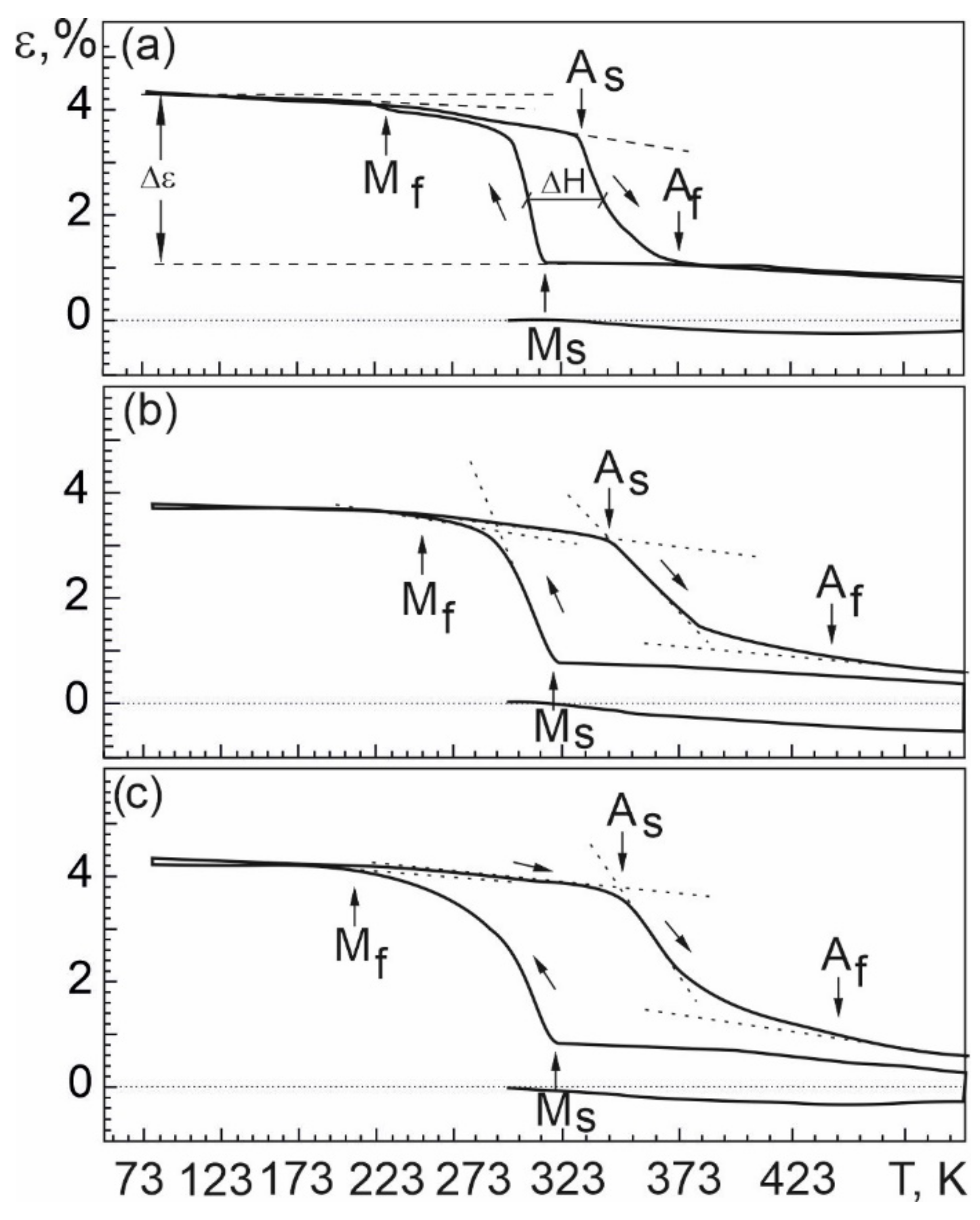
4.4. Shape Memory Effect in Nb-Doped TiNi-Based Alloys
5. Conclusions
- Structural studies showed that all alloys at room temperature consist of intermetallic compounds with the TiNi (B2, B19′), Ti2Ni, and Ni56Ti29Nb15 compositions. It was found that in the Ti50Ni48.2Nb1.5Mo0.3 alloy, a microstructural state without eutectic is formed during crystallization, in contrast to alloys with 0.5 and 1 at% Nb. It was established that the doping of TiNi alloys with niobium leads to an increase in the stability of high-temperature B2 phase. An increase in the lattice parameter and atomic volume of the B2 phase indicates that some of the Nb atoms are dissolved in the B2 matrix phase. The observed significant change in the structural-phase state has a significant effect on the features of the martensitic transition in the free state and under load.
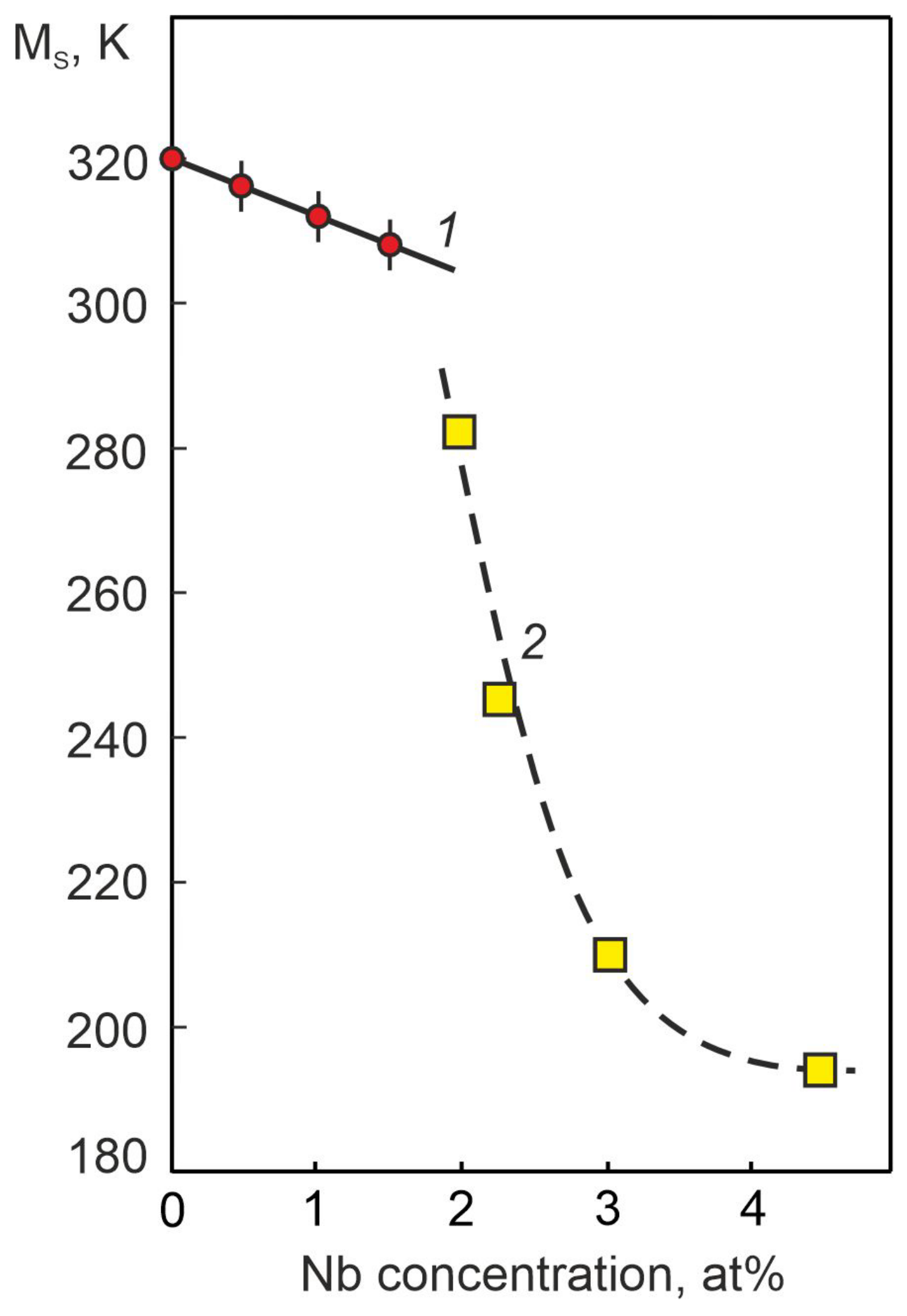
- In order to determine the characteristics of martensitic transformation in the free state and under load in TiNiNb based alloys, temperature dependences of electrical resistivity and temperature dependences of strain accumulation and recovery under multiple shape memory effects were obtained. The dependencies indicate that a single stage B2–B19′ MT occurs in the alloys studied. From the experimental data, characteristic temperatures and intervals of MT were determined. Using the thermodynamic description of thermoelastic MT and the experimental values of the characteristic temperatures based on the dependences obtained in the free state and under load, the influence of Nb alloying on the ratio of the reversible and irreversible components of the non-chemical free energy was evaluated. These studies play an important role in determining the behavior of the alloys under different operating conditions, namely in the free state and under load.
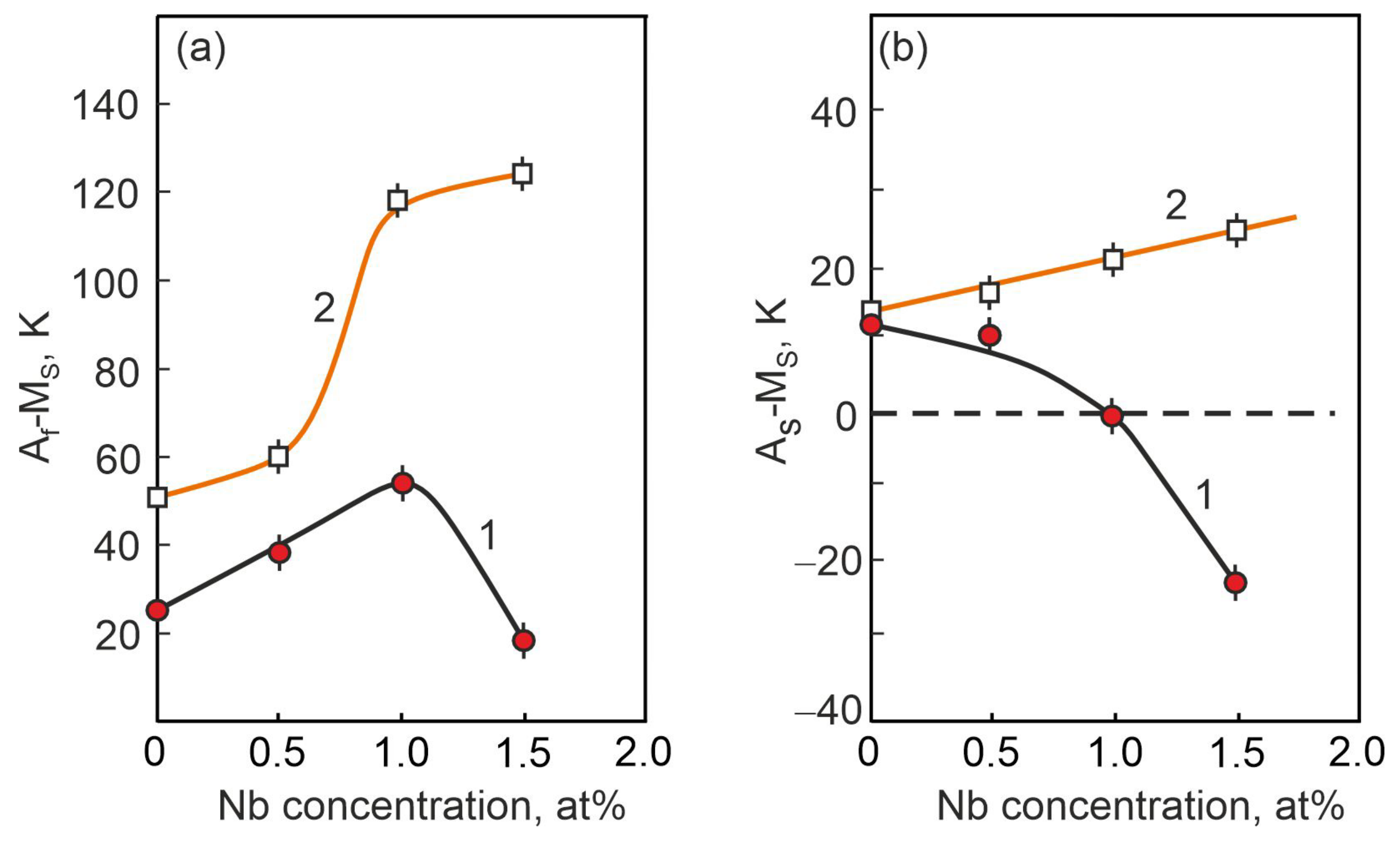
- The width of the thermal hysteresis Af − Ms, corresponding to the irreversible energy dissipation during MT, was determined. In the experiments under load, it was found that the alloys show a significant increase in the irreversible free energy dissipation during MT, whereas in the free state the energy dissipation during MT is much lower in the same alloys. This indicates that the irreversible component of the non-chemical free energy is higher in the loaded alloys during MT than in the unloaded alloys, and that particle precipitation has an additional influence on the dissipation energy during interfacial boundary motion under load.
- The temperature difference AS − MS between the beginning of the direct and the beginning of the reverse MT, determined by the ratio between the reversible and irreversible energies, was established. Based on the analysis of the concentration dependence of the temperature interval AS − MS during MT under load, it was found that alloying with Nb causes the reversible Gibbs free energy to be more than twice as large as the irreversible Gibbs free energy . In the same alloy, a completely different concentration dependence of the temperature interval AS − MS MT occurring under load is observed when the irreversible Gibbs free energy exceeds more than twice the reversible Gibbs free energy.
- The MT mechanism strongly depends on the concentration of the alloying element, and this is reflected in the change in the ratio between the reversible and irreversible Gibbs free energies at MT flow without load and under load. These changes in the concentration dependences of the MT temperature intervals in the alloys studied in the free state and under load depend on the precipitation of particles along the grain boundaries and in the grain body and on the changes in lattice parameter and atomic volume in the austenitic B2 phase.
- Based on the analysis of the concentration dependences of the temperature T0 of the chemical equilibrium of the austenitic and martensitic phases, it was found that for the MT to occur under load, in alloys with an alloying element concentration of more than 1.0 at% Nb, a more significant overcooling is required than for MT without load.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lagoudas, D. Shape Memory Alloys: Modeling and Engineering Applications; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2008; p. 436. [Google Scholar]
- Otsuka, K.; Shimizu, K.; Suzuki, Y. Shape Memory Alloys; Funakubo, H.M., Ed.; Nova Science Publishers, Inc.: Hapog, NY, USA, 1990; p. 224. [Google Scholar]
- Piao, M.; Miyazaki, S.; Otsuka, K. Characteristic of deformation and transformation in Ti44Ni47Nb9 shape memory alloy materials. Mater. Trans. JIM 1992, 4, 346–353. [Google Scholar] [CrossRef]
- He, X.M.; Rong, L.J.; Yan, D.S.; Li, Y.Y. TiNiNb wide hysteresis shape memory alloy with low niobium content. Mater. Sci. Eng. A 2004, 371, 193–197. [Google Scholar] [CrossRef]
- Cai, W.; Meng, X.L.; Zhao, L.C. Recent development of TiNi-based shape memory alloys. Curr. Opin. Solid. State Mater. Sci. 2005, 9, 296–302. [Google Scholar] [CrossRef]
- Picornell, C.; Pons, J.; Paulscn, A. Burst-like reverse martensitic transformation during heating, cooling and under isothermal conditions in stabilized Ni-Ti-Nb. Scr. Mater. 2020, 180, 23–28. [Google Scholar] [CrossRef]
- Choi, E.; Nam, T.H.; Chung, Y.S.; Kim, Y.W.; Lee, S.Y. Behavior of NiTiNb SMA wires under recovery stress or prestressing. Nano Res. Lett. 2012, 7, 66. [Google Scholar] [CrossRef] [PubMed]
- Xi, R.; Jiang, H.; Kustov, S. Influence of Nb addition and process parameters on the microstructure and phase transformation behavior of NiTiNb ternary shape memory alloys fabricated by laser powder bed fusion. Scr. Mater. 2023, 222, 114996. [Google Scholar] [CrossRef]
- Fan, Q.C.; Zhang, Y.; Zhang, Y.H.; Wang, Y.Y.; Yang, E.H.; Huang, S.K.; Wen, Y.H. Influence of Ni/Ti ratio and Nb addition on martensitic transformation behavior of NiTiNb alloys. J. Alloy. Compd. 2019, 790, 1167–1176. [Google Scholar] [CrossRef]
- He, X.M.; Rong, L.J. Effect of deformation on the stress-induced martensitic transformation in (Ni47Ti44)100−xNbx shape memory alloys with wide hysteresis. Met. Mater. Int. 2006, 12, 279–288. [Google Scholar] [CrossRef]
- Bao, Z.; Guo, S.; Xiao, F.; Zhao, X. Development of NiTiNb in-situ composite with high damping capacity and high yield strength. Prog. Nat. Sci. 2011, 21, 293–300. [Google Scholar] [CrossRef]
- He, X.M.; Zhao, L.Z.; Zhang, S.F.; Duo, S.W.; Zhang, R.F. Study of the thermal physical properties of Ti47Ni44Nb9 wide hysteresis shape memory alloy. Mater. Sci. Eng. A 2006, 441, 167–169. [Google Scholar] [CrossRef]
- Piotrowski, B.; Zineb, B.; Patoor, E.; Eberhardt, A. Modeling of niobium precipitates effect on the Ni47Ti44Nb9 shape memory alloy behavior. Int. J. Plast. 2012, 36, 130–147. [Google Scholar] [CrossRef]
- Rius, J.M.; Cladera, A.; Mas, B.; Ribas, C. Shear behaviour of beams strengthened using different Ni-Ti-Nb shape memory alloy wire configurations and design proposal based on the compression chord capacity model (CCCM). Eng. Struct. 2022, 268, 114724. [Google Scholar] [CrossRef]
- Fu, X.; Guojun, M.; Xinqing, Z.; Huibin, X. Effects of Nb content on yield strength of NiTiNb alloys in martensite state. Chin. J. Aeronaut. 2009, 22, 658–662. [Google Scholar] [CrossRef][Green Version]
- Zhang, F.; Zhang, L.; Wang, F.; Zhang, H. Effects of Nb additions on the precipitate morphology and hardening behavior of Ni-rich Ni55Ti45 alloys. J. Alloys Compd. 2018, 735, 2453–2461. [Google Scholar] [CrossRef]
- Silva, J.D.; Macieira, G.F.C.; Santos, E.S.; Santos, L.A.; Buono, V.T.L. Role of Nb on the phase stability and morphology of Ti-Ni-Cu-Nb alloys. J. Mater. Res. Technol. 2022, 20, 1428–1436. [Google Scholar] [CrossRef]
- Mirkin, L.I. X-ray Diffraction Analysis: Indexing of Radiographs; Science: Moscow, Russia, 1981; p. 496. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Kireeva, I.V.; Panchenko, E.Y.; Timofeeva, E.E. Mechanisms of Thermoelastic Martensitic Transformations in High-Strength Single Crystals of Alloys Based on Iron and Titanium Nickelide; Chumlyakov, Y.I., Ed.; NTL: Tomsk, Russia, 2016; p. 244. [Google Scholar]
- Ortin, J.; Planes, A. Thermodynamic analysis of thermal measurements inthermoelastic martensitic transformation. Acta. Mettall. 1988, 36, 1873–1889. [Google Scholar] [CrossRef]
- Doroczi, L.; Palanki, Z.; Szabo, S.; Beke, D.L. Stress dependence of non-chemical free energy contribution in Cu-Al-Ni shape memory alloys. Mater. Sci. Eng. 2004, 378, 274–277. [Google Scholar] [CrossRef]
- Guanjun, Y.; Shiming, H. Experimental investigation on the 800 °C isothermal section of the Ti-Ni-Nb ternary system. Rare Met. Mater. Eng. 1997, 26, 18–22. [Google Scholar]
- Massalski, T.B. Binary Alloy Phase Diagrams; American Society for Metals: Chardon, OH, USA, 1984; Volume 1, 224p. [Google Scholar]
- Matsumoto, S.; Tokunaga, T.; Ohtani, H.; Hasebc, M. Thermodynamic analysis of the phase equilibria of the Nb-Ni-Ti system. Mater. Trans. 2005, 46, 2920–2930. [Google Scholar] [CrossRef]
- He, X.M.; Xiang, J.H.; Li, M.S.; Duo, S.W.; Guo, S.B.; Zhang, R.F.; Rong, L.J. Temperature memory effect induced by incomplete transformation in TiNi-based shape memory alloy. J. Alloys Compd. 2006, 422, 338–341. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, X.; Yang, Y.; Xu, H. Wide hysteresis NiTi(Nb) shape memory alloys with low Nb content (4.5 at.%). Mater. Sci. Eng. A 2006, 438–440, 575–578. [Google Scholar] [CrossRef]
- Abramov, V.Y.; Aleksandrova, N.M.; Borovkov, D.V.; Khmelevskaya, I.Y. Martensitic transformation and functional properties of thermally and thermomechanically treated Ti-Ni-Nb based alloys. Mater. Sci. Eng. A 2006, 438–440, 553–557. [Google Scholar] [CrossRef]
- Shi, H.; Frenzel, J.; Martinez, G.T.; Van Rompaey, S.; Bakulin, A.; Kulkova, S.; Van Aert, D. Schryvers, Site occupation of Nb atoms in ternary Ni-Ti-Nb shape memory alloys. Acta Mater. 2014, 74, 85–95. [Google Scholar] [CrossRef]
- Prokoshkin, S.D.; Korotitskiy, A.V.; Brailovski, V. On the lattice parameters of phases in binary TiNi shape memory alloys. Acta Mater. 2004, 52, 4479–4492. [Google Scholar] [CrossRef]
- Lobodyuk, V.A.; Estrin, E.I. Martensitic Transformations; Phizmatlit: Moscow, Russia, 2009; p. 352. [Google Scholar]










| Structural Component | Composition, at% | |||
|---|---|---|---|---|
| Ti | Ni | Mo | Nb | |
| B2 matrix | 41.3 ± 0.5 | 58.3 ± 0.5 | 0.14 ± 0.1 | 0.3 ± 0.5 |
| Ti2Ni particles | 65.4 ± 0.5 | 34.6 ± 0.5 | – | – |
| Ni56Ti29Nb15 particles | 29.8 ± 0.5 | 55.9 ± 0.5 | – | 14.3 ± 0.5 |
| Structural Component | Composition, at% | |||
|---|---|---|---|---|
| Ti | Ni | Mo | Nb | |
| B2 matrix | 40.1 ± 0.5 | 59.2 ± 0.5 | 0.2 ± 0.1 | 0.4 ± 0.1 |
| Ti2Ni particles | 63.3 ± 0.5 | 36.7 ± 0.5 | – | – |
| Ni56Ti29Nb15 particles | 30.3 ± 0.5 | 53.6 ± 0.5 | – | 16.1 ± 0.5 |
| Structural Component | Composition, at% | |||
|---|---|---|---|---|
| Ti | Ni | Mo | Nb | |
| B2 matrix | 38.0 ± 0.5 | 61.2 ± 0.5 | 0.3 ± 0.1 | 0.5 ± 0.1 |
| Ti2Ni particles | 61.5 ± 0. 5 | 38.6 ± 0.5 | – | – |
| Ni56Ti29Nb15 particles | 29.3 ± 0.5 | 54.8 ± 0.5 | – | 16.0 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchenko, E.S.; Klopotov, A.A.; Baigonakova, G.A.; Zhukov, I.A. Regularities in the Evolution of Thermoelastic Martensitic Transformations during Cooling/Heating in the Free State and under Load of Titanium Nickelide Alloyed with Niobium. Materials 2024, 17, 175. https://doi.org/10.3390/ma17010175
Marchenko ES, Klopotov AA, Baigonakova GA, Zhukov IA. Regularities in the Evolution of Thermoelastic Martensitic Transformations during Cooling/Heating in the Free State and under Load of Titanium Nickelide Alloyed with Niobium. Materials. 2024; 17(1):175. https://doi.org/10.3390/ma17010175
Chicago/Turabian StyleMarchenko, Ekaterina S., Anatoly A. Klopotov, Gulsharat A. Baigonakova, and Ilya A. Zhukov. 2024. "Regularities in the Evolution of Thermoelastic Martensitic Transformations during Cooling/Heating in the Free State and under Load of Titanium Nickelide Alloyed with Niobium" Materials 17, no. 1: 175. https://doi.org/10.3390/ma17010175
APA StyleMarchenko, E. S., Klopotov, A. A., Baigonakova, G. A., & Zhukov, I. A. (2024). Regularities in the Evolution of Thermoelastic Martensitic Transformations during Cooling/Heating in the Free State and under Load of Titanium Nickelide Alloyed with Niobium. Materials, 17(1), 175. https://doi.org/10.3390/ma17010175






