Three-Dimensional Vibration Model of Cylindrical Shells via Carrera Unified Formulation
Abstract
:1. Introduction
2. Theoretical Formulations
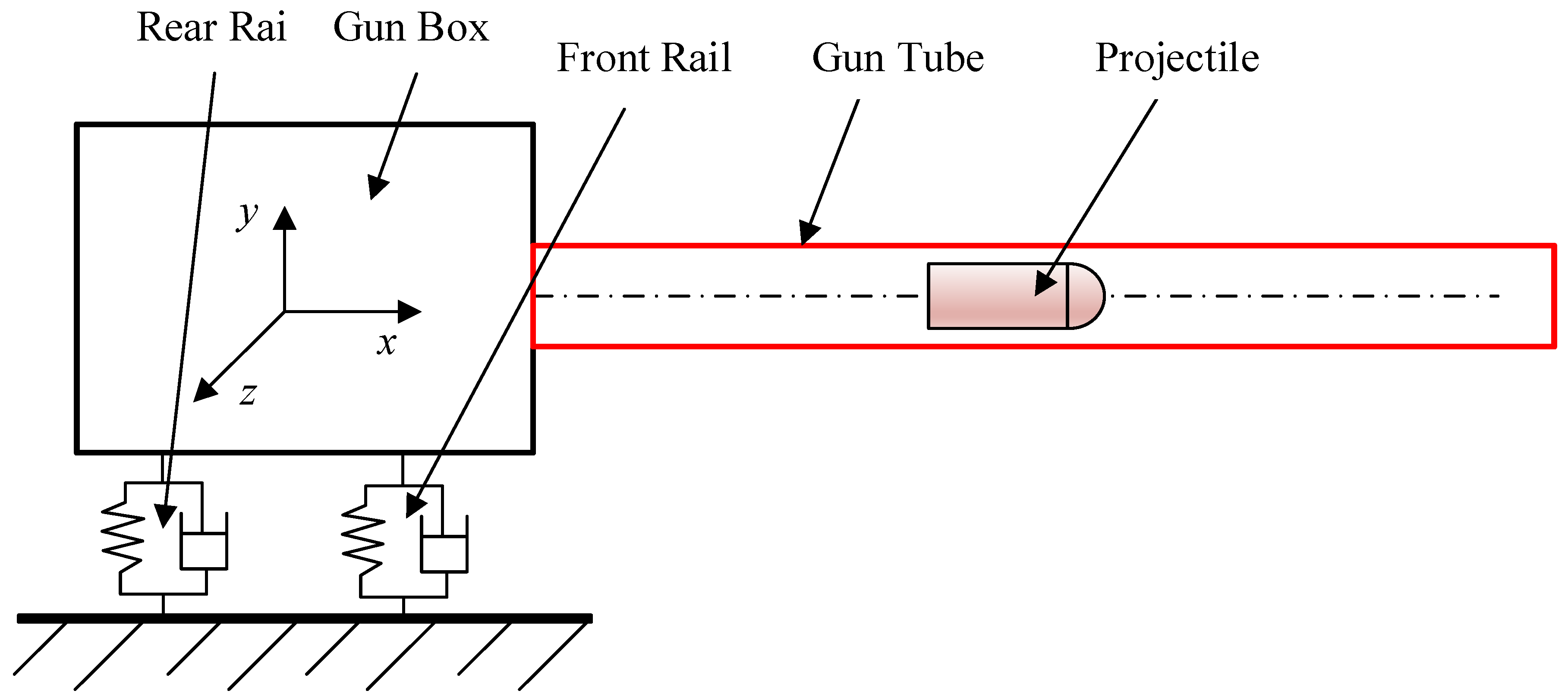
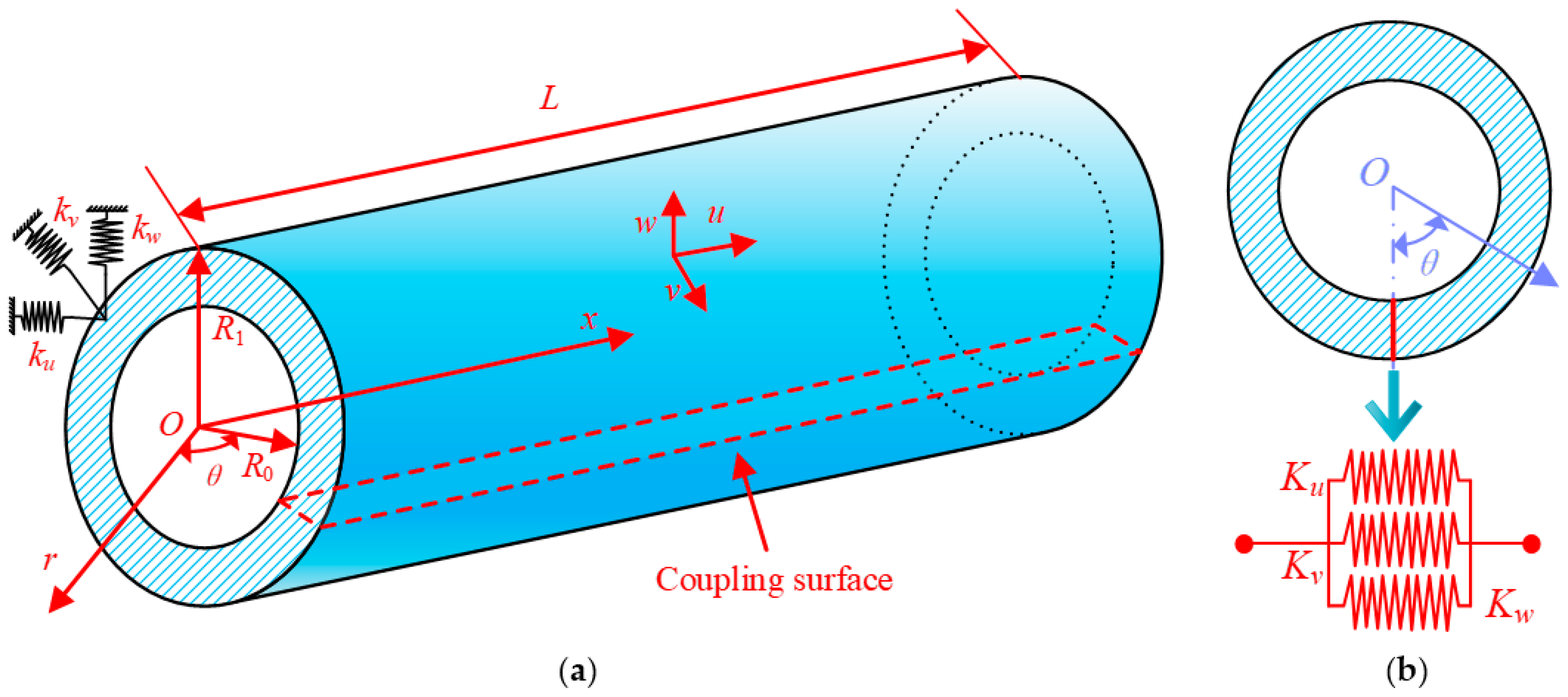
2.1. Model Description
2.2. Energy Expressions
2.3. The Unified Formulation with Chebyshev Discretization
2.4. Solving Procedures
3. Results and Discussion
3.1. Spring Parameters and Convergence Study
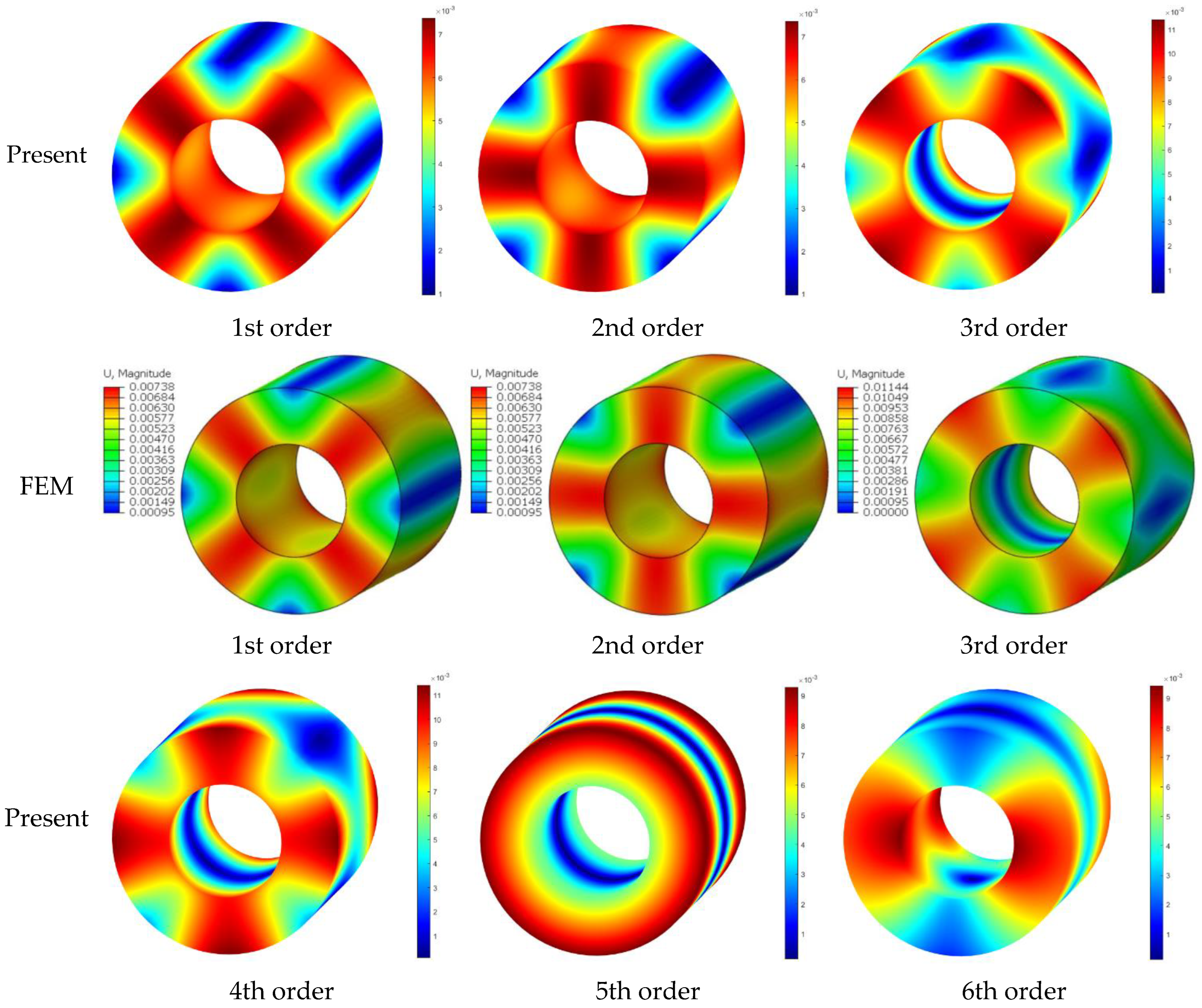
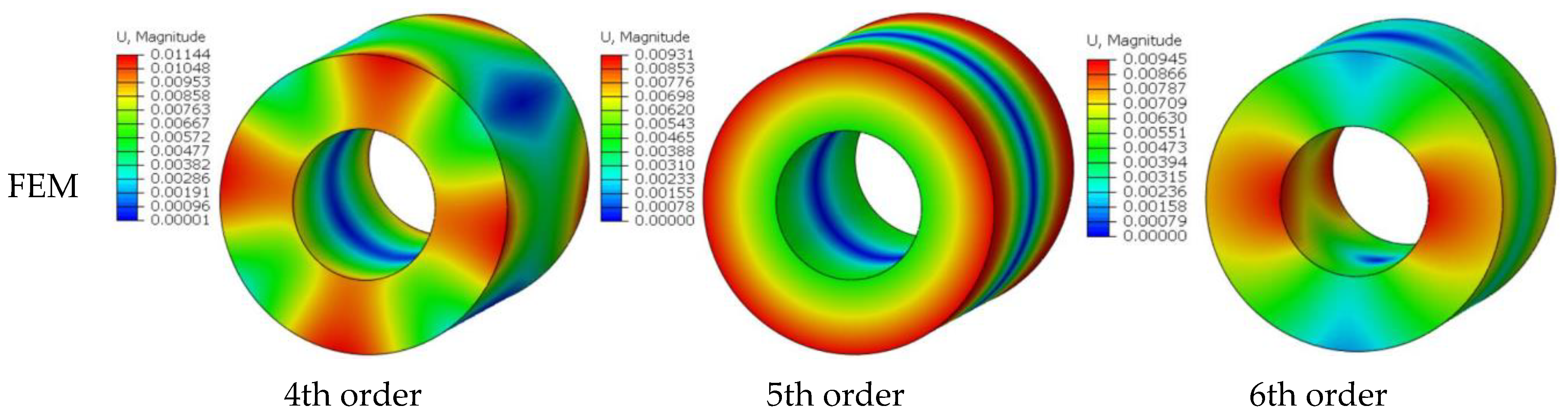
3.2. Results Validation
3.3. Numerical Study
4. Conclusions
- (1)
- The CUF model used in this paper is extended with Chebyshev polynomials and Taylor series for displacements in the axial, circumferential, and radial directions of the cylindrical shell, which effectively reduces the 3D model’s dimensionality.
- (2)
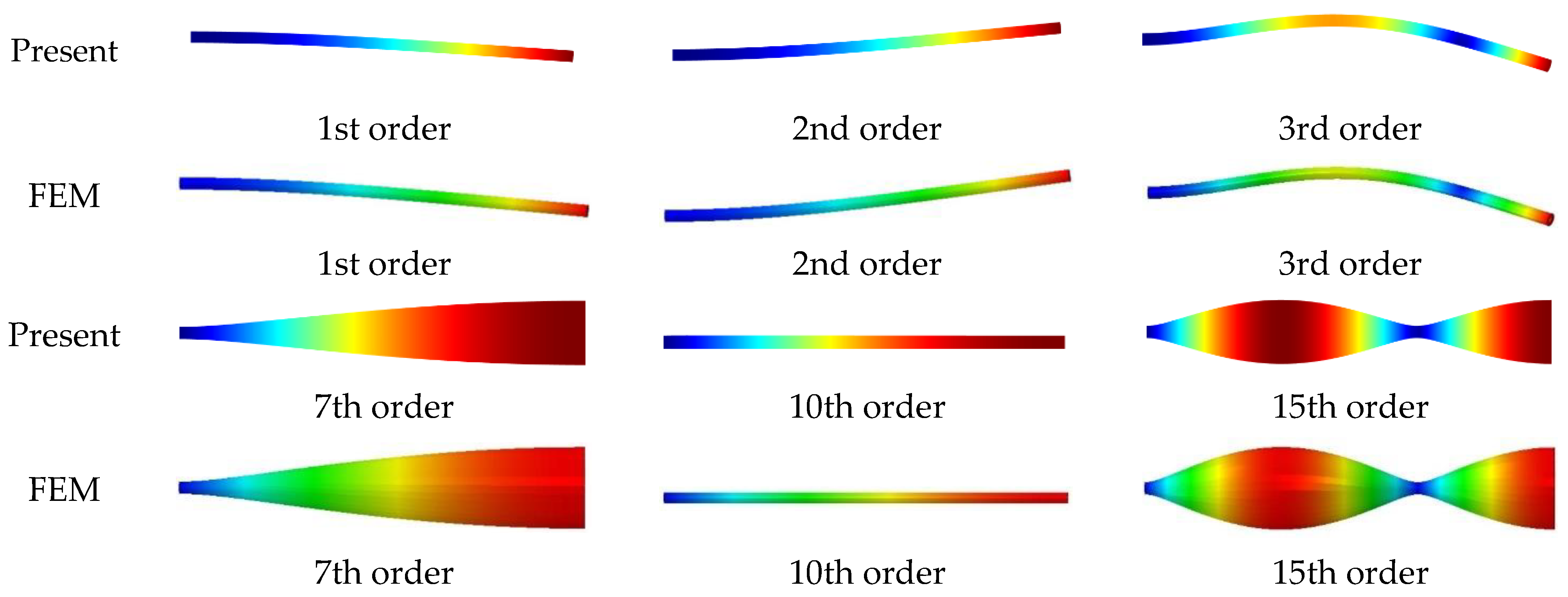
- The model presented in this study can be used to investigate the free vibration features of elastically constrained, 3D cylindrical shells. The model has good convergence, according to the results of the pertinent calculations. Additionally, the model’s great computational correctness and universality can be demonstrated by comparison with relevant literature and finite element results.
- (3)
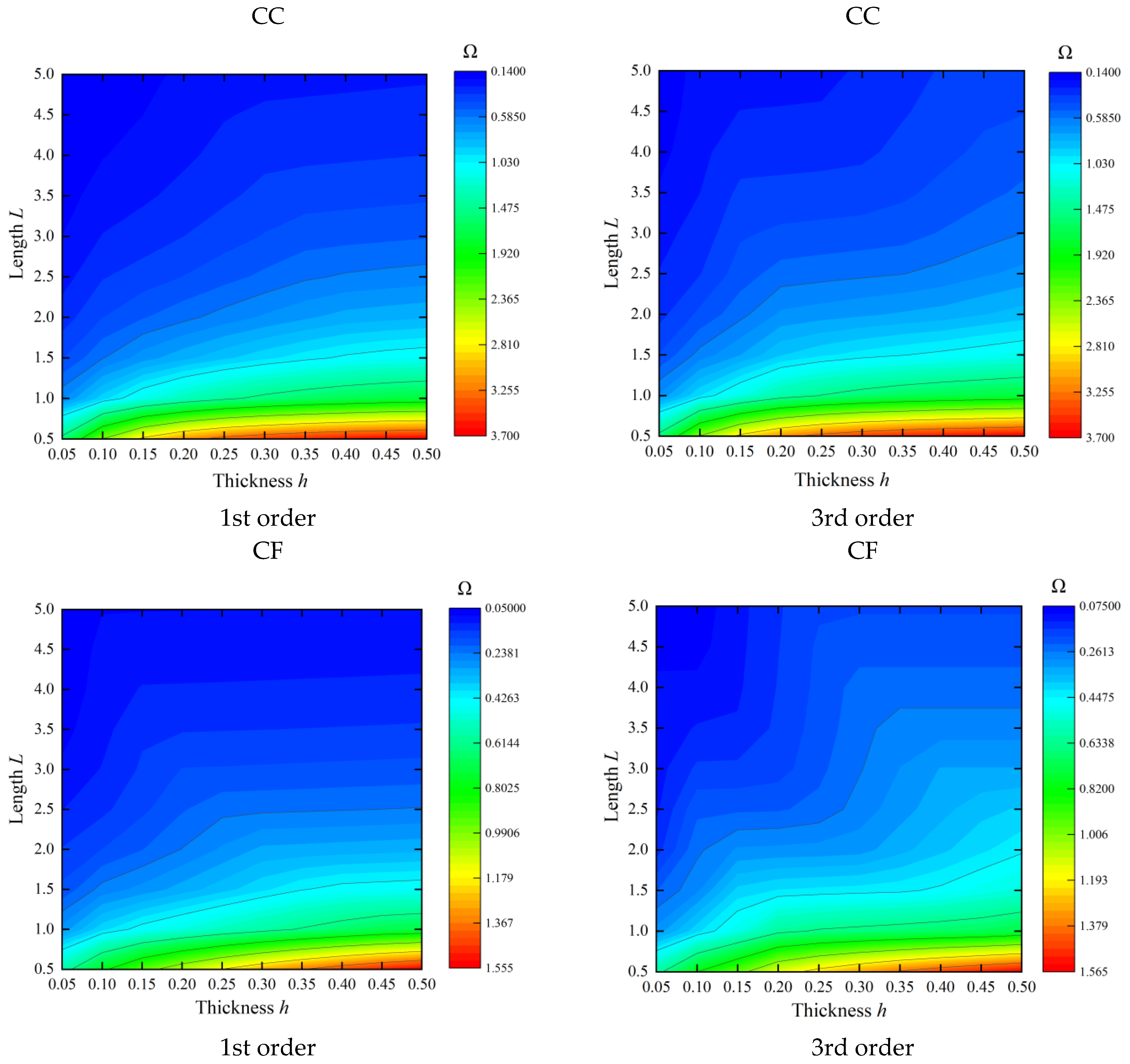
- The frequency parameter of the shell decreases with increasing length, since the longer the shell, the lower the stiffness, thus the higher the proneness to vibration. The frequency parameter of the shell decreases with increasing radius, mainly because the mass of the shell increases with increasing radius. The frequency of the cylindrical shell structure increases with thickness, and the longer the length, the slower the decreasing trend of its frequency with the increase of the thickness of shells.
- (4)
- The main drawback of the study in this paper is the inability to analyze the cylindrical shell structure with variable thickness characteristics, and the strong nonlinear characteristics are not considered.
- (5)
- The research in this paper can provide support for the optimal design of cylindrical shell-like gun tube structures and dynamics performance prediction in the future, and can be further extended to the vibration characteristics analysis of composite cylindrical shells.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Expressions for the Mass Matrix M and Stiffness Matrix K
References
- Zhao, Y.; Zhou, Q.; Yue, P. Research on Vibration Characteristics of Gun Barrel Based on Contact Model. AIP Conf. Proc. 2017, 1829, 020017. [Google Scholar]
- Koç, M.A. Development of an Intelligent Software Based on Adaptive Neural-Fuzzy Inference Systems for Predicting Muzzle Vibration of a Gun Barrel. Arab. J. Sci. Eng. 2022, 47, 8829–8846. [Google Scholar] [CrossRef]
- Liew, K.M.; Hung, K.C. Three-dimensional vibratory characteristics of solid cylinders and some remarks on simplified beam theories. Int. J. Solids Struct. 1995, 32, 3499–3513. [Google Scholar] [CrossRef]
- Loy, C.T.; Lam, K.Y. Vibration of thick cylindrical shells on the basis of three-dimensional theory of elasticity. J. Sound Vib. 1999, 226, 719–737. [Google Scholar] [CrossRef]
- Zhou, D.; Cheung, Y.K.; Lo, S.H.; Au, F.T.K. 3D vibration analysis of solid and hollow circular cylinders via Chebyshev–Ritz method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1575–1589. [Google Scholar] [CrossRef]
- Mofakhami, M.R.; Toudeshky, H.H.; Hashemi, S.H. Finite cylinder vibrations with different end boundary conditions. J. Sound Vib. 2006, 297, 293–314. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Davar, A.; Malekzadeh Fard, K. Free vibration analysis of homogeneous isotropic circular cylindrical shells based on a new three-dimensional refined higher-order theory. Int. J. Mech. Sci. 2012, 56, 1–25. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Farid, M.; Zahedinejad, P.; Karami, G. Three-dimensional free vibration analysis of thick cylindrical shells resting on two-parameter elastic supports. J. Sound Vib. 2008, 313, 655–675. [Google Scholar] [CrossRef]
- Ye, T.; Jin, G.; Shi, S.; Ma, X. Three-dimensional free vibration analysis of thick cylindrical shells with general end conditions and resting on elastic foundations. Int. J. Mech. Sci. 2014, 84, 120–137. [Google Scholar] [CrossRef]
- Atashipour, S.R.; Mohammadi, Z.; Folkow, P.D. A direct approach for three-dimensional elasto-static and elasto-dynamic solutions in curvilinear cylindrical coordinates with application to classical cylinder problems. Eur. J. Mech.—A/Solids 2022, 95, 104646. [Google Scholar] [CrossRef]
- Xiang, S.; Bi, Z.-y.; Jiang, S.-x.; Jin, Y.-x.; Yang, M.-s. Thin plate spline radial basis function for the free vibration analysis of laminated composite shells. Compos. Struct. 2011, 93, 611–615. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The GDQ method for the free vibration analysis of arbitrarily shaped laminated composite shells using a NURBS-based isogeometric approach. Compos. Struct. 2016, 154, 190–218. [Google Scholar] [CrossRef]
- Wang, Q.; Cui, X.; Qin, B.; Liang, Q.; Tang, J. A semi-analytical method for vibration analysis of functionally graded (FG) sandwich doubly-curved panels and shells of revolution. Int. J. Mech. Sci. 2017, 134 (Suppl. C), 479–499. [Google Scholar] [CrossRef]
- Fan, J.; Huang, J.; Juxiang, Z.; Jie, Z. The Walsh series method for free vibration analysis of functionally graded cylindrical shells. Compos. Struct. 2018, 206, 853–864. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, A.; Qin, B.; Wang, Q.; Zhong, R. Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation. Eur. Phys. J. Plus 2020, 135, 582. [Google Scholar] [CrossRef]
- Liu, T.; Wang, A.; Wang, Q.; Qin, B. Wave based method for free vibration characteristics of functionally graded cylindrical shells with arbitrary boundary conditions. Thin-Walled Struct. 2020, 148, 106580. [Google Scholar] [CrossRef]
- Chenchen, G.; Liu, T.; Wang, Q.; Bin, Q.; Shao, W.; Wang, A. Spectral-Tchebychev technique for the free vibration analysis of composite laminated stepped and stiffened cylindrical shells with arbitrary boundary conditions. Compos. Struct. 2021, 272, 114193. [Google Scholar] [CrossRef]
- Qin, Z.; Chu, F.; Zu, J. Free vibrations of cylindrical shells with arbitrary boundary conditions: A comparison study. Int. J. Mech. Sci. 2017, 133, 91–99. [Google Scholar] [CrossRef]
- Rahimi, A.; Alibeigloo, A.; Safarpour, M. Three-dimensional static and free vibration analysis of graphene platelet–reinforced porous composite cylindrical shell. J. Vib. Control 2020, 26, 1627–1645. [Google Scholar] [CrossRef]
- Zheng, D.; Du, J.; Liu, Y. Vibration characteristics analysis of an elastically restrained cylindrical shell with arbitrary thickness variation. Thin-Walled Struct. 2021, 165, 107930. [Google Scholar] [CrossRef]
- Su, Z.; Jin, G.; Ye, T. Three-dimensional vibration analysis of thick functionally graded conical, cylindrical shell and annular plate structures with arbitrary elastic restraints. Compos. Struct. 2014, 118, 432–447. [Google Scholar] [CrossRef]
- Qin, B.; Wang, Q.; Zhong, R.; Zhao, X.; Shuai, C. A three-dimensional solution for free vibration of FGP-GPLRC cylindrical shells resting on elastic foundations: A comparative and parametric study. Int. J. Mech. Sci. 2020, 187, 105896. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Nguyen-Trong, N.; Khatir, S.; Nguyen-Xuan, H.; Abdel-Wahab, M. A three-dimensional solution for free vibration and buckling of annular plate, conical, cylinder and cylindrical shell of FG porous-cellular materials using IGA. Compos. Struct. 2021, 259, 113216. [Google Scholar] [CrossRef]
- Tong, B.; Li, Y.; Zhu, X.; Zhang, Y. Three-dimensional vibration analysis of arbitrary angle-ply laminated cylindrical shells using differential quadrature method. Appl. Acoust. 2019, 146, 390–397. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Nali, P. Plates and Shells for Smart Structures: Classical and Advanced Theories for Modeling and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 36. [Google Scholar]
- Petrolo, M.; Carrera, E.; Cinefra, M.; Zappino, E. Finite Element Analysis of Structures through Unified Formulation; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Carrera, E.; Giunta, G.; Petrolo, M. Beam Structures: Classical and Advanced Theories; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Carrera, E.; Miglioretti, F.; Petrolo, M. Accuracy of refined finite elements for laminated plate analysis. Compos. Struct. 2011, 93, 1311–1327. [Google Scholar] [CrossRef]
- Carrera, E.; Elishakoff, I.; Petrolo, M. Who needs refined structural theories? Compos. Struct. 2021, 264, 113671. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the shells of revolution. Numerical evaluation. Mech. Adv. Mater. Struct. 2022, 1–23. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for shells of revolution. I. Higher-order theory. Acta Mech. 2022, 234, 109–136. [Google Scholar] [CrossRef]
- Carrera, E.; Zozulya, V.V. Carrera unified formulation (CUF) for the shells of revolution. II. Navier close form solutions. Acta Mech. 2022, 234, 137–161. [Google Scholar] [CrossRef]
- Armenàkas, A.E.; Gazis, D.C.; Herrmann, G. Free Vibrations of Circular Cylindrical Shells; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
| Authors | Materials | Elastic Theory | Method |
|---|---|---|---|
| Xiang et al. [11] | Laminated composites | First-order shear deformation theory | Meshless global collocation method |
| Tornabene et al. [12] | Higher-order shear deformation theory | Generalized Differential Quadrature method | |
| Wang et al. [13] | Functionally graded sandwich materials | First-order shear deformation theory | Fourier series expression method |
| Fan et al. [14] | Functionally graded materials | Walsh series method | |
| Chen et al. [15] | Functionally graded graphene platelets-reinforced materials | Chebyshev–Lagrangian approach | |
| Liu et al. [16] | Functionally graded materials | Wave-based method | |
| Guo et al. [17] | Laminated composites | Spectral-Tchebychev technique | |
| Qin et al. [18] | Isotropic materials | Sanders shell theory | Rayleigh—Ritz method |
| Rahimi et al. [19] | Graphene platelet-reinforced porous composites | 3D elastic theory | Differential quadrature method |
| Zheng et al. [20] | Isotropic materials | Donnell—Mushtari shell theory | Modified Fourier series method |
| Boundary Conditions | Spring Parameters | ||
|---|---|---|---|
| ku | kv | kw | |
| C | 1014 | 1014 | 1014 |
| S | 0 | 1014 | 1014 |
| F | 0 | 0 | 0 |
| E1 | 104 | 104 | 104 |
| Z | M × N | Modes | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 3 | 8 × 8 | 0.6582 | 0.6858 | 0.7163 | 0.7207 | 1.1780 | 1.2040 |
| 10 × 10 | 0.5814 | 0.5828 | 0.6440 | 0.6445 | 1.1781 | 1.1787 | |
| 12 × 12 | 0.5782 | 0.5782 | 0.6415 | 0.6416 | 1.1781 | 1.1789 | |
| 14 × 14 | 0.5782 | 0.5782 | 0.6416 | 0.6417 | 1.1781 | 1.1792 | |
| 16 × 16 | 0.5782 | 0.5782 | 0.6417 | 0.6417 | 1.1781 | 1.1792 | |
| 18 × 18 | 0.5782 | 0.5782 | 0.6417 | 0.6417 | 1.1781 | 1.1792 | |
| 4 | 8 × 8 | 0.6576 | 0.6855 | 0.7158 | 0.7203 | 1.1780 | 1.2036 |
| 10 × 10 | 0.5810 | 0.5824 | 0.6437 | 0.6441 | 1.1781 | 1.1783 | |
| 12 × 12 | 0.5779 | 0.5779 | 0.6412 | 0.6412 | 1.1781 | 1.1785 | |
| 14 × 14 | 0.5779 | 0.5779 | 0.6413 | 0.6413 | 1.1781 | 1.1788 | |
| 16 × 16 | 0.5779 | 0.5779 | 0.6414 | 0.6414 | 1.1781 | 1.1788 | |
| 18 × 18 | 0.5779 | 0.5779 | 0.6414 | 0.6414 | 1.1781 | 1.1788 | |
| Z | M × N | Modes | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 3 | 8 × 8 | 66.284 | 99.632 | 141.104 | 159.373 | 218.621 | 251.441 |
| 10 × 10 | 12.368 | 13.422 | 75.151 | 75.310 | 208.602 | 208.671 | |
| 12 × 12 | 12.033 | 12.034 | 75.022 | 75.035 | 208.373 | 208.474 | |
| 14 × 14 | 12.027 | 12.027 | 74.989 | 75.002 | 208.291 | 208.381 | |
| 16 × 16 | 12.024 | 12.024 | 74.970 | 74.982 | 208.247 | 208.327 | |
| 18 × 18 | 12.022 | 12.022 | 74.960 | 74.971 | 208.226 | 208.297 | |
| 4 | 8 × 8 | 66.110 | 99.516 | 140.831 | 159.131 | 218.567 | 251.287 |
| 10 × 10 | 12.365 | 13.415 | 75.150 | 75.308 | 208.599 | 208.668 | |
| 12 × 12 | 12.033 | 12.034 | 75.021 | 75.035 | 208.370 | 208.472 | |
| 14 × 14 | 12.027 | 12.027 | 74.988 | 75.001 | 208.288 | 208.378 | |
| 16 × 16 | 12.024 | 12.024 | 74.969 | 74.981 | 208.244 | 208.324 | |
| 18 × 18 | 12.022 | 12.022 | 74.959 | 74.970 | 208.223 | 208.295 | |
| Method | Mode Number | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Liew [3] | 0.9594 | 0.9594 | 0.9742 | 1.5467 | 1.7751 | 1.7751 | 1.9483 | 2.5938 | 2.5938 |
| Ye [9] | 0.9595 | 0.9595 | 0.9742 | 1.5467 | 1.7751 | 1.7751 | 1.9483 | 2.5938 | 2.5938 |
| Present | 0.9595 | 0.9595 | 0.9742 | 1.5467 | 1.7751 | 1.7751 | 1.9483 | 2.5939 | 2.5939 |
| Diff L | 0.01% | 0.01% | 0 | 0 | 0 | 0 | 0 | 0.004% | 0.004% |
| Diff Y | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.004% | 0.004% |
| Mode Number | Method | |||
|---|---|---|---|---|
| Present | FEM | Ye [9] | Zhou [5] | |
| 1 | 0.9703 | 0.9686 | 0.9700 | 0.9700 |
| 2 | 0.9703 | 0.9686 | ||
| 3 | 1.0454 | 1.0429 | 1.0451 | 1.0451 |
| 4 | 1.0454 | 1.0429 | ||
| 5 | 1.5708 | 1.5695 | ||
| 6 | 1.6041 | 1.6036 | 1.6041 | 1.6041 |
| 7 | 1.6041 | 1.6036 | ||
| 8 | 1.8932 | 1.8891 | 1.8932 | 1.8932 |
| 9 | 1.8932 | 1.8891 | ||
| 10 | 1.9354 | 1.9288 | 1.9351 | 1.9351 |
| 11 | 1.9354 | 1.9288 | ||
| 12 | 2.0424 | 2.0413 | ||
| 13 | 2.1513 | 2.1489 | ||
| 14 | 2.2883 | 2.2834 | ||
| 15 | 2.2885 | 2.2835 | ||
| 16 | 2.3047 | 2.2969 | ||
| 17 | 2.3488 | 2.3421 | ||
| 18 | 2.3490 | 2.3421 | ||
| 19 | 2.4807 | 2.4764 | 2.4807 | 2.4807 |
| 20 | 2.4807 | 2.4764 | ||
| L/R | Method | Mode Number | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 2 | Ye [9] | 0.01814 | 0.01906 | 0.03100 | |||||
| Ref. [33] | 0.01814 | 0.01907 | 0.03100 | ||||||
| Ref. [7] | 0.01814 | 0.01906 | 0.03100 | ||||||
| Present | 0.01814 | 0.01814 | 0.01907 | 0.01907 | 0.02627 | 0.02640 | 0.03100 | 0.03100 | |
| 1 | Ye [9] | 0.03642 | 0.03971 | ||||||
| Ref. [33] | 0.03643 | 0.03927 | |||||||
| Ref. [7] | 0.03641 | 0.03969 | |||||||
| Present | 0.03184 | 0.03184 | 0.03643 | 0.03644 | 0.03972 | 0.03972 | 0.04036 | 0.04066 | |
| 0.5 | Ye [9] | 0.07616 | 0.07681 | ||||||
| Ref. [33] | 0.07618 | 0.07684 | |||||||
| Ref. [7] | 0.07607 | 0.07675 | |||||||
| Present | 0.03184 | 0.03184 | 0.06368 | 0.06368 | 0.07614 | 0.07617 | 0.07617 | 0.07684 | |
| B.C. | Method | Mode Number | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| FF | FEM | 0.2987 | 0.2992 | 0.8180 | 0.8193 | 1.5883 | 1.5906 | 2.5927 | 2.5964 |
| Present | 0.3015 | 0.3015 | 0.8253 | 0.8255 | 1.6021 | 1.6027 | 2.6144 | 2.6160 | |
| Error | 0.908% | 0.761% | 0.894% | 0.761% | 0.870% | 0.760% | 0.837% | 0.758% | |
| CF | FEM | 0.0471 | 0.0472 | 0.2938 | 0.2943 | 0.8164 | 0.8177 | 1.5521 | 1.5825 |
| Present | 0.0476 | 0.0476 | 0.2965 | 0.2966 | 0.8237 | 0.8240 | 1.5599 | 1.5959 | |
| Error | 0.940% | 0.780% | 0.917% | 0.781% | 0.889% | 0.776% | 0.505% | 0.849% | |
| CC | FEM | 0.2981 | 0.2986 | 0.8142 | 0.8154 | 1.5768 | 1.5791 | 2.5680 | 2.5715 |
| Present | 0.3009 | 0.3010 | 0.8215 | 0.8219 | 1.5900 | 1.5914 | 2.5882 | 2.5916 | |
| Error | 0.923% | 0.796% | 0.894% | 0.800% | 0.834% | 0.781% | 0.788% | 0.782% | |
| E1E1 | FEM | 0.2990 | 0.2994 | 0.8183 | 0.8195 | 1.5885 | 1.5908 | 2.5930 | 2.5966 |
| Present | 0.3015 | 0.3015 | 0.8253 | 0.8255 | 1.6019 | 1.6027 | 2.6138 | 2.6160 | |
| Error | 0.850% | 0.699% | 0.861% | 0.734% | 0.842% | 0.745% | 0.805% | 0.749% | |
| CE1 | FEM | 0.0472 | 0.0473 | 0.2940 | 0.2944 | 0.8166 | 0.8178 | 1.5521 | 1.5826 |
| Present | 0.0477 | 0.0477 | 0.2966 | 0.2966 | 0.8237 | 0.8240 | 1.5599 | 1.5959 | |
| Error | 1.163% | 1.004% | 0.886% | 0.747% | 0.875% | 0.763% | 0.505% | 0.841% | |
| B.C. | L | Mode Number | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| FF | 0.5 | 1.4111 | 1.4114 | 1.4471 | 1.4478 | 1.8848 | 1.9471 | 1.9475 | 2.3868 |
| 1 | 0.9424 | 1.0116 | 1.0116 | 1.4502 | 1.4507 | 1.4547 | 1.4554 | 1.4753 | |
| 2 | 0.3468 | 0.3468 | 0.4712 | 0.7431 | 0.7431 | 0.7554 | 0.9424 | 1.1672 | |
| CF | 0.5 | 0.6446 | 0.6447 | 0.9423 | 1.5273 | 1.5278 | 1.5369 | 1.6856 | 1.6858 |
| 1 | 0.2224 | 0.2224 | 0.4712 | 0.7670 | 0.7943 | 0.7944 | 1.4135 | 1.4589 | |
| 2 | 0.0638 | 0.0638 | 0.2356 | 0.3080 | 0.3080 | 0.3821 | 0.6919 | 0.6920 | |
| CC | 0.5 | 1.6850 | 1.6853 | 1.8844 | 2.2074 | 2.2077 | 3.0542 | 3.0805 | 3.1789 |
| 1 | 0.7525 | 0.7526 | 0.9423 | 1.4839 | 1.4841 | 1.5372 | 1.6250 | 1.6256 | |
| 2 | 0.2965 | 0.2965 | 0.4712 | 0.6361 | 0.6362 | 0.7669 | 0.9424 | 1.0349 | |
| E1E1 | 0.5 | 1.4111 | 1.4114 | 1.4471 | 1.4478 | 1.8848 | 1.9471 | 1.9476 | 2.3868 |
| 1 | 0.9424 | 1.0116 | 1.0116 | 1.4502 | 1.4507 | 1.4547 | 1.4554 | 1.4753 | |
| 2 | 0.3468 | 0.3468 | 0.4712 | 0.7431 | 0.7431 | 0.7554 | 0.9424 | 1.1672 | |
| CS | 0.5 | 1.4839 | 1.4841 | 1.5373 | 1.8844 | 2.0442 | 2.0446 | 2.1701 | 2.1703 |
| 1 | 0.6361 | 0.6362 | 0.7670 | 0.9423 | 1.4496 | 1.4498 | 1.5763 | 1.5769 | |
| 2 | 0.2309 | 0.2310 | 0.3821 | 0.4712 | 0.5895 | 0.5896 | 0.9424 | 0.9998 | |
| SS | 0.5 | 1.4056 | 1.4058 | 1.5403 | 1.5407 | 1.8844 | 1.9310 | 1.9315 | 2.3953 |
| 1 | 0.5356 | 0.5357 | 0.9423 | 1.4057 | 1.4059 | 1.4753 | 1.5380 | 1.5387 | |
| 2 | 0.1679 | 0.1679 | 0.4712 | 0.5356 | 0.5357 | 0.7554 | 0.9424 | 0.9636 | |
| SF | 0.5 | 0.9423 | 1.4502 | 1.4507 | 1.4851 | 1.4854 | 2.1343 | 2.1345 | 2.1419 |
| 1 | 0.4712 | 0.7431 | 0.7431 | 1.4135 | 1.4546 | 1.4552 | 1.4753 | 1.4814 | |
| 2 | 0.2356 | 0.2495 | 0.2495 | 0.6407 | 0.6407 | 0.7068 | 0.7554 | 1.0665 | |
| B.C. | R | Mode Number | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| FF | 0.5 | 1.0189 | 1.0190 | 1.1123 | 1.1123 | 2.2115 | 2.2115 | 2.7943 | 2.7945 |
| 1 | 0.2577 | 0.2577 | 0.3409 | 0.3409 | 0.7227 | 0.7227 | 0.8544 | 0.8545 | |
| 2 | 0.0644 | 0.0644 | 0.1153 | 0.1154 | 0.1817 | 0.1817 | 0.2876 | 0.2876 | |
| CF | 0.5 | 0.7455 | 0.7456 | 1.0968 | 1.0969 | 1.5707 | 1.9305 | 1.9305 | 2.4139 |
| 1 | 0.5667 | 0.5668 | 0.8178 | 0.8179 | 0.9481 | 0.9481 | 1.4415 | 1.4482 | |
| 2 | 0.4558 | 0.4559 | 0.4891 | 0.4905 | 0.6044 | 0.6044 | 0.7467 | 0.7647 | |
| CC | 0.5 | 1.7689 | 1.7689 | 2.1506 | 2.1507 | 3.1326 | 3.1328 | 3.1414 | 3.1955 |
| 1 | 1.4034 | 1.4035 | 1.4648 | 1.4648 | 1.8130 | 1.8228 | 2.0447 | 2.0447 | |
| 2 | 1.0391 | 1.0407 | 1.0830 | 1.0832 | 1.1400 | 1.1932 | 1.2511 | 1.2512 | |
| E1E1 | 0.5 | 1.0189 | 1.0190 | 1.1123 | 1.1123 | 2.2115 | 2.2115 | 2.7943 | 2.7945 |
| 1 | 0.2577 | 0.2577 | 0.3409 | 0.3409 | 0.7227 | 0.7228 | 0.8544 | 0.8545 | |
| 2 | 0.0644 | 0.0644 | 0.1154 | 0.1154 | 0.1817 | 0.1817 | 0.2876 | 0.2876 | |
| CS | 0.5 | 1.5776 | 1.5777 | 1.9193 | 1.9194 | 2.5359 | 3.0256 | 3.0257 | 3.0658 |
| 1 | 1.2647 | 1.2648 | 1.3200 | 1.3201 | 1.7241 | 1.7332 | 1.9743 | 1.9743 | |
| 2 | 0.9271 | 0.9288 | 0.9864 | 0.9866 | 1.0426 | 1.0946 | 1.1882 | 1.1882 | |
| SS | 0.5 | 1.4071 | 1.4071 | 1.7505 | 1.7505 | 2.8449 | 2.8450 | 3.0125 | 3.0127 |
| 1 | 1.1398 | 1.1398 | 1.1980 | 1.1980 | 1.6504 | 1.6585 | 1.9478 | 1.9478 | |
| 2 | 0.8332 | 0.8350 | 0.9115 | 0.9116 | 0.9633 | 1.0001 | 1.0001 | 1.0117 | |
| SF | 0.5 | 1.0454 | 1.0455 | 1.5707 | 1.7566 | 1.7567 | 2.3758 | 2.3758 | 2.8304 |
| 1 | 0.2843 | 0.2843 | 0.7610 | 0.7611 | 1.4231 | 1.4295 | 1.4784 | 1.4785 | |
| 2 | 0.0863 | 0.0863 | 0.2174 | 0.2174 | 0.3946 | 0.3971 | 0.7157 | 0.7304 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, W.; Liu, T.; Li, C.; Wang, Q. Three-Dimensional Vibration Model of Cylindrical Shells via Carrera Unified Formulation. Materials 2023, 16, 3345. https://doi.org/10.3390/ma16093345
Liang W, Liu T, Li C, Wang Q. Three-Dimensional Vibration Model of Cylindrical Shells via Carrera Unified Formulation. Materials. 2023; 16(9):3345. https://doi.org/10.3390/ma16093345
Chicago/Turabian StyleLiang, Weige, Tao Liu, Chi Li, and Qingshan Wang. 2023. "Three-Dimensional Vibration Model of Cylindrical Shells via Carrera Unified Formulation" Materials 16, no. 9: 3345. https://doi.org/10.3390/ma16093345
APA StyleLiang, W., Liu, T., Li, C., & Wang, Q. (2023). Three-Dimensional Vibration Model of Cylindrical Shells via Carrera Unified Formulation. Materials, 16(9), 3345. https://doi.org/10.3390/ma16093345








