Development of a Unified Specimen for Adhesive Characterisation—Part 1: Numerical Study on the Mode I (mDCB) and II (ELS) Fracture Components
Abstract
1. Introduction
2. Numerical Details
2.1. Finite Element Model
2.1.1. Partitions
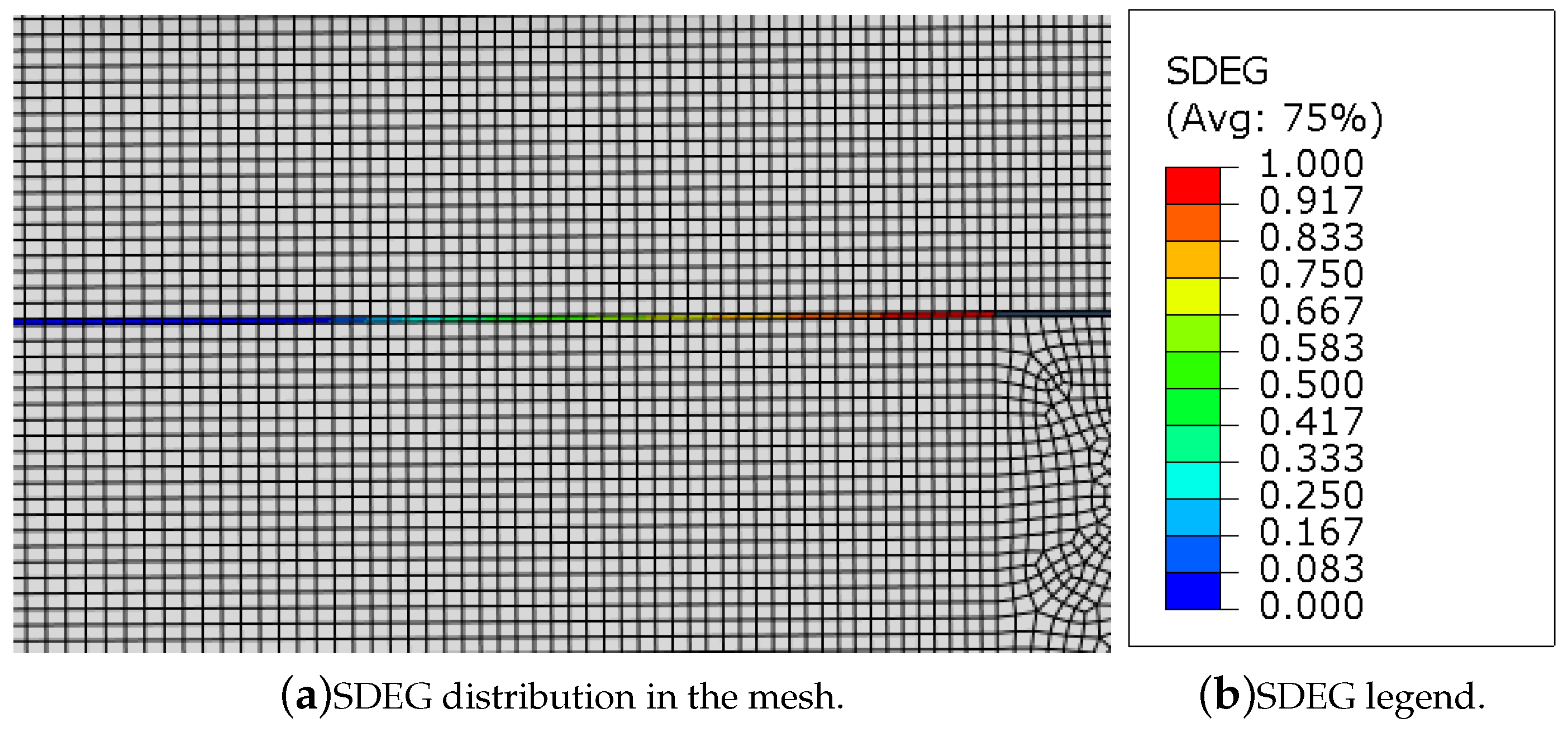
2.1.2. Mesh
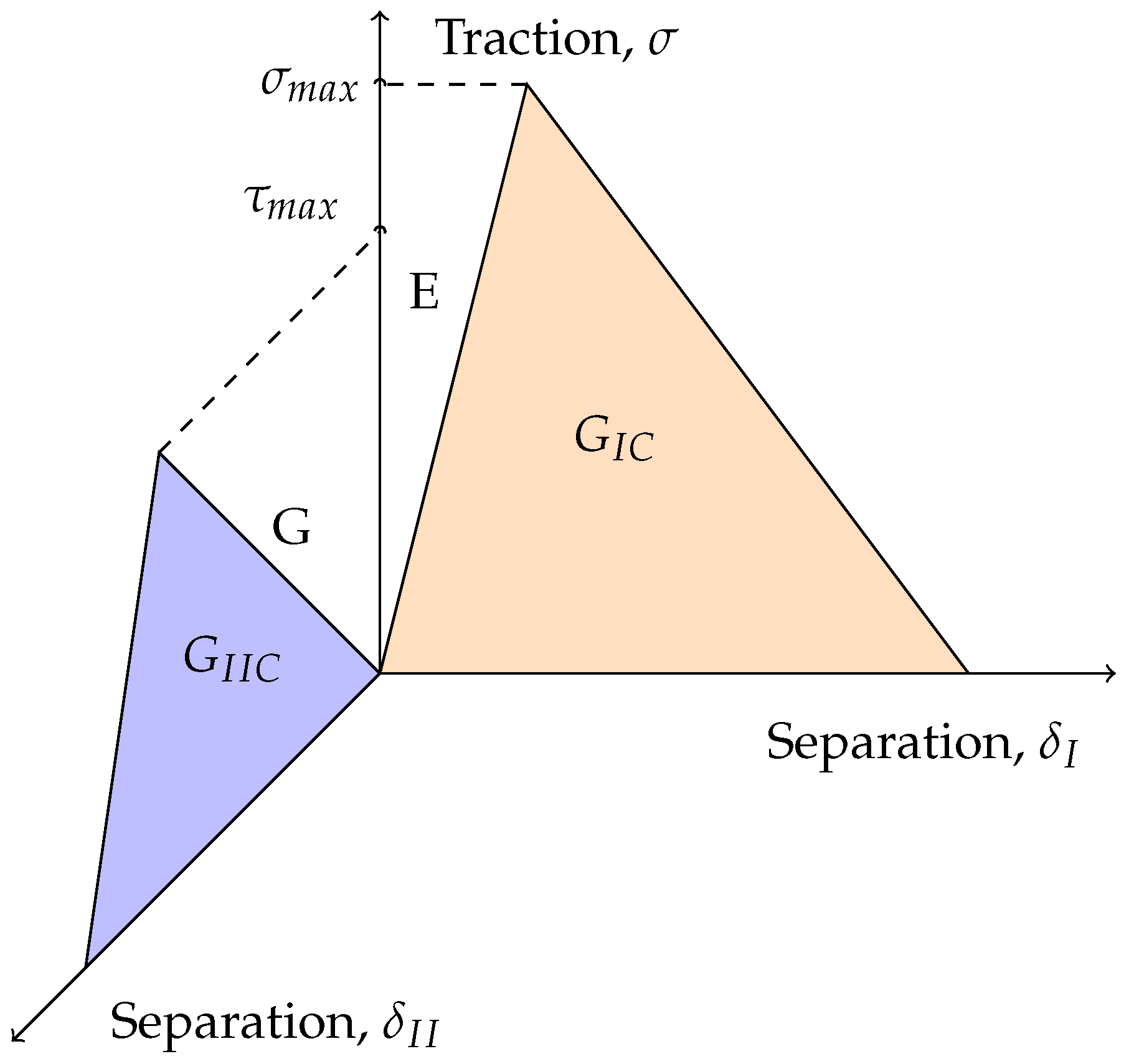
2.1.3. Cohesive Element Formulation
2.1.4. Material Properties
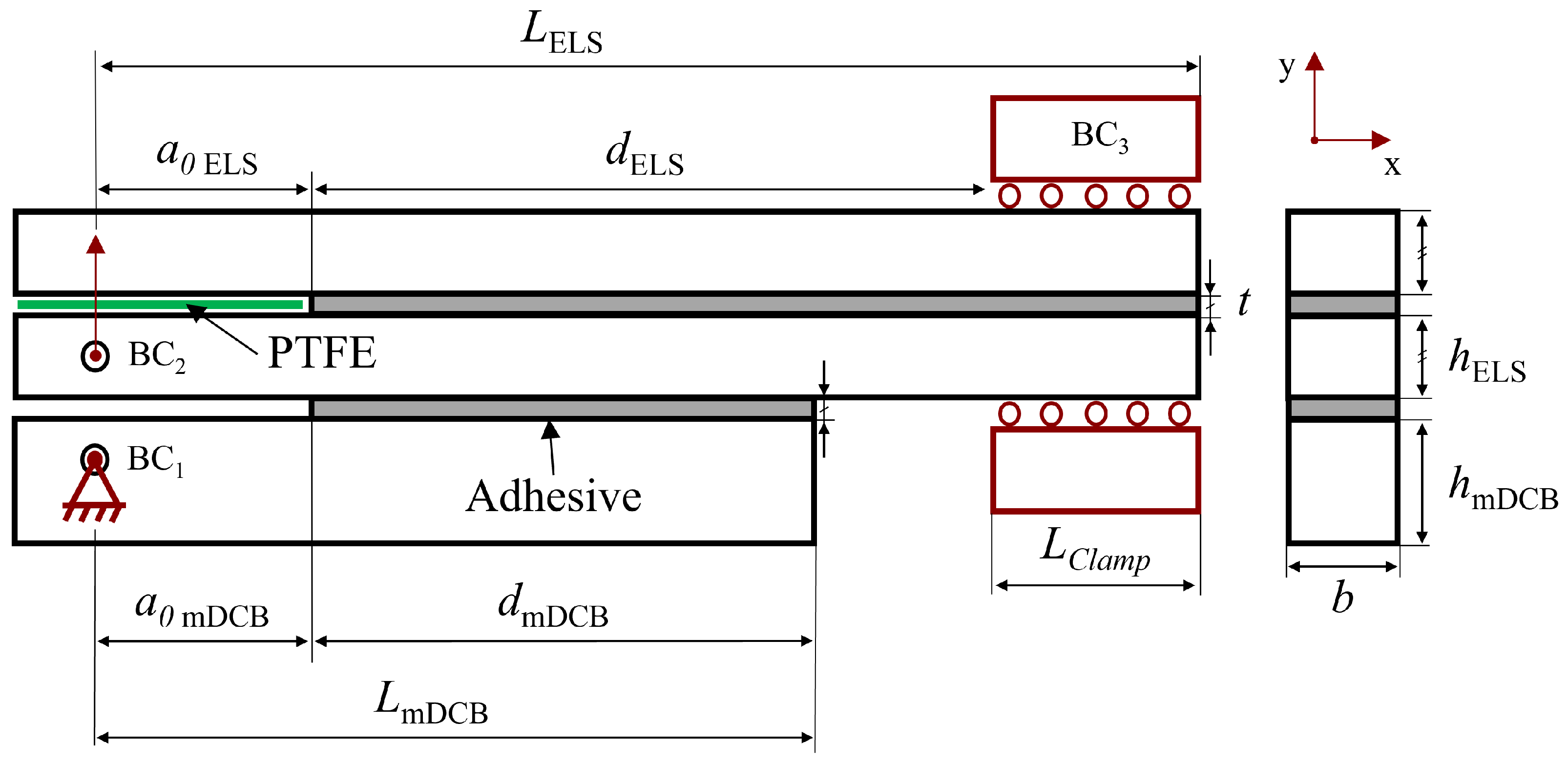
2.1.5. Boundary Conditions
2.2. Analysed Conditions
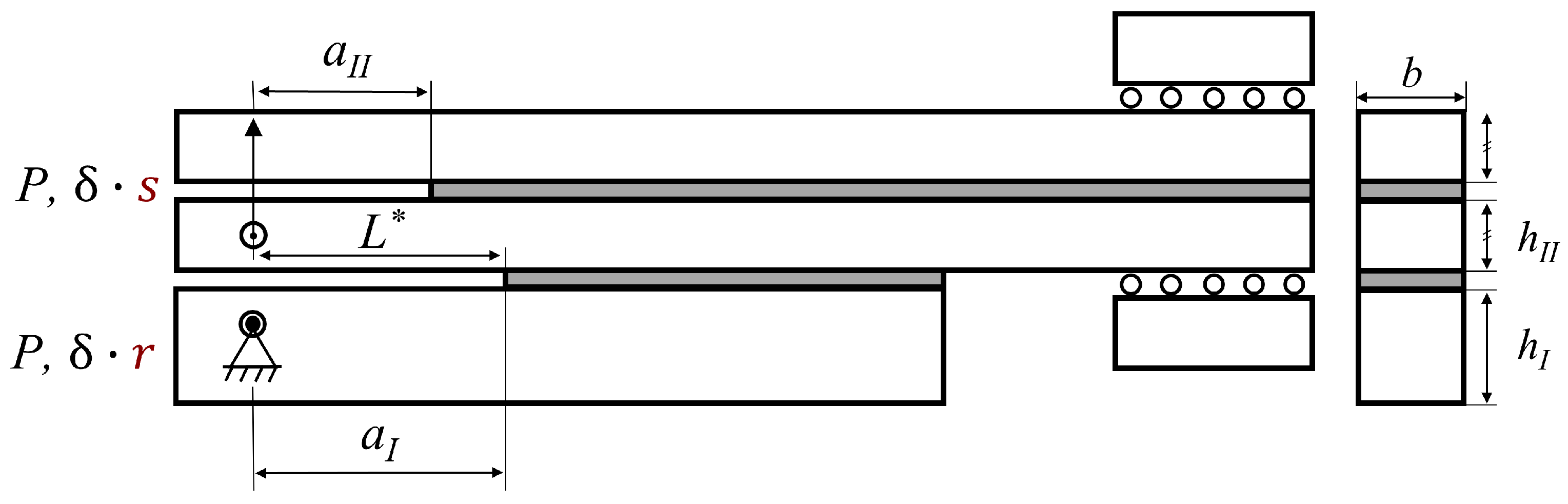
2.2.1. ELS Test
Parametric Study
Fracture Process Zone Analyses
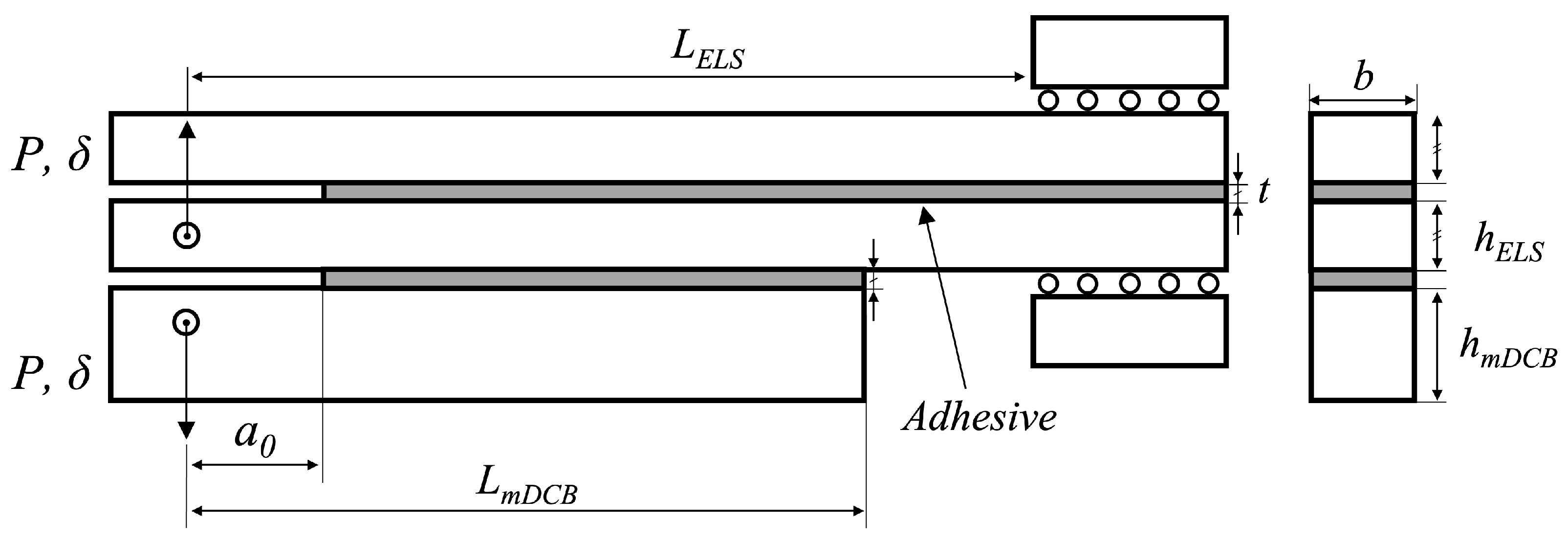
2.2.2. Modified DCB Test
Parametric Study
2.2.3. Data Reduction Methods
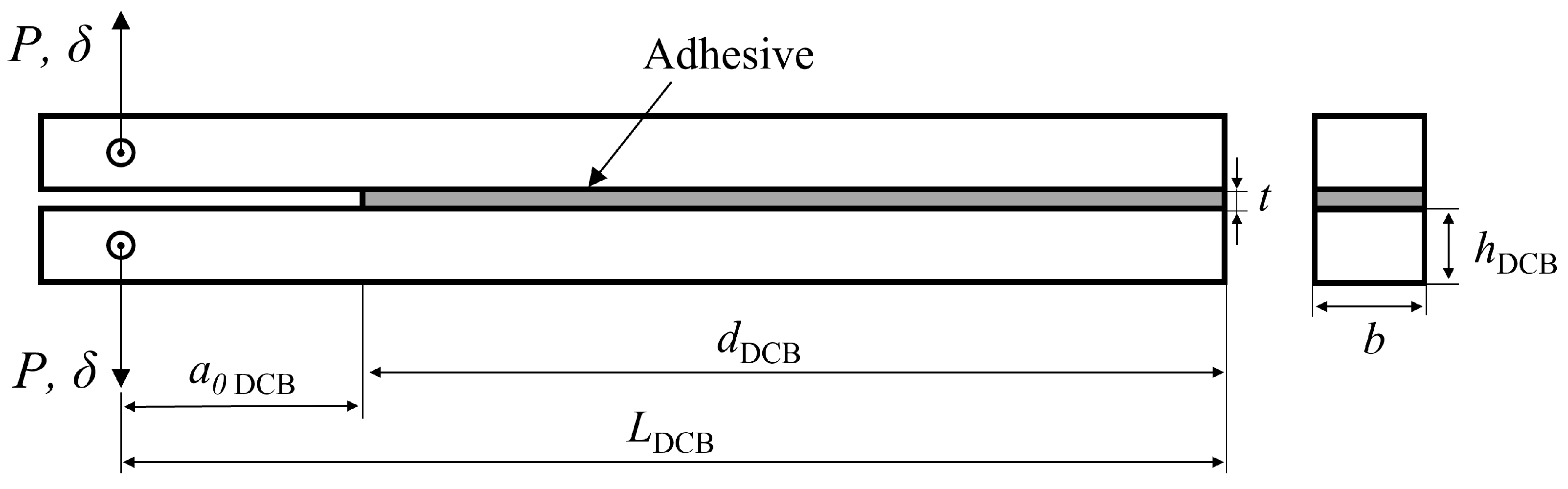
Mode I—CBBM for DCB Test
Mode I—CBBM for mDCB Test
Mode II—CBBM for ELS Test
3. Numerical Results and Discussion
3.1. End-Loaded Split (ELS) Test Specimen
3.1.1. Parametric Study
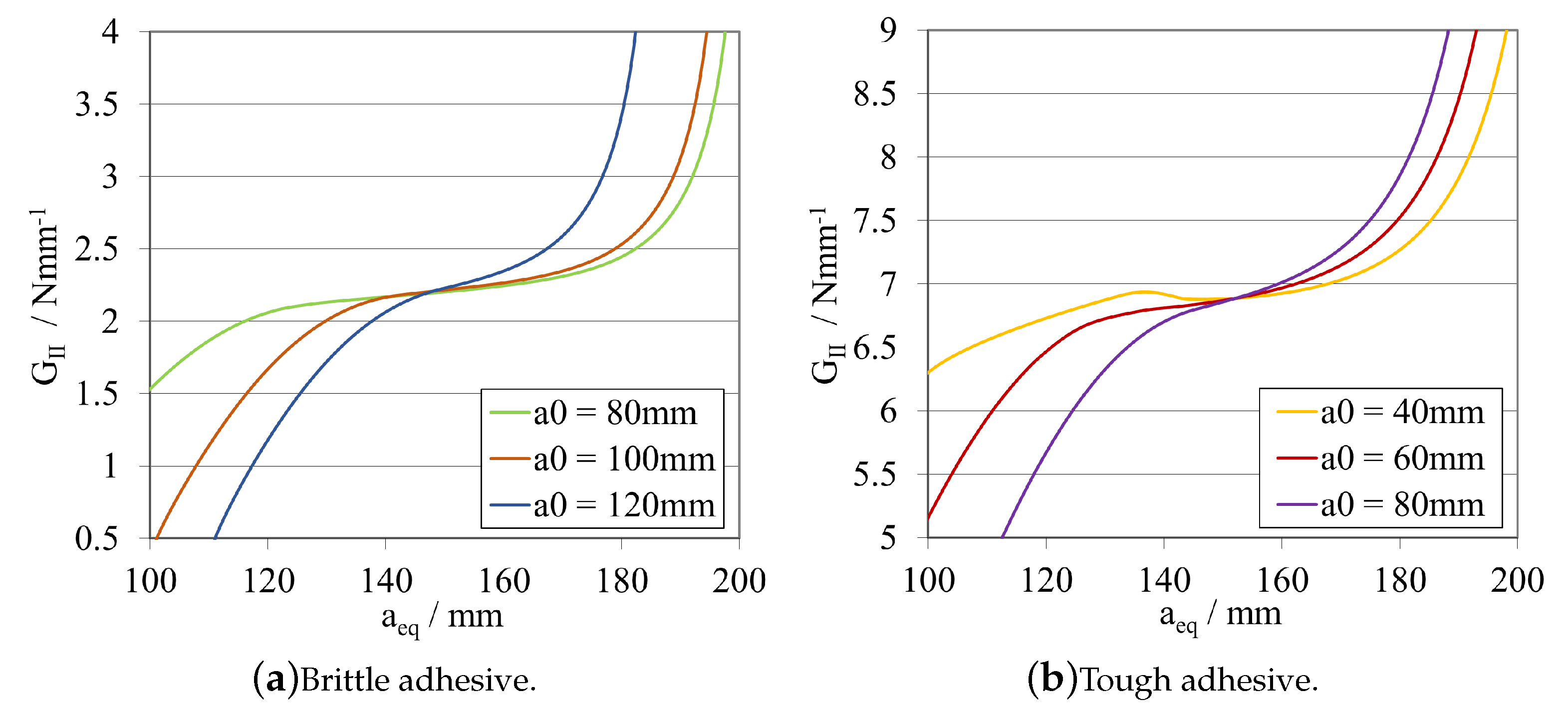
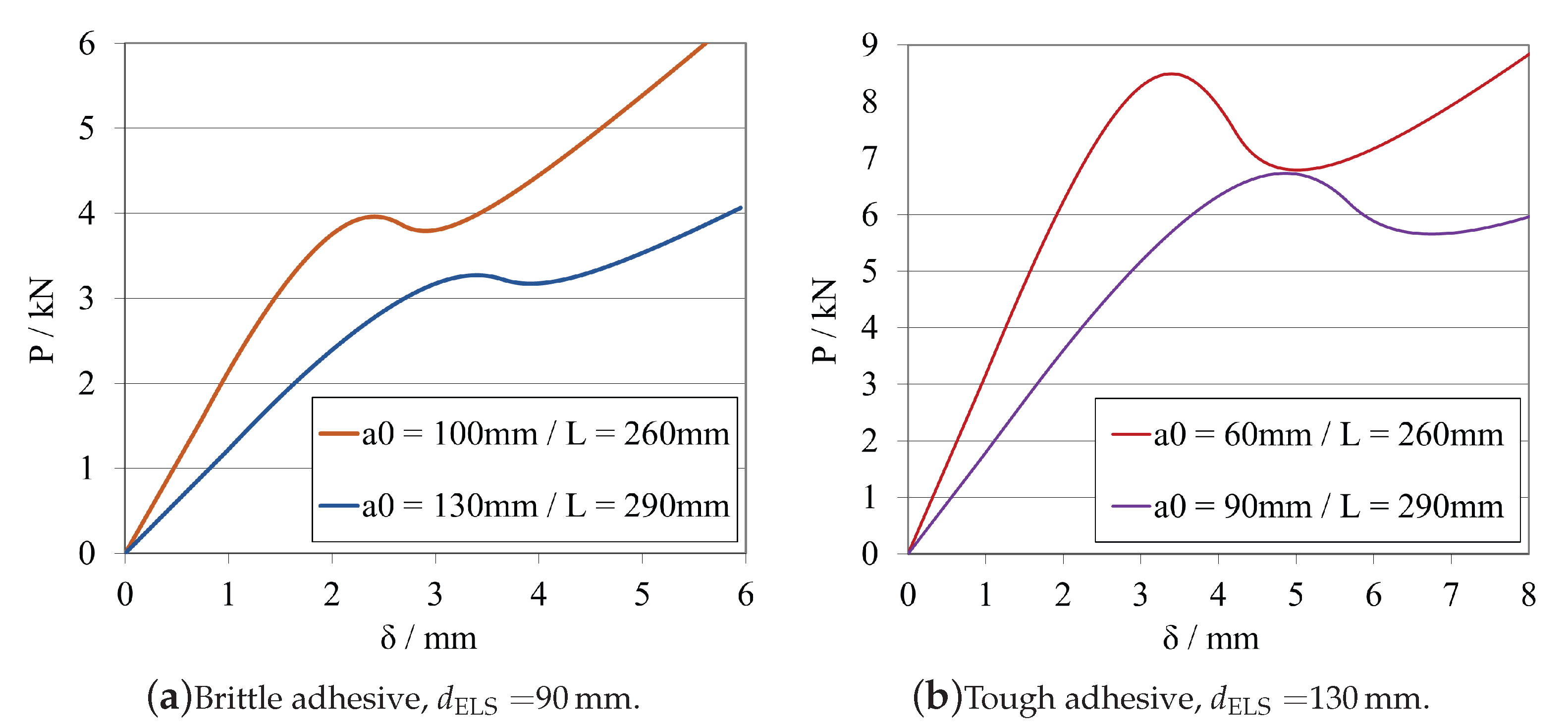
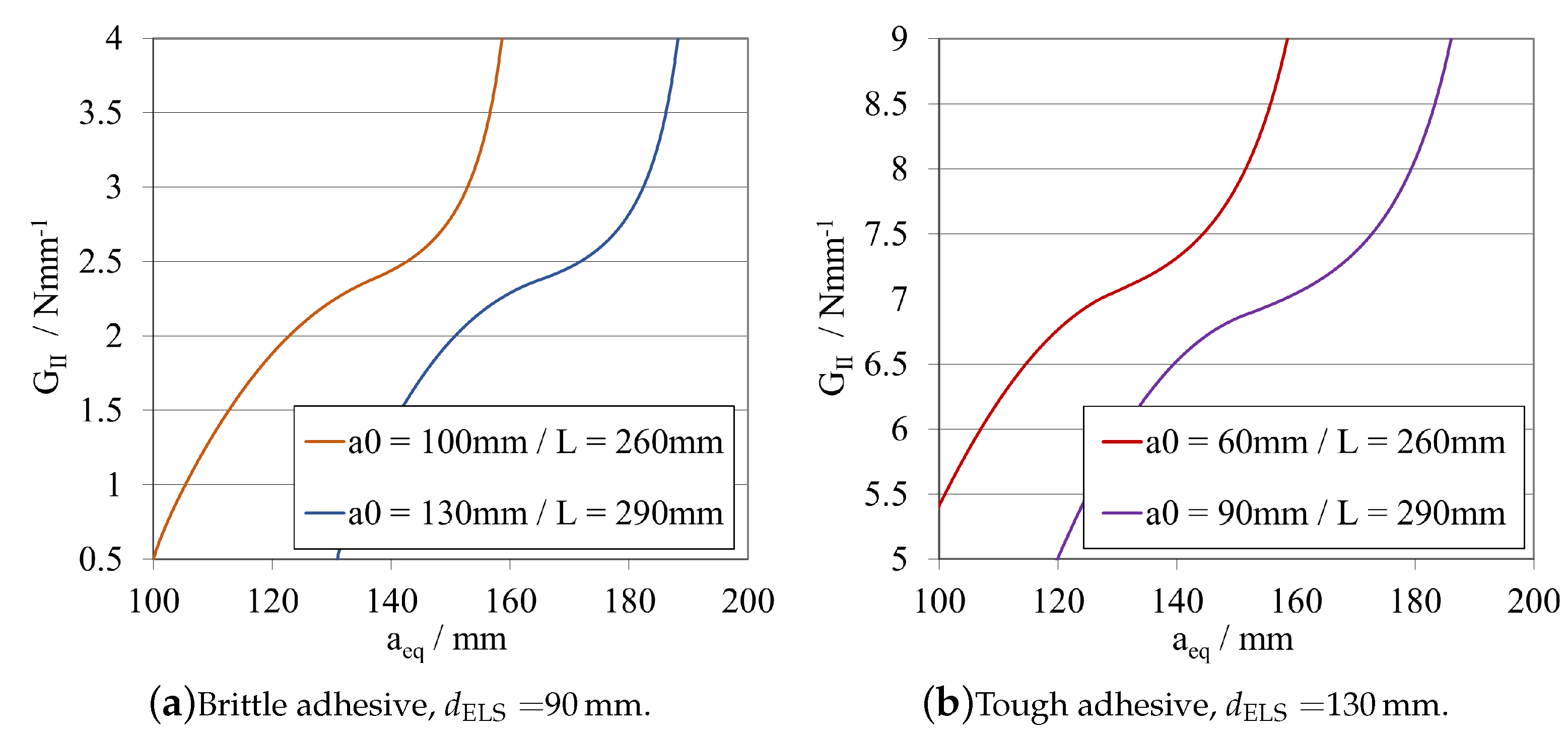
Initial Crack Length—
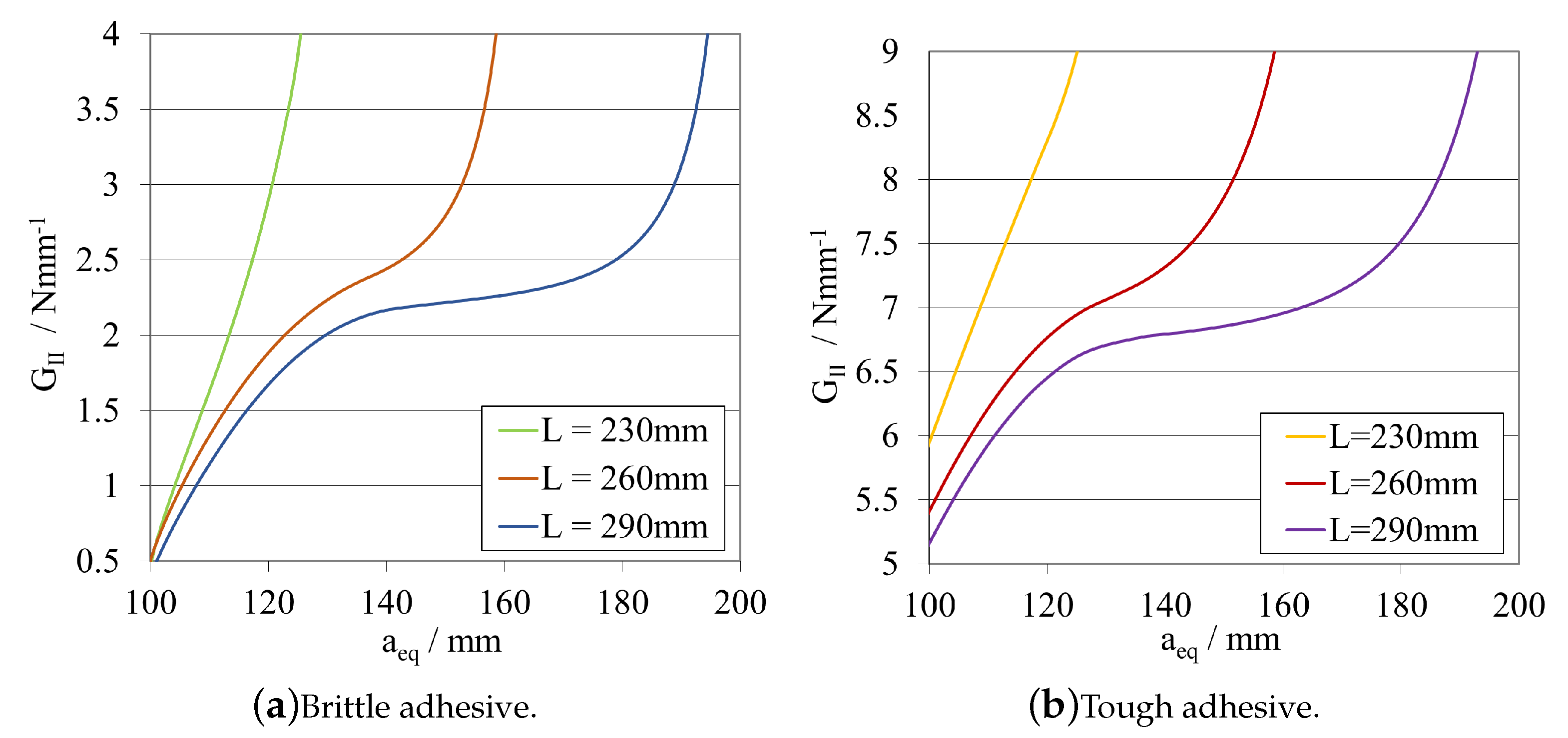
Total Length—
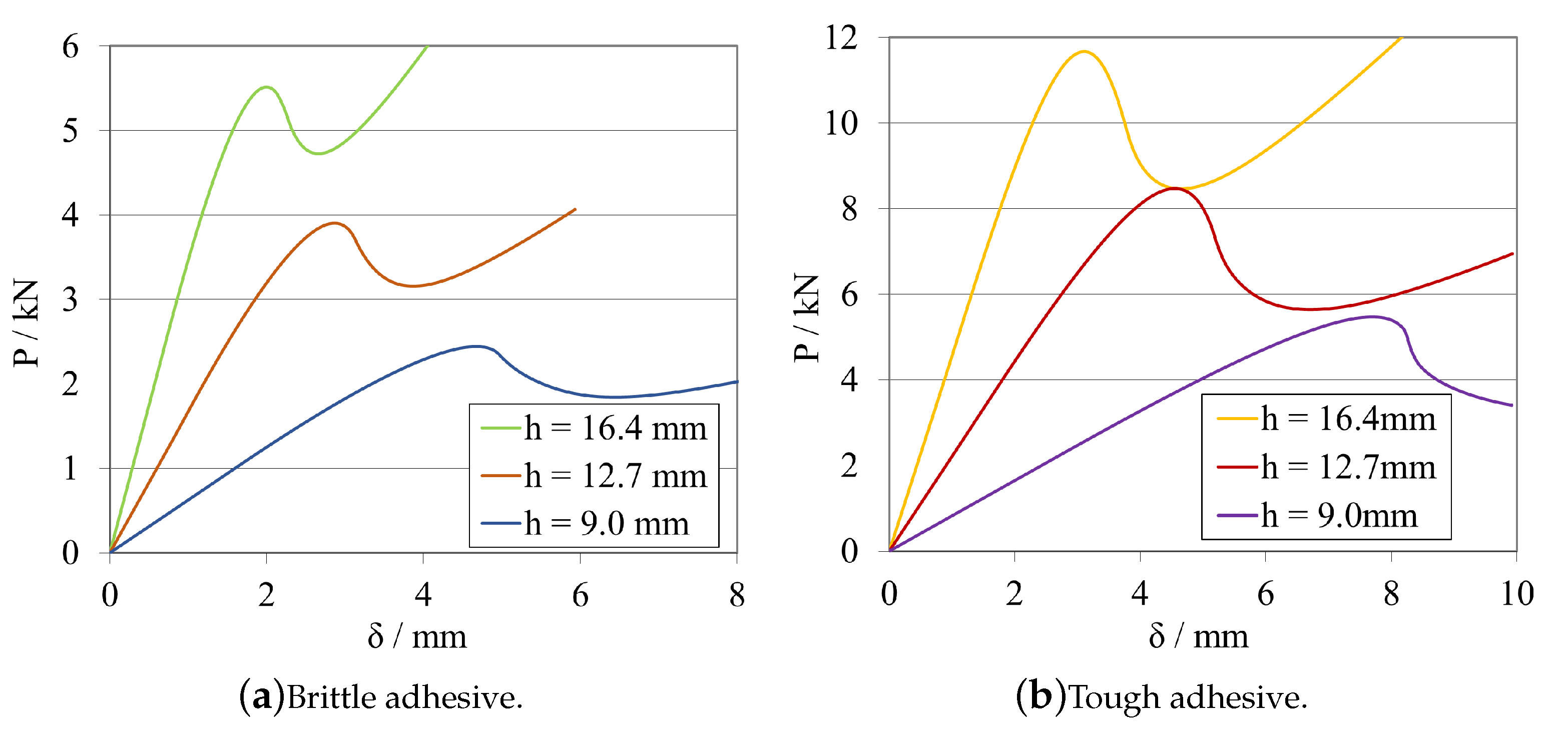
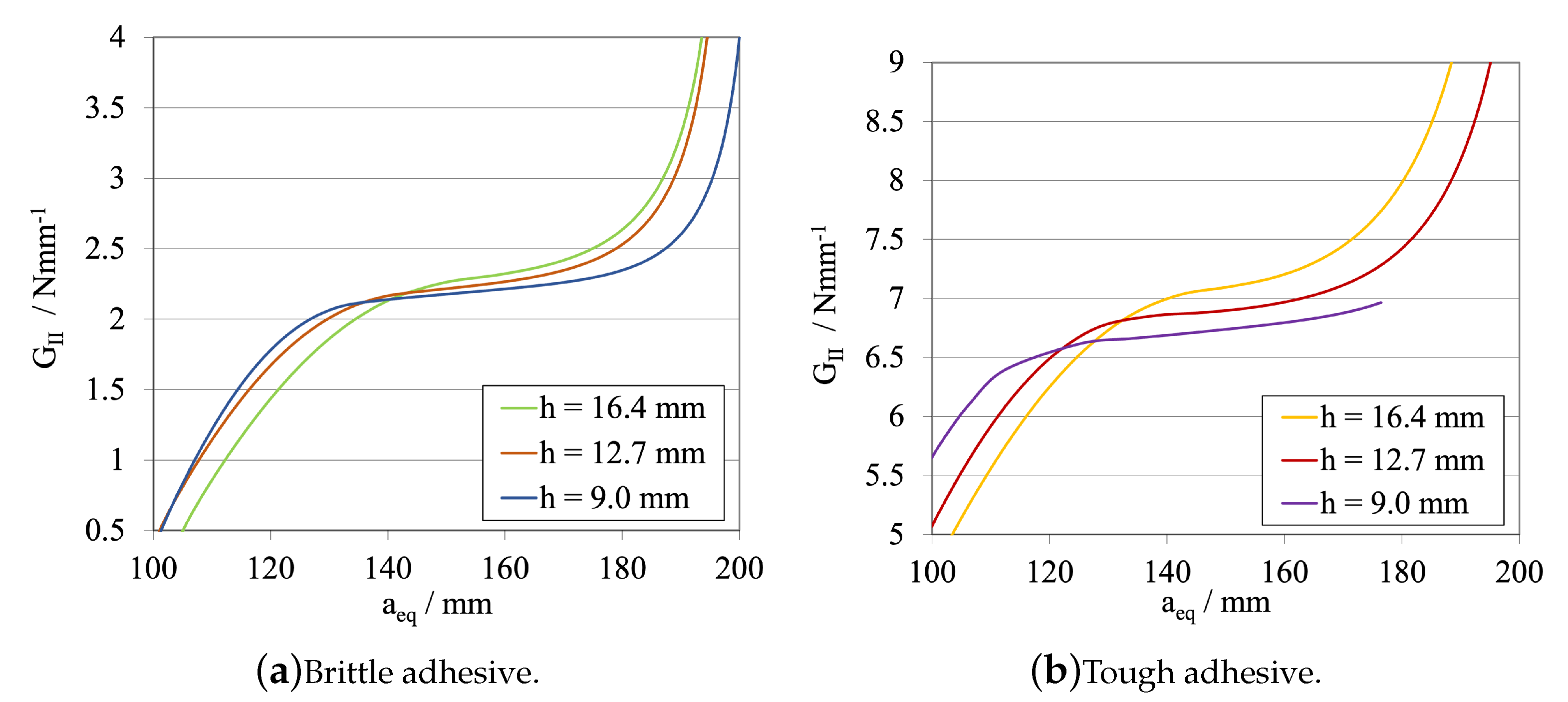
Substrate Height—
Mid Span Length—d
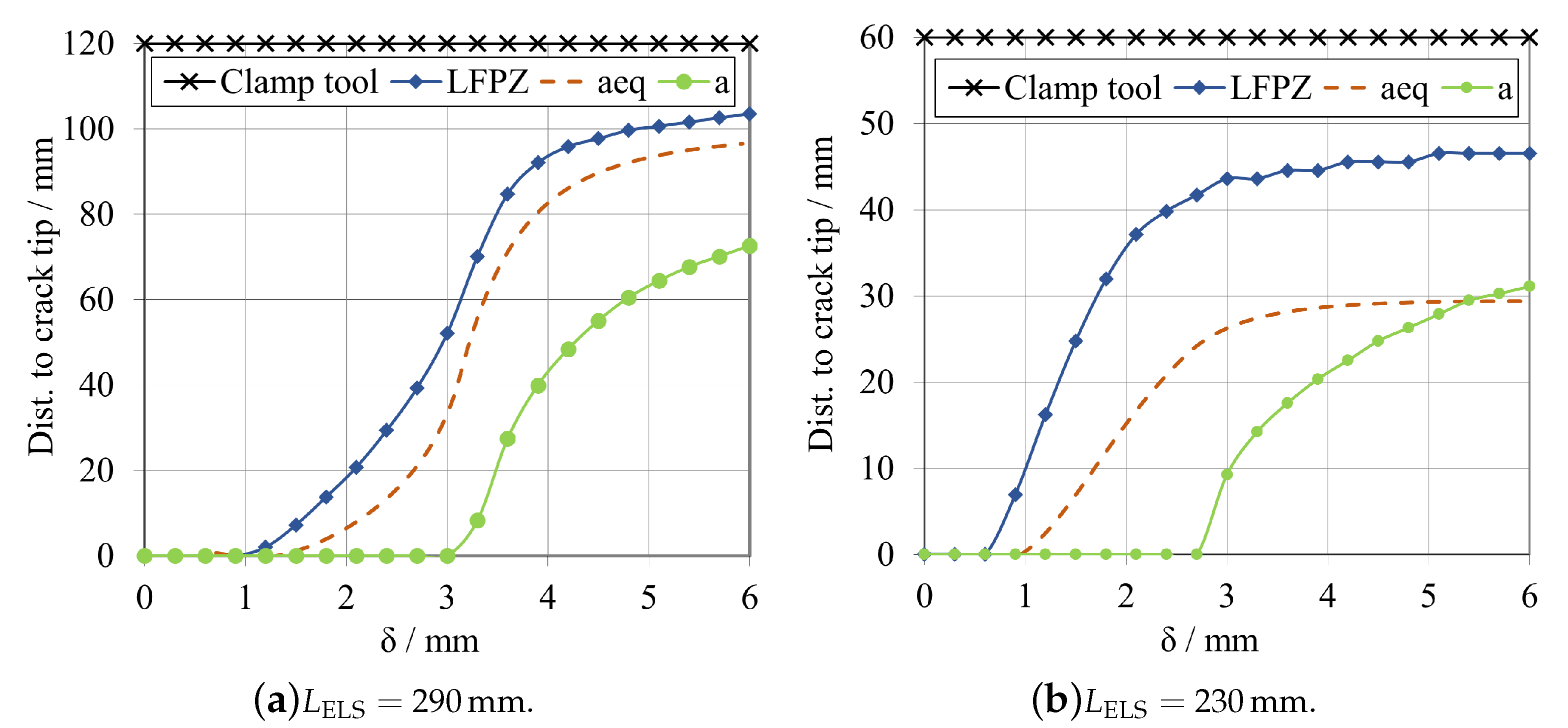
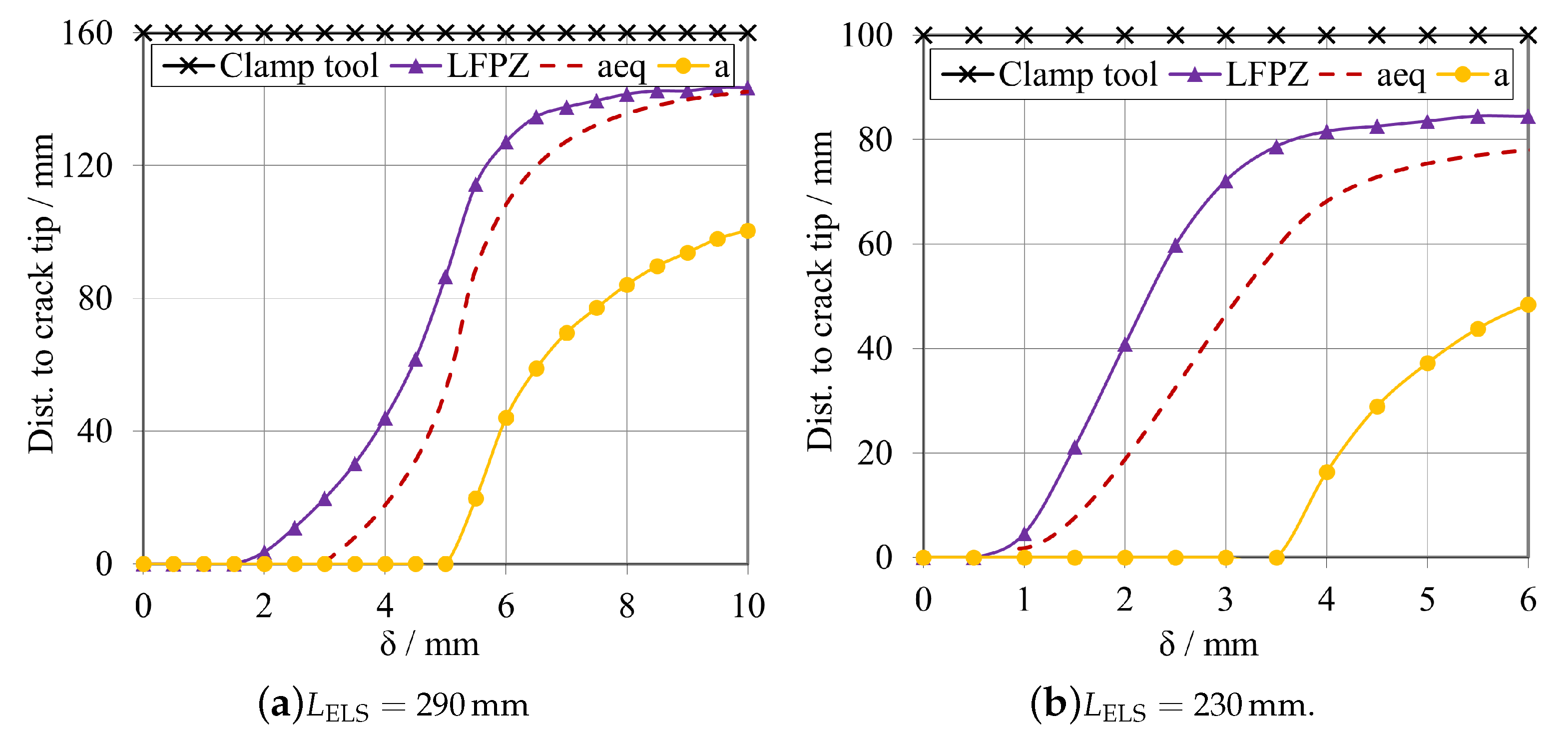
3.1.2. Fracture Process Zone (FPZ) Study
Brittle Adhesive
Tough Adhesive
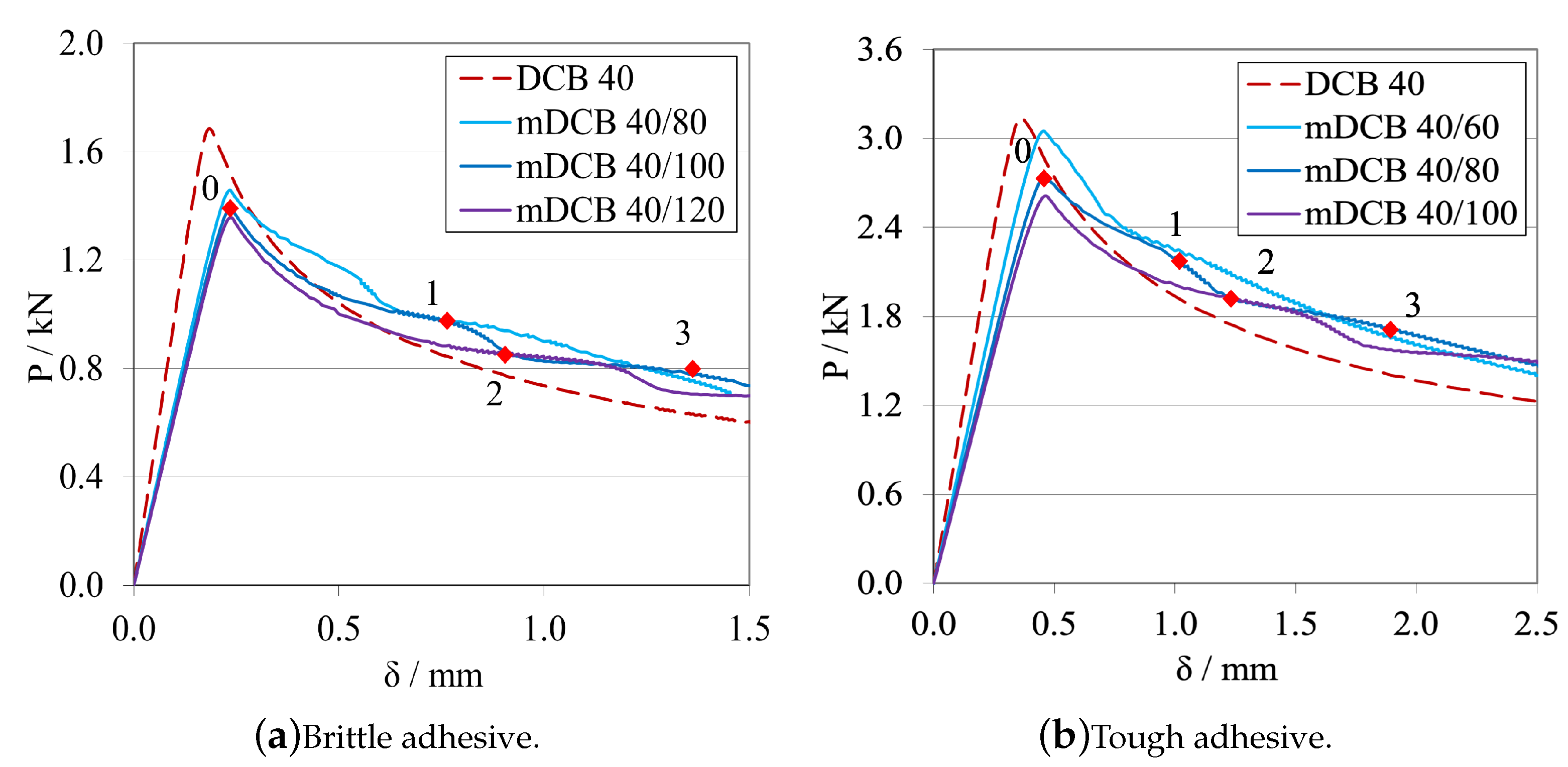
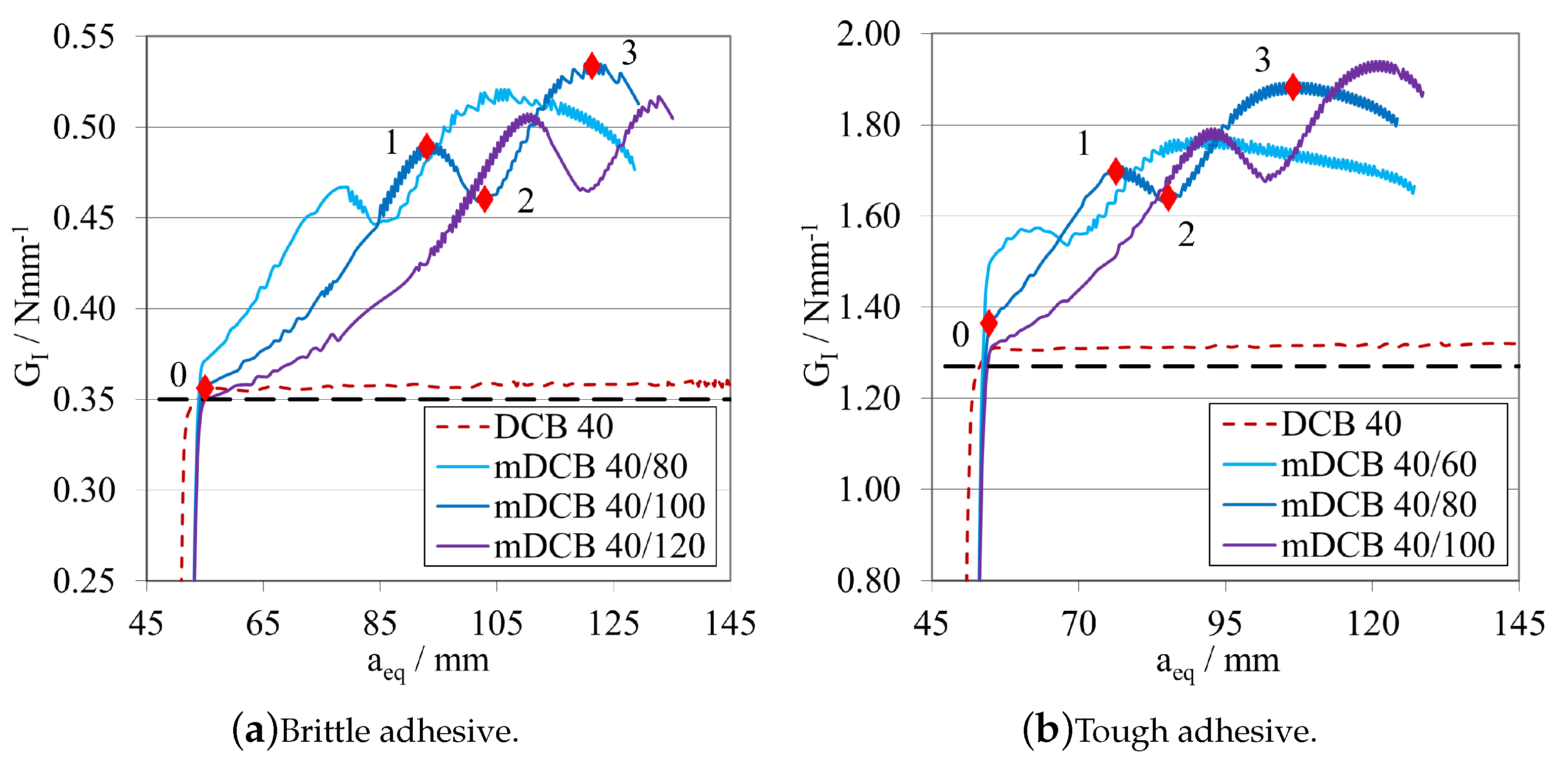
3.2. Modified Double Cantilever Beam (mDCB) Test Specimen
Parametric Study
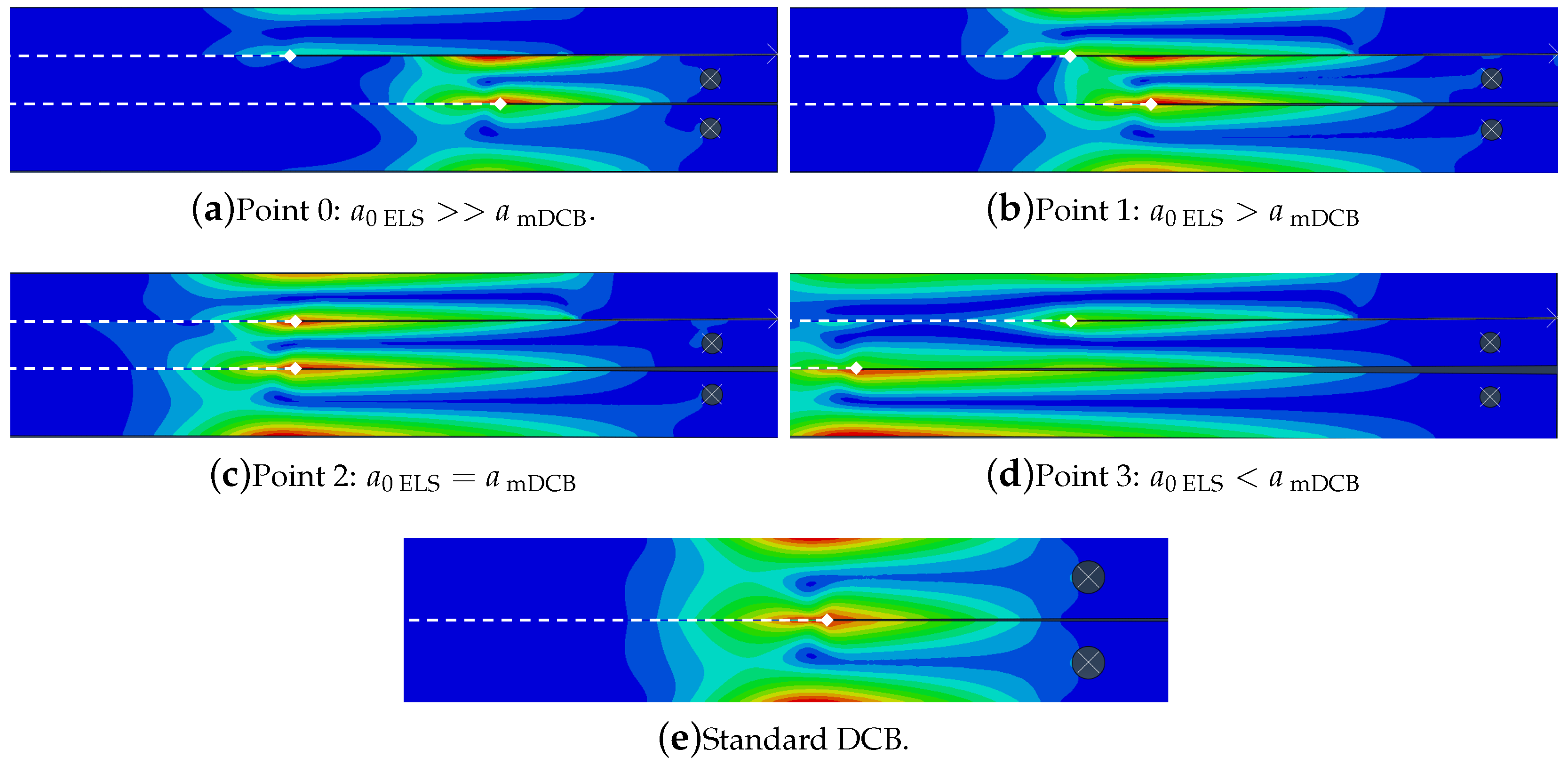
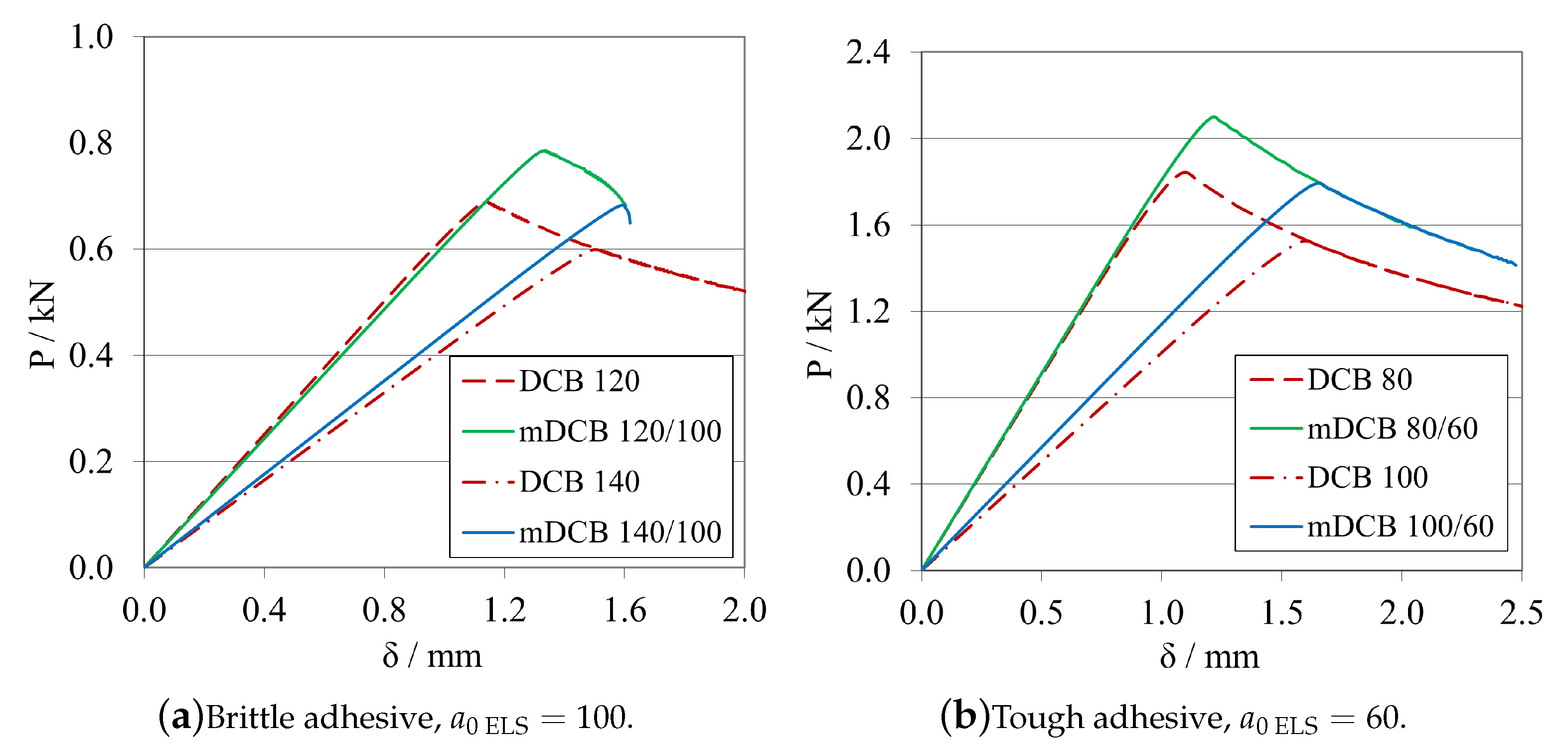
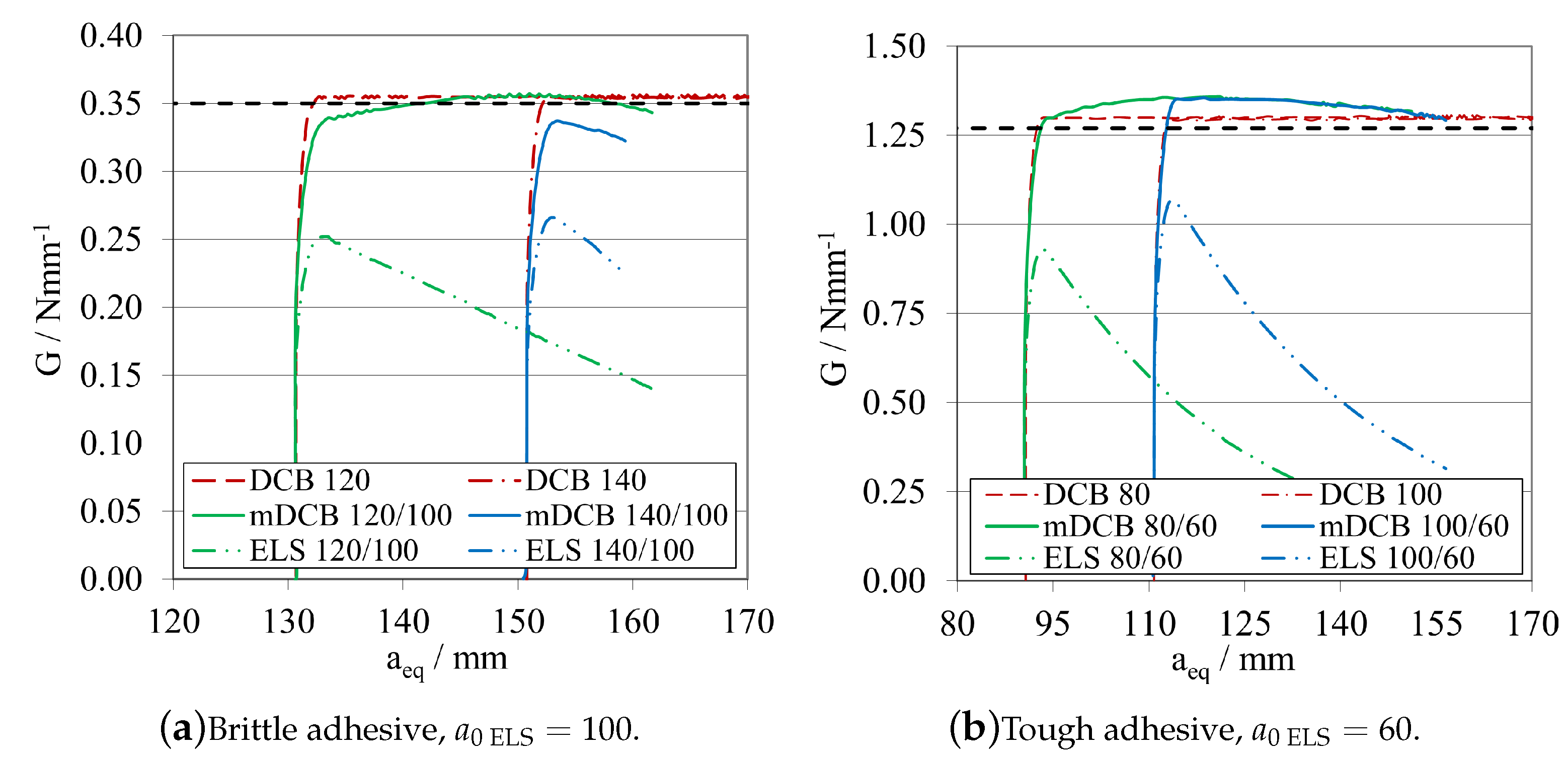
Initial Crack Length Study—
Initial Crack Length Study—
Final Crack Length Relation—
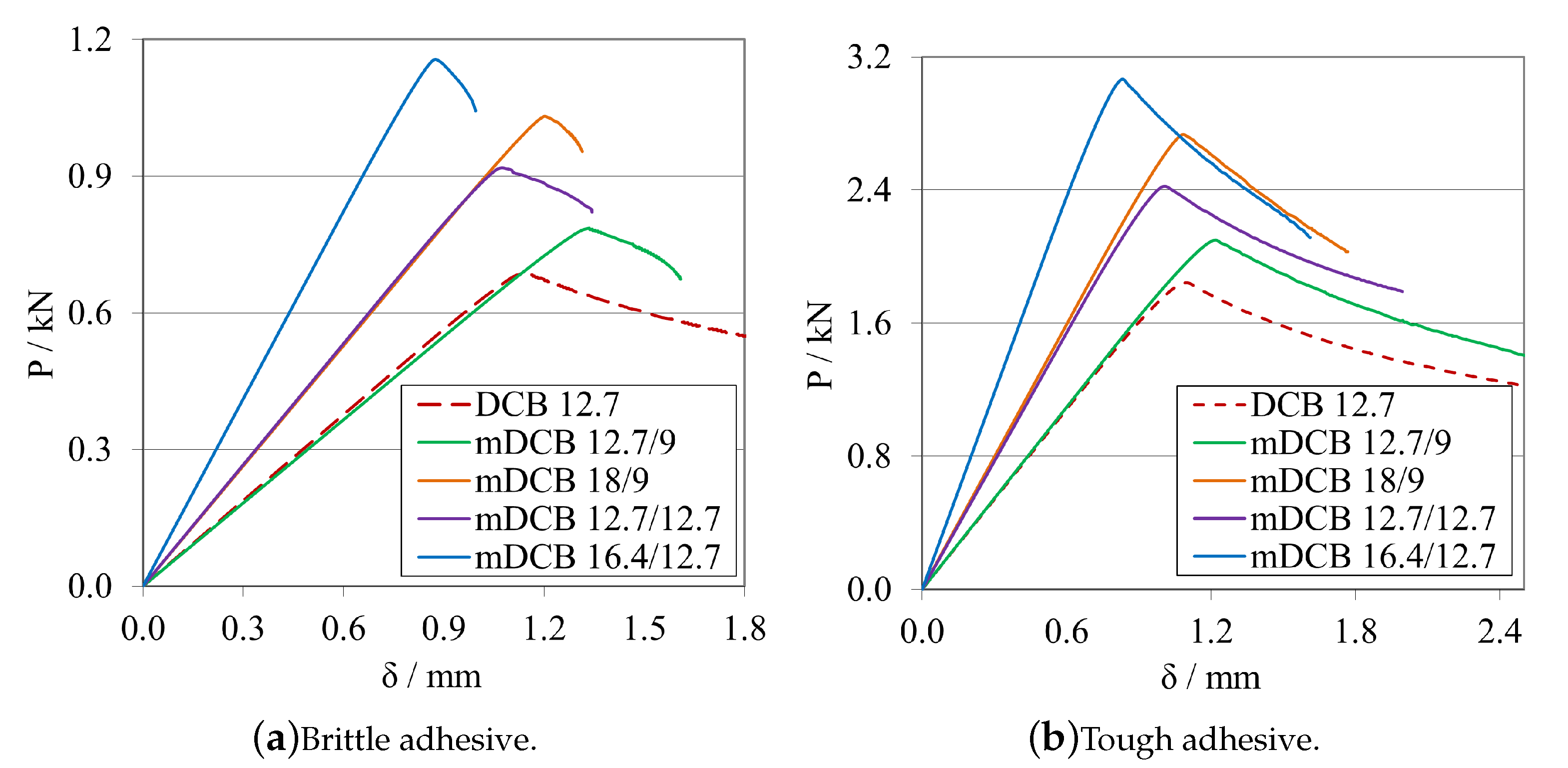
Substrate Height Study— and
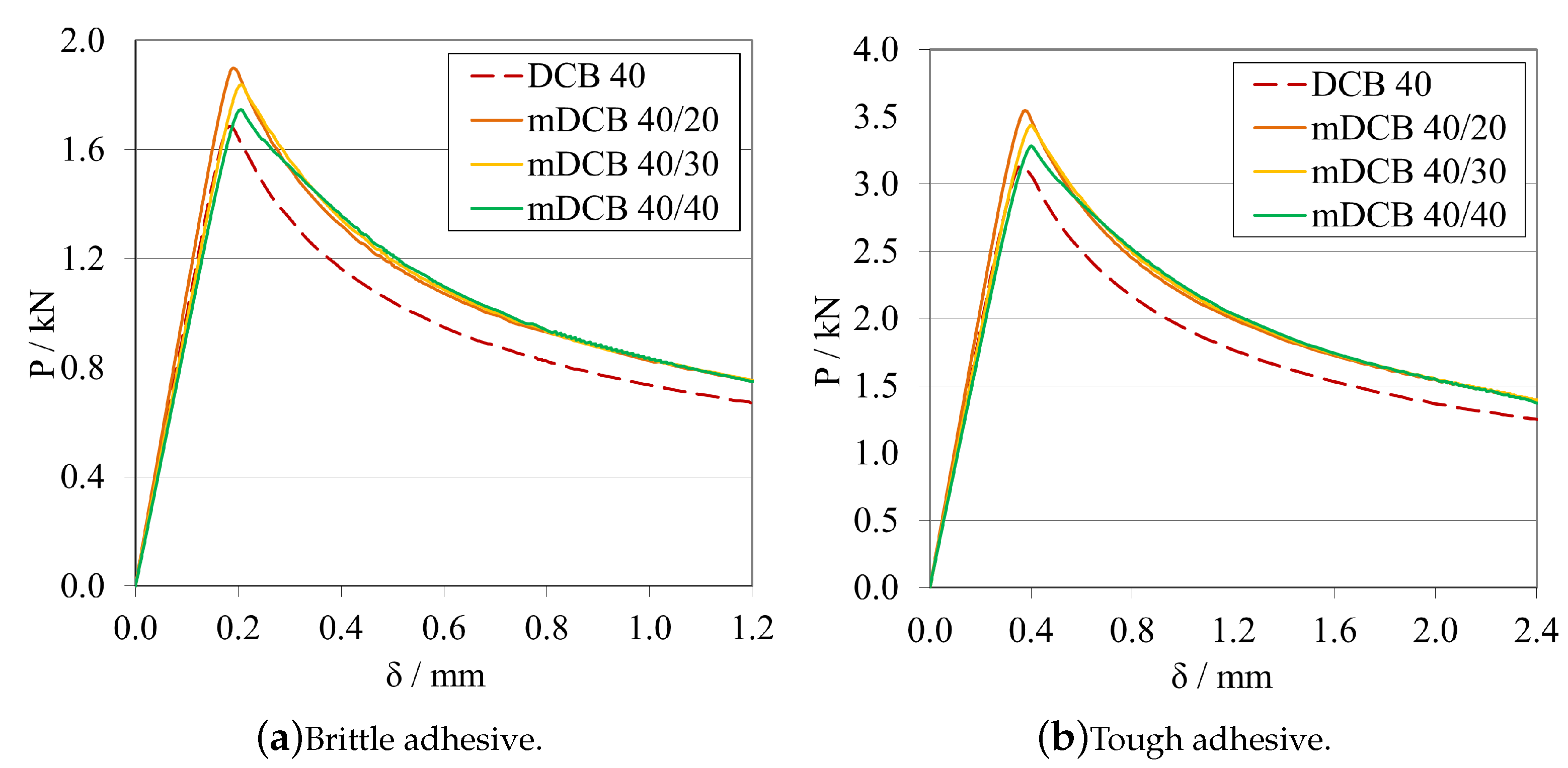
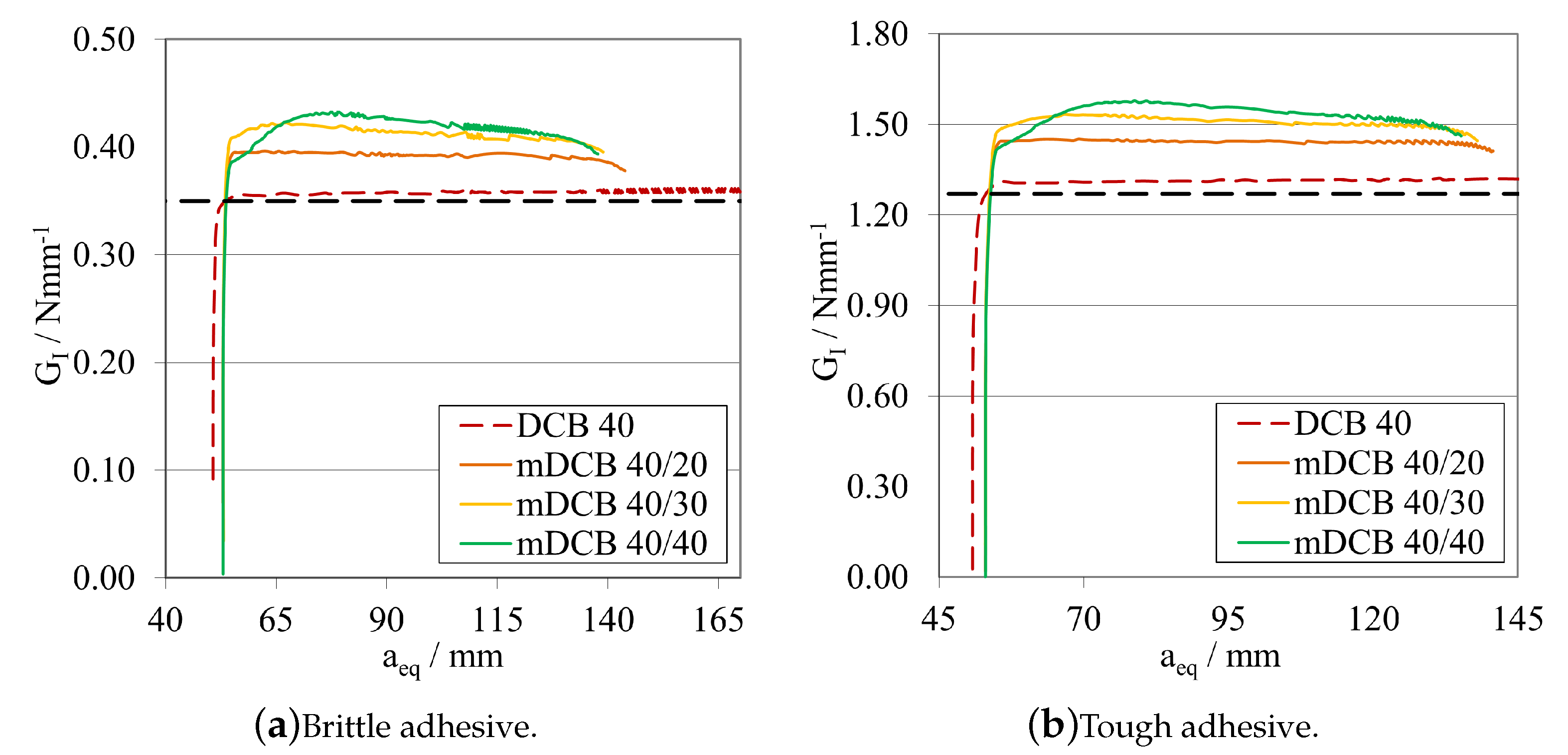
Validation for Flexible/Ductile Adhesives
4. Conclusions
- The mid span length, , is the most important parameter since it is related to a proper full development of the fracture process zone. This parameter should be large enough to prevent the FPZ reaching the vicinity of the clamping tool before its full development, as seen in Section 3.1.2. This can be tailored depending on the adhesive, higher values for more ductile adhesives, and vice versa for brittle adhesives.
- As a general rule, a sufficiently high —that is experimentally possible—should be used to allow a more stable crack propagation for a wide range of adhesives. As can be observed in Figure 10 and Figure 11, for lower values of , an unstable crack propagation occurs for both adhesives, and no plateau region can be achieved in the R-curves.
- The height of the specimen interacts directly with both propagation stability (better for lower values) and substrate plasticity phenomenon (better for higher values), demonstrating opposite effects. The maximum load, for both adhesives, more than doubled when the height changed from 9 mm to 16.4 mm, while there was also a significant increase in the stiffness value. As such, a compromise between both phenomena should be chosen.
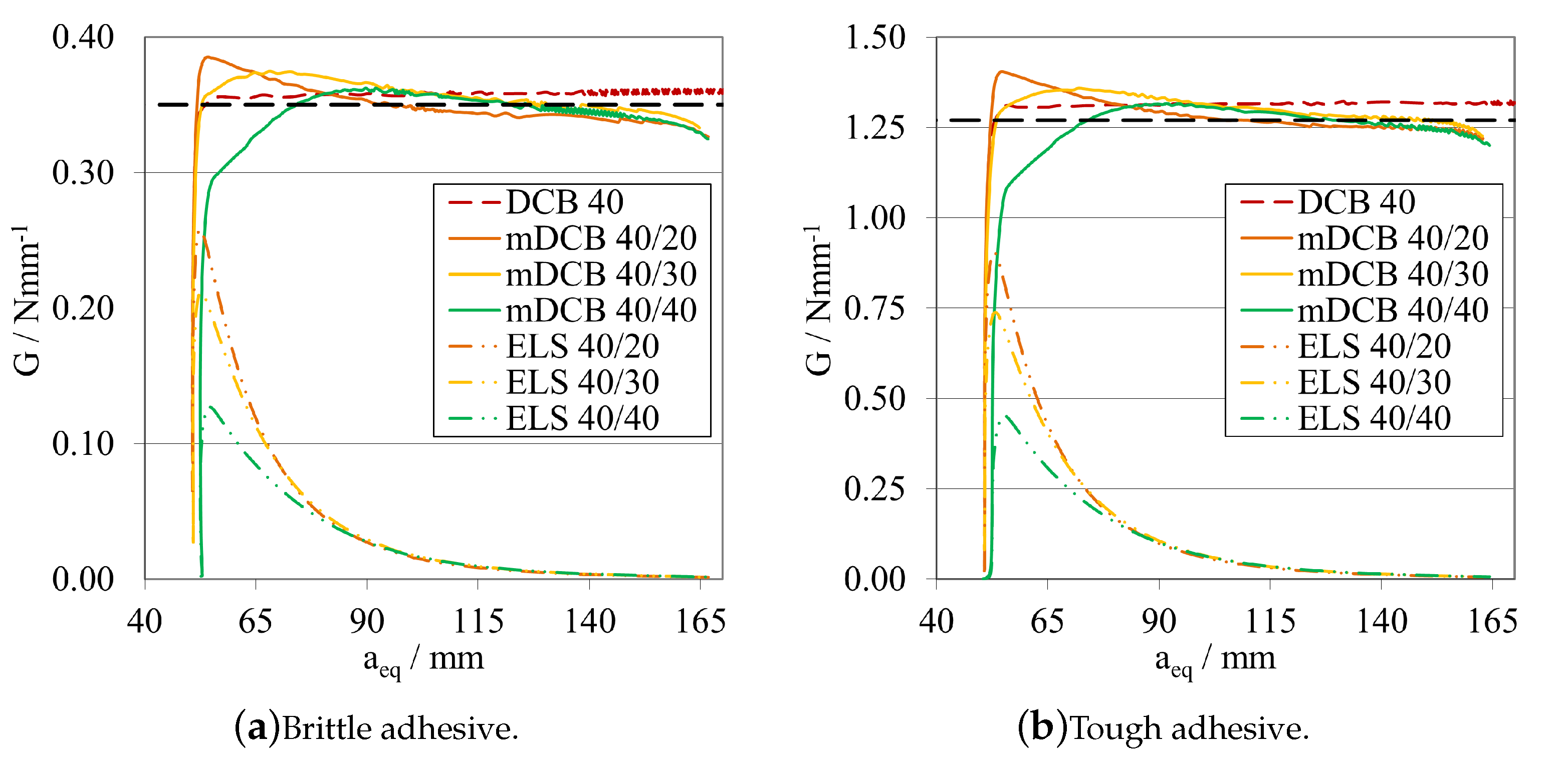
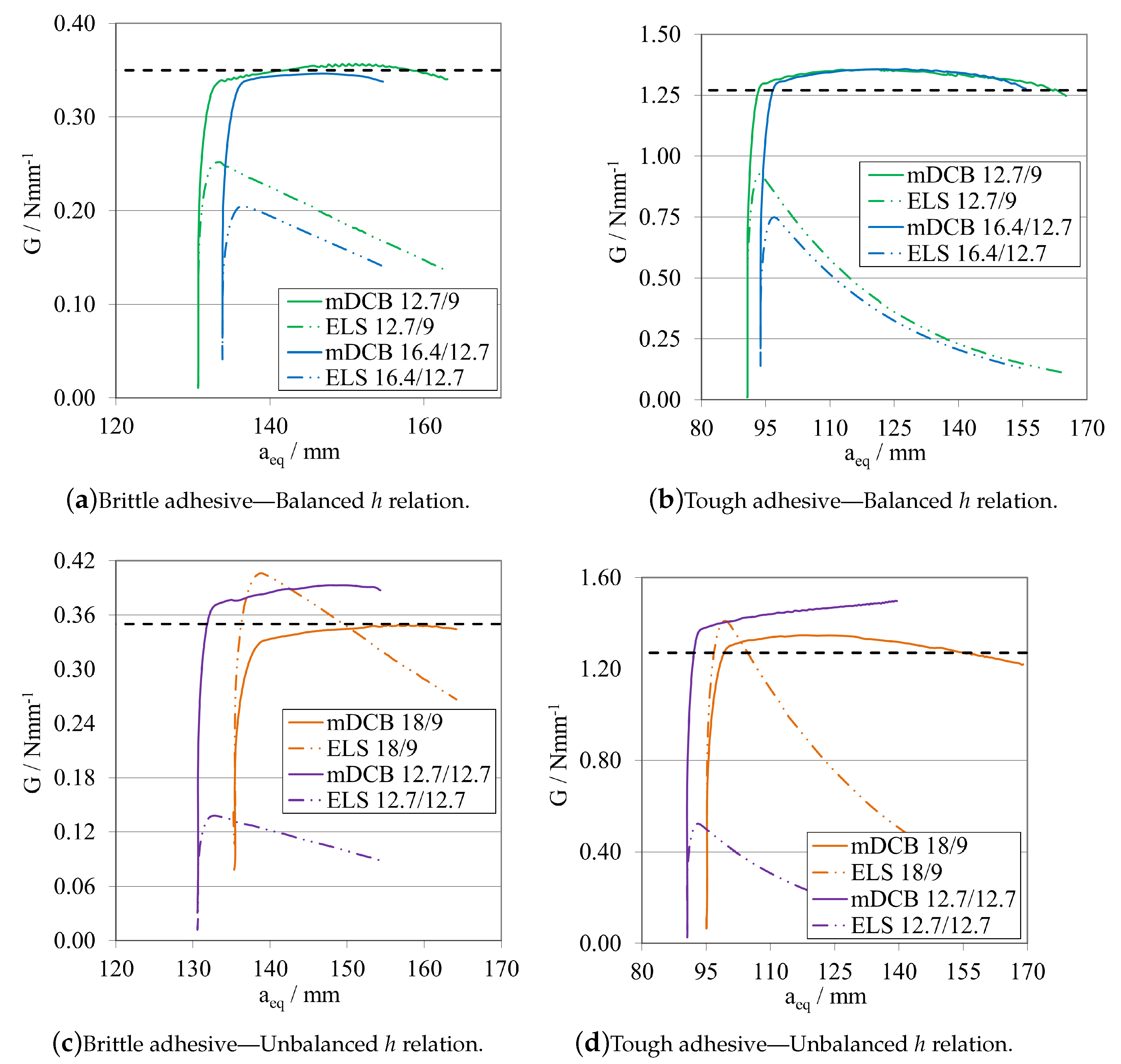
- The modified DCB test must have a relation of crack lengths where is smaller than , recommending a minimum relative distance of 20 , to prevent all the phenomena presented in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. This is done to isolate the mDCB crack tip and reduce interference of the stress concentration associated with the ELS specimen’s crack tip on the mode I test—Figure 20.
- When considering the height of the substrates, a balanced configuration () should be preferred, as the characterisation procedure presented better results for these configurations—Figure 27.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- da Silva, L.F.M.; Öchsner, A.; Adams, R.D. Handbook of Adhesion Technology; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- da Silva, L.F.M.; Dillard, D.A.; Blackman, B.R.K.; Adams, R.D. Testing Adhesive Joints: Best Practices; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cognard, J.Y.; Créac’Hcadec, R. Analysis of the non-linear behavior of an adhesive in bonded assemblies under shear loadings. Proposal of an improved TAST. J. Adhes. Sci. Technol. 2009, 23, 1333–1355. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Hadavinia, H.; Kinloch, A.J.; Paraschi, M.; Williams, J.G. The calculation of adhesive fracture energies in mode I: Revisiting the tapered double cantilever beam (TDCB) test. Eng. Fract. Mech. 2003, 70, 233–248. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Kinloch, A.J.; Paraschi, M.; Teo, W. S Measuring the mode I adhesive fracture energy, GIC, of structural adhesive joints: The results of an international round-robin. Int. J. Adhes. Adhes. 2003, 23, 293–305. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; Campilho, R.D.S.G.; Gonçalves, J.P. M Crack equivalent concept applied to the fracture characterization of bonded joints under pure mode I loading. Compos. Sci. Technol. 2008, 68, 2224–2230. [Google Scholar] [CrossRef]
- Moore, D.R.; Pavan, A.; Williams, J.G. Fracture Mechanics Testing Methods for Polymers Adhesives and Composites; ESIS Publication 28; ESIS: Philadelphia, PA, USA, 2006. [Google Scholar]
- Chaves, F.J.P.; da Silva, L.F.M.; de Moura, M.F.S.F.; Dillard, D.A.; Esteves, V.H.C. Fracture Mechanics Tests in Adhesively Bonded Joints: A Literature Review. J. Adhes. 2014, 90, 955–992. [Google Scholar] [CrossRef]
- Pérez-Galmés, M.; Renart, J.; Sarrado, C.; Rodríguez-Bellido, A.; Costa, J. A data reduction method based on the J-integral to obtain the interlaminar fracture toughness in a mode II end-loaded split (ELS) test. Compos. Part A Appl. Sci. Manuf. 2016, 90, 670–677. [Google Scholar] [CrossRef]
- Silva, M.A.L.; Morais, J.J.L.; de Moura, M.F.S.F.; Lousada, J.L. Mode II wood fracture characterization using the ELS test. Eng. Fract. Mech. 2007, 74, 2133–2147. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; de Morais, A.B. Equivalent crack-based analyses of ENF and ELS tests. Eng. Fract. Mech. 2008, 75, 2584–2596. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Brunner, A.J.; Williams, J.G. Mode II fracture testing of composites: A new look at an old problem. Eng. Fract. Mech. 2006, 73, 2443–2455. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; Dourado, N.; Morais, J.J.L.; Pereira, F.A.M. Numerical analysis of the ENF and ELS tests applied to mode II fracture characterization of cortical bone tissue. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 149–158. [Google Scholar] [CrossRef]
- El Moustaphaoui, A.; Chouaf, A.; Kimakh, K. Experimental and numerical study of the delamination of Ceiba plywood under mode I, mode II and mixed-mode (I+ II) loading using the DCB, ELS and MMF tests. Int. J. Fract. 2021, 231, 1–20. [Google Scholar] [CrossRef]
- Blackman, B.R.K.; Kinloch, A.J.; Paraschi, M. The determination of the mode II adhesive fracture resistance, GIIC, of structural adhesive joints: An effective crack length approach. Eng. Fract. Mech. 2005, 72, 877–897. [Google Scholar] [CrossRef]
- Budzik, M.K.; Jumel, J. Inverse End Loaded Split test configuration for stable mode II crack propagation in bonded joint: Macroscopic analysis—Effective crack length approach. Int. J. Fract. 2017, 207, 27–39. [Google Scholar] [CrossRef]
- Wang, H.; Vu-Khanh, T.; Le, V.N. Effects of large deflection on mode II fracture test of composite materials. J. Compos. Mater. 1995, 29, 833–849. [Google Scholar] [CrossRef]
- Wang, H.; Vu-Khanh, T. Use of end-loaded-split (ELS) test to study stable fracture behaviour of composites under mode II loading. Compos. Struct. 1996, 36, 71–79. [Google Scholar] [CrossRef]
- Davies, P.; Blackman, B.R.K.; Brunner, A.J. Standard test methods for delamination resistance of composite materials: Current status. Appl. Compos. Mater. 1998, 5, 345–364. [Google Scholar] [CrossRef]
- de Morais, A.B.; de Moura, M.F.S.F. Evaluation of initiation criteria used in interlaminar fracture tests. Eng. Fract. Mech. 2006, 73, 2264–2276. [Google Scholar] [CrossRef]
- Pérez-Galmés, M.; Renart, J.; Sarrado, C.; Costa, J. Suitable specimen dimensions for the determination of mode II fracture toughness of bonded joints by means of the ELS test. Eng. Fract. Mech. 2018, 202, 350–362. [Google Scholar] [CrossRef]
- Toolabi, M.; Blackman, B.R.K. Guidelines for selecting the dimensions of adhesively bonded en-loaded split joints: An approach based on numerical cohesive zone length. Eng. Fract. Mech. 2018, 203, 250–265. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; Morais, J.J.L.; Dourado, N. A new data reduction scheme for mode I wood fracture characterization using the double cantilever beam test. Eng. Fract. Mech. 2008, 75, 3852–3865. [Google Scholar] [CrossRef]
- Williams, J.G. End corrections for orthotropic DCB specimens. Compos. Sci. Technol. 1989, 35, 367–376. [Google Scholar] [CrossRef]
- Wang, Y.; Williams, J.G. Corrections for mode II fracture toughness specimens of composites materials. Compos. Sci. Technol. 1992, 43, 251–256. [Google Scholar] [CrossRef]
- Sun, F.; Blackman, B.R.K. Using digital image correlation to automate the measurement of crack length and fracture energy in the mode I testing of structural adhesive joints. Eng. Fract. Mech. 2021, 255, 107957. [Google Scholar] [CrossRef]
- Zugliani, P.A.; Banea, M.D.; Budhe, S.; Carbas, R.J.; da Silva, L.F.M.; Rohem, N.R.F.; de Barros, S. Bonded composite repair of metallic pipeline using energy release rate method. J. Adhes. Sci. Technol. 2019, 33, 2141–2156. [Google Scholar] [CrossRef]
- Chaves, F.J.P.; de Moura, M.F.S.F.; da Silva, L.F.M.; Dillard, D.A. Numerical validation of a crack equivalent method for mixed-mode I+II fracture characterization of bonded joints. Eng. Fract. Mech. 2013, 107, 38–47. [Google Scholar] [CrossRef]
- Cheperanov, G.P. Crack propagation in continuous media. USSR J. Appl. Math. Mech. Transl. 1967, 31, 504. [Google Scholar]
- Rice, J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Bucci, R.J.; Landes, J.D.; Paris, P.C.; Rice, J.R. Integral Estimation Procedures; ASTM International: Hershey, PA, USA, 1972. [Google Scholar]
- Sadeghi, M.Z.; Zimmermann, J.; Gabener, A.; Schroeder, K.U. The applicability of J-integral approach in the determination of mixed-mode fracture energy in a ductile adhesive. Int. J. Adhes. Adhes. 2018, 83, 2–8. [Google Scholar] [CrossRef]
- Jia, Z.; Yuan, G.; Hui, D.; Feng, X.; Zou, Y. Effect of high strain rate and low temperature on mode II fracture toughness of ductile adhesive. Int. J. Adhes. Adhes. 2018, 86, 105–112. [Google Scholar]
- Cui, H. Simulation of ductile adhesive failure with experimentally determined cohesive law. Compos. Part B Eng. 2016, 92, 193–201. [Google Scholar]
- Goutianos, S.; Sørensen, B.F. The application of J integral to measure cohesive laws under large-scale yielding. Eng. Fract. Mech. 2016, 155, 145–165. [Google Scholar] [CrossRef]
- Sun, F.; Blackman, B.R.K. A DIC method to determine the Mode I energy release rate G, the J-integral and the traction-separation law simultaneously for adhesive joints. Eng. Fract. Mech. 2020, 234, 107097. [Google Scholar] [CrossRef]
- Yu, J.; Wang, Y.; Li, Z.; Zhang, Q.; Jian, X.; Zhang, Z. Using DIC technique to characterize the mode II interface fracture of layered system composed of multiple materials. Compos. Struct. 2019, 230, 111413. [Google Scholar] [CrossRef]
- Monsef, S.A.; Pérez-Galmés, M.; Renart, J.; Turon, A.; Maimí, P. The influence of mode II test configuration on the cohesive law of bonded joints. Compos. Struct. 2020, 234, 111689. [Google Scholar] [CrossRef]
- Lélias, G.; Paroissien, E.; Lachaud, F.; Morlier, J. Experimental characterization of cohesive zone models for thin adhesive layers loaded in mode I, mode II, and mixed-mode I/II by the use of a direct method. Int. J. Solids Struct. 2019, 158, 90–115. [Google Scholar] [CrossRef]
- Sørensen, B.F.; Kirkegaard, P. Determination of mixed mode cohesive laws. Eng. Fract. Mech. 2006, 73, 2642–2661. [Google Scholar] [CrossRef]
- Loh, L.; Marzi, S. A novel experimental methodology to identify fracture envelopes and cohesive laws in mixed-mode I+ III. Eng. Fract. Mech. 2019, 214, 304–319. [Google Scholar] [CrossRef]
- Faria, A.R.A.C.; Correia, D.S.; Marques, E.A.S.; Carbas, R.J.C.; da Silva, L.F.M. Novel mechanical characterization method applied to non-structural adhesives: Adherend material sensitivity. Univ. Porto—J. Mech. Solids 2022, 1, 25–30. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Riccio, A.; Saputo, S.; Raimondo, A.; Sellitto, A. Modeling low velocity impact phenomena on composite structures. In Dynamic Response and Failure of Composite Materials and Structures; Elsevier: Amsterdam, The Netherlands, 2017; pp. 129–158. [Google Scholar]
- da Silva, L.F.M.; da Silva, R.A.M.; Chousal, J.A.G.; Pinto, A.M.G. Alternative Methods to Measure the Adhesive Shear Displacement in the Thick Adherend Shear Test. J. Adhes. Sci. Technol. 2008, 22, 15–29. [Google Scholar] [CrossRef]
- Correia, D.S.; Carbas, R.J.C.; Marques, E.A.S.; das Neves, P.J.C.; da Silva, L.F.M. Experimental study on aluminium to tungsten carbide/polycrystalline diamond (WC/PCD) adhesive bonding for milling tools. Int. J. Adhes. Adhes. 2022, 114, 103121. [Google Scholar] [CrossRef]
- Simulia. ABAQUS Version 6.6 Documentation; Simulia: Johnston, IA, USA, 2006. [Google Scholar]





| Property | Brittle Adhesive | Tough Adhesive | Steel |
|---|---|---|---|
| E / MPA | 4890 | 3880 | 210,000 |
| / − | − | − | 0.3 |
| G / MPA | 1560 1 | 1447 | − |
| / MPA | 41.0 1 | 65.6 | − |
| / MPA | 30.2 1 | 41.6 | − |
| / | 0.35 2 | 1.27 | − |
| / | 2.40 2 | 7.22 | − |
| Boundary Conditions | Mode I Test | Mode II Test |
|---|---|---|
| {0, 0, -} | Deactivated | |
| {0, , -} | {0, , -} | |
| {-, -, 0} | {-, 0, 0} | |
| Interactions | Mode I Test | Mode II Test |
| Surf. to surf. contact | Surf. to surf. contact |
| b | t | ||||
|---|---|---|---|---|---|
| 290 | 40 | 25 | 70 |
| 290 | 190 | 40 | 40 | 9 |
| 290 | 40 |
| b | t | |||||||
|---|---|---|---|---|---|---|---|---|
| 290 | 190 | 100 / 60 | 120 / 80 | 9 | 70 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correia, D.S.; Costa, I.D.; Simões, B.D.; Marques, E.A.S.; Carbas, R.J.C.; da Silva, L.F.M. Development of a Unified Specimen for Adhesive Characterisation—Part 1: Numerical Study on the Mode I (mDCB) and II (ELS) Fracture Components. Materials 2023, 16, 2951. https://doi.org/10.3390/ma16082951
Correia DS, Costa ID, Simões BD, Marques EAS, Carbas RJC, da Silva LFM. Development of a Unified Specimen for Adhesive Characterisation—Part 1: Numerical Study on the Mode I (mDCB) and II (ELS) Fracture Components. Materials. 2023; 16(8):2951. https://doi.org/10.3390/ma16082951
Chicago/Turabian StyleCorreia, Daniel S., Inês D. Costa, Beatriz D. Simões, Eduardo A. S. Marques, Ricardo J. C. Carbas, and Lucas F. M. da Silva. 2023. "Development of a Unified Specimen for Adhesive Characterisation—Part 1: Numerical Study on the Mode I (mDCB) and II (ELS) Fracture Components" Materials 16, no. 8: 2951. https://doi.org/10.3390/ma16082951
APA StyleCorreia, D. S., Costa, I. D., Simões, B. D., Marques, E. A. S., Carbas, R. J. C., & da Silva, L. F. M. (2023). Development of a Unified Specimen for Adhesive Characterisation—Part 1: Numerical Study on the Mode I (mDCB) and II (ELS) Fracture Components. Materials, 16(8), 2951. https://doi.org/10.3390/ma16082951










