Adsorbent Material Based on Carbon Black and Bismuth with Tunable Properties for Gold Recovery
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials Synthesis and Characterization
- −
- scanning electron microscopy (SEM) using a Quanta FEG 250 microscope (FEI, Hilsboro, OR, USA), in order to get information regarding material surface morphology;
- −
- X-ray energy dispersive spectroscopy—in order to get material elemental composition;
- −
- material specific surface was determined by using Brunauer-Emmet–Teller (BET) method, with a Quantachrome Nova 1200 E system. All samples were degassed under vacuum, at room temperature for 24 h. Adsorption–desorption isotherms were recorded a 77 K under nitrogen atmosphere;
- −
- X-ray diffraction (XRD)—measurements were done using Ultima IV (RIGAKU, Tokyo, Japan) instrument operating with Cu K radiation;
- −
- thermal analysis was performed using a thermos-analyzer system Mettler TGA/SDTA 851/LF/1100. The sample with a mass of about 10 mg was placed in alumina crucibles of 150 μL. The experiments were performed under an air atmosphere with a heating rate of 10 °C/min;
- −
- Atomic force microscopy (AFM), was performed using scanning probe microscopy platform (MultiView-2000 system, Nanonics Imaging Ltd., Jerusalem, Israel).
2.2. Gold Recovery by Adsorption Processes
2.2.1. pH Effect
2.2.2. Contact Time and Temperature Effect
2.2.3. Initial Concentration Effect
2.3. Kinetic, Thermodynamic, and Equilibrium Parameters for Adsorption Process
2.3.1. Kinetic Study
2.3.2. Thermodynamic Studies
2.3.3. Activation Energy
2.3.4. Equilibrium Study: Isotherms Models
3. Results and Discussion
3.1. Material Characterization
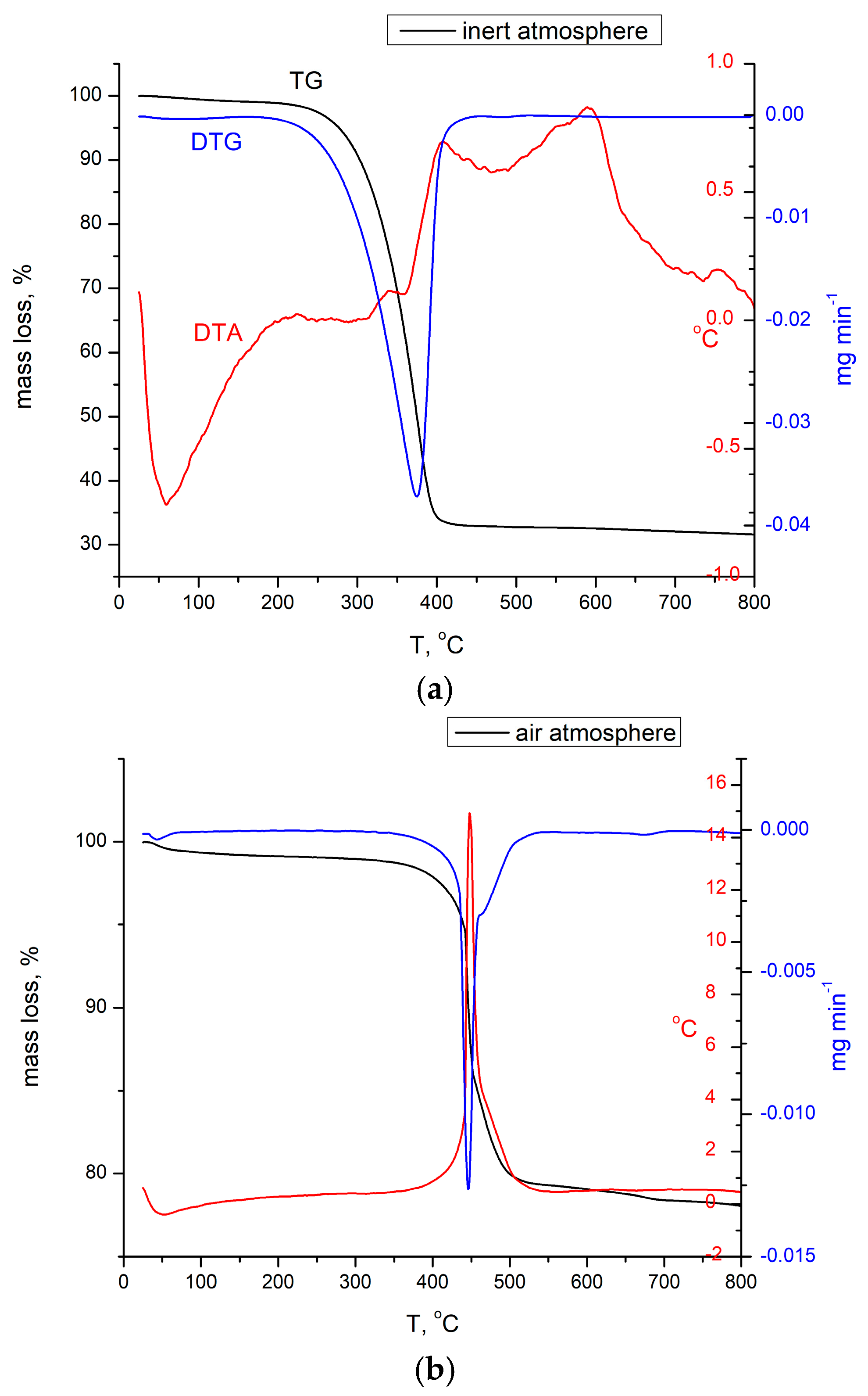
3.1.1. Thermogravimetric Analysis, TG
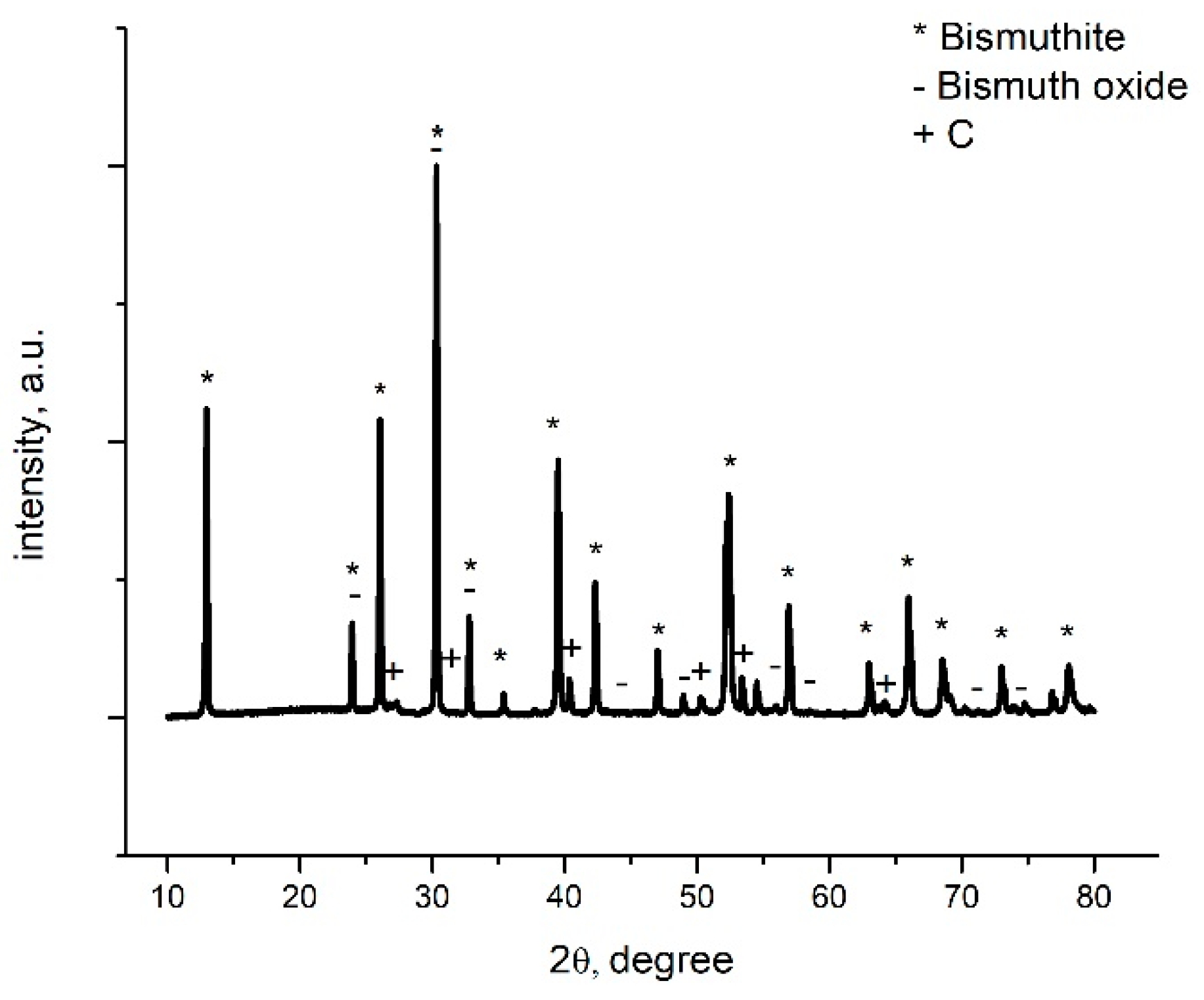
3.1.2. X-ray Diffraction (XRD)
3.1.3. Scanning Electron Microscopy (SEM)
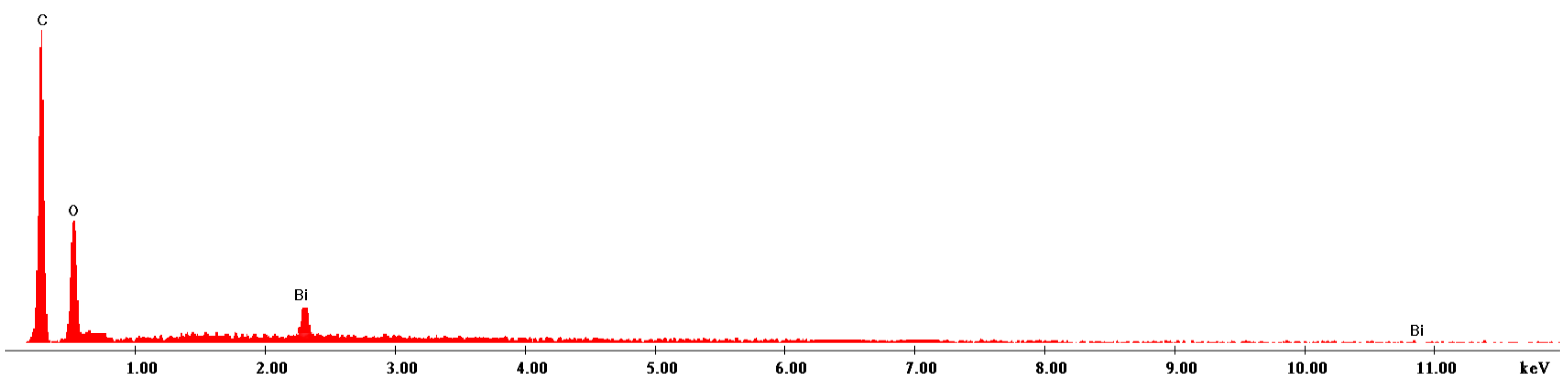
3.1.4. Energy Dispersive X-ray Spectroscopy, EDX
3.1.5. Brunauer–Emmet–Teller (BET) Specific Surface Determination
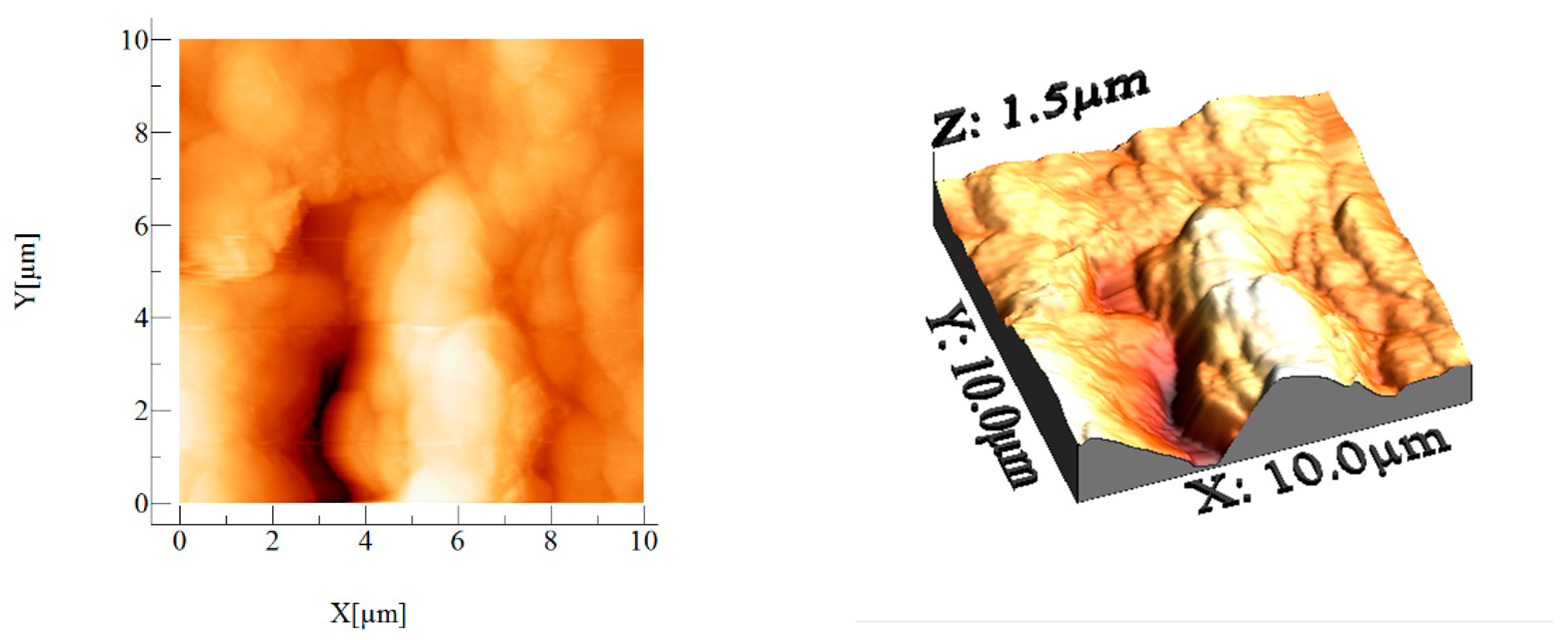
3.1.6. Atomic Force Microscopy, AFM
3.2. Gold Recovery by Adsorption Processes
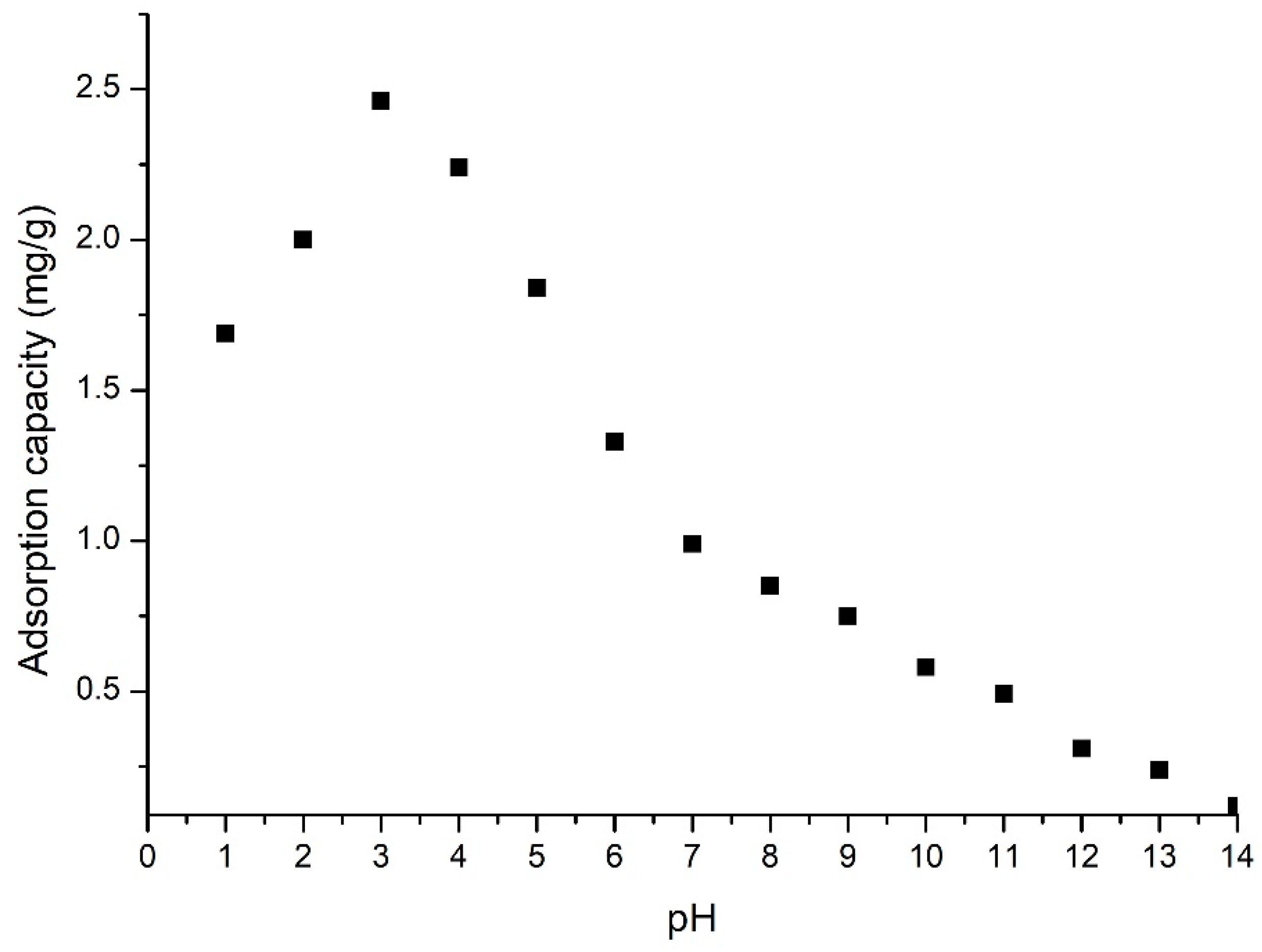
3.2.1. pH Effect
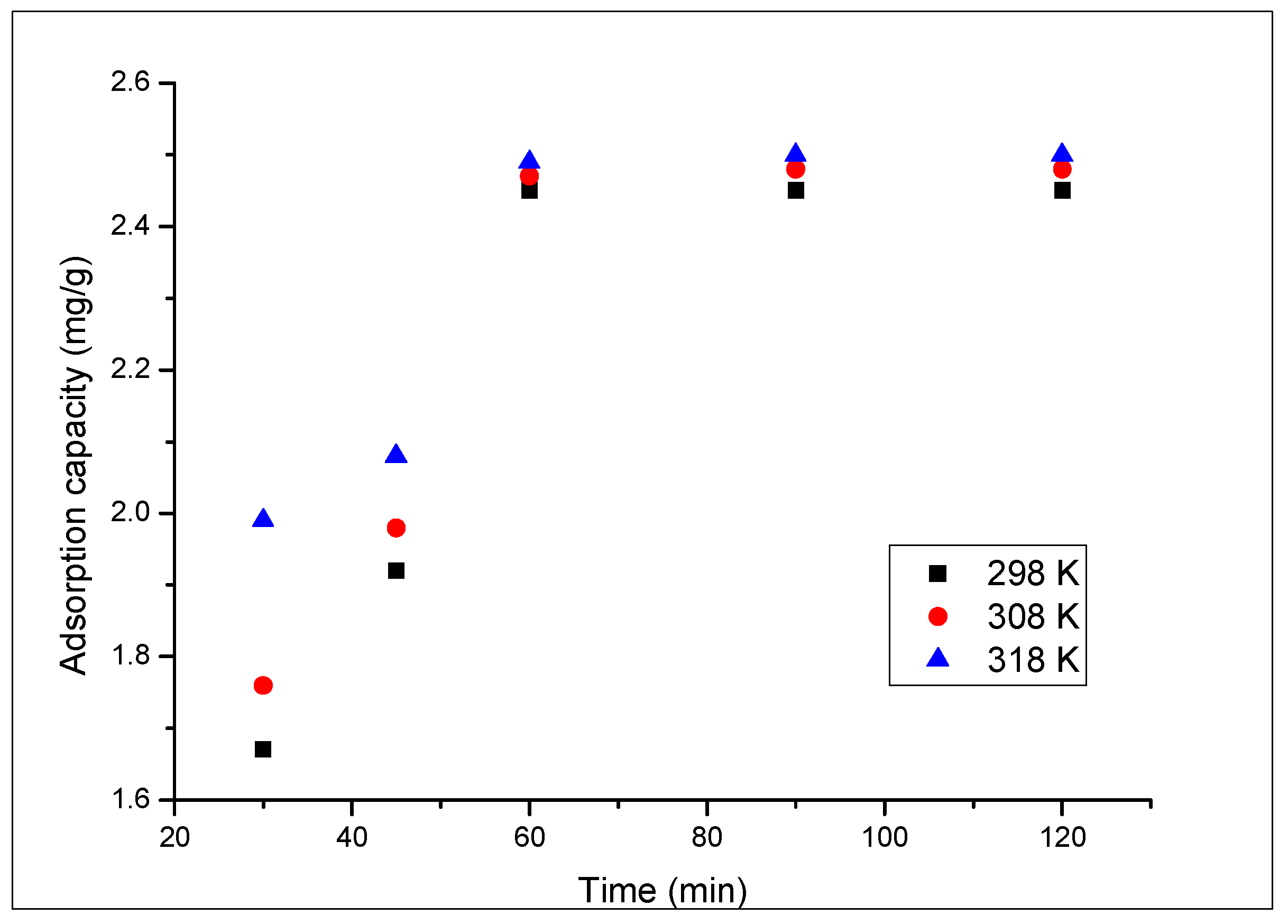
3.2.2. Contact Time and Temperature Effect
3.3. Kinetic, Thermodynamic, and Equilibrium Parameters for Adsorption Process
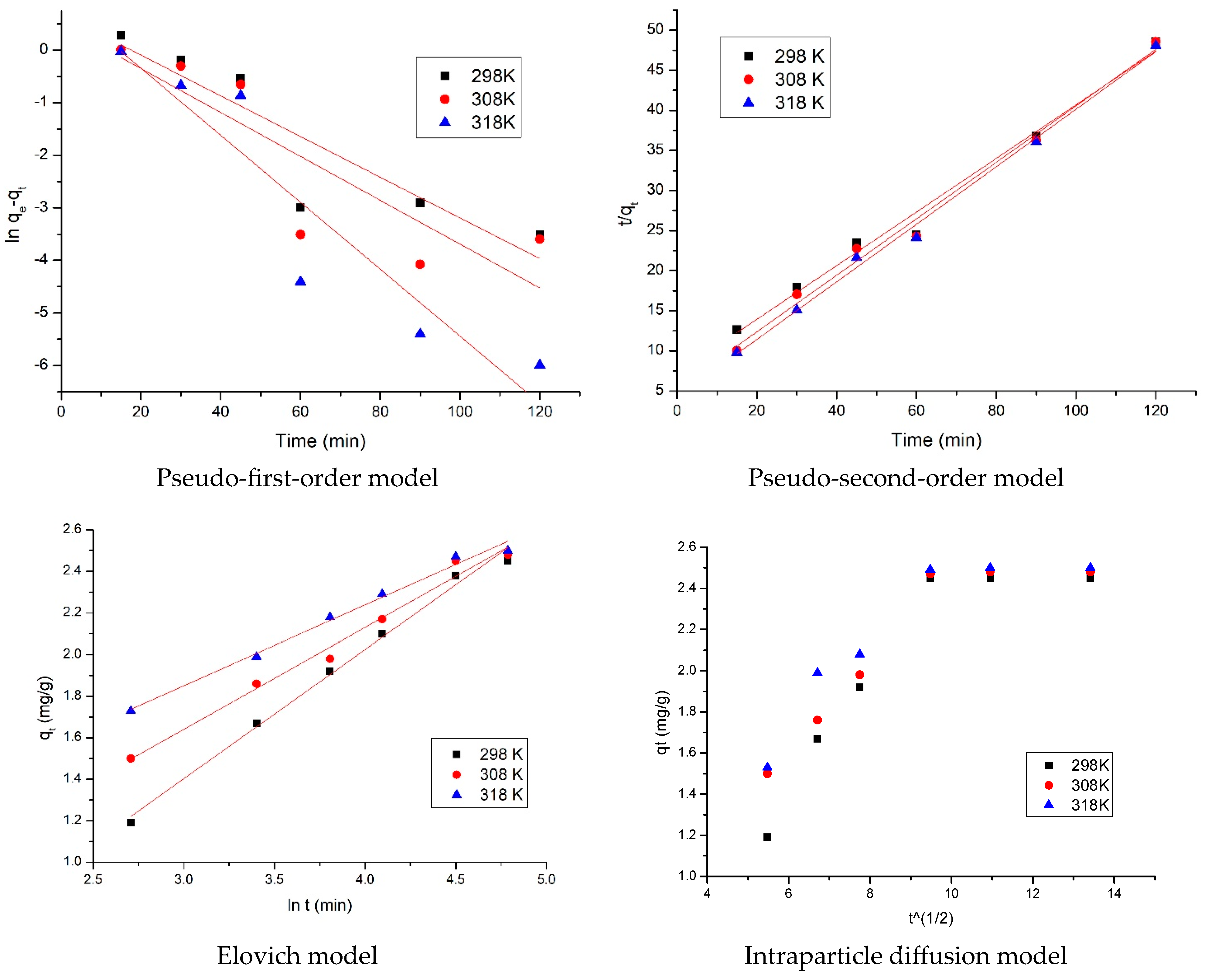
3.3.1. Kinetic Study
3.3.2. Thermodynamic Study
3.3.3. Activation Energy
3.3.4. Equilibrium Study: Adsorption Isotherms
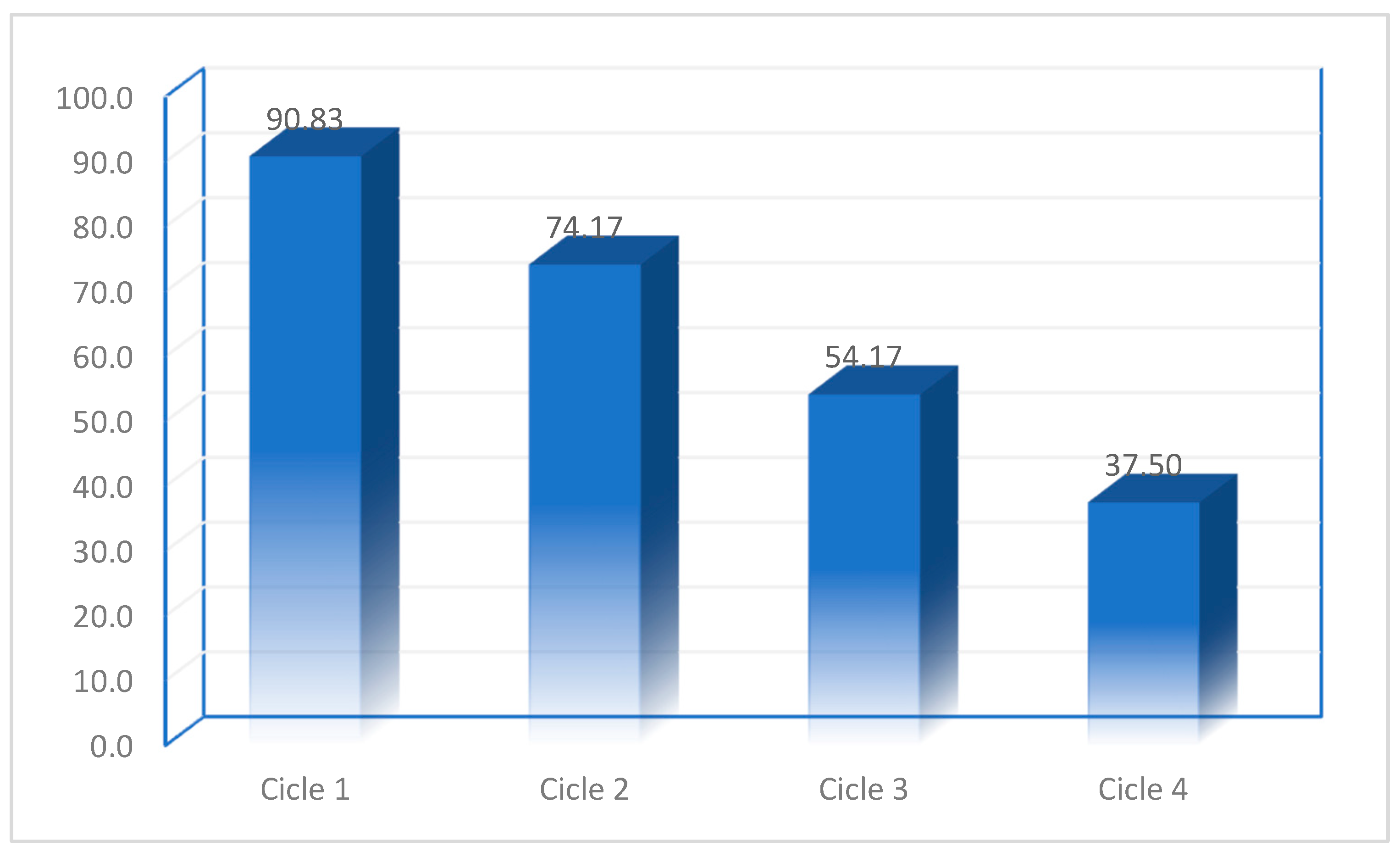
3.3.5. Regeneration Degree of Adsorbent
3.3.6. Material Usage in Case of Real Solution
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Negrea, A.; Ronka, S.; Ciopec, M.; Duteanu, N.; Negrea, P.; Mihailescu, M. Kinetics, Thermodynamics and Equilibrium Studies for Gold Recovery from Diluted Waste Solution. Materials 2021, 14, 5325. [Google Scholar] [CrossRef]
- Reith, F.; Rea, M.A.D.; Sawley, P.; Zammit, C.M.; Nolze, G.; Reith, T.; Rantanen, K.; Bissett, A. Biogeochemical cycling of gold: Transforming gold particles from arctic Finland. Chem. Geol. 2018, 483, 511–529. [Google Scholar] [CrossRef]
- Philips, G.N. Conglomerate-hosted gold deposits: What is so special? In Proceedings of the Gold18@Perth, An Australian Institute of Geoscientists symposium organised in conjunction with Geoscientists Symposia, Perth, WA, Australia, 2–3 August 2018.
- Saradesh, K.M.; Vinodkumar, G.S. Metallurgical processes for hardening of 22Karat Gold for light weight and high strength jewelry manufacturing. J. Mater. Res. Technol. 2020, 9, 2009–2020. [Google Scholar] [CrossRef]
- Corti, C.W. Metallurgy of Microalloyed 24 Carat Golds. Gold Bull. 1999, 32, 39–47. [Google Scholar] [CrossRef]
- Tamai, T.; Yamakawa, M. Contact Resistance Property of Gold Plated Contact Covered with Contact Lubricant Under High Temperature. IEICE Trans. Electron. 2017, E100.C, 702–708. [Google Scholar] [CrossRef]
- Côrtes, L.N.; Tanabe, E.H.; Bertuol, D.A.; Dotto, G.L. Biosorption of gold from computer microprocessor leachate solutions using chitin. Waste Manag. 2015, 45, 272–279. [Google Scholar] [CrossRef]
- Wang, R.; Xu, Z. Recycling of non-metallic fractions from waste electrical and electronic equipment (WEEE): A review. Waste Manag. 2014, 34, 1455–1469. [Google Scholar] [CrossRef]
- Wong, M.H.; Wu, S.C.; Deng, W.J.; Yu, X.Z.; Luo, Q.; Leung, A.O.W.; Wong, C.S.C.; Luksemburg, W.J.; Wong, A.S. Export of toxic chemicals—A review of the case of uncontrolled electronic-waste recycling. Environ. Pollut. 2007, 149, 131–140. [Google Scholar] [CrossRef]
- Syed, S. A green technology for recovery of gold from non-metallic secondary sources. Hydrometallurgy 2006, 82, 48–53. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, S.; Liu, B.; Zheng, H.; Chang, C.-C.; Ekberg, C. Recovery of precious metals from electronic waste and spent catalysts: A review. Resour. Conserv. Recycl. 2019, 141, 284–298. [Google Scholar] [CrossRef]
- Hoffmann, J.E. Recovering precious metals from electronic scrap. Jom 1992, 44, 43–48. [Google Scholar] [CrossRef]
- Lee, J.-C.; Song, H.T.; Yoo, J.-M. Present status of the recycling of waste electrical and electronic equipment in Korea. Resour. Conserv. Recycl. 2007, 50, 380–397. [Google Scholar] [CrossRef]
- Sum, E.Y.L. The recovery of metals from electronic scrap. Jom 1991, 43, 53–61. [Google Scholar] [CrossRef]
- Ghosh, B.; Ghosh, M.K.; Parhi, P.; Mukherjee, P.S.; Mishra, B.K. Waste Printed Circuit Boards recycling: An extensive assessment of current status. J. Clean. Prod. 2015, 94, 5–19. [Google Scholar] [CrossRef]
- Morin, D.; Lips, A.; Pinches, T.; Huisman, J.; Frias, C.; Norberg, A.; Forssberg, E. BioMinE—Integrated project for the development of biotechnology for metal-bearing materials in Europe. Hydrometallurgy 2006, 83, 69–76. [Google Scholar] [CrossRef]
- Andrews, D.; Raychaudhuri, A.; Frias, C. Environmentally sound technologies for recycling secondary lead. J. Power Sources 2000, 88, 124–129. [Google Scholar] [CrossRef]
- Chmielewski, A.G.; Urbański, T.S.; Migdał, W. Separation technologies for metals recovery from industrial wastes. Hydrometallurgy 1997, 45, 333–344. [Google Scholar] [CrossRef]
- Quinet, P.; Proost, J.; Van Lierde, A. Recovery of precious metals from electronic scrap by hydrometallurgical processing routes. Min. Metall. Explor. 2005, 22, 17–22. [Google Scholar] [CrossRef]
- Sheng, P.P.; Etsell, T.H. Recovery of gold from computer circuit board scrap using aqua regia. Waste Manag. Res. 2007, 25, 380–383. [Google Scholar] [CrossRef] [PubMed]
- Fleming, C.A. Hydrometallurgy of precious metals recovery. Hydrometallurgy 1992, 30, 127–162. [Google Scholar] [CrossRef]
- Pilśniak, M.; Trochimczuk, A.W.; Apostoluk, W. The Uptake of Gold(I) from Ammonia Leaching Solution by Imidazole Containing Polymeric Resins. Sep. Sci. Technol. 2009, 44, 1099–1119. [Google Scholar] [CrossRef]
- Udayakumar, S.; Bin Abd Razak, M.I.; Ismail, S. Recovering valuable metals from Waste Printed Circuit Boards (WPCB): A short review. In Proceedings of the 14th AUN/SEED-Net Regional Conference on Materials (RCM) and 4th International Postgraduate Conference on Materials, Minerals and Polymer (MAMIP), online, 1–2 December 2021. [Google Scholar]
- Duong, D.D. Adsorption Analysis: Equilibria and Kinetics. Series on Chemical Engineering; Imperial College Press: London, UK, 1998; Volume 2. [Google Scholar]
- El-Naas, M.; Alhaija, M.A. Modeling of Adsorption Processes, Mathematical Modelling; Nova Publishers: Hauppauge, NY, USA, 2013; pp. 579–600. [Google Scholar]
- Lahuri, A.H.; Adnan, R.; Mansor, M.; Farah, N.; Nordin, N. Adsorption Kinetics for Carbon dioxide Capture using Bismuth(III) Oxide Impregnated on Activated Carbon. Malays. J. Chem. 2020, 22, 33–46. [Google Scholar]
- Hakim, A.; Abu Tahari, M.N.; Marliza, T.S.; Wan Isahak, W.N.R.; Yusop, M.R.; Mohamed Hisham, M.W.; Yarmoa, M.A. Study of CO2 adsorption and desorption on activated carbon supported iron oxide by temperature programmed desorption. J. Teknol. 2015, 77, 75–84. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Sato, H.; Kaneeda, M.; Kondo, J.N. Synthesis and analysis of CO2 adsorbents based on cerium oxide. J. CO2 Util. 2014, 8, 34–38. [Google Scholar] [CrossRef]
- Hakim, A.; Marliza, T.S.; Abu Tahari, N.M.; Isahak, R.; Yusop, R.M.; Hisham, W.M.M.; Yarmo, A.M. Studies on CO2 Adsorption and Desorption Properties from Various Types of Iron Oxides (FeO, Fe2O3, and Fe3O4). Ind. Eng. Chem. Res. 2016, 55, 7888–7897. [Google Scholar] [CrossRef]
- Rosynek, M.P.; Magnuson, D.T. Infrared study of carbon dioxide adsorption on lanthanum sesquioxide and trihydroxide. J. Catal. 1977, 48, 417–421. [Google Scholar] [CrossRef]
- Okawa, Y.; Tanaka, K.-I. STM investigation of the reaction of Ag O added rows with CO2 on a Ag (110) surface. Surf. Sci. 1995, 344, L1207–L1212. [Google Scholar] [CrossRef]
- Takahashi, H.; Yuki, K.; Nitta, T. Chemical modification of rutile TiO2(110) surface by ab initio calculations for the purpose of CO2 adsorption. Fluid Phase Equilibria 2002, 194–197, 153–160. [Google Scholar] [CrossRef]
- Isahak, W.N.R.W.; Ramli, Z.A.C.; Ismail, M.W.; Ismail, K.; Yusop, R.M.; Hisham, M.W.M.; Yarmo, M.A. Adsorption–desorption of CO2 on different type of copper oxides surfaces: Physical and chemical attractions studies. J. CO2 Util. 2013, 2, 8–15. [Google Scholar] [CrossRef]
- Hess, G.; Froitzheim, H.; Baumgartner, C. The adsorption and catalytic decomposition of CO2 on Fe (111) surfaces studied with high resolution EELS. Surf. Sci. 1995, 331–333, 138–143. [Google Scholar] [CrossRef]
- Bagherisereshki, E.; Tran, J.; Lei, F.; AuYeung, N. Investigation into SrO/SrCO3 for high temperature thermochemical energy storage. Sol. Energy 2018, 160, 85–93. [Google Scholar] [CrossRef]
- Lahuri, A.H.; Abu Tahari, M.; Isahak, W.; Yusop, R.; Wahab, M.; Yarmo, A. Temperature Programmed Desorption of Carbon Dioxide for Activated Carbon Supported Nickel Oxide: The Adsorption and Desorption Studies. Adv. Mater. Res. 2014, 1087, 45–49. [Google Scholar]
- Ma, W.; Wang, N.; Lu, Y.; Lu, Z.; Tang, X.; Li, S. Synthesis of magnetic biomass carbon-based Bi2O3 photocatalyst and mechanism insight by a facile microwave and deposition method. New J. Chem. 2019, 43, 2888–2898. [Google Scholar] [CrossRef]
- Karnan, T.; Selvakumar, S.A.S.; Adinaveen, T.; Suresh, J. Visible light induced photocatalytic degradation of azo dye by Bi2O3 nanoparticles synthesized using greener route. Int. J. Sci. Eng. Res. 2016, 7, 266–270. [Google Scholar]
- Ayekoe, P.Y.; Robert, D.; Gone, D.L. Facile synthesis of TiO2/Bi2O3 heterojunctions for the photocatalytic degradation of water contaminants. J. Mater. Environ. Sci. 2018, 9, 2247–2253. [Google Scholar]
- Al-Ghouti, M.A.; Da’ana, D.A. Guidelines for the use and interpretation of adsorption isotherm models: A review. J. Hazard. Mater. 2020, 393, 122383. [Google Scholar] [CrossRef]
- Yagub, M.T.; Sen, T.K.; Afroze, S.; Ang, H.M. Dye and its removal from aqueous solution by adsorption: A review. Adv. Colloid Interface Sci. 2014, 209, 172–184. [Google Scholar] [CrossRef]
- Namal, O.O.; Kalipci, E. Adsorption kinetics of methylene blue using alkali and microwave-modified apricot stones. Sep. Sci. Technol. 2019, 54, 1722–1738. [Google Scholar] [CrossRef]
- Lagergren, S. About the theory of so-called adsorption of soluble substabces. Kungl. Sven. Vetensk. Handl. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S. Review of second-order models for adsorption systems. J. Hazard. Mater. 2006, 136, 681–689. [Google Scholar] [CrossRef]
- Ho, Y.S.; Mckay, G. The kinetics of sorption of basic dyes from aqueous solution by sphagnum moss peat. Can. J. Chem. Eng. 1998, 76, 822–827. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of Adsorption on Carbon from Solution. J. Sanit. Eng. Div. 1963, 89, 31–59. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Equilibria and Capacities for Adsorption on Carbon. J. Sanit. Eng. Div. 1964, 90, 79–108. [Google Scholar] [CrossRef]
- Ebelegi, A.; Nimibofa, A.; Donbebe, W. Interpretation of Adsorption Thermodynamics and Kinetics. Open J. Phys. Chem. 2020, 10, 166–182. [Google Scholar] [CrossRef]
- Teng, H.; Hsieh, C.-T. Activation Energy for Oxygen Chemisorption on Carbon at Low Temperatures. Ind. Eng. Chem. Res. 1999, 38, 292–297. [Google Scholar] [CrossRef]
- Cheung, C.W.; Porter, J.F.; McKay, G. Sorption kinetic analysis for the removal of cadmium ions from effluents using bone char. Water Res. 2001, 35, 605–612. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry; Oxford University Press: Oxford, UK, 2005; p. 1008. [Google Scholar]
- Fujiwara, K.; Ramesh, A.; Maki, T.; Hasegawa, H.; Ueda, K. Adsorption of platinum (IV), palladium (II) and gold (III) from aqueous solutions onto l-lysine modified crosslinked chitosan resin. J. Hazard. Mater. 2007, 146, 39–50. [Google Scholar] [CrossRef]
- Iftekhar, S.; Srivastava, V.; Sillanpää, M. Synthesis and application of LDH intercalated cellulose nanocomposite for separation of rare earth elements (REEs). Chem. Eng. J. 2017, 309, 130–139. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Y.; Cheng, Z. Removal of heavy metal ions using chitosan and modified chitosan: A review. J. Mol. Liq. 2016, 214, 175–191. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–470. [Google Scholar]
- McKay, G.; Otterburn, M.S.; Sweeney, A.G. The removal of colour from effluent using various adsorbents—III. Silica: Rate processes. Water Res. 1980, 14, 15–20. [Google Scholar] [CrossRef]
- Sips, R. On the Structure of a Catalyst Surface. J. Chem. Phys. 1948, 16, 490–495. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Mihăilescu, M.; Negrea, A.; Ciopec, M.; Davidescu, C.M.; Negrea, P.; Duţeanu, N.; Rusu, G. Gold (III) adsorption from dilute waste solutions onto Amberlite XAD7 resin modified with L-glutamic acid. Sci. Rep. 2019, 9, 8757. [Google Scholar] [CrossRef] [PubMed]
- Chassary, P.; Vincent, T.; Sanchez Marcano, J.; Macaskie, L.E.; Guibal, E. Palladium and platinum recovery from bicomponent mixtures using chitosan derivatives. Hydrometallurgy 2005, 76, 131–147. [Google Scholar] [CrossRef]
- Zhang, S.; Ning, S.; Liu, H.; Zhou, J.; Wang, S.; Zhang, W.; Wang, X.; Wei, Y. Highly-efficient separation and recovery of ruthenium from electroplating wastewater by a mesoporous silica-polymer based adsorbent. Microporous Mesoporous Mater. 2020, 303, 110293. [Google Scholar] [CrossRef]
- Iftekhar, S.; Srivastava, V.; Sillanpää, M. Enrichment of lanthanides in aqueous system by cellulose based silica nanocomposite. Chem. Eng. J. 2017, 320, 151–159. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Kumara, N.T.R.N.; Hamdan, N.; Petra, M.I.; Tennakoon, K.U.; Ekanayake, P. Equilibrium Isotherm Studies of Adsorption of Pigments Extracted from Kuduk-kuduk (Melastoma malabathricum L.) Pulp onto TiO2 Nanoparticles. J. Chem. 2014, 2014, 468975. [Google Scholar] [CrossRef]
- Liu, R.; Liang, P. Determination of gold by nanometer titanium dioxide immobilized on silica gel packed microcolumn and flame atomic absorption spectrometry in geological and water samples. Anal. Chim. Acta 2007, 604, 114–118. [Google Scholar] [CrossRef] [PubMed]
- Pu, Q.S.; Su, Z.X.; Hu, Z.H.; Chang, X.J.; Yang, M. 2-mercaptobenzothiazole-bonded silica gel as selective adsorbent for preconcentration of gold, platinum and palladium prior to their simultaneous inductively coupled plasma optical emission spectrometric determination. J. Anal. At. Spectrom. 1998, 13, 249–253. [Google Scholar] [CrossRef]
- Wang, L.; Tian, C.; Mu, G.; Sun, L.; Zhang, H.; Fu, H. Magnetic nanoparticles/graphitic carbon nanostructures composites: Excellent magnetic separable adsorbents for precious metals from aqueous solutions. Mater. Res. Bull. 2012, 47, 646–654. [Google Scholar] [CrossRef]
- Soleimani, M.; Kaghazchi, T. Adsorption of gold ions from industrial wastewater using activated carbon derived from hard shell of apricot stones—An agricultural waste. Bioresour. Technol. 2008, 99, 5374–5383. [Google Scholar] [CrossRef] [PubMed]
- Vilvanathan, S.; Shanthakumar, S. Column adsorption studies on nickel and cobalt removal from aqueous solution using native and biochar form of Tectona grandis. Environ. Prog. Sustain. Energy 2017, 36, 1030–1038. [Google Scholar] [CrossRef]
- Abdolali, A.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Zhang, J.; Liang, S.; Chang, S.W.; Nguyen, D.D.; Liu, Y. Application of a breakthrough biosorbent for removing heavy metals from synthetic and real wastewaters in a lab-scale continuous fixed-bed column. Bioresour. Technol. 2017, 229, 78–87. [Google Scholar] [CrossRef] [PubMed]

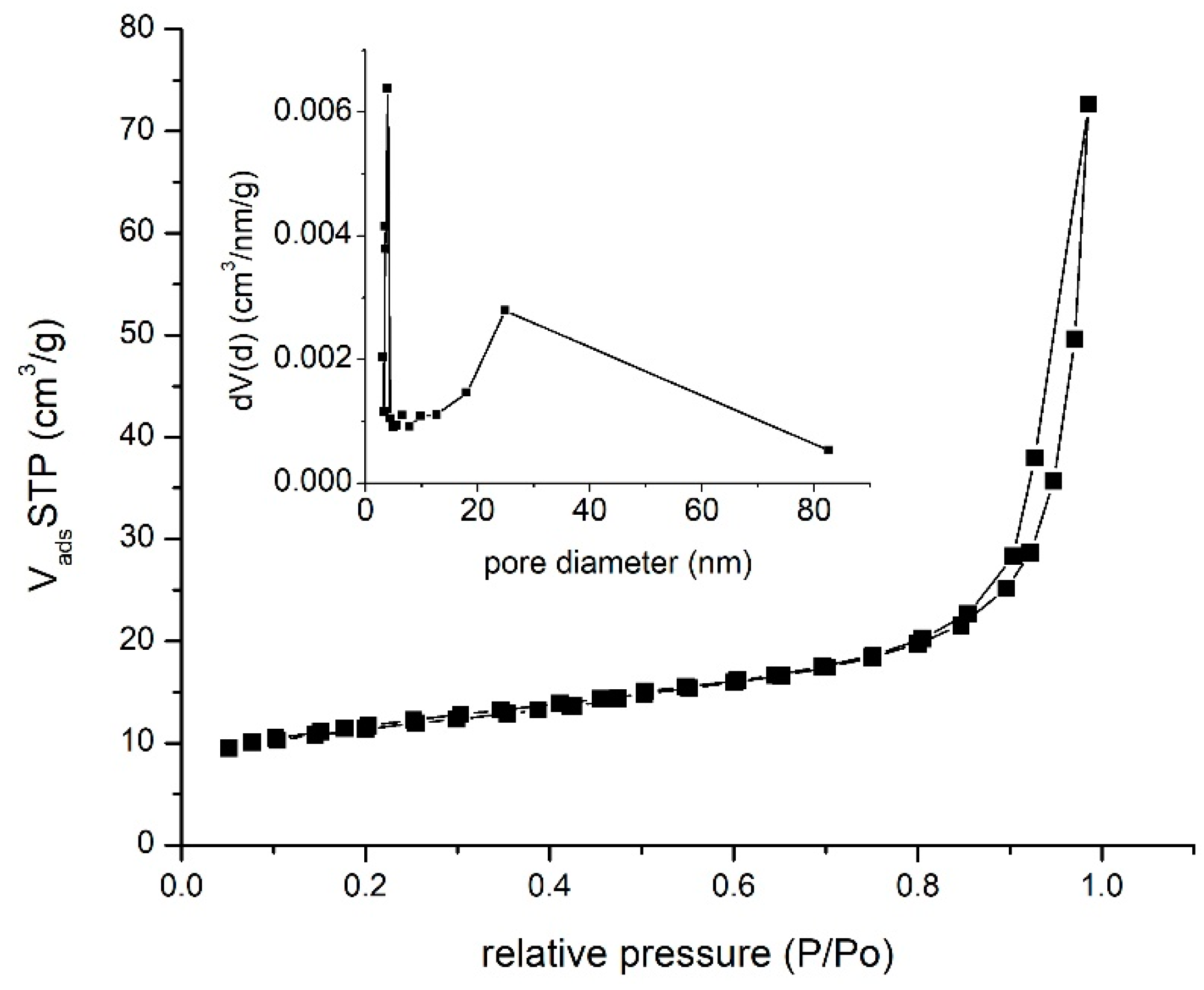


| Surface Area, m2/g | BJH Desorption, nm | Average Pore Diameter nm | Total Pore Volume, cc/g |
|---|---|---|---|
| 41.00 | 3.95 | 11.48 | 1.126 × 10−1 cc/g for pores smaller than 137.1 nm |
| Sample | Material Area (µm2) | (µm) | (µm) | (µm) | (µm) | (µm) | ||
|---|---|---|---|---|---|---|---|---|
| BCp/BC | 114.388 | 0.179 | 0.237 | 0.677 | −0.776 | 1.454 | −0.273 | 3.529 |
| Pseudo-First Order | ||||
| Temperature (K) | (mg g−1) | (min−1) | (mg g−1) | |
| 298 | 2.45 | 0.0387 | 2.19 | 0.7911 |
| 308 | 2.48 | 0.0399 | 2.57 | 0.7542 |
| 318 | 2.50 | 0.0498 | 2.60 | 0.8753 |
| Pseudo-second order | ||||
| Temperature (K) | (mg g−1) | (g mg−1∙min−1) | (mg g−1) | |
| 298 | 2.45 | 1.0060 | 2.49 | 0.9961 |
| 308 | 2.48 | 1.2010 | 2.48 | 0.9935 |
| 318 | 2.50 | 1.4760 | 2.51 | 0.9948 |
| Elovich Model | ||||
| Temperature (K) | (mg g−1 min−1) | (mg g−1 min−1) | ||
| 298 | 1.61 | 3.38 | 0.9911 | |
| 308 | 2.04 | 1.44 | 0.9811 | |
| 318 | 2.57 | 0.51 | 0.9880 | |
| Intraparticle diffusion model (IPD) | ||||
| Temperature (K) | (mg·g−1 min−1/2) | |||
| 298 | 0.158 | 0.597 | 0.7311 | |
| 308 | 0.161 | 0.929 | 0.7675 | |
| 318 | 0.185 | 1.126 | 0.7131 | |
(kJ/mol) | (J/mol·K) | (kJ/mol) | |||
|---|---|---|---|---|---|
| 91.4 | 328.4 | 298 K | 308 K | 318 K | 0.9993 |
| −6.42 | −9.70 | −12.99 | |||
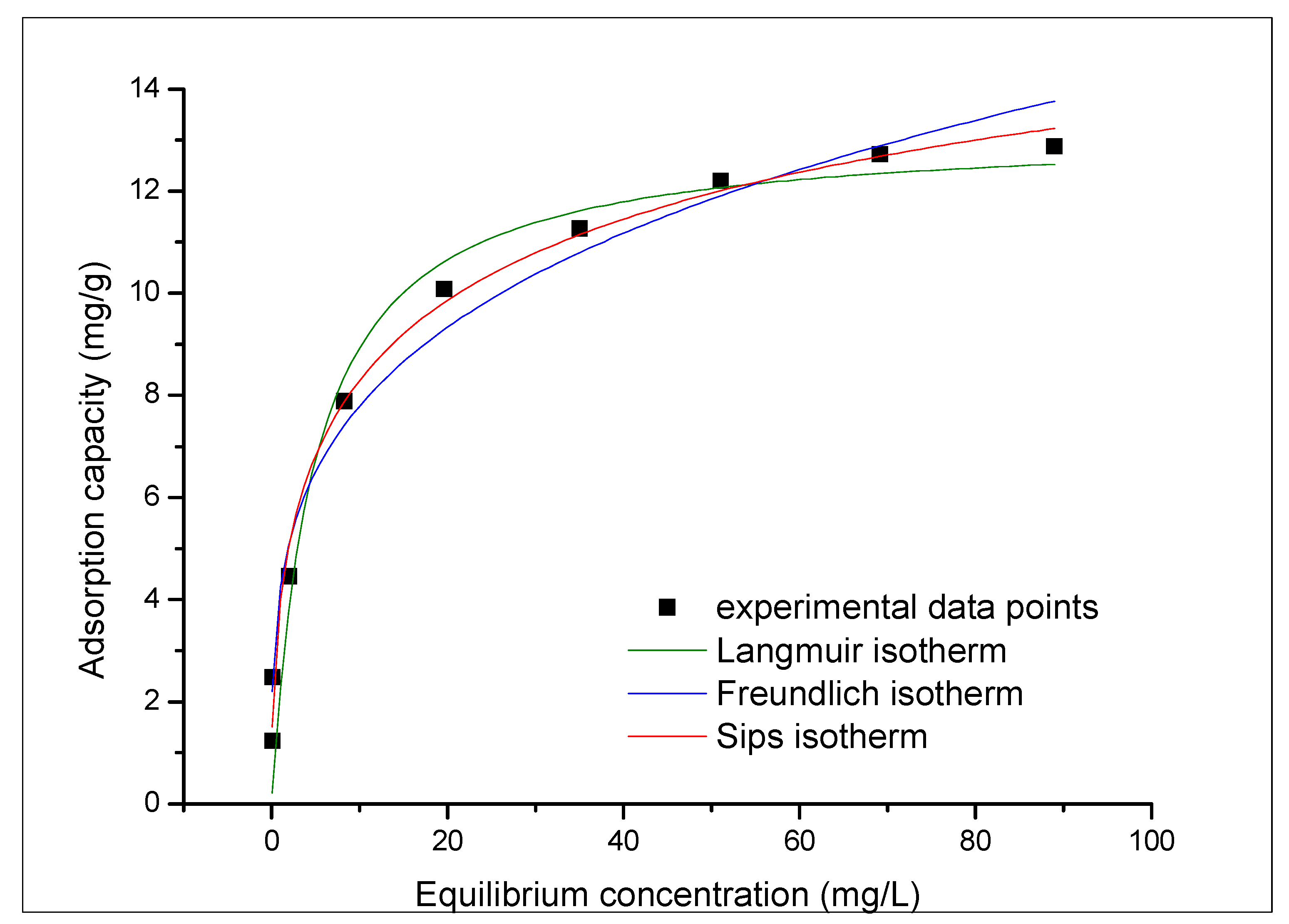
| Langmuir Isotherm | |||
| (mg/g) | (L/mg) | (mg/g) | |
| 12.70 | 0.290 | 13.20 | 0.9506 |
| Freundlich Isotherm | |||
| (mg/g) | |||
| 4.28 | 0.26 | 0.9769 | |
| Sips Isotherm | |||
| (mg/g) | |||
| 0.56 | 13.10 | 0.21 | 0.9986 |
| Material | Adsorption Capacity for Au(III) Recovery by Adsorption Process, mg/g | References |
|---|---|---|
| Nanometer TiO2 immobilized on silica gel | 3.56 | [66] |
| 2-Mercaptobenzothiazole-bonded silica gel | 4.50 | [67] |
| Nanoparticles/graphitic carbon | 7.92 | [68] |
| Activated carbon | between 6 and 30, based on AC type | [69] |
| BCb/BC | 12.70 | This paper |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ianăşi, C.; Svera, P.; Popa, A.; Lazău, R.; Negrea, A.; Negrea, P.; Duteanu, N.; Ciopec, M.; Nemes, N.-S. Adsorbent Material Based on Carbon Black and Bismuth with Tunable Properties for Gold Recovery. Materials 2023, 16, 2837. https://doi.org/10.3390/ma16072837
Ianăşi C, Svera P, Popa A, Lazău R, Negrea A, Negrea P, Duteanu N, Ciopec M, Nemes N-S. Adsorbent Material Based on Carbon Black and Bismuth with Tunable Properties for Gold Recovery. Materials. 2023; 16(7):2837. https://doi.org/10.3390/ma16072837
Chicago/Turabian StyleIanăşi, Cătălin, Paula Svera (m. Ianăşi), Alexandru Popa, Radu Lazău, Adina Negrea, Petru Negrea, Narcis Duteanu, Mihaela Ciopec, and Nicoleta-Sorina Nemes. 2023. "Adsorbent Material Based on Carbon Black and Bismuth with Tunable Properties for Gold Recovery" Materials 16, no. 7: 2837. https://doi.org/10.3390/ma16072837
APA StyleIanăşi, C., Svera, P., Popa, A., Lazău, R., Negrea, A., Negrea, P., Duteanu, N., Ciopec, M., & Nemes, N.-S. (2023). Adsorbent Material Based on Carbon Black and Bismuth with Tunable Properties for Gold Recovery. Materials, 16(7), 2837. https://doi.org/10.3390/ma16072837










