Accelerating Density Functional Calculation of Adatom Adsorption on Graphene via Machine Learning
Abstract
1. Introduction
2. Modeling and Dataset
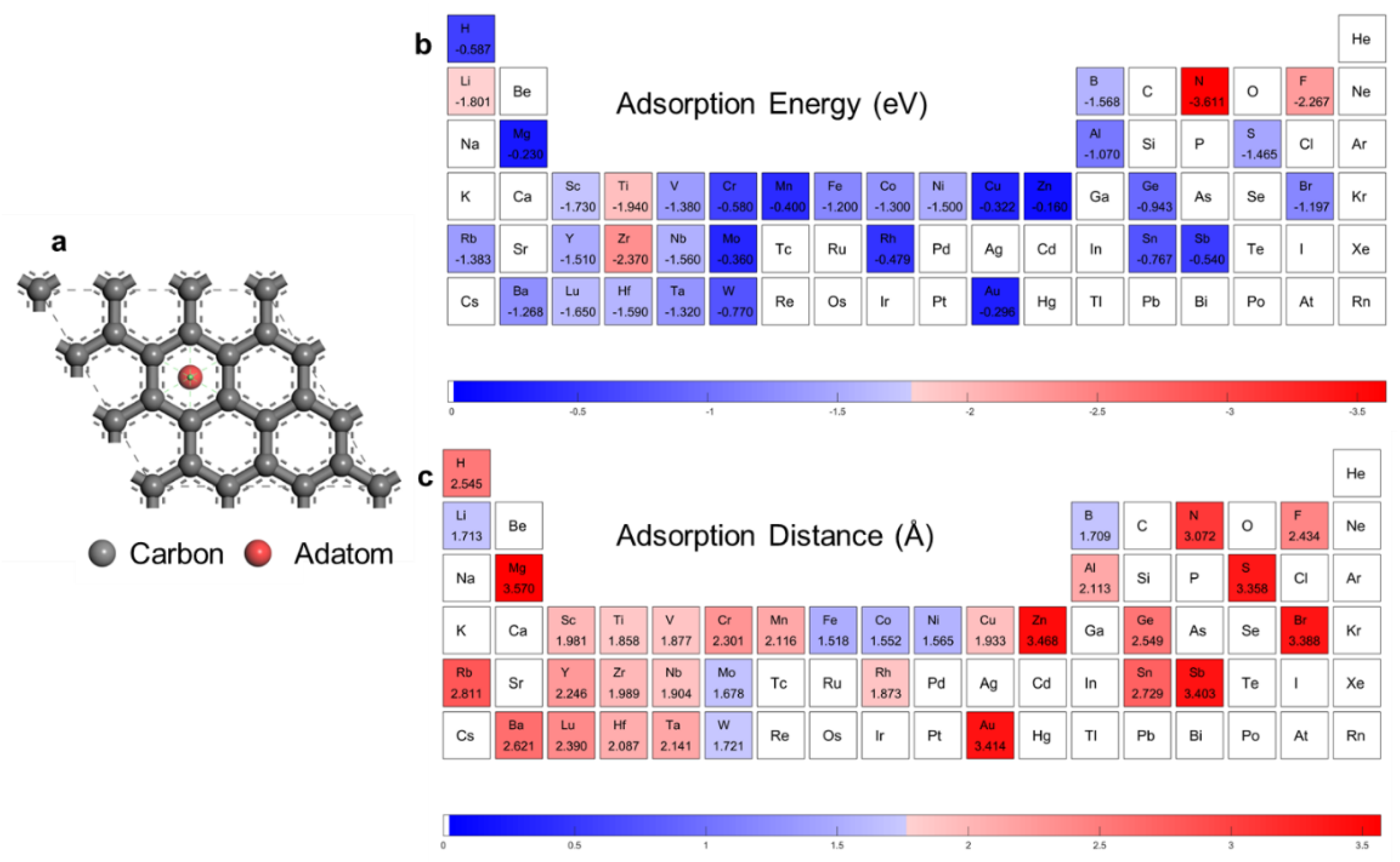
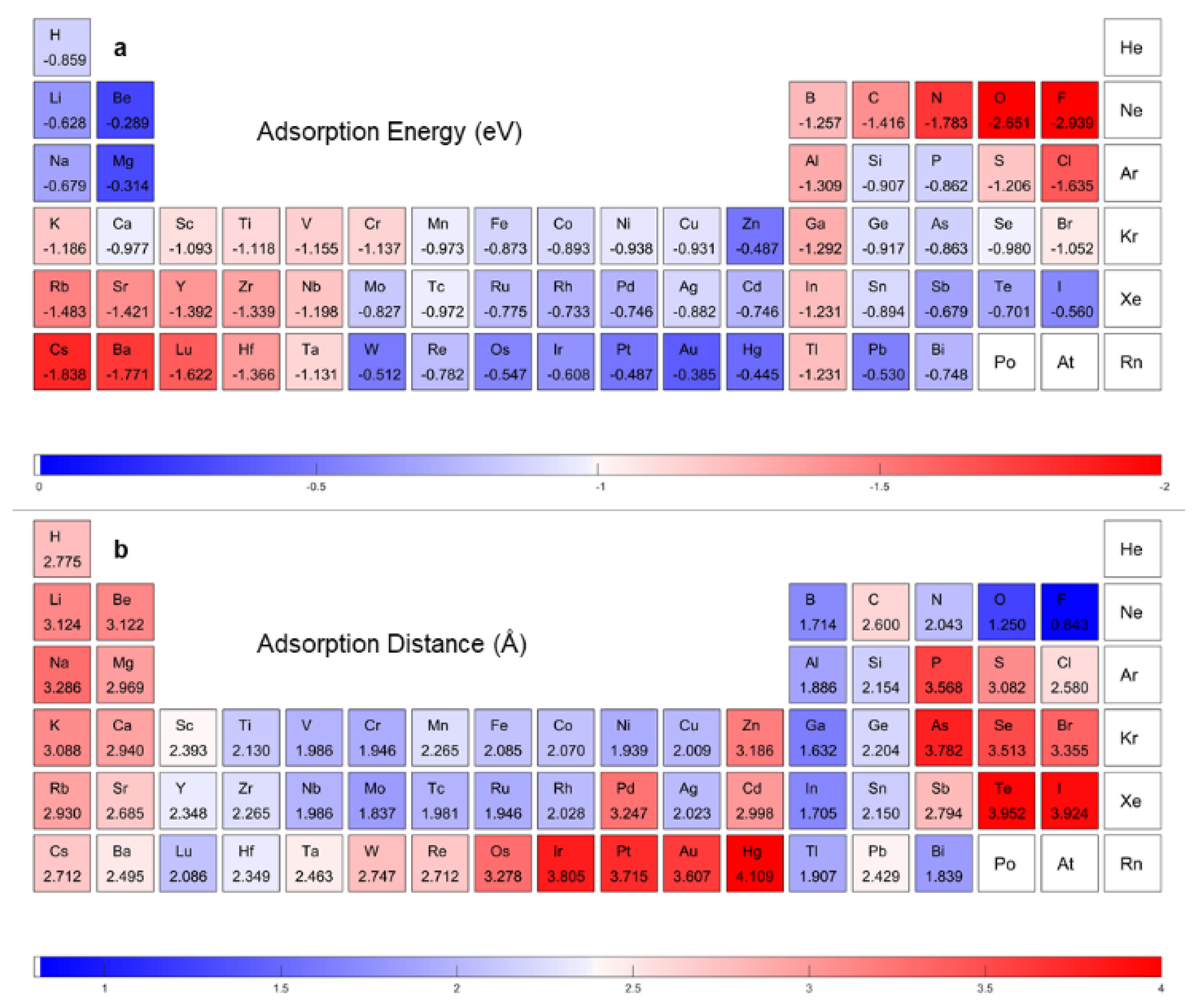
2.1. First Principles Calculations
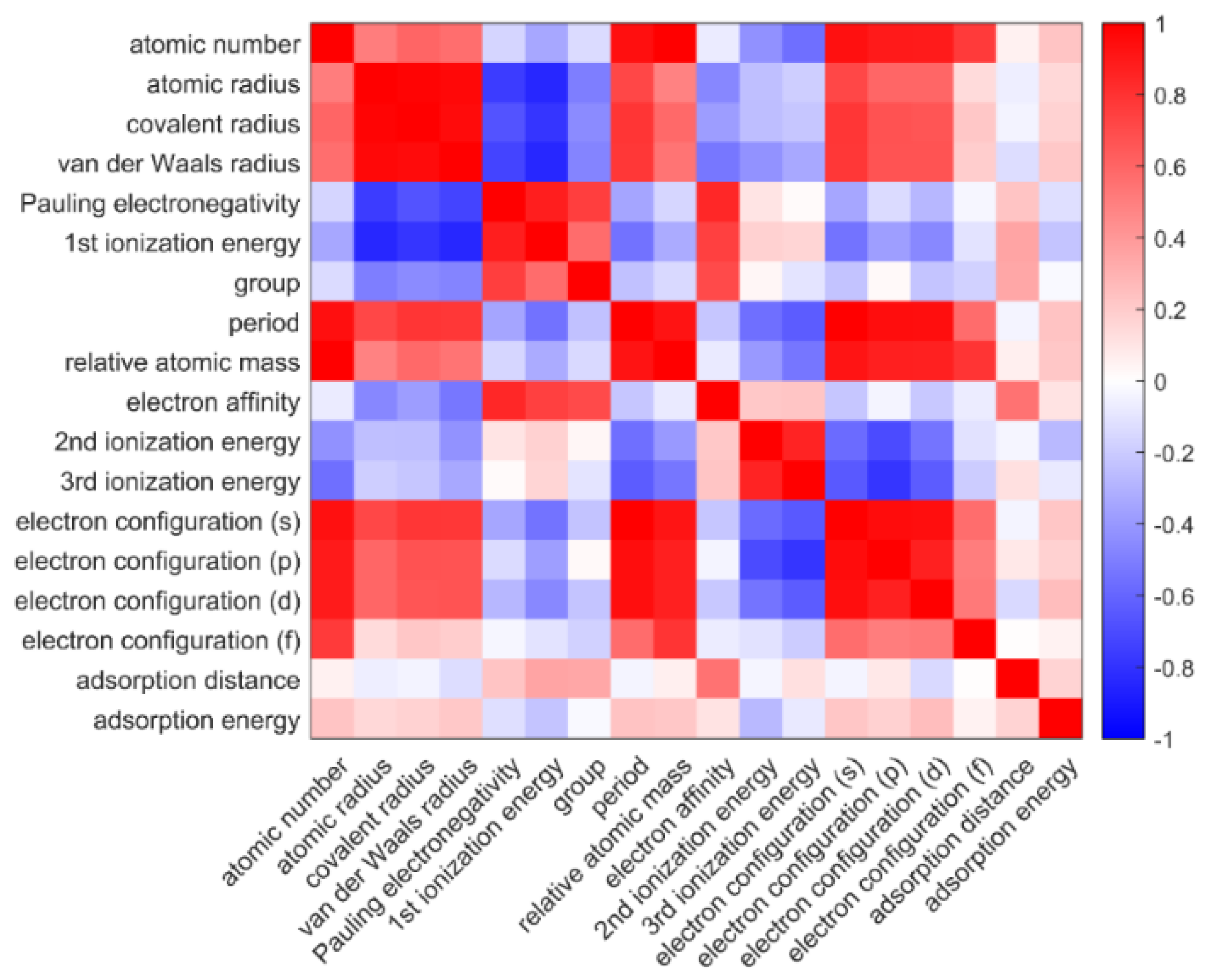
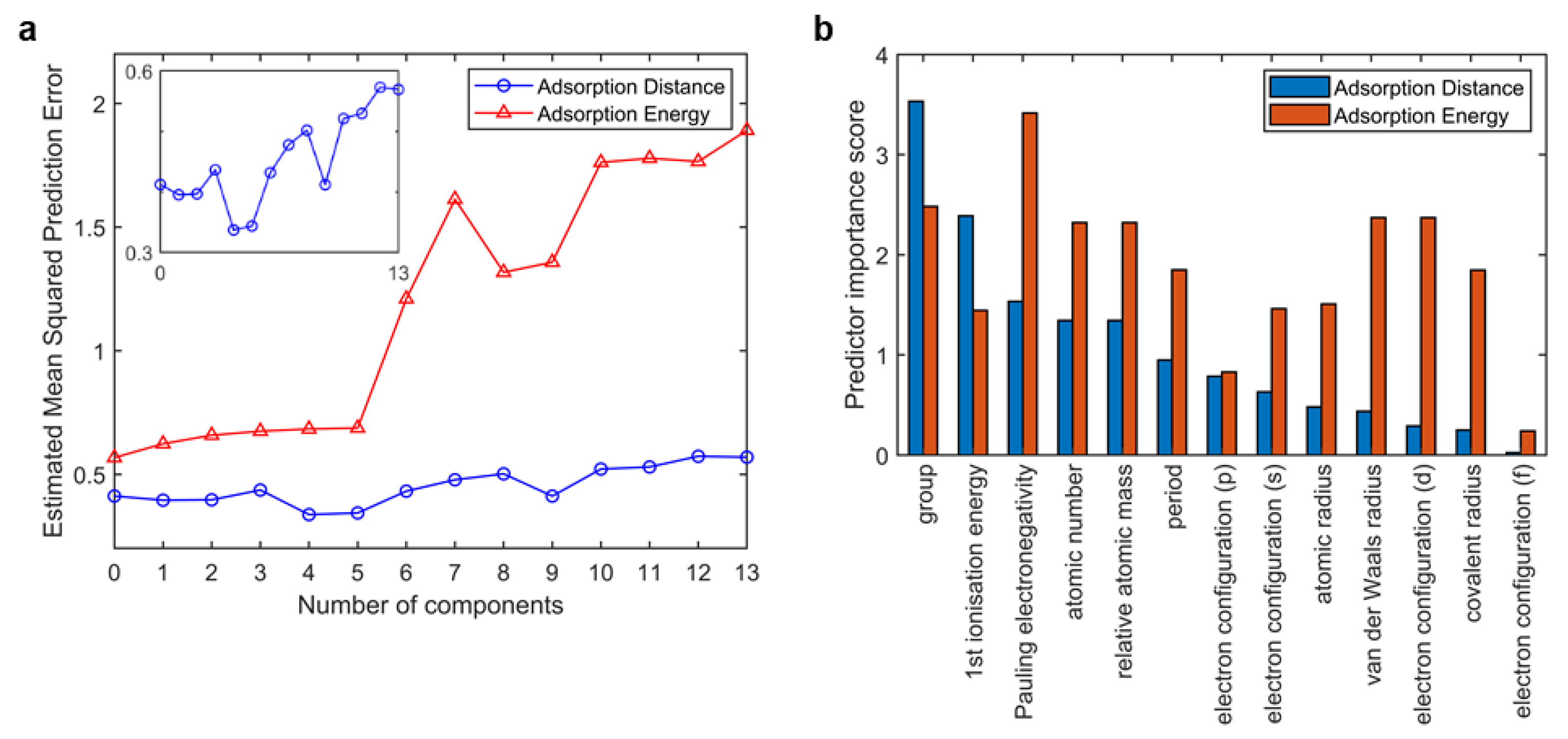
2.2. Feature Engineering
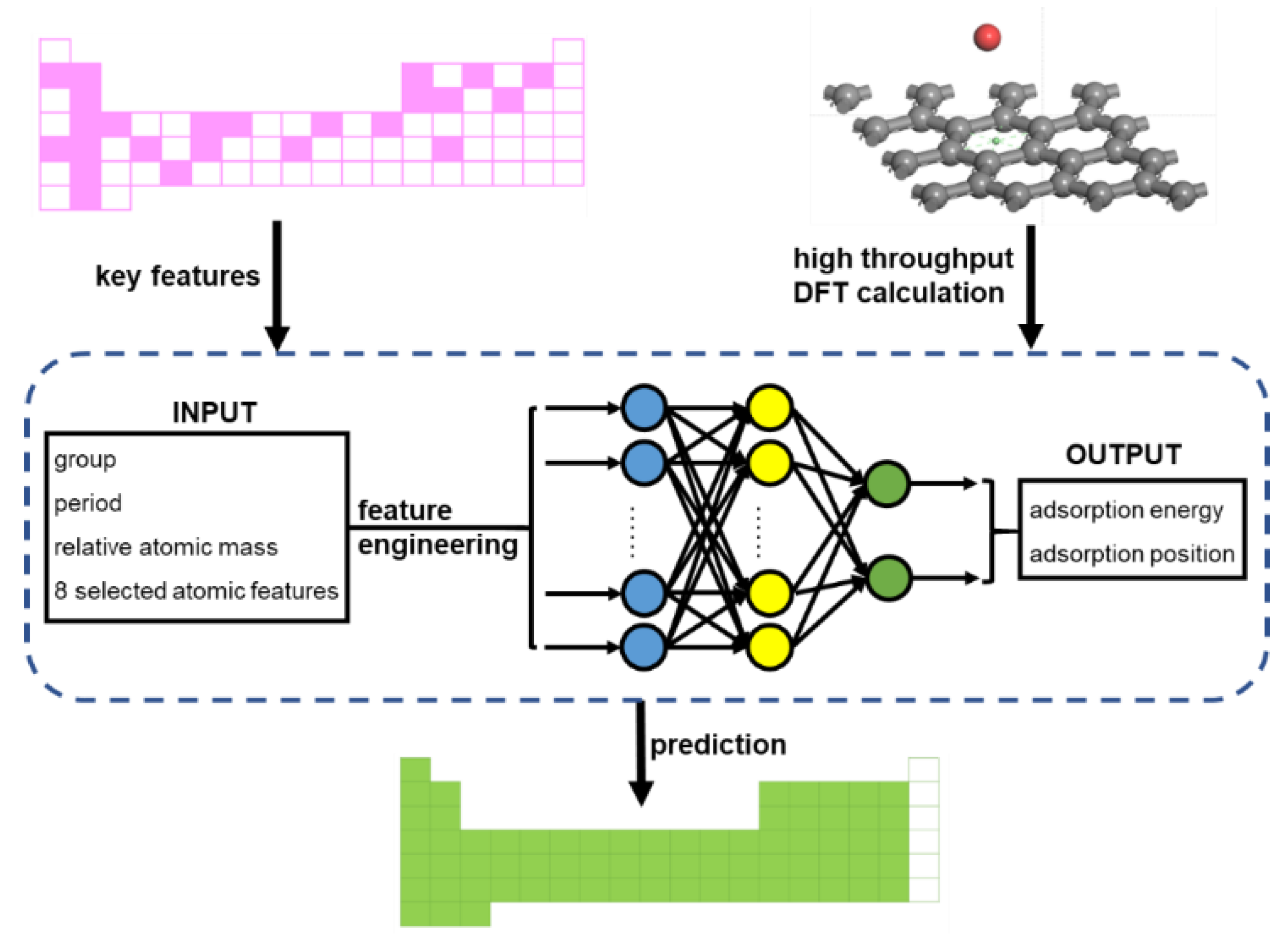
2.3. Machine Learner Design
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, S.; Yu, Q.; Yu, X.; Rong, P.; Jiang, L.; Jiang, J. Graphene-supported metal single-atom catalysts: A concise review. Sci. China Mater. 2020, 63, 903–920. [Google Scholar] [CrossRef]
- Zhuo, H.Y.; Zhang, X.; Liang, J.X.; Yu, Q.; Xiao, H.; Li, J. Theoretical Understandings of Graphene-based Metal Single-Atom Catalysts: Stability and Catalytic Performance. Chem. Rev. 2020, 120, 12315–12341. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, Y.; Zhang, J. A Review of High Density Solid Hydrogen Storage Materials by Pyrolysis for Promising Mobile Applications. Ind. Eng. Chem. Res. 2021, 60, 2737–2771. [Google Scholar] [CrossRef]
- Manadé, M.; Viñes, F.; Illas, F. Transition metal adatoms on graphene: A systematic density functional study. Carbon 2015, 95, 525–534. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, C.; Xiao, W.; Ameyama, K.; Ma, C. Enhanced mechanical properties of Al5083 alloy with graphene nanoplates prepared by ball milling and hot extrusion. Mater. Sci. Eng. A 2016, 658, 8–15. [Google Scholar] [CrossRef]
- Güler, Ö.; Bağcı, N. A short review on mechanical properties of graphene reinforced metal matrix composites. J. Mater. Res. Technol. 2020, 9, 6808–6833. [Google Scholar] [CrossRef]
- Chu, K.; Wang, J.; Liu, Y.-p.; Geng, Z.-r. Graphene defect engineering for optimizing the interface and mechanical properties of graphene/copper composites. Carbon 2018, 140, 112–123. [Google Scholar] [CrossRef]
- Chen, Y.C.; Liu, Y.; Zhou, F.; Chen, M.; Qu, N.; Liao, M.Q.; Zhu, J.C. The interface properties of defective graphene on aluminium: A first-principles calculation. Comput. Mater. Sci. 2021, 188, 110157. [Google Scholar] [CrossRef]
- Shahid, M.; Farooqi, Z.H.; Begum, R.; Arif, M.; Irfan, A.; Azam, M. Extraction of cobalt ions from aqueous solution by microgels for in-situ fabrication of cobalt nanoparticles to degrade toxic dyes: A two fold-environmental application. Chem. Phys. Lett. 2020, 754, 137645. [Google Scholar] [CrossRef]
- Arif, M. Extraction of iron (III) ions by core-shell microgel for in situ formation of iron nanoparticles to reduce harmful pollutants from water. J. Environ. Chem. Eng. 2023, 11, 109270. [Google Scholar] [CrossRef]
- Ajmal, M.; Siddiq, M.; Aktas, N.; Sahiner, N. Magnetic Co–Fe bimetallic nanoparticle containing modifiable microgels for the removal of heavy metal ions, organic dyes and herbicides from aqueous media. RSC Adv. 2015, 5, 43873–43884. [Google Scholar] [CrossRef]
- Arif, M.; Shahid, M.; Irfan, A.; Nisar, J.; Wang, X.; Batool, N.; Ali, M.; Farooqi, Z.H.; Begum, R. Extraction of copper ions from aqueous medium by microgel particles for in-situ fabrication of copper nanoparticles to degrade toxic dyes. Z. Phys. Chem. 2022, 236, 1219–1241. [Google Scholar] [CrossRef]
- Huang, F.; Deng, Y.; Chen, Y.; Cai, X.; Peng, M.; Jia, Z.; Ren, P.; Xiao, D.; Wen, X.; Wang, N.; et al. Atomically Dispersed Pd on Nanodiamond/Graphene Hybrid for Selective Hydrogenation of Acetylene. J. Am. Chem. Soc. 2018, 140, 13142–13146. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y. Unveiling the Active Structure of Single Nickel Atom Catalysis: Critical Roles of Charge Capacity and Hydrogen Bonding. J. Am. Chem. Soc. 2020, 142, 5773–5777. [Google Scholar] [CrossRef] [PubMed]
- Back, S.; Lim, J.; Kim, N.Y.; Kim, Y.H.; Jung, Y. Single-atom catalysts for CO2 electroreduction with significant activity and selectivity improvements. Chem. Sci. 2017, 8, 1090–1096. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Zhang, L.; Zhang, X.; Dai, G.; Zhang, J.; Wang, X.; You, H. Hollow AuAg Alloy Nanourchins: Twin Plane and Surface Treatment for Enhanced Methanol Electrooxidation Performance. ACS Appl. Energy Mater. 2019, 3, 723–732. [Google Scholar] [CrossRef]
- Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 2011, 134, 074106. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. Npj Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Xie, T.; France-Lanord, A.; Wang, Y.; Shao-Horn, Y.; Grossman, J.C. Graph dynamical networks for unsupervised learning of atomic scale dynamics in materials. Nat. Commun. 2019, 10, 2667. [Google Scholar] [CrossRef]
- Schutt, K.T.; Kessel, P.; Gastegger, M.; Nicoli, K.A.; Tkatchenko, A.; Muller, K.R. SchNetPack: A Deep Learning Toolbox For Atomistic Systems. J. Chem. Theory Comput. 2019, 15, 448–455. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [PubMed]
- Rupp, M.; Tkatchenko, A.; Muller, K.R.; von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Vandermause, J.; Sun, L.; Cepellotti, A.; Kozinsky, B. Bayesian force fields from active learning for simulation of inter-dimensional transformation of stanene. Npj Comput. Mater. 2021, 7, 40. [Google Scholar] [CrossRef]
- Song, Y.; Siriwardane, E.M.D.; Zhao, Y.; Hu, J. Computational Discovery of New 2D Materials Using Deep Learning Generative Models. ACS Appl. Mater. Interfaces 2021, 13, 53303–53313. [Google Scholar] [CrossRef]
- Tran, K.; Ulissi, Z.W. Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution. Nat. Catal. 2018, 1, 696–703. [Google Scholar] [CrossRef]
- Cooper, A.M.; Kästner, J.; Urban, A.; Artrith, N. Efficient training of ANN potentials by including atomic forces via Taylor expansion and application to water and a transition-metal oxide. Npj Comput. Mater. 2020, 6, 54. [Google Scholar] [CrossRef]
- Choudhury, A. The Role of Machine Learning Algorithms in Materials Science: A State of Art Review on Industry 4.0. Arch. Comput. Methods Eng. 2021, 28, 3361–3381. [Google Scholar] [CrossRef]
- Hu, Y.J.; Zhao, G.; Zhang, B.; Yang, C.; Zhang, M.; Liu, Z.K.; Qian, X.; Qi, L. Local electronic descriptors for solute-defect interactions in bcc refractory metals. Nat. Commun. 2019, 10, 4484. [Google Scholar] [CrossRef]
- Tian, Y.L.; Ren, J.F.; Yue, W.W.; Chen, M.N.; Hu, G.C.; Yuan, X.B. Adsorption of chloroform on N-doped and Al-doped graphene: A first-principle study. Chem. Phys. Lett. 2017, 685, 344–348. [Google Scholar] [CrossRef]
- Dai, J.; Yuan, J.; Giannozzi, P. Gas adsorption on graphene doped with B, N, Al, and S: A theoretical study. Appl. Phys. Lett. 2009, 95, 232105. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Ma, Z.; Pei, Y. Structure and Catalytic Activity of Gold Clusters Supported on Nitrogen-Doped Graphene. J. Phys. Chem. C 2021, 125, 5006–5019. [Google Scholar] [CrossRef]

| Interface | (Å) | (Å) | (eV) | (eV) |
|---|---|---|---|---|
| Graphene/Mg+Zn | 3.13 | 3.40 | 6.340 | −0.487 |
| Graphene/Mg+Li | 3.04 | 3.42 | 6.377 | −0.628 |
| Graphene/Mg+Ca | 3.27 | 2.82 | 6.379 | −0.977 |
| Graphene/Mg+Al | 3.27 | 3.65 | 6.470 | −1.309 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, N.; Chen, M.; Liao, M.; Cheng, Y.; Lai, Z.; Zhou, F.; Zhu, J.; Liu, Y.; Zhang, L. Accelerating Density Functional Calculation of Adatom Adsorption on Graphene via Machine Learning. Materials 2023, 16, 2633. https://doi.org/10.3390/ma16072633
Qu N, Chen M, Liao M, Cheng Y, Lai Z, Zhou F, Zhu J, Liu Y, Zhang L. Accelerating Density Functional Calculation of Adatom Adsorption on Graphene via Machine Learning. Materials. 2023; 16(7):2633. https://doi.org/10.3390/ma16072633
Chicago/Turabian StyleQu, Nan, Mo Chen, Mingqing Liao, Yuan Cheng, Zhonghong Lai, Fei Zhou, Jingchuan Zhu, Yong Liu, and Lin Zhang. 2023. "Accelerating Density Functional Calculation of Adatom Adsorption on Graphene via Machine Learning" Materials 16, no. 7: 2633. https://doi.org/10.3390/ma16072633
APA StyleQu, N., Chen, M., Liao, M., Cheng, Y., Lai, Z., Zhou, F., Zhu, J., Liu, Y., & Zhang, L. (2023). Accelerating Density Functional Calculation of Adatom Adsorption on Graphene via Machine Learning. Materials, 16(7), 2633. https://doi.org/10.3390/ma16072633







