Effect of Ambient Temperature on the Mechanical Properties of High Ductility Concrete
Abstract
1. Introduction
2. Materials and Methods
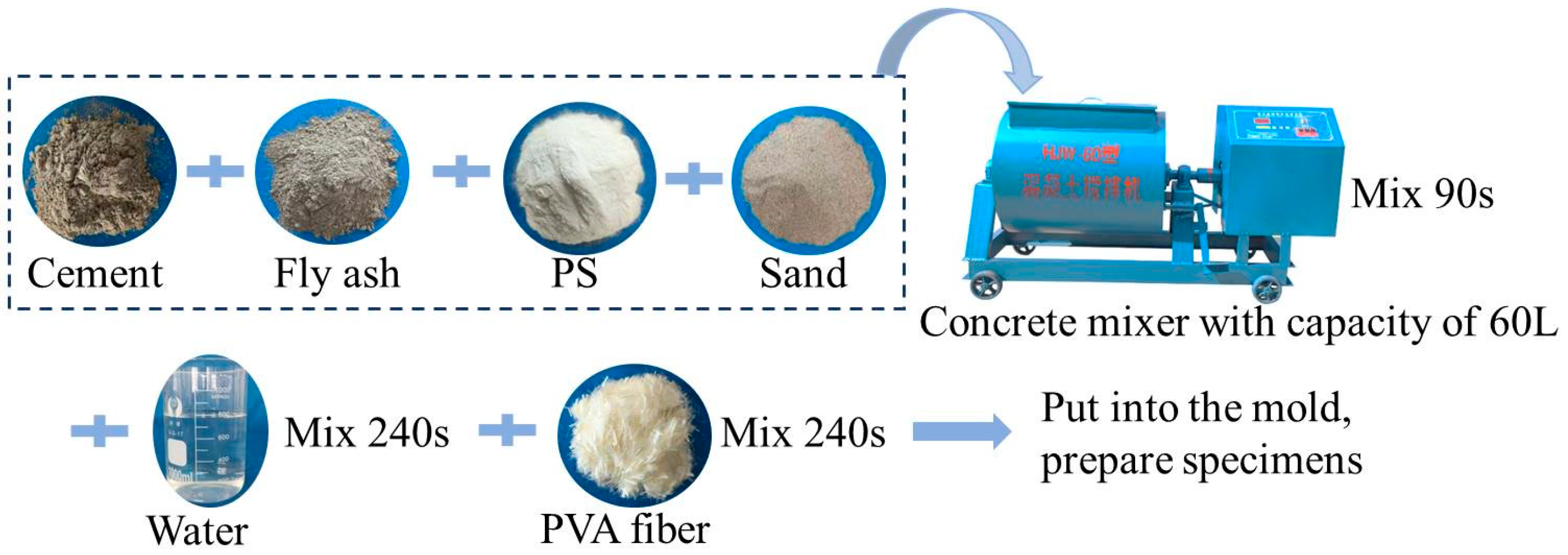
2.1. Raw Materials and Mix Proportions
2.2. Specimen Preparation Process
2.3. Test Methods
2.3.1. Optimization of HDC Mix Proportion
2.3.2. Fiber Dispersion Method
2.3.3. Mechanical Property Testing of HDC after Different Temperature Treatments
2.3.4. Microscopic Performance Testing
3. Results and Discussion
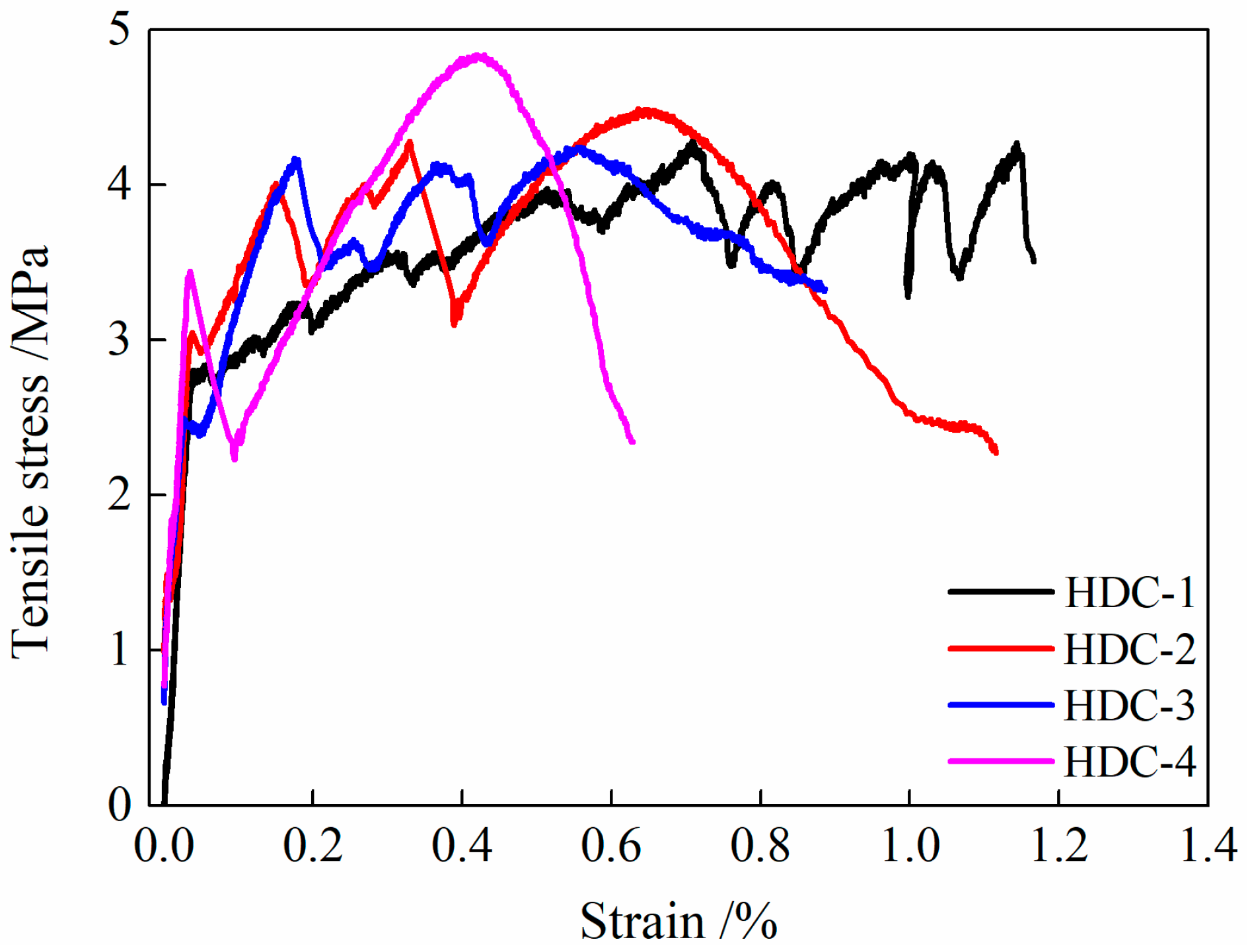
3.1. Optimal Proportioning of HDC
3.2. Fiber Dispersion Property
3.3. Compressive Performance
3.3.1. Failure Mode of Prism
3.3.2. Characteristic Parameters
3.3.3. Structural Design Parameters
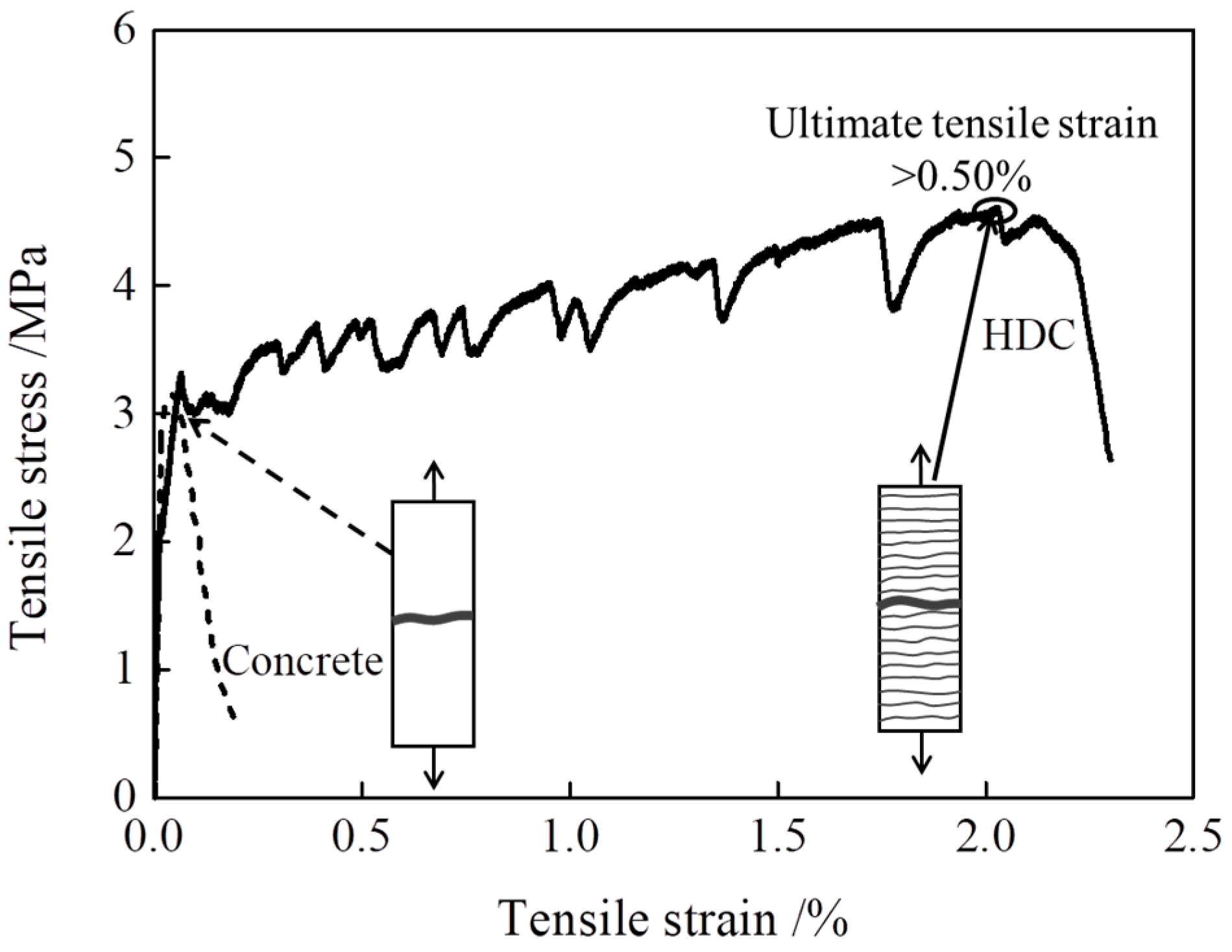
3.4. Tensile Performance
3.4.1. Failure Mode
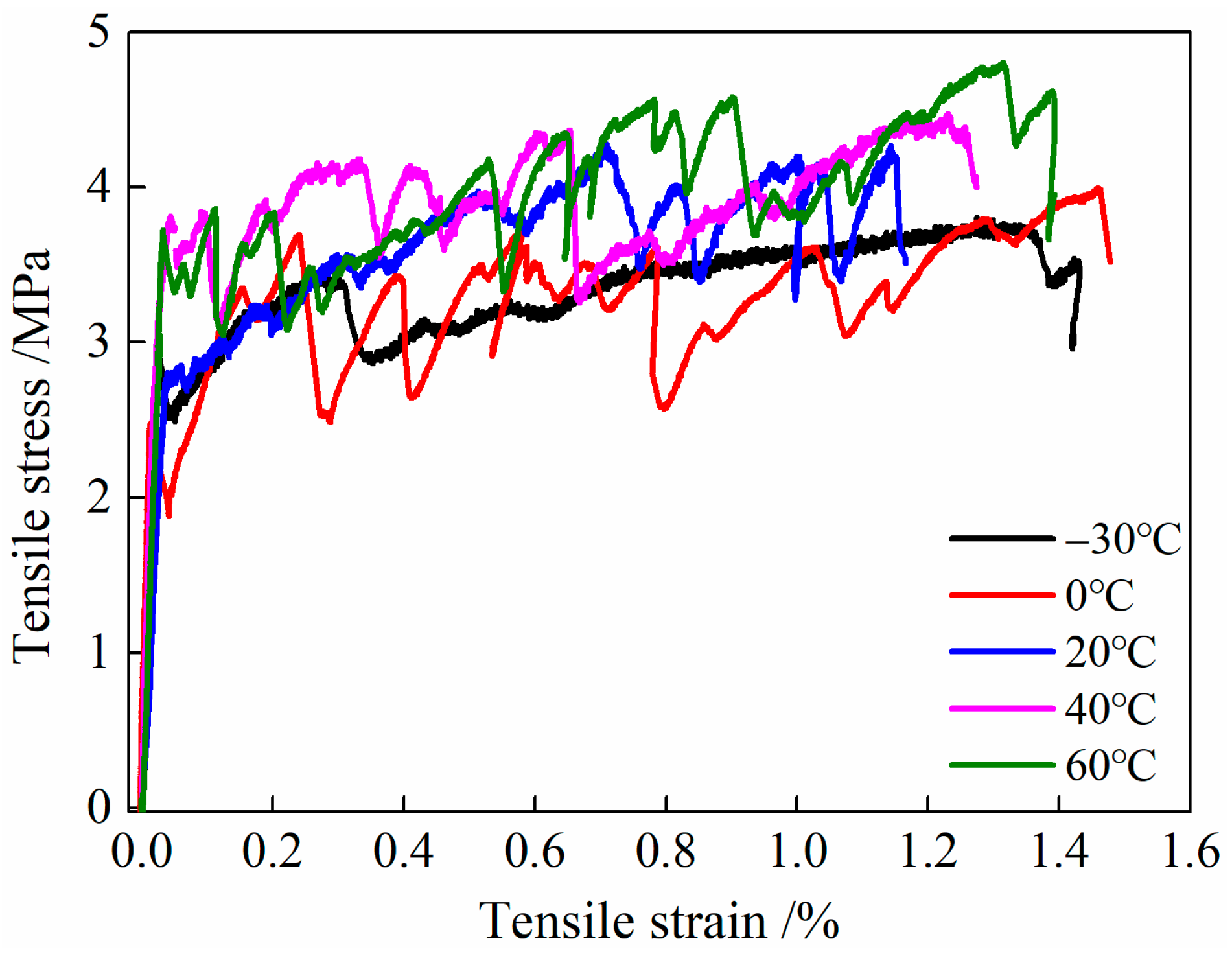
3.4.2. Tensile Stress–Strain Relationship Curve
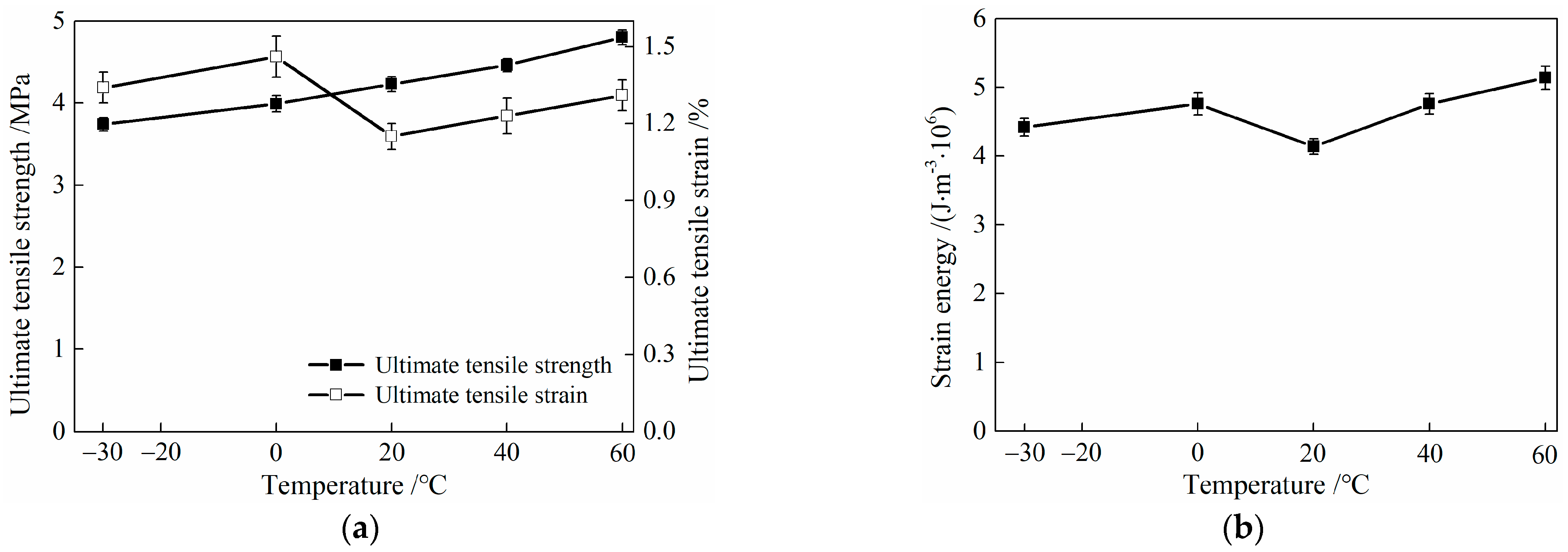
3.4.3. Characteristic Parameters
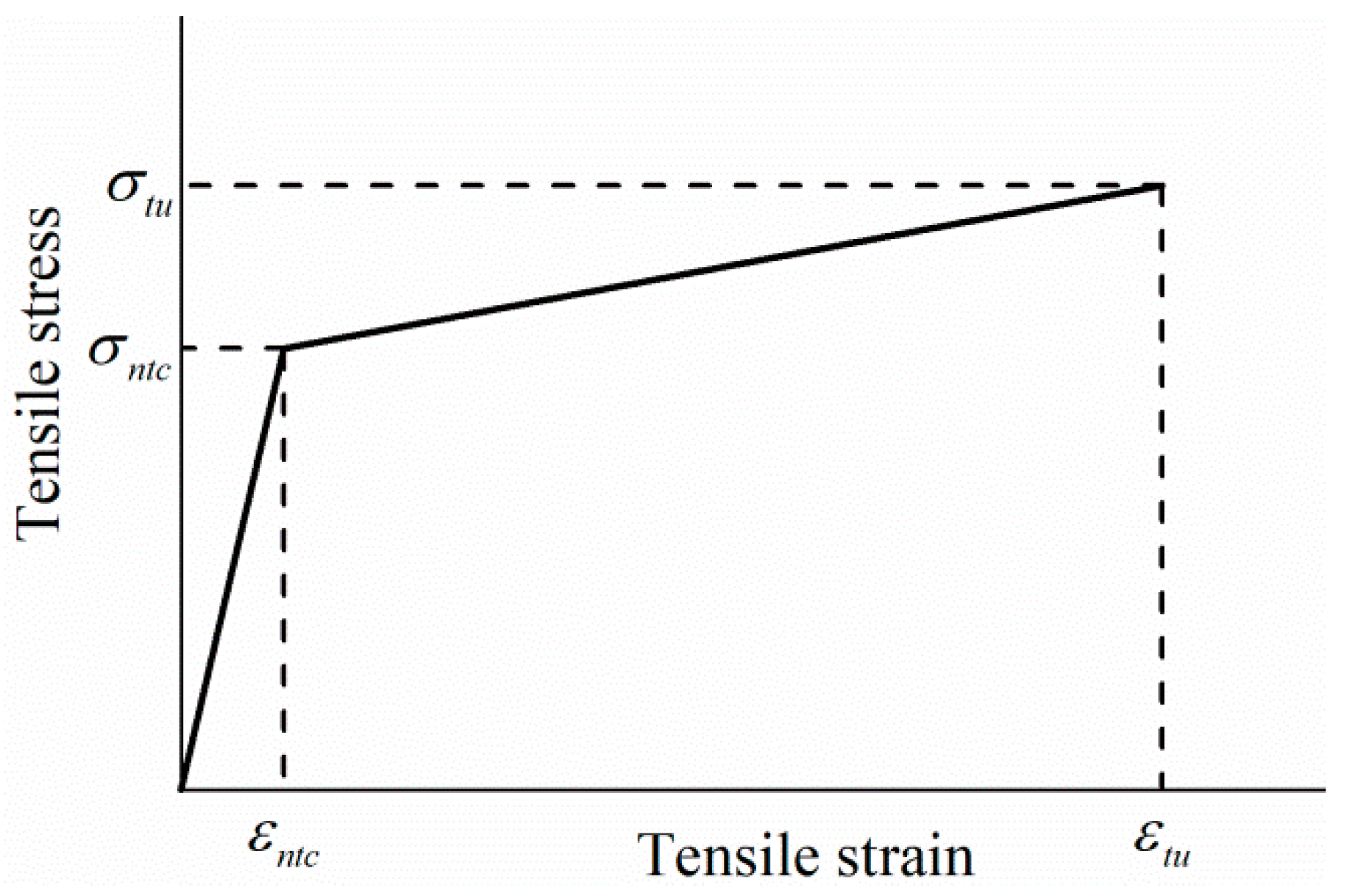
3.4.4. Tensile Stress–Strain Relationship Model
3.4.5. Structural Design Parameters
3.5. Flexural Performance
3.5.1. Failure Mode
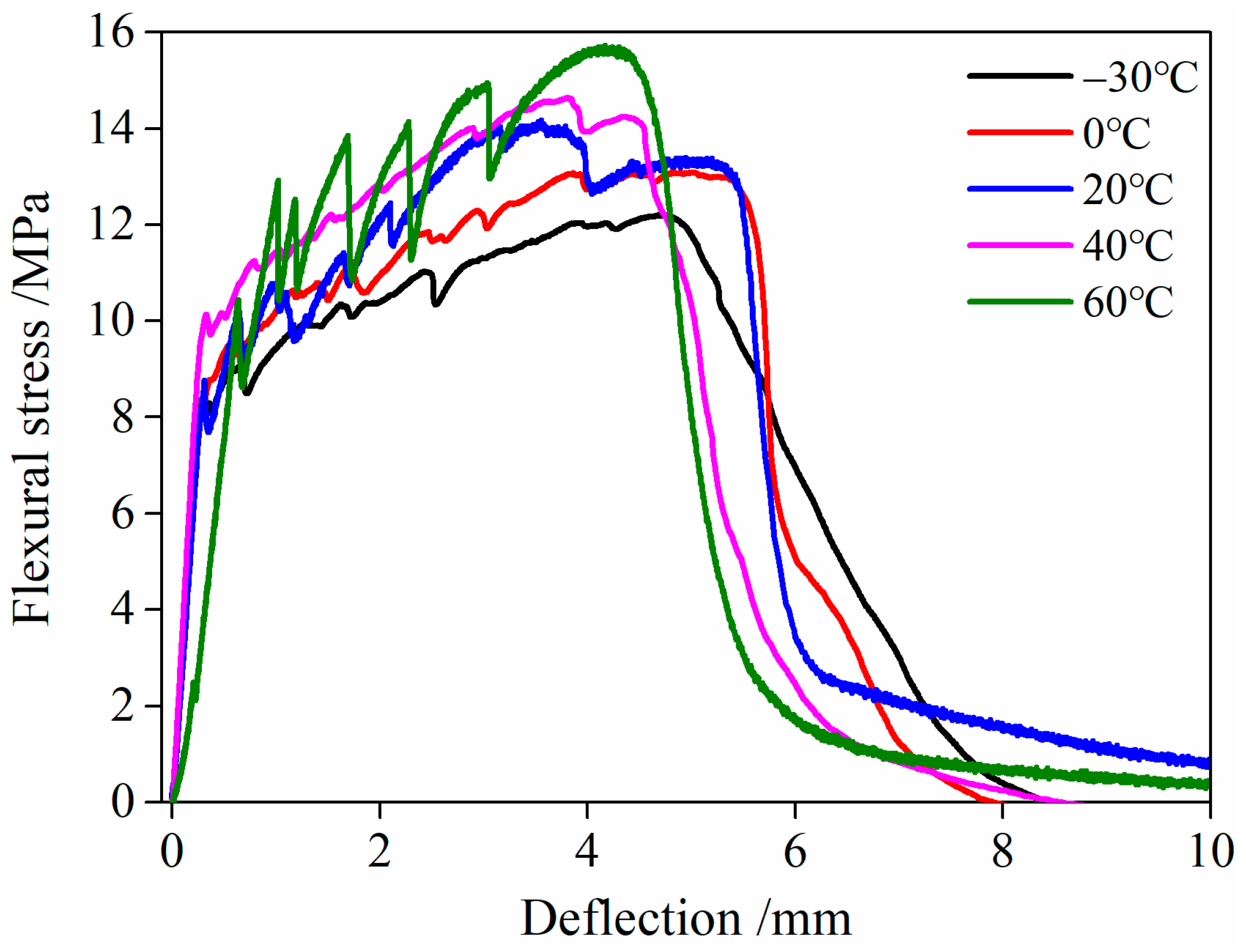
3.5.2. Flexural Stress–Deflection Relationship Curve
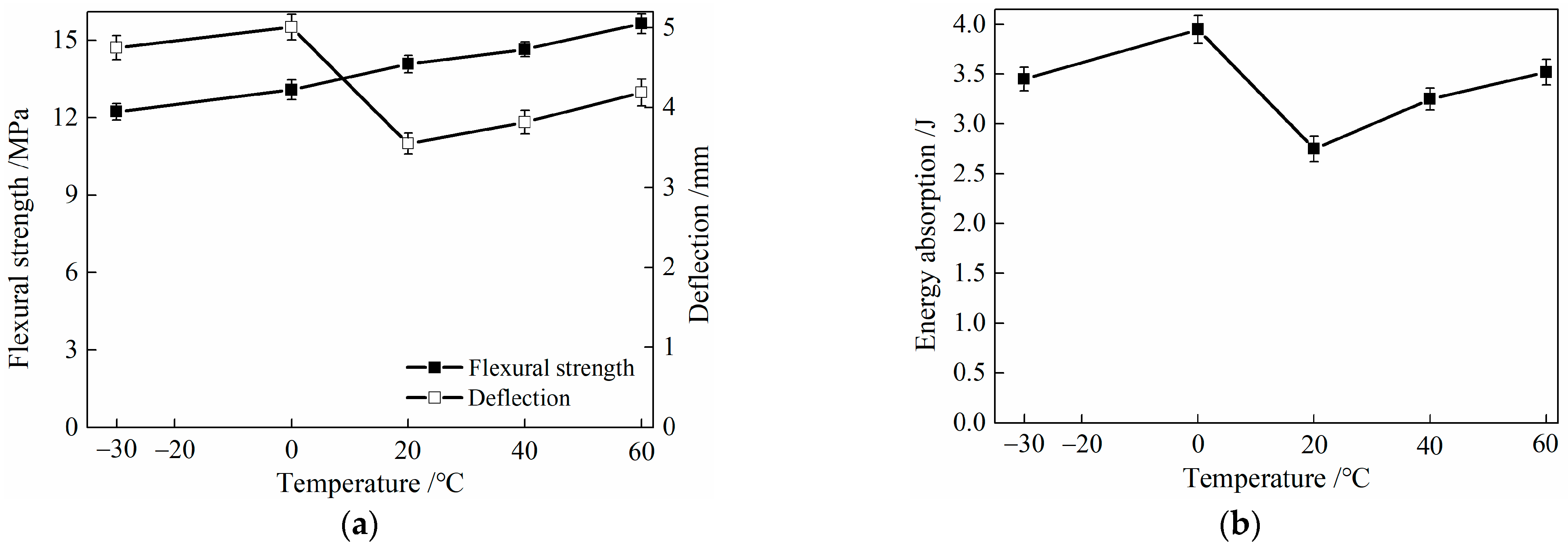
3.5.3. Characteristic Parameters
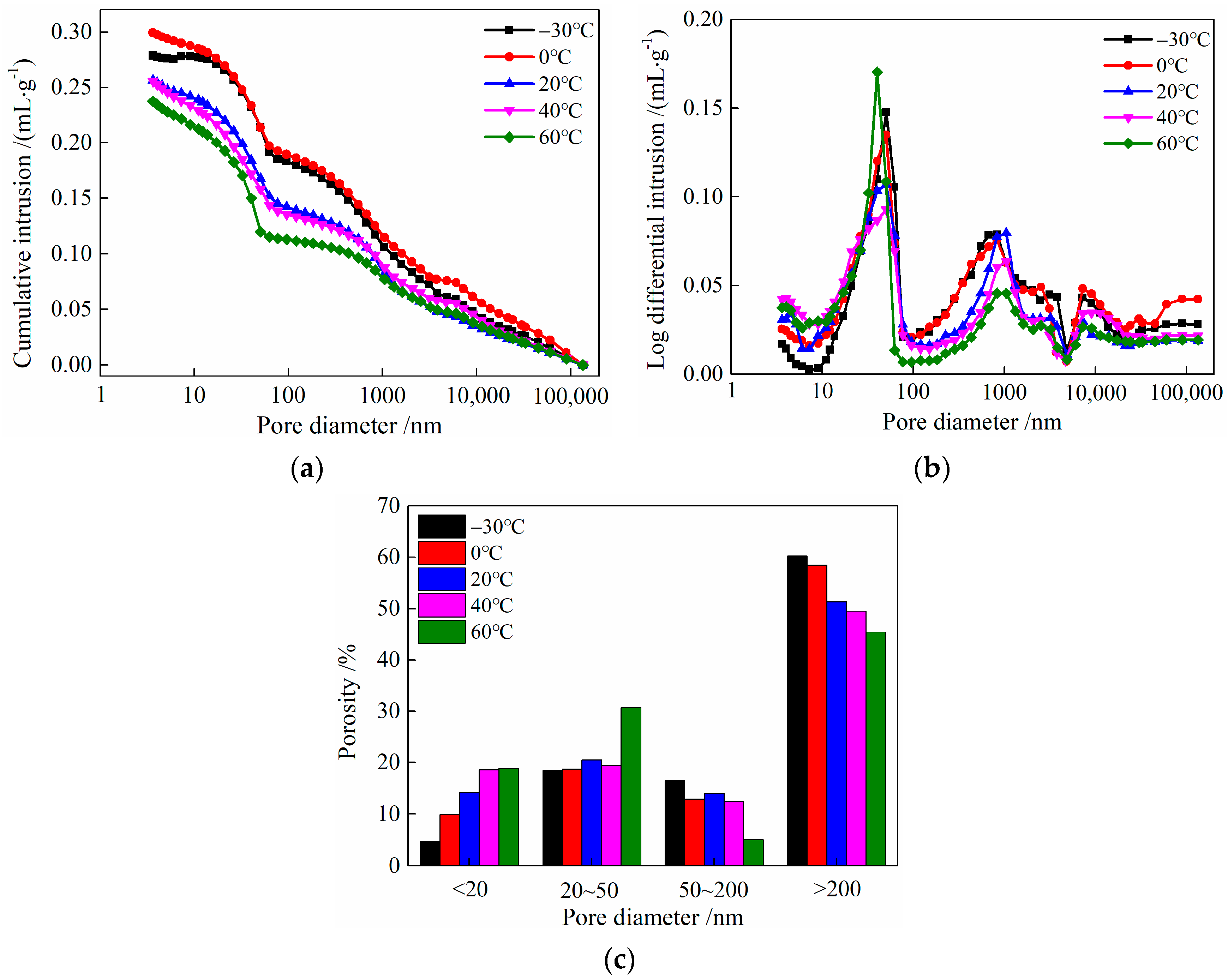
3.6. Pore Structure
4. Conclusions
- Compared with HDC treated at room temperature (20 °C), the cubic compressive strength, axial compressive strength, and elastic modulus of HDC treated at low temperatures (−30 and 0 °C) decrease, while those treated at high temperatures (40 and 60 °C) increase. The Poisson’s ratio of HDC remained almost constant after treatment at different temperatures. In the design of HDC bridge deck link slabs, the compressive strength indicators of HDC under room temperature can be used without considering the temperature effect.
- After treatment at different temperatures, multiple cracking is observed in the tensile specimens of HDC, and the stress–strain curves show strain-hardening stages. The constitutive relationship can be simplified as a bilinear model. Compared with HDC treated at room temperature (20 °C), the ultimate tensile strength of HDC decreases after treatment at low temperatures (−30 and 0 °C), while it increases after treatment at high temperatures (40 and 60 °C). The ultimate tensile strain and strain energy of HDC increase after treatment at low and high temperatures. In the design of HDC bridge deck link slabs, the effect of temperature on the tensile properties of HDC should be considered.
- HDC exhibits deflection hardening in its flexural stress–deflection relationship, and the failure mode is multiple cracking. After subjecting the material to low temperatures (−30 and 0 °C), the flexural strength of HDC decreases, while the ultimate deflection and energy absorption increase, compared to its performance at room temperature (20 °C). However, after being exposed to high temperatures (40 and 60 °C), the flexural strength, ultimate deflection, and energy absorption of HDC increase. When analyzing the structural property of HDC bridge deck link slabs, it is important to consider the influence of temperature on the flexural property parameters of HDC.
- The porosity of harmless and less harmful pores in HDC gradually increases as the temperature increases within the range of −30 to 60 °C, while the porosity of harmful and more harmful pores decreases. After being treated at a high temperature of 60 °C, both the critical pore size and most probable pore size of HDC decrease.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinoma International Engineering Co., Ltd. Standard Test Method for the Mechanical Properties of Ductile Fiber Reinforced Cementitious Composites: JC/T 2461-2018; China Building Materials Press: Beijing, China, 2018. [Google Scholar]
- Guo, L.P.; Wang, M.; Ding, C.; Chai, L.J. Effect of incorporating reclaimed asphalt pavement on macroscopic and microstructural properties of high ductility cementitious composites. Constr. Build. Mater. 2020, 260, 119956. [Google Scholar]
- Su, L.; Wang, S.L.; Gao, Y.; Liu, J.L.; Shao, X.D. In situ experimental study on the behavior of UHPC composite orthotropic steel bridge deck. Materials 2020, 13, 253. [Google Scholar] [CrossRef]
- Li, Y.H.; Zhang, N.; Sun, R.J.; Guan, Y.H.; Liu, L.M.; Tian, C.J.; Ling, Y.F.; Zhang, H.Z.; Šavija, B. Behavior of engineered cementitious composites (ECCs) subjected to coupled sustained flexural load and salt frost. Materials 2023, 16, 165. [Google Scholar] [CrossRef] [PubMed]
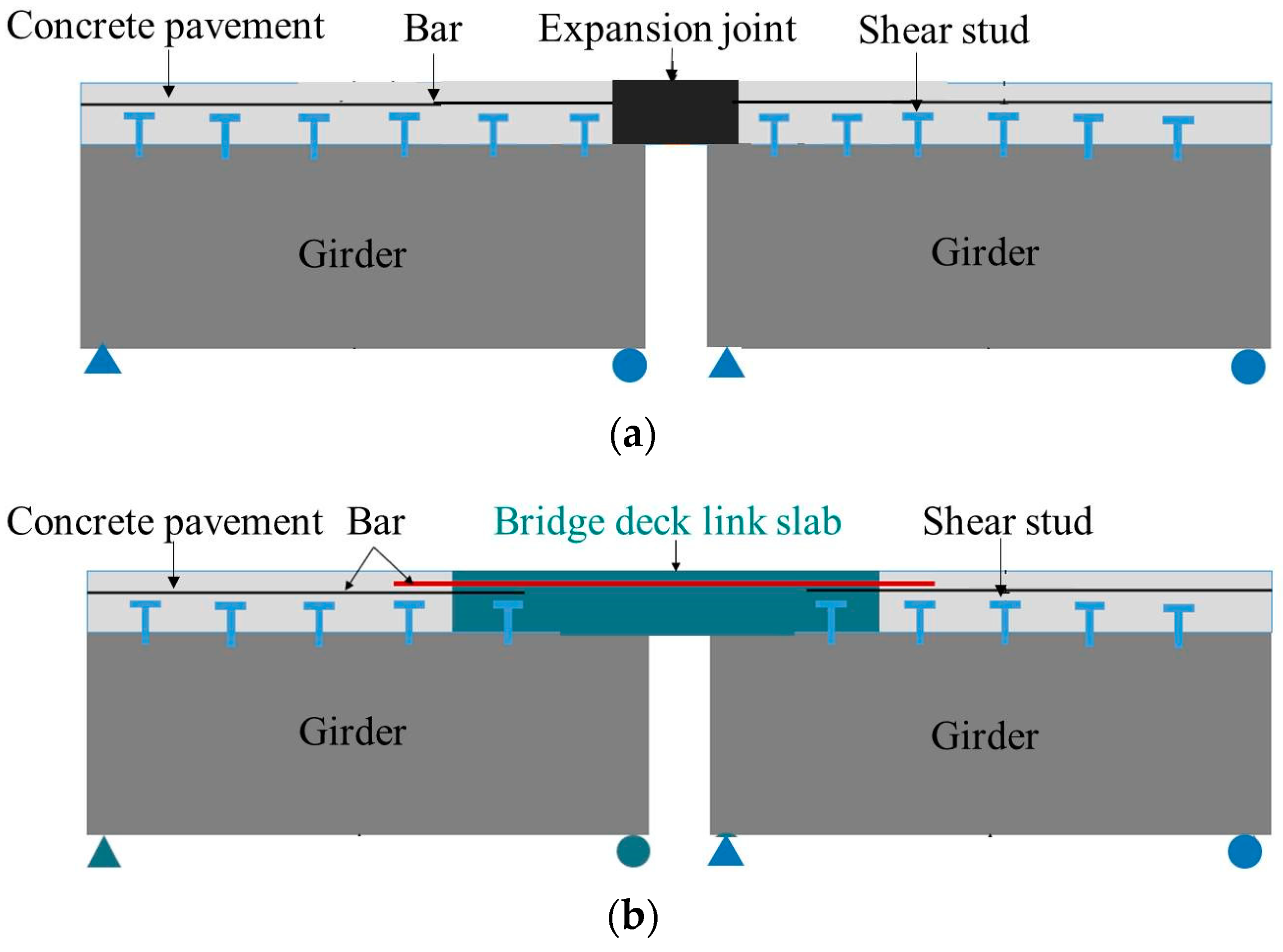
- Lepech, M.D.; Li, V.C. Application of ECC for bridge deck link slabs. Mater. Struct. 2009, 42, 1185–1195. [Google Scholar] [CrossRef]
- Guo, L.P.; Zhu, C.D.; Fan, Y.G.; Chen, B.; Chen, Z.K. Design and application of high ductility cementitious composite (HDCC) for bridge deck link slab repairing. China Concr. Cem. Prod. 2016, 36–39. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, M.J.; Yoo, D.Y. Combined effect of SCMs and curing temperature on mechanical properties of high-strength strain-hardening cementitious composites. J. Reinf. Plast. Comp. 2022, 41, 331–346. [Google Scholar] [CrossRef]
- Nematollahi, B.; Sanjayan, J.; Qiu, J.S.; Yang, E.H. Micromechanics-based investigation of a sustainable ambient temperature cured one-part strain hardening geopolymer composite. Constr. Build. Mater. 2017, 131, 552–563. [Google Scholar] [CrossRef]
- Shaaban, I.G.; Rizzuto, J.P.; El-Nemr, A.; Bohan, L.; Ahmed, H.; Tindyebwa, H. Mechanical properties and air permeability of concrete containing waste tyres extracts. J. Mater. Civil Eng. 2021, 33, 04020472.1–04020472.12. [Google Scholar] [CrossRef]
- Yu, J.T.; Lin, J.H.; Zhang, Z.G.; Li, V.C. Mechanical performance of ECC with high-volume fly ash after sub-elevated temperatures. Constr. Build. Mater. 2015, 99, 82–89. [Google Scholar] [CrossRef]
- Dong, F.Y.; Yu, K.Q.; Yu, J.T.; Wang, Y.C.; Liu, K.K. Effects of environmental temperature on the mechanical properties of polyethylene fiber-engineered cementitious composites. Struct. Concr. 2022, 23, 3114–3125. [Google Scholar] [CrossRef]
- Li, L.L.; Shi, J.P.; Kou, J.L.; Yan, Z.J. Mechanical properties of high-ductility concrete at different temperatures. Mag. Concrete Res. 2023. [Google Scholar] [CrossRef]
- Lei, D.Y.; Guo, L.P.; Chen, B.; Curosu, I.; Mechtcherine, V. The connection between microscopic and macroscopic properties of ultra-high strength and ultra-high ductility cementitious composites (UHS-UHDCC). Compos. Part B Eng. 2019, 164, 144–157. [Google Scholar] [CrossRef]
- Ding, C.; Guo, L.P.; Chen, B. Orientation distribution of polyvinyl alcohol fibers and its influence on bridging capacity and mechanical performances for high ductility cementitious composites. Constr. Build. Mater. 2020, 247, 118491. [Google Scholar] [CrossRef]
- Chai, L.J.; Guo, L.P.; Chen, B.; Xu, Y.H. Interactive effects of freeze-thaw cycle and carbonation on tensile property of ecological high ductility cementitious composites for bridge deck link slab. Constr. Build. Mater. 2018, 186, 773–781. [Google Scholar] [CrossRef]
- CCCC Highway Consultants Co., Ltd. General Specifications for Design of Highway Bridges and Culverts: JTG D60-2015; China Communications Press: Beijing, China, 2015. [Google Scholar]
- Zhang, L.H. Research on Preperation, Key Performance and Mechanism of Eco-High Ductility Cementitious Composites. Master’s Thesis, Southeast University, Nanjing, China, 2014. [Google Scholar]
- Chen, Z.K. Optimized Design and Key Performance of Domestic Green High Ductility Cementitious Composites. Master’s Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Zhang, L.H.; Guo, L.P.; Sun, W.; Zhang, W.X.; Chen, Z.K. Rheological property and fiber dispersion of high ductility cementitious composites. J. Southeast Univ. (Nat. Sci. Ed.) 2014, 44, 1037–1040. [Google Scholar]
- Chai, L.J. Design and Key Performance of Jointless Link Slab for Bridge Deck Made by ecological High Ductility Cementitious Composites. Ph.D. Thesis, Southeast University, Nanjing, China, 2020. [Google Scholar]
- Chai, L.J.; Guo, L.P.; Chen, B.; Xu, Y.H.; Ding, C. Mechanical properties of ecological high ductility cementitious composites produced with recycled crumb rubber and recycled asphalt concrete. J. Mater. Cycles Waste 2019, 21, 488–502. [Google Scholar] [CrossRef]
- Ismail, M.K.; Sherir, M.A.A.; Siad, H.; Hassan, A.A.A.; Lachemi, M. Properties of self-consolidating engineered cementitious composite modified with rubber. J. Mater. Civil Eng. 2018, 30, 04018031.1–04018031.9. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, M.J.; Oh, T.; Jang, Y.S.; Park, J.J.; Yoo, D.Y. Mechanical properties of high-strength strain-hardening cementitious composites (HS-SHCC) with hybrid supplementary cementitious materials under various curing conditions. J. Build. Eng. 2022, 57, 104912. [Google Scholar] [CrossRef]
- Bhat, P.S.; Chang, V.; Li, M. Effect of elevated temperature on strain-hardening engineered cementitious composites. Constr. Build. Mater. 2014, 69, 370–380. [Google Scholar] [CrossRef]
- Liu, T.W.; Li, X.P.; Che, J.L. Study on bond performance between corroded deformed steel bar and DS-ECC. Materials 2022, 15, 9009. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Structures GB 50010-2010; China Architecture & Building Press: Beijing, China, 2010. [Google Scholar]
- Chai, L.J.; Guo, L.P.; Chen, B.; Cao, Y.Z. Effects of curing age on compressive and tensile stress-strain behaviors of ecological high ductility cementitious composites. J. Southeast Univ. (Engl. Ed.) 2020, 36, 73–80. [Google Scholar]
- Chai, L.J.; Guo, L.P.; Chen, B.; Tang, Y.J.; Fei, X.P. Tensile behaviors of ecological high ductility cementitious composites exposed to interactive freeze-thaw-carbonation and single carbonation. J. Southeast Univ. (Engl. Ed.) 2019, 35, 367–373. [Google Scholar]
- Yang, Y.N. Multi-Scale Constitutive Relation and Design Theory of Ecological High Ductility Cementitious Composites under Variable Temperature Conditions. Master’s Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Yu, J.; Leung, C.K.Y. Strength improvement of strain-hardening cementitious composites with ultrahigh-volume fly ash. J. Mater. Civil Eng. 2017, 29, 05017003. [Google Scholar] [CrossRef]
- Şahmaran, M.; Özbay, E.; Yücel, H.E.; Lachemi, M.; Li, V.C. Frost resistance and microstructure of engineered cementitious composites: Influence of fly ash and micro poly-vinyl-alcohol fiber. Cem. Concr. Compos. 2012, 34, 156–165. [Google Scholar] [CrossRef]
- Li, H.D. Experimental Research on Ultra High Toughness Cementitious Composites. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2008. [Google Scholar]
- Vantadori, S.; Carpinteri, A.; Guo, L.P.; Ronchei, C.; Zanichelli, A. Synergy assessment of hybrid reinforcements in concrete. Compos. Part B Eng. 2018, 147, 197–206. [Google Scholar] [CrossRef]
- Shen, A.Q.; Lin, S.L.; Guo, Y.C.; He, T.Q.; Lyu, Z.H. Relationship between flexural strength and pore structure of pavement concrete under fatigue loads and freeze-thaw interaction in seasonal frozen regions. Constr. Build. Mater. 2018, 174, 684–692. [Google Scholar] [CrossRef]
- Nam, J.; Kim, G.; Lee, B.; Hasegawa, R.; Hama, Y. Frost resistance of polyvinyl alcohol fiber and polypropylene fiber reinforced cementitious composites under freeze thaw cycling. Compos. Part B Eng. 2016, 90, 241–250. [Google Scholar] [CrossRef]







| Specimen ID | C | FA | S | PS | W | PVA |
|---|---|---|---|---|---|---|
| HDC-1 | 680 | 600 | 384 | 1.01 | 384 | 26 |
| HDC-2 | 768 | 512 | 384 | 1.54 | 397 | 26 |
| HDC-3 | 768 | 512 | 384 | 1.31 | 323 | 26 |
| HDC-4 | 768 | 512 | 384 | 1.92 | 253 | 26 |
| Test Program | Dimension/(mm × mm × mm) | Amount |
|---|---|---|
| Cubic compressive strength | 100 × 100 × 100 | 3 |
| Uniaxial tensile property | 13 × 30 × 100 (Dimension of pure tension zone) | 6 |
| Test Program | Dimension/(mm × mm × mm) | Amount |
|---|---|---|
| Cubic compressive strength | 100 × 100 × 100 | 3 |
| Axial compressive property | 100 × 100 × 300 | 3 |
| Uniaxial tensile property | 13 × 30 × 100 (Dimension of pure tension zone) | 6 |
| Flexural property | 15 × 75 × 300 | 3 |
| Specimen ID | Cubic Compressive Strength/MPa | Ultimate Tensile Strength /MPa | Ultimate Tensile Strain /% |
|---|---|---|---|
| HDC-1 | 48.0 ± 0.99 | 4.23 ± 0.09 | 1.15 ± 0.05 |
| HDC-2 | 47.8 ± 2.4 | 4.47 ± 0.15 | 0.64 ± 0.07 |
| HDC-3 | 50.2 ± 3.2 | 4.22 ± 0.23 | 0.55 ± 0.04 |
| HDC-4 | 59.0 ± 1.9 | 4.83 ± 0.17 | 0.42 ± 0.05 |
| Temperature /°C | Cubic Compressive Strength /MPa | Axial Compressive Strength /MPa | Elastic Modulus /GPa | Poisson’s Ratio | |
|---|---|---|---|---|---|
| −30 | 46.7 ± 1.02 (−2.71%) | 42.0 ± 1.11 (−2.55%) | 23.2 ± 0.6 (−2.52%) | 0.23 | 0.90 |
| 0 | 47.1 ± 1.13 (−1.88%) | 42.5 ± 1.23 (−1.41%) | 23.5 ± 0.7 (−1.26%) | 0.23 | 0.90 |
| 20 | 48.0 ± 0.99 (~) | 43.1 ± 0.98 (~) | 23.8 ± 0.8 (~) | 0.23 | 0.90 |
| 40 | 50.9 ± 1.15 (6.04%) | 45.7 ± 1.18 (6.03%) | 24.0 ± 0.98 (0.84%) | 0.23 | 0.90 |
| 60 | 52.7 ± 1.19 (9.79%) | 47.6 ± 1.32 (10.44%) | 24.1 ± 0.88 (1.26%) | 0.23 | 0.90 |
| Temperature /°C | Ultimate Tensile Strength /MPa | Ultimate Tensile Strain /% | Strain Energy /(J/m3 × 106) |
|---|---|---|---|
| −30 | 3.74 ± 0.08 (−11.58%) | 1.34 ± 0.06 (16.52%) | 4.42 (6.76%) |
| 0 | 3.99 ± 0.10 (−5.67%) | 1.46 ± 0.08 (26.96%) | 4.76 (14.98%) |
| 20 | 4.23 ± 0.09 (~) | 1.15 ± 0.05 (~) | 4.14 (~) |
| 40 | 4.46 ± 0.08 (5.44%) | 1.23 ± 0.07 (6.96%) | 4.76 (14.98%) |
| 60 | 4.80 ± 0.09 (13.48%) | 1.31 ± 0.06 (13.91%) | 5.14 (24.15%) |
| Temperature /°C | Elastic Stage | Strain-Hardening Stage | ||||
|---|---|---|---|---|---|---|
| /MPa | /MPa | /MPa | /% | |||
| −30 | 11.16 × 103 | 0.94 | 79.91 | 0.94 | 2.79 | 0.025 |
| 0 | 16.76 × 103 | 0.98 | 69.55 | 0.84 | 1.56 | 0.014 |
| 20 | 10.21 × 103 | 0.99 | 60.70 | 0.81 | 2.86 | 0.028 |
| 40 | 15.62 × 103 | 0.99 | 57.82 | 0.80 | 3.28 | 0.021 |
| 60 | 13.89 × 103 | 0.99 | 95.43 | 0.88 | 2.92 | 0.021 |
| Temperature /°C | Ultimate Load /kN | Flexural Strength /MPa | Ultimate Deflection /mm | Energy Absorption /J |
|---|---|---|---|---|
| −30 | 0.86 ± 0.32 (−13.13%) | 12.23 ± 0.32 (−13.13%) | 4.75 ± 0.15 (33.80%) | 3.45 (25.45%) |
| 0 | 0.92 ± 0.38 (−7.07%) | 13.08 ± 0.38 (−7.07%) | 5.01 ± 0.16 (41.13%) | 3.95 (43.64%) |
| 20 | 0.99 ± 0.34 (~) | 14.08 ± 0.34 (~) | 3.55 ± 0.13 (~) | 2.75 (~) |
| 40 | 1.03 ± 0.28 (4.04%) | 14.65 ± 0.28 (4.04%) | 3.82 ± 0.15 (7.61%) | 3.25 (18.18%) |
| 60 | 1.10 ± 0.38 (11.11%) | 15.64 ± 0.38 (11.11%) | 4.19 ± 0.17 (18.03%) | 3.52 (28.00%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, L.; Chen, B.; Guo, L.; Ren, B.; Chen, Z.; Huang, T. Effect of Ambient Temperature on the Mechanical Properties of High Ductility Concrete. Materials 2023, 16, 2465. https://doi.org/10.3390/ma16062465
Chai L, Chen B, Guo L, Ren B, Chen Z, Huang T. Effect of Ambient Temperature on the Mechanical Properties of High Ductility Concrete. Materials. 2023; 16(6):2465. https://doi.org/10.3390/ma16062465
Chicago/Turabian StyleChai, Lijuan, Bo Chen, Liping Guo, Biaokun Ren, Zhichun Chen, and Tianyong Huang. 2023. "Effect of Ambient Temperature on the Mechanical Properties of High Ductility Concrete" Materials 16, no. 6: 2465. https://doi.org/10.3390/ma16062465
APA StyleChai, L., Chen, B., Guo, L., Ren, B., Chen, Z., & Huang, T. (2023). Effect of Ambient Temperature on the Mechanical Properties of High Ductility Concrete. Materials, 16(6), 2465. https://doi.org/10.3390/ma16062465





