Liquefaction Potential of Saturated Sand Reinforced by Cement-Grouted Micropiles: An Evolutionary Approach Based on Shaking Table Tests
Abstract
1. Introduction
2. Shaking Table Tests
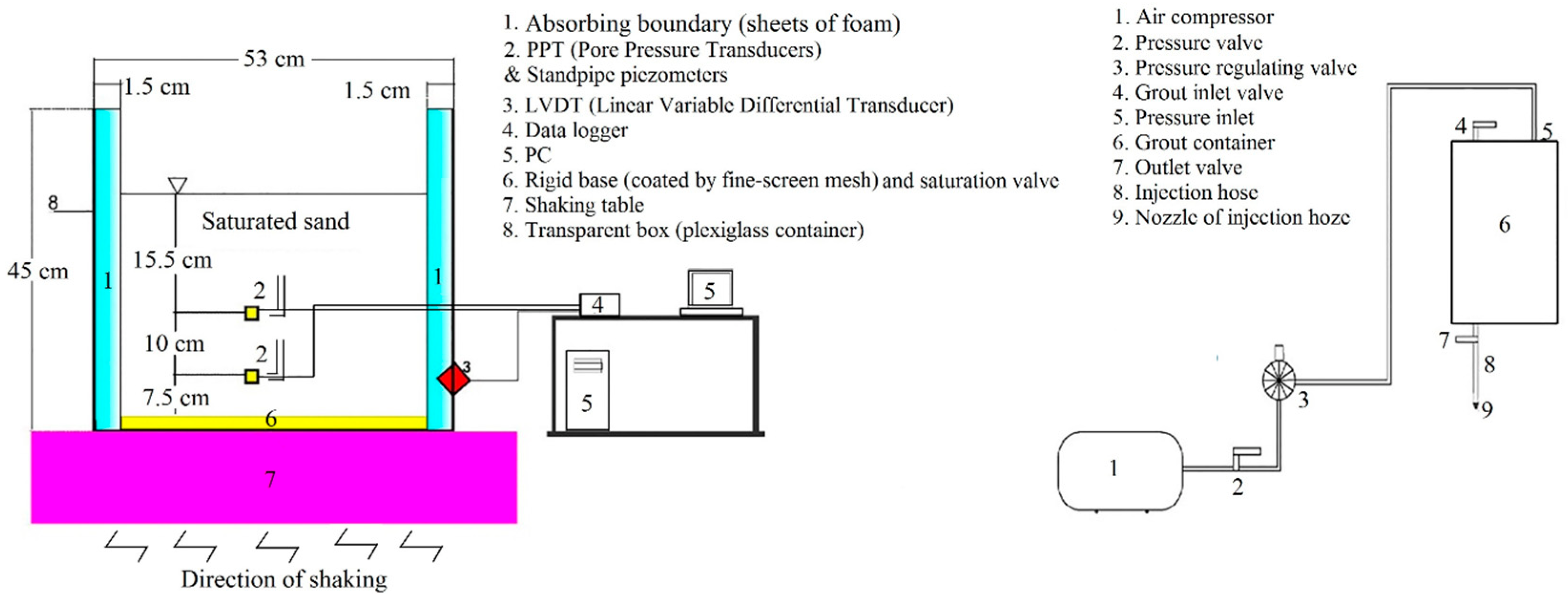
2.1. Rigid Transparent Box
2.2. Instrumentation
2.3. Grout-Injection Set-Up
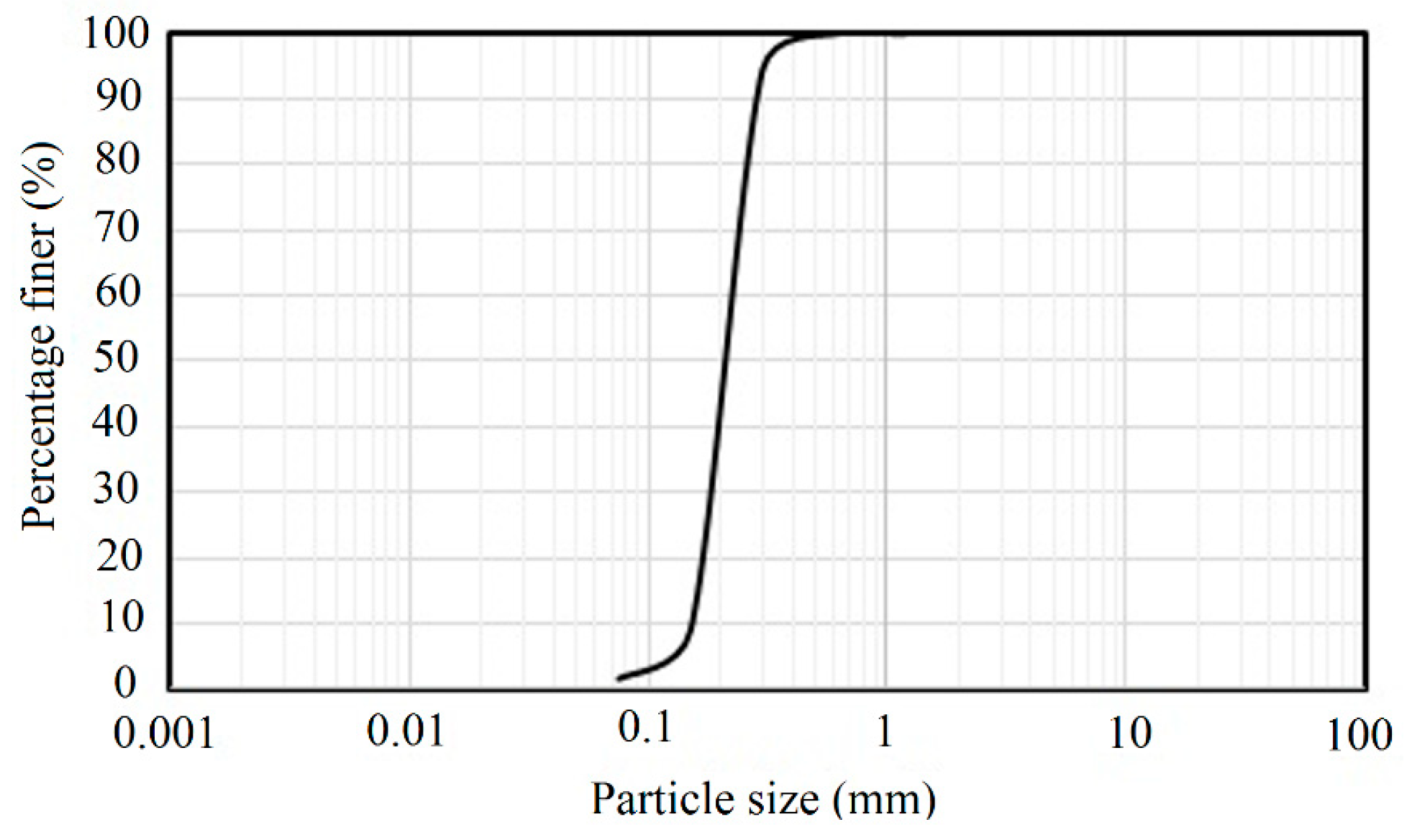
3. Material Properties
4. Physical Model
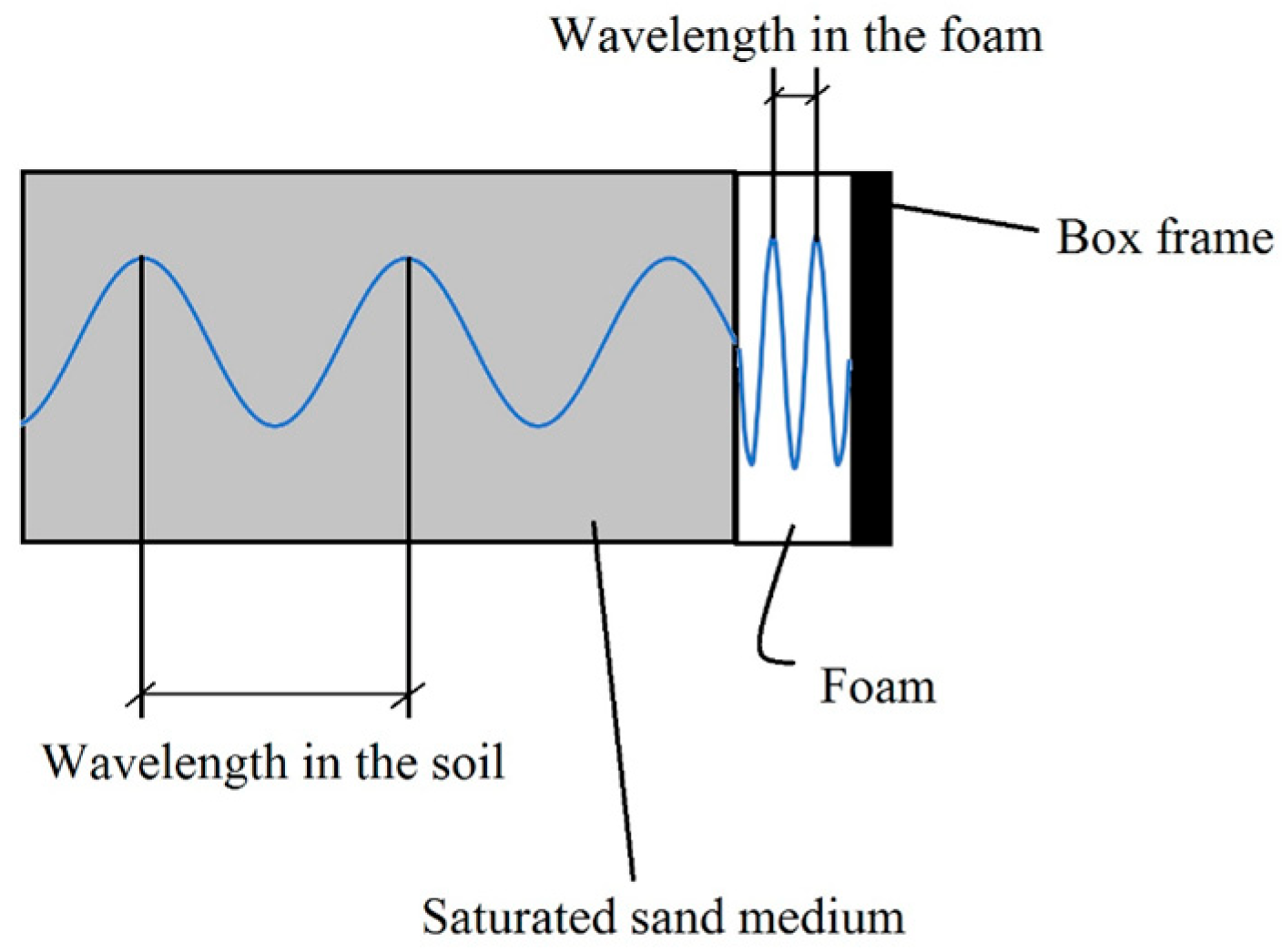
4.1. Boundary Condition
4.2. Scaling of Micropiles
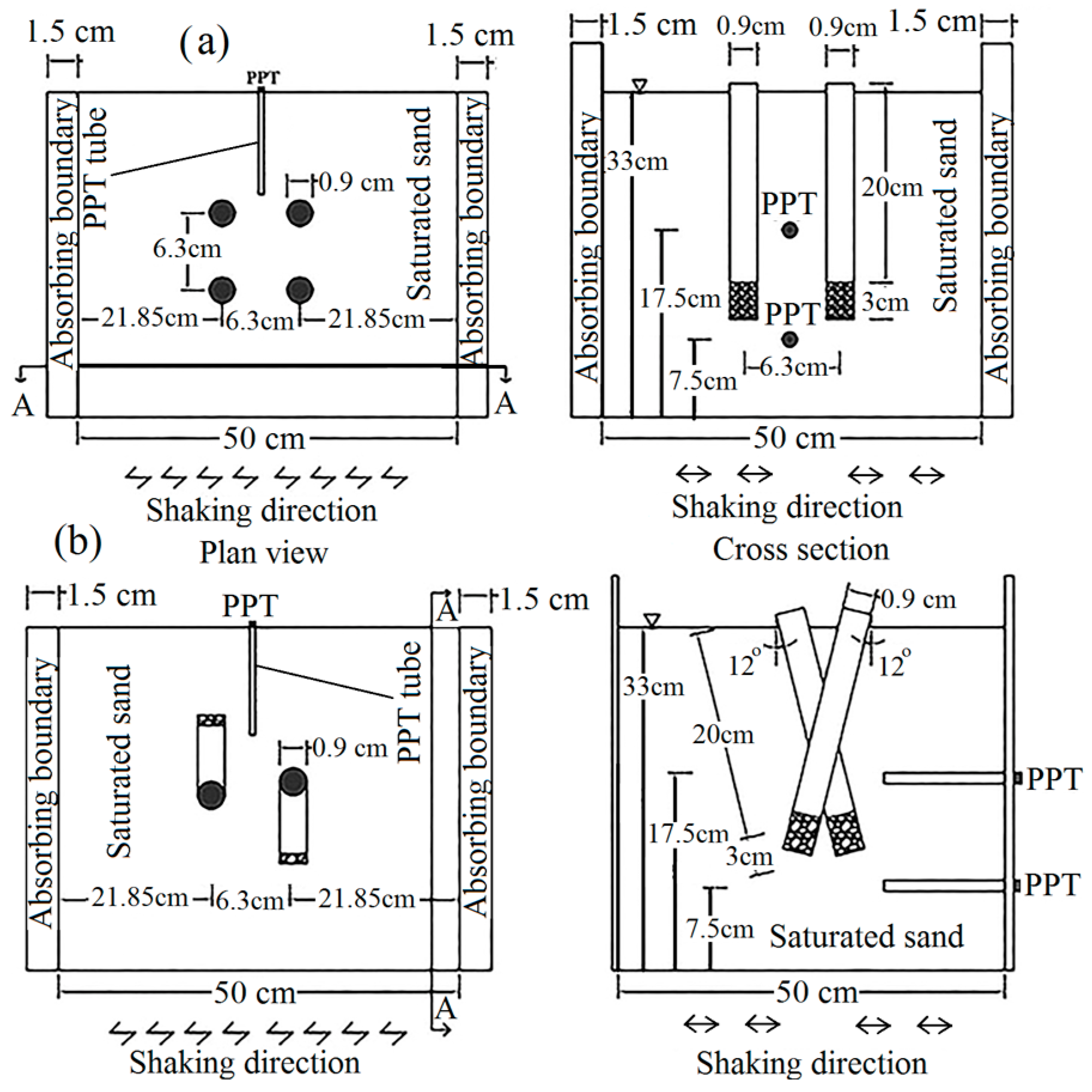
4.3. Model Preparation
5. Experimental Results
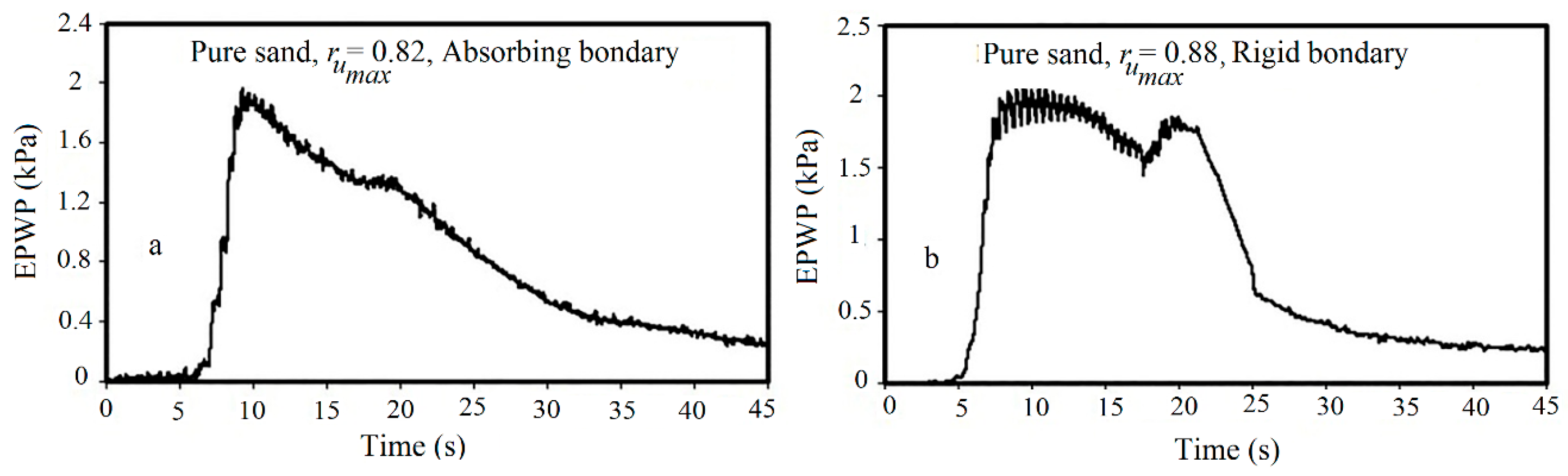
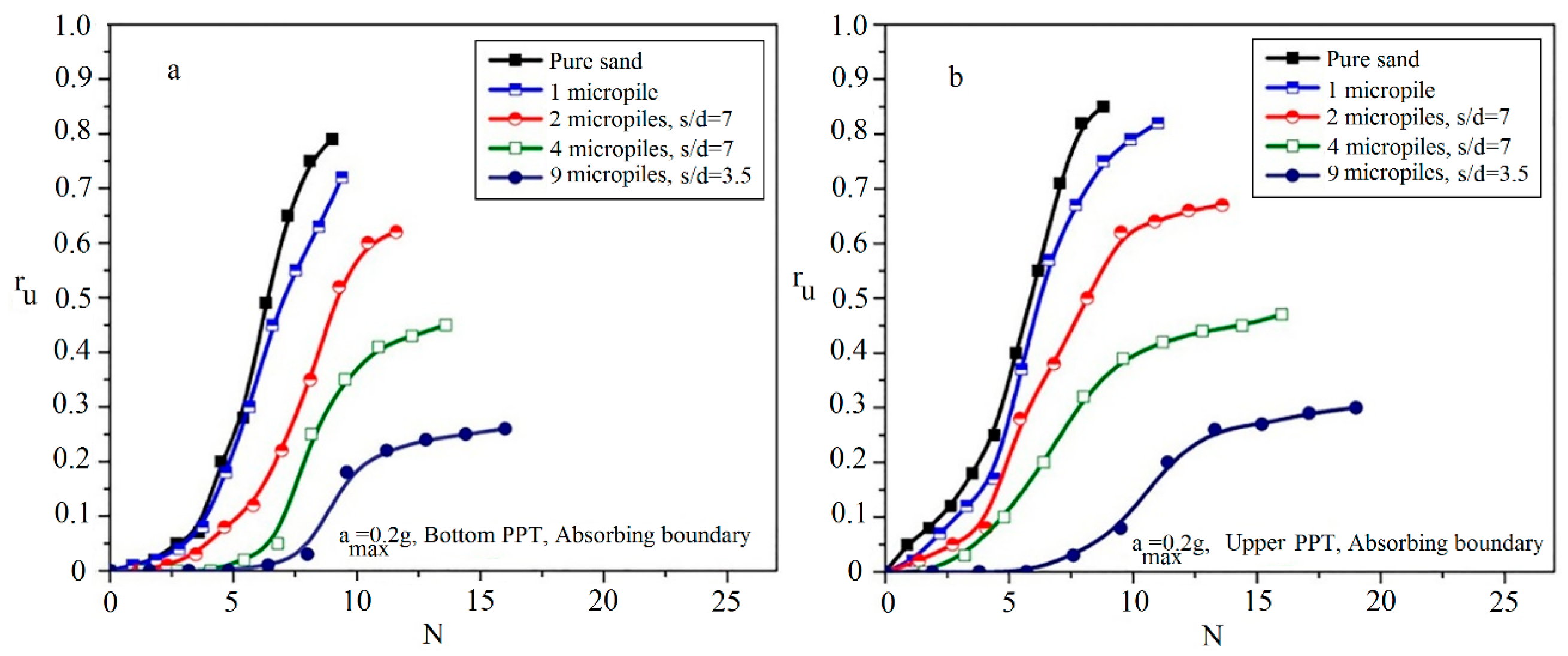
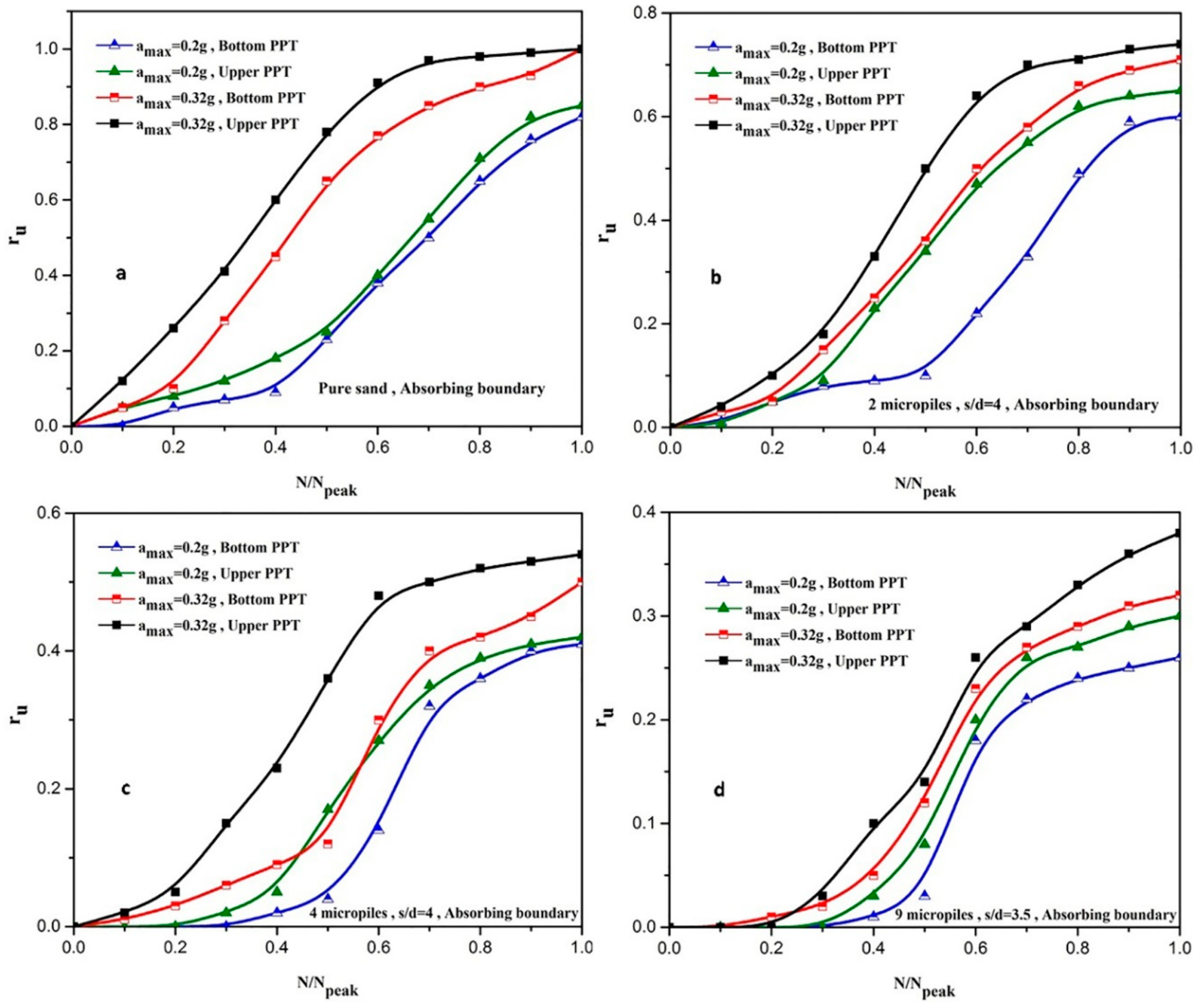
5.1. Effect of Boundary Conditions on Excess Pore Water Pressure Ratio (ru)
5.2. Effects of Different Arrangements of Micropiles on ru Values
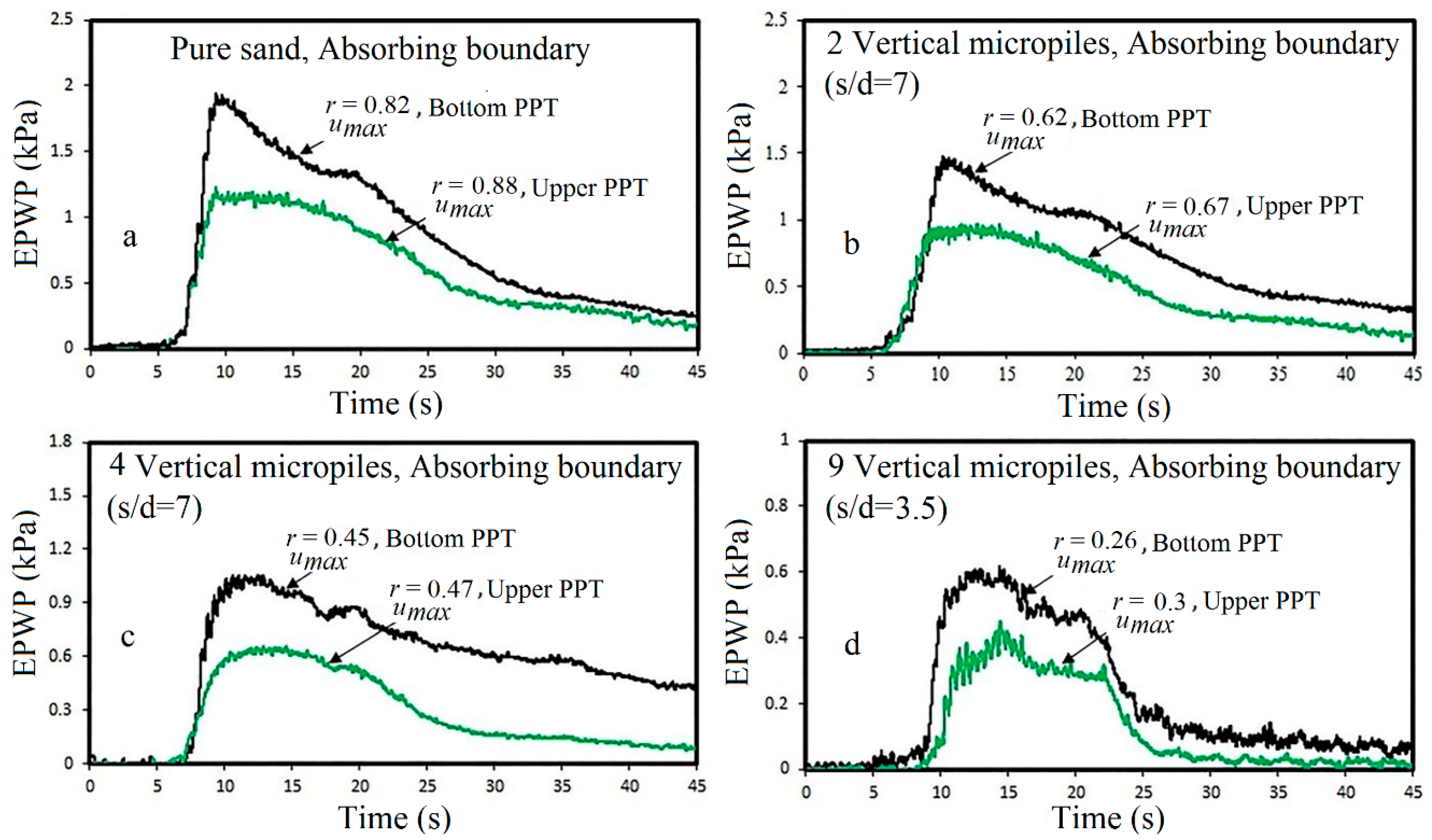
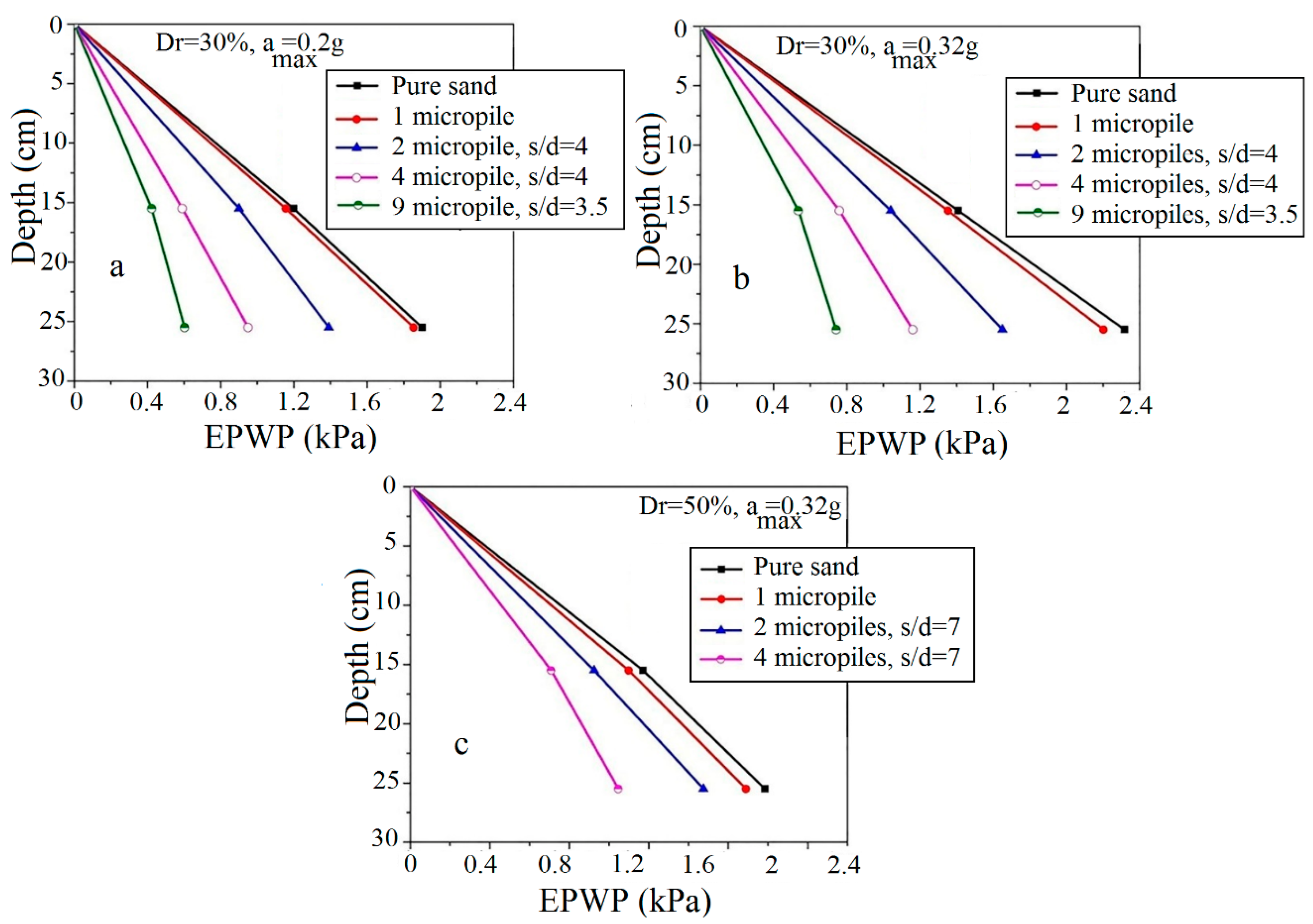
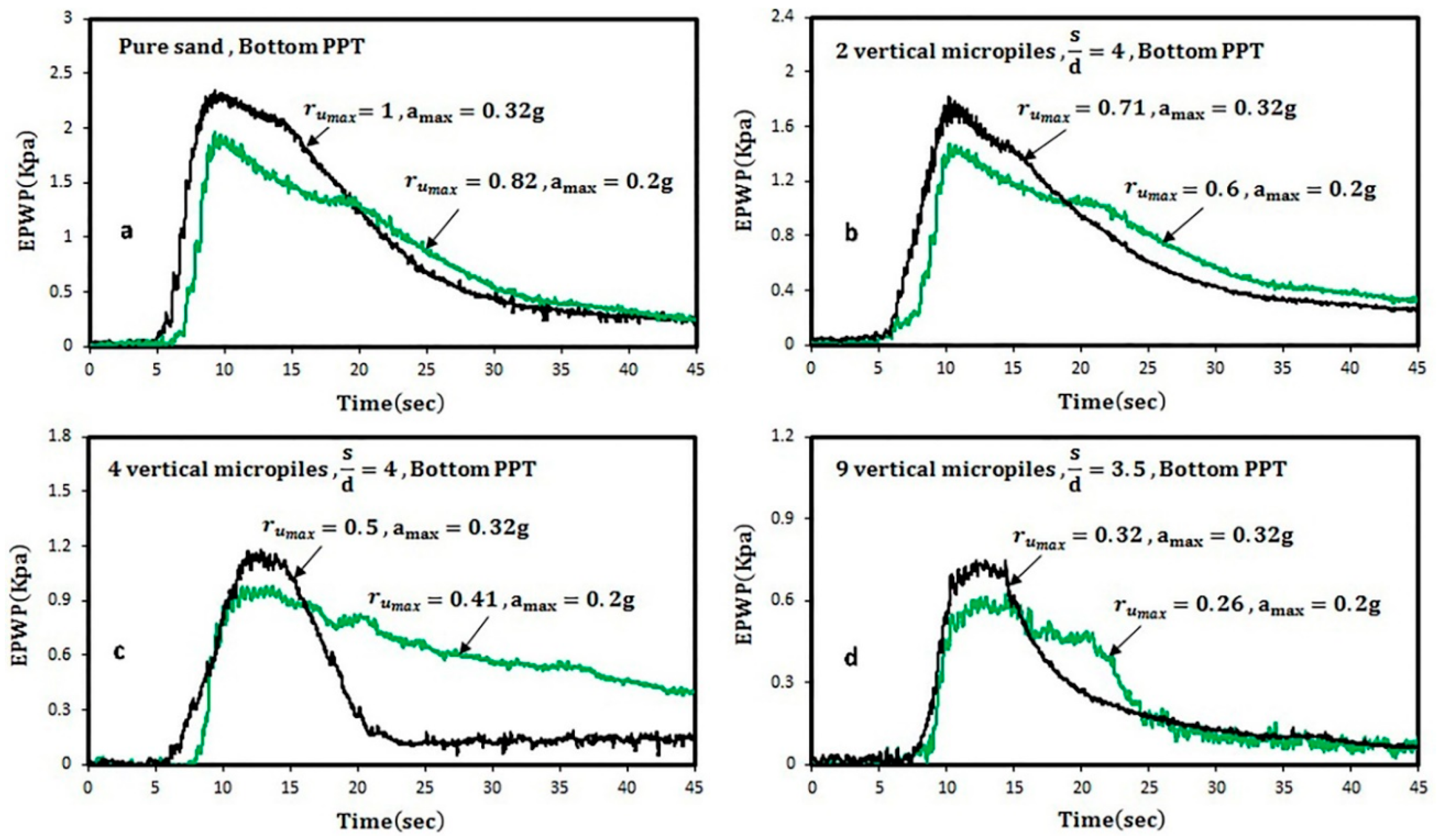
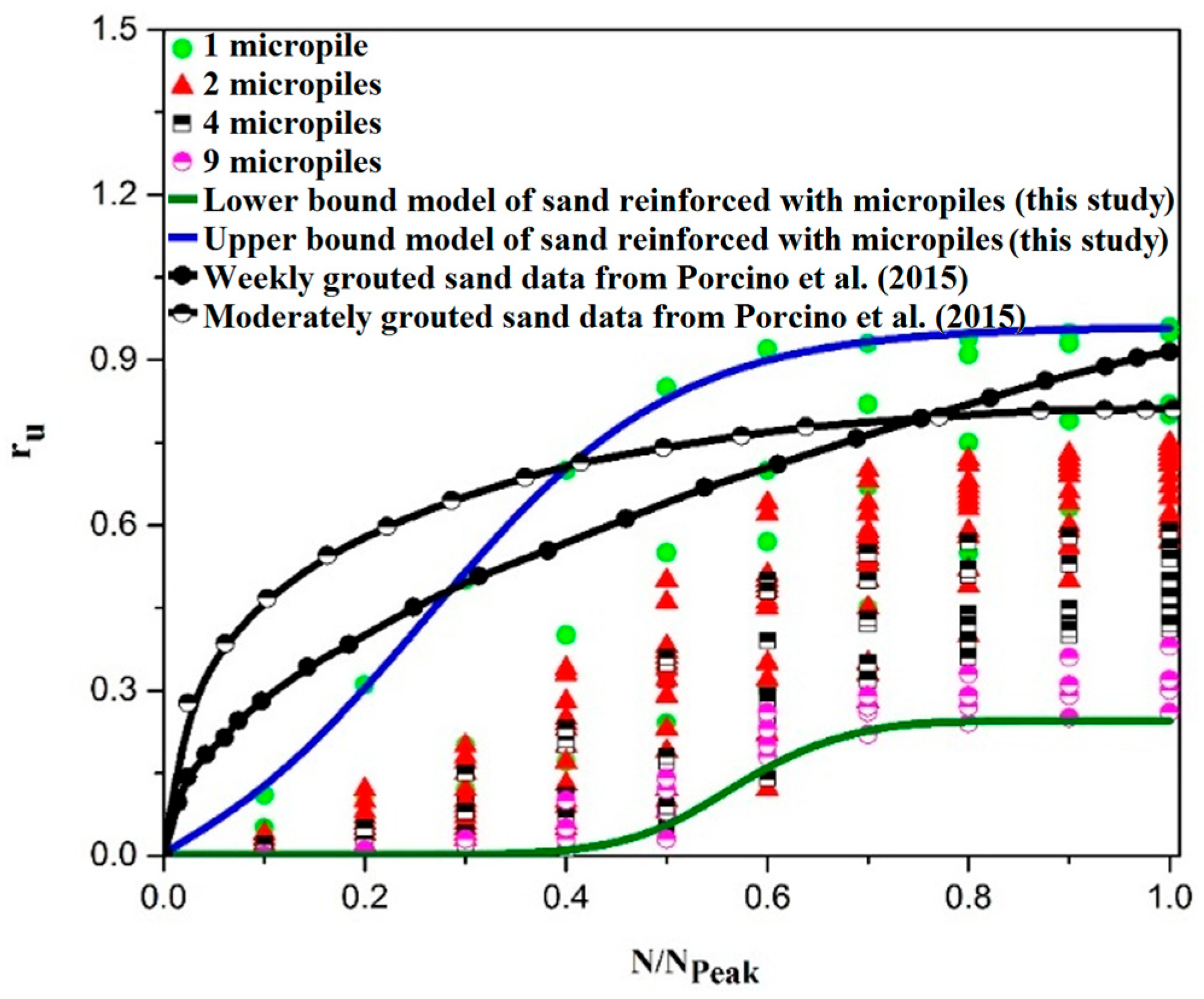
5.2.1. Effect of the Number of Micropiles
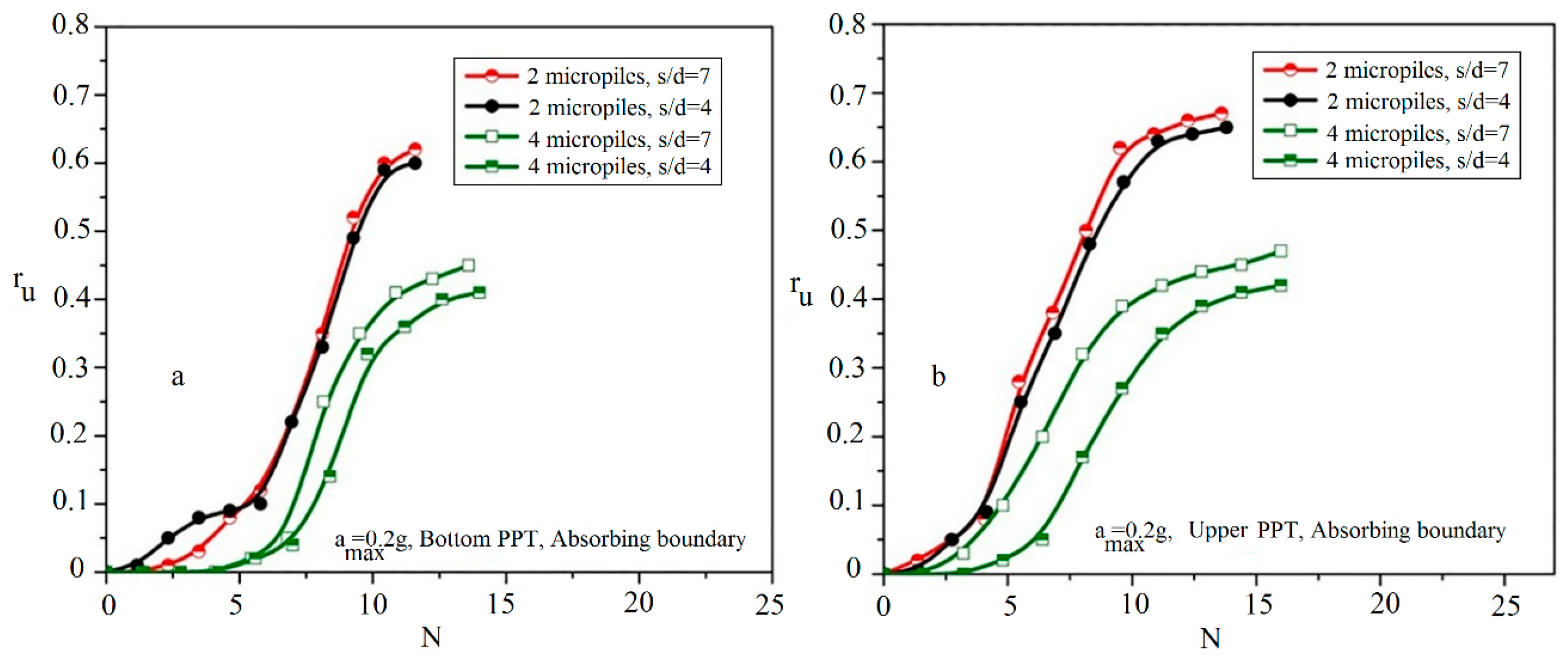
5.2.2. Effects of Micropiles Spacing Ratio (Smic/dmic)
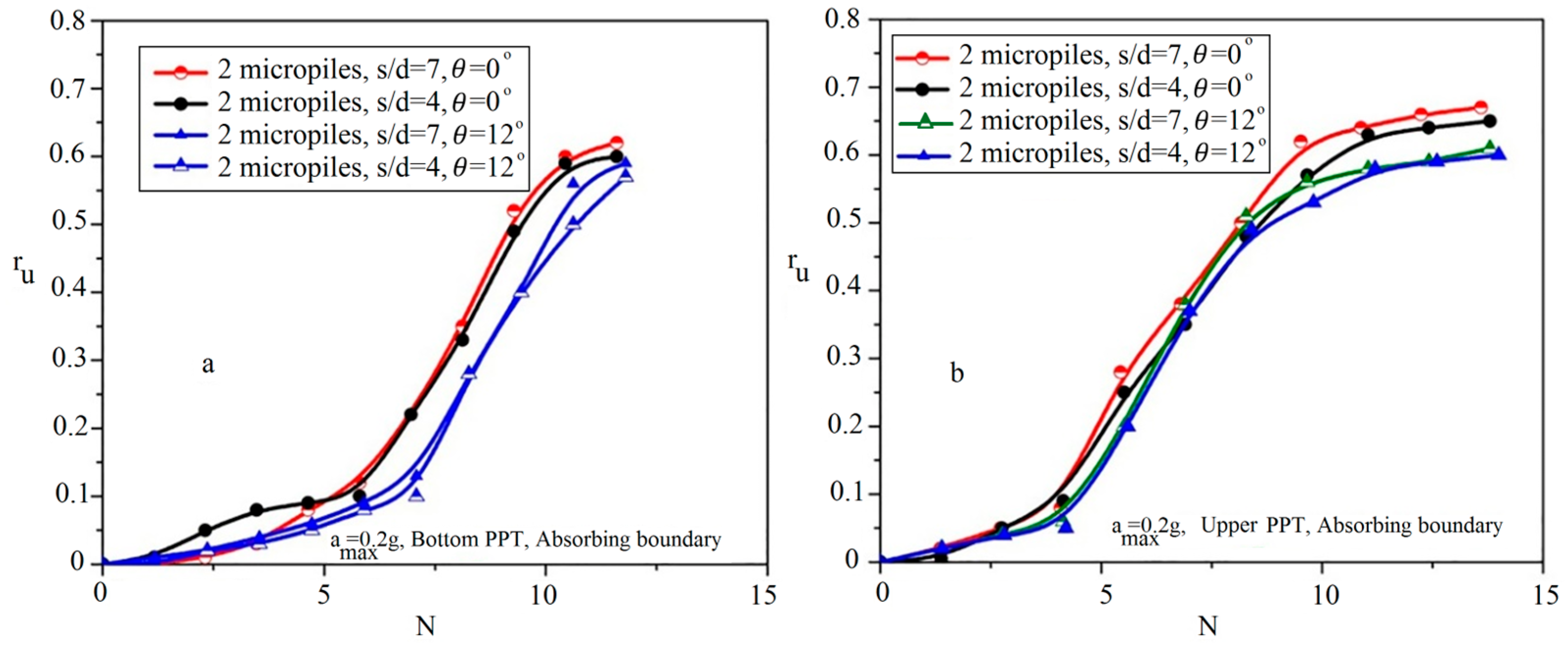
5.2.3. Effects of Micropiles’ Inclination
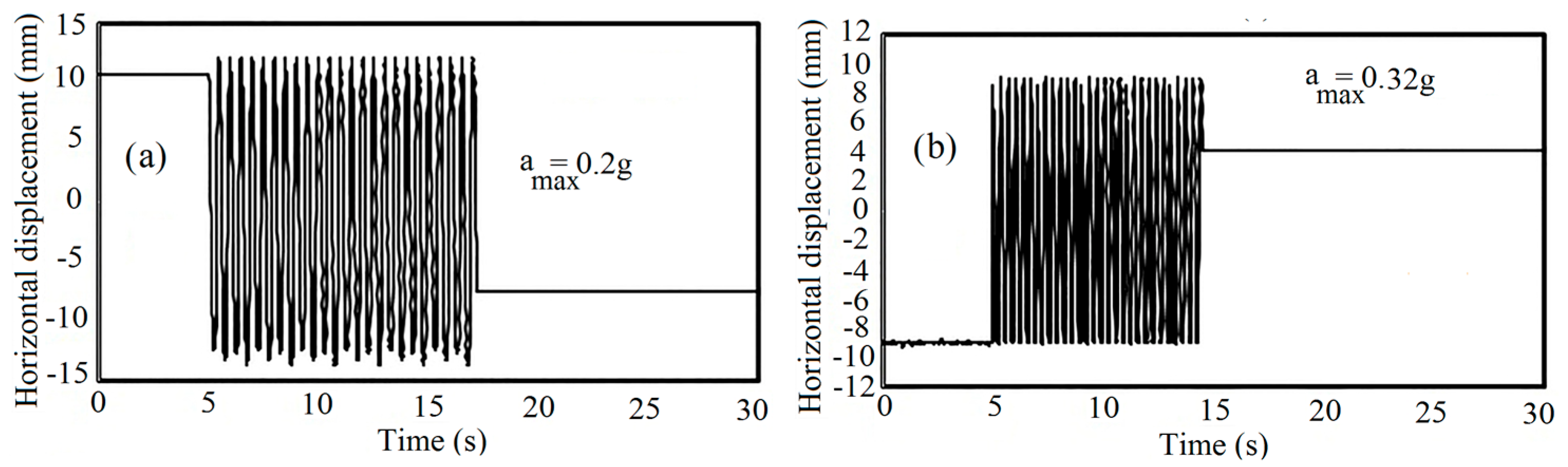
5.3. Effect of Different Scaled Accelerations on ru Values
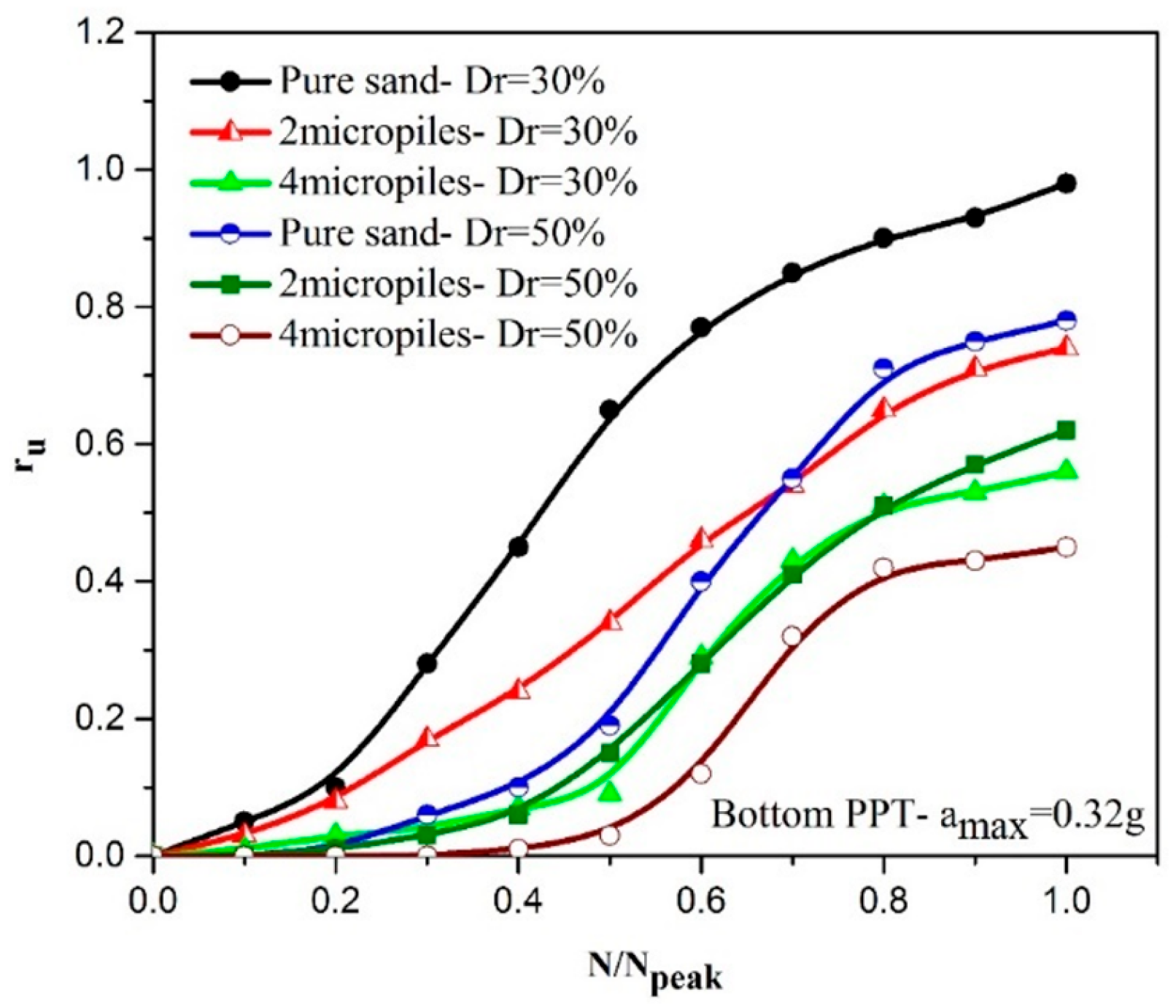
5.4. Effect of the Relative Density of Soil on ru Values
6. Data Processing and Modeling
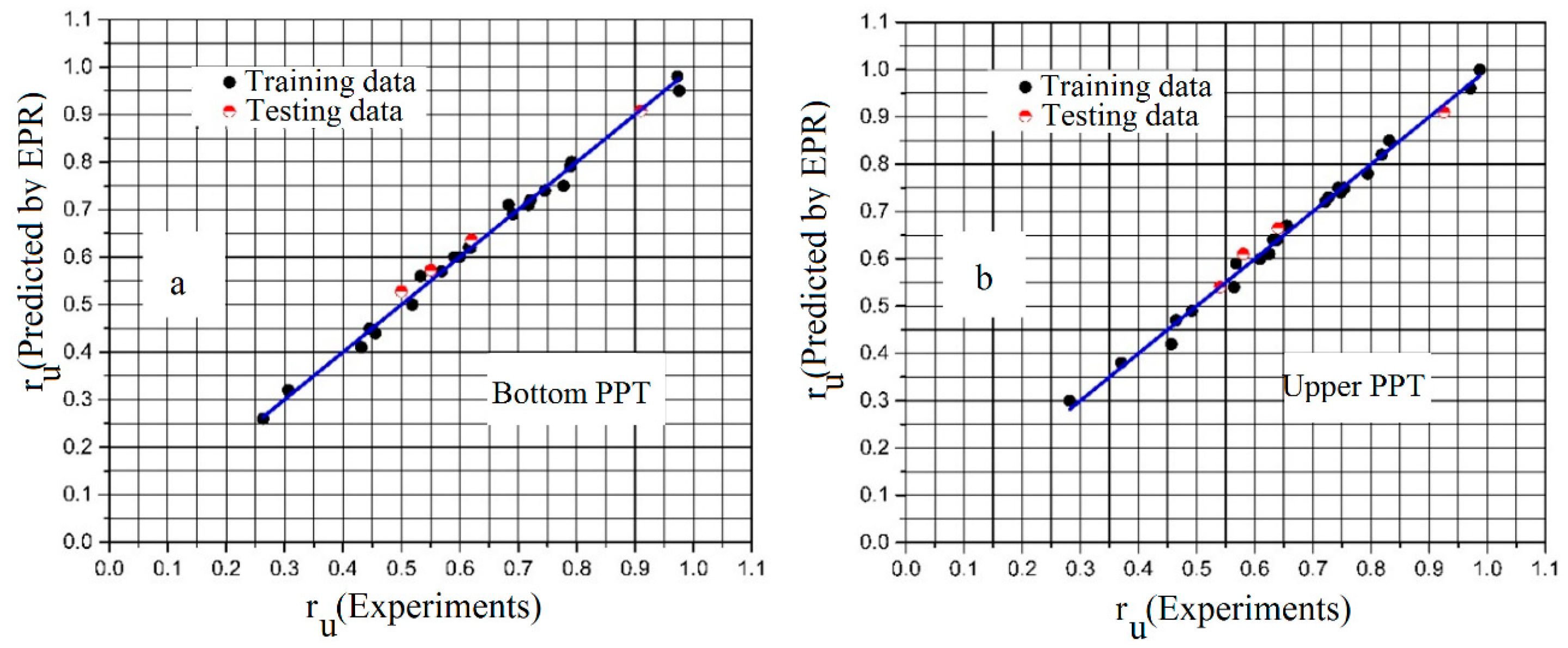
6.1. Predictive Model for the Potential of Liquefaction
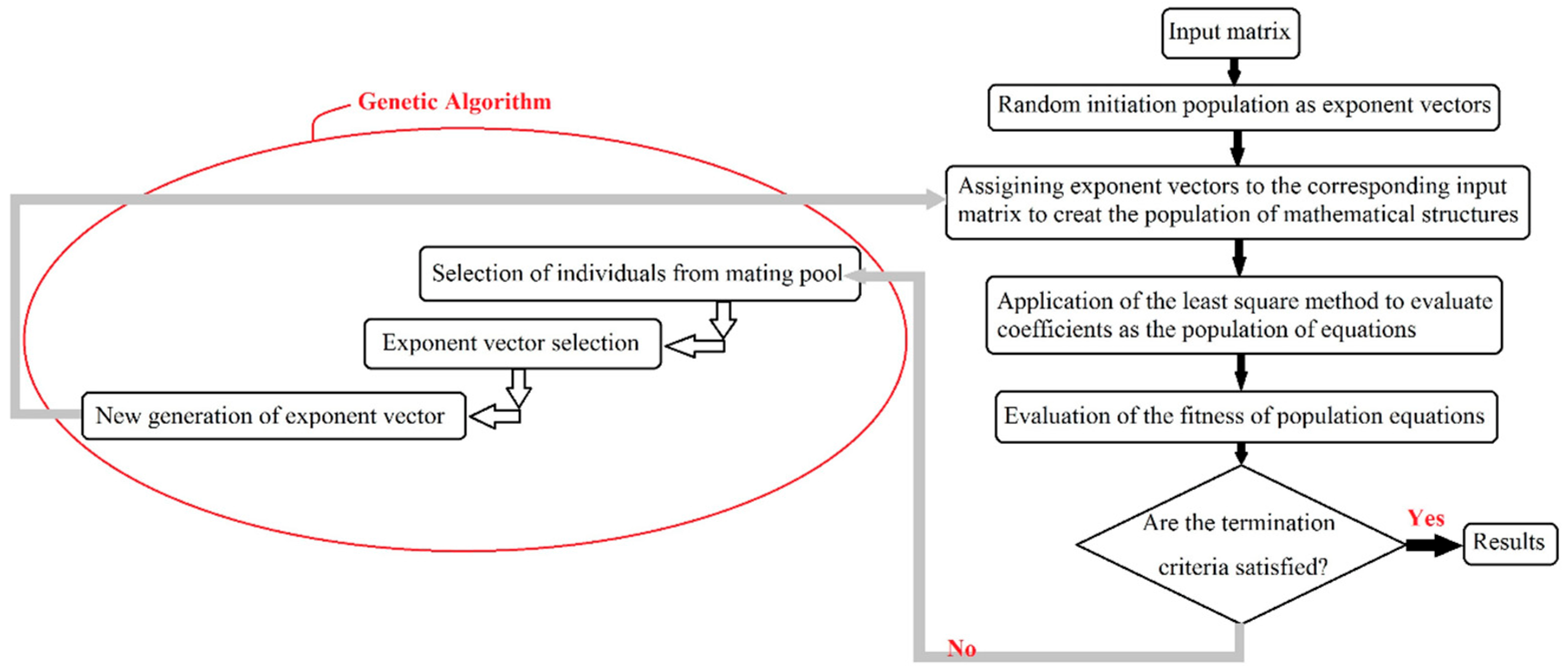
6.2. Evolutionary Polynomial Regression Modeling (EPR)
7. Multiple-Variable Parametric (MVP) Study on the Potential of Liquefaction
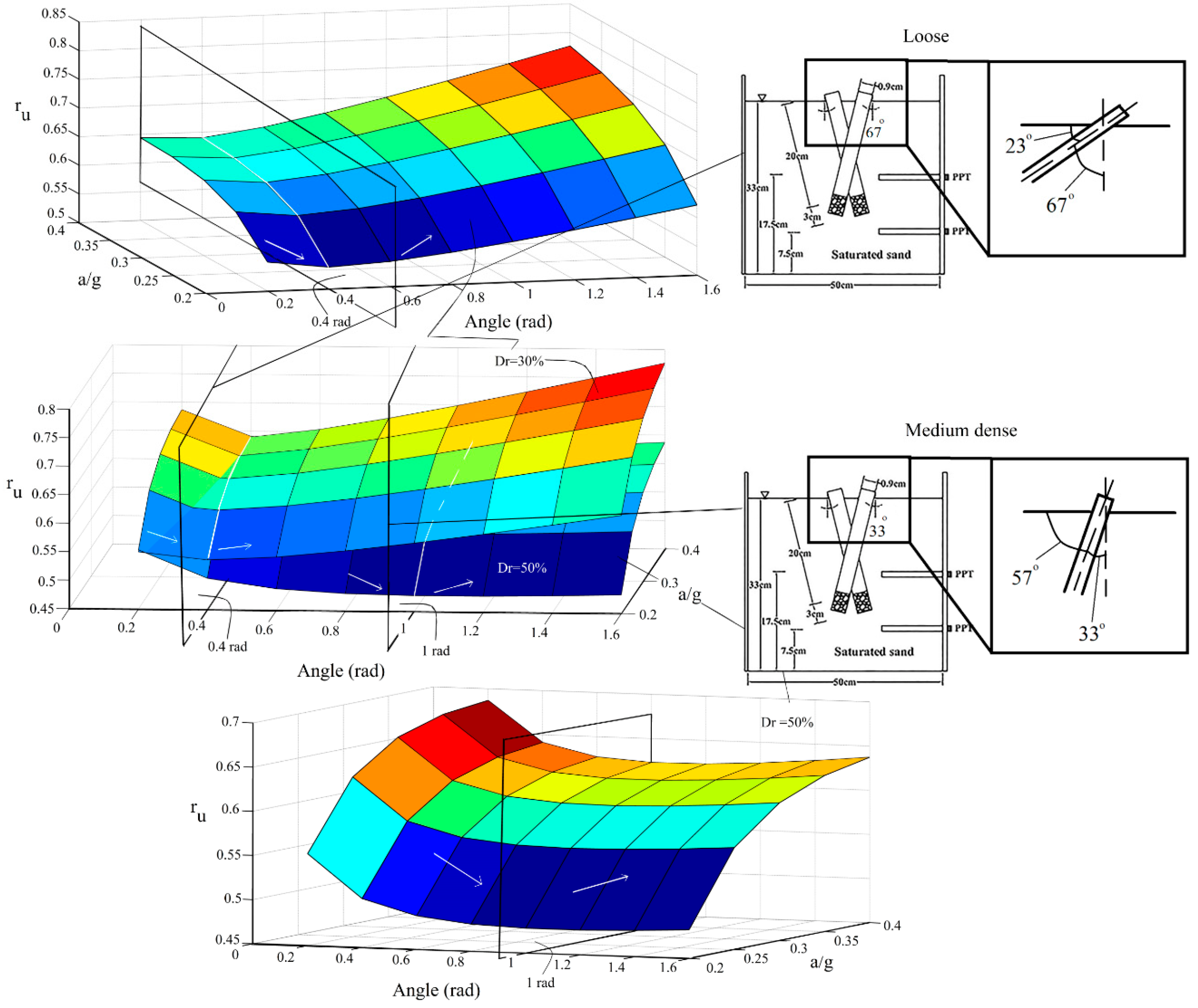
7.1. Simultaneous Effects of a/g, Inclination Angle, and Relative Density
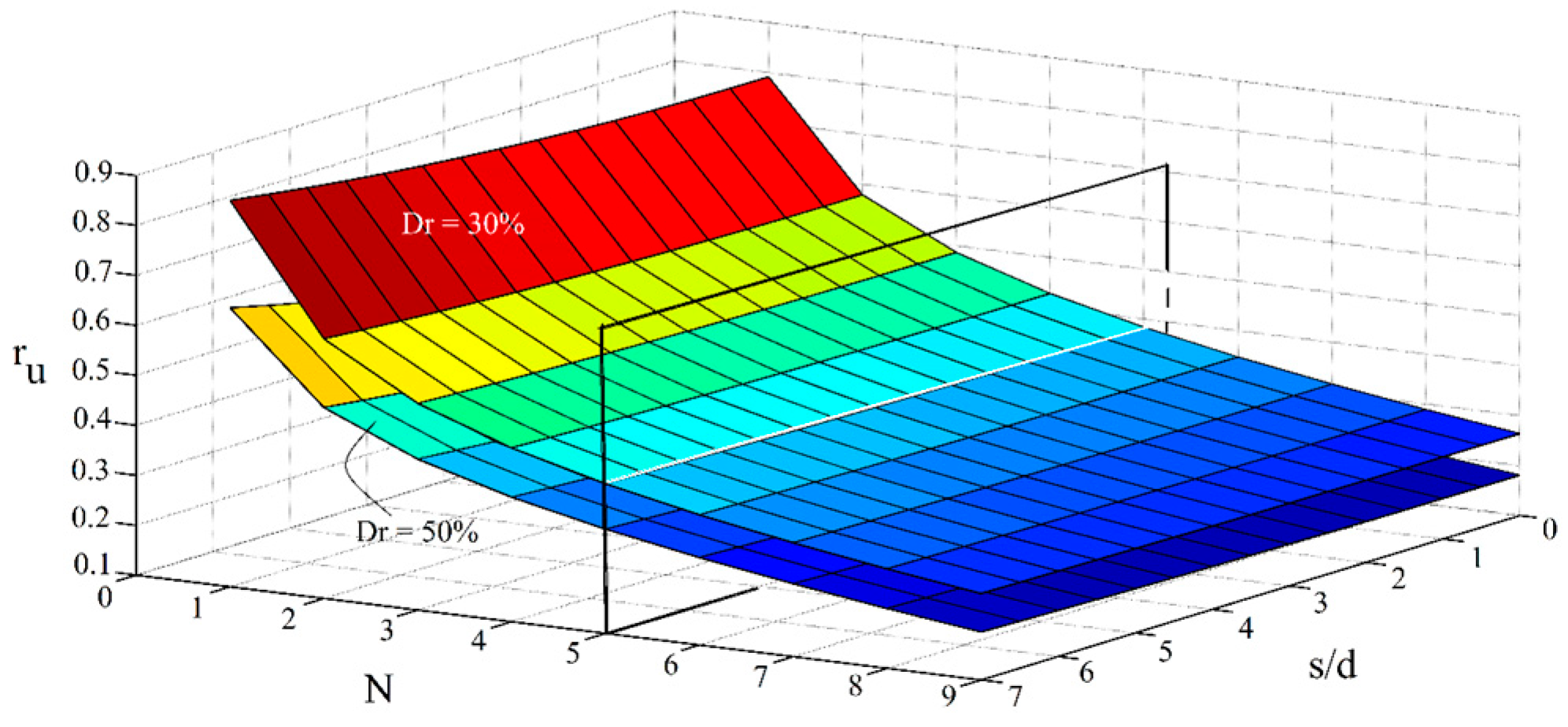
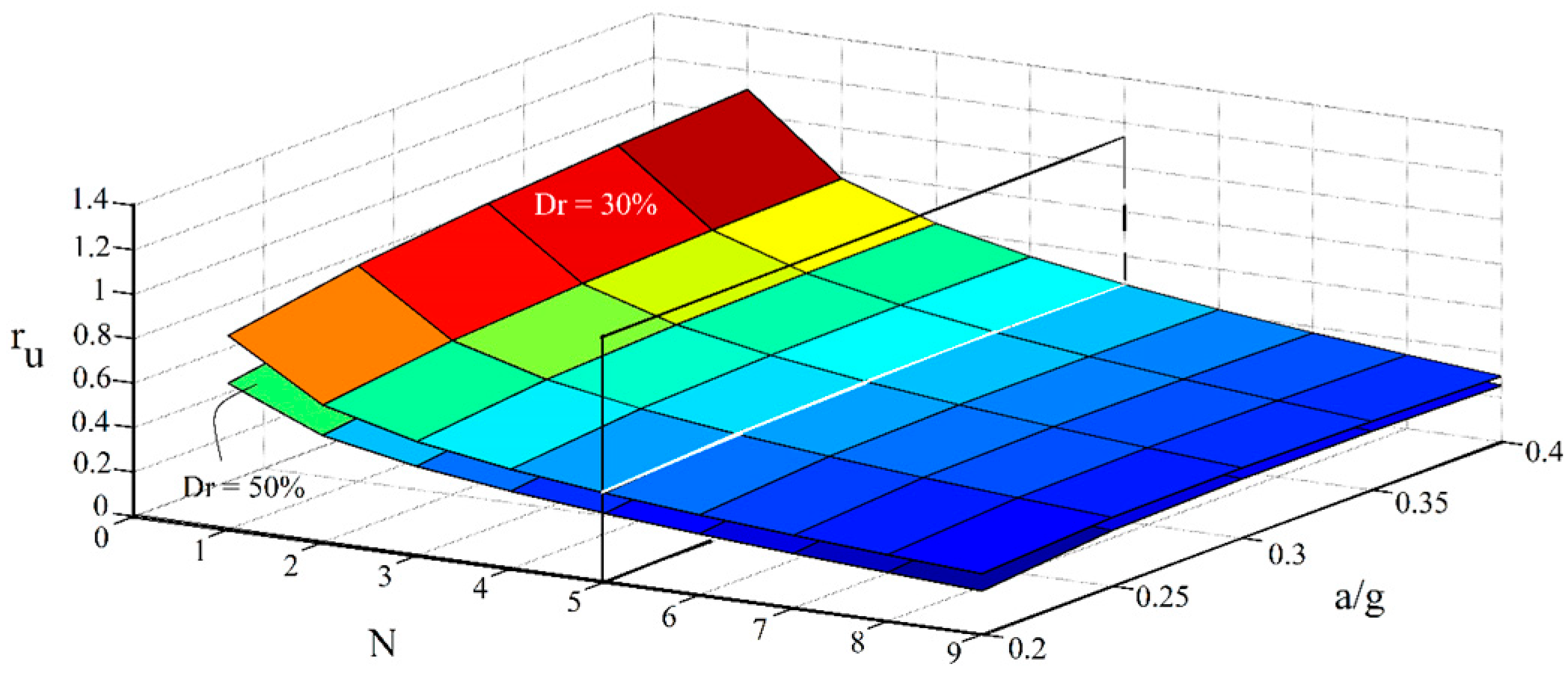
7.2. Simultaneous Effects of Number of Micropiles, Spacing Ratio, and a/g
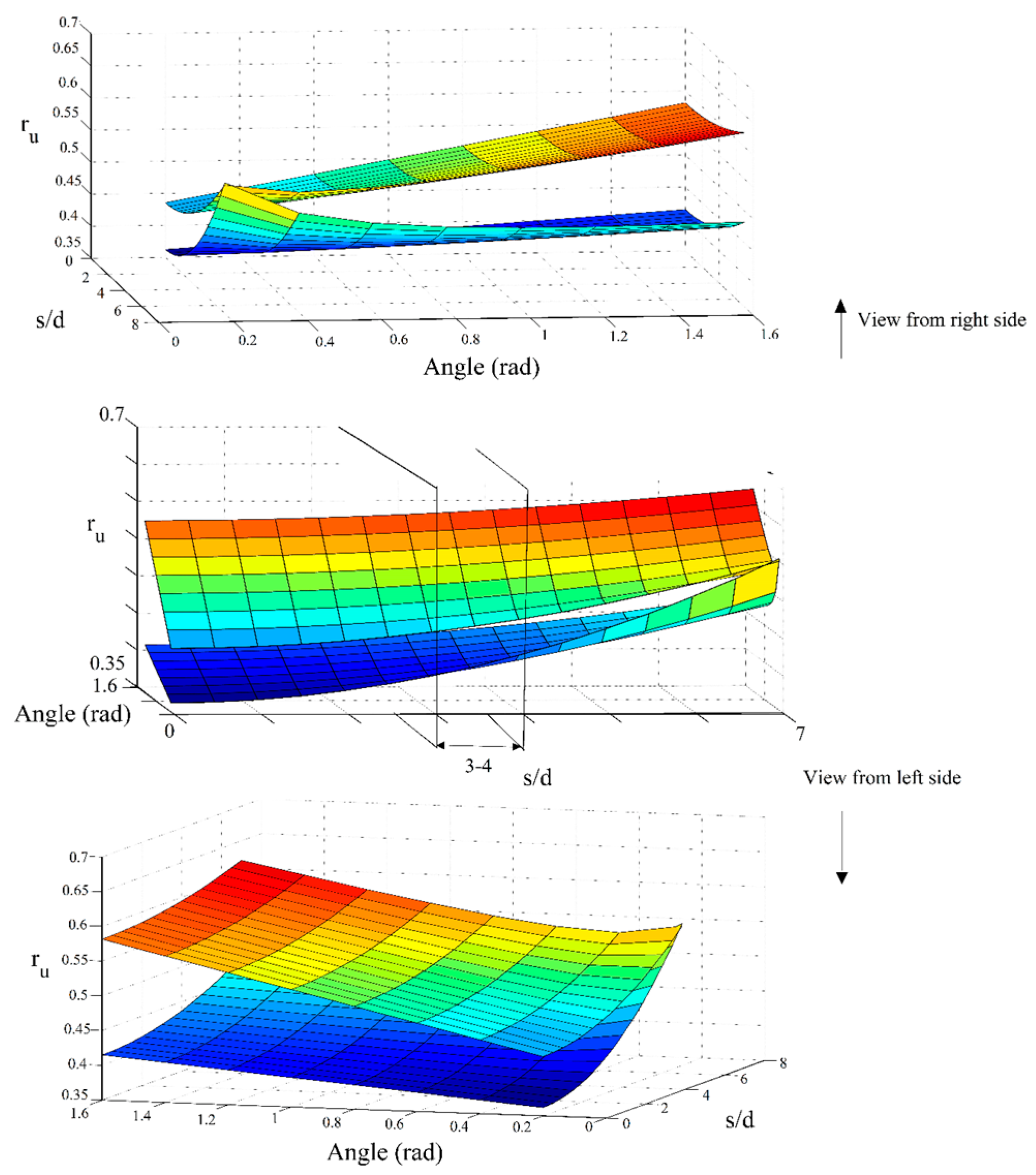
7.3. Simultaneous Effects of Spacing Ratio, Inclination Angle, and Relative Density
8. Conclusions
- A more accurate response for the excess pore water pressure is obtained using foam sheets as the artificial lateral boundaries by a reduction in reflected and generated waves, in which its effect is well illustrated by a 7% decrease in rumax.
- The application of only one micropile has a negligible effect on the liquefaction potential of the soil at different seismic excitations. On the other hand, 2, 4 and 9 micropiles reduce rumax values averagely by 27%, 46%, and 66%, respectively. Therefore, the results clearly show that micropile reinforcement is an effective technique to decrease the liquefaction potential of sands, especially in samples with nine micropiles.
- The spacing ratio of micropiles has a small effect on rumax and Npeak values in the reinforced sand by two vertical micropiles, while its effect is more considerable in specimens reinforced by four vertical micropiles.
- The reinforced sand by two inclined micropiles exhibits a greater resistance to liquefaction compared with vertical micropiles.
- The results indicate that specimens of reinforced sand in all micropile arrangements have more liquefaction resistance in comparison with pure sand, due to the increase in the required number of cycles (Npeak) to liquefy.
- With increasing the scaled input acceleration, the liquefaction potential of pure and reinforced sand increases. Moreover, the dissipation of pore water pressure occurred faster with an increase in the applied excitations due to the separation between soil and micropiles.
- The increase in relative density of the sand significantly reduces the liquefaction potential. In addition, this positive effect has a better efficiency in loose sand compared with the medium sand.
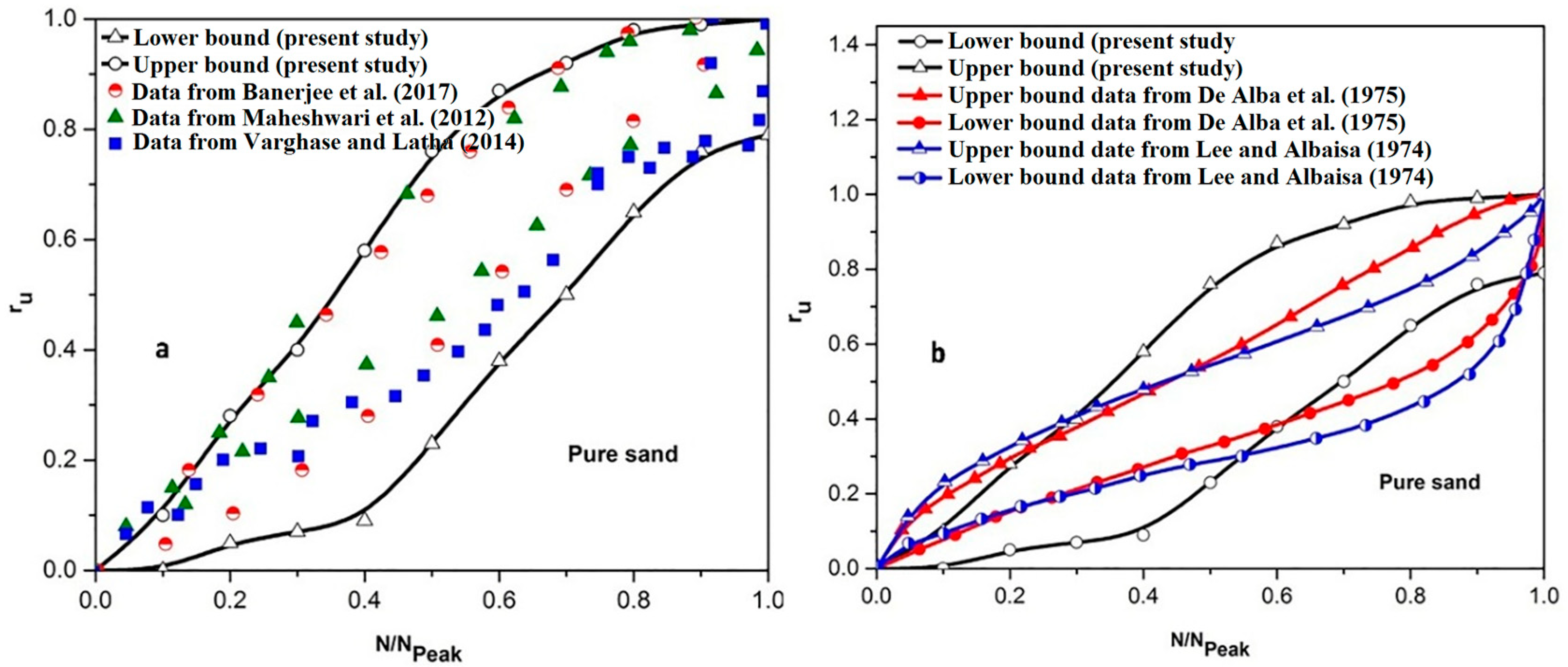
- New upper and lower bounds are suggested for the prediction of the liquefaction potential of micropile-induced sand, which can be an efficient controlling tool for design engineers.
- High-accuracy EPR models are proposed for the prediction of ru of the sand reinforced with micropiles.
- The impact of N, Dr, and a/g on ru is more significant compared with other affecting parameters.
- Inclined micropiles have a better performance in the mitigation of liquefaction potential for loose sands compared with the medium-dense sand.
- The applicable range of inclination of micropiles in medium-dense sands is less than its applicable range for loose sands.
- Critical, boundary inclination angle in dense sands (33°) is lower than loose sands (67°).
- The range of (3–4) is introduced as the optimum range for the spacing ratio of micropiles (in view of both material consumption and enhancing the soil’s resistivity against the liquefaction).
- With inclining micropiles, the effect of the spacing ratio on the liquefaction potential is amplified.
- The number of micropiles plays a more important role in the liquefaction potential compared with the spacing ratio and the scaled input acceleration. With the application of at least five micropiles, the effects of s/d and a/g are shown to be negligible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yegian, M.K.; Nogole-Sadat, M.A.A.; Ghahraman, V.G.; Darai, H. Liquefaction Case Histories from 1990 Manjil Earthquake, Iran. In Proceedings of the Third International Conference on Case Histories in Geotechnical Engineering, Saint Louis, MO, USA, 1–4 June 1993. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
- Zengin, E.; Erguler, Z.A. Assessment of Liquefaction Susceptibility of Kutahya Soils Based on Recent Earthquakes in Turkey. In Proceedings of the EGU General Assembly 2014, Vienna, Austria, 27 April–2 May 2014; p. 2480. [Google Scholar]
- Ecemis, N.; Valizadeh, H.; Karaman, M. Sand-granulated rubber mixture to prevent liquefaction-induced uplift of buried pipes: A shaking table study. Bull. Earthq. Eng. 2021, 19, 2817–2838. [Google Scholar] [CrossRef]
- Özcebe, A.G.; Giretti DBozzoni, F.; Fioravante, V.; Lai, C.G. Centrifuge and numerical modelling of earthquake-induced soil liquefaction under free-field conditions and by considering soil–structure interaction. Bull. Earthq. Eng. 2021, 19, 47–75. [Google Scholar] [CrossRef]
- Han, Z.; Xiao, J.; Wei, Y. Spatial Distribution Characteristics of Microbial Mineralization in Saturated Sand Centrifuge Shaking Table Test. Materials 2022, 15, 6102. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhong, X.; Lv, J.; Wang, G.; Hu, R. Experimental Study on Different Improvement Schemes of EICP-Lignin Solidified Silt. Materials 2023, 16, 999. [Google Scholar] [CrossRef]
- Konrad, J.-M.; Watts, B.D. Undrained shear strength for liquefaction flow failure analysis. Can. Geotech. J. 1995, 32, 783–794. [Google Scholar] [CrossRef]
- Konrad, J.-M. A methodology to evaluate the susceptibility of soils for liquefaction flow failures. In Physics and Mechanics of Soil Liquefaction; Lade, P.V., Yamamuro, J.A., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1999; p. 213. [Google Scholar]
- Baziar, M.H.; Ghorbani, A. Evaluation of lateral spreading using artificial neural networks. Soil Dyn. Earthq. Eng. 2005, 25, 1–9. [Google Scholar] [CrossRef]
- Özener, P.T.; Özaydın, K.; Berilgen, M.M. Investigation of liquefaction and pore water pressure development in layered sands. Bull. Earthq. Eng. 2009, 7, 199–219. [Google Scholar] [CrossRef]
- Jafarian, Y.; Abdollahi, A.S.; Vakili, R.; Baziar, M.H.; Noorzad, A. On the efficiency and predictability of strain energy for the evaluation of liquefaction potential: A numerical study. Comput. Geotech. 2011, 38, 800–808. [Google Scholar] [CrossRef]
- El Takch, A.; Sadrekarimi, A.; El Naggar, M.H. Cyclic resistance and liquefaction behavior of silt and sandy silt soils. Soil Dyn. Earthq. Eng. 2016, 83, 98–109. [Google Scholar] [CrossRef]
- Ghorbani, A.; Mersa, A.N.; Veiskarami, M.; Hamidzadeh, N.; Hasanzadehshooiili, H. Shaking table tests to parametrically evaluate post-shaking settlements and pore water pressure build-up in marine sands. Arab. J. Geosci. 2021, 14, 693. [Google Scholar] [CrossRef]
- Ghorbani, A.; Eslami, A. Energy-based model for predicting liquefaction potential of sandy soils using evolutionary polynomial regression method. Comput. Geotech. 2021, 129, 103867. [Google Scholar] [CrossRef]
- Bozzoni, F.; Bonì, R.; Conca, D.; Lai, C.G.; Zuccolo, E.; Meisina, C. Megazonation of earthquake-induced soil liquefaction hazard in continental Europe. Bull. Earthq. Eng. 2021, 19, 4059–4082. [Google Scholar] [CrossRef]
- Bahadori, H.; Farzalizadeh, R.; Barghi, A.; Hasheminezhad, A. A comparative study between gravel and rubber drainage columns for mitigation of liquefaction hazards. J. Rock Mech. Geotech. Eng. 2018, 10, 924–934. [Google Scholar] [CrossRef]
- Fallahzadeh, M.; Haddad, A.; Jafarian, Y.; Lee, C.J. Seismic performance of end-bearing piled raft with countermeasure strategy against liquefaction using centrifuge model tests. Bull. Earthq. Eng. 2019, 17, 5929–5961. [Google Scholar] [CrossRef]
- Padmanabhan, G.; Shanmugam, G.K.; Berilgen, M.M. Liquefaction and reliquefaction resistance of saturated sand deposits treated with sand compaction piles. Bull. Earthq. Eng. 2021, 19, 4235–4259. [Google Scholar] [CrossRef]
- Dou, P.; Xu, C.; Du, X.; Chen, S. Influence of structure on the aseismic stability and dynamic responses of liquefiable soil. Bull. Earthq. Eng. 2022, 20, 55–76. [Google Scholar] [CrossRef]
- Hasheminezhad, A.; Farzalizadeh, R.; Rahimi, H.; Bahadori, H. Seismic performance assessment of wall-type gravel and rubber drains in liquefaction mitigation of sands. Bull. Earthq. Eng. 2022, 20, 3699–3714. [Google Scholar] [CrossRef]
- FHWA NHI (Federal Highway Administration-National Highway Institute). Micropile Design and Construction—Reference Manual; FHWA NHI-05-039; U.S. Department of Transportation: McLean, VA, USA, 2005; p. 436. [Google Scholar]
- Juran, I.; Hasan, J.; Weinstein, G.M.; Sourisseau, L. FOREVER: Synthesis of the Results of the National Project on Micropiles; International Center for Ground Improvement, Polytechnic University: Southlake, TX, USA, 2003. [Google Scholar]
- Shahrour, J.I.; Juran, I. Seismic behaviour of micropile systems. Proc. Inst. Civ. Eng. Ground Improv. 2004, 8, 109–120. [Google Scholar] [CrossRef]
- McManus, K.J.; Charton, G.; Turner, J.P. Effect of Micropiles on Seismic Shear Strain. In Proceedings of the GeoSupport Conference 2004, Orlando, FL, USA, 29–31 January 2004; Society of Civil Engineers (ASCE): Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- McManus, K.J.; Turner, J.P.; Charton, G. Inclined reinforcement to prevent soil liquefaction. In Proceedings of the Annual NZSEE Technical Conference, Wairakei, New Zealand, 11–13 March 2005; pp. 41–51. [Google Scholar]
- Tsukada, Y.; Miura, K.; Tsubokawa, Y.; Otani, Y.; You, G.L. Mechanism of bearing capacity of spread footings reinforced with micropiles. Soils Found. 2006, 46, 367–376. [Google Scholar] [CrossRef]
- Esmaeili, M.; Nik, M.G.; Khayyer, F. Experimental and numerical study of micropiles to reinforce high railway embankments. Int. J. Geomech. 2012, 13, 729–744. [Google Scholar] [CrossRef]
- Kavand, A.; Haeri, S.M.; Raisianzadeh, J.; Afzalsoltani, S. Effectiveness of a vertical micropile system for mitigation of liquefaction induced lateral spreading effects on pile foundations: 1 g large scale shake table tests. Sci. Iran. 2021, 29, 1038–1058. [Google Scholar] [CrossRef]
- Sližytė, D. The interaction estimation of piles bored in sand. Statyba 2001, 7, 405–412. [Google Scholar] [CrossRef]
- Juran, I.; Benslimane, A.; Hanna, S. Engineering analysis of dynamic behavior of micropile systems. Transp. Res. Rec. J. Transp. Res. Board 2001, 1772, 91–106. [Google Scholar] [CrossRef]
- Ousta, R.; Shahrour, I. Three-dimensional analysis of the seismic behaviour of micropiles used in the reinforcement of saturated soil. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 183–196. [Google Scholar] [CrossRef]
- Mitrani, H.; Madabhushi, S.P.G. Centrifuge tests investigating inclined grout micro-piles as a method of liquefaction remediation for existing buildings. Earthq. Eng. Soil Dyn. 2005, 3, 245–256. [Google Scholar]
- Shahrour, I.; Hassan, S.A.; Mhamed, S. 3D elastoplastic analysis of the seismic performance of inclined micropiles. Comput. Geotech. 2012, 39, 1–7. [Google Scholar]
- Ghorbani, A.; Hasanzadehshooiili, H.; Ghamari, E. 3D finite element analysis of seismic soil-micropile-structure interaction. In Proceedings of the 2nd International Conference on Civil Engineering and Building Materials (CEBM), Hong Kong, China, 17–18 November 2012; Chang, S.-Y., Al Bahar, S.K., Zhao, J., Eds.; CRC Press: Hong Kong, China, 2012; pp. 265–269. [Google Scholar]
- Moayed, R.Z.; Naeini, S.A. Improvement of loose sandy soil deposits using micropiles. KSCE J. Civ. Eng. 2012, 16, 334–340. [Google Scholar] [CrossRef]
- Sližytė, D.; Medzvieckas, J. Evaluation of Gravity Retaining Walls from Jet Grouting Piles Installed in Sands. Procedia Eng. 2013, 57, 1070–1077. [Google Scholar] [CrossRef]
- Ghorbani, A.; Hasanzadehshooiili, H.; Ghamari, E.; Medzvieckas, J. Comprehensive three dimensional finite element analysis, parametric study and sensitivity analysis on the seismic performance of soil–micropile-superstructure interaction. Soil Dyn. Earthq. Eng. 2014, 58, 21–36. [Google Scholar] [CrossRef]
- Abdollahi, K.; Mortezaei, A. A new expression for determining the bending stiffness of circular micropile groups. Soil Dyn. Earthq. Eng. 2015, 77, 58–70. [Google Scholar] [CrossRef]
- Saha, R.; Dutta, S.C.; Haldar, S. Seismic response of soil-pile raft-structure system. J. Civ. Eng. Manag. 2015, 21, 144–164. [Google Scholar] [CrossRef]
- Ortega, J.M.; Esteban, M.D.; Rodriguez, R.R.; Pator, J.L.; Ibanco, F.J.; Sánchez, I.; Climent, M.Á. Long-Term Behaviour of Fly Ash and Slag Cement Grouts for Micropiles Exposed to a Sulphate Aggressive Medium. Materials 2017, 10, 598. [Google Scholar] [CrossRef] [PubMed]
- Sales, M.M.; Prezzi, M.; Salgado, R.; Choi, Y.S.; Lee, J. Load-settlement behaviour of model pile groups in sand under vertical load. J. Civ. Eng. Manag. 2017, 23, 1148–1163. [Google Scholar] [CrossRef]
- Vali, R.; Khotbehsara, E.M.; Saberian, M.; Li, J.; Mehrinejad, M.; Jahandari, S. A three-dimensional numerical comparison of bearing capacity and settlement of tapered and under-reamed piles. Int. J. Geotech. Eng. 2019, 13, 236–248. [Google Scholar] [CrossRef]
- Norkus, A.; Martinkus, V. Experimental study on bearing resistance of short displacement pile groups in dense sands. J. Civ. Eng. Manag. 2019, 25, 551–558. [Google Scholar] [CrossRef]
- Mashhoud, H.J.; Yin, J.H.; Komak Panah, A.; Leung, Y.F. A 1-g shaking table investigation on response of a micropile system to earthquake excitation. Acta Geotech. 2020, 15, 827–846. [Google Scholar] [CrossRef]
- Ghorbani, A.; Jahanpour, R.; Hasanzadehshooiili, H. Evaluation of liquefaction potential of marine sandy soil with piles considering nonlinear seismic soil–pile interaction; A simple predictive model. Mar. Georesour. Geotechnol. 2020, 38, 1–22. [Google Scholar] [CrossRef]
- Abdlrahem, M.A.; El Naggar, M.H. Axial performance of micropile groups in cohesionless soil from full-scale tests. Can. Geotech. J. 2020, 57, 1006–1024. [Google Scholar] [CrossRef]
- Orang, M.J.; Boushehri, R.; Motamed, R.; Prabhakaran, A.; Elgamal, A. An experimental evaluation of helical piles as a liquefaction-induced building settlement mitigation measure. Soil Dyn. Earthq. Eng. 2021, 151, 106994. [Google Scholar] [CrossRef]
- Saadatinezhad, M.; Lakirouhani, A.; Jabin Asli, S. Seismic response of non-connected piled raft foundations. Int. J. Geotech. Eng. 2021, 15, 66–80. [Google Scholar] [CrossRef]
- Sadeghian, F.; Jahandari, S.; Haddad, A.; Rasekh, H.; Li, J. Effects of variations of voltage and pH value on the shear strength of soil and durability of different electrodes and piles during electrokinetic phenomenon. J. Rock Mech. Geotech. Eng. 2021, 14, 625–636. [Google Scholar] [CrossRef]
- Sabri, M.M.S.; Vatin, N.I.; Ponomarev, A.B.; Nurmukhametov, R.R.; Kostyukov, I.I. Settlement of Soil Reinforced with Vertical Fiberglass Micro-Piles. Materials 2022, 15, 4744. [Google Scholar] [CrossRef] [PubMed]
- Komak Panah, A.; Mashhoud, H.J.; Yin, J.H.; Leung, Y.F. Shaking Table Investigation of Effects of Inclination Angle on Seismic Performance of Micropiles. Int. J. Geomech. 2018, 18, 04018142. [Google Scholar] [CrossRef]
- Ghorbani, A.; Somti Foumani, M.A. The experimental study on the micropile effect on liquefaction potential of Anzali saturated sand. Sharif J. Civ. Eng. 2020, 36, 15–24. (In Farsi) [Google Scholar]
- Munoz, H.; Kiyota, T. Deformation and localisation behaviours of reinforced gravelly backfill using shaking table tests. J. Rock Mech. Geotech. Eng. 2020, 12, 102–111. [Google Scholar] [CrossRef]
- Alainachi, I.; Fall, M. Chemically induced changes in the geotechnical response of cementing paste backfill in shaking table test. J. Rock Mech. Geotech. Eng. 2021, 13, 513–528. [Google Scholar] [CrossRef]
- Wood, D.M. Geotechnical Modelling; CRC Press: Boca Raton, FL, USA, 2003; Volume 1. [Google Scholar]
- Teymur, B.; Madabhushi, S.P.G. Experimental study of boundary effects in dynamic centrifuge modelling. Géotechnique 2003, 53, 655–663. [Google Scholar] [CrossRef]
- Krishna, A.M.; Latha, G.M. Container boundary effects in shaking table tests on reinforced soil wall models. Int. J. Phys. Model. Geotech. 2009, 9, 1–14. [Google Scholar] [CrossRef]
- Fishman, K.L.; Mander, J.B.; Richards, R. Laboratory study of seismic free-field response of sand. Soil Dyn. Earthq. Eng. 1995, 14, 33–43. [Google Scholar] [CrossRef]
- Lee, C.J.; Wei, Y.C.; Kuo, Y.C. Boundary effects of a laminar container in centrifuge shaking table tests. Soil Dyn. Earthq. Eng. 2012, 34, 37–51. [Google Scholar] [CrossRef]
- Dewoolkar, M.M.; Ko, H.Y.; Pak, R.Y.S. Experimental developments for studying static and seismic behavior of retaining walls with liquefiable backfills. Soil Dyn. Earthq. Eng. 2000, 19, 583–593. [Google Scholar] [CrossRef]
- Soudkhah, M.; Pak, R.Y. Wave absorbing-boundary method in seismic centrifuge simulation of vertical free-field ground motion. Comput. Geotech. 2012, 43, 155–164. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Scarpa, F.; Bianchi, M. Dynamic response of a geotechnical rigid model container with absorbing boundaries. Soil Dyn. Earthq. Eng. 2015, 69, 46–56. [Google Scholar] [CrossRef]
- Takahashi, A.; Takemura, J. Liquefaction-induced large displacement of pile-supported wharf. Soil Dyn. Earthq. Eng. 2005, 25, 811–825. [Google Scholar] [CrossRef]
- Ha, I.S.; Olson, S.M.; Seo, M.W.; Kim, M.M. Evaluation of reliquefaction resistance using shaking table tests. Soil Dyn. Earthq. Eng. 2011, 31, 682–691. [Google Scholar] [CrossRef]
- Lee, K.L.; Albaisa, A. Earthquake induced settlements in saturated sands. J. Geotech. Eng. Div. 1974, 100, 387–406. [Google Scholar] [CrossRef]
- De Alba, P.; Chan, C.K.; Seed, H.B. Determination of Soil Liquefaction Characteristics by Large-Scale Laboratory Tests; Springfield: Seattle, WA, USA, 1975. [Google Scholar]
- Abendroth, R.E.; Greimann, L.F. Pile behavior established from model tests. J. Geotech. Eng. 1990, 116, 571–587. [Google Scholar] [CrossRef]
- Moccia, F. Seismic Soil Pile Interaction: Experimental Evidence. Ph.D. Thesis, University of Napoli “Federico II”, Napoli, Italy, 2009. [Google Scholar]
- Porcino, D.; Marcianò, V.; Granata, R. Cyclic liquefaction behaviour of a moderately cemented grouted sand under repeated loading. Soil Dyn. Earthq. Eng. 2015, 79, 36–46. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids; Dover; Courier Corporation: New York, NY, USA, 1953. [Google Scholar]
- Lombardi, D.; Bhattachaya, S. Shaking table tests on rigid soil container with absorbing boundaries. In Proceedings of the Fifthteenth World Conference on Earthquake Engineering (15 WCEE), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Zienkiewicz, O.C.; Chang, C.T.; Bettess, T. Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Limits of validity. Geotechnique 1980, 30, 385–395. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Dover Publications: Cambridge, UK, 1932. [Google Scholar]
- Iai, S. Similitude for Shaking Table Tests on Soil-Structure-Fluid Model in 1 g Gravitational Field. Soils Found. 1989, 29, 105–118. [Google Scholar] [CrossRef]
- Ueng, T.S.; Wu, C.W.; Cheng, H.W.; Chen, C.H. Settlements of saturated clean sand deposits in shaking table tests. Soil Dyn. Earthq. Eng. 2010, 30, 50–60. [Google Scholar] [CrossRef]
- Varghese, R.M.; Latha, G.M. Shaking table tests to investigate the influence of various factors on the liquefaction resistance of sands. Nat. Hazards 2014, 73, 1337–1351. [Google Scholar] [CrossRef]
- Maheshwari, B.K.; Singh, H.P.; Saran, S. Effects of reinforcement on liquefaction resistance of solani sand. J. Geotech. Geoenviron. Eng. 2012, 138, 831–840. [Google Scholar] [CrossRef]
- Banerjee, R.; Konai, S.; Sengupta, A.; Deb, K. Shake Table Tests and Numerical Modeling of Liquefaction of Kasai River Sand. Geotech. Geol. Eng. 2017, 35, 1327–1340. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.A. A symbolic data-driven technique based on evolutionary polynomial regression. J. Hydroinforma. 2006, 8, 207–222. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.A. Advances in data-drive analyses and modelling using EPR-MOGA. J. Hydroinforma. 2009, 11, 225–236. [Google Scholar] [CrossRef]
- Rezania, M.; Javadi, A.A.; Giustolisi, O. An evolutionary-based data mining technique for assessment of civil engineering systems. Eng. Comput. 2008, 25, 500–517. [Google Scholar] [CrossRef]
- Ahangar-Asr, A.; Faramarzi, A.; Mottaghifard, N.; Javadi, A.A. Modeling of permeability and compaction characteristics of soils using evolutionary polynomial regression. Comput. Geosci. 2011, 37, 1860–1869. [Google Scholar] [CrossRef]
- Ghorbani, A.; Hasanzadehshooiili, H. Prediction of UCS and CBR of microsilica-lime stabilized sulfate silty sand using ANN and EPR models; application to the deep soil mixing. Soils Found. 2018, 58, 34–49. [Google Scholar] [CrossRef]
- Shariatmadari, N.; Karimpour-Fard, M.; Hasanzadehshooiili, H.; Hoseinzadeh, S.; Karimzadeh, Z. Effects of drainage condition on the stress-strain behavior and pore pressure buildup of sand-PET mixtures. Constr. Build. Mater. 2020, 233, 117295. [Google Scholar] [CrossRef]
- Shariatmadari, N.; Hasanzadehshooiili, H.; Ghadir, P.; Saeidi, F.; Moharrami, F. Compressive Strength of Sandy Soils Stabilized with Alkali Activated Volcanic Ash and Slag. J. Mater. Civ. Eng. 2021, 33, 04021295. [Google Scholar] [CrossRef]
- Ghorbani, A.; Hasanzadehshooiili, H.; Eslami, A. Parametric Evaluation of Simultaneous Effects of Damaged Zone Parameters and Rock Strength Properties on GRC. Adv. Civ. Eng. 2021, 2021, 2237918. [Google Scholar] [CrossRef]

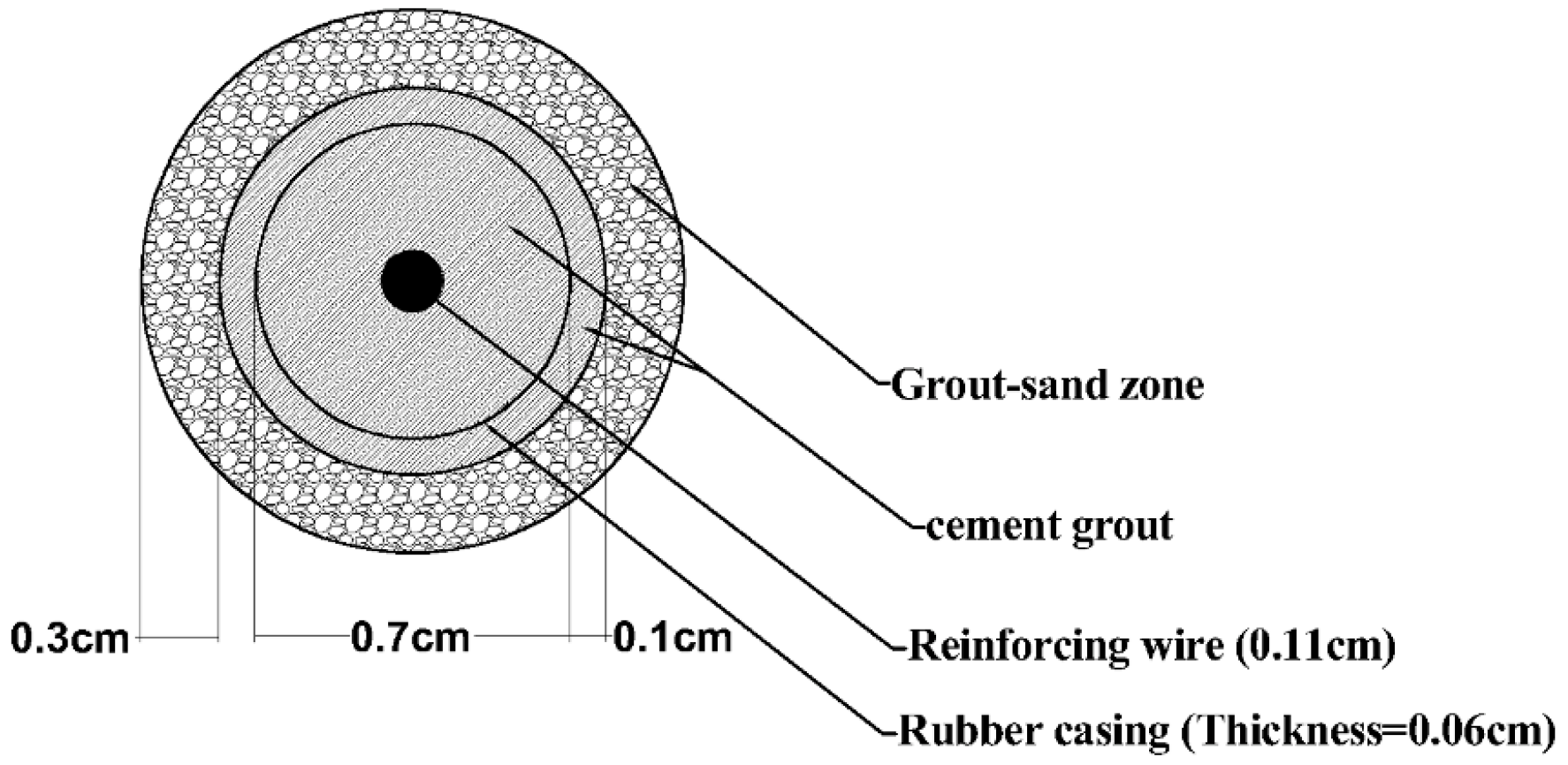

| Quantity | General | 1 g (Laboratory) | Scaling Factor (Model/Prototype) |
|---|---|---|---|
| Length | |||
| Mass density | 1 | ||
| Acceleration | 1 | ||
| Stiffness | |||
| Stress | |||
| Strain | |||
| Displacement | |||
| Time | |||
| Shear wave velocity | |||
| Frequency | |||
| EI |
| Parameter | Model | Prototype |
|---|---|---|
| Material | Soft rubber | Steel |
| Length of casing (m) | 0.2 | 3.2 |
| Casing thickness (cm) | 0.06 | 1 |
| Inner diameter of micropile (cm) | 0.7 | 11 |
| Radius of neat grout around the micropiles (cm) | 0.1 | 2 |
| Radius of grouted sand (cm) | 0.3 | 5 |
| Diameter of reinforcement element (cm) | 0.12 | 1.8 |
| Young’s modulus of casing (GPa) | 0.006 | 200 |
| Young’s modulus of grouted sand (GPa) | 0.2 | 0.2 |
| Young’s modulus of grout (GPa) | 30 | 30 |
| Young’s modulus of reinforcement element (GPa) | 100 | 200 |
| Test | Lateral Boundary | Duration (s) | Frequency (Hz) | Max. Acceleration (g) | Relative Density (%) | Number of Micropiles | ||
|---|---|---|---|---|---|---|---|---|
| 1 | Rigid | 12.5 | 2 | 0.2 | 30 | - | - | - |
| 2 | 12.5 | 2 | 2 | 7 | 90 | |||
| 3 | Absorbing | 12.5 | 2 | 0.2 | 30 | - | - | - |
| 4 | 12.5 | 2 | 1 | - | 90 | |||
| 5 | 12.5 | 2 | 2 | 7 | 90 | |||
| 6 | 12.5 | 2 | 2 | 4 | 90 | |||
| 7 | 12.5 | 2 | 2 | 7 | 78 | |||
| 8 | 12.5 | 2 | 2 | 4 | 78 | |||
| 9 | 12.5 | 2 | 4 | 7 | 90 | |||
| 10 | 12.5 | 2 | 4 | 4 | 90 | |||
| 11 | 12.5 | 2 | 9 | 3.5 | 90 | |||
| 12 | Absorbing | 9.5 | 3 | 0.32 | 30 | - | - | - |
| 13 | 9.5 | 3 | 1 | - | 90 | |||
| 14 | 9.5 | 3 | 2 | 7 | 90 | |||
| 15 | 9.5 | 3 | 2 | 4 | 90 | |||
| 16 | 9.5 | 3 | 2 | 7 | 78 | |||
| 17 | 9.5 | 3 | 2 | 4 | 78 | |||
| 18 | 9.5 | 3 | 4 | 7 | 90 | |||
| 19 | 9.5 | 3 | 4 | 4 | 90 | |||
| 20 | 9.5 | 3 | 9 | 3.5 | 90 | |||
| 21 | Absorbing | 9.5 | 3 | 0.32 | 50 | - | - | - |
| 22 | 9.5 | 3 | 1 | - | 90 | |||
| 23 | 9.5 | 3 | 2 | 7 | 90 | |||
| 24 | 9.5 | 3 | 4 | 7 | 90 |
| Test | Bottom PPT | Upper PPT | ||||||
|---|---|---|---|---|---|---|---|---|
| Percentage of Reduction in Relative to the Pure Sand | Percentage of Increase in Relative to the Pure Sand | Percentage of Reduction in Relative to the Pure Sand | Percentage of Increase in Relative to the Pure Sand | |||||
| 1 | 0.88 | - | 8.8 | - | 0.9 | - | 8.7 | - |
| 2 | 0.68 | 22.7 | 11.2 | 27.27 | 0.7 | 22.2 | 13.4 | 54.02 |
| 3 | 0.82 | - | 9 | - | 0.85 | - | 8.8 | - |
| 4 | 0.8 | 2.4 | 9.4 | 4.44 | 0.82 | 3.5 | 11 | 25 |
| 5 | 0.62 | 24.39 | 11.6 | 28.89 | 0.67 | 21.2 | 13.6 | 54.5 |
| 6 | 0.6 | 26.83 | 11.6 | 28.89 | 0.64 | 24.7 | 13.8 | 56.8 |
| 7 | 0.6 | 26.83 | 11.8 | 31.11 | 0.61 | 28.2 | 13.8 | 56.8 |
| 8 | 0.57 | 30.49 | 11.8 | 31.11 | 0.6 | 29.4 | 14 | 59.1 |
| 9 | 0.45 | 45.12 | 13.6 | 51.11 | 0.47 | 44.7 | 16 | 81.8 |
| 10 | 0.41 | 50 | 14 | 55.56 | 0.42 | 50.6 | 16 | 81.8 |
| 11 | 0.26 | 68.29 | 16 | 77.78 | 0.3 | 64.71 | 19 | 115.91 |
| 12 | 1 | - | 13.2 | - | 1 | - | 12.9 | - |
| 13 | 0.95 | 5 | 13.5 | 2.27 | 0.96 | 4 | 15.6 | 21 |
| 14 | 0.74 | 26 | 16.5 | 25 | 0.75 | 25 | 19.5 | 51.2 |
| 15 | 0.71 | 29 | 16.5 | 25 | 0.74 | 26 | 19.8 | 53.5 |
| 16 | 0.72 | 28 | 17.4 | 31.82 | 0.73 | 27 | 20.1 | 55.8 |
| 17 | 0.69 | 31 | 17.7 | 34.1 | 0.72 | 28 | 20.4 | 58.1 |
| 18 | 0.56 | 44 | 20.1 | 52.27 | 0.59 | 41 | 22.5 | 74.4 |
| 19 | 0.5 | 50 | 20.4 | 54.55 | 0.54 | 46 | 23.1 | 79 |
| 20 | 0.32 | 68 | 23.4 | 77.27 | 0.38 | 62 | 27 | 109.3 |
| 21 | 0.75 | - | 16.5 | - | 0.81 | - | 16.2 | - |
| 22 | 0.71 | 5.3 | 17.1 | 3.6 | 0.76 | 6.1 | 18 | 11 |
| 23 | 0.62 | 17.33 | 19.5 | 18.18 | 0.64 | 21 | 21.9 | 35.18 |
| 24 | 0.44 | 41.33 | 24 | 45.45 | 0.49 | 39.5 | 26.4 | 63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorbani, A.; Hasanzadehshooiili, H.; Somti Foumani, M.A.; Medzvieckas, J.; Kliukas, R. Liquefaction Potential of Saturated Sand Reinforced by Cement-Grouted Micropiles: An Evolutionary Approach Based on Shaking Table Tests. Materials 2023, 16, 2194. https://doi.org/10.3390/ma16062194
Ghorbani A, Hasanzadehshooiili H, Somti Foumani MA, Medzvieckas J, Kliukas R. Liquefaction Potential of Saturated Sand Reinforced by Cement-Grouted Micropiles: An Evolutionary Approach Based on Shaking Table Tests. Materials. 2023; 16(6):2194. https://doi.org/10.3390/ma16062194
Chicago/Turabian StyleGhorbani, Ali, Hadi Hasanzadehshooiili, Mohammad Ali Somti Foumani, Jurgis Medzvieckas, and Romualdas Kliukas. 2023. "Liquefaction Potential of Saturated Sand Reinforced by Cement-Grouted Micropiles: An Evolutionary Approach Based on Shaking Table Tests" Materials 16, no. 6: 2194. https://doi.org/10.3390/ma16062194
APA StyleGhorbani, A., Hasanzadehshooiili, H., Somti Foumani, M. A., Medzvieckas, J., & Kliukas, R. (2023). Liquefaction Potential of Saturated Sand Reinforced by Cement-Grouted Micropiles: An Evolutionary Approach Based on Shaking Table Tests. Materials, 16(6), 2194. https://doi.org/10.3390/ma16062194





