The Microzone Structure Regulation of Diamond/Cu-B Composites for High Thermal Conductivity: Combining Experiments and First-Principles Calculations
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments
2.2. DFT Calculations
3. Results and Discussion
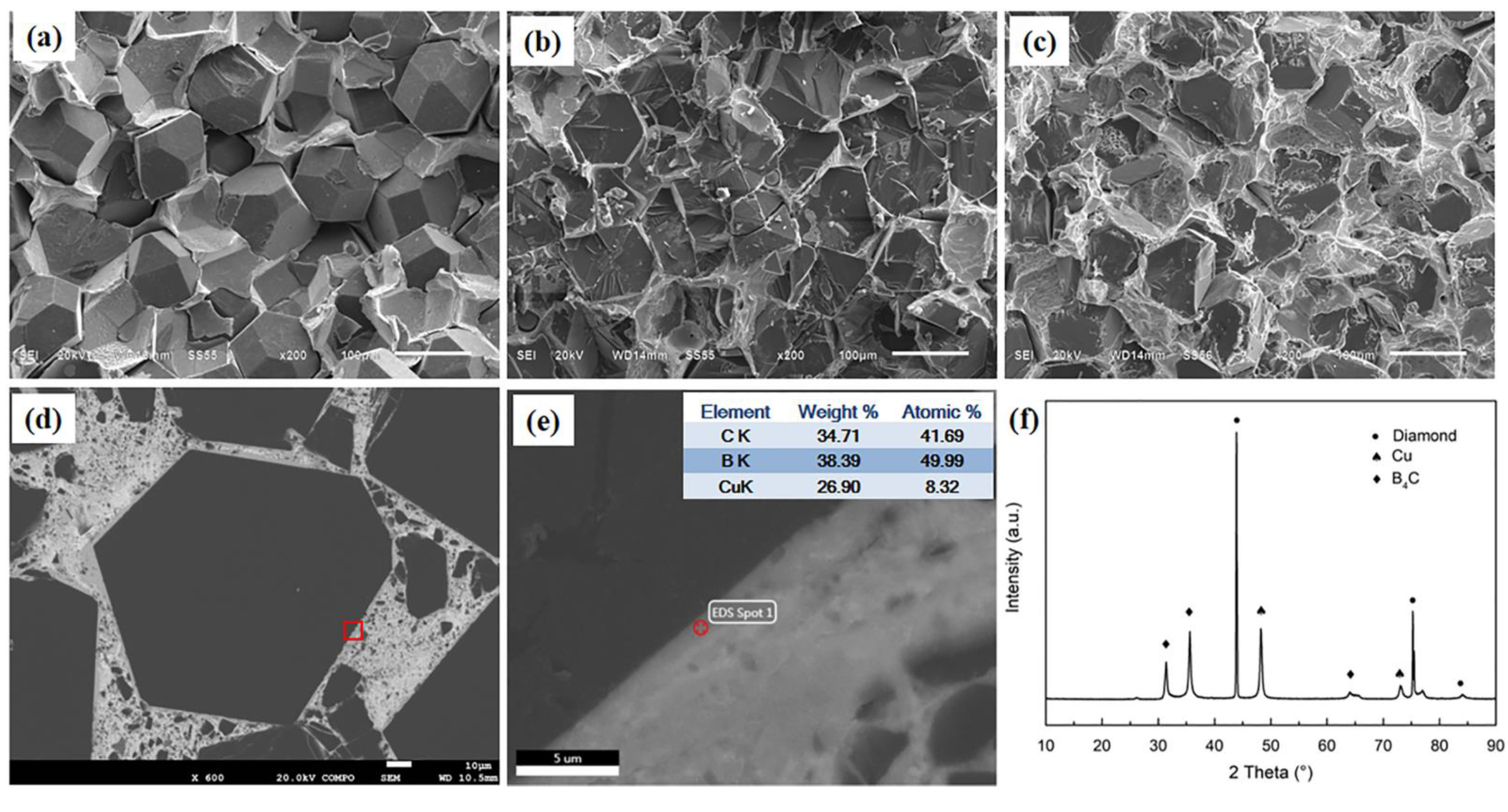
3.1. Microstructures and Phase Constitutions
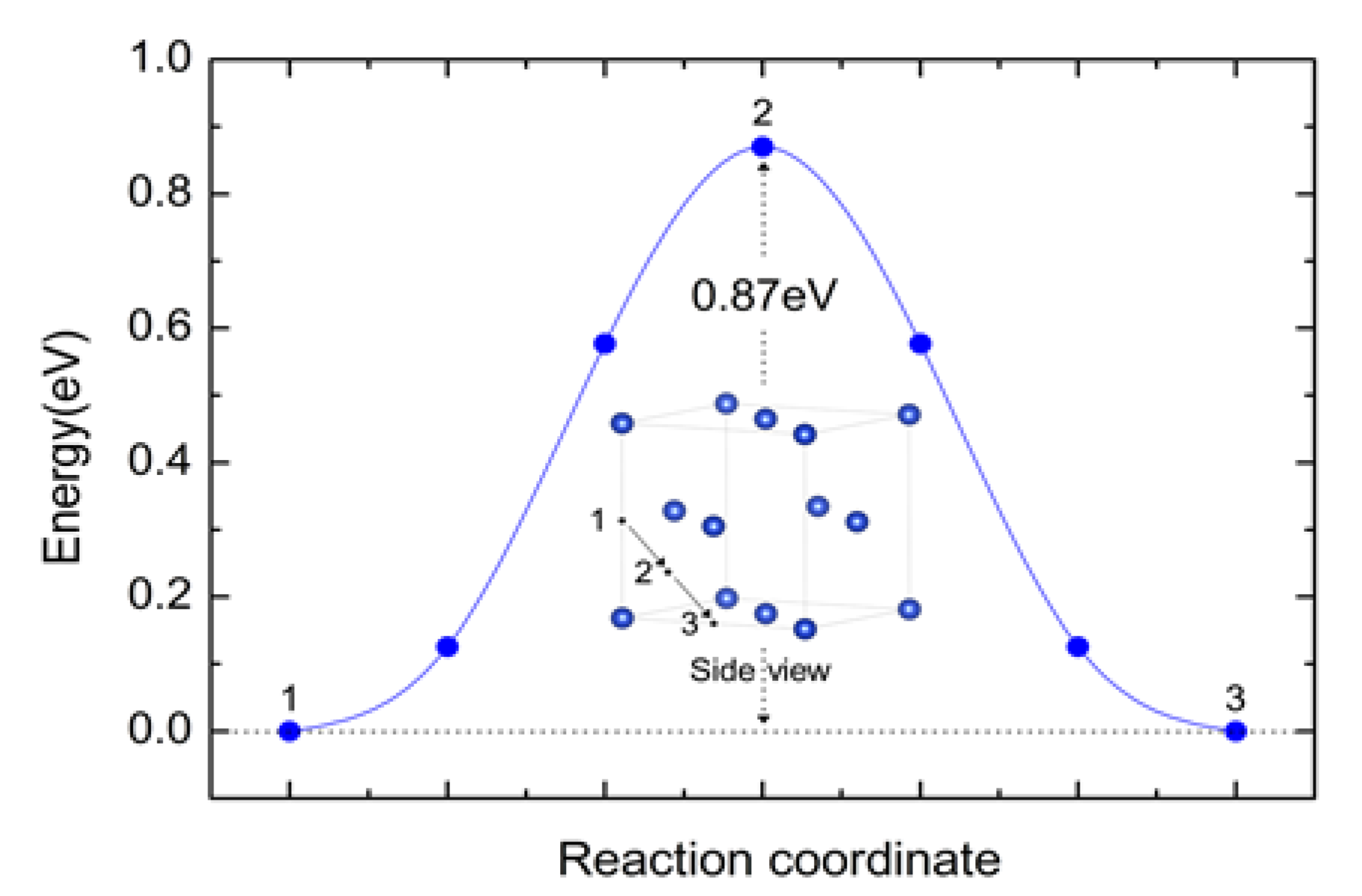
3.2. The Formation Kinetics and Thermodynamics of Carbide Interlayer B4C
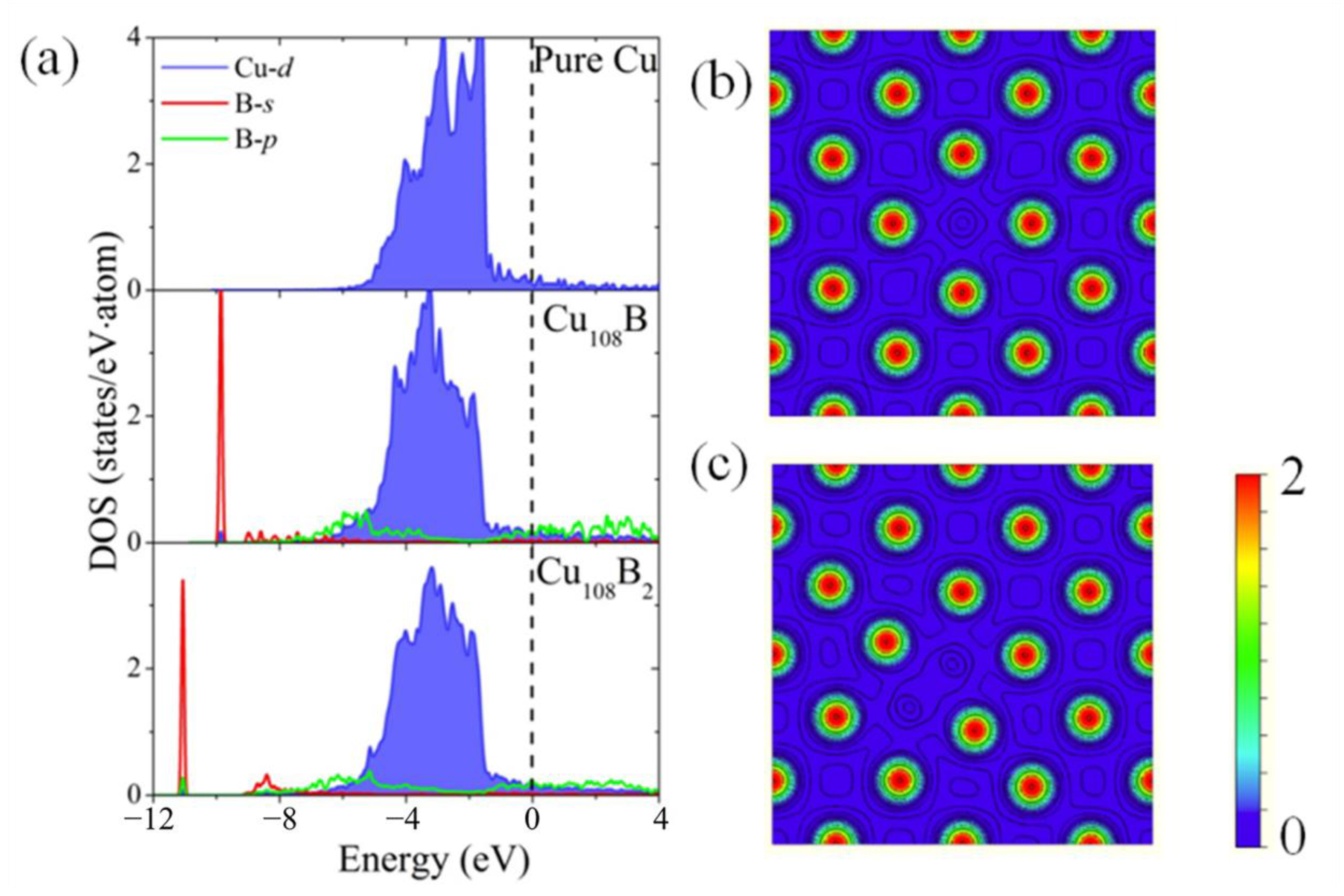
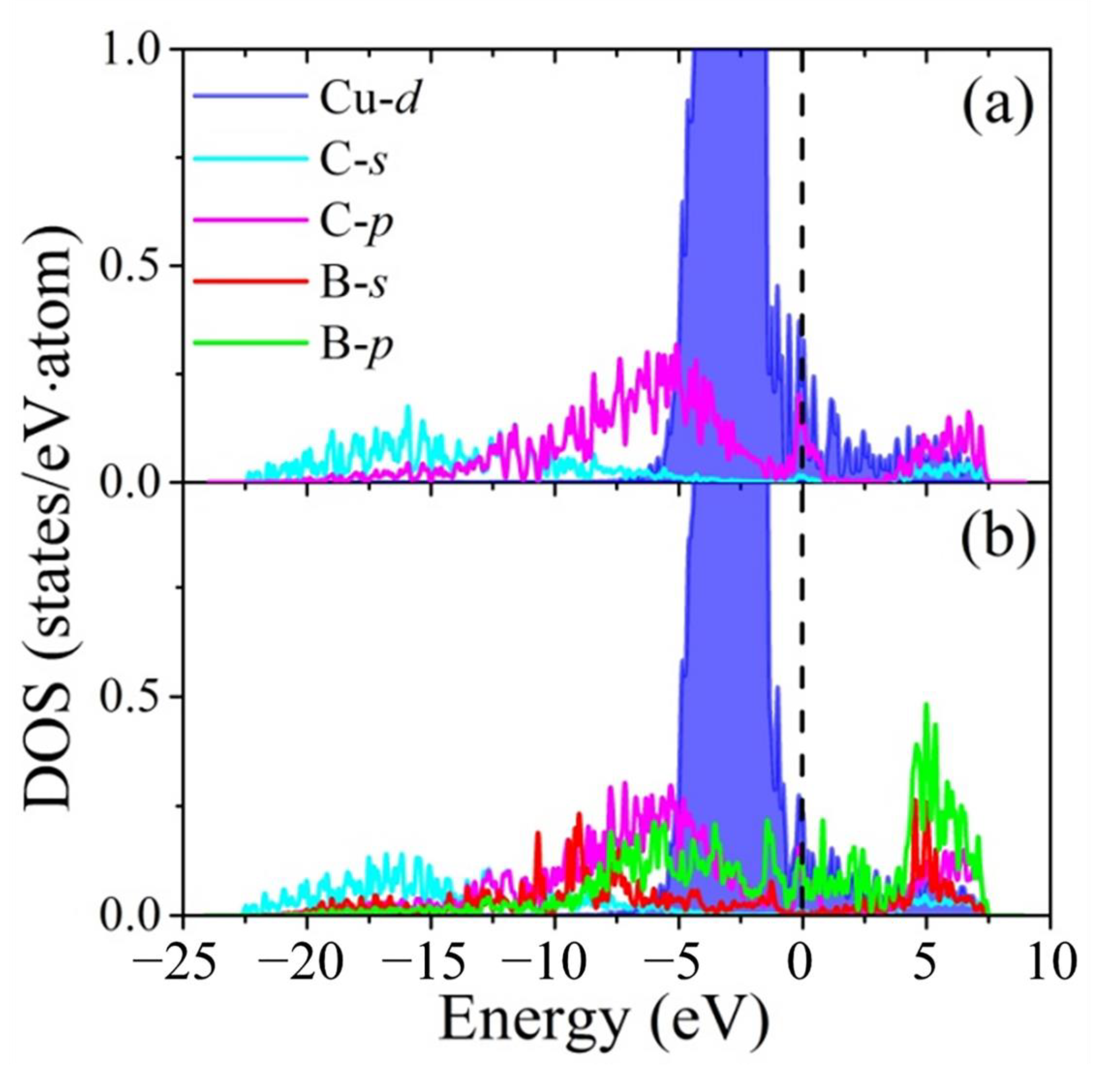
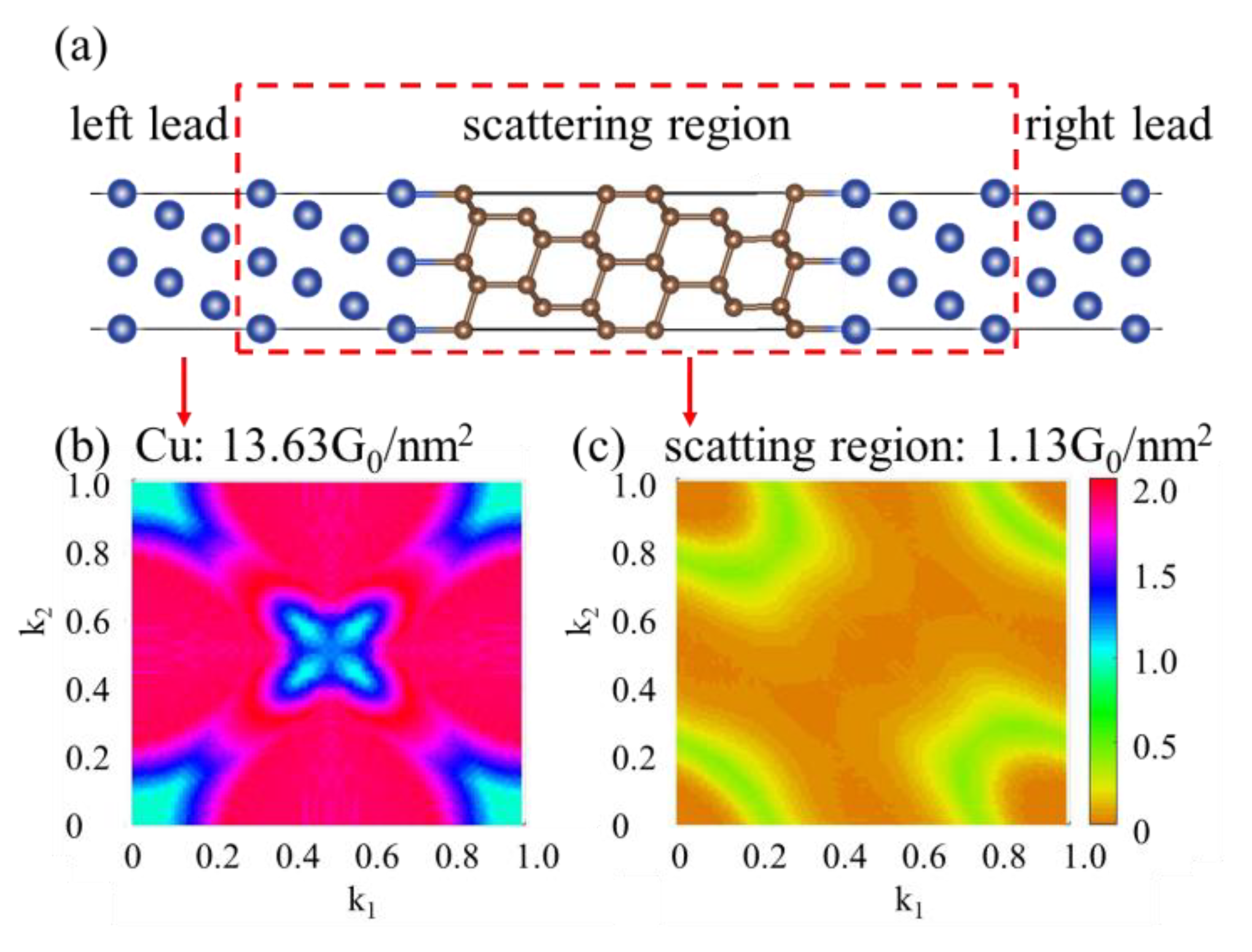
3.3. The Enhancement Mechanisms of Interfacial Heat Conduction
4. Conclusions
- Diamond/Cu-B composites achieved the highest thermal conductivity of 694 W/mK with a boron addition of 0.5 wt.%. The addition of boron improves the interface bonding, thus increasing the thermal conductivity of diamond/Cu composites.
- The calculation results demonstrate that boron can diffuse toward the interface region with an energy barrier of 0.87 eV, and these boron elements are energetically favorable to form the B4C phase. By adjusting the preparation process and boron concentration, the interface between B4C and diamond can be transformed from a straight interface to a dentate interface.
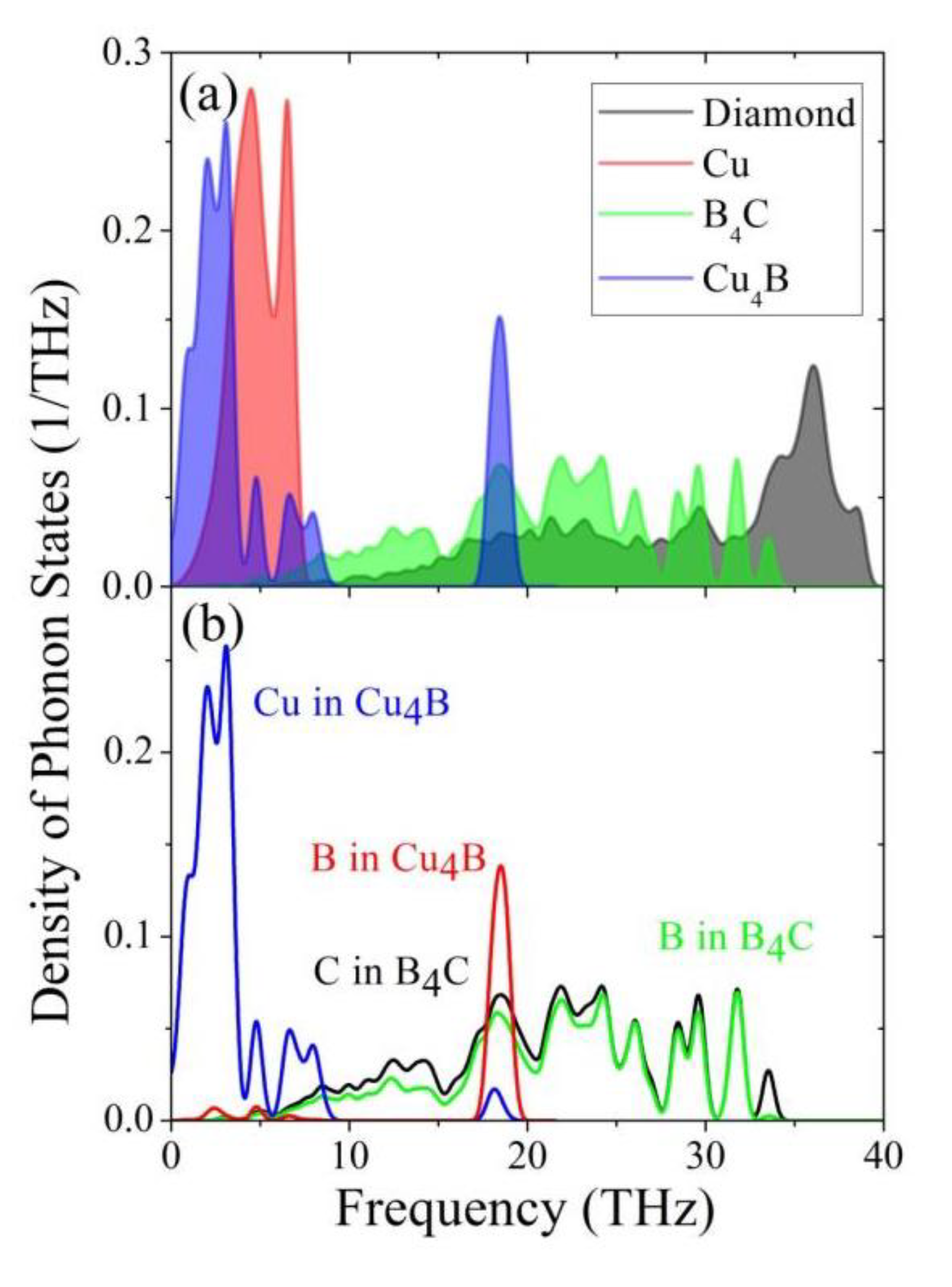
- The B4C phonon spectrum is distributed in the range of the copper and diamond phonon spectrum. The overlapping of phonon spectra and the dentate structure together enhance the interface phononic transport efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, Z.; Guo, H.; Zhang, X.; Huang, S. Enhancing thermal conductivity of Copper/diamond composites by regulating distribution of bimodal diamond particles. Diam. Relat. Mater. 2019, 100, 107564. [Google Scholar] [CrossRef]
- Chang, G.; Sun, F.; Duan, J.; Che, Z.; Wang, X.; Wang, J.; Kim, M.; Zhang, H. Effect of Ti interlayer on interfacial thermal conductance between Cu and diamond. Acta Mater. 2018, 160, 235–246. [Google Scholar] [CrossRef]
- Sun, Y.; He, L.; Zhang, C.; Meng, Q.; Liu, B.; Gao, K.; Wen, M.; Zheng, W. Enhanced tensile strength and thermal conductivity in copper diamond composites with B4C coating. Sci. Rep. 2017, 7, 10727. [Google Scholar] [CrossRef]
- Bai, G.; Wang, L.; Zhang, Y.; Wang, X.; Wang, J.; Kim, M.; Zhang, H. Tailoring interface structure and enhancing thermal conductivity of Cu/diamond composites by alloying boron to the Cu matrix. Mater. Charact. 2019, 152, 265–275. [Google Scholar] [CrossRef]
- Ciupiński, Ł.; Kruszewski, M.; Grzonka, J.; Chmielewski, M.; Zielińsk, R.; Moszczyńska, D.; Michalski, A. Design of interfacial Cr3C2 carbide layer via optimization of sintering parameters used to fabricate copper/diamond composites for thermal management applications. Mater. Des. 2017, 120, 170–185. [Google Scholar] [CrossRef]
- Lei, L.; Bolzoni, L.; Yang, F. High thermal conductivity and strong interface bonding of a hot-forged Cu/Ti-coated-diamond composite. Carbon 2020, 168, 553–563. [Google Scholar] [CrossRef]
- Abyzov, A.; Kidalov, S.; Shakhov, F. High thermal conductivity composite of diamond particles with tungsten coating in a copper matrix for heat sink application. Appl. Therm. Eng. 2012, 48, 72–80. [Google Scholar] [CrossRef]
- Chu, K.; Jia, C.; Guo, H.; Li, W. Microstructure and thermal conductivity of Cu-B/diamond composites. J. Compos. Mater. 2013, 47, 2945–2953. [Google Scholar] [CrossRef]
- Cao, H.; Tian, Z.; Lu, M.; Ji, G.; Yan, X.; Di, C.; Yuan, M.; Guo, Q.; Su, Y.; Addad, A.; et al. Graphene interlayer for enhanced interface thermal conductance in metal matrix composites: An approach beyond surface metallization and matrix alloying. Carbon 2019, 150, 60–68. [Google Scholar] [CrossRef]
- Jia, S.; Bolzoni, L.; Li, T.; Yang, F. Unveiling the interface characteristics and their influence on the heat transfer behavior of hot-forged Cu-Cr/Diamond composites. Carbon 2021, 172, 390–401. [Google Scholar] [CrossRef]
- Jia, S.; Yang, F. High thermal conductive copper/diamond composites: State of the art. J. Mater. Sci. 2021, 56, 2241–2274. [Google Scholar] [CrossRef]
- Azina, C.; Cornu, I.; Silvain, J.; Lu, Y.; Battaglia, J. Effect of titanium and zirconium carbide interphases on the thermal conductivity and interfacial heat transfers in copper/diamond composite materials. AIP Adv. 2019, 9, 055315. [Google Scholar] [CrossRef]
- Guo, H.; Qi, Y.; Li, X. Adhesion at diamond/metal interfaces: A density functional theory study. J. Appl. Phys. 2010, 107, 033722. [Google Scholar] [CrossRef]
- Wang, X.; Smith, J. Copper/Diamond Adhesion and Hydrogen Termination. Phys. Rev. Lett. 2001, 87, 186103. [Google Scholar] [CrossRef]
- Pepper, S. Effect of Electronic Structure of the Diamond Surface on the Strength of the Diamond-Metal Interface. J. Vac. Sci. Technol. 1982, 20, 643–646. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, S.; Lu, Z.; Pu, J.; Zhang, G. Adhesive transfer at copper/diamond interface and adhesion reduction mechanism with fluorine passivation: A first-principles study. Carbon 2018, 127, 548–556. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Y.; Zhang, T.; Zhao, N.; Shi, C.; He, C.; Liu, E. Adhesion, bonding and mechanical properties of Mo doped diamond/Al (Cu) interfaces: A first principles study. Appl. Surf. Sci. 2020, 527, 146817. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, P.J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Waldron, D.; Haney, P.; Larade, B.; MacDonald, A.; Guo, H. Nonlinear spin current and magnetoresistance of molecular tunnel junctions. Phys. Rev. Lett. 2006, 96, 166804. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.; Probert, M. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Liu, F.; Zou, R.; Hu, N.; Ning, H.; Yan, C.; Liu, Y.; Wu, L.; Mo, F.; Fu, S. Enhancement of thermal energy transport across the graphene/h-BN heterostructure interface. Nanoscale 2019, 11, 4067–4072. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Wang, Z.; Guo, Y.; Wang, Y. Enhancing Mechanism of Interfacial Metal Element on the Thermal Transport across Cu-Graphene Interfaces Revealed by Molecular Dynamics Simulations. Mater. Today Commun. 2020, 25, 101431. [Google Scholar] [CrossRef]


| BSUB | BOIS | BTIS | |
|---|---|---|---|
| This work | 1.90 | 1.63 | 3.09 |
| Density (g/cm3) | Specific Heat Capacity (J/(gK)) | Thermal Diffusivity Coefficient (mm2/s) | Thermal Conductivity (W/(mK)) | |
|---|---|---|---|---|
| Diamond/Cu | 5.52 | 0.46 | 102.95 | 261 |
| Diamond/Cu-0.5 wt.%B | 5.73 | 0.46 | 263.30 | 694 |
| Diamond/Cu-1.0 wt.%B | 5.75 | 0.46 | 244.76 | 647 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Xiao, W.; Guo, H.; Xue, B.; Yang, H.; Zhang, X.; Huang, S.; Sun, M.; Xie, H. The Microzone Structure Regulation of Diamond/Cu-B Composites for High Thermal Conductivity: Combining Experiments and First-Principles Calculations. Materials 2023, 16, 2021. https://doi.org/10.3390/ma16052021
Xie Z, Xiao W, Guo H, Xue B, Yang H, Zhang X, Huang S, Sun M, Xie H. The Microzone Structure Regulation of Diamond/Cu-B Composites for High Thermal Conductivity: Combining Experiments and First-Principles Calculations. Materials. 2023; 16(5):2021. https://doi.org/10.3390/ma16052021
Chicago/Turabian StyleXie, Zhongnan, Wei Xiao, Hong Guo, Boyu Xue, Hui Yang, Ximin Zhang, Shuhui Huang, Mingmei Sun, and Haofeng Xie. 2023. "The Microzone Structure Regulation of Diamond/Cu-B Composites for High Thermal Conductivity: Combining Experiments and First-Principles Calculations" Materials 16, no. 5: 2021. https://doi.org/10.3390/ma16052021
APA StyleXie, Z., Xiao, W., Guo, H., Xue, B., Yang, H., Zhang, X., Huang, S., Sun, M., & Xie, H. (2023). The Microzone Structure Regulation of Diamond/Cu-B Composites for High Thermal Conductivity: Combining Experiments and First-Principles Calculations. Materials, 16(5), 2021. https://doi.org/10.3390/ma16052021







