Performance of Medium-Rise Buildings with Reinforced Concrete Shear Walls Designed for High Seismic Hazard
Abstract
1. Introduction
2. Methodology for the Seismic Assessment
- Build a mathematical model that represents the structure.
- Select an appropriate set of ground motion pairs representing seismic events that may result in the structure’s collapse, considering the site’s seismic risk.
- Scale the pairs of ground motions such that the pseudo-spectral acceleration in the fundamental period of the structure, , for each pair has a value low enough that the inelastic response is negligible.
- Analyze the mathematical model for each scaled ground motion pair and determine the maximum value of the drift that occurs among all its levels.
- Increase the intensity of the effective spectral pseudo-acceleration in the fundamental period, , to which each ground motion pair is scaled.
- Analyze the structure for each incrementally scaled ground motion pair and record the maximum value of the ground drift.
- Repeat steps 5 and 6 above for each pair of ground motions until the analysis predicts a collapse of the structure.
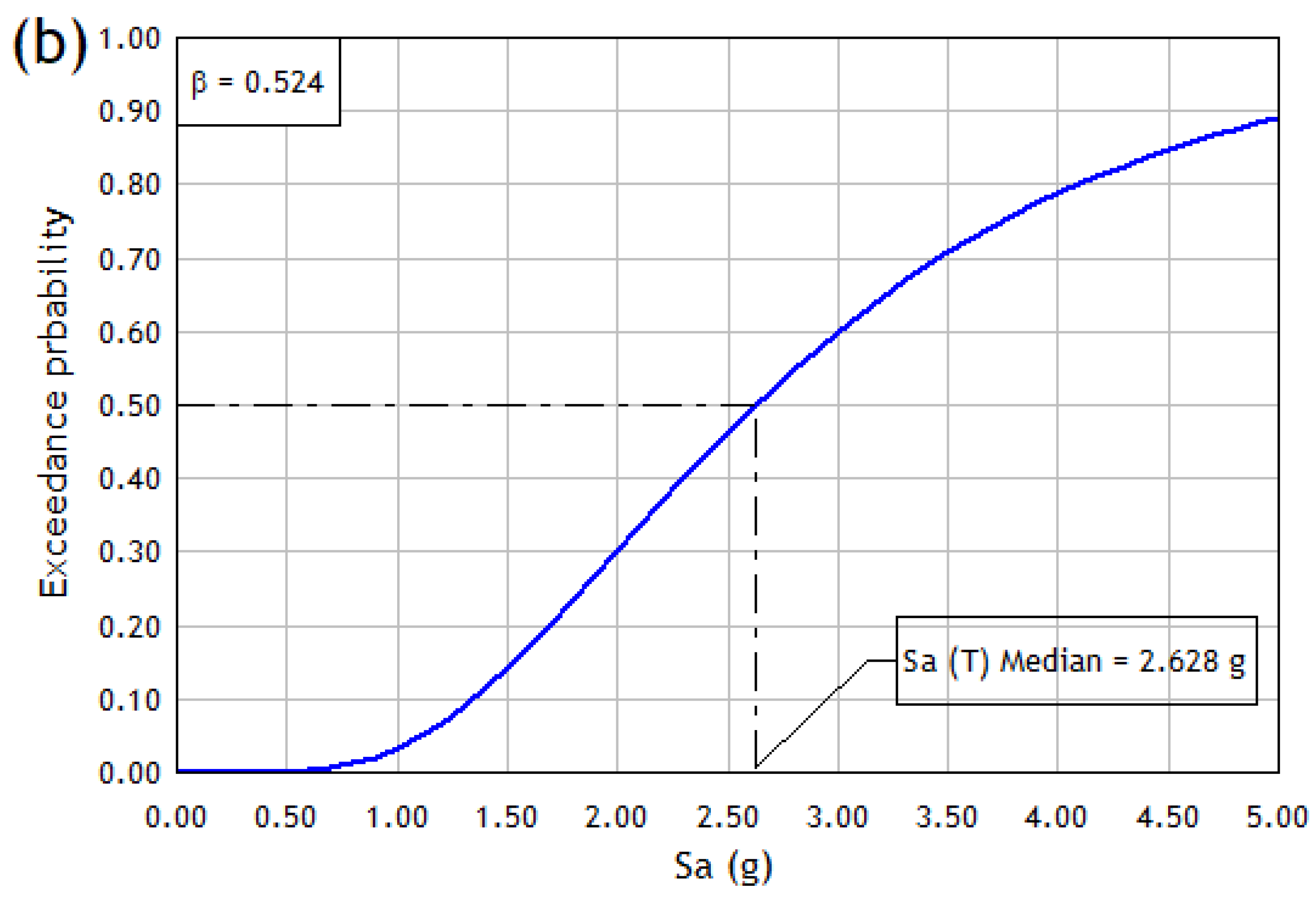
- Determine the value of the spectral pseudo-acceleration in which 50% of the ground motion pairs produce collapse predictions. This value of is taken as the mean collapse capacity, .
- Determine a scattering for the collapse fragility.
- Three mechanisms of collapse are distinguished in this methodology. One is a lateral failure or lateral dynamic instability, characterized by the loss of lateral stiffness and development of P-delta instability. Another collapse mechanism is loss of vertical bearing capacity in resistant gravity or seismic components due to earthquake-induced drift. Finally, collapse can be defined as exceeding non-simulated failure criteria, such as maximum force or deformation where components can no longer resist the load reliably.
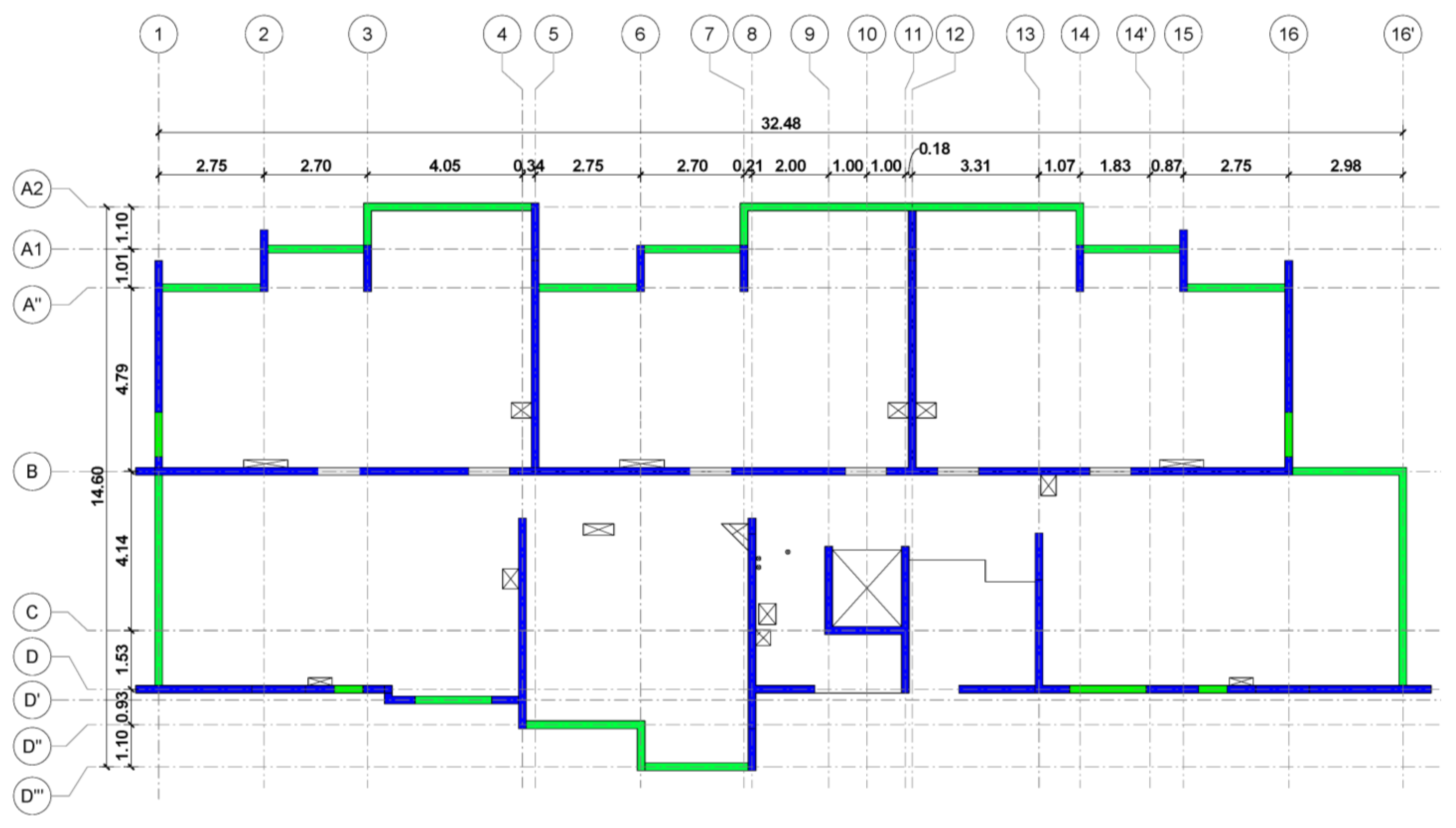
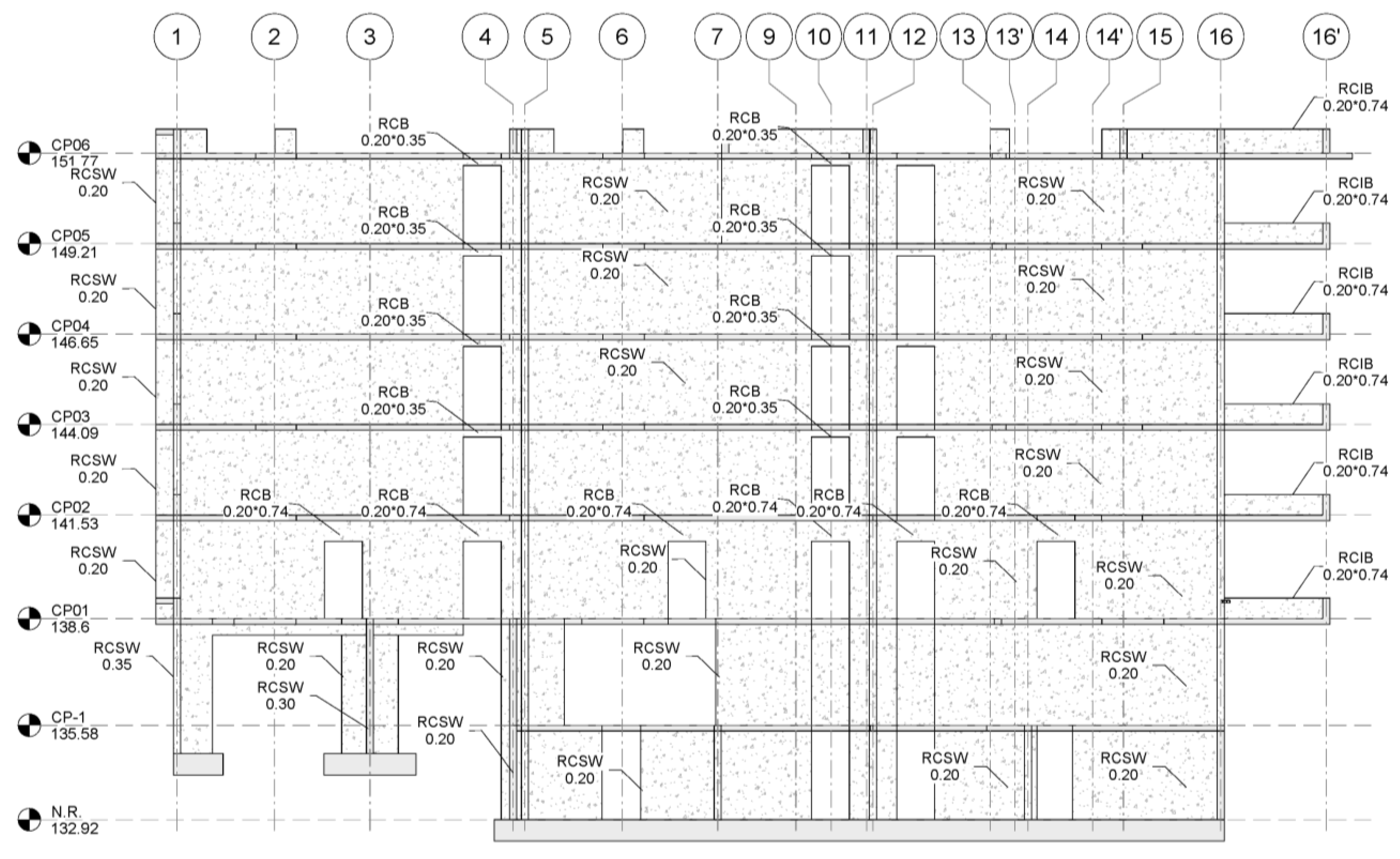
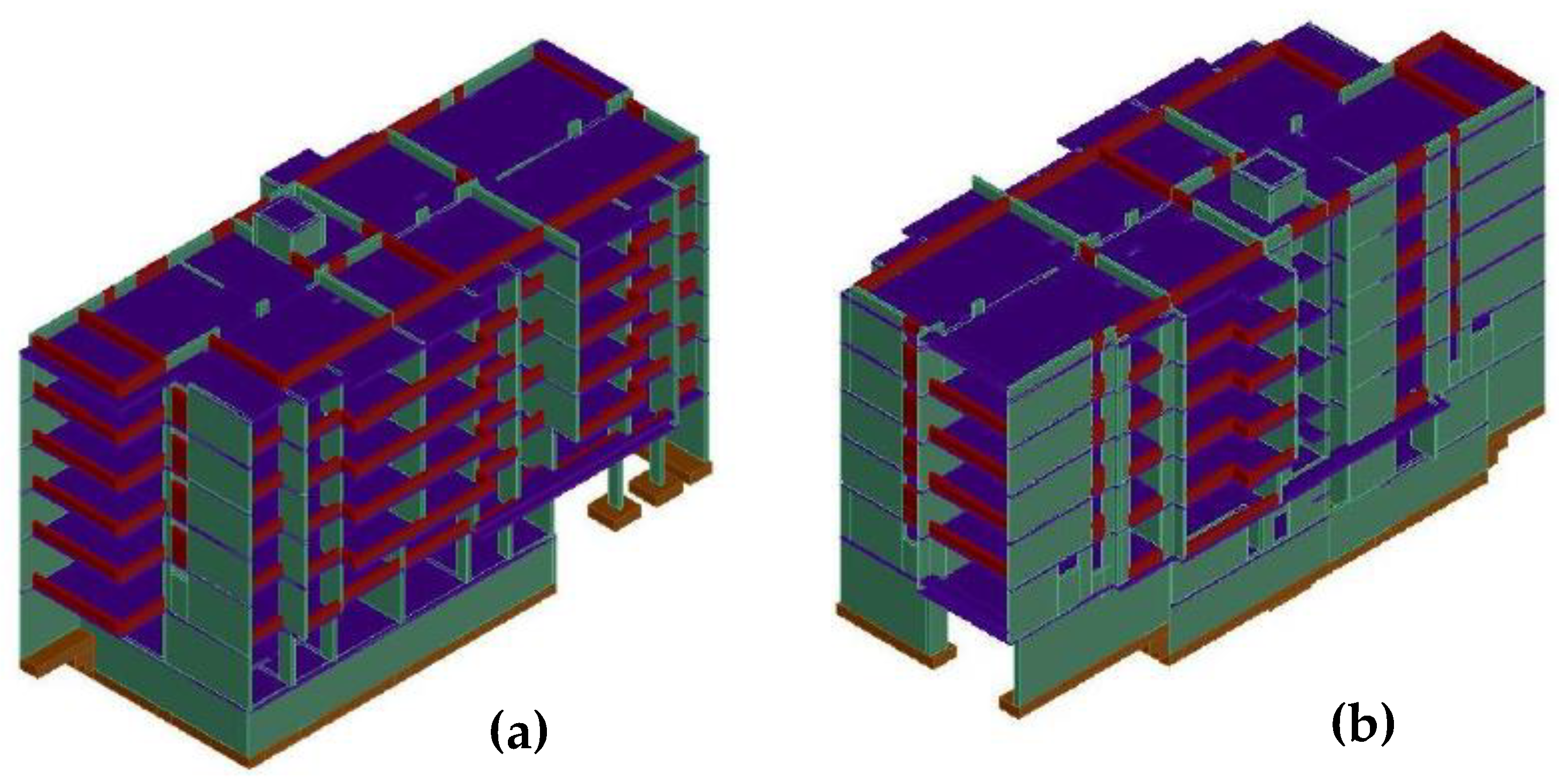
3. Case Studied
4. Results and Discussion
- To ensure better continuity in the IDA curve generated by the discrete points obtained for different intensity levels, scale increments between approximately 10% and 30% of the actual intensity value of the seismic event were used, depending on the maximum level of demand required to bring the structure to a limit state of collapse.
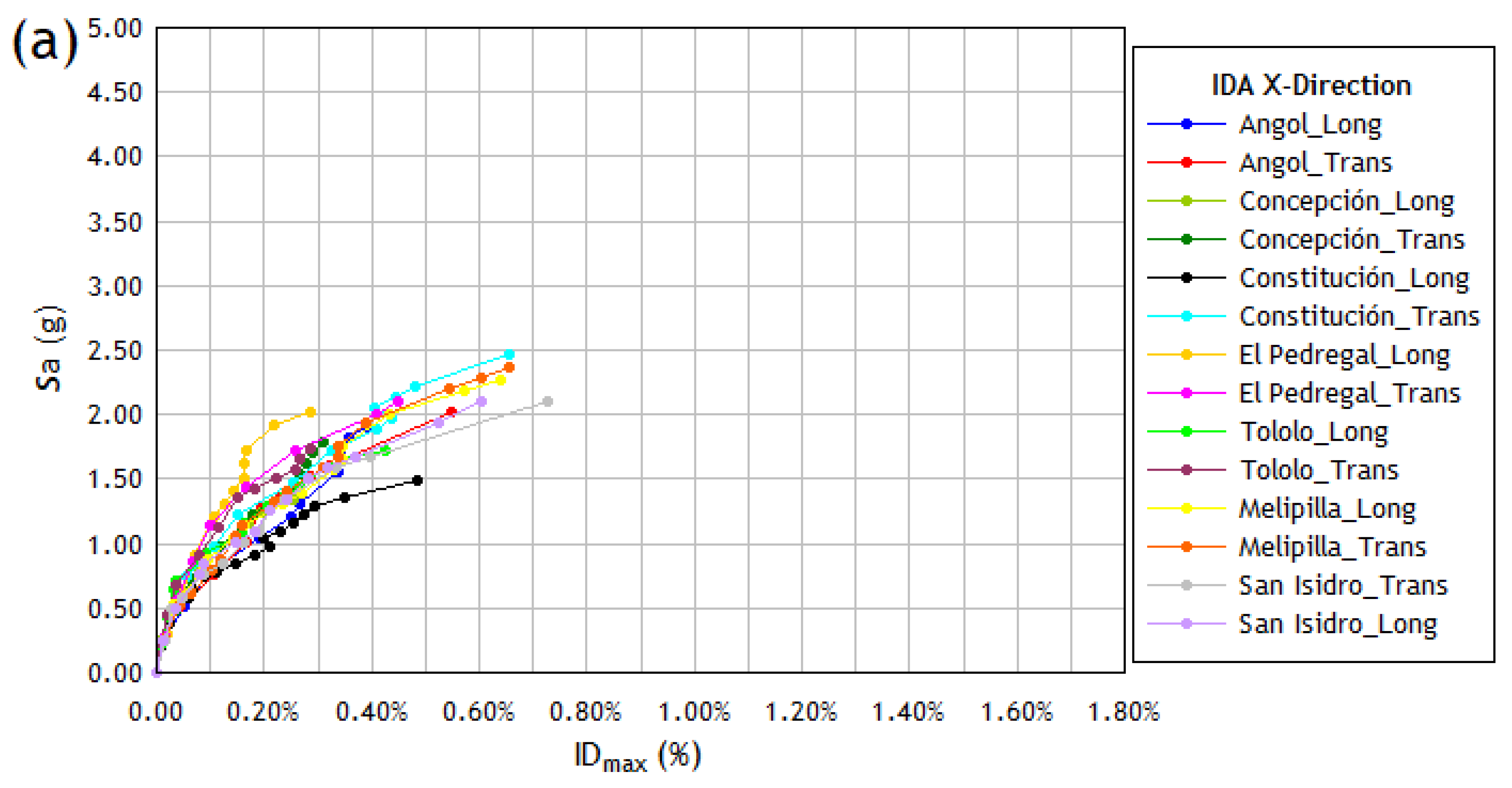
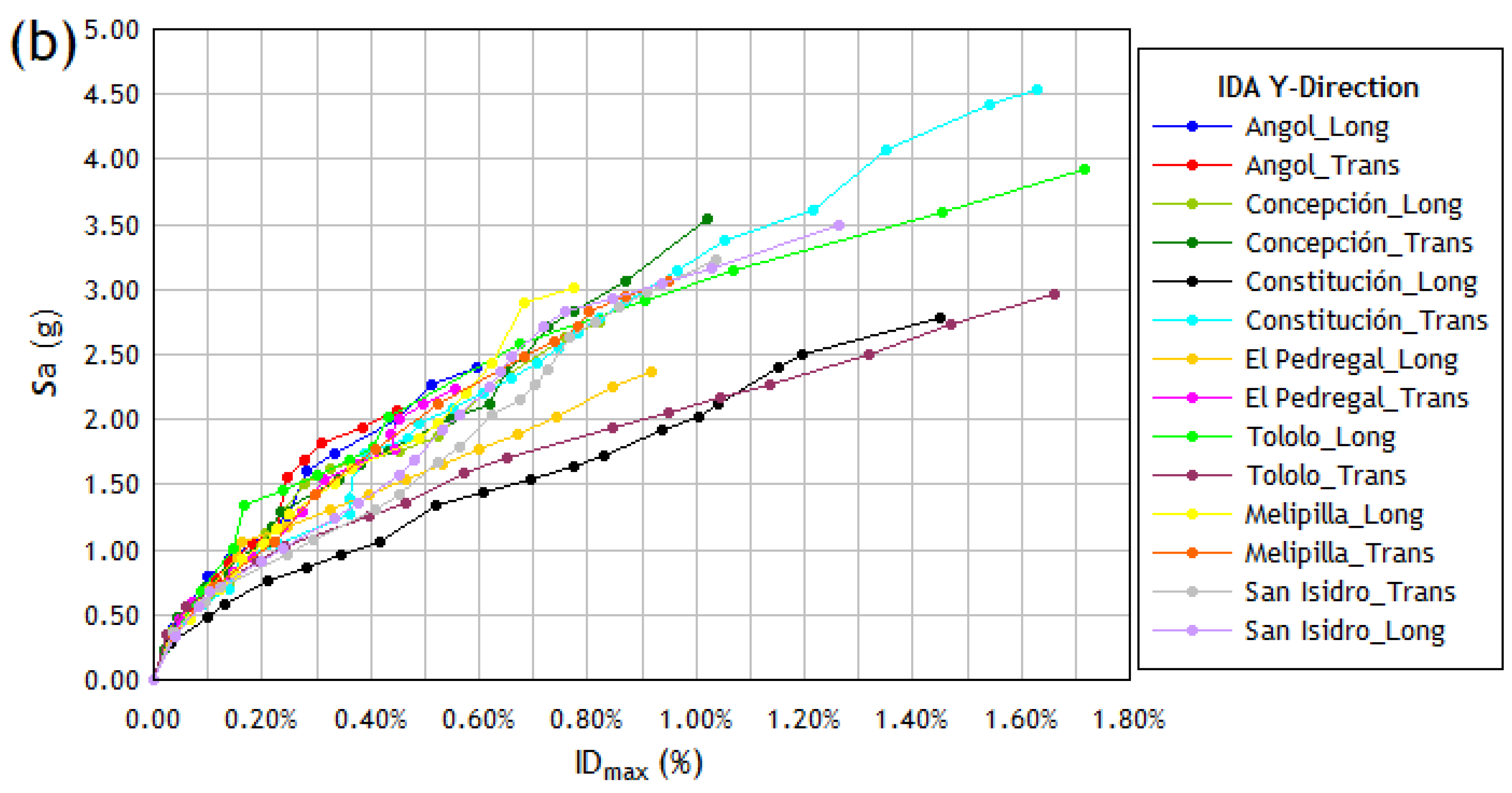
- Orthogonal components of the seismic records were assigned as input demand in each main direction of the structure (i.e., 14 components of each seismic event were used as demand in both the X and Y directions) to obtain the structure’s response with a higher degree of accuracy. This implies that a collapse brittleness curve will be obtained for each principal direction of the structure. Thus, the analysis was carried out considering the effect of each component on the numerical model independently.
- As previously stated, global dynamic instability occurs when a slight increase in the intensity of the seismic event results in a considerable increase in the structural response, i.e., when the IDA curve tends to flatten. The maximum value of IM that signals the beginning of structural collapse will be the one where the local tangent reaches 20% of the elastic slope, which is obtained when the building is subjected to a reduced scale accelerogram (for example, using a scale factor λ = 0.3).
- Obtain the acceleration at the center of gravity of the building roof for each case from time–history analysis.
- Obtain the Fourier amplitude spectrum of the acceleration at the center of gravity of the roof and take the frequency of maximum spectral amplitude.
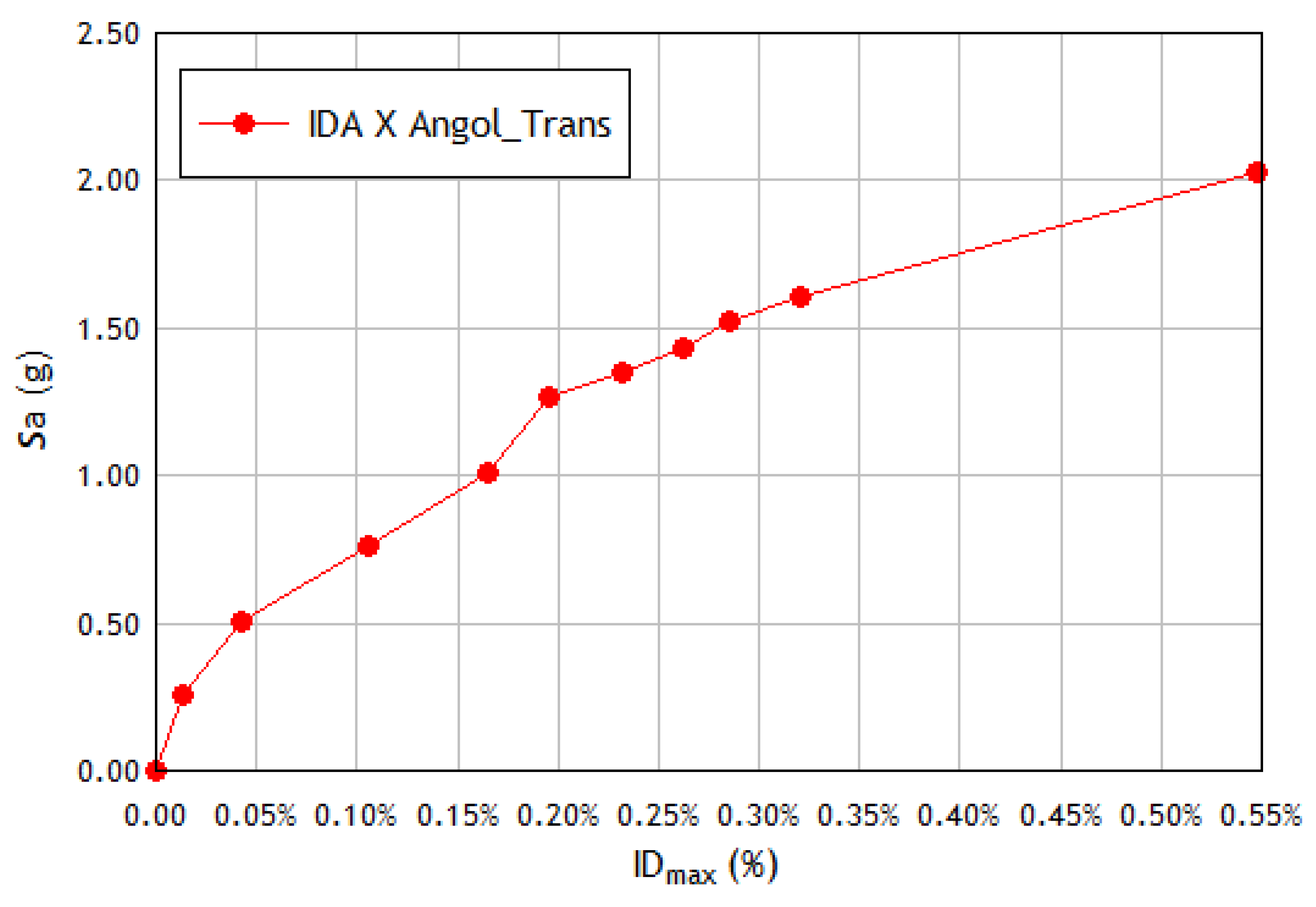
- Plot the intensity measure against the damage indicator parameter to obtain the IDA curve, where the parameter chosen to quantify the damage to the structure () is the maximum drift of the story .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- INN. Seismic design of buildings. In Norma Chilena Oficial—Nch433.of 1996 Modified 2012; Instituto Nacional de Normalización: Santiago de Chile, Chile, 2012. (In Spanish) [Google Scholar]
- Priestley, M.N.J. Myths and fallacies in earthquake engineering. Bull. New Zealand Soc. Earthq. Eng. 1997, 19, 54–63. [Google Scholar] [CrossRef]
- ACHISINA. Performance-Based Seismic Design an Alternative Procedure for Seismic Analysis and Design of Buildings; Chilean Society of Earthquake Engineering: Santiago de Chile, Chile, 2017. (In Spanish) [Google Scholar]
- Erdil, B.; Ceylan, H.A. Detailed Comparison of Preliminary Seismic Vulnerability Assessment Methods for RC Buildings, Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 711–725, dic. 2019. [Google Scholar] [CrossRef]
- Xiong, C.; Lu, X.; Lin, X. Damage assessment of shear wall components for RC frame–shear wall buildings using story curvature as engineering demand parameter. Eng. Struct. 2019, 189, 77–88. [Google Scholar] [CrossRef]
- Carrillo, J.; Oyarzo-Vera, C.; Blandón, C. Damage assessment of squat, thin and lightly-reinforced concrete walls by the Park & Ang damage index. J. Build. Eng. 2019, 26, 100921. [Google Scholar] [CrossRef]
- Pejovic, J.R.; Serdar, N.N. Estimation of inter-story drifts at onset of damage states for RC high-rise buildings. Earthq. Struct. 2021, 21, 63–78. [Google Scholar] [CrossRef]
- ATC. ATC 40: Seismic Evaluation and Retrofit of Concrete Buildings Vol.1 Report no’s 96-01; Applied Technology Council: Redwood City, CA, USA, 1996. [Google Scholar]
- Vamvatsikos, D. Seismic Performance, Capacity and Reliability of Structures as Seen Through Incremental Dynamic Analysis. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Angulo, C.; Diaz, K.; Gutiérrez, J.; Casadey, R.; Pannillo, G.; Muñoz-La Rivera, F.; Vielma, J.C. Using BIM for the Assessment of the Seismic Performance of Educational Buildings. Int. J. Saf. Secur. Eng. 2020, 10, 77–82. [Google Scholar] [CrossRef]
- Bertero, V. Strength and Deformation Capacities of Buildings under Extreme Environments. Struct. Eng. Struct. Mech. 1977, 53, 29–79. [Google Scholar]
- Luco, N.; Cornell, C.A. Effects of random connection fractures on the demands and reliability for a 3-story pre-Northridge SMRF structure. In Proceedings of the 6th US National Conference on Earthquake Engineering, Seattle, WA, USA, 31 May–4 June 1998; Volume 244, pp. 1–12. [Google Scholar]
- Luco, N.; Cornell, C.A. Effects of connection fractures on SMRF seismic drift demands. J. Struct. Eng. 2000, 126, 127–136. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, A. Seismic Hazard Analysis of Nonlinear Structures. II: Applications. J. Struct. Eng. 1994, 120, 3345–3365. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, A. Seismic hazard analysis of nonlinear structures. I: Methodology. J. Struct. Eng. 1994, 120, 3320–3344. [Google Scholar] [CrossRef]
- Yun, S.-Y.; Hamburger, R.; Cornell, A.; Foutch, D.A. Seismic Performance Evaluation for Steel Moment Frames. J. Struct. Eng. 2002, 128, 534–545. [Google Scholar] [CrossRef]
- Mehanny, S.S.F.; Deierlein, G.G. Seismic Damage and Collapse Assessment of Composite Moment Frames. J. Struct. Eng. 2001, 127, 1045–1053. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. The incremental dynamic analysis and its application to performance-based earthquake engineering. In Proceedings of the 12th European Conference on Earthquake Engineerig, London, UK, 9–13 September 2002; Volume 40, pp. 1375–1392. [Google Scholar]
- Vamvatsikos, D.; Cornell, A. Incremental Dynamic Analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- FEMA P-58-1; Seismic Performance Assessment of Buildings Volume 1—Methodology. Federal Emergency Management Agency: Washington, DC, USA, 2018.
- Ugalde, D.; Lopez-Garcia, D.; Parra, P.F. Fragility-based analysis of the influence of effective stiffness of reinforced concrete members in shear wall buildings. Bull. Earthq. Eng. 2020, 18, 2061–2082. [Google Scholar] [CrossRef]
- Nair, S.S.; Hemalatha, G.; Raja, R.; Stephen, E.A. Seismic Vulnerability Studies of a G+17 storey building in Abu Dhabi—UAE using Fragility Curves. Int. J. Eng. 2021, 34, 5. [Google Scholar] [CrossRef]
- Bonett, R. Vulnerability and Seismic Risk of Buildings. Application to Urban Environments in High and Moderate Seismic Prone areas. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, España, 2003. [Google Scholar]
- Li, G.; Li, R.; Yu, D. Experimental and Analytical Lateral Performance of Shear Walls with Variable Phases of Deformation. J. Struct. Eng. 2022, 148, 10. [Google Scholar] [CrossRef]
- Aryan, H.; Gencturk, B.; Alkhrdaji, T. In-plane shear strengthening of reinforced concrete diaphragms using fiber reinforced polymer composites. Adv. Struct. Eng. 2022. Published online. [Google Scholar] [CrossRef]
- Akl, A.; Ezzeldin, M. Seismic collapse risk assessment of low-aspect-ratio reinforced concrete shear walls using the FEMA P695 methodology. J. Struct. Eng. 2023, 149, 04022237. [Google Scholar] [CrossRef]
- Loa, G.; Tarque, N.; Condori, C. Experimental and numerical modelling studies of slender reinforced concrete walls with single-layer reinforcement in Peru. Eng. Struct. 2022, 273, 115029. [Google Scholar] [CrossRef]
- Kolozvari, K.; Hori, Y.; Yasumoto, H.; Suzuki, Y.; Nakashima, M.; Naeim, F. A comparative study of seismic analysis, design, and collapse safety margins of tall buildings in the united states and Japan: Part II: Comparison of seismic capacity and collapse safety margin. Earthq. Spectra 2022, 38, 2319–2335. [Google Scholar] [CrossRef]
- Soltani, M.; Raissi Dehkordi, M.; Eghbali, M.; Samadian, D.; Salmanmohajer, H. Influence of infill walls on resilience index of RC schools using the BIM analysis and FEMA P-58 methodology. Int. J. Civ. Eng. 2022. [Google Scholar] [CrossRef]
- Momeni, H.; Dolatshahi, K.M. Predictive equations for drift ratio and damage assessment of RC shear walls using surface crack patterns. Eng. Struct. 2019, 190, 410–421. [Google Scholar] [CrossRef]
- Belletti, B.; Martinelli, E.; Michelini, E.; Tavano, M.; Vecchi, F. Seismic risk assessment of existing RC frame-buildings with shear walls. In Seismic Behaviour and Design of Irregular and Complex Civil Structures IV; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Durga, M.; Satyabrata, C. Effect of damage limit states on the seismic fragility of reinforced concrete frame-shear wall buildings. Disaster Adv. 2021, 14, 57–68. [Google Scholar] [CrossRef]
- Desai, K.; Sheth, R.; Patel, K. Performance evaluation using fragility analysis of rc frame-wall structures. Reliab. Theory Appl. 2021, 16, 187–195. [Google Scholar]
- Pavel, F.; Calotescu, I.; Stanescu, D.; Badiu, A. Life-cycle and seismic fragility assessment of code-conforming reinforced concrete and steel structures in Bucharest, Romania. Int. J. Disaster Risk Sci. 2018, 9, 263–274. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, X.; Hu, L. Seismic fragility analysis of RC frame-shear wall structures. In Proceedings of the IABSE Symposium: Engineering for Progress, Nature and People, Madrid, Spain, 3–5 September 2014; pp. 372–379. [Google Scholar] [CrossRef]
- Hoult, R.; Goldsworthy, H.; Lumantarna, E. Fragility functions for RC shear wall buildings in Australia. Earthq. Spectra 2019, 55, 333–360. [Google Scholar] [CrossRef]
- Sadraddin, H.L.; Shao, X.; Hu, Y. Fragility assessment of high-rise reinforced concrete buildings considering the effects of shear wall contributions. Struct. Des. Tall Spec. Build. 2016, 25, 1089–1102. [Google Scholar] [CrossRef]
- Martínez, J. Characterization of Seismic Vulnerability Using Fragility Curves and Damage Probability Matrices for Reinforced Concrete Structural Typologies. Application to the City of Valdivia, Los Ríos Region. Bachelor’s Thesis, Universidad Austral de Chile, Valdivia, Chile, 2012. (In Spanish). [Google Scholar]
- Porcu, M.C.; Vielma, J.C.; Pais, G.; Osorio, D.; Vielma-Quintero, J.C. Some issues on the seismic assessment of shear-wall buildings through code-compliant dynamic analyses. Buildings 2022, 12, 694. [Google Scholar] [CrossRef]
- Alwashali, H.; Maeda, M.; Ogata, Y.; Aizawa, N.; Tsurugai, K. Residual seismic performance of damaged reinforced concrete walls. Eng. Struct. 2021, 243, 112673. [Google Scholar] [CrossRef]
- Kolozvari, K.; Terzic, V.; Miller, R.; Saldana, D. Assessment of dynamic behavior and seismic performance of a high-rise RC coupled wall building. Eng. Struct. 2018, 176, 606–620. [Google Scholar] [CrossRef]
- Petrone, F.; McKenna, F.; Do, T.; McCallen, D.A. Versatile numerical model for the nonlinear analysis of squat-to-tall reinforced-concrete shear walls. Eng. Struct. 2021, 242, 112406. [Google Scholar] [CrossRef]
- Wallace, J.W.; Moehle, J. Behavior, design, and modeling of structural walls and coupling beams—Lessons from recent laboratory tests and earthquakes. Int. J. Concr. Struct. Mater. 2012, 6, 3–18. [Google Scholar] [CrossRef]
- Antoniou, K.; Tsionis, G.; Fardis, M.N. Inelastic shears in ductile RC walls of mid-rise wall-frame buildings and comparison to Eurocode 8. Bull. Earthq. Eng. 2015, 13, 841–869. [Google Scholar] [CrossRef]
- Wallace, J.W. Modelling issues for tall reinforced concrete core wall buildings. Struct. Des. Tall Spec. Build 2007, 16, 615–632, dic. 2007. [Google Scholar] [CrossRef]
- D’Ayala, D.; Meslem, A.; Vamvatsikos, D.; Porter, K.; Rossetto, T.; Silva, V. Guidelines for Analytical Vulnerability Assessment of Low/Mid-Rise Buildings, Vulnerability Global Component Project; GEM Technical Report 2014-12; Global Earthquake Model Foundation: Pavia, Italy, 2015. [Google Scholar] [CrossRef]
- Tojo, T.; Tanaka, K.; Yamamoto, S.; Tsunashima, N.; Suzuki, T.; Takada, A.; Yabushita, N. Evaluation of seismic performance for the complex structure of planar arrangement with reinforced concrete shear walls. AIJ J. Technol. Des. 2020, 26, 91–96. [Google Scholar] [CrossRef]
- Alwaeli, W.; Mwafy, A.; Pilakoutas, K.; Guadagnini, Y.M. Multi-level nonlinear modeling verification scheme of RC high-rise wall buildings. Bull. Earthq. Eng. 2017, 15, 2035–2053. [Google Scholar] [CrossRef]
- FEMA. Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings; Report No. FEMA-350; SAC Joint Venture, Federal Emergency Management Agency: Washington, DC, USA, 2000.
- FEMA. Recommended seismic evaluation and upgrade criteria for existing welded steel momentframe. Report No. FEMA-351, SAC Joint Venture; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Seismosoft. SeismoMatch—A Computer Program for Spectrum Matching of Earthquake Records. Available online: www.seismosoft.com (accessed on 31 January 2021).
- Ureta, R. Response of Reinforced Concrete Shear Wall Buildings during the 2010, Chile Earthquake. Ph.D. Thesis, Pontificia Universidad Católica de Chile, Santiago de Chile, Chile, 2016. [Google Scholar]
- Ramos, L.; Hube, M. Seismic response of reinforced concrete wall buildings with nonlinear coupling slabs. Eng. Struct. 2021, 234, 111888. [Google Scholar] [CrossRef]
- Morales, A.; Ceresa, P.; Hube, M. Seismic shear and moment demands in reinforced concrete wall buildings. In Proceedings of the 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Crete, Greece, 24–26 June 2019; pp. 4115–4127. [Google Scholar] [CrossRef]
- Jiang, H.; Huang, Y.; He, L.; Huang, T.; Zhang, S. Seismic performance of RC frame-shear wall structures with vertical setback. Structures 2021, 33, 4203–4217. [Google Scholar] [CrossRef]
- Pais, G. Non-Linear Seismic Analysis on a Multi-Storey Building with Chilean Typology. Master’s Thesis, Università Degli Studi di Cagliari, Cagliari, Italy, 2019. (In Italian). [Google Scholar]
- Seismosoft. SeismoStruct—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures. Available online: http://www.seismosoft.com (accessed on 31 January 2021).
- Calvi, G.; Pinho, R.; Magenes, G.; Bommer, J.; Restrepo-Vélez, L.; Crowley, H. Development of seismic vulnerability assessment methodologies over the past 30 years. ISET J. Earthq. Technol. 2006, 43, 75–104. [Google Scholar]
- Gómez, M.A.; Díaz, G.Y.; Vielma, J.C. Nonlinear numerical assessment of the seismic response of hillside RC buildings. Earthq. Eng. Eng. Vib. 2021, 20, 423–440. [Google Scholar] [CrossRef]
- Vielma, J.C.; Porcu, M.C.; Fuentes, M. Non-linear analyses to assess the seismic performance of RC buildings retrofitted with FRP. Rev. Int. Métodos Numér. Cálc. Diseñoing. 2020. Online first. Available online: https://www.scipedia.com/public/Vielma-Perez_et_al_2019a (accessed on 3 October 2022).
- Chang, G.A.; Mander, J.B. Seismic Energy Based Fatigue Damage Analysis of Bridge Columns: Part 1—Evaluation of Seismic Capacity; NCEER Technical Report No. NCEER-94-0006; State University of New York: Buffalo, NY, USA, 1994. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. In Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Katsanos, E.; Sextos, A.; Elnashai, A. Prediction of inelastic response periods of buildings based on intensity measures and analytical model parameters. Eng. Struct. 2014, 71, 161–177. [Google Scholar] [CrossRef]
- Vielma, J.C.; Porcu, M.; López, N. Intensity Measure Based on a Smooth Inelastic Peak Period for a More Effective Incremental Dynamic Analysis. Appl. Sci. 2020, 10, 8632. [Google Scholar] [CrossRef]
- Milutinovic, Z.; Trandafilovski, G. Risk-UE An Advanced Approach to Earthquake Risk Scenarios with Applications to Different European Towns; Report to WP4: Vulnerability of Current Buildings; European Commission: Brussels, Belgium, 2003.
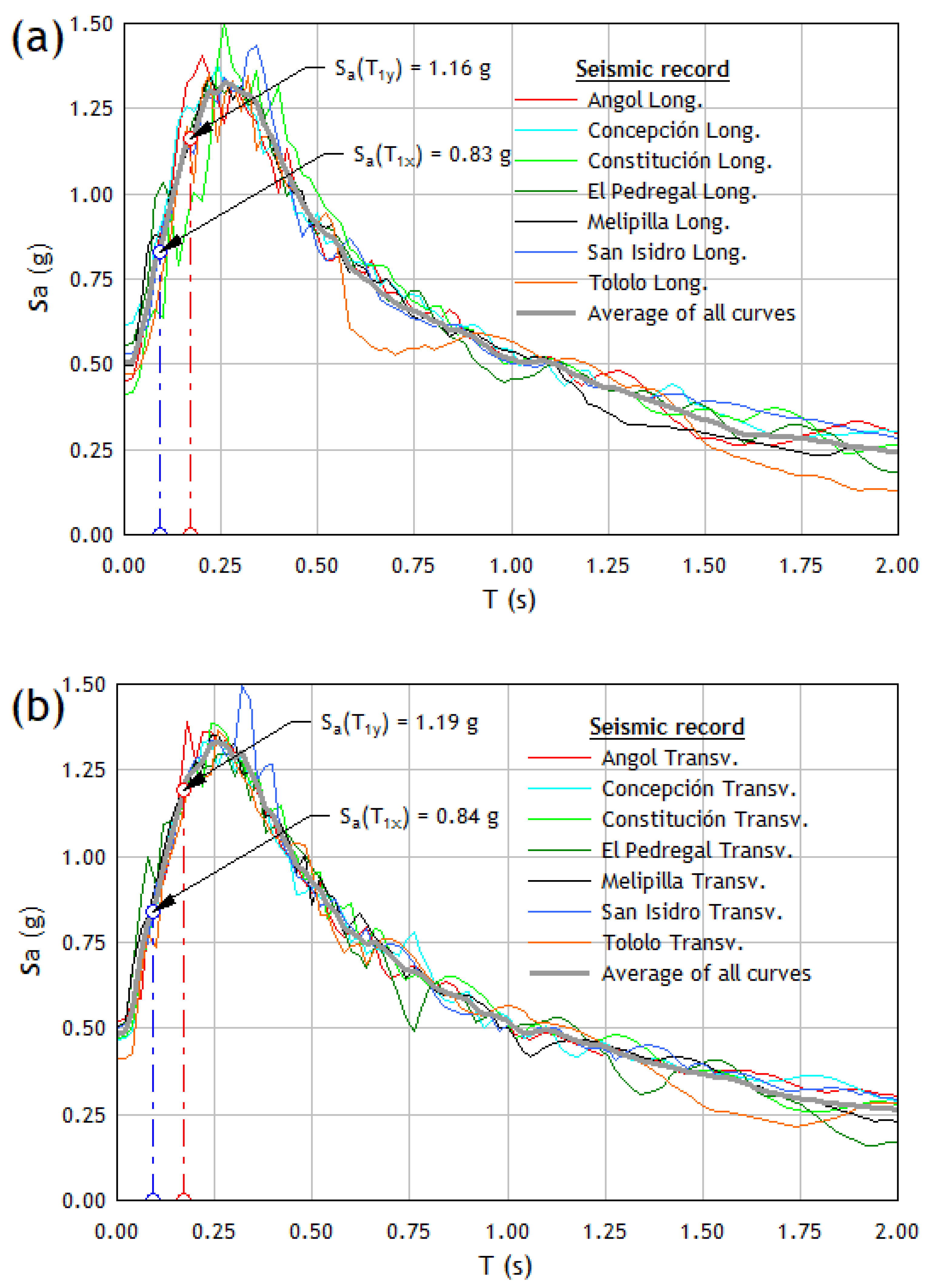



| Earthquake | Date | Magnitude (Mw) | Coord. Epicenter | Station | Component | PGA (g) | Significative Duration (s) |
|---|---|---|---|---|---|---|---|
| Valparaiso | 03-03-85 | 8.0 (CSN) | 33.240° S | Melipilla | Transv. | 0.496 | 19.82 |
| Long. | 0.499 | 18.80 | |||||
| 7.4 (USGS) | 71.850° W | San Isidro | Transv. | 0.532 | 36.20 | ||
| Long. | 0.503 | 39.80 | |||||
| Bio-Bio | 27-02-2010 | 8.8 (CSN) | 36.290° S | Angol | Transv. | 0.446 | 45.89 |
| Long. | 0.523 | 44.84 | |||||
| Concepcion | Transv. | 0.617 | 56.49 | ||||
| 8.8 (USGS) | 73.239° W | Long. | 0.466 | 59.25 | |||
| Constitucion | Transv. | 0.415 | 38.43 | ||||
| Long. | 0.473 | 51.42 | |||||
| Coquimbo | 16-09-2015 | 8.4 (CSN) | 31.553° S | El Pedregal | Transv. | 0.557 | 36.43 |
| Long. | 0.504 | 33.02 | |||||
| 8.3 (USGS) | 71.864° W | Tololo | Transv. | 0.470 | 42.02 | ||
| Long. | 0.412 | 43.30 |
| Mode | Period [s] | Frequency [Hz] | Participative Mass [%] | |||||
|---|---|---|---|---|---|---|---|---|
| Ux | Uy | Uz | Rx | Ry | Rz | |||
| 1 | 0.169 | 5.904 | 1.87 | 43.23 | 0.00 | 25.59 | 0.62 | 15.96 |
| 2 | 0.153 | 6.552 | 4.06 | 20.07 | 0.10 | 12.64 | 1.01 | 41.82 |
| 3 | 0.090 | 11.058 | 56.46 | 0.00 | 0.06 | 0.00 | 17.24 | 5.14 |
| 4 | 0.087 | 11.536 | 0.06 | 0.04 | 0.00 | 0.04 | 0.02 | 0.01 |
| 5 | 0.051 | 19.655 | 0.01 | 0.33 | 14.26 | 4.03 | 6.62 | 0.09 |
| 6 | 0.050 | 19.965 | 0.09 | 0.03 | 2.03 | 0.15 | 0.19 | 0.02 |
| 7 | 0.050 | 19.989 | 0.08 | 0.23 | 5.28 | 1.59 | 0.54 | 0.02 |
| 8 | 0.049 | 20.553 | 0.21 | 0.00 | 7.88 | 1.76 | 8.47 | 0.01 |
| 9 | 0.047 | 21.393 | 0.61 | 0.10 | 0.06 | 0.48 | 0.62 | 0.34 |
| 10 | 0.046 | 21.937 | 0.00 | 0.00 | 0.54 | 0.00 | 0.31 | 0.11 |
| IDA X | Scale Factor λ | ||
|---|---|---|---|
| Constitución_Long | 1.6 | 0.199 | 1.036 |
| Tololo_Long | 1.6 | 0.164 | 1.151 |
| Concepción_Long | 1.3 | 0.171 | 1.159 |
| San_Isidro_Trans | 1.5 | 0.210 | 1.257 |
| ElPedregal_Transv | 1.5 | 0.168 | 1.433 |
| San_Isidro_Long | 1.8 | 0.281 | 1.511 |
| Angol_Transv | 1.8 | 0.285 | 1.521 |
| Tololo_Transv | 2.2 | 0.265 | 1.655 |
| Concepción_Transv | 2.1 | 0.290 | 1.705 |
| Melipilla_Long | 2.0 | 0.344 | 1.748 |
| Angol_Long | 2.1 | 0.358 | 1.824 |
| ElPedregal_Long | 1.9 | 0.218 | 1.918 |
| Melipilla_Transv | 2.2 | 0.387 | 1.933 |
| Constitución_Transv | 2.5 | 0.403 | 2.049 |
| IDA Y | Scale Factor λ | ||
|---|---|---|---|
| Tololo_Transv | 0.5 | 0.060 | 0.569 |
| ElPedregal_Long | 0.9 | 0.161 | 1.065 |
| Angol_Transv | 1.4 | 0.308 | 1.813 |
| ElPedregal_Transv | 1.8 | 0.498 | 2.122 |
| Angol_Long | 1.7 | 0.514 | 2.270 |
| Constitución_Long | 2.6 | 1.198 | 2.498 |
| Tololo_Long | 2.3 | 0.675 | 2.578 |
| Concepción_Long | 2.1 | 0.761 | 2.628 |
| Concepción_Transv | 2.3 | 0.727 | 2.716 |
| San_Isidro_Long | 2.5 | 0.759 | 2.823 |
| Melipilla_Transv | 2.4 | 0.804 | 2.835 |
| Melipilla_Long | 2.5 | 0.684 | 2.895 |
| San_Isidro_Transv | 2.5 | 0.910 | 2.983 |
| Constitución_Transv | 3.5 | 1.349 | 4.067 |
| Direction X | Direction Y | ||
|---|---|---|---|
| β | β | ||
| 1.655 | 0.524 | 2.628 | 0.524 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alarcón, C.; López, Á.; Vielma, J.C. Performance of Medium-Rise Buildings with Reinforced Concrete Shear Walls Designed for High Seismic Hazard. Materials 2023, 16, 1859. https://doi.org/10.3390/ma16051859
Alarcón C, López Á, Vielma JC. Performance of Medium-Rise Buildings with Reinforced Concrete Shear Walls Designed for High Seismic Hazard. Materials. 2023; 16(5):1859. https://doi.org/10.3390/ma16051859
Chicago/Turabian StyleAlarcón, Claudio, Álvaro López, and Juan Carlos Vielma. 2023. "Performance of Medium-Rise Buildings with Reinforced Concrete Shear Walls Designed for High Seismic Hazard" Materials 16, no. 5: 1859. https://doi.org/10.3390/ma16051859
APA StyleAlarcón, C., López, Á., & Vielma, J. C. (2023). Performance of Medium-Rise Buildings with Reinforced Concrete Shear Walls Designed for High Seismic Hazard. Materials, 16(5), 1859. https://doi.org/10.3390/ma16051859







