Numerical Simulation for Hydrogen-Assisted Cracking: An Explicit Phase-Field Formulation
Abstract
1. Introduction
2. Method
2.1. Classical Phase-Field Fracture Model and Governing Equation
2.2. Hydrogen Diffusion Equation
2.3. Spectral Decomposition of Strain Energy
2.4. C0 Shell Element
2.5. Finite Element Implementation of Computational Framework
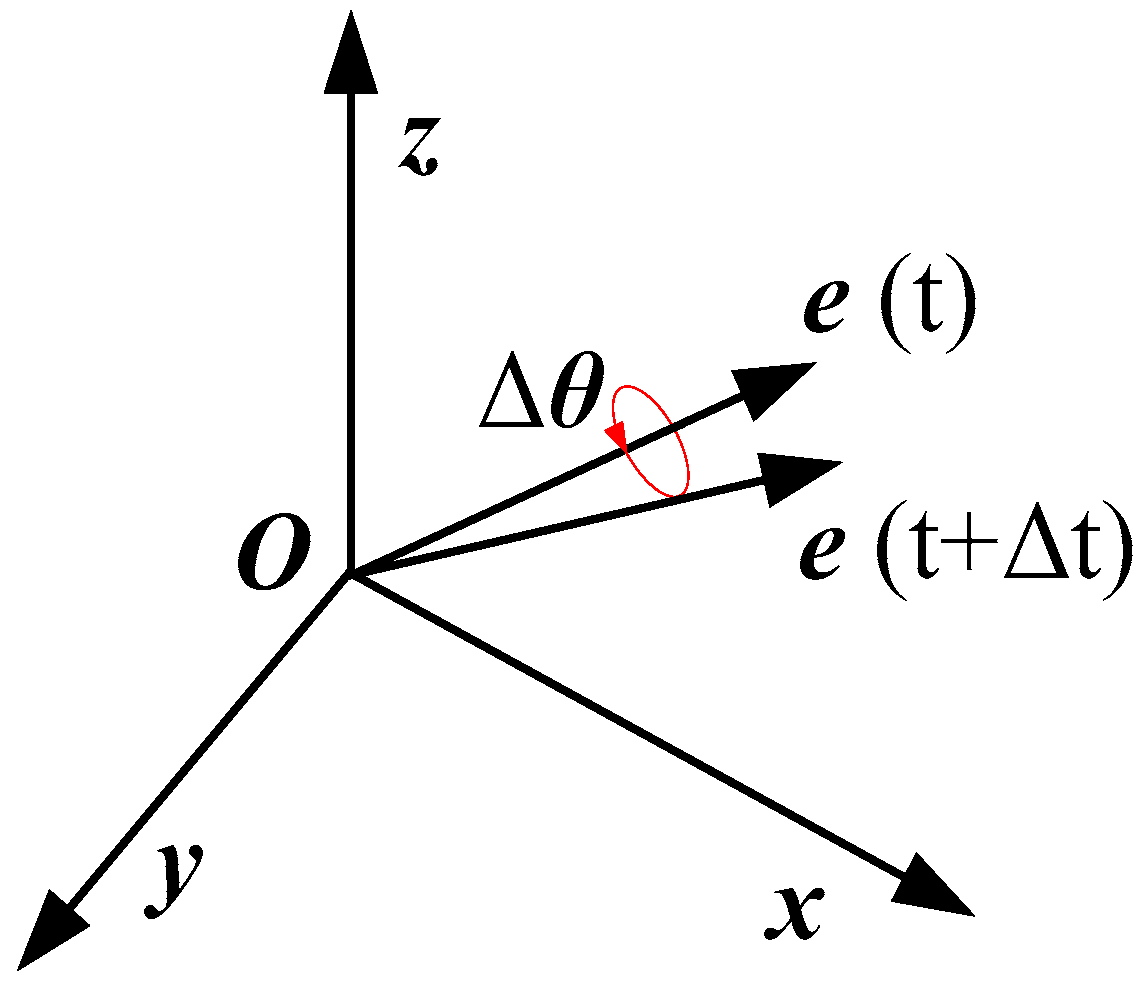
2.6. Central Difference Method and Rodriguez Transformation
3. Numerical Experiment
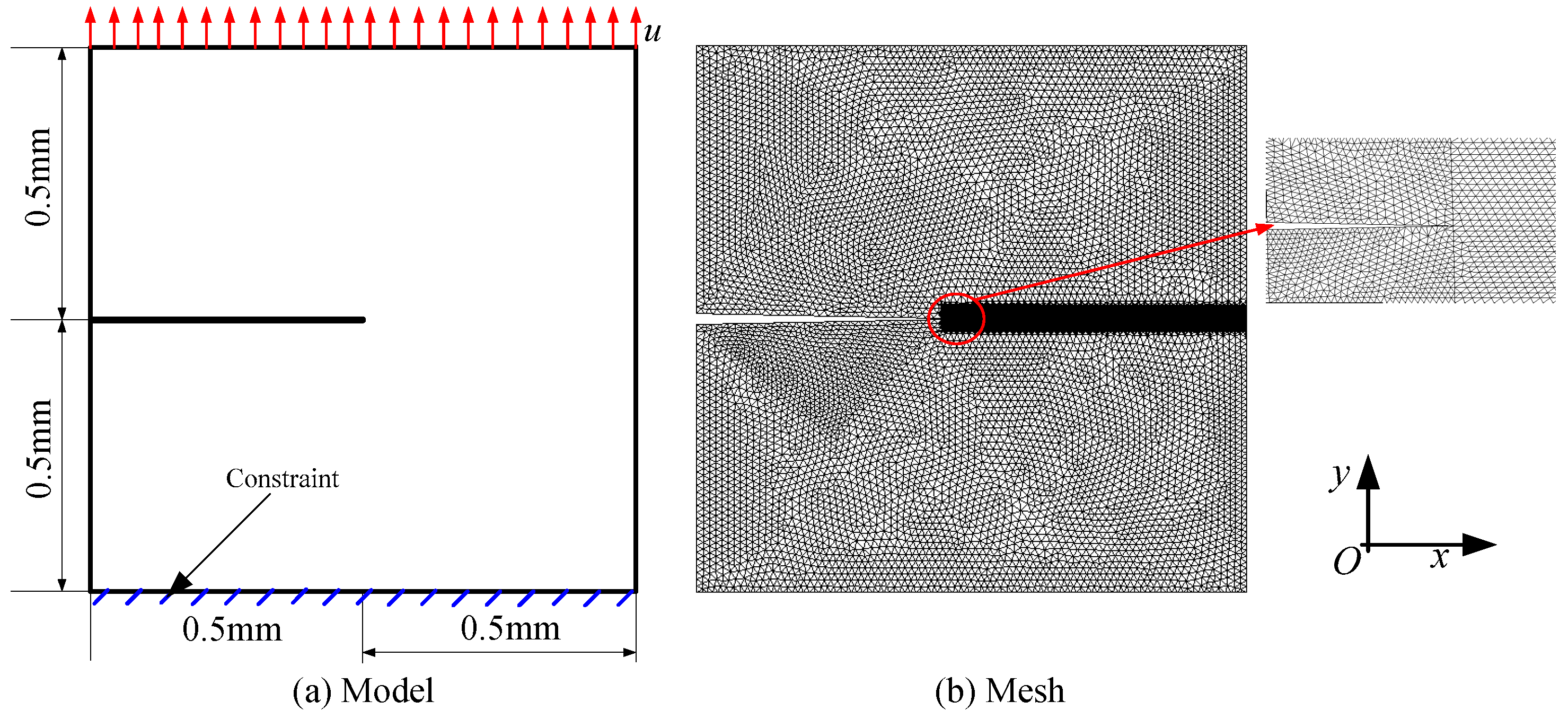
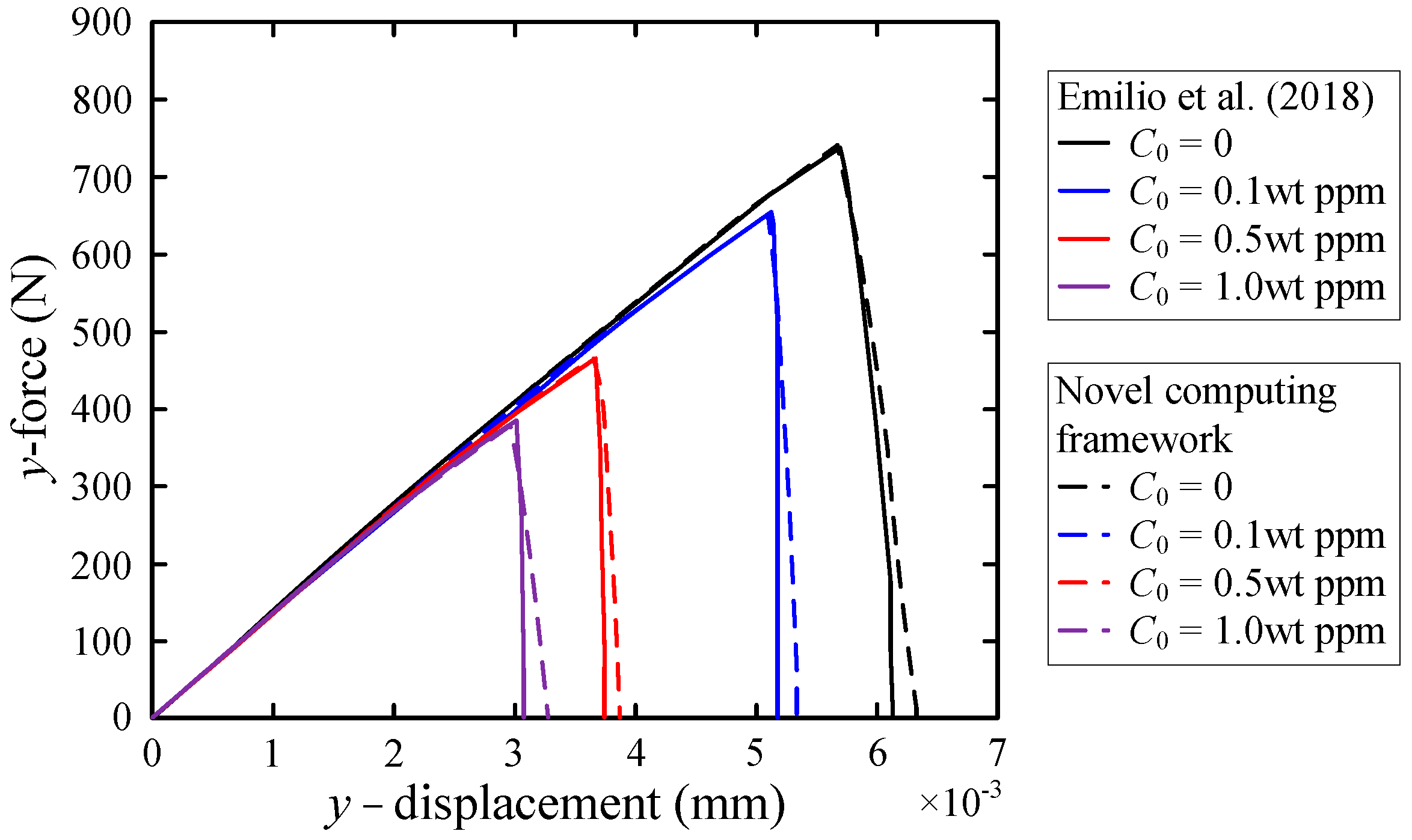
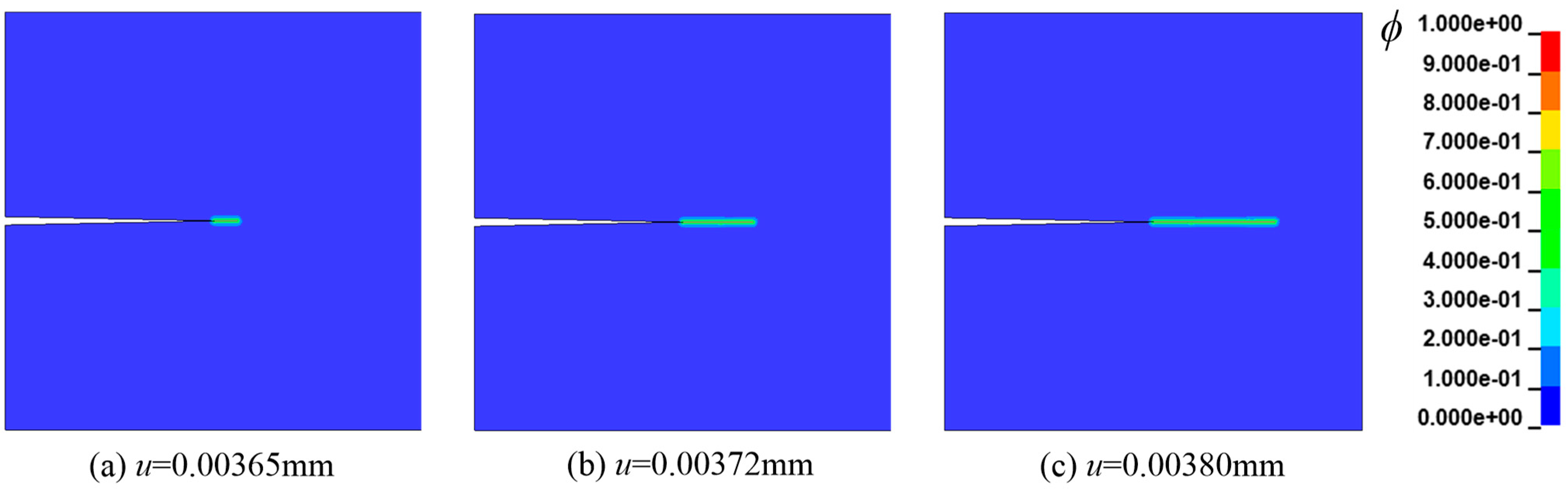
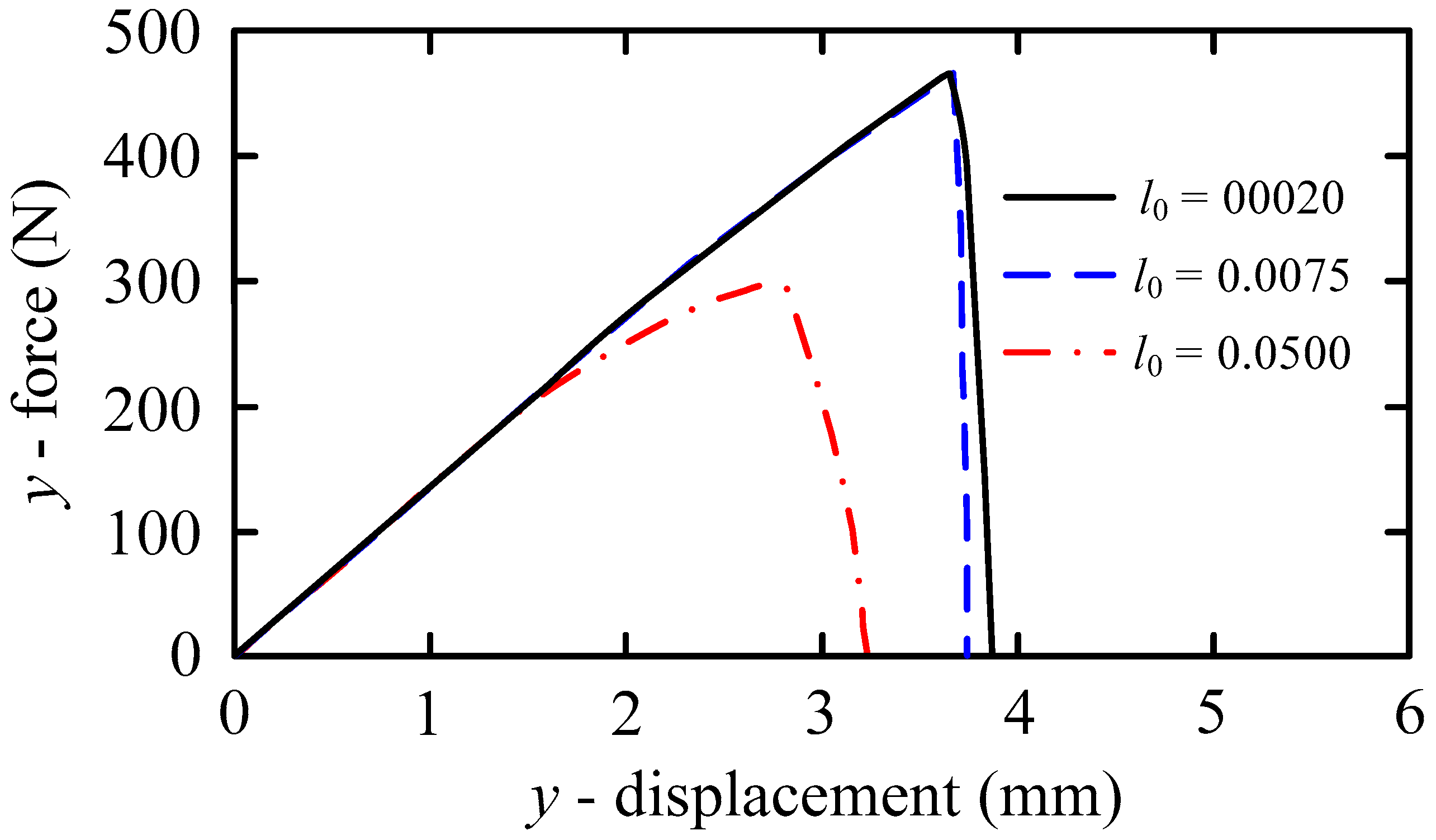
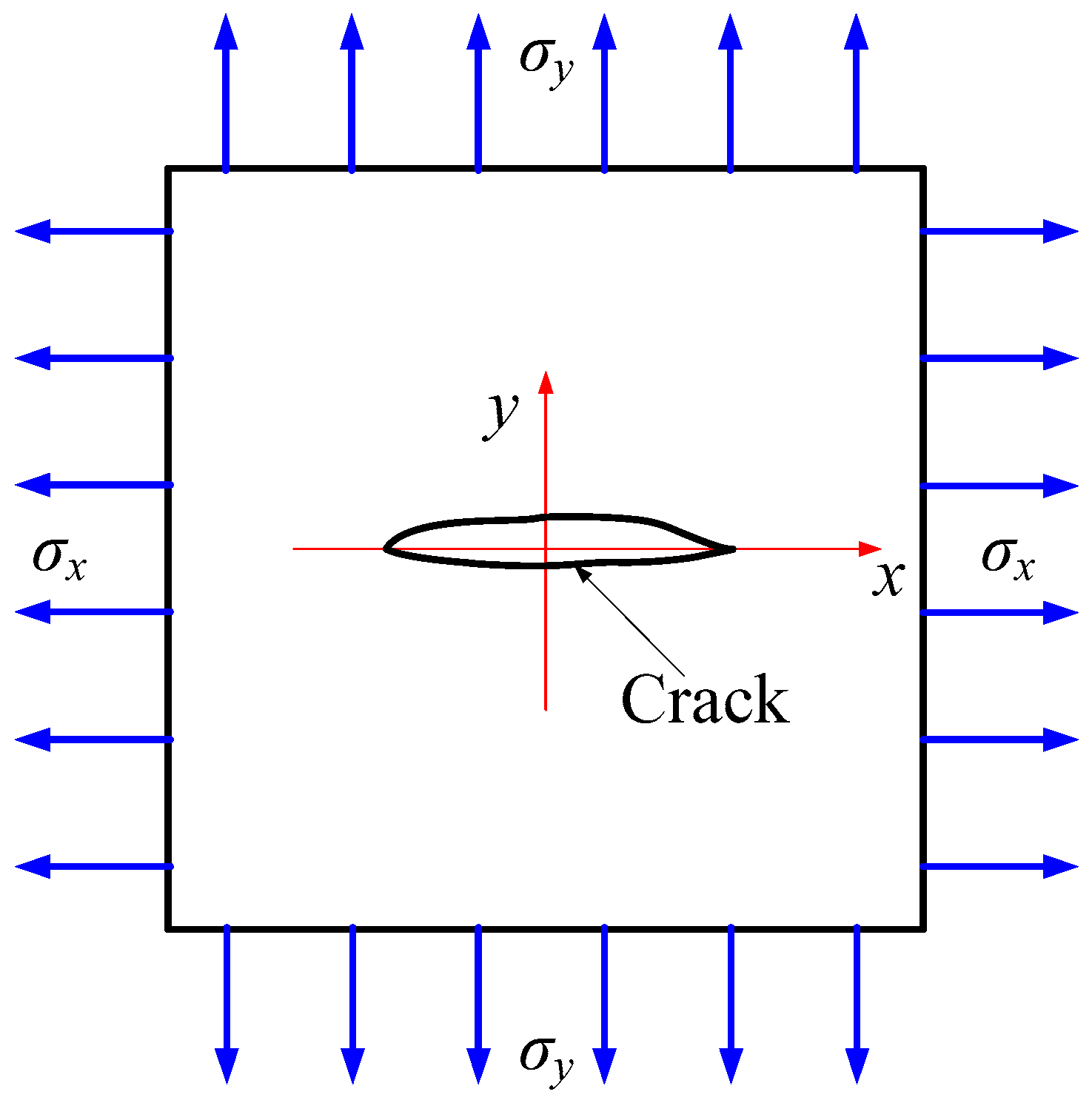
3.1. Mode I Failure of Square Plate in a Hydrogenous Environment
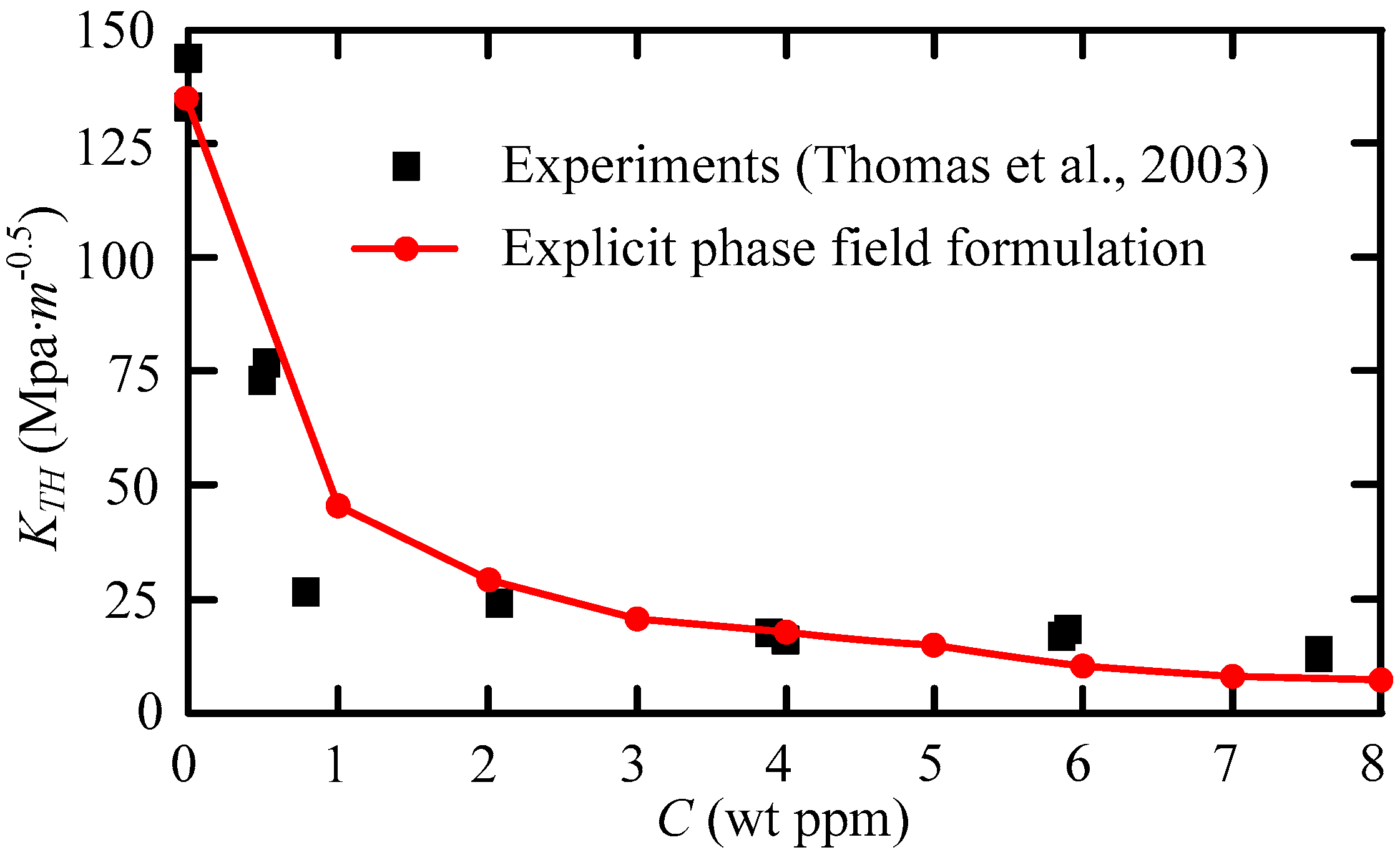
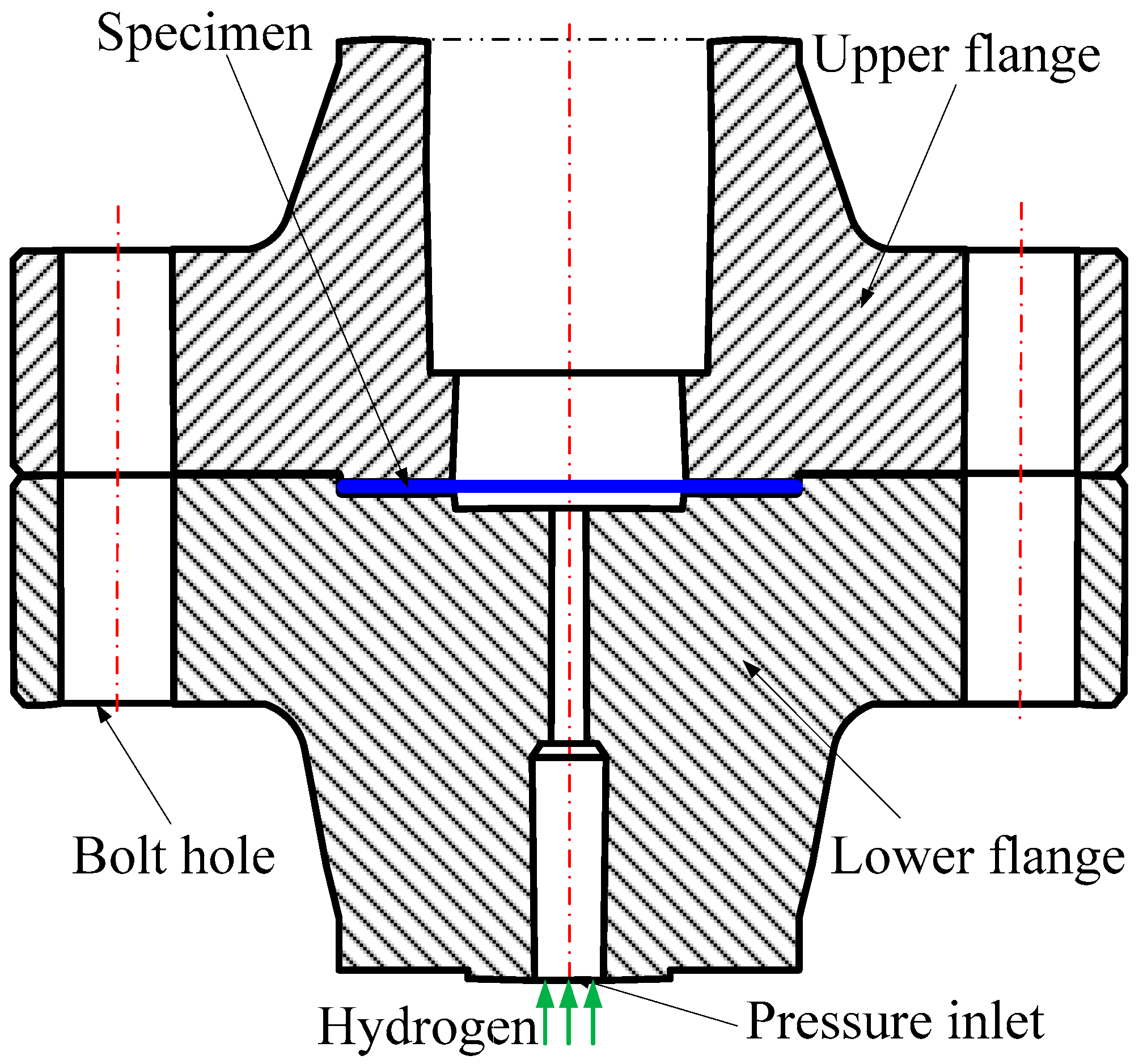
3.2. Mode I Failure of CT Specimen with Internal Hydrogen
- The simulation results are in good agreement with the experimental results;
- In the range of 0~1 ppm, KTH decreases sharply with the increase in hydrogen content. In this case, the internal hydrogen embrittlement is especially severe for this kind of high strength steel, and at 1~8 ppm, it is not sensitive to the amount of hydrogen.
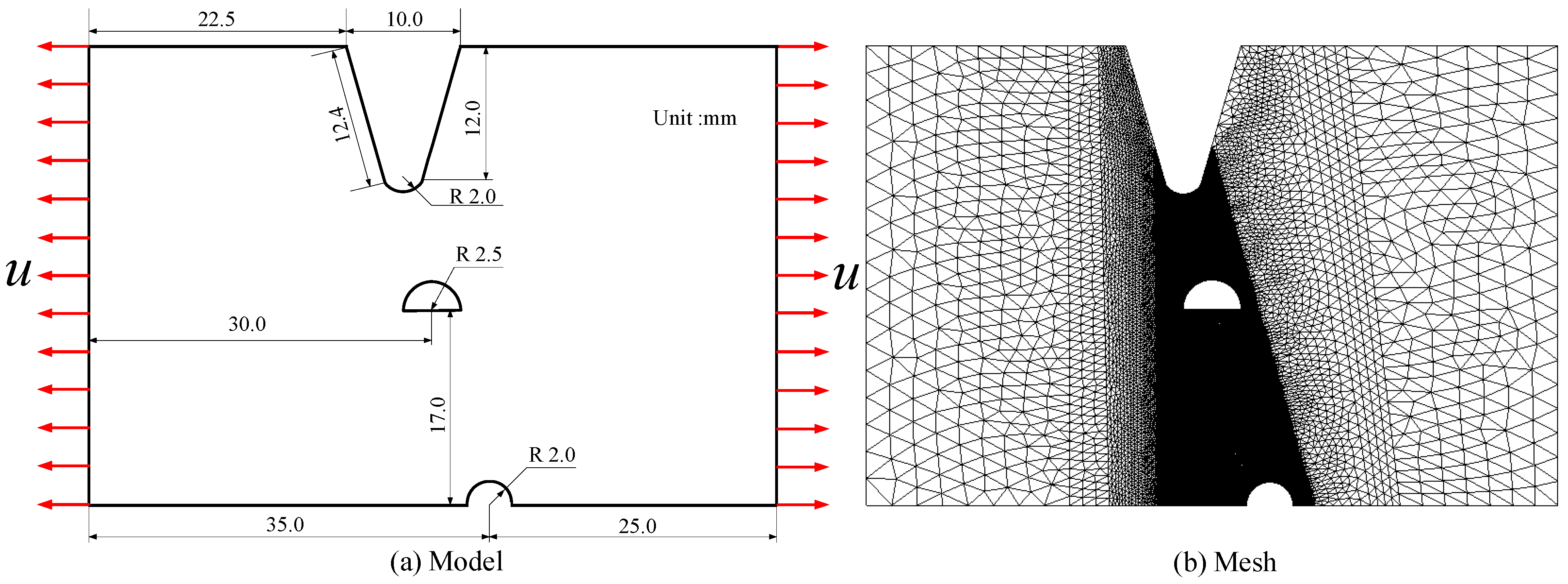
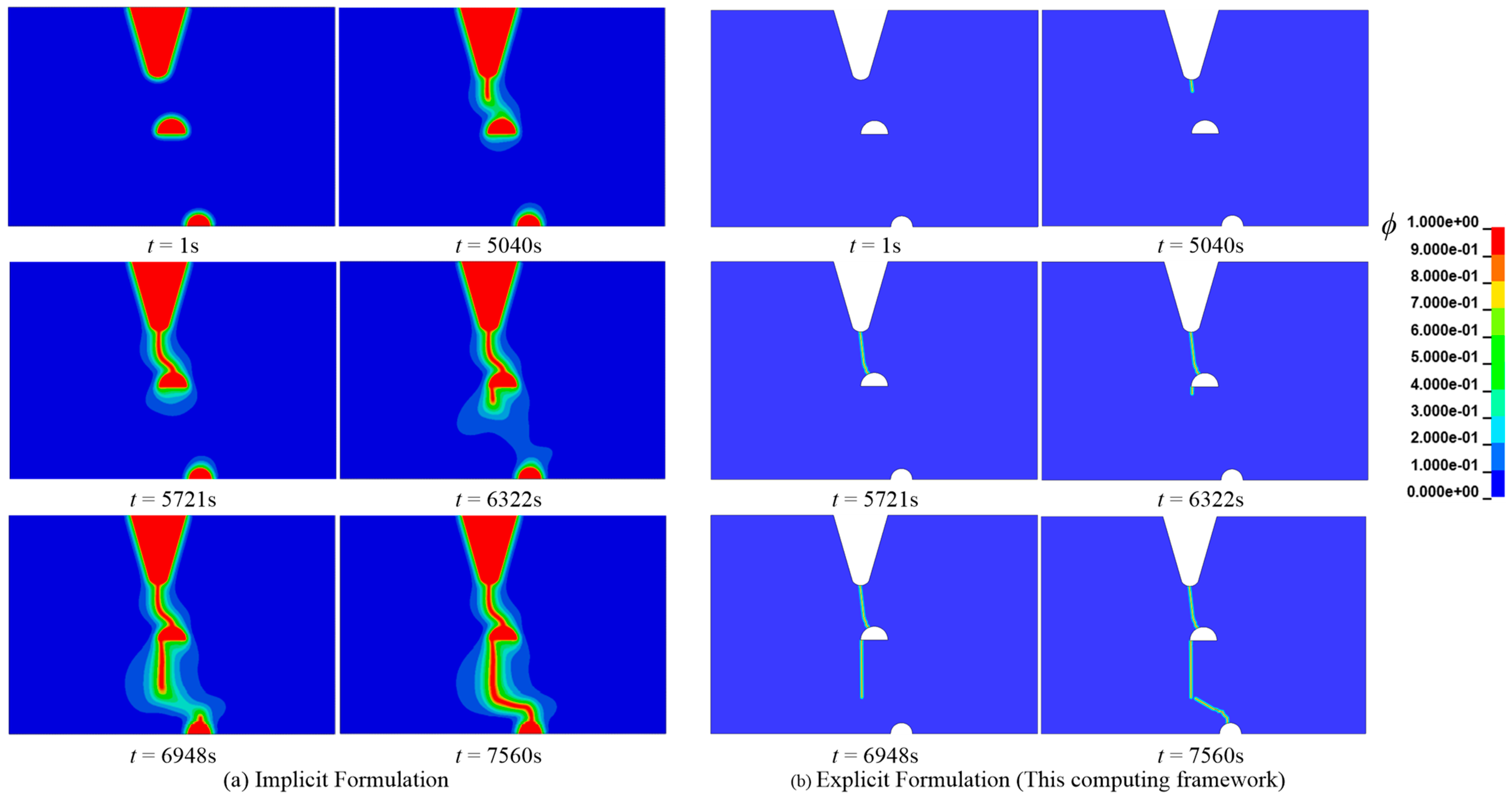
3.3. Mode I Failure for a Plate with Corrosion Pits
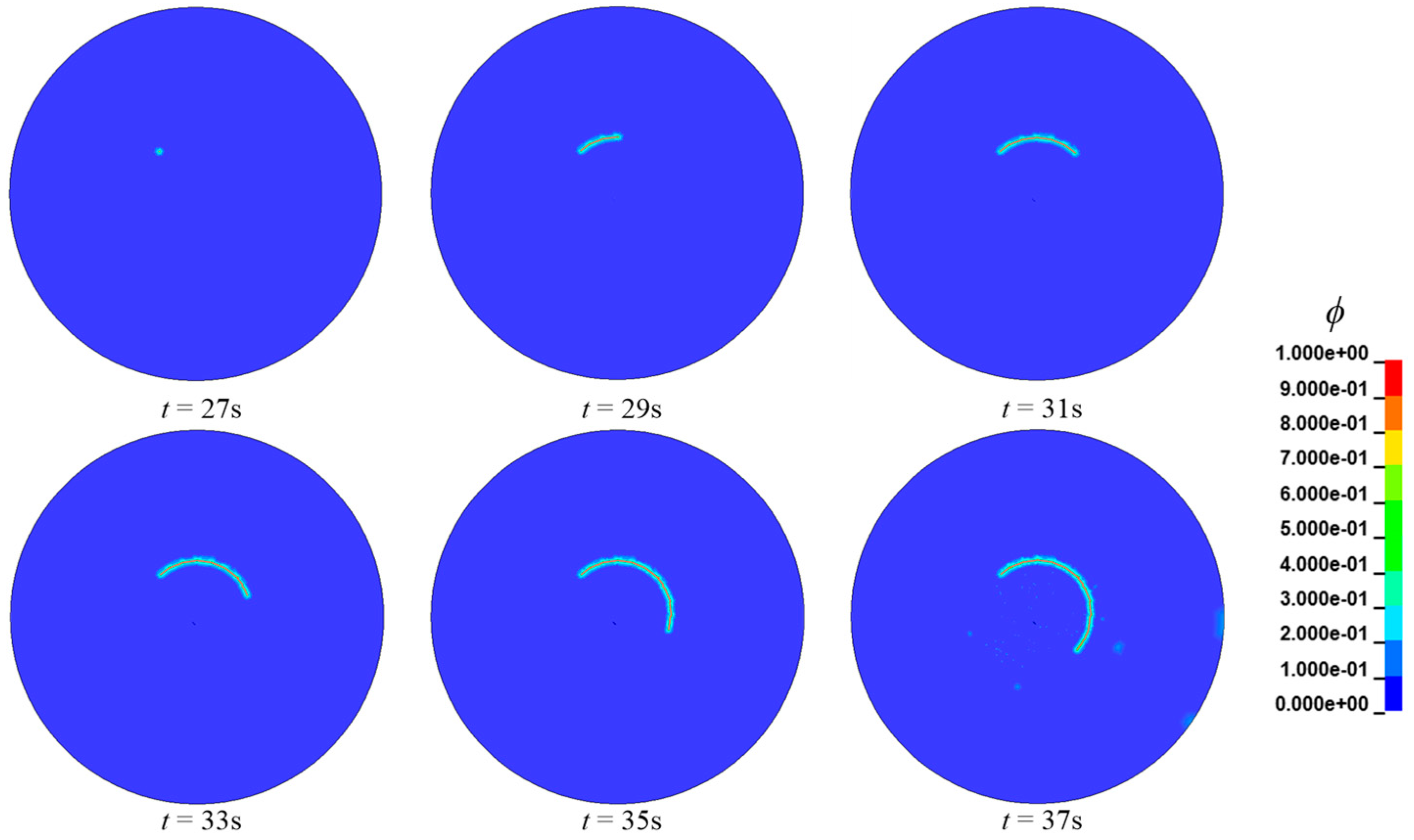
3.4. Mode II Failure for Disk Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Zhang, K. Analysis of Hydrogen-Assisted Brittle Fracture Using Phase-Field Damage Modelling Considering Hydrogen Enhanced Decohesion Mechanism. Metals 2022, 12, 1032. [Google Scholar] [CrossRef]
- Wu, J.Y.; Mandal, T.K.; Nguyen, V.P. A phase-field regularized cohesive zone model for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2020, 358, 112614. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Golahmar, A.; Niordson, C.F. A phase field formulation for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2018, 342, 742–761. [Google Scholar] [CrossRef]
- Moshtaghi, M.; Loder, B.; Safyari, M.; Willidal, T.; Hojo, T.; Mori, G. Hydrogen trapping and desorption affected by ferrite grain boundary types in shielded metal and flux-cored arc weldments with Ni addition. Int. J. Hydrogen Energy 2022, 47, 20676–20683. [Google Scholar] [CrossRef]
- Shimotomai, M. Heuristic Design of advanced martensitic steels that are highly resistant to hydrogen embrittlement by ε-carbide. Metals 2021, 11, 370. [Google Scholar] [CrossRef]
- Kim, S.G.; Shin, S.H.; Hwang, B. Machine learning approach for prediction of hydrogen environment embrittlement in austenitic steels. J. Mater. Res. Technol. 2022, 19, 2794–2798. [Google Scholar] [CrossRef]
- Komoda, R.; Kubota, M.; Staykov, A.; Ginet, P.; Barbier, F.; Furtado, J.; Prost, L.; Nagao, A. Effect of gas pressure on hydrogen environment embrittlement of carbon steel A106 in carbon monoxide mixed hydrogen gas. Metall. Mater. Trans. A 2022, 53, 74–85. [Google Scholar] [CrossRef]
- Michler, T.; Wackermann, K.; Schweizer, F. Review and assessment of the effect of hydrogen gas pressure on the embrittlement of steels in gaseous hydrogen environment. Metals 2021, 11, 637. [Google Scholar] [CrossRef]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.D.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.R.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modelling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef]
- Martin, M.L.; Dadfarnia, M.; Nagao, A.; Wang, S.; Sofronis, P. Enumeration of the hydrogen-enhanced localized plasticity mechanism for hydrogen embrittlement in structural materials. Acta Mater. 2019, 165, 734–750. [Google Scholar] [CrossRef]
- Kholtobina, A.S.; Ecker, W.; Pippan, R.; Razumovskiy, V.I. Effect of alloying elements on hydrogen enhanced decohesion in bcc iron. Comput. Mater. Sci. 2021, 188, 110215. [Google Scholar] [CrossRef]
- He, S.; Ecker, W.; Pippan, R.; Razumovskiy, V.I. Hydrogen-enhanced decohesion mechanism of the special Σ5 (0 1 2)[1 0 0] grain boundary in Ni with Mo and C solutes. Comput. Mater. Sci. 2019, 167, 100–110. [Google Scholar] [CrossRef]
- Shi, Y.; Joseph, S.; Saunders, E.A.; Sandala, R.S.; Walker, A.; Lindley, T.C.; Dye, D. AgCl-induced hot salt stress corrosion cracking in a titanium alloy. Corros. Sci. 2021, 187, 109497. [Google Scholar] [CrossRef]
- Yuan, S.; Zhu, Y.; Huang, M.; Liang, S.; Li, Z. Dislocation-density based crystal plasticity model with hydrogen-enhanced localized plasticity in polycrystalline face-centered cubic metals. Mech. Mater. 2020, 148, 103472. [Google Scholar] [CrossRef]
- Wilson, B.T.; Robson, J.D.; Shanthraj, P.; Race, C.P. Simulating intergranular hydrogen enhanced decohesion in aluminium using density functional theory. Model. Simul. Mater. Sci. Eng. 2022, 30, 035009. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M.B.; Ngo, T.D. Influence of hydrogen-enhanced plasticity and decohesion mechanisms of hydrogen embrittlement on the fracture resistance of steel. Eng. Fail. Anal. 2021, 123, 105312. [Google Scholar] [CrossRef]
- Djukic, M.; Bakic, G.; Šijački-Žeravčić, V.; Rajicic, B.; Sedmak, A.; Wasim, M.; Perišić, J. The synergistic action of HELP and HEDE mechanisms of hydrogen embrittlement in steels. In Proceedings of the Research Symposium on Hydrogen-Materials Interactions, Kyushu, Japan, 28–29 January 2021; Kyushu University: Fukuoka, Japan, 2021. [Google Scholar]
- Yang, L.; Yang, Y.; Zheng, H. A phase field numerical manifold method for crack propagation in quasi-brittle materials. Eng. Fract. Mech. 2021, 241, 107427. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Jianying, W. On the theoretical and numerical aspects of the unified phase-field theory for damage and failure in solids and structures. Chin. J. Theor. Appl. Mech. 2021, 53, 301–329. [Google Scholar]
- Mandal, T.K.; Nguyen, V.P.; Wu, J.Y. Comparative study of phase-field damage models for hydrogen assisted cracking. Theor. Appl. Fract. Mech. 2021, 111, 102840. [Google Scholar] [CrossRef]
- Chen, P.; Ma, Y.; Peng, F.; Zhou, L. Simulating hydrogen embrittlement fracture based on phase field method. Xibei Gongye Daxue Xuebao/J. Northwestern Polytech. Univ. 2022, 40, 504–511. [Google Scholar] [CrossRef]
- Bui, T.Q.; Hu, X. A review of phase-field models, fundamentals and their applications to composite laminates. Eng. Fract. Mech. 2021, 248, 107705. [Google Scholar] [CrossRef]
- Diehl, P.; Lipton, R.; Wick, T.; Tyagi, M. A comparative review of peridynamics and phase-field models for engineering fracture mechanics. Comput. Mech. 2022, 69, 1259–1293. [Google Scholar] [CrossRef]
- Carlsson, J.; Isaksson, P. A statistical geometry approach to length scales in phase field modelling of fracture and strength of porous microstructures. Int. J. Solids Struct. 2020, 200, 83–93. [Google Scholar] [CrossRef]
- Wu, J.Y.; Chen, W.X. On the phase-field modeling of fully coupled chemo- mechanical deterioration and fracture in calcium leached cementitious solids. Int. J. Solids Struct. 2022, 238, 111380. [Google Scholar] [CrossRef]
- Alvaro, A.; Jensen, I.T.; Kheradmand, N.; Løvvik, O.M.; Olden, V. Hydrogen embrittlement in nickel, visited by first principles modeling, cohesive zone simulation and nanomechanical testing. Int. J. Hydrogen Energy 2015, 40, 16892–16900. [Google Scholar] [CrossRef]
- Livermore Software Technology. LS-DYNA® Keyword User’s Manual Volume II Material Models; LS-DYNA R13; Livermore Software Technology: Livermore, CA, USA, 2021. [Google Scholar]
- Hallquist, J.O. Ls-Dyna Theory Manual; Livermore Software Technology: Livermore, CA, USA, 2019. [Google Scholar]
- Abdollahzadeh, M.A.; Kefal, A.; Yildiz, M. A comparative and review study on shape and stress sensing of flat/curved shell geometries using C0-continuous family of iFEM elements. Sensors 2020, 20, 3808. [Google Scholar] [CrossRef]
- Wang, D.; Xu, W.; Chen, S.; Zang, M. An extrinsic cohesive shell model for dynamic fracture analyses. Theor. Appl. Fract. Mech. 2018, 97, 165–176. [Google Scholar] [CrossRef]
- Wang, T.; Ye, X.; Liu, Z.; Chu, D.; Zhuang, Z. Modeling the dynamic and quasi-static compression-shear failure of brittle materials by explicit phase field method. Comput. Mech. 2019, 64, 1537–1556. [Google Scholar] [CrossRef]
- Ren, H.L.; Zhuang, X.Y.; Anitescu, C.; Rabczuk, T. An explicit phase field method for brittle dynamic fracture. Comput. Struct. 2019, 217, 45–56. [Google Scholar] [CrossRef]
- Soares, D., Jr. A locally stabilized central difference method. Finite Elem. Anal. Des. 2019, 155, 1–10. [Google Scholar] [CrossRef]
- Garoz, D.; Gilabert, F.A.; Sevenois RD, B.; Spronk, S.W.F.; Van Paepegem, W. Consistent application of periodic boundary conditions in implicit and explicit finite element simulations of damage in composites. Compos. Part B Eng. 2019, 168, 254–266. [Google Scholar] [CrossRef]
- Zheng, M.; Yuan, Z.; Tong, Q.; Zhang, G.; Zhu, W. A novel unconditionally stable explicit integration method for finite element method. Vis. Comput. 2018, 34, 721–733. [Google Scholar] [CrossRef]
- Maritz, M.F. Rotations in Three Dimensions. SIAM Rev. 2021, 63, 395–404. [Google Scholar] [CrossRef]
- Hectors, K.; De Waele, W. An X-FEM based framework for 3D fatigue crack growth using a B-spline crack geometry description. Eng. Fract. Mech. 2022, 261, 108238. [Google Scholar] [CrossRef]
- Thomas RL, S.; Scully, J.R.; Gangloff, R.P. Internal hydrogen embrittlement of ultrahigh-strength AERMET 100 steel. Metall. Mater. Trans. A 2003, 34, 327–344. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, K.; Lu, D.; Zeng, B. Hydrogen-Assisted Brittle Fracture Behavior of Low Alloy 30CrMo Steel Based on the Combination of Experimental and Numerical Analyses. Materials 2021, 14, 3711. [Google Scholar] [CrossRef]
- Sun, Y.; Cheng, Y.F. Hydrogen-induced degradation of high-strength steel pipeline welds: A critical review. Eng. Fail. Anal. 2022, 133, 105985. [Google Scholar] [CrossRef]
- Klinsmann, M.; Rosato, D.; Kamlah, M.; McMeeking, R.M. An assessment of the phase field formulation for crack growth. Comput. Methods Appl. Mech. Eng. 2015, 294, 313–330. [Google Scholar] [CrossRef]
- Beghini, M.; Benamati, G.; Bertini, L. Hydrogen embrittlement characterization by disk pressure tests: Test analysis and application to high chromium martensitic steels. J. Eng. Mater. Technol. 1996, 118, 179–185. [Google Scholar] [CrossRef]
- Safyari, M.; Moshtaghi, M.; Kuramoto, S. Effect of strain rate on environmental hydrogen embrittlement susceptibility of a severely cold-rolled Al–Cu alloy. Vacuum 2020, 172, 109057. [Google Scholar] [CrossRef]
- Kuperman, A.M.; Sergeev, A.Y.; Turusov, R.A.; Solodilov, V.I. Influence of a Sealing Layer on the Physical and Mechanical Properties of the Shell of a High-Pressure Vessel for Hydrogen Storage. Russ. J. Phys. Chem. B 2022, 16, 1172–1179. [Google Scholar] [CrossRef]
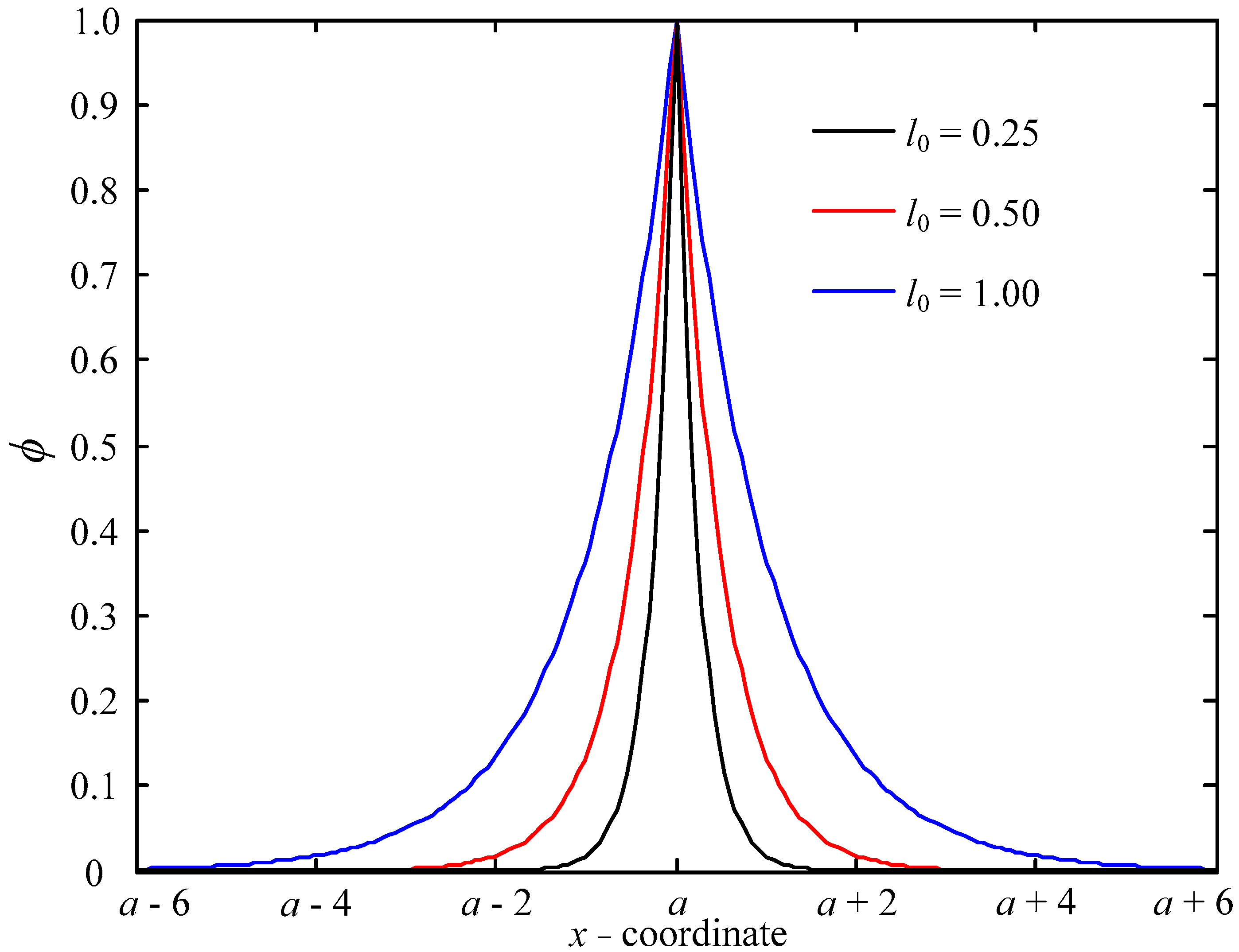

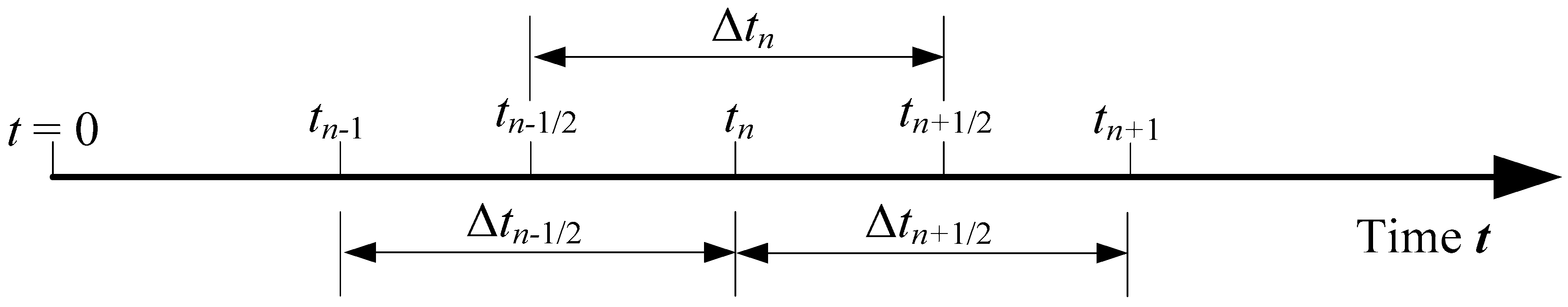

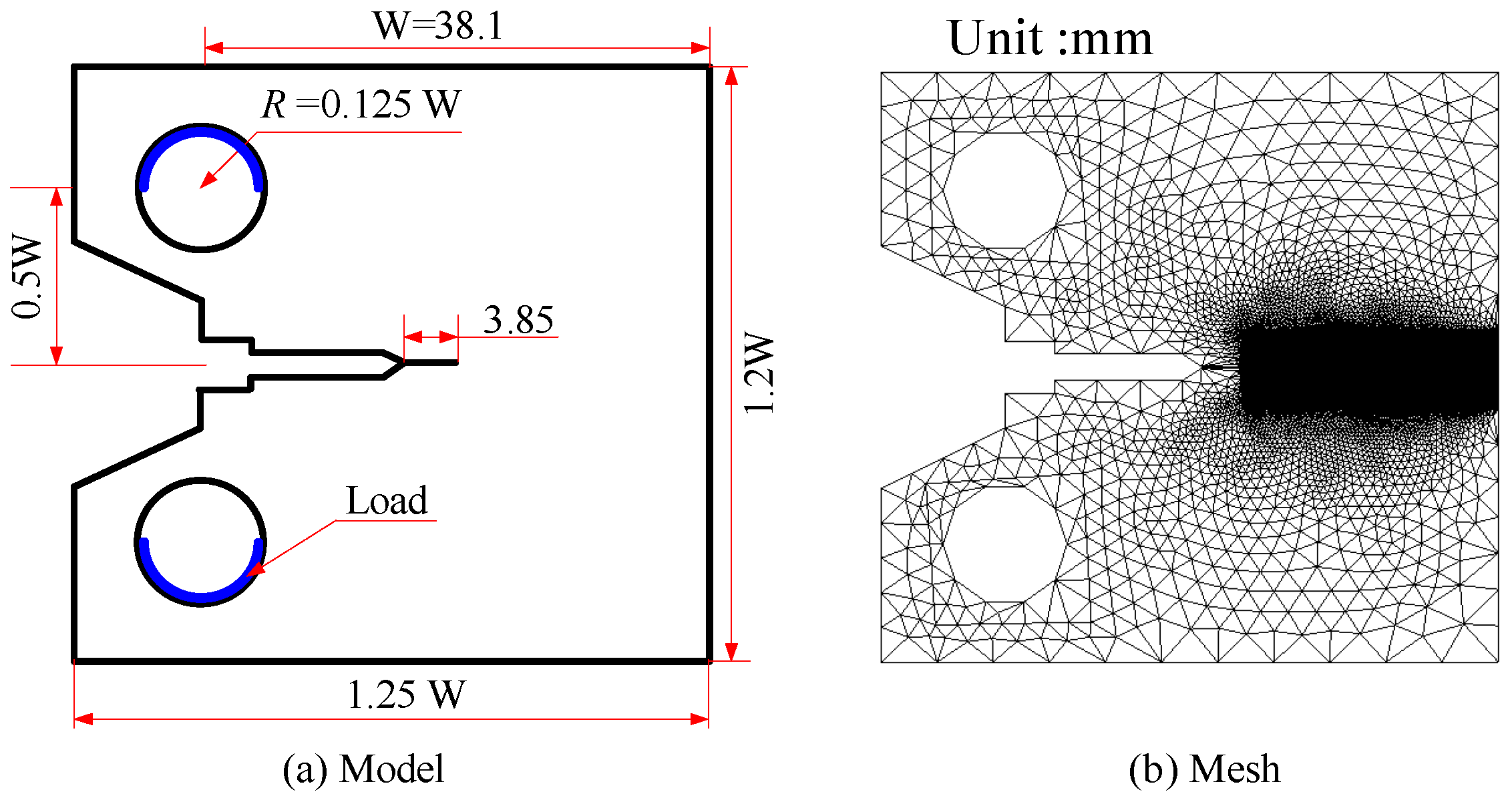
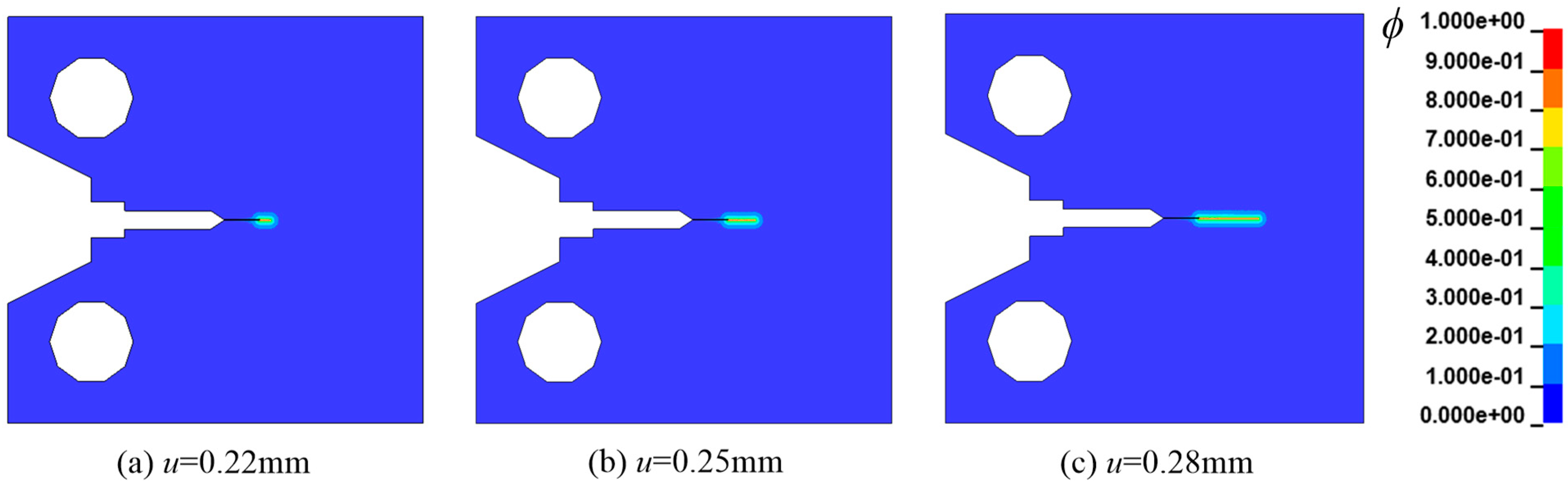


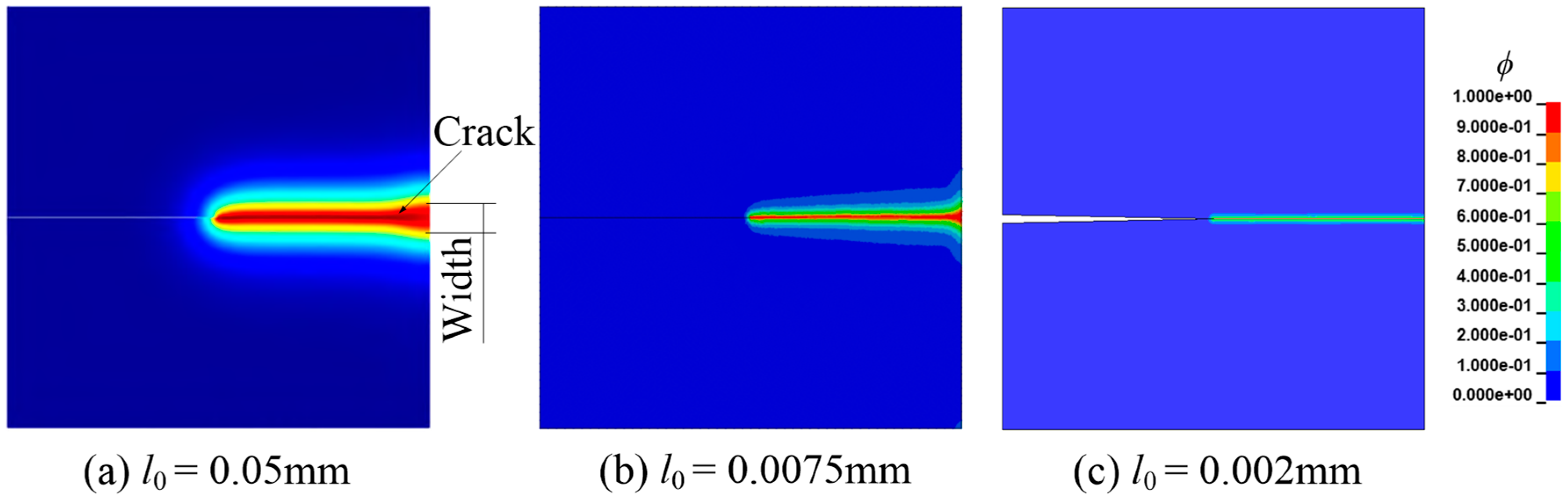
| Parameter | Settings | Parameter | Settings |
|---|---|---|---|
| Young’s modulus, E | 210 GPa | χ | 0.89 |
| Poisson’s ratio, ν | 0.3 | 2000 mm3/mol | |
| Density, ρ | 7900 kg/m3 | D | 2 × 10−4 mm2/s |
| Gc(0) | 2.7 Mpa mm | l0 | 0.002 |
| Parameter | Settings | Parameter | Settings |
|---|---|---|---|
| Young’s modulus, E | 194.4 GPa | χ | 0.89 |
| Poisson’s ratio, ν | 0.3 | 2000 mm3/mol | |
| Density, ρ | 7900 kg/m3 | D | 2 × 10−4 mm2/s |
| Gc(0) | 30 kJ/ m2 | l0 | 0.15 |
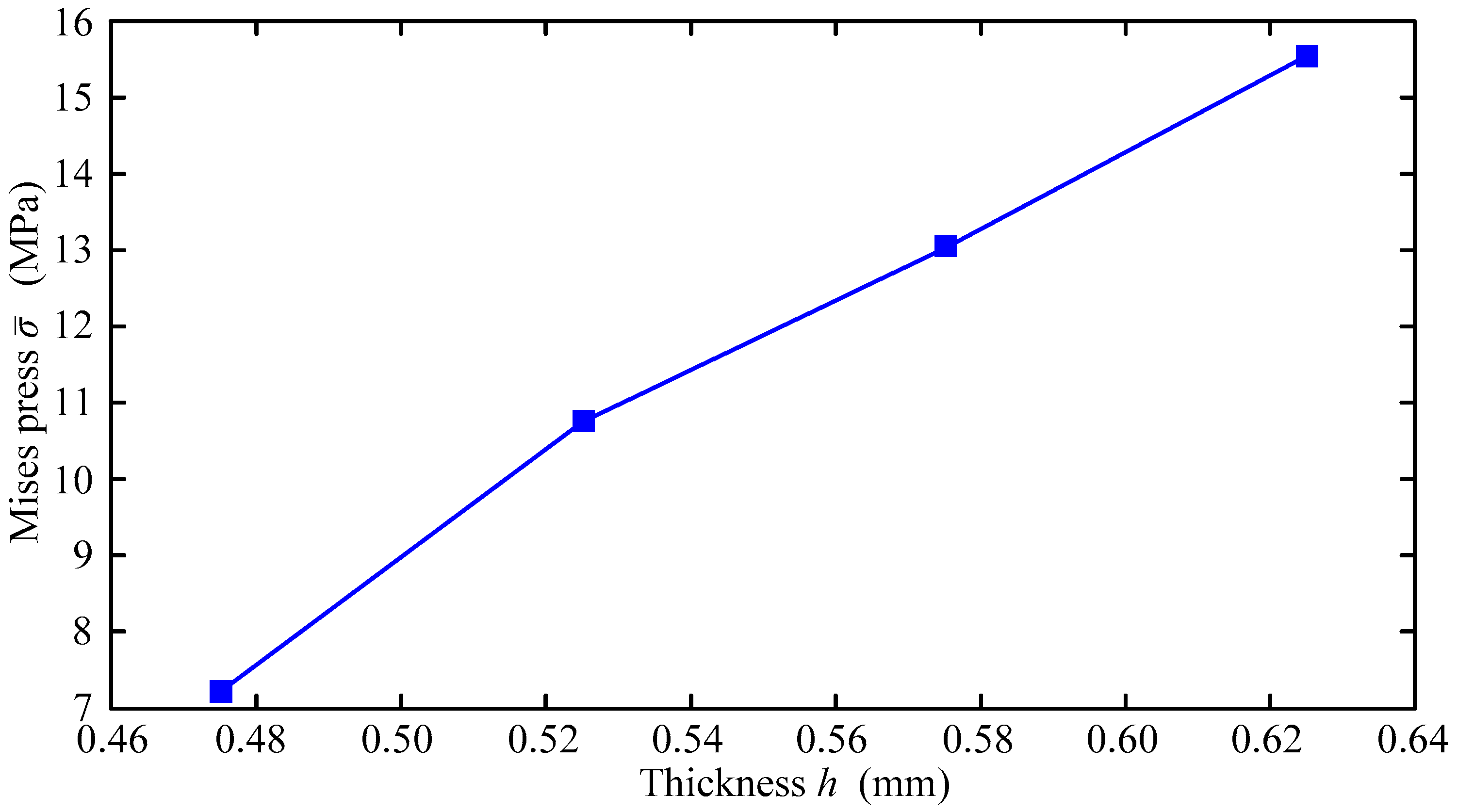
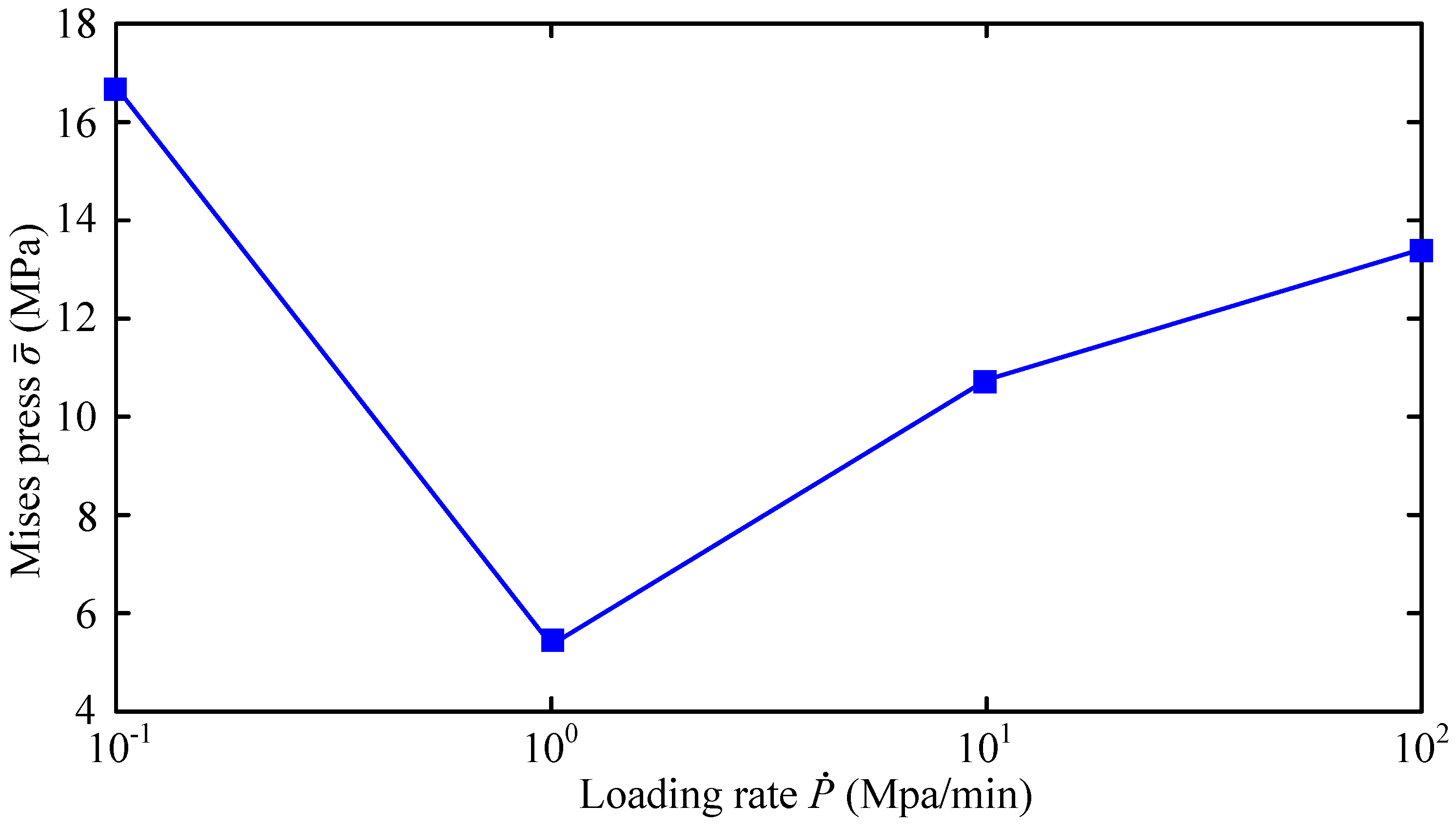
| C0 (ppm) | Thick (mm) | Exp. Press (MPa) | Sim. Press (MPa) | Error (%) |
|---|---|---|---|---|
| 0.0 | 0.525 | 26.10 | 26.34 | 0.92 |
| 1.5 | 0.531 | 27.20 | 27.11 | 0.33 |
| 1.9 | 0.479 | 24.70 | 25.50 | 3.24 |
| 2.5 | 0.520 | 26.10 | 24.89 | 4.64 |
| 3.0 | 0.520 | 12.50 | 13.37 | 6.96 |
| 3.5 | 0.525 | 11.70 | 10.75 | 8.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Ma, F.; Chen, H. Numerical Simulation for Hydrogen-Assisted Cracking: An Explicit Phase-Field Formulation. Materials 2023, 16, 1708. https://doi.org/10.3390/ma16041708
Wang D, Ma F, Chen H. Numerical Simulation for Hydrogen-Assisted Cracking: An Explicit Phase-Field Formulation. Materials. 2023; 16(4):1708. https://doi.org/10.3390/ma16041708
Chicago/Turabian StyleWang, Di, Fangping Ma, and Hao Chen. 2023. "Numerical Simulation for Hydrogen-Assisted Cracking: An Explicit Phase-Field Formulation" Materials 16, no. 4: 1708. https://doi.org/10.3390/ma16041708
APA StyleWang, D., Ma, F., & Chen, H. (2023). Numerical Simulation for Hydrogen-Assisted Cracking: An Explicit Phase-Field Formulation. Materials, 16(4), 1708. https://doi.org/10.3390/ma16041708