A New Method for Inversion of Dam Foundation Hydraulic Conductivity Using an Improved Genetic Algorithm Coupled with an Unsaturated Equivalent Continuum Model and Its Application
Abstract
1. Introduction
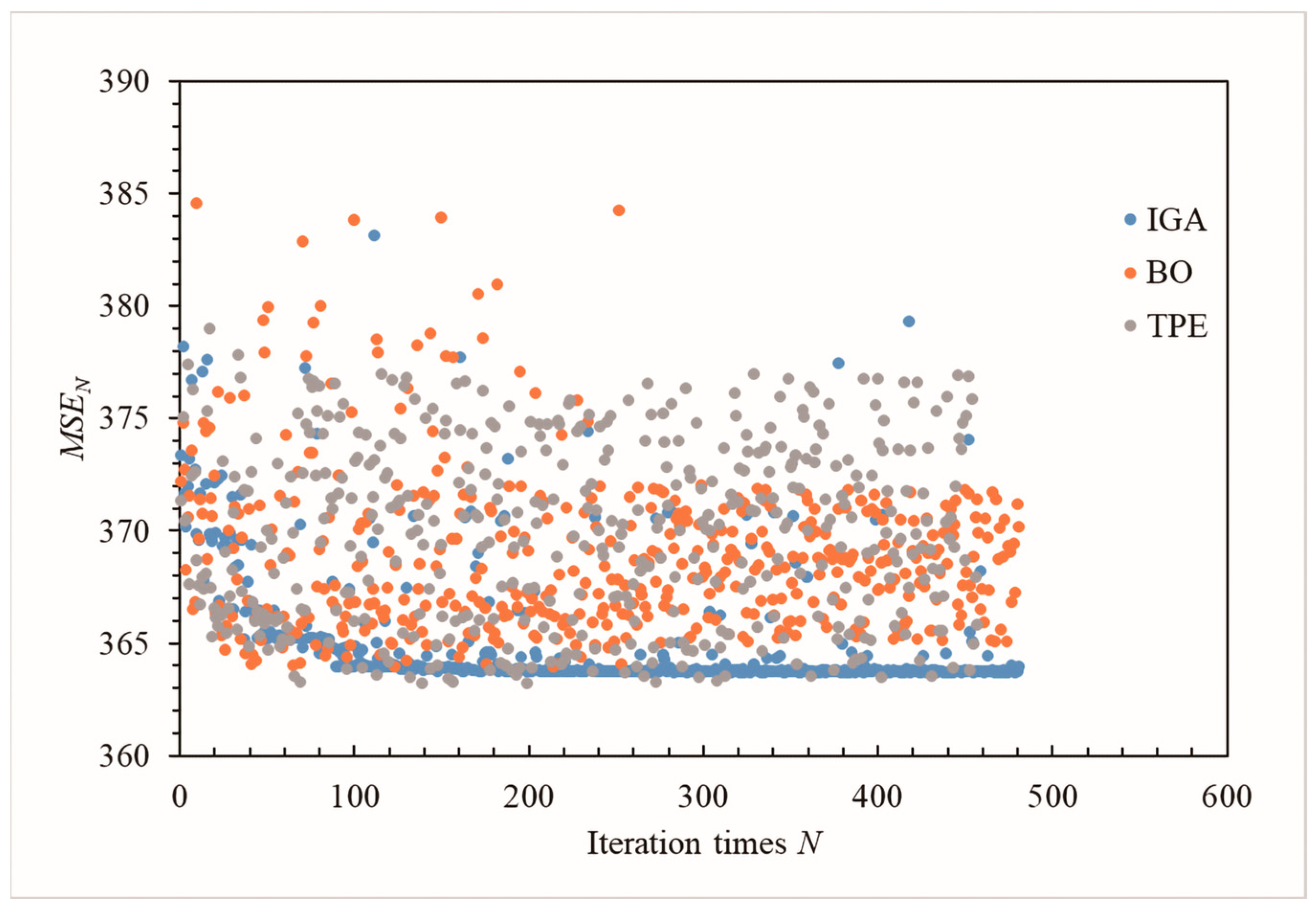
- The standard GA algorithm is improved by creating a new genetic operation to overcome the premature convergence shortage of the standard GA in the hydraulic conductivity inversion problem. The improved genetic algorithm (IGA) has a faster convergence speed than BO and TEP on hydraulic conductivity inversion.
- A new method and code for the inversion of dam foundation hydraulic conductivity by coupling the improved GA and the UECM is proposed, which fully considers engineering practicability. The realization of the three-dimensional finite element solution of the UECM is based on our previous research.
- The geological survey and design data of the Hami concrete-face rockfill dam are used to verify the new method for the inversion of dam foundation hydraulic conductivity, and an engineering application case of the new method is presented.
- Some suggestions are given for the inversion dam foundation hydraulic conductivity, the three-dimensional seepage field calculation, and the anti-seepage curtain layout of a concrete-face rockfill dam.
2. Method
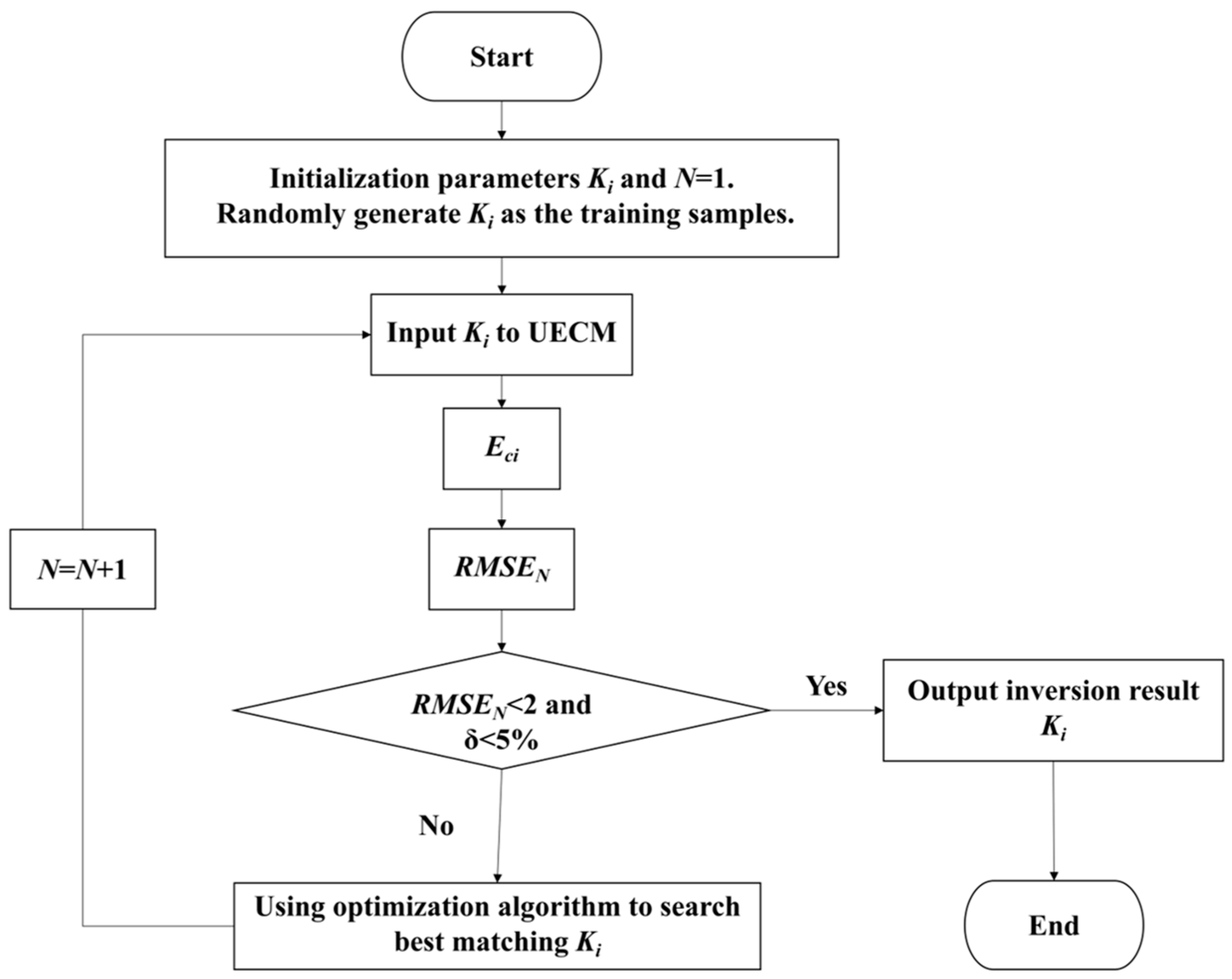
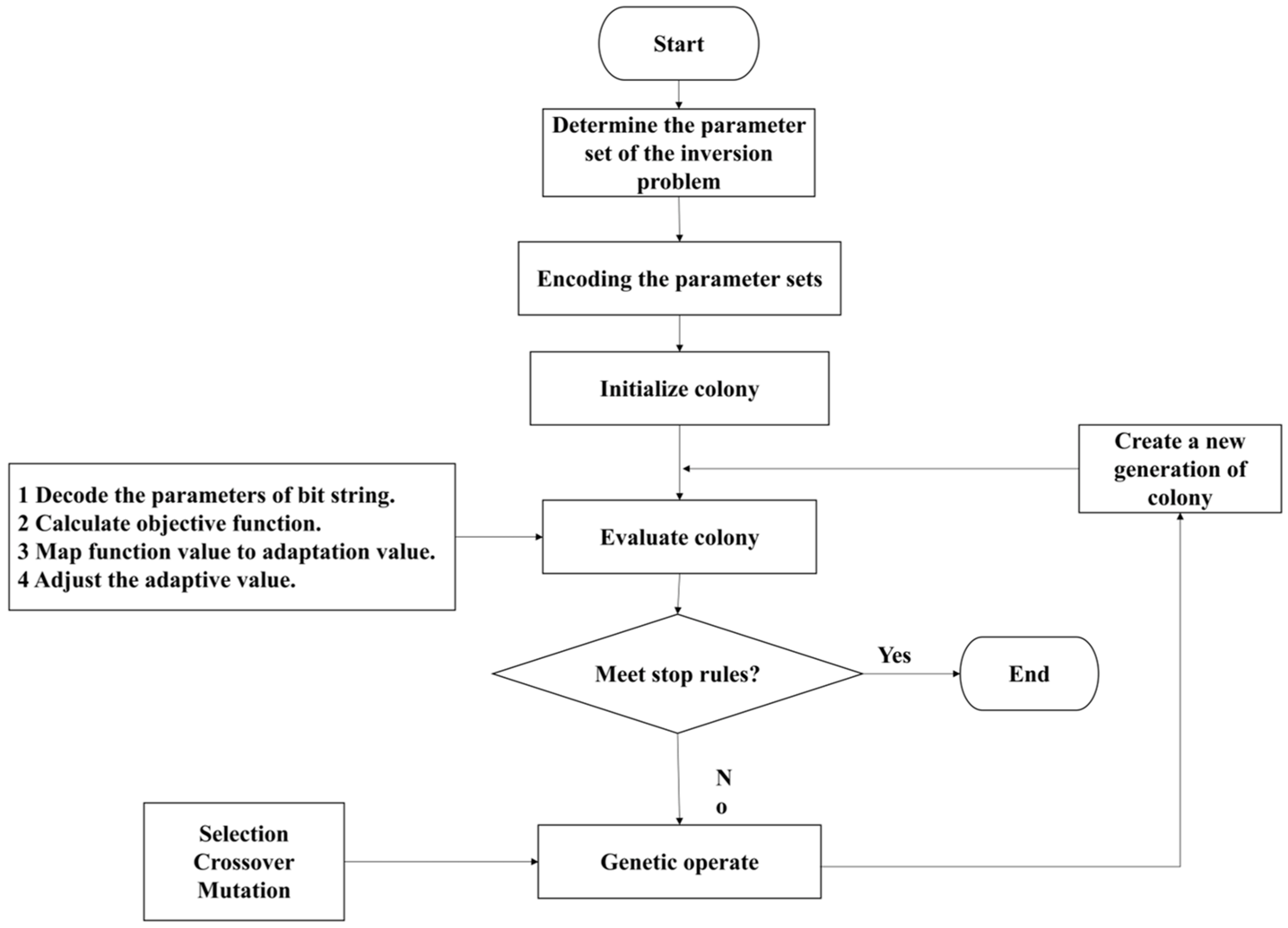
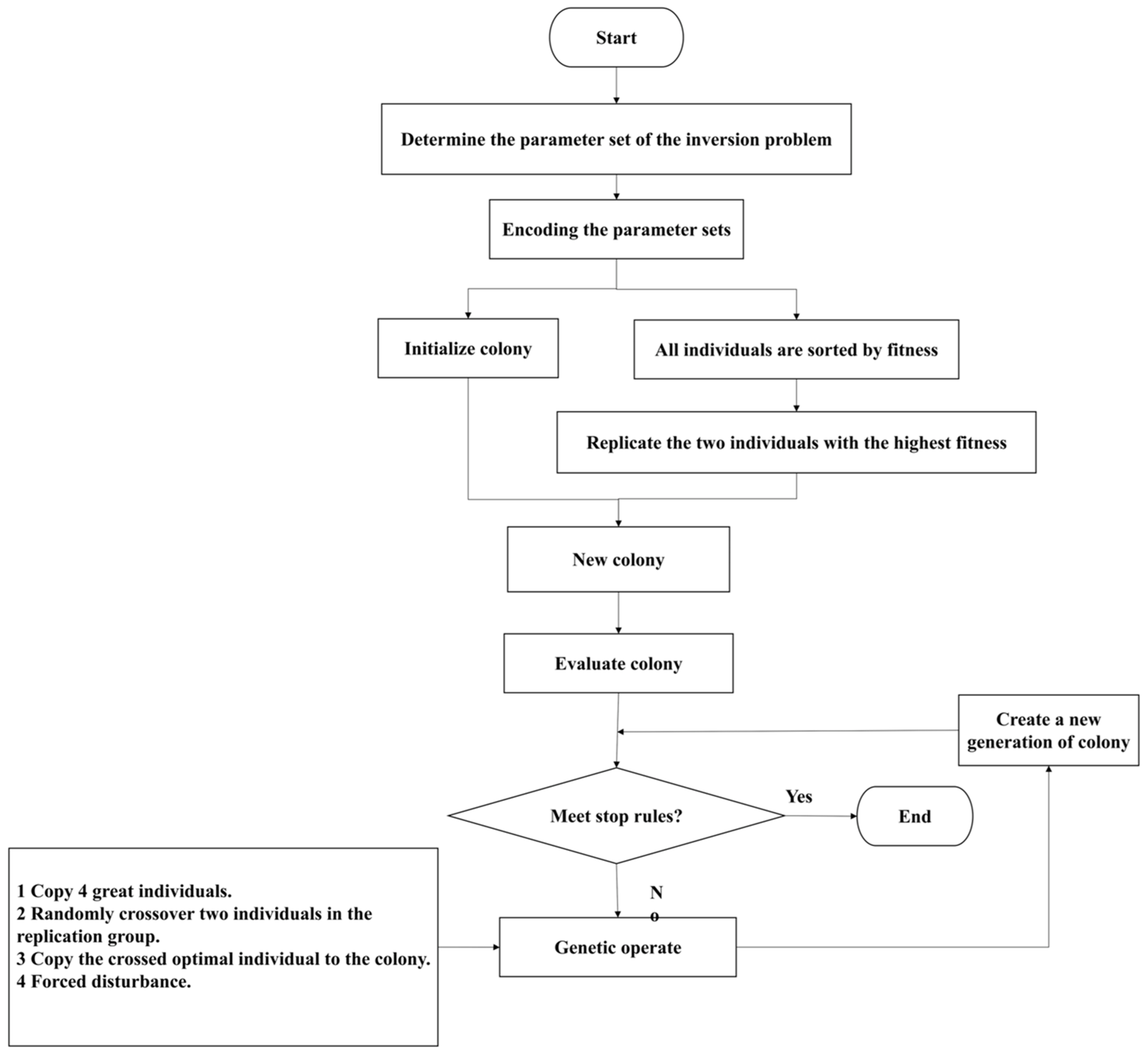
2.1. An Improved Genetic Algorithm for Inversion of Dam Foundation’s Hydraulic Conductivity
2.2. Seepage Field Calculation by the Unsaturated Equivalent Continuum Model
2.2.1. Basic Differential Model
2.2.2. Definite Solution Condition
2.2.3. Solution Method
2.2.4. Iterative Format
2.2.5. Seepage Discharge
2.3. Other Deep Learning Methods
3. Engineering Example
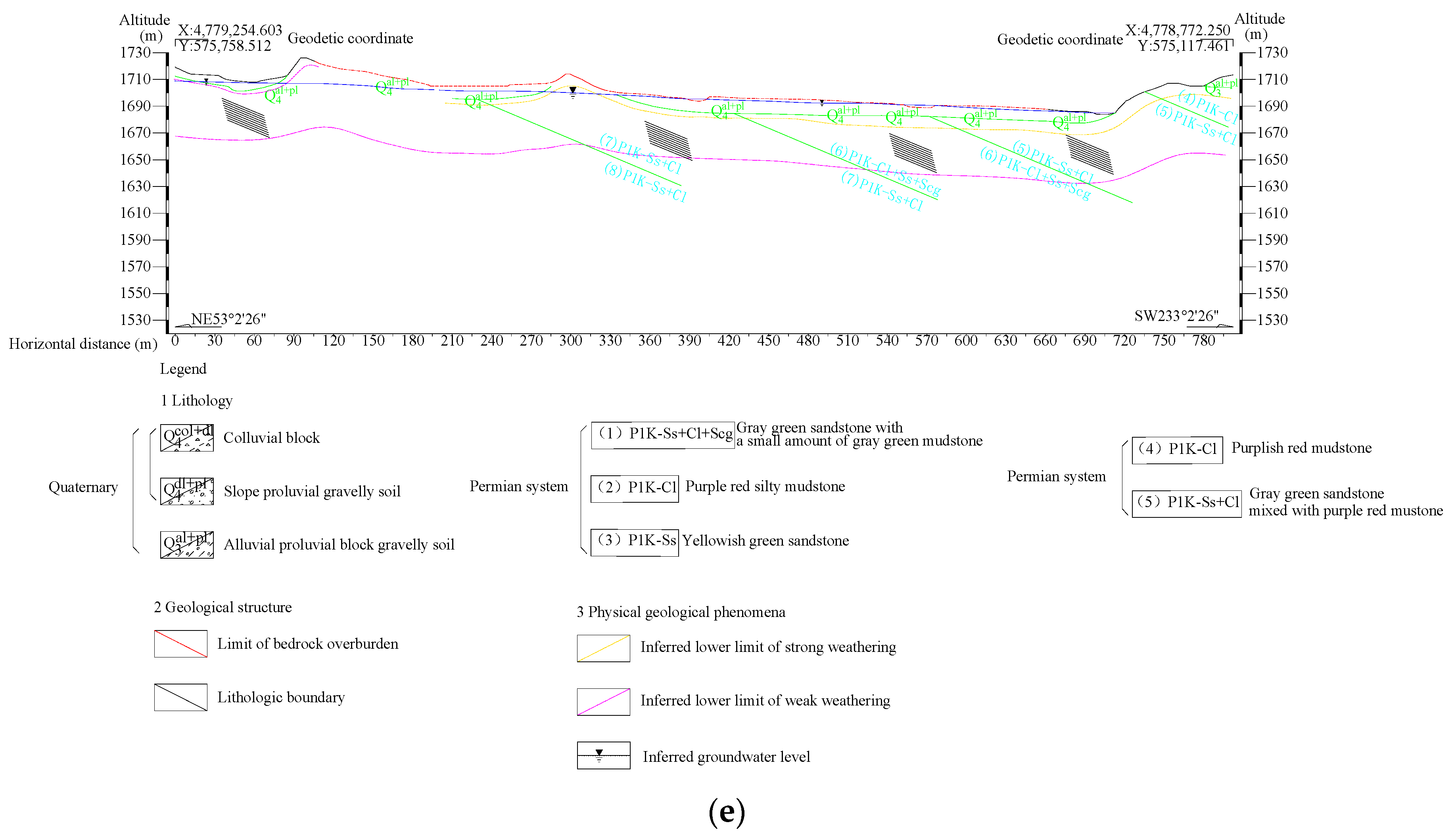
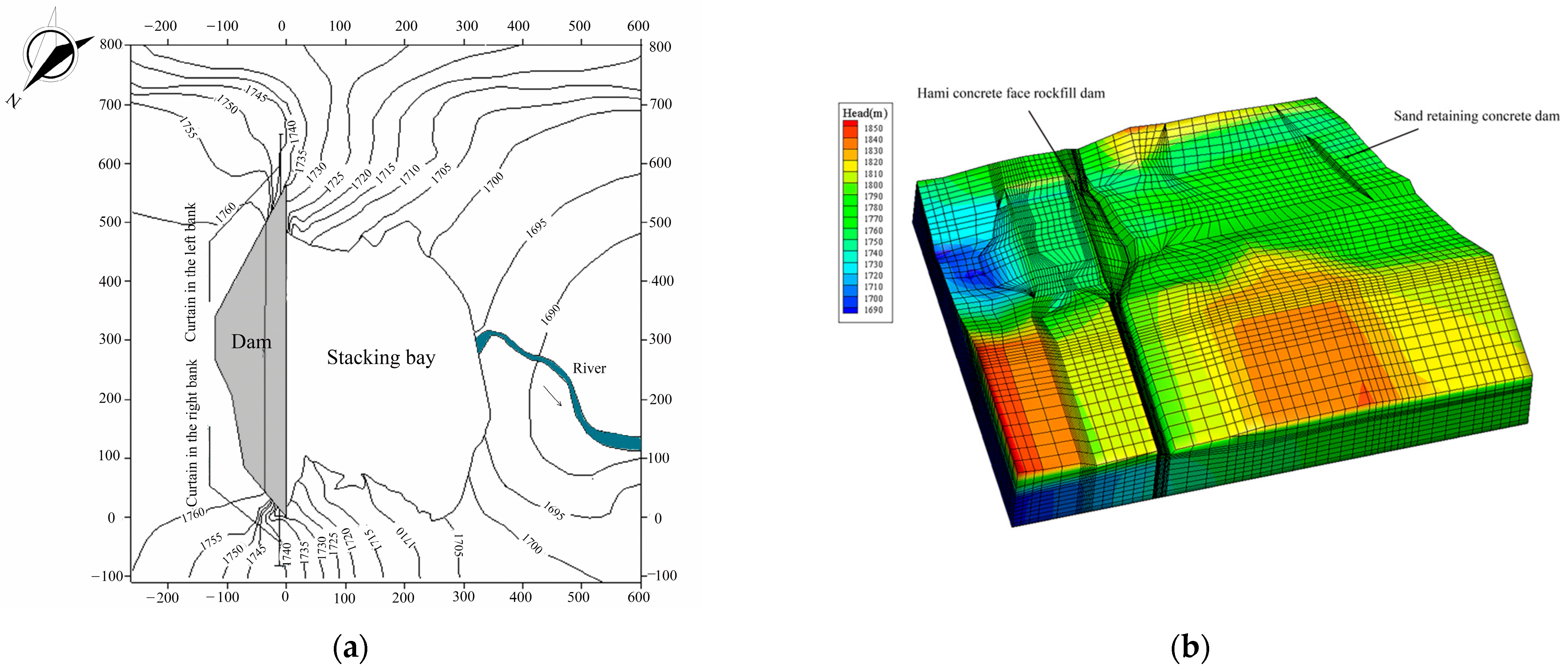
3.1. Project Overview and Data Collection
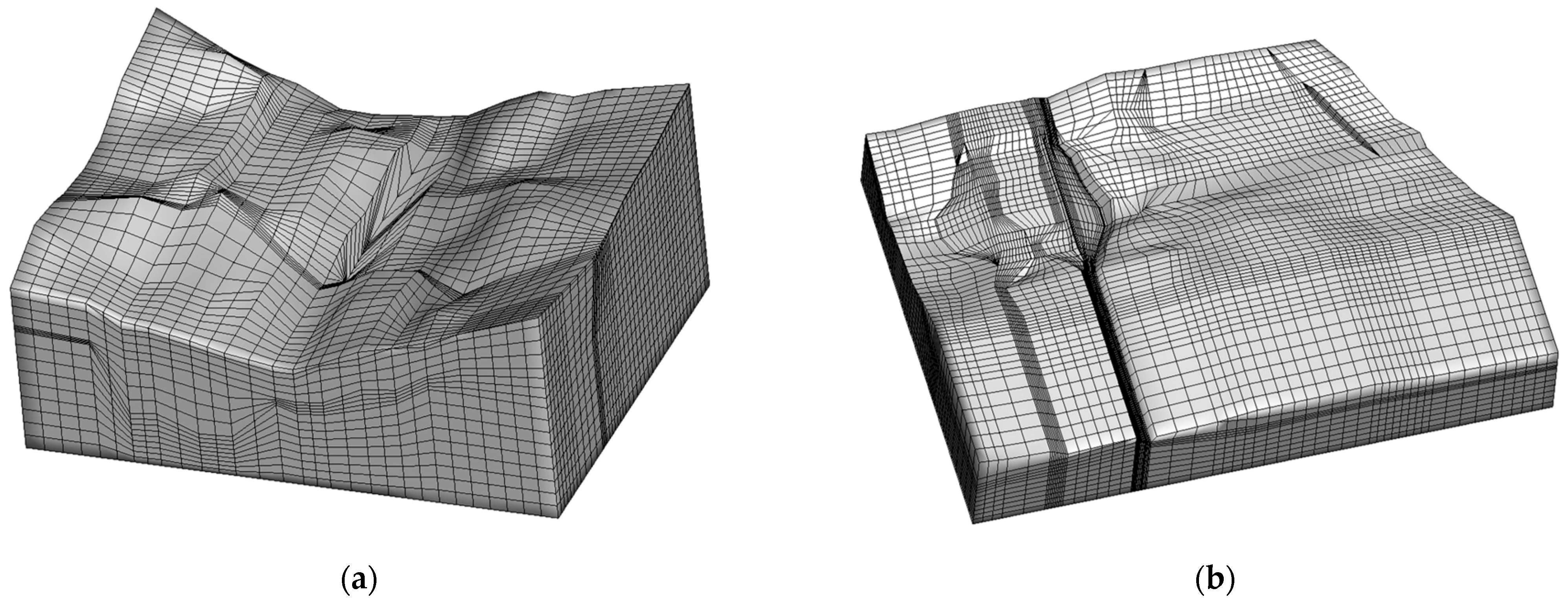
3.2. Three-Dimensional Finite Element Mesh Model and Boundary Conditions of the Dam
3.3. Sensitivity Analysis on the Structure of the Mesh
4. Results and Discussion
4.1. Inversion Results of Dam Foundation Hydraulic Conductivity
4.1.1. Inversion Results of IGA
4.1.2. Comparison of the Improved Genetic Algorithm and Other Algorithms for Inversion of the Hydraulic Conductivity of the Dam Foundation
4.2. Influence of Different Layout Schemes of Dam Grouting Curtain on Dam Three-Dimensional Seepage Field
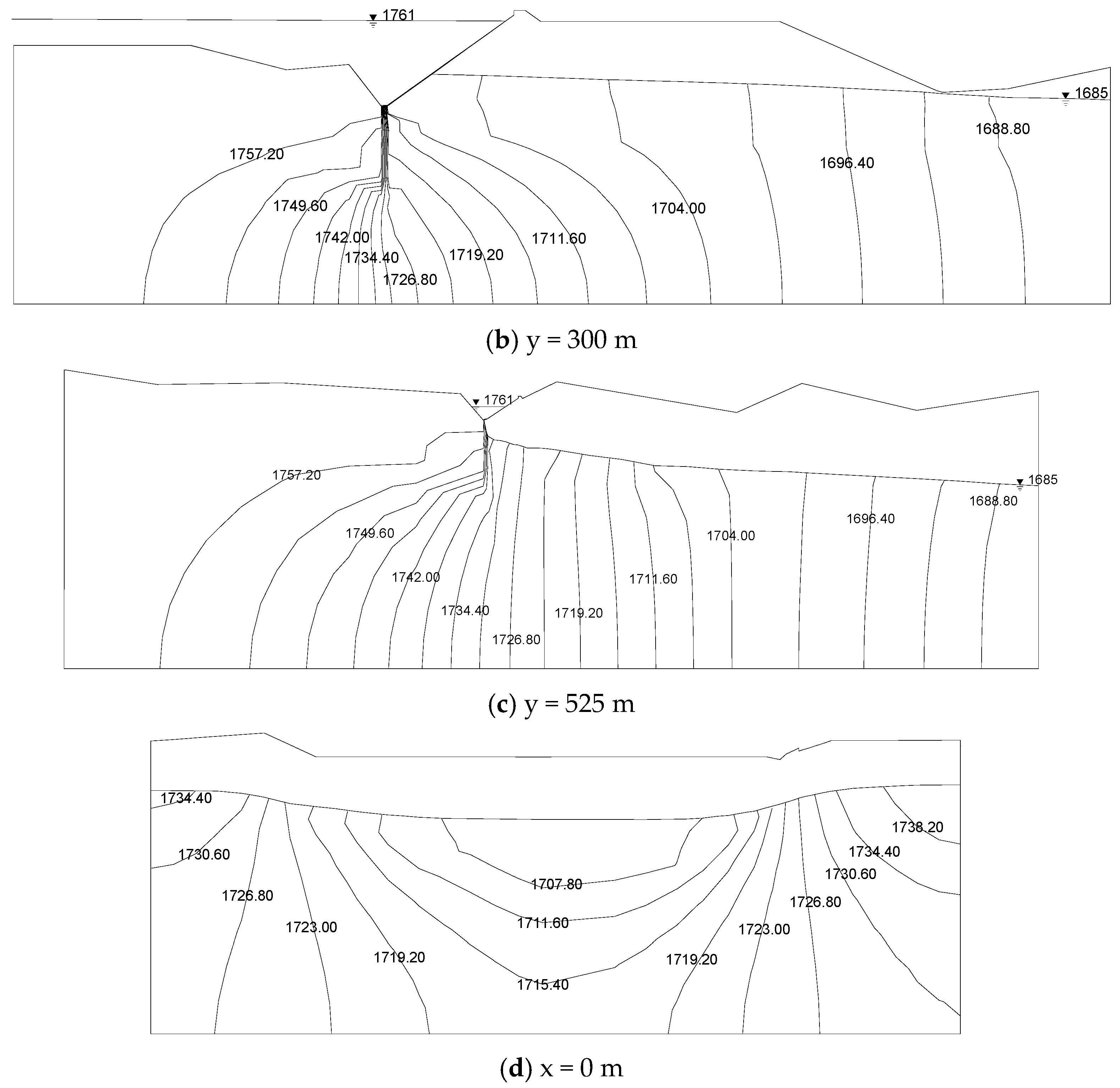
4.2.1. The Three-Dimensional Seepage Field
4.2.2. Suggestions on Optimization of Grouting Curtain
5. Conclusions
- The standard GA algorithm is improved by making a new genetic operation to overcome the premature convergence shortage of the standard GA in the hydraulic conductivity inversion problem and is more efficient compared to the BO and TEP algorithms. When using this method to invert other dams’ hydraulic conductivity, it will be necessary to adjust the number of copies of excellent individuals according to the total number of samples to adapt to different sample sizes.
- A new method and code for the inversion of dam foundation hydraulic conductivity by coupling the improved GA and the UECM is proposed, which fully considers engineering practicability. The result of the IGA–UECM to calculate the dam seepage field is reasonable and is expected to be widely used in dam seepage inversion.
- When the UECM is used to calculate the seepage field of a concrete-face rockfill dam, the range of calculation area should be adjusted according to the terrain. For example, the faults affecting the seepage around the dam should be considered in the model for dams with faults nearby.
- For the Hami concrete-face rockfill dam, the seepage discharge of the grouting curtain designed layout is 26.13 L/s. Compared to the change in grouting curtain size, the construction quality of the curtain grouting has the most significant impact on the water head reduction, the seepage gradient, and the seepage discharge of the anti-seepage system of the dam. The seepage stability of the Hami dam can still be ensured when the hydraulic conductivity of the grouting curtain is 2.5 times larger, owing to the poor construction quality of the curtain grouting. During construction management and control, it will be necessary to prevent the hydraulic conductivity of the grouting curtain from growing beyond 2.5 times.
- The grouting curtain should be designed to extend to the impermeable layer as far as possible to reduce the impact of grouting construction quality on the anti-seepage effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.; Chen, L.; Xu, M.; Tong, X. Review of Dam-Break Research of Earth-Rock Dam Combining with Dam Safety Management. Procedia Eng. 2012, 28, 382–388. [Google Scholar] [CrossRef]
- Cooke, J.B.; Sherard, J.L. Concrete-Face Rockfill DAM: II. Design. J. Geotech. Eng. 1987, 113, 1113–1132. [Google Scholar] [CrossRef]
- Ma, H.; Chi, F. Technical Progress on Researches for the Safety of High Concrete-Faced Rockfill Dams. Engineering 2016, 2, 332–339. [Google Scholar] [CrossRef]
- Warren, A.L. Investigation of Dam Incidents and Failures. Forensic Eng. 2011, 164, 33–41. [Google Scholar] [CrossRef]
- Hou, J.; Wang, D.G.; Luo, F.Q.; Zhang, Y.H. A Review on the Numerical Inversion Methods of Relative Permeability Curves. Procedia Eng. 2012, 29, 375–380. [Google Scholar] [CrossRef]
- Miyamoto, A.; Watanabe, K.; Ikeda, K.; Sato, M. Variational Bayes Method for NIRS-DOT Inverse Problem and Its Phase Transition. Neurosci. Res. 2010, 68, e217. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Fernández-Muñiz, Z.; Pallero, J.L.G.; Pedruelo-González, L.M. From Bayes to Tarantola: New Insights to Understand Uncertainty in Inverse Problems. J. Appl. Geophys. 2013, 98, 62–72. [Google Scholar] [CrossRef]
- Iglesias, M.A.; Law, K.J.H.; Stuart, A.M. Ensemble Kalman Methods for Inverse Problems. Inverse Probl. 2013, 29, 045001. [Google Scholar] [CrossRef]
- Huang, D.Z.; Schneider, T.; Stuart, A.M. Iterated Kalman Methodology for Inverse Problems. J. Comput. Phys. 2022, 463, 111262. [Google Scholar] [CrossRef]
- Direct Search Solution of an Inverse Problem in Elastoplasticity: Identification of Cohesion, Friction Angle and in Situ Stress by Pressure Tunnel Tests. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 21. [CrossRef]
- Strauss, T.; Fan, X.; Sun, S.; Khan, T. Statistical Inversion of Absolute Permeability in Single-Phase Darcy Flow. Procedia Comput. Sci. 2015, 51, 1188–1197. [Google Scholar] [CrossRef]
- Bekker, J.; Davis, J. Learning from Positive and Unlabeled Data: A Survey. Mach. Learn. 2020, 109, 719–760. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, G.; Liu, C.; Cheng, L.; Sha, D. Bagging-Based Positive-Unlabeled Learning Algorithm with Bayesian Hyperparameter Optimization for Three-Dimensional Mineral Potential Mapping. Comput. Geosci. 2021, 154, 104817. [Google Scholar] [CrossRef]
- Ares-Pena, F.J.; Rodriguez-Gonzalez, J.A.; Villanueva-Lopez, E.; Rengarajan, S.R. Genetic Algorithms in the Design and Optimization of Antenna Array Patterns. IEEE Trans. Antennas Propag. 1999, 47, 506–510. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 4, 2951–2959. [Google Scholar] [CrossRef]
- Rong, G.; Li, K.; Su, Y.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sens. 2021, 13, 4694. [Google Scholar] [CrossRef]
- Zhou, S.; Song, W. Deep Learning-Based Roadway Crack Classification Using Laser-Scanned Range Images: A Comparative Study on Hyperparameter Selection. Autom. Constr. 2020, 114, 103171. [Google Scholar] [CrossRef]
- Mahdaddi, A.; Meshoul, S.; Belguidoum, M. EA-Based Hyperparameter Optimization of Hybrid Deep Learning Models for Effective Drug-Target Interactions Prediction. Expert Syst. Appl. 2021, 185, 115525. [Google Scholar] [CrossRef]
- Kunang, Y.N.; Nurmaini, S.; Stiawan, D.; Suprapto, B.Y. Attack Classification of an Intrusion Detection System Using Deep Learning and Hyperparameter Optimization. J. Inf. Secur. Appl. 2021, 58, 102804. [Google Scholar] [CrossRef]
- Sui, A.; Deng, Y.; Wang, Y.; Yu, J. A Deep Learning Model Designed for Raman Spectroscopy with a Novel Hyperparameter Optimization Method. Spectrochim Acta A Mol. Biomol. Spectrosc. 2022, 280, 121560. [Google Scholar] [CrossRef]
- Bhoskar, T.; Kulkarni, O.K.; Kulkarni, N.K.; Patekar, S.L.; Kakandikar, G.M.; Nandedkar, V.M. Genetic Algorithm and Its Applications to Mechanical Engineering: A Review. Mater. Today Proc. 2015, 2, 2624–2630. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Sobey, A. A Comparative Review between Genetic Algorithm Use in Composite Optimisation and the State-of-the-Art in Evolutionary Computation. Compos. Struct. 2020, 233, 111739. [Google Scholar] [CrossRef]
- Pandey, H.M. State of the Art: Genetic Algorithms and Premature Convergence. In State of the Art on Grammatical Inference Using Evolutionary Method; Academic Press: Cambridge, MA, USA, 2022; pp. 35–124. [Google Scholar] [CrossRef]
- Andre, J.; Siarry, P.; Dognon, T. An Improvement of the Standard Genetic Algorithm Fighting Premature Convergence in Continuous Optimization. Adv. Eng. Softw. 2001, 32, 49–60. [Google Scholar] [CrossRef]
- Ding, Y.; Zhou, K.; Bi, W. Feature Selection Based on Hybridization of Genetic Algorithm and Competitive Swarm Optimizer. Soft Comput. 2020, 24, 11663–11672. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Birgé, L.; Massart, P. Gaussian Model Selection. J. Eur. Math. Soc. 2001, 3, 203–268. [Google Scholar] [CrossRef]
- Pelikan, M. Bayesian Optimization Algorithm. In Hierarchical Bayesian Optimization Algorithm; Studies in Fuzziness and Soft Computing, Volume 170; Springer: Berlin/Heidelberg, Germany, 2005; pp. 31–48. [Google Scholar] [CrossRef]
- Chen, M.; Ludtke, S.J. Deep Learning-Based Mixed-Dimensional Gaussian Mixture Model for Characterizing Variability in Cryo-EM. Nat. Methods 2021, 18, 930–936. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Ullah, A.; Khan, S.N.; Selim, M.M. Mesoscopic Simulation for Magnetized Nanofluid Flow within a Permeable 3D Tank. IEEE Access 2021, 9, 135234–135244. [Google Scholar] [CrossRef]
- Ullah, A.; Ikramullah; Selim, M.M.; Abdeljawad, T.; Ayaz, M.; Mlaiki, N.; Ghafoor, A. A Magnetite–Water-Based Nanofluid Three-Dimensional Thin Film Flow on an Inclined Rotating Surface with Non-Linear Thermal Radiations and Couple Stress Effects. Energies 2021, 14, 5531. [Google Scholar] [CrossRef]
- Rizk, D.; Ullah, A.; Ikramullah; Elattar, S.; Alharbi, K.A.M.; Sohail, M.; Khan, R.; Khan, A.; Mlaiki, N. Impact of the KKL Correlation Model on the Activation of Thermal Energy for the Hybrid Nanofluid (GO+ZnO+Water) Flow through Permeable Vertically Rotating Surface. Energies 2022, 15, 2872. [Google Scholar] [CrossRef]
- Hu, M.; Wang, Y.; Rutqvist, J. Development of a Discontinuous Approach for Modeling Fluid Flow in Heterogeneous Media Using the Numerical Manifold Method. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1932–1952. [Google Scholar] [CrossRef]
- Lisjak, A.; Kaifosh, P.; He, L.; Tatone, B.S.A.; Mahabadi, O.K.; Grasselli, G. A 2D, Fully-Coupled, Hydro-Mechanical, FDEM Formulation for Modelling Fracturing Processes in Discontinuous, Porous Rock Masses. Comput. Geotech. 2017, 81, 1–18. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; An, X.; Ma, G. Modelling Rock Fracturing and Blast-Induced Rock Mass Failure via Advanced Discretisation within the Discontinuous Deformation Analysis Framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Fan, L.F.; Wang, M.; Wu, Z.J. Effect of Nonlinear Deformational Macrojoint on Stress Wave Propagation Through a Double-Scale Discontinuous Rock Mass. Rock Mech. Rock Eng. 2021, 54, 1077–1090. [Google Scholar] [CrossRef]
- Regassa, B.; Xu, N.; Mei, G. An Equivalent Discontinuous Modeling Method of Jointed Rock Masses for DEM Simulation of Mining-Induced Rock Movements. Int. J. Rock Mech. Min. Sci. 2018, 108, 1–14. [Google Scholar] [CrossRef]
- Chen, S.-K.; He, Q.-D.; Cao, J.-G. gang Seepage Simulation of High Concrete-Faced Rockfill Dams Based on Generalized Equivalent Continuum Model. Water Sci. Eng. 2018, 11, 250–257. [Google Scholar] [CrossRef]
- Li, A.; Liu, Y.; Dai, F.; Liu, K.; Wei, M. Continuum Analysis of the Structurally Controlled Displacements for Large-Scale Underground Caverns in Bedded Rock Masses. Tunn. Undergr. Space Technol. 2020, 97, 103288. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Battaglia, G.J. Mean Square Error. AMP J. Technol. 1996, 5, 31–36. [Google Scholar]
- Zehan, L.; Zhenzhong, S.; Wenwu, Q.; Sufan, X.; Lei, G. Anti-Seepage Evaluation of Reinforcement Effect for Fengchan Earth Dam. Key Eng. Mater. 2017, 753, 290–294. [Google Scholar]
- Zhang, H.; Shen, Z.; Liu, D.; Xu, L.; Gan, L.; Long, Y. A Suggested Equivalent Method for a Drainage Structure to Analyze Seepage in Tailings Dam. Materials 2022, 15, 7154. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Shen, Z.; Chen, G.; Zhang, W.; Xu, L.; Ren, J.; Wang, F. Optimization Design and Assessment of the Effect of Seepage Control at Reservoir Sites under Karst Conditions: A Case Study in Anhui Province, China. Hydrogeol. J. 2021, 29, 1831–1855. [Google Scholar] [CrossRef]
- Zhenzhong, S.; Xiaohu, C.; Yuelin, S. Analysis of the Steady Seepage Field with Free Surface Using Element Free Galerkin Method. J. Xi Shiyou Univ. 2007, 22, 92–96. [Google Scholar]
- Hartmann, R.; Houston, P. Adaptive Discontinuous Galerkin Finite Element Methods for the Compressible Euler Equations. J. Comput. Phys. 2002, 183. [Google Scholar] [CrossRef]
- Hughes, T.J.R. Multiscale Phenomena: Green’s Functions, the Dirichlet-to-Neumann Formulation, Subgrid Scale Models, Bubbles and the Origins of Stabilized Methods. Comput. Methods Appl. Mech. Eng. 1995, 127, 387–401. [Google Scholar] [CrossRef]
- Riks, E. An Incremental Approach to the Solution of Snapping and Buckling Problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Fox, G.A.; Wilson, G.V.; Simon, A.; Langendoen, E.J.; Akay, O.; Fuchs, J.W. Measuring Streambank Erosion Due to Ground Water Seepage: Correlation to Bank Pore Water Pressure, Precipitation and Stream Stage. Earth Surf. Process. Landf. 2007, 32, 1558–1573. [Google Scholar] [CrossRef]
- Mirebeau, J.M. Optimal Meshes for Finite Elements of Arbitrary Order. Constr. Approx. 2010, 32, 339–383. [Google Scholar] [CrossRef]
- Dziwinski, P.; Bartczuk, L. A New Hybrid Particle Swarm Optimization and Genetic Algorithm Method Controlled by Fuzzy Logic. IEEE Trans. Fuzzy Syst. 2020, 28, 1140–1154. [Google Scholar] [CrossRef]
- Lin, B.; Huang, Y.; Zhang, J.; Hu, J.; Chen, X.; Li, J. Cost-Driven Off-Loading for DNN-Based Applications over Cloud, Edge, and End Devices. IEEE Trans. Ind. Inform. 2020, 16, 5456–5466. [Google Scholar] [CrossRef]
- Petrosov, D.A.; Lomazov, V.A.; Petrosova, N.V. Model of an Artificial Neural Network for Solving the Problem of Controlling a Genetic Algorithm Using the Mathematical Apparatus of the Theory of Petri Nets. Appl. Sci. 2021, 11, 3899. [Google Scholar] [CrossRef]
- Santiago, A.; Dorronsoro, B.; Fraire, H.J.; Ruiz, P. Micro-Genetic Algorithm with Fuzzy Selection of Operators for Multi-Objective Optimization: ΜFAME. Swarm Evol. Comput. 2021, 61, 100818. [Google Scholar] [CrossRef]
- Li, A.D.; Xue, B.; Zhang, M. Improved Binary Particle Swarm Optimization for Feature Selection with New Initialization and Search Space Reduction Strategies. Appl. Soft Comput. 2021, 106, 107302. [Google Scholar] [CrossRef]
- Costa-Carrapiço, I.; Raslan, R.; González, J.N. A Systematic Review of Genetic Algorithm-Based Multi-Objective Optimisation for Building Retrofitting Strategies towards Energy Efficiency. Energy Build. 2020, 210, 109690. [Google Scholar] [CrossRef]
- Wang, Z.L.; Ogawa, T.; Adachi, Y. Influence of Algorithm Parameters of Bayesian Optimization, Genetic Algorithm, and Particle Swarm Optimization on Their Optimization Performance. Adv. Theory Simul. 2019, 2, 1900110. [Google Scholar] [CrossRef]
- Cui, W.J.; Chai, J.R.; Xu, Z.G.; Wu, M.H. Application of Improved Genetic Algorithm to Optimization of Grouting Curtain of Dam Foundation. Yantu Lixue/Rock Soil Mech. 2008, 29, 3349–3352. [Google Scholar]
- Wang, Y.; Liu, J. Inverse Analysis of Fully Coupled Dynamic Water Flow and Stress in Fractured Rock Masses. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2008, 27, 1652–1658. [Google Scholar]
- Yao, L.; Li, J. Parameter Identification of 3D Groundwater Flow Model with Improved Genetic Algorithm. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2004, 23, 625–630. [Google Scholar]
- Jia, S.P.; Wu, G.J.; Chen, W.Z. Application of Finite Element Inverse Model Based on Improved Particle Swarm Optimization and Mixed Penalty Function. Yantu Lixue/Rock Soil Mech. 2011, 32, 598–603. [Google Scholar]
- Zhang, X.; Chen, X.; Li, J. Improving Dam Seepage Prediction Using Back-Propagation Neural Network and Genetic Algorithm. Math. Probl. Eng. 2020, 2020, 1404295. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Zuo, K.; Khan, M.J. An Improved Genetic Algorithm Optimization Fuzzy Controller Applied to the Wellhead Back Pressure Control System. Mech. Syst. Signal Process. 2020, 142, 106708. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Xu, L.; Shen, Z.; Ma, B. A New Approach for Mechanical Parameter Inversion Analysis of Roller Compacted Concrete Dams Using Modified PSO and RBFNN. Clust. Comput. 2022, 25, 4633–4652. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Wang, X.; Gan, L.; Shao, W.; Tang, P.; Zhang, H.; Yu, S. Effect of Calcium Leaching on the Fracture Properties of Concrete. Constr. Build. Mater. 2023, 365, 130018. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Shen, Z.; Shao, W.; Gan, L.; Yuan, Y.; Tang, P.; Zhao, S.; Chen, Y. Reduction of the Calcium Leaching Effect on the Physical and Mechanical Properties of Concrete by Adding Chopped Basalt Fibers. Constr. Build. Mater. 2023, 365, 130080. [Google Scholar] [CrossRef]






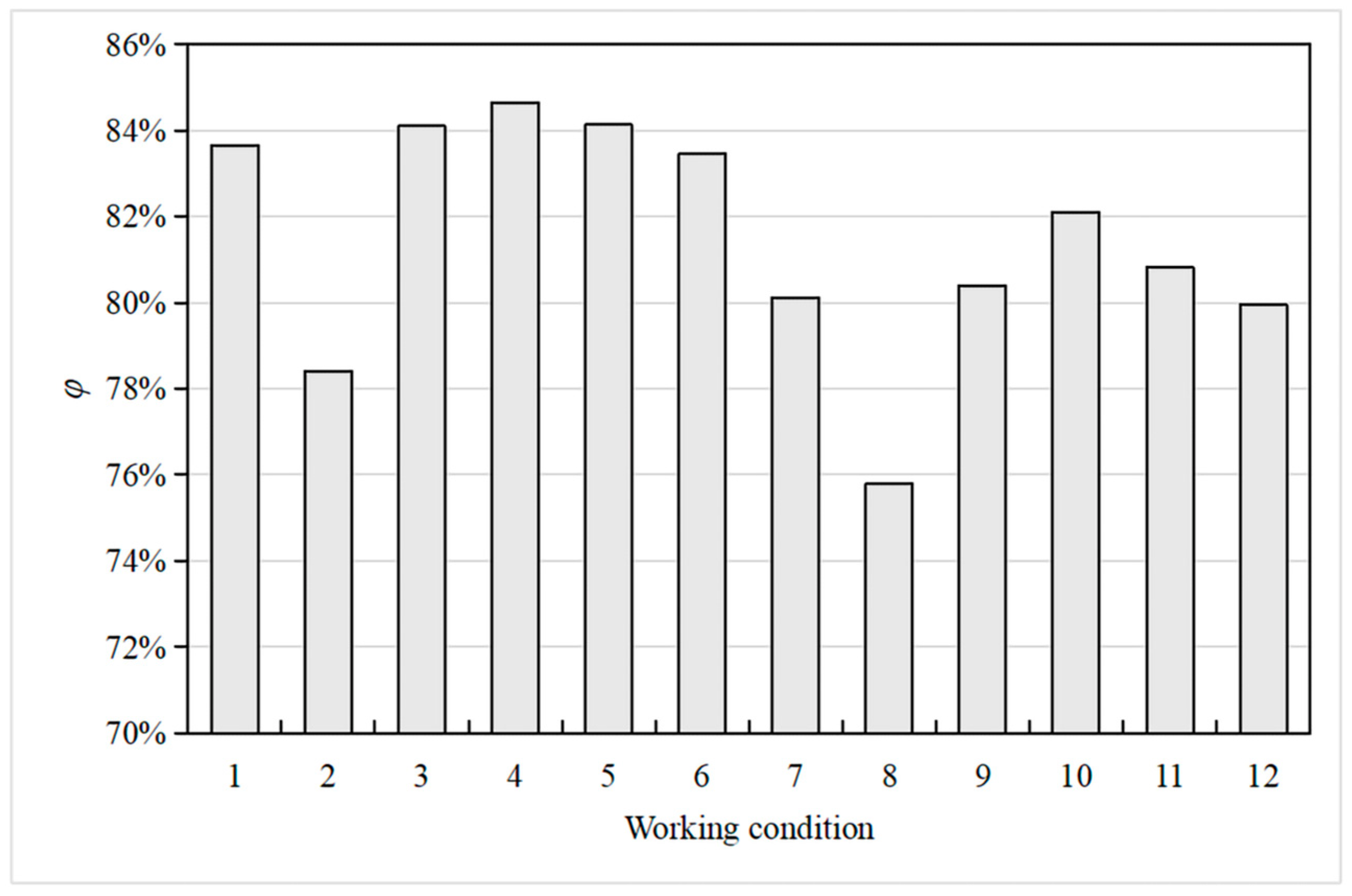
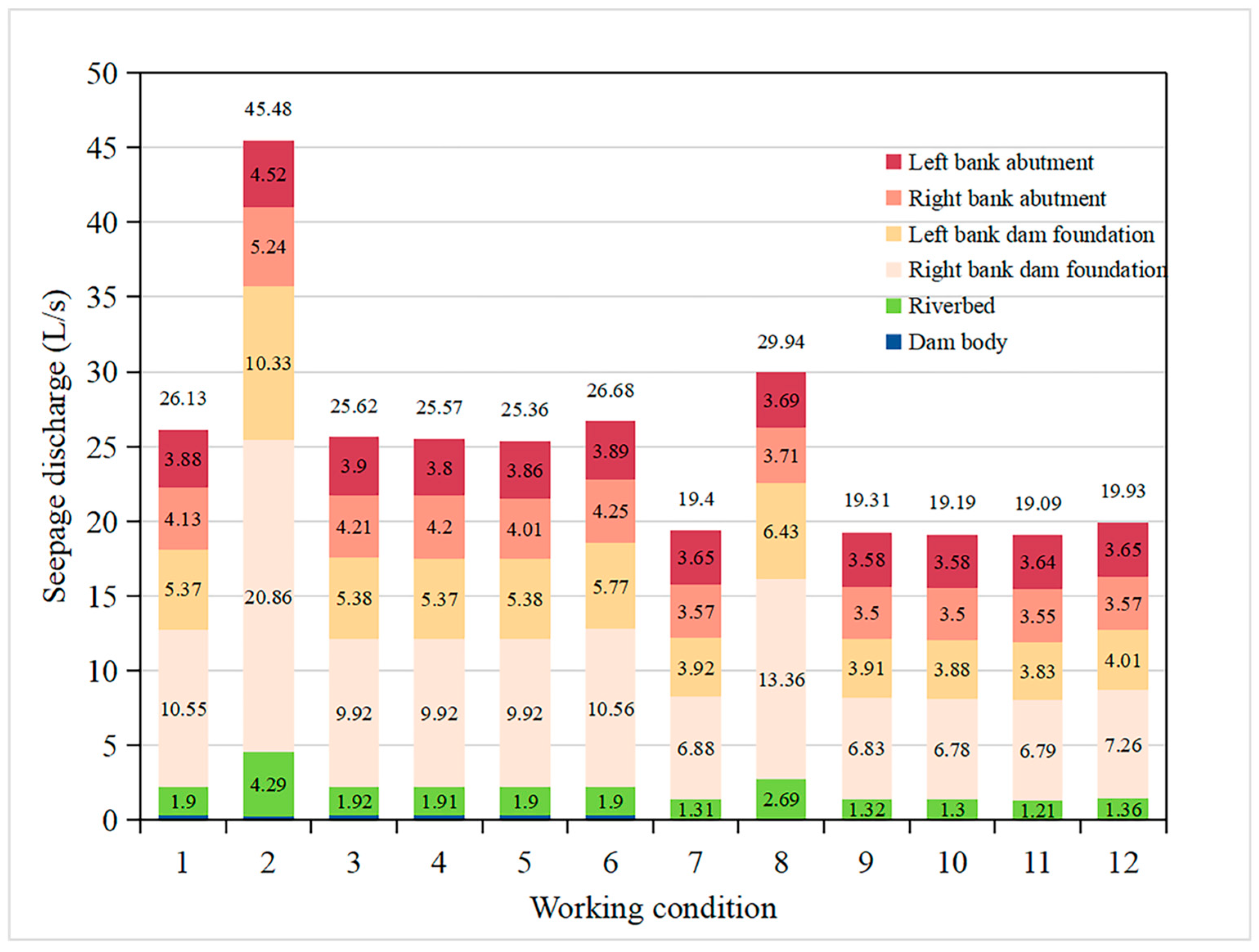
| Rock Layer | Number | Hydraulic Conductivity (cm/s) |
|---|---|---|
| 10 Lu–100 Lu | K1 (highly weathered) | (0.5–10) × 10−3 |
| K2 (slightly weathered) | (1.0–10) × 10−4 | |
| 3 Lu–10 Lu | K3 | (1.0–9.0) × 10−5 |
| 1 Lu–3 Lu | K4 | (0.5–5.0) × 10−5 |
| Fault zone | K5 | (1.0–10) × 10−6 |
| Number | EM1 | EM2 | EM3 | EM4 | EM5 | EM6 | EM7 | EM8 | EM9 | EM10 | EM11 | EM12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E (m) | 1825.8 | 1740.8 | 1752.0 | 1750.0 | 1738.1 | 1739.0 | 1717.0 | 1717.4 | 1716.2 | 1715.7 | 1716.3 | 1710.9 |
| x | 166.51 | 163.60 | −29.35 | 15.25 | 184.49 | 69.93 | −23.25 | −81.72 | 61.15 | 125.10 | 3.59 | −248.61 |
| y | 0.00 | 90.00 | 150.00 | 150.00 | 150.00 | 150.00 | 300.00 | 300.00 | 300.00 | 300.00 | 400.00 | 550.00 |
| Condition | Description | |
|---|---|---|
| HM-1 | Normal water level at 1761.00 m | The grouting curtain is arranged in the design scheme. |
| HM-2 | The hydraulic conductivity of the grouting curtain is 2.5 times larger than that of the design scheme. | |
| HM-3 | The grouting curtain is 10 m deeper than the design scheme. | |
| HM-4 | The grouting curtain is 20 m deeper than the design scheme. | |
| HM-5 | The grouting curtain is extended by 20 m to the left and right banks. | |
| HM-6 | The grouting curtain is shortened by 20 m to the left and right banks. | |
| HM-7 | Dead water level at 1732 m | The grouting curtain is arranged in the design scheme. |
| HM-8 | The hydraulic conductivity of the grouting curtain is 2.5 times larger than that of the design scheme. | |
| HM-9 | The grouting curtain is 10 m deeper than the design scheme. | |
| HM-10 | The grouting curtain is 20 m deeper than the design scheme. | |
| HM-11 | The grouting curtain is extended by 20 m to the left and right banks. | |
| HMX-12 | The grouting curtain is shortened by 20 m to the left and right banks. | |
| Rock Layer | Number | Hydraulic Conductivity (cm/s) |
|---|---|---|
| 10 Lu–100 Lu | K1 | 4.5 × 10−3 |
| K2 | 6.4 × 10−4 | |
| 3 Lu–10 Lu | K3 | 3.1 × 10−5 |
| 1 Lu–3 Lu | K4 | 2.2 × 10−5 |
| Fault zone | K5 | 1.1 × 10−6 |
| Working Condition | HM-1 | HM-2 | HM-3 | HM-4 | HM-5 | HM-6 | HM-7 | HM-8 | HM-9 | HM-10 | HM-11 | HM-12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum seepage gradient | 7.14 | 6.66 | 7.25 | 7.31 | 7.58 | 7.11 | 3.76 | 3.26 | 3.81 | 3.86 | 3.91 | 3.45 |
| Location | III | III | II | II | II | III | III | III | III | III | III | II |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Shen, Z.; Xu, L.; Gan, L.; Tan, J. A New Method for Inversion of Dam Foundation Hydraulic Conductivity Using an Improved Genetic Algorithm Coupled with an Unsaturated Equivalent Continuum Model and Its Application. Materials 2023, 16, 1662. https://doi.org/10.3390/ma16041662
Peng J, Shen Z, Xu L, Gan L, Tan J. A New Method for Inversion of Dam Foundation Hydraulic Conductivity Using an Improved Genetic Algorithm Coupled with an Unsaturated Equivalent Continuum Model and Its Application. Materials. 2023; 16(4):1662. https://doi.org/10.3390/ma16041662
Chicago/Turabian StylePeng, Jiayi, Zhenzhong Shen, Liqun Xu, Lei Gan, and Jiacheng Tan. 2023. "A New Method for Inversion of Dam Foundation Hydraulic Conductivity Using an Improved Genetic Algorithm Coupled with an Unsaturated Equivalent Continuum Model and Its Application" Materials 16, no. 4: 1662. https://doi.org/10.3390/ma16041662
APA StylePeng, J., Shen, Z., Xu, L., Gan, L., & Tan, J. (2023). A New Method for Inversion of Dam Foundation Hydraulic Conductivity Using an Improved Genetic Algorithm Coupled with an Unsaturated Equivalent Continuum Model and Its Application. Materials, 16(4), 1662. https://doi.org/10.3390/ma16041662








