The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation
Abstract
1. Introduction
2. Numerical Models of Vibro-Acoustic Interactions in Cracked Beams
2.1. Crack Models
- (1)
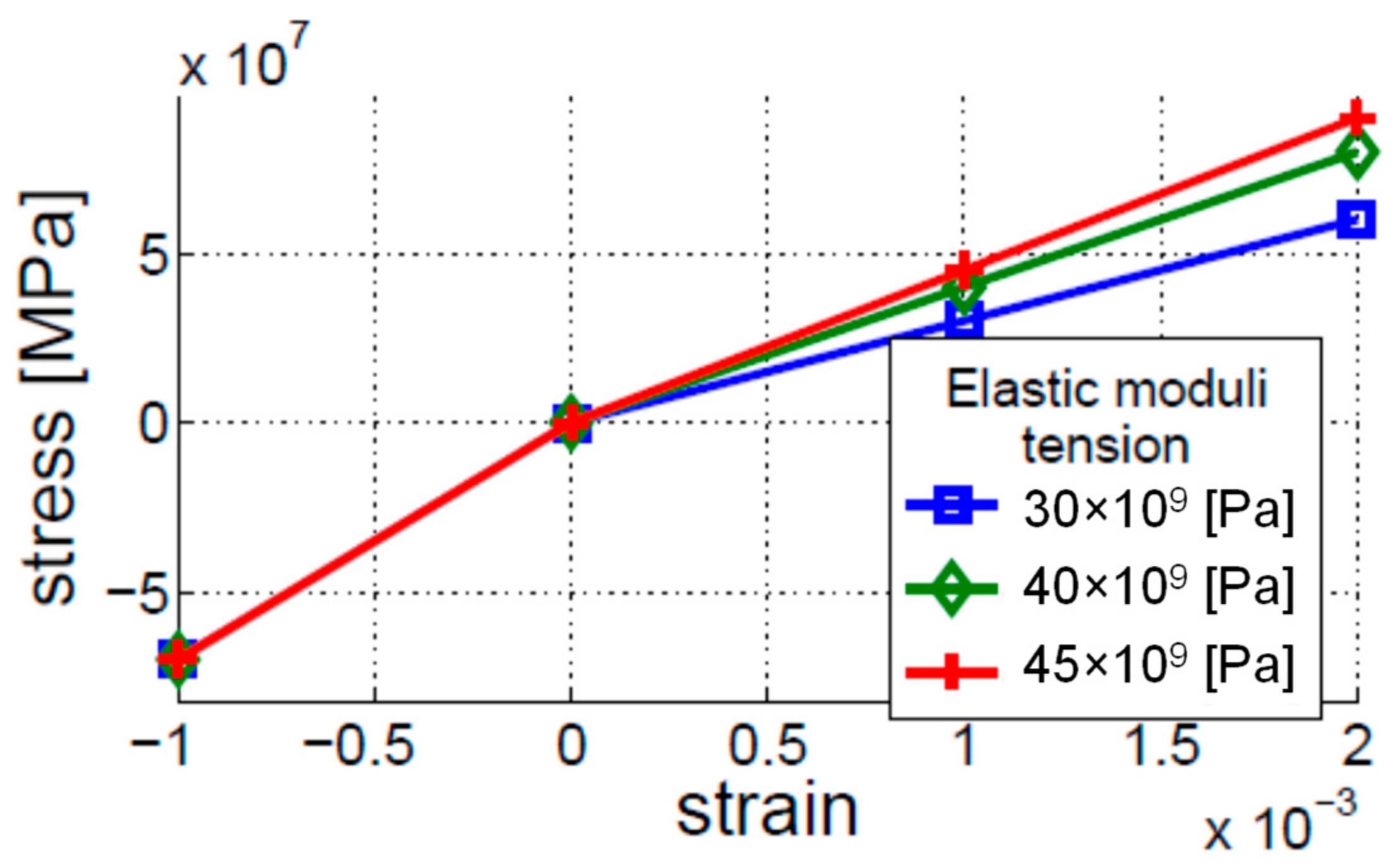
- Bi-linear model of elasticity
- (2)
- Open crack model
- (3)
- Breathing crack model
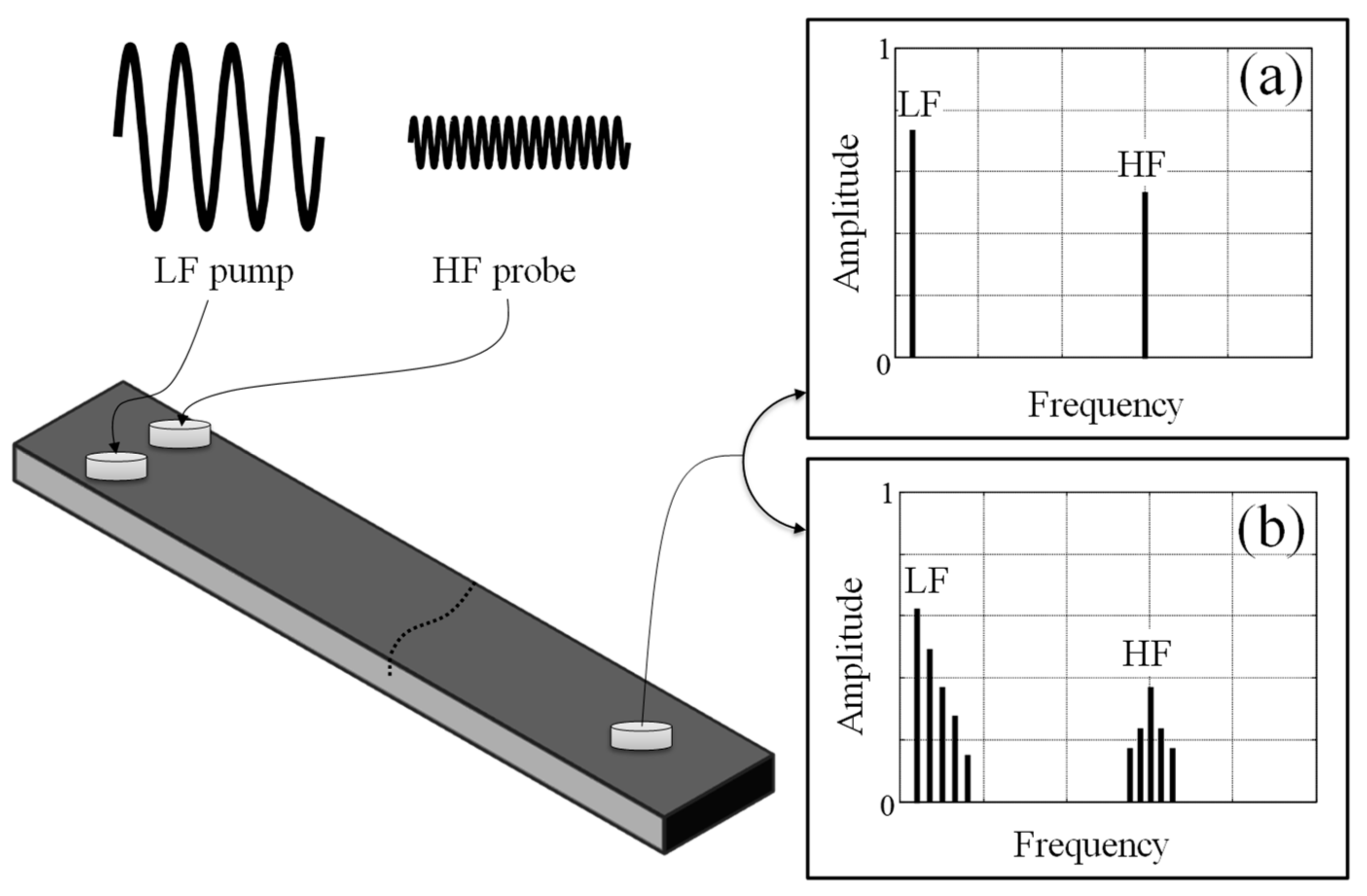
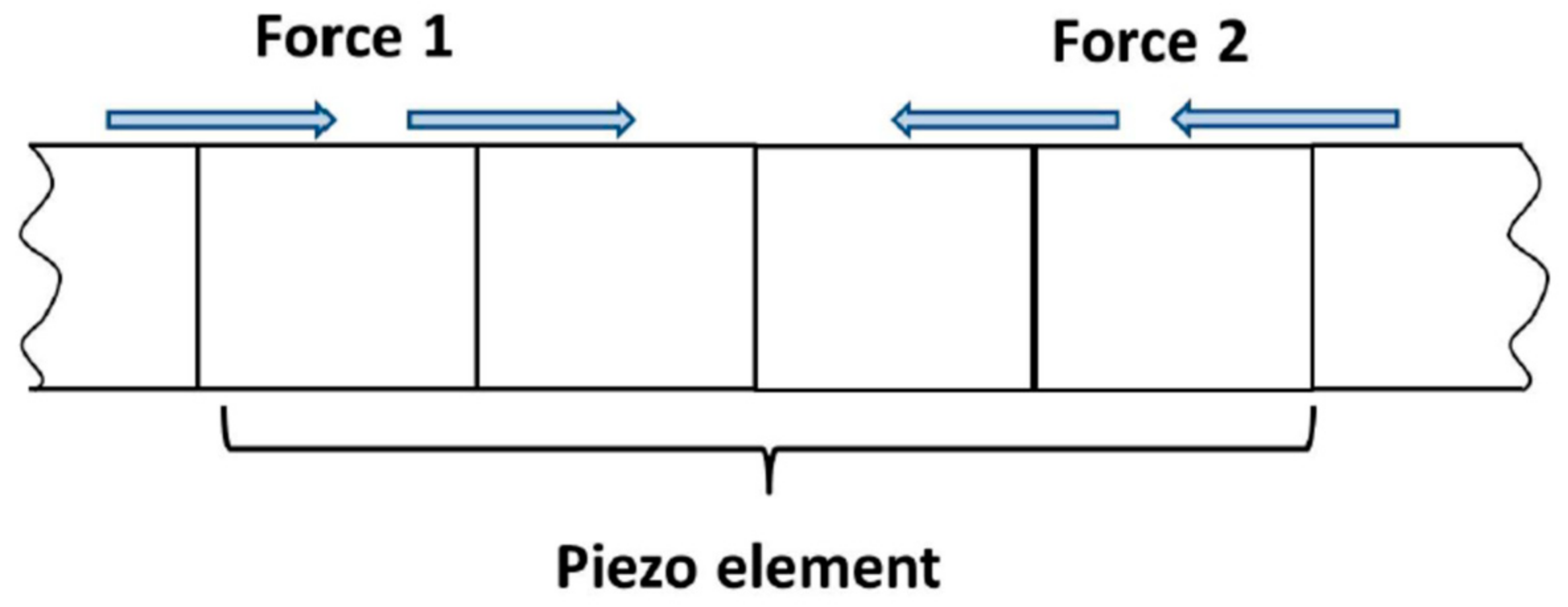
2.2. Modal and Ultrasonic Excitation
2.3. Vibro-Acoustic Responses and Indicators of Nonlinearity
3. Numerical Simulation Results
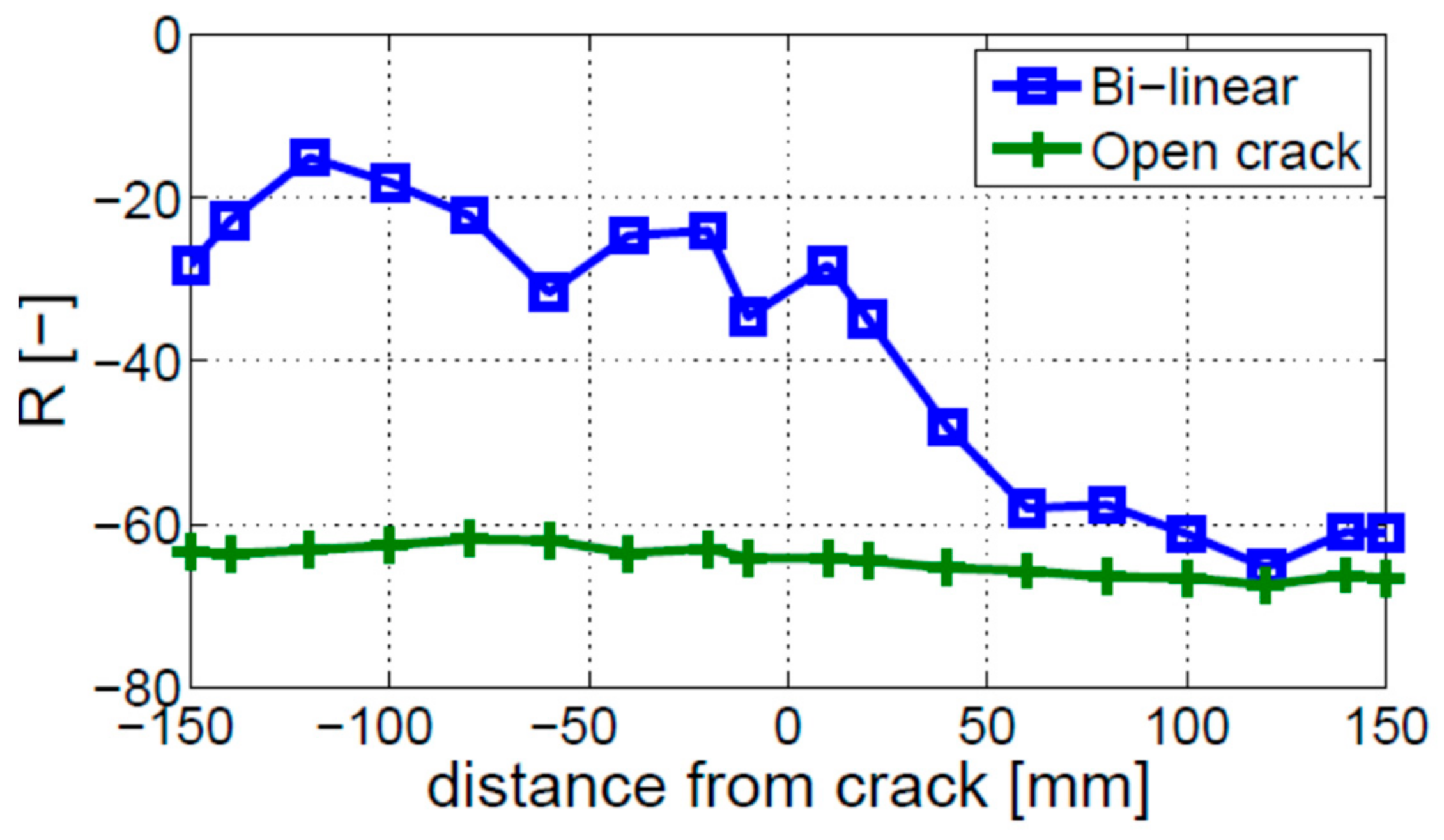
3.1. Bi-Linear Crack Model
3.2. Open Crack Model
3.3. Breathing Crack Model
3.4. Summary of Numerical Investigations
- The open crack model is not able to describe the nonlinear vibro-acoustic modulations, as expected, and cannot be used for the analysis of the crack localization effect.
- The proportionality between the input excitation amplitude and modulation intensity level was not observed in the numerically simulated results that involved the bi-linear and breathing crack models.
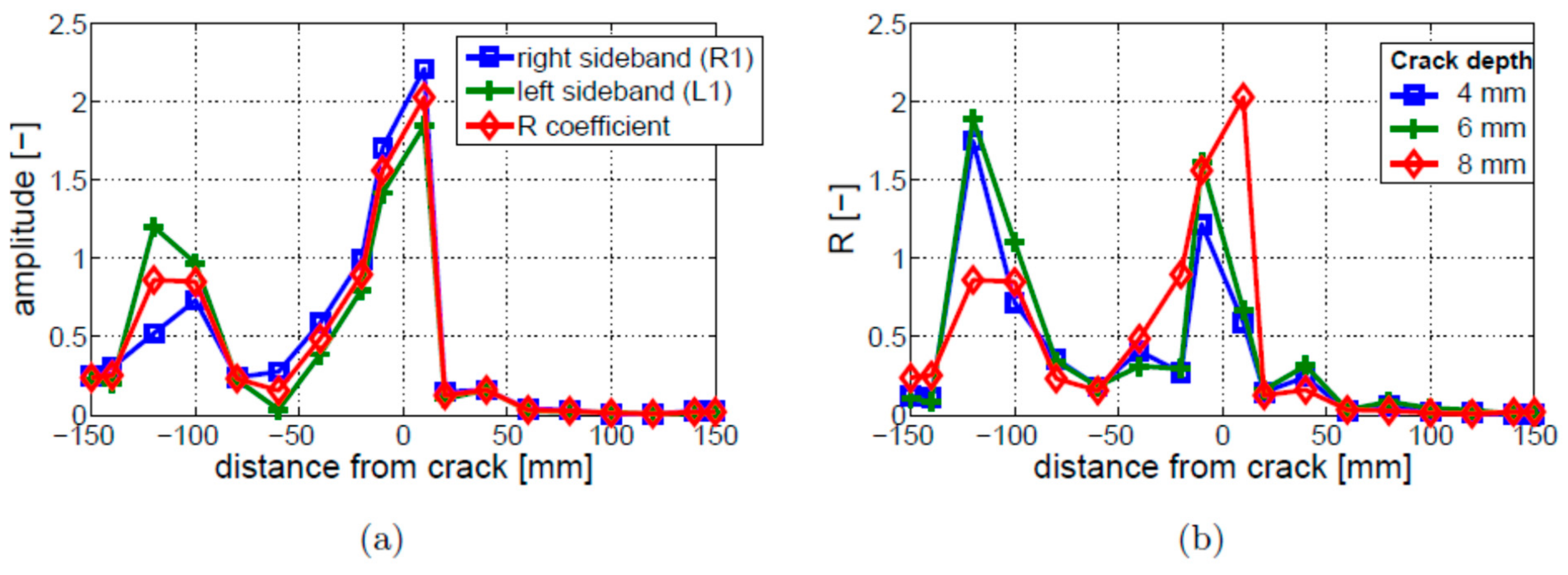
- The amplitudes of the first left and right sidebands were found to be similar in the breathing crack model and different in the bi-linear model.
- The proportionality between the crack depth and the modulation intensity level was observed for the bi-linear crack model. This relation is more complex in the breathing crack model and strongly depends on the ultrasonic HF excitation modeling approach.
- The crack localization effect was found in the bi-linear and breathing crack models, although the distribution of nonlinearity along the beam is significantly different for both crack models. The distribution of nonlinearity is also affected by the ultrasonic HF excitation modeling approach.
4. Experimental Validation
4.1. Experimental Setup and Test Procedure
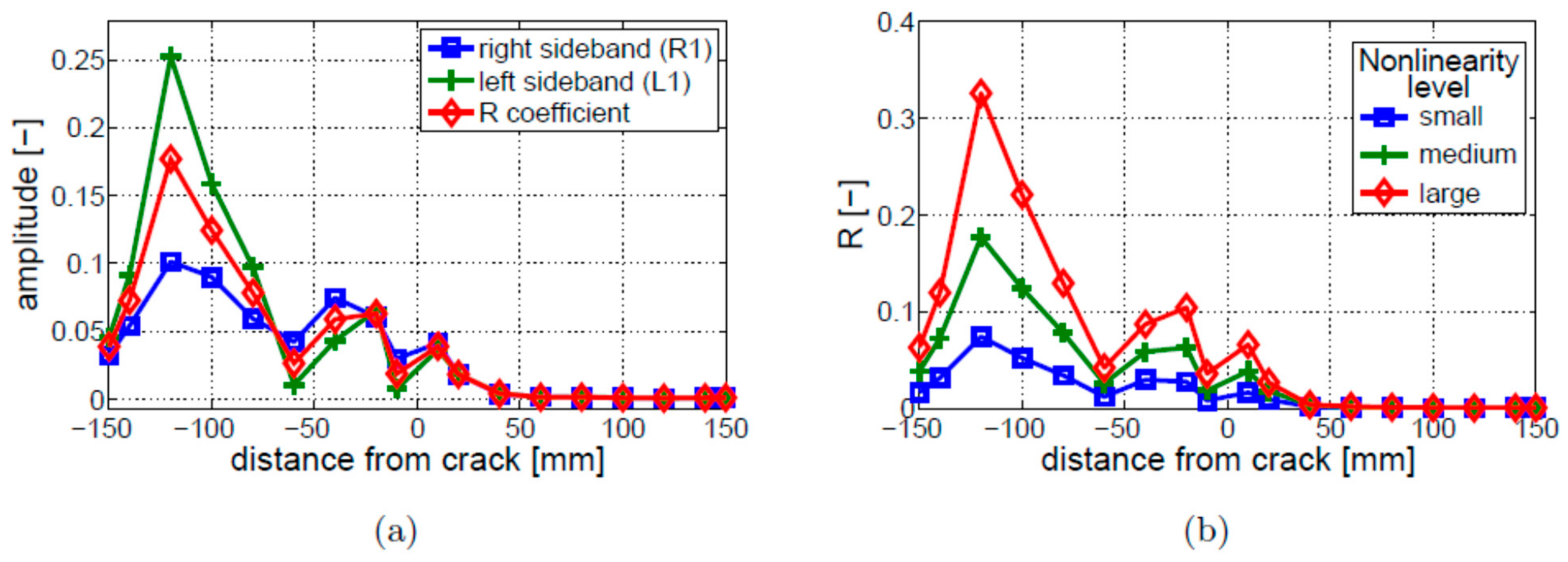
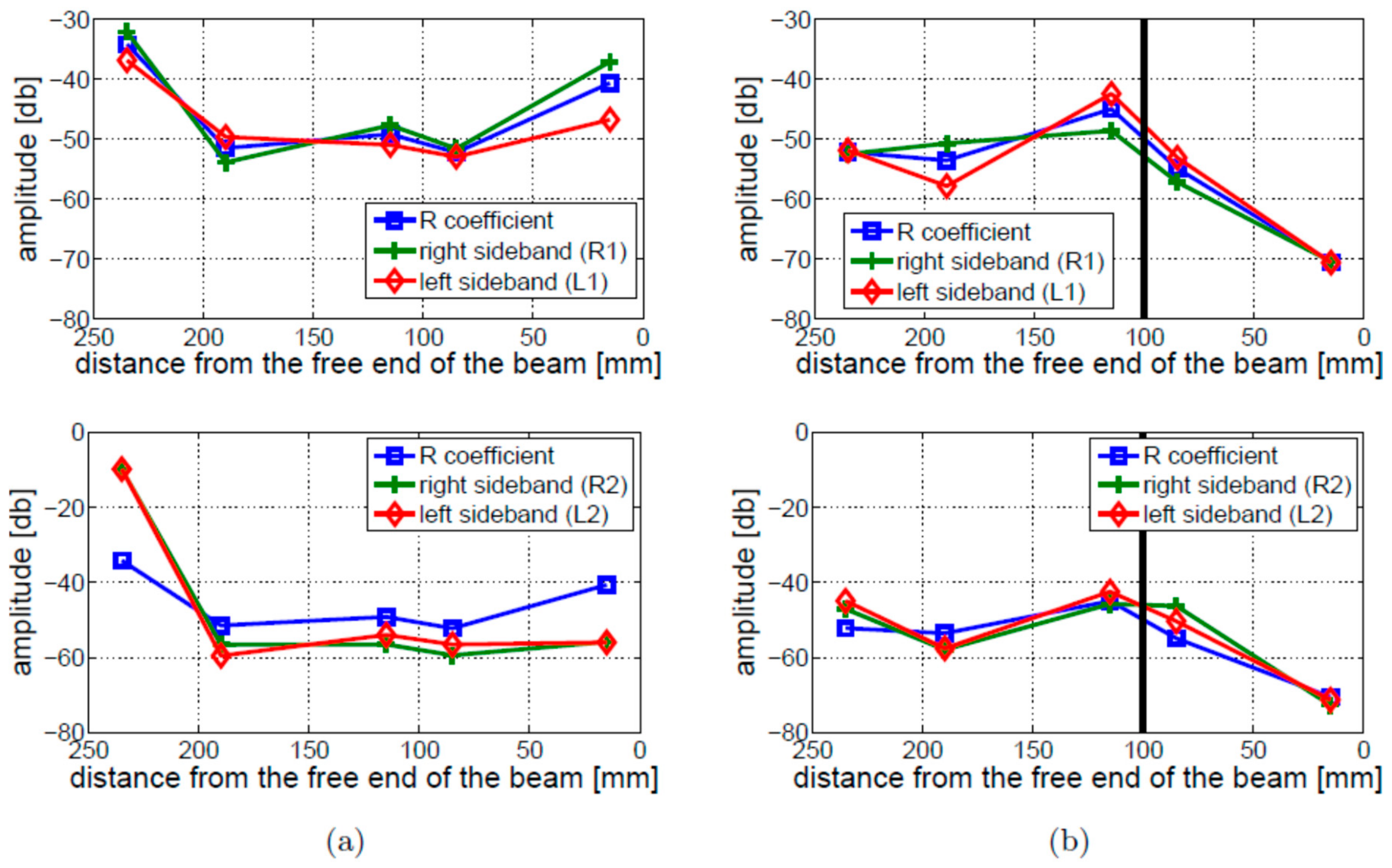
4.2. Level of Nonlinearity
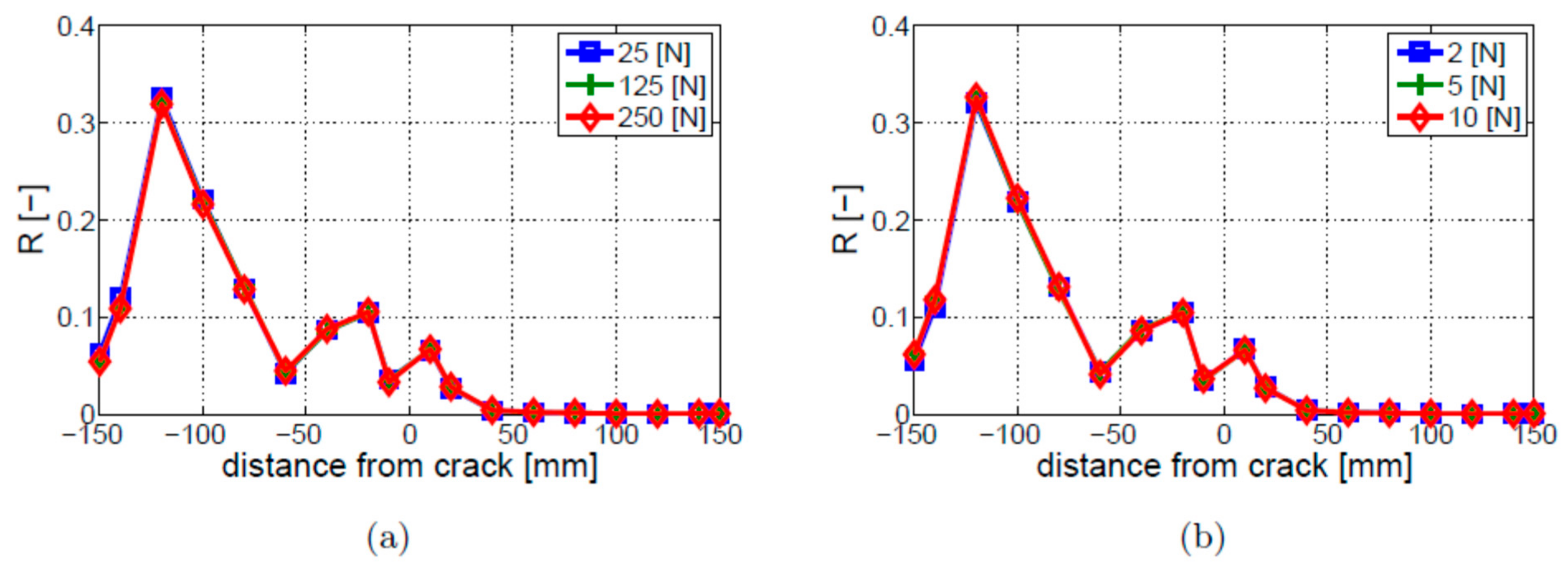
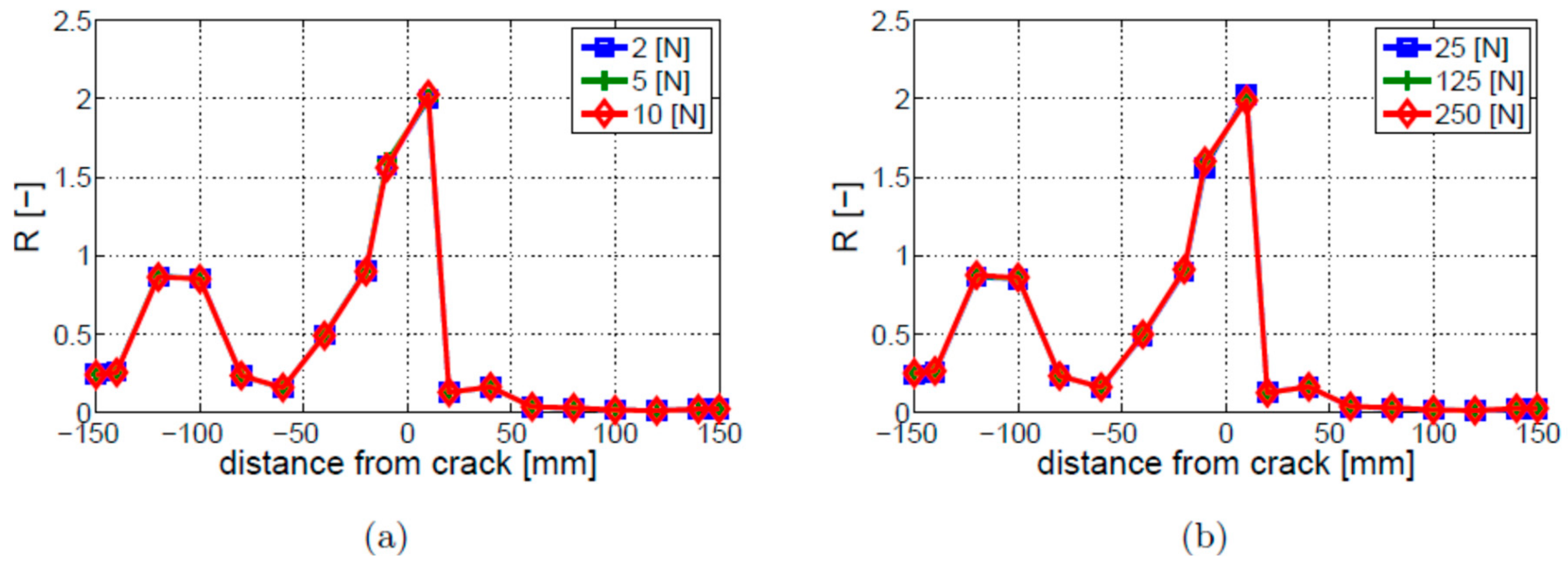
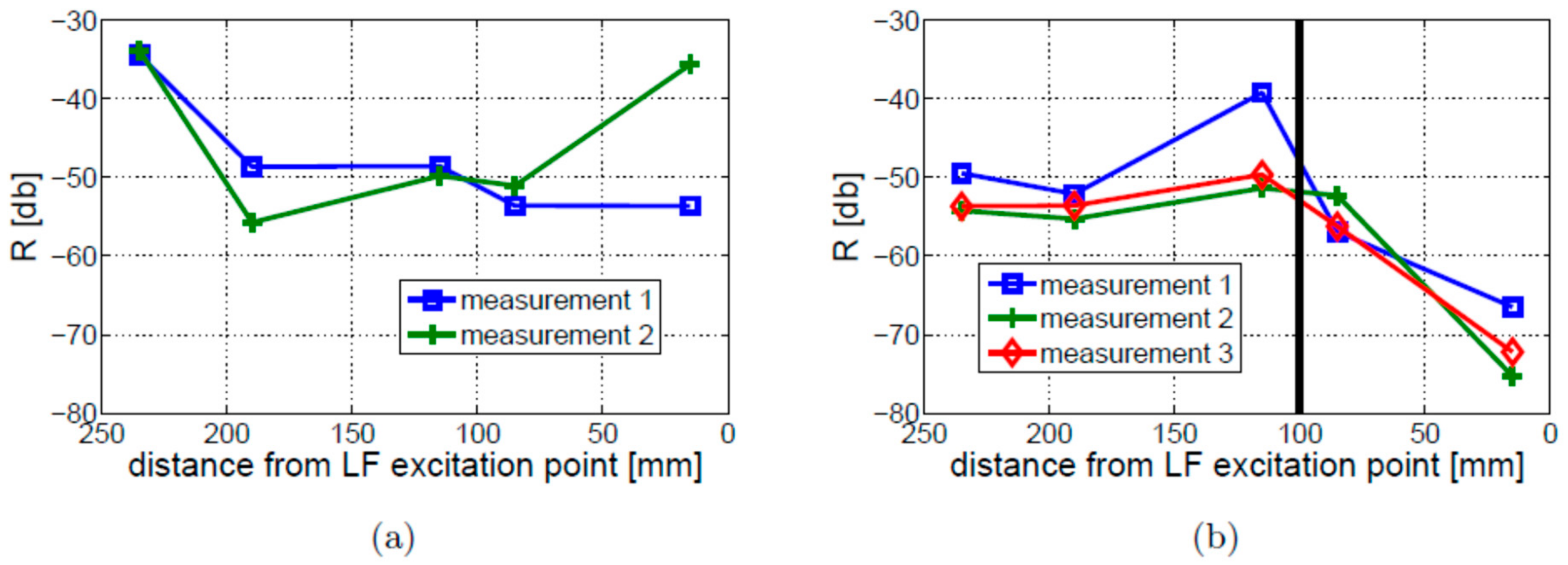
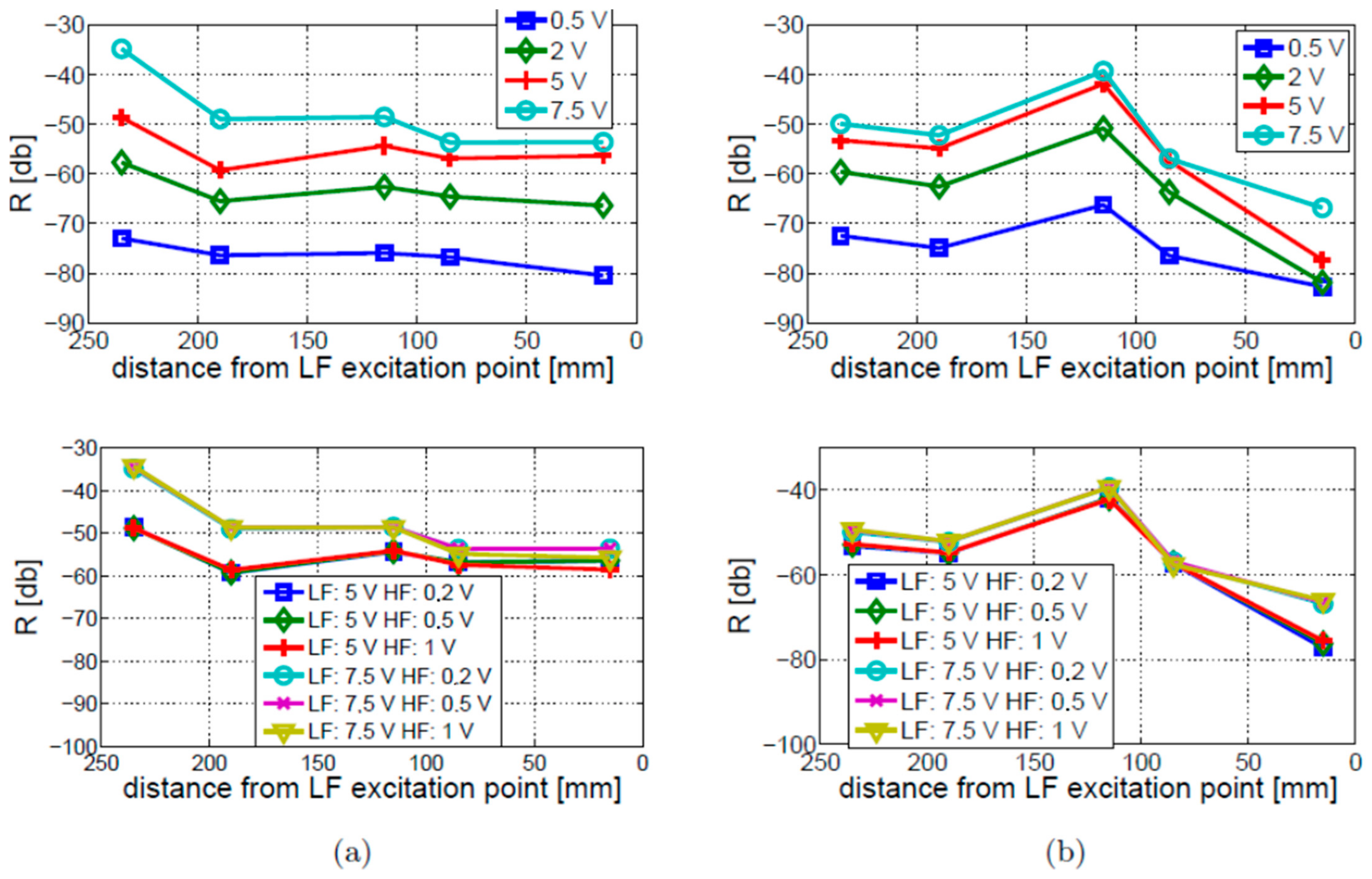
4.3. Excitation Amplitude
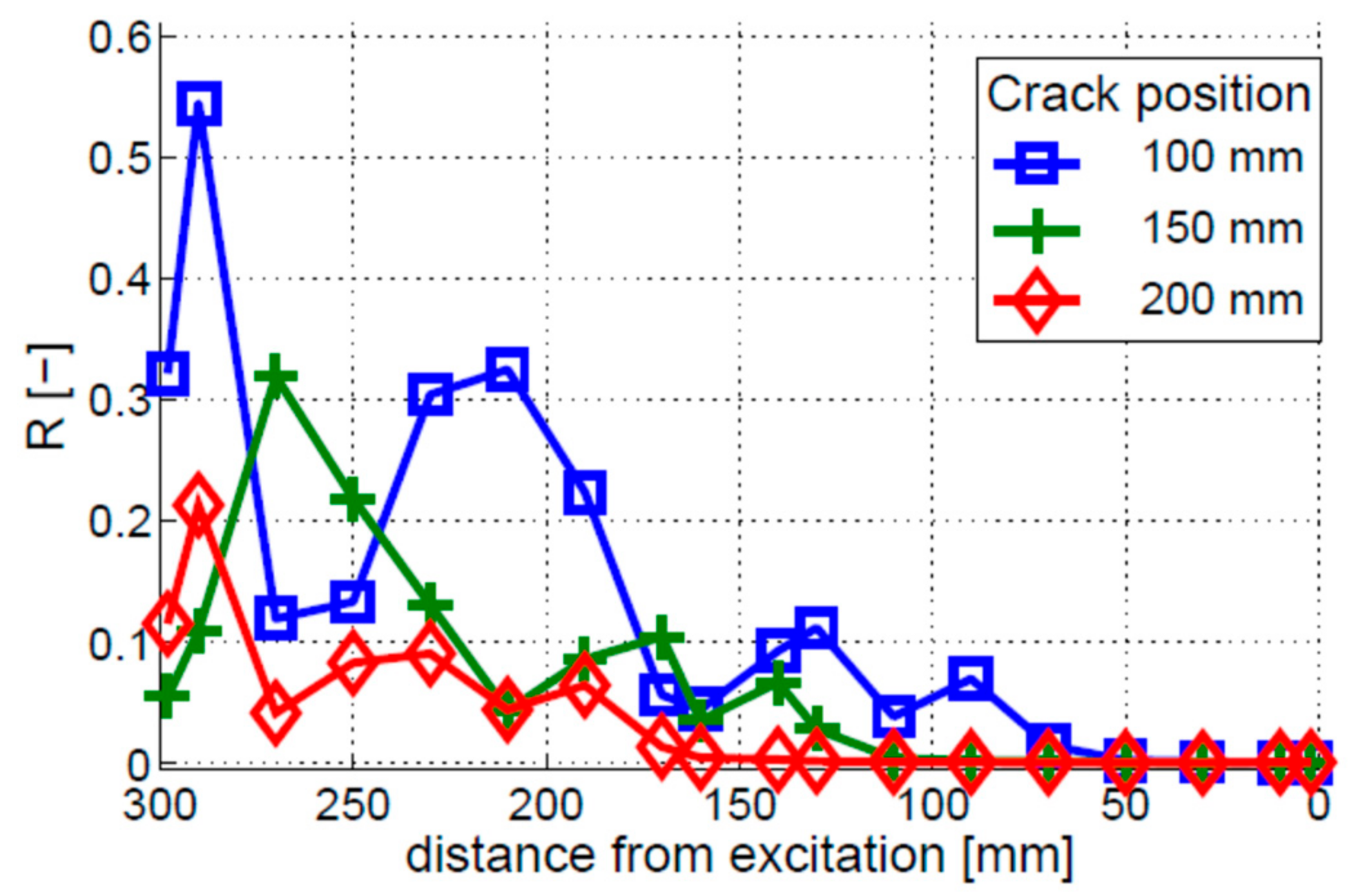
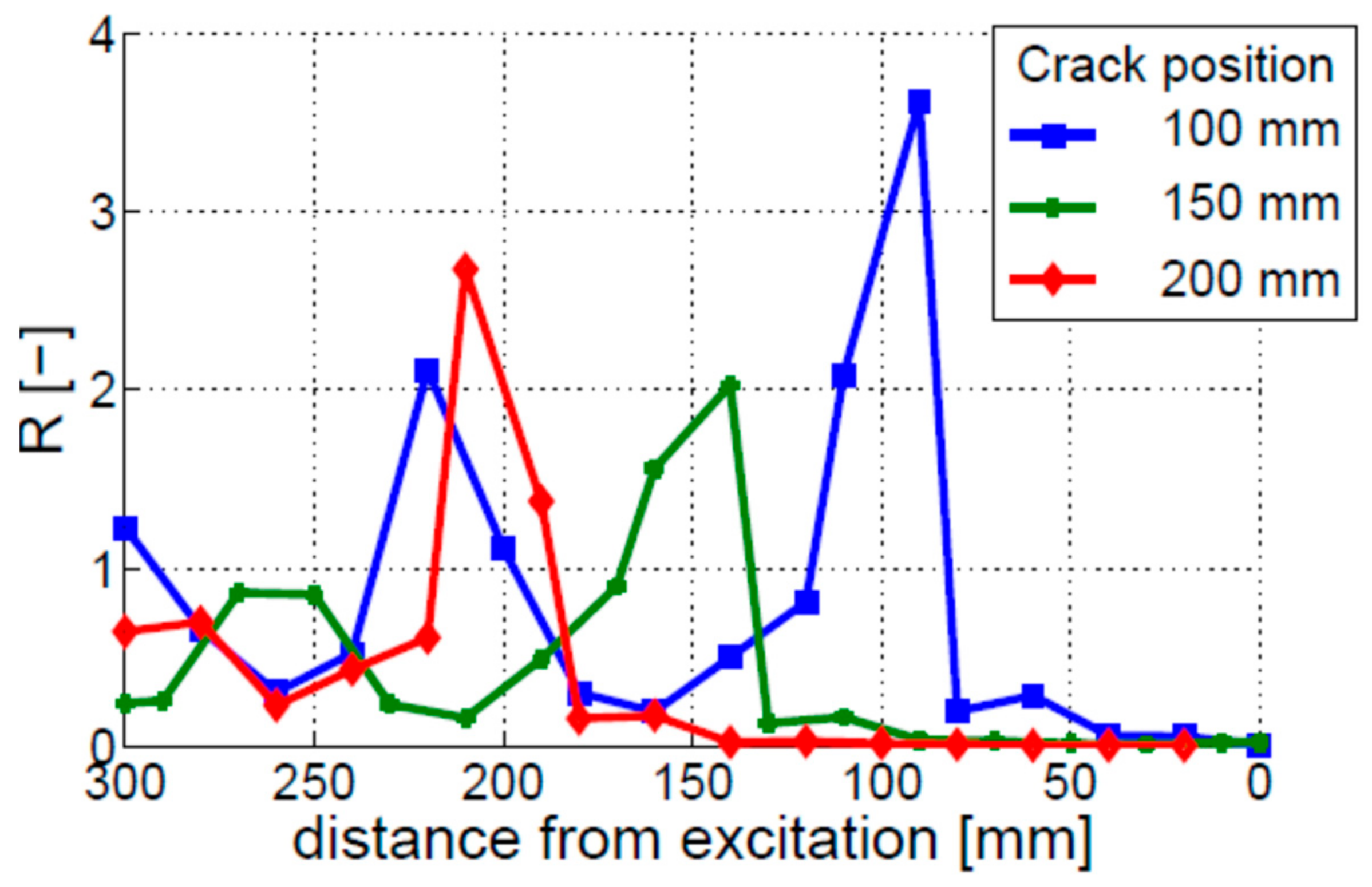
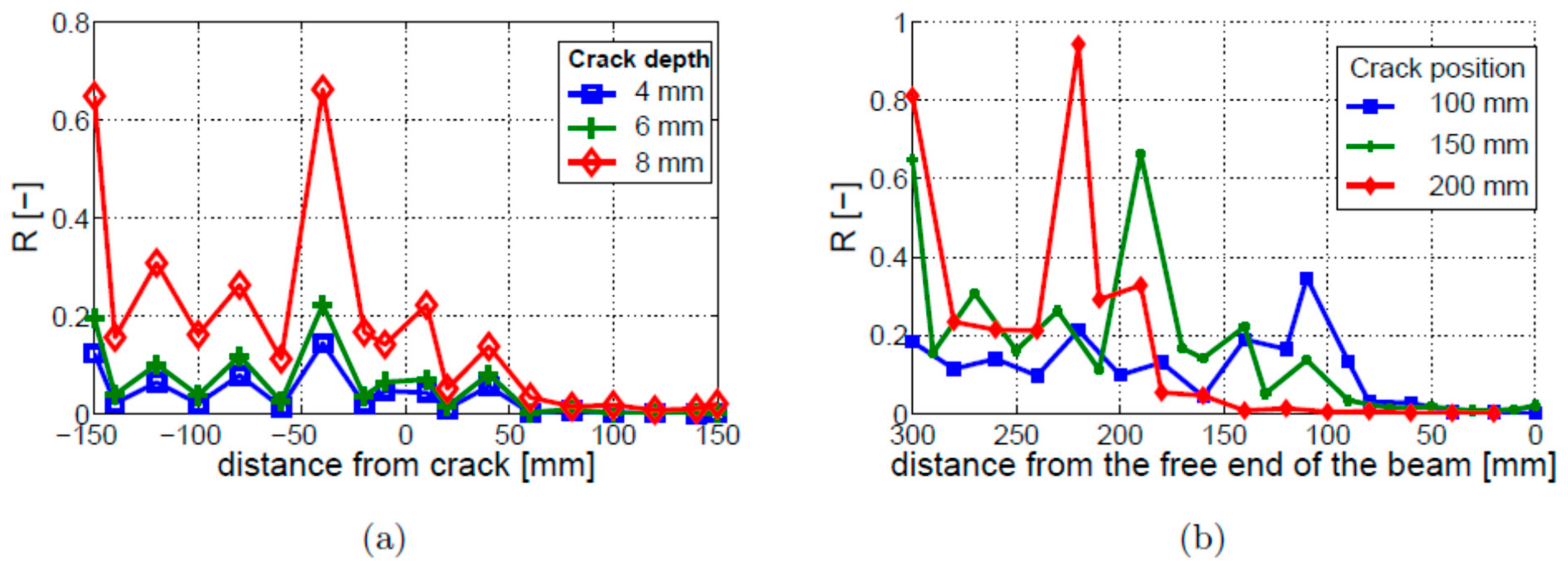
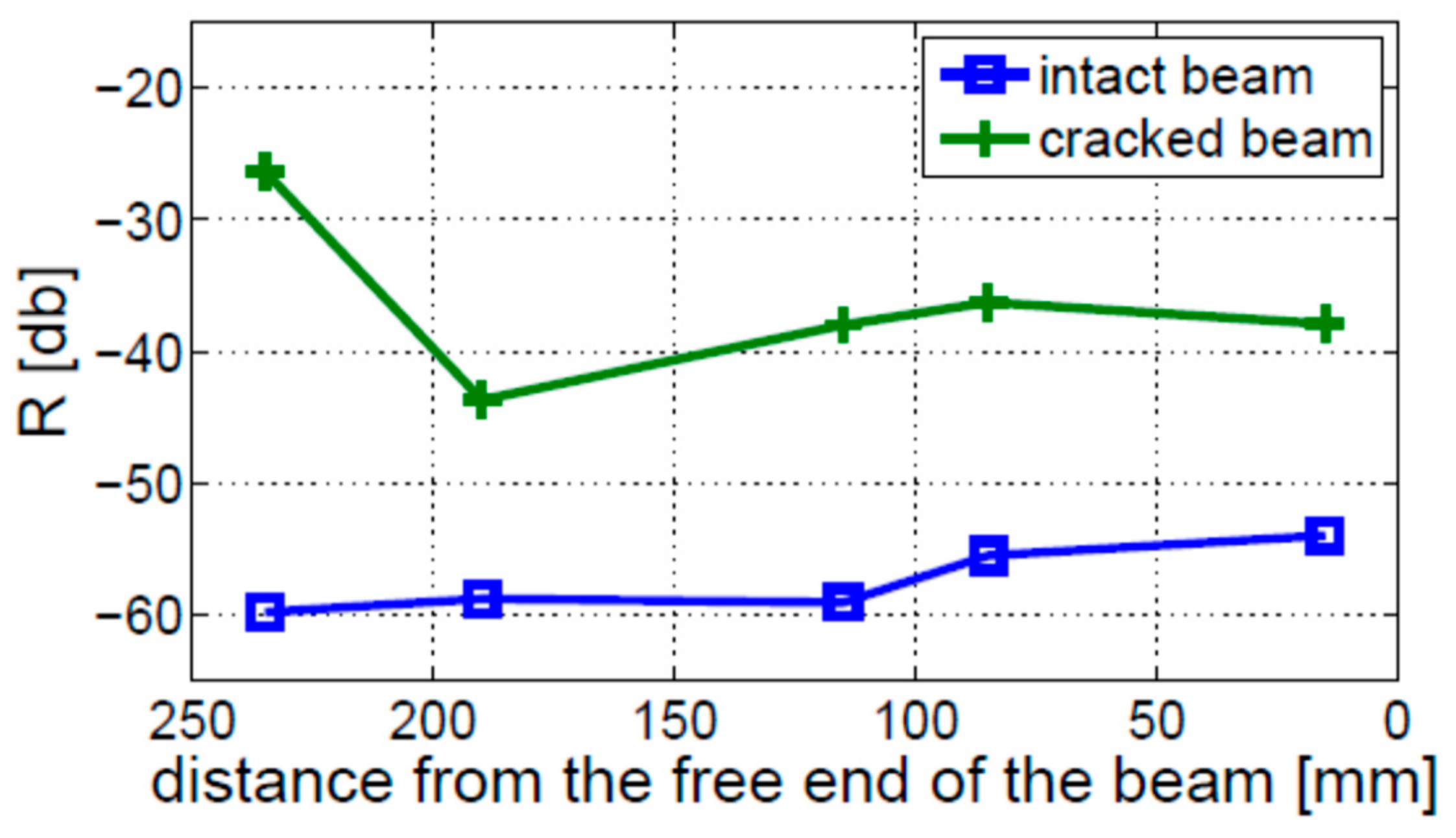
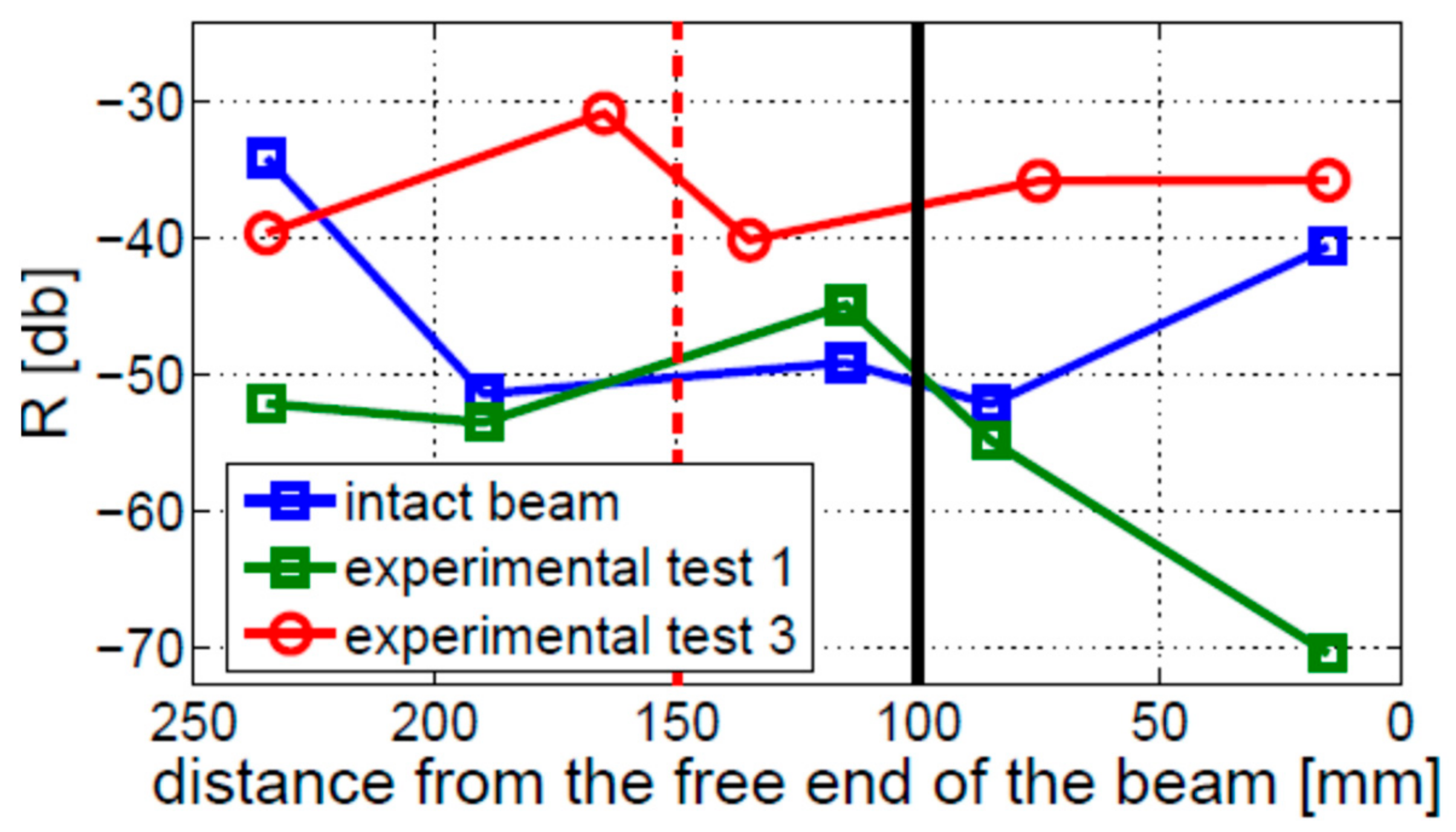
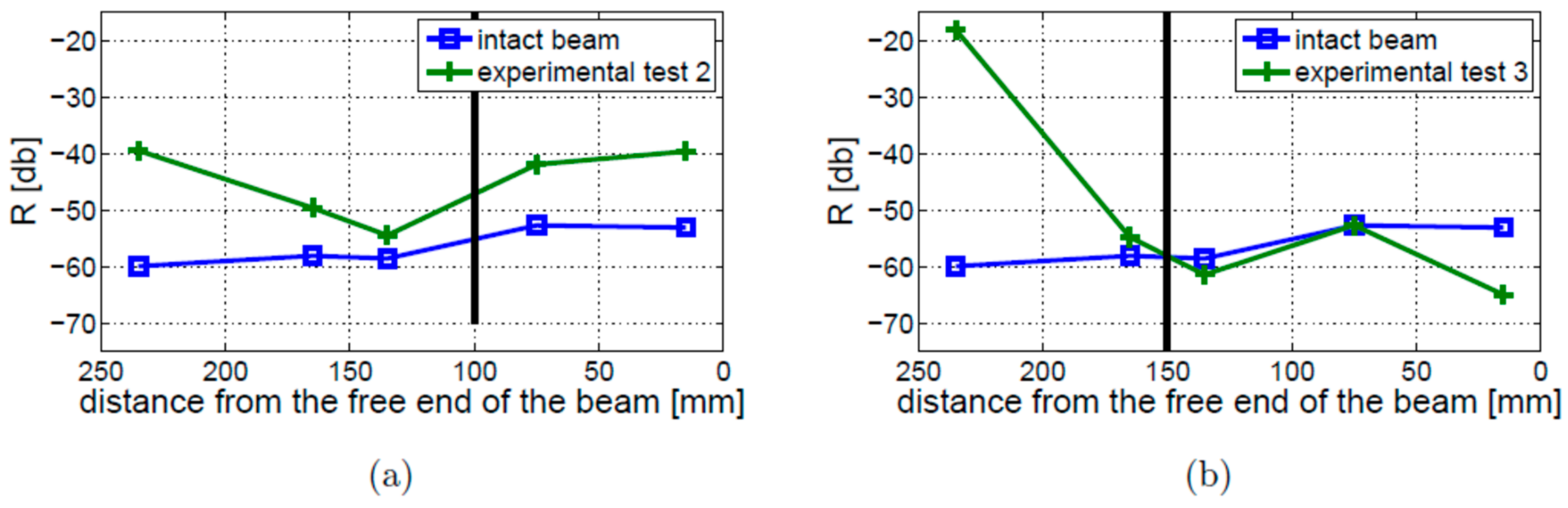
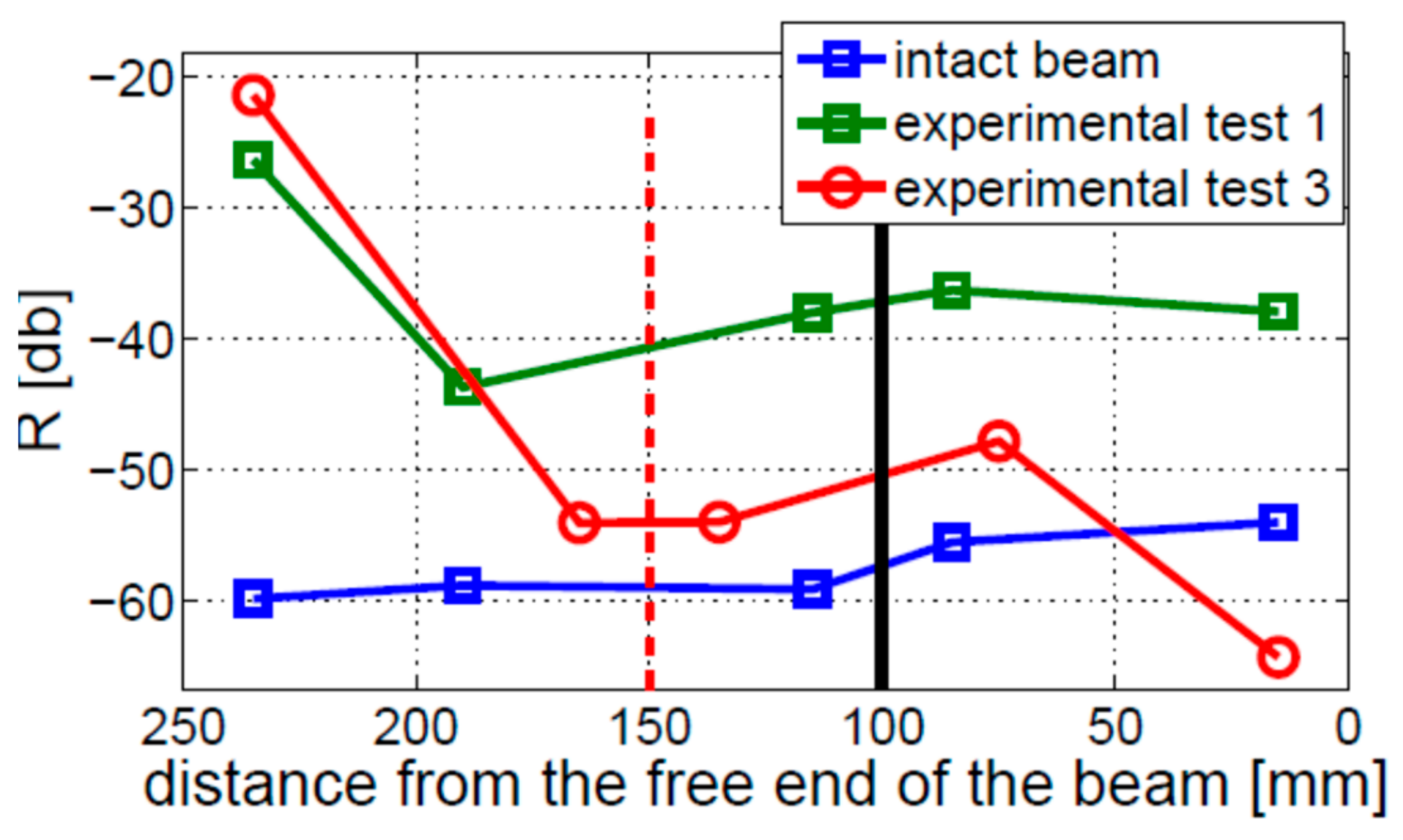
4.4. Crack Depth and Location
4.5. Summary of Experimental Results
- The amplitudes of the first two pairs of sidebands are similar. The free–free beam produces similar results compared to the fixed–free beam results in the repeatability tests.
- The values of the R coefficient are proportional to the LF vibration excitation amplitudes for the cracked and intact beams. However, the dependency of the R coefficient on the HF ultrasonic excitation amplitudes has not been found.
- The amplitude of modulation sidebands cannot be used reliably to detect cracks in beams with fixed–free boundary conditions, regardless of the crack size and position. In contrast, cracks can be detected for all investigated crack sizes and locations in beams with free–free boundary conditions.
- The crack localization effect was found in the beam with the fixed–free boundary conditions but not observed in the beams with free–free boundary conditions.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Breazeale, M.A.; Ford, J. Ultrasonic studies of the nonlinear behavior of solids. J. Appl. Phys. 1965, 36, 3486–3490. [Google Scholar] [CrossRef]
- Hikata, A.; Chick, B.B.; Elbaum, C. Dislocation contribution to the second harmonic generation of ultrasonic waves. J. Appl. Phys. 1965, 36, 229–236. [Google Scholar] [CrossRef]
- Krautkrämer, J.; Krautkrämer, H. Ultrasonic Testing of Materials; Springer Science & Business Media: Dordrecht, Germany, 2013. [Google Scholar]
- Boller, C.; Chang, F.; Fujino, Y. Encyclopedia of Structural Health Monitoring; John Wiley: New York, NY, USA, 2009. [Google Scholar]
- Herrmann, J.; Kim, J.-Y.; Jacobs, L.J.; Qu, J.; Littles, J.W.; Savage, M.F. Assessment of material damage in a nickel-base superalloy using nonlinear Rayleigh surface waves. J. Appl. Phys. 2006, 99, 124913. [Google Scholar] [CrossRef]
- Chillara, V.K.; Lissenden, C.J. Nonlinear guided waves in plates: A numerical perspective. Ultrasonics 2014, 54, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Radecki, R.; Su, Z.; Packo, P.; Staszewski, W.J. Modelling nonlinearity of guided ultrasonic waves in fatigued materials using a nonlinear local interaction simulation approach and a spring model. Ultrasonics 2017, 84, 272–289. [Google Scholar] [CrossRef]
- Shengbo, S.; Cheng, L. Mixed third harmonic shear horizontal wave generation: Interaction between primary shear horizontal wave and second harmonic Lamb wave. Smart Mater. Struct. 2019, 28, 085042. [Google Scholar]
- Delsanto, P.P. (Ed.) Universality of Nonclassical Nonlinearity: Applications to Non-Destructive Evaluations and Ultrasonics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gusev, V.; Tournat, V.; Castagnede, B. Nonlinear acoustic phenomena in micro-inhomogeneous media. In Materials and Acoustic Handbook; Potel, C., Bruneau, M., Eds.; ISTE Ltd.: London, UK, 2009. [Google Scholar]
- Stepinski, T.; Uhl, T.; Staszewski, W. Advanced Structural Damage Detection: From Theory to Engineering Applications; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Kundu, T. (Ed.) Nonlinear Ultrasonics and Vibro-Acoustical Techniques for Non-Destructive Evaluation; Springer: New York, NY, USA, 2019. [Google Scholar]
- Zaitsev, V.; Sutin, A.; Belyaeva, I.Y.; Nazarov, V. Nonlinear Interaction of Acoustical Waves Due to Cracks and Its Possible Usage for Cracks Detection. J. Vib. Control 1995, 1, 335–344. [Google Scholar] [CrossRef]
- Johnson, P.A. The New Wave in Acoustic Testing. Mater. World 1999, 7, 544–546. [Google Scholar]
- Van Den Abeele, K.; Johnson, P.; Sutin, A. Nonlinear elastic wave spectroscopy (NEWS) techniques to discern material damage, part I: Nonlinear wave modulation spectroscopy (NWMS). J. Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar] [CrossRef]
- Donskoy, D.; Sutin, A.; Ekimov, A. Nonlinear acoustic interaction on contact interfaces and its use for nondestructive testing. NDT E Int. 2001, 34, 231–238. [Google Scholar] [CrossRef]
- Pieczonka, L.; Klepka, A.; Martowicz, A.; Staszewski, W.J. Nonlinear vibro-acoustic wave modulations for structural damage detection: An overview. Opt. Eng. 2016, 55, 011005. [Google Scholar] [CrossRef]
- Pieczonka, L.; Zietek, L.; Klepka, A.; Staszewski, W.J.; Aymerich, F.; Uhl, T. Impact damage imaging in composites using nonlinear vibro-acoustic wave modulations. Struct. Control Health Monit. 2018, 25, e2063. [Google Scholar] [CrossRef]
- Dziedziech, K.; Pieczonka, L.; Kijanka, P.; Staszewski, W.J. Enhanced nonlinear crack-wave interactions for structural damage detection based on guided ultrasonic waves. Struct. Control Health Monit. 2016, 23, 1108–1120. [Google Scholar] [CrossRef]
- Karve, P.; Mahadevan, S. On the performance of vibro-acoustic-modulation-based diagnosis of breathing cracks in thick, elastic slabs. Struct. Control Health Monit. 2020, 27, e2470. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.; Martowicz, A.; Uhl, T.; Silberschmidt, V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Donskoy, D.; Liu, D. Vibro-acoustic modulation baseline-free non-destructive testing. J. Sound Vib. 2021, 492, 115808. [Google Scholar] [CrossRef]
- Dorendorf, L.; Lalkovski, N.; Rutner, M. Physical explanation for vibro-acoustic modulation due to local and global nonlinearities in a structure and its experimental and numerical validation. J. Sound Vib. 2022, 528, 116885. [Google Scholar] [CrossRef]
- Zaitsev, V.; Gusev, V.; Castagnede, B. Observation of the “Luxemburg–Gorky effect” for elastic waves. Ultrasonics 2002, 40, 627–631. [Google Scholar] [CrossRef]
- Klepka, A.; Staszewski, W.; Jenal, R.; Szwedo, M.; Iwaniec, J.; Uhl, T. Nonlinear acoustics for fatigue crack detection—Experimental investigations of vibro-acoustic wave modulations. Struct. Health Monit. 2012, 11, 197–211. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cim. 2001, 24, 1–46. [Google Scholar] [CrossRef]
- Solodov, I.; Wackerl, J.; Pfleiderer, K.; Busse, G. Nonlinear self-modulation and subharmonic acoustic spectroscopy for damage detection and location. Appl. Phys. Lett. 2004, 84, 5386–5388. [Google Scholar] [CrossRef]
- Solodov, I.; Döring, D.; Busse, G. New opportunities for NDT using non-linear interaction of elastic waves with defect. J. Mech. Eng. 2011, 57, 169–182. [Google Scholar] [CrossRef]
- Kober, J.; Prevorovsky, Z. Theoretical investigation of nonlinear ultrasonic wave modulation spectroscopy at crack interface. NDT E Int. 2014, 61, 10–15. [Google Scholar] [CrossRef]
- Alnutayfat, A.; Hassiotis, S.; Liu, D.; Sutin, A. Sideband Peak Count in a Vibro-Acoustic Modulation Method for Crack Detection. Acoustics 2022, 4, 74–86. [Google Scholar] [CrossRef]
- Li, Y.F.; Matar, O.B.; Li, B.S.; Chen, X. Pseudo-Spectral simulation of 1D nonlinear propagation in heterogeneous elastic media. Wave Motion 2015, 52, 54–65. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C.; Zhao, Y.; Hu, N.; Deng, M. Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave. Materials 2020, 13, 3318. [Google Scholar] [CrossRef]
- Nazarov, V.E.; Radostin, A.; Ostrovsky, L.; Soustova, I.A. Wave processes in media with hysteretic nonlinearity. Part I. Acoust. Phys. 2003, 49, 344–353. [Google Scholar] [CrossRef]
- Nazarov, V.E.; Radostin, A.V.; Ostrovsky, L.A.; Soustova, I.A. Wave processes in media with hysteretic nonlinearity: Part II. Acoust. Phys. 2003, 49, 444–448. [Google Scholar] [CrossRef]
- Guyer, R.A.; McCall, K.R.; Boitnott, G.N. Hysteresis, Discrete Memory, and Nonlinear Wave Propagation in Rock: A New Paradigm. Phys. Rev. Lett. 1995, 74, 3491–3494. [Google Scholar] [CrossRef]
- Osika, M.; Radecki, R.; Ziaja-Sujdak, A.; Staszewski, W.J. An insight into amplitude-depended modulation transfer due to nonlinear shear wave interaction with contact interfaces. In Proceedings of the 16th International Conference Dynamical Systems—Theory and Application (DSTA), Lodz, Poland, 6–9 December 2021; pp. 535–536. [Google Scholar]
- Radecki, R.; Ziaja-Sujdak, A.; Osika, M.; Staszewski, W.J. Numerical and theoretical investigations of modulation transfer due to nonlinear shear interaction at frictional interfaces. In Proceedings of the 16th International Conference Dynamical Systems—Theory and Application (DSTA), Lodz, Poland, 6–9 December 2021; pp. 537–538. [Google Scholar]
- Martowicz, A.; Packo, P.; Staszewski, W.J.; Uhl, T. Modelling of nonlinear vibro-acoustic wave interaction in cracked aluminium plates using local interaction simulation approach. In Proceedings of the ECCOMAS 2012, Vienna, Austria, 10–14 September 2012. [Google Scholar]
- Martowicz, A.; Ruzzene, M.; Staszewski, W.J. Non-local modeling and simulation of wave propagation and crack growth. In Proceedings of the 40th Annual Review of Progress in Quantitative Nondestructive Evaluation, Baltimore, MD, USA, 21–26 July 2013; AIP Publishing: New York, NY, USA, 2014; Volume 33A, pp. 513–520. [Google Scholar]
- Martowicz, A.; Staszewski, W.J.; Ruzzene, M.; Uhl, T. Vibroacoustic wave interaction in cracked plate modeled with peridynamics. In Proceedings of the 11th World Congress on Computational Mechanics (WCCM XI), Barcelona, Spain, 20–25 July 2014; pp. 1–2. [Google Scholar]
- Malfense Fierro, G.P.; Ciampa, F.; Meo, M. Phase symmetry analysis for nonlinear ultrasonic modulated signals. Struct. Control Health Monit. 2020, 27, e2516. [Google Scholar] [CrossRef]
- Hexagon, A.B. Marc Advanced Nonlinear Simulation Solution. Available online: https://hexagon.com/products/marc (accessed on 2 January 2023).
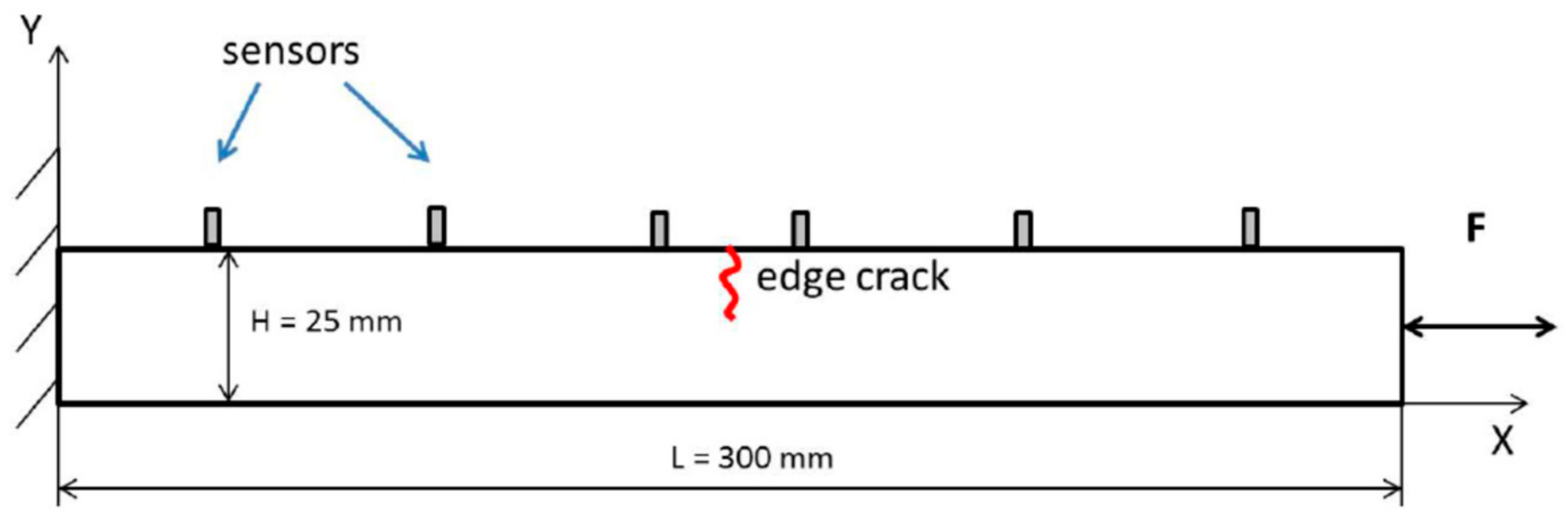




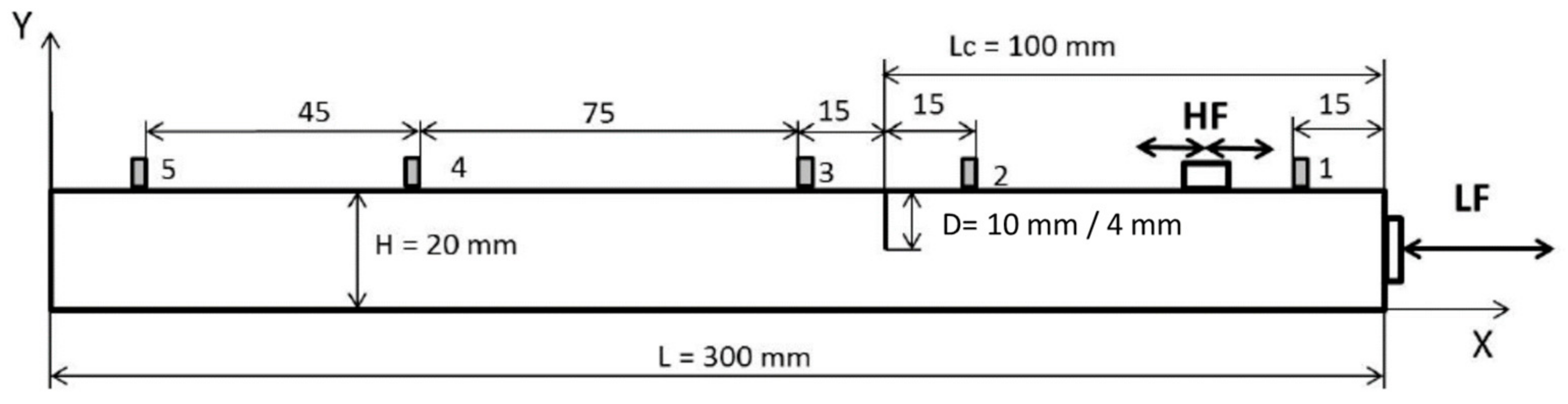

| Experimental Test | Crack Depth [mm] | Crack Position [mm] |
|---|---|---|
| Test 1 | 10 | 100 |
| Test 2 | 4 | 100 |
| Test 3 | 10 | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Broda, D.; Mendrok, K.; Silberschmidt, V.V.; Pieczonka, L.; Staszewski, W.J. The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation. Materials 2023, 16, 1653. https://doi.org/10.3390/ma16041653
Broda D, Mendrok K, Silberschmidt VV, Pieczonka L, Staszewski WJ. The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation. Materials. 2023; 16(4):1653. https://doi.org/10.3390/ma16041653
Chicago/Turabian StyleBroda, Dariusz, Krzysztof Mendrok, Vadim V. Silberschmidt, Lukasz Pieczonka, and Wieslaw J. Staszewski. 2023. "The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation" Materials 16, no. 4: 1653. https://doi.org/10.3390/ma16041653
APA StyleBroda, D., Mendrok, K., Silberschmidt, V. V., Pieczonka, L., & Staszewski, W. J. (2023). The Study of Localized Crack-Induced Effects of Nonlinear Vibro-Acoustic Modulation. Materials, 16(4), 1653. https://doi.org/10.3390/ma16041653










