Measuring and Predicting the Effects of Residual Stresses from Full-Field Data in Laser-Directed Energy Deposition
Abstract
1. Introduction
2. Aim and Structure of the Approach
3. Materials and Methods
3.1. Thermal Expansion Coefficient
3.2. Incremental Hole Drilling
4. Stochastic Modeling and Optimization
4.1. Evaluation of the Thermal Expansion Coefficient
4.1.1. Development of the Metamodel
4.1.2. Numerical Modeling of Thin-Wall Specimens
4.1.3. Results
4.2. Stochastic Modeling of the Displacement Field for Incremental Hole Drilling
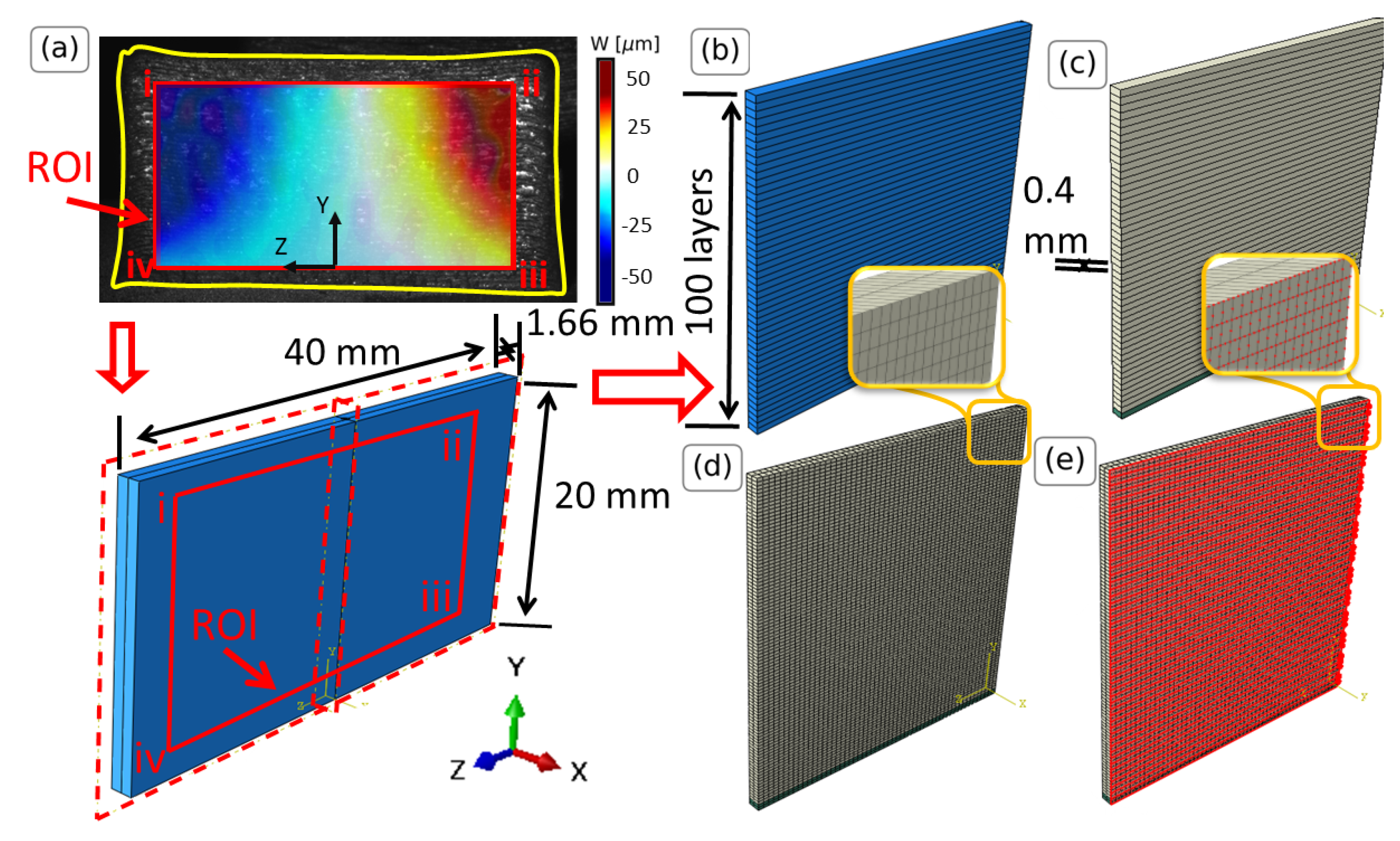
4.2.1. Numerical Modeling of the Incremental Hole Drilling
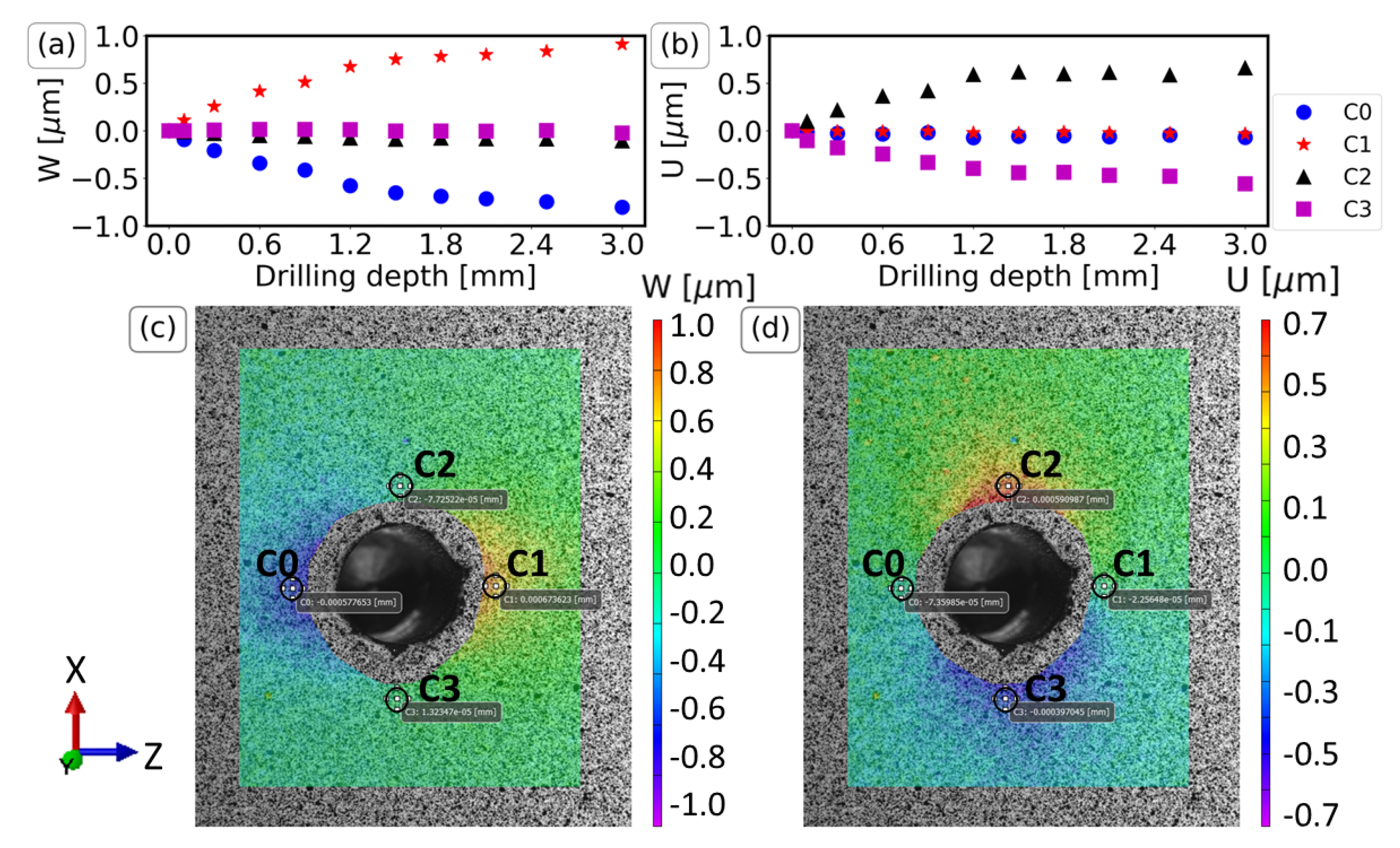
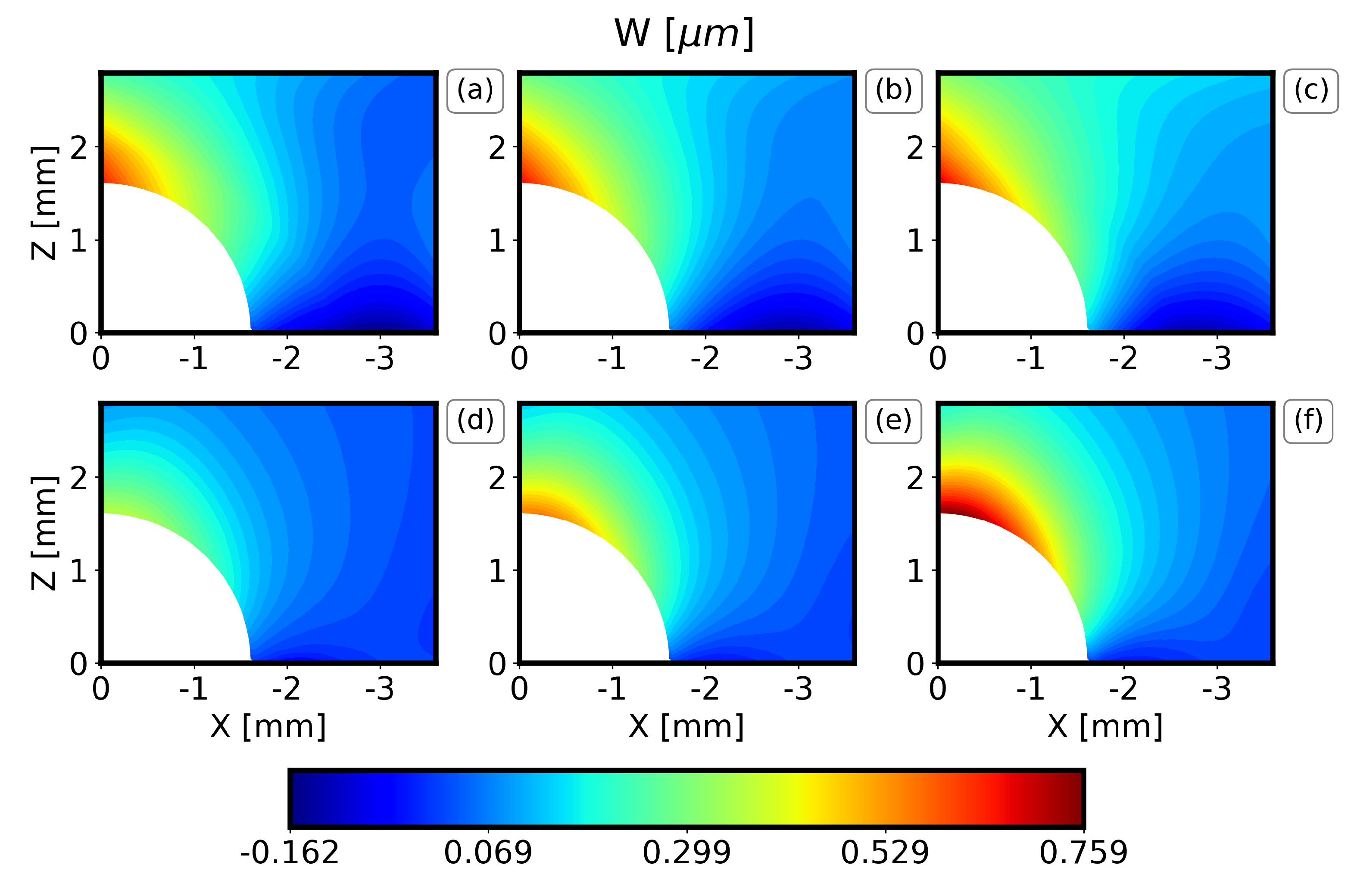
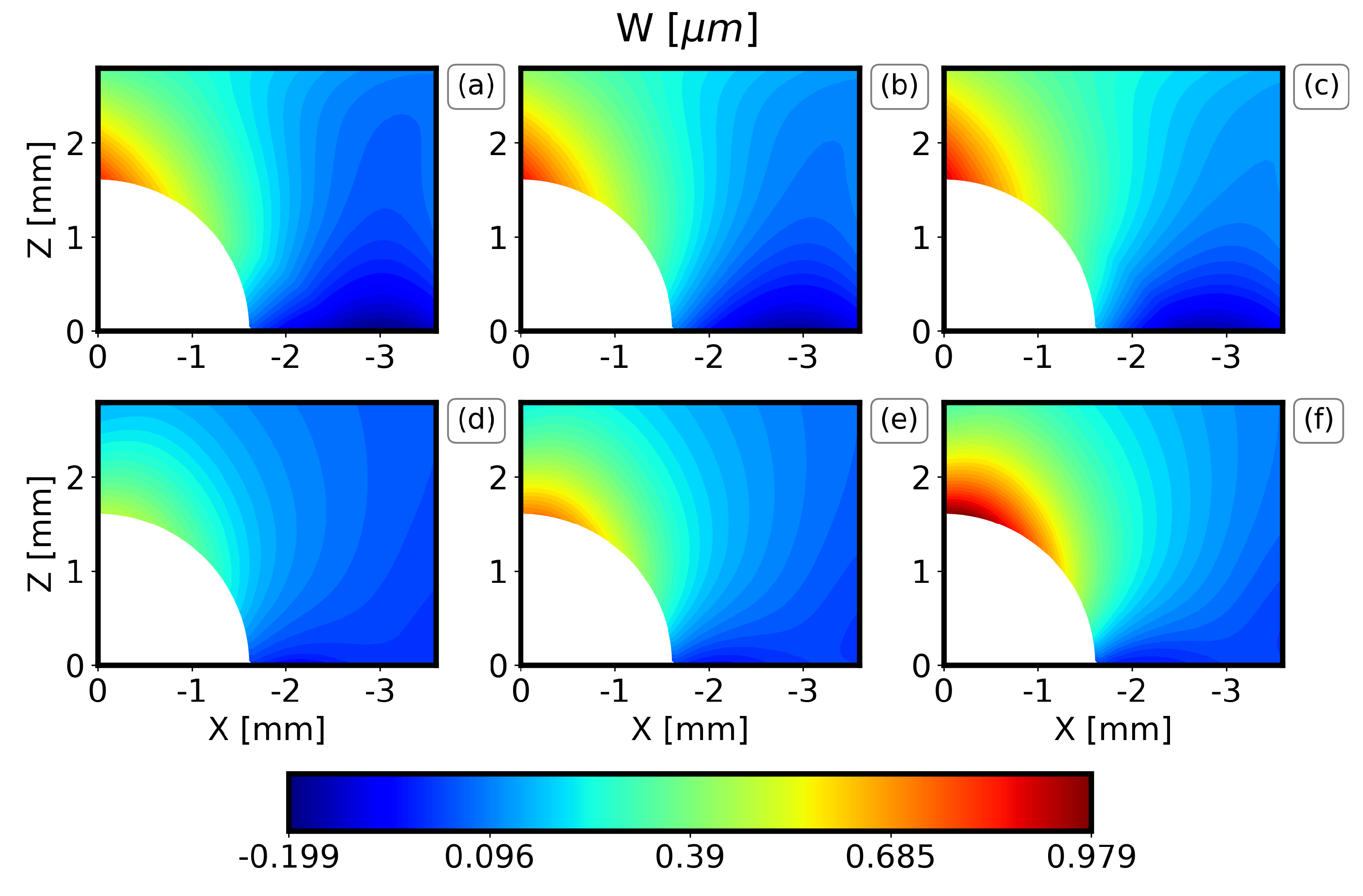
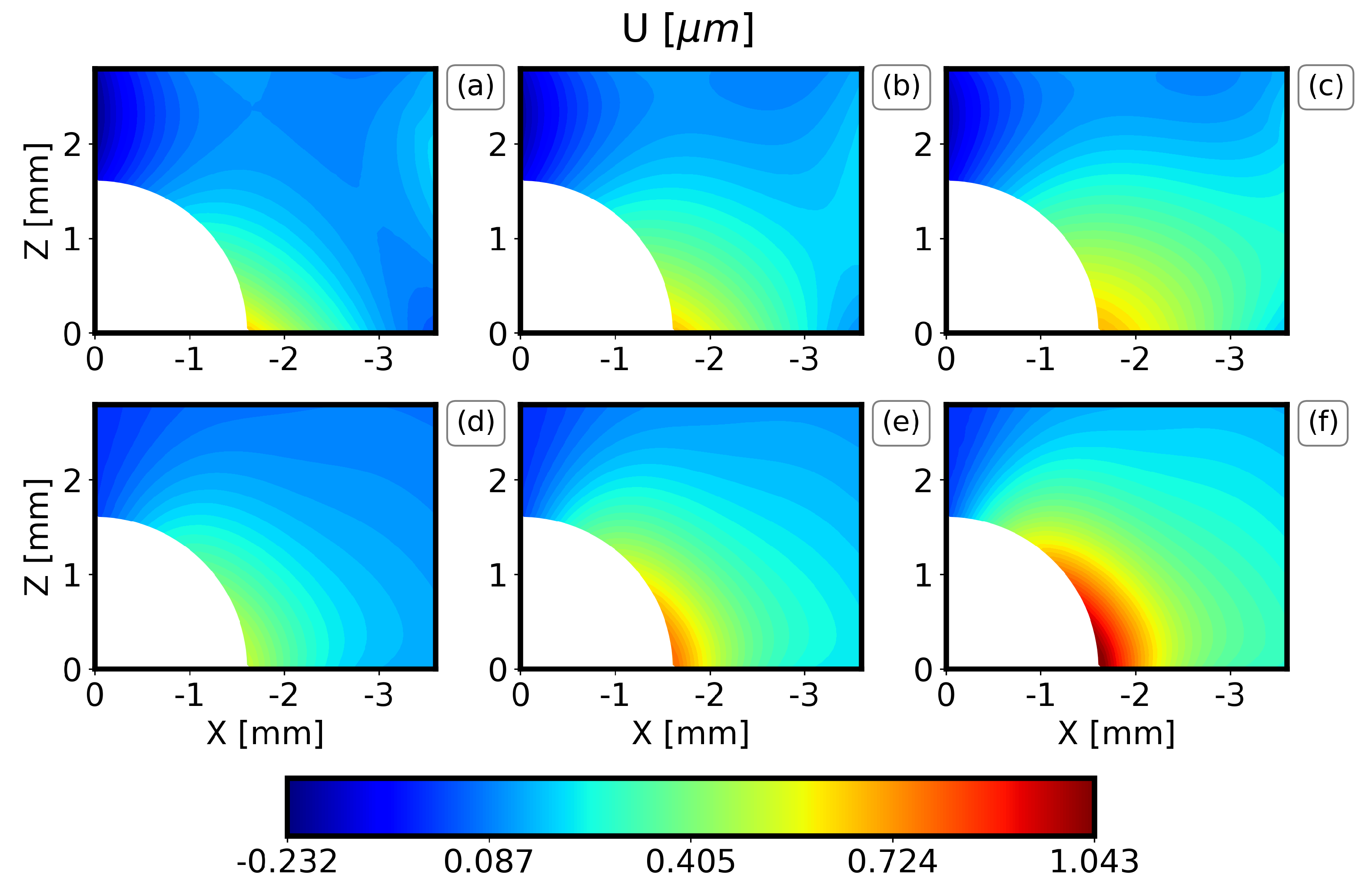
4.2.2. Results of the Displacement Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Thompson, S.M.; Bian, L.; Shamsaei, N.; Yadollahi, A. An overview of Direct Laser Deposition for additive manufacturing; Part I: Transport phenomena, modeling and diagnostics. Addit. Manuf. 2015, 8, 36–62. [Google Scholar]
- Arias-González, F.; Barro, O.; del Val, J.; Lusquiños, F.; Fernández-Arias, M.; Comesaña, R.; Riveiro, A.; Pou, J. Chapter 4—Laser-directed energy deposition: Principles and applications. In Additive Manufacturing; Pou, J., Riveiro, A., Davim, J.P., Eds.; Handbooks in Advanced Manufacturing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 121–157. [Google Scholar] [CrossRef]
- Shamsaei, N.; Yadollahi, A.; Bian, L.; Thompson, S.M. An overview of Direct Laser Deposition for additive manufacturing; Part II: Mechanical behavior, process parameter optimization and control. Addit. Manuf. 2015, 8, 12–35. [Google Scholar]
- Beuth, J.; Klingbeil, N. The role of process variables in laser-based direct metal solid freeform fabrication. JOM 2001, 53, 36–39. [Google Scholar]
- Polyzos, E.; Van Hemelrijck, D.; Pyl, L. Analytical model for the estimation of the hygrothermal residual stresses in generally layered laminates. Eng. Fract. Mech. 2021, 247, 107667. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar]
- Liang, X.; Cheng, L.; Chen, Q.; Yang, Q.; To, A.C. A modified method for estimating inherent strains from detailed process simulation for fast residual distortion prediction of single-walled structures fabricated by directed energy deposition. Addit. Manuf. 2018, 23, 471–486. [Google Scholar]
- Liang, X.; Chen, Q.; Cheng, L.; Hayduke, D.; To, A.C. Modified inherent strain method for efficient prediction of residual deformation in direct metal laser sintered components. Comput. Mech. 2019, 64, 1719–1733. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Huang, W. In situ measurements and thermo-mechanical simulation of Ti–6Al–4V laser solid forming processes. Int. J. Mech. Sci. 2019, 153, 119–130. [Google Scholar]
- Gouge, M.; Denlinger, E.; Irwin, J.; Li, C.; Michaleris, P. Experimental validation of thermo-mechanical part-scale modeling for laser powder bed fusion processes. Addit. Manuf. 2019, 29, 100771. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Croom, B.P.; Burdick, J.; Henkel, D.; Li, X. Revealing mechanisms of residual stress development in additive manufacturing via digital image correlation. Addit. Manuf. 2018, 22, 1–12. [Google Scholar] [CrossRef]
- Wu, Q.; Mukherjee, T.; Liu, C.; Lu, J.; DebRoy, T. Residual stresses and distortion in the patterned printing of titanium and nickel alloys. Addit. Manuf. 2019, 29, 100808. [Google Scholar]
- Lord, J.D.; Penn, D.; Whitehead, P. The application of digital image correlation for measuring residual stress by incremental hole drilling. Appl. Mech. Mater. 2008, 13, 65–73. [Google Scholar] [CrossRef]
- Carpenter Additive. PowderRange 316L Datasheet. 2020. Available online: https://www.carpenteradditive.com/hubfs/Resources/Data%20Sheets/PowderRange_316L_Datasheet.pdf (accessed on 10 January 2023).
- Polyzos, E.; Pyl, L. Stochastic analytical and numerical modelling of interface stressses for generally layered 3D-printed composites. In Proceedings of the 20th European Conference on Composite Mechanics, Lausanne, Switzerland, 26–30 June 2022; pp. 320–328. [Google Scholar]
- Hinderdael, M.; Ertveldt, J.; Jardon, Z.; Pyl, L.; Guillaume, P. Residual stress characterization during laser-based Directed Energy Deposition using in-situ Digital Image Correlation based on specular light reflection on as-built surfaces of thin walls. In Proceedings of the Procedia-CIRP, 12th CIRP Conference on Photonic Technologies (LANE 2022), Fürth, Germany, 4–8 September 2022. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sudret, B. Polynomial chaos expansions and stochastic finite element methods. In Risk and Reliability in Geotechnical Engineering; CRC: Boca Raton, FL, USA, 2014; pp. 265–300. [Google Scholar]
- Polyzos, E.; Katalagarianakis, A.; Van Hemelrijck, D.; Pyl, L. Delamination analysis of 3D-printed nylon reinforced with continuous carbon fibers. Addit. Manuf. 2021, 46, 102144. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series; Cambridge University Press: Cambridge, UK, 2004; Volume 96. [Google Scholar]
- Gil, A.; Segura, J.; Temme, N.M. Numerical Methods for Special Functions; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Merriman, M. A List of Writings Relating to the Method of Least Squares: With Historical and Critical Notes; Academy: Cambridge, MA, USA, 1877; Volume 4. [Google Scholar]
- Feinberg, J.; Petter, H. Chaospy: An open source tool for designing methods of uncertainty quantification. J. Comput. Sci. 2015, 11, 46–57. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2009. [Google Scholar]
- Hagart-Alexander, C. Chapter 21—Temperature Measurement. In Instrumentation Reference Book, 4th ed.; Boyes, W., Ed.; Butterworth-Heinemann: Boston, MA, USA, 2010; pp. 269–326. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.; He, Y. Deformation Prediction and Experimental Study of 316L Stainless Steel Thin-Walled Parts Processed by Additive-Subtractive Hybrid Manufacturing. Materials 2021, 14, 5582. [Google Scholar]
- Mackey, G.W. Harmonic analysis as the exploitation of symmetry—A historical survey. Bull. Am. Math. Soc. 1980, 3, 543–698. [Google Scholar] [CrossRef]





| L1 Metamodel | (10C) | (10C) |
|---|---|---|
| ML | 13.91 ± 2.06 | 17.04 ± 0.30 |
| PC | 13.76 ± 2.97 | 15.01 ± 1.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polyzos, E.; Pulju, H.; Mäckel, P.; Hinderdael, M.; Ertveldt, J.; Van Hemelrijck, D.; Pyl, L. Measuring and Predicting the Effects of Residual Stresses from Full-Field Data in Laser-Directed Energy Deposition. Materials 2023, 16, 1444. https://doi.org/10.3390/ma16041444
Polyzos E, Pulju H, Mäckel P, Hinderdael M, Ertveldt J, Van Hemelrijck D, Pyl L. Measuring and Predicting the Effects of Residual Stresses from Full-Field Data in Laser-Directed Energy Deposition. Materials. 2023; 16(4):1444. https://doi.org/10.3390/ma16041444
Chicago/Turabian StylePolyzos, Efstratios, Hendrik Pulju, Peter Mäckel, Michael Hinderdael, Julien Ertveldt, Danny Van Hemelrijck, and Lincy Pyl. 2023. "Measuring and Predicting the Effects of Residual Stresses from Full-Field Data in Laser-Directed Energy Deposition" Materials 16, no. 4: 1444. https://doi.org/10.3390/ma16041444
APA StylePolyzos, E., Pulju, H., Mäckel, P., Hinderdael, M., Ertveldt, J., Van Hemelrijck, D., & Pyl, L. (2023). Measuring and Predicting the Effects of Residual Stresses from Full-Field Data in Laser-Directed Energy Deposition. Materials, 16(4), 1444. https://doi.org/10.3390/ma16041444





