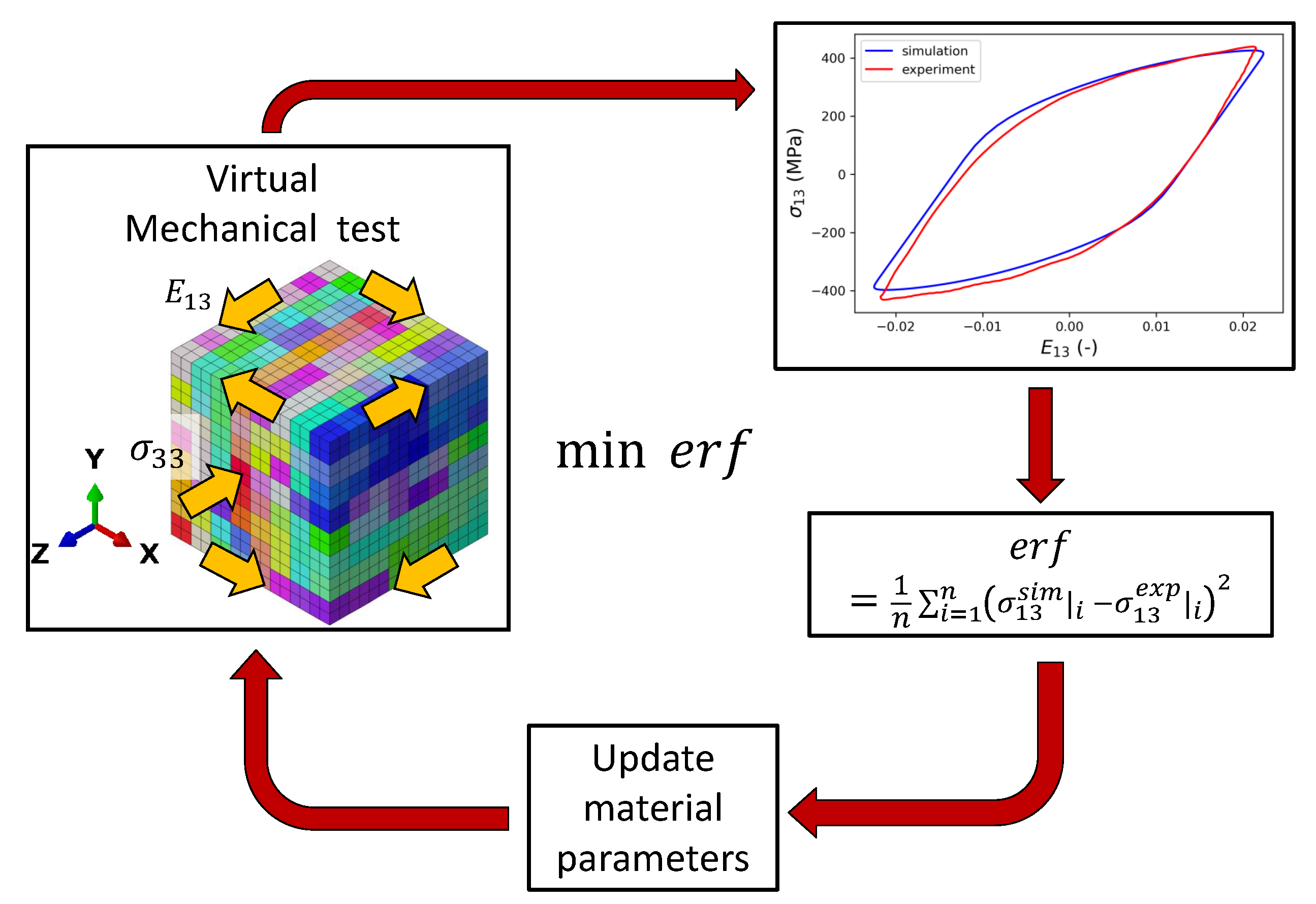
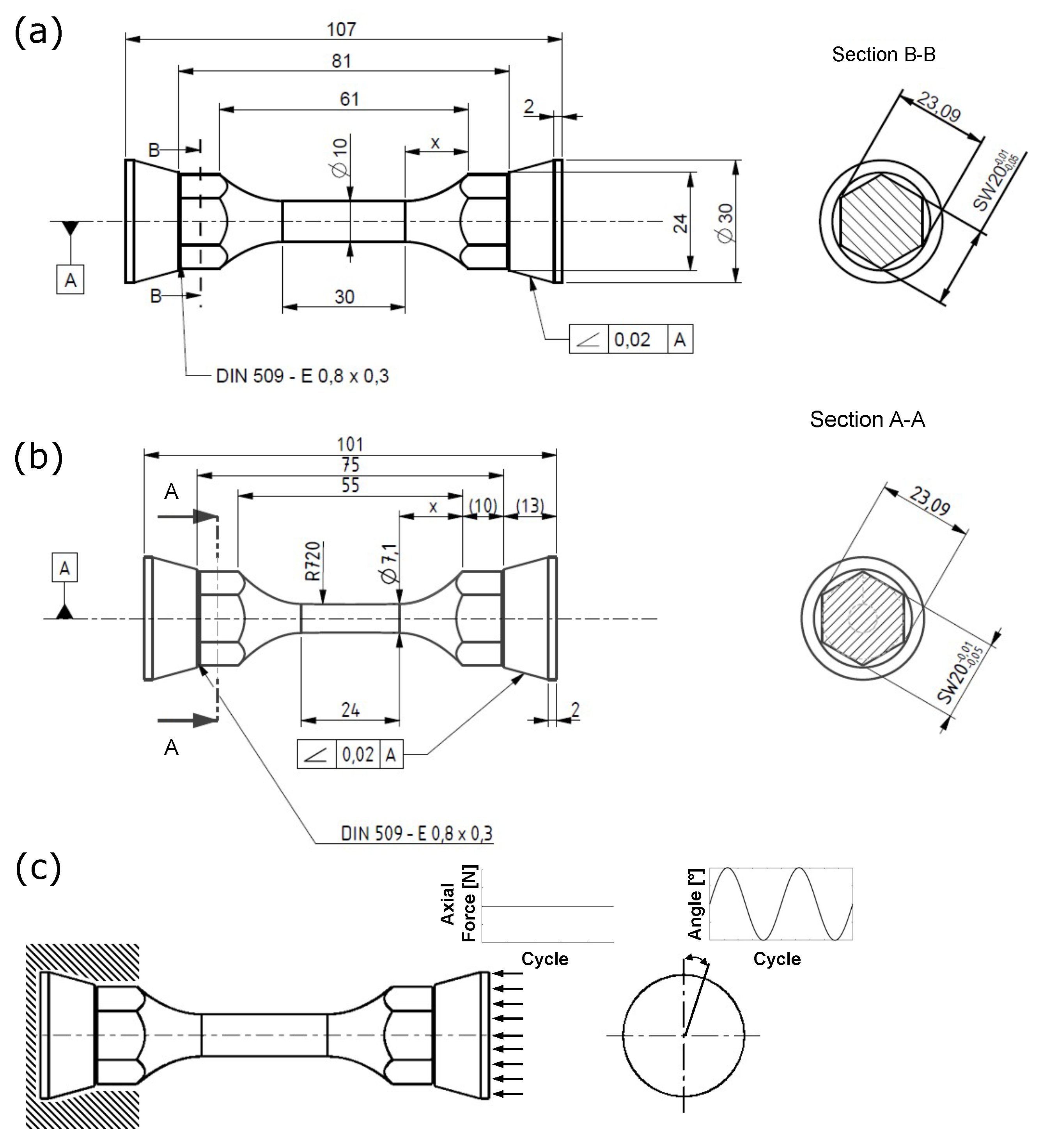
In this section, the results obtained from numerical models are compared with experimental findings. Due to the multiaxial and heterogeneous stress and strain fields in the gauge section of the specimens, the material parameters cannot be assessed directly from the results of the HPTF test, but the constitutive parameters for J2 and CPFE model must be obtained using an inverse procedure instead, as shown in
Appendix C. In the first step, a FE model of the gauge section of the test specimens is applied to characterize the material response under HPTF loading using a J2/von Mises plasticity model with Chaboche kinematic hardening and isotropic softening. In the second step, a representative volume element (RVE) is introduced that considers the mean grain size and crystallographic texture resulting from the EBSD analysis of the tested specimens, as described above. In FE simulations of this RVE, boundary conditions are applied that mimic the HPTF loading on a volume element close to the surface of the gauge section of the experimental specimens. The plastic deformation of each grain in the RVE is described by the CP model introduced above. It is noted here that in the present study, we do not attempt to model the grain shapes or even microstructural details as annealing twins, but we focus on the determination of the material parameters, which requires the use of a numerically efficient model. Furthermore, a parametric study of the CP kinematic hardening parameters is shown in
Appendix A, emphasizing the importance of axial creep experiments for the calibration of parameters.
4.1. J2 Plasticity
The parameters for the J2 model are calibrated using data from uniaxial fatigue experiments. The parameters controlling the stress–strain hysteresis loop, i.e., , , , and , are obtained in an iterative process in which the difference between experimental and numerical hysteresis loops are minimized by systematically varying those material parameters. For this purpose, a representative hysteresis loop is chosen from the regime of load cycles in which the mean stress has already saturated. In contrast, the isotropic softening parameters, i.e., , Q, and b, are gained from the comparison of the maximum stress obtained during each load cycle between simulation and experiment. To obtain the hysteresis loop in the regime where the amplitude is constant, the experimental hysteresis loop from the 5000th cycle is used for calibration of the kinematic hardening parameters. The isotropic softening parameters are calibrated by simulating the initial 300 cycles.
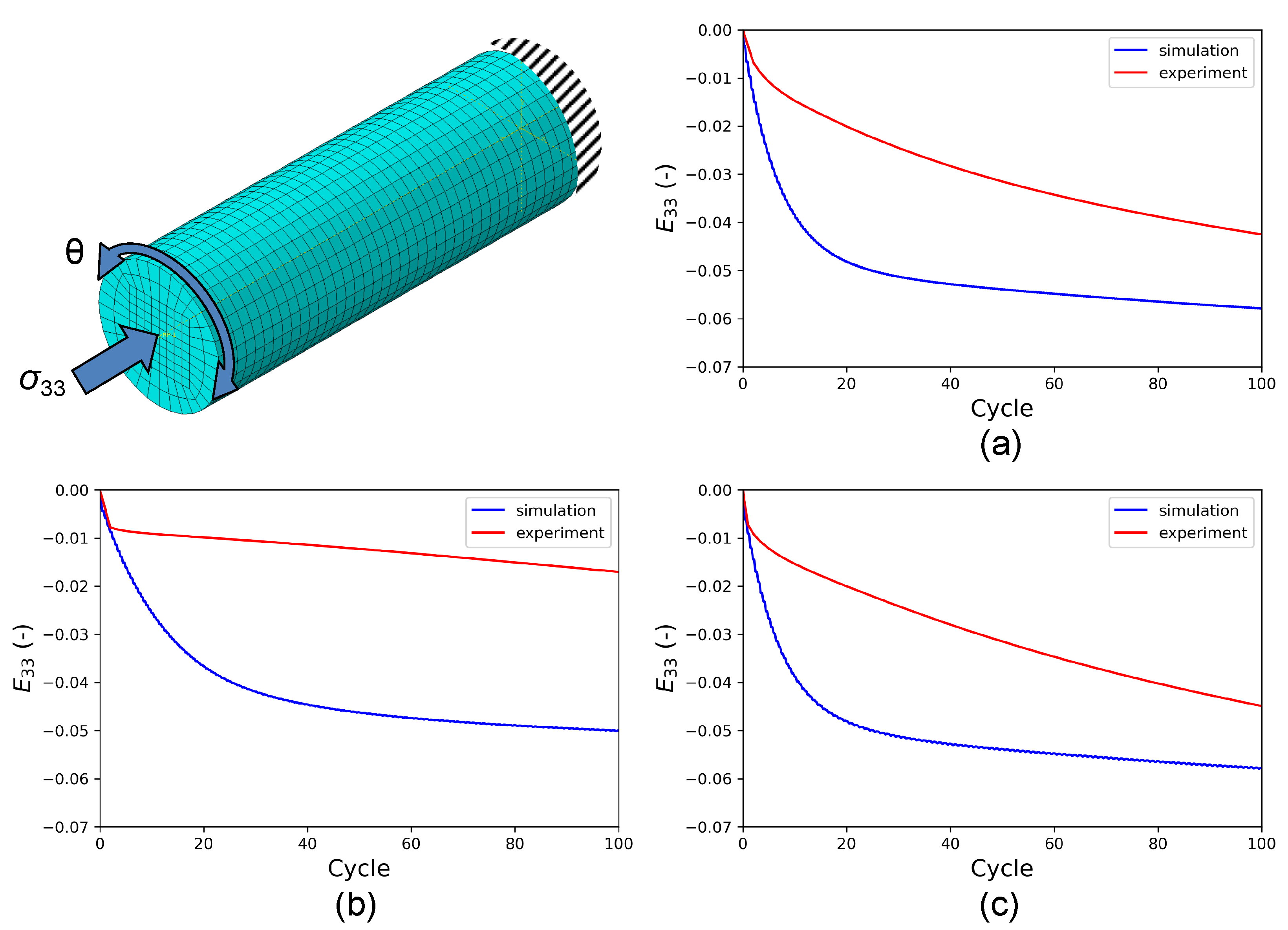
Figure 6 shows the comparison of the saturated hysteresis, i.e., the hysteresis loop in the regime where the stress amplitude is constant, and the maximum stress obtained from simulation and experiments; the corresponding calibrated J2 material parameters are given in
Table 4.
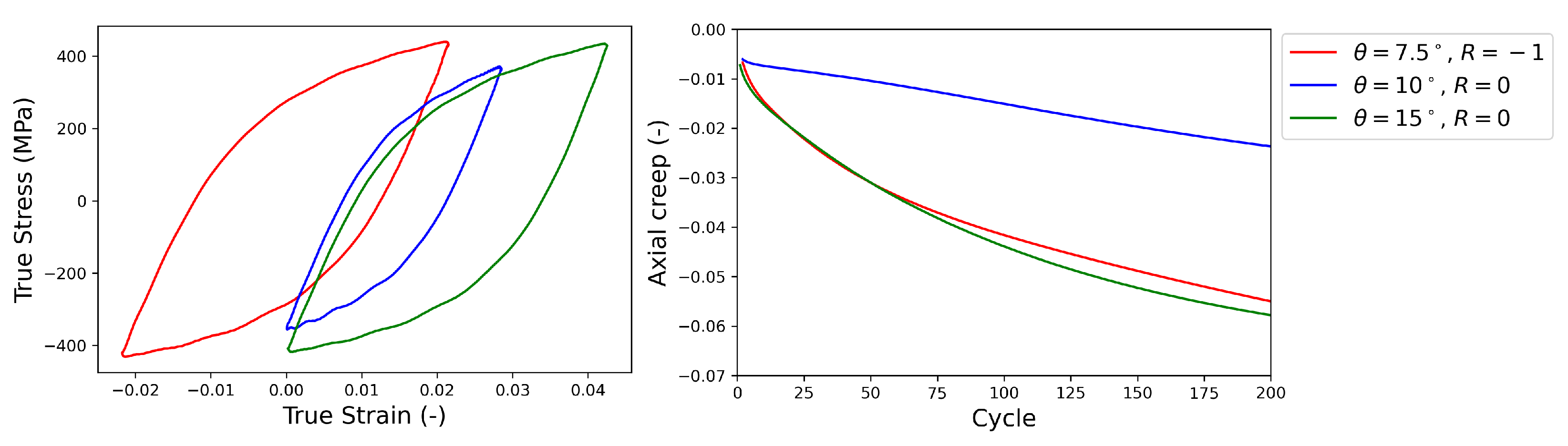
Keeping the J2 material parameters constant, HPTF simulations are performed with the same FE model, see
Figure 7, in which the resulting axial creep strain
obtained from the experiment and the HPTF simulations also are shown. It is seen that the simulations result in a similar axial creep behavior under different HPTF loading conditions, which stands in stark contrast to the experiment where the axial creep behavior is very sensitive to the torsional loading. Furthermore, the axial creep strains obtained from the FE simulations with material parameters fitted to uniaxial fatigue experiments grossly overestimate the experimentally found creep strains under HPTF loading, which points out the limitations of the J2 plasticity model. The reason for these deficits in the J2 model in predicting the axial creep behavior correctly can be attributed to the associated flow rule used here, see Equation (
7), where the plastic strain increment is proportional to the deviatoric stress reduced by the back stress. Hence, as long as constant stress is applied along the axial direction, the plastic strain in this direction will not be sensitive to the amplitude of the cyclic torsional load, which is clearly seen in the simulation results for axial creep in
Figure 7. Since this is a fundamental restriction, no attempt is made to test other modeling strategies for J2 plasticity, although in the literature, it has been demonstrated that an associated flow rule in combination with a three-surface hardening-recovery model for kinematic hardening could be successfully parameterized to describe the material behavior of thin-walled tubular specimens under monotonic-cyclic loading [
15].
To understand the distributions of axial stress and axial plastic strain in the J2 model, these quantities are shown along a cut through the gauge section in
Figure 8. The contour plots indicate that both, axial stress and plastic strain, are rather constant in each cross-section of the model. The axial stress, however, exhibits elevated compressive stresses close to the symmetry axis, where high hydrostatic stress components are observed.
4.2. Crystal Plasticity
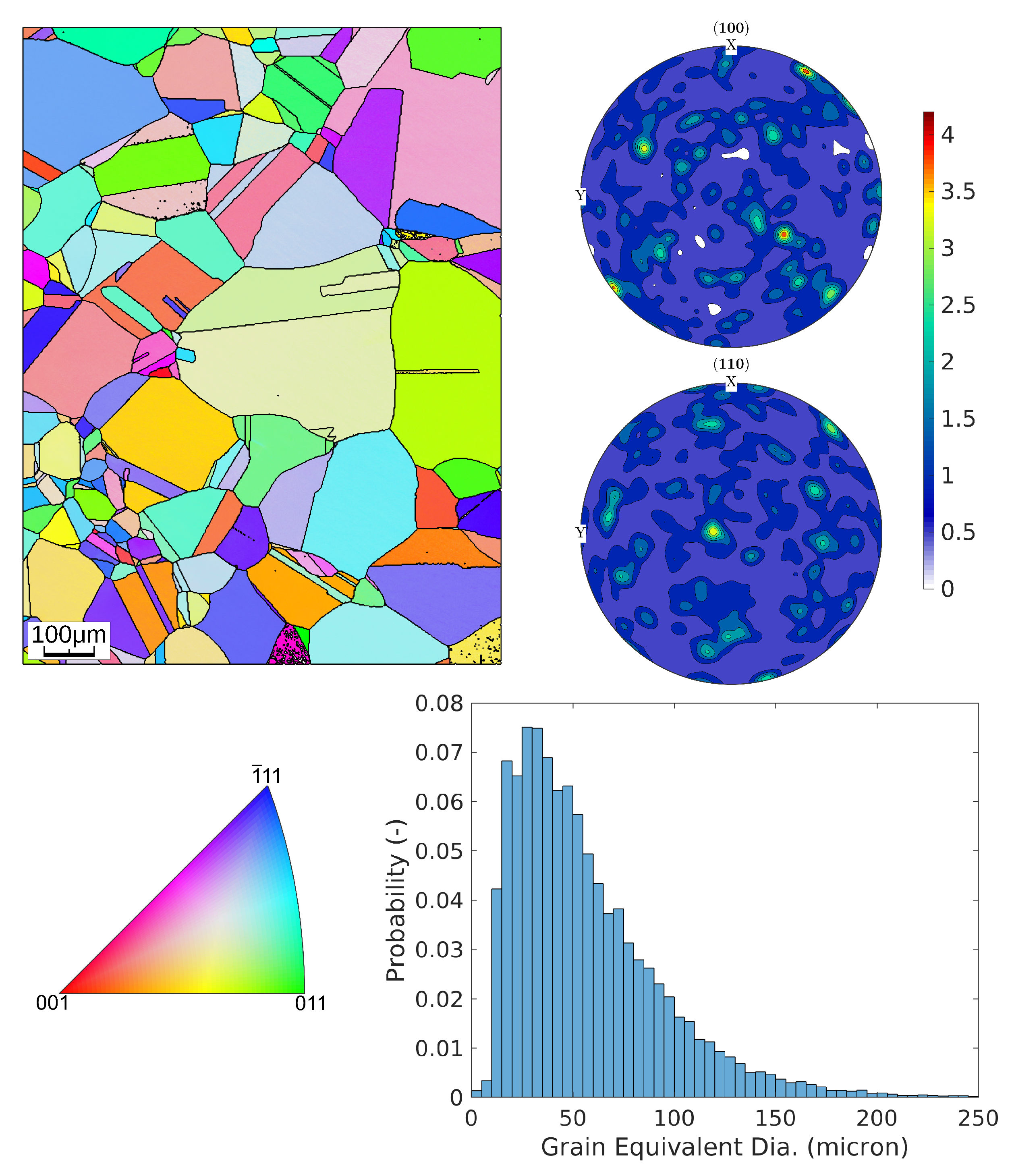
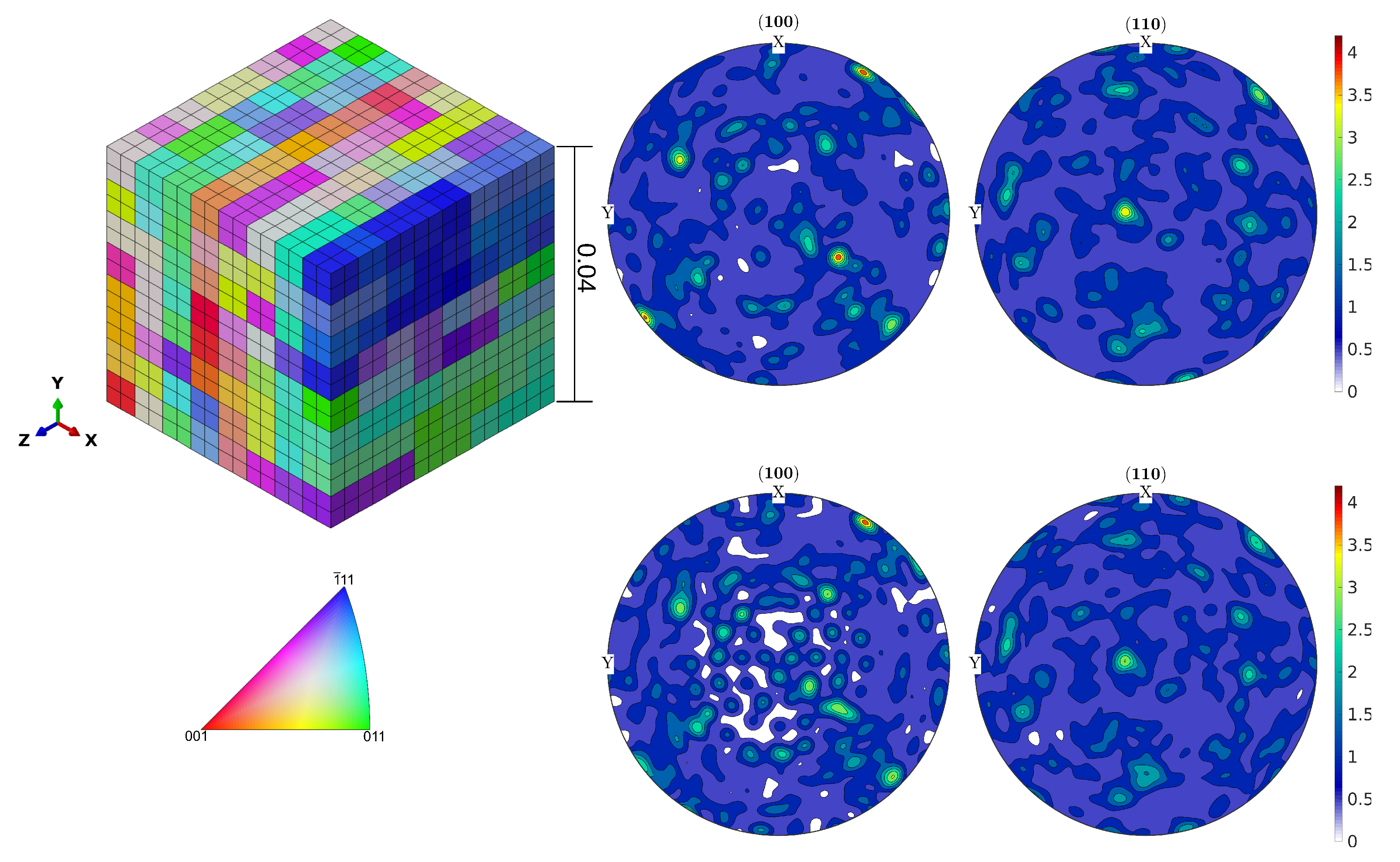
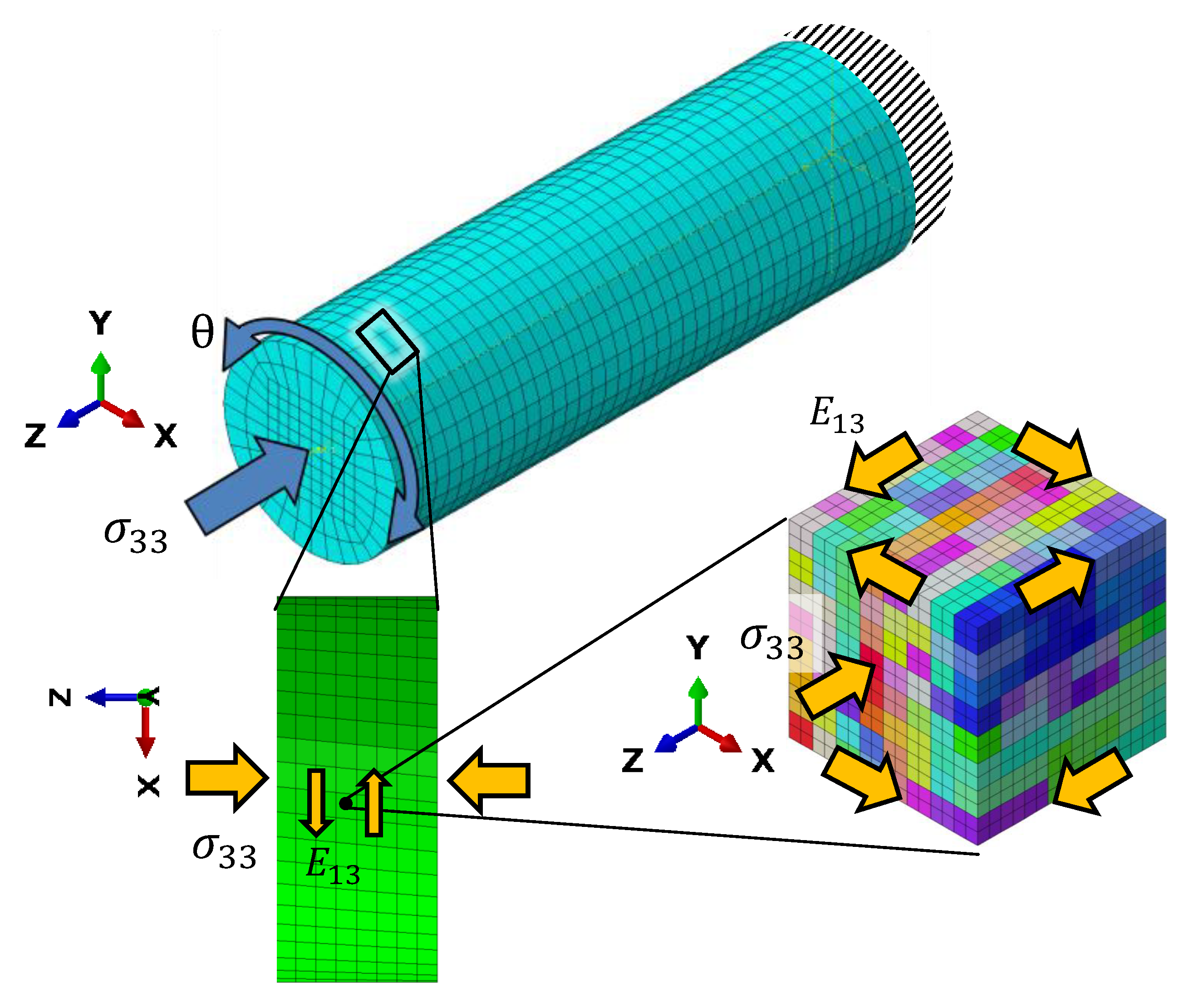
Since the RVE with 512 grains is much smaller than the dimension of the experimental specimens, we cannot directly apply torsional loading on this RVE. Instead, we consider a small volume element close to the surface of the cylindrical FE model representing the gauge section of the experimental specimens, which has been used for the J2 plasticity calculations, see
Figure 9. The distortions experienced by this volume element during the different HPTF loading cases are applied as boundary conditions to the CPFEM model to achieve a comparable loading situation on the length scale of the RVE. The major distortion occurs in the X–Z and Y–Z shear directions (tensor components
and
, respectively). The RVE is subject to displacement boundary conditions resulting in X–Z shear, and a distributed force boundary condition in the Z direction, the magnitude of the force is adjusted such that the homogenized stress in the RVE matches the required axial pressure for the given HPTF load, and similarly, the shear displacement is adjusted to match the strain obtained from the saturated hysteresis loop of the HPTF experiment. Furthermore, as shown in the J2 model, the axial plastic strain and the axial stress are rather homogeneous throughout the gauge section, which justifies the application of the distortions of a volume element close to the surface as boundary conditions to the RVE, as the plastic strains observed in the RVE will be representative for the entire gauge section.
It is noted here, that the RVE is exposed to periodic boundary conditions to avoid free surfaces, which would severely influence the stress field within the RVE and produce finite size effects. This simplification is justified because we do not attempt to study crack initiation, for which free surface effects might play a crucial role.
In the first step to calibrate the CP parameters, the HPTF experiment with
and
is used. Only the kinematic hardening parameters
and
can be calibrated in this way, whereas the isotropic hardening parameters
,
, and
are temporarily set to zero and will be calibrated in a second step as described below. To validate the correctness and generality of the CP parameters obtained by this procedure, the calibrated model is verified by comparing the simulation results with experiments for
,
and
,
.
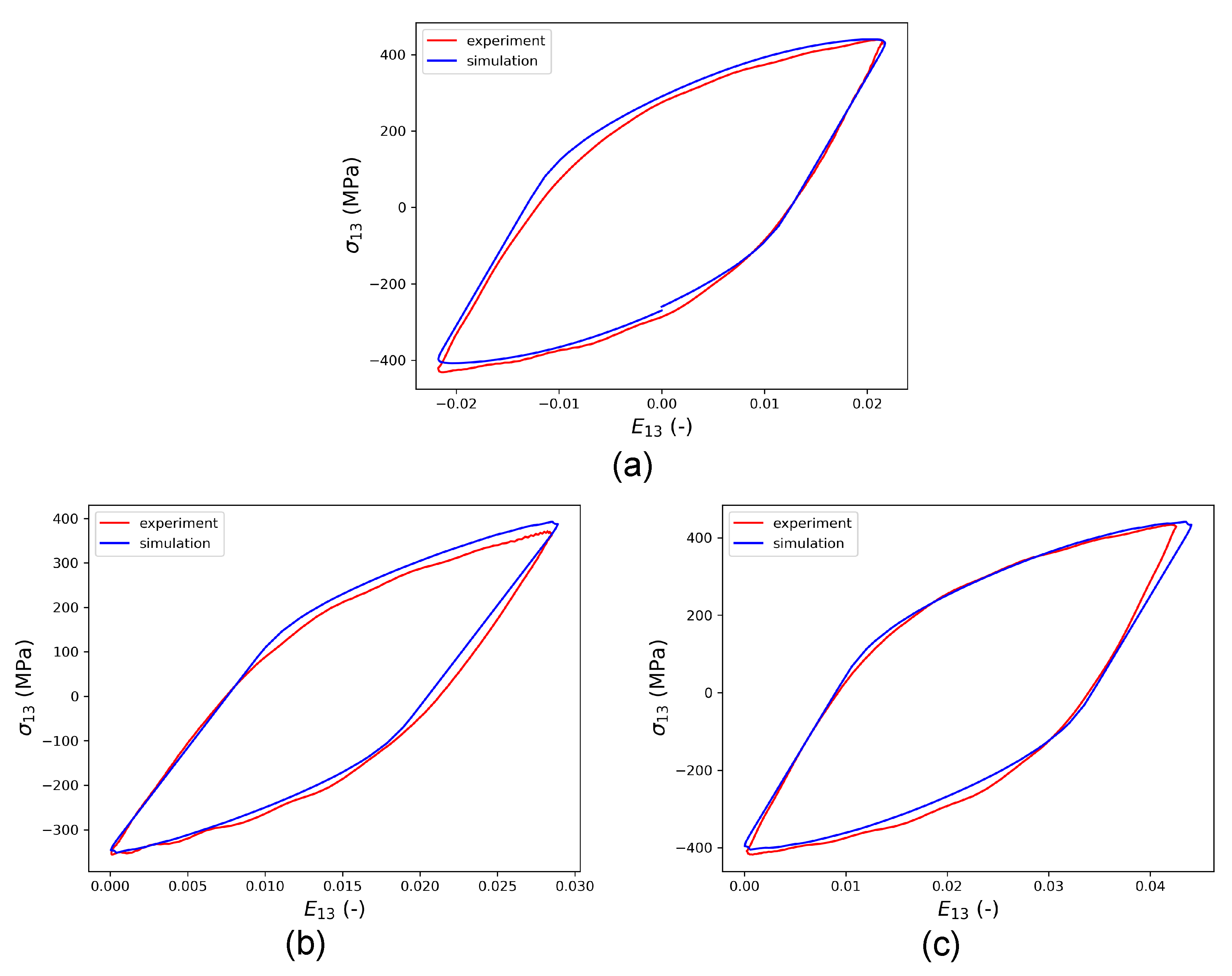
Figure 10 shows that the stress–strain hysteresis loops obtained from HPTF simulations using the RVE model closely match the experiments for all loading cases, which confirms the predictive capability of the parameterized model.
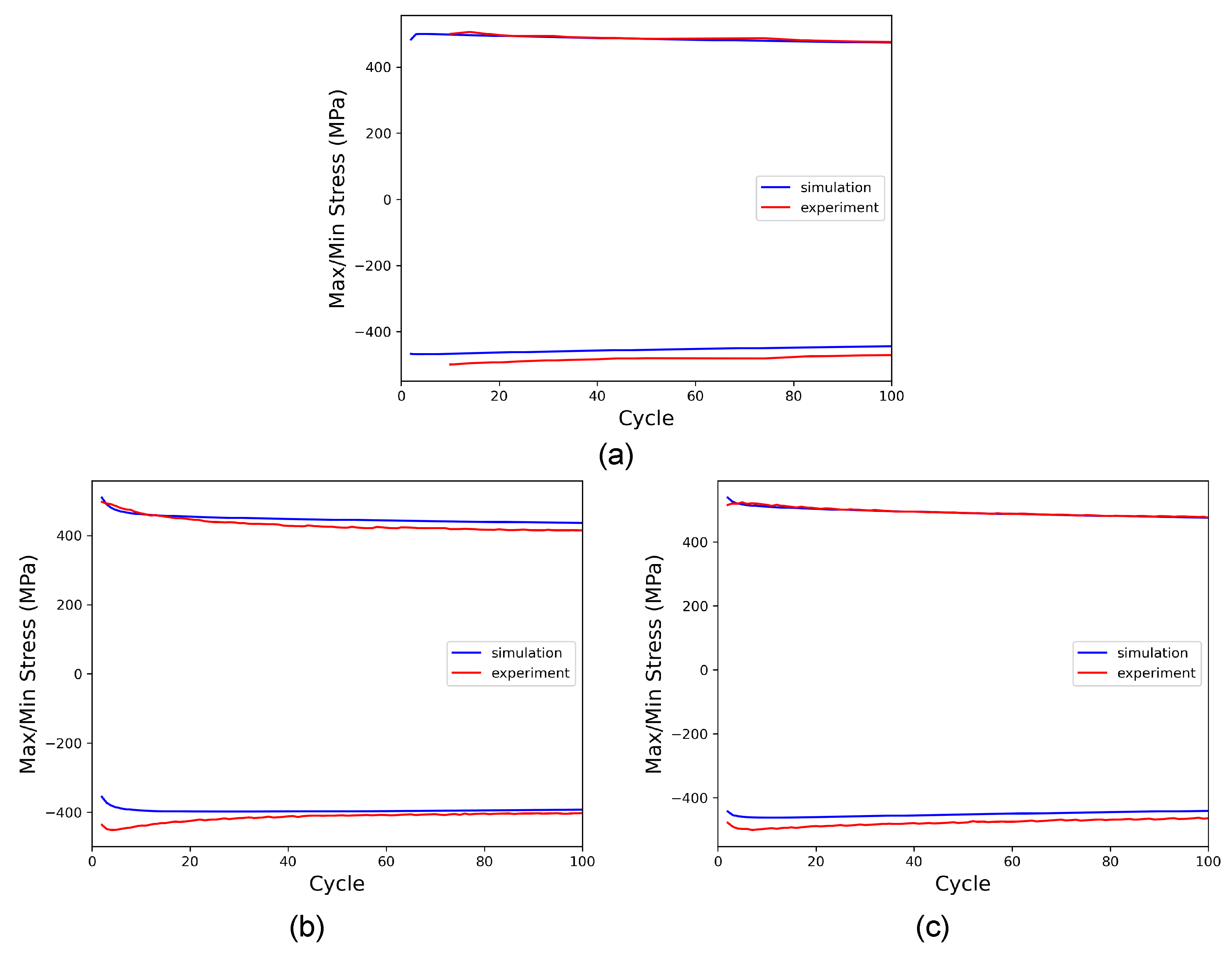
The calibration of the isotropic hardening parameters (
,
, and
) and the remaining kinematic hardening parameter
m, requires matching the evolution of maximum and minimum stress recorded during all cycles between simulation and experiment. Again, this is done for loading with (
), and the result is validated by comparison with the other cases. As seen in
Figure 11, a satisfying agreement between simulation and experiment could be achieved in this way. All resulting CP parameters are given in
Table 5 and referred to as set 1.
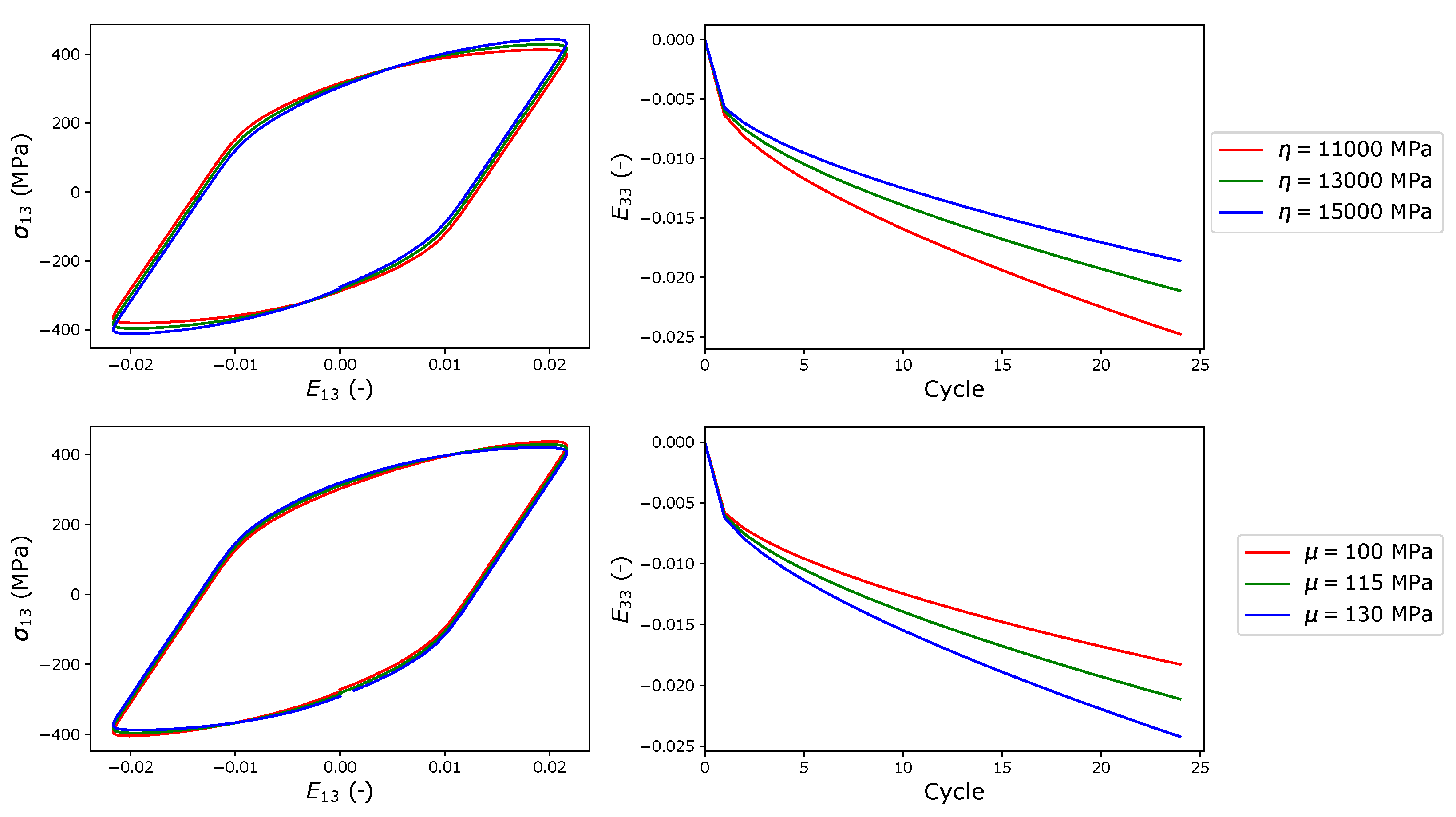
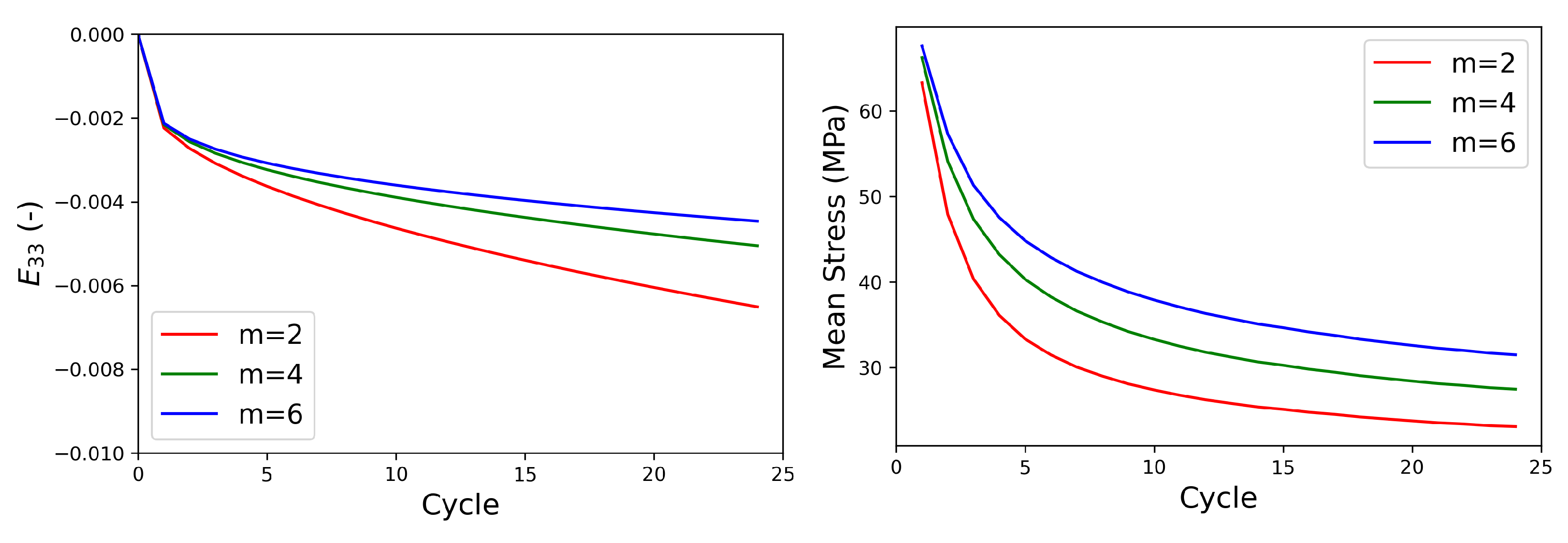
As indicated in the parametric study shown in
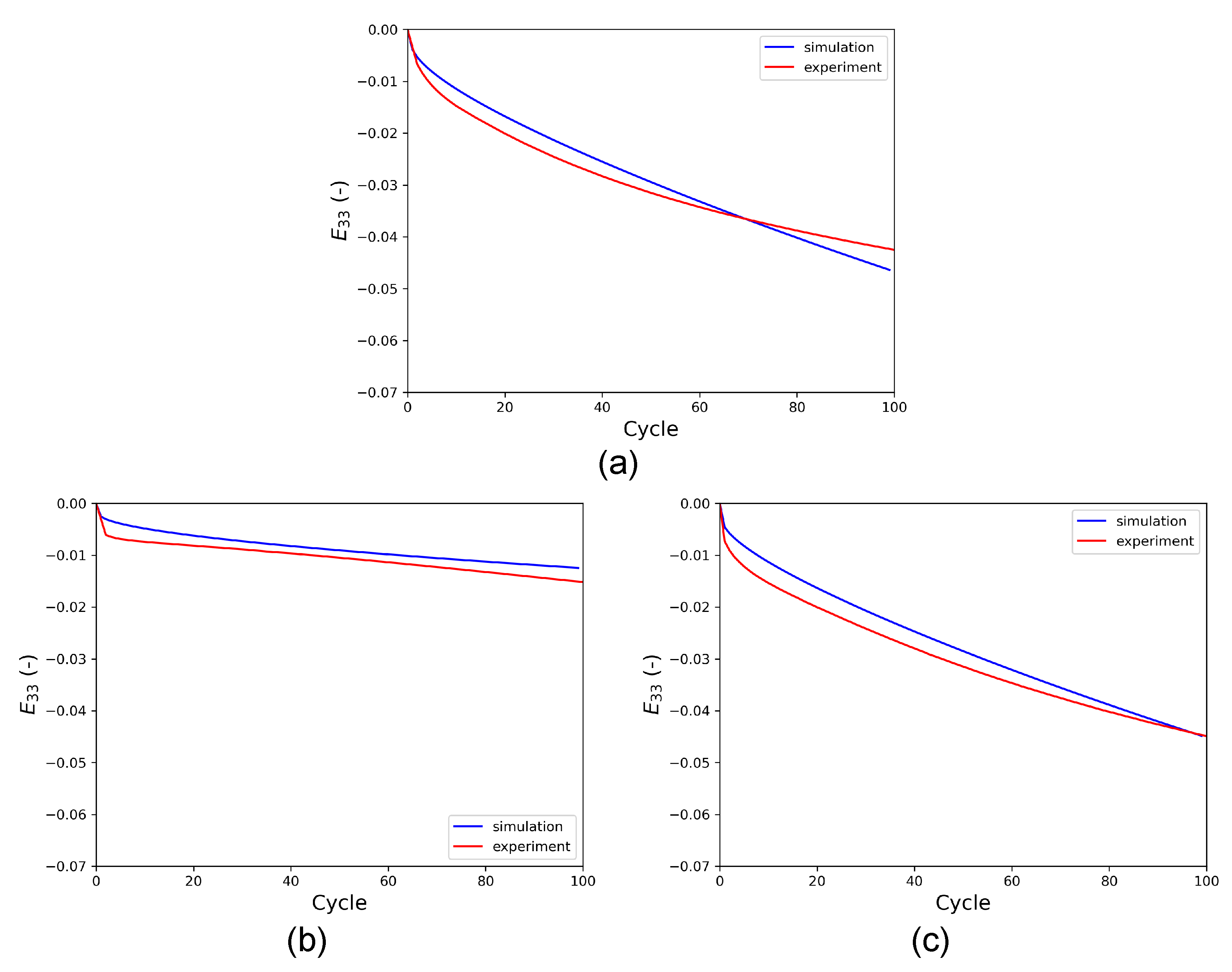
Appendix A, the axial creep behavior is also employed for the calibration of the CP parameters.
Figure 12 shows the axial creep in the RVE during HPTF simulations. The results indicate that the CPFE model does not only predict the cyclic properties but also the axial creep behavior for the different HPTF loading cases very well.
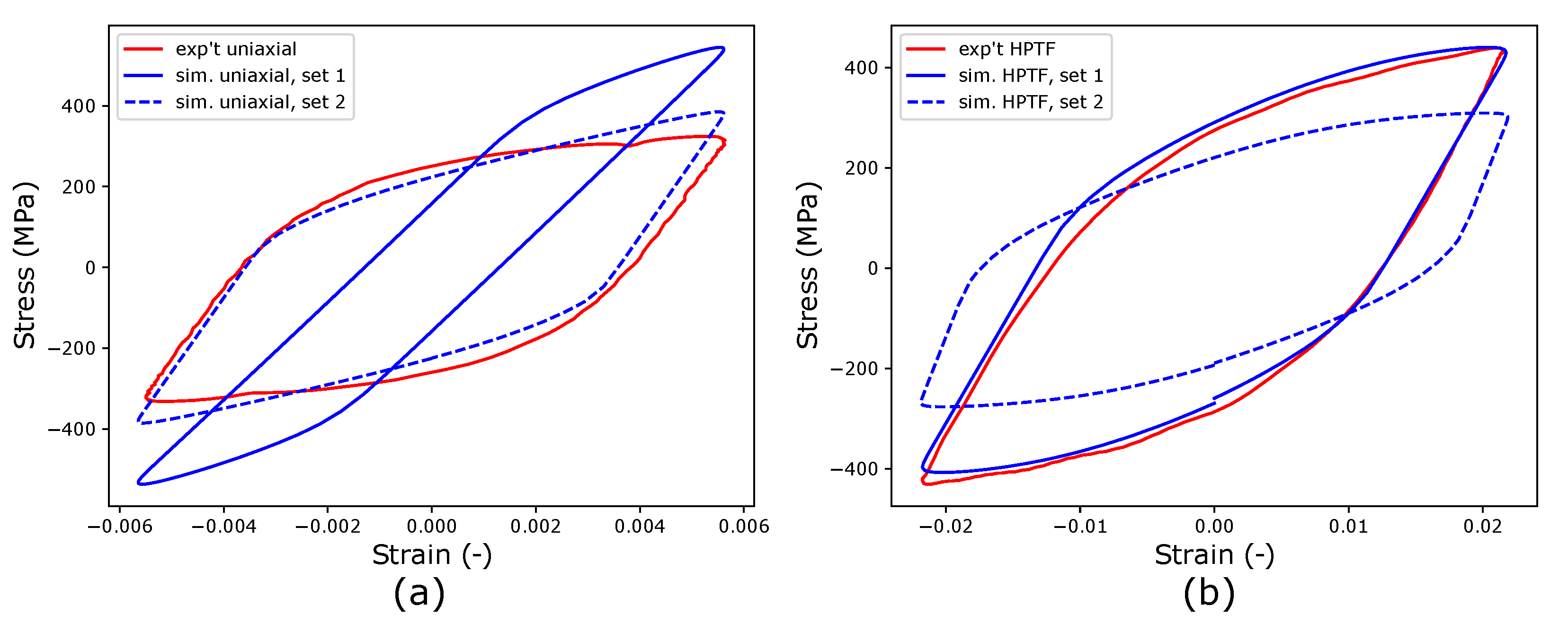
In the next step, the CPFE model calibrated with HPTF experiments (set 1) is used to predict material behavior under uniaxial fatigue loading. It is pointed out here that it is expected that the material parameters fitted to more complex loading situations should be able to describe the material behavior under uniaxial loading (see, for example, the study of de Castro e Susa [
36], where the authors tested various protocols to determine material parameters for cyclic plasticity using inverse procedures. However, the comparison of the simulation and experiments shown in
Figure 13a exhibits the limitations of this approach, as the predicted and measured stress–strain hysteresis loops for uniaxial loading differ significantly from the parameters of set 1 that yield good comparability between experiment and simulation for the HPFT case, as seen in
Figure 13b.
To understand the reason for this discrepancy in the prediction of the CPFE model, the experimental stress–strain hysteresis loops for HPTF and uniaxial fatigue tests are analyzed more closely.
Figure 14 shows the comparison of the experimental results for saturated hysteresis loops under HPTF loading (
) and uniaxial fatigue loading (
). Since the elastic stiffness in the former case is dominated by the materials’ shear modulus and in the latter case by Young’s modulus, the stress is normalized by the respective elastic quantities, which are estimated from the stiffness parameters given in
Table 3 as Young’s modulus
GPa and shear modulus
GPa.
It is seen that the effective slopes of the elastic branches of the HPTF and uniaxial hysteresis loops are significantly different, even after the proper scaling is applied, and that the elastic response of the material under uniaxial fatigue is approximately 1.46 times stiffer than under HPTF loading.
Due to this difference in the elastic slope, the effective elastic parameters required for the uniaxial fatigue simulations are different from those used for the HPTF simulation, which can be controlled by the scaling factor
in this work. A similar change in the stress–strain relationship due to pre-straining has been reported in the experimental work of Vrh et al. [
37]. A degradation of Young’s modulus by more than 20% during fatigue tests was reported for dual-phase steels in [
38]. It can be interpreted from the experimental work of Wilshire and Willis [
39], Stout et al. [
40], and Schneider et al. [
41] that the magnified effect of defects (especially dislocation structures) due to pre-straining in HPTF experiments can lead to the change in the stress–strain behavior. It is also pointed out here that the temperature increase during the HPTF experiments is significantly higher than that during the uniaxial tests (200 K vs. 50 K), which might also lead to a reduction in the elastic stiffness and the yield stress of the austenitic steel.
To demonstrate the possibility of calibrating the material parameters used for CPFE simulations to describe uniaxial fatigue behavior, the scaling parameter for elastic properties
, the critical resolved shear stress
, and the isotropic hardening parameters ({
}) are re-calibrated to match uniaxial experiments, while keeping the kinematic hardening parameters unchanged. The re-calibrated uniaxial parameters, referred to as set 2, are given in
Table 6. The CPFE results obtained for both loading cases are plotted in
Figure 13 as set 2. It is seen that this data set describes the stress–strain hysteresis under uniaxial loading very well, whereas the results for HPTF are not represented in an acceptable manner for set 2. A closer analysis of the material parameters of set 1 and set 2 reveals that the ratio of the fitted elastic constants in the CP models of both loading cases amounts to 1.51, which is close to the ratio of the effective stiffness values read from the experimental curves, which takes a value of 1.46. Furthermore, the scaling parameter
used to adapt the elastic constants from DFT calculations to fit the uniaxial experiments is 0.95 and thus close to unity, which demonstrates the predictive capabilities of DFT methods concerning the calculation of elastic parameters. Generally, this finding that the transfer of crystal parameters obtained by inverse analysis of data referring to one experiment cannot be simply transferred to predict another experiment indicates a limitation in our current constitutive models and their parameters.
However, this analysis also reveals, that the kinematic hardening parameters obtained from uniaxial fatigue or HPTF loading are consistent, whereas the effective elastic parameters and, with them, some basic plastic properties, such as critical resolved shear stress and isotropic hardening parameters, take different values for the two different loading cases. The difference in these parameters can possibly be attributed to the higher temperatures that occur during HPTF testing or to different dislocation structures that result from multiaxial vs. uniaxial deformations. However, more research is required to draw a firm conclusion and to derive a model that describes these differences quantitatively. It is also pointed out here, that care needs to be taken when transferring material parameters obtained for particular loading cases to different scenarios.