A Novel Method to Describe Large-Range Stress-Strain Relations of Elastic-Plastic Materials Based on Energy Equivalence Principle
Abstract
1. Introduction
2. Theoretical Model
2.1. Energy Equivalence Principle
2.2. Linear Elastic Load-Displacement Model
2.3. Fully Plastic Load-Displacement Model
2.4. Elastic-Plastic Load-Displacement Model
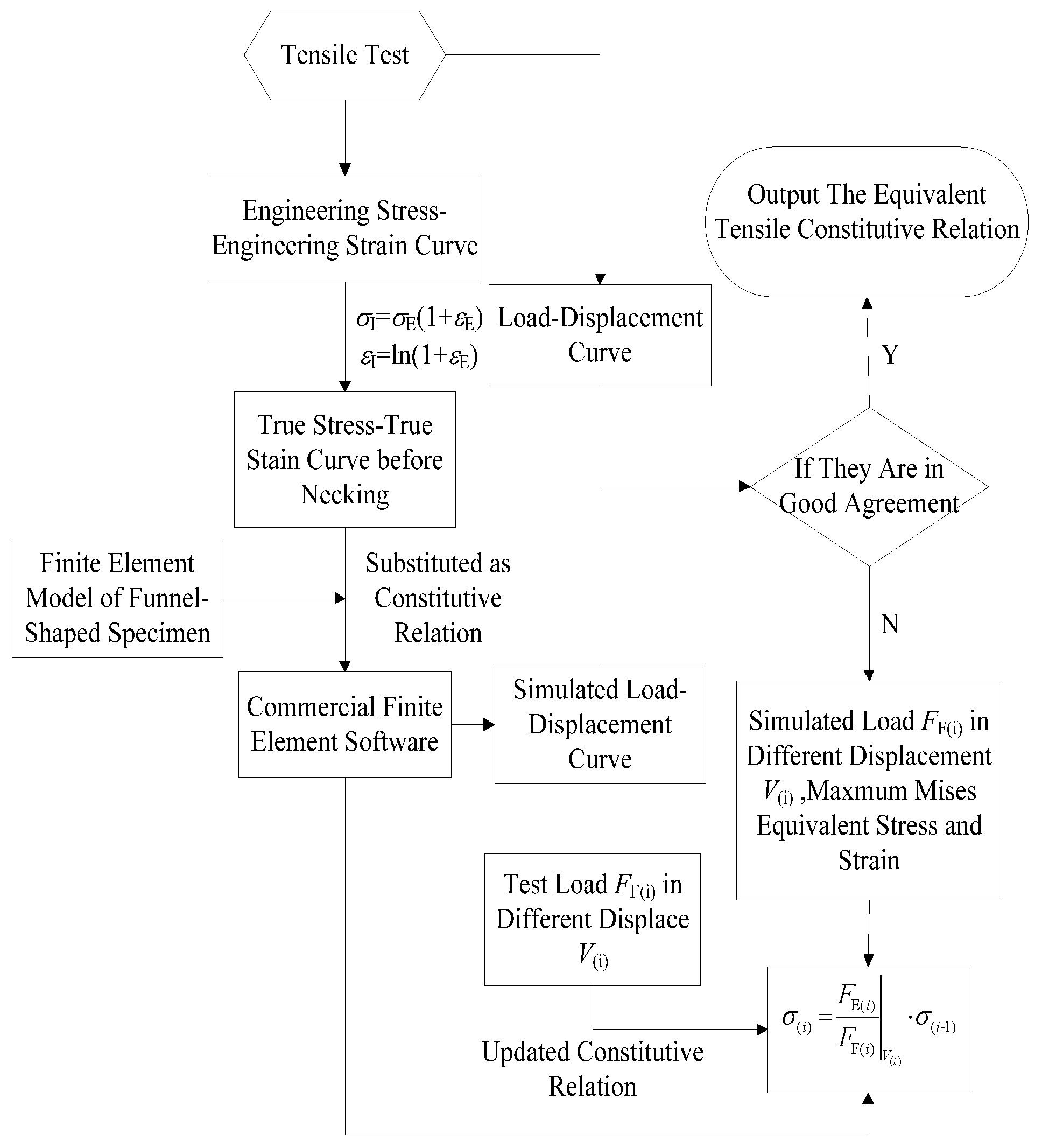
2.5. Acquisition of Uniaxial Stress-Strain Relation
3. Verification of the Models
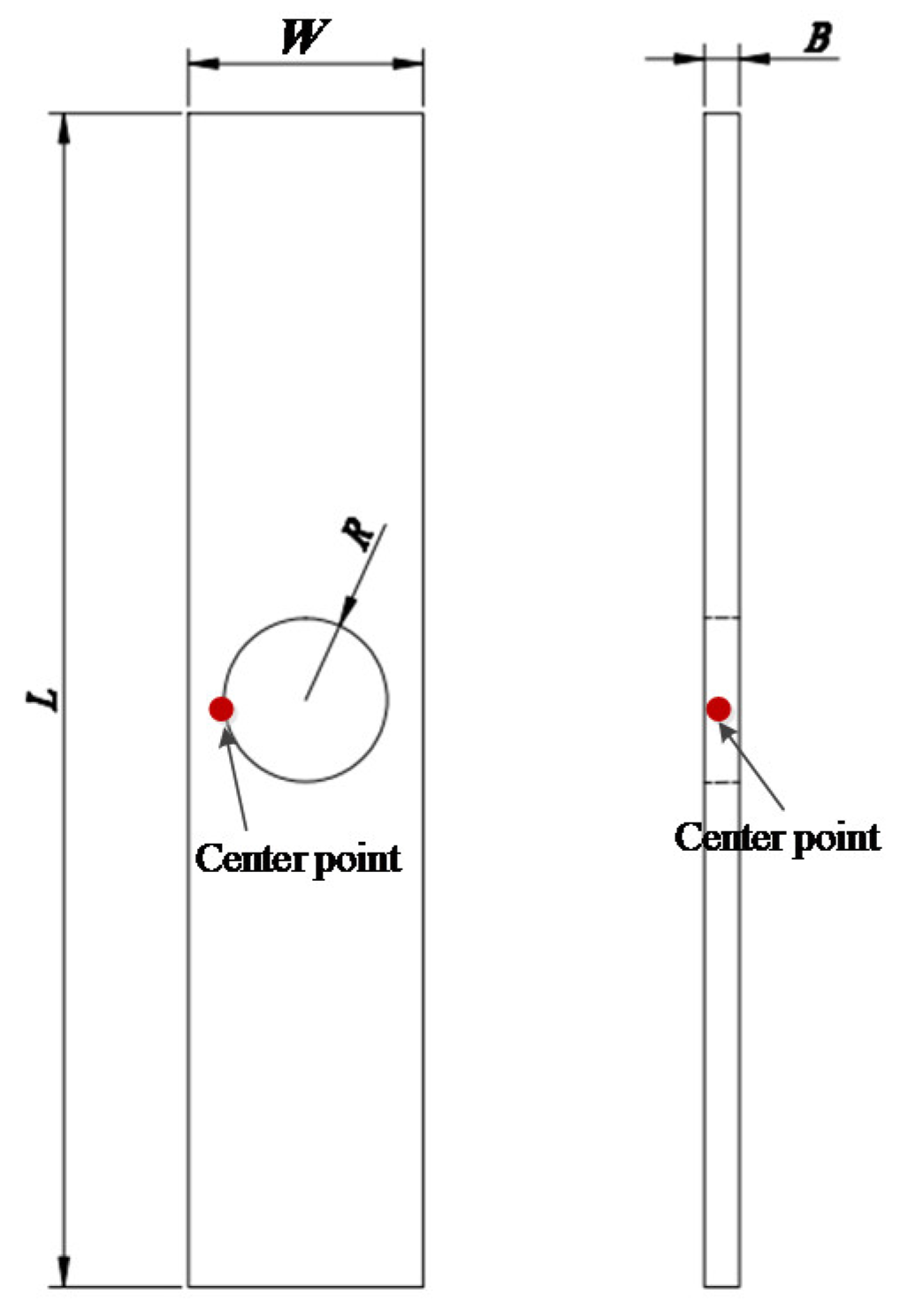
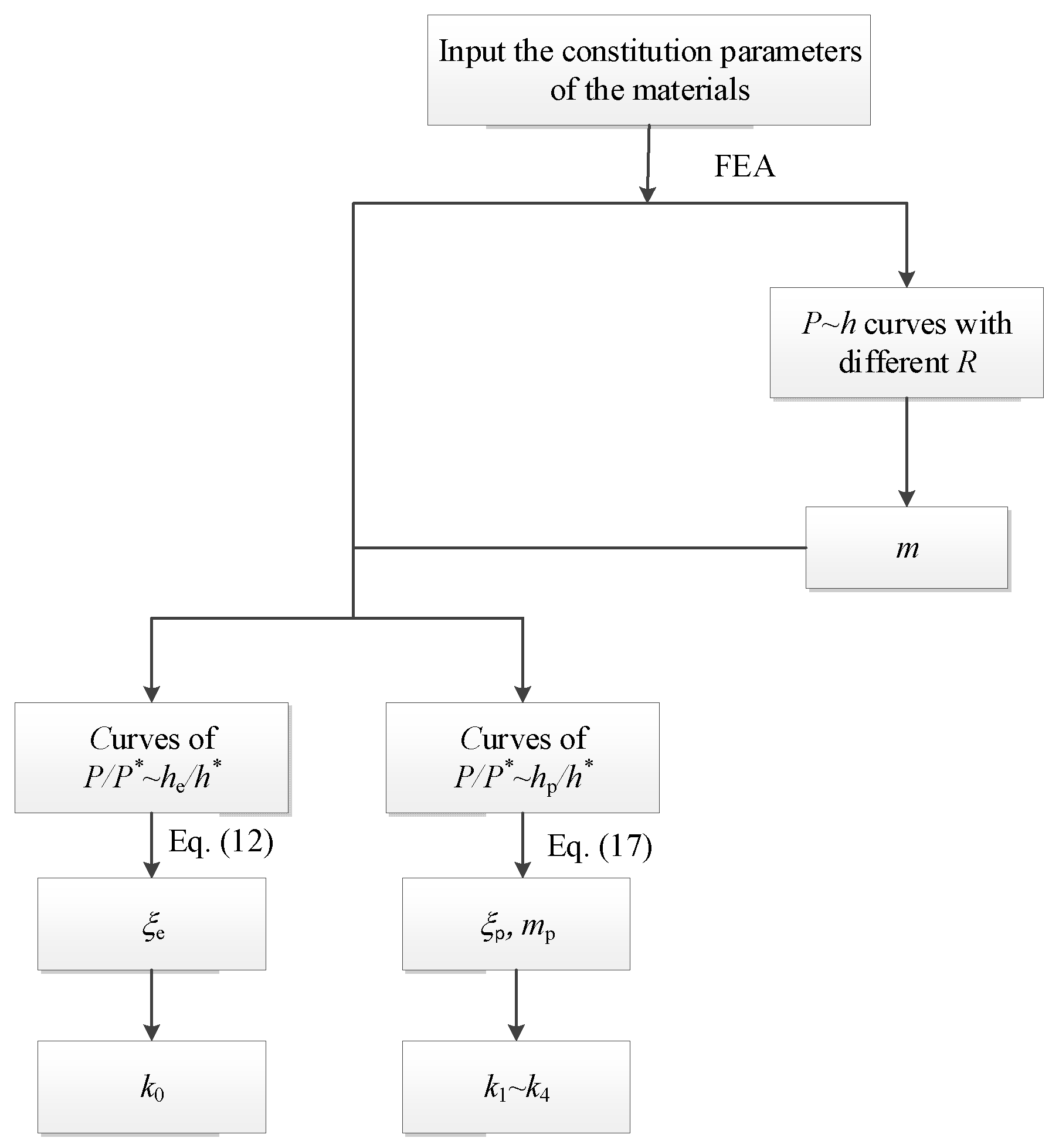
3.1. Parameters Determination by FEA
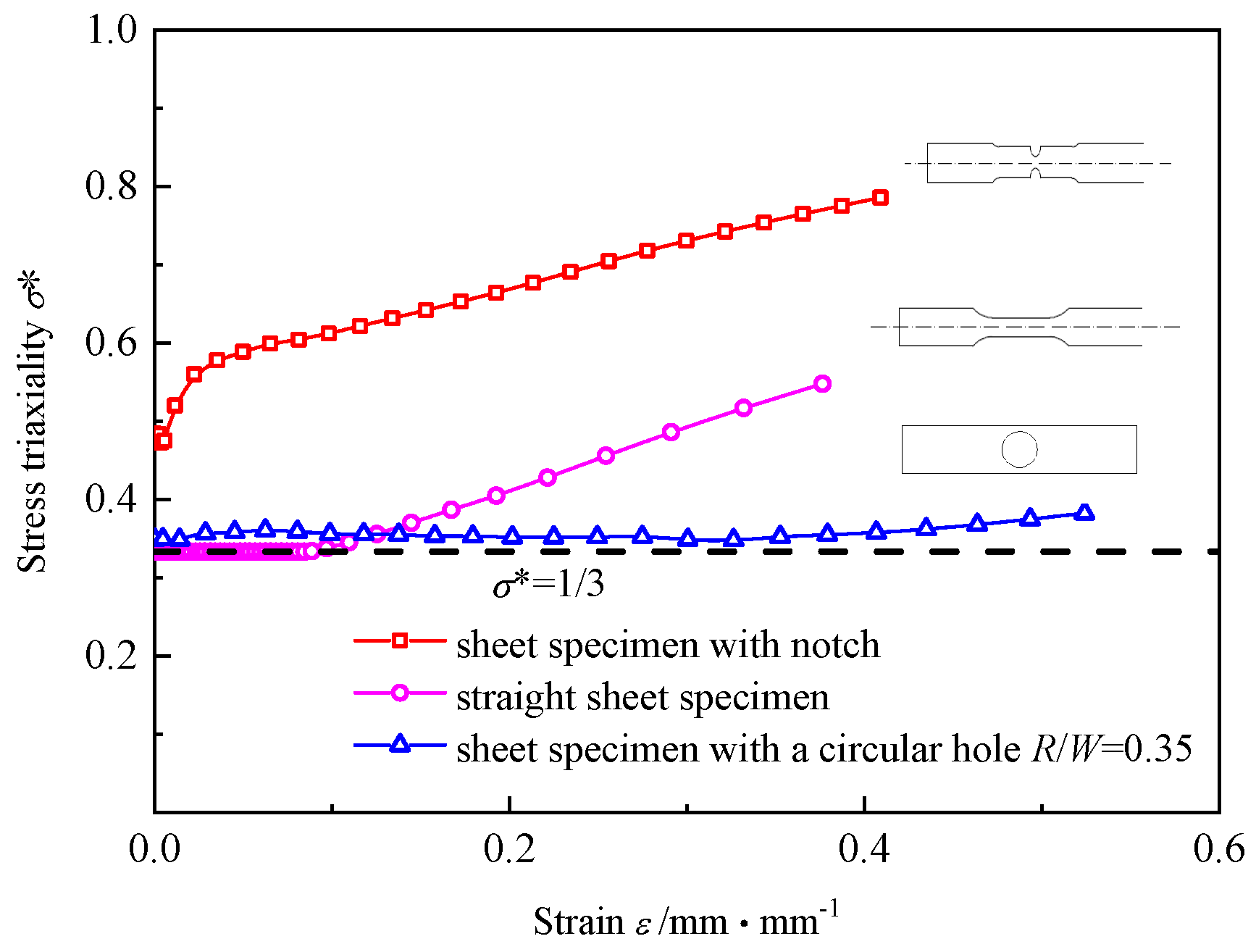
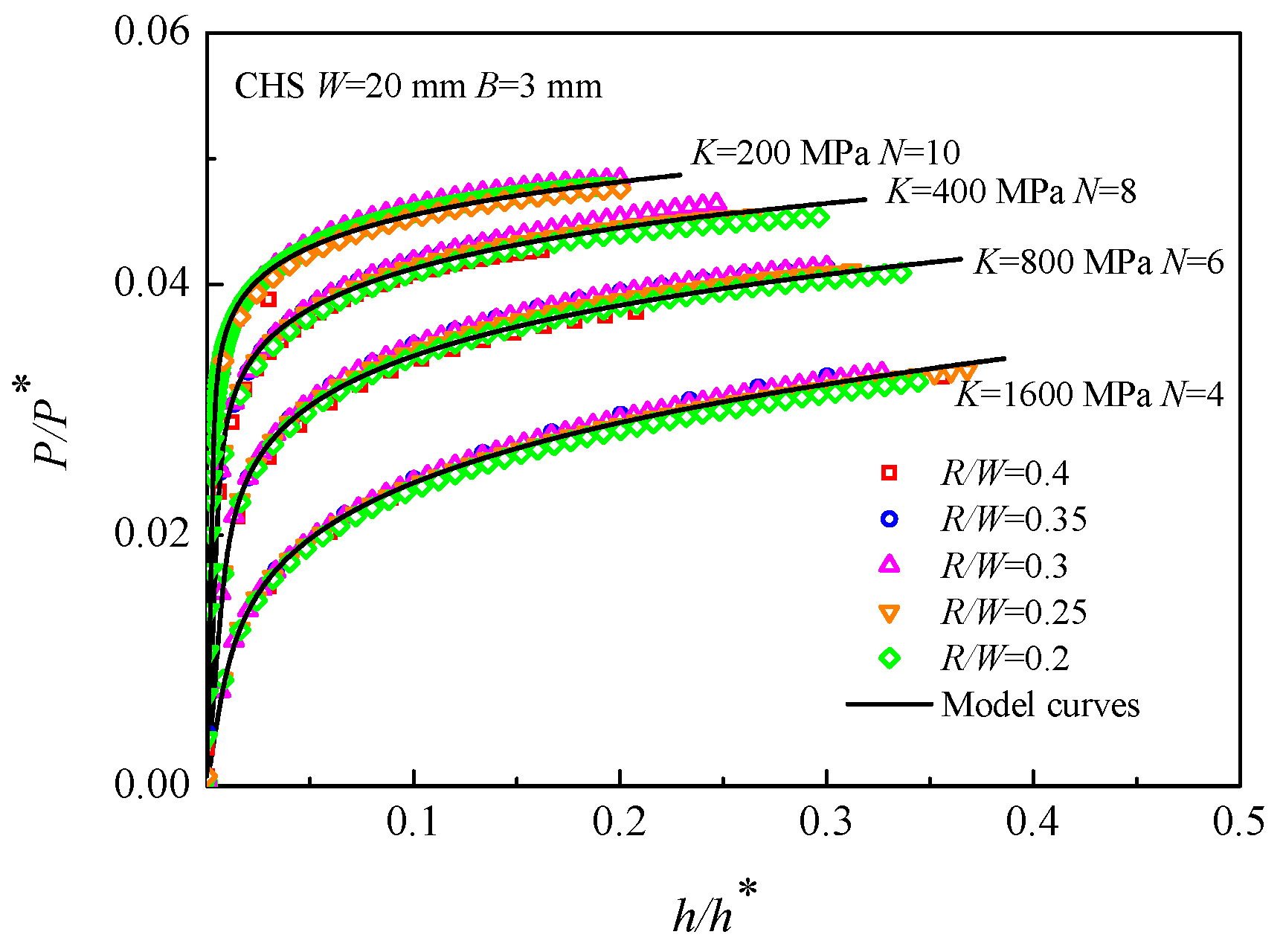
3.2. Influence of R/W on the CHS-LD Model
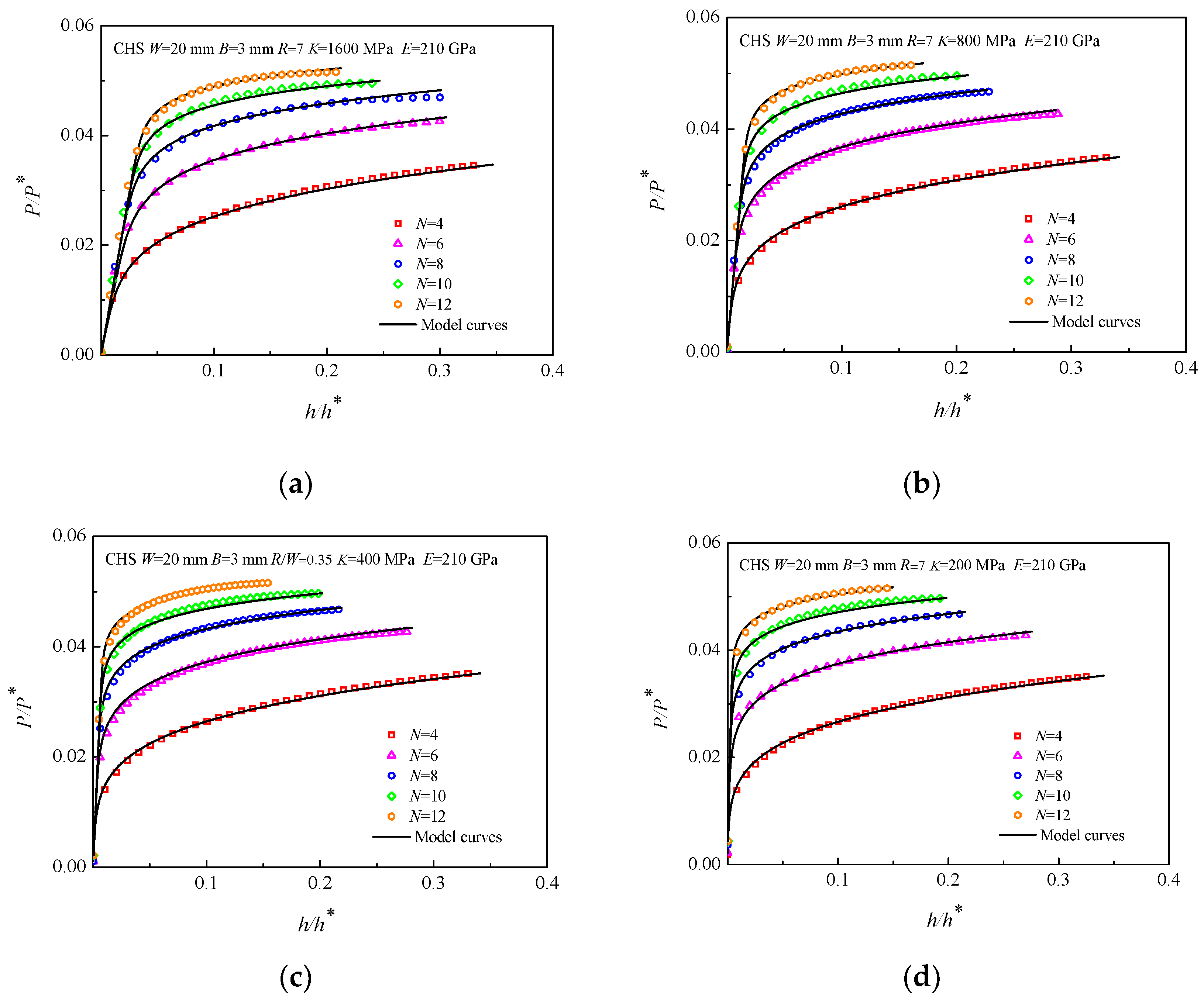
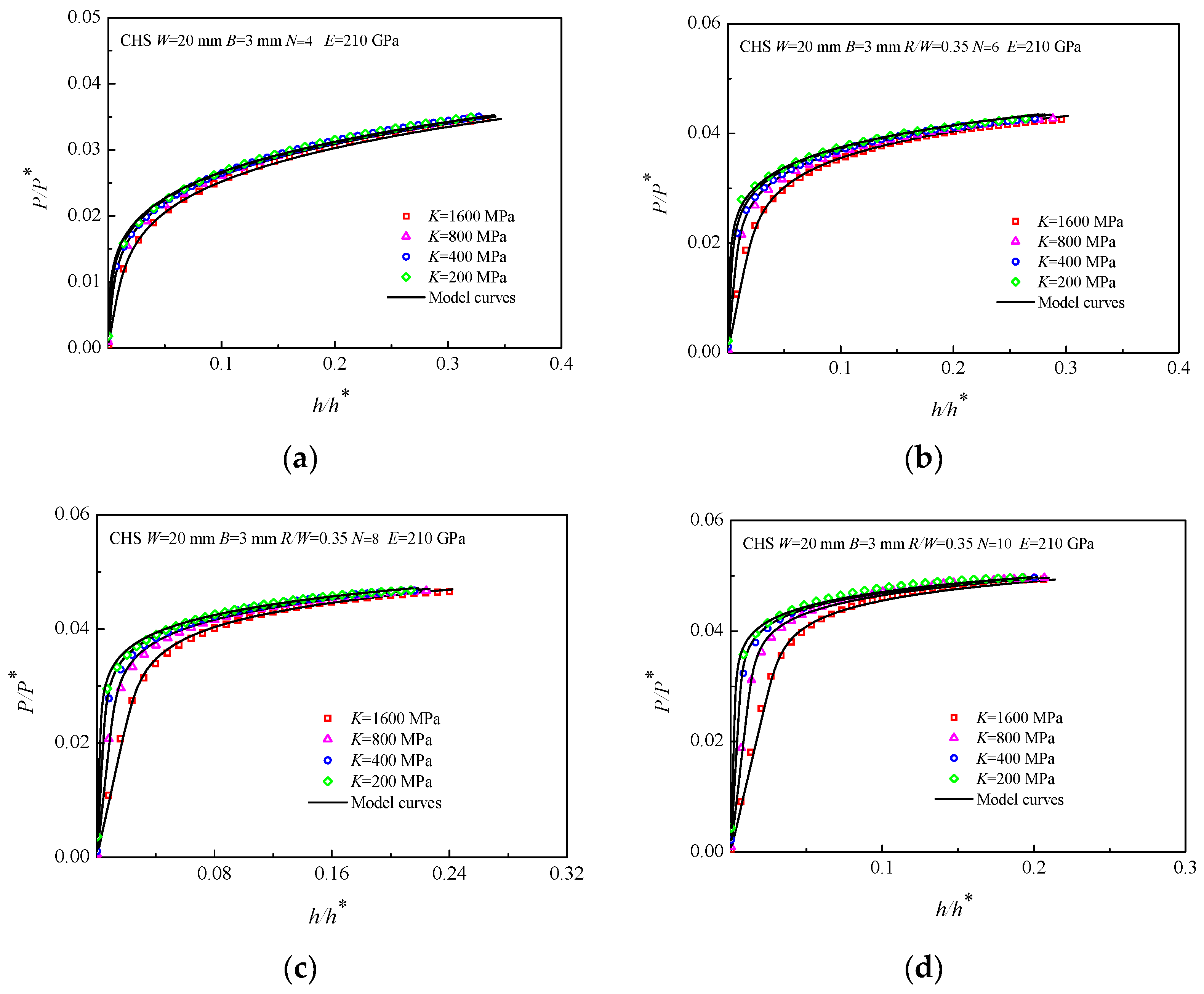
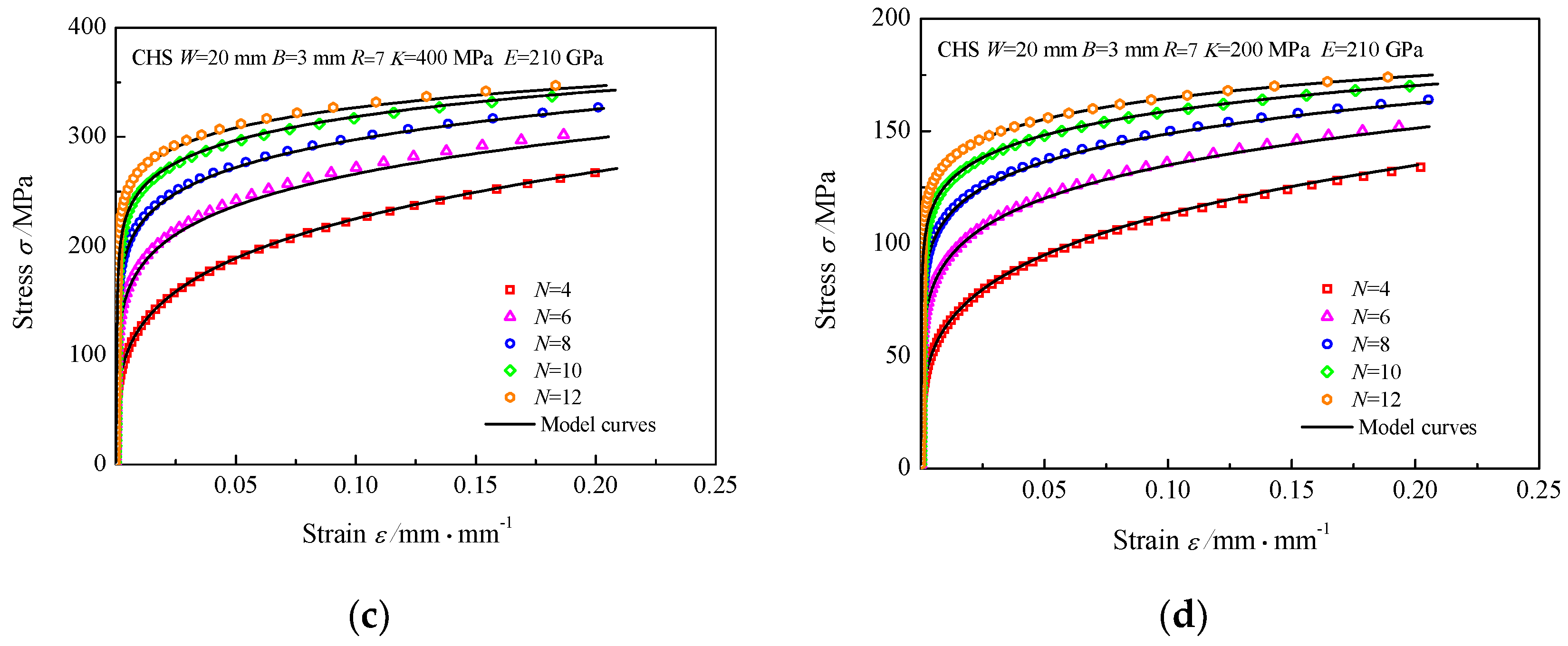
3.3. Effect of Constitutive Parameters on the CHS-LD Model
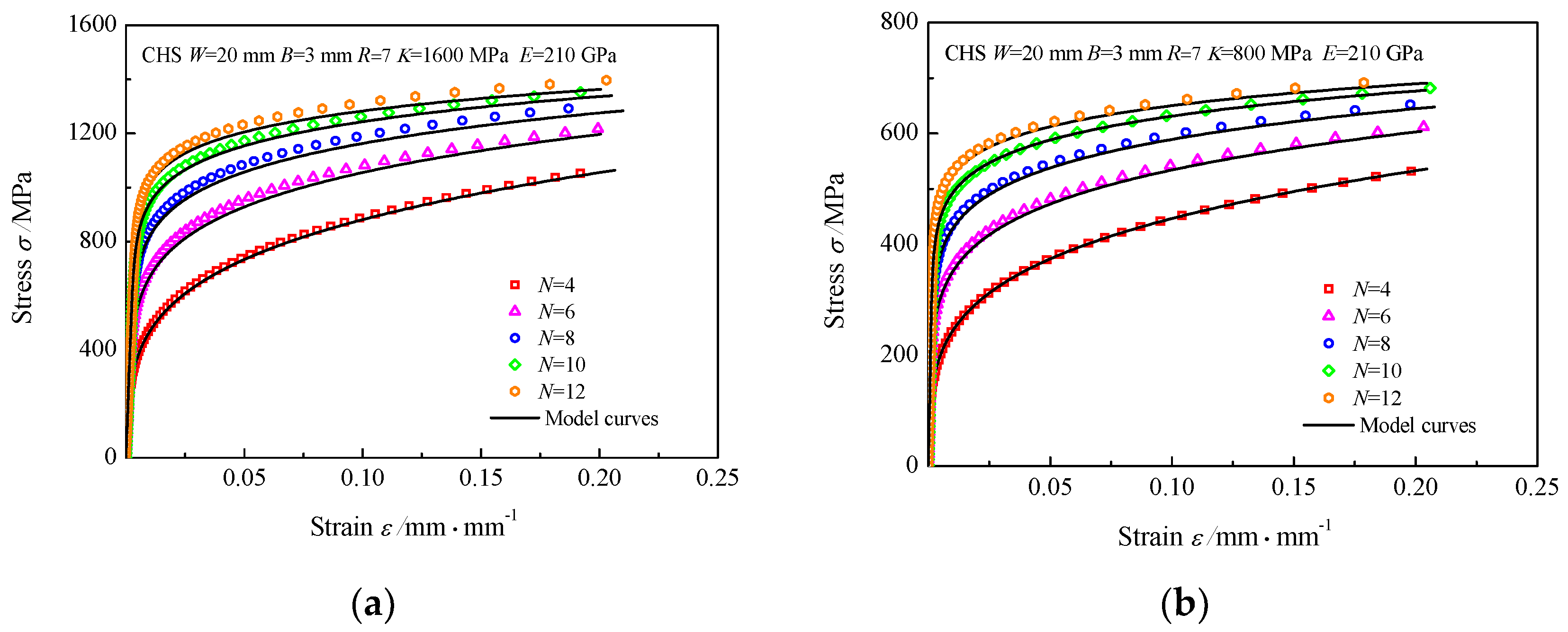
3.4. Verification of the CHS-SS Model
4. Experimental Verifications
4.1. Materials and Experimental Condition
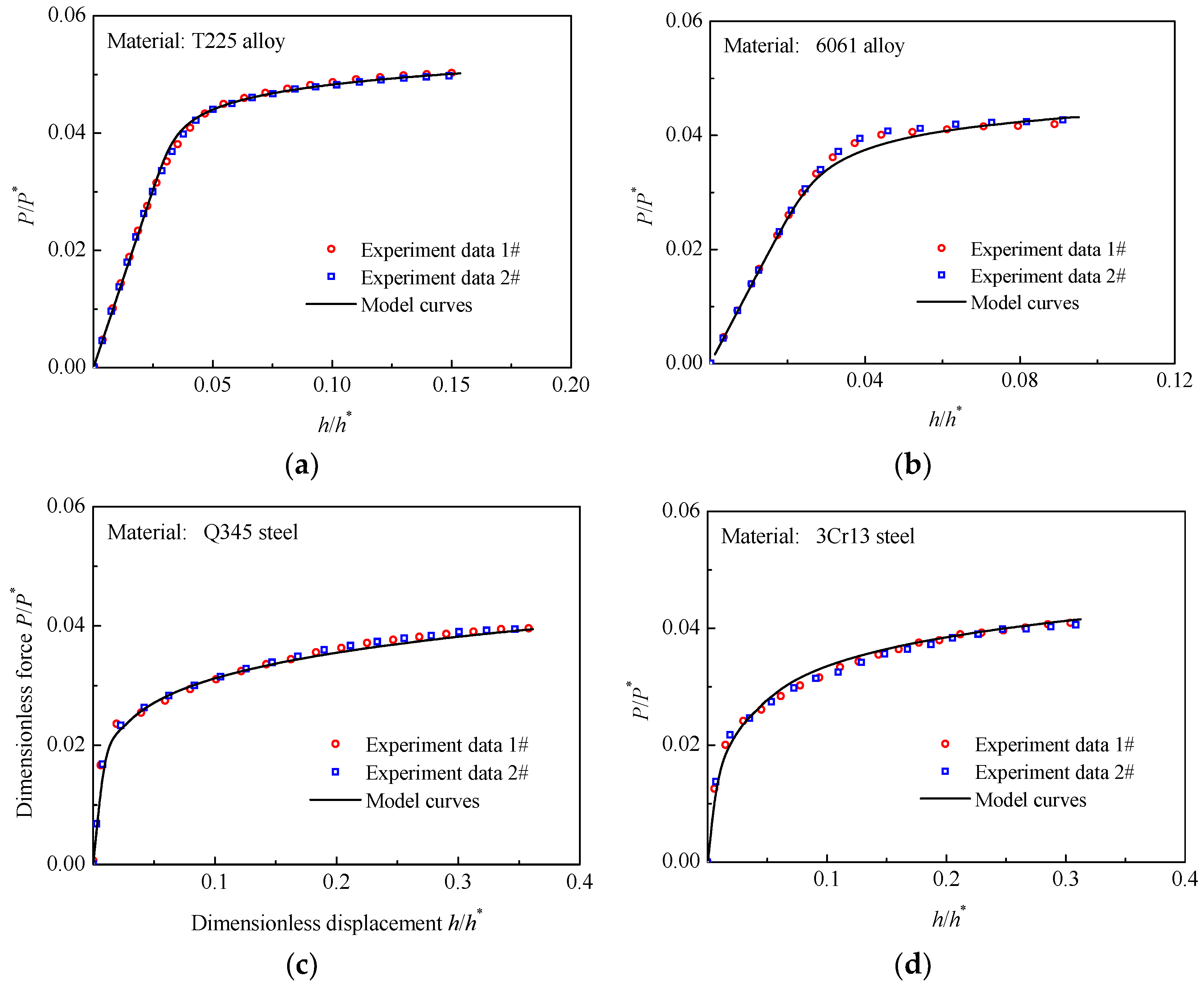
4.2. Verification of the CHS-LD Model
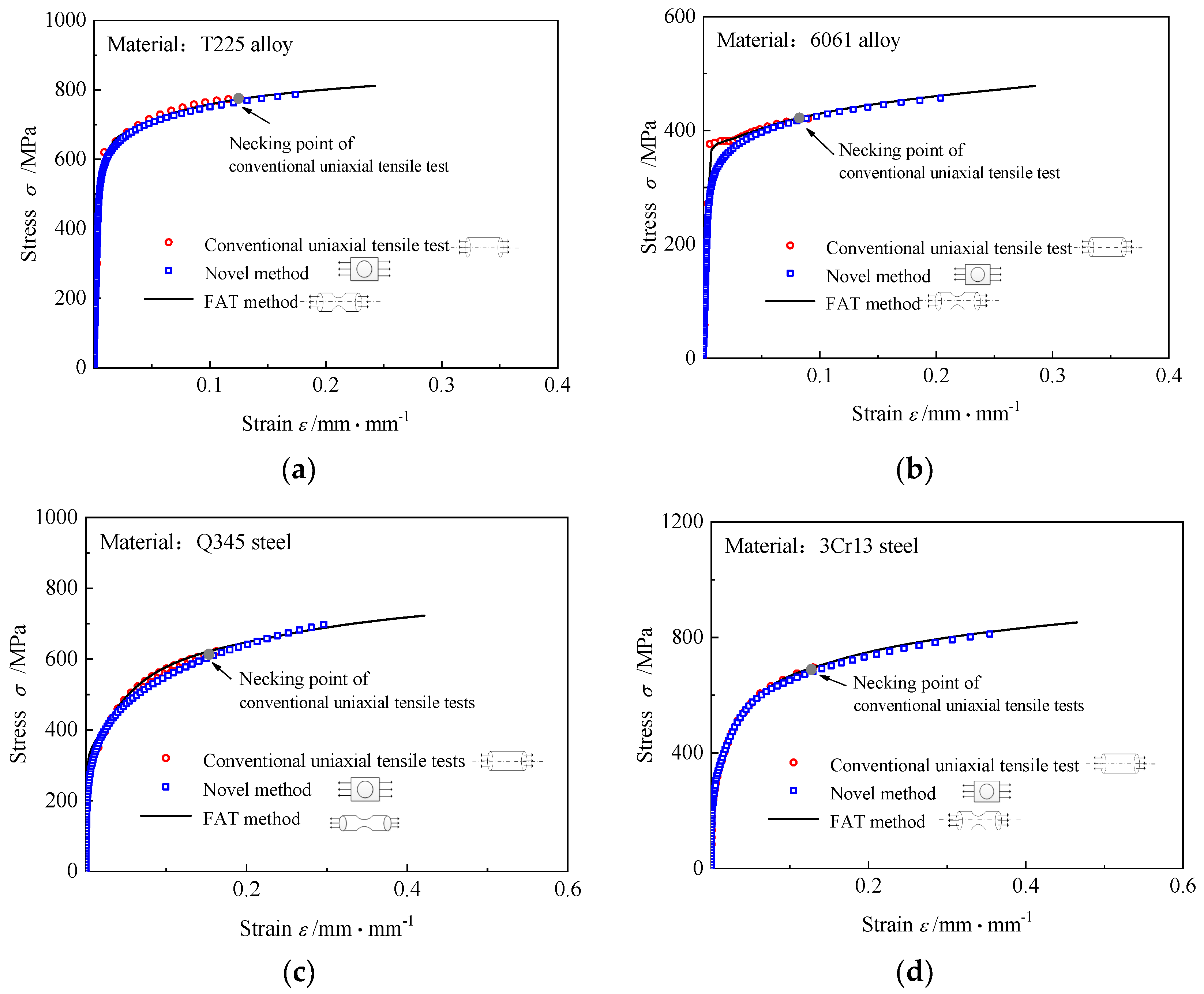
4.3. Verification of the Novel Method to Obtain Stress-Strain Relation
5. Conclusions and Discussions
- (1)
- The numerical simulations of CHS specimens fabricated from various materials were conducted, and the P/P*~h/h* curves obtained by the CHS-LD model are consistent with the FEA results. In addition, the geometric parameter R/W has little influence on the CHS-LD model, and K and E have the main effect on the elastic deformation stage of the CHS-LD model, whereas N has the clearest effect on the CHS-LD model.
- (2)
- Corresponding to the simulated load-displacement relations, the stress-strain relations of the materials predicted by the CHS-SS model match the initial stress-strain relations fed into finite element software well.
- (3)
- The P/P*~h/h* curves predicted by the CHS-LD model are all in good correspondence with the experimental P/P*~h/h* curves of the materials including T225 titanium alloy, 6061 aluminum alloy, Q345 steel, and 3Cr13 steel. Moreover, the average absolute relative errors between the two types of P/P*~h/h* curves are all less than 2%.
- (4)
- Compared with conventional uniaxial tensile tests and the FAT method, the novel method proposed in the study achieves the analytic description of uniaxial stress-strain relations, and it only requires a small amount of FEA. In addition, the range of the uniaxial true stress-strain relations obtained using the novel method has been significantly increased compared with that of the conventional uniaxial tensile tests.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bridgman, P.W. Studies in Large Flow and Fracture; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Earl, J.C.; Brown, D.K. Distribution of stress and plastic strain in circumferentially notched tension specimens. Eng. Fract. Mech. 1976, 8, 599–611. [Google Scholar] [CrossRef]
- Clausing, D. Stress and strain distribution in a tension specimen with a circumferentially notch. J. Mater. 1969, 4, 566–582. [Google Scholar]
- Chen, C. A Collection of Metal Fracture Research; Metallurgical Industry Press Co., Ltd.: Beijing, China, 1978. [Google Scholar]
- Ling, Y. Uniaxial true stress-strain after necking. AMP J. Technol. 1996, 5, 37–48. [Google Scholar]
- Hyun, H.C.; Kim, M.; Bang, S.; Lee, H. On acquiring true stress-strain curves for sheet specimens using tensile test and FE analysis based on a local necking criterion. J. Mater. Res. 2014, 29, 695–707. [Google Scholar] [CrossRef]
- Alves, M.; Jones, N. Influence of hydrostatic stress on failure of axisymmetric notched specimens. J. Mech. Phys. Solids 1999, 47, 643–667. [Google Scholar] [CrossRef]
- La Rosa, G.; Mirone, G.; Risitano, A. Effect of stress triaxiality corrected plastic flow on ductile damage evolution in the framework of continuum damage mechanics. Eng. Fract. Mech. 2001, 68, 417–434. [Google Scholar] [CrossRef]
- Mirone, G. A new model for the elastoplastic characterization and the stress–strain determination on the necking section of a tensile specimen. Int. J. Solids Struct. 2004, 41, 3545–3564. [Google Scholar] [CrossRef]
- Li, G.C. Necking in uniaxial tension. Int. J. Mech. Sci. 1983, 25, 47–57. [Google Scholar] [CrossRef]
- Norris, J.D.M.; Moran, B.; Scudder, J.K.; Qui, D.F. A computer simulation of the tension test. J. Mech. Phys. Solids 1978, 26, 1–19. [Google Scholar] [CrossRef]
- Matic, P. Numerically predicting ductile material behavior from tensile specimen response. Theor. Appl. Fract. Mech. 1985, 4, 13–28. [Google Scholar] [CrossRef]
- Matic, P.; Kirby, G.C.; Jolles, M.I. The relation of tensile specimen size and geometry effects to unique constitutive parameters for elastic-plastic materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1988, 417, 309–333. [Google Scholar]
- Matic, P.; Kirby, G.C.; Jolles, M.I.; Father, P.R. Ductile alloy constitutive response by correlation of iterative finite element simulation with laboratory video images. Eng. Fract. Mech. 1991, 40, 395–419. [Google Scholar] [CrossRef]
- Zhano, K.S.; Li, Z.H. Numerical analysis of the stress-strain curve and fracture initiation for ductile material. Eng. Fract. Mech. 1994, 49, 235–241. [Google Scholar] [CrossRef]
- Zhang, K.S. Technical Note Fracture Prediction and Necking Analysis. Eng. Fract. Mech. 1995, 52, 575–582. [Google Scholar] [CrossRef]
- Cabezas, E.E.; Celentano, D.J. Experimental and numerical analysis of the tensile test using sheet specimens. Finite Elem. Anal. Des. 2003, 40, 555–575. [Google Scholar] [CrossRef]
- Michael, B. Numerical analysis and modeling of large deformation and necking behavior of tensile specimens. Finite Elem. Anal. Des. 1998, 28, 303–319. [Google Scholar] [CrossRef]
- Dumoulin, S.; Tabourot, L.; Chappuis, C. Determination of the equivalent stress~quivalent strain relationship of a copper sample under tensile loading. J. Mater. Process. Technol. 2003, 133, 79–83. [Google Scholar] [CrossRef]
- Joun, M.S.; Eom, J.G.; Lee, M.C. A new method for acquiring true stress–strain curves over a large range of strains using a tensile test and finite element method. Mech. Mater. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Joun, M.; Choi, I.; Eom, J.; Lee, M. Finite element analysis of tensile testing with emphasis on necking. Comput. Mater. Sci. 2007, 41, 63–69. [Google Scholar] [CrossRef]
- Kamaya, M.; Wilkinson, A.J.; Titchmarsh, J.M. Quantification of plastic strain of stainless steel and nickel alloy by electron backscatter diffraction. Acta Mater. 2006, 54, 539–548. [Google Scholar] [CrossRef]
- Kawakubo, K.M. A procedure for determining the true stress–strain curve over a large range of strains using digital image correlation and finite element analysis. Mech. Mater. 2011, 43, 243–253. [Google Scholar] [CrossRef]
- Di, Y.; Lixun, C.; Chen, B. A new approach on necking constitutive relationships of elastic-plastic materials at elevated temperatures. Chin. J. Aeronaut. 2016, 29, 1626–1634. [Google Scholar] [CrossRef]
- Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Girardi, M.; Padovani, C.; Pellegrini, D.; Robol, L. A finite element model updating method based on global optimization. Mech. Syst. Signal Process. 2021, 152, 107372. [Google Scholar] [CrossRef]
- Neggers, J.; Hoefnagels, J.; Geers, M.; Hild, F.; Roux, S. Time-resolved integrated digital image correlation. Int. J. Numer. Methods Eng. 2015, 103, 157–182. [Google Scholar] [CrossRef]
- Gamot, J.; Lasserre, T.; Richard, L.; Neggers, J.; Swiergiel, N.; Hild, F. Calibrating thermoelastic stress analysis with integrated digital image correlation: Application to fatigue cracks. J. Strain Anal. Eng. Des. 2019, 54, 320–330. [Google Scholar] [CrossRef]
- Obers, S.; Overal, J.J.; Wong, W.J.; Walters, C.L. The effect of the yield to tensile strength ratio on stress/strain concentrations around holes in high-strength steels. Mar. Struct. 2022, 84, 103205. [Google Scholar] [CrossRef]
- Di, Y.; Lixun, C.; Chen, B. A new fracture criterion for elastic-plastic materials based on a finite element aided testing method. Mater. Sci. Eng. A 2016, 673, 633–647. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Goldman, N.L.; Hutchinson, J.W. Fully plastic crack problems: The center-cracked strip under plane strain. Int. J. Solids Struct. 1975, 11, 575–591. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Singular behavior at the end of a tensile crack in a hardening material. J. Mech. Phys. Solids 1968, 16, 13–31. [Google Scholar] [CrossRef]
- Peng, Y.; Cai, L.X.; Chen, H.; Chen, B.; Yi, H. A novel semi-analytical method based on equivalent energy principle to obtain J resistance curves of elastic-plastic materials. Int. J. Mech. Sci. 2018, 148, 31–38. [Google Scholar] [CrossRef]
- Chen, H.; Cai, L.X. Unified elastoplastic model based on a strain energy equivalence principle. Appl. Math. Model. 2017, 52, 664–671. [Google Scholar] [CrossRef]
- Chen, H.; Cai, L.X. An elastoplastic energy model for predicting the deformation behaviors of various structure components. Appl. Math. Model. 2019, 68, 405–421. [Google Scholar] [CrossRef]
- Chen, H.; Cai, L.X.; Bao, C. Equivalent-energy indentation method to predict the tensile properties of light alloys. Mater. Des. 2019, 162, 322–330. [Google Scholar] [CrossRef]


| Element Model | Number of Nodes | Number of Elements | Configuration Size |
|---|---|---|---|
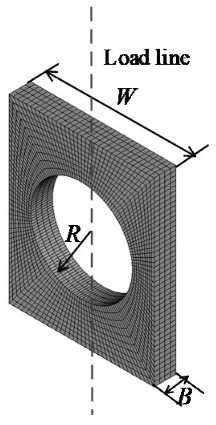 | 35,903 (R = 7 mm) | 29,748 (R = 7 mm) | W = 20 mm B = 3 mm R = 4 mm, 5 mm, 6 mm, 7 mm, 8 mm |
| m | k0 | k1 | k2 | k3 | k4 | |
|---|---|---|---|---|---|---|
| CHS | 1.80 | 0.00901 | 0.450 | 0.00102 | 0.161 | 0.980 |
| Materials | E/GPa | K/MPa | N | W/mm | R/mm | B/mm |
|---|---|---|---|---|---|---|
| T225 | 110 | 907 | 13.2 | 20 | 7.5 | 3 |
| 6061 | 72.6 | 453 | 14.3 | 20 | 7 | 3 |
| Q345 | 209 | 829 | 6.45 | 20 | 7.5 | 3 |
| 3Cr13 | 204 | 969 | 6.12 | 20 | 7.5 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Cai, L.; Wang, L.; Lang, L. A Novel Method to Describe Large-Range Stress-Strain Relations of Elastic-Plastic Materials Based on Energy Equivalence Principle. Materials 2023, 16, 892. https://doi.org/10.3390/ma16030892
Yu S, Cai L, Wang L, Lang L. A Novel Method to Describe Large-Range Stress-Strain Relations of Elastic-Plastic Materials Based on Energy Equivalence Principle. Materials. 2023; 16(3):892. https://doi.org/10.3390/ma16030892
Chicago/Turabian StyleYu, Simiao, Lixun Cai, Ling Wang, and Lin Lang. 2023. "A Novel Method to Describe Large-Range Stress-Strain Relations of Elastic-Plastic Materials Based on Energy Equivalence Principle" Materials 16, no. 3: 892. https://doi.org/10.3390/ma16030892
APA StyleYu, S., Cai, L., Wang, L., & Lang, L. (2023). A Novel Method to Describe Large-Range Stress-Strain Relations of Elastic-Plastic Materials Based on Energy Equivalence Principle. Materials, 16(3), 892. https://doi.org/10.3390/ma16030892







