Mechanical Properties of Sugar Beet Roots under Impact Loading Conditions
Abstract
1. Introduction
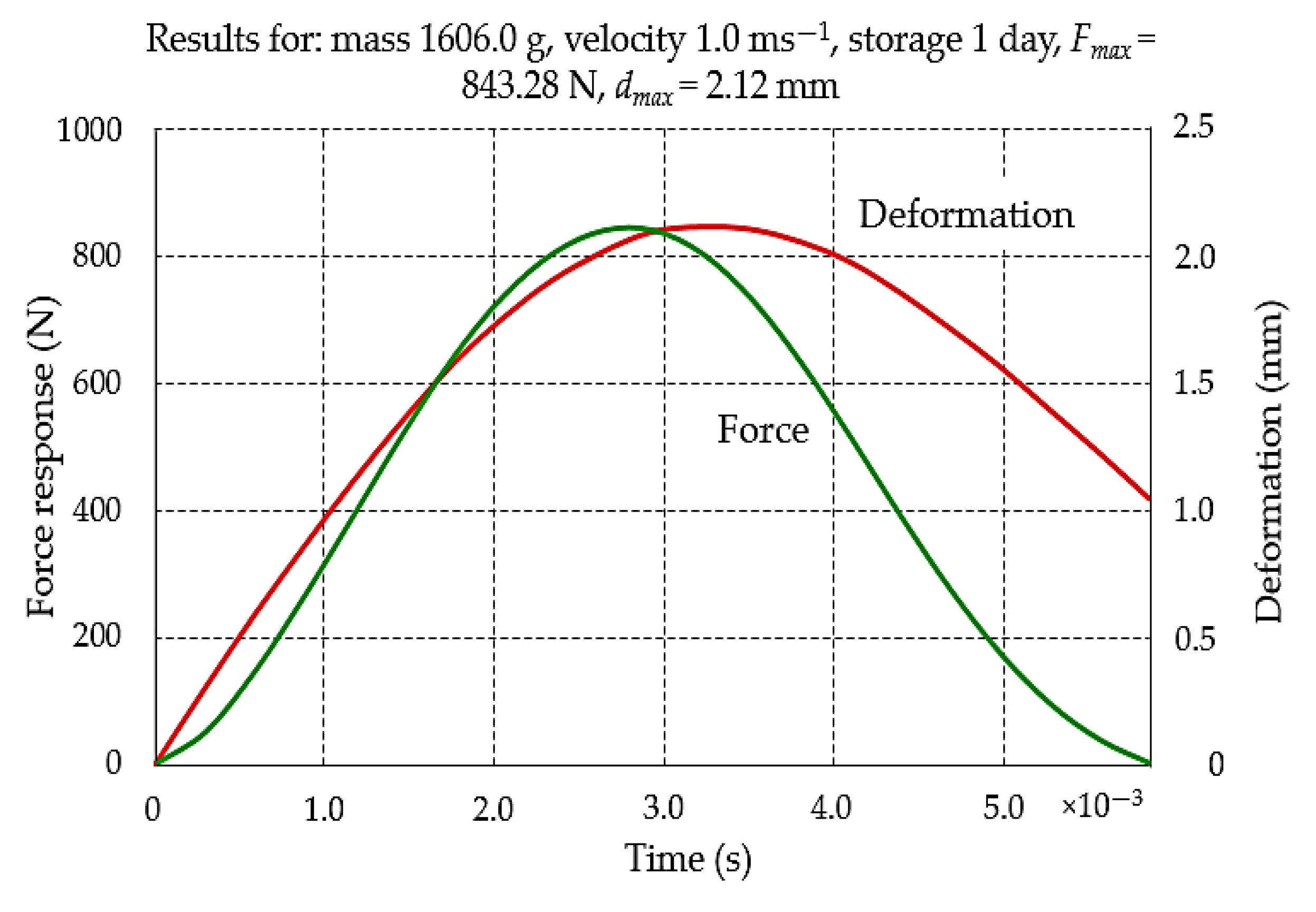
- Time courses of the beet root’s reaction and force response to the impact.
- The course of deformation during the impact in time as a sequence of images.
2. Materials and Methods
2.1. Materials
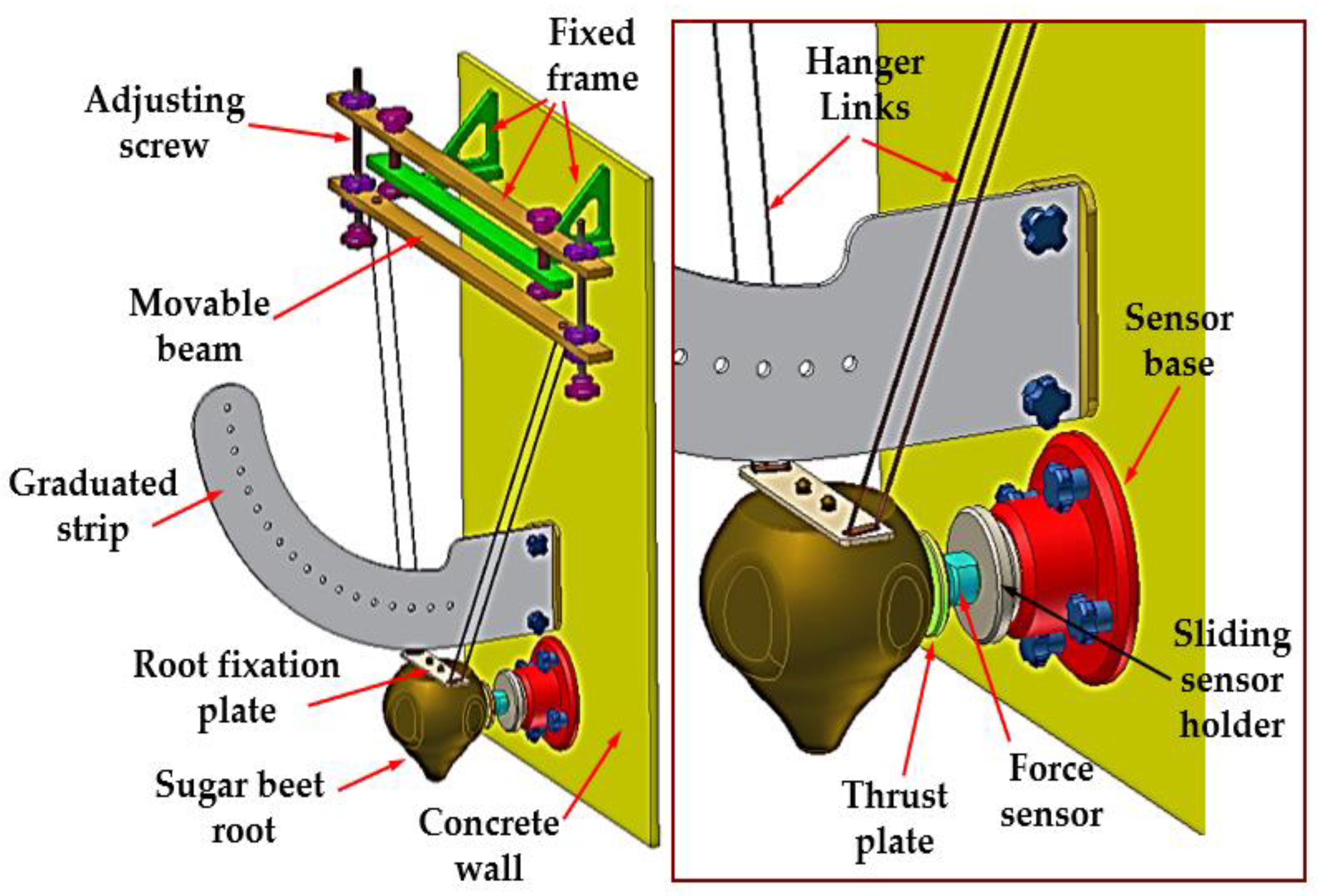
2.2. Research Stand
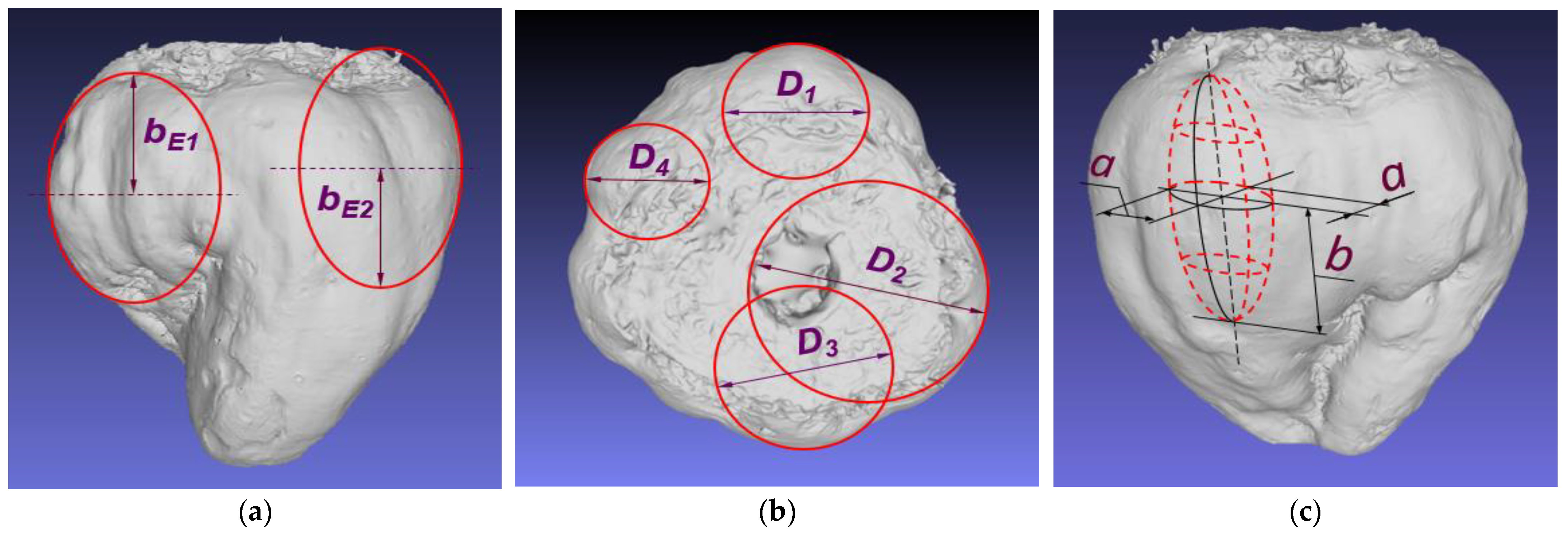
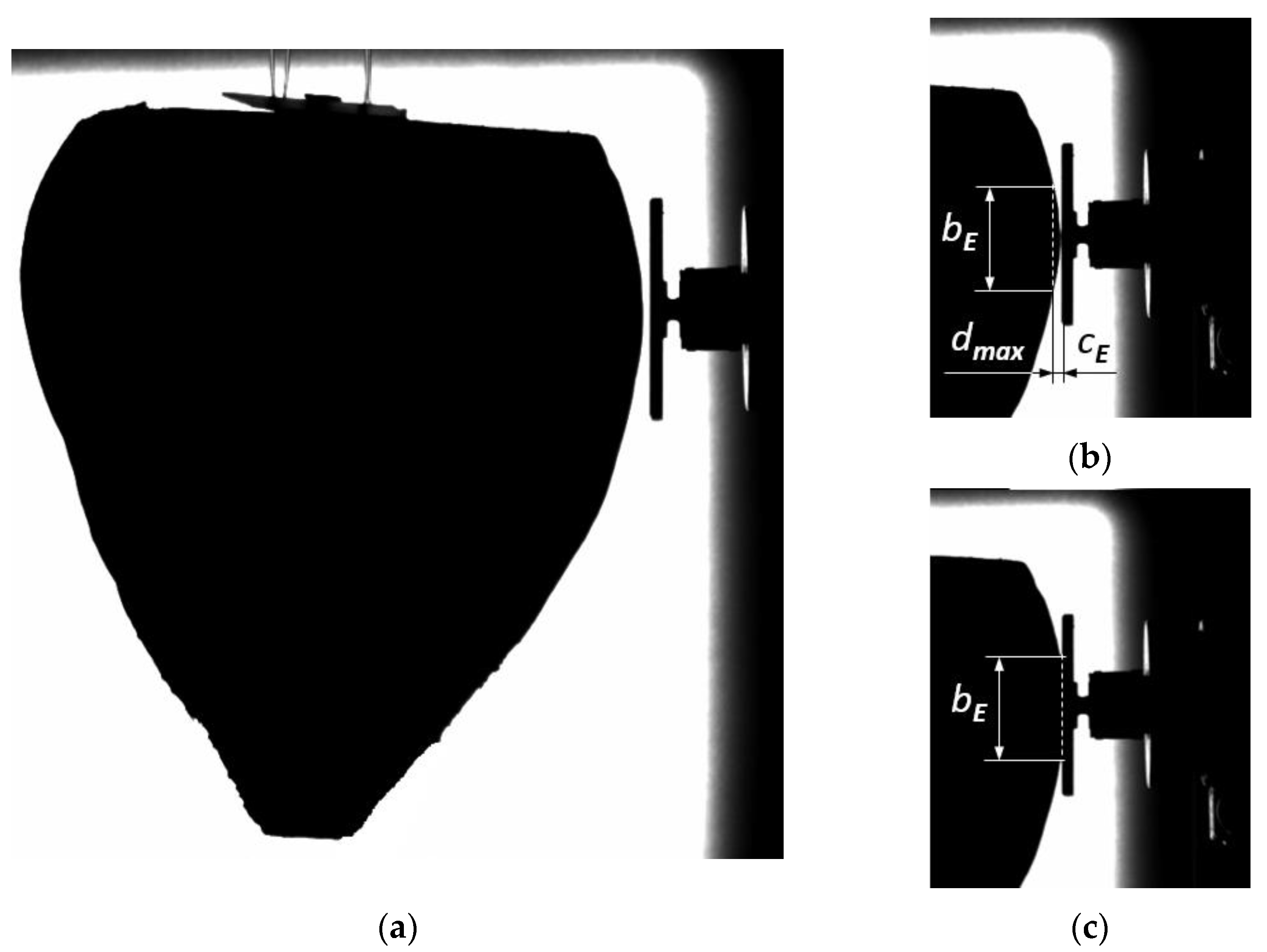
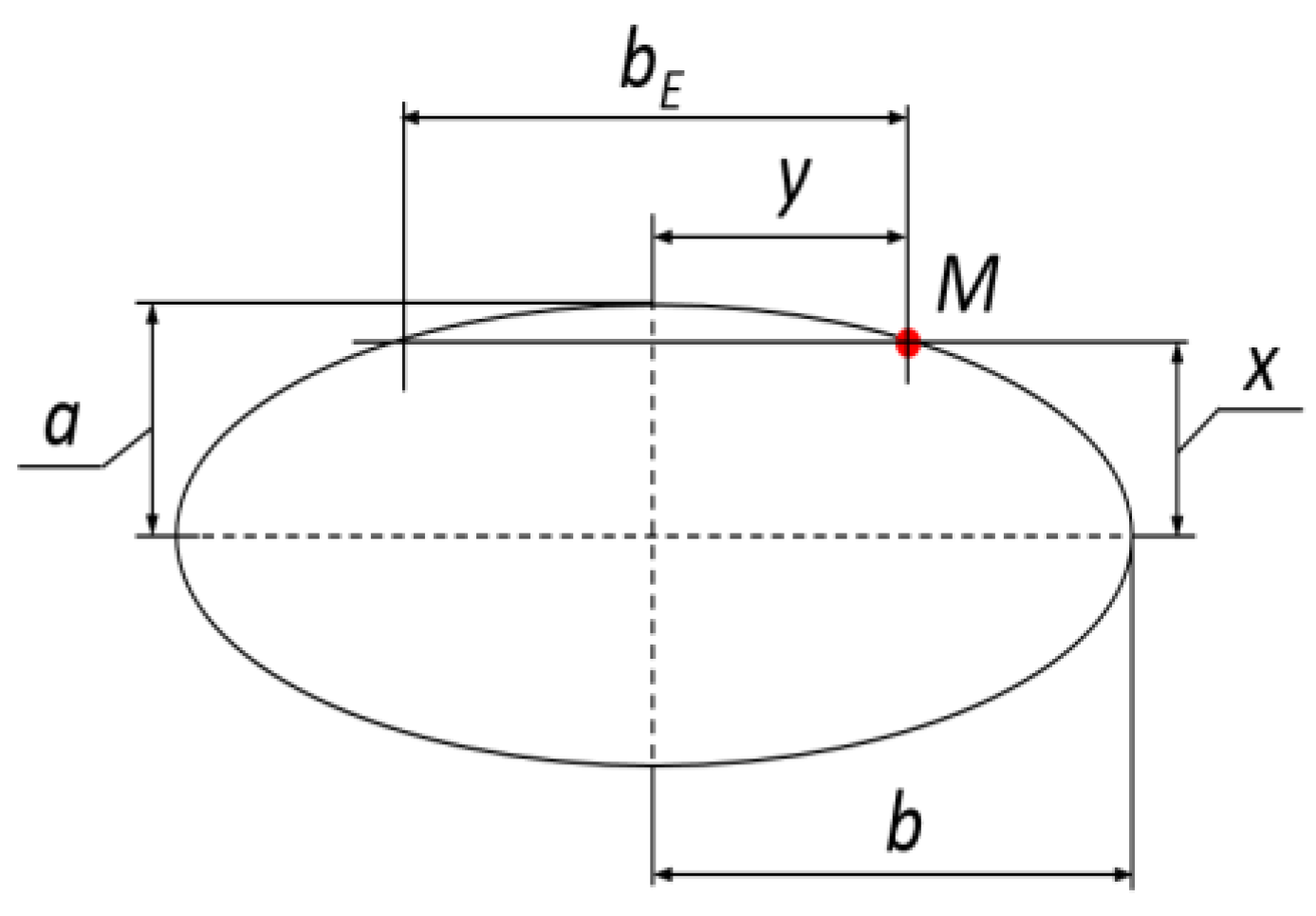
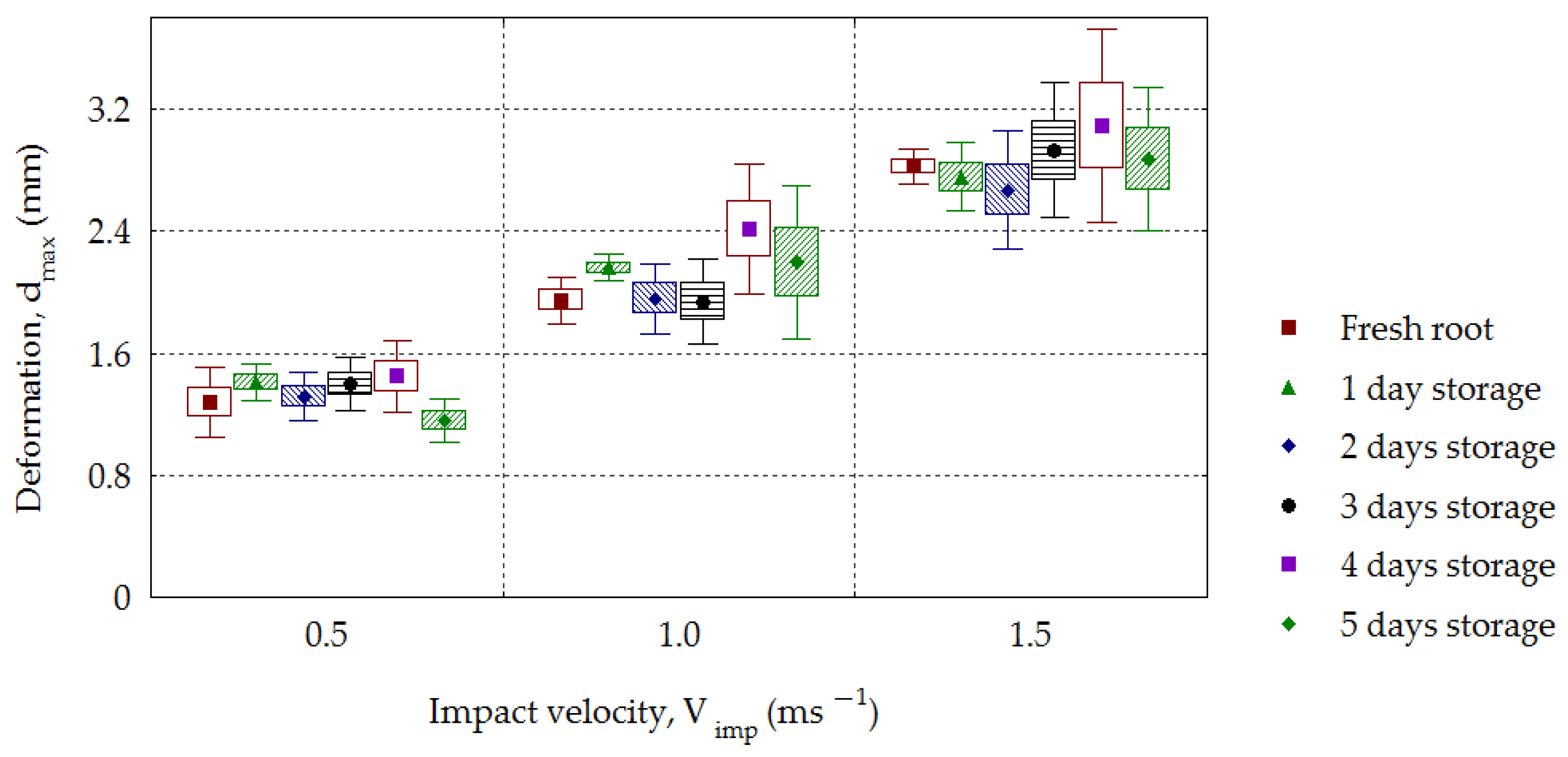
2.3. Volume of Deformation of the Root
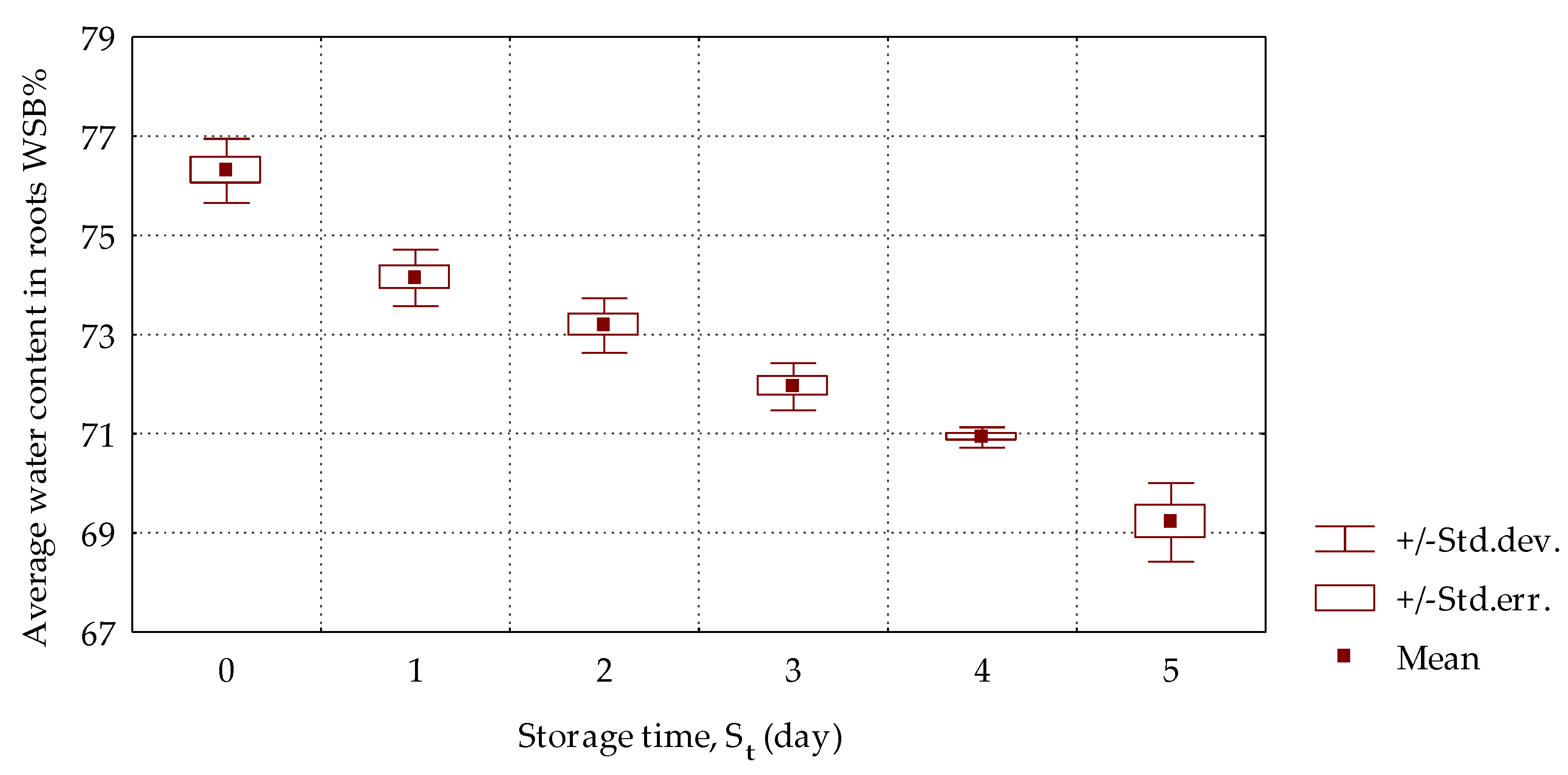
2.4. Moisture Content
2.5. Apparatus and Slotted Section
2.6. Measurements
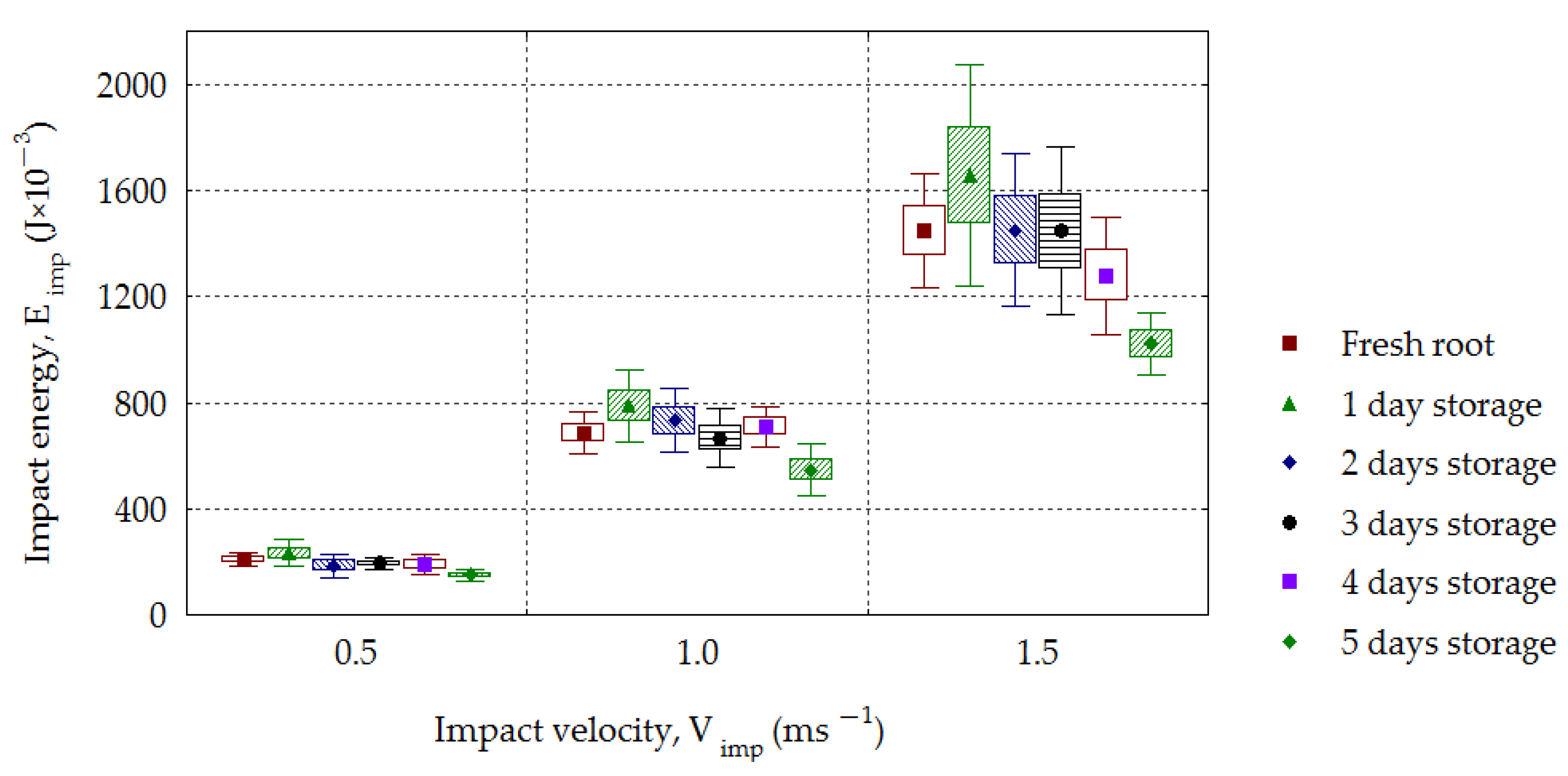
- Eimp—The energy of the mechanical impact J,
- Eel—The energy of beet material response to the mechanical impact J,
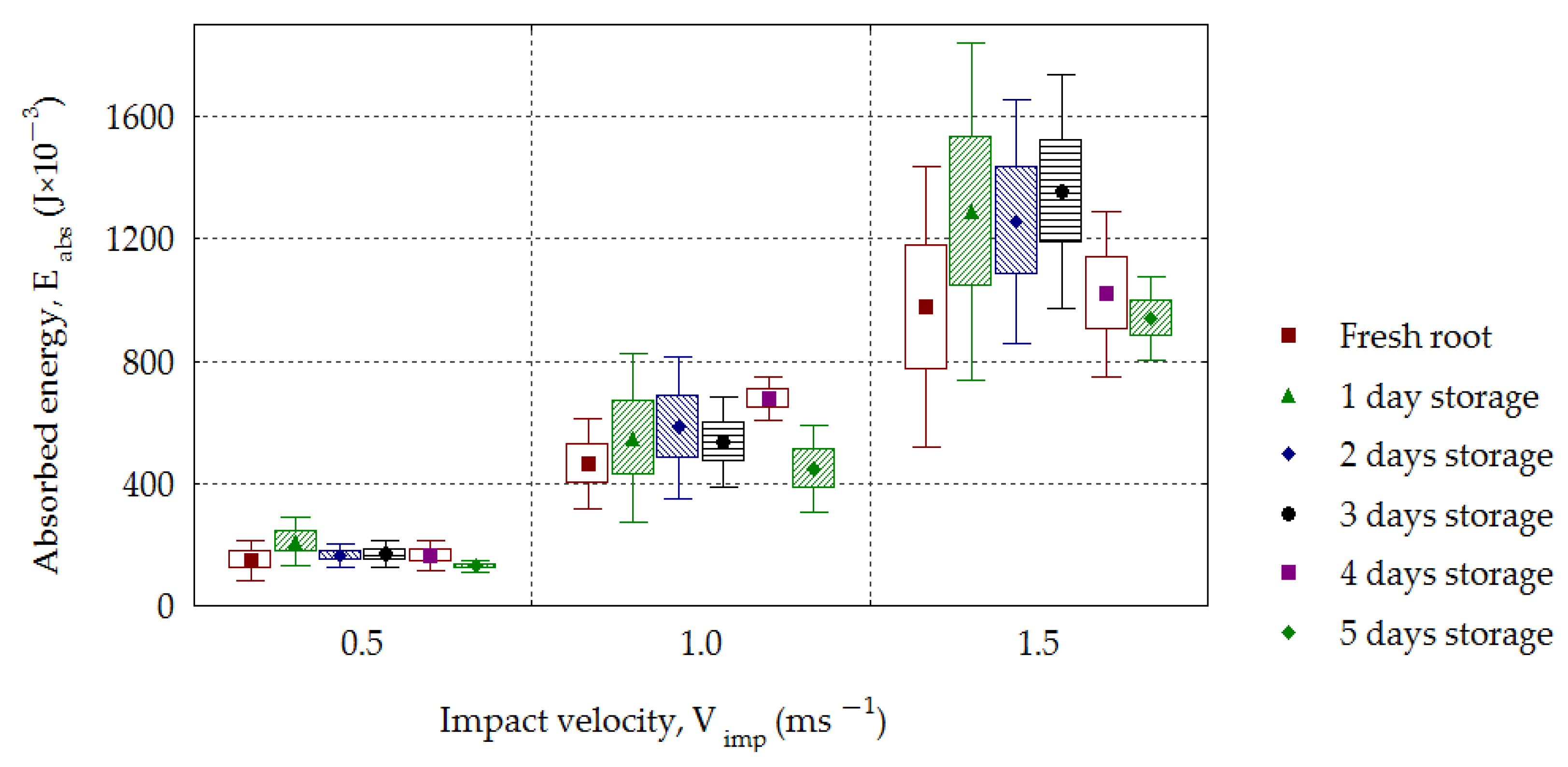
- Eabs—The energy absorbed during the mechanical impact (the surface area between the curves Fimp(d) and Freb(d) in the part from d = 0 to d = dmax).
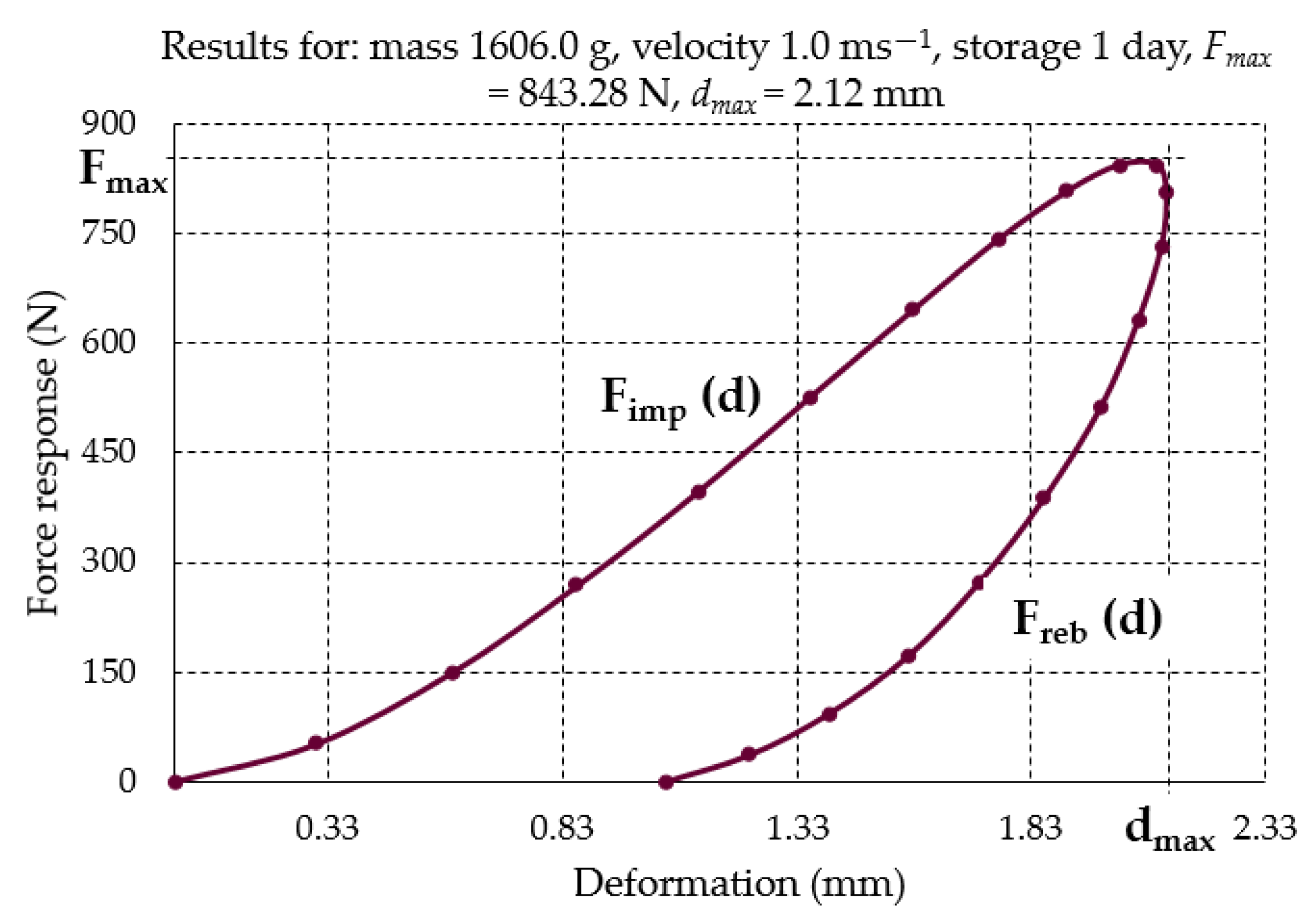
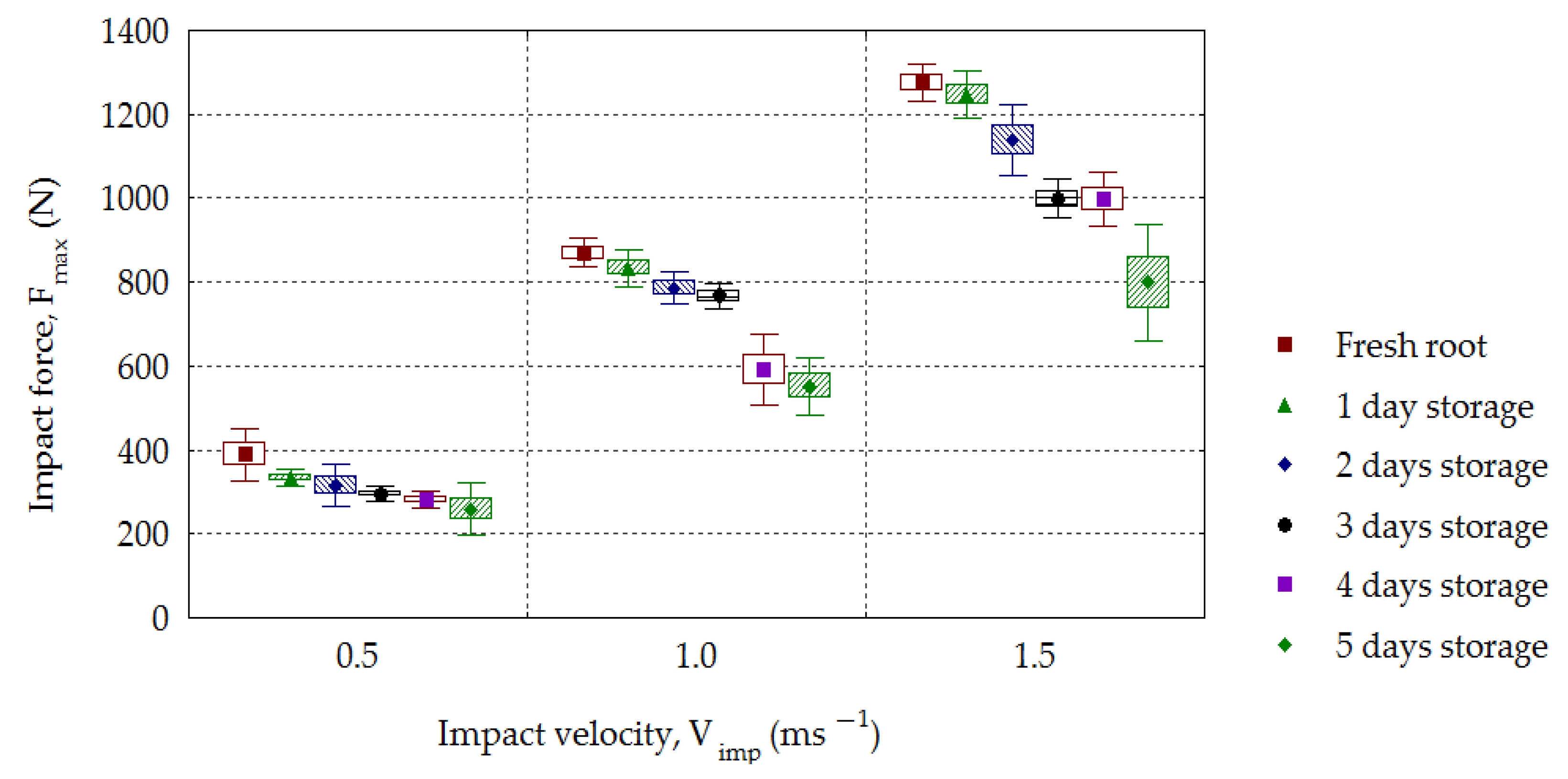
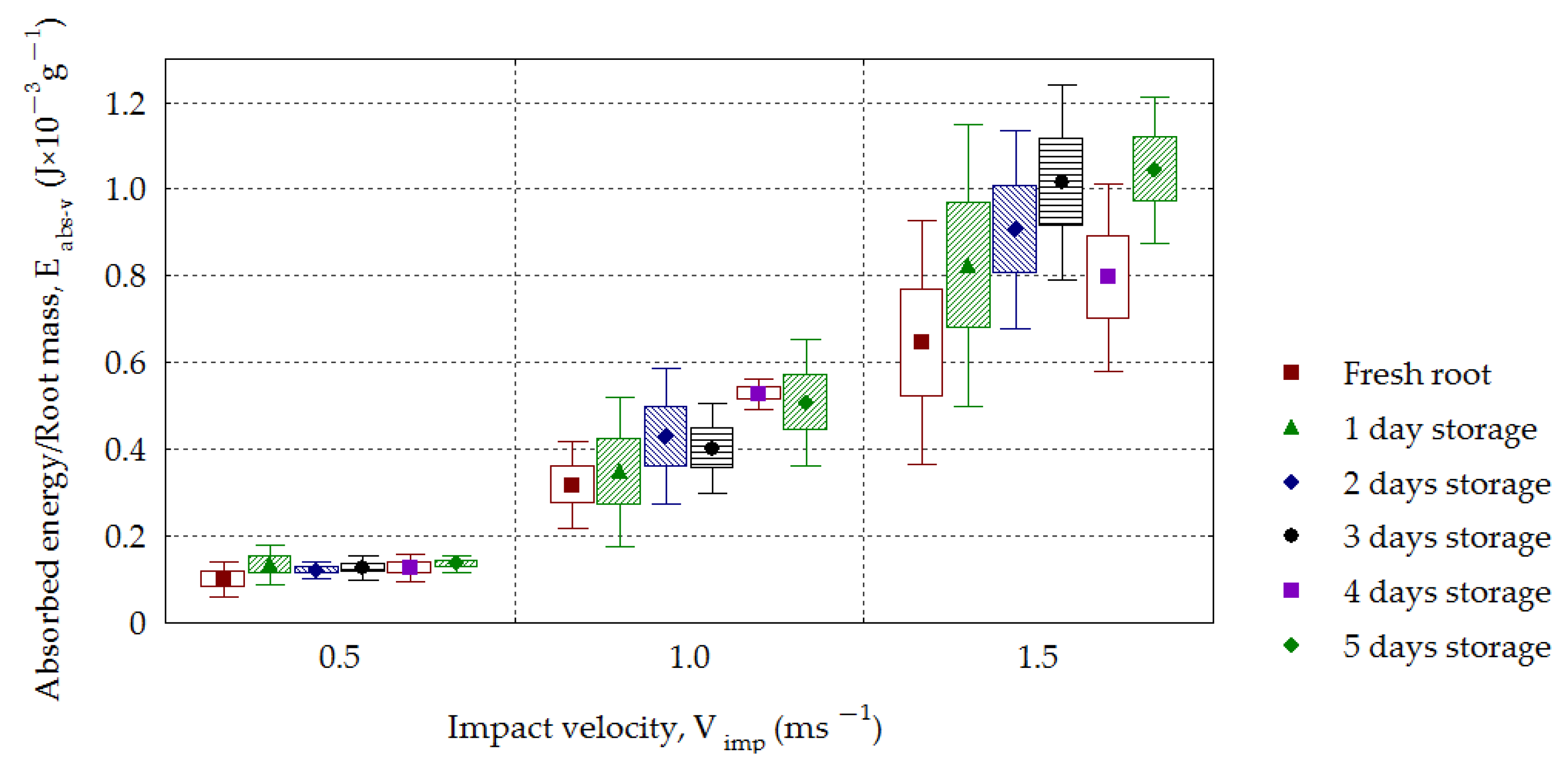
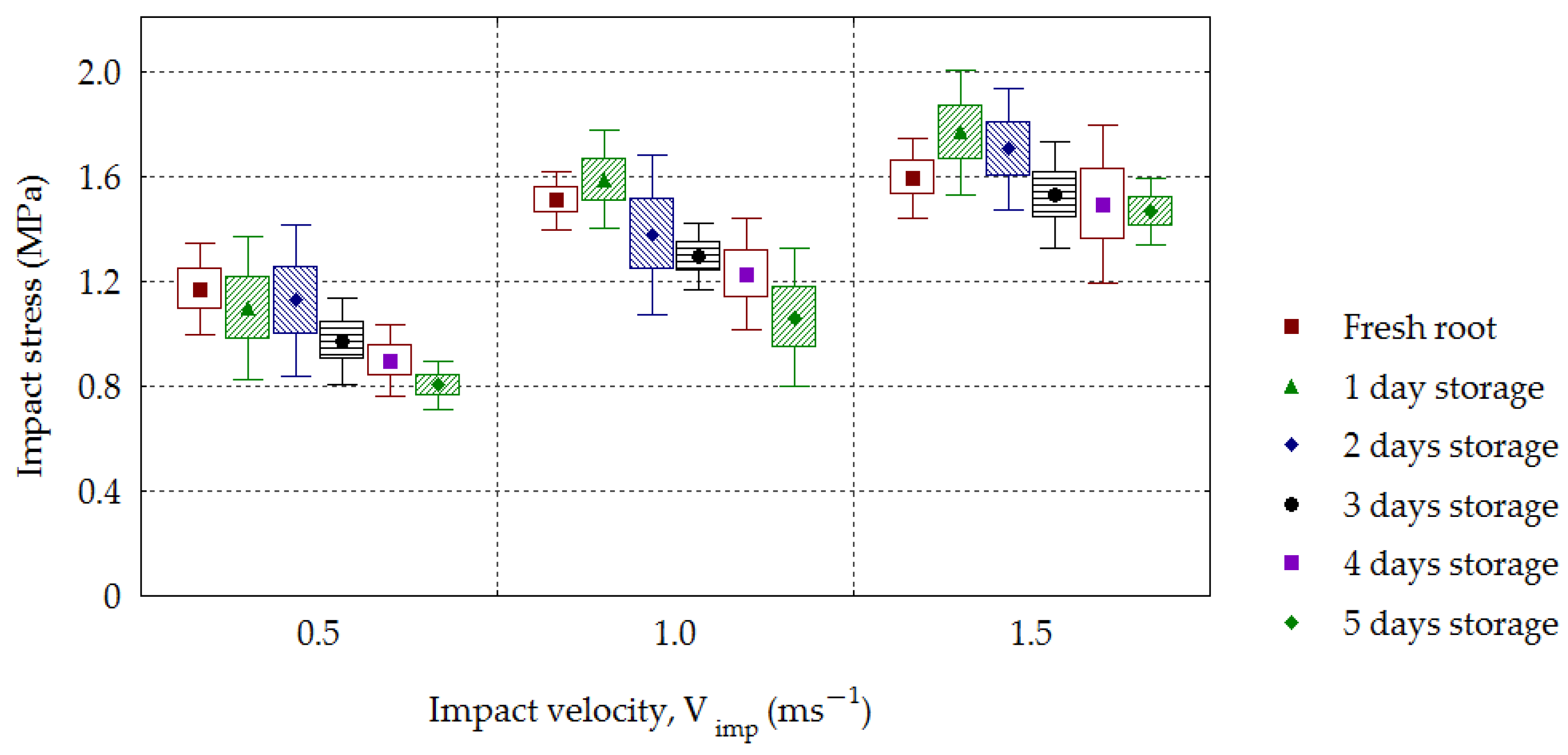
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jarimopas, B.; Singh, S.P.; Sayasoonthorn, S.; Singh, J. Comparison of package cushioning materials to protect postharvest impact damage to apples. Packag. Technol. Sci. 2007, 20, 315–324. [Google Scholar] [CrossRef]
- Van Zeebroeck, M.; Van Linden, V.; Ramon, H.; De Baerdemaeker, J.; Nicolai, B.M.; Tijskens, E. Impact damage of apples during transport and handling. Postharvest Biol. Technol. 2007, 45, 157–167. [Google Scholar] [CrossRef]
- Opara, U.L.; Fadiji, T. Compression damage susceptibility of apple fruit packed inside ventilated corrugated paperboard package. Sci. Hortic. 2018, 227, 154–161. [Google Scholar] [CrossRef]
- Van Zeebroeck, M.; Van Linden, V.; Darius, P.; De Ketelaere, B.; Ramon, H.; Tijskens, E. The effects of fruit factors on the bruise susceptibility of apples. Postharvest Biol. Technol. 2007, 46, 10–19. [Google Scholar] [CrossRef]
- Valero, C.; Crisosto, C.H.; Slaughter, D. Relationship between nondestructive firmness measurements and commercially important ripening fruit stages for peaches, nectarines and plums. Postharvest Biol. Technol. 2007, 44, 248–253. [Google Scholar] [CrossRef]
- Van Linden, V.; De Ketelaere, B.; Desmet, M.; De Baerdemaeker, J. Determination of bruise susceptibility of tomato fruit means of an instrumented pendulum. Postharvest Biol. Technol. 2006, 40, 7–14. [Google Scholar] [CrossRef]
- Blahovec, J. Shape of bruise spots in impacted potatoes. Postharvest Biol. Technol. 2006, 38, 278–284. [Google Scholar] [CrossRef]
- Spackman, V.M.T.; Cobb, A.H. An enzyme-based method for the rapid determination of sucrose, glucose and fructose in sugar beet roots and the effects of impact damage and postharvest storage in clamps. J. Sci. Food Agric. 2001, 82, 80–86. [Google Scholar] [CrossRef]
- Hoffmann, C.M. Sugar beet from field clamps-harvest quality and storage loss. Sugar Ind. 2018, 143, 639–647. [Google Scholar] [CrossRef]
- He, L.; Fu, H.; Xia, H.; Manoj, K.; Zhang, Q.; Whiting, M. Evaluation of a localized shake-and-catch harvesting system for fresh market apples. Agric. Eng. Int. CIGR J. 2018, 19, 36–44. [Google Scholar]
- Tabatabaekoloor, R. Engineering properties and bruise susceptibility of peach fruits (Prunus persica). Agric. Eng. Int. CIGR J. 2013, 15, 244–252. [Google Scholar]
- Hussein, Z.; Fawole, O.A.; Opara, U.L. Investigating bruise susceptibility of pomegranate cultivars during postharvest handling. AFJRD 2017, 2, 33–39. [Google Scholar]
- Hoffmann, C.M.; Schnepel, K. Susceptibility to root tip breakage increases storage losses of sugar beet genotypes. Sugar Ind. 2016, 141, 625–632. [Google Scholar] [CrossRef]
- Hoffmann, C.M.; Engelhardt, M.; Gallmeier, M.; Gruber, M.; Märländer, B. Importance of harvesting system and variety for storage losses of sugar beet. Sugar Ind. 2018, 143, 474–484. [Google Scholar] [CrossRef]
- Nasirahmadi, A.; Wilczek, U.; Hensel, O. Sugar Beet Damage Detection during Harvesting Using Different Convolutional Neural Network Models. Agriculture 2021, 11, 1111. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. Response of Apple Flesh to Compression under the Quasi-Static and Impact Loading Conditions. Materials 2022, 15, 7743. [Google Scholar] [CrossRef]
- Van Zeebroeck, M.; Tijskens, E.; Van Liedekerke, P.; Deli, V.; De Baerdemaeker, J.; Ramon, H. Determination of the dynamical behaviour of biological materials during impacts using pendulum device. J. Sound Vib. 2003, 266, 465–480. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. Methodological aspects of determining apple mechanical properties during impact. Int. J. Food Prop. 2016, 19, 1325–1334. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. Impact characteristics of pears. Postharvest Biol. Technol. 2019, 147, 100–106. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. Stress relaxation of the apples at different deformation velocities and temperature. Trans. ASABE 2019, 62, 115–121. [Google Scholar] [CrossRef]
- Polat, R.; Aktas, T.; Ikinci, A. Selected Mechanical Properties and Bruise Susceptibility of Nectarine Fruit. Int. J. Food Prop. 2012, 15, 1369–1380. [Google Scholar] [CrossRef]
- Ahmadi, E. Bruise susceptibilities of kiwifruit as affected by impact and fruit properties. Res. Agric. Eng. 2012, 58, 107–113. [Google Scholar] [CrossRef]
- Abedi, G.; Ahmadi, E. Design and evaluation a pendulum device to study postharvest mechanical damage in fruits: Bruise modeling of red delicious apple. AJCS 2013, 7, 962–968. [Google Scholar]
- Gorzelany, J.; Puchalski, C. Application of the non-desctructive method to investigations of mechanical properties of sugar beet roots. Acta Agrophys. 2003, 2, 61–71. [Google Scholar]
- Lien, C.C.; Ting, C.H. Assessing guava maturity by statistical analyses of dropped fruit impact responses. Postharvest Biol. Technol. 2014, 95, 20–27. [Google Scholar] [CrossRef]
- Słupska, M.; Syguła, E.; Komarnicki, P.; Szulczewski, W.; Stopa, R. Simple Method for Apples’ Bruise Area Prediction. Materials 2022, 15, 139. [Google Scholar] [CrossRef]
- Komarnicki, P.; Stopa, R.; Szyjewicz, D.; Kuta, Ł.; Klimza, T. Influence of Contact Surface Type on the Mechanical Damages of Apples Under Impact Loads. Food Bioproc. Tech. 2017, 10, 1479–1494. [Google Scholar] [CrossRef]
- Geyer, M.O.; Praeger, U.; Konig, C.; Graf, A.; Truppel, I.; Schluter, O.; Herold, B. Measuring behavior of an acceleration measuring unit implanted in potatoes. Trans. ASABE 2009, 52, 1267–1274. [Google Scholar] [CrossRef]
- Komarnicki, P.; Stopa, R.; Szyjewicz, D.; Młotek, M. Evaluation of bruise resistance of pears to impact load. Postharvest Biol. Technol. 2016, 114, 36–44. [Google Scholar] [CrossRef]
- Kabas, O. Methods of Measuring Bruise Volume of Pear (Pyrus Communis L.). Int. J. Food Prop. 2010, 13, 1178–1186. [Google Scholar] [CrossRef]
- Opara, U.L.; Pathare, P.B. Bruise damage measurement and analysis of fresh horticultural produce—A review. Postharvest Biol. Technol. 2014, 91, 9–24. [Google Scholar] [CrossRef]
- Alizadeh, H.; Segerlind, L.J. Some material properties of sugar beet roots. Appl. Eng. Agric. 1997, 13, 507–510. [Google Scholar] [CrossRef]
- Bentini, M.; Caprara, C.; Rondelli, V. Mechanical properties of sugar beet roots. Trans. ASAE 2005, 48, 1429–1439. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, D. Experimental Study on Compression Property of Sugar Beet; Paper number 141905757, Montreal, Quebec Canada July 13–16; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2014. [Google Scholar] [CrossRef]
- Nedomova, Š.; Kumbar, V.; Pytel, R.; Buchar, J. Mechanical properties of sugar beet root during storage. Int. Agrophys. 2017, 31, 507–513. [Google Scholar] [CrossRef]
- Kleuker, G.; Hoffmann, C.M. Method development for the determination of textural properties of sugar beet roots. Sugar Ind. 2019, 144, 392–400. [Google Scholar] [CrossRef]
- Kleuker, G.; Hoffmann, C.M. Influence of tissue strength on root damage and storage losses of sugar beet. Sugar Ind. 2020, 145, 435–443. [Google Scholar] [CrossRef]
- Kołodziej, P.; Gołacki, K.; Boryga, M. Impact characteristics of sugar beet root during postharvest storage. Int. Agrophys. 2019, 33, 355–361. [Google Scholar] [CrossRef]
- Trnka, J.; Kumbár, V.; Nedomova, Š.; Pytel, R.; Buchar, J. Influence of sugar beet storage duration on root response to non-destructive impacts. Int. Agrophys. 2018, 32, 421–428. [Google Scholar] [CrossRef]
- Pan, L.; Lu, R.; Zhu, Q.; McGarth, J.M.; Tu, K. Measurement of moisture, soluble solids, sucrose content and mechanical properties in sugar beet using portable visible and near-infrared spectroscopy. Postharvest Biol. Technol. 2015, 102, 42–50. [Google Scholar] [CrossRef]
- Shafie, M.M.; Rajabipour, A.; Castro-García, S.; Jiménez-Jiménez, F.; Mobli, H. Effect of Fruit Properties on Pomegranate Bruising. Int. J. Food Prop. 2015, 18, 1837–1846. [Google Scholar] [CrossRef]
- Kitthawee, U.; Pathaveerat, S.; Srirungruang, T.; Slaughter, D. Mechanical bruising of young coconut. Biosyst. Eng. 2011, 109, 211–219. [Google Scholar] [CrossRef]
- ASAE. Moisture measurement-forages. In ASAE Standards; ASAE: St. Joseph, MI, USA, 1992; Volume 406, Chapter S358.2. [Google Scholar]
- Stropek, Z.; Gołacki, K. Studies concerning the response of potatoes to impact. Int. Agrophys. 2022, 36, 115–122. [Google Scholar] [CrossRef]
- Brusewitz, G.H.; McCollum, T.G.; Zhang, X. Impact bruise resistance of peaches. Trans. ASAE 1991, 34, 962–965. [Google Scholar] [CrossRef]
- Fu, Q.; Fu, J.; Chen, Z.; Han, L.; Ren, L. Effect of impact parameters and moisture content on kernel loss during corn snapping. Int. Agrophys. 2019, 33, 493–502. [Google Scholar] [CrossRef]
- Yu, P.; Li, C.; Takeda, F.; Krewer, G. Visual bruise assessment and analysis of mechanical impact measurement in southern highbush blueberries. Appl. Eng. Agric. 2014, 30, 29–37. [Google Scholar] [CrossRef]
- Scheffler, O.C.; Coetzee, C.J.; Opara, U.L. A discrete element model (DEM) for predicting apple damage during handling. Biosyst. Eng. 2018, 172, 29–48. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. Viscoelastic response of apple flesh in a wide range of mechanical loading rates. Int. Agrophys. 2018, 32, 335–340. [Google Scholar] [CrossRef]
- De Kleine, M.E.; Karkee, M. Evaluating a non-newtonian shear-thickening surface during fruit impacts. Trans. ASABE 2015, 58, 907–915. [Google Scholar] [CrossRef]
- Du, D.; Wang, B.; Wang, J.; Yao, F.; Hong, X. Prediction of bruise susceptibility of harvested kiwifruit (Actinidia chinensis) using finite element method. Postharvest Biol. Technol. 2019, 152, 36–44. [Google Scholar] [CrossRef]
- Azam, M.M.; Eissa, A.H. Comprehensive Evaluation of Dynamic Impact as a Measure of Potato Quality. Eur. J. Biophys. 2015, 3, 59–68. [Google Scholar] [CrossRef]
- Ahmadi, E.; Barikloo, H.; Kashafi, M. Viscoelastic finite element analysis of the dynamic behavior of apple under impact loading with regard its different layers. Comput. Electron. Agric. 2016, 121, 1–11. [Google Scholar] [CrossRef]
- Lu, L.X.; Wang, Z.W. Dropping bruise fragility and bruise boundary of apple fruit. Trans. ASABE 2007, 50, 1323–1329. [Google Scholar] [CrossRef]
- Stropek, Z.; Gołacki, K. A new method for measuring impact related bruises in fruits. Postharvest Biol. Technol. 2015, 110, 131–139. [Google Scholar] [CrossRef]
- Vursavus, K.; Ozguven, F. Determining the strength properties of the Dixired peach variety. Turk. J. Agric. For. 2003, 27, 155–160. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kołodziej, P.; Stropek, Z.; Gołacki, K. Mechanical Properties of Sugar Beet Roots under Impact Loading Conditions. Materials 2023, 16, 1281. https://doi.org/10.3390/ma16031281
Kołodziej P, Stropek Z, Gołacki K. Mechanical Properties of Sugar Beet Roots under Impact Loading Conditions. Materials. 2023; 16(3):1281. https://doi.org/10.3390/ma16031281
Chicago/Turabian StyleKołodziej, Paweł, Zbigniew Stropek, and Krzysztof Gołacki. 2023. "Mechanical Properties of Sugar Beet Roots under Impact Loading Conditions" Materials 16, no. 3: 1281. https://doi.org/10.3390/ma16031281
APA StyleKołodziej, P., Stropek, Z., & Gołacki, K. (2023). Mechanical Properties of Sugar Beet Roots under Impact Loading Conditions. Materials, 16(3), 1281. https://doi.org/10.3390/ma16031281





